النقاط الفردية للدالة وتصنيفها. نقاط مفردة معزولة. بقايا وصيغ لحسابها

النماذج الموصوفة بأنظمة من معادلتين تفاضليتين مستقلتين.

طائرة المرحلة. صورة المرحلة. طريقة isocline. الخطوط المتساوية الرئيسية. حالة مستقرة مستقرة. الأنظمة الخطية. أنواع النقاط الرئيسية: العقدة ، السرج ، التركيز ، المركز. مثال: تفاعلات كيميائية من الدرجة الأولى.

تم الحصول على النتائج الأكثر إثارة للاهتمام حول النمذجة النوعية لخصائص الأنظمة البيولوجية من خلال نماذج من معادلتين تفاضليتين ، مما يسمح بإجراء دراسة نوعية باستخدام الطريقة طائرة المرحلة. ضع في اعتبارك نظامًا من معادلتين تفاضليتين عاديتين مستقلتين للشكل العام

(4.1)

الفوسفور (س ، ص) ، س (س ، ص)- وظائف مستمرة محددة في بعض المجالات جيطائرة اقليدية ( س ، ص- الإحداثيات الديكارتية) وفي هذه المنطقة مشتقات مستمرة من الرتبة لا تقل عن الأول.

منطقة جييمكن أن تكون إما غير محدودة أو محدودة. إذا كانت المتغيرات س ، صلها معنى بيولوجي محدد (تركيزات المواد ، وفرة الأنواع) ، وغالبًا ما تكون المنطقة جيهو الربع الموجب لنصف المستوى الأيمن:

0 £ x< ¥ ,0 £ ذ< ¥ .

يمكن أيضًا تقييد تركيزات المواد أو وفرة الأنواع من الأعلى بحجم الوعاء أو منطقة الموائل. ثم يكون نطاق المتغيرات بالشكل:

0 £ x< x 0 , 0 £ ذ< y 0 .

المتغيرات س ، صتغيير في الوقت وفقًا لنظام المعادلات (4.1) ، بحيث تتوافق كل حالة من حالات النظام مع زوج من قيم المتغيرات ( س ، ص).

على العكس من ذلك ، لكل زوج من المتغيرات ( س ، ص) يتوافق مع حالة معينة من النظام.

ضع في اعتبارك مستوى بمحاور إحداثيات يتم رسم قيم المتغيرات عليها س ، ص. كل نقطة مهذا المستوى يتوافق مع حالة معينة من النظام. يسمى هذا المستوى بمستوى الطور ويصور مجمل جميع حالات النظام. النقطة M (x ، y) تسمى النقطة الموضحة أو الممثلة.

اسمحوا في الوقت الأولي ر = ر 0 يمثل إحداثيات النقطة م 0 (x(ر 0)، ذ(ر 0)). في كل لحظة تالية في الوقت المناسب رستتحرك نقطة التصوير وفقًا للتغييرات في قيم المتغيرات x(ر)، ذ(ر). مجموعة من النقاط م(x(ر)، ذ (ر)) على مستوى الطور ، حيث يتوافق موضعها مع حالات النظام في عملية تغيير المتغيرات بمرور الوقت س (ر), ص (ر)وفقا للمعادلات (4.1) ، يسمى مسار المرحلة.

تعطي مجموعة مسارات الطور للقيم الأولية المختلفة للمتغيرات "صورة" مرئية بسهولة للنظام. بناء صورة المرحلةيسمح لك باستخلاص استنتاجات حول طبيعة التغييرات في المتغيرات س ، صدون معرفة الحلول التحليلية لنظام المعادلات الأصلي(4.1).

لتصوير صورة طور ، من الضروري إنشاء حقل متجه للاتجاهات لمسارات النظام في كل نقطة من مستوى الطور. بتحديد الزيادةد ر> 0 ،نحصل على الزيادات المقابلة د xو د ذمن التعبيرات:

د س = ف (س ، ص)د ر,

د ص = س (س ، ص)د ر.

اتجاه متجه dy / dxعند نقطة ( س ، ص) يعتمد على علامة الوظائف الفوسفور (س ، ص) ، س (س ، ص)ويمكن إعطاؤه من خلال الجدول:

الفوسفور (س ، ص)> 0 ، س (س ، ص)> 0
الفوسفور (س ، ص)<0,Q(x,y)<0
الفوسفور (س ، ص)> 0 ، س (س ، ص)<0
الفوسفور (س ، ص)<0,Q(x,y)>0

.(4.2)

حل هذه المعادلة ص = ذ(س ، ج), أو ضمنيًا F(س ، ص)= ج ،أين معهو ثابت التكامل ، يعطي عائلة منحنيات متكاملة للمعادلة (4.2) - مسارات المرحلةنظام (4.1) على متن الطائرة س ، ص.

طريقة Isocline

لبناء صورة طور ، يستخدم المرء طريقة isocline -يتم رسم الخطوط على مستوى الطور الذي يتقاطع مع منحنيات متكاملة بزاوية واحدة محددة. من السهل الحصول على معادلة isocline من (4.2). هيا نضع

أين أ– ثابت معين. المعنى أيمثل ظل منحدر الظل لمسار الطور ويمكن أن يأخذ قيمًا من -¥ ل + ¥ . الاستبدال بدلاً من dy / dxفي (4.2) الكمية أنحصل على معادلة isocline:

.(4.3)

تحدد المعادلة (4.3) عند كل نقطة من المستوى المماس الوحيد لمنحنى التكامل المقابل ، باستثناء النقطة التي يكون فيها الفوسفور (س ، ص)= 0 ، س (س ، ص) = 0 ، حيث يصبح اتجاه الظل غير محدد ، حيث تصبح قيمة المشتق غير محددة:

.

هذه النقطة هي نقطة التقاطع لجميع الخطوط المتساوية - نقطة خاصة.إنه يتلاشى في نفس الوقت المشتقات الزمنية للمتغيرات xو ذ.

وهكذا ، عند النقطة المفردة ، تكون معدلات تغير المتغيرات مساوية للصفر. لذلك ، فإن النقطة الفردية للمعادلات التفاضلية لمسارات الطور (4.2) تتوافق مع حالة النظام الثابتة(4.1) ، وإحداثياتها هي القيم الثابتة للمتغيرات س ، ص.

ذات أهمية خاصة الخطوط المتساوية الرئيسية:

dy / dx = 0 ، ص(س ، ص)=0 – المتساوي من الظل الأفقي و

dy / dx =¥ س(س ، ص)=0 – المتساوي من الظل الرأسي.

من خلال إنشاء خطوط متساوية رئيسية وإيجاد نقطة تقاطعها (س ، ص) ، إحداثياتها تستوفي الشروط:

وبالتالي سنجد نقطة تقاطع جميع الخطوط المتساوية لمستوى الطور ، حيث يكون اتجاه الظل لمسارات الطور غير محدد. هذه - نقطة فرديةالذي يتوافق حالة النظام الثابتة(الشكل 4.2).

يحتوي النظام (4.1) على العديد من الحالات الثابتة حيث توجد نقاط تقاطع للخطوط المتساوية الرئيسية على مستوى الطور.

يتوافق كل مسار طور مع مجموعة من حركات النظام الديناميكي الذي يمر عبر نفس الحالات ويختلف عن بعضها البعض فقط في بداية المرجع الزمني.

إذا تم استيفاء شروط نظرية كوشي ، ثم من خلال كل نقطة من الفضاء س ، ص ، ريمر عبر منحنى متكامل واحد. وينطبق الشيء نفسه ، بفضل الاستقلالية ، على مسارات الطور: يمر مسار طور فريد من خلال كل نقطة من مستوى الطور.

حالة مستقرة مستقرة

دع النظام يكون في حالة توازن.

ثم تقع النقطة التمثيلية في إحدى النقاط الفريدة للنظام ، والتي ، بحكم التعريف:

.

يتم تحديد ما إذا كانت النقطة الفردية مستقرة أم لا من خلال ما إذا كانت النقطة التمثيلية تغادر أم لا بانحراف بسيط عن الحالة الثابتة. كما هو مطبق على نظام من معادلتين ، تعريف الاستقرار في اللغةه, دكما يلي.

تكون حالة التوازن مستقرة إذا كانت لأي منطقة معينة من الانحرافات عن حالة التوازن (ه )يمكن تحديد المنطقة د (ه )، المحيطة بحالة التوازن وامتلاك خاصية عدم وجود مسار يبدأ داخل المنطقة د ، لن تصل أبدًا إلى الحدود ه . (الشكل 4.4)

لفئة كبيرة من الأنظمة - أنظمة خشنة – طبيعة السلوك الذي لا يتغير مع تغيير طفيف في نوع المعادلات ، يمكن الحصول على معلومات حول نوع السلوك في محيط الحالة الثابتة من خلال دراسة ليس الأصل ، ولكن المبسطة خطيالنظام.

الأنظمة الخطية.

ضع في اعتبارك نظامًا من معادلتين خطيتين:

.(4.4)

هنا ا ب ت ث- الثوابت ، س ، ص- الإحداثيات الديكارتية على مستوى الطور.

سيتم البحث عن الحل العام في النموذج:

.(4.5)

عوّض بهذه التعبيرات في (4.4) واختزل بـ ه ل ر:

(4.6)

النظام الجبري للمعادلات (4.6) ذات المجهول أ ، بله حل غير صفري فقط إذا كان محدده ، المكون من معاملات المجهول ، يساوي صفرًا:

.

بتوسيع هذا المحدد ، نحصل على المعادلة المميزة للنظام:

.(4.7)

يعطي حل هذه المعادلة قيم المؤشرل 1,2 ، والتي يمكن تحتها القيم غير الصفرية أو بحلول المعادلة (4.6). هذه القيم

.(4.8)

إذا كان التعبير الجذري سالبًال 1,2 الأعداد المترافقة المعقدة. افترض أن كلا جذري المعادلة (4.7) لهما أجزاء غير صفرية حقيقية وأنه لا توجد جذور متعددة. ثم يمكن تمثيل الحل العام للنظام (4.4) كمجموعة خطية من الأس مع الأسل 1 , ل 2 :

(4.9)

لتحليل طبيعة المسارات المحتملة للنظام على مستوى الطور ، نستخدم تحويل تنسيق خطي متجانس ،والتي ستجلب النظام إلى الشكل الكنسي:

,(4.10)

مما يسمح بتمثيل أكثر ملاءمة على مستوى الطور مقارنة بالنظام الأصلي (4.4). دعونا نقدم إحداثيات جديدةξ , η حسب الصيغ:

(4.1)

من المعروف من مسار الجبر الخطي أنه إذا كانت الأجزاء الحقيقية لا تساوي الصفرل 1 , ل 2 يمكن دائمًا تحويل النظام الأصلي (4.4) بمساعدة التحويلات (4.11) إلى الشكل المتعارف عليه (4.10) ويمكن دراسة سلوكه على مستوى الطورξ , η . ضع في اعتبارك الحالات المختلفة التي قد تطرح نفسها هنا.

الجذور λ 1 , λ 2 - ساري المفعول ومن نفس العلامة

في هذه الحالة ، معاملات التحويل حقيقية ، ننتقل من المستوى الحقيقيس ، صإلى المستوى الحقيقي ξ ، η. بقسمة ثاني المعادلات (4.10) على الأولى نحصل عليها:

.(4.12)

دمج هذه المعادلة ، نجد:

أين. (4.13)

دعونا نتفق على فهم من قبل λ 2 جذر المعادلة المميزة بمعامل كبير لا ينتهك عمومية تفكيرنا. ثم ، لأنه في الحالة قيد النظر الجذور λ 1 , λ2 - ساري المفعول ومن نفس العلامة ،أ>1 ، ونحن نتعامل مع منحنيات متكاملة من النوع المكافئ.

جميع المنحنيات المتكاملة (باستثناء المحور η الذي يتوافق مع ) تلمس أصل المحور ξ, وهو أيضًا منحنى متكامل للمعادلة (4.11). أصل الإحداثيات هو نقطة مفردة.

دعونا الآن نكتشف اتجاه حركة النقطة التمثيلية على طول مسارات المرحلة. إذا λ 1 ، λ 2 سلبية ، إذن ، كما يتضح من المعادلات (4.10) ، | ξ | ، | η | تنخفض بمرور الوقت. تقترب نقطة التمثيل من الأصل ، لكنها لا تصل إليه أبدًا. خلاف ذلك ، سيتعارض هذا مع نظرية كوشي ، التي تنص على أن مسار طور واحد فقط يمر عبر كل نقطة من مستوى الطور.

هذه نقطة فريدة تمر من خلالها منحنيات متكاملة ، تمامًا مثل عائلة من القطع المكافئ يمر عبر الأصل ، ويسمى عقدة (الشكل. 4.5)

حالة التوازن من نوع العقدة عند λ 1 ، λ 2 < 0 مستقر وفقًا لـ Lyapunov ، نظرًا لأن نقطة التمثيل تتحرك على طول جميع المنحنيات المتكاملة نحو أصل الإحداثيات. هذه عقدة مستقرة. إذا λ 1 ، λ 2 > 0 ، إذن | ξ | ، | η | تزداد مع الوقت وتبتعد النقطة التمثيلية عن الأصل. في هذه الحالة ، النقطة الفريدة– عقدة غير مستقرة .

على مستوى المرحلة س ، ص سيبقى الطابع النوعي العام لسلوك المنحنيات المتكاملة ، لكن ظل المنحنيات المتكاملة لن يتطابق مع محاور الإحداثيات. سيتم تحديد زاوية ميل هذه الظلال بنسبة المعاملات α , β , γ , δ في المعادلات (4.11).

الجذور λ 1 , λ 2 صالحة ولها علامات مختلفة.

تحويل منإحداثيات س ، ص للإحداثيات ξ, η مرة أخرى حقيقي. معادلات المتغيرات الأساسية مرة أخرى لها الشكل (4.10) ، ولكن الآن العلامات λ 1 ، λ 2 مختلف. معادلة مسار الطور لها الشكل:

أين ، (4.14)

تكامل (4.14) نجد

(4.15)

هذه تحدد المعادلة عائلة من المنحنيات ذات النوع الزائدي ، حيث ينسق كلا المحورينهي الخطوط المقاربة (في أ=1 سيكون لدينا عائلة من القطوع الزائدة متساوية الساقين). محاور الإحداثيات هي أيضًا منحنيات متكاملة في هذه الحالة– ستكون هذه المنحنيات المتكاملة الوحيدة التي تمر عبر الأصل. كلوالتي تتكون من ثلاث مسارات: من حركتين نحو حالة توازن (أو بعيدًا عن حالة توازن) وعن حالة توازن. جميع المنحنيات التكاملية الأخرى– هي القطوع الزائدة التي لا تمر من خلال الأصل (الشكل. 4.6) تسمى هذه النقطة الفريدة "سرج ». تتصرف خطوط المستوى بالقرب من السرج الجبلي مثل مسارات الطور بالقرب من السرج.

دعونا نفكر في طبيعة حركة النقطة التمثيلية على طول مسارات الطور بالقرب من حالة التوازن. دعونا ، على سبيل المثال ،λ 1> 0، λ 2<0 . ثم يتم وضع النقطة التمثيلية على المحور ξ ، سوف تبتعد عن الأصل ، وتوضع على المحور η – سوف يقترب إلى أجل غير مسمى من أصل الإحداثيات, دون الوصول إليه في وقت محدد. أينما كانت نقطة التمثيل في اللحظة الأولى (باستثناء النقطة المفرد والنقاط على الخط المقارب η =0), سوف يتحرك في النهاية بعيدًا عن حالة التوازن ، حتى لو تحرك في البداية على طول أحد المنحنيات المتكاملة نحو نقطة مفردة.

من الواضح أن النقطة الفريدة من نوع السرج دائمًا غير مستقرة . فقط في ظل ظروف أولية مُختارة خصيصًا على خط التقاربη =0 سيقترب النظام من حالة التوازن. ومع ذلك ، فإن هذا لا يتعارض مع التأكيد على أن النظام غير مستقر. إذا كنت تعول, أن جميع الحالات الأولية للنظام على مستوى الطور هي احتمالية بالتساوي ، ثم احتمال مثل هذه الحالة الأولية التي تتوافق مع الحركة في الاتجاهل نقطة المفرد تساوي الصفر. لذلك ، فإن أي حركة حقيقية ستزيل النظام من حالة التوازن.العودة إلى الإحداثياتس ، ص ،نحصل على نفس الصورة النوعية لطبيعة حركة المسارات حول الأصل.

الحد الفاصل بين الحالات المدروسة للعقدة والسرج هو الحالمتي أحد المؤشرات المميزة ، على سبيل المثال λ 1 , والذي يحدث عند محدد النظام- التعبير adbc = 0(انظر الصيغة 4.8 ). في هذه الحالة ، معاملات الجانب الأيمن من المعادلات (4.4) متناسبة مع بعضها البعض:

والنظام لديه لتوازنه ينص على جميع نقاط الخط:

المنحنيات المتكاملة المتبقية هي عائلة من الخطوط المتوازية مع ميل ، حيث تقترب النقاط التمثيلية من حالة التوازن أو تبتعد عنها ، اعتمادًا على علامة الجذر الثاني للمعادلة المميزة λ 2 = أ + د.(الشكل 4.7 ) في هذه الحالة ، تعتمد إحداثيات حالة التوازن على القيمة الأولية للمتغيرات.

الجذور λ 1 , λ 2 – مركبالمترافقة

في هذه الحالة ، حقيقيxو ذونحن سوف لها اقترانات معقدة ξ , η (4.10) . ومع ذلك ، من خلال إدخال تحويل وسيط آخر ، من الممكن أيضًا في هذه الحالة تقليل الاعتبار إلى تحويل متجانس خطي حقيقي. هيا نضع:

(4.16)

أين أ ، ب ،و ش ، ضد – القيم الحقيقية. يمكن إثبات أن التحول منس ، صل ش ، ضد هو ، وفقًا لافتراضاتنا ، حقيقي وخطي ومتجانس مع محدد غير صفري. بسبب المعادلات(4.10 ، 4.16) لدينا:

أين

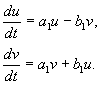(4.17)

قسمة ثاني المعادلات على الأول، نحن نحصل:

وهو أسهل في الاندماج, إذا انتقلنا إلى نظام الإحداثيات القطبية (ص φ ) . بعد التبديلنصل من حيث:

.(4.18)

وهكذا ، على مستوى المرحلةش ، ضدنحن نتعامل مع عائلة من اللوالب اللوغاريتمية ، لكل منهانقطة التقارب في الأصل.النقطة المفردة وهي نقطة التقارب لجميع المنحنيات المتكاملة التي لها شكل اللوالب, صديق متداخل فيصديق ، اتصل التركيز ( شكل 4.8 ) .

دعونا نفكر في طبيعة حركة نقطة التمثيل على طول مسارات المرحلة. ضرب أول المعادلتين (4.17) فيش، والثاني ل الخامسوإضافة ، نحصل على:

أين

يترك أ 1 < 0 (أ 1 = إعادةλ ) . ثم تقترب نقطة التمثيل من الأصل باستمرار دون الوصول إليه في وقت محدد. هذا يعني أن مسارات الطور عبارة عن حلزونات ملتوية وتتوافق مع التذبذبات المثبطةالمتغيرات. هذه - تركيز ثابت .

في حالة التركيز المستقر ، كما في حالة العقدة المستقرة ، لا يتم استيفاء شرط Lyapunov فحسب ، بل أيضًا شرط أكثر صرامة. وبالتحديد ، بالنسبة لأي انحرافات أولية ، سيعود النظام في النهاية أقرب ما يكون إلى موضع التوازن. يسمى هذا الاستقرار ، الذي لا تزداد فيه الانحرافات الأولية فحسب ، بل تتحلل ، تميل إلى الصفر الاستقرار المطلق .

إذا في الصيغة (4.18) أ 1 >0 ، ثم تبتعد نقطة التمثيل عن الأصل ، ونحن نتعامل معها تركيز غير مستقر . عند التحرك من الطائرةش ، ضدإلى مستوى الطورx, ذستبقى اللوالب أيضًا لولبية ، لكنها ستتشوه.

النظر الآن في حالة متىأ 1 =0 . مسارات المرحلة على متن الطائرةش ، ضدستكون هناك دوائر التي على متن الطائرةس ، صتناسب الحذف:

وهكذا ، فيأ 1=0 من خلال نقطة خاصةس = 0، ص = 0 لا يمر منحنى متكامل. تسمى هذه النقطة المفردة المعزولة ، التي تكون المنحنيات المتكاملة بالقرب منها منحنيات مغلقة ، على وجه الخصوص ، القطع الناقصة المضمنة في بعضها البعض وتحيط بالنقطة المفردة ، بالمركز.

وبالتالي ، فإن ستة أنواع من التوازن ممكنة ، اعتمادًا على طبيعة جذور المعادلة المميزة (4.7). عرض مسارات المرحلة على المستوى س ، صلهذه الحالات الست في الشكل. 4.9

أرز. 4.9أنواع صور الطور في جوار حالة ثابتة لنظام المعادلات الخطية (4.4).

الأنواع الخمسة لحالات التوازن تقريبية ، ولا تتغير طبيعتها مع التغييرات الصغيرة بما فيه الكفاية في الجوانب اليمنى من المعادلات (4.4). في هذه الحالة ، يجب أن تكون التغييرات صغيرة ليس فقط في الجانب الأيمن ، ولكن أيضًا في مشتقاتها من الدرجة الأولى. الحالة السادسة للتوازن - المركز - ليست خشنة. مع التغييرات الصغيرة في معلمات الجانب الأيمن من المعادلات ، ينتقل إلى تركيز ثابت أو غير مستقر.

مخطط التشعب

دعونا نقدم التدوين:

. (4.11)

ثم يمكن كتابة المعادلة المميزة بالشكل:

. (4.12)

لنفترض أن طائرة ذات إحداثيات ديكارتية مستطيلة س , د ووضع علامة عليها المناطق المقابلة لنوع أو آخر من حالة التوازن ، والتي تحددها طبيعة جذور المعادلة المميزة

.(4.13)

سيكون شرط استقرار حالة التوازن هو وجود جزء حقيقي سلبي من yل 1 و ل 2 . الشرط الضروري والكافي لهذا هو تحقيق عدم المساواةس > 0, د > 0 . في الرسم التخطيطي (4.15) ، يتوافق هذا الشرط مع النقاط الموجودة في الربع الأول من مستوى المعلمة. ستكون النقطة الفريدة هي التركيز إذال 1 و ل 2 مركب. هذا الشرط يتوافق مع تلك النقاط في المستوى الذي , أولئك. النقاط بين فرعين من القطع المكافئس 2 = 4 د. نقاط نصف المحور س = 0, د> 0 ، تتوافق مع حالات التوازن لنوع المركز. على نفس المنوال،ل 1 و ل 2 - صالحة لكنها علامات مختلفة ، أي. ستكون النقطة الفريدة سرجًا إذا د<0, إلخ. نتيجة لذلك ، نحصل على مخطط تقسيم لمستوى المعلمة س, د، إلى مناطق تتوافق مع أنواع مختلفة من حالات التوازن.

أرز. 4.10.مخطط التشعب

لنظام المعادلات الخطية 4.4

إذا كانت معاملات النظام الخطي ا ب ت ثتعتمد على بعض المعلمات ، فعندما يتم تغيير هذه المعلمة ، ستتغير القيم أيضًاس , د . عند المرور عبر الحدود ، تتغير طبيعة صورة المرحلة نوعياً. لذلك ، تسمى هذه الحدود حدود التشعب - على الجانبين المتقابلين للحدود ، يحتوي النظام على صورتين طوبولوجيتين مختلفتين طوبولوجيًا ، وبالتالي ، نوعان مختلفان من السلوك.

يوضح الرسم التخطيطي كيف يمكن أن تحدث هذه التغييرات. إذا استبعدنا حالات خاصة - أصل الإحداثيات - فمن السهل أن نرى أن السرج يمكن أن يدخل في عقدة أو مستقر أو غير مستقر عند عبور المحور ص. يمكن أن تنتقل العقدة المستقرة إلى سرج أو تركيز ثابت ، وما إلى ذلك. لاحظ أن العقدة المستقرة - التركيز الثابت والعقدة غير المستقرة - انتقالات التركيز غير المستقرة ليست ثنائية التشعب ، حيث لا تتغير طوبولوجيا مساحة الطور في هذه الحالة. سنتحدث بمزيد من التفصيل عن طوبولوجيا فضاء الطور وانتقالات التشعب في المحاضرة 6.

في ظل انتقالات التشعب ، تتغير طبيعة استقرار النقطة المفردة. على سبيل المثال ، يمكن أن يتحول التركيز الثابت من خلال المركز إلى تركيز غير مستقر. يسمى هذا التشعب تشعب أندرونوف-هوبفبأسماء العلماء الذين درسوه. مع هذا التشعب في الأنظمة غير الخطية ، تولد دورة حدية ، ويصبح النظام ذاتي التأرجح (انظر المحاضرة 8).

مثال. نظام التفاعلات الكيميائية الخطية

مادة Xيتدفق إلى الداخل من الخارج بمعدل ثابت ، ويتحول إلى مادة Y وبمعدل يتناسب مع تركيز المادة ص، خارج مجال التفاعل. جميع التفاعلات من الدرجة الأولى ، باستثناء تدفق المادة من الخارج ، الذي له ترتيب صفري. يبدو مخطط التفاعل كما يلي:

(4.14)

ويصفه نظام المعادلات:

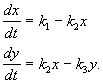(4.15)

نحصل على تركيزات ثابتة من خلال مساواة الجانبين الأيمن بالصفر:

.(4.16)

ضع في اعتبارك صورة المرحلة للنظام. دعونا نقسم المعادلة الثانية للنظام (4.16) على الأولى. نحن نحصل:

.(4.17)

تحدد المعادلة (4.17) سلوك المتغيرات على مستوى الطور. دعونا نبني صورة مرحلية لهذا النظام. أولاً ، نرسم الخطوط المتساوية الرئيسية على مستوى الطور. معادلة خط متساوي للظل الرأسي:

معادلة الخط المتساوي للظل الأفقي:

تقع النقطة المفردة (الحالة الثابتة) عند تقاطع الخطوط المتساوية الرئيسية.

الآن دعونا نحدد في أي زاوية تتقاطع محاور الإحداثيات مع المنحنيات المتكاملة.

إذا س = 0 ، إذن.

وهكذا ، ظل منحدر منحدر المماس لمنحنيات متكاملة ص = ص (س) ،عبور المحور ص س = 0، سالبة في نصف المستوى العلوي (تذكر أن المتغيرات س ، صلها قيم تركيز ، وبالتالي فنحن مهتمون فقط بالربع الأيمن العلوي من مستوى الطور). في هذه الحالة ، تزداد قيمة ظل زاوية ميل الظل مع زيادة المسافة من الأصل.

تأمل المحور ص = 0. عند تقاطع هذا المحور ، يتم وصف المنحنيات المتكاملة بالمعادلة

في يكون ظل منحدر المنحنيات المتكاملة التي تعبر محور الإحداثي موجبًا ويزيد من صفر إلى ما لا نهاية مع زيادة x.

في .

بعد ذلك ، مع زيادة أخرى ، يتناقص ظل المنحدر في القيمة المطلقة ، ويبقى سالبًا ويميل إلى -1 عند x ® ¥ . من السهل تكوين الصورة الكاملة لمسارات الطور بمعرفة اتجاه المماس للمنحنيات المتكاملة على الخطوط المتساوية الرئيسية وعلى محاور الإحداثيات.

سيتم تحديد طبيعة استقرار النقطة المفردة باستخدام طريقة Lyapunov. المحددات المميزة للنظام لها الشكل:

.

بتوسيع المحدد ، نحصل على المعادلة المميزة للنظام: ، بمعنى آخر. جذور المعادلة المميزة كلاهما سلبي. لذلك ، فإن الحالة الثابتة للنظام هي عقدة مستقرة. في نفس الوقت تركيز المادة Xيميل إلى حالة ثابتة دائمًا بشكل رتيب ، يمكن أن يمر تركيز المادة Y عبر min أو max. الأنظمة التذبذبية في مثل هذا النظام مستحيلة.

يترك zq - نقطة مفردة للدالة f (z) ، t.s. و (ض)ولكنه تحليلي في هذه المرحلة (على وجه الخصوص ، قد لا يتم تعريفه عند ذلك). إذا كان هناك مثل هذا الحي المثقوب للنقطة zq (أي المجموعة O z - zq f (z) هو aliatic ، إذن zoاتصل نقطة مفردة معزولةالمهام و (ض).يتم الاحتفاظ بهذا التعريف أيضًا في الحالة zn =أوه ، إذا كان اليود عبارة عن منطقة مثقوبة من نقطة zq = oo فهم المجموعة ض>انا - ظهور بعض الدوائر المتمركزة في الأصل. بعبارة أخرى ، النقطة الفريدة يُقال أن zq معزول إذا كان هناك حي من هذه النقطة حيث توجد نقاط مفردة أخرى مختلفة عنها ذق. في كل مكان أدناه ، نأخذ في الاعتبار النقاط الفردية فقط للشخصية ذات القيمة الواحدة (الوظيفة و (ض)يفترض أن تكون فريدة).

حسب سلوك الوظيفة و (ض)في ض -> زقهناك ثلاثة أنواع من النقاط الفردية. نقطة مفردة معزولة وظائف zq و (ض)اتصل:

1) نقطة مفردة قابلة للإزالةإذا كان هناك حد محدود

2) عمودإذا كان هناك حد

3) نقطة أساسيةإذا و (ض) ليس له حد نهائي ولا نهائي لـ ض-> ذق.

مثال 26.1. دعونا نظهر أن جميع الأنواع الثلاثة من النقاط الفردية قد تحققت. يعتبر F(ض)= نقطة zq = 0 معزول

نقطة واحدة من هذه الوظيفة. باستخدام الصيغة (22.12) نحصل على التوسع

مما يترتب على وجود ليم فاي (ض)= 1. لذلك ، zq = 0 تساوي

هي نقطة مفردة قابلة للإزالة للوظيفة فاي (ض).

دور f'j (ض) =--- له عمود عند نقطة zo= 1 بسبب

2 ص"X

النظر الآن في الوظيفة ) ض (ض)= e 1 ^ r وأظهر ذلك zo = O هي نقطة فردية أساسية لهذه الوظيفة. عند الكفاح ضللصفر على طول المحور الحقيقي ، الحدين الأيمن والأيسر للدالة f (ض)مختلف: ليم مع 1 / 1 = 0 ، ليم مع 1 / * =نظام التشغيل. هذا يعني،

س-> 0-0 س-> 0 + 0

ماذا او ما f: أنا (ض)ليس له حد نهائي أو لانهائي لـ 2 -> أوه ، أي zq = 0 هي نقطة مفردة أساسًا لهذه الوظيفة. (لاحظ أن النقطة تميل z-iyلصفر في وظيفة المحور التخيلي

ليس له حدود على الإطلاق.)

بالطبع ، هناك أيضًا نقاط مفردة غير معزولة. على سبيل المثال. الوظيفة لها أقطاب عند النقاط ض ن = -, ص= ± 1، ± 2، ...

لذلك، Zq = 0 هي نقطة مفردة غير معزولة لهذه الوظيفة: في أي حي (صغير عشوائيًا) من هذه النقطة توجد نقاط مفردة أخرى ز ص.

يترك zo-نقطة مفردة معزولة نهائية لوظيفة ما و (ض).ثم و (ض)يشبه في بعض الجوار المثقوب 0 Zo من النقطة zoيمكن اعتبار هذا الحي بمثابة حلقة نصف قطرها الداخلي r = 0. وفقًا لنظرية 25.1 ، في الحي قيد النظر ، الوظيفة و (ض)يمكن توسيعها في سلسلة Laurent (25.2). سنبين أن سلوك الوظيفة لـ 2 -> zq (أي نوع النقطة المفردة zo)يعتمد على شكل الجزء الرئيسي من التحلل (25.2) ؛ يفسر هذا الظرف أصل مصطلح "الجزء الرئيسي".

نظرية 2G.2. نقطة مفردة معزولة zo للدالة f (z) قابلة للإزالة إذا وفقط إذا كان توسع Lorap في حي مثقوب من هذه النقطة يحتوي على OID

أولئك. يتكون من الجزء الصحيح فقط, وجميع معاملات الجزء الرئيسي تساوي الرمز النقطي.

دليل. 1. اسمحوا zoهي نقطة مفردة قابلة للإزالة. دعونا نثبت أن توسيع لوران للدالة و (ض)له شكل (26.1). منذ نقطة المفرد zoقابل للإزالة ، ثم هناك حد محدود و (ض) = أ.لذلك، و (ض)يحدها في بعض حي مثقوب 0 z - zq من النقطة زوأولئك. ) (ض) للجميع ضمن هذا الحي. خذ تم العثور على R. U р /؟ | ، واستخدم الصيغ (25.3) لمعاملات سلسلة Laurent:

لمعاملات الجزء الرئيسي من التوسع ن =- 1 ، -2 ، ... لمثل هذه القيم صلدينا ص ~ ن-e 0 في ص-> 0. منذ القيمة صيمكن اختياره بشكل تعسفي صغير ، إذن السيد ~ "يمكن أن تكون صغيرة بشكل تعسفي. منذ | c t، | ^ السيد ~ نو cn لا تعتمد على p ، ثم cn = 0 لـ و= - 1 ، -2 ، ... ، التي كان من المقرر إثباتها.

2. لنفترض الآن أن توسعة لوران لها الشكل (26.1). السلسلة (26.1) هي سلسلة طاقة و. لذلك ، تتلاقى ليس فقط في الثقب ، ولكن أيضًا في الحي بأكمله ض-ذق بما في ذلك النقطة زو.مجموعها S (ض)تحليلي ل ض و S (ض) = ) (ض)في 0 ض - zoتم العثور على R.لذلك ، هناك حد محدود ) (ض)\ u003d Pm 5 (r) \ u003d 5 (r) - لذلك ، النقطة المفرد zq

Z-> Zo Z- * Zo

للاستعمال لمرة واحدة. لقد تم إثبات النظرية.

تعليق. ويترتب على إثبات النظرية أنه في الجوار المثقوب 0 z - zo لنقطة مفردة قابلة للإزالة ، الوظيفة و (ض)يتطابق مع الوظيفة S (r) ، وهي دالة تحليلية في الحي بأكمله ض - zo. لذلك ، إذا وضعنا / (ث) = S (zq) ، ثم ، دون تغيير قيم الوظيفة و (ض)في أي نقطة من الجوار المثقوب ، نجعل هذه الوظيفة تحليلية في r ، أي "إزالة" الميزة. هذا ما يفسر مصطلح "التفرد القابل للإزالة". من الطبيعي اعتبار هذه النقاط عادية وليست نقاط مفردة للوظيفة و (ض).

ضع في اعتبارك ، على سبيل المثال ، الوظيفة

في المثال 26.1 ، تبين أن Pm (n) = 1. أي نقطة فردية

zq = 0 قابل للإزالة. ضبط / i (0) = 1 ، وبالتالي نحذف التفرد ونحصل على وظيفة تحليلية عند النقطة zq = 0 (وفي المستوى C بأكمله).

دعونا الآن نميز الأقطاب من حيث توسعات لوران.

نظرية 26.3. النقطة المفردة المعزولة Zo للدالة f (z) هي قطب إذا وفقط إذا, عندما يكون الجزء الرئيسي من توسعة Laurent مع المركز Zq عددًا محدودًا فقط من المتميزين

من صفر معاملات مع n:

دليل. 1. اسمحوا zq - قطب ، أي ليم / ( ض) = oo.

دعونا نثبت أن توسيع لوران للدالة و (ض)له شكل (2G.2). منذ ليم و (ض)= س س. ثم يوجد حي مثقوب للنقطة

كي ذق. حيث و (ض)تحليلي وليس له أصفار. ثم الوظيفة ز (ض) = 1 /و (ض)سيكون أيضًا تحليليًا في هذا الحي المثقوب ، وليم ز (ض)= 0. لذلك ، زوهل يمكن التخلص منها * -؟ * 0

نقطة مفردة للوظيفة ز (ض).دعونا نعيد تعريف ز (ض)في هذه النقطة zoوضع ز (zo)= 0. ثم ز (ض)يصبح تحليليًا في المنطقة المجاورة بالكامل للنقطة (غير المثقوبة) ض 0 ،و ض 0سيكون صفره المعزول. للدلالة به نتعدد (ترتيب) هذا الصفر. كما هو موضح في الفقرة 23 ، في منطقة مجاورة للنقطة وظيفة zq ز (ض)قابلة للتمثيل في النموذج (انظر (23.2))

و (ض $) و 0 و ص> (ض)تحليلي في بعض المناطق المجاورة للنقطة zo-لأن ip (ض)مستمر عند النقطة zoو ز> (zo) و 0 "إذن ip (ض)ليس له أصفار في بعض الأحياء من هذه النقطة أيضًا. لذلك وظيفة 1 / -p (z)سيكون أيضًا تحليليًا في هذا الحي ، وبالتالي يتوسع فيه في سلسلة تايلور:

بفك الأقواس وتغيير تسميات المعاملات ، نكتب التوسع الأخير في النموذج

حيث c_jv = 1> س و 0. وهكذا ، فإن الجزء الرئيسي من توسعة لوران لـ f (r) يحتوي فقط على عدد محدود من المصطلحات ؛ لقد وصلنا إلى المساواة المطلوبة (26.2).

2. دعونا في حي مثقوب من نقطة ذوظيفة ) (ض)يمثلها توسع لوران (26.2) (في شكل موسع أكثر ، انظر (26.3)) ، الجزء الرئيسي منها يحتوي فقط على عدد محدود من المصطلحات ، و مع-د" F 0. يجب أن نثبت ذلك ZQ - عمود الوظيفة و (ض).ضرب المساواة (26.3) في (جي - جيس) رابعا ، نحصل على الوظيفة

السلسلة في (26.4) هي سلسلة قوى تتقارب مع وظيفة تحليلية ليس فقط في الثقب ، ولكن أيضًا في المنطقة المجاورة للنقطة بأكملها زق. لذلك ، فإن الوظيفة ح (ض)يصبح تحليليًا في هذا الحي إذا قمنا بتوسيعه من خلال الإعداد ح (zo)= s_dg F 0. ثم

وهكذا فإن النقطة o هي قطب ، وقد تم إثبات النظرية 26.3.

تعدد (ترتيب) الدالة الصفرية ز (ض)= 1 // (ص) يسمى ترتيب القطبوظيفة / (ص). إذا ن-ترتيب القطب هو عشر ، إذن ز (ض)= (ص - Zo) N ip (z) ،و اذهب) F 0 ، وكما هو موضح في الجزء الأول من إثبات النظرية 26.3 ، فإن توسيع f (r) له شكل (26.3) ، حيث c_ / v F 0. على العكس من ذلك ، إذا توسعت f (r) في السلسلة (26.3) و ه-ي و 0 ، إذن

t.s. ن-ترتيب قطب الوظيفة f (r). في هذا الطريق، ترتيب القطب zq للوظيفة/ (ز) يساوي عدد المعامل الرئيسي غير الصفري للجزء الرئيسي من توسع لوران في المنطقة المثقوبة للنقطة zq(أي يساوي هذا الرقم ن،ما s_dg F 0 و ص= 0 في ص > ن).

دعنا نثبت التأكيد التالي ، وهو مناسب) للتطبيقات.

النتيجة الطبيعية 26.4. النقطة zq هي قطب من الرتبة N للخيال/ (ز) إذا وفقط إذا/ (ز) تمثيل في الشكل

حيث h (z) هي دالة تحليلية في منطقة مجاورة لنقطةذ وح (zo) و 0.

دليل. دور cp (z) = l / h (z)تحليلي في بعض المناطق المجاورة للنقطة r. حالة النتيجة الطبيعية 26.4 تعادل ما يلي:

لذا ذق - تعدد الصفر نالمهام ز (ض).ومن هنا قطب التعددية نوظائف / (2).

المثال الثاني 26.5. ابحث عن نقاط مفردة معزولة للدالة وتحديد نوعها.

D e u c tio n. النقاط التي عندها (ض 2 + 1 ) (ض+ H) 2 = 0. إذا ض 2 L- 1 = 0 ثم 2 = ± صإذا (ض 4- ح) 2 = 0 ثم ض= -3. لذلك ، للدالة ثلاث نقاط مفردة ض= ص ، 22 = -ر ، ض3 = - 3. النظر ض:

ز -قطب من الدرجة الأولى (استخدمنا Corollary 26.4). يمكن إثبات أن 22 = -أناأيضا قطب من الدرجة الأولى. لمدة ساعتين لدينا:

دعونا ننتقل إلى النظر في النقاط الفردية بشكل أساسي.

نظرية 26.6. النقطة المفردة المعزولة zq للدالة f (z) هي بشكل أساسي مفردة إذا وفقط إذا كان الجزء الرئيسي من توسعة Laurent المتمركزة في zq يختلف كثيرًا عن. صفر ، المعاملات مع p.

دليل. النظرية 26.6 تتبع مباشرة من النظريتين 26.2 و 26.3. في الواقع ، إذا كانت النقطة zq مفرد بشكل أساسي ، فلا يمكن أن يكون الجزء الرئيسي من توسعة Laurent غائبًا أو يحتوي على عدد محدود من المصطلحات (وإلا فإن النقطة سيكون Zq إما قابل للإزالة أو عمودًا). لذلك ، يجب أن يكون عدد المصطلحات في الجزء الرئيسي غير محدود.

على العكس من ذلك ، إذا كان الجزء الرئيسي يحتوي على عدد غير محدود من الأعضاء ، إذن لا يمكن أن يكون Zq نقطة قابلة للإزالة ولا قطبًا. وبالتالي ، فإن هذه النقطة هي في الأساس نقطة مفردة.

وفقًا للتعريف ، تتميز النقطة المفردة أساسًا بحقيقة أن الوظيفة f (2) ليس لها حد محدود ولا حد لانهائي لـ ض ->ذق. يتم إعطاء فكرة أكثر اكتمالاً عن مدى عدم انتظام سلوك الوظيفة في حي نقطة مفردة أساسًا من خلال النظرية التالية.

نظرية 26.7 (نظرية سوتشوكي). إذا كان zq مفردًا بشكل أساسي ، فإن نقطة الدالة f (z), ثم لأي عدد مركبلام ، بما في ذلك A =أوه ، هناك تسلسل من النقاط z n مثل z n -> zo وليم و (زن) = أ.

ن-> نظام التشغيل

دليل. لنتأمل الحالة أولاً أ =س. في الجزء الأول من إثبات نظرية 2G.2 ، أثبتنا أنه إذا و (ض)يحد في بعض الجوار المثقوب للنقطة r0 ، ثم جميع المعاملات ج ، ن = - 1 ، - 2 ، ... للجزء الرئيسي تساوي الصفر (وبالتالي ، يمكن إزالة التفرد في th). نظرًا لأن r ، من خلال الافتراض ، هي نقطة مفردة بشكل أساسي ، فإن الوظيفة / (r) غير محدودة في أي حي مثقوب للنقطة r. دعونا نأخذ بعض الحي الضيق 0 Z مثل هذا و (زي)> 1 (إذا | / (r) | z - zo R / 2 هناك نقطة ض-2 ، أين | / (dd) | > 2 ، إلخ: في الحي المثقوب O 71. من الواضح أن rn -e go و lim / (r «) = oo. وهكذا ، في الحالة A = oo ، Theorem 26.7

ثبت.

دعنا الآن أ وس. افترض أولاً أن هناك حيًا مثقوبًا 0

= -yy---- سيكون تحليليًا في هذا الحي المثقوب ، وبالتالي ،

/ (G) - أ

وبالتالي ، r هي نقطة مفردة معزولة للوظيفة Φ (r). دعونا تظهر. أن r0 هي نقطة مفردة أساسًا لـ Φ (r). فليكن خطأ. ثم يوجد حد lim Φ (r) ، إما محدود أو لانهائي. لأن

/ (r) = A + ، ثم Hsh / (r) موجود أيضًا ، وهو ما يتعارض مع الشرط

F (ز) ~ : - * z 0

وجهة نظر النظرية. وبالتالي فإن r0 هي نقطة مفردة أساسًا للوظيفة Φ (r). وفقًا لما تم إثباته أعلاه ، هناك سلسلة من النقاط r n مثل r n o و lim Φ (r n) = oo. من هنا

لقد أثبتنا التأكيد المطلوب على افتراض أن f (r) و أفي بعض الجوار المثقوب من النقطة ص. لنفترض الآن أن هذا ليس صحيحًا ، أي في أي حي صغير مثقوب بشكل تعسفي من النقطة هناك مثل هذه النقطة G "،أن f (r ") = A. ثم لأي صفي الجوار المثقوب 0 f (z u) = L. وهكذا يكون التأكيد المطلوب صحيحًا ص-yuo

في جميع الأحوال ، وثبت نظرية 26.7.

وفقًا لنظرية (Sokhotsky's) 26.7 ، في أي منطقة مثقوبة (صغيرة بشكل تعسفي) لنقطة مفردة بشكل أساسي ، تأخذ الدالة f (r) قيمًا قريبة بشكل تعسفي من أي رقم في المستوى المركب الممتد C.

لدراسة النقاط الفردية المعزولة ، غالبًا ما تكون توسعات تايلور المعروفة للوظائف الأولية الأساسية مفيدة.

مثال 2G.8. حدد نوع النقطة المفردة zq = 0 للدالة

حل و e. نفك البسط والمقام في سلسلة Taylor في قوى r. الاستعاضة عن (22.11) 3 ضبدلاً من r وطرح 1 ، نحصل على

باستخدام (22.12) نحصل على توسيع المقام:

تتلاقى السلسلة في هذه التوسعات في المستوى المركب بأكمله €. لدينا

و / 2 (2) متشابهتان في منطقة مجاورة للنقطة zo = 0 (وحتى في الطائرة بأكملها) و / 2 (20) F 0 ، إذن ح (ض)هو أيضًا تحليلي في بعض المناطق المجاورة للنقطة gF 0. وفقًا لـ Corollary 26.4 ، النقطة Zo = 0 هو عمود الترتيب ن = 4.

المثال الثاني 26.9. ابحث عن نقاط مفردة لوظيفة و (ض)= sin j - وتحديد نوعها.

P e in e و e تحتوي الوظيفة على نقطة مفردة نهائية zq = 1. في نقاط أخرى من C ، الدالة ث =- تحليلي ومن هنا تأتي وظيفة الخطيئة ثسيكون تحليليًا.

الاستبدال في توسيع الجيب (22.12) - بدلاً من r نحصل عليه

لقد حصلنا على توسيع دالة الخطيئة في سلسلة Laurent في منطقة مثقوبة من النقطة 20 = 1. نظرًا لأن التوسع الناتج يحتوي على عدد لا نهائي من الحدود مع قوى سالبة (r - 1) ، إذن zq = 1 هي نقطة مفردة أساسية (في هذه الحالة ، يتكون توسع Laurent من الجزء الرئيسي فقط ، والجزء الصحيح مفقود).

لاحظ أنه في هذه الحالة كان من الممكن أيضًا تحديد طبيعة التفرد مباشرة من التعريف ، دون اللجوء إلى توسيع السلسلة. في الواقع ، هناك متواليات (r ") و (2") متقاربة zo= 1 ، وهكذا و (ض "ن)= 1، / (2 ") = 0 (حدد هذه التسلسلات بنفسك). و (ض)ليس له حدود عندما ض -> 1 ومن هنا جاءت النقطة zq - 1 مفرد بشكل أساسي.

دعونا نقدم مفهوم توسع لوران لوظيفة في منطقة مجاورة لنقطة ما Zq = 00 واعتبر العلاقة بين التوسع وطبيعة التفرد في هذه المرحلة. لاحظ أن تعريفات نقطة مفردة معزولة ونوعها (قابل للإزالة ، أو قطب ، أو فردي بشكل أساسي) تنتقل إلى العلبة zq = oc دون تغيير. لكن النظريات 26.2. يجب تغيير 26.3 و 26.6 ، المتعلقين بطبيعة توسعات Laurent. النقطة هي أن الأعضاء ج ن (ض - 2o) ص. ص= -1 ، -2 ، ... ، الجزء الرئيسي ، تحديد "عدم انتظام" الوظيفة بالقرب من نقطة النهاية Zq ، نظرًا لأن 2 تميل إلى oo ، فسوف تتصرف "بشكل صحيح" (تميل إلى 0). على العكس من ذلك ، فإن أعضاء الجزء العادي مع ص= 1،2 ، ... سوف تميل إلى oo ؛ يحددون طبيعة التفرد في Zq = oo. لذلك ، فإن الجزء الرئيسي من التوسع في حي oo سيكون الشروط ذات القوى الإيجابية فوصحيح - مع السلبية.

دعنا نقدم متغير جديد ث = 12. دور تلفزيون = 1/2 ، ممتد بحيث u (oo) = 0 ، واحد لواحد ويقوم بتعيين الحي بشكل مطابق ض> صنقاط zq = 00 بجوار | w | wq = 0. إذا كانت الوظيفة و (ض)تحليلات في حي مثقوب ص z Zq = oc ، ثم الوظيفة G (w) = f (l / w)سيكون التحليلي في الحي الأصفر 0 wo = 0. منذ 2 -> oo سيكون هناك ث-> 0 إذن

لذا ز (ث)لديه في هذه النقطة wq = 0 هي حالة تفرد من نفس النوع مثل و (ض)في هذه النقطة Zq = 00. دعونا نوسع الدالة G (w) في سلسلة Laurent في منطقة مثقوبة من النقطة wo = 0:

المجاميع الموجودة على الجانب الأيمن من (26.5) تمثل الأجزاء الصحيحة والرئيسية من التوسيع ، على التوالي. دعنا ننتقل إلى المتغير ض ،أستعاض ث = 1/ ض:

دلالة ص\ u003d -A * ، 6 * \ u003d 6_ "\ u003d مع صويلاحظ ذلك جي (ل / ض) = و (ض)، نحن نحصل

يسمى التحلل (2G.G) توسيع لوران للدالة f (z) في حي مثقوب من النقطة zq= س س. المبلغ الأول في (2G.6) يسمى الجزء الصحيح، والمبلغ الثاني هو الجزء الرئيسيهذا التحلل. نظرًا لأن هذه المبالغ تتوافق مع الأجزاء الصحيحة والرئيسية من التوسيع (26.5) ، فإن التوسيع (26.6) يلبي نظائر النظريات 26.2 و 26.3 و 26.6. وبالتالي ، فإن النظرية التالية هي نظير للنظرية 26.2.

نظرية 26.10.2020 نقطة مفردة معزولةزق - نظام التشغيل (المهام/ (ز) قابل للإزالة فقط إذا كان توسيع لوران في منطقة مثقوبة من هذه النقطة له الشكل فقط

t.s. يتكون من الجزء الصحيح فقط.

نضع / (س س) = شارك.الوظيفة التي تحددها السلسلة (26.7) متقاربة في الجوار ض> صالنقاط 2o \ u003d oc ، تسمى تحليلي عند النقطة ضس = س س. (لاحظ أن هذا التعريف يعادل تحليل الوظيفة جي (دبليو) عند النقطة wo = 0.)

مثال 26.11. تحقق من النقطة المفردة zq = oo للدالة

بما أن الحد محدود إذن zo = oo هي نقطة مفردة قابلة للإزالة للوظيفة f (r). إذا وضعنا / (oo) = lim ي (ض)= 0 إذن و (ض)سيصبح

عرة عند نقطة زو= نظام التشغيل. دعونا نوضح كيفية إيجاد التوسع المقابل (26.7). دعنا ننتقل إلى المتغير ث = 1 م.أستعاض ض= 1 /؟ e ، نحصل عليه

(المساواة الأخيرة صالحة في المنطقة المجاورة للنقطة ww = 0 ، لكننا سنوسع التعريف (7 (0) = 0). الوظيفة الناتجة لها نقاط مفردة ث =± أنا ، ث =-1/3 ، وعند النقطة Wq = 0 تحليلي. وظيفة التوسيع ز (ث)بالدرجات ث(كما حدث في المثال 25.7) والاستبدال في سلسلة القدرة الناتجة ث = 1 / ضيمكن للمرء الحصول على توسيع (26.7) الوظيفة و (ض).

نظرية 26.3 للقضية zo= oo ستتم إعادة كتابتها بالشكل التالي.

نظرية 26.12.2019 نقطة مفردة معزولةاذهب = نظام التشغيل الدالة f (z) هي قطب إذا وفقط إذا كان الجزء الرئيسي من توسعة لوران (26.6) ليس له سوى عدد محدود من المعاملات غير الصفريةمع":

هنا السلسلة هي الجزء العادي ، وكثير الحدود بين قوسين هو الجزء الرئيسي من التوسع. يُعرَّف تعدد القطب في المحيط بأنه تعدد القطب wq = 0 وظائف ز (ض).من السهل أن نرى أن تعدد القطب يتطابق مع الرقم نفي (26.8).

س ص | (i 2 + 1) (z + 3) 2

مهمة. تبين أن الوظيفة و (ض) =-- -- يوجد في

هدف zo =طلب قطب 3.

تتم إعادة كتابة النظرية 26.6 حول نقطة مفردة أساسية للحالة zo= os حرفيًا تقريبًا ، ولا نتطرق إليه بالتفصيل.

تعمل سلسلة تايلور كأداة فعالة لدراسة الوظائف التحليلية في الدائرة zol لدراسة الوظائف التحليلية في منطقة حلقية ، اتضح أنه من الممكن بناء توسعات في القوى الموجبة والسالبة (z - zq) من النموذج الذي يعمم توسعات تايلور. السلسلة (1) ، التي تُفهم على أنها مجموع سلسلتين ، تسمى سلسلة Laurent. من الواضح أن منطقة تقارب السلسلة (1) هي الجزء المشترك من مناطق التقارب لكل سلسلة (2). دعنا نجدها. منطقة التقارب في السلسلة الأولى هي دائرة يتم تحديد نصف قطرها بواسطة صيغة Cauchy-Hadamard. داخل دائرة التقارب ، تتقارب السلسلة (3) إلى دالة تحليلية ، وفي أي دائرة ذات نصف قطر أصغر ، تتقارب تمامًا وبشكل موحد. السلسلة الثانية هي سلسلة قوى فيما يتعلق بالمتغير. السلسلة (5) تتقارب داخل دائرة التقارب الخاصة بها إلى الوظيفة التحليلية للمتغير المركب m- * oo ، وفي أي دائرة ذات نصف قطر أصغر تتقارب بشكل مطلق وموحد ، مما يعني أن منطقة تقارب السلسلة (4) هي مظهر الدائرة - إذا كان هناك منطقة مشتركة لتقارب السلسلة (3) و (4) - حلقة دائرية تكون فيها السلسلة (1) يتقارب لوظيفة تحليلية. علاوة على ذلك ، في أي حلقة ، يتقارب بشكل مطلق وموحد. مثال 1. تحديد منطقة التقارب لسلسلة راد لوران يمكن تمثيل النقاط المفردة المعزولة وتصنيفها (z) ، وهو أحادي القيمة وغير سياسي في حلقة دائرية ، في هذه الحلقة كمجموع لسلسلة متقاربة معاملاتها يتم تحديد وحساب Cn بشكل فريد من خلال الصيغ حيث 7p عبارة عن دائرة نصف قطرها m دعونا نصلح نقطة عشوائية z داخل الحلقة R نقوم ببناء دوائر بمراكز عند النقطة r والتي يلبي أنصاف أقطارها المتباينات وننظر في حلقة جديدة.وفقًا لنظرية كوشي المتكاملة لمجال متصل بشكل مضاعف ، دعونا نحول كل تكاملات في المجموع (8) بشكل منفصل. بالنسبة لجميع النقاط £ على طول الدائرة 7 د * ، يتم استيفاء العلاقة بين مجموع سلسلة متقاربة بشكل موحد 1 1. لذلك ، يمكن تمثيل الكسر ^ في vi- / "/ بطريقة مختلفة نوعًا ما ، لجميع النقاط ξ على الدائرة ir> لدينا العلاقة لذلك ، يمكن تمثيل الكسر ^ على أنه مجموع سلسلة متقاربة بشكل موحد في الصيغ (10) و (12) هي وظائف تحليلية في حلقة دائرية. لذلك ، وفقًا لنظرية كوشي ، لا تتغير قيم التكاملات المقابلة إذا تم استبدال الدائرتين 7 / r و 7r / بأي دائرة. هذا يسمح لنا بدمج الصيغتين (10) و (12). استبدال التكاملات على الجانب الأيمن من الصيغة (8) بتعبيراتها (9) و (11) ، على التوالي ، نحصل على التوسع المطلوب. نظرًا لأن z هو أمر تعسفي نقطة الحلقة ، يترتب على ذلك أن السلسلة (14) تتقارب مع الوظيفة f (z) في كل مكان في هذه الحلقة ، وفي أي حلقة تتقارب السلسلة مع هذه الوظيفة بشكل مطلق وموحد. دعونا الآن نثبت أن تحلل الشكل (6) فريد من نوعه. افترض حدوث تحلل آخر ، ثم في كل مكان داخل الحلقة R ، لدينا على المحيط ، تتلاقى السلسلة (15) بشكل موحد. اضرب طرفي المساواة (حيث m هو عدد صحيح ثابت ، ودمج كلا من مصطلح السلسلة بمصطلح واحد. ونتيجة لذلك ، نحصل على الجانب الأيسر ، وعلى الجانب الأيمن - Csh. وهكذا ، (4، \ u003d St. نظرًا لأن m رقم تعسفي ، فإن آخر سلسلة مساواة (6) ، التي تُحسب معاملاتها بالصيغ (7) ، تسمى سلسلة Laurent للوظيفة f (z) في الحلقة 7) لمعاملات سلسلة Laurent نادرًا ما تُستخدم عمليًا ، لأنها تتطلب ، كقاعدة عامة ، حسابات مرهقة. عادةً ، إذا أمكن ، يتم استخدام توسعات تيلور الجاهزة للوظائف الأولية. بناءً على تفرد التوسيع ، تؤدي أي طريقة شرعية إلى نفس النتيجة. مثال 2 ضع في اعتبارك توسعات سلسلة Laurent لوظائف المجالات المختلفة ، بافتراض أن Fuiscius / (r) له نقطتان فرديتان: لذلك ، هناك ثلاثة مجالات حلقة وتتركز عند النقطة r = 0. في كل منها تكون الوظيفة f (r) تحليلية: أ) الدائرة هي الجزء الخارجي للدائرة (الشكل 27). دعونا نجد توسعات Laurent للوظيفة / (z) في كل من هذه المناطق. نمثل / (ض) كمجموع الكسور الأولية أ) علاقة تحويل الدائرة (16) على النحو التالي باستخدام صيغة مجموع شروط التقدم الهندسي ، نحصل على ب) تظل الحلقة الخاصة بالوظيفة -z متقاربة في هذه الحلقة ، نظرًا لأن السلسلة (19) للوظيفة j ^ j لـ | z | > 1 يتباعد. لذلك ، نقوم بتحويل الوظيفة / (z) على النحو التالي: تطبيق الصيغة (19) مرة أخرى ، نحصل على أن هذه السلسلة تتقارب من أجلها. بالتعويض عن الامتدادات (18) و (21) في العلاقة (20) ، نحصل على ج) المظهر الخارجي للدالة -z مع | z | > 2 تباعد ، وسلسلة (21) للوظيفة دعونا نمثل الوظيفة / (ض) بالشكل التالي: /<*> باستخدام الصيغتين (18) و (19) ، نحصل على OR 1 يوضح هذا المثال أنه بالنسبة لنفس الوظيفة f (z) ، فإن توسع Laurent ، بشكل عام ، له شكل مختلف لحلقات مختلفة. مثال 3. ابحث عن تحلل سلسلة Laurent الثمانية لوظيفة Laurent series نقاط مفردة معزولة وتصنيفها في المنطقة الحلقيّة A نستخدم تمثيل الوظيفة f (z) بالشكل التالي: وقم بتحويل المصطلح الثاني باستخدام صيغة مجموع شروط التقدم الهندسي ، نحصل على استبدال التعبيرات التي تم العثور عليها في الصيغة (22) ، لدينا مثال 4. قم بتوسيع الدالة في سلسلة Laurent المجاورة لـ Thin zq = 0. لأي واحد معقد ، لدينا دع هذا التوسيع صالح لأي نقطة z Ф 0. في هذه الحالة ، المنطقة الحلقيّة هي المستوي المعقد بأكمله بنقطة واحدة مطروحة z - 0. يمكن تحديد هذه المنطقة بالعلاقة التالية: هذه الوظيفة تحليلية في المنطقة من الصيغ (13) لمعاملات سلسلة Laurent ، وبنفس المنطق كما في الفقرة السابقة ، يمكن للمرء الحصول على متباينات Kouiw. إذا كانت الوظيفة f (z) محدودة بدائرة ، حيث M ثابت) ، فإن النقاط المفردة المعزولة تسمى النقطة zo نقطة مفردة معزولة للوظيفة f (z) إذا كان هناك جوار حلقي للنقطة ( تسمى هذه المجموعة أحيانًا أيضًا الحي المثقوب للنقطة 2o) ، حيث تكون الوظيفة f (z) ذات قيمة واحدة وتحليلية. عند النقطة zo نفسها ، إما أن الوظيفة غير محددة أو ليست أحادية القيمة أو تحليلية. يتم تمييز ثلاثة أنواع من النقاط الفردية اعتمادًا على سلوك الوظيفة / (z) عند الاقتراب من النقطة zo. يُقال أن النقطة المفردة المعزولة هي: 1) قابلة للإزالة إذا كان هناك منتهي 2) pmusach إذا 3) نقطة مفردة بشكل أساسي إذا كانت الوظيفة f (z) ليس لها حد لـ نظرية 16. النقطة المفردة المعزولة z0 للدالة f (z) هي نقطة مفردة قابلة للإزالة إذا وفقط إذا كان توسع Laurent للوظيفة f (z) في حي من النقطة zo لا يحتوي على جزء رئيسي ، أي ، له شكل Let zo - نقطة مفردة قابلة للإزالة. ثم هناك واحدة محدودة ، وبالتالي فإن الوظيفة f (z) محدودة في المنطقة التناسلية للنقطة r. لقد حددنا بحكم عدم المساواة Cauchy نظرًا لأنه من الممكن اختيار ρ صغيرًا كما نرغب ، فكل المعاملات عند القوى السالبة (z - 20) تساوي صفرًا: على العكس ، دع لوران توسع الدالة / (r) في منطقة مجاورة للنقطة zq يحتوي فقط على الجزء الصحيح ، أي أنه يحتوي على الشكل (23) وبالتالي ، هو تايلور. من السهل ملاحظة أنه بالنسبة إلى z - * z0 ، فإن الوظيفة / (r) لها قيمة حدية: النظرية 17. يمكن إزالة النقطة المفردة المعزولة zq للوظيفة f (z) إذا وفقط إذا كانت الوظيفة J (z) يحدها في بعض الجوار المثقوب من النقطة zq ، Zgmechai لا. لنفترض أن r0 نقطة مفردة قابلة للإزالة لـ f (r). بافتراض أننا توصلنا إلى أن الدالة f (r) تحليلية في بعض الدوائر المتمركزة عند النقطة th. هذا يحدد اسم النقطة - المتاح. نظرية 18. النقطة المفردة المعزولة zq للدالة f (z) هي قطب إذا وفقط إذا كان الجزء الرئيسي من توسع لوران للدالة f (z) في منطقة مجاورة للنقطة يحتوي على رقم منتهي (وموجب) من الشروط غير الصفرية ، على سبيل المثال ، لها الشكل 4 لنفترض أن z0 يكون عمودًا. منذ ذلك الحين يوجد حي مثقوب للنقطة z0 حيث تكون الوظيفة f (z) تحليلية وغير صفرية. ثم يتم تحديد دالة تحليلية في هذا الحي ، وبالتالي ، فإن النقطة zq هي نقطة مفردة قابلة للإزالة (صفر) للوظيفة أو حيث h (z) هي دالة تحليلية ، h (z0) ∩ 0. تحليلية في حي من النقطة zq ، ومن هنا نحصل على ذلك ، لنفترض الآن أن الوظيفة f (z) لها تحلل للصيغة (24) في منطقة مثقوبة من النقطة zo. هذا يعني أنه في هذا الحي تكون الوظيفة f (z) تحليلية مع الوظيفة. بالنسبة للوظيفة g (z) ، يكون التوسيع صالحًا ومن الواضح أن zq هي نقطة مفردة قابلة للإزالة للوظيفة g (z) وموجودة ، ثم تميل الوظيفة عند 0 - عمود الوظيفة هناك واحد أكثر بساطة حقيقة. النقطة Zq هي عمود للدالة f (z) إذا وفقط إذا كان يمكن تمديد الوظيفة g (z) = y إلى دالة تحليلية في منطقة مجاورة للنقطة zq عن طريق ضبط g (z0) = 0. الترتيب لقطب الوظيفة f (z) يسمى ترتيب الصفر للدالة jfa. تشير النظريتان 16 و 18 إلى التأكيد التالي. نظرية 19. النحافة المفردة المعزولة هي في الأساس مفردة إذا وفقط إذا كان الجزء الرئيسي من توسع لوران في منطقة مثقوبة من هذه النقطة يحتوي على عدد لا نهائي من المصطلحات غير الصفرية. مثال 5. النقطة المفردة للدالة هي zo = 0. لدينا نقاط مفردة معزولة من سلسلة Laurent وتصنيفها لذلك ، zo = 0 هي نقطة مفردة قابلة للإزالة. يحتوي توسيع الدالة / (z) في سلسلة Laurent بالقرب من نقطة الصفر على الجزء الصحيح فقط: Example7. f (z) = النقطة المفردة للدالة f (z) هي zq = 0. ضع في اعتبارك سلوك هذه الوظيفة على المحورين الحقيقي والخيالي: على المحور الحقيقي عند x 0 ، على المحور التخيلي ، لذلك ، ليس محدودًا ولا حد لانهائي f (z) عند z - * 0 غير موجود. ومن ثم فإن النقطة r0 = 0 هي نقطة مفردة أساسًا للوظيفة f (z). لنجد توسعة لوران للدالة f (z) في منطقة مجاورة لنقطة الصفر. لأي مجمع لدينا دعونا. ثم تحتوي توسعة لوران على عدد لا نهائي من الحدود مع قوى سالبة لـ z.

تعريف.تسمى النقطة المفردة للوظيفة معزول، إذا كانت هناك وظيفة تحليلية في منطقة ما من هذه النقطة (أي التحليلية في الحلقة).

يرتبط تصنيف النقاط المفردة المعزولة لوظيفة ما بسلوك هذه الوظيفة في منطقة مجاورة لنقطة مفردة.

تعريف.النقطة تسمى للاستعمال لمرة واحدة نقطة مفردة للدالة إذا كان هناك حد محدود لهذه الوظيفة عند.

مثال 5أظهر أن الوظيفة لها ميزة تفرد قابلة للإزالة في نقطة ما.

المحلول.بتذكير الحد الملحوظ الأول ، نحسب

هذا يعني أن الوظيفة المعينة لها تفرد قابل للإزالة في هذه النقطة.

المهمة 4.أظهر أن النقطة قابلة للإزالة من أجل.

تعريف.النقطة تسمى عمود وظيفة ، إذا زادت هذه الوظيفة إلى أجل غير مسمى ، فهذا هو.

دعونا ننتبه إلى العلاقة بين مفاهيم الصفر وقطب الوظيفة التحليلية. دعنا نمثل الوظيفة كـ.

إذا كانت النقطة عبارة عن صفر بسيط للدالة ، فإن الوظيفة لها قطب بسيط

إذا كانت النقطة هي الترتيب صفر للدالة ، فعندئذٍ بالنسبة للوظيفة يكون القطب طلب.

مثال 6أظهر أن الوظيفة لها عمود من الدرجة الثالثة في نقطة ما.

المحلول.بافتراض أننا حصلنا عليها. نظرًا لأننا نميل إلى الصفر ، وفقًا لأي قانون ، لدينا. ثم ، ومعها تزيد الوظيفة نفسها إلى أجل غير مسمى. لذلك ، فإن النقطة المفردة هي قطب. بالنسبة للدالة ، من الواضح أن هذه النقطة هي صفر ثلاثي. ومن ثم ، بالنسبة لهذه الوظيفة ، فإن النقطة هي قطب من الرتبة الثالثة.

المهمة 5.أظهر أن النقطة لها عمود بسيط.

تعريف.النقطة تسمى خاصة بشكل أساسي نقطة الوظيفة إذا لم يكن هناك في هذه المرحلة حد محدود أو لانهائي للوظيفة (لم يتم تعريف سلوك الوظيفة).

اسمحوا أن تكون نقطة أساسية مفردة للوظيفة. ثم بالنسبة لأي رقم مركب تم تعيينه مسبقًا ، يوجد تسلسل من النقاط المتقاربة ، والتي تميل القيم على طولها إلى: ( نظرية سوتشوكي).

مثال 7أظهر أن الوظيفة في نقطة ما لها تفرُّد أساسي.

المحلول.ضع في اعتبارك سلوك وظيفة معينة بالقرب من النقطة. على طول الجزء الإيجابي من المحور الحقيقي (أي) لدينا و ؛ إذا كان على طول الجزء السلبي من المحور الحقيقي (أي) ، ثم و. لذلك لا يوجد حد ل. بحكم التعريف ، فإن الوظيفة لها تفرد أساسي في نقطة ما.

دعونا نفكر في سلوك الوظيفة عند الصفر من وجهة نظر نظرية Sochocki. يجب أن يكون أي عدد معقد بخلاف الصفر واللانهاية.

من المساواة نجد. بافتراض أننا حصلنا على سلسلة من النقاط ،. بوضوح، . في كل نقطة من هذا التسلسل ، فإن الدالة تساوي ، وبالتالي

المهمة 6.أظهر أن الوظيفة لها تفرد أساسي في نقطة ما.

تعتبر النقطة في اللانهاية دائمًا خاصة بالنسبة للوظيفة. تسمى النقطة بالنقطة المفردة المعزولة لوظيفة ما إذا لم يكن لهذه الوظيفة نقاط مفردة أخرى خارج بعض الدوائر المتمركزة في الأصل.

يمكن أيضًا أن يمتد تصنيف النقاط الفردية المعزولة إلى الحالة.

المثال 8أظهر أن الوظيفة لها قطب مزدوج عند اللانهاية.

المحلول.ضع في اعتبارك الوظيفة ، حيث هي دالة تحليلية في منطقة مجاورة للنقطة ، و. هذا يعني أن للدالة صفرًا مزدوجًا عند اللانهاية ، ولكن بالنسبة للدالة ، فإن النقطة هي قطب مزدوج.

المثال 9أظهر أن الوظيفة لها تفرد أساسي في اللانهاية.

المحلول.تم النظر في مشكلة مماثلة في العدد 7. ضع في اعتبارك سلوك وظيفة في المنطقة المجاورة لنقطة بعيدة بشكل لا نهائي. على طول الجزء الموجب من المحور الحقيقي ، وعلى طول الجزء السلبي من المحور الحقيقي. هذا يعني أنه لا يوجد حد للدالة في نقطة ما ، وبحكم التعريف ، فإن هذه النقطة هي في الأساس مفردة.

يمكن الحكم على طبيعة تفرد وظيفة في نقطة ما الجزء الرئيسي توسع لوران في حي من هذه النقطة.

نظرية 1.للنقطة أن تكون للاستعمال لمرة واحدة نقطة واحدة للوظيفة ، فمن الضروري والكافي أن توسع لوران المقابل لا تحتوي على الجزء الرئيسي.

المهمة 6.باستخدام توسعة تايلور للوظيفة في منطقة مجاورة للنقطة ، أظهر أن لها خاصية تفرد قابلة للإزالة عند الصفر.

نظرية 2.للنقطة أن تكون عمود وظائف ضرورية وكافية بحيث الجزء الرئيسي توسع لوران المقابل تحتوي على عدد محدود من الأعضاء :

يحدد رقم الحد الأعلى السلبي ترتيب القطب.

في هذه الحالة ، يمكن تمثيل الوظيفة كـ

أين هي الوظيفة التحليلية عند النقطة ، هو ترتيب القطب.

المثال 10أظهر أن الوظيفة لها أقطاب بسيطة عند النقاط.

المحلول.دعونا نفكر في نقطة. نستخدم توسعة Laurent لهذه الوظيفة بالقرب من هذه النقطة ، التي تم الحصول عليها في المثال 2:

نظرًا لأن أعلى قوة سالبة (وفقط) في الجزء الرئيسي من هذا التمدد تساوي واحدًا ، فإن النقطة هي قطب بسيط لهذه الوظيفة.

يمكن الحصول على هذه النتيجة بطريقة أخرى. دعونا نمثل في الشكل ونضع - هذه وظيفة تحليلية عند النقطة و. ومن ثم ، بسبب (8) هذه الوظيفة لها قطب بسيط عند النقطة.

طريقة أخرى: ضع في اعتبارك وظيفة بها صفر بسيط عند النقطة. ومن ثم ، في هذه المرحلة يكون لها قطب بسيط.

وبالمثل ، إذا كتبنا الوظيفة في النموذج ، حيث يتم تحليل الوظيفة عند النقطة ، ومن الواضح على الفور أن النقطة هي عمود بسيط للدالة.

المهمة 7.بيّن أن للوظيفة قطبًا من الرتبة الثانية عند النقطة وقطبًا من الرتبة الرابعة عند النقطة.

نظرية 3.للنقطة أن تكون خاصة بشكل أساسي نقطة من الوظيفة ، فمن الضروري والكافي أن الجزء الرئيسي توسعة لوران في منطقة مجاورة للنقطة يحتوي على عدد لا حصر له من الأعضاء .

المثال 11.حدد طبيعة التفرد عند نقطة الوظيفة

المحلول.في التوسيع المعروف لجيب التمام ، نضع بدلاً من:

ومن ثم ، فإن توسع لوران في حي نقطة له الشكل

هنا الجزء الصحيح هو مصطلح واحد. والجزء الرئيسي يحتوي على عدد لا نهائي من المصطلحات ، لذا فإن النقطة هي في الأساس مفردة.

المهمة 8.أظهر أنه عند نقطة ما يكون للوظيفة تفرد أساسي.

ضع في اعتبارك بعض الوظائف واكتب توسعة Laurent الخاصة بها عند النقطة:

دعونا نجري الاستبدال ، بينما تذهب النقطة إلى النقطة. الآن ، في منطقة مجاورة لنقطة عند اللانهاية ، لدينا

يبقى لإدخال تسمية جديدة. نحن نحصل

أين هو الجزء الرئيسي ، وهو الجزء المعتاد من توسعة لوران للوظيفة في المنطقة المجاورة لنقطة بعيدة بشكل لا نهائي. وهكذا ، في توسعة لوران لدالة في منطقة مجاورة لنقطة ، يكون الجزء الرئيسي عبارة عن سلسلة في قوى موجبة ، بينما الجزء الصحيح هو سلسلة في قوى سالبة. مع مراعاة هذا

ومع ذلك ، فإن المعايير المذكورة أعلاه لتحديد طبيعة التفرد تظل صالحة لنقطة بعيدة بشكل لا نهائي.

المثال 12.اكتشف طبيعة تفرد الوظيفة عند النقطة. ، ثم في مرحلة ما قد يتضح أنه غير معزول.

المثال 15الوظيفة في نقطة بعيدة غير محدودة لها تفرد أساسي. بيّن أن نقطة الوظيفة ليست نقطة مفردة معزولة.

المحلول.للدالة عدد لا نهائي من الأعمدة عند أصفار المقام ، أي عند النقاط. منذ ذلك الحين ، فإن النقطة ، في أي حي يوجد به أعمدة ، هي نقطة النهاية للأقطاب.

نقطة فردية

في الرياضيات.

1) النقطة المفردة للمنحنى المعطاة بواسطة المعادلة F ( س ، ص) = 0 ، - النقطة M 0 ( س 0 ، ص 0) ، حيث كلا المشتقتين الجزئيتين للدالة F ( س ، ص) تلاشى:

إذا ، بالإضافة إلى ذلك ، ليست كل المشتقات الجزئية الثانية للدالة F ( س ، ص) عند النقطة M 0 تساوي صفرًا ، ثم O. t. يسمى مزدوج. إذا اختفت جميع المشتقات الثانية ، إلى جانب تلاشي المشتقات الأولى عند النقطة M 0 ، ولكن لم تكن كل المشتقات الثالثة تساوي صفرًا ، فإن O. t. تسمى ثلاثية ، وهكذا. عند دراسة هيكل منحنى بالقرب من O. t مزدوج ، تلعب علامة التعبير دورًا مهمًا

إذا كانت> 0 ، فإن O. t يسمى معزول ؛ على سبيل المثال ، المنحنى ص 2 - س 4 + 4 س 2= 0 الأصل هو معزول O. t. (انظر أرز. واحد ). إذا كانت Δ x 2 + y 2 + a 2) 2 - 4 أ 2 × 2 - أ 4= 0 أصل الإحداثيات هو العقدي O. t (انظر أرز. 2 ). إذا كانت Δ = 0 ، فإن منحنى O. t إما معزول أو يتميز بحقيقة أن الفروع المختلفة للمنحنى لها ظل مشترك في هذه النقطة ، على سبيل المثال: الظل وتشكيل نقطة ، مثل المنحنى ص 2 - × 3= 0 (انظر أرز. 3 ، أ) ؛ ب) من النوع الثاني - توجد فروع مختلفة من المنحنى على نفس الجانب من الظل المشترك ، مثل المنحنى (ص - س 2)2 - × 5= 0 (انظر أرز. 3 ، ب)؛ ج) نقطة الاتصال الذاتي (لمنحنى ص 2 - × 4= 0 الأصل نقطة اتصال ذاتي ؛ (سم. أرز. 3 ، الخامس). جنبا إلى جنب مع O. t. هناك العديد من O. t. مع أسماء خاصة ؛ على سبيل المثال ، النقطة المقاربة هي قمة اللولب مع عدد لا حصر له من المنعطفات (انظر الشكل. أرز. 4 ) ونقطة الانقطاع ونقطة الزاوية وما إلى ذلك.

2) النقطة المفردة للمعادلة التفاضلية هي النقطة التي يختفي عندها كل من البسط والمقام في الجانب الأيمن من المعادلة التفاضلية في وقت واحد (انظر المعادلات التفاضلية)

حيث P و Q وظائف قابلة للتفاضل باستمرار. بافتراض وجود O. t في أصل الإحداثيات واستخدام صيغة Taylor (انظر صيغة Taylor) ، يمكننا تمثيل المعادلة (1) في النموذج

حيث P 1 ( س ، ص) و س 1 ( س ، ص) متناهية الصغر بالنسبة إلى

أي إذا كانت 1 ≠ λ 2 و λ 1 λ 2> 0 أو λ 1 = λ 2 ، إذن O. t. هي عقدة ؛ تدخل جميع المنحنيات المتكاملة التي تمر عبر نقاط منطقة صغيرة بما فيه الكفاية من العقدة. إذا كانت 1 ≠ λ 2 و λ 1 λ 2 i β و α ≠ 0 و β ≠ 0 ، فإن O. t. جميع المنحنيات المتكاملة التي تمر عبر نقاط في حي صغير بدرجة كافية من البؤرة عبارة عن حلزونات مع عدد لا حصر له من المنعطفات في أي حي صغير عشوائيًا من البؤرة. إذا أخيرًا ، λ 1،2 = ± أناβ ، β ≠ 0 ، ثم حرف O. t. لا يتم تحديده من خلال المصطلحات الخطية في توسعات P ( س ، ص) و Q ( س ، ص) ، كما كان الحال في جميع الحالات المذكورة أعلاه ؛ هنا يمكن أن يكون O. ر بؤرة أو مركزًا ، أو يمكن أن يكون له طابع أكثر تعقيدًا. في حي المركز ، يتم إغلاق جميع المنحنيات المتكاملة وتحتوي على المركز بداخلها. لذلك ، على سبيل المثال ، النقطة (0 ، 0) هي عقدة المعادلات في" = 2ش / س(λ 1 = 1 ، λ 2 = 2 ؛ انظر أرز. 5 ، أ) و ذ" = ش / س(λ 1 = λ 2 = 1 ؛ انظر أرز. 5 ، ب) ، سرج للمعادلة ص "= -ص / س(λ 1 = -1 ، λ 2 = 1 ؛ سم. أرز. 6 ) ، بؤرة المعادلة ص "=(س + ص) / (س - ص) (λ 1 = 1 - أنا، λ 2 = 1 + أنا؛ سم. أرز. 7 ) ومركز المعادلة ص "= -x / ص(λ 1 = -أنا، λ 2 = أنا؛ سم. أرز. ثمانية ).

إذا كانت x و y) و Q ( س ، ص) تحليليًا ، يمكن تقسيم جوار O. t ذات الترتيب الأعلى إلى مناطق: D 1 - مملوءة بمنحنيات متكاملة ، يتم تضمين طرفيها في O. t. (مناطق إهليلجية) ، D 2 - مملوءة مع منحنيات متكاملة ، يتم تضمين أحد طرفيها في O. t. (مناطق مكافئ) ، و D 3 - مناطق يحدها منحنيان متكاملان مدرجان في O. t. ، يوجد بينهما منحنيات متكاملة من نوع القطع الزائدة (المناطق الزائدية) (انظر. أرز. 9 ). إذا لم تكن هناك منحنيات متكاملة تدخل في نقطة O ، فإن النقطة O تسمى نقطة من النوع المستقر. يتكون حي O. t المستقر من منحنيات متكاملة مغلقة تحتوي على O. t داخل نفسها ، والتي توجد بينها اللوالب (انظر الشكل. أرز. 10 ).

دراسة المعادلات التفاضلية O. t ، أي في جوهرها ، دراسة سلوك العائلات ذات المنحنيات المتكاملة في حي O.t M. Lyapunov a ، A. Poincaré وغيرها).

3) النقطة المفردة لوظيفة تحليلية أحادية القيمة هي النقطة التي يتم فيها انتهاك تحليل الوظيفة (انظر الوظائف التحليلية). إذا كان هناك حي O. t. أ، خالية من O. t. ، ثم النقطة أيسمى معزولة O. ر أهو O. t معزول ويوجد منتهي يسمى O. t قابل للإزالة. F(أ)= ب، من الممكن تحقيقه أستصبح نقطة عادية للوظيفة المصححة. على سبيل المثال ، نقطة ض= 0 هو O.T. قابل للإزالة للوظيفة f 1 ( ض) = F(ض)، إذا ض≠ 0 و F 1 (0) ، = 1 نقطة ض= 0 نقطة عادية [ F 1 (ض) تحليلي في هذه النقطة ض= 0]. إذا أ- معزولة O. t وتسمى a قطب أو نقطة مفردة بشكل غير أساسي للوظيفة F(ض) ، إذا كانت سلسلة Laurent) تعمل F(ض) في حي O. t معزول لا يحتوي على قوى سالبة ض - أ، إذا أ- قابل للإزالة O. t. ، يحتوي على عدد محدود من القوى السالبة ض - أ، إذا أ- القطب (في هذه الحالة ، ترتيب القطب صتُعرَّف بأنها أعلى قوة لـ - نقطة مفردة أساسًا. على سبيل المثال ، للوظيفة

ص = 2 ، 3 ، ...)

نقطة ض= 0 هو عمود الترتيب ص، للوظيفة

نقطة ض= 0 هي نقطة مفردة أساسية.

على حدود دائرة التقارب لسلسلة قوى يجب أن يكون هناك O.m واحد على الأقل للدالة الممثلة داخل هذه الدائرة بواسطة سلسلة الأس المعطاة. جميع النقاط الحدودية لمجال وجود دالة تحليلية أحادية القيمة (حدود طبيعية) هي نقاط حدودية لهذه الوظيفة. وبالتالي ، فإن جميع نقاط دائرة الوحدة | ض| = 1 خاص بالدالة

بالنسبة لوظيفة التحليل متعددة القيم ، فإن مفهوم "O. T. " أكثر صعوبة. بالإضافة إلى O. t. ، في أوراق منفصلة لسطح Riemann لوظيفة ما (أي ، O. t للعناصر التحليلية أحادية القيمة) ، فإن أي نقطة فرع هي أيضًا O. t للدالة. يتم تصنيف نقاط التفرع المعزولة لسطح ريمان (أي نقاط التفرع مثل عدم وجود وظائف أخرى في أي ورقة في بعض أحيائهم) على النحو التالي. إذا كانت a نقطة فرع معزولة ذات ترتيب محدود وكان هناك نقطة متناهية a ، فإنها تسمى القطب الحرج. إذا أهي نقطة فرع معزولة بترتيب لانهائي ويسمى a متسامي O. t. تسمى جميع نقاط التفرع الأخرى المعزولة بالنقاط الفردية الحرجة بشكل أساسي. أمثلة: dot ض= 0 نقطة حرجة عادية للوظيفة f ( ض) = تسجيل الدخول ضونقطة مفردة أساسية حاسمة للوظيفة F (ض) = سجل الخطيئة ض.

أي O. t. ، باستثناء واحد قابل للإزالة ، هو عقبة أمام الاستمرار التحليلي ، أي الاستمرار التحليلي على طول منحنى يمر عبر O. t غير قابل للإزالة.

الموسوعة السوفيتية العظمى. - م: الموسوعة السوفيتية. 1969-1978 .

تعرف على "Special Point" في القواميس الأخرى:

النقاط هنا. انظر أيضًا النقطة الفردية (المعادلات التفاضلية). الميزة أو التفرد في الرياضيات هي النقطة التي لا يتم فيها تعريف كائن رياضي (عادة وظيفة) أو يكون له سلوك غير منتظم (على سبيل المثال ، النقطة التي عندها ... ... ويكيبيديا

الوظيفة التحليلية هي النقطة التي يتم فيها انتهاك شروط التحليل. إذا تم تحديد دالة تحليلية f (z) في بعض المناطق المجاورة للنقطة z0 في كل مكان ... موسوعة فيزيائية

الوظيفة التحليلية هي النقطة التي يتم عندها انتهاك تحليل الوظيفة ... قاموس موسوعي كبير

نقطة فردية- - [Ya.N. Luginsky، MS Fezi Zhilinskaya، YuS Kabirov. القاموس الإنجليزي الروسي للهندسة الكهربائية وصناعة الطاقة ، موسكو ، 1999] موضوعات الهندسة الكهربائية والمفاهيم الأساسية EN المفرد نقطة ... دليل المترجم الفني

1) الوقت الإضافي للدالة التحليلية f (z) هو عقبة أمام الاستمرار التحليلي لعنصر من عناصر الوظيفة f (z) لمتغير معقد z على طول مسار ما على مستوى هذا المتغير. دع وظيفة التحليل f (z) تحدد من قبل البعض ... ... موسوعة رياضية

الوظيفة التحليلية ، النقطة التي يتم عندها انتهاك تحليل الوظيفة. * * * نقطة واحدة هي نقطة مفردة لوظيفة تحليلية ، وهي النقطة التي يتم فيها انتهاك تحليل الوظيفة ... قاموس موسوعي

نقطة فردية- ypatingasis taškas statusas T sritis automatika atitikmenys: engl. نقطة المفرد vok. المفرد بونت م روس. نقطة مفردة ، fpranc. نقطة الجسيم ، م ؛ نقطة المفرد ، م ... Automatikos terminų žodynas