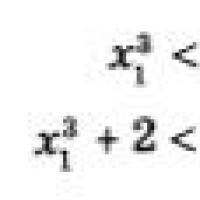Moment of inertia of the ring section. Moments of inertia of simple sections. Axial moments of inertia of a right triangle
DEFINITION
Axial (or equatorial) moment of inertia section relative to the axis is called a quantity that is defined as:
Expression (1) means that to calculate the axial moment of inertia, the sum of the products of infinitesimal areas () multiplied by the squares of the distances from them to the axis of rotation is taken over the entire area S:
The sum of the axial moments of inertia of the section relative to mutually perpendicular axes (for example, relative to the X and Y axes in the Cartesian coordinate system) gives the polar moment of inertia () relative to the intersection point of these axes:
DEFINITION
Polar moment inertia is the moment of inertia section relative to a certain point.
Axial moments of inertia are always greater than zero, since in their definitions (1) under the integral sign there is the value of the area of the elementary area (), always positive, and the square of the distance from this area to the axis.
If we are dealing with a section of complex shape, then often in calculations we use the fact that the axial moment of inertia of a complex section relative to the axis is equal to the sum of the axial moments of inertia of the parts of this section relative to the same axis. However, it should be remembered that it is impossible to sum up the moments of inertia that are found relative to different axes and points.
The axial moment of inertia relative to the axis passing through the center of gravity of the section has the smallest value of all moments relative to the axes parallel to it. The moment of inertia about any axis () provided that it is parallel to the axis passing through the center of gravity is equal to:
where is the moment of inertia of the section relative to the axis passing through the center of gravity of the section; - cross-sectional area; - distance between axles.
Examples of problem solving
EXAMPLE 1
| Exercise | What is the axial moment of inertia of an isosceles triangular cross-section relative to the Z axis passing through the center of gravity () of the triangle, parallel to its base? The height of the triangle is . |
| Solution | Let us select a rectangular elementary area on a triangular section (see Fig. 1). It is located at a distance from the axis of rotation, the length of one side is , the other side is . From Fig. 1 it follows that:
The area of the selected rectangle, taking into account (1.1), is equal to: To find the axial moment of inertia, we use its definition in the form: |
| Answer |
EXAMPLE 2
| Exercise | Find the axial moments of inertia relative to the perpendicular axes X and Y (Fig. 2) of a section in the form of a circle whose diameter is equal to d. |
| Solution | To solve the problem, it is more convenient to start by finding the polar moment relative to the center of the section (). Let us divide the entire section into infinitely thin rings of thickness , the radius of which will be denoted by . Then we find the elementary area as: |
For simple sections, static moments and moments of inertia are found using formulas (2.1)-(2.4) using integration. Consider, for example, calculating the axial moment of inertia J x for an arbitrary section shown in Fig. 2.9. Considering that in a rectangular coordinate system the area element dF=dxdy, we get
wherex^(y) and x in (y) - coordinates of contour points at some fixed value u.
Performing integration over x, we find
Magnitude b(y) represents the section width at level at(see Fig. 2.9), and the product b(y)dy = dF - area of the shaded elementary strip parallel to the axis Oh. Taking this into account, the formula for / is transformed to the form
A similar expression can be obtained for the moment of inertia Jy.
Rectangle. Let us find the moments of inertia about the main central axes, which, in accordance with property 2 (§ 2.5), coincide with the symmetry axes of the rectangle (Fig. 2.10). Since the width of the section is constant, then using formula (2.14) we obtain
Moment of inertia about the axis Oh x x x we determine by the first of formulas (2.6): 
Moments of inertia / and J are found similarly. Let us write down the formulas for the axial moments of inertia of a rectangle:
Arbitrary triangle. First, let's find the moment of inertia about the axis 0 ( x v passing through the base of the triangle (Fig. 2.11). Section width b(y()) at the level y ( is found from the similarity of triangles:
Substituting this quantity into formula (2.14) and performing integration, we obtain
Moments about the axes Oh And 0 2 x 2, parallel to the base and passing through the center of gravity and through the vertex of the triangle, respectively, we find using formulas (2.6):
In these formulas b ( =h/ 3 and b 2 = -2h/3 - respectively, the ordinates of the center of gravity of the triangle ABOUT in the coordinate system O x x 1 y 1 And 0 2 x 2 y t
1 ° 2 r Г* аУ 1
TL P *2
g >4 ™_ °2 1
D__V_!_*_ / ^ *3
V XV* ;-7^Лт^
U_ У-_XI - UZ__у
ABOUT,| b *, 0 b/ b 2 %*1
Rice. 2.11 Rice. 2.12
Let us write the formulas for the axial moments of inertia of the triangle relative to the axes parallel to the base:
Right and isosceles triangles. For a right triangle (Fig. 2.12), we determine the centrifugal moment of inertia J relative to the central axes Oh And OU, parallel to the legs. This can be done using formula (2.3). However, the solution to the problem can be simplified by applying the following technique. Using the median 0 { 0 3 divide the given triangle into two isosceles triangles 0 ( 0 3 A And Ofi 3 B. Axes 0 3 x 3 and 0 3 y 3 are the axes of symmetry for these triangles and, based on property 2 (§ 2.5), will be the main axes of each of them separately, and therefore of the entire triangle O x AB. Therefore, the centrifugal moment of inertia J=0. Centrifuge-
moment of the triangle about the axes Oh And OU we find using the last of formulas (2.6):
Let us write down the formulas for the moments of inertia of a right triangle: 
Moment of inertia of an isosceles triangle about the axis of symmetry OU(Fig. 2.13) we define, using the fourth of formulas (2.17), as the doubled moment of inertia of a right triangle with a base h and height b/ 2:
Thus, the moments of inertia of an isosceles triangle about the main central axes Oh And OU determined by formulas
Circle. First, it is convenient to calculate the polar moment of inertia of a circle using formula (2.4), using the polar coordinate system (Fig. 2.14).
Considering that dF-rdrdQ, we'll find
Since the polar moment according to (2.4) is equal to the sum of two axial moments, we obtain
Ring. The moments of inertia of the ring (Fig. 2.15) are found as the difference between the moments of inertia of two circles with radii I 2 And R ( :
Semicircle(rice. 2.16). Let us select an area element in the plane of the semicircle dF with polar coordinates G, 0 and Cartesian coordinates x v y v for which, in accordance with Fig. 2.16 we have:
Using formulas (2.1) and (2.5), we find, respectively, the static moment of the semicircle relative to the axis 0 ( x ( and ordinate at 0 center of gravity ABOUT in the coordinate system 0 ( x ( Uy
Relative to axes 0, x, and 0 ( y v which are the main axes for the semicircle, the axial moments of inertia are equal to half the moments of inertia of the circle:
The moment of inertia about the main central axis is determined using the first formula (2.6):
Ellipse. To calculate the axial moment of inertia of an ellipse with semi-axes A And b relative to the axis Oh(Fig. 2.17) we proceed as follows. Let us draw a circle around the ellipse and select two elementary stripes of width dx and height 2ук for circle and 2 uh for an ellipse. The moments of inertia of these two strips can be determined by the first of formulas (2.15) for a rectangle:
Integrating these expressions ranging from -A before A, we get 
Rice. 2.16
Rice. 2.17
From the equations of a circle and an ellipse we have
With this in mind
A similar expression can be obtained for the moment of inertia about the axis OU. As a result, for the ellipse we will have the following formulas for axial moments:
Rolled rods. The geometric characteristics of the sections of rolled rods (I-beams, channels, angles) are given in the tables of rolled steel assortments (see appendix).
Bodies m per square of distance d between axes:
J = J c + m d 2 , (\displaystyle J=J_(c)+md^(2),)Where m- total body weight.
For example, the moment of inertia of a rod relative to an axis passing through its end is equal to:
J = J c + m d 2 = 1 12 m l 2 + m (l 2) 2 = 1 3 m l 2. (\displaystyle J=J_(c)+md^(2)=(\frac (1)(12))ml^(2)+m\left((\frac (l)(2))\right)^ (2)=(\frac (1)(3))ml^(2).)Axial moments of inertia of some bodies
| Body | Description | Axis position a | Moment of inertia J a |
|---|---|---|---|
| Material point mass m | On distance r from a point, stationary | ||
| Hollow thin-walled cylinder or radius ring r and masses m | Cylinder axis | m r 2 (\displaystyle mr^(2)) | |
| Solid cylinder or radius disk r and masses m | Cylinder axis | 1 2 m r 2 (\displaystyle (\frac (1)(2))mr^(2)) | |
| Hollow thick-walled mass cylinder m with outer radius r 2 and inner radius r 1 | Cylinder axis | m r 2 2 + r 1 2 2 (\displaystyle m(\frac (r_(2)^(2)+r_(1)^(2))(2))) | |
| Solid cylinder length l, radius r and masses m | 1 4 m ⋅ r 2 + 1 12 m ⋅ l 2 (\displaystyle (1 \over 4)m\cdot r^(2)+(1 \over 12)m\cdot l^(2)) | ||
| Hollow thin-walled cylinder (ring) length l, radius r and masses m | The axis is perpendicular to the cylinder and passes through its center of mass | 1 2 m ⋅ r 2 + 1 12 m ⋅ l 2 (\displaystyle (1 \over 2)m\cdot r^(2)+(1 \over 12)m\cdot l^(2)) | |
| Straight Thin Length Rod l and masses m | The axis is perpendicular to the rod and passes through its center of mass | 1 12 m l 2 (\displaystyle (\frac (1)(12))ml^(2)) | |
| Straight Thin Length Rod l and masses m | The axis is perpendicular to the rod and passes through its end | 1 3 m l 2 (\displaystyle (\frac (1)(3))ml^(2)) | |
| Thin-walled radius sphere r and masses m | The axis passes through the center of the sphere | 2 3 m r 2 (\displaystyle (\frac (2)(3))mr^(2)) | |
| Radius ball r and masses m | The axis passes through the center of the ball | 2 5 m r 2 (\displaystyle (\frac (2)(5))mr^(2)) | |
| Radius cone r and masses m | Cone axis | 3 10 m r 2 (\displaystyle (\frac (3)(10))mr^(2)) | |
| Isosceles triangle with altitude h, basis a and mass m | The axis is perpendicular to the plane of the triangle and passes through the vertex | 1 24 m (a 2 + 12 h 2) (\displaystyle (\frac (1)(24))m(a^(2)+12h^(2))) | |
| Regular triangle with side a and mass m | The axis is perpendicular to the plane of the triangle and passes through the center of mass | 1 12 m a 2 (\displaystyle (\frac (1)(12))ma^(2)) | |
| Square with side a and mass m | The axis is perpendicular to the plane of the square and passes through the center of mass | 1 6 m a 2 (\displaystyle (\frac (1)(6))ma^(2)) | |
| Rectangle with sides a And b and mass m | The axis is perpendicular to the plane of the rectangle and passes through the center of mass | 1 12 m (a 2 + b 2) (\displaystyle (\frac (1)(12))m(a^(2)+b^(2))) | |
| Regular n-gon of radius r and mass m | The axis is perpendicular to the plane and passes through the center of mass | m r 2 6 [ 1 + 2 cos (π / n) 2 ] (\displaystyle (\frac (mr^(2))(6))\left) | |
| Torus (hollow) with guide circle radius R, radius of the generating circle r and mass m | The axis is perpendicular to the plane of the torus guide circle and passes through the center of mass | I = m (3 4 r 2 + R 2) (\displaystyle I=m\left((\frac (3)(4))\,r^(2)+R^(2)\right)) |
Deriving formulas
Thin-walled cylinder (ring, hoop)
Derivation of the formula
The moment of inertia of a body is equal to the sum of the moments of inertia of its constituent parts. Let us divide a thin-walled cylinder into elements with mass dm and moments of inertia dJ i. Then
J = ∑ d J i = ∑ R i 2 d m . (1) . (\displaystyle J=\sum dJ_(i)=\sum R_(i)^(2)dm.\qquad (1).)Since all elements of a thin-walled cylinder are at the same distance from the axis of rotation, formula (1) is transformed into the form
J = ∑ R 2 d m = R 2 ∑ d m = m R 2 . (\displaystyle J=\sum R^(2)dm=R^(2)\sum dm=mR^(2).)Thick-walled cylinder (ring, hoop)
Derivation of the formula
Let there be a homogeneous ring with an outer radius R, inner radius R 1, thick h and density ρ. Let's break it into thin rings thick dr. Mass and moment of inertia of a thin radius ring r will be
d m = ρ d V = ρ ⋅ 2 π r h d r ; d J = r 2 d m = 2 π ρ h r 3 d r . (\displaystyle dm=\rho dV=\rho \cdot 2\pi rhdr;\qquad dJ=r^(2)dm=2\pi \rho hr^(3)dr.)Let us find the moment of inertia of the thick ring as an integral
J = ∫ R 1 R d J = 2 π ρ h ∫ R 1 R r 3 d r = (\displaystyle J=\int _(R_(1))^(R)dJ=2\pi \rho h\int _ (R_(1))^(R)r^(3)dr=) = 2 π ρ h r 4 4 | R 1 R = 1 2 π ρ h (R 4 − R 1 4) = 1 2 π ρ h (R 2 − R 1 2) (R 2 + R 1 2) . (\displaystyle =2\pi \rho h\left.(\frac (r^(4))(4))\right|_(R_(1))^(R)=(\frac (1)(2 ))\pi \rho h\left(R^(4)-R_(1)^(4)\right)=(\frac (1)(2))\pi \rho h\left(R^(2 )-R_(1)^(2)\right)\left(R^(2)+R_(1)^(2)\right).)Since the volume and mass of the ring are equal
V = π (R 2 − R 1 2) h ; m = ρ V = π ρ (R 2 − R 1 2) h , (\displaystyle V=\pi \left(R^(2)-R_(1)^(2)\right)h;\qquad m= \rho V=\pi \rho \left(R^(2)-R_(1)^(2)\right)h,)we obtain the final formula for the moment of inertia of the ring
J = 1 2 m (R 2 + R 1 2) . (\displaystyle J=(\frac (1)(2))m\left(R^(2)+R_(1)^(2)\right).)Homogeneous disc (solid cylinder)
Derivation of the formula
Considering a cylinder (disk) as a ring with zero internal radius ( R 1 = 0 ), we obtain the formula for the moment of inertia of the cylinder (disk):
J = 1 2 m R 2 . (\displaystyle J=(\frac (1)(2))mR^(2).)Solid cone
Derivation of the formula
Let's break the cone into thin disks with a thickness dh, perpendicular to the axis of the cone. The radius of such a disk is equal to
r = R h H , (\displaystyle r=(\frac (Rh)(H)),)Where R– radius of the cone base, H– height of the cone, h– distance from the top of the cone to the disk. The mass and moment of inertia of such a disk will be
d J = 1 2 r 2 d m = 1 2 π ρ r 4 d h = 1 2 π ρ (R h H) 4 d h ; (\displaystyle dJ=(\frac (1)(2))r^(2)dm=(\frac (1)(2))\pi \rho r^(4)dh=(\frac (1)( 2))\pi \rho \left((\frac (Rh)(H))\right)^(4)dh;)Integrating, we get
J = ∫ 0 H d J = 1 2 π ρ (R H) 4 ∫ 0 H h 4 d h = 1 2 π ρ (R H) 4 h 5 5 | 0 H == 1 10 π ρ R 4 H = (ρ ⋅ 1 3 π R 2 H) 3 10 R 2 = 3 10 m R 2 . (\displaystyle (\begin(aligned)J=\int _(0)^(H)dJ=(\frac (1)(2))\pi \rho \left((\frac (R)(H)) \right)^(4)\int _(0)^(H)h^(4)dh=(\frac (1)(2))\pi \rho \left((\frac (R)(H) )\right)^(4)\left.(\frac (h^(5))(5))\right|_(0)^(H)==(\frac (1)(10))\pi \rho R^(4)H=\left(\rho \cdot (\frac (1)(3))\pi R^(2)H\right)(\frac (3)(10))R^( 2)=(\frac (3)(10))mR^(2).\end(aligned)))Solid homogeneous ball
Derivation of the formula
Let's break the ball into thin disks of thickness dh, perpendicular to the axis of rotation. The radius of such a disk located at a height h from the center of the sphere, we find it using the formula
r = R 2 − h 2 . (\displaystyle r=(\sqrt (R^(2)-h^(2))).)The mass and moment of inertia of such a disk will be
d m = ρ d V = ρ ⋅ π r 2 d h ; (\displaystyle dm=\rho dV=\rho \cdot \pi r^(2)dh;) d J = 1 2 r 2 d m = 1 2 π ρ r 4 d h = 1 2 π ρ (R 2 − h 2) 2 d h = 1 2 π ρ (R 4 − 2 R 2 h 2 + h 4) d h. (\displaystyle dJ=(\frac (1)(2))r^(2)dm=(\frac (1)(2))\pi \rho r^(4)dh=(\frac (1)( 2))\pi \rho \left(R^(2)-h^(2)\right)^(2)dh=(\frac (1)(2))\pi \rho \left(R^( 4)-2R^(2)h^(2)+h^(4)\right)dh.)We find the moment of inertia of the ball by integration:
J = ∫ − R R d J = 2 ∫ 0 R d J = π ρ ∫ 0 R (R 4 − 2 R 2 h 2 + h 4) d h = = π ρ (R 4 h − 2 3 R 2 h 3 + 1 5 h 5) | 0 R = π ρ (R 5 − 2 3 R 5 + 1 5 R 5) = 8 15 π ρ R 5 = = (4 3 π R 3 ρ) ⋅ 2 5 R 2 = 2 5 m R 2 . (\displaystyle (\begin(aligned)J&=\int _(-R)^(R)dJ=2\int _(0)^(R)dJ=\pi \rho \int _(0)^(R )\left(R^(4)-2R^(2)h^(2)+h^(4)\right)dh=\\&=\pi \rho \left.\left(R^(4) h-(\frac (2)(3))R^(2)h^(3)+(\frac (1)(5))h^(5)\right)\right|_(0)^( R)=\pi \rho \left(R^(5)-(\frac (2)(3))R^(5)+(\frac (1)(5))R^(5)\right) =(\frac (8)(15))\pi \rho R^(5)=\\&=\left((\frac (4)(3))\pi R^(3)\rho \right) \cdot (\frac (2)(5))R^(2)=(\frac (2)(5))mR^(2).\end(aligned)))Thin-walled sphere
Derivation of the formula
To derive this, we use the formula for the moment of inertia of a homogeneous ball of radius R :
J 0 = 2 5 M R 2 = 8 15 π ρ R 5 . (\displaystyle J_(0)=(\frac (2)(5))MR^(2)=(\frac (8)(15))\pi \rho R^(5).)Let us calculate how much the moment of inertia of the ball will change if, at a constant density ρ, its radius increases by an infinitesimal amount dR .
J = d J 0 d R d R = d d R (8 15 π ρ R 5) d R = = 8 3 π ρ R 4 d R = (ρ ⋅ 4 π R 2 d R) 2 3 R 2 = 2 3 m R 2 . (\displaystyle (\begin(aligned)J&=(\frac (dJ_(0))(dR))dR=(\frac (d)(dR))\left((\frac (8)(15))\ pi \rho R^(5)\right)dR=\\&=(\frac (8)(3))\pi \rho R^(4)dR=\left(\rho \cdot 4\pi R^ (2)dR\right)(\frac (2)(3))R^(2)=(\frac (2)(3))mR^(2).\end(aligned)))Thin rod (axis passes through the center)
Derivation of the formula
Let's break the rod into small fragments of length dr. The mass and moment of inertia of such a fragment are equal to
d m = m d r l ; d J = r 2 d m = m r 2 d r l . (\displaystyle dm=(\frac (mdr)(l));\qquad dJ=r^(2)dm=(\frac (mr^(2)dr)(l)).)Integrating, we get
J = ∫ − l / 2 l / 2 d J = 2 ∫ 0 l / 2 d J = 2 m l ∫ 0 l / 2 r 2 d r = 2 m l r 3 3 | 0 l / 2 = 2 m l l 3 24 = 1 12 m l 2 . (\displaystyle J=\int _(-l/2)^(l/2)dJ=2\int _(0)^(l/2)dJ=(\frac (2m)(l))\int _ (0)^(l/2)r^(2)dr=(\frac (2m)(l))\left.(\frac (r^(3))(3))\right|_(0) ^(l/2)=(\frac (2m)(l))(\frac (l^(3))(24))=(\frac (1)(12))ml^(2.)Thin rod (axis passes through the end)
Derivation of the formula
When the axis of rotation moves from the middle of the rod to its end, the center of gravity of the rod moves relative to the axis by a distance l ⁄ 2. According to Steiner's theorem, the new moment of inertia will be equal to
J = J 0 + m r 2 = J 0 + m (l 2) 2 = 1 12 m l 2 + 1 4 m l 2 = 1 3 m l 2 . (\displaystyle J=J_(0)+mr^(2)=J_(0)+m\left((\frac (l)(2))\right)^(2)=(\frac (1)( 12))ml^(2)+(\frac (1)(4))ml^(2)=(\frac (1)(3))ml^(2.)Dimensionless moments of inertia of planets and satellites
Their dimensionless moments of inertia are of great importance for studies of the internal structure of planets and their satellites. Dimensionless moment of inertia of a body of radius r and masses m is equal to the ratio of its moment of inertia relative to the axis of rotation to the moment of inertia of a material point of the same mass relative to a fixed axis of rotation located at a distance r(equal to mr 2). This value reflects the distribution of mass over depth. One of the methods for measuring it near planets and satellites is to determine the Doppler shift of the radio signal transmitted by an AMS flying near a given planet or satellite. For a thin-walled sphere, the dimensionless moment of inertia is 2/3 (~0.67), for a homogeneous ball it is 0.4, and in general, the smaller the greater the mass of the body is concentrated at its center. For example, the Moon has a dimensionless moment of inertia close to 0.4 (equal to 0.391), so it is assumed that it is relatively homogeneous, its density changes little with depth. The dimensionless moment of inertia of the Earth is less than that of a homogeneous ball (equal to 0.335), which is an argument in favor of the existence of a dense core.
Centrifugal moment of inertia
The centrifugal moments of inertia of a body relative to the axes of a rectangular Cartesian coordinate system are the following quantities:
J x y = ∫ (m) x y d m = ∫ (V) x y ρ d V , (\displaystyle J_(xy)=\int \limits _((m))xydm=\int \limits _((V))xy\ rho dV,) J x z = ∫ (m) x z d m = ∫ (V) x z ρ d V , (\displaystyle J_(xz)=\int \limits _((m))xzdm=\int \limits _((V))xz\ rho dV,) J y z = ∫ (m) y z d m = ∫ (V) y z ρ d V , (\displaystyle J_(yz)=\int \limits _((m))yzdm=\int \limits _((V))yz\ rho dV,)Where x , y And z- coordinates of a small body element with volume dV, density ρ and mass dm .
The OX axis is called main axis of inertia of the body, if the centrifugal moments of inertia J xy And J xz are simultaneously equal to zero. Three main axes of inertia can be drawn through each point of the body. These axes are mutually perpendicular to each other. Moments of inertia of the body relative to the three main axes of inertia drawn at an arbitrary point O bodies are called main moments of inertia of this body.
The main axes of inertia passing through the center of mass of the body are called main central axes of inertia of the body, and the moments of inertia about these axes are its main central moments of inertia. The axis of symmetry of a homogeneous body is always one of its main central axes of inertia.
Geometric moments of inertia
Geometric moment of inertia of volume
J V a = ∫ (V) r 2 d V , (\displaystyle J_(Va)=\int \limits _((V))r^(2)dV,)where, as before r- distance from element dV to the axis a .
Geometric moment of inertia of area relative to the axis - a geometric characteristic of the body, expressed by the formula:
J S a = ∫ (S) r 2 d S , (\displaystyle J_(Sa)=\int \limits _((S))r^(2)dS,)where integration is performed over the surface S, A dS- element of this surface.
Dimension JSa- length to the fourth power ( d i m J S a = L 4 (\displaystyle \mathrm (dim) J_(Sa)=\mathrm (L^(4)) )), respectively, the SI unit of measurement is 4. In construction calculations, literature and rolled metal assortments, it is often indicated in cm 4.
The moment of resistance of the section is expressed through the geometric moment of inertia of the area:
W = J S a r m a x . (\displaystyle W=(\frac (J_(Sa))(r_(max))).)Here rmax- maximum distance from the surface to the axis.
| Geometric moments of inertia of the area of some figures | |
|---|---|
| Rectangle height h (\displaystyle h) and width b (\displaystyle b): | J y = b h 3 12 (\displaystyle J_(y)=(\frac (bh^(3))(12)))
J z = h b 3 12 (\displaystyle J_(z)=(\frac (hb^(3))(12))) |
| Rectangular box section with height and width along external contours H (\displaystyle H) And B (\displaystyle B), and for internal h (\displaystyle h) And b (\displaystyle b) respectively | J z = B H 3 12 − b h 3 12 = 1 12 (B H 3 − b h 3) (\displaystyle J_(z)=(\frac (BH^(3))(12))-(\frac (bh^( 3))(12))=(\frac (1)(12))(BH^(3)-bh^(3)))
J y = H B 3 12 − h b 3 12 = 1 12 (H B 3 − h b 3) (\displaystyle J_(y)=(\frac (HB^(3))(12))-(\frac (hb^( 3))(12))=(\frac (1)(12))(HB^(3)-hb^(3))) |
| Circle diameter d (\displaystyle d) | J y = J z = π d 4 64 (\displaystyle J_(y)=J_(z)=(\frac (\pi d^(4))(64))) |
Moment of inertia relative to the plane
The moment of inertia of a rigid body relative to a certain plane is a scalar quantity equal to the sum of the products of the mass of each point of the body by the square of the distance from this point to the plane in question.
If through an arbitrary point O (\displaystyle O) draw coordinate axes x , y , z (\displaystyle x,y,z), then the moments of inertia relative to the coordinate planes x O y (\displaystyle xOy), y O z (\displaystyle yOz) And z O x (\displaystyle zOx) will be expressed by the formulas:
J x O y = ∑ i = 1 n m i z i 2 , (\displaystyle J_(xOy)=\sum _(i=1)^(n)m_(i)z_(i)^(2)\ ,) J y O z = ∑ i = 1 n m i x i 2 , (\displaystyle J_(yOz)=\sum _(i=1)^(n)m_(i)x_(i)^(2)\ ,) J z O x = ∑ i = 1 n m i y i 2 . (\displaystyle J_(zOx)=\sum _(i=1)^(n)m_(i)y_(i)^(2)\ .)In the case of a solid body, summation is replaced by integration.
Central moment of inertia
Central moment of inertia (moment of inertia about point O, moment of inertia about the pole, polar moment of inertia) J O (\displaystyle J_(O)) is the quantity determined by the expression:
J a = ∫ (m) r 2 d m = ∫ (V) ρ r 2 d V , (\displaystyle J_(a)=\int \limits _((m))r^(2)dm=\int \limits _((V))\rho r^(2)dV,)The central moment of inertia can be expressed in terms of the principal axial moments of inertia, as well as in terms of the moments of inertia about the planes:
J O = 1 2 (J x + J y + J z) , (\displaystyle J_(O)=(\frac (1)(2))\left(J_(x)+J_(y)+J_(z) \right),) J O = J x O y + J y O z + J x O z . (\displaystyle J_(O)=J_(xOy)+J_(yOz)+J_(xOz).)Tensor of inertia and ellipsoid of inertia
The moment of inertia of a body relative to an arbitrary axis passing through the center of mass and having a direction specified by the unit vector s → = ‖ s x , s y , s z ‖ T , | s → | = 1 (\displaystyle (\vec (s))=\left\Vert s_(x),s_(y),s_(z)\right\Vert ^(T),\left\vert (\vec (s) )\right\vert =1), can be represented in the form of a quadratic (bilinear) form:
I s = s → T ⋅ J ^ ⋅ s → , (\displaystyle I_(s)=(\vec (s))^(T)\cdot (\hat (J))\cdot (\vec (s)) ,\qquad) (1)where is the inertia tensor. The inertia tensor matrix is symmetrical and has dimensions 3 × 3 (\displaystyle 3\times 3) and consists of components of centrifugal moments:
By choosing the appropriate coordinate system, the inertia tensor matrix can be reduced to diagonal form. To do this, you need to solve the eigenvalue problem for the tensor matrix J ^ (\displaystyle (\hat (J))):
Where Q ^ (\displaystyle (\hat (Q)))- orthogonal matrix of transition to the own basis of the inertia tensor. In the proper basis, the coordinate axes are directed along the main axes of the inertia tensor, and also coincide with the main semi-axes of the inertia tensor ellipsoid. Quantities J X , J Y , J Z (\displaystyle J_(X),J_(Y),J_(Z))- main moments of inertia. Expression (1) in its own coordinate system has the form:
from which we obtain the equation of the ellipsoid in its own coordinates. Dividing both sides of the equation by I s (\displaystyle I_(s))
and making replacements:
ξ = s x I s , η = s y I s , ζ = s z I s , (\displaystyle \xi =(s_(x) \over (\sqrt (I_(s)))),\eta =(s_(y ) \over (\sqrt (I_(s)))),\zeta =(s_(z) \over (\sqrt (I_(s)))),)we obtain the canonical form of the ellipsoid equation in coordinates ξ η ζ (\displaystyle \xi \eta \zeta ):
ξ 2 ⋅ J X + η 2 ⋅ J Y + ζ 2 ⋅ J Z = 1. (\displaystyle \xi ^(2)\cdot J_(X)+\eta ^(2)\cdot J_(Y)+\zeta ^( 2)\cdot J_(Z)=1.)The distance from the center of the ellipsoid to a certain point is related to the value of the moment of inertia of the body along a straight line passing through the center of the ellipsoid and this point.
The axial moment of inertia is the sum, taken over the entire section, of the products of elementary areas and the square of the distance to a certain axis lying in the plane of the section under consideration. The magnitude of the axial moment of inertia characterizes the beam's ability to resist bending deformation.
J – Axial moment of inertia
J x = 
J y = 
Axial moment of resistance is called the ratio of the axial moment of inertia to the distance to the fibers of the section furthest from the neutral axis.
W – Axial moment of resistance.
W x = , W y =
Polar moment of inertia is called, taken over the entire section, the sum of the products of elementary areas by the squares of their distances to the center of gravity of the section. i.e. until the coordinate axes intersect.
The polar moment of inertia characterizes the ability of a part to resist torsional deformation.
Polar moment of inertia.
=
.
Polar moment of resistance is called the ratio of the polar moment of inertia to the distance to the most distant points of the section from the center of gravity of the section under consideration.
Polar moment of resistance
1. Rectangular section.
J y = (mm 4), J x = (mm 4)
W x = 
(mm 3), W y = 
(mm 3)
2. Round section
J x = J y = (mm 4), = (mm 4)
W y = W x = 
(mm 3), = 
(mm 3)
3. Ring section
J x = J y = - = 
(mm 4) , α=d/D
W y = W x =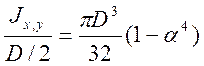 
(mm 3)
= 
(mm 4)
=
(mm 3)
4. Box section.
J x = 
=
(mm 4)
J y = 
=
(mm 4)
W x = 
(mm 3)
W y = 
(mm 3)
Calculations of parts with uniform stress distribution.
This type of parts includes rods with eyes and pins, as well as hydraulic and pneumatic cylinders and other pressure vessels, bimetallic elements (thermal relays).
Traction calculation.
1) Tensile force F is applied to the rod.
The traction rod perceives a longitudinal load, under the influence of which it stretches. In this case, the magnitude of the absolute elongation is determined by the expanded Hooke’s law:
σ р =Eε. , σ р =F/A, 
, σ р =F/A<=[
σ р ]= σ T / n -
tensile traction strength condition, (A=H*B, A=).
As a result of interaction with the finger, the lugs are crushed over the contact area.
Bearing strength condition:
σ cm =F/A<=[σ см ]= 2σ T / n , A=d*b.
The fingers are calculated for shear from interaction with the eyes:
τ av =F/A<=[τ ср ]= 0,5σ T / n; A=*i, i - количество платежей среза (i=2).
2) Compressive force F2 is applied to the rod.
The thrust rod works in compression. The magnitude of absolute shortening is also determined by Hooke’s law:
σ c =F/A<=[σ с ]=[σ р ]=σ T / n. – Для коротких стержней тяги.
Long rod - when the length exceeds 3 times one of the cross-sectional dimensions. Here there is a possibility of instantaneous bending of the rod rod.
σ с =<=[σ с ]=[σ р ]=σ T / n, φ – коэффициент продольного изгиба, величина табличная – зависит от материала, гибкости стержня и характера закрепления концов стержня.
The eyelet and fingers are calculated similarly to the previous calculation.
Calculation of thin-walled vessels.
Thin-walled vessels include hydraulic and pneumatic cylinders, receivers, pipelines, etc.
Depending on the shape, the vessels are:
cylindrical (hydraulic and pneumatic cylinders, some types of receivers, pipelines);
spherical (some types of receivers, bottoms and covers of cylindrical vessels, membranes, etc.);
torus (curvilinear sections of pipelines, sensitive elements of pointer pressure gauges).
In all vessels, under the influence of internal forces of liquid or gas, stresses arise in the walls in the longitudinal and cross sections.
Cylindrical vessels.
A thin cylindrical shell is loaded with internal pressure P. - Calculated as the cross section of the cylinder.
Torus vessels.
They are calculated as curved cylindrical ones.
15.10.04 Calculation of stresses arising when temperature changes.
When temperature fluctuates, a part fixed between rigid supports experiences compressive or tensile deformation. When the temperature increases (decreases) by Dt, the rod must lengthen (shorten) by the amount of absolute elongation (shortening):
Dl= at* l* Dt, where a t is the temperature coefficient of linear expansion (for steel 12*10 -6 °C -1), then the value of absolute elongation (shortening): Δε t = Δ l t / l = α t* Dt, but because Since the rod is fixed rigidly, it cannot lengthen (shorten), so compression (tension) stresses will arise in its material, the values of which are determined by Hooke’s law:
σ с,р =E*ε t =E*α t *Δt.
The moments of inertia of the section of a beam (beam, rod), like the cross-sectional area, are one of the main geometric characteristics of the element involved in strength calculations. Let me remind you that in strength of strength materials a beam is an element whose one of the dimensions is length...
Significantly larger than the other two - width and height. It is the last two overall dimensions plus the shape that, along with the properties of the material, influence the strength characteristics of the beam.
The geometric moments of inertia of a section should not be confused with the moments of inertia of bodies, although their meaning is very similar. The moment of inertia of a body around a certain axis is the sum of the products masses elementary “volumetric” points of the body by the squared distances from the axis to these points. The moment of inertia of a section (flat figure) is the sum of the products areas elementary “flat” points of this section into the squares of the distances from them to the axis under consideration.
Formulas for calculating axial moments of inertia, as well as radii of inertia and moments of resistance of almost thirty elementary figures, from which any cross-section of a beam can be composed, can be taken in the section “Elements of resistance of materials” of chapter No. 1 “General technical information” of volume No. 1 of the “Designer’s Handbook” mechanical engineer" V.I. Anuriev. This three-volume reference book, which is the main reference book for several generations of mechanical engineers and has undergone about ten reprints, continues to be in demand and relevant today. I think every engineer should have it, especially since finding it on the Internet is not a problem. Of course, the formulas we are interested in can be found in other reference literature.
For I-beams, channels, angles, pipes and other rolled and bent profiles, widely used in mechanical engineering and construction, the geometric characteristics of sections, including moments of inertia, can be found in the tables of GOSTs, OSTs and other regulatory documents that regulate their production.
Beams and rods composed of two or more elementary profiles are used to increase the strength and rigidity of elements in the absence of an adequate replacement with a single profile in terms of weight and dimensions. In practice, these are paired corners, two-branch columns, beams with a belt reinforced with a sheet strip, and other cases.
Geometric characteristics of a composite section. Calculation in Excel.
In the article, we considered as an example a composite figure consisting of a triangle and a rectangle with a semicircle cutout. Let's continue with this example. Although you will probably never see a beam with such a bizarre cross-section in practice, it will suit us for a not very complex and illustrative example!
Launch MS Excel or OOo Calc and get started!
General rules for formatting spreadsheets used in blog articles can be found here.
From the above-mentioned article we already know the coordinates of the centers of gravity, the areas of the cross-sectional elements and the area of the entire composite section. In this article we will continue the work we started and calculate other geometric characteristics.
Initial data:
Items 1 , 2 , 3 copy from the file and fill the range of cells D3:F6.
4. Let's calculate the axial and centrifugal moments of inertia of the elements relative to their own central axes Ixi , Iyi , Ixiyi in cm4, using the formulas from the “Handbook of Mechanical Designers” by V.I. Anuriev
in cell D7: =80*40^3/12/10000 =42,667
Ix1 = a 1 *(b1 ^3)/12
in cell D8: =40*80^3/12/10000 =170,667
Iy1 = b1 *(a1 ^3)/12
in cell D9: =0 =0,000
Ix1 y1 = 0 (element with axial symmetry)
in cell E7: =24*42^3/36/10000 =4,939
Ix2 = a 2 *(h 2 ^3)/36
in cell E8: =42*24^3/48/10000 =1,210
Iy2 = h 2 *(a 2 ^3)/48
in cell E9: =0 =0,000
Ix2 y2 = 0 (element with axial symmetry)
in cell F7: =- (PI()/8*26^4-8/9/PI()*26^4)/10000=-5,016
Ix3 =- (π /8)*(r 3 ^4) — (8/(9* π ))*(r 3 ^4)
in cell F8: =-PI()/8*26^4/10000 =-17,945
Iy3 =- (π /8)*(r 3 ^4)
in cell F9: =0 =0,000
Ix3 y3 = 0 (element with axial symmetry)
The axial moments of inertia of the third element - the semicircle - are negative because it is a cutout in a rectangle - an empty space!
Calculation of geometric characteristics:
Items 5 , 6 , 7 copy from the file and fill in the combined cells D11E11F11...D15E15F15.
8. Let us calculate the axial and centrifugal moments of inertia of the section relative to the central axes x0 and y0 drawn through the center of gravity Ix 0 , Iy 0 , Ix0 y0 in cm4
in merged cell D16E16F16: =((D5-D15)^2*D6+(E5-D15)^2*E6+(F5-D15)^2*F6)/10000+D7+E7+F7=90,122
Ix0 = Σ ((yci — Yc )^2* Fi )+ ΣIxi
in merged cell D17E17F17: =((D4-D14)^2*D6+(E4-D14)^2*E6+(F4-D14)^2*F6)/10000+D8+E8+F8=159,678
Iy0 = Σ ((xci — Xc )^2* Fi )+ ΣIyi
in merged cell D18E18F18: =((D5-D15)*(D4-D14)*D6+(E5-D15)*(E4-D14)*E6+(F5-D15)*(F4-D14)*F6)/10000+D9+E9+F9=-50,372
Ix0y0 = Σ ((yci -Yc )*(xci -Xc )*Fi )+Σ Ixiyi
9. Let us calculate the main central moments of inertia of the section IV And Iu in cm4
in merged cell D19E19F19: =($D$16+$D$17)/2+((($D$16-$D$17)/2)^2+$D$18^2)^0.5=186,111
Iv =(Ix0 +Iy0 )/2+(((Ix0 -Iy0 )/2)^2+Ix0y0 ^2)^0.5
in merged cell D20E20F20: =($D$16+$D$17)/2- ((($D$16-$D$17)/2)^2+$D$18^2)^0.5=63,689
Iu =(Ix0 +Iy0 )/2- (((Ix0 -Iy0 )/2)^2+Ix0y0 ^2)^0.5
10. Let's find the angle of inclination of the main axis v to the central axis x0 α in degrees
in merged cell D21E21F21: =ATAN(D18/(D20-D16))/PI()*180=62,311
α =arctg (Ix0y0 /(Iu -Ix0 ))
11. And in conclusion, we calculate the radii of gyration of the composite section iv And iu in mm
in the merged cell D22E22F22: =(D19*10000/D11)^0.5 =26,540
iv =(IV / F 0 )^0,5
in merged cell D23E23F23: =(D20*10000/D11)^0.5 =15,526
iu =(Iu / F 0 )^0,5
The task is completed - the moments of inertia and radii of gyration of a composite section of three simple elements are calculated! All necessary data for constructing the ellipse of inertia have been obtained.
An Excel file with a calculation program allows you to easily perform a complete calculation of the geometric characteristics of the cross section of a beam consisting of two or three simple elements. If necessary, it is easy to expand the capabilities of the calculation module to a larger number of elements.
For receiving information about new articles and for downloading working program files please subscribe for announcements in the window located at the end of each article or in the window at the top of the page.
Do not forget confirm subscription by clicking on the link in a letter that will immediately come to you at the specified mail (may arrive in the folder « Spam » )!!!
I will read your comments with interest, dear readers!!! Share your thoughts!
I beg respecting the author's work download the file with the calculation program after subscription for article announcements!
