გეომეტრიულად თუ გეომეტრიულად. გეომეტრიული პროგრესია. ყოვლისმომცველი სახელმძღვანელო მაგალითებით (2020). რატომ არის საჭირო გეომეტრიული პროგრესია და მისი ისტორია?

განვიხილოთ გარკვეული სერია.

7 28 112 448 1792...

აბსოლუტურად ნათელია, რომ მისი რომელიმე ელემენტის ღირებულება წინაზე ზუსტად ოთხჯერ მეტია. ეს ნიშნავს, რომ ეს სერია პროგრესია.

გეომეტრიული პროგრესია არის რიცხვების უსასრულო თანმიმდევრობა, რომლის მთავარი მახასიათებელია ის, რომ შემდეგი რიცხვი მიიღება წინადან კონკრეტულ რიცხვზე გამრავლებით. ეს გამოიხატება შემდეგი ფორმულით.

a z +1 =a z ·q, სადაც z არის შერჩეული ელემენტის რიცხვი.

შესაბამისად, z ∈ N.

პერიოდი, როდესაც სკოლაში სწავლობენ გეომეტრიულ პროგრესიას, არის მე-9 კლასი. მაგალითები დაგეხმარებათ გაიგოთ კონცეფცია:

0.25 0.125 0.0625...

ამ ფორმულის საფუძველზე, პროგრესიის მნიშვნელი შეიძლება მოიძებნოს შემდეგნაირად:

არც q და არც b z არ შეიძლება იყოს ნული. ასევე, პროგრესიის თითოეული ელემენტი არ უნდა იყოს ნულის ტოლი.

შესაბამისად, რიგის შემდეგი რიცხვის გასარკვევად, ბოლო უნდა გაამრავლოთ q-ზე.

ამ პროგრესიის დასაყენებლად, თქვენ უნდა მიუთითოთ მისი პირველი ელემენტი და მნიშვნელი. ამის შემდეგ შესაძლებელია ნებისმიერი შემდგომი ტერმინის და მათი ჯამის პოვნა.

ჯიშები

q და a 1-დან გამომდინარე, ეს პროგრესია იყოფა რამდენიმე ტიპად:

• თუ 1 და q ერთზე მეტია, მაშინ ასეთი თანმიმდევრობა არის გეომეტრიული პროგრესია, რომელიც იზრდება ყოველი მომდევნო ელემენტთან ერთად. ამის მაგალითი წარმოდგენილია ქვემოთ.

მაგალითი: a 1 =3, q=2 - ორივე პარამეტრი ერთზე მეტია.

შემდეგ რიცხვების თანმიმდევრობა შეიძლება ჩაიწეროს ასე:

3 6 12 24 48 ...

• თუ |q| არის ერთზე ნაკლები, ანუ მასზე გამრავლება გაყოფის ტოლფასია, მაშინ მსგავსი პირობების მქონე პროგრესია არის კლებადი გეომეტრიული პროგრესია. ამის მაგალითი წარმოდგენილია ქვემოთ.

მაგალითი: a 1 =6, q=1/3 - a 1 მეტია ერთზე, q ნაკლებია.

შემდეგ რიცხვების თანმიმდევრობა შეიძლება ჩაიწეროს შემდეგნაირად:

6 2 2/3 ... - ნებისმიერი ელემენტი 3-ჯერ აღემატება მის მიმდევარ ელემენტს.

• ალტერნატიული ნიშანი. თუ ქ<0, то знаки у чисел последовательности постоянно чередуются вне зависимости от a 1 , а элементы ни возрастают, ни убывают.

მაგალითი: a 1 = -3, q = -2 - ორივე პარამეტრი ნულზე ნაკლებია.

შემდეგ რიცხვების თანმიმდევრობა შეიძლება ჩაიწეროს ასე:

3, 6, -12, 24,...

ფორმულები

გეომეტრიული პროგრესიების მოსახერხებელი გამოყენების მრავალი ფორმულა არსებობს:

• Z-ტერმინის ფორმულა. საშუალებას გაძლევთ გამოთვალოთ ელემენტი კონკრეტული რიცხვის ქვეშ წინა რიცხვების გამოთვლის გარეშე.

მაგალითი:ქ = 3, ა 1 = 4. საჭიროა პროგრესის მეოთხე ელემენტის დათვლა.

გამოსავალი:ა 4 = 4 · 3 4-1 = 4 · 3 3 = 4 · 27 = 108.

• პირველი ელემენტების ჯამი, რომელთა რაოდენობა უდრის ზ. საშუალებას გაძლევთ გამოთვალოთ მიმდევრობის ყველა ელემენტის ჯამი მდეზინკლუზიური.

მას შემდეგ, რაც (1-ქ) არის მნიშვნელში, შემდეგ (1 - q)≠ 0, შესაბამისად q არ არის 1-ის ტოლი.

შენიშვნა: თუ q=1, მაშინ პროგრესია იქნება უსასრულოდ განმეორებადი რიცხვების სერია.

გეომეტრიული პროგრესიის ჯამი, მაგალითები:ა 1 = 2, ქ= -2. გამოთვალეთ S5.

გამოსავალი:ს 5 = 22 - გაანგარიშება ფორმულის გამოყენებით.

• თანხა თუ |ქ| < 1 и если z стремится к бесконечности.

მაგალითი:ა 1 = 2 , ქ= 0.5. იპოვეთ თანხა.

გამოსავალი:სზ = 2 · = 4

სზ = 2 + 1 + 0.5 + 0.25 + 0.125 + 0.0625 = 3.9375 4

ზოგიერთი თვისება:

• დამახასიათებელი თვისება. თუ შემდეგი პირობა მუშაობს ნებისმიერზეზ, მაშინ მოცემული რიცხვების სერია არის გეომეტრიული პროგრესია:

ზ 2 = ზ -1 · აz+1

• ასევე, ნებისმიერი რიცხვის კვადრატი გეომეტრიულ პროგრესიაში იპოვება მოცემულ სერიაში ნებისმიერი ორი სხვა რიცხვის კვადრატების მიმატებით, თუ ისინი თანაბარ მანძილზე არიან ამ ელემენტისგან.

ზ 2 = ზ - ტ 2 + ზ + ტ 2 , სადტ- მანძილი ამ ციფრებს შორის.

• ელემენტებიგანსხვავდება q-შიერთხელ.
• პროგრესიის ელემენტების ლოგარითმები ასევე ქმნიან პროგრესიას, ოღონდ არითმეტიკულს, ანუ თითოეული მათგანი წინაზე მეტია გარკვეული რიცხვით.

ზოგიერთი კლასიკური პრობლემის მაგალითები

უკეთ რომ გავიგოთ, რა არის გეომეტრიული პროგრესია, მე-9 კლასის ამონახსნების მაგალითები დაგეხმარებათ.

• პირობები:ა 1 = 3, ა 3 = 48. იპოვექ.

გამოსავალი: ყოველი მომდევნო ელემენტი უფრო დიდია ვიდრე წინაქ ერთხელ.აუცილებელია ზოგიერთი ელემენტის გამოხატვა სხვების თვალსაზრისით მნიშვნელის გამოყენებით.

აქედან გამომდინარე,ა 3 = ქ 2 · ა 1

ჩანაცვლებისასქ= 4

• პირობები:ა 2 = 6, ა 3 = 12. გამოთვალეთ S 6.

გამოსავალი:ამისათვის უბრალოდ იპოვეთ q, პირველი ელემენტი და შეცვალეთ იგი ფორმულაში.

ა 3 = ქ· ა 2 , შესაბამისად,ქ= 2

a 2 = q · a 1,Ამიტომაც a 1 = 3

S 6 = 189

• · ა 1 = 10, ქ= -2. იპოვნეთ პროგრესიის მეოთხე ელემენტი.

გამოსავალი: ამისათვის საკმარისია მეოთხე ელემენტის გამოხატვა პირველი და მნიშვნელის მეშვეობით.

a 4 = q 3· a 1 = -80

განაცხადის მაგალითი:

• ბანკის კლიენტმა შეიტანა დეპოზიტი 10,000 რუბლის ოდენობით, რომლის პირობებით ყოველწლიურად კლიენტს დაემატება მისი 6% ძირითად თანხაზე. რა თანხა იქნება ანგარიშზე 4 წლის შემდეგ?

გამოსავალი: საწყისი თანხა 10 ათასი რუბლია. ეს ნიშნავს, რომ ინვესტიციიდან ერთი წლის შემდეგ ანგარიშს ექნება 10,000 + 10,000 · 0,06 = 10000 1,06

შესაბამისად, ანგარიშზე არსებული თანხა კიდევ ერთი წლის შემდეგ გამოისახება შემდეგნაირად:

(10000 · 1.06) · 0.06 + 10000 · 1.06 = 1.06 · 1.06 · 10000

ანუ ყოველწლიურად თანხა 1,06-ჯერ იზრდება. ეს ნიშნავს, რომ 4 წლის შემდეგ ანგარიშზე თანხის ოდენობის საპოვნელად საკმარისია იპოვოთ პროგრესიის მეოთხე ელემენტი, რომელიც მოცემულია პირველი ელემენტის ტოლი 10 ათასის და მნიშვნელის ტოლი 1,06-ის.

S = 1.06 1.06 1.06 1.06 10000 = 12625

ჯამის გამოთვლის ამოცანების მაგალითები:

გეომეტრიული პროგრესია გამოიყენება სხვადასხვა ამოცანებში. თანხის საპოვნელად შეიძლება მოყვანილი იყოს შემდეგი მაგალითი:

ა 1 = 4, ქ= 2, გამოთვალეთS 5.

გამოსავალი: გაანგარიშებისთვის საჭირო ყველა მონაცემი ცნობილია, თქვენ უბრალოდ უნდა ჩაანაცვლოთ ისინი ფორმულაში.

ს 5 = 124

• ა 2 = 6, ა 3 = 18. გამოთვალეთ პირველი ექვსი ელემენტის ჯამი.

გამოსავალი:

გეომში. პროგრესიით, ყოველი შემდეგი ელემენტი q-ჯერ მეტია წინაზე, ანუ ჯამის გამოსათვლელად თქვენ უნდა იცოდეთ ელემენტია 1 და მნიშვნელიქ.

ა 2 · ქ = ა 3

ქ = 3

ანალოგიურად, თქვენ უნდა იპოვოთა 1 , იცისა 2 დაქ.

ა 1 · ქ = ა 2

a 1 =2

ს 6 = 728.

გაკვეთილი თემაზე "უსასრულოდ კლებადი გეომეტრიული პროგრესია"

გაკვეთილის მიზანი:სტუდენტების ახალი ტიპის მიმდევრობის გაცნობა - უსასრულოდ კლებადი გეომეტრიული პროგრესია.

Დავალებები:

რიცხვითი მიმდევრობის ლიმიტის საწყისი იდეის ჩამოყალიბება; უსასრულო პერიოდული წილადების ჩვეულებრივად გადაქცევის სხვა ხერხის გაცნობა უსასრულოდ კლებადი გეომეტრიული პროგრესიის ჯამის ფორმულის გამოყენებით;

სკოლის მოსწავლეთა პიროვნების ინტელექტუალური თვისებების განვითარება, როგორიცაა ლოგიკური აზროვნება, შეფასებითი მოქმედებების უნარი და განზოგადება;

აქტიურობის, ურთიერთდახმარების, კოლექტივიზმისა და თემისადმი ინტერესის ხელშეწყობა.

აღჭურვილობა:კომპიუტერული კლასი, პროექტორი, ეკრანი.

გაკვეთილის ტიპი:გაკვეთილი - ახალი თემის შესწავლა.

გაკვეთილების დროს

მე . ორგ. მომენტი. დაასახელეთ გაკვეთილის თემა და მიზანი.

II . მოსწავლეთა ცოდნის განახლება.1. საშინაო დავალების შემოწმება.

1) არითმეტიკული და გეომეტრიული პროგრესიებთან დაკავშირებული ძირითადი ფორმულების შემოწმება. დაფაზე ორი მოსწავლე ამზადებს ჩანაწერებს ფორმულებზე.

2) დანარჩენი სტუდენტები აკეთებენ მათემატიკური კარნახი თემაზე „ჯამის ფორმულები“.

Დავალებები:

№1. იპოვეთ არითმეტიკული პროგრესიის პირველი ხუთი წევრის ჯამი, თუ მისი პირველი წევრია 6 (1-ლი ვარიანტი), -20 (მე-2 ვარიანტი), ხოლო მეხუთე წევრი არის -6 (1-ლი ვარიანტი), 20 (მე-2 ვარიანტი).

№2. იპოვეთ არითმეტიკული პროგრესიის პირველი ხუთი წევრის ჯამი, თუ მისი პირველი წევრია -20 (1-ლი ვარიანტი), 6 (მე-2 ვარიანტი) და სხვაობა არის 10 (1-ლი ვარიანტი), -3 (მე-2 ვარიანტი).

№3. იპოვეთ გეომეტრიული პროგრესიის პირველი ხუთი წევრის ჯამი, თუ მისი პირველი წევრი უდრის 1-ს (1-ლი ვარიანტი), -1-ის (მე-2 ვარიანტი), ხოლო მნიშვნელი არის -2 (1-ლი ვარიანტი), 2 (მე-2 ვარიანტი).

კარნახის ბოლოს შერჩევით მოწმდება ორი მოსწავლის ნამუშევარი შეფასებისთვის, დანარჩენები ასრულებენ თვითტესტს დაფის ფლანგებზე დაწერილი მზა გადაწყვეტილებების გამოყენებით.

გადაწყვეტილებები:

Დავალებები

1. არითმეტიკული პროგრესია მოცემულია ფორმულით ა ნ = 7 – 4 ნ. იპოვე ა 10 . (-33)

2. არითმეტიკული პროგრესიაში ა 3 = 7 და ა 5 = 1 . იპოვე ა 4 . (4)

3. არითმეტიკული პროგრესიაში ა 3 = 7 და ა 5 = 1 . იპოვე ა 17 . (-35)

4. არითმეტიკული პროგრესიაში ა 3 = 7 და ა 5 = 1 . იპოვე ს 17 . (-187)

5. გეომეტრიული პროგრესიისთვის
იპოვნეთ მეხუთე ტერმინი.

6. გეომეტრიული პროგრესიისთვის
იპოვე ნწევრი.

7. ექსპონენტურად ბ 3 = 8 და ბ 5 = 2 . იპოვე ბ 4 . (4)

8. ექსპონენტურად ბ 3 = 8 და ბ 5 = 2 . იპოვე ბ 1 და ქ .

9. ექსპონენტურად ბ 3 = 8 და ბ 5 = 2 . იპოვე ს 5 . (62)

III . ახალი თემის სწავლა(პრეზენტაციის დემონსტრირება).

განვიხილოთ კვადრატი, რომლის გვერდიც ტოლია 1. დავხატოთ სხვა კვადრატი, რომლის გვერდი არის პირველი კვადრატის ნახევარი, შემდეგ მეორე, რომლის გვერდიც არის მეორეს ნახევარი, შემდეგ შემდეგი და ა.შ. ყოველ ჯერზე ახალი კვადრატის გვერდი უდრის წინა კვადრატის ნახევარს.

შედეგად მივიღეთ კვადრატების გვერდების თანმიმდევრობა გეომეტრიული პროგრესიის ფორმირება მნიშვნელთან ერთად.

და, რაც ძალიან მნიშვნელოვანია, რაც მეტს ავაშენებთ ასეთ კვადრატებს, მით უფრო პატარა იქნება კვადრატის მხარე. Მაგალითად,

იმათ. n რიცხვის მატებასთან ერთად პროგრესირების პირობები ნულს უახლოვდება.

ამ ფიგურის გამოყენებით, შეგიძლიათ განიხილოთ სხვა თანმიმდევრობა.

მაგალითად, კვადრატების ფართობების თანმიმდევრობა:

. და კიდევ, თუ ნიზრდება განუსაზღვრელი ვადით, შემდეგ ფართობი უახლოვდება ნულს, რამდენადაც გსურთ.

მოდით შევხედოთ სხვა მაგალითს. ტოლგვერდა სამკუთხედი, რომლის გვერდები ტოლია 1 სმ. ავაშენოთ შემდეგი სამკუთხედი 1-ლი სამკუთხედის გვერდების შუა წერტილებში წვეროებით, სამკუთხედის შუა ხაზის შესახებ თეორემის მიხედვით - მე-2-ის გვერდი უდრის პირველის გვერდის ნახევარს, მე-3-ის გვერდს. უდრის მე-2 მხარის ნახევარს და ა.შ. ისევ ვიღებთ სამკუთხედების გვერდების სიგრძის თანმიმდევრობას.

ზე
.

თუ განვიხილავთ გეომეტრიულ პროგრესიას უარყოფითი მნიშვნელით.

შემდეგ, ისევ, მზარდი რიცხვებით ნპროგრესის მიდგომის პირობები ნულოვანი.

მივაქციოთ ყურადღება ამ მიმდევრობების მნიშვნელებს. ყველგან მნიშვნელები აბსოლუტური მნიშვნელობით 1-ზე ნაკლები იყო.

შეგვიძლია დავასკვნათ: გეომეტრიული პროგრესია იქნება უსასრულოდ კლებადი, თუ მისი მნიშვნელის მოდული 1-ზე ნაკლებია.

ფრონტალური სამუშაო.

განმარტება:

გეომეტრიულ პროგრესიას ამბობენ, რომ უსასრულოდ მცირდება, თუ მისი მნიშვნელის მოდული ერთზე ნაკლებია.
.

განმარტების გამოყენებით შეგიძლიათ გადაწყვიტოთ გეომეტრიული პროგრესია უსასრულოდ მცირდება თუ არა.

დავალება

არის თუ არა მიმდევრობა უსასრულოდ კლებადი გეომეტრიული პროგრესია, თუ იგი მოცემულია ფორმულით:

;
.

გამოსავალი:

. ჩვენ ვიპოვით ქ .

;
;
;
.

ეს გეომეტრიული პროგრესია უსასრულოდ მცირდება.

ბ)ეს თანმიმდევრობა არ არის უსასრულოდ კლებადი გეომეტრიული პროგრესია.

განვიხილოთ კვადრატი, რომლის გვერდიც ტოლია 1. გაყავით შუაზე, ერთი ნახევარი შუაზე და ა.შ. ყველა მიღებული მართკუთხედის ფართობი ქმნის უსასრულოდ კლებულ გეომეტრიულ პროგრესიას:

ამ გზით მიღებული ყველა მართკუთხედის ფართობის ჯამი იქნება 1-ლი კვადრატის ფართობის ტოლი და 1-ის ტოლი.

მაგრამ ამ ტოლობის მარცხენა მხარეს არის უსასრულო რაოდენობის წევრთა ჯამი.

განვიხილოთ პირველი n წევრის ჯამი.

გეომეტრიული პროგრესიის პირველი n წევრის ჯამის ფორმულის მიხედვით უდრის .

თუ ნიზრდება შეუზღუდავად, მაშინ

ან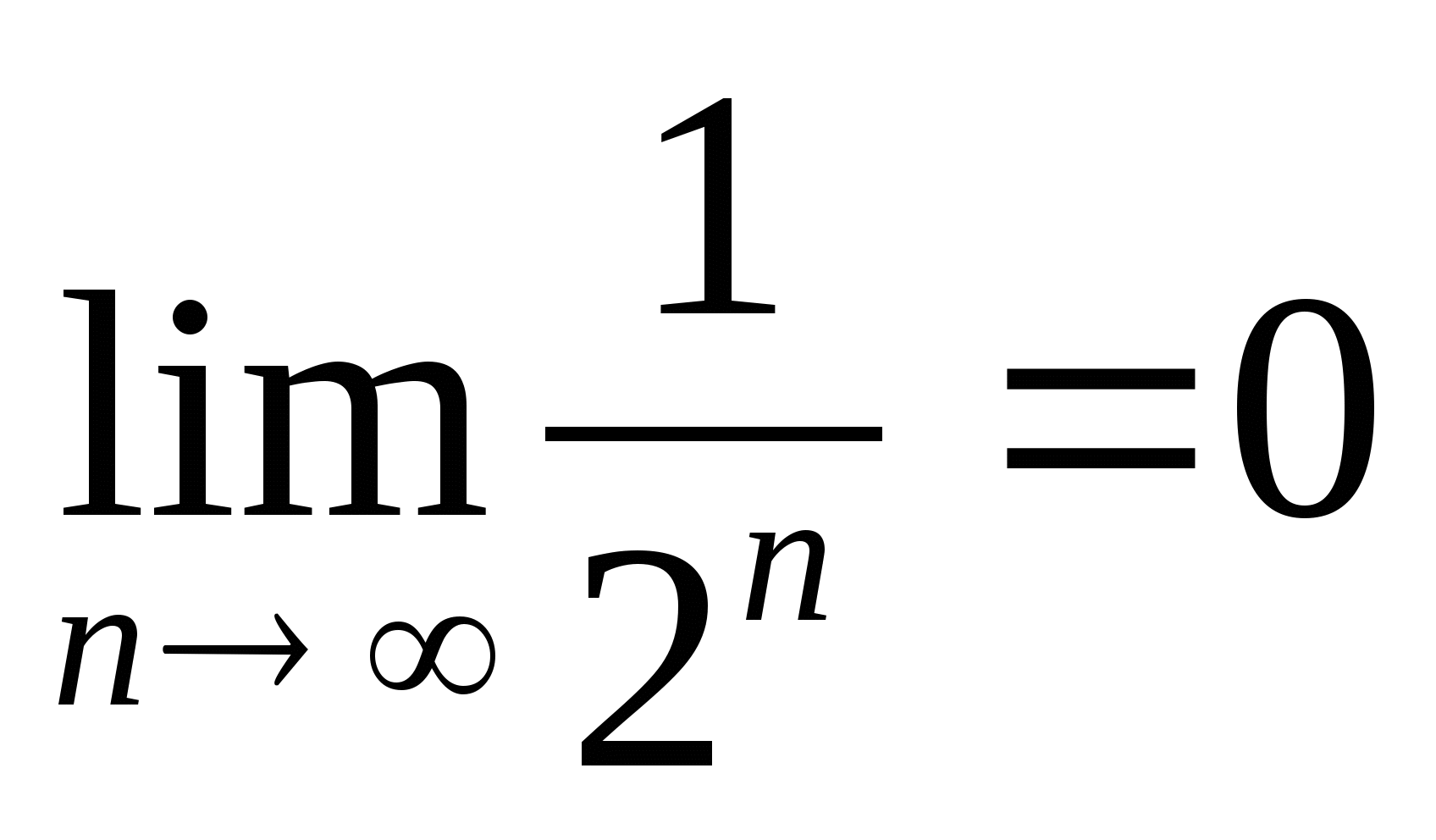
. Ამიტომაც
, ე.ი.
.

უსასრულოდ კლებადი გეომეტრიული პროგრესიის ჯამიარის თანმიმდევრობის ლიმიტი ს 1 , ს 2 , ს 3 , …, ს ნ , … .

მაგალითად, პროგრესისთვის
,

იმიტომ რომ

უსასრულოდ კლებადი გეომეტრიული პროგრესიის ჯამიშეგიძლიათ იპოვოთ ფორმულის გამოყენებით
.

III . გააზრება და კონსოლიდაცია(დავალებების შესრულება).

დავალება No2. იპოვეთ უსასრულოდ კლებადი გეომეტრიული პროგრესიის ჯამი, რომლის პირველი წევრი არის 3, ხოლო მეორე წევრი არის 0.3.

გამოსავალი:

დავალება No3. სახელმძღვანელო, გვ.160, No433(1)

იპოვეთ უსასრულოდ კლებადი გეომეტრიული პროგრესიის ჯამი:

გამოსავალი:

დავალება No4. ჩაწერეთ უსასრულო პერიოდული ათობითი წილადი 0,(5) საერთო წილადად.

1 მეთოდი. მოდით x=0,(5)= 0.555... / 10 მე-2 მეთოდი. 0,(5)=0.555…=

დავალება No5. სახელმძღვანელო, გვ.162, No445(3) (დამოუკიდებელი გადაწყვეტა)

ჩაწერეთ უსასრულო პერიოდული ათობითი წილადი 0,(12) საერთო წილადად.

პასუხი: 0,(12)= 4/33.

IV . შეჯამება.

რა თანმიმდევრობას გაეცანით დღეს?

განსაზღვრეთ უსასრულოდ კლებადი გეომეტრიული პროგრესია.

როგორ დავამტკიცოთ, რომ გეომეტრიული პროგრესია უსასრულოდ მცირდება?

მიეცით ფორმულა უსასრულოდ კლებადი გეომეტრიული პროგრესიის ჯამისთვის.

ვ . Საშინაო დავალება.

გეომეტრიული პროგრესია არის რიცხვითი თანმიმდევრობა, რომლის პირველი წევრი არ არის ნულოვანი და ყოველი მომდევნო წევრი უდრის წინა წევრს გამრავლებული იმავე არანულოვანი რიცხვით. გეომეტრიული პროგრესია აღინიშნება b1,b2,b3, …, bn,…

გეომეტრიული პროგრესიის თვისებები

გეომეტრიული შეცდომის ნებისმიერი ტერმინის შეფარდება მის წინა წევრთან იგივე რიცხვის ტოლია, ანუ b2/b1 = b3/b2 = b4/b3 = ... = bn/b(n-1) = b( n+1)/bn =…. ეს პირდაპირ გამომდინარეობს არითმეტიკული პროგრესიის განმარტებიდან. ამ რიცხვს გეომეტრიული პროგრესიის მნიშვნელი ეწოდება. როგორც წესი, გეომეტრიული პროგრესიის მნიშვნელი აღინიშნება ასო q-ით.

გეომეტრიული პროგრესიის დაზუსტების ერთ-ერთი გზაა მისი პირველი წევრის b1 და გეომეტრიული შეცდომის q მნიშვნელის დაზუსტება. მაგალითად, b1=4, q=-2. ეს ორი პირობა განსაზღვრავს გეომეტრიულ პროგრესიას 4, -8, 16, -32, ....

თუ q>0 (q არ არის 1-ის ტოლი), მაშინ პროგრესი არის მონოტონური მიმდევრობა. მაგალითად, მიმდევრობა, 2, 4,8,16,32, ... არის მონოტონურად მზარდი მიმდევრობა (b1=2, q=2).

თუ გეომეტრიულ ცდომილებაში მნიშვნელი არის q=1, მაშინ გეომეტრიული პროგრესიის ყველა წევრი იქნება ერთმანეთის ტოლი. ასეთ შემთხვევებში, პროგრესი ითვლება მუდმივი თანმიმდევრობით.

ფორმულა პროგრესის მე-n ტერმინისთვის

იმისათვის, რომ რიცხვითი მიმდევრობა (bn) იყოს გეომეტრიული პროგრესია, აუცილებელია, რომ მისი ყოველი წევრი, მეორედან დაწყებული, იყოს მეზობელი წევრების გეომეტრიული საშუალო. ანუ აუცილებელია შემდეგი განტოლების შესრულება - (b(n+1))^2 = bn * b(n+2), ნებისმიერი n>0-სთვის, სადაც n ეკუთვნის N ნატურალური რიცხვების სიმრავლეს.

გეომეტრიული პროგრესიის მე-n წევრის ფორმულა არის:

bn=b1*q^(n-1), სადაც n ეკუთვნის N ნატურალური რიცხვების სიმრავლეს.

მოდით შევხედოთ მარტივ მაგალითს:

გეომეტრიულ პროგრესიაში b1=6, q=3, n=8 იპოვეთ bn.

გამოვიყენოთ ფორმულა გეომეტრიული პროგრესიის n-ე წევრისთვის.

გეომეტრიული პროგრესია არის რიცხვების მიმდევრობის ახალი ტიპი, რომელსაც ჩვენ ვაპირებთ გავეცნოთ. წარმატებული გაცნობისთვის, სულაც არ არის ცუდი ცოდნა და გაგება. მაშინ გეომეტრიულ პროგრესირებასთან დაკავშირებით პრობლემები არ იქნება.)

რა არის გეომეტრიული პროგრესია? გეომეტრიული პროგრესიის კონცეფცია.

ტურს, როგორც ყოველთვის, საფუძვლებით ვიწყებთ. მე ვწერ რიცხვების დაუმთავრებელ თანმიმდევრობას:

1, 10, 100, 1000, 10000, …

შეგიძლიათ დააფიქსიროთ ნიმუში და გითხრათ, რომელი რიცხვები იქნება შემდეგი? წიწაკა გამჭვირვალეა, მერე მოჰყვება რიცხვები 100 000, 1 000 000 და ა.შ. დიდი გონებრივი ძალისხმევის გარეშეც კი ყველაფერი ნათელია, არა?)

ᲙᲐᲠᲒᲘ. Სხვა მაგალითი. მე ვწერ ამ თანმიმდევრობას:

1, 2, 4, 8, 16, …

შეგიძლიათ თქვათ, რომელი რიცხვები იქნება შემდეგი რიცხვი 16-ის შემდეგ და სახელი მერვემიმდევრობის წევრი? თუ გაარკვიეთ, რომ ეს იქნებოდა ნომერი 128, მაშინ ძალიან კარგი. ასე რომ, ბრძოლის ნახევარი გაგებაშია მნიშვნელობადა ძირითადი პუნქტებიგეომეტრიული პროგრესი უკვე გაკეთდა. შეგიძლიათ კიდევ გაიზარდოთ.)

ახლა კი კვლავ გადავდივართ შეგრძნებებიდან მკაცრ მათემატიკაზე.

გეომეტრიული პროგრესიის ძირითადი პუნქტები.

საკვანძო წერტილი #1

გეომეტრიული პროგრესია არის რიცხვების თანმიმდევრობა.ასევეა პროგრესი. არაფერი გამორჩეული. მხოლოდ ეს თანმიმდევრობაა მოწყობილი განსხვავებულად.აქედან გამომდინარე, ბუნებრივია, მას სხვა სახელი აქვს, დიახ ...

საკვანძო წერტილი #2

მეორე საკვანძო პუნქტით, კითხვა უფრო რთული იქნება. მოდით ცოტა უკან დავბრუნდეთ და გავიხსენოთ არითმეტიკული პროგრესიის ძირითადი თვისება. Აქ არის: თითოეული წევრი განსხვავდება წინაგან იმავე რაოდენობით.

შესაძლებელია თუ არა მსგავსი საკვანძო თვისების ჩამოყალიბება გეომეტრიული პროგრესიისთვის? ცოტა დაფიქრდით... დაწვრილებით დააკვირდით მოყვანილ მაგალითებს. გამოიცანით? დიახ! გეომეტრიული პროგრესიით (ნებისმიერი!) მისი თითოეული წევრი განსხვავდება წინაგან იგივე რაოდენობის ჯერ.ყოველთვის!

პირველ მაგალითში ეს რიცხვი არის ათი. მიმდევრობის რომელი წევრიც არ უნდა აიღოთ, ის უფრო დიდია ვიდრე წინა ათჯერ.

მეორე მაგალითში ეს არის ორი: თითოეული ტერმინი უფრო დიდია ვიდრე წინა ორჯერ.

სწორედ ამ საკვანძო პუნქტია, რომ გეომეტრიული პროგრესია არითმეტიკული პროგრესიისგან განსხვავდება. არითმეტიკული პროგრესიის დროს მიიღება ყოველი მომდევნო წევრი დამატებითიგივე მნიშვნელობა წინა ტერმინთან შედარებით. Და აქ - გამრავლებაწინა ვადა იმავე ოდენობით. ეს არის მთელი განსხვავება.)

საკვანძო წერტილი #3

ეს საკვანძო წერტილი სრულიად იდენტურია არითმეტიკული პროგრესიისთვის. კერძოდ: გეომეტრიული პროგრესიის თითოეული წევრი დგას თავის ადგილზე.ყველაფერი ზუსტად ისეა, როგორც არითმეტიკულ პროგრესში და კომენტარები, ვფიქრობ, ზედმეტია. არის პირველი ტერმინი, არის ასი პირველი და ა.შ. მოდით გავცვალოთ მინიმუმ ორი ტერმინი - ნიმუში (და მასთან ერთად გეომეტრიული პროგრესია) გაქრება. რაც დარჩება არის მხოლოდ რიცხვების თანმიმდევრობა ყოველგვარი ლოგიკის გარეშე.

Სულ ეს არის. ეს არის გეომეტრიული პროგრესიის მთელი აზრი.

ვადები და აღნიშვნები.

მაგრამ ახლა, როდესაც გავიგეთ გეომეტრიული პროგრესიის მნიშვნელობა და ძირითადი პუნქტები, შეგვიძლია გადავიდეთ თეორიაზე. წინააღმდეგ შემთხვევაში, რა არის თეორია მნიშვნელობის გაგების გარეშე, არა?

როგორ აღვნიშნოთ გეომეტრიული პროგრესია?

როგორ იწერება გეომეტრიული პროგრესია ზოგადი ფორმით? Არაა პრობლემა! პროგრესირების თითოეული ტერმინი ასევე იწერება ასოს სახით. მხოლოდ არითმეტიკული პროგრესირებისთვის, ჩვეულებრივ ასო გამოიყენება "A", გეომეტრიულისთვის – ასო "ბ". წევრის ნომერიჩვეულებისამებრ, მითითებულია ინდექსი ქვედა მარჯვენა მხარეს. ჩვენ უბრალოდ ჩამოვთვლით თავად პროგრესიის წევრებს, გამოყოფილი მძიმეებით ან მძიმით.

Ამგვარად:

b 1,ბ 2 , ბ 3 , ბ 4 , ბ 5 , ბ 6 , …

მოკლედ, ეს პროგრესი იწერება ასე: (b n) .

ან ასე, სასრული პროგრესებისთვის:

b 1, b 2, b 3, b 4, b 5, b 6.

b 1, b 2, …, b 29, b 30.

ან მოკლედ:

(b n), ნ=30 .

სინამდვილეში, ეს არის მთელი აღნიშვნა. ყველაფერი იგივეა, მხოლოდ ასოა განსხვავებული, დიახ.) ახლა კი პირდაპირ განსაზღვრებაზე გადავდივართ.

გეომეტრიული პროგრესიის განმარტება.

გეომეტრიული პროგრესია არის რიცხვითი თანმიმდევრობა, რომელშიც პირველი წევრი არ არის ნულოვანი და ყოველი მომდევნო წევრი ტოლია წინა წევრის გამრავლებული იმავე არანულოვანი რიცხვით.

ეს არის მთელი განმარტება. სიტყვებისა და ფრაზების უმეტესობა თქვენთვის გასაგები და ნაცნობია. თუ, რა თქმა უნდა, გესმით გეომეტრიული პროგრესიის მნიშვნელობა "თითებზე" და ზოგადად. მაგრამ ასევე არის რამდენიმე ახალი ფრაზა, რომელსაც განსაკუთრებული ყურადღება მინდა მივაქციო.

პირველი, სიტყვები: „რომლის პირველი წევრი არანულოვანი".

ეს შეზღუდვა პირველ ვადაზე შემთხვევით არ დაწესებულა. როგორ ფიქრობთ, რა მოხდება, თუ პირველი წევრი ბ 1 ნულის ტოლი იქნება? რის ტოლი იქნება მეორე წევრი, თუ თითოეული წევრი წინაზე მეტია? იგივე რამდენჯერ?ვთქვათ სამჯერ? ვნახოთ... გავამრავლოთ პირველი წევრი (ე.ი. 0) 3-ზე და მივიღოთ... ნული! რაც შეეხება მესამე წევრს? ასევე ნულოვანი! და მეოთხე წევრიც არის ნული! Და ასე შემდეგ…

ჩვენ უბრალოდ ვიღებთ ჩანთას, ნულების თანმიმდევრობას:

0, 0, 0, 0, …

რა თქმა უნდა, ასეთ თანმიმდევრობას აქვს სიცოცხლის უფლება, მაგრამ ეს არ არის პრაქტიკული ინტერესი. Ყველაფერი ნათელია. მისი ნებისმიერი წევრი არის ნული. ნებისმიერი რაოდენობის ტერმინების ჯამიც ნულია... რა საინტერესო საქმის გაკეთება შეგიძლია? არაფერი…

შემდეგი საკვანძო სიტყვები: "გამრავლებული იმავე არანულოვანი რიცხვით."

ამ იმავე ნომერს ასევე აქვს თავისი განსაკუთრებული სახელი - გეომეტრიული პროგრესიის მნიშვნელი. დავიწყოთ გაცნობა.)

გეომეტრიული პროგრესიის მნიშვნელი.

ყველაფერი ისეთივე მარტივია, როგორც მსხლის ჭურვი.

გეომეტრიული პროგრესიის მნიშვნელი არის არანულოვანი რიცხვი (ან რაოდენობა), რომელიც მიუთითებსრამდენჯერპროგრესირების ყოველი ტერმინი წინაზე მეტი.

ისევ, არითმეტიკული პროგრესიის მსგავსად, ამ განმარტებაში საკვანძო სიტყვაა სიტყვა "მეტი". ეს ნიშნავს, რომ მიღებულია გეომეტრიული პროგრესიის თითოეული ტერმინი გამრავლებასწორედ ამ მნიშვნელს წინა წევრი.

Ნება მომეცი აგიხსნა.

რომ გამოვთვალოთ, ვთქვათ მეორედიკ, უნდა მიიღოს პირველიწევრი და გამრავლებაის მნიშვნელისკენ. გაანგარიშებისთვის მეათედიკ, უნდა მიიღოს მეცხრეწევრი და გამრავლებაის მნიშვნელისკენ.

თავად გეომეტრიული პროგრესიის მნიშვნელი შეიძლება იყოს ნებისმიერი რამ. აბსოლუტურად ვინმეს! მთლიანი, წილადი, დადებითი, უარყოფითი, ირაციონალური - ყველაფერი. ნულის გარდა. ეს არის ის, რასაც სიტყვა "არა-ნულოვანი" განმარტებაში გვეუბნება. რატომ არის საჭირო ეს სიტყვა აქ - ამის შესახებ მოგვიანებით.

გეომეტრიული პროგრესიის მნიშვნელიყველაზე ხშირად მითითებულია ასოებით ქ.

როგორ მოვძებნოთ ქ? Არაა პრობლემა! პროგრესის ნებისმიერი ტერმინი უნდა ავიღოთ და გაყოფა წინა ტერმინზე. განყოფილება არის წილადი. აქედან მოდის სახელწოდება - "პროგრესიის მნიშვნელი". მნიშვნელი, ის ჩვეულებრივ წილადში ზის, დიახ...) თუმცა, ლოგიკურად, მნიშვნელობა ქუნდა ეწოდოს კერძოგეომეტრიული პროგრესია, მსგავსი განსხვავებაარითმეტიკული პროგრესირებისთვის. მაგრამ ჩვენ დავთანხმდით დარეკვას მნიშვნელი. და ჩვენ არც ბორბალს ხელახლა გამოვიგონებთ.)

მოდით განვსაზღვროთ, მაგალითად, რაოდენობა ქამ გეომეტრიული პროგრესისთვის:

2, 6, 18, 54, …

ყველაფერი ელემენტარულია. ავიღოთ ნებისმიერირიგითი ნომერი. რასაც გვინდა, ვიღებთ. პირველის გარდა. მაგალითად, 18. და გაყავით წინა ნომერი. ანუ 6-ზე.

ჩვენ ვიღებთ:

ქ = 18/6 = 3

Სულ ეს არის. ეს არის სწორი პასუხი. ამ გეომეტრიული პროგრესიისთვის, მნიშვნელი არის სამი.

ახლა ვიპოვოთ მნიშვნელი ქკიდევ ერთი გეომეტრიული პროგრესიისთვის. მაგალითად, ეს:

1, -2, 4, -8, 16, …

Ერთი და იგივე. რა ნიშნებიც არ უნდა ჰქონდეთ თავად წევრებს, ჩვენ მაინც ვიღებთ ნებისმიერირიგითობის ნომერი (მაგალითად, 16) და გაყავით წინა ნომერი(ანუ -8).

ჩვენ ვიღებთ:

დ = 16/(-8) = -2

და ეს.) ამჯერად პროგრესიის მნიშვნელი უარყოფითი აღმოჩნდა. მინუს ორი. ხდება.)

ახლა ავიღოთ ეს პროგრესი:

1, 1/3, 1/9, 1/27, …

და ისევ, მიუხედავად რიგითობის რიცხვების ტიპისა (მთელი რიცხვები, ლუწი წილადები, თუნდაც უარყოფითი, თუნდაც ირაციონალური), ვიღებთ ნებისმიერ რიცხვს (მაგალითად, 1/9) და ვყოფთ წინა რიცხვზე (1/3). წილადებთან მუშაობის წესების მიხედვით, რა თქმა უნდა.

ჩვენ ვიღებთ:

სულ ესაა.) აქ მნიშვნელი წილადი აღმოჩნდა: ქ = 1/3.

რას ფიქრობთ ამ "პროგრესზე"?

3, 3, 3, 3, 3, …

ცხადია აქ ქ = 1 . ფორმალურად, ეს ასევე გეომეტრიული პროგრესიაა, მხოლოდ იდენტური წევრები.) მაგრამ ასეთი პროგრესი არ არის საინტერესო სასწავლო და პრაქტიკული გამოყენებისთვის. იგივეა, რაც პროგრესიები მყარი ნულებით. ამიტომ, ჩვენ არ განვიხილავთ მათ.

როგორც ხედავთ, პროგრესიის მნიშვნელი შეიძლება იყოს ნებისმიერი - მთელი რიცხვი, წილადი, დადებითი, უარყოფითი - ყველაფერი! ეს არ შეიძლება იყოს უბრალოდ ნული. ვერ ვხვდები რატომ?

კარგი, მოდით გამოვიყენოთ კონკრეტული მაგალითი, რომ ვნახოთ რა მოხდება, თუ ავიღებთ მნიშვნელად ქნულ.) მოდით, მაგალითად, გვქონდეს ბ 1 = 2 , ა ქ = 0 . მაშინ რის ტოლი იქნება მეორე წევრი?

ჩვენ ვითვლით:

ბ 2 = ბ 1 · ქ= 2 0 = 0

რაც შეეხება მესამე წევრს?

ბ 3 = ბ 2 · ქ= 0 0 = 0

გეომეტრიული პროგრესიების სახეები და ქცევა.

ყველაფერი მეტ-ნაკლებად ნათელი იყო: თუ პროგრესის განსხვავება დდადებითია, შემდეგ პროგრესირება იზრდება. თუ განსხვავება უარყოფითია, მაშინ პროგრესი მცირდება. მხოლოდ ორი ვარიანტია. მესამე არ არსებობს.)

მაგრამ გეომეტრიული პროგრესიის ქცევით, ყველაფერი ბევრად უფრო საინტერესო და მრავალფეროვანი იქნება!)

არ აქვს მნიშვნელობა, როგორ მოიქცნენ აქ ტერმინები: ისინი იზრდებიან და მცირდებიან და განუსაზღვრელი ვადით უახლოვდებიან ნულს, და ნიშნებსაც კი ცვლიან, მონაცვლეობით თავს იყრიან „პლუსში“ და შემდეგ „მინუსში“! და ამ მრავალფეროვნებაში თქვენ უნდა შეძლოთ კარგად გაგება, დიახ...

მოდით გავარკვიოთ?) დავიწყოთ უმარტივესი შემთხვევით.

მნიშვნელი დადებითია ( ქ >0)

დადებითი მნიშვნელით, პირველ რიგში, გეომეტრიული პროგრესიის ტერმინები შეიძლება შევიდეს პლუს უსასრულობა(ანუ გაზრდა ლიმიტის გარეშე) და შეიძლება შევიდეს მინუს უსასრულობა(ანუ შემცირების გარეშე). ჩვენ უკვე მიჩვეულები ვართ პროგრესირების ამ ქცევას.

Მაგალითად:

(b n): 1, 2, 4, 8, 16, …

აქ ყველაფერი მარტივია. მიიღება პროგრესირების თითოეული ტერმინი წინაზე მეტი. უფრო მეტიც, თითოეული ტერმინი გამოდის გამრავლებაწინა წევრი ჩართულია დადებითინომერი +2 (ე.ი. ქ = 2 ). ასეთი პროგრესიის ქცევა აშკარაა: პროგრესიის ყველა წევრი იზრდება უსაზღვროდ, გადის სივრცეში. პლუს უსასრულობა...

ახლა კი აქ არის პროგრესი:

(b n): -1, -2, -4, -8, -16, …

აქაც მიიღება პროგრესირების ყოველი ტერმინი გამრავლებაწინა წევრი ჩართულია დადებითინომერი +2. მაგრამ ასეთი პროგრესიის ქცევა ზუსტად საპირისპიროა: პროგრესიის ყოველი ტერმინი მიიღება წინაზე ნაკლებიდა მისი ყველა პირობა მცირდება შეზღუდვის გარეშე, მიდის მინუს უსასრულობამდე.

ახლა მოდით დავფიქრდეთ: რა საერთო აქვს ამ ორ პროგრესს? ასეა, მნიშვნელი! Აქ და იქ ქ = +2 . დადებითი ნომერი.ორი. Და აქ მოქმედებაეს ორი პროგრესი ფუნდამენტურად განსხვავებულია! ვერ ვხვდები რატომ? დიახ! ეს ყველაფერი პირველი წევრი!სწორედ ის უწოდებს მელოდიას, როგორც იტყვიან.) თავად ნახეთ.

პირველ შემთხვევაში, პროგრესის პირველი ვადა დადებითი(+1) და, მაშასადამე, ყველა მომდევნო წევრი მიღებული გამრავლებით დადებითიმნიშვნელი ქ = +2 , ასევე იქნება დადებითი.

მაგრამ მეორე შემთხვევაში, პირველი ვადა უარყოფითი(-1). მაშასადამე, პროგრესიის ყველა შემდგომი პირობა, მიღებული გამრავლებით დადებითი ქ = +2 , ასევე მიიღება უარყოფითი.რადგან „მინუს“ „პლუს“ ყოველთვის იძლევა „მინუსს“, დიახ.)

როგორც ხედავთ, არითმეტიკული პროგრესიისგან განსხვავებით, გეომეტრიულ პროგრესიას შეუძლია სრულიად განსხვავებულად მოიქცეს არა მხოლოდ დამოკიდებულია მნიშვნელიდანქ, არამედ დამოკიდებულია პირველი წევრიდან, დიახ.)

გახსოვდეთ: გეომეტრიული პროგრესიის ქცევა ცალსახად განისაზღვრება მისი პირველი ტერმინით ბ 1 და მნიშვნელიქ .

ახლა კი ჩვენ ვიწყებთ ნაკლებად ნაცნობი, მაგრამ ბევრად უფრო საინტერესო შემთხვევების ანალიზს!

ავიღოთ, მაგალითად, ეს თანმიმდევრობა:

(b n): 1, 1/2, 1/4, 1/8, 1/16, …

ეს თანმიმდევრობაც გეომეტრიული პროგრესიაა! ამ პროგრესის ყოველი ტერმინიც გამოდის გამრავლებაწინა წევრი, იგივე რაოდენობით. ეს უბრალოდ რიცხვია - წილადი: ქ = +1/2 . ან +0,5 . მეტიც (მნიშვნელოვანია!) ნომერი ერთზე ნაკლები:ქ = 1/2<1.

რატომ არის ეს გეომეტრიული პროგრესია საინტერესო? სად მიდიან მისი წევრები? მოდით შევხედოთ:

1/2 = 0,5;

1/4 = 0,25;

1/8 = 0,125;

1/16 = 0,0625;

…….

რა საინტერესო რამ შეგიძლიათ შეამჩნიოთ აქ? პირველ რიგში, პროგრესირების კუთხით კლება დაუყოვნებლივ შესამჩნევია: მისი თითოეული წევრი ნაკლებიწინა ზუსტად 2 ჯერ.ან, გეომეტრიული პროგრესიის განმარტების მიხედვით, თითოეული ტერმინი მეტიწინა 1/2 ჯერ, იმიტომ პროგრესიის მნიშვნელი ქ = 1/2 . და როდესაც მრავლდება ერთზე ნაკლებ დადებით რიცხვზე, შედეგი ჩვეულებრივ მცირდება, დიახ...

Რა მეტიჩანს ამ პროგრესის ქცევაში? მცირდება მისი წევრები? შეუზღუდავი, მიდიხარ მინუს უსასრულობამდე? არა! ისინი ქრება განსაკუთრებული გზით. თავდაპირველად ისინი საკმაოდ სწრაფად მცირდება, შემდეგ კი უფრო და უფრო ნელა. და იმავდროულად დარჩენის დროს დადებითი. თუმცა ძალიან, ძალიან პატარა. და თვითონ რისკენ ისწრაფვიან? ვერ გამოიცანით? დიახ! ისინი ნულისკენ ისწრაფვიან!) მეტიც, მიაქციეთ ყურადღება, ჩვენი პროგრესის წევრები ნულიდან არიან არასოდეს მიაღწიო!მხოლოდ უახლოვდება მას უსასრულოდ ახლოს. Ეს ძალიან მნიშვნელოვანია.)

მსგავსი ვითარება მოხდება შემდეგ პროგრესში:

(b n): -1, -1/2, -1/4, -1/8, -1/16, …

Აქ ბ 1 = -1 , ა ქ = 1/2 . ყველაფერი იგივეა, მხოლოდ ახლა ტერმინები ნულს მიუახლოვდება მეორე მხრიდან, ქვემოდან. სულ დარჩენა უარყოფითი.)

ისეთი გეომეტრიული პროგრესია, რომლის ტერმინები მიუახლოვდით ნულს ლიმიტის გარეშე(არ აქვს მნიშვნელობა დადებითი თუ უარყოფითი მხრიდან), მათემატიკაში განსაკუთრებული სახელი აქვს - უსასრულოდ კლებადი გეომეტრიული პროგრესია.ეს პროგრესი იმდენად საინტერესო და უჩვეულოა, რომ განიხილება კიდეც ცალკე გაკვეთილი .)

ასე რომ, ჩვენ განვიხილეთ ყველაფერი შესაძლო დადებითიმნიშვნელები არის როგორც დიდი, ასევე პატარა. ჩვენ არ განვიხილავთ თავად ერთეულს მნიშვნელად ზემოთ ჩამოთვლილი მიზეზების გამო (გაიხსენეთ მაგალითი სამეულების თანმიმდევრობით...)

მოდით შევაჯამოთ:

დადებითიდა ერთზე მეტი (ქ>1), შემდეგ პროგრესირების პირობები:

ა) გაზრდა შეზღუდვის გარეშე (თუბ 1 >0);

ბ) შემცირება შეუზღუდავად (თუბ 1 <0).

თუ გეომეტრიული პროგრესიის მნიშვნელი დადებითი და ერთზე ნაკლები (0< ქ<1), то члены прогрессии:

ა) უსასრულოდ ახლოს ნულთან ზემოთ(თუბ 1 >0);

ბ) უახლოვდება ნულს უსასრულოდ ახლოს ქვემოდან(თუბ 1 <0).

ახლა რჩება საქმის განხილვა უარყოფითი მნიშვნელი.

მნიშვნელი უარყოფითია ( ქ <0)

მაგალითისთვის შორს არ წავალთ. რატომ, ზუსტად, შაგი ბებია?!) ​​მოდით, მაგალითად, პროგრესის პირველი ტერმინი იყოს ბ 1 = 1 , და ავიღოთ მნიშვნელი q = -2.

ჩვენ ვიღებთ შემდეგ თანმიმდევრობას:

(b n): 1, -2, 4, -8, 16, …

და ასე შემდეგ.) პროგრესირების ყოველი ტერმინი მიიღება გამრავლებაწინა წევრი ჩართულია უარყოფითი რიცხვი-2. ამ შემთხვევაში, ყველა წევრი, რომელიც დგას კენტ ადგილებზე (პირველი, მესამე, მეხუთე და ა.შ.) იქნება დადებითიდა ლუწი ადგილებში (მეორე, მეოთხე და ა.შ.) – უარყოფითი.ნიშნები მკაცრად ალტერნატიულია. პლუს-მინუს-პლუს-მინუს... ამ გეომეტრიულ პროგრესიას ჰქვია - მზარდი ნიშანი მონაცვლეობით.

სად მიდიან მისი წევრები? მაგრამ არსად.) დიახ, აბსოლუტური მნიშვნელობით (ანუ მოდული)ჩვენი პროგრესის წევრები იზრდებიან შეუზღუდავად (აქედან გამომდინარე სახელწოდება „იზრდება“). მაგრამ ამავე დროს, პროგრესის თითოეული წევრი მონაცვლეობით აგდებს სიცხეში, შემდეგ სიცივეში. ან "პლუს" ან "მინუს". ჩვენი პროგრესი მერყევია... მეტიც, რყევების ფარგლები ყოველ ნაბიჯზე სწრაფად იზრდება, დიახ.) ამიტომ პროგრესიის წევრების მისწრაფებები სადღაც მიდის. კონკრეტულადᲐქ არა.არც პლიუს უსასრულობამდე, არც მინუს უსასრულობამდე და არც ნულამდე - არსად.

ახლა განვიხილოთ წილადის მნიშვნელი ნულსა და მინუს ერთს შორის.

მაგალითად, ასეც იყოს ბ 1 = 1 , ა q = -1/2.

შემდეგ მივიღებთ პროგრესს:

(b n): 1, -1/2, 1/4, -1/8, 1/16, …

და ისევ გვაქვს ნიშნების მონაცვლეობა! მაგრამ, წინა მაგალითისგან განსხვავებით, აქ უკვე აშკარაა ტერმინების ნულის მიახლოების ტენდენცია.) მხოლოდ ამჯერად ჩვენი ტერმინები ნულს უახლოვდება არა მკაცრად ზემოდან ან ქვემოდან, არამედ ისევ. ყოყმანობს. დადებითი და უარყოფითი მნიშვნელობების მონაცვლეობით მიღება. მაგრამ ამავე დროს ისინი მოდულებისულ უფრო და უფრო უახლოვდებიან სანუკვარ ნულს.)

ამ გეომეტრიულ პროგრესიას ე.წ უსასრულოდ კლებადი ნიშანი, მონაცვლეობა.

რატომ არის ეს ორი მაგალითი საინტერესო? და ის ფაქტი, რომ ორივე შემთხვევაში ხდება ნიშნების მონაცვლეობა!ეს ხრიკი დამახასიათებელია მხოლოდ უარყოფითი მნიშვნელის მქონე პროგრესიებისთვის, დიახ.) ამიტომ, თუ რომელიმე დავალებაში ხედავთ გეომეტრიულ პროგრესიას ალტერნატიული ტერმინებით, უკვე დანამდვილებით გეცოდინებათ, რომ მისი მნიშვნელი 100% უარყოფითია და შეცდომას არ დაუშვებთ. ნიშანში.)

სხვათა შორის, უარყოფითი მნიშვნელის შემთხვევაში, პირველი წევრის ნიშანი საერთოდ არ ახდენს გავლენას თავად პროგრესიის ქცევაზე. პროგრესირების პირველი ტერმინის ნიშნის მიუხედავად, ნებისმიერ შემთხვევაში შეინიშნება ტერმინების ნიშანი. ერთადერთი კითხვაა, რა ადგილებში(ლუწი ან კენტი) იქნება წევრები კონკრეტული ნიშნებით.

გახსოვდეთ:

თუ გეომეტრიული პროგრესიის მნიშვნელი უარყოფითი , მაშინ პროგრესის პირობების ნიშნები ყოველთვის არის ალტერნატიული.

ამავე დროს, თავად წევრები:

ა) გაზრდა შეუზღუდავადმოდული, თუქ<-1;

ბ) უსასრულოდ მივუდგეთ ნულს, თუ -1< ქ<0 (прогрессия бесконечно убывающая).

Სულ ეს არის. გაანალიზებულია ყველა ტიპიური შემთხვევა.)

გეომეტრიული პროგრესიის სხვადასხვა მაგალითების ანალიზის პროცესში პერიოდულად ვიყენებდი სიტყვებს: "მიდრეკილია ნულისკენ", "მიდრეკილია პლუს უსასრულობისკენ", "მიდრეკილია მინუს უსასრულობისკენ"... არა უშავს.) ეს მეტყველების ფიგურები (და კონკრეტული მაგალითები) მხოლოდ საწყისი შესავალია. მოქმედებასხვადასხვა რიცხვების თანმიმდევრობა. გეომეტრიული პროგრესიის მაგალითის გამოყენებით.

რატომ უნდა ვიცოდეთ პროგრესის ქცევა? რა მნიშვნელობა აქვს სად მიდის? ნულისკენ, პლიუს უსასრულობამდე, მინუს უსასრულობამდე... რას გვეშველება ეს?

საქმე ისაა, რომ უკვე უნივერსიტეტში, უმაღლესი მათემატიკის კურსზე, დაგჭირდებათ მრავალფეროვან რიცხვითი მიმდევრობით მუშაობის უნარი (ნებისმიერი, არა მხოლოდ პროგრესიით!) და ზუსტად წარმოიდგინოთ, როგორია ესა თუ ის მიმდევრობა. იქცევა - იზრდება თუ არა შეუზღუდავად, მიდრეკილია თუ არა კონკრეტული რიცხვისკენ (და არა აუცილებლად ნულისკენ), ან საერთოდ არ მიდრეკილია არაფერზე... მათემატიკური კურსის განმავლობაში ამ თემას ეთმობა მთელი განყოფილება. ანალიზი - ლიმიტების თეორია.და ცოტა უფრო კონკრეტულად - კონცეფცია რიცხვთა თანმიმდევრობის ლიმიტი.ძალიან საინტერესო თემაა! აზრი აქვს კოლეჯში წასვლას და ამის გარკვევას.)

ზოგიერთი მაგალითი ამ განყოფილებიდან (მიმდევრობა, რომელსაც აქვს ლიმიტი) და კერძოდ, უსასრულოდ კლებადი გეომეტრიული პროგრესიასკოლაში იწყებენ შეგუებას. ჩვენ შევეჩვიეთ.)

უფრო მეტიც, თანმიმდევრობის ქცევის კარგად შესწავლის უნარი მომავალში დიდ სარგებელს მოგცემთ და ძალიან გამოგადგებათ ფუნქციის კვლევა.ყველაზე მრავალფეროვანი. მაგრამ ფუნქციებთან კომპეტენტურად მუშაობის უნარი (წარმოებულების გამოთვლა, მათი სრულად შესწავლა, მათი გრაფიკების აგება) უკვე მკვეთრად ზრდის თქვენს მათემატიკურ დონეს! გაქვთ რაიმე ეჭვი? Არ არის საჭიროება. ასევე დაიმახსოვრე ჩემი სიტყვები.)

მოდით შევხედოთ გეომეტრიულ პროგრესს ცხოვრებაში?

ჩვენს ირგვლივ ცხოვრებაში ჩვენ ვხვდებით გეომეტრიულ პროგრესირებას ძალიან, ძალიან ხშირად. თუნდაც ამის ცოდნის გარეშე.)

მაგალითად, სხვადასხვა მიკროორგანიზმები, რომლებიც ყველგან გვახვევენ უზარმაზარი რაოდენობით და რომლებსაც მიკროსკოპის გარეშეც კი ვერ ვხედავთ, ზუსტად მრავლდებიან გეომეტრიული პროგრესიით.

ვთქვათ, ერთი ბაქტერია მრავლდება შუაზე გაყოფით და შთამომავლობას აძლევს 2 ბაქტერიას. თავის მხრივ, თითოეული მათგანი, გამრავლებისას, ასევე იყოფა შუაზე, რაც 4 ბაქტერიის საერთო შთამომავლობას იძლევა. შემდეგი თაობა გამოიმუშავებს 8 ბაქტერიას, შემდეგ 16 ბაქტერიას, 32, 64 და ასე შემდეგ. ყოველი მომდევნო თაობის დროს ბაქტერიების რაოდენობა ორმაგდება. გეომეტრიული პროგრესიის ტიპიური მაგალითი.)

ასევე, ზოგიერთი მწერი - ბუგრები და ბუზები - ექსპონენტურად მრავლდება. და ზოგჯერ კურდღლებიც, სხვათა შორის.)

ყოველდღიურ ცხოვრებასთან უფრო ახლოს გეომეტრიული პროგრესიის კიდევ ერთი მაგალითია ე.წ საერთო ინტერესი.ეს საინტერესო ფენომენი ხშირად გვხვდება საბანკო დეპოზიტებში და ე.წ პროცენტის კაპიტალიზაცია.რა არის ეს?

თქვენ თვითონ, რა თქმა უნდა, ჯერ კიდევ ახალგაზრდა ხართ. სკოლაში სწავლობ, ბანკებში არ დადიხარ. მაგრამ თქვენი მშობლები უკვე მოზრდილები და დამოუკიდებელი ადამიანები არიან. ისინი მიდიან სამსახურში, შოულობენ ფულს დღიური პურის სანაცვლოდ და ფულის ნაწილს ბანკში დებენ და ზოგავენ.)

დავუშვათ, რომ მამაშენს სურს დაზოგოს გარკვეული თანხა თურქეთში ოჯახური დასვენებისთვის და დებს 50000 რუბლს ბანკში წელიწადში 10%-ით სამი წლის განმავლობაში. წლიური საპროცენტო კაპიტალიზაციით.უფრო მეტიც, მთელი ამ პერიოდის განმავლობაში დეპოზიტით არაფრის გაკეთება არ შეიძლება. თქვენ არ შეგიძლიათ არც დეპოზიტის შევსება და არც ანგარიშიდან თანხის ამოღება. რამდენ მოგებას მიიღებს ამ სამი წლის შემდეგ?

პირველ რიგში, ჩვენ უნდა გავარკვიოთ, რა არის წლიური 10%. Ეს ნიშნავს, რომ წელიწადშისაწყის დეპოზიტზე ბანკი 10%-ს დაამატებს. რისგან? რა თქმა უნდა, დან საწყისი დეპოზიტის თანხა.

ჩვენ ვიანგარიშებთ ანგარიშის ზომას ერთი წლის შემდეგ. თუ საწყისი დეპოზიტის თანხა იყო 50,000 რუბლი (ანუ 100%), მაშინ ერთი წლის შემდეგ რამდენი პროცენტი იქნება ანგარიშზე? მართალია, 110%! 50000 რუბლიდან.

ასე რომ, ჩვენ ვიანგარიშებთ 50,000 რუბლის 110% -ს:

50000 · 1.1 = 55000 რუბლი.

იმედი მაქვს გესმით, რომ მნიშვნელობის 110%-ის პოვნა ნიშნავს ამ მნიშვნელობის 1.1 რიცხვზე გამრავლებას? თუ არ გესმით, რატომ არის ასე, გაიხსენეთ მეხუთე და მეექვსე კლასები. სახელდობრ - კავშირი პროცენტებსა და წილადებსა და ნაწილებს შორის.)

ამრიგად, პირველი წლის ზრდა იქნება 5000 რუბლი.

რამდენი თანხა იქნება ანგარიშზე ორ წელიწადში? 60000 რუბლი? სამწუხაროდ (უფრო სწორად, საბედნიეროდ), ყველაფერი არც ისე მარტივია. პროცენტის კაპიტალიზაციის მთელი ხრიკი იმაში მდგომარეობს, რომ ყოველი ახალი პროცენტის დარიცხვისას, იგივე პროცენტები უკვე განიხილება ახალი თანხიდან!იმისგან ვინც უკვეარის ანგარიშზე Ამ მომენტში.ხოლო წინა პერიოდისთვის დარიცხული პროცენტი ემატება დეპოზიტის თავდაპირველ თანხას და, ამრიგად, თავად იღებს მონაწილეობას ახალი პროცენტის გამოთვლაში! ანუ ისინი ხდებიან საერთო ანგარიშის სრული ნაწილი. ან გენერალური კაპიტალი.აქედან მოდის სახელი - პროცენტის კაპიტალიზაცია.

ეკონომიკაშია. მათემატიკაში კი ასეთ პროცენტებს უწოდებენ საერთო ინტერესი.ან პროცენტის პროცენტი.) მათი ხრიკი ისაა, რომ თანმიმდევრობით გაანგარიშებისას ყოველ ჯერზე პროცენტები გამოითვლება ახალი მნიშვნელობიდან.და არა ორიგინალიდან...

ამიტომ, გამოთვალოთ თანხა მეშვეობით ორი წელი, უნდა გამოვთვალოთ იმ თანხის 110%, რომელიც იქნება ანგარიშზე წელიწადში.ანუ უკვე 55000 რუბლიდან.

ჩვენ ვითვლით 55,000 რუბლის 110% -ს:

55000 · 1.1 = 60500 რუბლი.

ეს ნიშნავს, რომ პროცენტული ზრდა მეორე წლისთვის იქნება 5,500 რუბლი, ხოლო ორი წლის განმავლობაში - 10,500 რუბლი.

ახლა უკვე შეგიძლიათ გამოიცნოთ, რომ სამი წლის შემდეგ ანგარიშზე თანხა იქნება 60,500 რუბლის 110%. ეს არის ისევ 110% წინადან (შარშან)თანხები.

აქ ჩვენ ვფიქრობთ:

60500 · 1.1 = 66550 რუბლი.

ახლა ჩვენ ვაწყობთ ჩვენს ფულად თანხებს წლის მიხედვით თანმიმდევრობით:

50000;

55000 = 50000 1.1;

60500 = 55000·1,1 = (50000·1,1)·1,1;

66550 = 60500 1.1 = ((50000 1.1) 1.1) 1.1

მაშ როგორ არის? რატომ არა გეომეტრიული პროგრესია? პირველი წევრი ბ 1 = 50000 , და მნიშვნელი ქ = 1,1 . თითოეული ტერმინი მკაცრად 1,1-ჯერ აღემატება წინას. ყველაფერი მკაცრად შეესაბამება განმარტებას.)

და რამდენ დამატებით საპროცენტო ბონუსს "დააგროვებს" მამაშენი, როცა მისი 50000 რუბლი სამი წელია მის საბანკო ანგარიშზე დევს?

ჩვენ ვითვლით:

66550 - 50000 = 16550 რუბლი

არც ისე ბევრი, რა თქმა უნდა. მაგრამ ეს იმ შემთხვევაში, თუ საწყისი დეპოზიტის თანხა მცირეა. რა მოხდება, თუ მეტია? ვთქვათ, არა 50, არამედ 200 ათასი რუბლი? მაშინ ზრდა სამი წლის განმავლობაში იქნება 66,200 რუბლი (თუ მათემატიკას გააკეთებთ). რაც უკვე ძალიან კარგია.) რა მოხდება, თუ წვლილი კიდევ უფრო დიდია? Ის არის...

დასკვნა: რაც უფრო მაღალია საწყისი დეპოზიტი, მით უფრო მომგებიანი ხდება პროცენტის კაპიტალიზაცია. ამიტომ საპროცენტო კაპიტალიზაციით დეპოზიტებს ბანკები აწვდიან გრძელვადიან პერიოდს. ვთქვათ ხუთი წლის განმავლობაში.

ასევე, ყველა სახის მავნე დაავადებას, როგორიცაა გრიპი, წითელა და კიდევ უფრო საშინელი დაავადებები (იგივე SARS 2000-იანი წლების დასაწყისში ან ჭირი შუა საუკუნეებში) მოსწონს ექსპონენტურად გავრცელება. აქედან გამომდინარეობს ეპიდემიების მასშტაბები, დიახ...) და ყველაფერი იმის გამო, რომ გეომეტრიული პროგრესია მთელი დადებითი მნიშვნელი (ქ>1) - რამ, რომელიც ძალიან სწრაფად იზრდება! გაიხსენეთ ბაქტერიების გამრავლება: ერთი ბაქტერიიდან მიიღება ორი, ორიდან - ოთხი, ოთხიდან - რვა და ასე შემდეგ... იგივეა ნებისმიერი ინფექციის გავრცელება.)

უმარტივესი ამოცანები გეომეტრიული პროგრესიის შესახებ.

დავიწყოთ, როგორც ყოველთვის, მარტივი პრობლემით. წმინდა მნიშვნელობის გასაგებად.

1. ცნობილია, რომ გეომეტრიული პროგრესიის მეორე წევრი არის 6, ხოლო მნიშვნელი -0,5. იპოვეთ პირველი, მესამე და მეოთხე ტერმინები.

ასე რომ, ჩვენ გვეძლევა გაუთავებელიგეომეტრიული პროგრესია, მაგრამ ცნობილია მეორე ვადაეს პროგრესი:

b 2 = 6

გარდა ამისა, ჩვენ ასევე ვიცით პროგრესიის მნიშვნელი:

q = -0.5

და თქვენ უნდა იპოვოთ პირველი, მესამედა მეოთხეამ პროგრესის წევრები.

ასე რომ, ჩვენ ვიმოქმედებთ. თანმიმდევრობას ვწერთ პრობლემის პირობების მიხედვით. პირდაპირ ზოგადი ფორმით, სადაც მეორე ტერმინი არის ექვსი:

b 1, 6,ბ 3 , ბ 4 , …

ახლა დავიწყოთ ძებნა. ჩვენ ვიწყებთ, როგორც ყოველთვის, უმარტივესით. შეგიძლიათ გამოთვალოთ, მაგალითად, მესამე ტერმინი ბ 3? შეიძლება! მე და შენ უკვე ვიცით (პირდაპირ გეომეტრიული პროგრესიის გაგებით), რომ მესამე ტერმინი (ბ 3)მეორეზე მეტი (ბ 2 ) ვ "q"ერთხელ!

ასე რომ, ჩვენ ვწერთ:

b 3 =ბ 2 · ქ

ამ გამოსახულებაში ექვსს ვცვლით ნაცვლად ბ 2და -0.5 ნაცვლად ქდა ვითვლით. და მინუსსაც არ უგულებელვყოფთ, რა თქმა უნდა...

b 3 = 6·(-0.5) = -3

Ამგვარად. მესამე ვადა უარყოფითი გამოდგა. გასაკვირი არ არის: ჩვენი მნიშვნელი ქ- უარყოფითი. და პლუსის მინუსზე გამრავლება, რა თქმა უნდა, იქნება მინუსი.)

ახლა ჩვენ ვითვლით პროგრესის მომდევნო, მეოთხე ტერმინს:

b 4 =ბ 3 · ქ

b 4 = -3·(-0.5) = 1.5

მეოთხე ვადა ისევ პლიუსით. მეხუთე წევრი ისევ იქნება მინუს, მეექვსე იქნება პლუსი და ა.შ. ნიშნები ერთმანეთს ენაცვლება!

ასე რომ, მესამე და მეოთხე ტერმინები იქნა ნაპოვნი. შედეგი არის შემდეგი თანმიმდევრობა:

ბ 1 ; 6; -3; 1.5; ...

ახლა რჩება მხოლოდ პირველი ტერმინის პოვნა ბ 1ცნობილი მეორეს მიხედვით. ამისათვის ჩვენ გადავდივართ სხვა მიმართულებით, მარცხნივ. ეს ნიშნავს, რომ ამ შემთხვევაში ჩვენ არ გვჭირდება პროგრესიის მეორე წევრის გამრავლება მნიშვნელზე, არამედ გაყოფა.

ვყოფთ და ვიღებთ:

სულ ესაა.) პრობლემის პასუხი ასეთი იქნება:

-12; 6; -3; 1,5; …

როგორც ხედავთ, გადაწყვეტის პრინციპი იგივეა, რაც . Ჩვენ ვიცით ნებისმიერიწევრი და მნიშვნელიგეომეტრიული პროგრესია - ჩვენ შეგვიძლია ვიპოვოთ მისი ნებისმიერი სხვა წევრი. ჩვენ ვიპოვით იმას, რაც გვსურს.) ერთადერთი განსხვავება ისაა, რომ შეკრება/გამოკლება იცვლება გამრავლებით/გაყოფით.

გახსოვდეთ: თუ ვიცით გეომეტრიული პროგრესიის მინიმუმ ერთი წევრი და მნიშვნელი, მაშინ ყოველთვის შეგვიძლია ვიპოვოთ ამ პროგრესიის ნებისმიერი სხვა წევრი.

შემდეგი პრობლემა, ტრადიციის თანახმად, არის OGE-ს რეალური ვერსიიდან:

2.

...; 150; X; 6; 1.2; ...

მაშ როგორ არის? ამჯერად არც პირველი ტერმინია, არც მნიშვნელი ქ, მხოლოდ რიცხვების თანმიმდევრობაა მოცემული... რაღაც უკვე ნაცნობი, არა? დიახ! მსგავსი პრობლემა უკვე მოგვარებულია არითმეტიკული პროგრესიით!

ასე რომ, ჩვენ არ გვეშინია. Ერთი და იგივე. თავი გავაქნიოთ და გავიხსენოთ გეომეტრიული პროგრესიის ელემენტარული მნიშვნელობა. ჩვენ ყურადღებით ვაკვირდებით ჩვენს თანმიმდევრობას და ვხვდებით სამი ძირითადის გეომეტრიული პროგრესიის რომელი პარამეტრია (პირველი წევრი, მნიშვნელი, ტერმინი ნომერი) დამალული მასში.

წევრების ნომრები? წევრობის ნომრები არ არის, დიახ... მაგრამ არის ოთხი თანმიმდევრულინომრები. მე ვერ ვხედავ აზრს იმის ახსნაში, თუ რას ნიშნავს ეს სიტყვა ამ ეტაპზე.) არსებობს ორი მეზობელი ცნობილი ნომრები?ჭამე! ეს არის 6 და 1.2. ასე რომ, ჩვენ შეგვიძლია ვიპოვოთ პროგრესიის მნიშვნელი.ამიტომ ვიღებთ რიცხვს 1.2 და ვყოფთ წინა ნომერზე.ექვსამდე.

ჩვენ ვიღებთ:

ჩვენ ვიღებთ:

x= 150·0.2 = 30

პასუხი: x = 30 .

როგორც ხედავთ, ყველაფერი საკმაოდ მარტივია. მთავარი სირთულე მხოლოდ გამოთვლებშია. განსაკუთრებით რთულია უარყოფითი და წილადი მნიშვნელების შემთხვევაში. ამიტომ ვისაც პრობლემები აქვს, გაიმეორეთ არითმეტიკა! როგორ ვიმუშაოთ წილადებთან, როგორ ვიმუშაოთ უარყოფით რიცხვებთან და ასე შემდეგ... თორემ აქ უმოწყალოდ შეანელებთ.

ახლა მოდით ცოტათი შევცვალოთ პრობლემა. ახლა ის საინტერესო გახდება! ამოვიღოთ მისგან ბოლო რიცხვი 1.2. ახლა მოვაგვაროთ ეს პრობლემა:

3. იწერება გეომეტრიული პროგრესიის რამდენიმე თანმიმდევრული პირობა:

...; 150; X; 6; ...

იპოვეთ პროგრესიის ვადა, რომელიც მითითებულია ასო x.

ყველაფერი იგივეა, მხოლოდ ორი მიმდებარე ცნობილიახლა პროგრესის წევრები არ გვყავს. ეს არის მთავარი პრობლემა. რადგან სიდიდე ქორი მეზობელი ტერმინის მეშვეობით შეგვიძლია ადვილად განვსაზღვროთ ჩვენ არ შეგვიძლია.გვაქვს თუ არა შანსი დავალების შესრულებაში? Რა თქმა უნდა!

მოდით ჩამოვწეროთ უცნობი ტერმინი" x„პირდაპირ გეომეტრიული პროგრესიის მნიშვნელობით! ზოგადად.

Დიახ დიახ! ზუსტად უცნობი მნიშვნელით!

ერთის მხრივ, X-სთვის შეგვიძლია დავწეროთ შემდეგი თანაფარდობა:

x= 150·ქ

მეორეს მხრივ, ჩვენ გვაქვს სრული უფლება აღვწეროთ იგივე X-ის მეშვეობით შემდეგიწევრი, ექვსის მეშვეობით! ექვსი გაყავით მნიშვნელზე.

Ამგვარად:

x = 6/ ქ

ცხადია, ახლა ჩვენ შეგვიძლია გავაიგივოთ ორივე ეს თანაფარდობა. ვინაიდან ჩვენ გამოვხატავთ იგივესიდიდე (x), მაგრამ ორი სხვადასხვა გზები.

ჩვენ ვიღებთ განტოლებას:

ყველაფრის გამრავლება ქ, გამარტივებით და შემოკლებით, ვიღებთ განტოლებას:

q2 = 1/25

ჩვენ ვხსნით და ვიღებთ:

q = ±1/5 = ±0.2

უი! მნიშვნელი ორმაგი აღმოჩნდა! +0.2 და -0.2. და რომელი უნდა აირჩიოთ? Ჩიხი?

დამშვიდდი! დიახ, პრობლემა ნამდვილად არის ორი გამოსავალი!ამაში ცუდი არაფერია. ეს ხდება.) არ გაგიკვირდებათ, როდესაც, მაგალითად, ჩვეულებრივი პრობლემის გადაჭრისას ორ ფესვს იღებთ? აქაც იგივე ამბავია.)

ამისთვის q = +0.2ჩვენ მივიღებთ:

X = 150 0.2 = 30

და ამისთვის ქ = -0,2 იქნება:

X = 150·(-0.2) = -30

ორმაგ პასუხს ვიღებთ: x = 30; x = -30.

რას ნიშნავს ეს საინტერესო ფაქტი? და რაც არსებობს ორი პროგრესიით, აკმაყოფილებს პრობლემის პირობებს!

ამათ მსგავსად:

…; 150; 30; 6; …

…; 150; -30; 6; …

ორივე შესაფერისია.) როგორ ფიქრობთ, რატომ გვქონდა განხეთქილება პასუხებში? მხოლოდ პროგრესის კონკრეტული წევრის (1,2) აღმოფხვრის გამო, რომელიც მოდის ექვსის შემდეგ. და გეომეტრიული პროგრესიის მხოლოდ წინა (n-1) და მომდევნო (n+1) ტერმინები ვიცით, ცალსახად ვეღარაფერს ვიტყვით მათ შორის მდგარ n-ე წევრზე. არსებობს ორი ვარიანტი - პლუსთან და მინუსთან ერთად.

მაგრამ პრობლემა არ არის. როგორც წესი, გეომეტრიული პროგრესირების ამოცანებში არის დამატებითი ინფორმაცია, რომელიც იძლევა ერთმნიშვნელოვან პასუხს. მოდით ვთქვათ სიტყვები: "ალტერნატიული პროგრესი"ან "პროგრესია დადებითი მნიშვნელით"და ასე შემდეგ... სწორედ ეს სიტყვები უნდა გამოდგეს, თუ რომელი ნიშანი, პლუსი თუ მინუსი უნდა აირჩეს საბოლოო პასუხის მომზადებისას. თუ ასეთი ინფორმაცია არ არის, მაშინ დიახ, დავალება ექნება ორი გამოსავალი.)

ახლა ჩვენ თვითონ გადავწყვიტეთ.

4. დაადგინეთ არის თუ არა რიცხვი 20 გეომეტრიული პროგრესიის წევრი:

4 ; 6; 9; …

5. მონაცვლეობითი გეომეტრიული პროგრესიის ნიშანი მოცემულია:

…; 5; x ; 45; …

იპოვეთ ასოში მითითებული პროგრესირების ვადა x .

6. იპოვეთ გეომეტრიული პროგრესიის მეოთხე დადებითი წევრი:

625; -250; 100; …

7. გეომეტრიული პროგრესიის მეორე წევრი უდრის -360-ს, ​​ხოლო მისი მეხუთე წევრი უდრის 23,04-ს. იპოვეთ ამ პროგრესის პირველი წევრი.

პასუხები (აშლილობის დროს): -15; 900; არა; 2.56.

გილოცავ, თუ ყველაფერი გამოვიდა!

რაღაც არ ჯდება? სადმე იყო ორმაგი პასუხი? ყურადღებით წაიკითხეთ დავალების პირობები!

ბოლო პრობლემა არ გამოდგება? იქ არაფერია რთული.) უშუალოდ ვმუშაობთ გეომეტრიული პროგრესიის მნიშვნელობის მიხედვით. კარგად, შეგიძლიათ დახატოთ სურათი. ეს ეხმარება.)

როგორც ხედავთ, ყველაფერი ელემენტარულია. თუ პროგრესი ხანმოკლეა. რა მოხდება, თუ გრძელია? ან ძალიან დიდია საჭირო წევრის რაოდენობა? მსურს, არითმეტიკული პროგრესიის ანალოგიით, როგორმე მივიღო მოსახერხებელი ფორმულა, რომელიც გაადვილებს პოვნას ნებისმიერინებისმიერი გეომეტრიული პროგრესიის ტერმინი მისი ნომრით.ბევრჯერ, ბევრჯერ გამრავლების გარეშე ქ. და არის ასეთი ფორმულა!) დეტალები შემდეგ გაკვეთილზე.

გეომეტრიული პროგრესია არის რიცხვითი თანმიმდევრობა, რომლის პირველი წევრი არ არის ნულოვანი და ყოველი მომდევნო წევრი უდრის წინა წევრს გამრავლებული იმავე არანულოვანი რიცხვით.

აღინიშნება გეომეტრიული პროგრესია b1,b2,b3, …, bn, ….

გეომეტრიული შეცდომის ნებისმიერი ტერმინის შეფარდება მის წინა წევრთან იგივე რიცხვის ტოლია, ანუ b2/b1 = b3/b2 = b4/b3 = ... = bn/b(n-1) = b( n+1)/bn =…. ეს პირდაპირ გამომდინარეობს არითმეტიკული პროგრესიის განმარტებიდან. ამ რიცხვს გეომეტრიული პროგრესიის მნიშვნელი ეწოდება. როგორც წესი, გეომეტრიული პროგრესიის მნიშვნელი აღინიშნება ასო q-ით.

ერთფეროვანი და მუდმივი თანმიმდევრობა

გეომეტრიული პროგრესიის დაზუსტების ერთ-ერთი გზაა მისი პირველი წევრის b1 და გეომეტრიული შეცდომის q მნიშვნელის დაზუსტება. მაგალითად, b1=4, q=-2. ეს ორი პირობა განსაზღვრავს გეომეტრიულ პროგრესიას 4, -8, 16, -32, ....

თუ q>0 (q არ არის 1-ის ტოლი), მაშინ პროგრესია არის ერთფეროვანი თანმიმდევრობა.მაგალითად, მიმდევრობა, 2, 4,8,16,32, ... არის მონოტონურად მზარდი მიმდევრობა (b1=2, q=2).

თუ გეომეტრიულ ცდომილებაში მნიშვნელი არის q=1, მაშინ გეომეტრიული პროგრესიის ყველა წევრი იქნება ერთმანეთის ტოლი. ასეთ შემთხვევებში ამბობენ, რომ პროგრესია მუდმივი თანმიმდევრობა.

გეომეტრიული პროგრესიის მე-n წევრის ფორმულა

იმისათვის, რომ რიცხვითი მიმდევრობა (bn) იყოს გეომეტრიული პროგრესია, აუცილებელია, რომ მისი ყოველი წევრი, მეორედან დაწყებული, იყოს მეზობელი წევრების გეომეტრიული საშუალო. ანუ აუცილებელია შემდეგი განტოლების შესრულება
(b(n+1))^2 = bn * b(n+2), ნებისმიერი n>0-სთვის, სადაც n ეკუთვნის N ნატურალური რიცხვების სიმრავლეს.

გეომეტრიული პროგრესიის მე-n წევრის ფორმულა არის:

bn=b1*q^(n-1),

სადაც n ეკუთვნის N ნატურალური რიცხვების სიმრავლეს.

გეომეტრიული პროგრესიის პირველი n წევრის ჯამის ფორმულა

გეომეტრიული პროგრესიის პირველი n წევრის ჯამის ფორმულას აქვს ფორმა:

Sn = (bn*q - b1)/(q-1), სადაც q არ არის 1-ის ტოლი.

მოდით შევხედოთ მარტივ მაგალითს:

გეომეტრიულ პროგრესიაში b1=6, q=3, n=8 იპოვეთ Sn.

S8-ის საპოვნელად ვიყენებთ გეომეტრიული პროგრესიის პირველი n პუნქტების ჯამის ფორმულას.

S8= (6*(3^8 -1))/(3-1) = 19680.