1. Концептот на асимптоти

Една од важните фази на конструирање на графикони на функции е пребарувањето на асимптоти. Сме сретнале асимптоти повеќе од еднаш: при конструирање графикони на функции, y=tgx, y=сtgx. Ги дефиниравме како линии кон кои графикот на функцијата „се стреми“, но никогаш не ги преминува. Дојде време да се даде прецизна дефиниција на асимптоти.

Постојат три вида асимптоти: вертикални, хоризонтални и коси. На цртежот, асимптотите обично се означуваат со точки.

Да го разгледаме следниот вештачки конструиран график на функцијата (сл. 16.1), чиј пример ги прикажува сите видови асимптоти:

Дозволете ни да го дефинираме секој тип на асимптота:

1. Директно x=aповикани вертикална асимптота функции ако .

2. Директно y=cповикани хоризонтална асимптота функции ако .

3. Директно y=kx+bповикани коси асимптота функции ако .

Геометриски, дефиницијата на кос асимптота значи дека при →∞ графикот на функцијата се приближува до права линија колку што сакаме y=kx+b, т.е. тие се речиси идентични. Разликата помеѓу практично идентични изрази се стреми кон нула.

Забележете дека хоризонталните и коси асимптоти се разгледуваат само под условот →∞. Понекогаш тие се разликуваат во хоризонтални и коси асимптоти на →+∞ и →-∞.

1. Алгоритам за пребарување на асимптоти

За да најдете асимптоти, можете да го користите следниов алгоритам:

Може да има една, неколку или никакви вертикални асимптоти.

• Ако c е број, тогаш y=c– хоризонтална асимптота;
• Ако c е бесконечност, тогаш нема хоризонтални асимптоти.

Ако функцијата е сооднос од два полиноми, тогаш ако функцијата има хоризонтални асимптоти, нема да бараме коси асимптоти - тие не постојат.

Ајде да погледнеме примери за наоѓање асимптоти на функција:

Пример 16.1.Најдете ги асимптотите на кривата.

Решение X-1≠0; X≠1.

Ајде да провериме дали линијата е права x= 1 вертикална асимптота. За да го направите ова, ја пресметуваме границата на функцијата во точката x= 1: .

x= 1 - вертикална асимптота.

Со= .

Со= = . Бидејќи Со=2 (број), тогаш y=2– хоризонтална асимптота.

Бидејќи функцијата е однос на полиноми, ако има хоризонтални асимптоти, тврдиме дека нема коси асимптоти.

x= 1 и хоризонтална асимптота y=2.За јасност, графикот на оваа функција е претставен на сл. 16.2.

Пример 16.2. Најдете ги асимптотите на кривата.

Решение. 1. Најдете го доменот на дефиниција на функцијата: X-2≠0; X≠2.

Ајде да провериме дали линијата е права x= 2 вертикална асимптота. За да го направите ова, ја пресметуваме границата на функцијата во точката x= 2: .

Затоа, го добивме тоа, x= 2 - вертикална асимптота.

2. За пребарување хоризонтални асимптоти, наоѓаме: Со= .

Бидејќи несигурноста се појавува во границата, го користиме правилото на L'Hopital: Со= = . Бидејќи Со– бесконечност, тогаш нема хоризонтални асимптоти.

3. За пребарување на коси асимптоти, наоѓаме:

Добивме несигурност на формата, ајде да го користиме правилото на L'Hopital: = =1. Значи, 1. Ајде да најдеме бспоред формулата: .

б= = =

Разбрав б= 2. Потоа y=kx+b –коси асимптота. Во нашиот случај изгледа вака: y=x+2.

Ориз. 16.3

Така, оваа функција има вертикална асимптота x= 2 и коси асимптота y=x+2.За јасност, графикот на функцијата е прикажан на сл. 16.3.

Контролни прашања:

Предавање 17. ОПШТА ШЕМА ЗА ПРОУЧУВАЊЕ ФУНКЦИЈА И ИЗГРАДУВАЊЕ ГРАФИК

Во ова предавање ќе го сумираме целиот претходно изучен материјал. Крајната цел на нашето долго патување е да можеме да ја испитаме секоја аналитички дадена функција и да го изградиме нејзиниот график. Важни делови од нашето истражување ќе бидат проучувањето на функцијата за екстреми, определувањето на интервали на монотоност, конвексност и конкавност на графикот, пребарување на точки на флексија и асимптоти на графикот на функцијата.

Имајќи ги предвид сите горенаведени аспекти, ви претставуваме шема за изучување на функција и цртање график .

1. Најдете го доменот на дефинирање на функцијата.

2. Испитајте ја функцијата за парен-непар паритет:

· ако , тогаш функцијата е парна (графот на парна функција е симетричен во однос на оската ОУ);

· ако , тогаш функцијата е непарна (графикот на непарната функција е симетричен во однос на потеклото);

· инаку функцијата не е ниту парна ниту непарна.

3. Истражете ја функцијата за периодичност (меѓу функциите што ги проучуваме, само тригонометриските функции можат да бидат периодични).

4. Најди ги пресечните точки на функционалниот график со координатните оски:

· О: на=0 (равенката ја решаваме само ако можеме да користиме методи кои ни се познати);

· ОУ: X=0.

5. Најдете го првиот извод на функцијата и критичните точки од првиот вид.

6. Најдете интервали на монотоност и екстреми на функцијата.

7. Најдете го вториот извод на функцијата и критичните точки од вториот вид.

8. Најдете ги интервалите конвексност-конкавност на графикот на функцијата и точките на флексија.

9. Најдете ги асимптотите на графикот на функцијата.

10. Конструирај график на функцијата. При изградбата, треба да се земе предвид случаи на можна локација на графикот во близина на асимптоти :

11. Доколку е потребно, изберете контролни точки за попрецизна конструкција.

Ајде да разгледаме шема за проучување на функција и конструирање на нејзиниот график користејќи конкретни примери:

Пример 17.1. Графиконирајте ја функцијата.

Решение. 1. Оваа функција е дефинирана на целата бројна линија освен X= 3, бидејќи во овој момент именителот оди на нула.

2. За да одредиме дали функцијата е парна или непарна, наоѓаме:

Го гледаме тоа и, според тоа, не е ниту парна ниту непарна функција.

3. Функцијата е непериодична.

4. Најдете ги пресечните точки со координатните оски. Да се ​​најде точката на пресек со оската Ода прифатиме на=0. Ја добиваме равенката: . Значи, точката (0; 0) е точката на пресек со координатните оски.

5. Да го најдеме изводот на функцијата користејќи го правилото за диференцијација на дропките: = = = = .

За да најдеме критични точки, наоѓаме точки во кои изводот на функцијата е еднаков на 0 или не постои.

Ако =0, значи . Производот тогаш е еднаков на 0 кога барем еден од факторите е еднаков на 0: или .

X-3) 2 е еднакво на 0, т.е. не постои кога X=3.

Значи, функцијата има три критични точки од првиот вид: ; ; .

6. На бројната оска означуваме критични точки од првиот вид, а точката ја означуваме со пробиена точка, бидејќи функцијата не е дефинирана во него.

На секој интервал го ставаме дериватот = знаци:

т.мин

т.макс

Во интервали каде што , оригиналната функција се зголемува (на (-∞;0]), каде што - се намалува (на ).

Точка X=0 е максималната точка на функцијата. За да го најдеме максимумот на функцијата, ја наоѓаме вредноста на функцијата во точката 0: .

Точка X=6 е минималната точка на функцијата. За да го најдеме минимумот на функцијата, ја наоѓаме вредноста на функцијата во точка 6: .

Резултатите од истражувањето може да се внесат во табела. Бројот на редови во табелата е фиксен и еднаков на четири, а бројот на колони зависи од функцијата што се проучува. Во ќелиите од првата линија, последователно се внесуваат интервали во кои критичните точки го делат доменот на дефинирање на функцијата, вклучувајќи ги и самите критични точки. За да избегнете грешки при конструирање точки кои не припаѓаат на доменот на дефиниција, не можете да ги вклучите во табелата.

Втората линија од табелата ги содржи знаците на изводот на секој од интервалите што се разгледуваат и вредноста на изводот во критичните точки. Во согласност со знаците на изводот на функцијата, во третата линија се означени интервалите на зголемување, намалување и екстреми на функцијата.

Последната линија служи за означување на максимумот и минимумот на функцијата.

X	(-∞;0)		(0;3)		(3;6)		(6;+ ∞)
	+		-		-		+
f(x)
заклучоци		макс				мин

7. Да го најдеме вториот извод на функцијата како извод на првиот извод: = =

Ајде да го ставиме во броител X-3 за загради и извршете го намалувањето:

Да прикажеме слични поими во броителот: .

Да најдеме критични точки од вториот вид: точки во кои вториот извод на функцијата е еднаков на нула или не постои.

0 ако =0. Оваа дропка не може да биде еднаква на нула, затоа, нема точки во кои вториот извод на функцијата е еднаков на нула.

Не постои ако именителот ( X-3) 3 е еднакво на 0, т.е. не постои кога X=3. : О, ОУ, потекло, мерни единици за секоја оска.

Пред да нацртате функција, треба:

Нацртајте ги асимптотите со точки;

· означете ги пресечните точки со координатните оски;

Ориз. 17.1

означете го максимумот и минимумот на функцијата, а се препорачува максимумот и минимумот на функцијата да се означат директно на цртежот со лакови: k или ;

· користејќи ги добиените податоци за интервалите на зголемување, намалување, конвексност и конкавност конструирај график на функцијата. Гранките на графиконот треба да „тежнеат“ кон асимптоти, но не и да ги пресекуваат.

· проверете дали графикот на функцијата одговара на спроведеното истражување: ако функцијата е парна или непарна, тогаш дали е забележана симетрија; Дали интервалите на зголемување и намалување, конвексност и конкавност и точки на флексија одговараат на теоретски пронајдените?

11. За попрецизна конструкција, можете да изберете неколку контролни точки. На пример, да ги најдеме вредностите на функциите во точките -2 и 7:

Ние го прилагодуваме распоредот земајќи ги предвид контролните точки.

Контролни прашања:

1. Кој е алгоритамот за графички приказ на функцијата?
2. Може ли функцијата да има екстремум во точки надвор од нејзиниот домен на дефиниција?

ГЛАВА 3. 3. ИНТЕГРАЛНО ПРЕСМЕТУВАЊЕ НА ФУНКЦИЈА

- (од грчки негативен дел., и symptotos коинцидираат заедно). Права линија која постојано се приближува кон кривата и ја среќава само во бесконечност. Речник на странски зборови вклучен во рускиот јазик. Чудинов А.Н., 1910. АСИМПТОТА од... ... Речник на странски зборови на рускиот јазик

АСИМПТОТА- (од грчкиот asymptotos не се совпаѓа), права линија до која се приближува бесконечна гранка на крива без ограничување, на пример асимптота на хипербола ... Модерна енциклопедија

АСИМПТОТА- (од грчкиот asymptotos не се совпаѓа) крива со бесконечна гранка, права линија до која оваа гранка се приближува без ограничување, на пример, асимптота на хипербола ... Голем енциклопедиски речник

асимптота- Права линија со крива која постепено се приближува кон неа. асимптота Права линија кон која кривата на некоја функција, имајќи бесконечна гранка, се стреми (без да ја достигне) кога нејзиниот аргумент се зголемува без ограничување или... Водич за технички преведувач

Асимптота- (од грчкиот asymptotos non-coinciding), права линија до која се приближува бесконечна гранка на крива без ограничување, на пример асимптота на хипербола. ... Илустриран енциклопедиски речник

АСИМПТОТА- женски, геом. права линија, секогаш се приближува до кривата (хипербола), но никогаш не се приближува со неа. Пример за објаснување на ова: ако кој било број се подели на половина, тогаш тој ќе се намали до бесконечност, но никогаш нема да стане нула. ... Даловиот објаснувачки речник

асимптота- именка, број на синоними: 1 ред (182) ASIS Dictionary of Synonyms. В.Н. Тришин. 2013… Речник на синоними

Асимптота- (од грчки зборови: а, сонце, пиптв) неусогласено. Под симптом се подразбира линија која, неодредено продолжена, се доближува до дадена крива линија или некој нејзин дел, така што растојанието помеѓу заедничките линии станува помало... ...

Асимптота- површина е права линија што ја пресекува површината на најмалку две точки во бесконечност... Енциклопедија на Брокхаус и Ефрон

АСИМПТОТА- (асимптота) Вредноста кон која се стреми оваа функција при менување на аргументот (аргументот), но не ја постигнува за која било конечна вредност на аргументот. На пример, ако вкупната цена на излезот x е дадена со функцијата TC=a+bx, каде што a и b се константи... Економски речник

Асимптота- права линија кон која се стреми кривата на некоја функција (без воопшто да ја достигне), имајќи бесконечна гранка, кога нејзиниот аргумент се зголемува или намалува без ограничување. На пример, во функцијата: y = c + 1/x вредноста на y се приближува со... ... Економски и математички речник

Колку асимптоти може да има графикот на функцијата?

Ниту еден, еден, два, три,... или бескрајно многу. Нема да одиме далеку за примери; да се потсетиме на елементарните функции. Параболата, кубната парабола и синусниот бран воопшто немаат асимптоти. Графикот на експоненцијална, логаритамска функција има една асимптота. Арктангентата и лактангентата имаат два од нив, а тангентата и котангентата имаат бесконечно многу. Не е невообичаено графикот да има и хоризонтални и вертикални асимптоти. Хипербола, секогаш ќе те сака.

Што значи да се најдат асимптоти на графикот на функцијата?

Ова значи да се пронајдат нивните равенки и да се исцртаат прави линии доколку проблемот го бара тоа. Процесот вклучува пронаоѓање на границите на функцијата.

Вертикални асимптоти на графикот на функцијата

Вертикалната асимптота на графикот, по правило, се наоѓа на точката на бесконечна дисконтинуитет на функцијата. Едноставно е: ако во одредена точка функцијата претрпи бесконечен дисконтинуитет, тогаш правата линија наведена со равенката е вертикалната асимптота на графикот.

Забелешка: Ве молиме имајте предвид дека записот се користи за да се однесува на два сосема различни концепти. Дали точката е имплицирана или равенка на права зависи од контекстот.

Така, за да се утврди присуството на вертикална асимптота во точка, доволно е да се покаже дека барем една од едностраните граници е бесконечна. Најчесто ова е точката каде што именителот на функцијата е нула. Во суштина, веќе најдовме вертикални асимптоти во последните примери од лекцијата за континуитет на функција. Но, во некои случаи постои само една еднострана граница, а ако е бесконечна, тогаш повторно - сакајте и фаворизирајте ја вертикалната асимптота. Наједноставна илустрација: и ординатна оска.

Од горенаведеното, следува и очигледен факт: ако функцијата е континуирана вклучена, тогаш нема вертикални асимптоти. Поради некоја причина на ум ми дојде парабола. Навистина, каде можете да „залепите“ права линија овде? ...да... разбирам... Следбениците на чичко Фројд станаа хистерични =)

Конверзната изјава е генерално неточна: на пример, функцијата не е дефинирана на целата бројна линија, туку е целосно лишена од асимптоти.

Закосени асимптоти на графикот на функцијата

Коси (како посебен случај - хоризонтални) асимптоти може да се извлечат ако аргументот на функцијата се стреми кон „плус бесконечност“ или кон „минус бесконечност“. Според тоа, графикот на функцијата не може да има повеќе од 2 наклонети асимптоти. На пример, графикот на експоненцијална функција има една хоризонтална асимптота во, а графикот на арктангенсот at има две такви асимптоти, а притоа различни.

Кога графикот на двете места се приближува до една коси асимптота, тогаш вообичаено е да се комбинираат „бесконечностите“ под еден запис. На пример, ...точно погодивте: .

Асимптоти на графикот на функција

Духот на асимптотата талкаше низ страницата долго време за конечно да се материјализира во посебна статија и да донесе особено задоволство на читателите кои се збунети целосно проучување на функцијата. Пронаоѓањето на асимптоти на графиконот е еден од ретките делови на оваа задача што е опфатен во училишниот курс само на прегледен начин, бидејќи настаните се вртат околу пресметката функционални граници, но сепак припаѓаат на вишата математика. За посетителите кои малку ја разбираат математичката анализа, мислам дека навестувањето е јасно ;-) ... застани, застани, каде одиш? Граници- тоа е лесно!

Примери на асимптоти се сретнаа веднаш во првата лекција за графикони на елементарни функции, а темата сега добива детално разгледување.

Значи, што е асимптота?

Замислете променлива точка, кој „патува“ по графикот на функцијата. Асимптота е директно, до кој неодредено затворањеграфикот на функцијата се приближува додека нејзината променлива точка се движи до бесконечност.

Забелешка : Дефиницијата е значајна, ако ви треба формулација во пресметковна нотација, ве молиме погледнете го учебникот.

На авионот, асимптотите се класифицираат според нивната природна локација:

1) Вертикални асимптоти, кои се дадени со равенка од формата , каде што „алфа“ е реален број. Популарен претставник ја дефинира самата оска на ординатите,
со мало чувство на гадење се сеќаваме на хиперболата.

2) Коси асимптотитрадиционално напишано равенка на права линијасо коефициент на агол. Понекогаш посебен случај се идентификува како посебна група - хоризонтални асимптоти. На пример, истата хипербола со асимптота.

Ајде брзо, ајде да ја погодиме темата со краток рафал од митралез:

Колку асимптоти може да има графикот на функцијата?

Ниту еден, еден, два, три,... или бескрајно многу. Нема да одиме далеку за примери, да се потсетиме елементарни функции. Параболата, кубната парабола и синусниот бран воопшто немаат асимптоти. Графикот на експоненцијална, логаритамска функција има една асимптота. Арктангентата и лактангентата имаат два од нив, а тангентата и котангентата имаат бесконечно многу. Не е невообичаено графикот да има и хоризонтални и вертикални асимптоти. Хипербола, секогаш ќе те сака.

Што значи ?

Вертикални асимптоти на графикот на функцијата

Вертикалната асимптота на графикот обично се наоѓа на точката на бесконечен дисконтинуитетфункции. Едноставно е: ако во одредена точка функцијата претрпи бесконечен дисконтинуитет, тогаш правата линија наведена со равенката е вертикалната асимптота на графикот.

Забелешка : Имајте предвид дека записот се користи за да се однесува на два сосема различни концепти. Дали точката е имплицирана или равенка на права зависи од контекстот.

Така, за да се утврди присуството на вертикална асимптота во точка, доволно е да се покаже тоа барем еденод еднострани граници бесконечна. Најчесто ова е точката каде што именителот на функцијата е нула. Во суштина, веќе најдовме вертикални асимптоти во последните примери од лекцијата на континуитет на функција. Но, во некои случаи постои само една еднострана граница, а ако е бесконечна, тогаш повторно - сакајте и фаворизирајте ја вертикалната асимптота. Наједноставната илустрација: и оската на ординатите (види. Графикони и својства на елементарните функции).

Од горенаведеното, следува и очигледен факт: ако функцијата е континуирано вклучена, тогаш нема вертикални асимптоти. Поради некоја причина на ум ми дојде парабола. Навистина, каде можете да „залепите“ права линија овде? ...да... разбирам... Следбениците на чичко Фројд станаа хистерични =)

Конверзната изјава е генерално неточна: на пример, функцијата не е дефинирана на целата бројна линија, туку е целосно лишена од асимптоти.

Закосени асимптоти на графикот на функцијата

Коси (како посебен случај - хоризонтални) асимптоти може да се извлечат ако аргументот на функцијата се стреми кон „плус бесконечност“ или кон „минус бесконечност“. Затоа графикот на функцијата не може да има повеќе од две коси асимптоти. На пример, графикот на експоненцијална функција има една хоризонтална асимптота на , а графикот на арктангенсот во има две такви асимптоти, а притоа различни.

Кога графикот на двете места се приближува до една коси асимптота, тогаш „бесконечностите“ обично се комбинираат под еден запис. На пример, ...точно погодивте: .

Општо правило:

Ако има две конечнаграница , тогаш правата линија е кос асимптота на графикот на функцијата кај . Ако барем еденод наведените граници е бесконечна, тогаш нема коси асимптота.

Забелешка : формулите остануваат валидни ако „x“ се стреми само кон „плус бесконечност“ или само кон „минус бесконечност“.

Да покажеме дека параболата нема коси асимптоти:

Границата е бесконечна, што значи дека нема коси асимптота. Забележете дека при наоѓањето на границата потребата исчезна бидејќи одговорот е веќе добиен.

Забелешка : Ако имате (или ќе имате) потешкотии да ги разберете знаците плус-минус, минус-плус, ве молиме погледнете ја помошта на почетокот на лекцијата
на бесконечно мали функции, каде ви кажав како правилно да ги толкувате овие знаци.

Очигледно е дека ниту една квадратна, кубна функција, полином од 4 и повисоки степени исто така нема коси асимптоти.

Сега да се увериме дека графикот исто така нема коси асимптота. За да ја откриеме несигурноста користиме Правилото на L'Hopital:
, што требаше да се провери.

Кога функцијата расте бесконечно, но нема права линија до која би се приближил нејзиниот график бескрајно блиску.

Ајде да преминеме на практичниот дел од лекцијата:

Како да се најдат асимптоти на графикот на функција?

Токму така е формулирана типичната задача и вклучува пронаоѓање на СИТЕ асимптоти на графикот (вертикална, наклонета/хоризонтална). Иако, попрецизно во поставувањето на прашањето, зборуваме за истражување за присуство на асимптоти (на крајот на краиштата, можеби и ги нема). Да почнеме со нешто едноставно:

Пример 1

Најдете асимптоти на графикот на функцијата

РешениеУдобно е да се подели на две точки:

1) Прво проверуваме дали има вертикални асимптоти. Именителот оди на нула во , и веднаш е јасно дека во овој момент функцијата страда бескраен јаз, а правата линија дадена со равенката е вертикална асимптота на графикот на функцијата. Но, пред да се извлече таков заклучок, неопходно е да се најдат еднострани граници:

Ве потсетувам на техниката за пресметување на која слично се фокусирав во статијата Континуитет на функцијата. Точки на прекин. Во изразот под знакот за граница заменуваме . Нема ништо интересно во броителот:
.

Но, во именителот излегува бесконечно мал негативен број:
, ја одредува судбината на лимитот.

Границата на левата страна е бесконечна и, во принцип, веќе е можно да се донесе пресуда за присуството на вертикална асимптота. Но, унилатералните граници се потребни не само за ова - тие ПОМАГААТ ДА СЕ РАЗБИРА КАКОлоцирајте го графикот на функцијата и изградете го ПРАВИЛНО. Затоа, мора да ја пресметаме и границата на десната рака:

Заклучок: едностраните граници се бесконечни, што значи дека правата линија е вертикална асимптота на графикот на функцијата на .

Првата граница конечни, што значи дека е неопходно да се „продолжи разговорот“ и да се најде втората граница:

Втората граница исто така конечни.

Така, нашата асимптота е:

Заклучок: правата линија дадена со равенката е хоризонтална асимптота на графикот на функцијата на .

Да се ​​најде хоризонталната асимптота
можете да користите поедноставена формула:

Доколку постои конечниграница, тогаш правата линија е хоризонтална асимптота на графикот на функцијата на .

Лесно е да се види дека броителот и именителот на функцијата истиот редослед на раст, што значи дека бараната граница ќе биде конечна: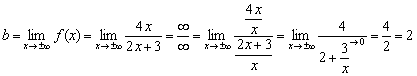

Одговори:

Според условот, не треба да го завршите цртежот, туку ако е во полн ек студија за функција