Линии од втор ред на авион. Линии од прв ред Како да се одреди редоследот на линијата
Линии од втор ред.
Елипса и нејзината канонска равенка. Заокружете
По темелно проучување прави линии во рамнинатаПродолжуваме да ја проучуваме геометријата на дводимензионалниот свет. Влоговите се удвоени и ве поканувам да ја посетите живописната галерија на елипси, хиперболи, параболи, кои се типични репрезентативци линии од втор ред. Екскурзијата е веќе започната, а најпрвин кратка информација за целата изложба на различни катови од музејот:
Концептот на алгебарска линија и нејзиниот редослед
Линија на авион се нарекува алгебарски, ако во афин координатен системнеговата равенка има форма , каде што е полином кој се состои од членови на формата ( – реален број, – ненегативни цели броеви).
Како што можете да видите, равенката на алгебарската линија не содржи синуси, косинуси, логаритми и други функционални Beau Monde. Влегуваат само X и Y ненегативни цели броевистепени.
Линиски редоследеднаква на максималната вредност на поимите вклучени во него.
Според соодветната теорема, концептот на алгебарска линија, како и неговиот редослед, не зависат од изборот афин координатен систем, затоа, за полесно постоење, претпоставуваме дека сите последователни пресметки се одвиваат во Декартови координати.
Општа равенкалинијата од втор ред има форма , каде 
– произволни реални броеви (Вообичаено е да се напише со фактор два), а коефициентите не се еднакви на нула во исто време.
Ако , тогаш равенката се поедноставува на 
, а ако коефициентите не се еднакви на нула во исто време, тогаш тоа е точно општа равенка на „рамна“ линија, што претставува линија од прв ред.
Многумина го разбраа значењето на новите термини, но, сепак, за 100% да го совладаме материјалот, ги ставаме прстите во штекерот. За да го одредите редоследот на линиите, треба да повторите сите термининеговите равенки и најдете за секоја од нив збир на степенидојдовни променливи.
На пример:
терминот содржи „x“ до 1 сила;
терминот содржи „Y“ до 1 сила;
Во поимот нема променливи, така што збирот на нивните моќи е нула.
Сега да откриеме зошто равенката ја дефинира линијата второсо цел:
терминот содржи „x“ до втора сила;
збирот го има збирот на моќите на променливите: 1 + 1 = 2;
терминот содржи „Y“ до втора сила;
сите други термини - помалкустепени.
Максимална вредност: 2
Ако дополнително додадеме, да речеме, на нашата равенка, тогаш таа веќе ќе определи линија од трет ред. Очигледно е дека општата форма на равенката на линијата од 3 ред содржи „целосен сет“ поими, збирот на моќите на променливите во кој е еднаков на три:
, каде што коефициентите не се еднакви на нула во исто време.
Во случај да додадете еден или повеќе соодветни термини кои содржат 
, тогаш веќе ќе зборуваме за Линии од 4 ред, итн.
Ќе мора да се сретнеме со алгебарски линии од 3, 4 и повисоки редови повеќе од еднаш, особено кога се запознаваме со поларен координатен систем.
Сепак, да се вратиме на општата равенка и да се потсетиме на нејзините наједноставни училишни варијации. Како примери, се појавува парабола, чија равенка може лесно да се сведе на општа форма, и хипербола со еквивалентна равенка. Сепак, не е се така мазно...
Значаен недостаток на општата равенка е тоа што речиси секогаш не е јасно која линија ја дефинира. Дури и во наједноставниот случај, нема веднаш да сфатите дека ова е хипербола. Таквите распореди се добри само за маскенбал, така што типичен проблем се разгледува во текот на аналитичката геометрија доведување на равенката на линијата од 2 ред во канонска форма.
Која е канонската форма на равенката?
Ова е општо прифатена стандардна форма на равенка, кога за неколку секунди станува јасно каков геометриски објект дефинира. Покрај тоа, канонската форма е многу погодна за решавање на многу практични задачи. Така, на пример, според канонската равенка „рамно“ директно, прво, веднаш е јасно дека ова е права линија, и второ, точката што и припаѓа и векторот на насока се лесно видливи.
Очигледно е дека било кој Линија од 1 реде права линија. На вториот кат веќе не чека чуварот, туку многу поразновидна дружина од девет статуи:
Класификација на линии од втор ред
Користејќи посебен сет на дејства, секоја равенка на линија од втор ред се сведува на една од следниве форми:
(и се позитивни реални броеви)
1) 
– канонска равенка на елипсата;
2) – канонска равенка на хипербола;
3) 
– канонска равенка на парабола;
4) – имагинаренелипса;
5) – пар линии кои се вкрстуваат;
6) – пар имагинаренлинии кои се пресекуваат (со една валидна точка на пресек на почетокот);
7) – пар паралелни прави;
8) – пар имагинаренпаралелни линии;
9) – пар совпаѓачки линии.
Некои читатели може да имаат впечаток дека списокот е нецелосен. На пример, во точката бр. 7, равенката го одредува парот директно, паралелно со оската и се поставува прашањето: каде е равенката што ги одредува правите паралелни со оската на ординатите? Одговори не се смета за канонски. Правите линии го претставуваат истиот стандарден случај, ротиран за 90 степени, а дополнителниот внес во класификацијата е излишен, бидејќи не носи ништо суштински ново.
Така, постојат девет и само девет различни типови линии од втор ред, но во пракса најчести се елипса, хипербола и парабола.
Ајде прво да ја погледнеме елипсата. Како и обично, се фокусирам на оние точки кои се од големо значење за решавање на проблемите, а ако ви треба детално изведување на формули, докази на теореми, ве молиме погледнете го, на пример, учебникот на Базилев/Атанасјан или Александров.
Елипса и нејзината канонска равенка
Правопис.
Канонската равенка на елипса има форма , каде се позитивни реални броеви и . Подоцна ќе ја формулирам самата дефиниција за елипса, но засега е време да се одмориме од продавницата за зборување и да решиме заеднички проблем:
Како да се изгради елипса?
Да, само земете го и само нацртајте го. Задачата се јавува често, а значителен дел од учениците не се справуваат правилно со цртежот:
Пример 1
Конструирај ја елипсата дадена со равенката
Решение: Прво, да ја доведеме равенката во канонска форма: 
Зошто да се донесе? Една од предностите на канонската равенка е тоа што ви овозможува веднаш да одредите темиња на елипсата, кои се наоѓаат на точки. Лесно е да се види дека координатите на секоја од овие точки ја задоволуваат равенката.
Во овој случај : 
Линиски сегментповикани главната оскаелипса;
линиски сегмент – мала оска;
број 
повикани полу-главна осовинаелипса;
број 
– мала оска.
во нашиот пример: .
За брзо да замислите како изгледа одредена елипса, само погледнете ги вредностите на „a“ и „be“ на нејзината канонска равенка.
Сè е во ред, мазно и убаво, но има едно предупредување: го направив цртежот користејќи ја програмата. И можете да го направите цртежот користејќи која било апликација. Меѓутоа, во суровата реалност, на масата има карирано парче хартија, а глувците танцуваат во кругови на нашите раце. Луѓето со уметнички талент, се разбира, можат да се расправаат, но имате и глувци (иако помали). Не залудно човештвото измисли владетел, компас, транспортер и други едноставни уреди за цртање.
Поради оваа причина, веројатно нема да можеме точно да нацртаме елипса знаејќи ги само темињата. Во ред е ако елипсата е мала, на пример, со полуоски. Алтернативно, можете да ја намалите скалата и, соодветно, димензиите на цртежот. Но, генерално, многу е пожелно да се најдат дополнителни поени.
Постојат два пристапи за изградба на елипса - геометриски и алгебарски. Не ми се допаѓа конструкцијата со помош на компас и линијар бидејќи алгоритмот не е најкраток и цртежот е значително натрупан. Во случај на итност, ве молиме погледнете го учебникот, но во реалноста е многу порационално да се користат алатките на алгебрата. Од равенката на елипсата во нацртот брзо изразуваме: 
Равенката потоа се распаѓа на две функции: 
– го дефинира горниот лак на елипсата; 
– го дефинира долниот лак на елипсата.
Елипсата дефинирана со канонската равенка е симетрична во однос на координатните оски, како и во однос на потеклото. И ова е одлично - симетријата е скоро секогаш предвесник на гратис. Очигледно, доволно е да се справиме со првата координатна четвртина, па ни треба функцијата 
. Моли да се најдат дополнителни поени со апсциси 
. Ајде да допреме три СМС пораки на калкулаторот: 
Се разбира, исто така е убаво што ако се направи сериозна грешка во пресметките, веднаш ќе стане јасно за време на изградбата.
Ајде да ги означиме точките на цртежот (црвено), симетричните точки на преостанатите лакови (сини) и внимателно да ја поврземе целата компанија со линија: 
Подобро е да се нацрта почетната скица многу тенко, а дури потоа да се притисне со молив. Резултатот треба да биде сосема пристојна елипса. Патем, дали би сакале да знаете што е оваа крива?
Дефиниција на елипса. Фокуси на елипса и ексцентричност на елипсата
Елипсата е посебен случај на овал. Зборот „овален“ не треба да се разбере во филистинска смисла („детето нацрта овална“ итн.). Ова е математички термин кој има детална формулација. Целта на оваа лекција не е да се разгледа теоријата на овали и нивните различни типови, на кои практично не им се обрнува внимание во стандардниот курс на аналитичката геометрија. И, во согласност со поактуелните потреби, веднаш преминуваме на строгата дефиниција на елипса:
Елипсае множество од сите точки на рамнината, збирот на растојанијата до секоја од две дадени точки, т.н. триковиелипса, е константна големина, нумерички еднаква на должината на главната оска на оваа елипса: .
Во овој случај, растојанијата помеѓу фокусите се помали од оваа вредност: .
Сега сè ќе стане појасно: 
Замислете дека сината точка „патува“ по елипса. Значи, без разлика која точка на елипсата ќе ја земеме, збирот на должините на отсечките секогаш ќе биде ист:
Да се увериме дека во нашиот пример вредноста на збирот е навистина еднаква на осум. Ментално поставете ја точката „um“ на десното теме на елипсата, а потоа: , што треба да се провери.
Друг метод за негово цртање се заснова на дефиницијата за елипса. Високата математика понекогаш е причина за напнатост и стрес, па време е да имате уште една сесија за истовар. Ве молиме земете хартија Whatman или голем лист картон и закачете го на масата со два клинци. Тоа ќе бидат трикови. Заврзете зелена нишка на испакнатите глави на ноктите и повлечете ја до крај со молив. Оводот за молив ќе заврши во одредена точка што припаѓа на елипсата. Сега почнете да го движите моливот по листот хартија, држејќи ја зелената нишка затегната. Продолжете со процесот додека не се вратите на почетната точка... одлично... цртежот може да го проверат докторот и наставникот =)
Како да ги пронајдете фокусите на елипсата?
Во горниот пример, ги прикажав „готовите“ фокусни точки, а сега ќе научиме како да ги извлечеме од длабочините на геометријата.
Ако елипсата е дадена со канонска равенка, тогаш нејзините фокуси имаат координати 
, каде е растојание од секој фокус до центарот на симетријата на елипсата.
Пресметките се поедноставни отколку едноставни: 
! Специфичните координати на фокуси не можат да се идентификуваат со значењето на „це“!Повторувам дека ова е ДИСТЕНЦИЈА од секој фокус до центарот(што во општиот случај не мора да се наоѓа токму на потеклото).
И, според тоа, растојанието помеѓу фокусите, исто така, не може да се поврзе со канонската положба на елипсата. Со други зборови, елипсата може да се премести на друго место и вредноста ќе остане непроменета, додека фокусите природно ќе ги променат своите координати. Ве молиме земете го ова предвид додека дополнително ја истражувате темата.
Ексцентричност на елипсата и нејзиното геометриско значење
Ексцентричноста на елипсата е сооднос што може да земе вредности во опсегот.
Во нашиот случај:
Ајде да дознаеме како обликот на елипсата зависи од нејзината ексцентричност. За ова поправете ги левите и десните темињана разгледуваната елипса, односно вредноста на полуглавната оска ќе остане константна. Тогаш формулата за ексцентричност ќе добие форма: .
Да почнеме да ја приближуваме вредноста на ексцентричноста до единството. Ова е можно само доколку. Што значи тоа? ...сетете се на триковите 
. Ова значи дека фокусите на елипсата ќе се „раздвојат“ долж оската на апсцисата до страничните темиња. И, бидејќи „зелените сегменти не се гумени“, елипсата неизбежно ќе почне да се израмнува, претворајќи се во потенок и потенок колбас нанижан на оска.
Така, колку е поблиску вредноста на ексцентричноста на елипсата до единството, толку е поиздолжена елипсата.
Сега да го моделираме спротивниот процес: фокусите на елипсата 
тргнаа еден кон друг, приближувајќи се кон центарот. Ова значи дека вредноста на „ce“ станува сè помала и, соодветно, ексцентричноста се стреми кон нула: .
Во овој случај, „зелените сегменти“, напротив, ќе „станат преполни“ и ќе почнат да ја „туркаат“ линијата на елипсата нагоре и надолу.
Така, Колку е поблиску вредноста на ексцентричноста до нула, толку елипсата е повеќе слична со... погледнете го ограничувачкиот случај кога фокусите успешно се обединуваат на потекло:
Круг е посебен случај на елипса
Навистина, во случај на еднаквост на полуоските, канонската равенка на елипсата ја добива формата , која рефлексно се трансформира во равенката на круг со центар на почетокот на радиусот „а“, добро позната уште од училиште.
Во практиката почесто се користи ознаката со „зборувачка“ буква „ер“: . Радиусот е должината на сегментот, при што секоја точка на кругот е отстранета од центарот за растојание од радиус.
Забележете дека дефиницијата за елипса останува целосно точна: фокусите се совпаѓаат, а збирот на должините на совпаѓачките отсечки за секоја точка на кругот е константа. Бидејќи растојанието помеѓу фокусите е , тогаш ексцентричноста на кој било круг е нула.
Изградбата на круг е лесно и брзо, само користете компас. Сепак, понекогаш е неопходно да се дознаат координатите на некои од неговите точки, во овој случај одиме на познатиот начин - ја доведуваме равенката до веселата форма Матанов:
– функција на горниот полукруг;
– функција на долниот полукруг.
Потоа ги наоѓаме потребните вредности, разликуваат, интегрираати прави други добри работи.
Написот, се разбира, е само за референца, но како можете да живеете во светот без љубов? Креативна задача за самостојно решение
Пример 2
Составете ја канонската равенка на елипса ако се познати едно од нејзините фокуси и полумала оска (центарот е на почетокот). Најдете темиња, дополнителни точки и повлечете линија на цртежот. Пресметајте ја ексцентричноста.
Решение и цртање на крајот од часот
Ајде да додадеме акција:
Ротирајте и паралелно преведете елипса
Да се вратиме на канонската равенка на елипсата, имено, на состојбата, чија мистерија ги измачува љубопитните умови уште од првото спомнување на оваа крива. Така ја погледнавме елипсата 
, но дали во пракса не е можно да се исполни равенката 
? На крајот на краиштата, и овде, сепак, се чини дека е елипса!
Овој вид на равенка е ретка, но се среќава. И всушност дефинира елипса. Ајде да демистифицираме: 
Како резултат на изградбата, добиена е нашата родна елипса, ротирана за 90 степени. Тоа е, 
- Ова неканонски влезелипса 
. Рекорд!- равенката 
не дефинира друга елипса, бидејќи на оската нема точки (фокуси) кои би ја задоволиле дефиницијата за елипса.
Преземете од Depositfiles
Предавање бр.9. Тема 3: Линии од втор ред
Нека е дадена линија дефинирана со равенка од втор степен во некои DSC
каде се коефициентите 
не се еднакви на нула во исто време. Оваа линија се нарекувакрива или линија од втор ред.
Може да се случи да нема поени 
со реални координати кои ја задоволуваат равенката (1). Во овој случај, се верува дека равенката (1) дефинира имагинарна линија од втор ред. На пример, 
Ова е равенка на имагинарен круг.
Да разгледаме три важни специјални случаи на равенката (1).
3.1. Елипса
Елипсата е дефинирана со равенката
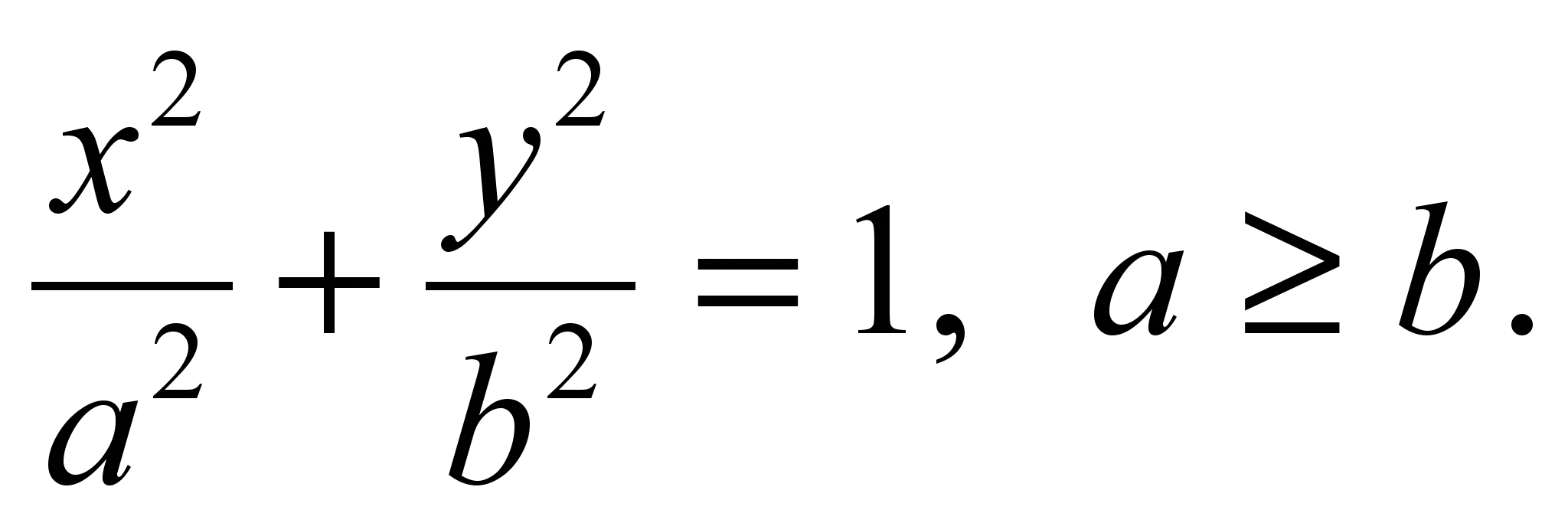(2)
Шансите АИ б се нарекуваат полу-големи и полу-мали оски, соодветно, а равенката (2) еканонски равенка на елипсата.
Да ставиме 
и означете на оскатаЗА Xпоени 
повиканитрикови елипса. Тогаш елипсата може да се дефинира како
локус на точки, збирот на растојанијата од кои до фокусите е константна вредност еднаква на 2А.
на
б
М К
— АФ 1 О Ф 2 а x
— б
Ајде да го покажеме. Нека поентата 
моменталната точка на елипсата. Во овој случај добиваме Тогаш еднаквоста мора да остане
Да го претставиме изразот (3) во форма
и квадрат од двете страни на изразот
Од тука добиваме 
Уште еднаш, да го квадрираме овој израз и да ја користиме релацијата 
, Потоа
(4)
Делење на двете страни на изразот (4) со 
, конечно ја добиваме канонската равенка на елипсата 
Да ја испитаме равенката (2). Ако замениме во равенката, тогаш равенката (2) нема да се промени. Ова значи дека елипсата е симетрична во однос на координатните оски. Затоа, да го разгледаме подетално делот од елипсата што се наоѓа во првата четвртина. Тоа е дефинирано со равенката 
Очигледно е дека елипсата минува низ точките 
. Откако ќе ја завршиме шематската конструкција во првиот квартал, симетрично ќе го прикажеме неговиот график во сите четвртини. Така, елипсата е континуирана затворена крива. Точките се нарекувааттемиња на елипсата.
Став 
повиканиексцентричностелипса. За елипса 
.
Директно 
се нарекуваатдиректори на елипсата.
Следното својство на директорите е точно::
Односот на растојанијата од фокусот и дирекцијата за точките на елипсата е константна вредност еднаква на ексцентричноста, т.е. 
Тоа се докажува на ист начин како и еднаквоста (3).
Забелешка 1. Заокружете 
е посебен случај на елипса. За неа 
3.2. Хипербола
Канонската равенка на хипербола има форма
тие. во равенката (1) треба да ставиме
Шансите АИ б се нарекуваат реални и имагинарни полуоски, соодветно.
Ставање 
, означете на оскатаЗА Xпоени 
повиканитрикови хипербола. Тогаш хиперболата може да се дефинира како
локус на точки, разликата во растојанија од кои до фокусите во апсолутна вредност е 2А, т.е.
на
ДО М
Ф 1 —А ЗА АФ 2 X
Доказот е сличен на оној за елипсата. Врз основа на формата на равенката на хипербола, заклучуваме и дека нејзиниот график е симетричен во однос на оските на координатниот систем. Делот од хиперболата што лежи во првата четвртина ја има равенката 
Од оваа равенка е јасно дека за доволно големиXхиперболата е блиску до права линија 
. По шематска конструкција во првиот квартал, симетрично го прикажуваме графикот во сите четвртини.
Поени 
се нарекуваатврвови хипербола. Директно 
се нарекуваатасимптоти - тоа се правите линии кон кои се стремат гранките на хиперболата без да ги пресечат.
Врската се викаексцентричностхипербола. За хипербола 
.
Директните линии се нарекуваатдиректорки хипербола. За директорите на хиперболата, важи својството слично на она за директорите на елипсата.
Пример. Најдете ја равенката на елипса чии темиња се во фокусите, а фокусите се на темињата на хиперболата 
.
По услов 
А
Конечно добиваме 
10.3. Парабола
Параболата е дефинирана со канонската равенка 
тие. во равенката (1) треба да ставиме
ДО 
коефициентРповикани ДОна
фокален параметар. М
Да означиме на оската О Xточка 
наречен фокус
- елипса;
- парабола;
- хипербола.
Криви од втор редна рамнина се линии дефинирани со равенки во кои променливата координира xИ yсе содржани во вториот степен. Тие вклучуваат елипса, хипербола и парабола.
Општата форма на равенката на кривата од втор ред е како што следува:
Каде А, Б, Ц, Д, Е, Ф- бројки и најмалку еден од коефициентите А, Б, Цне е еднаква на нула.
При решавање на проблеми со криви од втор ред, најчесто се разгледуваат канонските равенки на елипсата, хиперболата и параболата. Лесно е да се премине на нив од општите равенки; пример 1 за проблеми со елипсови ќе биде посветен на ова.
Елипса дадена со канонската равенка
Дефиниција на елипса.Елипса е множество од сите точки на рамнината за кои збирот на растојанијата до точките наречени фокуси е константна вредност поголема од растојанието помеѓу фокусите.
Фокусите се означени како на сликата подолу.
Канонската равенка на елипса има форма:
Каде аИ б (а > б) - должините на полуоските, т.е., половина од должините на сегментите отсечени со елипсата на координатните оски.
Правата линија што минува низ фокусите на елипсата е нејзината оска на симетрија. Друга оска на симетрија на елипсата е права линија што минува низ средината на отсечка нормална на овој сегмент. Точка ЗАпресекот на овие линии служи како центар на симетрија на елипсата или едноставно центар на елипсата.
Оската на апсцисата на елипсата се сече на точките ( а, ЗА) И (- а, ЗА), а оската на ординатите е во точки ( б, ЗА) И (- б, ЗА). Овие четири точки се нарекуваат темиња на елипсата. Отсечката помеѓу темињата на елипсата на оската x се нарекува нејзина главна оска, а на ординатна оска - нејзината помала оска. Нивните отсечки од врвот до центарот на елипсата се нарекуваат полуоски.
Ако а = б, тогаш равенката на елипсата добива форма . Ова е равенка на круг со радиус а, а круг е посебен случај на елипса. Елипса може да се добие од круг со радиус а, ако го компресирате во а/бпати по оската Ој .
Пример 1.Проверете дали правата дадена со општа равенка е 
, елипса.
Решение. Ја трансформираме општата равенка. Го користиме преносот на слободниот член на десната страна, поделбата по член по член на равенката со ист број и намалувањето на дропките:
Одговори. Равенката добиена како резултат на трансформациите е канонската равенка на елипсата. Затоа, оваа линија е елипса.
Пример 2.Составете ја канонската равенка на елипса ако нејзините полуоски се 5 и 4, соодветно.
Решение. Ја разгледуваме формулата за канонската равенка на елипса и ја заменуваме: полуголемата оска е а= 5, полуминорната оска е б= 4. Ја добиваме канонската равенка на елипсата:
Точки и , означени со зелено на главната оска, каде
се нарекуваат трикови.
повикани ексцентричностелипса.
Став б/аја карактеризира „растеченоста“ на елипсата. Колку е помал овој однос, толку повеќе елипсата е издолжена по главната оска. Сепак, степенот на издолжување на елипсата почесто се изразува преку ексцентричност, формулата за која е дадена погоре. За различни елипси, ексцентричноста варира од 0 до 1, секогаш останувајќи помала од единството.
Пример 3.Составете ја канонската равенка на елипсата ако растојанието помеѓу фокусите е 8 и главната оска е 10.
Решение. Ајде да направиме неколку едноставни заклучоци:
Ако главната оска е еднаква на 10, тогаш нејзината половина, односно полуоската а = 5 ,
Ако растојанието помеѓу фокусите е 8, тогаш бројот вод фокалните координати е еднаква на 4.
Заменуваме и пресметуваме:
Резултатот е канонската равенка на елипсата:
Пример 4.Составете ја канонската равенка на елипса ако нејзината главна оска е 26, а нејзината ексцентричност е .
Решение. Како што следува и од големината на главната оска и од равенката на ексцентричност, полуглавната оска на елипсата а= 13. Од равенката за ексцентричност го изразуваме бројот в, потребна за пресметување на должината на малата полуоска:
.
Го пресметуваме квадратот на должината на малата полуоска:
Ја составуваме канонската равенка на елипсата:
Пример 5.Определи ги фокусите на елипсата дадени со канонската равенка.
Решение. Најдете го бројот в, кој ги одредува првите координати на фокусите на елипсата:
.
Ги добиваме фокусите на елипсата:
Пример 6.Фокусите на елипсата се наоѓаат на оската Волсиметрично за потеклото. Составете ја канонската равенка на елипсата ако:
1) растојанието помеѓу фокусите е 30, а главната оска е 34
2) мала оска 24, а еден од фокусите е во точката (-5; 0)
3) ексцентричност, а едно од фокусите е во точката (6; 0)
Ајде да продолжиме да ги решаваме проблемите со елипсата заедно
Ако е произволна точка на елипсата (означена со зелено во горниот десен дел од елипсата на цртежот) и е растојанието до оваа точка од фокусите, тогаш формулите за растојанијата се како што следува:
За секоја точка што припаѓа на елипсата, збирот на растојанија од фокусите е константна вредност еднаква на 2 а.
Линии дефинирани со равенки
се нарекуваат директоркиелипса (на цртежот има црвени линии по должината на рабовите).
Од двете равенки погоре следува дека за која било точка на елипсата
,
каде и се растојанијата на оваа точка до насоките и .
Пример 7.Дадена е елипса. Напишете равенка за нејзините директори.
Решение. Ја гледаме директската равенка и откриваме дека треба да ја најдеме ексцентричноста на елипсата, т.е. Ги имаме сите податоци за ова. Ние пресметуваме:
.
Ја добиваме равенката на насоките на елипсата:
Пример 8.Составете ја канонската равенка на елипса ако нејзините фокуси се точки, а директорите се прави.
1. Линии од втор ред на Евклидовата рамнина.
2. Инваријанти на равенките на линијата од втор ред.
3. Определување на типот на правите од втор ред од инваријантите на неговата равенка.
4. Линии од втор ред на афината рамнина. Теорема на уникатност.
5. Центри од линии од втор ред.
6. Асимптоти и дијаметри на линии од втор ред.
7. Намалување на равенките на линиите од втор ред до наједноставни.
8. Главни насоки и дијаметри на линии од втор ред.
БИБЛИОГРАФИЈА
1. Линии од втор ред во Евклидовата рамнина.
Дефиниција:
Евклидска рамнинае простор со димензија 2,
(дводимензионален реален простор).Прави од втор ред се линии на пресек на кружен конус со рамнини кои не минуваат низ неговото теме.
Овие редови често се наоѓаат во различни прашања од природните науки. На пример, движењето на материјална точка под влијание на централното поле на гравитација се случува по една од овие линии.
Ако рамнината на сечење ги пресекува сите праволиниски генератрики на една празнина на конусот, тогаш делот ќе произведе линија наречена елипса(Сл. 1.1, а). Ако рамнината за сечење ги пресекува генератриките на двете шуплини на конусот, тогаш делот ќе произведе линија наречена хипербола(Сл. 1.1,6). И, конечно, ако рамнината за сечење е паралелна со една од генератриките на конусот (на 1,1, В- ова е генераторот АБ),тогаш делот ќе произведе линија наречена парабола.Ориз. 1.1 дава визуелна претстава за обликот на предметните линии.
Слика 1.1
Општата равенка на линијата од втор ред е како што следува:
(1)
(1*)
Елипса е множество точки на рамнината за кои збирот на растојанијата до двафиксни точкиФ 1 ИФ 2 оваа рамнина, наречена фокуси, е константна вредност.
Во овој случај, совпаѓањето на фокусите на елипсата не е исклучено. Очигледно ако фокусите се совпаѓаат, тогаш елипсата е круг.
За да ја изведеме канонската равенка на елипсата, го избираме потеклото O на Декартовиот координатен систем во средината на отсечката Ф 1 Ф 2 , и секирите ОИ ОУДа го насочиме како што е прикажано на сл. 1.2 (ако трикови Ф 1 И Ф 2 се совпаѓаат, тогаш О се совпаѓа со Ф 1 И Ф 2, и за оската Оможе да земете која било оска што минува низ ЗА).
Нека должината на сегментот Ф 1 Ф 2 Ф 1 И Ф 2 соодветно имаат координати (-с, 0) и (с, 0). Да означиме со 2аконстантата наведена во дефиницијата за елипса. Очигледно, 2a > 2c, т.е. a > c (Ако М- точка на елипсата (види Сл. 1.2), потоа | М.Ф. ] |+ | М.Ф. 2 | = 2 а, а бидејќи збирот на две страни М.Ф. 1 И М.Ф. 2 тријаголник М.Ф. 1 Ф 2 повеќе трета страна Ф 1 Ф 2 = 2c, потоа 2a > 2c. Природно е да се исклучи случајот 2a = 2c, оттогаш поентата Мсе наоѓа на сегментот Ф 1 Ф 2 а елипсата дегенерира во сегмент. ).
Нека М (x, y)(сл. 1.2). Да ги означиме со r 1 и r 2 растојанијата од точката Мдо поени Ф 1 И Ф 2 соодветно. Според дефиницијата за елипса еднаквостр 1 + р 2 = 2а(1.1)
е неопходен и доволен услов за локацијата на точката M (x, y) на дадена елипса.
Користејќи ја формулата за растојание помеѓу две точки, добиваме
(1.2)Од (1.1) и (1.2) следува дека сооднос
(1.3)претставува неопходен и доволен услов за местоположба на точка M со координати x и y на дадена елипса.Според тоа, релацијата (1.3) може да се смета како елипса равенка.Користејќи го стандардниот метод на „уништување на радикали“, оваа равенка се сведува на формата
(1.4) (1.5)Бидејќи равенката (1.4) е алгебарски заклучокелипса равенка (1.3), потоа координатите x и yкоја било точка Мелипсата ќе ја задоволи и равенката (1.4). Бидејќи за време на алгебарските трансформации поврзани со ослободување од радикали, може да се појават „дополнителни корени“, мора да се погрижиме дека која било точка М,чии координати ја задоволуваат равенката (1.4), се наоѓа на оваа елипса. За да го направите ова, очигледно, доволно е да се докаже дека вредностите на р 1 и р 2 за секоја точка ја задоволува релацијата (1.1). Па нека ги координатите XИ напоени Мја задоволува равенката (1.4). Замена на вредноста во 2од (1.4) на десната страна на изразот (1.2) за r 1, по едноставни трансформации наоѓаме дека сосема слично наоѓаме дека (1.6)
т.е. р 1 + р 2 = 2а,и затоа точката М се наоѓа на елипса. Се нарекува равенката (1.4). канонска равенка на елипса.Количини АИ бсе повикуваат соодветно главни и помали полуоски на елипсата(имињата „големи“ и „мали“ се објаснуваат со фактот дека а>б).
Коментар. Ако полуоските на елипсата АИ бсе еднакви, тогаш елипсата е круг чиј радиус е еднаков на Р = а = б, а центарот се совпаѓа со потеклото.
Хипербола е множество точки на рамнината за кои е апсолутната вредност на разликата во растојанија до две фиксни точкиФ 1 ИФ 2 на оваа рамнина, наречена фокуси, постои константна вредност (Трикови Ф 1 И Ф 2 природно е хиперболите да се сметаат за различни, бидејќи ако константата наведена во дефиницијата за хипербола не е еднаква на нула, тогаш нема ниту една точка на рамнината ако тие се совпаѓаат Ф 1 И Ф 2 , што би ги задоволило барањата за дефиниција на хипербола. Ако оваа константа е нула и Ф 1 се совпаѓа со Ф 2 , тогаш која било точка на рамнината ги задоволува барањата за дефиниција на хипербола. ).
За да ја изведеме канонската равенка на хипербола, го избираме потеклото на координатите во средината на сегментот Ф 1 Ф 2 , и секирите ОИ ОУДа го насочиме како што е прикажано на сл. 1.2. Нека должината на сегментот Ф 1 Ф 2 еднакво на 2 секунди. Потоа во избраниот координатен систем точките Ф 1 И Ф 2 соодветно имаат координати (-с, 0) и (с, 0) Да означиме со 2 Аконстантата наведена во дефиницијата за хипербола. Очигледно 2а< 2с, т. е. а< с.
Нека М- точка на рамнината со координати (x, y)(Сл. 1,2). Да ги означиме со r 1 и r 2 растојанијата М.Ф. 1 И М.Ф. 2 . Според дефиницијата за хипербола еднаквост
(1.7)е неопходен и доволен услов за локацијата на точката М на дадена хипербола.
Користејќи ги изразите (1.2) за r 1 и r 2 и релацијата (1.7), го добиваме следново неопходен и доволен услов за локација на точка M со координати x и y на дадена хипербола:
. (1.8)Користејќи го стандардниот метод на „уништување на радикали“, ја намалуваме равенката (1.8) на формата
(1.9) (1.10)Мора да се погрижиме равенката (1.9), добиена со алгебарски трансформации на равенката (1.8), да не добила нови корени. За да го направите ова, доволно е да го докажете тоа за секој поен М,координати XИ накои ја задоволуваат равенката (1.9), вредностите на r 1 и r 2 ја задоволуваат релацијата (1.7). Спроведувајќи аргументи слични на оние што беа дадени при изведување на формулите (1.6), ги наоѓаме следните изрази за количините од интерес за нас r 1 и r 2:
(1.11)Така, за предметната точка Мние имаме
, и затоа се наоѓа на хипербола.Се повикува равенката (1.9). канонската равенка на хипербола.Количини АИ бсе нарекуваат реални и имагинарни, соодветно полуоски на хиперболата.
Парабола е збир на точки на рамнината за кои е растојанието до некоја фиксна точкаФоваа рамнина е еднаква на растојанието до некоја фиксна права линија, исто така лоцирана во рамнината што се разгледува.
(MIF-2, бр. 3, 2005)
Линии од втор ред на авион
Стр. 1. Дефиниција за линија од втор ред
Размислете за рамнина на која е наведен правоаголен Декартов координатен систем (XOY). Тогаш која било точка М е уникатно одредена со нејзините координати (x, y). Покрај тоа, секој пар на броеви (x, y) дефинира одредена точка на рамнината. Координатите на точките може да задоволат одредени услови, на пример, некоја равенка f(x, y) = 0 во однос на непознатите (x, y). Во овој случај велат дека равенката f(x, y)=0 дефинира одредена фигура на рамнината. Ајде да погледнеме примери.
Пример 1.Размислете за функцијата y= f( x). Координатите на точките на графикот на оваа функција ја задоволуваат равенката y– f( x) = 0.
Пример 2.Равенка (*), каде а, б, в– некои бројки дефинираат одредена права линија на рамнината. (Се повикуваат равенките од формата (*). линеарна).
Пример 3.Графикот на хипербола се состои од точки чии координати ја задоволуваат равенката https://pandia.ru/text/80/134/images/image004_92.gif" width="161" height="25">.
Дефиниција 1. Равенка на формата (**), каде што барем еден од коефициентите е DIV_ADBLOCK75">
Ќе ги разгледаме геометриските и физичките својства на линиите споменати погоре. Да почнеме со елипса.
https://pandia.ru/text/80/134/images/image008_54.gif" width="79" height="44 src="> (1).
Се нарекува равенката (1). канонскиравенка на елипсата.
Обликот на елипсата може да се процени од Слика 1.
Ајде да го ставиме. Точките се нарекуваат триковиелипса. Постојат голем број на интересни својства поврзани со трикови, за кои ќе разговараме подолу.
Дефиниција 4. Хипербола е фигура на рамнина чии координати на сите точки ја задоволуваат равенката
(2).
Се нарекува равенката (2). канонскихипербола равенка. Типот на хипербола може да се процени од Слика 2.
Ајде да го ставиме. Точките се нарекуваат триковихипербола. Параметар аповикани валиден, и параметарот б- имагинарна полуоскахиперболи, соодветно вол– вистински и ох– имагинарна оска на хиперболата.
https://pandia.ru/text/80/134/images/image016_34.gif" width="61" height="41">, се нарекуваат асимптоти. За големи вредности на параметри xточките на асимптотите се приближуваат до гранките на хиперболата бескрајно блиску. На слика 2, асимптотите се прикажани со испрекинати линии.
Дефиниција 5. Парабола е фигура на рамнина чии координати на сите точки ја задоволуваат равенката
https://pandia.ru/text/80/134/images/image018_28.gif" width="47" height="45 src=">.
Стр. 3. Својства на LVP фокусите
За секој LVP во А.2. беа посочени посебни точки - трикови. Овие точки играат голема улога во објаснувањето на важните својства на елипсата, хиперболата и параболата. Овие својства ги формулираме во форма на теореми.
Теорема. 1. Елипсата е збир на точкиМ, така што збирот на растојанијата од овие точки до фокусите е еднаков на 2а:
https://pandia.ru/text/80/134/images/image020_26.gif" width="115" height="23 src="> (5).
За да формулираме слично својство за парабола, дефинираме директорка. Тоа е директно г, дадена со равенката https://pandia.ru/text/80/134/images/image022_23.gif" width="103" height="21 src="> (6).
Стр. 4. Фокуси и тангенти
https://pandia.ru/text/80/134/images/image024_24.gif" align="right" width="322" height="386 src=">.gif" width="52" height="24 src="> припаѓа на соодветниот HDL. Подолу се дадени равенките за тангентите што минуваат низ оваа точка:
- за елипса, (7)
- за хипербола, (8)
- за парабола. (9)
Ако нацртаме отсечки од двете фокуси до точката на тангенција со елипса или хипербола (тие се нарекуваат фокални радиусипоени), тогаш ќе се открие нешто извонредно имот(види Сл. 5 и 6): фокусните радиуси формираат еднакви агли со тангентата нацртана во оваа точка.
Овој имот има интересна физичка интерпретација. На пример, ако сметаме дека контурата на елипсата е пресликана, тогаш зраците на светлината од точкаст извор поставен на еден фокус, по рефлексијата од ѕидовите на колото, нужно ќе поминат низ вториот фокус.
Слично својство за парабола доби голема практична примена. Факт е дека фокалниот радиус на која било точка на параболата прави агол со тангентата повлечена до оваа точка еднаков на аголот помеѓу тангентата и оската на параболата.
Физички ова се толкува на следниов начин: зраците на точката поставена во фокусот на параболата, по рефлексијата од нејзините ѕидови, се шират паралелно со оската на симетрија на параболата. Затоа огледалата на фенерите и рефлектори имаат параболична форма. Патем, ако во него влезе млаз светлина (радио бранови) паралелно со оската на параболата, тогаш, по рефлексијата од ѕидовите, сите негови зраци ќе поминат низ фокусот. По овој принцип работат станиците за вселенски комуникации, како и радарите.
5. Уште малку физика
HDL најдоа широка употреба во физиката и астрономијата. Така, беше откриено дека едно релативно лесно тело (на пример, сателит) се движи во гравитационото поле на помасивно тело (планета или ѕвезда) по должината на траекторијата што претставува еден од LVP. Во овој случај, помасивното тело е во фокусот на оваа траекторија.
За прв пат овие својства беа детално проучени Јоханес Кеплер и тие беа наречени Кеплерови закони.
Тест бр.1 за ученици од 10-то одделение
Прашања за самотестирање (5 поени по задача)
М.10.1.1.Дефинирајте HDL. Наведете неколку примери на равенки кои го дефинираат LVP.
М.10.1.2.Пресметај ги координатите на фокусите на а) елипса, б) хипербола, ако а=13, б=5.
М.10.1.3.Состави ја канонската равенка на а) елипса, б) хипербола, ако се знае дека оваа права минува низ точки со координати (5, 6) и (-8, 7).
М.10.1.4.Проверете дали правата линија дадена со равенката (9) всушност ја пресекува параболата дадена со равенката (3) само во точката со координати . ( Забелешка: прво заменете ја равенката на тангентата со равенката на параболата, а потоа уверете се дека дискриминантот на добиената квадратна равенка е нула.)
М.10.1.5.Напишете равенка за тангентата на хиперболата со реална полуоска 8 и имагинарна полуоска - 4 во точката со координати x=11 ако втората координата на точката е негативна.
Практична работа (10 поени)
М.10.1.6.Конструирајте неколку елипси користејќи го следниот метод: прицврстете лист хартија на иверица и залепете неколку копчиња во хартијата (но не до крај). Земете парче конец и врзете ги краевите. Фрлете ја добиената јамка над двете копчиња (фокусните точки на идната елипса), повлечете ја конецот со остриот крај на моливот и внимателно повлечете линија, внимавајќи конецот да е затегнат. Со менување на димензиите на јамката, можете да изградите неколку конфокални елипси. Обидете се да објасните користејќи теорема 1 дека добиените линии се навистина елипсови и објаснете како, знаејќи го растојанието помеѓу копчињата и должината на конецот, можете да ги пресметате полуоските на елипсата.
