Алгоритам за елиминирање на левата рекурзија. Лева рекурзија. Рекурзивно спуштање со враќање

Особеноста на формалните граматики е тоа што тие овозможуваат да се дефинира бесконечен сет на синџири на јазик користејќи конечен сет на правила (се разбира, множеството синџири на јазикот може да биде и конечен, но дури и за едноставни реални јазици. овој услов обично не е исполнет). Примерот за граматика за потпишани децимални цели броеви погоре дефинира бесконечно множество цели броеви користејќи 15 правила.

Способноста да се користи конечен сет на правила се постигнува во оваа форма на граматичка нотација преку рекурзивни правила. Рекурзијата во граматичките правила се изразува во тоа што еден од нетерминалните симболи се дефинира преку себе. Рекурзијата може да биде директна (експлицитна) - тогаш симболот се дефинира преку себе во едно правило, или индиректна (имплицитна) - тогаш истото се случува преку синџир на правила.

Во граматиката G дискутирана погоре, директната рекурзија е присутна во правилото:<чс>-»<чс><цифра>, а во нејзината еквивалентна граматика Г“ - во правилото: Т-ВТФ.

За да не биде бесконечна рекурзијата, за нетерминалниот симбол на граматиката што учествува во неа, мора да има и други правила што ја дефинираат, заобиколувајќи се себеси и дозволуваат да се избегне бесконечна рекурзивна дефиниција (инаку овој симбол едноставно би не се потребни во граматиката). Овие правила се<чс>-»<цифра>- во граматиката на Г и Т->Ф - во граматиката на Г."

Во теоријата на формалните јазици ништо повеќе не може да се каже за рекурзија. Но, за поцелосно да го разберете значењето на рекурзијата, можете да прибегнете кон семантиката на јазикот - во примерот дискутиран погоре, ова е јазикот на потпишаните децимални цели броеви. Да го разгледаме неговото значење.

Дефиниција за граматика. Форма на екуса-маура „ЗО /

Ако се обидете да дефинирате што е број, тогаш можете да започнете со фактот дека секој број сам по себе е број. Понатаму, можете да забележите дека било кои две цифри се исто така број, потоа три цифри, итн. ограничен со било што). Сепак, можете да забележите дека секогаш кога генерираме нов број, едноставно додаваме единица десно (бидејќи сме навикнати да пишуваме од лево кон десно) на веќе напишаната серија на броеви. И оваа серија на броеви, почнувајќи од една цифра, е исто така број. Тогаш дефиницијата за концептот „број“ може да се конструира на овој начин: „број е која било цифра или друг број на кој се додава која било цифра десно“. Токму тоа ја формира основата на правилата на граматиките G и G“ и се рефлектира во втората линија од правилата во правилата.<чс>-><цифра> [ <чс><цифра>и T->F | ТФ. Другите правила во овие граматики ви дозволуваат да додадете знак на број (прва линија правила) и да го дефинирате концептот на „цифра“ (трета линија правила). Тие се елементарни и не бараат објаснување.

Принципот на рекурзија (понекогаш наречен „принцип на повторување“, кој не ја менува суштината) е важен концепт во идејата за формални граматики. На еден или друг начин, експлицитно или имплицитно, рекурзијата е секогаш присутна во граматиките на сите реални програмски јазици. Токму тоа ви овозможува да изградите бесконечен број јазични синџири и невозможно е да се зборува за нивната генерација без да се разбере принципот на рекурзија. Типично во граматиката на вистински јазик? програмирањето не содржи едно, туку цел сет на правила конструирани со помош на рекурзија.

Други начини за поставување граматики

Формата Бакус-Наур е удобен од формална гледна точка, но не секогаш лесно разбирлив начин на пишување формални граматики. Рекурзивните дефиниции се добри за формална анализа на јазичните низи, но не се погодни од човечка гледна точка. На пример, какви правила<чс>-><цифра> | <чс><цифра>ја рефлектираат способноста да се конструира број со додавање на кој било број на цифри десно, почнувајќи од една, што не е очигледно и бара дополнително објаснување.

Но, при креирањето на програмски јазик, важно е неговата граматика да биде разбрана не само од оние кои ќе креираат компајлери за овој јазик, туку и од корисниците на јазикот - идни развивачи на програми. Затоа, постојат и други начини за опишување на правилата на формалните граматики кои се насочени кон поголема разбирливост кај луѓето.

Пишување граматички правила

користејќи металикови

Пишувањето граматички правила со помош на метазнаци претпоставува дека низата граматички правила може да содржи специјални знаци - мета-

358 Поглавје 9. Формални јазици и граматики

Симболи - кои имаат посебно значење и се толкуваат на посебен начин. Најчесто користени метакарактери се () (загради), (квадратни загради), () (виткани загради), „,“ (запирка) и „“ (наводници). Овие метакарактери го имаат следново значење:

□ Заградите значат дека од сите синџири наведени во нив
знаци на дадено место од граматичкото правило може да има само еден це
пупка;

□ квадратните загради значат дека синџирот наведен во нив може да се појави
правилата на граматиката може или не може да се појават на дадено место (односно, тие можат
може да биде во него еднаш или воопшто не);

□ кадравите загради значат дека низата наведена во нив може да не се појави
граматичките правила се појавуваат на дадено место повеќе од еднаш, се појавуваат еднаш
еднаш или онолку пати по желба;

□ запирка се користи за одвојување низи од знаци во круг
загради;

□ Наводниците се користат во случаи кога е потребен еден од металиковите
вклучи во синџирот на вообичаен начин - тоа е, кога еден од заградите или зад
петтиот мора да биде присутен во синџирот на јазични знаци (ако самиот цитат
треба да се вклучи во синџир на знаци, тогаш мора да се повтори двапати - ова
принципот им е познат на развивачите на програми).

Вака би требало да изгледаат правилата на граматиката G, дискутирани погоре, ако се напишани со помош на метазнаци:

<число> -» [(+.-)]<цифра>{<цифра>}

<цифра> ->0|1|2|3|4|5|6|7|8|9

На вториот ред од правилата не му требаат коментари, а првото правило гласи вака: „бројот е синџир од знаци, кој може да започне со симболите + или -, потоа мора да содржи една цифра, која може да биде проследена со низа од кој било број цифри“. За разлика од формата Бакус-Наур, во форма на пишување со помош на метасимболи, како што можете да видите, прво, нејасен не-терминален симбол е отстранет од граматиката<чс>, и второ, успеавме целосно да ја елиминираме рекурзијата. Граматиката на крајот стана појасна.

Формата на пишување правила со помош на метасимболи е удобен и разбирлив начин за претставување на правилата на граматиката. Во многу случаи, ви овозможува целосно да се ослободите од рекурзијата со тоа што ќе го замените со симболот за повторување () (виткани загради). Како што ќе биде јасно од понатамошниот материјал, оваа форма е најчеста за еден од видовите граматики - редовни граматики.

Снимање граматички правила во графичка форма

Кога се пишуваат правила во графичка форма, целата граматика е претставена во форма на збир на специјално конструирани дијаграми. Оваа форма беше предложена при опишувањето на граматиката на јазикот Паскал, а потоа стана широко распространета во литературата. Не е достапен за сите видови граматики, туку само

Дефиниција за граматика. Бакус-Наур форма 359

За типови без контекст и обични, но тоа е доволно за да може да се користи за опишување на граматиките на добро познатите програмски јазици.

Во оваа форма на нотација, секој не-краен симбол на граматиката одговара на дијаграм конструиран во форма на насочен график. Графикот ги има следниве типови темиња:

□ влезна точка (на никаков начин не е означена на дијаграмот, едноставно започнува од таму)
влезен лак на графикот);

□ не-терминален симбол (означен со правоаголник на дијаграмот, во кој
кој се внесува ознаката на симболот);

□ синџир на терминални симболи (на дијаграмот означен со овална, круг
или правоаголник со заоблени рабови, внатре во кој е впишан
пупка);

□ нодална точка (на дијаграмот означена со задебелена точка или засенчена
круг);

□ излезна точка (не е означена на кој било начин, излезниот лак на графикот едноставно влегува во неа).

Секој дијаграм има само една влезна и една излезна точка, но било кој број темиња од другите три типа. Темењата се поврзани едни со други со насочени графички лаци (линии со стрелки). Лаците можат да излезат само од влезната точка и само да влезат во влезната точка. Останатите темиња на лакот можат и да влезат и да излезат (во правилно конструирана граматика, секое теме мора да има најмалку еден влез и најмалку еден излез).

За да изградите синџир од симболи што одговараат на кој било симбол на граматиката што не е терминал, треба да го земете предвид дијаграмот за овој симбол. Потоа, почнувајќи од влезната точка, треба да се движите по лаците на графиконот на дијаграмот низ кои било темиња до излезната точка. Во овој случај, поминувајќи низ темето означено со не-терминален симбол, овој симбол треба да се стави во добиениот синџир. Кога поминувате низ теме означено со синџир на терминални симболи, овие симболи треба да се стават и во синџирот што се добива. При минување низ нодалните точки на дијаграмот, не треба да се вршат никакви дејства на добиениот синџир. Во зависност од можниот пат на движење, можете да поминете низ кое било теме на графикот на дијаграмот еднаш, не еднаш или онолку пати колку што сакате. Веднаш штом ќе стигнеме до излезната точка на дијаграмот, изградбата на добиениот синџир е завршена.

Добиениот синџир, пак, може да содржи симболи што не се терминални. За да ги замените со низи од терминални симболи, повторно треба да ги земете предвид соодветните дијаграми. И така натаму додека не останат само терминалните знаци во синџирот. Очигледно, за да се конструира синџир на симболи на даден јазик, мора да се започне со разгледување со дијаграмот на целниот граматички симбол.

Ова е пригоден начин за опишување на правилата на граматиката, работење со слики и затоа фокусирано исклучиво на луѓе. Дури и едноставната презентација на неговите основни принципи овде се покажа доста незгодна, додека суштината

Поглавје 9. формални јазици и граматики

Методот е прилично едноставен. Ова може лесно да се види ако го погледнете описот на концептот „број“ од граматиката G користејќи ги дијаграмите на сл. 9.1.

Ориз. 9.1. Графички приказ на граматиката на потпишаните децимални цели броеви: на врвот - за концептот „број“; подолу - за концептот на „цифра“

Како што беше споменато погоре, овој метод главно се користи во литературата при презентирање на граматиките на програмските јазици. Погодно е за корисници - развивачи на програми, но сè уште нема практична примена во компајлери.

Класификација на јазици и граматики

Различни видови граматики веќе се споменати погоре, но не е посочено како и врз која основа се поделени на типови. За една личност, јазиците можат да бидат едноставни или сложени, но ова е чисто субјективно мислење, кое често зависи од личноста на личноста.

За компајлери, јазиците исто така може да се поделат на едноставни и сложени, но во овој случај постојат строги критериуми за оваа поделба. Како што ќе биде прикажано подолу, зависи од тоа на кој тип припаѓа одреден програмски јазик.

Рованија, комплексноста на препознавачот за овој јазик зависи. Колку е покомплексен јазикот, толку се поголеми пресметковните трошоци на компајлерот за анализа на синџирите на изворната програма напишана на овој јазик, и затоа, покомплексни се самиот компајлер и неговата структура. За некои типови јазици, во принцип е невозможно да се изгради компајлер кој би ги анализирал изворните текстови на овие јазици во прифатливо време врз основа на ограничени компјутерски ресурси (затоа сè уште е невозможно да се креираат програми на природни јазици, за на пример, на руски или англиски).

Класификација на граматики.

(Време: 1 сек. Меморија: 16 MB Тежина: 20%)

Во теоријата на формалните граматики и автомати (TFGiA), важна улога има т.н. граматики без контекст(КС-граматики). KS-граматика е четворка која се состои од множество N од не-терминални симболи, множество T терминални симболи, множество P од правила (продукции) и почетен симбол S што припаѓа на множеството N.

Секое производство p од P има форма A –> а, каде што A е не-терминален знак (A од N), а a е низа што се состои од терминални и нетерминални знаци. Процесот на излез на зборови започнува со линија која го содржи само почетниот знак S. После тоа, на секој чекор, еден од не-крајните знаци вклучени во тековната линија се заменува со десната страна на една од продукциите во која е лева страна. Ако после таква операција се добие низа што содржи само терминални знаци, тогаш излезниот процес завршува.

Во многу теоретски проблеми погодно е да се разгледа т.н нормални формиграматичар Процесот на доведување на граматиката во нормална форма често започнува со елиминирање на левата рекурзија. Во овој проблем ќе го разгледаме само неговиот посебен случај, наречен непосредна лева рекурзија. Правилото за заклучување A -> R се вели дека содржи непосредна лева рекурзија ако првиот знак од низата R е A.

Дадена е CS граматиката. Треба да го најдеме бројот на правила кои содржат непосредна лева рекурзија.

Внесени податоци

Првата линија од влезната датотека INPUT.TXT содржи n (1 ≤ n ≤ 1000) правила во граматиката. Секоја од следните n линии содржи едно правило. Не-терминалните симболи се означуваат со големи букви од англиската азбука, терминалните симболи - со мали букви. Левата страна на производот е одвоена од десната страна со симболите –>. Должината на десната страна на производот е од 1 до 30 знаци.

Класификација на формалните граматики според Чомски

· Граматика од тип 0 (општа форма). Правилата имаат форма α→β

· Граматички тип 1 (во зависност од контекстот, KZ)

Правилата имаат форма αAβ → αγβ. γ припаѓа на V +, т.е. граматиката не се скратува

α, β се нарекуваат лев и десен контекст

· Граматика тип 2 (без контекст, KS)

Правилата се од формата A → α. α припаѓа на V*, т.е. граматиката може да се скратува => Јазиците на КС не се содржани во КС

Најблиску до BPF

· Граматика тип 3 (автоматска, редовна)

Правилата се од формата A → aB, A → a, A → ε

Автоматските јазици се содржани во CS јазиците

Пример. Граматика која генерира јазик на регуларни изрази во заграда.

S → (S) | СС | ε

Генерација (заклучок)

Ознаки

=>+ (1 или повеќе)

=>* (0 или повеќе)

Реченичка форма на граматикае низа што може да се изведе од почетниот знак.

Реченица (реченица) граматикае реченица која се состои само од терминали.

Јазик L(G) граматика- ова е збир на сите нејзини предлози.

Ознаки:

Лев, десен излез (генерација).

Лев и десен излез за реченицата i + i * i

Излезно стебло (синтаксичко дрво, анализирано дрво) на низа од реченици. За разлика од генерирањето, информациите за редоследот на заклучоците се исклучени од него.

Анализирај ја круната на дрвото - синџир на ознаки од лист од лево кон десно

Граматиката која произведува повеќе од едно анализирано дрво за некоја реченица се нарекува двосмислена.

Пример за двосмислена граматика. Граматика на аритметички изрази.

E → E+E | E*E | јас

Две анализирани стебла за синџирот i + i * i

Пример за двосмислена граматика. Граматика на условен исказ

S → ако b тогаш S

| ако b тогаш S друго S

Две анализирани стебла за синџирот ако b тогаш ако b тогаш a

Претворете во еквивалентна недвосмислена граматика:

S → ако b тогаш S

| ако b тогаш S2 друго S

S2 → ако b тогаш S2 друго S2

44. Формални јазици и граматики: непразни, конечни и бесконечни јазици

45.Еквивалентност и минимизирање на автоматите

Еквивалентност на машините со конечни состојби

Нека S е азбука (конечно множество симболи) и S* збир на сите зборови во азбуката S. Да означиме со e празен збор, т.е. воопшто не содржи букви (симболи од S), туку знакот × - операција на доделување (спојување) зборови.

Значи, aav × va = aavva. Знакот × на операцијата припишување често се испушта.

Зборовите во азбуката S ќе бидат означени со мали грчки букви a, b, g, .... Очигледно, e е единицата за операцијата за наведување:

Очигледно е и дека операцијата припишување е асоцијативна, т.е. (ab)g = a(bg).

Така, множеството S* од сите зборови во азбуката S во однос на операцијата за доделување е полугрупа со идентитет, т.е. моноид;

S* се нарекува слободен моноид над азбуката S.

Минимизирање на државната машина

Машините за различни состојби можат да функционираат на ист начин дури и ако имаат различен број на состојби. Важна задача е да се најде машина за минимална конечна состојба која имплементира дадено автоматско мапирање.

Природно е да се наречат две состојби на еквивалент на автомат, кој не може да се разликува со ниту еден влезен збор.

Дефиниција 1: Две состојби p и q на машина со конечни состојби

A = (S,X,Y,s0,d,l) се нарекуваат еквивалентни (означени со p~q) ако ("aО X*)l*(p,a) =l*(q, a)

46. ​​Еквивалентност на Туринг машините со една лента и со повеќе ленти

Очигледно е дека концептот на k-лента MT е поширок од концептот на „обична“ машина со една лента. ДЕФИНИЦИЈА 6. (k+1)-машина за лента M′ со програма w симулира k-лента машина M ако за кое било множество влезни зборови (x1, x2, …, xk) резултатот од работата M′ се совпаѓа со резултатот од работата М на истите влезни податоци. Се претпоставува дека зборот w најпрво е напишан на (k+1)-тата лента M′. Резултатот се подразбира како состојба на првите k MT ленти во моментот на запирање, и ако M не застане на даден влез, тогаш машината што го симулира исто така не треба да застане на овој влез.

ДЕФИНИЦИЈА 7. А (k+1)-лента MT M* се нарекува универзална Тјуринг машина за машини со k-лента ако за која било машина со k-лента M постои програма w на која M* симулира M. 12 Ве молиме запомнете: во дефиницијата за универзален MT истата машина M′ мора да симулира различни машини со k-лента (на различни програми w). Размислете за следнава теорема. ТЕОРЕМА 3. За кој било k≥1, постои универзална (k+1)–Туринг лента. Доказ. Да ја докажеме теоремата конструктивно, т.е. Да покажеме како може да се конструира потребната универзална машина М*. Да ја разгледаме само општата градежна шема, испуштајќи сложени детали. Главната идеја е да се постави опис на симулираната Тјуринг машина на дополнителна (k+1)-та лента и да се користи овој опис за време на процесот на симулација.

ДЕФИНИЦИЈА 8. Ќе речеме дека Тјуринговата машина М пресметува делумна функција f:A*→A* ако за која било x∈A* напишана на првата лента на машината M: ако f(x) е дефинирана, тогаш M запира , и во моментот кога запира, зборот f(x) е напишан на последната лента од машината; ако f(x) не е дефинирана, тогаш машината М не запира.

ДЕФИНИЦИЈА 9. Ќе кажеме дека машините M и M′ се еквивалентни ако пресметаат иста функција. Концептот на еквивалентност е „послаб“ од симулацијата: ако машината M′ симулира машина M, тогаш машината M′ е еквивалентна на M; обратното, општо земено, не е точно. Од друга страна, симулацијата бара M′ да има барем толку ленти како M, додека за еквивалентноста не е потребна 15. Токму ова својство ни овозможува да ја формулираме и докажеме следната теорема.

ТЕОРЕМА 4. За која било машина со k-лента M со временска сложеност T(n), постои еквивалентна машина со една лента M′ со временска сложеност T′ (n) = O(T 2 (n)).

48. Еквивалентни трансформации на КС-граматики: исклучување на верижни правила, отстранување на произволно граматичко правило

Дефиниција.Добро граматичко правило , Каде , V A се нарекува синџир.

Изјава.За KS-граматика Γ што содржи верижни правила, можно е да се конструира еквивалентна граматика Γ" што не содржи синџири на правила.

Идејата на доказот е како што следува. Ако граматичката шема ја има формата

R = (..., ,..., , ... , а },

тогаш таквата граматика е еквивалентна на граматика со шема

R" = (..., а ,...},

бидејќи излезот во граматиката со дијаграмот на колото R на синџирот а :

а

може да се добие во граматика со шемата R“ користејќи го правилото а .

Во принцип, доказот за последната изјава може да се направи на следниов начин. Ајде да го поделиме R на две подмножества R 1 и R 2, вклучувајќи ги во R 1 сите правила на формата

За секое правило од R 1 наоѓаме множество правила S( ), кои се изградени вака:

Ако *а во Р 2 има правило α, каде што α е синџирот на речникот (V t V A)*, потоа во S( ) овозможете го правилото α.

Ајде да конструираме нова шема R“ со комбинирање на правилата R 2 и сите конструирани множества S( ). Добиваме граматика „G“ = (V t, V A , I, R“), која е еквивалентна на дадената и не содржи правила на формата .

Како пример, да го извршиме исклучокот на правилата на синџирот од граматиката на G 1.9 со шемата:

R=( +|,

*|,

()|а)

Прво, да ги поделиме граматичките правила на две подмножества:

R 1 = ( , },

R2 = ( +, *, ()|а)

За секое правило од R 1 конструираме соодветно подмножество.

S( ) = { *, ()|а ),

S( ) = { ()|а)

Како резултат на тоа, ја добиваме саканата граматичка шема без правила на синџир во форма:

R2U S( ) U S( ) = { + | * | () | а,

* | () | а,

() | а)

Последниот тип на трансформација што се разгледува е поврзан со отстранување на правилата со празна десна страна од граматиката.

Дефиниција.Љубезно правило $ се нарекува поништувачко правило.

49.Еквивалентни трансформации на КС-граматики: отстранување на бескорисни симболи.

Нека се даде произволна КС-граматика Г . Нетерминален А оваа граматика се нарекува продуктивни , ако има терминален синџир (вклучувајќи празен) таков што А Þ * а непродуктивни.

Теорема. Секоја CS граматика е еквивалентна на CS граматика без непродуктивни нетерминали.

Нетерминален А граматика Г повикани остварливи , доколку постои таков синџир а , Што С Þ * а . Во спротивно се нарекува нетерминалот недостижни.

Теорема. Секоја KS-граматика е еквивалентна на KS-граматика без недостапни нетерминали.

Се нарекува не-терминален симбол во граматиката на KS бескорисни (или излишни) , ако е или недостижна или непродуктивна.

Теорема. Секоја CS-граматика е еквивалентна на CS-граматика во која нема бескорисни нетерминали.

Пример.Елиминирајте ги бескорисните симболи во граматиката

С® aC | А; А ® такси; Б ® б ; В ® а.

Чекор 1. Градиме многу остварливиликови: {С} ® { С, Ц, А}® { С, Ц, А, Б}. Сите не-терминали се достапни. Нема недостижни, граматиката не се менува.

Чекор 2. Градиме многу продуктивниликови: {Ц, Б}® { С, Ц, Б}. Го добиваме тоа А - непродуктивен. Го исфрламе и сите правила со него надвор од граматиката. Добиваме

С® aC; Б ® б ; В ® а.

Чекор 3. Градиме многу остварливисимболи на новата граматика: {С} ® { С, Ц}. Го добиваме тоа Б недостижни. Го исфрламе и сите правила со него надвор од граматиката. Добиваме

С® aC; В ® а.

Ова е конечниот резултат.

50. Еквивалентни трансформации на КС-граматики: елиминирање на левата рекурзија, лево факторизација

Отстранување на левата рекурзија

Главната тешкотија при користење на предвидувачка анализа е да се најде граматика за влезниот јазик што може да се користи за да се изгради табела за анализа со уникатно дефинирани влезови. Понекогаш, со некои едноставни трансформации, граматиката што не е LL(1) може да се сведе на еквивалентна LL(1) граматика. Меѓу овие трансформации, најефективни се левата факторизација и отстранување лева рекурзија. Тука треба да се наведат две точки. Прво, не секоја граматика станува LL(1) по овие трансформации, и второ, по таквите трансформации добиената граматика може да стане помалку разбирлива.

Директната лева рекурзија, односно рекурзија на формата, може да се отстрани на следниот начин. Прво ги групираме А-правилата:

каде што ниту една од низите не започнува со A. Потоа го заменуваме овој сет на правила со

каде што А" е нов не-терминал. Од не-терминалот А можете да ги изведете истите синџири како порано, но сега не можете лева рекурзија. Оваа постапка ги отстранува сите директни лево рекурзии, но левата рекурзија која вклучува два или повеќе чекори не е отстранета. Даден подолу алгоритам 4.8ви овозможува да избришете сè лево рекурзииод граматиката.

Лево факторизација

Главната идеја на левата факторизација е дека во случај кога не е јасно која од двете алтернативи треба да се користи за проширување на нетерминалот А, треба да се сменат правилата А за да се одложи одлуката додека нема доволно информации за донесе правилна одлука.

Ако - две А -правила и влезниот синџир започнува со непразна низа, излез од не знаеме дали да се прошириме според првото или второто правило. Можете да ја одложите одлуката со проширување. Потоа, откако ќе анализирате од што може да се заклучите, можете да се проширите за или за . Лево факторизирани правила имаат форма

51. Туринг машински јазик.

Машината Тјуринг вклучува неограничено во двете насоки лента(Можни се туринг машини кои имаат неколку бесконечни ленти), поделени на ќелии и контролен уред(исто така наречен глава за читање-пишување (ГЗЧ)), способен да биде во еден од збир на држави. Бројот на можни состојби на контролниот уред е конечен и прецизно наведен.

Контролниот уред може да се движи лево и десно по лентата, да чита и пишува знаци од некоја конечна азбука во ќелии. Се издвојува посебно празенсимбол кој ги исполнува сите ќелии на лентата, освен оние од нив (конечниот број) на кои се запишани влезните податоци.

Контролниот уред работи според правила за транзиција, кои го претставуваат алгоритмот, остварливиоваа Тјуринг машина. Секое правило за транзиција ѝ дава инструкции на машината, во зависност од моменталната состојба и симболот забележан во тековната ќелија, да напише нов симбол во оваа ќелија, да премине во нова состојба и да помести една ќелија налево или надесно. Некои состојби на машината на Туринг може да се означат како терминал, а одењето на било кој од нив значи крај на работата, стопирање на алгоритмот.

Туринговата машина се нарекува детерминистички, ако секоја комбинација на симбол на состојба и лента во табелата одговара на најмногу едно правило. Ако постои пар „лента симбол - состојба“ за кој има 2 или повеќе инструкции, таквата Тјуринг машина се нарекува недетерминистички.

LL(k)-граматика ако, за даден стринг и првите k знаци (ако ги има) изведени од , постои најмногу едно правило што може да се примени на A за да се добие излезот од некоја терминална низа,

Ориз. 4.4.

почнувајќи со и продолжувајќи со споменатите k терминали.

Граматиката се нарекува LL(k)-граматика ако е LL(k)-граматика за некои k.

Пример 4.7. Размислете за граматиката G = ((S, A, B), (0, 1, a, b), P, S), каде што P се состои од правила

S -> A | B, A -> aAb | 0, B -> aBbb | 1.

Еве . G не е LL (k)-граматика за кое било k. Интуитивно, ако започнеме со читање доволно долга низа знаци a , не знаеме кое од правилата S -> A и S -> B се применило прво додека не наидеме на 0 или 1.

Осврнувајќи се на точната дефиниција на LL (k)-грамата, поставуваме и y = a k 1b 2k . Потоа заклучоци

одговараат на заклучоците (1) и (2) од дефиницијата. Првите k знаци од низите x и y се исти. Сепак, заклучокот е лажен. Бидејќи k овде е произволно избрано, G не е LL -граматика.

Последици од дефиницијата за LL(k)-граматика

Теорема 4.6. КС-граматика е LL(k)-граматика ако и само ако за две различни правилаи од P крстосница празно со сите овие , Што .

Доказ. Потреба. Да претпоставиме дека и ги задоволуваме условите на теоремата и содржи x. Потоа, по дефиниција за ПРВА, за некои y и z има заклучоци

(Забележете дека овде го искористивме фактот што N не содржи бескорисни нетерминали, како што се претпоставува за сите граматички што се разгледуваат.) Ако |x|< k ; то y = z = e . Так как , то G не LL (k)- грамматика .

Адекватност. Да претпоставиме дека G не е LL(k)-граматика.

Потоа има два заклучоци

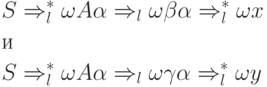
дека синџирите x и y се совпаѓаат во првите k позиции, но . Затоа и се различни правила од P и секое од множествата И го содржи синџирот FIRST k (x) што се совпаѓа со синџирот FIRST k (y).

Пример 4.8. Граматика G составена од две правила S -> aS | a нема да биде LL(1)-граматика, бидејќи

ПРВА 1 (аС) = ПРВА 1 (а) = а.

Интуитивно, ова може да се објасни на следниов начин: гледајќи го само овој прв знак при парсирање на синџир што започнува со симболот a, не знаеме кое од правилата S -> aS или S -> a треба да се примени на S. Од друга страна, G е LL(2)-граматика. Навистина, во ознаката на штотуку претставената теорема, ако , тогаш A = S и . Бидејќи за S се дадени само двете посочени правила, тогаш . Бидејќи FIRST2(aS) = aa и FIRST2(a) = a, тогаш според последната теорема G ќе биде LL (2)-граматика.

Отстранување на левата рекурзија

Главната тешкотија при користење на предвидувачка анализа е да се најде граматика за влезниот јазик што може да се користи за да се изгради табела за анализа со уникатно дефинирани влезови. Понекогаш, со некои едноставни трансформации, граматиката што не е LL(1) може да се сведе на еквивалентна LL(1) граматика. Меѓу овие трансформации, најефективни се левата факторизација и отстранувањето на левата рекурзија. Тука треба да се наведат две точки. Прво, не секоја граматика станува LL(1) по овие трансформации, и второ, по таквите трансформации добиената граматика може да стане помалку разбирлива.

Директната лева рекурзија, односно рекурзија на формата, може да се отстрани на следниот начин. Прво ги групираме А-правилата:

каде ниту една од линиите не започнува со А. Потоа го заменуваме овој сет на правила со

каде што А" е новиот нетерминал. Од нетерминалот А може да се заклучат истите синџири како порано, но сега нема лева рекурзија. Оваа постапка ги отстранува сите непосредни леви рекурзии, но не ја отстранува левата рекурзија која вклучува два или повеќе чекори. подолу алгоритам 4.8ви овозможува да ги отстраните сите леви рекурзии од граматиката.

Алгоритам 4.8. Отстранување на левата рекурзија.

Влез. КС-граматика Г без е-правила (од формата А -> е ).

Излезете. КС-граматика Г“ без лева рекурзија, еквивалентно на Г.

Метод. Следете ги чекорите 1 и 2.

(1) Подредете ги нетерминалите на граматиката G по кој било редослед.

(2) Направете ја следната постапка:

По (i-1)-тото повторување на надворешната јамка на чекор 2 за кое било правило на формата , каде што к< i , выполняется s >к. Како резултат на тоа, при следното повторување (од i), внатрешната јамка (за j) сукцесивно ја зголемува долната граница на m во кое било правило , додека не постои m >= i . Потоа, по отстранувањето на непосредната лева рекурзија за A i-правилата, m станува поголем од i.