Pag-andar ng pamamahagi. Probability theory panimula Distribution function dalawang constants

Kahulugan ng function ng pamamahagi

Hayaang ang $X$ ay isang random na variable, at ang $x$ ay ang probabilidad ng pamamahagi ng random variable na ito.

Kahulugan 1

Ang distribution function ay isang function na $F(x)$ na nagbibigay-kasiyahan sa kundisyon $F\left(x\right)=P(X

Kung hindi man, kung minsan ang distribution function ay tinatawag pinagsama-samang function ng pamamahagi o integral na batas ng pamamahagi.

Sa pangkalahatan, ang graph ng distribution function ay isang graph ng isang hindi bumababa na function na may hanay ng mga value na kabilang sa segment na $\left$ (at ang 0 at 1 ay kinakailangang kasama sa hanay ng mga value). Sa kasong ito, ang function ay maaaring o walang function jumps (Fig. 1)

Figure 1. Halimbawa ng distribution function graph

Distribution function ng isang discrete random variable

Hayaang maging discrete ang random variable na $X$. At hayaan ang isang serye ng pamamahagi nito para dito. Para sa ganoong halaga, ang probability distribution function ay maaaring isulat sa sumusunod na anyo:

Distribution function ng isang tuluy-tuloy na random variable

Hayaang maging tuloy-tuloy na ang random variable na $X$.

Ang graph ng distribution function ng naturang random variable ay palaging kumakatawan sa isang hindi bumababa na tuluy-tuloy na function (Larawan 3).

Isaalang-alang natin ngayon ang kaso kung saan pinaghalo ang random variable na $X$.

Ang graph ng distribution function ng naturang random variable ay palaging isang non-decreasing function na may minimum na value na 0 at maximum na value na 1, ngunit hindi ito tuluy-tuloy na function sa buong domain ng definition (iyon ay, ito ay may mga pagtalon sa mga indibidwal na punto) (Larawan 4).

Figure 4. Mixed random variable distribution function

Mga halimbawa ng mga problema sa paghahanap ng function ng pamamahagi

Halimbawa 1

Ang isang bilang ng mga pamamahagi ng paglitaw ng kaganapan $A$ sa tatlong mga eksperimento ay ibinigay.

Larawan 5.

Hanapin ang probability distribution function at i-plot ito.

Solusyon.

Dahil discrete ang random variable, magagamit natin ang formula na $\F\left(x\right)=\sum\limits_(x_i

Para sa $x>3$, $F\left(x\right)=0.2+0.1+0.3+0.4=1$;

Mula dito nakuha namin ang sumusunod na function ng pamamahagi ng posibilidad:

Larawan 6.

Buuin natin ang graph nito:

Larawan 7.

Halimbawa 2

Isinasagawa ang isang eksperimento kung saan maaaring mangyari o hindi mangyari ang $A$. Ang posibilidad na mangyari ang kaganapang ito ay $0.6$. Hanapin at buuin ang distribution function ng isang random variable.

Solusyon.

Dahil ang posibilidad na mangyari ang kaganapang $A$ ay katumbas ng $0.6$, kung gayon ang posibilidad na hindi mangyari ang kaganapang ito ay katumbas ng $1-0.6=0.4$.

Bumuo muna tayo ng serye ng pamamahagi para sa random variable na ito:

Larawan 8.

Dahil ang random variable ay discrete, nakita namin ang distribution function sa pamamagitan ng pagkakatulad sa Problema 1:

Kapag $x\le 0$, $F\left(x\right)=0$;

Para sa $x>1$, $F\left(x\right)=0.4+0.6=1$;

Kaya, nakukuha namin ang sumusunod na function ng pamamahagi:

Larawan 9.

Buuin natin ang graph nito:

Larawan 10.

Ang function ng pamamahagi ay ang pinaka-pangkalahatang anyo ng pagtukoy ng batas sa pamamahagi. Ito ay ginagamit upang tukuyin ang parehong discrete at tuloy-tuloy na random variable. Ito ay karaniwang itinalaga. Pag-andar ng pamamahagi tinutukoy ang posibilidad na ang isang random na variable ay kumukuha ng mga halaga na mas mababa sa isang nakapirming tunay na numero, i.e. Ang function ng pamamahagi ay ganap na naglalarawan ng isang random na variable mula sa isang probabilistikong punto ng view. Tinatawag din siya pinagsama-samang pagpapaandar ng pamamahagi.

Ang geometric na interpretasyon ng distribution function ay napakasimple. Kung ang isang random na variable ay itinuturing bilang isang random na punto sa axis (Larawan 6), na bilang isang resulta ng pagsubok ay maaaring tumagal ng isa o ibang posisyon sa axis, kung gayon ang distribution function ay ang posibilidad na ang random na punto bilang isang resulta ng pagsubok ay mahuhulog sa kaliwa ng punto.

Para sa isang discrete random variable na maaaring kumuha ng mga halaga, ang distribution function ay may form
kung saan ang hindi pagkakapantay-pantay ay nangangahulugan na ang pagsusuma ay nalalapat sa lahat ng mga halaga na mas mababa sa . Mula sa formula na ito ay sumusunod na ang distribution function ng isang discrete random variable ay isang stepped broken line (Fig. 7). Sa bawat bagong halaga ng isang random na variable, ang hakbang ay tumataas nang mas mataas ng isang halaga na katumbas ng posibilidad ng halagang ito. Ang kabuuan ng lahat ng jumps sa distribution function ay katumbas ng isa.

Ang tuluy-tuloy na random variable ay may tuluy-tuloy na distribution function, ang graph ng function na ito ay may hugis ng makinis na curve (Larawan 8).

Isaalang-alang natin ang mga pangkalahatang katangian ng mga function ng pamamahagi.

Ari-arian 1. Ang distribution function ay hindi negatibo, isang function sa pagitan ng zero at isa:

Ang bisa ng ari-arian na ito ay sumusunod mula sa katotohanan na ang distribution function ay tinukoy bilang ang posibilidad ng isang random na kaganapan na binubuo sa katotohanan na .

Ari-arian 2. Ang posibilidad ng isang random na variable na bumagsak sa isang agwat ay katumbas ng pagkakaiba sa pagitan ng mga halaga ng function ng pamamahagi sa mga dulo ng agwat na ito, i.e.

Ito ay sumusunod na ang posibilidad ng anumang indibidwal na halaga ng isang tuluy-tuloy na random variable ay zero.

Ari-arian 3. Ang distribution function ng isang random variable ay isang non-decreasing function, i.e. .

Ari-arian 4. Sa minus infinity ang distribution function ay katumbas ng zero, at sa plus infinity ito ay isa, i.e. At .

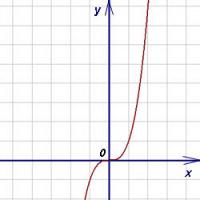
Halimbawa 1. Ang distribution function ng isang tuluy-tuloy na random variable ay ibinibigay ng expression

Hanapin ang coefficient at gumuhit ng graph. Tukuyin ang posibilidad na ang isang random na variable ay kukuha ng halaga sa pagitan bilang resulta ng eksperimento.

Random variable ay isang variable na maaaring tumagal sa ilang mga halaga depende sa iba't ibang mga pangyayari, at Ang random variable ay tinatawag na tuluy-tuloy , kung maaari itong kumuha ng anumang halaga mula sa anumang limitado o walang limitasyong pagitan. Para sa isang tuluy-tuloy na random na variable, imposibleng ipahiwatig ang lahat ng posibleng mga halaga, kaya itinalaga namin ang mga agwat ng mga halagang ito na nauugnay sa ilang mga probabilidad.

Kabilang sa mga halimbawa ng tuluy-tuloy na random na variable ang: ang diameter ng isang bahagi na dinidiin sa isang partikular na laki, ang taas ng isang tao, ang flight range ng isang projectile, atbp.

Dahil para sa tuluy-tuloy na random variable ang function F(x), Hindi katulad discrete random variables, ay walang mga jump kahit saan, kung gayon ang posibilidad ng anumang indibidwal na halaga ng isang tuluy-tuloy na random na variable ay zero.

Nangangahulugan ito na para sa isang tuluy-tuloy na random na variable ay walang saysay na pag-usapan ang tungkol sa pamamahagi ng posibilidad sa pagitan ng mga halaga nito: bawat isa sa kanila ay may zero na posibilidad. Gayunpaman, sa isang kahulugan, kabilang sa mga halaga ng isang tuluy-tuloy na random na variable mayroong "higit pa at mas malamang". Halimbawa, halos walang sinuman ang magdududa na ang halaga ng isang random na variable - ang taas ng isang random na nakatagpo na tao - 170 cm - ay mas malamang kaysa sa 220 cm, bagaman ang parehong mga halaga ay maaaring mangyari sa pagsasanay.

Distribution function ng tuluy-tuloy na random variable at probability density

Bilang isang batas sa pamamahagi na may katuturan lamang para sa tuluy-tuloy na mga random na variable, ipinakilala ang konsepto ng density ng pamamahagi o density ng probability. Ating lapitan ito sa pamamagitan ng paghahambing ng kahulugan ng distribution function para sa tuluy-tuloy na random variable at para sa discrete random variable.

Kaya, ang distribution function ng isang random variable (parehong discrete at tuloy-tuloy) o integral function ay tinatawag na function na tumutukoy sa posibilidad na ang halaga ng isang random variable X mas mababa sa o katumbas ng halaga ng limitasyon X.

Para sa isang discrete random variable sa mga punto ng mga halaga nito x1 , x 2 , ..., x ako,... ang masa ng mga probabilidad ay puro p1 , p 2 , ..., p ako,..., at ang kabuuan ng lahat ng masa ay katumbas ng 1. Ilipat natin ang interpretasyong ito sa kaso ng tuluy-tuloy na random variable. Isipin natin na ang isang mass na katumbas ng 1 ay hindi puro sa mga indibidwal na puntos, ngunit patuloy na "pinahiran" kasama ang abscissa axis Oh na may ilang hindi pantay na density. Probability ng isang random variable na bumabagsak sa anumang lugar Δ x ay bibigyang-kahulugan bilang masa bawat seksyon, at ang average na density sa seksyong iyon bilang ratio ng masa sa haba. Ipinakilala lang namin ang isang mahalagang konsepto sa teorya ng posibilidad: density ng pamamahagi.

Densidad ng posibilidad f(x) ng isang tuluy-tuloy na random na variable ay ang derivative ng distribution function nito:

.

Ang pag-alam sa function ng density, maaari mong mahanap ang posibilidad na ang halaga ng isang tuluy-tuloy na random na variable ay nabibilang sa closed interval [ a; b]:

ang posibilidad na ang isang tuluy-tuloy na random variable X kukuha ng anumang halaga mula sa pagitan [ a; b], ay katumbas ng isang tiyak na integral ng probability density nito mula sa a dati b:

.

Sa kasong ito, ang pangkalahatang formula ng function F(x) probability distribution ng isang tuluy-tuloy na random variable, na maaaring gamitin kung ang density function ay kilala f(x) :

.

Ang probability density graph ng isang tuluy-tuloy na random variable ay tinatawag na distribution curve nito (figure below).

Lugar ng isang figure (may shade sa figure) na nalilimitahan ng isang curve, mga tuwid na linya na iginuhit mula sa mga punto a At b patayo sa x-axis, at sa axis Oh, graphic na ipinapakita ang posibilidad na ang halaga ng tuluy-tuloy na random variable X ay nasa saklaw ng a dati b.

Mga katangian ng probability density function ng isang tuluy-tuloy na random variable

1. Ang posibilidad na ang isang random na variable ay kukuha ng anumang halaga mula sa pagitan (at ang lugar ng figure na nililimitahan ng graph ng function f(x) at axis Oh) ay katumbas ng isa:

2. Ang probability density function ay hindi maaaring kumuha ng mga negatibong halaga:

at sa labas ng pagkakaroon ng pamamahagi ay zero ang halaga nito

Densidad ng pamamahagi f(x), pati na rin ang function ng pamamahagi F(x), ay isa sa mga anyo ng batas sa pamamahagi, ngunit hindi katulad ng pagpapaandar ng pamamahagi, hindi ito pangkalahatan: ang density ng pamamahagi ay umiiral lamang para sa tuluy-tuloy na mga random na variable.

Banggitin natin ang dalawang pinakamahalagang uri ng pamamahagi ng tuluy-tuloy na random variable sa pagsasanay.

Kung ang distribution density function f(x) tuluy-tuloy na random variable sa ilang may hangganang pagitan [ a; b] ay tumatagal ng isang pare-parehong halaga C, at sa labas ng pagitan ay tumatagal ng isang halaga na katumbas ng zero, pagkatapos ito ang pamamahagi ay tinatawag na uniporme .

Kung ang graph ng distribution density function ay simetriko tungkol sa gitna, ang average na mga halaga ay puro malapit sa gitna, at kapag lumayo mula sa gitna, ang mga mas naiiba sa average ay kinokolekta (ang graph ng function ay kahawig ng isang seksyon ng isang kampana), pagkatapos ito ang pamamahagi ay tinatawag na normal .

Halimbawa 1. Ang probability distribution function ng isang tuluy-tuloy na random variable ay kilala:

Maghanap ng function f(x) probability density ng tuluy-tuloy na random variable. Bumuo ng mga graph ng parehong function. Hanapin ang posibilidad na ang tuluy-tuloy na random na variable ay kukuha ng anumang halaga sa pagitan mula 4 hanggang 8: .

Solusyon. Nakukuha namin ang probability density function sa pamamagitan ng paghahanap ng derivative ng probability distribution function:

Graph ng isang function F(x) - parabola:

Graph ng isang function f(x) - tuwid:

Hanapin natin ang posibilidad na ang tuluy-tuloy na random na variable ay kukuha ng anumang halaga sa hanay mula 4 hanggang 8:

Halimbawa 2. Ang probability density function ng isang tuluy-tuloy na random variable ay ibinibigay bilang:

Kalkulahin ang koepisyent C. Maghanap ng function F(x) probability distribution ng isang tuluy-tuloy na random variable. Bumuo ng mga graph ng parehong function. Hanapin ang posibilidad na ang tuluy-tuloy na random na variable ay kukuha ng anumang halaga sa hanay mula 0 hanggang 5: .

Solusyon. Coefficient C nakita namin, gamit ang property 1 ng probability density function:

Kaya, ang probability density function ng isang tuluy-tuloy na random variable ay:

Sa pamamagitan ng pagsasama, nakita namin ang function F(x) mga pamamahagi ng posibilidad. Kung x < 0 , то F(x) = 0 . Kung 0< x < 10 , то

.

x> 10, pagkatapos F(x) = 1 .

Kaya, ang kumpletong talaan ng probability distribution function ay:

Graph ng isang function f(x) :

Graph ng isang function F(x) :

Hanapin natin ang posibilidad na ang tuluy-tuloy na random na variable ay kukuha ng anumang halaga sa hanay mula 0 hanggang 5:

Halimbawa 3. Probability density ng tuluy-tuloy na random variable X ay ibinibigay ng pagkakapantay - pantay , at . Maghanap ng coefficient A, ang posibilidad na ang isang tuluy-tuloy na random na variable X kukuha ng anumang halaga mula sa interval ]0, 5[, ang distribution function ng isang tuluy-tuloy na random variable X.

Solusyon. Sa pamamagitan ng kondisyon ay nakarating tayo sa pagkakapantay-pantay

Samakatuwid, , mula saan . Kaya,

.

Ngayon nakita namin ang posibilidad na ang isang tuluy-tuloy na random variable X kukuha ng anumang halaga mula sa pagitan ]0, 5[:

Ngayon ay nakukuha natin ang distribution function ng random variable na ito:

Halimbawa 4. Hanapin ang probability density ng isang tuluy-tuloy na random variable X, na kumukuha lamang ng mga hindi negatibong halaga, at ang function ng pamamahagi nito .

Ang resulta ng anumang random na eksperimento ay maaaring mailalarawan sa qualitatively at quantitatively. Ng husay ang resulta ng isang random na eksperimento - random kaganapan. Anuman quantitative na katangian, na bilang resulta ng isang random na eksperimento ay maaaring tumagal ng isa sa isang bilang ng mga halaga, - random na halaga. Random na halaga ay isa sa mga pangunahing konsepto ng probability theory.

Hayaan ang isang arbitrary na puwang ng posibilidad. Random variable ay tinatawag na real numerical function x =x (w), w W na para sa anumang real x .

Kaganapan Nakaugalian na itong isulat sa anyong x< x. Sa sumusunod, ang mga random na variable ay ilalarawan ng maliliit na letrang Griyego na x, h, z, ...

Ang random variable ay ang bilang ng mga puntos na nakuha kapag naghahagis ng die, o ang taas ng isang estudyante na random na pinili mula sa isang study group. Sa unang kaso na kinakaharap natin discrete random variable(ito ay kumukuha ng mga halaga mula sa isang discrete number set M=(1, 2, 3, 4, 5, 6); sa pangalawang kaso - kasama tuloy-tuloy random variable(ito ay tumatagal ng mga halaga mula sa isang tuloy-tuloy na hanay ng numero - mula sa pagitan ng linya ng numero ako=).

Ang bawat random na variable ay ganap na tinutukoy ng nito function ng pamamahagi.

Kung ang x ay isang random na variable, kung gayon ang function F(x) = F x(x) = P(x< x) ay tinatawag na function ng pamamahagi random variable x. Dito P(x<x) - ang posibilidad na ang random variable na x ay kumukuha ng halagang mas mababa sa x.

Mahalagang maunawaan na ang distribution function ay ang "pasaporte" ng isang random variable: naglalaman ito ng lahat ng impormasyon tungkol sa random variable at samakatuwid ang pag-aaral ng isang random na variable ay binubuo sa pag-aaral nito mga function ng pamamahagi, na kadalasang simpleng tawag pamamahagi.

Ang distribution function ng anumang random variable ay may mga sumusunod na katangian:

Kung ang x ay isang discrete random variable na kumukuha ng mga halaga x 1 <x 2 < … <x i < … с вероятностями p 1 <p 2 < … <p i < …, то таблица вида

x 1	x 2	…	x i	…
p 1	p 2	…	p i	…

tinawag pamamahagi ng isang discrete random variable.

Ang distribution function ng isang random variable na may ganitong distribution ay may anyo

Ang isang discrete random variable ay may isang step distribution function. Halimbawa, para sa random na bilang ng mga puntos na nakuha sa isang throw ng isang die, ang distribution, distribution function, at ang graph ng distribution function ay:

1	2	3	4	5	6
1/6	1/6	1/6	1/6	1/6	1/6

Kung ang distribution function F x(x) ay tuloy-tuloy, pagkatapos ay ang random variable x ay tinatawag tuluy-tuloy na random variable.

Kung ang distribution function ng isang tuluy-tuloy na random variable naiba-iba, pagkatapos ay isang mas visual na representasyon ng random variable ang ibibigay ng probability density ng random variable p x(x), na nauugnay sa function ng pamamahagi F x(x) mga formula

At .

Mula dito, sa partikular, ito ay sumusunod na para sa anumang random na variable .

Kapag nilulutas ang mga praktikal na problema, madalas na kinakailangan upang mahanap ang halaga x, kung saan ang function ng pamamahagi F x(x) ang random variable x ay tumatagal ng isang ibinigay na halaga p, ibig sabihin. kailangang lutasin ang equation F x(x) = p. Mga solusyon ng naturang equation (mga kaukulang halaga x) sa probability theory ay tinatawag dami.

Dami x p ( p-quantile, level quantile p) random variable na mayroong function ng pamamahagi F x(x), tinatawag na solusyon xp mga equation F x(x) = p, p(0, 1). Para sa ilang p ang equation F x(x) = p maaaring may ilang mga solusyon, para sa ilan - wala. Nangangahulugan ito na para sa kaukulang random variable, ang ilang mga quantile ay hindi natatanging tinukoy, at ilang mga quantile ay hindi umiiral.

3. Ang distribution function ay hindi bumababa: kung, kung gayon

4. Pag-andar ng pamamahagi naiwan tuloy: para kahit kanino.

Tandaan. Ang huling pag-aari ay nagpapahiwatig kung anong mga halaga ang kinukuha ng function ng pamamahagi sa mga break point. Minsan ang kahulugan ng function ng pamamahagi ay binuo gamit ang isang maluwag na hindi pagkakapantay-pantay: . Sa kasong ito, ang continuity sa kaliwa ay pinapalitan ng continuity sa kanan: kapag . Hindi nito binabago ang anumang makabuluhang katangian ng function ng pamamahagi, kaya ang tanong na ito ay terminolohiya lamang.

Ang mga katangian 1-4 ay katangian, i.e. anumang function na nagbibigay-kasiyahan sa mga katangiang ito ay isang distribution function ng ilang random variable.

Ang distribution function ay natatanging tumutukoy sa probability distribution ng isang random variable. Sa katunayan, ito ay isang unibersal at pinaka-biswal na paraan ng paglalarawan sa pamamahagi na ito.

Kung mas lumalaki ang function ng pamamahagi sa isang naibigay na pagitan ng linya ng numero, mas mataas ang posibilidad ng isang random na variable na nahuhulog sa pagitan na ito. Kung ang posibilidad na mahulog sa isang pagitan ay zero, kung gayon ang pamamahagi ng function dito ay pare-pareho.

Sa partikular, ang posibilidad na ang isang random na variable ay kukuha ng isang ibinigay na halaga ay katumbas ng pagtalon sa distribution function sa isang naibigay na punto:

.

Kung tuluy-tuloy ang distribution function sa point , kung gayon ang posibilidad na kunin ang value na ito para sa isang random na variable ay zero. Sa partikular, kung ang distribution function ay tuloy-tuloy sa buong numerical axis (at ang kaukulang distribution ay tinatawag tuloy-tuloy), kung gayon ang posibilidad ng pagtanggap ng anumang ibinigay na halaga ay zero.

Mula sa kahulugan ng function ng pamamahagi, sumusunod na ang posibilidad ng isang random na variable na bumagsak sa isang agwat na sarado sa kaliwa at bukas sa kanan ay katumbas ng:

Gamit ang formula na ito at ang paraan sa itaas ng paghahanap ng posibilidad na matamaan ang anumang naibigay na punto, ang mga probabilidad ng isang random na variable na makapasok sa mga pagitan ng iba pang mga uri ay madaling matukoy: , at . Dagdag pa, sa pamamagitan ng measure extension theorem, maaari nating natatanging palawigin ang sukat sa lahat ng Borel set ng number line. Upang mailapat ang teorama na ito, kinakailangang ipakita na ang sukat na tinukoy sa mga pagitan ay sigma-additive sa mga ito; kapag pinatutunayan ito, ang mga katangian 1-4 ay ginagamit nang eksakto (sa partikular, ang pag-aari ng kaliwang pagpapatuloy 4, kaya hindi ito maaaring itapon).

Pagbuo ng isang random na variable na may ibinigay na distribusyon

Isaalang-alang natin ang isang random na variable na may function ng pamamahagi. Magpanggap na tayo tuloy-tuloy. Isaalang-alang ang random variable

.

Madaling ipakita na magkakaroon ito ng pare-parehong pamamahagi sa segment.