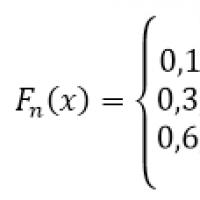Empirical function probability theory. Empirical distribution function, mga katangian. Serye ng pagkakaiba-iba. Polygon at histogram

Pagpapasiya ng empirical distribution function

Hayaang maging random variable ang $X$. Ang $F(x)$ ay ang distribution function ng isang ibinigay na random variable. Magsasagawa kami ng $n$ na mga eksperimento sa isang ibinigay na random na variable sa ilalim ng parehong mga kundisyon, independiyente sa bawat isa. Sa kasong ito, nakakakuha kami ng isang pagkakasunud-sunod ng mga halaga $x_1,\ x_2\ $, ... ,$\ x_n$, na tinatawag na sample.

Kahulugan 1

Ang bawat value na $x_i$ ($i=1,2\ $, ... ,$ \ n$) ay tinatawag na variant.

Ang isang pagtatantya ng theoretical distribution function ay ang empirical distribution function.

Kahulugan 3

Ang isang empirical distribution function na $F_n(x)$ ay isang function na tumutukoy para sa bawat value $x$ ang relatibong dalas ng kaganapan $X \

kung saan ang $n_x$ ay ang bilang ng mga opsyon na mas mababa sa $x$, ang $n$ ay ang sample size.

Ang pagkakaiba sa pagitan ng empirical function at theoretical ay ang theoretical function ay tumutukoy sa probabilidad ng kaganapan $X

Mga katangian ng empirical distribution function

Isaalang-alang natin ngayon ang ilang mga pangunahing katangian ng function ng pamamahagi.

Ang saklaw ng function na $F_n\left(x\right)$ ay ang segment na $$.

Ang $F_n\left(x\right)$ ay isang hindi bumababa na function.

Ang $F_n\left(x\right)$ ay isang left continuous function.

Ang $F_n\left(x\right)$ ay isang piecewise constant function at tumataas lamang sa mga punto ng value ng random variable na $X$

Hayaan ang $X_1$ ang pinakamaliit at $X_n$ ang pinakamalaking opsyon. Pagkatapos ay $F_n\left(x\right)=0$ para sa $(x\le X)_1$ at $F_n\left(x\right)=1$ para sa $x\ge X_n$.

Ipakilala natin ang isang teorama na nag-uugnay sa teoretikal at empirikal na mga pag-andar.

Teorama 1

Hayaan ang $F_n\left(x\right)$ ang empirical distribution function, at ang $F\left(x\right)$ ang theoretical distribution function ng pangkalahatang sample. Pagkatapos ang pagkakapantay-pantay ay humahawak:

\[(\mathop(lim)_(n\to \infty ) (|F)_n\left(x\right)-F\left(x\right)|=0\ )\]

Mga halimbawa ng mga problema sa paghahanap ng empirical distribution function

Halimbawa 1

Hayaang maitala sa distribusyon ng sampling ang sumusunod na data gamit ang isang talahanayan:

Larawan 1.

Hanapin ang sample size, gumawa ng empirical distribution function at i-plot ito.

Laki ng sample: $n=5+10+15+20=50$.

Ayon sa property 5, mayroon kami niyan para sa $x\le 1$ $F_n\left(x\right)=0$, at para sa $x>4$ $F_n\left(x\right)=1$.

halaga ng $x

Kaya nakukuha natin ang:

Larawan 2.

Larawan 3.

Halimbawa 2

20 lungsod ang random na napili mula sa mga lungsod ng gitnang bahagi ng Russia, kung saan nakuha ang sumusunod na data sa mga pamasahe sa pampublikong sasakyan: 14, 15, 12, 12, 13, 15, 15, 13, 15, 12, 15, 14 , 15, 13, 13, 12, 12, 15, 14, 14.

Gumawa ng empirical distribution function para sa sample na ito at i-plot ito.

Isulat natin ang mga sample na halaga sa pataas na pagkakasunud-sunod at kalkulahin ang dalas ng bawat halaga. Nakukuha namin ang sumusunod na talahanayan:

Larawan 4.

Laki ng sample: $n=20$.

Ayon sa property 5, mayroon kami niyan para sa $x\le 12$ $F_n\left(x\right)=0$, at para sa $x>15$ $F_n\left(x\right)=1$.

halaga ng $x

Kaya nakukuha natin ang:

Larawan 5.

I-plot natin ang empirical distribution:

Larawan 6.

Orihinalidad: $92.12\%$.

Serye ng pagkakaiba-iba. Polygon at histogram.

Saklaw ng pamamahagi- kumakatawan sa isang maayos na pamamahagi ng mga yunit ng populasyon na pinag-aaralan sa mga pangkat ayon sa isang tiyak na magkakaibang katangian.

Depende sa katangian na pinagbabatayan ng pagbuo ng serye ng pamamahagi, sila ay nakikilala katangian at pagkakaiba-iba mga hilera ng pamamahagi:

§ Ang mga serye ng pamamahagi na binuo sa pataas o pababang pagkakasunud-sunod ng mga halaga ng isang quantitative na katangian ay tinatawag pagkakaiba-iba.

Ang variation series ng distribution ay binubuo ng dalawang column:

Ang unang hanay ay nagbibigay ng mga quantitative na halaga ng iba't ibang katangian, na tinatawag mga pagpipilian at itinalaga. Discrete na opsyon - ipinahayag bilang isang integer. Ang pagpipiliang interval ay mula sa at hanggang. Depende sa uri ng mga opsyon, maaari kang bumuo ng isang discrete o interval variation series.
Ang ikalawang hanay ay naglalaman ng bilang ng tiyak na opsyon, na ipinahayag sa mga tuntunin ng mga frequency o frequency:

Mga frequency- ang mga ito ay ganap na mga numero, na nagpapakita ng bilang ng mga beses sa kabuuang isang naibigay na halaga ng isang katangian ay nangyayari, na nagsasaad. Ang kabuuan ng lahat ng mga frequency ay dapat na katumbas ng bilang ng mga yunit sa buong populasyon.

Mga frequency() ay mga frequency na ipinahayag bilang isang porsyento ng kabuuan. Ang kabuuan ng lahat ng mga frequency na ipinahayag bilang mga porsyento ay dapat na katumbas ng 100% sa mga fraction ng isa.

Graphic na representasyon ng serye ng pamamahagi

Ang serye ng pamamahagi ay biswal na ipinakita gamit ang mga graphical na larawan.

Ang serye ng pamamahagi ay inilalarawan bilang:

§ Polygon

§ Mga histogram

§ Naiipon

Polygon

Kapag gumagawa ng polygon, ang mga halaga ng iba't ibang katangian ay naka-plot sa pahalang na axis (x-axis), at ang mga frequency o frequency ay naka-plot sa vertical axis (y-axis).

1. Polygon sa Fig. 6.1 ay batay sa data mula sa micro-census ng populasyon ng Russia noong 1994.

Histogram

Upang makabuo ng isang histogram, ang mga halaga ng mga hangganan ng mga agwat ay ipinahiwatig kasama ang abscissa axis at, batay sa mga ito, ang mga parihaba ay itinayo, ang taas nito ay proporsyonal sa mga frequency (o mga frequency).

Sa Fig. 6.2. nagpapakita ng histogram ng distribusyon ng populasyon ng Russia noong 1997 ayon sa pangkat ng edad.

Fig.1. Pamamahagi ng populasyon ng Russia ayon sa mga pangkat ng edad

Empirical distribution function, mga katangian.

Ang empirical distribution function (sampling distribution function) ay isang function na tumutukoy para sa bawat value x ang relative frequency ng event X

Sa kaibahan sa empirical distribution function ng isang sample, ang population distribution function ay tinatawag na theoretical distribution function. Ang pagkakaiba sa pagitan ng mga function na ito ay ang teoretikal na function ay tumutukoy sa posibilidad ng kaganapan X

Habang tumataas ang n, ang relatibong dalas ng kaganapan X

Mga pangunahing katangian

Hayaang maayos ang isang elementarya na kinalabasan. Pagkatapos ay ang distribution function ng discrete distribution na ibinigay ng sumusunod na probability function:

saan, at - bilang ng mga sample na elemento na katumbas ng . Sa partikular, kung ang lahat ng mga elemento ng sample ay iba, kung gayon .

Ang matematikal na inaasahan ng distribusyon na ito ay:

Kaya, ang sample mean ay ang theoretical mean ng sampling distribution.

Katulad nito, ang sample variance ay ang theoretical variance ng isang sampling distribution.

Ang random variable ay may binomial distribution:

Ang sample distribution function ay isang walang pinapanigan na pagtatantya ng distribution function:

Ang variance ng sample distribution function ay may anyo:

Ayon sa malakas na batas ng malalaking numero, ang sample distribution function ay halos tiyak na converges sa theoretical distribution function:

halos tiyak sa .

Ang sample distribution function ay isang asymptotically normal na pagtatantya ng theoretical distribution function. Kung , kung gayon

Ayon sa pamamahagi sa .

Lecture 13. Ang konsepto ng istatistikal na pagtatantya ng mga random na variable

Hayaang malaman ang istatistikal na frequency distribution ng isang quantitative na katangian na X. Tukuyin natin sa pamamagitan ng bilang ng mga obserbasyon kung saan ang halaga ng katangian ay naobserbahang mas mababa sa x at ng n ang kabuuang bilang ng mga obserbasyon. Malinaw, ang relatibong dalas ng kaganapan X< x равна и является функцией x. Так как эта функция находится эмпирическим (опытным) путем, то ее называют эмпирической.

Empirical distribution function(sampling distribution function) ay isang function na tumutukoy para sa bawat value x ang relatibong dalas ng kaganapan X< x. Таким образом, по определению ,где - число вариант, меньших x, n – объем выборки.

Sa kaibahan sa empirical distribution function ng isang sample, ang population distribution function ay tinatawag theoretical distribution function. Ang pagkakaiba sa pagitan ng mga pag-andar na ito ay tinutukoy ng teoretikal na pag-andar probabilidad mga kaganapan X< x, тогда как эмпирическая – relatibong dalas ang parehong kaganapan.

Habang tumataas ang n, ang relatibong dalas ng kaganapan X< x, т.е. стремится по вероятности к вероятности этого события. Иными словами

Mga katangian ng empirical distribution function:

1) Ang mga halaga ng empirical function ay nabibilang sa segment

2) - hindi bumababa na pag-andar

3) Kung ang pinakamaliit na opsyon, kung gayon = 0 para sa , kung ang pinakamalaking opsyon, kung gayon = 1 para sa .

Ang empirical distribution function ng sample ay nagsisilbing tantiyahin ang theoretical distribution function ng populasyon.

Halimbawa. Bumuo tayo ng isang empirical function batay sa sample distribution:

Mga pagpipilian
Mga frequency

Hanapin natin ang sample size: 12+18+30=60. Ang pinakamaliit na opsyon ay 2, kaya =0 para sa x £ 2. Ang halaga ng x<6, т.е. , наблюдалось 12 раз, следовательно, =12/60=0,2 при 2< x £6. Аналогично, значения X < 10, т.е. и наблюдались 12+18=30 раз, поэтому =30/60 =0,5 при 6< x £10. Так как x=10 – наибольшая варианта, то =1 при x>10. Kaya, ang nais na empirical function ay may anyo:

Ang pinakamahalagang katangian ng mga pagtatantya sa istatistika

Hayaang kailangang pag-aralan ang ilang quantitative na katangian ng pangkalahatang populasyon. Ipagpalagay natin na mula sa mga teoretikal na pagsasaalang-alang posible na maitatag iyon alin ang eksaktong ang pamamahagi ay may isang palatandaan at ito ay kinakailangan upang tantiyahin ang mga parameter kung saan ito ay tinutukoy. Halimbawa, kung ang katangiang pinag-aaralan ay naipamahagi nang normal sa populasyon, kung gayon kinakailangan na tantiyahin ang inaasahan sa matematika at karaniwang paglihis; kung ang katangian ay may pamamahagi ng Poisson, kung gayon kinakailangan na tantiyahin ang parameter l.

Karaniwan, ang sample na data lamang ang magagamit, halimbawa, mga halaga ng isang quantitative na katangian na nakuha bilang resulta ng n independiyenteng mga obserbasyon. Isinasaalang-alang bilang mga independiyenteng random na mga variable maaari nating sabihin iyon upang makahanap ng istatistikal na pagtatantya ng isang hindi kilalang parameter ng isang teoretikal na pamamahagi ay nangangahulugan ng paghahanap ng isang function ng mga naobserbahang random na variable na nagbibigay ng tinatayang halaga ng tinantyang parameter. Halimbawa, upang matantya ang mathematical na inaasahan ng isang normal na distribusyon, ang papel ng function ay ginagampanan ng arithmetic mean.

Upang ang mga istatistikal na pagtatantya ay makapagbigay ng mga wastong pagtatantya ng mga tinantyang parameter, dapat nilang matugunan ang ilang mga kinakailangan, kung saan ang pinakamahalaga ay ang mga kinakailangan hindi inilipat At solvency mga pagtatasa.

Hayaan ay isang istatistikal na pagtatantya ng hindi kilalang parameter ng teoretikal na pamamahagi. Hayaang mahanap ang pagtatantya mula sa isang sample ng laki n. Ulitin natin ang eksperimento, i.e. kunin natin ang isa pang sample na may parehong laki mula sa pangkalahatang populasyon at, batay sa data nito, kumuha ng ibang pagtatantya. Ang pag-uulit ng eksperimento nang maraming beses, nakakakuha kami ng iba't ibang numero. Ang marka ay maaaring isipin bilang isang random na variable, at ang mga numero bilang mga posibleng halaga nito.

Kung ang pagtatantya ay nagbibigay ng tinatayang halaga sa kasaganaan, ibig sabihin. ang bawat numero ay mas malaki kaysa sa tunay na halaga, at bilang kinahinatnan, ang mathematical na inaasahan (average na halaga) ng random variable ay mas malaki kaysa sa:. Gayundin, kung nagbibigay ito ng pagtatantya may dehado, Yung .

Kaya, ang paggamit ng isang istatistikal na pagtatantya, ang matematikal na inaasahan na kung saan ay hindi katumbas ng tinantyang parameter, ay hahantong sa sistematikong (ng parehong tanda) na mga error. Kung, sa kabaligtaran, ito ay ginagarantiyahan laban sa mga sistematikong pagkakamali.

Walang kinikilingan tinatawag na istatistikal na pagtatantya, ang mathematical na inaasahan na katumbas ng tinantyang parameter para sa anumang laki ng sample.

Inilipat ay tinatawag na pagtatantya na hindi nakakatugon sa kundisyong ito.

Ang pagiging walang kinikilingan ng pagtatantya ay hindi pa ginagarantiyahan ang isang mahusay na pagtatantya para sa tinantyang parameter, dahil ang mga posibleng halaga ay maaaring napaka kalat sa paligid ng average na halaga nito, i.e. ang pagkakaiba ay maaaring maging makabuluhan. Sa kasong ito, ang pagtatantya na natagpuan mula sa data ng isang sample, halimbawa, ay maaaring maging makabuluhang malayo sa average na halaga, at samakatuwid mula sa parameter na tinatantya.

Epektibo ay isang istatistikal na pagtatantya na, para sa isang ibinigay na laki ng sample n, ay mayroon pinakamaliit na posibleng pagkakaiba .

Kapag isinasaalang-alang ang malalaking sample, kinakailangan ang mga pagtatantya ng istatistika solvency .

Mayaman ay tinatawag na istatistikal na pagtatantya, na, dahil ang n®¥ ay may posibilidad sa tinantyang parameter. Halimbawa, kung ang pagkakaiba ng isang walang pinapanigan na pagtatantya ay nagiging zero bilang n®¥, ang naturang pagtatantya ay lumalabas na pare-pareho.

Sample na average.

Hayaang kunin ang isang sample ng laki n upang pag-aralan ang pangkalahatang populasyon tungkol sa isang quantitative na katangian X.

Ang sample mean ay ang arithmetic mean ng isang katangian sa isang sample na populasyon.

Sample na pagkakaiba-iba.

Upang obserbahan ang pagpapakalat ng isang quantitative na katangian ng mga sample na halaga sa paligid ng average na halaga nito, isang buod na katangian ay ipinakilala - sample na pagkakaiba-iba.

Ang sample na pagkakaiba-iba ay ang arithmetic mean ng mga parisukat ng paglihis ng mga naobserbahang halaga ng isang katangian mula sa kanilang mean na halaga.

Kung ang lahat ng mga halaga ng sample na katangian ay iba, kung gayon

Nawastong pagkakaiba.

Ang sample na variance ay isang biased estimate ng population variance, i.e. ang mathematical na inaasahan ng sample na pagkakaiba-iba ay hindi katumbas ng tinantyang pangkalahatang pagkakaiba, ngunit katumbas ng

Upang itama ang sample na pagkakaiba, i-multiply lang ito sa fraction

Sample na koepisyent ng ugnayan ay matatagpuan sa pamamagitan ng formula

kung saan ang mga sample na standard deviations ng mga halaga at .

Ang sample correlation coefficient ay nagpapakita ng lapit ng linear na relasyon sa pagitan ng at : mas malapit sa pagkakaisa, mas malakas ang linear na relasyon sa pagitan ng at .

23. Ang frequency polygon ay isang putol na linya na ang mga segment ay nagkokonekta sa mga punto. Upang bumuo ng isang frequency polygon, ang mga variant ay naka-plot sa abscissa axis, at ang mga kaukulang frequency ay naka-plot sa ordinate axis, at ang mga punto ay konektado sa pamamagitan ng mga segment ng linya.

Ang relative frequency polygon ay itinayo sa katulad na paraan, maliban na ang mga relatibong frequency ay naka-plot sa ordinate axis.

Ang frequency histogram ay isang stepped figure na binubuo ng mga parihaba, ang mga base nito ay bahagyang pagitan ng haba h, at ang mga taas ay katumbas ng ratio. Upang makabuo ng isang frequency histogram, ang mga bahagyang agwat ay inilatag sa abscissa axis, at ang mga segment na parallel sa abscissa axis sa layo (taas) ay iginuhit sa itaas ng mga ito. Ang lugar ng i-th rectangle ay katumbas ng kabuuan ng mga frequency ng i-o interval, samakatuwid ang lugar ng frequency histogram ay katumbas ng kabuuan ng lahat ng frequency, i.e. laki ng sample.

Empirical distribution function

saan n x- bilang ng mga halaga ng sample na mas mababa sa x; n- laki ng sample.

22Tukuyin natin ang mga pangunahing konsepto ng mga istatistika ng matematika

.Pangunahing konsepto ng mga istatistika ng matematika. Populasyon at sample. Serye ng pagkakaiba-iba, serye ng istatistika. Nakapangkat na sample. Nakapangkat na serye ng istatistika. Polygon ng dalas. Sample distribution function at histogram.

Populasyon– ang buong hanay ng mga magagamit na bagay.

Sample– isang hanay ng mga bagay na random na pinili mula sa pangkalahatang populasyon.

Ang isang pagkakasunud-sunod ng mga pagpipilian na nakasulat sa pataas na pagkakasunud-sunod ay tinatawag pagkakaiba-iba malapit, at isang listahan ng mga opsyon at ang kanilang mga kaukulang frequency o relative frequency - serye ng istatistika: random na pinili mula sa pangkalahatang populasyon.

Polygon Ang mga frequency ay tinatawag na isang sirang linya, ang mga segment kung saan kumokonekta sa mga punto.

Histogram ng dalas ay isang stepped figure na binubuo ng mga parihaba, ang mga base nito ay bahagyang pagitan ng haba h, at ang mga taas ay katumbas ng ratio .

Sample (empirical) distribution function tawagan ang function F*(x), pagtukoy para sa bawat halaga X relatibong dalas ng kaganapan X< x.

Kung ang ilang tuluy-tuloy na feature ay pinag-aaralan, ang variation series ay maaaring binubuo ng napakalaking bilang ng mga numero. Sa kasong ito ito ay mas maginhawang gamitin pinagsama-samang sample. Upang makuha ito, ang agwat na naglalaman ng lahat ng naobserbahang mga halaga ng katangian ay nahahati sa ilang pantay na bahagyang pagitan ng haba h, at pagkatapos ay hanapin para sa bawat bahagyang pagitan n i– ang kabuuan ng mga frequency ng variant na kasama sa i ika agwat.

20. Ang batas ng malalaking numero ay hindi dapat unawain bilang alinmang pangkalahatang batas na nauugnay sa malalaking numero. Ang batas ng malalaking numero ay isang pangkalahatang pangalan para sa ilang mga theorems, mula sa kung saan ito ay sumusunod na sa isang walang limitasyong pagtaas sa bilang ng mga pagsubok, ang mga average na halaga ay may posibilidad sa ilang mga constants.

Kabilang dito ang theorems ng Chebyshev at Bernoulli. Ang theorem ni Chebyshev ay ang pinaka-pangkalahatang batas ng malalaking numero.

Ang patunay ng mga theorems, na pinagsama ng terminong "batas ng malalaking numero," ay batay sa hindi pagkakapantay-pantay ni Chebyshev, na nagtatatag ng posibilidad ng paglihis mula sa inaasahan ng matematika:

19Pamamahagi ng Pearson (chi - square) - pamamahagi ng isang random na variable

nasaan ang mga random variable X 1, X 2,…, X n independyente at may parehong distribusyon N(0,1). Sa kasong ito, ang bilang ng mga termino, i.e. n, ay tinatawag na "bilang ng mga antas ng kalayaan" ng pamamahagi ng chi-square.

Ang distribusyon ng chi-square ay ginagamit kapag tinatantya ang pagkakaiba-iba (gamit ang pagitan ng kumpiyansa), kapag sinusuri ang mga hypotheses ng kasunduan, homogeneity, kalayaan,

Pamamahagi t Ang t ng mag-aaral ay ang pamamahagi ng isang random na variable

nasaan ang mga random variable U At X malaya, U ay may karaniwang normal na distribusyon N(0.1), at X– pamamahagi ng chi – parisukat c n antas ng kalayaan. Kasabay nito n ay tinatawag na "bilang ng mga antas ng kalayaan" ng pamamahagi ng Mag-aaral.

Ginagamit ito kapag tinatantya ang inaasahan sa matematika, halaga ng pagtataya at iba pang mga katangian gamit ang mga agwat ng kumpiyansa, pagsubok ng mga hypotheses tungkol sa mga halaga ng mga inaasahan sa matematika, mga coefficient ng regression,

Ang pamamahagi ng Fisher ay ang pamamahagi ng isang random na variable

Ginagamit ang pamamahagi ng Fisher kapag sinusuri ang mga hypotheses tungkol sa kasapatan ng modelo sa pagsusuri ng regression, pagkakapantay-pantay ng mga pagkakaiba at sa iba pang mga problema ng mga inilapat na istatistika

18Linear regression ay isang tool sa istatistika na ginagamit upang mahulaan ang mga presyo sa hinaharap batay sa nakaraang data, at kadalasang ginagamit upang matukoy kung ang mga presyo ay sobrang init. Ang paraan ng least squares ay ginagamit upang makabuo ng "pinakamahusay na angkop" na tuwid na linya sa pamamagitan ng isang serye ng mga punto ng halaga ng presyo. Ang mga punto ng presyo na ginamit bilang input ay maaaring alinman sa mga sumusunod: bukas, malapit, mataas, mababa,

17. Ang dalawang-dimensional na random na variable ay isang ordered set ng dalawang random variable o .

Halimbawa: Dalawang dice ang inihagis. – ang bilang ng mga puntos na pinagsama sa una at pangalawang dice, ayon sa pagkakabanggit

Ang isang unibersal na paraan upang tukuyin ang batas sa pamamahagi ng isang dalawang-dimensional na random na variable ay ang distribution function.

15.m.o Mga discrete na random variable

Mga Katangian:

1) M(C) = C, C- pare-pareho;

2) M(CX) = C.M.(X);

3) M(X 1 + X 2) = M(X 1) + M(X 2), Saan X 1, X 2- mga independiyenteng random na variable;

4) M(X 1 X 2) = M(X 1)M(X 2).

Ang pag-asa sa matematika ng kabuuan ng mga random na variable ay katumbas ng kabuuan ng kanilang mga inaasahan sa matematika, i.e.

Ang pag-asa sa matematika ng pagkakaiba sa pagitan ng mga random na variable ay katumbas ng pagkakaiba ng kanilang mga inaasahan sa matematika, i.e.

Ang inaasahan sa matematika ng isang produkto ng mga random na variable ay katumbas ng produkto ng kanilang mga inaasahan sa matematika, i.e.

Kung ang lahat ng mga halaga ng isang random na variable ay nadagdagan (nababawasan) ng parehong numero C, kung gayon ang pag-asa sa matematika nito ay tataas (bumababa) ng parehong numero

14. Exponential(exponential)batas sa pamamahagi X ay may exponential distribution law na may parameter λ >0 kung ang probability density nito ay may anyo:

Inaasahan sa matematika: .

Pagpapakalat: .

Malaki ang papel ng exponential distribution law sa queuing theory at reliability theory.

13. Ang normal na batas sa pamamahagi ay nailalarawan sa dalas ng pagkabigo a (t) o density probability density f (t) ng anyo:

, (5.36)

kung saan ang σ ay ang standard deviation ng SV x;

m x– mathematical na inaasahan ng SV x. Ang parameter na ito ay madalas na tinatawag na sentro ng pagpapakalat o ang pinaka-malamang na halaga ng SV X.

x– isang random na variable, na maaaring kunin bilang oras, kasalukuyang halaga, halaga ng boltahe ng kuryente at iba pang mga argumento.

Ang normal na batas ay isang dalawang-parameter na batas, upang isulat na kailangan mong malaman m x at σ.

Ang normal na distribusyon (Gaussian distribution) ay ginagamit upang masuri ang pagiging maaasahan ng mga produkto na apektado ng isang bilang ng mga random na kadahilanan, na ang bawat isa ay may bahagyang epekto sa resultang epekto.

12. Unipormeng pamamahagi ng batas. Patuloy na random variable X ay may pare-parehong batas sa pamamahagi sa segment [ a, b], kung ang probability density nito ay pare-pareho sa segment na ito at katumbas ng zero sa labas nito, i.e.

Pagtatalaga: .

Inaasahan sa matematika: .

Pagpapakalat: .

Random na variable X, na ibinahagi ayon sa isang pare-parehong batas sa segment ay tinatawag random na numero mula 0 hanggang 1. Ito ay nagsisilbing panimulang materyal para sa pagkuha ng mga random na variable na may anumang batas sa pamamahagi. Ang unipormeng batas sa pamamahagi ay ginagamit sa pagsusuri ng mga error sa pag-ikot kapag nagsasagawa ng mga numerical na kalkulasyon, sa isang serye ng mga problema sa pagpila, sa istatistikal na pagmomodelo ng mga obserbasyon na napapailalim sa isang ibinigay na pamamahagi.

11. Kahulugan. Densidad ng pamamahagi ng mga probabilidad ng isang tuluy-tuloy na random variable X ay tinatawag na function f(x)– ang unang derivative ng distribution function F(x).

Ang density ng pamamahagi ay tinatawag din pag-andar ng kaugalian. Upang ilarawan ang isang discrete random variable, hindi katanggap-tanggap ang density ng pamamahagi.

Ang kahulugan ng density ng pamamahagi ay ipinapakita nito kung gaano kadalas lumilitaw ang isang random na variable X sa isang partikular na kapitbahayan ng isang punto X kapag inuulit ang mga eksperimento.

Pagkatapos ipakilala ang mga function ng pamamahagi at density ng pamamahagi, maaaring ibigay ang sumusunod na kahulugan ng isang tuluy-tuloy na random variable.

10. Probability density, probability distribution density ng random variable x, ay isang function p(x) na

at para sa anumang a< b вероятность события a < x < b равна
.

Kung ang p(x) ay tuloy-tuloy, kung gayon para sa sapat na maliit na ∆x ang posibilidad ng hindi pagkakapantay-pantay x< X < x+∆x приближенно равна p(x) ∆x (с точностью до малых более высокого порядка). Функция распределения F(x) случайной величины x, связана с плотностью распределения соотношениями

at kung ang F(x) ay differentiable, kung gayon

Pag-aralan natin ang ilang quantitative trait? pangkalahatang populasyon, at ipagpalagay na para sa anumang laki ng sample ay kilala ang frequency distribution ng katangiang ito. Sa pamamagitan ng pag-aayos ng sample size sa p, tukuyin ng p x bilang ng mga opsyon na mas mababa sa x. Kung gayon hindi mahirap makita na ang relasyon njn nagpapahayag ng relatibong dalas ng isang kaganapan (?

Ang ratio na ito ay nakasalalay sa isang nakapirming bilang x at, samakatuwid, ay ilang function ng dami na ito x. Ipahiwatig natin ito sa pamamagitan ng F*(x).

Kahulugan 1.10. Function F*(x) = -, na nagpapahayag ng kamag-anak

dalas ng kaganapan (? empirical function

pamamahagi (sampling distribution function o statistic distribution function).

Kaya, sa pamamagitan ng kahulugan

Alalahanin na ang function ng pamamahagi ng tampok ?, Ang populasyon ay tinukoy bilang ang posibilidad ng isang kaganapan (?

at sa kaibahan sa empirical distribution function ay tinatawag theoretical distribution function. Dahil ang empirical distribution function ay ang probabilidad ng parehong kaganapan, kung gayon ayon sa Bernoulli's theorem (tingnan ang seksyon 5.4), na may malaking sample size ay kaunti lang ang pagkakaiba nila sa isa't isa sa kahulugan na

kung saan ang e ay anumang arbitraryong maliit na positibong numero.

Ang kaugnayan (1.2) ay nagpapakita na kung ang theoretical distribution function ay hindi alam, ang empirical distribution function na natagpuan mula sa sample ay maaaring gamitin bilang sample estimate nito. Mula sa formula (1.2) sabay-sabay na sumusunod na ang pagtatantiyang ito ay pare-pareho (tingnan ang Depinisyon 2.4).

Magkomento 1.6. Saloobin nJn maaari ding bigyang kahulugan bilang ibahagi ang mga miyembro ng sample na nasa kaliwa ng isang nakapirming numerong x. Tukuyin natin ito sa pamamagitan ng co^.

Ngayon tingnan natin ang isang halimbawa ng pagbuo ng isang empirical distribution function para sa isang discrete sample.

Halimbawa 1.2. Ang pamamahagi ng sample ay kilala (Talahanayan 1.7).

Talahanayan 1.7

Pagpipilian x.
Dalas ako.

Buuin ang empirical distribution function nito.

Una, hanapin natin ang sample size:

Pagpipilian x x- ang pinakamaliit. kaya lang n x = 0 at F*(x)= 0 sa X% 3, pagkatapos n z = 6, ibig sabihin. sa kaliwa ng punto X= 3 mayroong anim na sample value. Kaya naman, F*(3) = - = 0.12. Sa kaliwa x = 5 matatagpuan

mga asawa n x=5 = 6 + 9= 15 sample na opsyon. kaya lang Fn(5) = - = 0.3. Kaya

Paano n x=1 = 6 + 9 + 18 = 33, pagkatapos Fn(7) = - = 0.66. Katulad din ang nahanap namin

33 + 12 = 45. Samakatuwid F* (9) = ^ = 0,9.

Ang opsyon x 5 = 9 ang pinakamalaki. Samakatuwid, para sa x > 9, ang buong sample ay nasa kaliwa ng puntong ito x. kaya lang n x>9= 50 at F*(x) = -= 1 para sa x > 9. 50

Kaya, mula sa mga kalkulasyon na isinagawa sa itaas, sumusunod na ang nais na empirical function ay natatanging tinukoy sa buong tunay na axis, piecewise constant at may anyo.

Ang graph ng function na ito ay kumakatawan sa isang step figure at ipinapakita sa Fig. 1.6. ?

Tulad ng para sa tanong ng pagbuo ng isang empirical function para sa tuluy-tuloy na mga sample, ang problemang ito ay nalutas, sa pangkalahatan, malayo sa hindi malabo. Ito ay dahil sa ang katunayan na ang mga halaga ng empirical function ay maaaring natatanging matagpuan lamang sa mga dulong punto ng mga bahagyang agwat kung saan ang pangunahing agwat na naglalaman ng sample na populasyon ay nahahati. Ngunit sa mga panloob na punto ng mga bahagyang agwat ay hindi ito tinukoy. Sa mga puntong ito ito ay higit na tinutukoy alinman sa pamamagitan ng isang piecewise constant function (tingnan ang nakaraang halimbawa) o sa pamamagitan ng ilang pagtaas ng tuluy-tuloy na function, halimbawa ng isang linear function, i.e. Ang linear approximation ay ginagamit upang bumuo ng empirical distribution function.

Halimbawa 1.3. Ayon sa Talahanayan 1.3, hanapin ang empirical distribution function ng mga empleyado ng enterprise ayon sa haba ng serbisyo.

Para sa katiyakan, ipinapalagay namin na ang mga bahagyang agwat na isinasaalang-alang ay sarado sa kaliwa at bukas sa kanan, i.e. naglalaman lamang sila ng kanilang mga kaliwang dulo. Hayaan ang x = 2. Pagkatapos kaganapan n 2 = 0 at F*(2)= 0. Kung x e (2; 6), pagkatapos ay sa puntong ito ang halaga p x ay hindi na tinukoy at kasama nito ang halaga ng empirical function ay hindi tinukoy. Halimbawa, kung x = 3, pagkatapos ay mula sa mga kondisyon ng problema imposibleng matukoy ang bilang ng mga manggagawa na may mas mababa sa tatlong taong karanasan sa trabaho, i.e. hindi mahanap ang dalas p x at samakatuwid F*(x).

Dagdag dito, pangangatwiran sa isang katulad na paraan, kami ay kumbinsido na ang mga kinakailangang function F*(x) kumukuha ng mga tiyak na halaga sa kaliwang endpoint ng mga bahagyang agwat, halimbawa: "6) = 4/100 = 0.04; "10) = 0.12; "14) = 0.24; "18) = 0.59; F*(22) = 0.78; "26) = 0.90"; "30) = 1, ngunit hindi ito tinukoy sa mga panloob na punto ng mga bahagyang pagitan. Upang tuluyang malutas ang problema, ang nais na pag-andar sa mga panloob na punto ng mga bahagyang pagitan ay higit na tinukoy sa pamamagitan ng isang putol-putol na pare-parehong pag-andar (Larawan 1.7) o sa pamamagitan ng ilang patuloy na pagtaas ng pag-andar (Larawan 1.8, kung saan ang nais na empirical function ay pinalawak ng isang linear function). ?