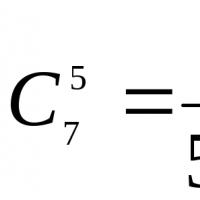Mga pangunahing formula ng combinatorics. Mga pamamaraan para sa paglutas ng mga problemang kombinatorial Elementary combinatorics

Upang gawing mas madaling i-navigate ang materyal, idaragdag ko ang nilalaman ng paksang ito:

Panimula. Mga set at seleksyon.

Sa paksang ito titingnan natin ang mga pangunahing konsepto ng combinatorics: mga permutasyon, kumbinasyon at pagkakalagay. Alamin natin ang kanilang kakanyahan at mga formula kung saan makikita mo ang kanilang dami.

Upang magtrabaho, kailangan namin ng ilang pantulong na impormasyon. Magsimula tayo sa isang pangunahing konsepto ng matematika bilang isang set. Ang konsepto ng isang set ay tinalakay nang detalyado sa paksang "Ang konsepto ng isang set. Paraan ng pagtukoy ng mga set".

Isang napakaikling kwento tungkol sa karamihan: Ipakita itago

Sa madaling salita: ang isang set ay isang koleksyon ng mga bagay. Sumulat ng mga set sa mga kulot na braces. Ang pagkakasunud-sunod ng pagkakasulat ng mga elemento ay hindi mahalaga; Ang pag-uulit ng mga elemento ay hindi pinapayagan. Halimbawa, ang hanay ng mga digit ng numerong 11115555999 ay magiging: $\(1,5,9\)$. Ang hanay ng mga katinig sa salitang "tiger cub" ay: $\(t, g, r, n, k\)$. Ang notasyong $5\sa A$ ay nangangahulugan na ang elemento 5 ay kabilang sa set na $A=\(1,5,9 \)$. Ang bilang ng mga elemento sa isang finite set ay tinatawag kapangyarihan ng set na ito at nagsasaad ng $|A|$. Halimbawa, para sa isang set na $A=\(1,5,9 \)$ na naglalaman ng 3 elemento, mayroon kaming: $|A|=3$.

Isaalang-alang ang isang tiyak na hindi walang laman na finite set na $U$, na ang cardinality ay $n$, $|U|=n$ (ibig sabihin, ang set na $U$ ay may $n$ na elemento). Ipakilala natin ang isang konsepto tulad ng sample(tinatawag itong tuple ng ilang may-akda). Sa pamamagitan ng isang sample ng volume na $k$ mula sa $n$ na mga elemento (pinaikling bilang $(n,k)$-sample) ang ibig naming sabihin ay isang set ng mga elemento $(a_1, a_2,\ldots, a_k)$, kung saan $a_i\in U$. Ang isang seleksyon ay tinatawag na ordered kung ang pagkakasunud-sunod ng mga elemento nito ay tinukoy. Magkaiba ang dalawang ordered sample na naiiba lang sa pagkakasunud-sunod ng mga elemento. Kung ang pagkakasunud-sunod ng mga elemento ng sample ay hindi makabuluhan, kung gayon ang sample ay tinatawag na unordered.

Tandaan na ang kahulugan ng isang seleksyon ay walang sinasabi tungkol sa mga pag-uulit ng elemento. Hindi tulad ng mga set na elemento, ang mga elemento ng pagpili ay maaaring ulitin.

Halimbawa, isaalang-alang ang hanay na $U=\(a,b,c,d,e\)$. Ang set na $U$ ay naglalaman ng 5 elemento, i.e. $|U|=5$. Ang isang sample na walang pag-uulit ay maaaring: $(a,b,c)$. Ang pagpipiliang ito ay naglalaman ng 3 elemento, i.e. ang laki ng sample na ito ay 3. Sa madaling salita, ito ay isang $(5,3)$-sample.

Ang isang sample na may mga pag-uulit ay maaaring ganito: $(a,a,a,a,a,c,c,d)$. Naglalaman ito ng 8 elemento, i.e. ang dami nito ay 8. Sa madaling salita, ito ay isang $(5,8)$-sample.

Isaalang-alang natin ang dalawa pang $(5,3)$-sample: $(a,b,b)$ at $(b,a,b)$. Kung ipagpalagay namin na ang aming mga sample ay hindi nakaayos, kung gayon ang sample na $(a,b,b)$ ay katumbas ng sample na $(b,a,b)$, i.e. $(a,b,b)=(b,a,b)$. Kung ipagpalagay namin na ang aming mga sample ay inayos, kung gayon $(a,b,b)\neq(b,a,b)$.

Tingnan natin ang isa pang halimbawa, medyo hindi gaanong abstract:) Ipagpalagay na mayroong anim na kendi sa isang basket, at lahat sila ay naiiba. Kung iuugnay natin ang unang kendi sa numero 1, ang pangalawang kendi sa numero 2, at iba pa, ang sumusunod na hanay ay maaaring iugnay sa mga kendi sa basket: $U=\(1,2,3,4, 5,6\)$. Isipin na random naming inilagay ang aming kamay sa isang basket upang makalabas ng tatlong kendi. Ang mga nabunot na kendi ang pinipili. Dahil kumukuha kami ng 3 kendi sa 6, nakakakuha kami ng (6,3)-sample. Ang pagkakasunud-sunod kung saan ang mga kendi ay inilalagay sa palad ay ganap na walang kaugnayan, kaya ang sample na ito ay hindi nakaayos. Buweno, at dahil ang lahat ng mga kendi ay iba, ang pagpili ay walang pag-uulit. Kaya, sa sitwasyong ito ay pinag-uusapan natin ang isang unordered (6,3) -sample na walang mga pag-uulit.

Ngayon lumapit tayo mula sa kabilang panig. Isipin natin na tayo ay nasa isang pabrika ng paggawa ng kendi, at ang pabrika na ito ay gumagawa ng apat na uri ng kendi. Ang set na $U$ sa sitwasyong ito ay ang mga sumusunod: $U=\(1,2,3,4 \)$ (bawat numero ay responsable para sa sarili nitong uri ng kendi). Ngayon isipin natin na ang lahat ng mga kendi ay ibinuhos sa isang solong chute, malapit sa kung saan tayo nakatayo. At, paglalagay ng aming mga palad, pumili kami ng 20 kendi mula sa daloy na ito. Ang isang dakot ng matamis ay isang sample. Ang pagkakasunud-sunod ba kung saan ang mga kendi ay inilalagay sa isang dakot na bagay? Naturally, hindi, kaya ang sample ay unordered. Mayroon lamang 4 na uri ng mga kendi, at pumili kami ng dalawampung piraso mula sa pangkalahatang daloy - ang pag-uulit ng mga varieties ay hindi maiiwasan. Kasabay nito, ang mga sample ay maaaring ibang-iba: maaaring mayroon din tayong lahat ng mga kendi ng parehong uri. Samakatuwid, sa sitwasyong ito tayo ay nakikitungo sa isang unordered (4,20) -sample na may mga pag-uulit.

Tingnan natin ang ilang higit pang mga halimbawa. Hayaang isulat ang magkakaibang 7 letra sa mga cube: k, o, n, f, e, t, a. Ang mga titik na ito ay bumubuo sa set na $U=\(k,o,n,f,e,m,a\)$. Sabihin nating mula sa mga cube na ito gusto nating gumawa ng "mga salita" ng 5 titik. Ang mga titik ng mga salitang ito (halimbawa, "konfe", "tenko" at iba pa) ay bumubuo ng (7,5)-mga seleksyon: $(k,o,n,f,e)$, $(t,e,n ,k ,o)$, atbp. Malinaw, ang pagkakasunud-sunod ng mga titik sa naturang sample ay mahalaga. Halimbawa, ang mga salitang "nokft" at "kfton" ay magkaiba (bagaman ang mga ito ay binubuo ng parehong mga titik), dahil ang pagkakasunud-sunod ng mga titik sa mga ito ay hindi tugma. Walang mga pag-uulit ng mga titik sa naturang "mga salita", dahil mayroon lamang pitong cube. Kaya, ang hanay ng mga titik ng bawat salita ay isang ordered (7,5)-sample na walang pag-uulit.

Isa pang halimbawa: gumagawa kami ng lahat ng uri ng walong digit na numero mula sa apat na digit 1, 5, 7, 8. Halimbawa, 11111111, 15518877, 88881111 at iba pa. Ang set na $U$ ay: $U=\(1,5,7,8\)$. Ang mga digit ng bawat binubuong numero ay bumubuo ng (4,8)-sample. Ang pagkakasunud-sunod ng mga digit sa isang numero ay mahalaga, i.e. ang sample ay iniutos. Ang mga pag-uulit ay pinahihintulutan, kaya narito tayo ay nakikitungo sa isang iniutos na (4,8)-sample na may mga pag-uulit.

Mga placement na walang pag-uulit ng $n$ na elemento ng $k$

Paglalagay nang walang pag-uulit ng $n$ na mga elemento ng $k$ - inayos ang $(n,k)$-pagpili nang walang pag-uulit.

Dahil ang mga elemento sa sample na isinasaalang-alang ay hindi maaaring ulitin, hindi kami makakapili ng higit pang mga elemento sa sample kaysa sa orihinal na hanay. Samakatuwid, para sa mga naturang sample ang sumusunod na hindi pagkakapantay-pantay ay totoo: $n≥ k$. Ang bilang ng mga placement na walang pag-uulit ng $n$ na mga elemento ng $k$ ay tinutukoy ng sumusunod na formula:

\begin(equation)A_(n)^(k)=\frac(n{(n-k)!} \end{equation} !}

Ano ang ibig sabihin ng "!": Ipakita itago

Nagre-record ng "n!" (basahin ang "en factorial") ay tumutukoy sa produkto ng lahat ng mga numero mula 1 hanggang n, i.e.

$$ n!=1\cdot2\cdot 3\cdot \ldots\cdot n $$

Sa pamamagitan ng kahulugan, ipinapalagay na $0!=1!=1$. Halimbawa, hanapin natin ang 5!:

$$ 5!=1\cdot 2\cdot 3\cdot 4\cdot 5=120. $$

Halimbawa Blg. 1

Ang alpabeto ay binubuo ng isang set ng mga simbolo $E=\(+,*,0,1,f\)$. Alamin natin ang bilang ng mga tatlong-character na salita sa alpabeto na ito na hindi naglalaman ng mga paulit-ulit na titik.

Sa pamamagitan ng tatlong-character na salita, ibig sabihin ay mga expression tulad ng "+*0" o "0f1". Ang set na $E$ ay may limang elemento, kaya ang mga titik ng tatlong-character na salita ay bumubuo ng (5,3)-mga seleksyon. Ang unang tanong ay: inorder ba ang mga sample na ito o hindi? Ang mga salita na naiiba lamang sa pagkakasunud-sunod ng kanilang mga titik ay itinuturing na iba, kaya ang pagkakasunud-sunod ng mga elemento sa sample ay mahalaga. Nangangahulugan ito na ang sample ay iniutos. Pangalawang tanong: pinapayagan ba ang pag-uulit o hindi? Ang sagot sa tanong na ito ay ibinibigay ng kondisyon: ang mga salita ay hindi dapat maglaman ng mga paulit-ulit na titik. Upang ibuod: ang mga titik ng bawat salita na nakakatugon sa mga kondisyon ng problema ay bumubuo ng isang ordered (5,3)-sample nang walang pag-uulit. Sa madaling salita, ang mga titik ng bawat salita ay bumubuo ng isang pagkakalagay nang walang pag-uulit ng 5 elemento ng 3. Narito ang mga halimbawa ng naturang mga pagkakalagay:

$$ (+,*,f), \; (*+,f), \; (1+,0) $$

Interesado kami sa kabuuang bilang ng mga pagkakalagay na ito. Ayon sa formula (1), ang bilang ng mga placement na walang pag-uulit ng 5 elemento ng 3 ay magiging ganito:

$$ A_(5)^(3)=\frac(5{(5-3)!}=\frac{5!}{2!}=60. $$ !}

Yung. maaari kang gumawa ng 60 tatlong-character na salita, ang mga titik na hindi na mauulit.

Sagot: 60.

Mga placement na may mga pag-uulit ng $n$ na elemento ng $k$

Paglalagay na may mga pag-uulit ng $n$ na mga elemento ng $k$ - inayos ang $(n,k)$-pagpili na may mga pag-uulit.

Ang bilang ng mga placement na may mga pag-uulit ng $n$ elemento ng $k$ ay tinutukoy ng sumusunod na formula:

\begin(equation)\bar(A)_(n)^(k)=n^k \end(equation)

Halimbawa Blg. 2

Ilang limang-digit na numero ang maaaring gawin mula sa hanay ng mga digit na $\(5,7,2\)$?

Mula sa hanay ng mga numerong ito maaari kang gumawa ng limang digit na numero 55555, 75222, at iba pa. Ang mga digit ng bawat naturang numero ay bumubuo ng isang (3,5)-sample: $(5,5,5,5,5)$, $(7,5,2,2,2)$. Tanungin natin ang ating sarili: anong uri ng mga sample ito? Una, ang mga digit sa mga numero ay maaaring paulit-ulit, kaya kami ay nakikitungo sa mga sample na may mga pag-uulit. Pangalawa, ang pagkakasunud-sunod ng mga digit sa isang numero ay mahalaga. Halimbawa, ang 27755 at 77255 ay magkaibang numero. Dahil dito, kami ay nakikitungo sa mga ordered (3,5)-sample na may mga pag-uulit. Nahanap namin ang kabuuang bilang ng mga naturang sample (ibig sabihin, ang kabuuang bilang ng kinakailangang limang-digit na numero) gamit ang formula (2):

$$ \bar(A)_(3)^(5)=3^5=243. $$

Samakatuwid, ang 243 limang-digit na numero ay maaaring gawin mula sa mga ibinigay na digit.

Sagot: 243.

Mga permutasyon nang walang pag-uulit ng $n$ na elemento

Ang permutasyon na walang pag-uulit ng $n$ na mga elemento ay isang inayos na $(n,n)$-pagpili nang walang pag-uulit.

Sa esensya, ang permutasyon nang walang pag-uulit ay isang espesyal na kaso ng paglalagay nang walang pag-uulit, kapag ang laki ng sample ay katumbas ng cardinality ng orihinal na hanay. Ang bilang ng mga permutasyon na walang pag-uulit ng $n$ elemento ay tinutukoy ng sumusunod na formula:

\begin(equation)P_(n)=n! \end(equation)

Sa pamamagitan ng paraan, ang formula na ito ay madaling makuha kung isasaalang-alang mo na $P_n=A_(n)^(n)$. Pagkatapos makuha namin:

$$ P_n=A_(n)^(n)=\frac(n{(n-n)!}=\frac{n!}{0!}=\frac{n!}{1}=n! $$ !}

Halimbawa Blg. 3

Mayroong limang servings ng ice cream mula sa iba't ibang kumpanya sa freezer. Sa ilang paraan maaari mong piliin ang pagkakasunud-sunod kung saan sila kinakain?

Hayaang tumutugma ang numero 1 sa unang ice cream, ang numero 2 sa pangalawa, at iba pa. Makukuha namin ang set na $U=\(1,2,3,4,5\)$, na kumakatawan sa mga nilalaman ng freezer. Ang pagkakasunud-sunod ng pagkain ay maaaring ang mga sumusunod: $(2,1,3,5,4)$ o ang mga sumusunod: $(5,4,3,1,2)$. Ang bawat set ay isang (5,5)-sample. Ito ay magiging maayos at walang pag-uulit. Sa madaling salita, ang bawat sample ay isang permutation ng 5 elemento ng orihinal na set. Ayon sa formula (3), ang kabuuang bilang ng mga permutasyong ito ay ang mga sumusunod:

$$ P_5=5!=120. $$

Dahil dito, mayroong 120 na mga order para sa pagpili ng pagkakasunud-sunod ng pagkain.

Sagot: 120.

Mga permutasyon na may mga pag-uulit

Ang permutasyon na may mga pag-uulit ay isang inayos na $(n,k)$-sample na may mga pag-uulit, kung saan ang elementong $a_1$ ay inuulit $k_1$ beses, $a_2$ ay inuulit $k_2$ beses, at iba pa, hanggang sa huling elemento $ a_r$, na inuulit ng $ k_r$ beses. Sa kasong ito, $k_1+k_2+\ldots+k_r=k$.

Ang kabuuang bilang ng mga permutasyon na may mga pag-uulit ay tinutukoy ng formula:

\begin(equation)P_(k)(k_1,k_2,\ldots,k_r)=\frac(k{k_1!\cdot k_2!\cdot \ldots \cdot k_r!} \end{equation} !}

Halimbawa Blg. 4

Binubuo ang mga salita batay sa alpabeto na $U=\(a,b,d\)$. Gaano karaming iba't ibang mga salita ang maaaring binubuo ng pitong karakter kung sa mga salitang ito ang titik "a" ay kailangang ulitin ng 2 beses; ang letrang "b" - 1 beses, at ang letrang "d" - 4 na beses?

Narito ang mga halimbawa ng mga salita sa paghahanap: "aabdddd", "daddabd" at iba pa. Ang mga titik ng bawat salita ay bumubuo ng isang (3,7)-sample na may mga pag-uulit: $(a,a,b,d,d,d,d)$, $(d,a,d,d,a,b,d )$ at iba pa. Ang bawat sample ay binubuo ng dalawang elemento "a", isang elemento "b" at apat na elemento "d". Sa madaling salita, $k_1=2$, $k_2=1$, $k_3=4$. Ang kabuuang bilang ng mga pag-uulit ng lahat ng mga simbolo, natural, ay katumbas ng laki ng sample, i.e. $k=k_1+k_2+k_3=7$. Ang pagpapalit ng mga datos na ito sa formula (4), magkakaroon tayo ng:

$$ P_7(2,1,4)=\frac(7{2!\cdot 1!\cdot 4!}=105. $$ !}

Samakatuwid, ang kabuuang bilang ng mga salita sa paghahanap ay 105.

Sagot: 105.

Mga kumbinasyong walang pag-uulit ng $n$ elemento ng $k$ bawat isa

Ang kumbinasyong walang pag-uulit ng $n$ elemento ng $k$ ay isang hindi nakaayos na $(n,k)$-sample na walang pag-uulit.

Ang kabuuang bilang ng mga kumbinasyon na walang pag-uulit ng $n$ elemento ng $k$ ay tinutukoy ng formula:

\begin(equation)C_(n)^(k)=\frac(n{(n-k)!\cdot k!} \end{equation} !}

Halimbawa Blg. 5

Ang basket ay naglalaman ng mga card na may mga integer na nakasulat sa mga ito mula 1 hanggang 10. 4 na card ang kinuha mula sa basket at ang mga numerong nakasulat sa mga ito ay idinagdag. Ilang magkakaibang hanay ng mga baraha ang maaaring makuha mula sa basket?

Kaya, sa problemang ito ang paunang hanay ay: $U=\(1,2,3,4,5,6,7,8,9,10\)$. Mula sa set na ito pumili kami ng apat na elemento (i.e., apat na card mula sa basket). Ang mga numero ng mga nahugot na elemento ay bumubuo ng isang (10,4) -selection. Ang mga pag-uulit sa pagpipiliang ito ay hindi pinapayagan, dahil ang mga numero ng lahat ng mga card ay iba. Ang tanong ay: mahalaga ba o hindi ang pagkakasunud-sunod ng mga napiling card? Iyon ay, halimbawa, ang mga sample na $(1,2,7,10)$ at $(10,2,1,7)$ ay pantay o hindi? Dito kailangan mong lumiko sa mga kondisyon ng problema. Ang mga card ay kinuha upang makita sa ibang pagkakataon ang kabuuan ng mga elemento. Nangangahulugan ito na ang pagkakasunud-sunod ng mga card ay hindi mahalaga, dahil ang pagbabago ng mga lugar ng mga termino ay hindi magbabago sa kabuuan. Halimbawa, ang sample na $(1,2,7,10)$ at ang sample na $(10,2,1,7)$ ay tumutugma sa parehong numero na $1+2+7+10=10+2+1+ 7= $20. Konklusyon: mula sa mga kondisyon ng problema ay sumusunod na kami ay nakikitungo sa mga hindi nakaayos na mga sample. Yung. kailangan nating hanapin ang kabuuang bilang ng mga unordered (10,4)-sample na walang pag-uulit. Sa madaling salita, kailangan nating hanapin ang bilang ng mga kumbinasyon ng 10 elemento ng 4. Gumagamit kami ng formula (5) para dito:

$$ C_(10)^(4)=\frac(10{(10-4)!\cdot 4!}=\frac{10!}{6!\cdot 4!}=210. $$ !}

Samakatuwid, ang kabuuang bilang ng mga hinanap na hanay ay 210.

Sagot: 210.

Mga kumbinasyon na may mga pag-uulit ng $n$ elemento ng $k$ bawat isa

Ang kumbinasyon na may mga pag-uulit ng $n$ na mga elemento ng $k$ ay isang hindi nakaayos na $(n,k)$-sample na may mga pag-uulit.

Ang kabuuang bilang ng mga kumbinasyon na may mga pag-uulit ng $n$ elemento ng $k$ ay tinutukoy ng formula:

\begin(equation)\bar(C)_(n)^(k)=\frac((n+k-1){(n-1)!\cdot k!} \end{equation} !}

Halimbawa Blg. 6

Isipin na tayo ay nasa isang pabrika ng kendi, sa tabi mismo ng isang conveyor kung saan lumilipat ang apat na uri ng mga kendi. Inilagay namin ang aming mga kamay sa batis na ito at bumunot ng dalawampung piraso. Ilang iba't ibang "kombinasyon ng kendi" ang maaari sa isang dakot?

Kung ipagpalagay natin na ang unang uri ay tumutugma sa numero 1, ang pangalawang uri - ang numero 2, at iba pa, kung gayon ang paunang hanay sa ating problema ay ang mga sumusunod: $U=\(1,2,3,4\) $. Mula sa set na ito pumili kami ng 20 elemento (ibig sabihin, ang parehong 20 kendi mula sa linya ng pagpupulong). Ang isang dakot ng matamis ay bumubuo ng isang (4,20)-sample. Naturally, magkakaroon ng mga pag-uulit ng mga varieties. Ang tanong, mahalaga ba ang pagkakasunud-sunod ng mga elemento sa sample o hindi? Mula sa mga kondisyon ng problema ay sumusunod na ang pagkakasunud-sunod kung saan ang mga elemento ay nakaayos ay hindi mahalaga. Walang pagkakaiba sa amin kung ang dakot ay naglalaman ng unang 15 lollipop, at pagkatapos ay 4 na tsokolate na kendi, o unang 4 na tsokolate na kendi, at pagkatapos ay 15 lollipop lamang. Kaya, kami ay nakikitungo sa isang unordered (4,20) sample na may mga pag-uulit. Upang mahanap ang kabuuang bilang ng mga sample na ito ginagamit namin ang formula (6):

$$ \bar(C)_(4)^(20)=\frac((4+20-1){(4-1)!\cdot 20!}=\frac{23!}{3!\cdot 20!}=1771. $$ !}

Samakatuwid, ang kabuuang bilang ng mga hinanap na kumbinasyon ay 1771.

Abstract sa paksa:

Nakumpleto ng 10th grade student “B”

sekondaryang paaralan Blg. 53

Glukhov Mikhail Alexandrovich

Naberezhnye Chelny

2002
Nilalaman

Mula sa kasaysayan ng combinatorics________________________________________________	3
Panuntunan ng kabuuan________________________________________________________________	4
	-
Panuntunan ng produkto________________________________________________	4
Mga halimbawa ng gawain________________________________________________________________	-
Mga intersecting set________________________________________________	5
Mga halimbawa ng gawain________________________________________________________________	-
Euler circles________________________________________________________________	-
Mga pagkakalagay nang walang pag-uulit _____________________________________________	6
Mga halimbawa ng gawain________________________________________________________________	-
Mga permutasyon nang walang pag-uulit________________________________________________	7
Mga halimbawa ng gawain________________________________________________________________	-
Mga kumbinasyon na walang pag-uulit ________________________________________________	8
Mga halimbawa ng gawain________________________________________________________________	-
Mga pagkakalagay at kumbinasyon nang walang pag-uulit______________________________	9
Mga halimbawa ng gawain________________________________________________________________	-
Mga permutasyon na may mga pag-uulit________________________________________________	9
Mga halimbawa ng gawain________________________________________________________________	-
Mga problema para sa malayang solusyon________________________________	10
Bibliograpiya________________________________	11

Mula sa kasaysayan ng combinatorics

Ang mga combinatorics ay tumatalakay sa iba't ibang uri ng mga koneksyon na maaaring mabuo mula sa mga elemento ng isang may hangganan na hanay. Ang ilang mga elemento ng combinatorics ay kilala sa India noong ika-2 siglo. BC e. Alam ng mga Nydian kung paano magkalkula ng mga numero, na ngayon ay tinatawag na "mga kumbinasyon". Noong ika-12 siglo Kinakalkula ni Bhaskara ang ilang uri ng kumbinasyon at permutasyon. Ito ay pinaniniwalaan na pinag-aralan ng mga siyentipiko ng India ang mga tambalan na may kaugnayan sa kanilang paggamit sa poetics, ang pag-aaral ng istruktura ng taludtod at mga akdang patula. Halimbawa, may kaugnayan sa pagkalkula ng mga posibleng kumbinasyon ng mga pantig na may diin (mahaba) at hindi nakadiin (maikli) ng isang talampakan ng n pantig. Bilang isang siyentipikong disiplina, nabuo ang combinatorics noong ika-17 siglo. Sa aklat na "The Theory and Practice of Arithmetic" (1656), ang Pranses na may-akda na si A. ay naglalaan din ng isang buong kabanata sa mga kumbinasyon at permutasyon.
B. Pascal sa kanyang "Treatise on the Arithmetic Triangle" at sa kanyang "Treatise on Numerical Orders" (1665) ay binalangkas ang doktrina ng binomial coefficients. Alam ni P. Fermat ang tungkol sa mga koneksyon sa pagitan ng mga mathematical square at figured na mga numero na may teorya ng mga compound. Ang terminong "combinatorics" ay nagsimulang gamitin pagkatapos mailathala ni Leibniz ang kanyang akdang "Discourse on the Art of Combination" noong 1665, na sa unang pagkakataon ay nagbigay ng siyentipikong batayan para sa teorya ng mga kumbinasyon at permutasyon. Unang pinag-aralan ni J. Bernoulli ang mga pagkakalagay sa ikalawang bahagi ng kanyang aklat na "Ars conjectandi" (ang sining ng hula) noong 1713. Ang modernong simbolismo ng mga kumbinasyon ay iminungkahi ng iba't ibang mga may-akda ng mga manwal na pang-edukasyon lamang noong ika-19 na siglo.

Ang buong iba't ibang mga formula ng kombinatoryal ay maaaring makuha mula sa dalawang pangunahing pahayag tungkol sa mga may hangganan na hanay - ang tuntunin ng kabuuan at ang tuntunin ng produkto.

Sum na Panuntunan

Kung ang mga finite set ay hindi nagsalubong, ang bilang ng mga elemento ng X U Y (o) ay katumbas ng kabuuan ng bilang ng mga elemento ng set X at ang bilang ng mga elemento ng set Y.

Ibig sabihin, kung mayroong X na aklat sa unang shelf, at Y na aklat sa pangalawa, maaari kang pumili ng aklat mula sa una o pangalawang shelf sa X+Y na paraan.

Mga sample na problema

Dapat tapusin ng mag-aaral ang praktikal na gawain sa matematika. Siya ay inalok ng pagpili ng 17 paksa sa algebra at 13 paksa sa geometry. Sa ilang paraan siya makakapili ng isang paksa para sa praktikal na gawain?

Solusyon: X=17, Y=13

Ayon sa sum rule X U Y=17+13=30 na paksa.

Mayroong 5 tiket para sa cash lottery, 6 na tiket para sa sports lottery at 10 tiket para sa car lottery. Sa ilang paraan maaari kang pumili ng isang tiket mula sa isang sports lotto o auto lottery?

Solusyon: Dahil ang cash at loterya ng damit ay hindi kasama sa pagpili, mayroon lamang 6 + 10 = 16 na pagpipilian.

Panuntunan ng produkto

Kung ang elementong X ay maaaring piliin sa k na paraan, at ang elementong Y sa m na paraan, kung gayon ang pares (X,Y) ay maaaring piliin sa k*m na paraan.

Ibig sabihin, kung mayroong 5 aklat sa unang shelf at 10 sa pangalawa, maaari kang pumili ng isang libro mula sa unang shelf at isa mula sa pangalawa sa 5 * 10 = 50 na paraan.

Mga sample na problema

Ang isang bookbinder ay dapat magbigkis ng 12 iba't ibang mga libro sa pula, berde at kayumanggi na mga binding. Sa ilang paraan niya ito magagawa?

Solusyon: Mayroong 12 mga libro at 3 kulay, na nangangahulugang ayon sa panuntunan ng produkto, 12 * 3 = 36 na mga opsyon sa pagbubuklod ay posible.

Ilang limang-digit na numero ang mayroon na pareho ang binasa mula kaliwa hanggang kanan at kanan pakaliwa?

Solusyon: Sa ganitong mga numero, ang huling digit ay magiging kapareho ng una, at ang penultimate digit ay kapareho ng pangalawa. Ang ikatlong digit ay magiging anuman. Ito ay maaaring ilarawan sa anyo XYZYX, kung saan ang Y at Z ay anumang mga numero, at ang X ay hindi zero. Nangangahulugan ito na ayon sa panuntunan ng produkto, ang bilang ng mga digit na maaaring basahin nang pantay mula kaliwa hanggang kanan at mula kanan papuntang kaliwa ay 9*10*10=900 na opsyon.

Mga intersecting set

Ngunit nangyayari na ang mga hanay ng X at Y ay nagsalubong, pagkatapos ay ginagamit nila ang formula

, kung saan ang X at Y ay mga set, at ang lugar ng intersection. Mga sample na problema

20 tao ang nakakaalam ng English at 10 ang nakakaalam ng German, kung saan 5 ang nakakaalam ng English at German. Ilang tao ang kabuuan?

Sagot: 10+20-5=25 tao.

Madalas ding ginagamit ang mga lupon ng Euler upang biswal na malutas ang problema. Halimbawa:

Sa 100 turistang bumibiyahe sa ibang bansa, 30 tao ang nagsasalita ng German, 28 - English, 42 - French 8 tao ang nagsasalita ng English at German nang sabay, 10 - English at French, 5 - German at French, 3 - lahat ng tatlo. ang mga turista ay hindi nagsasalita ng anumang wika?

Solusyon: Ipahayag natin sa graphical na paraan ang kalagayan ng problemang ito. Tukuyin natin sa pamamagitan ng isang lupon ang mga nakakaalam ng Ingles, isa pang lupon ng mga nakakaalam ng Pranses, at isang pangatlong lupon ng mga nakakaalam ng Aleman.

Tatlong turista ang nagsasalita ng lahat ng tatlong wika, na nangangahulugan na sa pangkalahatang bahagi ng mga bilog ay ipinasok namin ang numero 3. 10 tao ang nagsasalita ng Ingles at Pranses, at 3 sa kanila ay nagsasalita din ng Aleman. Dahil dito, 10-3=7 tao ang nagsasalita lamang ng Ingles at Pranses.

Katulad nito, nalaman namin na 8-3 = 5 tao ang nagsasalita lamang ng Ingles at Aleman, at 5-3 = 2 turista ang nagsasalita ng Aleman at Pranses. Inilalagay namin ang data na ito sa mga naaangkop na bahagi.

Alamin natin ngayon kung gaano karaming tao ang nagsasalita ng isa lamang sa mga nakalistang wika. 30 tao ang nakakaalam ng German, ngunit 5+3+2=10 sa kanila ang nagsasalita ng ibang mga wika, samakatuwid, 20 tao lang ang nakakaalam ng German. Katulad nito, nalaman namin na 13 tao ang nagsasalita ng Ingles nang nag-iisa, at 30 tao ang nagsasalita ng Pranses nang nag-iisa.

Ayon sa problema, 100 lang ang turista. 20+13+30+5+7+2+3=80 turista ang nakakaalam ng kahit isang wika, samakatuwid, 20 tao ang hindi nagsasalita ng alinman sa mga wikang ito.

Mga pagkakalagay nang walang pag-uulit.

Ilang numero ng telepono ang maaaring gawin mula sa 6 na numero bawat isa, upang ang lahat ng mga numero ay magkaiba?

Ito ay isang halimbawa ng problema sa paglalagay nang walang pag-uulit. Mayroong 10 numero ng 6 na nakalagay dito At ang mga opsyon kung saan ang parehong mga numero ay nasa iba't ibang mga order ay itinuturing na naiiba.

Kung ang isang X-set na binubuo ng n elemento, m≤n, kung gayon ang pagkakaayos nang walang pag-uulit ng n elemento ng set X sa m ay tinatawag na isang ordered set X na naglalaman ng m elemento ay tinatawag na isang ordered set X na naglalaman ng m elemento.

Ang bilang ng lahat ng mga kaayusan ng n elemento sa pamamagitan ng m ay tinutukoy ng

n! - n-factorial (factorial factor) ay ang produkto ng mga numero sa natural na serye mula 1 hanggang sa anumang numero n Gawain

Sa ilang paraan maaaring hilingin ng 4 na lalaki ang apat sa anim na babae na sumayaw?

Solusyon: hindi maaaring imbitahan ng dalawang lalaki ang parehong babae nang sabay. At ang mga pagpipilian kung saan ang parehong mga batang babae ay sumasayaw sa iba't ibang mga lalaki ay itinuturing na iba, samakatuwid:

Posible ang 360 na opsyon.

Mga permutasyon nang walang pag-uulit

Sa kaso ng n=m (tingnan ang mga pagkakalagay nang walang pag-uulit) ng n elemento ng m ay tinatawag na permutation ng set x.

Ang bilang ng lahat ng mga permutasyon ng n elemento ay tinutukoy ng P n.

Wasto para sa n=m:

Mga sample na problema

Ilang magkakaibang anim na digit na numero ang maaaring gawin mula sa mga digit na 0, 1, 2, 3, 4.5 kung ang mga numero ay hindi inuulit?

1) Hanapin ang bilang ng lahat ng permutasyon mula sa mga numerong ito: P 6 =6!=720

2) Ang 0 ay hindi maaaring nasa unahan ng isang numero, kaya ang bilang ng mga permutasyon kung saan ang 0 ay nasa unahan ay dapat ibawas sa numerong ito. At ito ay P 5 =5!=120.

P 6 -P 5 =720-120=600

Makulit na Unggoy

Oo, clubfoot si Mishka

Nagsimula kaming maglaro ng quartet

Tumigil, mga kapatid, tumigil! –

Sigaw ng unggoy, - teka!

Paano dapat pumunta ang musika?

Pagkatapos ng lahat, hindi ka nakaupo sa ganyan...

At sa ganitong paraan at nagpalit sila ng upuan - muli ang musika ay hindi maganda.

Isaalang-alang natin ang problema sa pagbibilang ng bilang ng mga sample mula sa isang ibinigay na set sa pangkalahatang anyo. Magkaroon ng ilang set N, na binubuo ng mga n mga elemento. Anumang subset na binubuo ng m ang mga elemento ay maaaring isaalang-alang nang hindi isinasaalang-alang ang kanilang pagkakasunud-sunod, o isinasaalang-alang ito, i.e. kapag binabago ang order, lumipat sa isa pa m– sampling.

Bumuo tayo ng mga sumusunod na kahulugan:

Mga pagkakalagay nang walang pag-uulit

Paglalagay nang walang pag-uulit ngn mga elemento sa pamamagitan ngm Nnaglalaman ngmiba't ibang elemento.

Mula sa kahulugan ay sumusunod na ang dalawang kaayusan ay magkaiba sa isa't isa, kapwa sa kanilang mga elemento at sa kanilang pagkakasunud-sunod, kahit na ang mga elemento ay pareho.

Teorama 3. Ang bilang ng mga pagkakalagay nang walang pag-uulit ay katumbas ng produkto m mga kadahilanan, ang pinakamalaki ay ang bilang n . Isulat:

Mga permutasyon nang walang pag-uulit

Mga permutasyon mula san Ang mga elemento ay tinatawag na iba't ibang pagkakasunud-sunod ng setN.

Mula sa kahulugang ito, sumusunod na ang dalawang permutasyon ay naiiba lamang sa pagkakasunud-sunod ng mga elemento at maaari silang ituring bilang isang espesyal na kaso ng mga pagkakalagay.

Teorama 4. Ang bilang ng iba't ibang permutasyon nang walang pag-uulit ay kinakalkula ng formula

Mga kumbinasyon nang walang pag-uulit

Isang kumbinasyon na walang pag-uulit ngn mga elemento sa pamamagitan ngm tinatawag ang anumang unordered subset ng isang setNnaglalaman ngm iba't ibang elemento.

Mula sa kahulugan ay sumusunod na ang dalawang kumbinasyon ay naiiba lamang sa mga elemento;

Teorama 5. Ang bilang ng mga kumbinasyon na walang pag-uulit ay kinakalkula gamit ang isa sa mga sumusunod na formula:

Halimbawa 1. May 5 upuan sa kwarto. Sa ilang paraan maaari mong ilagay ang mga ito sa kanila?

a) 7 tao; b) 5 tao; c) 3 tao?

Solusyon: a) Una sa lahat, kailangan mong pumili ng 5 tao sa 7 para maupo sa mga upuan. Pwedeng magawa
paraan. Sa bawat pagpipilian ng isang partikular na lima, maaari kang gumawa
muling pagsasaayos. Ayon sa multiplication theorem, ang kinakailangang bilang ng mga paraan ng landing ay pantay.

Komento: Ang problema ay maaaring malutas gamit lamang ang teorama ng produkto, pangangatwiran tulad ng sumusunod: para sa pag-upo sa unang upuan mayroong 7 mga pagpipilian, sa ika-2 upuan mayroong 6 na pagpipilian, sa ika-3 -5, sa ika-4 -4 at sa 5- ika-3. Kung gayon ang bilang ng mga paraan upang maupo ang 7 tao sa 5 upuan ay . Ang mga solusyon sa parehong mga pamamaraan ay pare-pareho, dahil

b) Ang solusyon ay malinaw -

V) - bilang ng mga halalan ng mga inookupahang upuan.

- ang bilang ng mga upuan para sa tatlong tao sa tatlong napiling upuan.

Ang kabuuang bilang ng mga halalan ay .

Hindi mahirap suriin ang mga formula
;

;

Ang bilang ng lahat ng subset ng isang set na binubuo ng n mga elemento.

Ulitin ang mga pagkakalagay

Sa pamamagitan ng paglalagay na may pag-uulit mula san mga elemento sa pamamagitan ngm bawat order na subset ng isang set ay tinatawagN, na binubuo ng mgam mga elemento upang maisama ang anumang elemento sa subset na ito mula 1 hanggangmbeses, o wala dito nang buo.

Ang bilang ng mga pagkakalagay na may pag-uulit ay tinutukoy ng at kinakalkula gamit ang formula, na isang kinahinatnan ng multiplication theorem:

Halimbawa 2. Hayaang ang N = (a, b, c) ay isang set ng tatlong titik. Tawagan natin ang anumang hanay ng mga titik na kasama sa hanay na ito bilang isang salita. Hanapin ang bilang ng mga salita na may haba na 2 na maaaring gawin mula sa mga titik na ito:
.

Komento: Malinaw, ang mga pagkakalagay na may pag-uulit ay maaari ding isaalang-alang kung kailan
.

Halimbawa 3. Kailangan mong gamitin ang mga titik (a, b) upang lumikha ng lahat ng posibleng salita na may haba 3. Sa ilang paraan ito magagawa?

Sagot:

Lektura 2

Ayon sa klasikal na kahulugan, ang pagkalkula ng posibilidad ng kaganapan A ay bumababa sa pagbibilang ng bilang ng mga resultang paborable dito. Ito ay kadalasang ginagawa gamit ang mga combinatorial na pamamaraan.

Ang Combinatorics ay isang sangay ng matematika na nag-aaral ng mga problema sa pagpili ng mga elemento mula sa isang naibigay na set at pag-aayos ng mga ito sa mga grupo ayon sa ibinigay na mga patakaran, lalo na ang problema sa pagbibilang ng bilang ng mga kumbinasyon (mga sample) na nakuha mula sa mga elemento ng isang tiyak na hanay. Ang bawat isa sa kanila ay nangangailangan ng pagbibilang ng bilang ng mga posibleng opsyon para sa pagsasagawa ng isang tiyak na aksyon at pagsagot sa tanong na "sa ilang paraan?"

Maraming mga problemang kombinatoryal ang maaaring malutas gamit ang sumusunod na dalawang mahahalagang tuntunin, na tinatawag na mga tuntunin ng pagpaparami at pagdaragdag, ayon sa pagkakabanggit.

Panuntunan sa pagpaparami(pangunahing prinsipyo): kung mula sa ilang limitadong hanay ang unang bagay (elemento x) ay maaaring mapili sa n mga paraan at pagkatapos ng bawat ganoong pagpipilian ang pangalawang bagay (elemento y) ay maaaring mapili sa m na paraan, kung gayon ang parehong mga bagay (x at y) sa tinukoy na pagkakasunud-sunod ay maaaring mapili sa n sa ´m na paraan.

Ang prinsipyong ito ay malinaw na umaabot sa kaso ng tatlo o higit pang mga bagay.

Halimbawa 1. Ilang tatlong-digit na numero ang maaaring gawin mula sa mga numero 1, 2, 3, 4, 5 kung:

a) ang mga numero ay hindi inuulit?

b) maaari bang ulitin ang mga numero?

Mayroong 5 iba't ibang paraan upang piliin ang numero para sa unang lugar (sa kaliwa sa isang tatlong-digit na numero). Matapos mapunan ang unang lugar, halimbawa, sa numero 2, may apat na numero na natitira upang punan ang pangalawang lugar. Upang punan ang ikatlong lugar, mayroong pagpipilian ng tatlong numero. Samakatuwid, ayon sa tuntunin ng multiplikasyon, mayroong 5 × 4 × 3 = 60 na paraan upang ayusin ang mga numero, ibig sabihin, ang kinakailangang bilang ng tatlong-digit na numero ay 60. (Narito ang ilan sa mga numerong ito: 243, 541, 514, 132, ...) Malinaw na kung ang mga numero ay maaaring ulitin, kung gayon mayroong 5×5×5= 125 tatlong-digit na mga numero (Narito ang ilan sa mga ito: 255, 333, 414, 111, 122, .. .)

Panuntunan ng kabuuan. Kung ang ilang bagay na x ay maaaring mapili sa n mga paraan, at ang isang bagay na y ay maaaring mapili sa m mga paraan, at ang una at pangalawang pamamaraan ay hindi magsalubong, kung gayon ang alinman sa mga tinukoy na bagay (x o y) ay maaaring mapili sa n+m mga paraan.

Nalalapat ang panuntunang ito sa anumang may hangganang bilang ng mga bagay.

Halimbawa 2. Mayroong 14 na babae at 6 na lalaki sa grupo ng mag-aaral. Sa ilang paraan mapipili ang dalawang mag-aaral ng parehong kasarian upang tapusin ang magkaibang gawain?

Ayon sa multiplication rule, dalawang babae ang maaaring piliin sa 14 × 13 = 182 na paraan, at dalawang lalaki ang maaaring piliin sa 6 × 5 = 30 na paraan. Dapat kang pumili ng dalawang mag-aaral ng parehong kasarian: dalawang babaeng mag-aaral o dalawang lalaking mag-aaral. Ayon sa panuntunan para sa pagdaragdag ng mga ganitong paraan ng pagpili, magkakaroon ng 182 + 30 = 212.

Ang paglutas ng probabilistic (at iba pang) problema ay kadalasang mas madali kung gagamit ka ng mga combinatorial formula. Tinutukoy ng bawat isa sa kanila ang bilang ng mga posibleng resulta sa ilang eksperimento (eksperimento), na binubuo ng pagpili ng random na m elemento mula sa n magkakaibang elemento ng set na isinasaalang-alang.

Mayroong dalawang mga scheme para sa pagpili ng m elemento (0< m £ n) из исходного множества: Walang balikan(walang pag-uulit) at Maligayang pagbabalik(na may pag-uulit). Sa unang kaso, ang mga napiling elemento ay hindi ibinalik; Maaari mong piliin ang lahat ng m elemento nang sabay-sabay o sunud-sunod na piliin ang mga ito nang paisa-isa. Sa pangalawang pamamaraan, ang pagpili ay isinasagawa elemento sa pamamagitan ng elemento na may obligadong pagbabalik ng napiling elemento sa bawat hakbang.

Scheme ng pagpili nang walang pagbabalik

Bigyan tayo ng isang set na binubuo ng n iba't ibang elemento.

Akomodasyon ng n elemento, m elemento bawat isa (0< m £ n) называется любое упорядоченное подмножество данного множества, содержащее m элементов.

Ito ay sumusunod mula sa kahulugan na ang mga pagkakalagay ay mga seleksyon (kombinasyon) na binubuo ng m mga elemento na naiiba sa isa't isa alinman sa komposisyon ng mga elemento o sa pagkakasunud-sunod ng kanilang pagkakaayos.

Ang bilang ng mga pagkakalagay ng n elemento ng m elemento ay tinutukoy ng simbolo (“A mula sa en sa pamamagitan ng em”) at kinakalkula ng formula

Upang lumikha ng isang pag-aayos, kailangan mong pumili ng m mga elemento mula sa isang set na may n mga elemento at ayusin ang mga ito, iyon ay, punan ang m mga lugar na may mga elemento ng set. Ang unang elemento ay maaaring mapili sa n mga paraan, ibig sabihin, alinman sa n elemento ay maaaring ilagay sa unang lugar. Ang pangalawang elemento ay maaaring mapili mula sa natitirang mga elemento ng n-1 sa mga n-1 na paraan. Mayroong n-2 na paraan upang piliin ang ikatlong elemento, n-3 paraan upang piliin ang ikaapat, at, sa wakas, para sa huling mth elemento mayroong (n-(m-1)) na mga paraan. Kaya, ayon sa tuntunin ng multiplikasyon, mayroong n(n-1)(n-2)...(n-(m-1)) na mga paraan upang piliin ang m elemento mula sa ibinigay na n elemento, ibig sabihin.

Halimbawa 3. Gumawa ng iba't ibang pagsasaayos ng 2 elemento mula sa set D = (a, b, c); bilangin ang kanilang numero.

Mula sa tatlong elemento ay maaaring mabuo ang mga sumusunod na kaayusan ng dalawang elemento: (a, b), (b, a), (a, c), (c, a), (b, c), (c, b). Ayon sa formula (1), ang kanilang numero ay: = 3×2 = 6.

Muling pagsasaayos ng n elemento ay isang pagsasaayos ng n elemento ng n elemento.

Ito ay sumusunod mula sa kahulugan na ang mga permutasyon ay mga seleksyon (kombinasyon) na binubuo ng n mga elemento at nagkakaiba sa isa't isa lamang sa pagkakasunud-sunod ng mga elemento. Ang bilang ng mga permutasyon ng n elemento ay tinutukoy ng simbolong P n (“pe mula sa en”) at kinakalkula ng formula

Ang formula (3) ay sumusunod mula sa kahulugan ng permutation:

Halimbawa 4. Bumuo ng iba't ibang permutasyon mula sa mga elemento ng set E = (2, 7, 8); bilangin ang kanilang numero.

Ang mga sumusunod na permutasyon ay maaaring gawin mula sa mga elemento ng set na ito: (2,7,8); (2,8,7); (7,2,8); (7,8,2); (8,2,7); (8,7,2). Ayon sa formula (3) mayroon tayong: P 3 = 3! = 1×2×3 = 6.

Halimbawa 5. Sa ilang paraan maaaring ayusin ang 5 magkaibang aklat sa isang istante?

Ang kinakailangang bilang ng mga paraan ay katumbas ng bilang ng mga permutasyon ng 5 elemento (mga aklat), i.e.

P 5 =5!=1×2×3×4×5 = 120.

Kumbinasyon ng n elemento ng m bawat isa (0< m £ n) элементов называется любое подмножество, которое содержит m элементов данного множества.

Ito ay sumusunod mula sa kahulugan na ang mga kumbinasyon ay mga sample (mga kumbinasyon), ang bawat isa ay binubuo ng m mga elemento na kinuha mula sa ibinigay na mga elemento, at kung saan ay naiiba sa bawat isa sa pamamagitan ng hindi bababa sa isang elemento, ibig sabihin, sila ay naiiba lamang sa komposisyon ng mga elemento.

Ang bilang ng mga kumbinasyon ng n elemento ng m elemento ay tinutukoy ng simbolo (“tse from en by em”) at kinakalkula ng formula

Ang bilang ng mga pagsasaayos ng n elemento sa pamamagitan ng m elemento ay matatagpuan tulad ng sumusunod: piliin ang m elemento mula sa isang set na naglalaman ng n elemento (ito ay maaaring gawin sa mga paraan); pagkatapos ay sa bawat isa sa mga resultang kumbinasyon (subsets) gawin ang lahat ng mga permutasyon upang mag-order ng mga subset (ito ay maaaring gawin sa P m na paraan). Samakatuwid, ayon sa panuntunan ng pagpaparami, maaari nating isulat:

Mula dito o

Maaaring ipakita na ang mga formula ay mayroong:

Halimbawa 5. Gumawa ng iba't ibang kumbinasyon ng 2 elemento mula sa set D - (a, b, c); bilangin ang kanilang numero.

Mula sa tatlong elemento ay maaaring mabuo ang mga sumusunod na kumbinasyon ng dalawang elemento: (a, b); (a,c); (b,c). Ang kanilang numero: (formula (4)).

Halimbawa 6. Sa ilang paraan maaari kang pumili ng 3 bulaklak mula sa isang plorera na naglalaman ng 10 pula at 4 na pink na carnation? Paano kung pumili ka ng 1 pulang carnation at 2 kulay rosas?

Dahil ang pagkakasunud-sunod kung saan ang mga bulaklak ay pinili ay hindi mahalaga, mayroong ilang mga paraan upang pumili ng 3 bulaklak mula sa isang plorera na naglalaman ng 14 na carnation. Gamit ang formula (4) makikita natin ang: . Susunod: maaari kang pumili ng pulang carnation sa iba't ibang paraan. Mayroong ilang mga paraan upang pumili ng dalawang pink na carnation mula sa magagamit na apat. Samakatuwid, ang isang palumpon ng isang pula at dalawang kulay-rosas na carnation ay maaaring binubuo, ayon sa panuntunan ng pagpaparami, sa iba't ibang paraan.

Scheme ng pagpili na may pagbabalik

Kung, pagkatapos pumili ng m elemento mula sa n, ang mga elemento ay ibinalik at inutusan, kung gayon ito ay sinasabing mga pagkakalagay na may mga pag-uulit.

Ang mga pagkakalagay na may mga pag-uulit ay maaaring magkaiba sa bawat isa sa mga elemento, ang kanilang pagkakasunud-sunod at ang bilang ng mga pag-uulit ng mga elemento. Ang bilang ng lahat ng mga pagkakalagay ng n elemento, m bawat isa ay may mga pag-uulit, ay tinutukoy ng isang simbolo at kinakalkula ng formula (6)

Halimbawa 7. Mula sa 3 elemento a, b, c, binubuo ang lahat ng mga pagkakalagay ng dalawang elemento na may mga pag-uulit.

Ayon sa formula (1.12), ang bilang ng mga pagkakalagay sa dalawa na may mga pag-uulit ay katumbas ng . Ito ay: (a,a), (a,b), (a,c), (b,b), (b,a), (b,c), (c,c), (c,a) , (c, b)

Halimbawa 8. Ilang limang-digit na numero ang maaaring gawin gamit ang mga digit:

a) Lahat ng limang-digit na mga numero na binubuo ng mga numerong 2, 5, 7, 8 ay naiiba sa isa't isa alinman sa pagkakasunud-sunod kung saan sila lumilitaw (halimbawa, 25558 at 52855), o sa mga numero mismo (halimbawa, 52788 at 78888). Samakatuwid, ang mga ito ay mga pag-aayos ng 4 na elemento ng 5 na may mga pag-uulit, i.e. . Kaya, ang kinakailangang bilang ng limang-digit na numero ay . Ang parehong resulta ay maaaring makuha gamit ang multiplication rule: ang unang digit mula sa kaliwa sa isang limang-digit na numero ay maaaring piliin sa apat na paraan, ang pangalawa sa apat na paraan, ang ikatlo sa apat, ang ikaapat sa apat, at ang ikalima sa apat. Sa kabuuan ay nakakakuha tayo ng 4×4×4×4×4=1024 limang-digit na numero.

b) Kung ang limang-digit na mga numero ay binubuo ng mga digit na 0, 1, 9, kung gayon ang unang digit sa kaliwa ay maaaring piliin sa dalawang paraan (ang 0 ay hindi maaaring sumakop sa unang posisyon), ang bawat isa sa natitirang apat na numero ay maaaring piliin sa tatlo mga paraan. Ayon sa tuntunin ng multiplikasyon, magkakaroon ng 2×3×3×3×3=162 na mga numero. (Kung hindi man: .)

Kung, kapag ang m elemento ay pinili mula sa n elemento, ang mga elemento ay ibinalik nang walang karagdagang pag-order, kung gayon ito ay sinasabing mga kumbinasyon na may mga pag-uulit.

Ang bilang ng lahat ng kumbinasyon ng n elemento ng m na may mga pag-uulit ay tinutukoy ng isang simbolo at kinakalkula ng formula

Halimbawa 9. Mula sa tatlong elemento a, b, c, binubuo ang lahat ng kumbinasyon ng dalawang elemento na may mga pag-uulit.

Ayon sa formula (7), ang bilang ng mga kumbinasyon ng dalawa na may mga pag-uulit ay katumbas ng . Ginagawa namin ang mga kumbinasyong ito na may mga pag-uulit: (a, a), (a. b), (a, c), (b,b), (b, c), (c, c).

Halimbawa 10. Sa ilang paraan maaari kang gumawa ng isang palumpon ng 5 bulaklak kung mayroong tatlong uri ng mga bulaklak na magagamit?

Ang set na isinasaalang-alang ay binubuo ng tatlong magkakaibang elemento, at ang mga sample ay may dami na katumbas ng 5. Dahil ang pagkakasunud-sunod ng mga bulaklak sa palumpon ay hindi mahalaga, ang kinakailangang bilang ng mga bouquet ay katumbas ng bilang ng mga kumbinasyon na may mga pag-uulit ng tatlong elemento. ng 5 bawat isa. Ayon sa formula (7) mayroon tayo

Hayaang ang isang set na may n elemento ay may k magkakaibang elemento, na ang unang elemento ay inuulit n 1 beses, ang 2nd elemento n 2 beses..., ang kth elemento n k beses, at n 1 +n 2 +... +n k =n .

Ang mga permutasyon ng n elemento ng isang naibigay na set ay tinatawag mga permutasyon na may mga pag-uulit ng n elemento.

Ang bilang ng mga permutasyon na may mga pag-uulit ng n elemento ay ipinahiwatig ng simbolo

Р n (n 1, n 2, …, n k) at kinakalkula ng formula

Halimbawa 11. Ilang magkakaibang limang-digit na numero ang maaaring gawin mula sa mga numerong 3, 3, 5, 5, 8?

Ilapat natin ang formula (8). Dito n=5, n 1 =2, n 2 =2, n 3 = 1. Ang bilang ng magkakaibang limang-digit na numero na naglalaman ng mga numero 3, 5 at 8 ay katumbas ng

Plano:

1. Mga elemento ng combinatorics.

2. Pangkalahatang mga patakaran ng combinatorics.

4. Paglalapat ng mga graph (scheme) sa paglutas ng mga problemang kombinatoryal.

1. Combinatorics at mga pinagmulan nito.

Kombinatorika ay isang larangan ng matematika kung saan pinag-aaralan ang mga tanong tungkol sa kung gaano karaming magkakaibang kumbinasyon, na napapailalim sa ilang mga kundisyon, ang maaaring gawin mula sa mga elementong kabilang sa isang naibigay na set.

Ang mga combinatorics ay nagmula noong ika-16 na siglo. Ang pagsusugal (mga card, dice) ay sumakop sa isang malaking lugar sa buhay ng mga privileged layer ng lipunan noong panahong iyon. Laganap ang mga loterya. Sa una, ang mga problemang kombinatoryal ay pangunahing tinatalakay sa pagsusugal: sa kung gaano karaming mga paraan ang isang tao ay makakakuha ng isang naibigay na bilang ng mga puntos sa pamamagitan ng paghagis ng 2 o 3 dice, o sa kung gaano karaming mga paraan ang isa ay makakakuha ng 2 hari sa isang partikular na laro ng baraha. Ang mga ito at iba pang mga problema ng pagsusugal ay ang puwersang nagtutulak sa pagbuo ng mga combinatorics at higit pa sa pagbuo ng teorya ng posibilidad.

Isa sa mga unang nagbilang ng bilang ng iba't ibang kumbinasyon kapag naglalaro ng dice ay ang Italian mathematician na si Tartaglia. Nag-compile siya ng mga talahanayan (ang bilang ng mga paraan na maaaring lumitaw ang mga k point sa r dice). Gayunpaman, hindi niya isinasaalang-alang na ang parehong halaga ng mga puntos ay maaaring lumabas sa iba't ibang paraan, kaya ang kanyang mga talahanayan ay naglalaman ng isang malaking bilang ng mga error.

Ang teoretikal na pag-aaral ng mga isyu sa combinatorics ay isinagawa noong ika-17 siglo ng mga French mathematician na sina Blaise Pascal at Fermat. Ang panimulang punto ng kanilang pananaliksik ay mga problema din sa pagsusugal.

Ang karagdagang pag-unlad ng combinatorics ay nauugnay sa mga pangalan ni J. Bernoulli, G. Leibniz, L. Euler. Gayunpaman, sa kanilang trabaho ang pangunahing papel ay nilalaro ng mga aplikasyon sa iba't ibang mga laro.

Sa ngayon, ang mga pamamaraan ng kombinatoryal ay ginagamit upang malutas ang mga problema sa transportasyon, sa partikular na mga problema sa pag-iskedyul, upang gumuhit ng mga plano sa produksyon at pagbebenta ng mga produkto, atbp.

2. Pangkalahatang mga patakaran ng combinatorics.

Panuntunan sa kabuuan: Kung ang ilang bagay na A ay maaaring piliin sa m na paraan, at ang isang bagay na B sa mga k na paraan, kung gayon ang bagay na "alinman sa A o B" ay maaaring piliin sa m + k na paraan.

Mga halimbawa:

1. Ipagpalagay natin na mayroong n magkakaibang kulay na mga bola sa isang kahon. 1 bola ay random na inalis. Sa ilang paraan ito magagawa?

Sagot: n paraan.

Ipamahagi natin ang mga n bola na ito sa dalawang kahon: ang una ay naglalaman ng m bola, ang pangalawa ay naglalaman ng mga k bola. 1 bola ay random na iginuhit mula sa isang random na piniling kahon. Sa ilang paraan ito magagawa?

Solusyon: Maaaring alisin ang bola mula sa unang kahon sa m paraan, at mula sa pangalawa sa k paraan. Kung gayon ang kabuuang bilang ng mga paraan ay m+k=n.

2. Marine semaphore.

Sa maritime semaphore, ang bawat titik ng alpabeto ay tumutugma sa isang tiyak na posisyon ng dalawang flag na nauugnay sa katawan ng signalman. Gaano karaming mga senyales ang maaaring magkaroon?

Solusyon: Ang kabuuang bilang ay ang kabuuan ng mga posisyon kapag ang parehong mga flag ay matatagpuan sa magkabilang panig ng katawan ng signalman at ang mga posisyon kapag sila ay matatagpuan sa parehong bahagi ng katawan ng signalman. Kapag binibilang ang bilang ng mga posibleng posisyon, inilalapat ang panuntunan sa kabuuan.

Panuntunan ng produkto: Kung ang object A ay maaaring mapili sa m na paraan, at pagkatapos ng bawat naturang pagpipilian ay maaaring pumili ng isa pang object B (anuman ang pagpili ng object A) sa mga k na paraan, kung gayon ang mga pares ng mga bagay na "A at B" ay maaaring mapili sa m * k mga paraan.

Mga halimbawa:

1. Ilang dalawang-digit na numero ang mayroon?

Solusyon: Ang bilang ng sampu ay maaaring tukuyin ng anumang numero mula 1 hanggang 9. Ang bilang ng isa ay maaaring tukuyin ng anumang numero mula 0 hanggang 9. Kung ang bilang ng sampu ay 1, kung gayon ang bilang ng isa ay maaaring maging anumang numero (mula sa 0 hanggang 9). Kaya, mayroong 10 dalawang-digit na numero, na ang bilang ng sampu ay 1. Pareho kaming nangangatuwiran para sa anumang iba pang bilang ng sampu. Pagkatapos ay maaari nating kalkulahin na mayroong 9 *10 = 90 dalawang-digit na numero.

2. May 2 drawer. Ang isa ay naglalaman ng m multi-kulay na mga cube, at ang isa ay naglalaman ng k multi-kulay na mga bola. Sa ilang paraan maaari mong piliin ang pares na "Cube-Ball"?

Solusyon: Ang pagpili ng bola ay hindi nakasalalay sa pagpili ng kubo, at vice versa. Samakatuwid, ang bilang ng mga paraan kung saan maaaring piliin ang isang pares ay m *k .

3. Populasyon na walang pag-uulit at sample na walang pag-uulit.

Populasyon na walang pag-uulit ay isang set ng ilang may hangganang bilang ng iba't ibang elemento a 1, a 2, a 3, ..., a n.

Halimbawa: Set ng n multi-colored shreds.

Dami ng samplingk (kn) ay isang pangkat ng m elemento ng isang naibigay na populasyon.

Halimbawa: Isang sari-saring laso na natahi mula sa m maraming kulay na mga scrap na pinili mula sa ibinigay na n .

Mga post mula san elemento bawat isak ang mga naturang sample ay tinatawag na mga naglalaman ng k elemento bawat isa, pinili mula sa mga ibinigay na elemento ng pangkalahatang populasyon nang walang pag-uulit, at naiiba sa bawat isa alinman sa komposisyon ng mga elemento o sa pagkakasunud-sunod ng kanilang pagkakaayos.

- bilang ng mga pagkakalagay mula sa n ni k.

Bilang ng mga pagkakalagay mula sa n ni k maaaring matukoy sa sumusunod na paraan: maaaring mapili ang unang bagay sa pagpili n mga paraan, pagkatapos ay mapipili ang pangalawang bagay n -1 paraan, atbp.

Sa pagbabago ng formula na ito, mayroon kaming:

Dapat itong tandaan 0!=1.

Mga halimbawa:

1. Mayroong 17 koponan na kalahok sa unang grupo ng Class A ng football championship. Ang mga medalya ay iginawad: ginto, pilak at tanso. Sa ilang paraan maaari silang laruin?

Solusyon:Ang mga kumbinasyon ng nanalong koponan ay naiiba sa bawat isa sa komposisyon at pagkakasunud-sunod ng mga elemento, i.e. ay mga pagkakalagay mula 17 hanggang 3.

2. Ang lipunang siyentipiko ay binubuo ng 25 katao. Kinakailangang maghalal ng isang pangulo ng lipunan, bise-presidente, kalihim ng siyensya at ingat-yaman. Sa ilang paraan ito magagawa?

Solusyon: Ang mga kumbinasyon ng pangkat ng pamamahala ng isang kumpanya ay naiiba sa bawat isa sa komposisyon at pagkakasunud-sunod ng mga elemento, i.e. ay mga pagkakalagay mula 25 hanggang 4.

Mga permutasyon nang walang pag-uulit mula sa nmga elementoay tinatawag na mga pagkakalagay nang walang pag-uulit mula sa n elemento ng n , ibig sabihin. ang mga pagkakalagay ay naiiba sa bawat isa lamang sa pagkakasunud-sunod ng mga elemento.

Bilang ng mga permutasyon.

Mga halimbawa:

1. Ilang magkakaibang limang-digit na numero ang maaaring gawin mula sa mga digit na 1, 2, 3, 4, 5, sa kondisyon na dapat silang binubuo ng magkakaibang mga digit?

Solusyon:Mayroon kaming mga permutasyon ng 5 elemento.2. Sa ilang paraan maaari kang mag-ipon ng 6 na maraming kulay na mga scrap sa isang makulay na laso?
Solusyon:Mayroon kaming mga permutasyon ng 6 na elemento.

Mga kumbinasyon na walang pag-uulit mula sa nmga elemento sa pamamagitan ngk ang mga naturang sample ay tinatawag na mga naglalaman ng k elemento bawat isa, pinili mula sa mga ibinigay na elemento ng pangkalahatang populasyon nang walang pag-uulit, at naiiba sa bawat isa lamang sa komposisyon ng mga elemento.

- bilang ng mga kumbinasyon ng n ni k

Mga elemento ng bawat isamaaaring ayusin ang mga kumbinasyonmga paraan. PagkataposMga halimbawa:

1. Kung 20 katao ang lalahok sa semi-final ng isang kampeonato sa chess, at tatlo lang ang makakarating sa final, kung gayon sa ilang paraan matutukoy ang tatlong ito?

Solusyon:Sa kasong ito, ang pagkakasunud-sunod kung saan matatagpuan ang triple na ito ay hindi makabuluhan. Samakatuwid, ang triplets na umabot sa finals ay kumbinasyon ng 20 by 3.

2. Sa ilang paraan maaari kang pumili ng tatlong delegado sa sampung tao para sa isang kumperensya?

Solusyon:Sa kasong ito, ang pagkakasunud-sunod kung saan matatagpuan ang triple na ito ay hindi makabuluhan. Samakatuwid, ang mga triplet ng mga delegado ay mga kumbinasyon ng 10 by 3.

Abstract:

4.Paggamit ng mga graph (schemes) sa paglutas ng mga problemang kombinatoryal.

Sa kaso kung saan ang bilang ng mga posibleng pagpipilian sa bawat hakbang ay depende sa kung aling mga elemento ang napili nang mas maaga, ang proseso ng pagbuo ng mga kumbinasyon ay maaaring ilarawan bilang isang "puno". Una, kung gaano karaming mga segment ang nakuha mula sa isang punto dahil may iba't ibang mga pagpipilian na maaaring gawin sa unang hakbang. Mula sa dulo ng bawat segment, gumuhit ng maraming segment na maaaring piliin sa ikalawang hakbang, kung napili ang elementong ito sa unang hakbang, atbp.

Gawain:

Kapag pinagsama-sama ang mga utos ng spacecraft, ang isyu ng sikolohikal na pagkakatugma ng mga kalahok sa paglalakbay ay isinasaalang-alang din. Ito ay kinakailangan upang bumuo ng isang spaceship crew ng 3 tao: isang kumander, isang inhinyero at isang doktor. Mayroong 4 na kandidato para sa posisyon ng kumander: a 1 , a 2 , a 3 , a 4 .Kapalit ng engineer 3:b 1, b 2, b 3. Para sa lugar ng doktor - 3: c 1, c 2, c 3. Ang inspeksyon ay nagpakita na ang kumanderAng a 1 ay psychologically compatible sa mga engineer b 1 at b 3 at mga doktor c 1 at c 3. Commander a 2 - kasama ang mga inhinyero b 1 at b 2. at lahat ng mga doktor. kumanderisang 3 - kasama ang mga inhinyerob 1 at b 2 at mga doktorc 1 at c 3. kumander a 4 - kasama ang lahat ng mga inhinyero at ang doktor c 2 . Bilang karagdagan, inhinyerob 1 hindi tugma sa doktor c 3, b 2 - kasama ang isang doktor c 1 at b 3 - kasama ang isang doktor c 2. Sa gaano karaming mga paraan maaaring binubuo ang mga tripulante ng barko sa ilalim ng mga kundisyong ito?

Solusyon:

Gumawa tayo ng kaukulang "puno".

Sagot: 10 kumbinasyon.

Ang nasabing puno ay isang graph at ginagamit upang malutas ang mga problemang kombinatoryal.