Mga function na walang minimum at maximum na mga puntos. Teoretikal na materyal. Patuloy kaming naghahanap ng extrema ng function nang magkasama

Ang extremum point ng isang function ay ang punto sa domain ng kahulugan ng function kung saan ang halaga ng function ay tumatagal sa isang minimum o maximum na halaga. Ang mga halaga ng function sa mga puntong ito ay tinatawag na extrema (minimum at maximum) ng function.

Kahulugan. Dot x1 function na domain f(x) ay tinatawag na maximum na punto ng function , kung ang halaga ng function sa puntong ito ay mas malaki kaysa sa mga halaga ng function sa mga puntong sapat na malapit dito, na matatagpuan sa kanan at kaliwa nito (iyon ay, ang hindi pagkakapantay-pantay ay humahawak f(x0 ) > f(x 0 + Δ x) x1 maximum.

Kahulugan. Dot x2 function na domain f(x) ay tinatawag na pinakamababang punto ng function, kung ang halaga ng function sa puntong ito ay mas mababa kaysa sa mga halaga ng function sa mga puntong sapat na malapit dito, na matatagpuan sa kanan at kaliwa nito (iyon ay, ang hindi pagkakapantay-pantay ay humahawak f(x0 ) < f(x 0 + Δ x) ). Sa kasong ito, sinasabi namin na ang function ay nasa punto x2 pinakamababa.

Sabihin nating punto x1 - maximum na punto ng function f(x). Pagkatapos ay sa pagitan hanggang sa x1 tumataas ang function, samakatuwid ang derivative ng function ay mas malaki kaysa sa zero ( f "(x) > 0 ), at sa pagitan pagkatapos x1 bumababa ang function, samakatuwid, derivative ng isang function mas mababa sa zero ( f "(x) < 0 ). Тогда в точке x1

Ipagpalagay din natin na ang punto x2 - pinakamababang punto ng function f(x). Pagkatapos ay sa pagitan hanggang sa x2 bumababa ang function, at ang derivative ng function ay mas mababa sa zero ( f "(x) < 0 ), а в интервале после x2 tumataas ang function, at ang derivative ng function ay mas malaki sa zero ( f "(x) > 0 ). Sa kasong ito din sa punto x2 ang derivative ng function ay zero o wala.

Fermat's theorem (isang kinakailangang tanda ng pagkakaroon ng extremum ng isang function). Kung ang punto x0 - matinding punto ng pag-andar f(x) pagkatapos sa puntong ito ang derivative ng function ay katumbas ng zero ( f "(x) = 0 ) o wala.

Kahulugan. Ang mga punto kung saan ang derivative ng isang function ay zero o wala ay tinatawag kritikal na puntos .

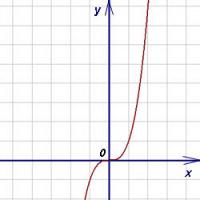
Halimbawa 1. Isaalang-alang natin ang pag-andar.

Sa punto x= 0 ang derivative ng function ay zero, samakatuwid ang point x= 0 ang kritikal na punto. Gayunpaman, tulad ng makikita sa graph ng function, tumataas ito sa buong domain ng kahulugan, kaya ang punto x Ang = 0 ay hindi ang extremum point ng function na ito.

Kaya, ang mga kundisyon na ang derivative ng isang function sa isang punto ay katumbas ng zero o wala ay mga kinakailangang kondisyon para sa isang extremum, ngunit hindi sapat, dahil ang iba pang mga halimbawa ng mga function ay maaaring ibigay kung saan ang mga kundisyong ito ay natutugunan, ngunit ang function ay walang extremum sa kaukulang punto. kaya lang dapat may sapat na ebidensya, na nagpapahintulot sa isa na hatulan kung mayroong extremum sa isang partikular na kritikal na punto at kung anong uri ito ng extremum - maximum o minimum.

Theorem (ang unang sapat na tanda ng pagkakaroon ng extremum ng isang function). Kritikal na punto x0 f(x) kung, kapag dumadaan sa puntong ito, ang derivative ng function ay nagbabago ng sign, at kung ang sign ay nagbabago mula sa "plus" hanggang sa "minus", kung gayon ito ay isang maximum na punto, at kung mula sa "minus" hanggang "plus", kung gayon ito ay isang minimum na punto.

Kung malapit sa punto x0 , sa kaliwa at sa kanan nito, pinapanatili ng derivative ang tanda nito, nangangahulugan ito na ang function ay bumababa lamang o tumataas lamang sa isang tiyak na kapitbahayan ng punto x0 . Sa kasong ito, sa punto x0 walang sukdulan.

Kaya, upang matukoy ang extremum point ng function, kailangan mong gawin ang mga sumusunod :

1. Hanapin ang derivative ng function.
2. I-equate ang derivative sa zero at tukuyin ang mga kritikal na puntos.
3. Sa isip o sa papel, markahan ang mga kritikal na punto sa linya ng numero at tukuyin ang mga palatandaan ng derivative ng function sa mga resultang pagitan. Kung ang tanda ng derivative ay nagbabago mula sa "plus" hanggang sa "minus", kung gayon ang kritikal na punto ay ang pinakamataas na punto, at kung mula sa "minus" hanggang "plus", kung gayon ang pinakamababang punto.
4. Kalkulahin ang halaga ng function sa mga extremum point.

Halimbawa 2. Hanapin ang extrema ng function .

Solusyon. Hanapin natin ang derivative ng function:

I-equate natin ang derivative sa zero upang mahanap ang mga kritikal na puntos:

.

Dahil para sa anumang mga halaga ng "x" ang denominator ay hindi katumbas ng zero, itinutumbas namin ang numerator sa zero:

Nakakuha ng isang kritikal na punto x= 3 . Tukuyin natin ang tanda ng derivative sa mga agwat na nililimitahan ng puntong ito:

sa saklaw mula sa minus infinity hanggang 3 - isang minus sign, iyon ay, bumababa ang function,

sa pagitan mula 3 hanggang plus infinity mayroong plus sign, iyon ay, tumataas ang function.

Ibig sabihin, period x= 3 ang pinakamababang punto.

Hanapin natin ang halaga ng function sa pinakamababang punto:

Kaya, ang extremum point ng function ay matatagpuan: (3; 0), at ito ang pinakamababang punto.

Theorem (ang pangalawang sapat na tanda ng pagkakaroon ng extremum ng isang function). Kritikal na punto x0 ay ang extremum point ng function f(x) kung ang pangalawang derivative ng function sa puntong ito ay hindi katumbas ng zero ( f ""(x) ≠ 0 ), at kung ang pangalawang derivative ay mas malaki sa zero ( f ""(x) > 0 ), pagkatapos ay ang pinakamataas na punto, at kung ang pangalawang derivative ay mas mababa sa zero ( f ""(x) < 0 ), то точкой минимума.

Tandaan 1. Kung sa punto x0 Kung ang una at pangalawang derivatives ay nawala, pagkatapos ay sa puntong ito imposibleng hatulan ang pagkakaroon ng isang extremum batay sa pangalawang sapat na pamantayan. Sa kasong ito, kailangan mong gamitin ang unang sapat na criterion para sa extremum ng isang function.

Puna 2. Ang pangalawang sapat na criterion para sa extremum ng isang function ay hindi naaangkop kahit na ang unang derivative ay hindi umiiral sa isang nakatigil na punto (kung gayon ang pangalawang derivative ay wala rin). Sa kasong ito, kailangan mo ring gamitin ang unang sapat na tanda ng isang extremum ng isang function.

Lokal na katangian ng extrema ng function

Mula sa mga kahulugan sa itaas, sumusunod na ang extremum ng isang function ay lokal sa kalikasan - ito ang pinakamalaki at pinakamaliit na halaga ng function kumpara sa mga kalapit na halaga.

Sabihin nating tinitingnan mo ang iyong mga kita sa loob ng isang taon. Kung noong Mayo ay nakakuha ka ng 45,000 rubles, at noong Abril 42,000 rubles at noong Hunyo 39,000 rubles, kung gayon ang mga kita sa Mayo ay ang pinakamataas na function ng kita kumpara sa mga kalapit na halaga. Ngunit noong Oktubre nakakuha ka ng 71,000 rubles, noong Setyembre 75,000 rubles, at noong Nobyembre 74,000 rubles, kaya ang mga kita sa Oktubre ay ang pinakamababa sa function ng kita kumpara sa mga kalapit na halaga. At madali mong makita na ang maximum sa mga halaga ng Abril-Mayo-Hunyo ay mas mababa kaysa sa minimum ng Setyembre-Oktubre-Nobyembre.

Sa pangkalahatan, sa pagitan ng isang function ay maaaring magkaroon ng ilang extrema, at maaaring lumabas na ang ilang minimum ng function ay mas malaki kaysa sa anumang maximum. Kaya, para sa function na ipinapakita sa figure sa itaas, .

Iyon ay, hindi dapat isipin ng isa na ang maximum at minimum ng isang function ay, ayon sa pagkakabanggit, ang pinakamalaki at pinakamaliit na halaga nito sa buong segment na isinasaalang-alang. Sa pinakamataas na punto, ang function ay may pinakamalaking halaga lamang kumpara sa mga halagang iyon na mayroon ito sa lahat ng mga punto na sapat na malapit sa pinakamataas na punto, at sa pinakamababang punto ito ay may pinakamaliit na halaga lamang kumpara sa mga halagang iyon. na mayroon itong sa lahat ng mga punto na sapat na malapit sa pinakamababang punto.

Samakatuwid, maaari nating linawin ang konsepto sa itaas ng mga extremum point ng isang function at tawagan ang mga minimum na puntos ng mga lokal na minimum na puntos, at ang maximum na mga puntos ng mga lokal na maximum na puntos.

Hinahanap namin ang extrema ng function nang magkasama

Halimbawa 3.

Solusyon: Ang function ay tinukoy at tuloy-tuloy sa buong linya ng numero. Ang hinango nito mayroon din sa buong linya ng numero. Samakatuwid, sa kasong ito, ang mga kritikal na punto ay ang mga kung saan, i.e. , mula saan at . Mga kritikal na punto at hatiin ang buong domain ng kahulugan ng function sa tatlong pagitan ng monotonicity: . Pumili tayo ng isang control point sa bawat isa sa kanila at hanapin ang sign ng derivative sa puntong ito.

Para sa pagitan, ang control point ay maaaring: hanapin. Ang pagkuha ng isang punto sa pagitan, nakukuha natin, at ang pagkuha ng isang punto sa pagitan, mayroon tayo. Kaya, sa pagitan at , at sa pagitan . Ayon sa unang sapat na criterion para sa isang extremum, walang extremum sa punto (dahil ang derivative ay nagpapanatili ng sign nito sa pagitan), at sa punto ang function ay may minimum (dahil ang derivative ay nagbabago ng sign mula minus hanggang plus kapag pumasa. sa pamamagitan ng puntong ito). Hanapin natin ang mga katumbas na halaga ng function: , a . Sa agwat ang pag-andar ay bumababa, dahil sa agwat na ito , at sa agwat ito ay tumataas, dahil sa agwat na ito .

Upang linawin ang pagbuo ng graph, makikita natin ang mga punto ng intersection nito sa mga coordinate axes. Kapag nakakuha tayo ng equation na ang mga ugat ay at , ibig sabihin, dalawang puntos (0; 0) at (4; 0) ng graph ng function ang matatagpuan. Gamit ang lahat ng impormasyong natanggap, bumuo kami ng isang graph (tingnan ang simula ng halimbawa).

Para sa self-checking sa panahon ng mga kalkulasyon, maaari mong gamitin online na derivative calculator .

Halimbawa 4. Hanapin ang extrema ng function at buuin ang graph nito.

Ang domain ng kahulugan ng isang function ay ang buong linya ng numero, maliban sa punto, i.e. .

Upang paikliin ang pag-aaral, maaari mong gamitin ang katotohanan na ang function na ito ay pantay, dahil . Samakatuwid, ang graph nito ay simetriko tungkol sa axis Oy at ang pag-aaral ay maaari lamang gawin para sa pagitan.

Paghahanap ng derivative at mga kritikal na punto ng function:

1) ;

2) ,

ngunit ang function ay naghihirap sa isang discontinuity sa puntong ito, kaya hindi ito maaaring maging isang extremum point.

Kaya, ang ibinigay na function ay may dalawang kritikal na punto: at . Isinasaalang-alang ang parity ng function, susuriin lamang namin ang punto gamit ang pangalawang sapat na criterion para sa isang extremum. Upang gawin ito, nakita namin ang pangalawang derivative at tukuyin ang sign nito sa: makuha natin . Dahil at , ito ang pinakamababang punto ng function, at .

Upang makakuha ng mas kumpletong larawan ng graph ng isang function, alamin natin ang pag-uugali nito sa mga hangganan ng domain ng kahulugan:

(dito ang simbolo ay nagpapahiwatig ng pagnanais x sa zero mula sa kanan, at x nananatiling positibo; katulad din ang ibig sabihin ng mithiin x sa zero mula sa kaliwa, at x nananatiling negatibo). Kaya, kung , pagkatapos . Susunod, hanapin namin

,

mga. kung , kung gayon .

Ang graph ng isang function ay walang mga intersection point sa mga axes. Ang larawan ay nasa simula ng halimbawa.

Para sa self-checking sa panahon ng mga kalkulasyon, maaari mong gamitin online na derivative calculator .

Patuloy kaming naghahanap ng extrema ng function nang magkasama

Halimbawa 8. Hanapin ang extrema ng function.

Solusyon. Hanapin natin ang domain ng kahulugan ng function. Dahil ang hindi pagkakapantay-pantay ay dapat masiyahan, nakukuha natin mula sa .

Hanapin natin ang unang derivative ng function.

Teorama. (isang kinakailangang kondisyon para sa pagkakaroon ng extremum) Kung ang function na f(x) ay naiba sa puntong x = x 1 at ang puntong x 1 ay isang extremum point, kung gayon ang derivative ng function ay naglalaho sa puntong ito.

Patunay. Ipagpalagay natin na ang function na f(x) ay may maximum sa puntong x = x 1.

Pagkatapos para sa sapat na maliit na positibong Dх>0 ang sumusunod na hindi pagkakapantay-pantay ay totoo:

A-priory:

Yung. kung Dх®0, ngunit Dх<0, то f¢(x 1) ³ 0, а если Dх®0, но Dх>0, pagkatapos ay f¢(x 1) £ 0.

At ito ay posible lamang kung sa Dх®0 f¢(x 1) = 0.

Para sa kaso kung ang function na f(x) ay may pinakamababa sa punto x 2, ang theorem ay napatunayan sa katulad na paraan.

Ang teorama ay napatunayan.

Bunga. Ang baligtad na pahayag ay hindi totoo. Kung ang derivative ng isang function sa isang partikular na punto ay katumbas ng zero, hindi ito nangangahulugan na ang function ay may extremum sa puntong ito. Ang isang mahusay na halimbawa nito ay ang function na y = x 3, ang derivative kung saan sa puntong x = 0 ay katumbas ng zero, ngunit sa puntong ito ang function ay mayroon lamang isang inflection, at hindi isang maximum o minimum.

Kahulugan. Mga kritikal na puntos ng isang function ay ang mga punto kung saan ang derivative ng function ay hindi umiiral o katumbas ng zero.

Ang teorama na tinalakay sa itaas ay nagbibigay sa atin ng mga kinakailangang kondisyon para sa pagkakaroon ng isang extremum, ngunit ito ay hindi sapat.

Halimbawa: f(x) = ôxô Halimbawa: f(x) =

y y

Sa puntong x = 0 ang function ay may pinakamababa, ngunit sa puntong x = 0 ang function ay wala

walang derivative. maximum, walang minimum, walang produksyon

Sa pangkalahatan, ang function na f(x) ay maaaring may extremum sa mga punto kung saan ang derivative ay wala o katumbas ng zero.

Teorama. (Sapat na mga kondisyon para sa pagkakaroon ng isang extremum)

Hayaang ang function na f(x) ay tuluy-tuloy sa pagitan (a, b), na naglalaman ng kritikal na punto x 1, at naiba sa lahat ng punto ng pagitan na ito (maliban, marahil, ang puntong x 1 mismo).

Kung, kapag dumadaan sa puntong x 1 mula kaliwa pakanan, ang derivative ng function na f¢(x) ay nagbabago ng sign mula sa “+” patungong “-“, pagkatapos ay sa puntong x = x 1 ang function na f(x) ay may isang maximum, at kung ang derivative ay nagbabago ng sign mula sa "- " hanggang sa "+" - kung gayon ang function ay may isang minimum.

Patunay.

Hayaan

Ayon sa teorama ni Lagrange: f(x) – f(x 1) = f¢(e)(x – x 1), kung saan ang x< e < x 1 .

Pagkatapos: 1) Kung x< x 1 , то e < x 1 ; f¢(e)>0; f¢(e)(x – x 1)<0, следовательно

f(x) – f(x 1)<0 или f(x) < f(x 1).

2) Kung x > x 1, kung gayon e > x 1 f¢(e)<0; f¢(e)(x – x 1)<0, следовательно

f(x) – f(x 1)<0 или f(x) < f(x 1).

Dahil ang mga sagot ay nagtutugma, maaari nating sabihin na f(x)< f(x 1) в любых точках вблизи х 1 , т.е. х 1 – точка максимума.

Ang patunay ng theorem para sa pinakamababang punto ay magkatulad.

Ang teorama ay napatunayan.

Batay sa itaas, maaari kang bumuo ng isang pinag-isang pamamaraan para sa paghahanap ng pinakamalaki at pinakamaliit na halaga ng isang function sa isang segment:

1) Hanapin ang mga kritikal na punto ng function.

2) Hanapin ang mga halaga ng function sa mga kritikal na punto.

3) Hanapin ang mga halaga ng function sa mga dulo ng segment.

4) Piliin ang pinakamalaki at pinakamaliit sa mga nakuhang halaga.

Pag-aaral ng isang function para sa isang extremum na paggamit

derivatives ng mas mataas na mga order.

Hayaan sa puntong x = x 1 f¢(x 1) = 0 at f¢¢(x 1) ay umiiral at tuluy-tuloy sa ilang kapitbahayan ng punto x 1.

Teorama. Kung f¢(x 1) = 0, kung gayon ang function na f(x) sa puntong x = x 1 ay may maximum kung f¢¢(x 1)<0 и минимум, если f¢¢(x 1)>0.

Patunay.

Hayaan ang f¢(x 1) = 0 at f¢¢(x 1)<0. Т.к. функция f(x) непрерывна, то f¢¢(x 1) будет отрицательной и в некоторой малой окрестности точки х 1 .

kasi f¢¢(x) = (f¢(x))¢< 0, то f¢(x) убывает на отрезке, содержащем точку х 1 , но f¢(x 1)=0, т.е. f¢(x) >0 sa x x 1 . Nangangahulugan ito na kapag dumadaan sa puntong x = x 1, ang derivative na f¢(x) ay nagbabago ng sign mula sa "+" hanggang sa "-", i.e.

sa puntong ito ang function na f(x) ay may maximum.

Para sa kaso ng isang minimum na function, ang theorem ay pinatunayan sa katulad na paraan.

Kung f¢¢(x) = 0, kung gayon ang katangian ng kritikal na punto ay hindi alam. Ang karagdagang pananaliksik ay kinakailangan upang matukoy ito.

Convexity at concavity ng isang curve.

Mga inflection point.

Kahulugan. Ang kurba ay matambok pataas sa pagitan (a, b) kung ang lahat ng mga punto nito ay nasa ibaba ng alinman sa mga tangent nito sa pagitan na ito. Ang isang curve convex paitaas ay tinatawag matambok, at tinatawag ang isang kurba na nakaharap nang matambok pababa malukong.

sa

Ang figure ay nagpapakita ng isang paglalarawan ng kahulugan sa itaas.

Teorama 1. Kung sa lahat ng punto ng pagitan (a, b) ang pangalawang derivative ng function na f(x) ay negatibo, kung gayon ang curve y = f(x) ay matambok paitaas (convex).

Patunay. Hayaan ang x 0 О (a, b). Gumuhit tayo ng tangent sa curve sa puntong ito.

Curve equation: y = f(x);

Tangent equation:

Dapat patunayan na .

Sa pamamagitan ng theorem ni Lagrange para sa f(x) – f(x 0): , x 0< c < x.

Ayon sa teorama ni Lagrange para sa

Hayaan ang x > x 0 pagkatapos x 0< c 1 < c < x. Т.к. x – x 0 >0 at c – x 0 > 0, at bilang karagdagan, ayon sa kundisyon

Kaya naman, .

Hayaan ang x< x 0 тогда x < c < c 1 < x 0 и x – x 0 < 0, c – x 0 < 0, т.к. по условию то

Parehong napatunayan na kung f¢¢(x) > 0 sa pagitan (a, b), kung gayon ang kurba y=f(x) ay malukong sa pagitan (a, b).

Ang teorama ay napatunayan.

Kahulugan. Tinatawag ang puntong naghihiwalay sa matambok na bahagi ng kurba mula sa malukong bahagi inflection point.

Ito ay malinaw na sa inflection point ang tangent intersects ang curve.

Teorama 2. Hayaang tukuyin ang kurba ng equation na y = f(x). Kung ang pangalawang derivative f¢¢(a) = 0 o f¢¢(a) ay wala at kapag dumadaan sa puntong x = a f¢¢(x) ay nagbabago ng sign, ang punto ng curve na may abscissa x = a ay isang inflection point.

Patunay. 1) Hayaan ang f¢¢(x)< 0 при х < a и f¢¢(x) >0 para sa x > a. Pagkatapos sa

x< a кривая выпукла, а при x >a ang kurba ay malukong, i.e. punto x = a – inflection point.

2) Hayaang f¢¢(x) > 0 para sa x< b и f¢¢(x) < 0 при x < b. Тогда при x < b кривая обращена выпуклостью вниз, а при x >b – matambok pataas. Kung gayon ang x = b ay ang inflection point.

Ang teorama ay napatunayan.

Asymptotes.

Kapag nag-aaral ng mga pag-andar, kadalasang nangyayari na kapag ang x-coordinate ng isang punto sa isang kurba ay gumagalaw sa infinity, ang kurba ay lumalapit nang walang katiyakan sa isang tiyak na tuwid na linya.

Kahulugan. Ang tuwid na linya ay tinatawag asymptote curve kung ang distansya mula sa variable na punto ng curve hanggang sa tuwid na linyang ito ay nagiging zero habang ang punto ay gumagalaw sa infinity.

Dapat tandaan na hindi lahat ng kurba ay may asymptote. Ang mga asymptotes ay maaaring tuwid o pahilig. Ang pag-aaral ng mga function para sa pagkakaroon ng mga asymptotes ay napakahalaga at nagbibigay-daan sa iyong mas tumpak na matukoy ang likas na katangian ng function at ang pag-uugali ng curve graph.

Sa pangkalahatan, ang isang kurba, na walang katiyakang papalapit sa asymptote nito, ay maaaring magsalubong dito, at hindi sa isang punto, tulad ng ipinapakita sa graph ng function sa ibaba . Ang pahilig na asymptote nito ay y = x.

Isaalang-alang natin nang mas detalyado ang mga pamamaraan para sa paghahanap ng mga asymptotes ng mga kurba.

Mga patayong asymptotes.

Mula sa kahulugan ng isang asymptote sumusunod na kung o o , kung gayon ang tuwid na linya x = a ay ang asymptote ng kurba y = f(x).

Halimbawa, para sa isang function, ang linyang x = 5 ay isang patayong asymptote.

Oblique asymptotes.

Ipagpalagay na ang curve y = f(x) ay may slanted asymptote y = kx + b.

Tukuyin natin ang punto ng intersection ng curve at ang patayo sa asymptote - M, P - ang punto ng intersection ng patayo na ito sa asymptote. Tukuyin natin ang anggulo sa pagitan ng asymptote at ng Ox axis bilang j. Ang perpendikular na MQ sa axis ng Ox ay nag-intersect sa asymptote sa punto N.

Pagkatapos MQ = y ay ang ordinate ng point ng curve, NQ = ay ang ordinate ng point N sa asymptote.

Ayon sa kondisyon: , ÐNMP = j, .

Ang anggulo j ay pare-pareho at hindi katumbas ng 90 0, kung gayon

Pagkatapos .

Kaya, ang tuwid na linya y = kx + b ay ang asymptote ng curve. Upang tumpak na matukoy ang linyang ito, kinakailangan upang makahanap ng isang paraan upang makalkula ang mga coefficient k at b.

Sa resultang expression, kinuha namin ang x sa mga bracket:

kasi x®¥, kung gayon , dahil b = const, pagkatapos .

Pagkatapos , samakatuwid,

.

kasi , Iyon , samakatuwid,

Tandaan na ang mga pahalang na asymptote ay isang espesyal na kaso ng oblique asymptotes para sa k = 0.

Halimbawa. .

1) Vertical asymptotes: y®+¥ x®0-0: y®-¥ x®0+0, samakatuwid, ang x = 0 ay isang vertical asymptote.

2) Oblique asymptotes:

Kaya, ang tuwid na linya y = x + 2 ay isang pahilig na asymptote.

I-plot natin ang function:

Halimbawa. Maghanap ng mga asymptotes at i-graph ang function.

Ang mga linyang x = 3 at x = -3 ay mga patayong asymptotes ng curve.

Hanapin natin ang oblique asymptotes:

y = 0 – pahalang na asymptote.

Halimbawa. Maghanap ng mga asymptotes at i-graph ang function .

Ang tuwid na linya x = -2 ay ang patayong asymptote ng kurba.

Hanapin natin ang oblique asymptotes.

Sa kabuuan, ang tuwid na linya y = x – 4 ay isang oblique asymptote.

Scheme ng pag-aaral ng function

Ang proseso ng pananaliksik sa pag-andar ay binubuo ng ilang mga yugto. Para sa pinaka kumpletong pag-unawa sa pag-uugali ng function at sa likas na katangian ng graph nito, kinakailangan upang mahanap:

1) Ang domain ng pagkakaroon ng function.

Kasama sa konseptong ito ang parehong domain ng mga halaga at ang domain ng kahulugan ng isang function.

2) Mga breaking point. (Kung bakante).

3) Mga pagitan ng pagtaas at pagbaba.

4) Pinakamataas at pinakamababang puntos.

5) Ang maximum at minimum na halaga ng isang function sa domain ng kahulugan nito.

6) Mga lugar ng convexity at concavity.

7) Mga inflection point (kung mayroon man).

8) Asymptotes (kung mayroon man).

9) Pagbuo ng isang graph.

Tingnan natin ang aplikasyon ng scheme na ito gamit ang isang halimbawa.

Halimbawa. I-explore ang function at buuin ang graph nito.

Nahanap namin ang domain ng pagkakaroon ng function. Obvious naman yun domain ng kahulugan ang function ay ang lugar (-¥; -1) È (-1; 1) È (1; ¥).

Sa turn, malinaw na ang mga tuwid na linya x = 1, x = -1 ay vertical asymptotes baluktot.

Saklaw ng mga halaga ng function na ito ay ang interval (-¥; ¥).

Mga break point Ang mga function ay mga puntos x = 1, x = -1.

Nahanap namin kritikal na mga punto.

Hanapin natin ang derivative ng function

Mga kritikal na puntos: x = 0; x = - ; x = ; x = -1; x = 1.

Hanapin natin ang pangalawang derivative ng function

Alamin natin ang convexity at concavity ng curve sa pagitan.

-¥ < x < - , y¢¢ < 0, кривая выпуклая

- < x < -1, y¢¢ < 0, кривая выпуклая

1 < x < 0, y¢¢ >0, malukong kurba

0 < x < 1, y¢¢ < 0, кривая выпуклая

1 < x < , y¢¢ >0, malukong kurba

< x < ¥, y¢¢ >0, malukong kurba

Paghahanap ng mga puwang dumarami At bumababa mga function. Upang gawin ito, tinutukoy namin ang mga palatandaan ng derivative ng function sa mga agwat.

-¥ < x < - , y¢ >0, tumataas ang function

- < x < -1, y¢ < 0, функция убывает

1 < x < 0, y¢ < 0, функция убывает

0 < x < 1, y¢ < 0, функция убывает

1 < x < , y¢ < 0, функция убывает

< x < ¥, y¢¢ >0, tumataas ang function

Makikita na ang puntong x = - ay isang punto maximum, at ang puntong x = ay isang punto pinakamababa. Ang mga halaga ng function sa mga puntong ito ay katumbas ng -3/2 at 3/2, ayon sa pagkakabanggit.

Tungkol sa patayo asymptotes nasabi na sa itaas. Ngayon hanapin natin pahilig na asymptotes.

Sa kabuuan, ang equation ng oblique asymptote ay y = x.

Buuin natin iskedyul Mga Tampok:

Mga pag-andar ng ilang mga variable

Kapag isinasaalang-alang ang mga function ng ilang variable, lilimitahan natin ang ating sarili sa isang detalyadong paglalarawan ng mga function ng dalawang variable, dahil lahat ng resultang nakuha ay magiging wasto para sa mga function ng isang arbitrary na bilang ng mga variable.

Kahulugan: Kung ang bawat pares ng magkaparehong independiyenteng mga numero (x, y) mula sa isang tiyak na hanay, ayon sa ilang panuntunan, ay nauugnay sa isa o higit pang mga halaga ng variable z, kung gayon ang variable na z ay tinatawag na function ng dalawang variable.

Kahulugan: Kung ang isang pares ng mga numero (x, y) ay tumutugma sa isang halaga z, kung gayon ang function ay tinatawag hindi malabo, at kung higit sa isa, kung gayon - polysemantic.

Kahulugan: Domain ng kahulugan Ang function na z ay ang hanay ng mga pares (x, y) kung saan umiiral ang function na z.

Kahulugan: Kapitbahayan ng isang punto Ang M 0 (x 0, y 0) ng radius r ay ang hanay ng lahat ng puntos (x, y) na nakakatugon sa kundisyon .

Kahulugan: Ang numero A ay tinatawag limitasyon function na f(x, y) bilang ang puntong M(x, y) ay patungo sa puntong M 0 (x 0, y 0), kung para sa bawat numero e > 0 mayroong numero r > 0 na para sa anumang punto M (x, y), kung saan totoo ang kundisyon

totoo rin ang kondisyon .

Isulat:

Kahulugan: Hayaang ang puntong M 0 (x 0, y 0) ay kabilang sa domain ng kahulugan ng function na f(x, y). Pagkatapos ay tinawag ang function na z = f(x, y). tuloy-tuloy sa puntong M 0 (x 0, y 0), kung

(1)

at ang puntong M(x, y) ay humahantong sa puntong M 0 (x 0, y 0) sa isang arbitraryong paraan.

Kung sa anumang puntong kondisyon (1) ay hindi nasiyahan, ang puntong ito ay tinatawag break point function na f(x, y). Ito ay maaaring sa mga sumusunod na kaso:

1) Ang function na z = f(x, y) ay hindi tinukoy sa puntong M 0 (x 0, y 0).

2) Walang limitasyon.

3) Umiiral ang limitasyong ito, ngunit hindi ito katumbas ng f(x 0 , y 0).

Ari-arian. Kung ang function na f(x, y, …) ay tinukoy at tuloy-tuloy sa isang closed at

bounded domain D, pagkatapos ay sa domain na ito ay may hindi bababa sa isang punto

N(x 0 , y 0 , …), para sa natitirang mga punto ang hindi pagkakapantay-pantay ay totoo

f(x 0 , y 0 , …) ³ f(x, y, …)

pati na rin ang punto N 1 (x 01, y 01, ...), na para sa lahat ng iba pang mga punto ay totoo ang hindi pagkakapantay-pantay

f(x 01 , y 01 , …) £ f(x, y, …)

pagkatapos f(x 0 , y 0 , …) = M – pinakamataas na halaga function, at f(x 01 , y 01 , ...) = m – pinakamaliit na halaga function na f(x, y, …) sa domain D.

Ang tuluy-tuloy na function sa isang closed at bounded na domain D ay umabot sa pinakamalaking value nito kahit isang beses at ang pinakamaliit na value nito nang isang beses.

Ari-arian. Kung ang function na f(x, y, …) ay tinukoy at tuloy-tuloy sa isang closed bounded domain D, at ang M at m ay, ayon sa pagkakabanggit, ang pinakamalaki at pinakamaliit na value ng function sa domain na ito, kung gayon para sa anumang punto m О may punto

N 0 (x 0 , y 0 , …) na ang f(x 0 , y 0 , …) = m.

Sa madaling salita, ang tuluy-tuloy na pag-andar ay tumatagal sa domain D ng lahat ng mga intermediate na halaga sa pagitan ng M at m. Ang isang kinahinatnan ng ari-arian na ito ay maaaring ang konklusyon na kung ang mga numero M at m ay may magkakaibang mga palatandaan, pagkatapos ay sa domain D ang function ay naglalaho ng hindi bababa sa isang beses.

Ari-arian. Function f(x, y, …), tuloy-tuloy sa isang closed bounded domain D, limitado sa rehiyong ito, kung mayroong isang bilang na K na para sa lahat ng mga punto sa rehiyon ang hindi pagkakapantay-pantay ay totoo .

Ari-arian. Kung ang isang function na f(x, y, …) ay tinukoy at tuloy-tuloy sa isang closed bounded domain D, kung gayon ito pare-parehong tuloy-tuloy sa lugar na ito, i.e. para sa anumang positibong numero e mayroong numerong D > 0 na para sa alinmang dalawang puntos (x 1, y 1) at (x 2, y 2) ng rehiyon na matatagpuan sa layong mas mababa sa D, ang hindi pagkakapantay-pantay ay nananatili

Ang mga katangian sa itaas ay katulad ng mga katangian ng mga pag-andar ng isang variable na tuluy-tuloy sa isang pagitan. Tingnan ang Properties ng mga function na tuloy-tuloy sa isang interval.

Derivatives at differentials ng mga function

ilang variable.

Kahulugan. Hayaang maibigay ang isang function na z = f(x, y) sa ilang domain. Kumuha tayo ng arbitrary point M(x, y) at itakda ang increment Dx sa variable na x. Pagkatapos ay tinatawag ang dami D x z = f(x + Dx, y) – f(x, y) bahagyang pagtaas ng function sa x.

Maaari mong isulat

.

Tapos tinawag na partial derivative mga function z = f(x, y) sa x.

pagtatalaga:

Ang partial derivative ng isang function na may kinalaman sa y ay natutukoy sa katulad na paraan.

Geometric na kahulugan ang partial derivative (sabihin natin) ay ang padaplis ng anggulo ng inclination ng tangent na iginuhit sa punto N 0 (x 0, y 0, z 0) sa seksyon ng ibabaw ng eroplano y = y 0.

Buong pagtaas at buong pagkakaiba.

padaplis na eroplano

Hayaang ang N at N 0 ay mga punto ng ibabaw na ito. Gumuhit tayo ng isang tuwid na linya NN 0. Ang eroplano na dumadaan sa puntong N 0 ay tinatawag padaplis na eroplano sa ibabaw kung ang anggulo sa pagitan ng secant NN 0 at ang eroplanong ito ay may posibilidad na zero, kapag ang distansya NN 0 ay may posibilidad na zero.

Kahulugan. Normal sa ibabaw sa punto N 0 ay isang tuwid na linya na dumadaan sa punto N 0 patayo sa tangent plane sa ibabaw na ito.

Sa anumang punto ang ibabaw ay may alinman lamang sa isang tangent na eroplano o wala ito sa lahat.

Kung ang ibabaw ay ibinigay ng equation na z = f(x, y), kung saan ang f(x, y) ay isang function na naiba-iba sa puntong M 0 (x 0, y 0), ang tangent plane sa puntong N 0 ( x 0,y 0, ( x 0 ,y 0)) ay umiiral at may equation:

Ang equation ng normal sa ibabaw sa puntong ito ay:

Geometric na kahulugan ang kabuuang pagkakaiba ng isang function ng dalawang variable na f(x, y) sa punto (x 0, y 0) ay ang pagtaas ng applicate (z coordinates) ng tangent plane patungo sa ibabaw kapag gumagalaw mula sa punto (x 0). , y 0) hanggang sa punto (x 0 + Dx, y 0 +Dу).

Tulad ng nakikita mo, ang geometric na kahulugan ng kabuuang kaugalian ng isang function ng dalawang variable ay isang spatial na analogue ng geometric na kahulugan ng kaugalian ng isang function ng isang variable.

Halimbawa. Hanapin ang mga equation ng tangent plane at normal sa ibabaw

sa puntong M(1, 1, 1).

Tangent plane equation:

Normal na equation:

Tinatayang mga kalkulasyon gamit ang kabuuang mga pagkakaiba.

Ang kabuuang pagkakaiba ng function na u ay katumbas ng:

Ang eksaktong halaga ng expression na ito ay: 1.049275225687319176.

Mga partial derivatives ng mas matataas na order.

Kung ang isang function na f(x, y) ay tinukoy sa ilang domain D, ang mga partial derivatives nito ay tutukuyin din sa parehong domain o bahagi nito.

Tatawagin natin itong mga derivatives mga partial derivative sa unang order.

Ang mga derivatives ng mga function na ito ay pangalawang order na bahagyang derivatives.

Sa patuloy na pag-iiba ng mga resultang pagkakapantay-pantay, nakakakuha kami ng mga partial derivatives ng mas matataas na order.

ibig sabihin

Pinakamahusay

ibig sabihin

Hindi bababa sa

Pinakamataas na punto

Pinakamababang punto

Ang mga problema sa paghahanap ng mga punto ng isang extremum function ay nalutas ayon sa isang karaniwang pamamaraan sa 3 hakbang.

Hakbang 1. Hanapin ang derivative ng function

• Alalahanin ang mga derivative formula para sa elementarya na mga function at ang mga pangunahing tuntunin ng pagkita ng kaibhan upang mahanap ang derivative.

y′(x)=(x3−243x+19)′=3x2−243.

Hakbang 2. Hanapin ang mga zero ng derivative

• Lutasin ang nagresultang equation upang mahanap ang mga zero ng derivative.

3x2−243=0⇔x2=81⇔x1=−9,x2=9.

Hakbang 3. Maghanap ng mga matinding puntos

• Gamitin ang paraan ng agwat upang matukoy ang mga palatandaan ng derivative;
• Sa pinakamababang punto, ang derivative ay katumbas ng zero at nagbabago ng sign mula minus hanggang plus, at sa pinakamataas na punto, mula plus hanggang minus.

Gamitin natin ang pamamaraang ito upang malutas ang sumusunod na problema:

Hanapin ang pinakamataas na punto ng function na y=x3−243x+19.

1) Hanapin ang derivative: y′(x)=(x3−243x+19)′=3x2−243;

2) Lutasin ang equation na y′(x)=0: 3x2−243=0⇔x2=81⇔x1=−9,x2=9;

3) Ang derivative ay positibo para sa x>9 at x<−9 и отрицательная при −9

Paano mahanap ang pinakamalaki at pinakamaliit na halaga ng isang function

Upang malutas ang problema sa paghahanap ng pinakamalaki at pinakamaliit na halaga ng isang function kailangan:

• Hanapin ang extremum point ng function sa segment (interval).
• Hanapin ang mga value sa dulo ng segment at piliin ang pinakamalaki o pinakamaliit na value mula sa mga value sa extremum point at sa dulo ng segment.

Tumutulong sa maraming gawain teorama:

Kung mayroon lamang isang extremum point sa isang segment, at ito ang pinakamababang punto, kung gayon ang pinakamaliit na halaga ng function ay makakamit dito. Kung ito ay isang maximum na punto, kung gayon ang pinakamalaking halaga ay naabot doon.

14. Konsepto at pangunahing katangian ng di-tiyak na integral.

Kung ang function f(x X, At k– numero, kung gayon

Sa madaling sabi: ang pare-pareho ay maaaring alisin sa integral sign.

Kung ang mga function f(x) At g(x) ay may mga antiderivative sa pagitan X, Iyon

Sa madaling sabi: ang integral ng kabuuan ay katumbas ng kabuuan ng mga integral.

Kung ang function f(x) ay may antiderivative sa pagitan X, pagkatapos ay para sa mga panloob na punto ng agwat na ito:

Sa madaling sabi: ang derivative ng integral ay katumbas ng integrand.

Kung ang function f(x) ay tuloy-tuloy sa pagitan X at naiba sa mga panloob na punto ng agwat na ito, kung gayon:

Sa madaling sabi: ang integral ng differential ng isang function ay katumbas ng function na ito kasama ang integration constant.

Bigyan natin ng mahigpit na kahulugan ng matematika mga konsepto ng di-tiyak na integral.

Ang isang pagpapahayag ng anyo ay tinatawag integral ng function f(x) , Saan f(x) - integrand function na ibinigay (kilala), dx - pagkakaiba x , na may simbolo na laging naroroon dx .

Kahulugan. Indefinite integral tinatawag na function F(x) + C , na naglalaman ng arbitrary na pare-pareho C , ang pagkakaiba nito ay katumbas ng integrand pagpapahayag f(x)dx , ibig sabihin. o Tinatawag ang function antiderivative function. Ang antiderivative ng isang function ay tinutukoy hanggang sa isang pare-parehong halaga.

Paalalahanan ka namin na - pag-andar ng kaugalian at tinukoy bilang mga sumusunod:

Paghahanap ng problema hindi tiyak na integral ay upang mahanap ang ganoong function derivative na katumbas ng integrand. Ang function na ito ay tinutukoy na tumpak sa isang pare-pareho, dahil ang derivative ng pare-pareho ay zero.

Halimbawa, ito ay kilala na , pagkatapos ito ay lumiliko na , narito ang isang arbitrary na pare-pareho.

paghahanap ng problema hindi tiyak na integral Ang mga pag-andar ay hindi kasing simple at kadali na tila sa unang tingin. Sa maraming pagkakataon, kailangang may kasanayan sa pagtatrabaho hindi tiyak na integral, dapat mayroong karanasan na kasama ng pagsasanay at palagian paglutas ng mga halimbawa ng hindi tiyak na integral. Ito ay nagkakahalaga ng pagsasaalang-alang sa katotohanan na hindi tiyak na integral mula sa ilang mga function (mayroong medyo marami sa kanila) ay hindi kinuha sa elementarya function.

15. Talaan ng mga pangunahing di-tiyak na integral.

Mga pangunahing formula

16. Definite integral bilang limitasyon ng integral sum. Geometric at pisikal na kahulugan ng integral.

Hayaang tukuyin ang function na y=ƒ(x) sa pagitan [a; b], a< b. Выполним следующие действия.

1. Gamit ang mga puntos na x 0 = a, x 1, x 2, ..., x n = B (x 0

2. Sa bawat bahagyang segment , i = 1,2,...,n, pumili ng arbitrary point na may i є at kalkulahin ang halaga ng function sa loob nito, ibig sabihin, ang halaga ƒ(may i).

3. I-multiply ang nahanap na halaga ng function ƒ (na may i) sa haba ∆x i =x i -x i-1 ng kaukulang partial segment: ƒ (na may i) ∆x i.

4. Gawin natin ang kabuuan S n ng lahat ng naturang produkto:

Ang kabuuan ng anyo (35.1) ay tinatawag na integral sum ng function na y = ƒ(x) sa pagitan [a; b]. Tukuyin natin sa pamamagitan ng λ ang haba ng pinakamalaking bahagyang bahagi: λ = max ∆x i (i = 1,2,..., n).

5. Hanapin natin ang limitasyon ng integral sum (35.1) kapag n → ∞ upang λ→0.

Kung sa kasong ito ang integral sum S n ay may limitasyon I, na hindi nakasalalay sa paraan ng paghahati ng segment [a; b] sa mga bahagyang segment, o sa pagpili ng mga puntos sa kanila, kung gayon ang numero I ay tinatawag na isang tiyak na integral ng function na y = ƒ(x) sa segment [a; b] at ipinahiwatig Kaya,

Ang mga numerong a at b ay tinatawag na lower at upper limits ng integration, ayon sa pagkakabanggit, ƒ(x) - ang integrand function, ƒ(x) dx - the integrand, x - ang variable ng integration, ang segment [a; b] - lugar (segment) ng pagsasama.

Function y=ƒ(x), kung saan sa pagitan [a; b] mayroong isang tiyak na integral na tinatawag na integrable sa pagitan na ito.

Bumuo tayo ngayon ng isang teorama para sa pagkakaroon ng isang tiyak na integral.

Theorem 35.1 (Cauchy). Kung ang function na y = ƒ(x) ay tuloy-tuloy sa pagitan [a; b], pagkatapos ay ang tiyak na integral

Tandaan na ang pagpapatuloy ng isang function ay isang sapat na kundisyon para sa integrability nito. Gayunpaman, ang isang tiyak na integral ay maaari ding umiral para sa ilang mga hindi tuluy-tuloy na function, lalo na para sa anumang function na nakatali sa isang pagitan na may hangganan na bilang ng mga discontinuity point dito.

Ipahiwatig natin ang ilang mga katangian ng tiyak na integral na direktang sumusunod mula sa kahulugan nito (35.2).

1. Ang tiyak na integral ay independiyente sa pagtatalaga ng variable ng integration:

Ito ay sumusunod mula sa katotohanan na ang integral sum (35.1), at samakatuwid ang limitasyon nito (35.2), ay hindi nakasalalay sa kung anong titik ang argumento ng isang naibigay na function ay tinutukoy ng.

2. Ang isang tiyak na integral na may parehong mga limitasyon ng pagsasama ay katumbas ng zero:

3. Para sa anumang tunay na numero c.

17. Newton-Leibniz formula. Mga pangunahing katangian ng isang tiyak na integral.

Hayaan ang function y = f(x) tuloy-tuloy sa segment At F(x) ay isa sa mga antiderivatives ng function sa segment na ito, kung gayon Formula ng Newton-Leibniz: .

Ang Newton-Leibniz formula ay tinatawag pangunahing pormula ng integral calculus.

Upang patunayan ang formula ng Newton-Leibniz, kailangan natin ang konsepto ng integral na may variable na upper limit.

Kung ang function y = f(x) tuloy-tuloy sa segment , pagkatapos para sa argumento ang integral ng form ay isang function ng itaas na limitasyon. Tukuyin natin ang function na ito , at ang function na ito ay tuloy-tuloy at ang pagkakapantay-pantay ay totoo .

Sa katunayan, isulat natin ang pagtaas ng function na tumutugma sa pagtaas ng argumento at gamitin ang ikalimang pag-aari ng tiyak na integral at ang corollary mula sa ikasampung pag-aari:

saan .

Muli nating isulat ang pagkakapantay-pantay na ito sa anyo . Kung aalalahanin natin ang kahulugan ng derivative ng isang function at pumunta sa limitasyon sa , makukuha natin . Iyon ay, ito ay isa sa mga antiderivatives ng function y = f(x) sa segment . Kaya, ang hanay ng lahat ng antiderivatives F(x) maaaring isulat bilang , kung saan SA– di-makatwirang pare-pareho.

Magkalkula tayo F(a), gamit ang unang katangian ng tiyak na integral: , samakatuwid, . Gamitin natin ang resultang ito kapag nagkalkula F(b): , yan ay . Ang pagkakapantay-pantay na ito ay nagbibigay ng mapapatunayang formula ng Newton-Leibniz .

Ang pagtaas ng isang function ay karaniwang tinutukoy bilang . Gamit ang notasyong ito, ang formula ng Newton-Leibniz ay kumukuha ng anyo .

Upang mailapat ang formula ng Newton-Leibniz, sapat na para sa amin na malaman ang isa sa mga antiderivatives y=F(x) pagsasama at pag-andar y=f(x) sa segment at kalkulahin ang pagtaas ng antiderivative na ito sa segment na ito. Ang mga pamamaraan ng artikulo ng pagsasama ay tumatalakay sa mga pangunahing paraan ng paghahanap ng antiderivative. Magbigay tayo ng ilang halimbawa ng pagkalkula ng mga tiyak na integral gamit ang formula ng Newton-Leibniz para sa paglilinaw.

Halimbawa.

Kalkulahin ang halaga ng tiyak na integral gamit ang Newton-Leibniz formula.

Solusyon.

Upang magsimula, tandaan namin na ang integrand ay tuloy-tuloy sa pagitan , samakatuwid, ay integrable dito. (Napag-usapan namin ang tungkol sa mga integrable function sa seksyon sa mga function kung saan mayroong isang tiyak na integral.)

Mula sa talahanayan ng mga hindi tiyak na integral, malinaw na para sa isang function ang hanay ng mga antiderivatives para sa lahat ng tunay na halaga ng argumento (at samakatuwid para sa ) ​​ay nakasulat bilang . Kunin natin ang antiderivative para sa C=0: .

Ngayon ay nananatiling gamitin ang Newton-Leibniz formula upang kalkulahin ang tiyak na integral: .

18. Mga geometriko na aplikasyon ng tiyak na integral.

GEOMETRICAL APPLICATIONS NG TIYAK NA INTEGRAL

Parihabang S.K.	Tinukoy ang function sa parametrically	Polyarnaya S.K.
Pagkalkula ng mga lugar ng mga figure ng eroplano
Kinakalkula ang haba ng arko ng isang kurba ng eroplano
Pagkalkula ng ibabaw na lugar ng rebolusyon

Pagkalkula ng dami ng katawan

Pagkalkula ng dami ng isang katawan mula sa mga kilalang lugar ng magkatulad na mga seksyon:

Dami ng katawan ng pag-ikot: ; .

Halimbawa 1. Hanapin ang lugar ng figure na nililimitahan ng curve y=sinx ng mga tuwid na linya

Solusyon: Paghahanap ng lugar ng figure:

Halimbawa 2. Kalkulahin ang lugar ng isang figure na may hangganan ng mga linya

Solusyon: Hanapin natin ang abscissa ng mga intersection point ng mga graph ng mga function na ito. Upang gawin ito, lutasin namin ang sistema ng mga equation

Mula dito makikita natin x 1 =0, x 2 =2.5.

19. Ang konsepto ng differential controls. First order differential equation.

Differential equation- isang equation na nag-uugnay sa halaga ng derivative ng isang function sa mismong function, ang mga halaga ng independent variable, at mga numero (parameter). Ang pagkakasunud-sunod ng mga derivatives na kasama sa equation ay maaaring magkakaiba (pormal na hindi ito limitado sa anumang bagay). Maaaring lumabas ang mga derivative, function, independent variable, at parameter sa isang equation sa iba't ibang kumbinasyon, o maaaring wala lahat maliban sa isang derivative. Hindi lahat ng equation na naglalaman ng derivatives ng isang hindi kilalang function ay isang differential equation. Halimbawa, ay hindi isang differential equation.

Mga partial differential equation(PDF) ay mga equation na naglalaman ng mga hindi kilalang function ng ilang mga variable at ang kanilang mga partial derivatives. Ang pangkalahatang anyo ng naturang mga equation ay maaaring kinakatawan bilang:

nasaan ang mga independiyenteng variable, at isang function ng mga variable na ito. Ang pagkakasunud-sunod ng mga partial differential equation ay maaaring matukoy sa parehong paraan tulad ng para sa ordinaryong differential equation. Ang isa pang mahalagang pag-uuri ng mga partial differential equation ay ang kanilang paghahati sa mga equation ng elliptic, parabolic at hyperbolic na mga uri, lalo na para sa second-order equation.

Ang parehong mga ordinaryong differential equation at partial differential equation ay maaaring nahahati sa linear At nonlinear. Ang isang differential equation ay linear kung ang hindi kilalang function at ang mga derivatives nito ay pumasok sa equation hanggang sa unang degree lamang (at hindi pinarami sa isa't isa). Para sa mga naturang equation, ang mga solusyon ay bumubuo ng isang affine subspace ng espasyo ng mga function. Ang teorya ng linear differential equation ay binuo ng mas malalim kaysa sa teorya ng nonlinear equation. Pangkalahatang view ng isang linear differential equation n-ika-utos:

saan p i(x) ay mga kilalang function ng independent variable, na tinatawag na coefficients ng equation. Function r(x) sa kanang bahagi ay tinatawag libreng miyembro(ang tanging termino na hindi nakasalalay sa hindi kilalang function) Ang isang mahalagang partikular na klase ng mga linear na equation ay mga linear differential equation na may pare-pareho ang mga koepisyent.

Ang isang subclass ng mga linear na equation ay homogenous differential equation - mga equation na hindi naglalaman ng libreng termino: r(x) = 0. Para sa mga homogenous na differential equation, ang superposition na prinsipyo ay mayroong: isang linear na kumbinasyon ng mga partial na solusyon ng naturang equation ang magiging solusyon din nito. Ang lahat ng iba pang mga linear differential equation ay tinatawag magkakaiba differential equation.

Ang mga nonlinear na differential equation sa pangkalahatang kaso ay walang nakabuo ng mga pamamaraan ng solusyon, maliban sa ilang mga espesyal na klase. Sa ilang mga kaso (gamit ang ilang mga pagtatantya) maaari silang bawasan sa linear. Halimbawa, ang linear equation ng isang harmonic oscillator ay maaaring ituring bilang isang approximation ng nonlinear equation ng isang mathematical pendulum para sa kaso ng maliliit na amplitude, kapag y≈ kasalanan y.

· - homogenous differential equation ng pangalawang order na may pare-parehong coefficient. Ang solusyon ay isang pamilya ng mga function , kung saan at mga arbitrary constants, na para sa isang partikular na solusyon ay tinutukoy mula sa hiwalay na tinukoy na mga paunang kondisyon. Ang equation na ito, sa partikular, ay naglalarawan ng galaw ng isang harmonic oscillator na may cyclic frequency na 3.

· Ang pangalawang batas ni Newton ay maaaring isulat sa anyo ng isang differential equation saan m- bigat ng katawan, x- ang coordinate nito, F(x, t) - puwersang kumikilos sa isang katawan na may coordinate x sa isang punto ng panahon t. Ang solusyon nito ay ang tilapon ng katawan sa ilalim ng pagkilos ng tinukoy na puwersa.

· Ang Bessel differential equation ay isang ordinaryong linear homogeneous equation ng pangalawang order na may variable coefficients: Ang mga solusyon nito ay ang Bessel functions.

· Isang halimbawa ng hindi homogenous na hindi linear na ordinary differential equation ng 1st order:

Sa susunod na pangkat ng mga halimbawa mayroong hindi kilalang function u depende sa dalawang variable x At t o x At y.

· Homogeneous linear partial differential equation ng unang order:

· One-dimensional wave equation - isang homogenous linear partial differential equation ng hyperbolic type ng second order na may pare-parehong coefficients, inilalarawan ang oscillation ng string kung - ang deflection ng string sa punto na may coordinate x sa isang punto ng panahon t, at ang parameter a nagtatakda ng mga katangian ng string:

· Ang equation ng Laplace sa two-dimensional space ay isang homogenous na linear na partial differential equation ng pangalawang order ng elliptic type na may pare-parehong coefficients, na nagmumula sa maraming pisikal na problema ng mechanics, thermal conductivity, electrostatics, hydraulics:

· Korteweg-de Vries equation, isang third-order nonlinear partial differential equation na naglalarawan ng mga nakatigil na nonlinear wave, kabilang ang mga soliton:

20. Differential equation na may separable applicable. Linear equation at Bernoulli's method.

Ang first-order linear differential equation ay isang equation na linear na may kinalaman sa isang hindi kilalang function at ang derivative nito. Ito ay may anyo na Buong kapangyarihan. Sa katunayan, kung hahanapin at papalitan mo ang mga equation ng mga uri na isinasaalang-alang, makakakuha ka ng isang tunay na pagkakapantay-pantay. Gaya ng nabanggit sa artikulo tungkol sa homogenous equation, kung ayon sa kondisyon ay kinakailangan na makahanap lamang ng isang partikular na solusyon, kung gayon ang pag-andar, para sa malinaw na mga kadahilanan, ay hindi nakakaabala sa amin, ngunit kapag kinakailangan upang makahanap ng isang pangkalahatang solusyon/integral, pagkatapos ay kinakailangan upang tiyakin na ang function na ito ay hindi nawala!

Dinala ko ang lahat ng sikat na variation ng Bernoulli equation sa isang malaking bag ng mga regalo at sinimulan kong ipamahagi ang mga ito. Isabit ang iyong mga medyas sa ilalim ng puno.

Halimbawa 1

Maghanap ng isang partikular na solusyon sa differential equation na tumutugma sa ibinigay na paunang kondisyon.
,

Marahil marami ang nagulat na ang unang regalo ay agad na inilabas sa bag kasama nito Cauchy na problema. Hindi ito aksidente. Kapag ang Bernoulli equation ay iminungkahi para sa isang solusyon, sa ilang kadahilanan ay madalas na kinakailangan upang makahanap ng isang partikular na solusyon. Mula sa aking koleksyon, gumawa ako ng random na pagpili ng 10 Bernoulli equation, at ang pangkalahatang solusyon (nang walang partikular na solusyon) ay kailangang matagpuan sa 2 equation lamang. Ngunit, sa katunayan, ito ay isang maliit na bagay, dahil ang isang pangkalahatang solusyon ay kailangang hanapin sa anumang kaso.

Solusyon: Ang diffuser na ito ay may anyo at samakatuwid ay ang equation ni Bernoulli

Isang simpleng algorithm para sa paghahanap ng extrema..

• Paghahanap ng derivative ng function
• Itinutumbas namin ang derivative na ito sa zero
• Nahanap namin ang mga halaga ng variable ng nagresultang expression (ang mga halaga ng variable kung saan ang derivative ay na-convert sa zero)
• Gamit ang mga halagang ito, hinahati namin ang linya ng coordinate sa mga pagitan (huwag kalimutan ang tungkol sa mga break point, na kailangan ding i-plot sa linya), ang lahat ng mga puntong ito ay tinatawag na "kahina-hinala" na mga punto para sa extremum
• Kinakalkula namin kung alin sa mga pagitan na ito ang derivative ay magiging positibo at alin ang magiging negatibo. Upang gawin ito, kailangan mong palitan ang halaga mula sa pagitan sa derivative.

Sa mga puntos na kahina-hinala para sa isang extremum, ito ay kinakailangan upang mahanap . Upang gawin ito, tinitingnan namin ang aming mga agwat sa linya ng coordinate. Kung, kapag dumadaan sa ilang punto, ang tanda ng derivative ay nagbabago mula plus hanggang minus, kung gayon ang puntong ito ay magiging maximum, at kung mula minus hanggang plus, kung gayon pinakamababa.

Upang mahanap ang pinakamalaki at pinakamaliit na halaga ng isang function, kailangan mong kalkulahin ang halaga ng function sa mga dulo ng segment at sa mga extremum point. Pagkatapos ay piliin ang pinakamalaki at pinakamaliit na halaga.

Tingnan natin ang isang halimbawa
Hanapin ang derivative at i-equate ito sa zero:

Inilalagay namin ang nakuha na mga halaga ng mga variable sa linya ng coordinate at kinakalkula ang tanda ng derivative sa bawat isa sa mga agwat. Well, halimbawa, para sa una ay kunin natin-2 , kung gayon ang derivative ay magiging pantay-0,24 , para sa pangalawang kukunin natin0 , kung gayon ang derivative ay magiging2 , at para sa pangatlo ay kukunin namin2 , kung gayon ang derivative ay magiging-0.24. Inilalagay namin ang naaangkop na mga palatandaan.

Nakikita namin na kapag dumadaan sa punto -1, ang derivative ay nagbabago ng sign mula minus hanggang plus, iyon ay, ito ang magiging pinakamababang punto, at kapag dumaan sa 1, babaguhin nito ang sign mula plus hanggang minus, ayon sa pagkakabanggit, ito ang magiging pinakamataas na punto.

Ang pag-andar at ang pag-aaral ng mga tampok nito ay sumasakop sa isa sa mga pangunahing kabanata sa modernong matematika. Ang pangunahing bahagi ng anumang function ay ang mga graph na naglalarawan hindi lamang ng mga katangian nito, kundi pati na rin ang mga parameter ng derivative ng function na ito. Unawain natin ang mahirap na paksang ito. Kaya ano ang pinakamahusay na paraan upang mahanap ang maximum at minimum na mga puntos ng isang function?

Tungkulin: kahulugan

Ang anumang variable na sa ilang paraan ay nakasalalay sa mga halaga ng isa pang dami ay maaaring tawaging isang function. Halimbawa, ang function na f(x 2) ay quadratic at tinutukoy ang mga halaga para sa buong set x. Sabihin natin na x = 9, kung gayon ang halaga ng ating function ay magiging katumbas ng 9 2 = 81.

Ang mga function ay may iba't ibang uri: logical, vector, logarithmic, trigonometric, numeric at iba pa. Ang mga ito ay pinag-aralan ng mga namumukod-tanging isip gaya ng Lacroix, Lagrange, Leibniz at Bernoulli. Ang kanilang mga gawa ay nagsisilbing pangunahing sa mga modernong paraan ng pag-aaral ng mga tungkulin. Bago hanapin ang pinakamababang puntos, napakahalagang maunawaan ang mismong kahulugan ng function at ang hinango nito.

Derivative at ang papel nito

Ang lahat ng mga function ay nakasalalay sa kanilang mga variable, na nangangahulugan na maaari nilang baguhin ang kanilang halaga anumang oras. Sa graph, ito ay ipapakita bilang isang curve na bumaba o tumataas sa kahabaan ng ordinate axis (ito ang buong hanay ng mga "y" na numero sa kahabaan ng patayong graph). Kaya, ang pagtukoy sa maximum at minimum na mga punto ng isang function ay tiyak na nauugnay sa mga "oscillations" na ito. Ipaliwanag natin kung ano ang relasyong ito.

Ang derivative ng anumang function ay naka-graph upang pag-aralan ang mga pangunahing katangian nito at kalkulahin kung gaano kabilis ang pagbabago ng function (ibig sabihin, nagbabago ang halaga nito depende sa variable na "x"). Sa sandaling tumaas ang function, tataas din ang graph ng derivative nito, ngunit anumang segundo ay maaaring magsimulang bumaba ang function, at pagkatapos ay bababa ang graph ng derivative. Ang mga puntong iyon kung saan nagbabago ang derivative mula sa isang minus sign patungo sa isang plus sign ay tinatawag na mga minimum na puntos. Upang malaman kung paano makahanap ng pinakamababang puntos, dapat mong mas maunawaan

Paano makalkula ang derivative?

Ang kahulugan at mga function ay nagpapahiwatig ng ilang mga konsepto mula sa Sa pangkalahatan, ang mismong kahulugan ng isang derivative ay maaaring ipahayag bilang mga sumusunod: ito ang dami na nagpapakita ng rate ng pagbabago ng function.

Ang mathematical na paraan ng pagtukoy nito ay tila kumplikado para sa maraming mga mag-aaral, ngunit sa katotohanan ang lahat ay mas simple. Kailangan mo lang sundin ang karaniwang plano para sa paghahanap ng derivative ng anumang function. Inilalarawan namin sa ibaba kung paano mo mahahanap ang pinakamababang punto ng isang function nang hindi inilalapat ang mga patakaran ng pagkita ng kaibhan at nang hindi sinasaulo ang talahanayan ng mga derivatives.

1. Maaari mong kalkulahin ang derivative ng isang function gamit ang isang graph. Upang gawin ito, kailangan mong ilarawan ang function mismo, pagkatapos ay kumuha ng isang punto dito (point A sa figure) Gumuhit ng isang linya nang patayo pababa sa abscissa axis (point x 0), at sa point A gumuhit ng tangent sa axis. graph ng function. Ang x-axis at ang tangent ay bumubuo ng isang tiyak na anggulo a. Upang kalkulahin ang halaga kung gaano kabilis tumaas ang isang function, kailangan mong kalkulahin ang tangent ng anggulong ito a.
2. Lumalabas na ang tangent ng anggulo sa pagitan ng tangent at ang direksyon ng x-axis ay ang derivative ng function sa isang maliit na lugar na may point A. Ang pamamaraang ito ay itinuturing na isang geometric na paraan para sa pagtukoy ng derivative.

Mga pamamaraan para sa pag-aaral ng function

Sa kurikulum ng matematika ng paaralan, posibleng mahanap ang pinakamababang punto ng isang function sa dalawang paraan. Napag-usapan na natin ang unang paraan gamit ang isang graph, ngunit paano natin matutukoy ang numerical value ng derivative? Upang gawin ito, kakailanganin mong matutunan ang ilang mga formula na naglalarawan sa mga katangian ng derivative at tumulong na i-convert ang mga variable tulad ng "x" sa mga numero. Ang sumusunod na pamamaraan ay pangkalahatan, kaya maaari itong mailapat sa halos lahat ng mga uri ng mga pag-andar (parehong geometriko at logarithmic).

1. Kinakailangang ipantay ang function sa derivative function, at pagkatapos ay pasimplehin ang expression gamit ang mga patakaran ng pagkita ng kaibhan.
2. Sa ilang mga kaso, kapag binigyan ng isang function kung saan ang variable na "x" ay nasa divisor, kinakailangan upang matukoy ang hanay ng mga katanggap-tanggap na halaga, hindi kasama ang puntong "0" mula dito (para sa simpleng dahilan na sa matematika ay hindi dapat kailanman. hatiin sa zero).
3. Pagkatapos nito, dapat mong baguhin ang orihinal na anyo ng function sa isang simpleng equation, na katumbas ng buong expression sa zero. Halimbawa, kung ganito ang hitsura ng function: f(x) = 2x 3 +38x, kung gayon ayon sa mga patakaran ng pagkita ng kaibhan, ang derivative nito ay katumbas ng f"(x) = 3x 2 +1. Pagkatapos ay binago namin ang expression na ito sa isang equation ng sumusunod na anyo: 3x 2 +1 = 0 .
4. Pagkatapos malutas ang equation at hanapin ang "x" na mga puntos, dapat mong i-plot ang mga ito sa x-axis at tukuyin kung ang derivative sa mga seksyong ito sa pagitan ng mga markang punto ay positibo o negatibo. Matapos ang pagtatalaga, magiging malinaw sa kung anong punto ang pag-andar ay nagsisimulang bumaba, iyon ay, nagbabago ang sign mula sa minus hanggang sa kabaligtaran. Sa ganitong paraan maaari mong mahanap ang parehong minimum at maximum na mga puntos.

Mga tuntunin ng pagkita ng kaibhan

Ang pinakapangunahing bahagi sa pag-aaral ng isang function at ang hinango nito ay ang kaalaman sa mga tuntunin ng pagkakaiba-iba. Tanging sa kanilang tulong maaari mong baguhin ang masalimuot na mga expression at malalaking kumplikadong mga function. Kilalanin natin sila, marami sa kanila, ngunit lahat sila ay napaka-simple dahil sa mga likas na katangian ng parehong kapangyarihan at logarithmic function.

1. Ang derivative ng anumang constant ay katumbas ng zero (f(x) = 0). Ibig sabihin, ang derivative f(x) = x 5 + x - 160 ay kukuha ng sumusunod na anyo: f" (x) = 5x 4 +1.
2. Derivative ng kabuuan ng dalawang termino: (f+w)" = f"w + fw".
3. Derivative ng isang logarithmic function: (log a d)" = d/ln a*d. Nalalapat ang formula na ito sa lahat ng uri ng logarithms.
4. Derivative ng power: (x n)"= n*x n-1. Halimbawa, (9x 2)" = 9*2x = 18x.
5. Ang derivative ng sinusoidal function: (sin a)" = cos a. Kung ang sin ng anggulo a ay 0.5, ang derivative nito ay √3/2.

Extremum na puntos

Napag-usapan na natin kung paano maghanap ng mga minimum na puntos, ngunit mayroon ding konsepto ng maximum na mga puntos ng isang function. Kung ang minimum ay tumutukoy sa mga puntong iyon kung saan nagbabago ang function mula sa isang minus sign patungo sa isang plus, kung gayon ang pinakamataas na puntos ay ang mga punto sa x-axis kung saan ang derivative ng function ay nagbabago mula sa plus hanggang sa kabaligtaran - minus.

Mahahanap mo ito gamit ang pamamaraang inilarawan sa itaas, ngunit dapat mong isaalang-alang na ipinapahiwatig nila ang mga lugar kung saan nagsisimulang bumaba ang function, iyon ay, ang derivative ay magiging mas mababa sa zero.

Sa matematika, kaugalian na gawing pangkalahatan ang parehong mga konsepto, na pinapalitan ang mga ito ng pariralang "mga punto ng extrema." Kapag hiniling sa iyo ng isang gawain na tukuyin ang mga puntong ito, nangangahulugan ito na kailangan mong kalkulahin ang derivative ng isang ibinigay na function at hanapin ang minimum at maximum na mga puntos.