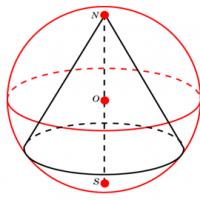
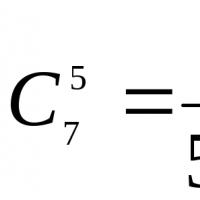Isang globo na nakasulat sa isang kono. Inscribed at circumscribed cones
Gaya ng Ibahagi 885 Views
Pagtatanghal ng mga aralin sa geometry ika-11 baitang. Sphere. Guro sa matematika ng Municipal Educational Institution Lyceum No. 18 I.V. Ang pagtatanghal ay ginawa ni Katerina Svintsova, isang estudyante ng 11-4 na baitang. Talaan ng mga Nilalaman:. 2. talaan ng nilalaman 3. panimula 13. mga kahulugan ng saklaw
I-download ang Presentasyon
Sphere
E N D - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Walang nauugnay na mga presentasyon.
Transcript ng Presentasyon
Sphere) Mayroong ilang mga kahulugan ng isang globo: 1. Isang saradong ibabaw. 2. Saklaw, ang mga limitasyon ng pamamahagi ng isang bagay. (Halimbawa, ang globo ng pagkilos ng grabidad). 3. Tagpuan, kapaligiran, kapaligirang panlipunan. (Halimbawa, industriya ng serbisyo)
Ang puntong ito ay tinatawag na sentro ng globo (punto O), at ang distansyang ito ay tinatawag na radius ng globo (Latin R). Tingnan ang fig. 1 Ang isang segment na nag-uugnay sa dalawang punto ng isang globo at dumadaan sa gitna nito ay tinatawag na diameter ng globo. Ang globo ay isang ibabaw na binubuo ng lahat ng mga punto sa espasyo na matatagpuan sa isang partikular na distansya mula sa isang partikular na punto. kanin. 1
Tandaan na ang isang globo ay maaaring makuha sa pamamagitan ng pag-ikot ng kalahating bilog sa paligid ng isang diameter. Tingnan ang fig. 2 Ang bahagi ng espasyo na matatagpuan sa loob ng globo ay tinatawag na bola. Tingnan ang fig. 3 Fig. 2 Ang sentro, radius at diameter ng isang globo ay tinatawag ding center, diameter at radius ng isang bola. kanin. 3
Isang mathematical na disiplina na nag-aaral ng mga geometric na imahe na matatagpuan sa isang globo, tulad ng planimetry na nag-aaral ng mga geometric na imahe na matatagpuan sa isang eroplano.
Ang isang globo, ay nagbibigay ng isang tiyak na bilog sa cross-section; Kapag nagsalubong ang dalawang malalaking bilog sa isang globo, bumubuo sila ng apat na spherical diagon. Gaya ng sa Fig. 4. kanin. 4
Ang magkatapat na mga punto na nagsasalubong sa isang pares ay bumubuo ng walong spherical na tatsulok sa globo. kanin. 5 Fig. 5
Sa isang tatsulok (Eulerian), ang bawat panig ay mas mababa sa kabuuan at mas malaki kaysa sa pagkakaiba ng iba pang dalawa; ang kabuuan ng lahat ng panig ay palaging mas mababa sa 2P. Ang kabuuan ng mga anggulo ng isang spherical triangle ay palaging mas mababa sa 3P at mas malaki kaysa sa P. Ang pagkakaiba s-P=E, kung saan ang s ay ang kabuuan ng mga anggulo ng isang spherical triangle, ay tinatawag na spherical excess.
Ito ay ganap na tinutukoy sa pamamagitan ng pagtukoy ng dalawang numero - ang mga numerong ito ay mga coordinate. Ang pagpapakilala ng mga coordinate sa isang globo ay nagpapahintulot sa isa na pag-aralan ang mga spherical figure gamit ang mga katulad na pamamaraan ng geometry. Kaya, dalawang equation
Tukuyin ang isang tiyak na linya sa globo. Ang haba ng arc M1 at M2 ng linyang ito ay kinakalkula ng formula Kung saan ang t1 at t2 ay ang halaga ng parameter na t, na tumutugma sa mga dulo ng M1 at M2 ng arc M1M2. Sa Fig. 6 Fig. 6
Isang mathematical na disiplina na nag-aaral ng mga ugnayan sa pagitan ng mga anggulo at gilid ng mga spherical triangle. Hayaang ang A, B, C ay ang mga anggulo a, b, c – ang magkabilang panig ng spherical triangle ABC Ang mga anggulo at gilid ng isang spherical triangle ay nauugnay sa mga sumusunod na pangunahing formula: sin a / sin A=sin b / sin. B=sin c /sin C, cos a =cos b cos c + sin b sin c cos A, sin a cos B=cos b sin c – sin b cos c cos A, Sin A cos b=cos B sin C + kasalanan B cos C cos a;
Sinusukat sila ng kaukulang mga gitnang anggulo, ang mga haba ng mga panig na ito ay katumbas ng aR, bR, cR, ayon sa pagkakabanggit, kung saan ang R ay ang radius ng globo. Sa pamamagitan ng pagbabago ng mga pagtatalaga ng mga anggulo at panig ayon sa panuntunan ng circular permutation, maaari kang sumulat ng iba pang mga formula ng spherical trigonometrya, katulad ng mga ipinahiwatig na mga formula na ito ay nagbibigay-daan sa iyo upang matukoy ang iba pang tatlong elemento ng isang spherical triangle (solve ang triangle) mula sa anumang tatlong elemento ng isang spherical triangle.
Kunin natin ang equation ng isang globo ng radius R na may sentro C (x0;y0;z0). (Larawan 7) Ang distansya mula sa isang di-makatwirang punto M (x;y;z) hanggang sa punto c ay kinakalkula ng formula Kung ang punto M ay nasa isang ibinigay na globo, kung gayon ang MC=R, o MC2=R2, i.e. ang mga coordinate ng point M ay nakakatugon sa equation (x – x0)2 + (y – y0)2 + (z – z0)2 = R2 (1) Kung ang point M (x; y; z) ay hindi nakalagay sa isang tuwid na tuwid sphere, kung gayon ang MC2 ay hindi katumbas ng R2, i.e. ang mga coordinate ng point M ay hindi nakakatugon sa equation (1). kanin. 7
Sa coordinate system, ang equation ng isang globo ng radius R na may sentrong C (x0; y0; z0) ay may anyo (x – x0)2 + (y – y0)2 + (z – z0)2 = R2
Mga eroplano
Ang distansya mula sa gitna nito hanggang sa eroplano a ay ang letrang d. Ipakilala natin ang isang coordinate system: ang Oxy plane ay tumutugma sa isang eroplano, at ang sentro C ng sphere ay nasa positibong semi-axis na Oz. Sa coordinate system na ito, ang point C ay may mga coordinate (0; 0; d), samakatuwid ang globo ay may equation na x2 + y2 + (z – d)2 = R2 (1) At ang eroplanong a ay tumutugma sa mga coordinate ng Oxy eroplano, at samakatuwid ang equation nito ay may view z = 0.(2)(ipaliwanag kung bakit)
Ang mga puntos na M (x; y; z) ay nakakatugon sa mga equation (1) at (2), pagkatapos ay ang point M ay namamalagi sa parehong eroplano at sa sphere, i.e. Ito ay karaniwan sa isang punto ng isang eroplano at isang globo. Kung ang sistema ng dalawang equation na ito (1) at (2) ay walang mga solusyon, kung gayon ang globo at ang eroplano ay walang mga karaniwang puntos. Kaya, ang tanong ng kamag-anak na posisyon ng globo at ang eroplano ay bumaba sa pag-aaral ng sistema ng mga equation Z = 0 X2 + y2 + (z – d)2 = R2 Ang pagpapalit ng z = 0 sa pangalawang equation, makuha namin ang X2 + y2 = R2 – d2 (3) Posibleng tatlong kaso, isaalang-alang natin ang mga ito.
Ay ang equation ng isang bilog na radius r = square root ng R2 – d2, na may sentro sa puntong She ng Oxy plane. Ang mga coordinate ng anumang punto M (x; y; 0) ng bilog na ito ay nakakatugon sa parehong equation ng eroplano at sa equation ng sphere, i.e. lahat ng mga punto ng bilog na ito ay karaniwang mga punto ng eroplano at ng globo. Fig. (8) Kaya, sa kasong ito, ang globo at ang eroplano ay nagsalubong sa isang bilog Kaya, kung ang distansya mula sa gitna ng globo hanggang sa eroplano ay mas mababa sa radius ng globo, kung gayon ang seksyon ng globo. sa pamamagitan ng eroplano ay isang bilog. Fig.(8)
Ang mga numerong x = 0, y = 0 lamang ang nakakasatisfy, i.e. Ang O ay ang tanging karaniwang punto ng globo at ng eroplano. Fig. (9) Kaya, kung ang distansya mula sa gitna ng globo hanggang sa eroplano ay katumbas ng radius ng globo, kung gayon ang globo at ang eroplano ay mayroon lamang isang karaniwang punto. kanin. (9)
Ang mga coordinate ng anumang punto ay hindi nakakatugon Dahil dito, kung ang distansya mula sa gitna ng globo hanggang sa eroplano ay mas malaki kaysa sa radius ng globo, ang toosphere at ang eroplano ay walang mga karaniwang punto. kanin. (10) Fig. (10)
Ang isang eroplano na mayroon lamang isang karaniwang punto na may isang globo ay tinatawag na isang tangent na eroplano sa globo, at ang kanilang karaniwang punto ay tinatawag na punto ng tangency sa pagitan ng eroplano at ng globo.
Ang radius ng isang sphere na iginuhit sa punto ng contact sa pagitan ng sphere at ng eroplano ay patayo sa tangent na eroplano
Isang eroplanong padaplis sa isang globo na may sentrong O sa puntong A. Patunayan: Ang OA ay patayo sa isang Patunay: Isaalang-alang natin ang pamamaraan sa pamamagitan ng kontradiksyon. Pagkatapos ang radius OA ay nakakiling sa eroplano at, samakatuwid, ang distansya mula sa gitna ng globo hanggang sa eroplano ay mas mababa kaysa sa radius ng globo. Samakatuwid, ang eroplano at ang globo ay nagsalubong sa isang bilog. Ngunit ito ay sumasalungat sa kondisyon, i.e. ang isang globo at isang eroplano ay may isang karaniwang punto lamang. Nangangahulugan ito na ang radius OA ay patayo sa eroplano. Ang teorama ay napatunayan.
Theorem: Kung ang isang radius ay patayo sa isang eroplanong dumadaan sa dulo nito na nakahiga sa isang globo, kung gayon ang eroplanong ito ay padaplis sa globo.
Isang eroplanong padaplis sa sphere na may sentrong O sa puntong A. Patunayan: Ang OA ay patayo sa isang Patunay: Mula sa mga kondisyon ng theorem, sumusunod na ang ibinigay na radius ay isang patayo na iginuhit mula sa gitna ng globo hanggang sa ibinigay na eroplano. Samakatuwid, ang distansya mula sa gitna ng globo hanggang sa eroplano ay katumbas ng radius ng globo, samakatuwid, ang globo at ang eroplano ay may isang karaniwang punto lamang. Nangangahulugan ito na ang eroplanong ito ay padaplis sa globo. Ang teorama ay napatunayan
Ang polyhedron ay sinasabing circumscribed tungkol sa isang globo (bola) kung ang globo ay dumampi sa lahat ng mukha nito. Ang isang globo ay sinasabing dumampi sa isang mukha ng isang polygon kung ang eroplano ng mukha ay padaplis sa globo at ang punto ng kontak ay kabilang sa mukha. Sa kasong ito, ang globo ay sinasabing nakasulat sa polyhedron.
Ang mga pagkakasunud-sunod ng mga lugar sa ibabaw ng polyhedra ay inilarawan sa paligid ng isang globo bilang ang pinakamalaking sukat ng bawat mukha ay may posibilidad na zero
Diretso. Ang eroplano ay nag-intersect sa sphere sa kahabaan ng isang bilog na L na may sentro O at radius R. Malinaw na ang lahat ng mga karaniwang punto ng globo at linya a (kung mayroon man) ay nasa eroplano a at, samakatuwid, sa bilog na L. 3 mga kaso ay maaari:
Ang mga tangent na segment na iginuhit mula sa punto A. Ang mga ito ay may mga sumusunod na katangian: ang mga tangent na segment sa isang sphere na iginuhit mula sa isang punto ay pantay at gumagawa ng mga pantay na anggulo na may isang tuwid na linya na dumadaan sa puntong ito at sa gitna ng globo.
Cylindrical surface Ang isang sphere ay sinasabing nakasulat sa isang cylindrical surface kung ito ay dumampi sa lahat ng nasasakupan nito. Patunayan natin na: May sphere tangent sa eroplano a at sa cylindrical na ibabaw.
Ang OH ay patayo sa eroplano a at tinutukoy namin sa pamamagitan ng letrang A ang punto ng intersection ng ray OH at ang globo S. (Fig. 11) Kung ang punto A at H ay nag-tutugma, pagkatapos ay gumuhit kami ng isang tuwid na linya sa pamamagitan ng punto A, parallel sa ang mga generator, at ipahiwatig sa pamamagitan ng letrang B ang punto ng intersection nito sa eroplano a. na may parallel na paglipat ng mga vectors AB, ang globo S ay nagbabago sa isang sphere S' ng radius r na may gitnang O' na nakahiga sa tuwid na linya OO1 (Larawan 12), kaya ang globo na ito ay humipo sa cylindrical na ibabaw. Ang distansya mula sa O' hanggang sa eroplano a ay katumbas ng O'B = OA (ipaliwanag kung bakit), i.e. katumbas ng radius r. Dahil dito, ang sphere S’ ay humipo sa eroplano a, i.e. ang ninanais ay napatunayan na. kanin. 11 Fig. 12
SURFACE Ang isang sphere ay sinasabing isinusulat sa isang conical surface kung ito ay dumampi sa lahat ng nasasakupan nito. Hayaan ang RA na maging isa sa mga generator ng kono. Isaalang-alang natin ang ilang eroplanong isang intersecting sa generatrix RA ng conical surface sa punto B na nakahiga sa ray RA. Patunayan natin sa ating sarili na mayroong isang sphere tangent sa eroplano a at sa conical surface. Tingnan ang fig. 13 Fig. 13
Isaalang-alang ang SABCD pyramid. Hayaang P ang perimeter ng base ABCD, na matatagpuan sa loob ng bilog na nagreresulta mula sa seksyon ng globo (ang hangganan ng bola) sa pamamagitan ng eroplanong ABCD. Ang radius ng bilog na ito ay r<=1. Продолжим отрезки АВ, ВС, CDи DA соответственно за точки B, C, Dи А до пересечения с окружностью в точках В1, С1, D1 и А1 соответственно. По неравенству треугольника
R<=Р1, где Р1 – периметр четырехугольника А1В1С1D1..Периметр любого выпуклого многоугольника, вписанного в окружность, меньше длинны этой окружности, поэтому р1<2Пr<=2ПДлинна каждого из ребер SA, SB, SC, SDне превосходит 2. поэтому если L – сумма длин всех сторон пирамиды, тоL=SA + SB + SC + SD + P < 2 + 2 + 2 + 2 + P1 < 8 + 2П< 15
Sa artikulong ito isasaalang-alang natin ang apat na problema sa stereometry. Ang isang kumbinasyon ng mga katawan ay ibinigay - isang kono at isang bola. Sa lahat ng mga gawain ay pinag-uusapan natin ang tungkol sa isang kono, na . Pansinin ko na sa kondisyon ang relatibong posisyon ng mga katawan na ito ay maaaring sabihin sa iba't ibang paraan, halimbawa: "Ang kono ay nakasulat sa isang bola" o "Ang isang globo ay inilarawan sa paligid ng kono."
Ang kakanyahan ay pareho - upang ilagay ito sa simpleng (di-matematika) na wika, ang kono ay "sa loob" ng globo, naglalaman ito ng bilog ng base at tuktok nito. Tingnan ang sketch:

Kapag naglutas, kailangan mong malaman ang mga formula para sa mga volume ng isang globo at isang kono.
Dami ng bola:

Dami ng kono:

*Kailangan mong malaman ang mga formula na ito!
Ang lugar ng base ng kono ay isang bilog, ito ay katumbas ng:
Isaalang-alang natin ang isang espesyal na kaso! Kung ang taas ng kono ay katumbas ng radius ng base nito, ang formula para sa dami ng kono ay magiging ganito:

Sketch:

Malinaw na ang gitnang seksyon ng naturang cone ay magiging isang right-angled isosceles triangle, at ang taas na iginuhit mula sa tamang anggulo ay hinahati din ito sa dalawang right-angled isosceles triangles:

Tandaan natin ang konsepto ng generator, madalas itong ginagamit sa mga problema sa cones, at gagamitin din sa mga gawain sa ibaba.
Formative ang kono ay isang segment na nag-uugnay sa tuktok ng kono sa punto ng base nito. Sa nakaraang sketch ito ay ipinahiwatig ng titik l .
Ang isang simpleng konklusyon ay nagmumungkahi mismo: ang kono ay may walang katapusang bilang ng mga generator at lahat sila ay pantay.
Sa pamamagitan ng paraan, mayroon nang ilang mga artikulo sa blog na may mga bola, maaari mong tingnan ang mga ito "" at "".
Ngayon tingnan natin ang mga gawain:
245351. Ang isang kono ay nakasulat sa isang bola. Ang radius ng base ng kono ay katumbas ng radius ng bola. Ang volume ng sphere ay 28. Hanapin ang volume ng kono.
Dahil sinasabing ang radius ng base ng kono ay katumbas ng radius ng bola, nagiging malinaw na ang base ng kono ay tumutugma sa eroplano ng gitnang seksyon ng bola.
Gumuhit tayo ng sketch ng kumbinasyong ito para sa kalinawan (ito ay isang axial section):

Sinasabi na ang taas ng isang kono ay katumbas ng radius ng base nito (at, siyempre, ang radius ng bola). Isulat natin ang mga formula para sa mga volume ng isang globo at isang kono:

Dahil ang dami ng bola ay kilala (ito ay katumbas ng 28), maaari nating kalkulahin ang radius. O sa halip, hindi natin kailangan ang radius mismo, ngunit ang cube nito:

Kaya, ang dami ng kono ay magiging katumbas ng:

* Ito ay posible na gawin nang walang mga kalkulasyon. Tingnan, kung ihahambing mo ang dalawang formula:
malinaw na ang volume ng globo ay 4 na beses ang volume ng kono.
Nangangahulugan ito na ang volume ng kono ay magiging 28/4 = 7.
Iyon ay, ang problema ay malulutas nang halos pasalita.
Sagot: 7
245352. Ang isang kono ay nakasulat sa isang bola. Ang radius ng base ng kono ay katumbas ng radius ng bola. Ang volume ng cone ay 6. Hanapin ang volume ng sphere.
Ang gawain ay kabaligtaran ng nauna, ang pagguhit ay pareho.
Mga formula:

Mula sa mga formula, malinaw na ang dami ng bola ay 4 na beses ang dami ng kono:

Kaya, ang kinakailangang dami ay 24.
Sagot: 24
316555. Ang isang globo ay nakapaligid sa isang kono (ang globo ay naglalaman ng circumference ng base ng kono at ang vertex nito). Ang gitna ng globo ay nasa gitna ng base ng kono. Ang generatrix ng kono ay katumbas ng. Hanapin ang radius ng globo.
Dito iba ang tunog ng kondisyon, ngunit ang mga katawan ay matatagpuan na may kaugnayan sa bawat isa sa eksaktong parehong paraan tulad ng sa mga nakaraang problema - ang kono ay nakasulat sa globo, ang base ng kono ay tumutugma sa gitnang seksyon ng globo.
Ang sketch ay pareho, markahan natin ang radius, ang taas na katumbas ng radius at ang generatrix:

Ang paglutas ng mga problema sa isang kono na nakasulat sa isang bola (kono na nakasulat sa isang globo) ay bumababa sa pagsasaalang-alang sa isa o higit pang mga tatsulok.
Ang isang kono ay nakasulat sa isang bola kung ang vertex at base circumference nito ay nasa ibabaw ng bola, iyon ay, sa isang globo. Ang gitna ng bola ay namamalagi sa axis ng kono.
Kapag nilutas ang mga problema na kinasasangkutan ng isang kono na nakasulat sa isang bola, ito ay maginhawa upang isaalang-alang ang seksyon ng isang kumbinasyon ng mga katawan sa pamamagitan ng isang eroplano na dumadaan sa axis ng kono at sa gitna ng bola. Ang seksyon ay isang malaking bilog ng bola (iyon ay, isang bilog na ang radius ay katumbas ng radius ng bola) na may isosceles triangle na nakasulat dito - ang axial section ng kono. Ang mga gilid ng tatsulok na ito ay ang bumubuo ng mga bahagi ng kono, ang base ay ang diameter ng kono.

Kung ang anggulo sa pagitan ng mga generator ay talamak, ang gitna ng circumscribed na bilog ay nasa loob ng tatsulok (naaayon, ang gitna ng bola na nakapaligid sa kono ay nasa loob ng kono).

Kung ang anggulo sa pagitan ng mga generator ay tama, ang gitna ng bilog ay nasa gitna ng base ng tatsulok (ang gitna ng bola ay tumutugma sa gitna ng base ng kono).
Kung ang anggulo sa pagitan ng mga generator ay mahina, ang gitna ng bilog ay nasa labas ng tatsulok (ang gitna ng circumscribed na bola ay nasa labas ng kono).
Kung ang pahayag ng problema ay hindi nagsasabi kung saan eksakto ang sentro ng circumscribed na bola, ipinapayong isaalang-alang kung paano maaaring makaapekto sa solusyon ang iba't ibang mga opsyon para sa lokasyon nito.
 Isaalang-alang ang isang kono at isang bola na nakapaligid dito ng isang eroplanong dumadaan sa axis ng kono at sa gitna ng bola. Dito SO=H ay ang taas ng kono, SB=l ay ang generatrix ng kono, SO1=O1B=R ay ang radius ng bola, OB=r ay ang radius ng base ng kono, ∠OSB=α ay ang anggulo sa pagitan ng taas at generatrix ng kono.
Isaalang-alang ang isang kono at isang bola na nakapaligid dito ng isang eroplanong dumadaan sa axis ng kono at sa gitna ng bola. Dito SO=H ay ang taas ng kono, SB=l ay ang generatrix ng kono, SO1=O1B=R ay ang radius ng bola, OB=r ay ang radius ng base ng kono, ∠OSB=α ay ang anggulo sa pagitan ng taas at generatrix ng kono.
Ang Triangle SO1B ay isosceles na may base SB (dahil SO1=O1B=R). Nangangahulugan ito na ang mga base na anggulo nito ay pantay: ∠OSB=∠O1BS=α, at ang O1F ay ang median, taas at bisector. Kaya SF=l/2.
Kapag nilulutas ang mga problema na kinasasangkutan ng isang kono na nakasulat sa isang bola, maaari mong isaalang-alang ang mga tamang tatsulok na SFO1 at SOB. Ang mga ito ay magkatulad (ayon sa talamak na anggulo S). Mula sa pagkakatulad ng mga tatsulok
![]()
Sa isang kanang tatsulok SOB ∠OBS=90º - ∠OSB=90º-α. Ayon sa Pythagorean theorem
Sa isang kanang tatsulok O1OB ∠OBO1=90º - ∠O1BS=90º - α - α=90º - 2α.
Isang sphere na nakasulat sa isang cylinder Ang isang sphere ay sinasabing nakalagay sa isang cylinder kung ito ay dumampi sa base at lateral surface nito (touch each generatrix). Sa kasong ito, ang silindro ay sinasabing circumscribed tungkol sa isang globo. Ang isang sphere ay maaaring ipasok sa isang silindro kung ang taas ng silindro ay katumbas ng diameter ng base nito. Ang sentro nito ay magiging punto O, na siyang gitna ng segment na kumukonekta sa mga sentro ng mga base O 1 at O 2 ng silindro. Ang radius ng sphere R ay magiging katumbas ng radius ng bilog ng base ng cylinder.













Isang sphere na nakapaligid sa isang silindro Ang isang silindro ay sinasabing nakalagay sa isang sphere kung ang mga bilog ng mga base ng silindro ay nasa sphere. Sa kasong ito, ang globo ay sinasabing nakapaligid sa silindro. Ang isang globo ay maaaring ilarawan sa paligid ng anumang silindro. Ang sentro nito ay magiging punto O, na siyang gitna ng segment na kumukonekta sa mga sentro ng mga base O 1 at O 2 ng silindro. Ang radius ng sphere R ay kinakalkula ng formula kung saan ang h ay ang taas ng cylinder, ang r ay ang radius ng base circle.






Isang silindro na nakasulat sa isang prisma Ang isang silindro ay tinatawag na nakasulat sa isang prisma kung ang mga base nito ay nakasulat sa mga base ng silindro. Sa kasong ito, ang prisma ay sinasabing naka-circumscribe sa isang silindro Ang isang silindro ay maaaring isulat sa isang prisma kung at kung ang isang bilog ay maaaring isulat sa base nito. Ang radius ng base ng silindro ay katumbas ng radius ng bilog na nakasulat sa base ng prisma. Ang taas ng silindro ay katumbas ng taas ng prisma.






A cylinder circumscribed about a prism Ang cylinder ay sinasabing circumscribed about a prism kung ang mga base nito ay circumscribed sa mga base ng cylinder. Sa kasong ito, ang prisma ay sinasabing nakasulat sa isang silindro Ang isang silindro ay maaaring ilarawan sa paligid ng isang prisma kung ang mga bilog ay maaaring ilarawan sa paligid ng mga base nito. Ang taas ng silindro ay katumbas ng taas ng prisma. ang radius ng bilog na inilarawan sa paligid ng base ng prisma. Ang radius ng base ng silindro ay







“Inscribed angle” - Ibinigay: __A. Pag-uulit ng materyal. Hanapin ang pagkakamali sa mga salita: Alam kung paano ito ipinahayag. Ang laki ng gitnang anggulo. Ang laki ng inscribed angle. Problema #1: Ihambing ang laki ng panlabas na anggulo at ang anggulo sa base. Paano magkatulad at magkaiba ang mga anggulong AOB at ACB? Ayon sa figure b). hanapin ang laki ng panlabas na anggulo. Konstruksyon ng mga patayong linya.
"Pagsukat ng mga anggulo" - Talamak, tuwid, mahina, tuwid na mga anggulo. Pagsukat ng mga anggulo. Ang isang protractor ay ginagamit upang bumuo ng mga anggulo. Maaari mong ilakip ang protractor sa ibang paraan. Tamang anggulo. Madilim na anggulo. Ang protractor ay ginagamit upang sukatin ang mga anggulo. Matalim na sulok. Nakabukang sulok. Anong anggulo ang ginagawa ng oras at minutong mga kamay ng orasan?
"Inscribed Angle Theorem" - Ano ang pangalan ng isang anggulo na may tuktok nito sa gitna ng bilog. Ang konsepto ng isang inscribed na anggulo. Hanapin ang anggulo sa pagitan ng mga chord. Sagot. Solusyon. Inscribed angle theorem. Tatsulok. Pagsasama-sama ng pinag-aralan na materyal. Matalim na sulok. Suriin ang iyong sarili. Hanapin ang anggulo sa pagitan nila. Tamang sagot. Pag-update ng kaalaman ng mga mag-aaral. Radius ng isang bilog.
"Anggulo at ang pagsukat nito" - Ang oras at minutong mga kamay ng orasan ay bumubuo ng isang malabo na anggulo sa 5 o'clock. Konstruksyon ng mga anggulo. Sa checkered na papel. Nakabukang sulok. Maling anggulo. Matalim na sulok. Ang protractor ay ginagamit upang sukatin ang mga anggulo. Ang tamang anggulo ay kalahating nakabukas na anggulo. Pagsukat ng mga anggulo. Gamit ang protractor. Ang mga anggulo ay sinusukat sa mga degree.
"Isang anggulo na nakasulat sa isang bilog" - Corollaries. Ipahiwatig ang mga inscribed na anggulo na ipinapakita sa figure. Nakasulat na anggulo. Aling anggulo ang tinatawag na sentral? Mga layunin ng aralin. Isang anggulo na ang vertex ay nasa isang bilog. Mga kaso ng lokasyon ng beam. Hanapin. Ang isang naka-inscribe na anggulo ay sinusukat ng kalahati ng arko kung saan ito nakasubtend. Alin sa mga anggulo na ipinapakita sa figure ang nakasulat?