1. Поняття асимптот

Одним із важливих етапів побудови графіків функцій є пошук асимптот. З асимптотами ми зустрічалися неодноразово: при побудові графіків функцій y=tgx, y=стgx. Ми визначали їх як лінії, до яких «прагне» графік функції, але ніколи їх не перетне. Настав час дати точне визначення асимптот.

Асимптоти бувають трьох видів: вертикальна, горизонтальна та похила. На кресленні асимптоти прийнято позначати пунктирними лініями.

Розглянемо наступний штучно складений графік функції (рис. 16.1), на прикладі якого добре видно всі види асимптоту:

Дамо визначення кожному виду асимптоту:

1. Пряма х = аназивається вертикальною асимптотою функції, якщо.

2. Пряма у = сназивається горизонтальною асимптотою функції, якщо.

3. Пряма у = kx + bназивається похилою асимптотою функції, якщо.

Геометрично визначення похилої асимптоти означає, що при ∞ графік функції скільки завгодно близько підходить до прямої у = kx + b, тобто. вони практично збігаються. Різниця практично однакових виразів прагне нуля.

Зазначимо, що горизонтальні та похилі асимптоти розглядаються лише за умови →∞. Іноді їх розрізняють на горизонтальні та похилі асимптоти при →+∞ і →-∞.

1. Алгоритм пошуку асимптот

Для пошуку асимптот можна використовувати наступний алгоритм:

Вертикальний асимптот може бути один, кілька або не зовсім.

• Якщо с – число, то у = с- Горизонтальна асимптота;
• Якщо з – нескінченність, то горизонтальних асимптотів немає.

Якщо функція є відношенням двох многочленів, то при наявності у функції горизонтальних асимптот похилі асимптоти шукати не будемо - їх немає.

Розглянемо приклади знаходження асимптот функції:

Приклад 16.1.Знайдіть асимптоти кривої.

Рішення х-1≠0; х≠1.

Перевіримо, чи є пряма х= 1 вертикальною асимптотою. Для цього обчислимо межу функції у точці х= 1: .

х= 1 – вертикальна асимптота.

з= .

з= = . Т.к. з=2 (число), то у=2- Горизонтальна асимптота.

Так як функція є відношенням багаточленів, то за наявності горизонтальних асимптот стверджуємо, що похилих асимптот немає.

х= 1 та горизонтальну асимптоту у=2.Для наочності графік цієї функції представлений на рис. 16.2.

Приклад 16.2. Знайдіть асимптоти кривої.

Рішення. 1. Знайдемо область визначення функції: х-2≠0; х≠2.

Перевіримо, чи є пряма х= 2 вертикальною асимптотою. Для цього обчислимо межу функції у точці х= 2: .

Отримали, що , отже, х= 2 – вертикальна асимптота.

2. Для пошуку горизонтальних асимптотів знаходимо: з= .

Оскільки в межі фігурує невизначеність, скористаємося правилом Лопіталя: з= = . Т.к. з- Безкінечність, то горизонтальних асимптот немає.

3. Для пошуку похилих асимптот знаходимо:

Отримали невизначеність виду, скористаємося правилом Лопіталя: = = 1. Отже, 1. Знайдемо bза формулою: .

b= = =

Отримали, що b= 2. Тоді у = kx + b -похила асимптота. У нашому випадку вона має вигляд: у = x +2.

Мал. 16.3

Таким чином, дана функція має вертикальну асимптоту. х= 2 і похилу асимптоту у = x +2.Для наочності графік функції представлено рис. 16.3.

Контрольні питання:

Лекція 17. ЗАГАЛЬНА СХЕМА ДОСЛІДЖЕННЯ ФУНКЦІЇ І ПОБУДУВАННЯ ГРАФІКА

У цій лекції ми підіб'ємо підсумок усьому раніше вивченому матеріалу. Кінцева мета нашого довгого шляху – вміти дослідити будь-яку аналітично задану функцію та будувати її графік. Важливими ланками нашого дослідження будуть дослідження функції на екстремуми, визначення інтервалів монотонності, опуклості та увігнутості графіка, пошук точок перегину, асимптот графіка функції.

З урахуванням усіх вищезгаданих аспектів наведемо схему дослідження функції та побудови графіка .

1. Знайти область визначення функції.

2. Дослідити функцію на парність-непарність:

· якщо , то функція парна (графік парної функції симетричний щодо осі Оу);

· Якщо , то функція непарна (графік непарної функції симетричний щодо початку координат);

· Інакше функція ні парна, ні непарна.

3. Дослідити функцію на періодичність (серед функцій, що ми вивчаємо, періодичними можуть бути тільки тригонометричні функції).

4. Знайти точки перетину графіка функції з осями координат:

· Ох: у=0 (вирішуємо рівняння лише тому випадку, якщо можемо використовувати відомі нам методи);

· Оу: х=0.

5. Знайти першу похідну функції та критичні точки першого роду.

6. Знайти інтервали монотонності та екстремуми функції.

7. Знайти другу похідну функції та критичні точки другого роду.

8. Знайти інтервали опуклості-увігнутості графіка функції та точки перегину.

9. Знайти асимптоти графіка функції.

10. Побудувати графік функції. При побудові слід врахувати випадки можливого розташування графіка поблизу асимптот :

11. При необхідності вибрати контрольні точки для більш точної побудови.

Розглянемо схему дослідження функції та побудови її графіка на конкретних прикладах:

Приклад 17.1. Побудуйте графік функції.

Рішення. 1. Ця функція визначена на всій числовій прямій за винятком х=3, т.к. у цій точці знаменник звертається у нуль.

2. Для визначення парності та непарності функції знайдемо:

Бачимо, що й, отже, функція ні парна, ні непарна.

3. Функція неперіодична.

4. Знайдемо точки перетину з осями координат. Для знаходження точки перетину з віссю Охприймемо у=0. Отримаємо рівняння: . Отже, точка (0; 0) – точка перетину з осями координат.

5. Знайдемо похідну функції за правилом диференціювання дробу: = = = = .

Для знаходження критичних точок знайдемо точки, у яких похідна функції дорівнює 0 чи немає.

Якщо =0, отже, . Добуток тоді дорівнює 0, коли хоча б один із множників дорівнює 0: або .

х-3) 2 дорівнює 0, тобто. не існує при х=3.

Отже, функція має три критичні точки першого роду: ; ; .

6. На числовій осі відзначимо критичні точки першого роду, причому точку відзначаємо точкою, що виколола, т.к. у ній функція не визначена.

Розставляємо похідні знаки = на кожному проміжку:

т.min

т.max

На проміжках, де , Вихідна функція зростає (при (-∞; 0] ), Де - Убуває (при ).

Крапка х=0 є точкою максимуму функції. Для знаходження максимуму функції знайдемо значення функції у точці 0: .

Крапка х=6 є точкою мінімуму функції. Для знаходження мінімуму функції знайдемо значення функції у точці 6: .

Результати досліджень можна занести до таблиці. Число рядків у таблиці фіксоване і дорівнює чотирьом, а число стовпців залежить від досліджуваної функції. У комірки першого рядка послідовно заносять інтервали, куди критичні точки розбивають область визначення функції, включаючи самі критичні точки. Щоб уникнути помилок при побудові точки, що не належать області визначення, можна до таблиці не включати.

У другому рядку таблиці розставляються знаки похідної кожному з аналізованих проміжків і значення похідної критичних точках. Відповідно до знаків похідної функції у третьому рядку відзначаються проміжки зростання, спадання, екстремуми функції.

Останній рядок служить для позначення максимуму та мінімуму функції.

х	(-∞;0)		(0;3)		(3;6)		(6;+ ∞)
	+		-		-		+
f(x)
Висновки		max				min

7. Знайдемо другу похідну функції як похідну від першої похідної: = =

Винесемо у чисельнику х-3 за дужки та виконаємо скорочення:

Наведемо в чисельнику такі доданки: .

Знайдемо критичні точки другого роду: точки, у яких друга похідна функції дорівнює нулю чи немає.

0 якщо =0. Даний дріб не може дорівнювати нулю, отже, точок, у яких друга похідна функції дорівнює нулю, немає.

Немає, якщо знаменник ( х-3) 3 дорівнює 0, тобто. не існує при х=3. :Ох, Оу, Початок відліку, одиниці виміру по кожній осі.

Перш ніж будувати графік функції, потрібно:

· Провести асимптоти пунктирними лініями;

· Відзначити точки перетину з осями координат;

Мал. 17.1

відзначити максимум і мінімум функції, причому рекомендується на кресленні позначити максимум і мінімум функції дугами: k або ;

· користуючись отриманими даними про проміжки зростання, спадання, опуклості та увігнутості, побудувати графік функції. Гілки графіка повинні «прагнути» асимптотам, але їх не перетинати.

· Перевірити, чи відповідає графік функції проведеному дослідженню: якщо функція парна або непарна, то чи дотримана симетрія; чи відповідають теоретично знайденим проміжки зростання та спадання, опуклості та увігнутості, точки перегину.

11. Для більш точної побудови можна вибрати кілька контрольних точок. Наприклад, знайдемо значення функції в точках -2 та 7:

Коригуємо графік з урахуванням контрольних точок.

Контрольні питання:

1. Яким є алгоритм побудови графіка функції?
2. Чи може функція мати екстремум у точках, що не належать області визначення?

ГЛАВА 3. 3. ІНТЕГРАЛЬНЕ ЗЛІЧЕННЯ ФУНКЦІЇ

- (Від грецьк. a отриц. Част., І symptotos збігається разом). Пряма лінія, що наближається до кривої і зустрічається з нею тільки в нескінченності. Словник іншомовних слів, що увійшли до складу російської мови. Чудінов А.Н., 1910. АСИМПТОТУ від ... Словник іноземних слів російської мови

АСИМПТОТА- (Від грецького asymptotos несупадаюча), пряма, до якої нескінченна гілка кривої наближається необмежено, наприклад асимптота гіперболи ... Сучасна енциклопедія

АСИМПТОТА- (від грец. asymptotos несупадний) кривою з нескінченною гілкою пряма, до якої ця гілка необмежено наближається, напр., асимптота гіперболи... Великий Енциклопедичний словник

асимптота- Пряма лінія, до якої поступово наближається крива. асимптота Пряма, до якої прагне (ніколи не досягаючи її) нескінченна гілка крива деякої функції, коли її аргумент необмежено зростає або … Довідник технічного перекладача

Асимптота- (Від грецького asymptotos несупадаюча), пряма, до якої нескінченна гілка кривої наближається необмежено, наприклад асимптота гіперболи. … Ілюстрований енциклопедичний словник

АСИМПТОТА- Жін., Геом. пряма риса, що вічно наближається до кривої (гіперболі), але ніколи з нею не сходить. Приклад, для пояснення цього: якщо якесь число все ділити навпіл, то воно применшуватиметься до нескінченності, але ніколи не стане банкрутом. Тлумачний словник Даля

асимптота- сущ., кіл у синонімів: 1 лінія (182) Словник синонімів ASIS. В.М. Тришин. 2013 … Словник синонімів

Асимптота- (Від грец. слів: a, sun, piptw) незбігається. Подасимптомом мається на увазі така лінія, яка, будучи невизначено продовжена, наближається до даної кривої лінії або до деякої її частини так, що відстань між загальними лініями робиться менше ...

Асимптота- Поверхні називається пряма лінія, що перетинає поверхню принаймні в двох нескінченно віддалених точках … Енциклопедія Брокгауза та Єфрона

АСИМПТОТА- (asymptote) Значення, до якого прагне дана функція при зміні аргументу (argument), але не досягає його за жодного кінцевого значення аргументу. Наприклад, якщо загальна вартість випуску х задається функцією ТС=а+bх, де а та b – константи … Економічний словник

Асимптота- Пряма, до якої прагне (ніколи не досягаючи її), що має нескінченну гілку крива деякої функції, коли її аргумент необмежено зростає або зменшується. Наприклад, функції: y = c + 1/x значення y наближається з… … Економіко-математичний словник

Скільки асимптот може мати графік функції?

Жодної, одна, дві, три, або нескінченно багато. За прикладами далеко не ходитимемо, згадаємо елементарні функції. Парабола, кубічна парабола, синусоїда зовсім не мають асимптоту. Графік експоненційної, логарифмічної функції має єдину асимптоту. У арктангенса, арккотангенса їх дві, а тангенса, котангенса - нескінченно багато. Не рідкість, коли графік укомплектований горизонтальними і вертикальними асимптотами. Гіпербола, буде завжди love you.

Що означає знайти асимптоти графіка функції?

Це означає з'ясувати їх рівняння, та й накреслити прямі лінії, якщо цього вимагає умова завдання. Процес передбачає знаходження меж функції.

Вертикальні асимптоти графіка функції

Вертикальна асимптота графіка, зазвичай, перебуває у точці нескінченного розриву функції. Все просто: якщо в точці функція зазнає нескінченного розриву, то пряма, задана рівнянням є вертикальною асимптотою графіка.

Зверніть увагу, що запис використовується для позначення двох абсолютно різних понять. Точка має на увазі або рівняння прямої - залежить від контексту.

Таким чином, щоб встановити наявність вертикальної асимптоти в точці досить показати, що хоча б одна з односторонніх меж нескінченна. Найчастіше це точка, де знаменник функції дорівнює нулю. Фактично, ми вже знаходили вертикальні асимптоти останніх прикладах уроку про безперервність функції. Але в ряді випадків існує тільки одна одностороння межа, і, якщо вона нескінченна, то знову - любіть і жалуйте вертикальну асимптоту. Найпростіша ілюстрація: і вісь ординат.

З вищесказаного також випливає очевидний факт: якщо функція безперервна, то вертикальні асимптоти відсутні. На думку чомусь спала парабола. Справді, де тут «устромиш» пряму? …так… розумію… послідовники дядечка Фрейда забилися в істериці =)

Зворотне твердження в загальному випадку неправильне: так, функція не визначена по всій числовій прямій, проте абсолютно обділена асимптотами.

Похилі асимптоти графіка функції

Похилі (як окремий випадок - горизонтальні) асимптоти можуть намалюватися, якщо аргумент функції прагне «плюс нескінченності» або «мінус нескінченності». Тому графік функції не може мати більше 2-х похилих асимптотів. Наприклад, графік експоненційної функції має єдину горизонтальну асимптоту при, а графік арктангенса при - двома такими асимптотами, причому різними.

Коли графік і там і там зближується з єдиною похилою асимптотою, то нескінченності прийнято об'єднувати під єдиним записом. Наприклад, …правильно здогадалися: .

Асимптоти графіка функції

Примара асимптоти давно бродила сайтом щоб, нарешті, матеріалізуватися в окремо взятій статті і привести в особливе захоплення читачів, спантеличених повним дослідженням функції. Знаходження асимптот графіка – одна з небагатьох частин зазначеного завдання, що висвітлюється у шкільному курсі лише в оглядовому порядку, оскільки події обертаються навколо обчислення меж функцій, А вони ставляться все-таки до вищої математики. Відвідувачі, які слабо знаються на математичному аналізі, натяк, думаю, зрозумілий;-) …стоп-стоп, ви куди? Межі- це легко!

Приклади асимптот зустрілися відразу на першому уроці про графіки елементарних функцій, і зараз тема отримує детальний розгляд.

Отже, що таке асимптота?

Уявіть змінну точку, Що «їздить» за графіком функції. Асимптота – це пряма, до якої необмежено близьконаближається графік функції при видаленні його змінної точки в нескінченність.

Примітка : визначення змістовно, якщо вам необхідне формулювання у позначеннях математичного аналізу, будь ласка, зверніться до підручника.

На площині асимптоти класифікують за їх природним розташуванням:

1) Вертикальні асимптоти, Які задаються рівнянням виду , Де «альфа» - дійсне число. Популярна представниця визначає саму вісь ординат,
з приступом легкої нудоти згадуємо гіперболу.

2) Похилі асимптотитрадиційно записуються рівнянням прямоїз кутовим коефіцієнтом. Іноді окремою групою виділяють окремий випадок. горизонтальні асимптоти. Наприклад, та ж гіпербола з асимптотою.

Швидко пішло-поїхало, ударимо по темі короткою автоматною чергою:

Скільки асимптот може мати графік функції?

Жодної, одна, дві, три, або нескінченно багато. За прикладами далеко не ходитимемо, згадаємо елементарні функції. Парабола, кубічна парабола, синусоїда зовсім не мають асимптоту. Графік експоненційної, логарифмічної функції має єдину асимптоту. У арктангенса, арккотангенса їх дві, а у тангенса, котангенса – дуже багато. Не рідкість, коли графік укомплектований горизонтальними і вертикальними асимптотами. Гіпербола, буде завжди love you.

Що значить ?

Вертикальні асимптоти графіка функції

Вертикальна асимптота графіка, як правило, знаходиться у точці нескінченного розривуфункції. Все просто: якщо в точці функція зазнає нескінченного розриву, то пряма, задана рівнянням є вертикальною асимптотою графіка.

Примітка : Зверніть увагу, що запис використовується для позначення двох абсолютно різних понять. Точка має на увазі або рівняння прямої - залежить від контексту.

Таким чином, щоб встановити наявність вертикальної асимптоти в точці, достатньо показати, що хоча б одинз односторонніх меж нескінченний. Найчастіше це точка, де знаменник функції дорівнює нулю. Фактично, ми вже знаходили вертикальні асимптоти в останніх прикладах уроку про безперервність функції. Але в ряді випадків існує тільки одна одностороння межа, і, якщо вона нескінченна, то знову - любіть і шануйте вертикальну асимптоту. Найпростіша ілюстрація: і вісь ординат (див. Графіки та властивості елементарних функцій).

Зі сказаного також випливає очевидний факт: якщо функція безперервна на, то вертикальні асимптоти відсутні. На думку чомусь спала парабола. Справді, де тут «устромиш» пряму? …так… розумію… послідовники дядечка Фрейда забилися в істериці =)

Зворотне твердження в загальному випадку неправильне: так, функція не визначена по всій числовій прямій, проте абсолютно обділена асимптотами.

Похилі асимптоти графіка функції

Похилі (як окремий випадок – горизонтальні) асимптоти можуть намалюватися, якщо аргумент функції прагне «плюс нескінченності» або «мінус нескінченності». Тому графік функції не може мати більше двох похилих асимптот. Наприклад, графік експоненційної функції має єдину горизонтальну асимптоту при , а графік арктангенса при – два такі асимптоти, причому різні.

Коли графік і там і там зближується з єдиною похилою асимптотою, то нескінченності прийнято об'єднувати під єдиним записом. Наприклад, …правильно здогадалися: .

Загальне практичне правило:

Якщо існують два кінцевихмежі то пряма є похилою асимптотою графіка функції при . Якщо хоча б одинз перелічених меж нескінченний, то похила асимптота відсутня.

Примітка : формули залишаються справедливими, якщо «ікс» прагне лише «плюс нескінченності» або лише «мінус нескінченності»

Покажемо, що парабола не має похилих асимптотів:

Межа нескінченна, отже, похила асимптота відсутня. Зауважте, що у знаходженні межі необхідність відпала, оскільки відповідь вже отримано.

Примітка : якщо у вас виникли (або виникнуть) труднощі з розумінням знаків «плюс-мінус», «мінус-плюс», будь ласка, перегляньте довідку на початку уроку
про нескінченно малі функції, де я розповів, як правильно інтерпретувати ці знаки.

Очевидно, що у будь-якої квадратичної, кубічної функції, багаточлена 4-го та вищих ступенів також немає похилих асимптот.

А тепер переконаємося, що при графіку теж немає похилої асимптоти. Для розкриття невизначеності використовуємо правило Лопіталя:
, Що і потрібно перевірити.

При функція необмежено зростає, проте не існує такої прямої, до якої б її графік наближався нескінченно близько.

Переходимо до практичної частини уроку:

Як знайти асимптоти графіка функції?

Саме так формулюється типове завдання, і воно передбачає знаходження ВСІХ асимптот графіка (вертикальних, похилих/горизонтальних). Хоча, якщо бути більш точним у постановці питання – йдеться про дослідження на наявність асимптот (адже таких може взагалі не виявитися). Почнемо з чогось простого:

Приклад 1

Знайти асимптоти графіка функції

Рішеннязручно розбити на два пункти:

1) Спочатку перевіряємо, чи є вертикальні асимптоти. Знаменник звертається в нуль при , і зрозуміло, що у цій точці функція терпить нескінченний розрив, А пряма, задана рівнянням є вертикальною асимптотою графіка функції . Але перш ніж оформити такий висновок, необхідно знайти односторонні межі:

Нагадую техніку обчислень, на якій я подібно зупинявся у статті Безперервність функції. Точки розриву. У вираз під знаком межі замість «ікса» підставляємо . У чисельнику нічого цікавого:
.

А ось у знаменнику виходить нескінченно мале негативне число:
, Воно і визначає долю межі.

Лівостороння межа нескінченна, і, в принципі, вже можна винести вердикт про наявність вертикальної асимптоти. Але односторонні межі потрібні не тільки для цього – вони ДОПОМАГАЮТЬ ЗРОЗУМІТИ, ЯКрозташований графік функції та побудувати його КОРЕКТНО. Тому обов'язково обчислимо і правосторонню межу:

Висновок: односторонні межі нескінченні, отже, пряма є вертикальною асимптотою графіка функції при .

Перша межа кінцевийОтже, необхідно «продовжити розмову» і знайти другу межу:

Друга межа теж кінцевий.

Таким чином, наша асимптота:

Висновок: Пряма, задана рівнянням є горизонтальною асимптотою графіка функції при .

Для знаходження горизонтальної асимптоти
можна користуватися спрощеною формулою:

Якщо існує кінцевиймежа, то пряма є горизонтальною асимптотою графіка функції при.

Неважко помітити, що чисельник та знаменник функції одного порядку зростання, а значить, межа буде кінцевою: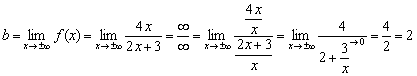

Відповідь:

За умовою не потрібно виконувати креслення, але якщо у розпалі дослідження функції