Funksiyaning yagona nuqtalari va ularning tasnifi. Izolyatsiya qilingan yagona nuqtalar. Qoldiqlar va ularni hisoblash formulalari

Ikki avtonom differensial tenglamalar tizimi tomonidan tasvirlangan modellar.

faza tekisligi. Fazali portret. izoklin usuli. asosiy izoklinlar. Barqaror holat barqarorligi. Chiziqli tizimlar. Asosiy nuqta turlari: tugun, egar, fokus, markaz. Misol: birinchi tartibli kimyoviy reaksiyalar.

Biologik tizimlar xususiyatlarini sifatli modellashtirish bo'yicha eng qiziqarli natijalar ikkita differentsial tenglamalar modellarida olingan bo'lib, bu usul yordamida sifatli o'rganish imkonini beradi. faza tekisligi. Umumiy shakldagi ikkita avtonom oddiy differentsial tenglamalar tizimini ko'rib chiqing

(4.1)

P(x,y), Q(x,y)- ba'zi sohalarda aniqlangan uzluksiz funktsiyalar G Evklid tekisligi ( x,y- Dekart koordinatalari) va bu sohada birinchidan past bo'lmagan tartibli uzluksiz hosilalarga ega.

Mintaqa G cheksiz yoki cheklangan bo'lishi mumkin. Agar o'zgaruvchilar x, y o'ziga xos biologik ma'noga ega (moddalarning kontsentratsiyasi, turlarning ko'pligi), ko'pincha maydon G o'ng yarim tekislikning musbat kvadranti:

0 £ x< ¥ ,0 £ y< ¥ .

Moddalarning kontsentratsiyasi yoki turlarning ko'pligi yuqoridan idishning hajmi yoki yashash joyining maydoni bilan ham cheklanishi mumkin. Keyin o'zgaruvchilar diapazoni quyidagi shaklga ega bo'ladi:

0 £ x< x 0 , 0 £ y< y 0 .

O'zgaruvchilar x, y vaqtni tenglamalar tizimiga (4.1) muvofiq o'zgartirish, shuning uchun tizimning har bir holati o'zgaruvchilarning juft qiymatlariga mos keladi ( x, y).

Aksincha, har bir o'zgaruvchi juftligi uchun ( x, y) tizimning muayyan holatiga mos keladi.

O'zgaruvchilar qiymatlari chizilgan koordinata o'qlari bo'lgan tekislikni ko'rib chiqing x,y. Har bir nuqta M bu tekislik tizimning ma'lum bir holatiga mos keladi. Bunday tekislik fazalar tekisligi deb ataladi va tizimning barcha holatlarining umumiyligini tasvirlaydi. M(x, y) nuqta tasvirlovchi yoki ifodalovchi nuqta deyiladi.

Dastlabki vaqtda ruxsat bering t=t 0 nuqta koordinatalarini ifodalaydi M 0 (x(t 0),y(t 0)). Vaqtning har bir keyingi daqiqasida t tasvirlash nuqtasi o'zgaruvchilar qiymatlari o'zgarishiga qarab harakatlanadi x(t),y(t). Nuqtalar to'plami M(x(t), y(t)) o'zgaruvchilarning vaqt o'tishi bilan o'zgarishi jarayonida tizimning holatiga mos keladigan faza tekisligida x(t), y(t)(4.1) tenglamalarga muvofiq, deyiladi fazali traektoriya.

O'zgaruvchilarning turli xil boshlang'ich qiymatlari uchun fazali traektoriyalar to'plami tizimning osongina ko'rinadigan "portretini" beradi. Bino fazali portret o'zgaruvchilarning o'zgarishi tabiati haqida xulosa chiqarish imkonini beradi x, y dastlabki tenglamalar tizimining analitik yechimlarini bilmasdan(4.1).

Fazali portretni tasvirlash uchun faza tekisligining har bir nuqtasida tizim traektoriyalari uchun yo'nalishlarning vektor maydonini qurish kerak. O'sishni belgilash orqaliD t>0,mos keladigan o'sishlarni olamiz D x va D y ifodalardan:

D x=P(x,y)D t,

D y=Q(x,y)D t.

vektor yo'nalishi dy/dx nuqtada ( x, y) funksiyalarning belgisiga bog'liq P(x, y), Q(x, y) va jadval bilan berilishi mumkin:

P(x,y)>0,Q(x,y)>0
P(x,y)<0,Q(x,y)<0
P(x,y)>0,Q(x,y)<0
P(x,y)<0,Q(x,y)>0

.(4.2)

Bu tenglamaning yechimi y=y(x, c), yoki bilvosita F(x,y)=c, qayerda Bilan integrasiya konstantasi bo‘lib, (4.2) tenglamaning integral egri chiziqlar oilasini beradi. fazali traektoriyalar tizim (4.1) tekislikda x, y.

Izoklin usuli

Fazali portretni yaratish uchun foydalaniladi izoklin usuli - integral egri chiziqlarni ma'lum bir burchak ostida kesib o'tadigan bosqichlar tekisligiga chiziqlar chiziladi. Izoklinal tenglamani (4.2) dan olish oson. Keling, qo'ying

qayerda A– ma'lum bir doimiy. Ma'nosi A faza traektoriyasiga tangens qiyaligining tangensini ifodalaydi va quyidagi qiymatlarni qabul qilishi mumkin -¥ ga + ¥ . O'rniga almashtirish dy/dx(4.2) dagi miqdor A izoklin tenglamasini olamiz:

.(4.3)

Tenglama (4.3) tekislikning har bir nuqtasida tegishli integral egri chiziqqa yagona tangensni belgilaydi, bu nuqtadan tashqari. P(x,y)= 0, Q (x,y) = 0 , bunda tangensning yo'nalishi noaniq bo'ladi, chunki hosilaning qiymati noaniq bo'ladi:

.

Bu nuqta barcha izoklinlarning kesishish nuqtasidir - maxsus nuqta. U bir vaqtning o'zida o'zgaruvchilarning vaqt hosilalarini yo'q qiladi x va y.

Shunday qilib, yagona nuqtada o'zgaruvchilarning o'zgarish tezligi nolga teng. Shuning uchun faza traektoriyalarining differensial tenglamalarining yagona nuqtasi (4.2) ga mos keladi. tizimning statsionar holati(4.1) va uning koordinatalari o'zgaruvchilarning statsionar qiymatlari x, y.

Ayniqsa qiziqish uyg'otadi Asosiy izoklinlar:

dy/dx=0, P(x,y)=0 – gorizontal tangenslarning izokliniyasi va

dy/dx=¥ , Q(x,y)=0 – vertikal tangenslarning izokliniyasi.

Asosiy izoklinallarni qurish va ularning kesishish nuqtasini topish orqali (x, y), koordinatalari quyidagi shartlarga javob beradi:

shu tariqa fazalar tekisligining barcha izoklinallarining kesishish nuqtasini topamiz, bunda faza traektoriyalariga teginishlar yo‘nalishi noaniq bo‘ladi. Bu - yagona nuqta, mos keladi tizimning statsionar holati(4.2-rasm).

(4.1) sistemada fazalar tekisligida asosiy izoklinallarning kesishish nuqtalari qancha bo'lsa, shuncha statsionar holatlar mavjud.

Har bir fazali traektoriya dinamik tizimning bir xil holatlardan o'tadigan va bir-biridan faqat vaqt ko'rsatkichining boshlanishi bilan farq qiladigan harakatlari to'plamiga mos keladi.

Agar Koshi teoremasining shartlari bajarilsa, u holda fazoning har bir nuqtasi orqali x, y, t bitta integral egri chiziqdan o'tadi. Fazali traektoriyalar uchun avtonomiya tufayli xuddi shunday: faza tekisligining har bir nuqtasidan o'ziga xos faza traektoriyasi o'tadi.

Barqaror holat barqarorligi

Tizim muvozanatda bo'lsin.

Keyin vakillik nuqtasi tizimning yagona nuqtalaridan birida joylashgan bo'lib, unda ta'rifga ko'ra:

.

Yagona nuqtaning turg'un yoki turg'un emasligi vakillik nuqtaning statsionar holatdan kichik og'ish bilan chiqib ketishi yoki chiqmasligi bilan aniqlanadi. Ikki tenglama tizimiga tatbiq qilinganidek, tilda barqarorlik ta'rifie, dquyida bayon qilinganidek.

Muvozanat holati barqaror bo'ladi, agar ma'lum bir sohada muvozanat holatidan og'ishlar bo'lsa. (e )maydoni belgilanishi mumkin d (e ), muvozanat holatini o'rab turgan va hudud ichida boshlanadigan hech qanday traektoriyaga ega bo'lmagan xususiyatga ega d , hech qachon chegaraga etib bormaydi e . (4.4-rasm)

Tizimlarning katta sinfi uchun - qo'pol tizimlar – xulq-atvorining tabiati tenglamalar turining ozgina o'zgarishi bilan o'zgarmaydigan, statsionar holatga yaqin joyda xatti-harakatlar turi haqida ma'lumotni asl nusxani emas, balki soddalashtirilganini o'rganish orqali olish mumkin. chiziqli tizimi.

Chiziqli tizimlar.

Ikki chiziqli tenglamalar tizimini ko'rib chiqing:

.(4.4)

Bu yerda a B C D- konstantalar, x, y- Fazalar tekisligidagi kartezian koordinatalari.

Umumiy yechim quyidagi shaklda izlanadi:

.(4.5)

Ushbu ifodalarni (4.4) o'rniga qo'ying va bilan kamaytiring e l t:

(4.6)

Noma'lumlar bilan algebraik tenglamalar tizimi (4.6). A, B Agar uning noma'lumlar koeffitsientlaridan tashkil topgan determinanti nolga teng bo'lsagina nolga teng bo'lmagan yechimga ega bo'ladi:

.

Ushbu determinantni kengaytirib, biz tizimning xarakteristik tenglamasini olamiz:

.(4.7)

Ushbu tenglamaning yechimi indikatorning qiymatlarini beradil 1,2 , uning ostida nolga teng bo'lmagan qiymatlar mumkin A va B(4.6) tenglamaning yechimlari. Bu qadriyatlar

.(4.8)

Agar radikal ifoda salbiy bo'lsa, u holdal 1,2 murakkab konjugat sonlar. Faraz qilaylik, (4.7) tenglamaning ikkala ildizi ham nolga teng bo‘lmagan haqiqiy qismlarga ega va bir nechta ildiz yo‘q. U holda (4.4) sistemaning umumiy yechimini ko‘rsatkichlar bilan ko‘rsatkichlarning chiziqli birikmasi sifatida ko‘rsatish mumkin.l 1 , l 2 :

(4.9)

Faza tekisligida tizimning mumkin bo'lgan traektoriyalarining tabiatini tahlil qilish uchun biz foydalanamiz chiziqli bir hil koordinatani o'zgartirish, bu tizimni olib keladi kanonik shakl:

,(4.10)

dastlabki tizim bilan solishtirganda faza tekisligida qulayroq ko'rinishga imkon beradi (4.4). Keling, yangi koordinatalarni kiritamizξ , η formulalar bo'yicha:

(4.1)

Chiziqli algebra kursidan ma'lumki, agar haqiqiy qismlar nolga teng bo'lmasal 1 , l 2 Dastlabki tizim (4.4) transformatsiyalar (4.11) yordamida har doim kanonik shaklga (4.10) aylantirilishi mumkin va uning faza tekisligidagi xatti-harakati o'rganilishi mumkin.ξ , η . Bu erda o'zini namoyon qilishi mumkin bo'lgan turli holatlarni ko'rib chiqing.

Ildizlar l 1 , λ 2 - haqiqiy va bir xil belgiga ega

Bunday holda, transformatsiya koeffitsientlari haqiqiydir, biz haqiqiy tekislikdan harakat qilamizx,yhaqiqiy tekislikka p, ē. (4.10) tenglamalarning ikkinchisini birinchisiga bo'lib, biz hosil bo'lamiz:

.(4.12)

Ushbu tenglamani integrallab, topamiz:

Qaerda .(4.13)

Keling, l bilan tushunishga rozi bo'laylik 2 katta modulli xarakterli tenglamaning ildizi, bu bizning fikrlashimizning umumiyligini buzmaydi. Keyin, chunki ko'rib chiqilayotgan holatda ildizlar l 1 , l2 - haqiqiy va bir xil belgiga ega;a>1 , va biz parabolik tipdagi integral egri chiziqlar bilan ishlaymiz.

Barcha integral egri chiziqlar (o'qdan tashqari η ga mos keladi ) o'qning boshiga teging ξ, bu ham (4.11) tenglamaning integral egri chizig'idir. Koordinatalarning kelib chiqishi yagona nuqtadir.

Endi vakillik nuqtasining faza traektoriyalari bo'yicha harakat yo'nalishini aniqlaymiz. Agar l 1 , l 2 manfiy bo'lsa, (4.10), |l|, |ē| tenglamalardan ko'rinib turibdiki vaqt o'tishi bilan kamayadi. Vakillik nuqtasi boshlang'ichga yaqinlashadi, lekin unga hech qachon etib bormaydi. Aks holda, bu fazalar tekisligining har bir nuqtasidan faqat bitta faza traektoriyasi o'tadi, degan Koshi teoremasiga zid keladi.

Xuddi parabolalar oilasi kabi integral egri chiziqlar o'tadigan shunday yagona nuqta kelib chiqishi orqali o'tadi, tugun deb ataladi (1-rasm). 4.5)

l da tugun tipidagi muvozanat holati 1 , l 2 < 0 Lyapunovga ko'ra barqaror, chunki ifodalovchi nuqta barcha integral egri chiziqlar bo'ylab koordinatalar boshiga qarab harakat qiladi. Bu barqaror tugun. Agar l 1 , l 2 > 0, keyin |l|, |ē| vaqt o'tishi bilan ortib boradi va vakillik nuqtasi koordinatadan uzoqlashadi. Bunday holda, yagona nuqta– beqaror tugun .

Faza tekisligida x, y integral egri chiziqlar harakatining umumiy sifat xarakteri saqlanib qoladi, lekin integral egri chiziqlarga teglar koordinata o'qlari bilan mos kelmaydi. Ushbu tangenslarning moyillik burchagi koeffitsientlar nisbati bilan aniqlanadi α , β , γ , δ (4.11) tenglamalarda.

Ildizlar l 1 , λ 2 amal qiladi va turli belgilarga ega.

dan aylantirish koordinatalar x,y koordinatalar uchun ξ, η yana haqiqiy. Kanonik o'zgaruvchilar uchun tenglamalar yana (4.10) ko'rinishga ega, ammo endi belgilar l 1 , l 2 boshqacha. Fazali traektoriya tenglamasi shaklga ega:

Qaerda, (4.14)

Integratsiyalash (4.14), biz topamiz

(4.15)

Bu Tenglama giperbolik tipdagi egri chiziqlar oilasini belgilaydi, bu erda ikkala koordinata o'qi asimptotlar (at a=1 bizda teng yonli giperbolalar oilasi bo'lar edi). Bu holatda koordinata o'qlari ham integral egri chiziqlardir– bular koordinatadan o'tuvchi yagona integral egri chiziqlar bo'ladi. Har birshundan uch fazali traektoriyalardan iborat: muvozanat holatiga (yoki muvozanat holatidan uzoqda) va muvozanat holatidan ikki harakatning. Boshqa barcha integral egri chiziqlar– Giperbolalar kelib chiqish joyidan o'tmaydi (1-rasm). 4.6) Bu yagona nuqta deyiladi "egar ». Tog'li egar yaqinidagi tekislik chiziqlari egar yaqinidagi faza traektoriyalari kabi harakat qiladi.

Vakillik nuqtasining muvozanat holatiga yaqin fazali traektoriyalar bo'ylab harakatining tabiatini ko'rib chiqaylik. Keling, masalan, l 1 >0 , l 2<0 . Keyin eksa ustida joylashgan vakillik nuqtasi ξ , boshlang'ichdan uzoqlashadi va o'qga joylashtiriladi η – koordinatalarning kelib chiqishiga cheksiz yaqinlashadi, chekli vaqt ichida erishmasdan. Vakillik nuqtasi boshlang'ich momentda bo'lgan joyda (singular nuqta va asimptotadagi nuqtalar bundan mustasno) η =0), u boshida integral egri chiziqlardan biri bo'ylab yagona nuqtaga qarab harakat qilsa ham, oxir-oqibat muvozanat holatidan uzoqlashadi..

Bu aniq egar tipidagi yagona nuqta har doim beqaror . Faqat asimptotada maxsus tanlangan dastlabki sharoitlardaη =0 tizim muvozanat holatiga yaqinlashadi. Biroq, bu tizimning beqaror ekanligi haqidagi da'voga zid emas. Agar hisoblasangiz, fazalar tekisligidagi tizimning barcha boshlang'ich holatlari bir xil ehtimolli bo'lsa, u holda yo'nalishdagi harakatga mos keladigan bunday boshlang'ich holatning ehtimolligi Kimga yagona nuqta nolga teng. Shuning uchun har qanday real harakat tizimni muvozanat holatidan olib tashlaydi.Koordinatalarga qaytishx,y,biz kelib chiqish atrofidagi traektoriyalar harakati tabiatining bir xil sifatli rasmini olamiz.

Tugun va egarning ko'rib chiqilgan holatlari orasidagi chegara holat qachon xarakterli ko'rsatkichlardan biri, masalan λ 1 , yo'qoladi, bu tizimning determinanti bo'lganda sodir bo'ladi- ifoda adbc=0(Qarang: formula 4.8 ). Bunda (4.4) tenglamalarning o'ng tomonlarining koeffitsientlari bir-biriga proporsional bo'ladi.:

va tizim o'zining muvozanat holati uchun chiziqning barcha nuqtalariga ega:

Qolgan integral egri chiziqlar qiyalikli parallel chiziqlar oilasidir , ular bo'ylab vakili nuqtalar l xarakterli tenglamaning ikkinchi ildizining belgisiga qarab muvozanat holatiga yaqinlashadi yoki undan uzoqlashadi. 2 = a+d.(4-rasm 7 ) Bu holda muvozanat holatining koordinatalari o'zgaruvchilarning boshlang'ich qiymatiga bog'liq.

Ildizlar l 1 , λ 2 – murakkabkonjugat

Bu holda, haqiqiyx va y Biz bo `lamiz murakkab konjugatlarga ega ξ , η (4.10) . Biroq, yana bitta oraliq transformatsiyani kiritish orqali, bu holda, ko'rib chiqishni haqiqiy chiziqli bir jinsli transformatsiyaga qisqartirish ham mumkin. Keling, qo'ying:

(4.16)

qayerda a, b, va u, v – haqiqiy qadriyatlar. dan o'zgarishini ko'rsatish mumkinx,y Kimga u, v Bizning taxminlarimiz bo'yicha, nolga teng bo'lmagan aniqlovchi bilan haqiqiy, chiziqli, bir hildir. Tenglamalar tufayli(4.10, 4.16) bizda:

qayerda

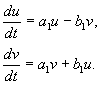(4.17)

Tenglamalarning ikkinchisini birinchisiga bo'lish, biz olamiz:

qaysi birlashtirish osonroq, qutb koordinata tizimiga o'tsak (r, φ ) . O'zgartirishdan keyin biz qayerdan olamiz:

.(4.18)

Shunday qilib, faza tekisligidau, vBiz logarifmik spirallar oilasi bilan shug'ullanamiz, ularning har biri mavjudkelib chiqishidagi asimptotik nuqta.Spiral shaklidagi barcha integral egri chiziqlarning asimptotik nuqtasi bo'lgan yagona nuqta, ichki do'stdo'stim, qo'ng'iroq qildi diqqat ( 4.8-rasm ) .

Keling, vakillik nuqtasining fazalar traektoriyalari bo'ylab harakatining tabiatini ko'rib chiqaylik. (4.17) tenglamalarning birinchisini ko'paytirishu, ikkinchisi esa v va qo'shsak, biz quyidagilarni olamiz:

Qayerda

Mayli a 1 < 0 (a 1 = Reλ ) . Keyin ifodalovchi nuqta chekli vaqt ichida yetib bormasdan, doimiy ravishda boshlang'ichga yaqinlashadi. Bu shuni anglatadiki, fazalar traektoriyalari burama spiraldir va sönümli tebranishlarga mos keladi. o'zgaruvchilar. Bu - barqaror diqqat .

Barqaror fokus holatida, barqaror tugun holatida bo'lgani kabi, nafaqat Lyapunov sharti, balki yanada qattiqroq talab ham qondiriladi. Ya'ni, har qanday boshlang'ich og'ishlar uchun tizim oxir-oqibat muvozanat holatiga kerakli darajada yaqinlashadi. Bunday barqarorlik deyiladi, unda dastlabki og'ishlar nafaqat o'smaydi, balki nolga moyil bo'ladi. mutlaq barqarorlik .

Agar formulada bo'lsa (4.18) a 1 >0 , keyin ifodalovchi nuqta boshlang'ichdan uzoqlashadi va biz bilan shug'ullanamiz beqaror diqqat . Samolyotdan harakatlanayotgandau, vfaza tekisligigax, yspirallar ham spiral bo'lib qoladi, lekin deformatsiyalanadi.

Endi qachon bo'lganini ko'rib chiqinga 1 =0 . Samolyotdagi fazali traektoriyalaru, vdoiralar bo'ladi qaysi samolyotdax,yellipslarga mos keladi:

Shunday qilib, daa 1=0 maxsus nuqta orqalix= 0,y= 0 integral egri chiziq o'tmaydi. Yonida integral egri chiziqlar yopiq egri chiziqlar, xususan, bir-biriga singib ketgan va singulyar nuqtani o'rab turgan ellipslar joylashgan bunday ajratilgan yagona nuqta markaz deyiladi.

Shunday qilib, xarakteristik tenglama (4.7) ildizlarining tabiatiga qarab, olti turdagi muvozanat mumkin. Tekislikdagi faza traektoriyalarining ko'rinishi x, y ushbu oltita holat uchun rasmda ko'rsatilgan. 4.9.

Guruch. 4.9.Chiziqli tenglamalar tizimi uchun statsionar holatning qo'shnisida fazali portretlarning turlari (4.4).

Besh turdagi muvozanat holatlari qo'pol bo'lib, ularning tabiati tenglamalarning o'ng tomonlarida etarlicha kichik o'zgarishlar bilan o'zgarmaydi (4.4). Bunday holda, o'zgarishlar nafaqat o'ng tomonda, balki ularning birinchi tartibli hosilalarida ham kichik bo'lishi kerak. Muvozanatning oltinchi holati - markaz - qo'pol emas. Tenglamalarning o'ng tomonining parametrlarida kichik o'zgarishlar bilan u barqaror yoki beqaror fokusga o'tadi.

Bifurkatsiya diagrammasi

Keling, belgi bilan tanishamiz:

. (4.11)

Keyin xarakteristik tenglamani quyidagi shaklda yozish mumkin:

. (4.12)

To'rtburchaklar Dekart koordinatalari bo'lgan tekislikni ko'rib chiqaylik s , D va unga xarakteristik tenglama ildizlarining tabiati bilan belgilanadigan muvozanat holatining u yoki bu turiga mos keladigan maydonlarni belgilang.

.(4.13)

Muvozanat holati barqarorligining sharti y ning manfiy real qismining mavjudligi bo'ladil 1 va l 2 . Buning zaruriy va yetarli sharti tengsizliklarni bajarishdirs > 0, D > 0 . Diagrammada (4.15) bu holat parametr tekisligining birinchi choragida joylashgan nuqtalarga mos keladi. Agar yagona nuqta diqqat markazida bo'ladil 1 va l 2 murakkab. Bu holat tekislikning o'sha nuqtalariga mos keladi , bular. parabolaning ikkita shoxlari orasidagi nuqtalars 2 = 4 D. Yarim o'q nuqtalari s = 0, D>0, markaz tipidagi muvozanat holatlariga mos keladi. Xuddi shunday,l 1 va l 2 - haqiqiy, lekin turli belgilar, ya'ni. birlik nuqta egar bo'ladi, agar D<0, va hokazo. Natijada, biz parametr tekisligining bo'linish diagrammasini olamiz s, D, har xil turdagi muvozanat holatlariga mos keladigan hududlarga.

Guruch. 4.10. Bifurkatsiya diagrammasi

chiziqli tenglamalar tizimi uchun 4.4

Agar chiziqli tizimning koeffitsientlari a B C D ba'zi parametrlarga bog'liq bo'lsa, bu parametr o'zgartirilganda qiymatlar ham o'zgaradis , D . Chegaralar orqali o'tayotganda, fazali portretning tabiati sifat jihatidan o'zgaradi. Shuning uchun bunday chegaralar bifurkatsiya chegaralari deb ataladi - chegaraning qarama-qarshi tomonlarida tizim ikkita topologik jihatdan turli xil fazali portretlarga va shunga mos ravishda ikki xil turdagi xatti-harakatlarga ega.

Diagrammada bunday o'zgarishlar qanday sodir bo'lishi ko'rsatilgan. Agar biz maxsus holatlarni - koordinatalarning kelib chiqishini istisno qilsak, egar y o'qini kesib o'tishda barqaror yoki barqaror bo'lmagan tugunga kirishi mumkinligini ko'rish oson. Barqaror tugun egarga yoki barqaror fokusga o'tishi mumkin va hokazo. E'tibor bering, barqaror tugun - barqaror fokus va beqaror tugun - beqaror fokus o'tishlari bifurkatsion emas, chunki bu holda fazalar bo'shlig'ining topologiyasi o'zgarmaydi. Faza fazosi topologiyasi va bifurkatsiya o’tishlari haqida 6-ma’ruzada batafsilroq to’xtalamiz.

Bifurkatsiya o'tishlari ostida yagona nuqtaning barqarorligi tabiati o'zgaradi. Misol uchun, markaz orqali barqaror fokus beqaror fokusga aylanishi mumkin. Bu bifurkatsiya deyiladi Andronov-Xopf bifurkatsiyasi uni tadqiq qilgan olimlarning nomlari bilan. Chiziqli bo'lmagan tizimlarda bu bifurkatsiya bilan chegara sikli tug'iladi va tizim o'z-o'zidan tebranuvchi holga keladi (8-ma'ruzaga qarang).

Misol. Chiziqli kimyoviy reaksiyalar tizimi

Modda X tashqaridan doimiy tezlikda oqadi, Y moddaga aylanadi va moddaning konsentratsiyasiga mutanosib tezlikda. Y, reaksiya sferasidan chiqariladi. Barcha reaksiyalar birinchi tartibli bo'lib, nol tartibli materiyaning tashqaridan kirib kelishi bundan mustasno. Reaktsiya sxemasi quyidagicha ko'rinadi:

(4.14)

va tenglamalar tizimi bilan tavsiflanadi:

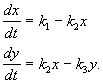(4.15)

O'ng tomonni nolga tenglashtirib, statsionar konsentratsiyalarni olamiz:

.(4.16)

Tizimning fazaviy portretini ko'rib chiqing. (4.16) sistemaning ikkinchi tenglamasini birinchisiga ajratamiz. Biz olamiz:

.(4.17)

(4.17) tenglama o'zgaruvchilarning fazalar tekisligidagi harakatini aniqlaydi. Keling, ushbu tizimning fazali portretini tuzamiz. Birinchidan, biz asosiy izoklinlarni faza tekisligida chizamiz. Vertikal tangenslar izokliniyasi tenglamasi:

Gorizontal tangenslarning izoklinli tenglamasi:

Yagona nuqta (statsionar holat) asosiy izoklinlar kesishmasida yotadi.

Endi koordinata o'qlari integral egri chiziqlarni qaysi burchakda kesishishini aniqlaylik.

Agar x= 0, keyin .

Shunday qilib, integral egri chiziqlarga teginish qiyaligi tangensi y=y(x), y o'qini kesib o'tish x=0, yuqori yarim tekislikda salbiy bo'ladi (esda tutingki, o'zgaruvchilar x, y konsentratsiya qiymatlariga ega va shuning uchun biz faqat faza tekisligining yuqori o'ng kvadrantiga qiziqamiz). Bunda tangensning qiyalik burchagi tangensining qiymati koordinata boshidan uzoqlashgan sari ortadi.

O'qni ko'rib chiqing y= 0. Ushbu o'qning kesishmasida integral egri chiziqlar tenglama bilan tavsiflanadi

Da abscissa o'qini kesib o'tuvchi integral egri chiziqlarning qiyaligi tangensi musbat va ortib borishi bilan noldan cheksizgacha ortadi. x.

Da .

Keyinchalik, keyingi o'sish bilan, qiyalik tangensi mutlaq qiymatda kamayadi, salbiy bo'lib qoladi va -1 ga intiladi. x ® ¥ . Asosiy izoklinlar va koordinata o'qlari bo'yicha integral egri chiziqlarga tegishlarning yo'nalishini bilib, faza traektoriyalarining butun rasmini qurish oson.

Singular nuqtaning barqarorligi tabiati Lyapunov usuli yordamida aniqlanadi. Tizimning xarakterli determinanti quyidagi shaklga ega:

.

Determinantni kengaytirib, biz tizimning xarakteristik tenglamasini olamiz: , ya'ni. xarakteristik tenglamaning ildizlari ikkala manfiy. Shuning uchun tizimning statsionar holati barqaror tugundir. Shu bilan birga, moddaning kontsentratsiyasi X Har doim monoton holda statsionar holatga intiladi, Y moddaning konsentratsiyasi min yoki max orqali o'tishi mumkin. Bunday tizimda tebranish rejimlari mumkin emas.

Mayli zq - f(z) funksiyaning birlik nuqtasi, t.s. f(z) lekin bu nuqtada analitik (xususan, unda aniqlanmasligi mumkin). Agar nuqtaning bunday teshilgan mahallasi mavjud bo'lsa zq (ya'ni, O z - to'plami zq f(z) aliatik, demak zo chaqirdi ajratilgan yagona nuqta funktsiyalari f(z). Bu ta'rif ishda ham saqlanib qolgan zn = oo, agar yod nuqtaning teshilgan mahallasi bo'lsa zq = oo to'plamni tushuning z > MEN - boshlang'ichda markazlashgan qandaydir doiraning ko'rinishi. Boshqacha qilib aytganda, yagona nuqta Agar bu nuqtaning qo'shnisi mavjud bo'lsa, zq izolyatsiya qilingan deb ataladi, unda boshqa birdan farqli nuqtalar mavjud. zq. Quyida hamma joyda biz faqat bitta qiymatli belgining yagona nuqtalarini ko'rib chiqamiz (funktsiya f(z) noyob deb hisoblanadi).

Funktsiyaning xatti-harakatiga qarab f(z) da z -> zq Yagona nuqtalarning uch turi mavjud. Izolyatsiya qilingan yagona nuqta zq funktsiyalari f(z) chaqirdi:

1) olinadigan yagona nuqta agar chekli chegara mavjud bo'lsa

2) qutb chegara bo'lsa

3) muhim nuqta, agar f(z) uchun na chekli, na cheksiz chegarasi bor z-> zq.

26.1. Keling, har uch turdagi birlik nuqtalarning amalga oshirilishini ko'rsataylik. O'ylab ko'ring f(z)= nuqta zq = 0 izolyatsiya qilingan

bu funktsiyaning yagona nuqtasi. (22.12) formuladan foydalanib, biz kengayishni olamiz

bundan lim borligi kelib chiqadi fi(z)= 1. Demak, zq = 0 bo'ladi

funksiyaning olinadigan yagona nuqtasidir fi(z).

Funktsiya f'j(z) =--- bir nuqtada qutbga ega zo= 1 chunki

2 r"X

Endi funktsiyani ko'rib chiqing )z(z)= e 1 ^ r va buni ko'rsating zo = O bu funksiyaning muhim birlik nuqtasidir. Intilish paytida z real o'q bo'ylab nolga, f funktsiyaning chap va o'ng chegaralari (z) har xil: lim Bilan 1 / 1 = 0,lim 1 /* = bilan os. Bu shuni anglatadiki,

x->0-0 x->0+0

nima f:i(z) 2 uchun na chekli, na cheksiz chegarasi bor -> Oh, ya'ni. zq = 0 bu funksiyaning mohiyatan yagona nuqtasidir. (E'tibor bering, nuqta tendentsiyaga qarab z-iy xayoliy o'q funktsiyasi bo'yicha nolga

umuman chegarasi yo'q.)

Albatta, izolyatsiyalanmagan yagona nuqtalar ham mavjud. Masalan. funksiya nuqtalarda qutblarga ega z n = -, P= ±1, ±2,...

Demak, Zq = 0 - bu funksiyaning izolyatsiyalanmagan yagona nuqtasi: bu nuqtaning istalgan (ixtiyoriy ravishda kichik) qo'shnisida boshqa yagona nuqtalar mavjud. g p.

Mayli zo- funktsiyaning oxirgi ajratilgan yagona nuqtasi f(z). Keyin f(z) nuqtaning ba'zi teshilgan mahallada 0 Zo o'xshash zo bu mahalla ichki radiusi r = 0 bo'lgan halqa sifatida qaralishi mumkin. 25.1 teoremaga ko'ra, ko'rib chiqilayotgan mahallada funktsiya f(z) Laurent seriyasida kengaytirilishi mumkin (25.2). Funktsiyaning 2 uchun xatti-harakatini ko'rsatamiz -> zq (ya'ni birlik nuqtaning turi zo) parchalanishning asosiy qismining shakliga bog'liq (25.2); bu holat "asosiy qism" atamasining kelib chiqishini tushuntiradi.

2G.2 TEOREMASI. f(z) funksiyaning izolyatsiyalangan yagona zo nuqtasi, agar bu nuqtaning teshilgan qo‘shnisidagi Lorap kengayishi oidga ega bo‘lsagina olinadigan bo‘ladi.

bular. faqat to'g'ri qismdan iborat, va asosiy qismning barcha koeffitsientlari o'qga teng.

Isbot. 1. Mayli zo olinadigan yagona nuqtadir. Funktsiyaning Loran kengayishi ekanligini isbotlaylik f(z)(26.1) shaklga ega. Yagona nuqtadan boshlab zo olinadigan, keyin cheklangan chegara lim mavjud f(z) = A. Demak, f(z) nuqtaning 0 z - zq ayrim teshilgan mahallada chegaralangan zo, bular. )(z) hamma uchun z shu mahalladan. Har qandayini oling R. U r /?|, va Loran seriyasining koeffitsientlari uchun (25.3) formulalardan foydalaning:

Kengayishning asosiy qismining koeffitsientlari uchun n =- 1,-2,... Bunday qiymatlar uchun P bizda ... bor p~n-e 0 da R-> 0. Qiymatdan boshlab R o'zboshimchalik bilan kichik tanlanishi mumkin, keyin janob ~" o'zboshimchalik bilan kichik bo'lishi mumkin. Buyon |c t,| ^ janob ~n va cn p ga bog'liq emas, keyin cn = 0 uchun va= - 1, -2,..., isbotlanishi kerak edi.

2. Keling, Laurent kengayishi (26.1) ko'rinishga ega deb faraz qilaylik. Seriya (26.1) quvvat seriyasidir va. shuning uchun nafaqat teshilgan, balki butun mahallada ham birlashadi z-zq shu jumladan nuqta zo; uning summasi S(z) uchun analitik hisoblanadi z va S(z) = )(z) 0 z da - zo R. Demak, chegaralangan chegara mavjud )(z)\u003d Pm 5 (r) \u003d 5 (r) - Shuning uchun yagona nuqta zq

Z->Zo Z-*Zo

bir martalik. Teorema isbotlangan.

Izoh. Teoremaning isbotidan kelib chiqadiki, teshilgan qo'shnida 0 z - zo olinadigan yagona nuqtada, funktsiya f(z) butun mahallada analitik bo‘lgan S(r) funksiyasiga to‘g‘ri keladi z - zo . Shuning uchun, agar /(th) = qo'ysak S(zq), keyin funktsiya qiymatlarini o'zgartirmasdan f(z) teshilgan mahallaning istalgan nuqtasida biz bu funktsiyani r-da analitik qilamiz, ya'ni. xususiyatni "o'chirish". Bu "olib tashlanadigan yagonalik" atamasini tushuntiradi. Bunday nuqtalarni funktsiyaning birlik nuqtalari sifatida emas, balki muntazam deb hisoblash tabiiydir f(z).

Masalan, funktsiyani ko'rib chiqing

26.1-misolda Pm (n) = 1. ya'ni. yagona nuqta

zq = 0 olinadigan. /i (0) = 1 ni o'rnatsak, biz shu bilan yagonalikni yo'q qilamiz va nuqtada analitik funktsiyani olamiz. zq = 0 (va butun C tekisligida).

Keling, qutblarni Loran kengayishlari nuqtai nazaridan tavsiflaylik.

26.3 teorema. f(z) funksiyaning izolyatsiyalangan yagona Zo nuqtasi qutb hisoblanadi, agar va faqat agar, Loran kengayishining asosiy qismi Zq markazga ega bo'lsa, faqat cheklangan sonli farqlar mavjud.

n bilan nol koeffitsientlardan:

Isbot. 1. Mayli zq - qutb, ya'ni. lim /( z) = oo.

Funktsiyaning Loran kengayishi ekanligini isbotlaylik f(z)(2G.2) shakliga ega. Limdan beri f(z)= oo. keyin nuqtaning teshilgan mahallasi mavjud

ki zq. unda f(z) analitik va nolga ega emas. Keyin funksiya g(z) = 1 /f(z) Bu teshilgan mahallada ham analitik bo'ladi va lim g(z)= 0. Shuning uchun, Zo bir martalik *-? *0

funksiyaning yagona nuqtasi g(z). Keling, qayta belgilaymiz g(z) nuqtada zo, qo'yish g(zo)= 0. Keyin g(z)(teshilmagan) nuqtaning butun qo'shnisida analitik bo'ladi z 0, va z0 uning ajratilgan nolga teng bo'ladi. tomonidan belgilang N bu nolning ko'pligi (tartibi). §23 da ko'rsatilganidek, nuqta qo'shnisida zq funktsiyasi g(z) shaklida ifodalanishi mumkin (qarang (23.2))

va (z$) f 0 va y>(z) nuqtaning ba'zi qo'shnilarida analitikdir zo- Chunki ip(z) nuqtada uzluksiz zo va g>(zo) F 0" keyin ip(z) Bu nuqtaning ayrim mahallalarida ham nolga ega emas. Shuning uchun funktsiya 1 /-p(z) Bu mahallada ham analitik bo'ladi va shuning uchun uni Teylor seriyasida kengaytiradi:

Qavslarni kengaytirib, koeffitsientlarning belgilarini o'zgartirib, biz oxirgi kengaytirishni shaklga yozamiz.

qaerda c_jv = 1>o f 0. Shunday qilib, f(r) ning Loran kengayishining asosiy qismi faqat cheklangan sonli hadlarni o'z ichiga oladi; biz kerakli tenglikka erishdik (26.2).

2. Nuqtaning teshilgan qo'shnisiga ruxsat bering th funktsiyasi )(z) Loran kengayishi (26.2) bilan ifodalanadi (kengaytirilgan shaklda, qarang (26.3)), uning asosiy qismida faqat cheklangan sonli atamalar mavjud va Bilan - d" f 0. Biz buni isbotlashimiz kerak Zq - funktsiya qutbi f(z). Tenglikni (26.3) ga ko'paytirish (G - G o) iV , funksiyani olamiz

(26.4) qator - bu nuqtaning nafaqat teshilgan qismida, balki butun qo'shnisida ham analitik funktsiyaga yaqinlashuvchi kuch qatoridir. Zq. Shuning uchun, funktsiya h(z) Agar biz uni o'rnatish orqali kengaytirsak, bu mahallada analitik bo'ladi h(zo)= s_dg f 0. Keyin

Shunday qilib, o nuqta qutb bo'lib, 26.3 teorema isbotlangan.

Nolinchi funksiyaning ko'pligi (tartibi). g(z)= 1//(r) deyiladi qutb tartibi funksiya /(r). Agar N- qutbning tartibi th, keyin g(z)= (r - Zo)N ip(z), va (ketish) F 0 va 26.3-teorema isbotining birinchi qismida ko'rsatilganidek, f(r) ning kengayishi (26.3) ko'rinishga ega bo'ladi, bu erda c_/v f 0. Aksincha, f(r) qatorga (26.3) kengaysa va e-z F 0, keyin

t.s. N- f(r) funksiyaning qutb tartibi. Shunday qilib, funksiyaning zq qutbining tartibi/(G) zq nuqtasining teshilgan qo'shnisida Loran kengayishining asosiy qismining etakchi nolga teng bo'lmagan koeffitsienti soniga teng.(ya'ni, bunday raqamga teng N, nima s_dg f 0 va sp= 0 da P > N).

Ilovalar uchun qulay bo'lgan quyidagi tasdiqni isbotlaylik.

Xulosa 26.4. zq nuqta fantastika N tartibli qutbdir/(G) agar va faqat agar/(G) shaklida ifodalaydi

Bu yerda h(z) nuqta qo‘shnisidagi analitik funksiya th va h(zo) f 0.

Isbot. Funktsiya cp(z) = l/h(z) r nuqtaning ba'zi qo'shnilarida analitikdir.Nulosa 26.4 sharti quyidagiga ekvivalentdir:

Shunday qilib zq - ko'plik nolga teng N funktsiyalari g(z). va shuning uchun ko'plik qutbi N funktsiyalari /(2).

II misol 26.5. Funksiyaning ajratilgan yagona nuqtalarini toping va ularning turini aniqlang.

D e u c tio n. Qaysi nuqtalar (z 2 + 1 )(z+ H) 2 = 0. Agar z 2 L- 1 = 0 keyin 2 = ±g agar (z 4- H) 2 = 0, u holda z= -3. Demak, funksiyaning uchta yagona nuqtasi bor z= r, 22 = -r, Z3 = - 3. O'ylab ko'ring z:

G - birinchi tartibli qutb (biz 26.4 xulosasidan foydalandik). 22 = ekanligini xuddi shunday isbotlash mumkin -i birinchi tartibli qutb ham. 2 soat davomida bizda:

Keling, mohiyatan alohida fikrlarni ko'rib chiqishga o'tamiz.

26.6 teorema. f(z) funksiyaning zq ajratilgan singulyar nuqtasi, agar markazlashgan Loran kengayishining asosiy qismi zq dan cheksiz ko‘p farq qilsagina, mohiyatan yagona hisoblanadi. nol, p bilan koeffitsientlar.

Isbot. 26.6 teorema bevosita 26.2 va 26.3 teoremalaridan kelib chiqadi. Haqiqatan ham, agar nuqta zq mohiyatan yagona bo'lsa, u holda Loran kengayishining asosiy qismi yo'q bo'lishi yoki cheklangan sonli atamalarni o'z ichiga olmaydi (aks holda nuqta Zq olinadigan yoki qutbli bo'ladi). Shuning uchun asosiy qismdagi atamalar soni cheksiz bo'lishi kerak.

Aksincha, agar asosiy qism cheksiz ko'p a'zolardan iborat bo'lsa, u holda Zq olinadigan nuqta ham, qutb ham bo'lishi mumkin emas. Binobarin, bu nuqta mohiyatan yagonadir.

Ta'rifga ko'ra, mohiyatan yagona nuqta f(2) funksiyaning na chekli, na cheksiz chegarasi bo'lmasligi bilan tavsiflanadi. z ->zq. Mohiyatan yagona nuqtaga yaqin joyda funktsiyaning harakati qanchalik tartibsiz ekanligi haqida to'liqroq fikr quyidagi teorema bilan berilgan.

26.7 teorema (Sochokki teoremasi). Agar zq mohiyatan birlik boʻlsa, f(z) funksiyaning nuqtasi), keyin har qanday kompleks son uchun L, shu jumladan A = oo, z n nuqtalar ketma-ketligi borki, z n -> zo va lim f(zn) = A.

n->os

Isbot. Avval ishni ko'rib chiqing A = oo. 2G.2 teorema isbotining birinchi qismida biz aniqladikki, agar f(z) r0 nuqtasining ba'zi bir teshilgan qo'shnisi bilan chegaralangan bo'lsa, u holda barcha koeffitsientlar c, n = - Asosiy qismning 1, - 2,... nolga teng (va, demak, thdagi yagonalik olib tashlanadi). Farazga ko'ra, r mohiyatan yagona nuqta bo'lganligi sababli, /(r) funksiya r nuqtaning har qanday teshilgan qo'shnisida chegaralanmagan. Keling, 0 Z tor mahallani olaylik f(zi) > 1 (agar |/(r)| z - zo R/2 nuqta bo'lsa z-2 , bu yerda |/(dd)| > 2 va boshqalar: teshilgan mahallada O 71. Ko'rinib turibdiki, rn -e go va lim /(r«) = oo. Shunday qilib, A = oo holatda, teorema 26.7

isbotlangan.

Keling A f oo. Avval 0-o'rinda teshilgan mahalla bor deb taxmin qiling

= -yy---- bu teshilgan mahallada analitik bo'ladi va shuning uchun

/(G) - A

demak, r PH(r) funksiyaning ajratilgan yagona nuqtasidir. Keling, ko'rsataylik. bu r0 PH(r) ning mohiyatan yagona nuqtasidir. Bu noto'g'ri bo'lsin. U holda chekli yoki cheksiz lim PH(r) chegarasi mavjud. Chunki

/(r) = A +, keyin Hsh /(r) ham mavjud, bu shartga zid keladi

F(g) ~ :-*z 0

teoremaning ko'rinishi. Shunday qilib, r0 PH(r) funksiyaning mohiyatan yagona nuqtasidir. Yuqorida isbotlangan narsaga ko'ra, r n nuqtalar ketma-ketligi mavjud bo'lib, r n o va lim PH(r n) = oo bo'ladi. Bu yerdan

Biz f(r) degan faraz ostida kerakli fikrni isbotladik. F A r nuqtasining ba'zi bir teshilgan mahallasida. Endi bu to'g'ri emas deb faraz qilaylik, ya'ni. nuqtaning har qanday o'zboshimchalik bilan kichik teshilgan mahallada shunday nuqta bor G", deb f(r") = A. Keyin har qanday uchun P teshilgan mahallada 0 f(z u) = L. Shunday qilib, talab qilingan tasdiq haqiqatdir P-yuo

hamma hollarda va 26.7 teorema isbotlangan.

(Soxotskiy) 26.7 teoremasiga ko'ra, mohiyatan yagona nuqtaning har qanday (o'zboshimchalik bilan kichik) teshilgan qo'shnisida f (r) funktsiyasi kengaytirilgan kompleks C tekisligidagi istalgan songa o'zboshimchalik bilan yaqin qiymatlarni oladi.

Izolyatsiya qilingan yagona nuqtalarni o'rganish uchun asosiy elementar funktsiyalarning taniqli Teylor kengaytmalari ko'pincha foydalidir.

2G.8 MISOL. Funksiya uchun zq = 0 yagona nuqta turini aniqlang

Yechilgan va e. Teylor qatoridagi pay va maxrajni r darajasida kengaytiramiz. (22.11) 3 ga almashtiramiz. z r ni va 1ni ayirish o'rniga, biz olamiz

(22.12) dan foydalanib, biz maxrajning kengayishini olamiz:

Ushbu kengaytmalardagi ketma-ketliklar butun kompleks tekislikda € birlashadi. Bizda ... bor

va /2(2) nuqta qo'shnisida o'xshashdir zo = 0 (va hatto butun tekislikda) va / 2 (20) F 0, keyin h(z) gF 0 nuqtasining ba'zi qo'shnilarida ham analitikdir. Xulosa 26.4 ga ko'ra, nuqta Zo = 0 - buyurtmaning qutbi N = 4.

II misol 26.9. Funktsiyaning yagona nuqtalarini toping f(z)= sin j - va ularning turini aniqlang.

P e in e va e. Funktsiya bitta yakuniy yagona nuqtaga ega zq = 1. C dan boshqa nuqtalarda funksiya w =--- analitik; shuning uchun gunoh funktsiyasi w analitik bo'ladi.

Sinusning kengayishida (22.12) o'rnini bosamiz - r o'rniga, biz olamiz

Biz 20 = 1 nuqtaning teshilgan qo'shnisida Laurent seriyasida gunoh funktsiyasining kengayishini oldik. Olingan kengayish manfiy kuchga ega cheksiz ko'p atamalarni o'z ichiga olganligi sababli (r - 1), u holda zq = 1 - muhim yagona nuqta (bu holda, Laurent kengayishi faqat asosiy qismdan iborat va to'g'ri qism yo'q).

E'tibor bering, bu holda, qatorni kengaytirishga murojaat qilmasdan, to'g'ridan-to'g'ri ta'rifdan yakkalik tabiatini aniqlash mumkin edi. Darhaqiqat, (r") va (2") ga yaqinlashuvchi ketma-ketliklar mavjud zo= 1 va shunga o'xshash f(z" n)= 1, /(2") = 0 (bunday ketma-ketlikni o'zingiz belgilang). f(z) qachon chegarasi yo'q z -> 1 va shuning uchun nuqta zq - 1 asosan birlikdir.

Funktsiyaning nuqta qo'shnisida Loran kengayishi tushunchasini kiritaylik Zq = 00 va bu nuqtada kengayish va yakkalikning tabiati o'rtasidagi bog'liqlikni ko'rib chiqing. E'tibor bering, izolyatsiya qilingan yagona nuqta va uning turi (olinadigan, qutb yoki asosan birlik) ta'riflari ish uchun o'tkaziladi. zq = oc o'zgarmagan. Lekin teoremalar 26.2. Laurent kengaytmalarining tabiati bilan bog'liq bo'lgan 26.3 va 26.6-ni o'zgartirish kerak. Gap shundaki, a'zolar c n (z - 2o) p. P= -1,-2,..., asosiy qism, oxirgi nuqtaga yaqin funktsiyaning "" tartibsizlik "ni belgilaydi Zq, chunki 2 oo ga moyil bo'lsa, ular "to'g'ri" harakat qiladilar (0 ga moyil). Aksincha, muntazam qism a'zolari bilan P= 1,2,... oo ga moyil bo'ladi; dagi birlik xususiyatini belgilaydilar Zq = oo. Shuning uchun, oo mahallasidagi kengaytirishning asosiy qismi ijobiy vakolatlarga ega bo'lgan shartlar bo'ladi P, va to'g'ri - salbiy bilan.

Keling, yangi o'zgaruvchini kiritamiz w = 12. Funktsiya tv= 1/2, u(oo) = 0 bo'lishi uchun kengaytirilgan, birma-bir va qo'shni hududni mos ravishda xaritalash z > R ball zq = 00 qo'shnisida |w| wq = 0. Agar funktsiya f(z) teshilgan mahallada tahlil R z Zq = oc, keyin funksiya G(w) = f(l/w) sariq mahallada analitik bo'ladi 0 wo = 0. 2 uchun beri -> oo bo'ladi w-> 0, keyin

Shunday qilib G(w) nuqtada bor wq = 0 - bir xil turdagi yagonalik f(z) nuqtada Zq = 00. G(w) funksiyani Laurent qatorida wo = 0 nuqtaning teshilgan mahallasida kengaytiramiz:

(26.5) ning o'ng tomonidagi summalar mos ravishda kengayishning to'g'ri va asosiy qismlarini ifodalaydi. Keling, o'zgaruvchiga o'tamiz z, almashtirish w = 1/z:

bildiruvchi P\u003d -A *, 6 * \u003d 6_ " \u003d p bilan va buni payqash G(l/z) = f(z), olamiz

Parchalanish (2G.G) deyiladi zq nuqtaning teshilgan qo'shnisida f(z) funksiyaning Loran kengayishi= oo. (2G.6) dagi birinchi summa chaqiriladi o'ng qism, ikkinchi summa esa asosiy qismi bu parchalanish. Bu summalar kengayishning (26.5) toʻgʻri va asosiy qismlariga toʻgʻri kelganligi sababli, kengaytirish (26.6) 26.2, 26.3 va 26.6 teoremalarning analoglarini qanoatlantiradi. Shunday qilib, quyidagi teorema 26.2 teoremaning analogidir.

26.10 teorema. Izolyatsiya qilingan yagona nuqtaZq - os (funktsiyalari/(G) Agar bu nuqtaning teshilgan mahallasidagi Loran kengayishi shaklga ega bo'lsagina olinadi.

t.s. faqat to'g'ri qismdan iborat.

Biz /(oo) = qo'yamiz co.(26.7) qator bilan aniqlangan funktsiya mahallada yaqinlashadi z > R nuqtalar 2o \u003d oc, chaqiriladi z nuqtada analitik o = oo. (E'tibor bering, bu ta'rif funktsiyaning analitikligiga ekvivalentdir G(w) nuqtada vo = 0.)

26.11-misol. Funksiyaning zq = oo birlik nuqtasini o‘rganing

Chegara chekli bo'lgani uchun, demak zo = oo f(r) funksiyaning olinadigan yagona nuqtasidir. Agar /(oo) = lim qo'ysak J(z)= 0, keyin f(z) aylanadi

nuqtada tik Zo= os. Keling, mos keladigan kengaytmani qanday topishni ko'rsatamiz (26.7). Keling, o'zgaruvchiga o'tamiz w = 1 fz. O'rnini bosish z= 1 /?e, olamiz

(oxirgi tenglik ww = 0 nuqtaning teshilgan qo'shnisida amal qiladi, lekin biz ta'rifni kengaytiramiz (7(0) = 0). Olingan funktsiya yagona nuqtalarga ega. w =±i, w =-1/3 va nuqtada Wq = 0 analitik hisoblanadi. Funktsiyani kengaytirish G(w) darajalar bo'yicha w(25.7-misolda qilinganidek) va natijada olingan quvvat qatoriga almashtirish w = 1/z funktsiyaning (26.7) kengayishini olish mumkin f(z).

Ish uchun teorema 26.3 zo= oo quyidagi shaklda qayta yoziladi.

26.12 teorema. Izolyatsiya qilingan yagona nuqta borish = ok f(z) funksiyasi qutb bo'ladi, agar Loran kengayishining asosiy qismi bo'lsa (26.6) faqat chekli sonli nolga teng bo'lmagan koeffitsientlarga ega Bilan":

Bu erda ketma-ket muntazam qism, qavs ichidagi ko'phad esa kengaytirishning asosiy qismidir. Ocdagi qutbning ko'pligi qutbning ko'pligi sifatida aniqlanadi wq = 0 funksiya G(z). Qutbning ko'pligi songa to'g'ri kelishini ko'rish oson N da (26.8).

Q p | (i 2 + 1) (z + 3) 2

Vazifa. Funktsiya ekanligini ko'rsating f(z) =-- -- bor

nuqta zo = oo qutb tartibi 3.

Muhim bir nuqtaga oid 26.6 teorema ish uchun qayta yoziladi zo= os deyarli so'zma-so'z va biz bu haqda batafsil to'xtalmaymiz.

Teylor qatori zol aylanasida analitik bo‘lgan funksiyalarni o‘rganishda samarali vosita bo‘lib xizmat qiladi. Halqasimon mintaqada analitik bo‘lgan funksiyalarni o‘rganish uchun musbat va manfiy darajalarda (z - zq) kengayishlarni qurish mumkinligi ma’lum bo‘ldi. Teylor kengayishlarini umumlashtiruvchi shakl. Ikki qatorning yig'indisi sifatida tushunilgan (1) seriya Loran seriyasi deb ataladi. Ko'rinib turibdiki, (1) qatorlarning yaqinlashish mintaqasi (2) qatorlarning har birining yaqinlashuv mintaqalarining umumiy qismidir. Keling, uni topamiz. Birinchi qatorning yaqinlashish maydoni aylana bo'lib, uning radiusi Koshi-Hadamard formulasi bilan aniqlanadi. Yaqinlashuv doirasi ichida (3) qator analitik funktsiyaga yaqinlashadi va har qanday kichikroq radiusli doirada u mutlaqo yaqinlashadi. va bir xilda. Ikkinchi qator o‘zgaruvchiga nisbatan darajali qatordir.(5) qator o‘zining yaqinlik doirasi doirasida m-*oo kompleks o‘zgaruvchining analitik funksiyasiga yaqinlashadi va har qanday kichikroq radiusli aylanada u mutlaqo va bir xil yaqinlashadi, ya'ni (4) qatorning yaqinlashish mintaqasi aylananing ko'rinishi - Agar (3) va (4) qatorlarning umumiy yaqinlashuv mintaqasi mavjud bo'lsa - (1) qatorlar joylashgan aylana halqa. analitik funksiyaga yaqinlashadi. Bundan tashqari, har qanday halqada u mutlaqo va bir xilda birlashadi. Misol 1. Rad Loran qatorining yaqinlashish mintaqasini aniqlang Izolyatsiya qilingan yagona nuqtalar va aylana halqada bir qiymatli va apolitik bo'lgan ularning tasnifi (z), bu halqada koeffitsientlari konvergent qatorlar yig'indisi sifatida ifodalanishi mumkin. Cn yagona tarzda aniqlanadi va formulalar bo'yicha hisoblanadi, bunda 7p m radiusli aylana bo'ladi. R halqasi ichidagi ixtiyoriy z nuqtasini o'rnatamiz. Radiuslari tengsizliklarni qanoatlantiruvchi r nuqtada markazlari bo‘lgan doiralar quramiz va yangi halqani ko‘rib chiqamiz.Ko‘paytmali bog‘langan soha uchun Koshi integral teoremasiga ko‘ra, yig‘indidagi (8) har bir integralni alohida o‘zgartiramiz. 7d* aylana bo‘ylab barcha £ nuqtalar uchun bir xil konvergent qator 1 1 yig‘indisi munosabati bajariladi. Shuning uchun ^ kasrni vi- /" shaklida ifodalash mumkin. aylana ir> munosabatiga egamiz Shuning uchun ^ kasrni (10) va (12) formulalardagi bir xil yaqinlashuvchi qator yig’indisi sifatida ifodalash mumkin, aylana halqadagi analitik funksiyalardir. Shuning uchun, Koshi teoremasi bo'yicha, agar 7/r va 7r/ aylanalar har qanday aylana bilan almashtirilsa, tegishli integrallarning qiymatlari o'zgarmaydi. Bu (10) va (12) formulalarni birlashtirish imkonini beradi.(8) formulaning o’ng tomonidagi integrallarni ularning mos ravishda (9) va (11) ifodalari bilan almashtirsak, kerakli kengaytmani olamiz.Z ixtiyoriy bo’lgani uchun. halqaning nuqtasidan kelib chiqadiki, (14) qator bu halqaning hamma joyida f(z) funksiyaga yaqinlashadi va har qanday halqada qator bu funksiyaga mutlaq va bir xil yaqinlashadi. Endi (6) shaklning parchalanishi yagona ekanligini isbotlaylik. Faraz qilaylik, yana bir parchalanish sodir bo'ladi, keyin R halqasining hamma joyida aylana bo'yicha (15) qatorlar bir xilda yaqinlashadi. Tenglikning har ikki tomonini ko'paytiring (bu erda m - sobit butun son va ikkala ketma-ket atamani muddat bo'yicha integrallash. Natijada, biz chap tomonda, o'ng tomonda esa - Csh. Shunday qilib, (4, \u003d St. m ixtiyoriy son bo'lgani uchun koeffitsientlari (7) formulalar bo'yicha hisoblangan oxirgi tenglik qatori (6) Loran qatori koeffitsientlari uchun 7-halqadagi f(z) funksiyaning Loran qatori deb ataladi. amalda kamdan kam qo'llaniladi, chunki ular qoida tariqasida og'ir hisob-kitoblarni talab qiladi.Odatda iloji bo'lsa elementar funksiyalarning tayyor Teylor kengaytmalari qo'llaniladi.Kengaytirishning o'ziga xosligidan kelib chiqqan holda har qanday qonuniy usul bir xil natijaga olib keladi. 2-misol. Fuiscija /(z) ning ikkita yagona nuqtasi bor deb faraz qilib, turli domenlar funksiyalarining Loran seriyali kengayishlarini ko'rib chiqing: Shunday qilib, uchta halqa sohasi mavjud. va markazlashgan nuqtada r = 0. har birida f(r) funksiya analitik bo'ladi: a) aylana aylananing tashqi ko'rinishidir (27-rasm). Ushbu mintaqalarning har birida /(z) funksiyaning Loran kengaytmalarini topamiz. /(z) ni elementar kasrlar yig‘indisi sifatida ifodalaymiz a) Doirani aylantirish munosabati (16) quyidagicha geometrik progressiya hadlari yig‘indisi formulasidan foydalanib, hosil qilamiz. b) -z funksiya uchun halqa bu halqada konvergent bo‘lib qoladi, chunki (19) seriya j^j funksiyasi uchun |z| > 1 farq qiladi. Shuning uchun /(z) funksiyani quyidagicha o'zgartiramiz: formula (19) ni yana qo'llagan holda, bu qator uchun yaqinlashishini olamiz. (18) va (21) kengaytmalarni (20) munosabatga almashtirib, c) -z funksiya uchun aylana tashqi tomonini |z| > 2 ajralish va funksiya uchun (21) qator /(z) funksiyani quyidagi ko‘rinishda ifodalaymiz: /<*> Formulalardan (18) va (19) foydalanib, biz OR 1 ni olamiz. Ushbu misol bir xil f(z) funksiyasi uchun Loran kengayishi, umuman olganda, turli halqalar uchun boshqa shaklga ega ekanligini ko'rsatadi. 3-misol. Loran qatori funksiyasining 8-Loran qatorining parchalanishini toping. Izolyatsiya qilingan birlik nuqtalar va ularning A halqasimon mintaqadagi tasnifi f (z) funksiyaning tasvirini quyidagi ko‘rinishda qo‘llaymiz: va ikkinchi hadni o‘zgartiramiz. geometrik progressiya hadlari yig'indisi formulasini olamiz. Topilgan ifodalarni formulaga (22) almashtirsak, bizda 4-misol bor. Laurent qatoridagi funktsiyani ingichka zq = 0 qo'shnisiga kengaytiring. Har qanday kompleks uchun , biz bor Let Bu kengayish har qanday z F 0 nuqtasi uchun amal qiladi. Bu holda, halqasimon mintaqa bitta tashqariga tashlangan z - 0 nuqtasi bo'lgan butun kompleks tekislikdir. Bu hududni quyidagi munosabat bilan aniqlash mumkin: Bu funksiya analitikdir. mintaqada Laurent seriyasining koeffitsientlari uchun formulalardan (13) oldingi banddagi kabi bir xil asoslar bilan Kouiw tengsizliklarini olish mumkin. agar f(z) funksiya aylana bilan chegaralangan bo‘lsa, bu erda M doimiy), u holda ajratilgan birlik nuqtalar Zo nuqta f(z) funksiyaning ajratilgan yagona nuqtasi deyiladi, agar nuqtaning halqasimon qo‘shnisi mavjud bo‘lsa. bu to'plam ba'zan 2o nuqtaning teshilgan qo'shnisi deb ham ataladi, bunda f(z) funksiya bir qiymatli va analitikdir. Zo nuqtaning o'zida funktsiya yo aniqlanmagan yoki bitta qiymatli va analitik emas. Zo nuqtaga yaqinlashganda /(z) funksiyaning harakatiga qarab uch xil birlik nuqtalar ajratiladi. Izolyatsiya qilingan birlik nuqta deyiladi: 1) agar chekli bo'lsa, olib tashlanishi mumkin 2) agar pmusach bo'lsa, 3) f(z) funksiyaning chegarasi bo'lmasa, mohiyatan yagona nuqta. Teorema 16. f(z) funksiyaning ajratilgan singulyar z0 nuqtasi, agar zo nuqta qo‘shnisidagi f(z) funksiyaning Loran kengayishi asosiy qismni o‘z ichiga olmasa, ya’ni, olib tashlanadigan singulyar nuqta hisoblanadi. Let zo shakliga ega - olinadigan yagona nuqta. U holda chekli mavjud bo'ladi va shuning uchun f(z) funksiya r nuqtaning prokologik qo'shniligida chegaralangan bo'ladi.Koshi tengsizliklari yordamida o'rnatamiz r ni biz xohlagancha kichik tanlash mumkin bo'lganligi sababli, u holda barcha manfiy darajalarda koeffitsientlar (z - 20) nolga teng: Aksincha, Loran funksiyasining kengayishi /(r) zq nuqtasining qo'shnisida faqat to'g'ri qismni o'z ichiga oladi, ya'ni u (23) ko'rinishga ega bo'lsin. va shuning uchun Teylor. z -* z0 uchun /(r) funksiya chegaraviy qiymatga ega ekanligini ko‘rish oson: 17-teorema. f(z) funksiyaning zq ajratilgan singulyar nuqtasi J(z) funksiya bo‘lgandagina olib tashlanishi mumkin. nuqta zq ba'zi teshilgan mahallada chegaralangan, Zgmechai emas. r0 f(r) ning olinadigan yagona nuqtasi bo'lsin. Faraz qilsak, f(r) funksiya th nuqtada markazlashgan qaysidir doirada analitikdir. Bu nuqta nomini belgilaydi - bir martalik. Teorema 18. f(z) funksiyaning ajratilgan zq nuqtasi qutb hisoblanadi, agar f(z) funksiyaning Loran kengayishining asosiy qismi nuqta qo‘shnisida chekli (va musbat) sonni o‘z ichiga olgan bo‘lsa. nolga teng bo'lmagan hadlar, ya'ni 4 ko'rinishga ega z0 qutb bo'lsin. O'shandan beri f(z) funksiya analitik va nolga teng bo'lmagan z0 nuqtasining teshilgan qo'shnisi mavjud. Keyin analitik funktsiya bu qo'shnilikda aniqlanadi va Demak, zq nuqta funktsiyaning olinadigan singulyar nuqtasi (nol) yoki h(z) analitik funktsiya, h(z0) ∩ 0. qo'shnilikda analitikdir. zq nuqtasini va demak, buni qayerdan olamiz Endi f(z) funksiya zo nuqtaning teshilgan qo'shnisida (24) ko'rinishdagi parchalanishga ega deb faraz qilaylik. Bu shuni anglatadiki, bu qo'shnilikda f(z) funksiya funktsiya bilan birgalikda analitikdir. g(z) funksiyasi uchun kengayish to'g'ri bo'ladi, shundan zq g(z) funksiyaning olinadigan singulyar nuqtasi ekanligi aniq bo'ladi va mavjud bo'ladi Keyin funksiya 0 ga intiladi - funktsiya qutbi Yana bitta oddiy narsa bor. haqiqat. Zq nuqta f(z) funktsiyaning qutbi bo'ladi, agar g(z) = y funksiyani g(z0) = 0 o'rnatish orqali zq nuqta qo'shnisidagi analitik funktsiyaga kengaytirish mumkin bo'lsa. f(z) funksiya qutbi jfa funksiyaning nol tartibi deyiladi. 16 va 18-teoremalar quyidagi tasdiqni bildiradi. Teorema 19. Izolyatsiya qilingan singulyar yupqa mohiyatan yagona hisoblanadi, agar bu nuqtaning teshilgan qo'shnisidagi Loran kengayishining asosiy qismi cheksiz ko'p nolga teng bo'lmagan hadlarni o'z ichiga olgan bo'lsa. Misol 5. Funksiyaning birlik nuqtasi zo = 0. Bizda Laurent Series Izolyatsiya qilingan yagona nuqtalar va ularning tasnifi bor. Shuning uchun zo = 0 olinadigan singulyar nuqtadir. Loran qatoridagi /(z) funksiyaning nol nuqtaga yaqin joyda kengayishi faqat to'g'ri qismni o'z ichiga oladi: 7-misol. f(z) = f(z) funksiyaning singulyar nuqtasi zq = 0. Bu funksiyaning haqiqiy va xayoliy o‘qlardagi xatti-harakatlarini ko‘rib chiqaylik: haqiqiy o‘qda x 0 da, xayoliy o‘qda Shuning uchun na chekli, na z -* 0 da f(z) cheksiz chegara mavjud emas. Demak, r0 = 0 nuqta f(z) funksiyaning mohiyatan birlik nuqtasidir. f(z) funksiyaning Loran kengayishini nol nuqtaga yaqin joyda topamiz. Har qanday kompleks C uchun biz o'rnatdik. Keyin Loran kengayishi z ning manfiy kuchiga ega bo'lgan cheksiz sonli atamalarni o'z ichiga oladi.

Ta'rif. Funktsiyaning yagona nuqtasi deyiladi izolyatsiya qilingan, agar bu nuqtaning ba'zi qo'shnilarida analitik funktsiya (ya'ni halqadagi analitik) bo'lsa.

Funktsiyaning ajratilgan yagona nuqtalarini tasniflash bu funksiyaning bir nuqta qo'shnisidagi xatti-harakati bilan bog'liq.

Ta'rif. Nuqta deyiladi bir martalik da bu funksiyaning chekli chegarasi bo'lsa, funksiyaning yagona nuqtasi.

5-misol Funktsiyaning bir nuqtada olinadigan singulyarlikka ega ekanligini ko'rsating.

Yechim. Birinchi ajoyib chegarani eslab, biz hisoblaymiz

Demak, berilgan funksiya nuqtada olib tashlanishi mumkin bo'lgan yagonalikka ega.

Vazifa 4. Nuqta uchun olinadigan ekanligini ko'rsating.

Ta'rif. Nuqta deyiladi qutb funktsiyasi, agar bu funktsiya uchun cheksiz ortadi, ya'ni.

Analitik funksiyaning nol va qutb tushunchalari orasidagi bog‘lanishga e’tibor qarataylik. Funktsiyani sifatida ifodalaylik.

Agar nuqta funksiyaning oddiy noli bo‘lsa, funksiya oddiy qutbga ega bo‘ladi

Agar nuqta funktsiya uchun nol tartib bo'lsa, u holda funktsiya uchun u qutbdir buyurtma.

6-misol Funktsiya nuqtada uchinchi tartib qutbga ega ekanligini ko'rsating.

Yechim. Faraz qilsak, olamiz. Biz nolga moyil bo'lganimizdek, har qanday qonunga ko'ra, bizda . Keyin , va u bilan funktsiyaning o'zi cheksiz ortadi. Shuning uchun, , ya'ni birlik nuqta qutbdir. Funktsiya uchun bu nuqta uch karra nolga teng. Demak, bu funksiya uchun nuqta uchinchi tartibli qutbdir.

Vazifa 5. Nuqtaning oddiy qutbga ega ekanligini ko'rsating.

Ta'rif. Nuqta deyiladi asosan maxsus funktsiyaning nuqtasi, agar bu nuqtada funksiyaning na chekli, na cheksiz chegarasi bo'lmasa (funktsiyaning harakati aniqlanmagan).

Funktsiyaning muhim yagona nuqtasi bo'lsin. Keyin har qanday oldindan tayinlangan kompleks raqam uchun ga yaqinlashuvchi nuqtalar ketma-ketligi mavjud bo'lib, ular bo'ylab qiymatlar : ( Sochokki teoremasi).

7-misol Nuqtadagi funksiya muhim o‘ziga xoslikka ega ekanligini ko‘rsating.

Yechim. Berilgan funktsiyaning nuqta yaqinidagi xatti-harakatlarini ko'rib chiqing. Chunki haqiqiy o'qning musbat qismi bo'ylab (ya'ni ) bizda va ; agar haqiqiy o'qning salbiy qismi bo'ylab (ya'ni), u holda va . Shunday qilib, uchun hech qanday chegara yo'q. Ta'rifga ko'ra, funktsiya nuqtada muhim o'ziga xoslikka ega.

Funksiyaning noldagi harakatini Sochokki teoremasi nuqtai nazaridan ko‘rib chiqamiz. Nol va cheksizlikdan boshqa har qanday kompleks son bo'lsin.

Tenglikdan topamiz. Faraz qilsak, biz nuqtalar ketma-ketligini olamiz. Shubhasiz, . Bu ketma-ketlikning har bir nuqtasida funksiya ga teng va shuning uchun

Vazifa 6. Funktsiyaning bir nuqtada muhim birlikka ega ekanligini ko'rsating.

Cheksizlikdagi nuqta har doim funktsiya uchun maxsus hisoblanadi. Nuqta funktsiyaning ajratilgan singulyar nuqtasi deyiladi, agar bu funktsiyaning bosh markazida joylashgan aylanadan tashqarida boshqa yagona nuqta bo'lmasa.

Izolyatsiya qilingan yagona nuqtalarning tasnifi, shuningdek, ish uchun kengaytirilishi mumkin.

8-misol Funktsiyaning cheksizlikda qo'sh qutbga ega ekanligini ko'rsating.

Yechim. Funktsiyani ko'rib chiqaylik, bu erda nuqta qo'shnisidagi analitik funktsiya va . Bu funktsiya cheksizlikda qo'sh nolga ega ekanligini anglatadi, lekin keyin funktsiya uchun nuqta qo'sh qutbdir.

9-misol Funktsiya cheksizlikda muhim birlikka ega ekanligini ko'rsating.

Yechim. Shunga o'xshash muammo pr.7da ko'rib chiqiladi. Cheksiz uzoq nuqtaga yaqin joyda funksiyaning harakatini ko'rib chiqing. Haqiqiy o'qning ijobiy qismi bo'ylab va haqiqiy o'qning salbiy qismi bo'ylab. Bu shuni anglatadiki, nuqtada funktsiyaning chegarasi yo'q va ta'rifga ko'ra, bu nuqta mohiyatan yagonadir.

Funktsiyaning bir nuqtadagi yagonaligining tabiati haqida xulosa chiqarish mumkin asosiy qismi Bu nuqta bir mahallada Laurent kengaytirish.

Teorema 1. Gap bo'lishi uchun bir martalik funktsiyaning yagona nuqtasi , tegishli Loran kengayishi zarur va etarli asosiy qismini o'z ichiga olmaydi.

Vazifa 6. Nuqtaning qo'shnisida funksiyaning Teylor kengayishidan foydalanib, uning nolga teng bo'lgan o'chiriladigan singulyarlikka ega ekanligini ko'rsating.

Teorema 2. Gap bo'lishi uchun qutb funktsiyalari , zarur va etarli bo'lishi uchun asosiy qismi mos keladigan Laurent kengayishi cheklangan sonli a'zolarni o'z ichiga olgan :

Eng yuqori salbiy atamaning soni qutb tartibini belgilaydi.

Bunday holda, funksiya sifatida ifodalanishi mumkin

bu yerda nuqtadagi funksiya analitik, , qutb tartibi.

10-misol Funktsiyaning nuqtalarda oddiy qutblari borligini ko'rsating.

Yechim. Keling, bir fikrni ko'rib chiqaylik. Biz 2-misolda olingan ushbu nuqtaga yaqin joyda ushbu funktsiyaning Laurent kengaytmasidan foydalanamiz:

Ushbu kengayishning asosiy qismidagi eng yuqori (va yagona) salbiy kuch birga teng bo'lgani uchun, nuqta bu funktsiyaning oddiy qutbidir.

Bu natijani boshqa yo'l bilan ham olish mumkin edi. Shaklda ifodalaymiz va qo'yamiz - bu nuqtada analitik bo'lgan funktsiya va . Demak, (8) tufayli bu funksiya nuqtada oddiy qutbga ega.

Boshqa usul: nuqtada oddiy nolga ega bo'lgan funksiyani ko'rib chiqing. Demak, bu nuqtada u oddiy qutbga ega.

Xuddi shunday funktsiyani , bu yerda va nuqtada funksiya analitik bo'lgan shaklda yozsak, nuqta funktsiyaning oddiy qutbi ekanligi darhol ayon bo'ladi.

Vazifa 7. Funktsiya nuqtada 2-tartibli qutbga va nuqtada 4-tartibli qutbga ega ekanligini ko'rsating.

Teorema 3. Gap bo'lishi uchun asosan maxsus funktsiyaning nuqtasi, bu zarur va etarli asosiy qismi nuqta bir mahallada Laurent kengaytirish cheksiz sonli a'zolarni o'z ichiga olgan .

11-misol. Funksiya nuqtasida birlik xususiyatini aniqlang

Yechim. Kosinusning taniqli kengayishida biz o'rniga quyidagilarni qo'yamiz:

Demak, nuqta qo'shnisida Loran kengayishi ko'rinishga ega

Bu erda to'g'ri qism bitta atamadir. Va asosiy qism cheksiz sonli atamalarni o'z ichiga oladi, shuning uchun nuqta mohiyatan birlikdir.

Vazifa 8. Bir nuqtada funktsiya muhim o'ziga xoslikka ega ekanligini ko'rsating.

Ba'zi funktsiyani ko'rib chiqing va uning Laurent kengayishini yozing:

Keling, o'rnini bosamiz, ammo nuqta nuqtaga o'tadi. Endi cheksiz nuqtaga yaqin joyda, biz bor

Yangi nomni joriy etish qoladi. olamiz

bu erda asosiy qism va cheksiz uzoq nuqta qo'shnisida funktsiyaning Loran kengayishining muntazam qismidir. Shunday qilib, funktsiyani nuqta qo'shnisida Loran kengayishida asosiy qism musbat darajalar qatori, to'g'ri qism esa manfiy darajalar qatoridir. Buni hisobga olgan holda

Biroq, birlik xususiyatini aniqlashning yuqoridagi mezonlari cheksiz uzoq nuqta uchun o'z kuchini saqlab qoladi.

12-misol. Funktsiyaning nuqtadagi birlik xususiyatini toping. , keyin bir nuqtada u izolyatsiyalanmagan bo'lib chiqishi mumkin.

15-misol Cheksiz uzoq nuqtadagi funksiya muhim birlikka ega. Funksiya uchun nuqta ajratilgan yagona nuqta emasligini ko'rsating.

Yechim. Funktsiya maxrajning nollarida, ya'ni , nuqtalarida cheksiz sonli qutblarga ega. Chunki , demak, har qanday mahallada qutblar joylashgan nuqta qutblar uchun chegara nuqtasidir.

yagona nuqta

matematikada.

1) F tenglama bilan berilgan egri chiziqning yagona nuqtasi ( x, y) = 0, - nuqta M 0 ( x 0 , y 0), bunda F funktsiyaning ikkala qisman hosilalari ( x, y) yo'qoladi:

Agar qo'shimcha ravishda F funktsiyasining barcha ikkinchi qisman hosilalari bo'lmasa ( x, y) nuqtada M 0 nolga teng, u holda O. t. qoʻsh deyiladi. Agar M 0 nuqtada birinchi hosilalarning yoʻqolishi bilan birga ikkinchi hosilalarning hammasi ham yoʻqolib ketsa, lekin uchinchi hosilalarning hammasi ham nolga teng boʻlmasa, O. t. uchlik deyiladi va hokazo. Qoʻsh O. t. yaqinidagi egri chiziq tuzilishini oʻrganishda ifoda belgisi muhim rol oʻynaydi.

Agar D > 0 boʻlsa, O. t. ajratilgan deyiladi; masalan, egri chiziq y 2 - x 4 + 4x 2= 0 kelib chiqishi izolyatsiya qilingan O. t. (qarang guruch. bitta ). Agar D x 2 + y 2 + a 2) 2 - 4a 2 x 2 - a 4= 0 koordinatalarning kelib chiqishi tugun O. t. (qarang guruch. 2 ). Agar D = 0 boʻlsa, O. t. egri chizigʻi yo izolyatsiya qilingan yoki egri chiziqning turli shoxlari shu nuqtada umumiy tangensga ega boʻlishi bilan tavsiflanadi, masalan: tangens va egri chiziq kabi nuqta hosil qiladi. y 2 - x 3= 0 (qarang guruch. 3 , a); b) 2-turdagi cho'qqi - egri chiziqning turli shoxlari egri chiziq kabi umumiy tangensning bir tomonida joylashgan. (y - x 2)2 - x 5= 0 (qarang guruch. 3 , b); c) o'z-o'zidan aloqa nuqtasi (egri chiziq uchun y 2 - x 4= 0 kelib chiqishi - o'z-o'zidan aloqa qilish nuqtasi; (sm. guruch. 3 , v). Koʻrsatilgan O. t. bilan bir qatorda maxsus nomli boshqa O. t.lar ham koʻp; Masalan, asimptotik nuqta cheksiz sonli burilishli spiralning cho'qqisidir (2-rasmga qarang). guruch. 4 ), uzilish nuqtasi, burchak nuqtasi va boshqalar.

2) Differensial tenglamaning yagona nuqtasi - bu differentsial tenglamaning o'ng tomonidagi pay va maxraj bir vaqtning o'zida yo'q bo'lib ketadigan nuqtadir (Differensial tenglamalarga qarang).

bu yerda P va Q uzluksiz differentsiallanuvchi funksiyalardir. O. t.ni koordinatalar boshida joylashgan deb hisoblab, Teylor formulasidan (Teylor formulasiga qarang) foydalanib, (1) tenglamani koʻrinishda ifodalashimiz mumkin.

bu erda P 1 ( x, y) va Q 1 ( x, y) ga nisbatan cheksiz kichikdir

Yaʼni, agar l 1 ≠ l 2 va l 1 l 2 > 0 yoki l 1 = l 2 boʻlsa, O. t. tugun; tugunning etarlicha kichik qo'shnisi nuqtalaridan o'tadigan barcha integral egri chiziqlar unga kiradi. Agar l 1 ≠ l 2 va l 1 l 2 i b, a ≠ 0 va b ≠ 0 bo‘lsa, O. t. fokus; Fokusning etarlicha kichik qo'shnisidagi nuqtalardan o'tadigan barcha integral egri chiziqlar fokusning har qanday o'zboshimchalik bilan kichik mahallasida cheksiz sonli burilishli spiraldir. Agar, nihoyat, l 1,2 = ± bo'lsa i b, b ≠ 0, u holda O. t.ning xarakteri P ning kengayishlarida chiziqli hadlar bilan aniqlanmaydi ( x, y) va Q ( x, y), yuqoridagi barcha holatlarda bo'lgani kabi; bu yerda O. t. fokus yoki markaz boʻlishi yoki murakkabroq xarakterga ega boʻlishi mumkin. Markazning qo'shnisida barcha integral egri chiziqlar yopiq bo'lib, ularning ichida markazni o'z ichiga oladi. Masalan, nuqta (0, 0) tenglamalar uchun tugundir da" = 2u/x(l 1 = 1, l 2 = 2; qarang guruch. 5 , a) va y" = u/x(l 1 = l 2 = 1; qarang guruch. 5 , b), tenglama uchun egar y" = -y/x(l 1 = -1, l 2 = 1 ; sm. guruch. 6 ), tenglama uchun fokus y" =(x + y) / (x - y) (l 1 = 1 - i, l 2 = 1 + i; sm. guruch. 7 ) va tenglama markazi y" = -x / y(l 1 = -i, l 2 = i; sm. guruch. sakkiz ).

Agar x, y) va Q ( x, y) analitik boʻlib, yuqori tartibli O. t.ning qoʻshnisini mintaqalarga boʻlish mumkin: D 1 - integral egri chiziqlar bilan toʻldirilgan, ikkala uchi O. t.ga (elliptik mintaqalar) kiradi, D 2 - toʻldirilgan. integral egri chiziqlar bilan, bir uchi O. t.ga kiradi (parabolik mintaqalar) va D 3 - O. t.ga kiruvchi ikkita integral egri chiziq bilan chegaralangan hududlar, ular orasida giperbolalar tipidagi integral egri chiziqlar mavjud. (giperbolik hududlar) (qarang. guruch. 9 ). Agar O. nuqtasiga kiruvchi integral egri chiziqlar boʻlmasa, O. nuqtasi barqaror tipdagi nuqta deyiladi. Turgʻun O. t.ning qoʻshnisi yopiq integral egri chiziqlardan iborat boʻlib, ular oʻrtasida spirallar joylashgan (1-rasmga qarang). guruch. 10 ).

O. t. differensial tenglamalarini oʻrganish, yaʼni mohiyatan O. t. M. Lyapunov a, A. Puankare va boshqalar qoʻshnisidagi integral egri chiziqlar oilalarining xatti-harakatlarini oʻrganish).

3) Bir qiymatli analitik funksiyaning yagona nuqtasi funksiyaning analitikligi buzilgan nuqtadir (qarang. Analitik funksiyalar). Agar O. t mahallasi mavjud boʻlsa. a, boshqa O. t.dan ozod, keyin nuqta a ajratilgan O. t deyiladi. Agar a ajratilgan O.T va mavjud boʻlgan cheklangan O.T olinadigan O.T deb ataladi. a nuqtadagi funksiya taʼrifini mos ravishda oʻzgartirish (yoki funksiya umuman aniqlanmagan boʻlsa, shu nuqtada uni qayta belgilash), yaʼni sozlash. f(a)= b, erishish mumkin a tuzatilgan funksiyaning oddiy nuqtasiga aylanadi. Masalan, nuqta z= 0 f 1 funksiyasi uchun olinadigan O.T. z) = f(z), agar z≠ 0 va f 1(0),=1, nuqta z= 0 oddiy nuqta [ f 1 (z) nuqtada analitikdir z= 0]. Agar a- ajratilgan O. t. va a funktsiyaning qutb yoki ahamiyatsiz yagona nuqtasi deyiladi. f(z), agar Loran seriyasi) funksiyalarini bajarsa f(z) izolyatsiya qilingan O. t.ning mahallasida salbiy kuchlar mavjud emas z - a, agar a- olinadigan O. t., cheklangan miqdordagi salbiy kuchlarni o'z ichiga oladi z - a, agar a- qutb (bu holda, qutbning tartibi R a ning eng yuqori kuchi sifatida aniqlanadi - mohiyatan yagona nuqta. Masalan, funksiya uchun

p = 2, 3, …)

nuqta z= 0 - tartibning qutbi R, funksiya uchun

nuqta z= 0 muhim yagona nuqtadir.

Darajalar qatorining yaqinlashish doirasi chegarasida berilgan daraja qatori bilan shu doira ichida ifodalangan funksiyaning kamida bitta O. t.i boʻlishi kerak. Bir qiymatli analitik funktsiyaning mavjudlik sohasining barcha chegara nuqtalari (tabiiy chegara) bu funksiyaning chegara nuqtalari hisoblanadi. Shunday qilib, birlik doiraning barcha nuqtalari | z| = 1 funksiya uchun maxsus

Ko‘p qiymatli analitik funksiya uchun “O. T.” qiyinroq. Funksiyaning Riman sirtining alohida varaqlarida (yaʼni bir qiymatli analitik elementlarning O. t.i) O. t.dan tashqari har qanday tarmoqlanish nuqtasi ham funksiyaning O. t.si hisoblanadi. Riman sirtining ajratilgan tarmoq nuqtalari (yaʼni, ularning ayrim mahallalarida hech qanday bargda boshqa O.t. funksiyalari mavjud boʻlmagan tarmoq nuqtalari) quyidagicha tasniflanadi. Agar a chekli tartibli ajratilgan tarmoq nuqtasi bo'lsa va u erda chekli a mavjud bo'lsa, u tanqidiy qutb deb ataladi. Agar a cheksiz tartibli ajratilgan tarmoq nuqtasi va a transsendental O. t deyiladi. Boshqa barcha ajratilgan tarmoq nuqtalari kritik mohiyatan birlik nuqtalar deyiladi. Misollar: nuqta z= 0 - f funktsiyaning oddiy kritik nuqtasi ( z) = jurnal z va funksiyaning muhim muhim yagona nuqtasi f (z) = gunoh jurnali z.

Har qanday O. t., olinadiganidan tashqari, analitik davom etish uchun toʻsiq boʻladi, yaʼni olib tashlanmaydigan O. t.dan oʻtuvchi egri chiziq boʻylab analitik davom etish mumkin emas.

Buyuk Sovet Entsiklopediyasi. - M.: Sovet Entsiklopediyasi. 1969-1978 .

Boshqa lug'atlarda "Maxsus nuqta" nima ekanligini ko'ring:

Bu yerda ballar. Yakka nuqta (differensial tenglamalar) ga ham qarang. Matematikadagi xususiyat yoki oʻziga xoslik matematik obʼyekt (odatda funksiya) aniqlanmagan yoki tartibsiz xatti-harakatlarga ega boʻlgan nuqtadir (masalan, ... ... Vikipediya.

Analitik funksiya analitiklik shartlari buzilgan nuqtadir. Agar f(z) analitik funksiya hamma joyda z0 nuqtasining ba'zi qo'shnilarida aniqlangan bo'lsa ... Jismoniy entsiklopediya

Analitik funktsiya - bu funktsiyaning analitikligi buzilgan nuqta ... Katta ensiklopedik lug'at

yagona nuqta- — [Ya.N.Luginskiy, M.S.Fezi Jilinskaya, Yu.S.Kabirov. Elektrotexnika va energetika sanoatining inglizcha ruscha lug'ati, Moskva, 1999] Elektrotexnika mavzulari, asosiy tushunchalar EN yagona nuqta ... Texnik tarjimon uchun qo'llanma

1) f(z) analitik funksiyaning OT z kompleks o‘zgaruvchining f(z) funksiyasi elementining analitik davom etishiga shu o‘zgaruvchining tekisligidagi qaysidir yo‘l bo‘ylab to‘siq bo‘ladi. Analitik f(z) funksiya ba'zi ... ... bilan aniqlansin. Matematik entsiklopediya

Analitik funksiya, funksiyaning analitikligi buzilgan nuqta. * * * SINGULAR NOKTA analitik funksiyaning SINGULAR NOKTA, funksiyaning analitikligi buzilgan nuqta ... ensiklopedik lug'at

yagona nuqta- ypatingasis taškas statusas T sritis automatika atitikmenys: engl. yagona nuqta vok. singularer Punkt, m rus. yagona nuqta, fpranc. nuqta zarrasi, m; nuqta singulier, m … Automatikos terminų žodynas