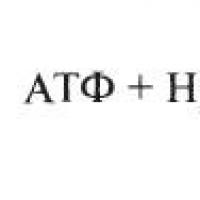Одной из отличительных черт бурного развития науки является широкое применение статистических методов и вычислительной техники в освоении информации. В настоящее время невозможно представить себе дисциплину, которая не пользовалась бы в процессе познания методами численного выражения закономерностей, связей, зависимости, измерения тенденции и т. д. Это, в частности, относится и к экономическим наукам.

В статистической литературе большое внимание уделяется изучению и применению отдельных статистических методов и приемов, но совсем недостаточно освещены вопросы целесообразности и последовательности использования того или иного статистического метода, их комплексного применения, сочетания различных методов. Абсолютизация того или иного метода исследования ничего, кроме вреда, не приносит. Только сочетание различных методов может дать заметный эффект. Именно с этих позиций и нужно оценивать роль и место статистического моделирования в системе познания различных процессов и явлений. В данной работе предпринята попытка систематизировать методику комплексного применения статистических методов в экономических исследованиях, рассмотрена целесообразность и последовательность использования статических методов и приемов при анализе статических и динамических процессов.

Первым этапом исследования является накопление (сбор) необходимых сведений об изучаемом объекте. Если наблюдений не очень много, то можно провести упорядочение, расположив их в порядке возрастания или убывания, т. е. построить ранжированные ряды. Если же наблюдений много, то приходится прибегать к их группировке. Статистические ряды носят самый разнообразный характер, имеют различное назначение и в разных целях могут использоваться в экономическом анализе. Одни статистические ряды являются вариационными рядами распределения. Эти ряды показывают распределение единиц изучаемой совокупности по отдельным группам, выделенным по какому-либо признаку. Другой разновидностью статистических рядов является последовательность чисел, отражающих величину того или иного показателя во времени. Это так называемые ряды динамики. Они позволяют анализировать изменение любых явлений во времени, об этом речь пойдет позже. Не умаляя значения временных рядов, следует отметить, что вариационным рядам распределения в статистическом анализе принадлежит особое место, ибо только при помощи распределения сложных совокупностей на качественно однородные группы можно изучать их структуру, соотношение между частями целого и т. п., без чего немыслим никакой экономический анализ. Ряды распределения могут строиться по качественным (атрибутивным) и по количественным признакам, по одному признаку и по нескольким, предоставляя тем самым широкие возможности исследователям при изучении сложных экономических явлений. Ряды распределения могут быть представлены либо в табличной форме, либо в геометрической, т. е. графической. Статистическая совокупность, представленная в виде ранжированного ряда распределения, графически изображается в виде огивы. Она строится так: на оси абсцисс наносятся номера элементов совокупности по ранжиру, а на оси ординат откладываются значения признака. Огива наглядно показывает интенсивность изменения изучаемого признака. Вариационные ряды распределения изображаются графически в виде полигонов и гистограмм. В виде полигонов обычно изображаются дискретные вариационные ряды распределения. При этом значения признака откладывают на оси абсцисс, а частоты (или частости) – на оси ординат. Вершины ординат соединяют прямыми линиями, в результате чего получают полигон (многоугольник). В виде полигона можно представить и интервальные вариационные ряды. Для этого за отдельные значения признака принимаются средние значения интервалов. Интервальные же вариационные ряды чаще всего изображают в виде гистограммы, в которой частоты выражают в виде прямоугольников соответствующей длины, а основания прямоугольников, опирающиеся на ось абсцисс, соответствуют интервалу значения признака (рис. 1).

Рис. 1. Гистограмма и полигон распределения

Различают одновершинные и многовершинные распределения. Многовершинность распределения, как правило, является признаком неоднородности изучаемой совокупности. Из разнообразия форм одновершинных кривых распределений можно выделить следующие наиболее характерные типы: симметричные, умеренно асимметричные, крайне асимметричные.

В практике обычно редко встречаются идеально симметричные распределения, чаще умеренно асимметричные, в которых частоты с одной стороны от центра рассеивания уменьшаются заметно быстрее, чем с другой. Асимметричное распределение в пределе становится крайне асимметричным – в этом случае наибольшая частота расположена на одном из концов распределения.

При решении некоторых вопросов удобнее пользоваться накопленными частотами распределения. Кривая накопленных частот распределения носит название «кумулята распределения». При построении кумуляты на оси абсцисс откладываются значения признака, на оси ординат – накопленные частоты. Построение вариационного ряда распределения и его графическое изображение позволяют получить первое представление о его наиболее характерных общих чертах. В то же время статистическое изучение совокупности не может ограничиться лишь простым упорядочением наблюдаемых величин. К тому же ряды распределения и их графики бывают довольно громоздкими, так как включают в себя всю исходную информацию. Поэтому наиболее рациональным путем статистического описания распределения будет вычисление определенных числовых характеристик, отражающих реальные свойства совокупности. К таким характеристикам прежде всего относятся характеристики центральной тенденции ряда распределения, т. е. нахождение его центрального значения; рассеивания значений признака относительно центра распределения; асимметрии и островершинности распределения. Изучение статистических характеристик распределений целесообразно начать с рассмотрения наиболее простых и в то же время чаще всего используемых в статистическом анализе, т. е. с изучения средних величин; затем научиться измерять вариацию, изучить меры скошенности и островершинности. Все эти показатели тех или иных особенностей распределения составляют единую систему статистических характеристик.

Однако применение тех или иных статистических методов предполагает прежде всего однородность изучаемой совокупности: нельзя, например, анализировать совокупность, состоящую из разных категорий хозяйств, включающую предприятия разной специализации и т. д. Для успешного решения задач необходимо глубокое понимание сущности изучаемого процесса или явления. Учитывая сложность, неоднородность экономических явлений и процессов, необходимо производить анализ таким образом, чтобы наиболее существенные различия между отдельными группами явлений не затушевывались, а выделялись для более успешного их изучения. В то же время объединение в группы сходных однотипных явлений помогает выявить их черты и особенности, которые при изучении каждого явления отдельно могут оставаться незамеченными. Выделение в каждой совокупности общественно/экономических типов явлений – главное условие ее научного анализа. А это можно осуществить, только применяя метод типологических группировок.

Массовые явления хозяйственной деятельности предприятий, являющиеся объектом статистического изучения, имеют сложный характер, обладают качественной общностью, свойственной данному явлению, но в то же время имеют и различия. Так, производством какой-либо продукции занимаются сельскохозяйственные предприятия и фермерские хозяйства и т. д. Стало быть, при характеристике производства данного вида продукции в регионе следует исходить из учета качественных особенностей предприятий, производящих эту продукцию, – в противном случае выводы будут неточными, а принимаемые на основании таких выводов решения – неэффективными.

Типологическая группировка данных – основной прием изучения экономических явлений, обеспечивающий качественную сопоставимость единиц совокупности и дающий возможность получения обобщенного количественного значения признака.

1.2. Методы измерения обобщающих характеристик совокупности

Метод группировок позволяет изучить состояние и взаимосвязи экономических явлений, если группы будут охарактеризованы показателями, раскрывающими наиболее существенные стороны изучаемого явления.

При анализе и планировании необходимо опираться не на случайные факты, а на показатели, выражающие основное, типичное, коренное. Такую характеристику дают различные виды средних величин, а также мода и медиана.

Вопрос об однородности совокупности не должен решаться формально по форме ее распределения. Его, как и вопрос о типичной средней, нужно решать, исходя из причин и условий, формирующих совокупность. Однородной является такая совокупность, единицы которой формируются под воздействием общих главных причин и условий, определяющих общий уровень данного признака, характерный для всей совокупности.

Согласно теории типологических группировок, решающее значение в оценке однородности совокупности принадлежит не форме распределения, а размеру вариации и условиям ее формирования. Для качественно однородной совокупности характерна вариация в определенных пределах, после чего начинается новое качество. Вместе с тем к этим границам для оценки качественной однородности совокупности надо подходить с точки зрения существа дела, а не формально, так как одно и то же количество в разных условиях выражает новое качество. Например, при одной и той же численности рабочих предприятия одних отраслей промышленности являются крупными, а других – мелкими.

Для всестороннего и углубленного изучения явлений, для объективной характеристики типов явлений, их взаимоотношений и процессов, обусловленных развитием системы как целого, необходимо сочетать групповые средние с общими средними. Сочетание таких средних и является одним из основных элементов анализа сложных систем. Это сочетание связывает в одно целое два органически дополняющих друг друга статистических метода: метод средних величин и метод группировки. При расчете средней индивидуальные варьирующие по группе значения заменяются одним средним значением. При этом случайные отклонения значения признака по отдельным единицам в сторону увеличения или уменьшения взаимно уравновешиваются и погашают друг друга, а в величине средней проявляется типичный размер признака, свойственный данной группе. Средняя величина служит характеристикой совокупности и в то же время относится к отдельному ее элементу – носителю качественных особенностей явления. Значение средней вполне конкретно, но одновременно и абстрактно; оно получено путем абстрагирования от случайного индивидуального по каждой единице с целью выявления того общего, типичного, что свойственно всем единицам и что формирует данную совокупность. При расчете средней величины численность единиц совокупности должна быть достаточно большой. Величина средней определяется как отношение общего объема явлений к числу единиц совокупности в группе. Для несгруппированных данных это будет средняя арифметическая простая:

а для сгруппированных данных, где каждое значение признака имеет свою частоту, – средняя арифметическая взвешенная:

где X i – значение признака; f i – частота этих значений признака.

Поскольку средняя арифметическая рассчитывается как отношение суммы значений признака к общей численности, она никогда не выходит за пределы этих значений. Средняя арифметическая обладает рядом свойств, которые широко используются в целях упорядочения расчетов.

1. Сумма отклонений индивидуальных значений признака от средней величины всегда равна нулю:

Доказательство. n

Разделив левую и правую часть на

2. Если значения признака (X i) изменить в k раз, то средняя арифметическая также изменится в x раз.

Доказательство.

Среднюю арифметическую из новых значений признака обозначим X, тогда:

Постоянную величину 1/k можно вынести за знак суммы, и тогда получим:

3. Если из всех значений признака X i вычесть или прибавить одно и то же постоянное число, то средняя арифметическая уменьшится или увеличится на эту величину.

Доказательство.

Средняя из отклонений значений признака от постоянного числа будет равна:

Точно так же доказывается это и в случае прибавления постоянного числа.

4. Если частоты всех значений признака уменьшить или увеличить в n раз, то средняя не изменится:

При наличии данных об общем объеме и известных значениях признака, но неизвестных частотах для определения среднего показателя используют формулу среднеарифметической взвешенной.

Например, имеются данные о ценах реализации капусты и общей выручке за различные сроки реализации (табл. 1).

Таблица 1.

Цена реализации капусты и общая выручка за различные сроки реализации

Так как средняя цена представляет отношение общей выручки к общему объему реализованной капусты, то вначале следует определить количество реализованной капусты по разным срокам реализации как отношение выручки к цене, а затем уже определить среднюю цену реализованной капусты.

В нашем примере средняя цена будет:

Если рассчитать в данном случае среднюю цену реализации по средней арифметической простой, то получим иной результат, который исказит истинное положение и завысит среднюю цену реализации, так как не будет учтен тот факт, что большая доля в реализации приходится на позднюю капусту с более низкой ценой.

Иногда требуется определить среднюю величину, когда значения признака даются в виде дробных чисел, т. е. обратных целым числам (например, при изучении производительности труда через обратный его показатель, трудоемкость). В таких случаях целесообразно использовать формулу средней гармонической:

Так, среднее время, необходимое для изготовления единицы продукции, есть средняя гармоническая. Если Х 1 = 1/4 часа, Х 2 = 1/2 часа, Х 3 = 1/3 часа, то средняя гармоническая этих чисел есть:

Для расчета средней величины из отношений двух одноименных показателей, например темпов роста, применяется средняя геометрическая, рассчитанная по формуле:

где Х 1 ? Х 2 … ? … Х 4 – отношение двух одноименных величин, например цепных темпов роста; n – численность совокупности отношений темпов роста.

Рассмотренные средние величины обладают свойством маорантности:

Пусть, например, имеем следующие значения Х (20; 40), тогда рассмотренные ранее виды средних величин будут равны:

При изучении состава совокупности о типичном размере признака можно судить по так называемым структурным средним – моде и медиане.

Модой называется наиболее часто встречающееся значение признака в совокупности. В интервальных вариационных рядах сначала находят модальный интервал. В найденном модальном интервале мода рассчитывается по формуле:

где Х 0 – нижняя граница модального интервала; d – величина интервала; f 1 , f 2 , f 3 – частоты предмодального, модального и послемодаль-ного интервалов.

Значение моды в интервальном ряду довольно просто можно отыскать на основе графика. Для этого в самом высоком столбце гистограммы от границ двух смежных столбцов проводят две линии. Из точки пересечения этих линий опускают перпендикуляр на ось абсцисс. Значение признака на оси абсцисс и будет модой (рис. 2).

Рис. 2

Для решения практических задач наибольший интерес представляет обычно мода, выраженная в виде интервала, а не дискретным числом. Объясняется это назначением моды, которая должна выявить наиболее распространенные размеры явления.

Средняя – величина, типичная для всех единиц однородной совокупности. Мода – тоже типичная величина, но она определяет непосредственно размер признака, свойственный хотя и значительной части, но все же не всей совокупности. Она имеет большое значение для решения некоторых задач, например для прогнозирования того, какие размеры обуви, одежды должны быть предназначены для массового производства, и т. д.

Медиана – значение признака, находящееся посредине ранжированного ряда. Она указывает на центр распределения единиц совокупности и делит ее на две равные части.

Медиана является лучшей характеристикой центральной тенденции, когда границы крайних интервалов открыты. Медиана является более приемлемой характеристикой уровня распределения и в том случае, если в ряду распределения имеются чрезмерно большие или чрезмерно малые значения, которые оказывают сильное влияние на среднюю величину, а на медиану – нет. Медиана, кроме того, обладает свойством линейного минимума: сумма абсолютных значений отклонений величины признака у всех единиц совокупности от медианы минимальная, т. е.

Это свойство имеет большое значение для решения некоторых практических задач – например, для расчета самого короткого из всех возможных расстояний для разных видов транспорта, для размещения станций техобслуживания таким образом, чтобы расстояние до всех обслуживаемых данной станцией машин было минимальным, и т. п.

При отыскании медианы сначала определяется ее порядковый номер в ряду распределения:

Далее, соответственно порядковому номеру, по накопленным частотам ряда находят саму медиану. В дискретном ряду – без всякого расчета, а в интервальном ряду, зная порядковый номер медианы, по накопленным частотам отыскивается медианный интервал, в котором путем простейшего приема интерполяции определяется уже значение медианы. Расчет медианы осуществляется по формуле:

где Х 0 – нижняя граница медианного интервала; d – величина интервала; f _ 1 – частота, накопленная до медианного интервала; f – частота медианного интервала.

Рассчитаем среднюю величину, моду и медиану на примере интервального распределения. Данные приведены в табл. 2.

Таким образом, в качестве центра распределения могут быть использованы различные показатели: средняя величина, мода и медиана,

и каждая из этих характеристик имеет свои особенности. Так, для средней величины характерно то, что все отклонения от нее отдельных значений признака взаимно погашаются, т. е.

Для медианы характерно то, что сумма отклонений индивидуальных значений признака от нее (без учета знаков) является минимальной. Мода же характеризует наиболее часто встречающееся значение признака. Поэтому в зависимости от того, какая из особенностей интересует исследователя, и должна выбираться одна из рассмотренных характеристик. В отдельных случаях рассчитываются все характеристики.

Их сравнение и выявление соотношений между ними помогает выяснить особенности распределения того или иного вариационного ряда. Так, в симметричных рядах, как в нашем случае, все три характеристики (средняя, мода и медиана) примерно совпадают. Чем больше расхождение между модой и средней величиной, тем более асимметричен ряд. Установлено, что для умеренно асимметричных рядов разность между модой и средней арифметической примерно в три раза превышает разность между медианой и средней арифметической:

Это соотношение можно использовать для определения одного показателя по двум известным. Из этого следует, что сочетание моды, медианы и средней важно и для характеристики типа распределения.

1.3. Методы исследования вариации и формы распределения признаков в однородной совокупности

Статистическое описание совокупности было бы неполным, если ограничиться лишь показателями центральной тенденции, т. е. средними величинами, модой и медианой, которые являются равнодействующими ряда изменяющихся значений признака. В одних случаях значение признака концентрируется возле некоторого центра очень тесно, в других случаях наблюдается значительное рассеивание, хотя средняя величина может быть одинаковой. В связи с этим средняя величина как показатель центральной тенденции не дает исчерпывающей характеристики изучаемой совокупности. Возникает необходимость изучения характера рассеивания признака. Хотя отклонения от средней и регулируются общими для всех единиц совокупности причинами, формирующими среднюю, но в то же время они обусловлены и индивидуальными причинами. Например, отклонения производительности труда отдельных рабочих, работающих в одной бригаде, а стало быть, находящихся в одинаковых условиях труда, вызваны не общими условиями и причинами, а индивидуальными обстоятельствами рабочих и их квалификацией, состоянием здоровья, настроением, сообразительностью и т. д. Поэтому изучение отклонений от средней их размеров и закономерности распределения представляет большой интерес для исследователя. Это важно прежде всего для оценки однородности совокупности, которую характеризует данная средняя величина, так как для качественно однородной совокупности характерна вариация в определенных границах. Стало быть, чем меньше вариация, тем качественно однороднее совокупность, тем типичнее и объективнее средняя величина, характеризующая ее.

Измерение вариации имеет большое значение и для изучения устойчивости изучаемых экономических явлений и процессов. Так, для сельского хозяйства очень важно не только получить среднюю урожайность сельскохозяйственных культур, но и обеспечить ее устойчивость во времени и пространстве, а для этого надо научиться рассчитывать показатели устойчивости, научиться измерять вариацию изучаемых явлений? ? 1,25а .

Для оценки вариации признака статистика знает и использует несколько показателей. Простейшим из них является размах вариации, рассчитываемый по формуле: X max – X min , т. е. как разность между максимальным и минимальным значением признака. Однако этот показатель далеко не совершенен, так как при его построении участвуют лишь крайние значения признака, которые могут быть случайными.

Более точно можно определить вариацию признака при помощи показателя, учитывающего отклонения всех значений признака от средней. Это так называемые абсолютные показатели: среднее линейное отклонение а и среднее квадратическое отклонение?. Среднее линейное отклонение – это средняя арифметическая из абсолютных значений отклонений отдельных значений признака от средней величины. Но сумма отклонений от средней

всегда равна нулю (одно из свойств средней величины), поэтому для расчета среднего линейного отклонения суммируют абсолютные отклонения без учета его знака:

Среднее квадратическое отклонение также может быть простое и взвешенное:

Среднее квадратическое отклонение является наиболее распространенным показателем вариации, оно несколько больше среднего линейного отклонения. Установлено, что в симметричных или умеренно асимметричных распределениях соотношение между ними можно записать в виде:

1,25а .

Следует иметь также в виду, что среднее линейное отклонение будет минимальным, если оно рассчитано от медианы, т. е.:

Среднее квадратическое отклонение минимально при вычислении его от средней арифметической, это же относится и к дисперсии, которая представляет собой квадрат среднего квадратического отклонения.

Дисперсия

широко применяется в дисперсионном анализе, но не как мера вариации, так как ее размерность не соответствует размерности признака.

Рассмотрим вычисление среднего линейного и среднего квадрати-ческого отклонения на примере данных, приведенных в табл. 3.

Таблица 3.

Анализ времени обработки деталей рабочими двух бригад

Средняя величина времени обработки детали составляет в обеих бригадах 124 мин. Для первой бригады Х 1 =992/8 = 124ми н. и для второй – Х 2 = 1240/10 = 124 мин.

Медианные значения также одинаковы в обеих бригадах. Так, для первой бригады Хме = (116+132)/2 = 124 мин. Для второй бригады – Хме = (122+126)/2 + 124 мин

Модальные значения в данном случае не могут быть определены, так как каждое из значений признаков не повторяется.

Исходя из полученных результатов, можно сделать вывод, что обе совокупности характеризуются одинаковыми показателями центра распределения, но они могут отличаться по характеру рассеяния отдельных значений признака вокруг этих центров.

Для характеристики рассеяния рассчитаем среднее линейное отклонение. Для первой бригады:

Сопоставление среднего линейного и среднего квадратического отклонений говорит о том, что вариации времени обработки деталей в первой бригаде значительно выше, чем во второй бригаде.

Следует также отметить, что среднее квадратическое отклонение в обоих случаях несколько больше, чем среднее линейное отклонение:

1 = 1,22а 1 ;

2 = 1,20а 2 .

Это говорит о том, что мы имеем дело с умеренно асимметричным распределением.

Рассмотренные показатели вариации (размах вариации, среднее линейное отклонение, среднее квадратическое отклонение) дают возможность сравнить степень однородности нескольких совокупностей, но в отношении лишь одного признака, поскольку это именованные величины, имеющие единицы измерения те же, что и сам признак.

Однако часто исследователю приходится сравнивать вариации различных признаков, а стало быть, эти показатели вариации не могут быть использованы.

Для характеристики вариации различных признаков рассчитывают относительные показатели вариации, приведенные к одному основанию, т. е. выраженные в процентах (доли размаха вариации, среднего линейного отклонения и среднего квадратического отклонения) от средней величины изучаемого признака.

Это так называемые коэффициент осцилляции, относительное отклонение и коэффициент вариации.

Коэффициент осцилляции рассчитывается по формуле:

В нашем примере эти показатели составляют:

Все рассчитанные относительные показатели вариации свидетельствуют также о более сильной вариации времени обработки деталей рабочими первой бригады по сравнению со второй, где среднее время обработки является более объективной, более типичной характеристикой работы данной бригады в целом, т. е. вторая бригада как совокупность более однородна.

Относительные показатели вариации, как уже было отмечено, позволяют сравнивать степень вариации признаков, имеющих одинаковые единицы измерения, но разные уровни средних. Например, урожайность зерновых культур и картофеля хотя и имеют одинаковые единицы измерения, но по абсолютным показателям вариации этих признаков сравнивать было бы неправильно, так как сами уровни урожайности зерновых и картофеля резко отличаются. Так, например, в регионе среднеквадратическое отклонение составило: по урожайности ржи – 5 центнеров с гектара (ц/га) и по урожайности картофеля – 20 ц/га, а сама урожайность ржи составила 25 ц/га, а картофеля – 200 ц/га. Коэффициент же вариации соответственно равен:

Это означает, что по урожайности картофеля совокупность хозяйств данной области более однородна, чем по урожайности ржи, т. е. урожайность картофеля более устойчива, чем урожайность ржи.

Сравнение абсолютных показателей вариации одного и того же признака разных совокупностей иногда приводит к иному выводу, чем при сопоставлении относительных показателей вариации.

Так, если в одной совокупности абсолютный показатель вариации больше, чем в другой, и средний уровень изучаемого признака в ней также значительно больше, чем в другой, то относительный показатель вариации может быть ниже.

Так, например, если среднее квадратическое отклонение урожайности ржи в одном районе составило 5 ц, в другом – 3 ц, а сама средняя урожайность, соответственно, составила 25 и 10 ц/га, то относительные показатели вариации приводят к иному выводу.

Следовательно, рост урожайности, связанный с некоторым повышением абсолютного показателя вариации, может и не снизить ее устойчивости.

Относительные показатели вариации необходимы также и для сравнения вариации различных признаков, имеющих разные единицы измерения, поскольку абсолютные показатели вариации в этом случае не могут быть использованы как мера вариации.

Например, при сравнении вариации урожайности и себестоимости той или иной культуры нельзя использовать абсолютные показатели вариации, так как они будут иметь разные единицы измерения: ц/га и руб. за 1 т. В этом случае целесообразно среднее квадратическое отклонение использовать для расчета так называемого нормированного отклонения:

характеризующее отклонение индивидуальных значений признака от средней (Xi ?X ) и приходящееся на единицу среднего квадратического отклонения. Нормированное отклонение позволяет сопоставлять между собой отклонения, выраженные в различных единицах измерения. Практически нормированные отклонения изменяются в пределах от 0 до 3.

Однако в совокупности могут встречаться отдельные единицы, у которых t > 3. Это будет свидетельствовать о неоднородности совокупности, и такие единицы совокупности целесообразно исключить как аномальные, нетипичные для данной совокупности.

Если совокупность мала (3 ? n ? 8), то однородность совокупности, т. е. проверку годности первичных данных, можно осуществить следующим образом. Вычисляют показатель, характеризующий отношение разности между сомнительным и соседним значениями ранжированного в порядке возрастания ряда к разности между крайними значениями, т. е.:

если вызывает сомнение первое в ряду значение признака, и:

если вызывает сомнение последнее в ряду значение признака.

Вычисленную величину Q сопоставляют с табличным ее значением для данного числа наблюдений и уровня вероятности. Если Q ф > Q табл, то сомнительное значение следует исключить из обработки. Если же Q ф < Q табл, то сомнительное значение не отбрасывается. Рассмотрим эту методику на примере.

Допустим, получены следующие результаты содержания золы в образцах корма в процентах: 2,25; 2,19; 2,11; 2,38; 2,32 и 3,21.

Располагаем данные анализа в порядке возрастания их значений: 2,11; 2,19; 2,25; 2,32; 2,38; 3,21.

Вычисляем:

Таблица 4. Значения Q в зависимости от степени надежности (p)

и общего числа значений признака (n)

Величина Q табл = 0,70. Следовательно, значение 3,21 должно быть исключено как нетипичное для данной совокупности.

При числе значений признака больше трех (и больше восьми) можно использовать другую методику определения пригодности первичных данных. По всем значениям признака в совокупности сначала рассчитывают среднюю величину (Х) и среднее квадратическое отклонение (?), затем на основании разницы (без учета знака) между максимально отклоняющимся значением (X max) и средней величиной находят величину критерия R max по формуле:

Значение R max сопоставляют с табличным его значением при данном числе значений признака для вероятности p = 0,99 (табл. 5).

Если R max > R табл, то сомнительное значение (X) следует исключить, если же R max < R табл, то значение (X max) следует принимать в расчет.

При n > 20 показатель R max ? 3 и условие пригодности имеет вид:

Таблица 5. Значения R max для степени надежности p = 0,99 в зависимости

от числа единиц совокупности n

Обратимся к предыдущему примеру и вычислим:

При расчете средней величины и среднего квадратического отклонения используют все значения признака. Затем рассчитываем:

Для n = 6, R табл _ 2,13; так как 2,22 > 2,13, то сомнительное значение 3,21 необходимо отбросить из статистической обработки. Если сомнение вызывает не одно, а несколько значений, то сначала производят указанные выше расчеты только для одного из них (наиболее отклоняющегося). После его исключения повторяют расчет для следующего сомнительного значения, вычисляя заново X и?.

При проверке годности данных с использованием любой методики может быть исключено не более одной трети единиц совокупности.

Если исключению подлежит более одной трети всех единиц совокупности, то данная совокупность считается неоднородной.

При изучении экономических явлений статистика встречается с разнообразной вариацией признаков, характеризующих отдельные единицы совокупностей. Величины признаков варьируют под воздействием различных причин и условий. Чем разнообразнее условия, влияющие на размер признака, тем больше его вариация.

Рассмотренные показатели центральной тенденции и показатели вариации представляют собой частные случаи некоторой единой системы статистических характеристик распределения. Такая единая система характеристик может быть представлена моментами статистического распределения. Если при вычислении моментов за произвольную постоянную принимается средняя арифметическая, то такие моменты называются центральными.

Общая формула центральных моментов k-го порядка имеет вид:

Иначе говоря, центральные моменты k-го порядка представляют собой среднюю арифметическую из k – x степеней отклонений значений признака от средней арифметической.

1. Центральный момент нулевого порядка равен единице при k = 0:

2. Центральный момент первого порядка равен нулю при k = 1:

3. Центральный момент второго порядка представляет собой дисперсию данного распределения при k = 2:

4. Центральный момент третьего порядка имеет вид:

Если распределение симметричное, то нетрудно видеть, что центральный момент третьего порядка равен нулю, так как минусовые отклонения (X i – X ) 3 в левой ветви распределения будут уравновешиваться положительными отклонениями в правой части. Такое взаимное погашение отклонений в симметричных рядах распределения сохраняет силу для всех нечетных центральных моментов.

Статистическая совокупность -

Совокупность называется однородной,

разнородной.

Вопрос 2. Признаки и их классификация

Признак - это качественная особенность единицы совокупности. По характеру отображения свойств единиц изучаемой совокупности признаки делятся на две основные группы;

признаки, имеющие непосредственное количественное выражение, например возраст, стаж работы, средний заработок и т. д. Они могут быть дискретными и непрерывными;

признаки, не имеющие непосредственного количественного выражения. В этом случае отдельные единицы совокупности различаются своим содержанием (например, отрасли - древесина, минеральные продукты, продтовары и т. д.). Такие признаки обычно называют атрибутивными (в философии «атрибут» - неотъемлемое свойство предмета).

Особенностью статистического исследования является то, что в нем изучаются только варьирующие признаки, т. е. признаки, принимающие различные значения (для атрибутивных признаков) или имеющие различные количественные уровни у отдельных единиц совокупности.

Вариация - это изменение величины либо значения признака при переходе от одного объекта (или группы объектов) к другому; точнее говоря - от одной единицы совокупности к другой. Обычно под вариацией мы понимаем обусловленное перекрещивающимся влиянием различных факторов на данное явление изменение величин только в пределах однородной совокупности.

Если же изменения изучаемого явления происходят в разные периоды времени, причем носят характер закономерности, то говорят уже не о вариации признака, а о его динамике.

Вопрос 3. Статистический показатель, система статистических показателей

Статистический показатель - это понятие (категория), отображающее количественные характеристики (размеры) соотношения признаков общественных явлений. Статистические показатели могут быть объемными (численность населения, объем продаж, товарооборот) и расчетными (средние величины). Они могут быть плановыми, отчетными и прогностическими (т.е. выступать в качестве прогнозных оценок). Статистические показатели следует отличать от статистических данных. Статистические данные - это конкретные численные значения статистических показателей. Они всегда определены не только качественно, но и количественно и зависят от конкретных условий места и времени.

Задачами статистики в этом направлении являются:

а) правильное определение содержания статистического показателя (валового национального продукта, национального дохода, экспорта, импорта и т. п.);

б) разработка методологии расчета статистического показателя.

Атрибуты статистического показателя:

1. Качественная сторона: объект, его свойство, категория.

2. Количественная сторона: число и единицы измерения.

3. Территориальные, отраслевые и иные границы объекта.

4. Интервал или момент времени.

Система статистических показателей - это совокупность статистических показателей, отражающая взаимосвязи, которые объективно существуют между явлениями. Для каждой общественно-экономической формации характерна определенная система взаимосвязи общественных явлений. Поэтому образуют систему и статистические показатели.

Система статистических показателей охватывает все стороны жизни общества на различных уровнях: страны, региона - макроуровень; предприятий, фирм, объединений и т. д. - микроуровень.

Системы статистических показателей имеют следующие особенности:

1) они носят исторический характер - меняются условия жизни населения, общества, меняются и системы статистических показателей;

2) методология расчета статистических показателей непрерывно совершенствуется.

Вопрос 4. Статистическая закономерность. Закон больших чисел

Статистическая закономерность – причинно-следственные связи, проявляющиеся в последовательности, повторяемости, регулярности массовых явлений и процессов общественной жизни, относящихся к определенному пространству и времени.
Закономерности, в которых необходимость неразрывно связана в каждом отдельном явлении со случайностью и лишь во множестве явлений проявляет себя как закон, называются статистическими.
Статистические закономерности обладают свойством устойчивости, т.е. стабильности и повторяемости при повторных наблюдениях.

Статистические закономерности изучают распределение единиц статистического множества по отдельным признакам под воздействием всей совокупности факторов.

Статистическая закономерность выступает как объективная закономерность сложного массового процесса и является формой причинной связи. Она обнаруживается в итоге массового статистического наблюдения. Этим обуславливается ее связь с законом больших чисел.

Статистическая закономерность с определенной вероятностью гарантирует устойчивость средних величин при сохранении постоянного комплекса условий, порождающих данное явление.

Свойство статистических закономерностей - проявляться лишь в массе явлений при обобщении данных по достаточно большому числу единиц, получило название закон больших чисел.

Закон больших чисел в наиболее простой форме гласит , что количественные закономерности массовых явлений отчетливо проявляются лишь в достаточно большом их числе.

Сущность - в числах, получающихся в результате массового наблюдения, выступают определенные правильности, которые не могут быть обнаружены в небольшом числе фактов.

Закон больших чисел выражает диалектику случайного и необходимого. В результате взаимопогашения случайных отклонений средние величины, исчисленные для величины одного и того же вида, становятся типичными, отражающими действия постоянных и существенных фактов в данных условиях места и времени.

Тенденции и закономерности, вскрытые с помощью закона больших чисел, имеют силу лишь как массовые тенденции, но не как законы для каждого отдельного случая.

Он характеризует лишь одну из форм проявления закономерностей в массовых количественных отношения х.

Так, цены на отдельные товары могут понижаться, на другие - повышаться, но совокупное изменение цен на все потребительские товары и услуги свидетельствует о неуклонном росте цен. Статистические совокупности часто называют массовыми явлениями.

Вопрос 7. Классификация стат.сводки и группировки.

Классификация сводки

от глубины обработки первичной информации , полученной в результате статистического наблюдения:

· простую;

· сложную.

Простая сводка предусматривает подсчет общих итогов по всей совокупности единиц статистического наблюдения. При этом определяется общий объем изучаемого явления.

Сложная сводка представляет собой комплекс процедур, которые включают группировку единиц совокупности, подсчет итогов характеристик единиц совокупности по каждой группе и по совокупности в целом, а также представление полученных результатов в виде статистических таблиц.

По признаку формы обработки информации :

· централизованную;

· децентрализованную.

Централизованная сводка предусматривает концентрацию всей исходной статистической информации в одном органе(Росстате, ФТС..), в котором он полностью обрабатывается При децентрализованной сводке обобщение исходных данных проводится последовательными этапами снизу доверху по иерархической системе (статистическая отчетность).

В зависимости от техники исполнения :

· автоматизированной

· ручной.

Классификация группировки

В зависимости от числа положенных в их основание признаков:

· простые

· многомерные (сложные)

Группировка, выполненная по одному признаку, называется простой.

Многомерная (сложная) группировка производится по двум и более признакам. Частным случаем многомер­ной группировки является комбинационная группировка, базирующаяся на двух и более признаках, взятых во взаи­мосвязи, в комбинации.

По отношениям между признаками:

· иерар­хические

· неиерархические

Иерархические группировки выполняются по двум и более признакам, при этом значения второго признака оп­ределяются областью значений первого (например, клас­сификация отраслей промышленности по подотраслям, товарных групп - по товарным позициям и т.д.).

Неиерархические (например, группировка по товарным группам в разрезе таможен или стран и т.д.).

По очередности обработки информации:

· п ервичные (составленные на основе первичных данных)

· и вторичные, являющиеся результатом перегруп­пировки ранее уже сгруппированных данных.

Статистические группировки и классификации делятпо преследуемым целям:

· типологическая, выделения качественно однородных совокупностей

· струк­турная, изучения структуры совокупности

· аналитическая (факторная) исследования существующих зависимостей

Вопрос 9. Ряды распределения. Атрибутивные и вариационные ряды распределения

Результаты сводки или группировки стат.наблюдения представляют собой статистические ряды рас­пределения .

При этом ряды распределения образованные по качественному признаку называют атрибутив.(напри­мер, распределение экспорта или импорта по товарным группам, по таможням, характеру сделки, категориям участни­ков ВЭД).

Если в качестве группировки выступает количе­ственный признак, то получается вариационный ряд распре­деления.

Атрибутивные ряды распределения

Изучение структуры в разрезе атрибутивных призна­ков целесообразно проводить по объемным показателям, таким как экспорт, импорт. Так, экспорт (импорт) можно подразделять по всем тем признакам, которые отражены в ГТД (товарные группы, страны, отрасли промышленнос­ти, таможенные режимы и т.д.).

Элементом структуры атрибутивного ряда являются группы значений, объединенных по качественному признаку (структура отраслей промышленности, страна, товарная по­зиция). Для более наглядного описания структуры ряда рас­пределения используют относительные величины (доли, %). Еще более наглядным является графическое изображение.

Пред­мет изучения вариационных рядов - подсчет частоты встречаемости значений исследуемого показателя и анализ частоты характеристик

Любой вариационный ряд состоит из элементов: ва­риантов и частот.

Вариантами (х) называются отдельные значения признака, которые он принимает в вариационном ряду, т.е. значения варьирующего признака.

Частоты (/) - это численность отдельных вариан­тов или каждой группы вариационного ряда, т.е. это чис­ла, показывающие, как часто встречаются те или иные ва­рианты в ряду распределения. Сумма всех частот определяет численность совокупности , ее объем. Например, при исследовании средней цены товара, частотой будет коли­чество килограммов товара, цена которого попадает в оп­ределенный интервал.

Частость, или относительная частота (м)-это от­ношение частоты к объему всей совокупности, т.е. часто­та, выраженная в процентах к итогу.

При проведении вариационного анализа исходные данные группируются в виде ряда распределения, рассчи­тываются статистические характеристики, описывающие форму распределения, строится его график. Затем делает­ся вывод о соотношении закономерности и случайности.

~В статистике вариационные ряды делятся на дискрет­ные, в которых значения признака выражены в виде изоли­рованных величин (чаще всего целых), и интервальные (не­прерывные), где значения признака заданы определенным интервалом. Например, участники ВЭД по товарообороту разделены на группы: 1000-10000 долл., 10000-20000 долл.

Статистическое распределение дискретного вариационного ряда - это перечень вариантов в возрастающем поряд­ке и соответствующих им частот (относительных частот).

Статистическое распределение непрерывного вариационного ряда - это последовательность интервалов в возрастающем порядке и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму вариантов, попавших в этот интервал)

Простые таблицы

Простые таблицы имеют в подлежащем перечень единиц совокупности, времени или территорий.

Групповые таблицы

Групповыми называются таблицы, имеющие в подлежащем группировку единиц совокупности по одному признаку.

Комбинационные таблицы

Комбинационные таблицы имеют в подлежащем группировку единиц совокупности по двум или более признакам.

По характеру разработки показателей сказуемого различают:

§ таблицы с простой разработкой показателей сказуемого, в которых имеет место параллельное расположение показателей сказуемого.

§ таблицы со сложной разработкой показателей сказуемого, в которых имеет место комбинирование показателей сказуемого: внутри групп, образованных по одному признаку, выделяют подгруппы по другому признаку.

Для достижения наибольшей выразительности статистической таблицы необходимо при ее оформлении придерживаться определенных правил

1 Форма статистической таблицы должна быть согласована с ранее существующими таблицами для обеспечения возможности сравнения данных за ряд отрезков времени

2 Название таблицы (общий заголовок) должна кратко и точно характеризовать основное ее содержание Это требование в равной степени касается и названий подлежащего и сказуемого таблицы Если общий заголовок недостаточно подробно сформулирован, то можно сделать примечания к нему.

3 В таблице должно быть указано, какой территории или какого периода или момента времени к приведенные данные, а также характер этих данных (фактич,норматив.,расчетные и т д.).

4 Показатели таблицы должны иметь единицы измерения

5 Все числовые значения данного показателя отмечаются с одинаковой точностью и др.

Относительные величины

Относительные величины представляют собой частное от деления двух величин и характеризуют количественное соотношение между ними.

При расчете относительных величин следует иметь в виду, что в числител е всегда находится показатель, отражающий то явление, которое изучается, а в знаменателе - показатель, с которым производится сравнение, принимаемый за основание или базу сравнения.

В завис-ти от базы сравнения- результат отношения может быть выражен в форме коэффициента или % .

Если значение основания или базы сравнения принимается за единицу (приравнивается к единице), то относительная величина (результат сравнения) является коэффициентом и показывает, во сколько раз изучаемая величина больше основания. (только если сравниваемая величина существенно больше той, с которой она сравнивается.) Если значение основания или базу сравнения принять за 100%, результат вычисления относительной величины будет выражаться также в %.

По своему значению они подразделяются на относительные величины структуры, сравнения, динамики, интенсивности, координации.

Относительные величины структуры характеризуют состав изучаемых совокупностей, исчисляются как отношение абсолютной величины каждого из элементов группировки к общему объему, т.е. как отношение части к целому. Сравнивая относительные величины структуры за разные периоды можно проследить структурные изменения. (Удел.вес (долю) экспорта и импорта в объеме внешнеторгового оборота…. а на долю экспорта – 3:4*100=75%).

Относительные величины сравнения отражают количественное соотношение одноименных показателей, т.е. показывают во сколько раз (или на сколько %) один показатель больше (меньше) другого. (коэффициент покрытия импорта экспортом. - экспорт превышает импорт в.=3 раза.)

Относительные величины динамики характеризуют изменение изучаемого явления во времени, т.е. показывают во сколько раз или на сколько %, уровень отчетного периода больше или меньше уровня базисного периода. (базис или цепной)

интенсивности - сколько единиц одной совокупности приходится на единицу другой. Рассчитываются делением абсолютной величины одной совокупности изучаемого явления на величину, характеризующую объем среды.(На 1 сотрудника в год пришлось – 500 деклараций).

координации - соотношение между отдельными частями стат. совокупности, и показывает во сколько раз сравниваемая часть больше или меньше части, которая принимается за базу сравнения. Относительная величина координации рассчитывается следующим образом.650: 6500= 10%, т.е. на 10 человек с высшим образованием приходится 1 чел. со средним техническим.

Средние величины

сглаживание различий в величине признака, которые возникают по тем или иным причинам. Средняя величина - один из распространенных способов обобщений количественных показателей.

Рассмотрим признак x (осредняемый признак) , по которому необходимо найти среднее значение . Значения осредняемого признака представлены рядом индивидуальных значений или вариант (х 1 , х 2 , х 3 ….х n) (например, вариационным рядом) с частотами индивидуальных значений (f 1 ,f 2 ,f 3 ,…f n) .

Сред. величина измер-ся в той же размер-ти, что и признак.

Каждая средняя величина характеризует изучаемую совокупность по какому-либо одному признаку.

суммарные

* средняя арифметическая;

* средняя геометрическая;

* средняя гармоническая;

Средняя арифметическая используется для характеристики абсолютных величин.

1. Если каждое значение признака в ряду встречается по одному разу, расчет производится по формуле простой (сумма всех значений, деленная на число этих значений
, где x 1 ,x 2 – знач-я признака (цена)

n - количество значений.

2. Если одно и то же значение признака встречается несколько раз, используют формулу средней арифметической взвешенной. ,

f i - частота повторения этого признака (вес товара).

Среднее арифметическое рассчитывается по разному в дискретных и интервальных вариационных рядах.

В дискретных рядах варианты признака умножаются на частоты, эти произведения суммируются и полученная сумма произведений делится на сумму частот.

В интервальных рядах значение признака задано в виде интервалов, поэтому нужно перейти к дискретному. В качестве вариантов X i используется середина соответствующих интервалов. - как полусумма нижней и верхней границ.

Средней гармонической величинойназывают величину, рассчитанную из обратных значений варьирующего признака. Она применяется и как обобщающая характеристика относительных величин.

Средняя гармоническая простая:

Средняя гармоническая взвешенная:

,

Средней геометрической принято именовать величину, исчисляемую как корень n –ной степени из произведения n отдельных вариантов признака.

Она также обычно используется для характеристики относительных величин и рассчитывается по формуле:

,

В случаях, когда некоторые либо все варианты (коэффициенты темпов роста, например) относятся к периодам, не одинаковым по продолжительности:

, (10.6)

где х - варианты; f i - веса; - сумма весов.

Определить длину интервала

(Хmаx - Хmin)/к

где Хmаx, Хmin - максимальное и минимальное значения показателя, соответственно;

к - число интервалов.

Вопрос 1. Статистическая совокупность. Однородность совокупности

Статистическая совокупность - это совокупность социально-экономических объектов или явлений общественной жизни, объединенных некоей качественной основой, общей связью, но отличающихся друг от друга отдельными признаками. Таковы, например, совокупность домохозяйств, совокупность семей, совокупность предприятий, фирм, объединений и т. п.. Совокупности могут быть однородными и разнородными.

Совокупность называется однородной, если один или несколько изучаемых существенных признаков ее объектов являются общими для всех единиц. Совокупность оказывается однородной именно с точки зрения этих признаков.

Совокупность, в которую входят явления разного типа, считается разнородной. Совокупность может быть однородна в одном отношении и разнородна в другом. В каждом отдельном случае однородность совокупности устанавливается путем проведения качественного анализа, выяснения содержания изучаемого общественного явления. Статистическая совокупность состоит из отдельных единиц (в статистике внешней торговли - отдельных партий товаров), имеющих свои свойства, особенности.

Единица совокупности- это первичный элемент статистической совокупности, являющийся носителем признаков, подлежащих регистрации, и основой ведущегося при обсле­довании счета.

Известно, что наличие в совокупности двух групп индивидуумов (например, мужчин и женщин), средние значения изучаемых признаков которых различаются между собой, может привести к ложной корреляции. Ложная корреляция возникает тогда, когда неоднородность проявляется по тем признакам, между которыми определяют связь. На проблему неоднородности указывал Коллер . Корреляция может быть вызвана, например, различием между полами, хотя при рассмотрении групп, состоящих только из мужчин или из женщин, связь между исследуемыми признаками отсутствует. На рис. 8.4 схематично изображен этот случай. Неоднородность данных может, наоборот, затушевать корреляцию или изменить ее знак.

Рис. 8.4. Схематичный пример возникновения корреляции из-за неоднородности данных. Между изучаемыми признаками и у как для группы мужчин, так и для группы женщин не существует связи. Но так как у группы мужчин все значения признаков и у больше, чем у женщин, то коэффициент корреляции, вычисленный в целом по обеим группам, получается значительным по величине

Так как факторный анализ исходит из корреляций между переменными, то неоднородность данных оказывает влияние также на факторное решение. На это обращал внимание уже Тэрстоун . Далее на нескольких примерах, сконструированных как модели, показывается влияние неоднородности на факторную структуру. Для этого привлекается числовой пример, с которым мы уже ранее имели дело (табл. 7.5 и 7.6).

К матрице данных рассмотренного примера добавляется вторая матрица с данными, представляющими результат наблюдения над теми же самыми 10 переменными у 200 индивидуумов. Определяется корреляционная матрица по всем данным. При этом переменные и 2-й группы наблюдений приводятся к стандартной форме. Среднее значение стандартизованных переменных равно нулю, а стандартное отклонение - единице. Коэффициенты корреляции между этими переменными равны коэффициентам корреляции, указанным в табл. 7.6, т. е. факторная структура двух корреляционных матриц известна, и они идентичны. Если ко всем значениям переменных второй группы данных прибавить постоянную величину, то их средние значения станут равными этой постоянной величине. Коэффициенты корреляции между переменными для этой группы данных не изменятся.

Если принять эту постоянную величину а равной 3, то объединенная совокупность данных будет отличаться своей неоднородностью. Можно показать, что если первоначальный коэффициент корреляции между двумя переменными, принадлежащими двум группам данных, равен , то коэффициент корреляции, вычисленный по объединенной совокупности данных при указанных выше условиях, будет равен

где являются постоянными, на величину которых смещаются средние значения переменных х и у. Через X и У обозначены переменные объединенной совокупности данйых. Введем новую переменную, обозначив ее через Y. Причем она будет принимать значение, равное нулю, для индивидуума, принадлежащего к первой группе данных, и принимать значение, равное единице, для индивидуума, принадлежащего ко второй группе данных . Коэффициент корреляции между этой новой переменной Y и переменной X для объединенной совокупности данных равен:

С помощью этих двух формул были вычислены соответствующие коэффиценты корреляции по элементам корреляционной матрицы, приведенной в табл. 7.6, причем вводились различные условия, вызывающие неоднородность данных. Затем по полученным корреляционным матрицам был проведен факторный анализ, включающий в себя варимакс-вращение, и было проведено сравнение с результатом варимакс-решения в табл. 7.5.

Пример 1. Прибавляем ко всем значениям первой переменной во второй группе данных постоянную . Коэффициенты корреляции между ней и другими переменными изменяются по сравнению со значениями, приведенными в табл. 7.6. В табл. 8.1 представлены лишь те коэффициенты корреляции, величина которых изменилась по сравнению с указанными в табл. 7.6.

Пример 2. Включаем в матрицу данных 11-ю переменную, чтобы проследить влияние неоднородности данных на факторное решение. Маркировочная переменная принимает значение, равное нулю, для индивидуума, принадлежащего к первой группе данных, и значение, равное единице, для индивидуума, принадлежащего ко второй группе данных.

Таблица 8.1. Коэффициенты корреляции, изменившиеся по сравнению с приведенными в табл. 7.6 из-за неоднородности данных

Коэффициенты корреляции между этой переменной и остальными переменными, вычисленными по выборке, состоящей из 400 индивидуумов, также указаны в табл. 8.1. Результаты факторизации корреляционных матриц этих двух примеров с применением варимакс-вращения приведены в табл. 8.4, где они противопоставлены первоначальному факторному решению, полученному по однородным данным. Если причиной неоднородности является преобразование одной переменной, то факторное отображение изменяется лишь постольку, поскольку общность этой переменной уменьшается. Лишь во втором примере маркировочная переменная 11 вызывает появление третьего фактора, фактора неоднородности, и значительно его нагружает. В то время как отдельные коэффициенты корреляции при введении неоднородности уменьшились, факторное отображение изменилось незначительно. Неоднородность, обусловленная новой переменной, вызвала появление нового фактора.

Пример 3. К значениям первых трех переменных второй матрицы исходных данных прибавляем постоянную , т. е. усиливаем неоднородность данных.

Пример 4. Дополнительно к условиям примера 3 вводим маркировочную переменную 11.

Корреляционная матрица этих двух примеров приведена в нижнем углу табл. 8.2. При сравнении с табл. 7.6. бросается в глаза, что из-за неоднородности данных некоторые коэффициенты корреляции изменяются очень сильно (например, коэффициент корреляции между 2-й и 3-й переменными изменил свое значение - 0,546 на + 0,524!). Несмотря на это, факторное отображение изменилось мало, что видно из табл. 8.4, так как наряду с неоднородностью еще действуют первоначальные связи между переменными и факторами. Но нагрузки переменных 1-3 на первый фактор уменьшились. В обоих последних примерах возникает третий фактор, вызванный неоднородностью данных. Он имеет значительные нагрузки от переменных 1-3, а также 11.

Примеры 5 и 6. К значениям первых пяти переменных прибавляем постоянную величину . Эти переменные нагружают первый фактор. Следовательно, неоднородность присуща тем переменным, которые определяют первый фактор. Такая ситуация осложняет обнаружение влияния неоднородности на этот фактор. В примере 6 дополнительно вводится маркировочная переменная. Корреляционная матрица для этих двух примеров приведена в правом верхнем углу табл. 8.2.

Таблица 8.2. Корреляционные матрицы для примеров 3 и 4 (в нижнем левом углу) и для примеров 5 и 6 (в верхнем правом углу)

(см. скан)

Из табл. 8.4 видно, что в результате процедур факторного анализа -деляются три фактора. Третий фактор определяется переменными 1-5 и его появление вызвано введением неоднородности. По сравнению с исходным факторным отображением нагрузки второго фактора остаются практически без изменения, а у некоторых нагрузок первого фактора изменяются знаки. Нагрузки факторов I и III от переменных 1-5 положительны и носят противоположный характер. Содержательная интерпретация первого фактора в данном примере вызвала бы значительные затруднения. Маркировочная переменная в примере 6 показывает, что неоднородность данных сыграла определенную роль в изменении нагрузок первого фактора.

Примеры 7 и 8. К значениям 1-й и 3-й переменных прибавляется постоянная к значениям 2-й переменной - постоянная Корреляционная матрица приведена в левом нижнем углу табл. 8.3. Некоторые коэффициенты корреляции в этой матрице значительно изменились по сравнению с элементами исходной матрицы и матрицы примеров 3 и 4. В примере 7 неоднородность данных полностью обусловливает появление третьего фактора, который имеет высокие положительные нагрузки от 1-й и 3-й переменных и высокую отрицательную нагрузку от 2-й переменной. Следовательно, неоднородность здесь выступает как отдельный фактор - фактор неоднородности 1. Маркировочная переменная показывает, что неоднородность данных почти не повлияла на факторы I и II.

Примеры 9 и 10. К значениям 1, 3 и 5-й переменных прибавляется постоянная а к значениям 2-й и 4-й переменных - постоянная Корреляционная матрица приведена в верхнем правом углу табл. 8.3. В этом случае фактор неоднородности совпадает с первым фактором. Следствием этого является усиление связи первых пяти переменных с первым фактором, и его нагрузки от этих переменных увеличиваются по сравнению с исходными. Структура фактора и знаки его нагрузок не изменяются. Факторное решение примера 10 после применения процедуры варимакс-вращения совпадает в основном с факторным решением примера 9 и из-за отсутствия места в таблице не приводится 2.

Приведенные примеры, в которых моделировалась неоднородность, позволяют сделать следующие выводы:

1. Неоднородность данных может привести к появлению фактора, обусловленного только этой неоднородностью Если он совпадает с каким-либо фактором, то нагрузки этого фактора увеличиваются по сравнению с исходными.

Таблица 8.3. Корреляционные матрицы для примеров 7 и 8 (в нижнем левом углу) и для примеров 9 и 10 (в верхнем правом углу)

(см. скан)

Таблица 8.4. Варимакс-решения, полученные для различных примеров

(см. скан)

Введение маркировочной переменной помогает выявить влияние фактора неоднородности.

2. Неоднородность данных изменяет факторное отображение. При больших изменениях в корреляционной матрице в факторном отображении совершенно неожиданно могут произойти лишь незначительные изменения. Факторный анализ менее чувствителен к влиянию неоднородности, чем отдельные коэффициенты корреляции, потому что неоднородность может появиться в факторном решении как отдельный фактор и его можно исключить. Но в некоторых случаях фактор неоднородности может совпадать с каким-либо действующим фактором. Тогда отображение этого фактора изменится.

3. Факторы, которые выделяются по матрице коэффициентов корреляций между переменными с помощью техники R, могут являться следствием как корреляции между переменными, так и неоднородностей в материале исследования. Это следует помнить при интерпретации факторов. Итак, имеются два типа факторов: факторы, которые определяются действием связей между переменными, и факторы, причиной которых является неоднородность данных. Кроме того, имеются смешанные факторы. В наших примерах процедуры факторного анализа осуществлялись вслепую, но мы смогли выявить все типы факторов и определить влияние неоднородности в каждом случае.

Если бы анализировались связи между индивидуумами по выборке переменных (т. е. использовалась бы техника Q для определения независимых друг от друга группировок индивидуумов), то результаты были бы аналогичные, а именно получили бы факторы, характеризующие различные группировки, и фактор, вызванный неоднородностью данных. Такой результат не является неожиданным, так как матрица исходных данных для обеих техник одна и та же. В зависимости от постановки задачи неоднородность может рассматриваться как фактор, искажающий результаты исследования, который нужно исключать, либо, наоборот, как фактор, вводимый специально для того, чтобы проследить изменение факторного решения. В любом случае неоднородность в данных не является препятствием проведения факторного анализа. Неоднородность как раз может быть выявлена благодаря факторному анализу и исключена из решения, особенно если для признака неоднородности подобрать маркировочную переменную. В принципе оба типа факторов всегда присутствуют в экспериментальном материале.

Для которой характерны принадлежность составных ее элементов к одному и тому же типу явления и сходство между элементами по существенным для данного исследования признакам.

Словарь бизнес-терминов. Академик.ру . 2001 .

Смотреть что такое "Совокупность Однородная" в других словарях:

СОВОКУПНОСТЬ, ОДНОРОДНАЯ - статистическая совокупность, для которой характерно принадлежность составных ее элементов к одному и тому же типу явления и сходство между элементами по существенным для данного исследования признакам. Статистическая совокупность может быть по… … Большой экономический словарь

Совокупность объектов или явлений общественной жизни, объединённых общей связью, но различающихся по ряду варьирующих признаков. Эти объекты или явления представляют собой элементы (единицы) С. с. Так, С. с. будет население, элементами… … Большая советская энциклопедия

однородная совокупность - (напр. ядерных энергетических установок) [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN homogeneous population … Справочник технического переводчика

Относительно однородная группа объектов или явлений, характеризующаяся наличием некоторых общих признаков и подвергающаяся изучению путем сбора количественных данных, их обработки и анализа … Большой медицинский словарь

множество - ▲ , совокупность однородный множество совокупность объектов, имеющих к л. общую характеристику; однородная совокупность; совокупность видов; неупорядоченная совокупность однородных попарно различных элементов; оно включает все такие элементы;… … Идеографический словарь русского языка

Лекция 1.3

РАЗВЕДОЧНЫЙ АНАЛИЗ ДАННЫХ

Основные узловые моменты разведочного анализа

Слайд 2

Цель разведочного анализа – представить наблюдаемые данные компактной и простой форме, позволяющей выявить имеющиеся в них закономерности и связи. Разведочный анализ включает преобразование данных и способы наглядного их представления, выявление аномальных значений, грубую оценку типа распределения, сглаживание.

Термин разведочный анализ применяется также в более широком смысле, чем предварительная обработка данных. Например, в многомерных процедурах, таких как факторный анализ, многомерное шкалирование данных, цель разведочного анализа, кроме анализа первичных данных, заключается в определении минимального числа факторов, которые удовлетворительно воспроизводят ковариационную (корреляционную) матрицу или матрицу близостей наблюдаемых переменных

Слайд 3

Согласно предыдущей лекции считаем, что у исследователя имеются наблюдения в виде матрицы «объект-признак» или вектора признака и частичное или полное отсутствие априорной информации о причинно-следственном механизме этих данных. При анализе обычно возникают следующие вопросы

1. Какой обработке подвергнуть наблюдения?

2. Какую модель выбрать?

3. Какие заключения можно сделать?

Для выбора способа обработки необходима модель наблюдаемых данных. Прежде чем произвести наблюдение необходимо указать природу и свойства измеряемой величины, т.е. использовать априорную информацию. Чем полнее априорная информация, тем точнее и с меньшими затратами можно получить необходимые результаты. Поэтому большое значение имеет формализация методов сбора, обработки и использования априорной информации. На основе анализа этой информации строится модель исследуемого явления, выбирается аппаратура, разрабатывается методика проведения эксперимента.

Слайд 4

Для получения более полной информации об изучаемом явлении проводится первичный анализ данных, получивший название разведочного анализа (Exploratory data analysis). Разведочный анализ необходим во всех случаях, за исключением лишь очень простых задач. Например, выбору семейства моделей исследуемого явления в большинстве случаев должен предшествовать предварительный и графический анализ данных. Для иллюстрации сказанного рассмотрим модель простой одномерной линейной регрессии. В соответствии с этой моделью предполагается, что наблюдения n пар (x 1 ,Y 1), …, (x n ,Y n ) можно описать уравнением

В качестве минимального предварительного анализа можно рассматривать график рассеяния точек (x j ,Y j ). В результате анализа графиков можно сделать заключение о постоянстве дисперсии Y i , о целесообразности преобразования переменных, выявить наличие аномальных наблюдений, для исключения которых необходимы специальные исследования. После такой обработки данных, предполагая, что верна модель (1), необходимо оценить параметры b 0 , b 1 и провести графический анализ остатков между наблюдаемыми и оцененными значениями Y i . На основе этого анализа можно подтвердить или предложить другую модель.

Слайд 5

Рассмотрим простейшие процедуры разведочного анализа, относящиеся к предварительной обработке данных . Они дополняют методы, изложенные в первой лекции при рассмотрении конкретных форм представления данных. Поясним необходимость проведения разведочного анализа на конкретных вопросах оценивания.

Оценка среднего . Рассмотрим простейший пример оценки истинного среднего m независимой случайной величины x по выборкеобъема n . Если вычислена оценка среднего, то возникает вопрос: «насколько сильно отличается оценка от ненаблюдаемого истинного значения?» Так как истинное значение m недоступно, то определяется доверительный интервал , который с заданной вероятностью накрывает истинное значение.

Отношение имеет t- распределение Стьюдента. Очень часто строят 95%-е доверительные интервалы, считая, что величина t распределена нормально. Для нормального распределения величина t будет равна 1,96, тогда как для t- распределения при числе степеней свободы v (v = n – 1), равных 1; 3 и 12, величина t , соответственно, равна 12,7; 4,3 и 2,18. Поэтому при малых объемах выборок использование нормального распределения вместо t- распределения приводит к большим ошибкам в интервальной оценке. Большое различие интервальных оценок связано с различием t- распределения от нормального в хвостах распределения.

Слайд 6

Хвосты реальных распределений имеют, как правило, больший разброс, чем у нормального распределения. Природа отличия реального распределения от нормального может быть различной:

1. Большинство измерений проводится в конкретных единицах, например, в миллиграммах, микронах, и их значения ограничены. Для нормального же закона распределения значения изменяются от – ¥ до + ¥.

2. Резкая асимметрия некоторых распределений (например,c 2 , F ) при малых выборках, обрывистые края у равномерного распределения.

3. Поведение на «хвостах» распределения. Одно или несколько резко выделяющихся значений от основной массы наблюдений могут существенно изменить среднее и катастрофически дисперсию. Неправдоподобные значения почти неизбежны в экспериментальных данных. Количество таких значений в медицинских данных достигает до 30%, а в специально поставленных экспериментах оно составляет около 1% от всех данных.

Оценка среднего среднеарифметическим имеет большие достоинства: несмещенность для генеральных совокупностей, имеющих математическое ожидание, достаточность, полнота и, соответственно, полная эффективность для нормального, пуассоновского, гамма-распределений и при достаточно широких условиях удобное асимптотически нормальное распределение, которое во многих случаях приближенно достигается уже при средних объемах выборок n . Имеются и недостатки такой оценки: эффективность ее равна нулю для равномерного распределения, а для некоторых выборок уже одно неправдоподобно большое наблюдение может сделать среднеарифметическую оценку бесполезной.

Слайд 7

Если нормальность распределения нарушается резко выделяющимися данными, то желательно применять робастные (robust – крепкий, здоровый, дюжий) оценки . Примером робастной оценки среднего, терпимой к отклонению хвостов распределения от нормального является медиана распределения. Она, как срединное значение наблюдений, не зависит от одного или нескольких неправдоподобно больших измерений.

Медиана, как робастная, не является эффективной оценкой относительно среднеарифметической оценки для нормального распределения.

Слайд 8

Мера разброса . На практике для характеристики величины разброса данных используются следующие меры: среднеквадратическое отклонение s или его квадрат – дисперсия s 2 , а также размах R. Оценки этих величин обозначают соответственно S , S 2 , R . Оценка разброса по S широко применяется, и оно полезно при линейных преобразованиях типа Y = b + aX. Для некоторых распределений s 2 = ∞, а размах применим; неправдоподобно большие отклонения в наблюдениях также могут сделать оценку дисперсии очень большой, что приводит к типу распределения, отличному от истинного.

Оценка разброса по выборочному размаху относится к быстрым процедурам. В связи с появлением быстродействующих ЭВМ вычислительные преимущества R по сравнению с S становятся все менее важными, но остаются преимущества, связанные с простотой вычисления R и возможностью для неспециалистов применять эту статистику. Так, размах практически совсем вытеснил S из систем контроля качества, в которых выборки малых объемов берутся через короткие интервалы времени и по средним значениям и размахам строятся контрольные карты.

Следует отметить, что размах можно использовать для распознавания больших неправдоподобных ошибок в вычислениях S для выборок из любой генеральной совокупности. Это следует из ограниченности отношения S/R .

Слайд 9

Подводя итог рассмотренным оценкам, необходимо сделать вывод, что имеются причины, чтобы не обрабатывать все данные одинаково. Прежде чем приступить к обработке наблюдений, необходимо проверить однородность выборки и, если она неоднородна, то разделить на слои. Наличие резко выделяющихся наблюдений также нарушает однородность выборки. В этом случае один из подходов базируется на обнаружении и удалении этих выделяющихся данных.

Удаление резко выделяющихся наблюдений обеспечивает безопасность оценки, однако обеспечивает эффективность только в случае определения четкой границы между удаленными и не удаленными данными. К явным резко выделяющимся данным примыкает зона «сомнительных» данных (рис. 1), которые не всегда можно распознать. Здесь легко допустить неправильные удаления и необоснованные сохранения, полной эффективности ожидать не приходится даже в идеале после удаления. Эти трудности можно преодолеть, применяя робастные методы оценивания. Робастные алгоритмы обеспечивают безопасность и эффективность оценивания при наличии резко выделяющихся и сомнительных данных.

Рис. 1. Плотность распределения. Разбиение данных на три группы.

Слайд 10

О качестве результатов Цель исследования – дать ответ на вопрос: можно полученные результаты применять на практике. Пригодность полученных результатов можно оценить методами перепроверок. Наиболее часто используются методики простой и двойной перепроверок.

Простая перепроверка. Проверка полученной модели проводится на данных, отличных от тех, по которым рассчитаны параметры модели. В этом случае можно выборку наблюдений делить на две (или больше) части. Одну часть используют для обработки, а другую – для проверки. После этого части можно менять местами, что может дать несколько больше информации, хотя здесь имеются определенные трудности, вытекающие из-за связи между двумя оценками качества модели.

Такую перепроверку можно осуществить и для многократного деления данных, например, можно выборку разделить на 10 равных частей. На любых 9 из них провести оценку модели, а на оставшейся одной части осуществить проверку. После этого повторить процедуру 9 раз, беря каждый раз новые 9 частей. В ряде случаев процедуру усложняют. Расчет осуществляют по всем данным без одного наблюдения, а проверку – на отброшенном значении. Расчеты повторяют для каждого из наблюдений выборки. Не следует обольщаться результатами простой проверки, так как контрольная выборка всегда будет больше похожа на рабочую, чем на выборку объектов, для которой будут использоваться результаты исследований.

Двойная перепроверка. Производится проверка на данных отличных, как от тех, по которым строилась модель, так и от тех, которые были использованы для расчета параметров модели. Медики такой метод проверки называют «дважды слепым». «Свежие данные» для перепроверки можно собирать после выбора модели и расчета параметров. Если получение таких данных невозможно, то можно обратиться к архивным данным при условии, что они оставались неизвестными, пока строилась модель и рассчитывались параметры этой модели. При двойной перепроверке важно, чтобы данные, используемые для проверки, являлись отличными от тех, по которым проводились оценки. Можно использовать данные разных лет, если они могут быть отнесены к одному времени, или данные других исследователей.

Слайд 11

Неоднородные выборки

Стандартные методы оценивания любой статистики выборочных данных построены на предположении, что выборка взята из однородной совокупности с простой структурой закона распределения. Между тем на практике выборки часто формируются под влиянием различных причин и условий, и они могут быть представлены в виде объединения некоторого множества однородных выборок, каждая из которых имеет простую структуру. Например, нельзя считать однородными доходы богатых и других граждан государства, так как они имеют различную экономическую основу; объекты различной стоимости, отличающиеся по народнохозяйственным последствиям . Примерами могут служить неоднородные последовательности динамических моделей в задачах анализа вибраций в машиностроении; сейсмограмм в геофизике; кардиограмм с нарушениями частоты биения сердца.

Природа неоднородности может быть различной. Например, возможны объединения из совокупностей с различными средними и дисперсиями или с одинаковыми средними, но с различными дисперсиями. Важный класс неоднородных выборок образуют также выборки, содержащие одно или несколько неправдоподобно больших или малых измерений . Обработка неоднородных

Пусть наблюдения состоят из трех однородных слоев, каждый из которых можно описать простой одномерной регрессией. Эти зависимости показаны на рис. 2, где прямые – линии регрессий каждой совокупности. Если обработать объединенную выборку этих совокупностей, то получим регрессионную зависимость, изображенную на рис. 2 пунктирной прямой. Очевидно, что регрессия по объединенным данным лишена всякого смысла.

Для определения однородности выборки необходим подробный содержательный анализ исследуемой совокупности. Этот анализ должен базироваться на существенном не случайном признаке, по которому исходная совокупность может быть представлена в виде объединения нескольких однородных совокупностей. Например, налоговые декларации можно разбить на группы по объемам доходов; учреждения – по числу служащих; фермы – по общей площади земель и валовым доходам. При разделении выборки на слои требуется ответить на вопросы, по какому признаку лучше производить расслоение, как определить границы между слоями, сколько должно быть слоев.

Слайд 12

Разделение неоднородной совокупности на однородные

Пусть выборка изучаемой совокупности x 1 , …, x n , содержит элементы двух независимых случайных величин с плотностями распределений f(x,q 1) и f(x,q 2). Обозначим через А – множество элементов выборки, принадлежащих к первой случайной величине, В – множество элементов выборки из второй совокупности. Требуется найти оценки 1 , 2 неизвестных параметров q 1 , q 2 и множества А и В. Для оценки этих четырех неизвестных используем метод максимума правдоподобия. Неизвестные q 1 , q 2 и А и В найдем из условия покоординатной максимизации функции правдоподобия

На каждом шаге максимизируется величина функции правдоподобия по одному из неизвестных . 1) < f(x i , 2),. Если f(x i , 1) = f(x i , 2), то оба варианта одинаково правдоподобны, что для непрерывных распределений является маловероятным событием. Далее берем следующий элемент и относим его в то или иное множество. Полученные множества сравниваем с множествами на предыдущем шаге. Если они отличаются, то переходим к шагу 2, в противном случае алгоритм останавливается, и задача считается решенной.

Недостатком алгоритма является то, что он останавливается на первом локальном максимуме функции правдоподобия. Частично этого недостаток можно избежать, решая задачу при различных начальных разбиениях на подмножества А и В. Если конечные результаты для нескольких начальных условий различны, то берется то решение, для которого значение функции правдоподобия больше. Отсюда следует, что приведенный алгоритм применим и для выборок, содержащих более двух слоев.