Udowodnić, że układ równań liniowych. Układ równań liniowych nazywa się określonym jeśli. Ochrona danych osobowych

Treść lekcji

Równania liniowe dwóch zmiennych

Uczeń ma 200 rubli na zjedzenie obiadu w szkole. Ciasto kosztuje 25 rubli, a filiżanka kawy kosztuje 10 rubli. Ile ciast i filiżanek kawy można kupić za 200 rubli?

Oznaczmy liczbę ciastek przez X i liczbę wypitych filiżanek kawy y. Następnie koszt ciastek będzie oznaczony wyrażeniem 25 X, a koszt filiżanek kawy w 10 y .

25X- cena X ciastka
10y — cena y filiżanki kawy

Całkowita kwota powinna wynosić 200 rubli. Następnie otrzymujemy równanie z dwiema zmiennymi X I y

25X+ 10y= 200

Ile pierwiastków ma to równanie?

Wszystko zależy od apetytu ucznia. Jeśli kupi 6 ciast i 5 filiżanek kawy, pierwiastkami równania będą liczby 6 i 5.

Mówi się, że para wartości 6 i 5 jest pierwiastkiem równania 25 X+ 10y= 200 . Zapisywane jako (6; 5), gdzie pierwsza liczba jest wartością zmiennej X, a drugi - wartość zmiennej y .

Liczby 6 i 5 nie są jedynymi pierwiastkami odwracającymi równanie 25 X+ 10y= 200 do tożsamości. W razie potrzeby za te same 200 rubli student może kupić 4 ciasta i 10 filiżanek kawy:

W tym przypadku pierwiastki równania 25 X+ 10y= 200 to para wartości (4; 10).

Co więcej, uczeń może w ogóle nie kupować kawy, ale kupować ciasta za całe 200 rubli. Następnie pierwiastki równania 25 X+ 10y= 200 będzie wartością 8 i 0

Lub odwrotnie, nie kupuj ciast, ale kup kawę za całe 200 rubli. Następnie pierwiastki równania 25 X+ 10y= 200 wartości będą wynosić 0 i 20

Spróbujmy wypisać wszystkie możliwe pierwiastki równania 25 X+ 10y= 200 . Umówmy się, że wartości X I y należą do zbioru liczb całkowitych. I niech te wartości będą większe lub równe zero:

X∈Z, y∈ Z;
x ≥ 0, y ≥ 0

Będzie to wygodne dla samego ucznia. Wygodniej jest kupować całe ciasta niż na przykład kilka całych ciast i połowę ciasta. Wygodniej jest też pić kawę w całych filiżankach niż np. kilka całych filiżanek i pół filiżanki.

Zauważ, że to dziwne X w żadnych okolicznościach niemożliwe jest osiągnięcie równości y. Następnie wartości X kolejne liczby będą wynosić 0, 2, 4, 6, 8. I wiedza X można łatwo określić y

W ten sposób otrzymaliśmy następujące pary wartości (0; 20), (2; 15), (4; 10), (6; 5), (8; 0). Pary te są rozwiązaniami lub pierwiastkami równania 25 X+ 10y= 200. Zamieniają to równanie w tożsamość.

Równanie postaci topór + by = c zwany równanie liniowe z dwiema zmiennymi. Rozwiązaniem lub pierwiastkami tego równania jest para wartości ( X; y), co czyni ją tożsamością.

Należy również zauważyć, że jeśli równanie liniowe z dwiema zmiennymi jest zapisane w postaci topór + b y = do , potem mówią, że jest to zapisane kanoniczny(normalna) forma.

Niektóre równania liniowe dwóch zmiennych można sprowadzić do postaci kanonicznej.

Na przykład równanie 2(16X+ 3y- 4) = 2(12 + 8X − y) można przywołać na myśl topór + by = c. Otwórzmy nawiasy po obu stronach tego równania i otrzymajmy 32X + 6y − 8 = 24 + 16X − 2y . Terminy zawierające niewiadome grupujemy po lewej stronie równania, a wyrazy wolne od niewiadomych po prawej. Wtedy otrzymamy 32x− 16X+ 6y+ 2y = 24 + 8 . Przedstawiamy podobne wyrazy po obu stronach, otrzymujemy równanie 16 X+ 8y= 32. Równanie to sprowadza się do postaci topór + by = c i jest kanoniczny.

Równanie 25 omówione wcześniej X+ 10y= 200 jest także równaniem liniowym z dwiema zmiennymi w postaci kanonicznej. W tym równaniu parametry A , B I C są równe odpowiednio wartościom 25, 10 i 200.

Właściwie równanie topór + by = c ma niezliczoną ilość rozwiązań. Rozwiązanie równania 25X+ 10y= 200, szukaliśmy jego pierwiastków tylko na zbiorze liczb całkowitych. W rezultacie otrzymaliśmy kilka par wartości, które zamieniły to równanie w tożsamość. Ale na zbiorze liczb wymiernych równanie 25 X+ 10y= 200 będzie miało nieskończenie wiele rozwiązań.

Aby uzyskać nowe pary wartości, należy przyjąć dowolną wartość X, następnie ekspres y. Weźmy na przykład zmienną X wartość 7. Następnie otrzymujemy równanie z jedną zmienną 25×7 + 10y= 200 w którym można wyrazić y

Pozwalać X= 15. Następnie równanie 25X+ 10y= 200 staje się 25 × 15 + 10y= 200. Stąd to znajdujemy y = −17,5

Pozwalać X= −3 . Następnie równanie 25X+ 10y= 200 staje się 25 × (-3) + 10y= 200. Stąd to znajdujemy y = −27,5

Układ dwóch równań liniowych z dwiema zmiennymi

Dla równania topór + by = c możesz przyjmować dowolne wartości tyle razy, ile chcesz X i znajdź wartości dla y. Wzięte osobno, takie równanie będzie miało niezliczoną ilość rozwiązań.

Ale zdarza się również, że zmienne X I y połączone nie jednym, ale dwoma równaniami. W tym przypadku tworzą one tzw układ równań liniowych na dwie zmienne. Taki układ równań może mieć jedną parę wartości (czyli inaczej: „jedno rozwiązanie”).

Może się również zdarzyć, że system nie będzie miał żadnych rozwiązań. Układ równań liniowych może mieć niezliczoną ilość rozwiązań w rzadkich i wyjątkowych przypadkach.

Dwa równania liniowe tworzą układ, gdy wartości X I y wprowadź do każdego z tych równań.

Wróćmy do pierwszego równania 25 X+ 10y= 200 . Jedną z par wartości tego równania była para (6; 5). To przypadek, gdy za 200 rubli można było kupić 6 ciast i 5 filiżanek kawy.

Sformułujmy problem tak, aby para (6; 5) stała się jedynym rozwiązaniem równania 25 X+ 10y= 200 . Aby to zrobić, utwórzmy kolejne równanie, które łączyłoby to samo X ciasta i y filiżanki kawy.

Podajmy treść problemu w następujący sposób:

„Student kupił kilka ciast i kilka filiżanek kawy za 200 rubli. Ciasto kosztuje 25 rubli, a filiżanka kawy kosztuje 10 rubli. Ile ciastek i filiżanek kawy kupił uczeń, jeśli wiadomo, że liczba ciastek jest o jedną jednostkę większa od liczby filiżanek kawy?

Mamy już pierwsze równanie. To jest równanie 25 X+ 10y= 200 . Utwórzmy teraz równanie warunku „liczba ciast jest o jedną jednostkę większa niż liczba filiżanek kawy” .

Liczba ciastek jest X, a liczba filiżanek kawy wynosi y. Możesz zapisać to zdanie, korzystając z równania x-y= 1. To równanie będzie oznaczać, że różnica między ciastami i kawą wynosi 1.

x = y+ 1 . To równanie oznacza, że ​​liczba ciast jest o jeden większa niż liczba filiżanek kawy. Dlatego, aby uzyskać równość, do liczby filiżanek kawy dodaje się jedną. Można to łatwo zrozumieć, jeśli zastosujemy model skal, który rozważaliśmy podczas badania najprostszych problemów:

Mamy dwa równania: 25 X+ 10y= 200 i x = y+ 1. Ponieważ wartości X I y, czyli 6 i 5 są zawarte w każdym z tych równań, wówczas razem tworzą system. Zapiszmy ten system. Jeżeli równania tworzą układ, wówczas są one otoczone znakiem układu. Symbolem systemowym jest nawias klamrowy:

Rozwiążmy ten system. Pozwoli nam to zobaczyć, jak dochodzimy do wartości 6 i 5. Istnieje wiele metod rozwiązywania takich układów. Przyjrzyjmy się najpopularniejszym z nich.

Metoda substytucyjna

Nazwa tej metody mówi sama za siebie. Jego istotą jest podstawienie jednego równania na drugie, po uprzednim wyrażeniu jednej ze zmiennych.

W naszym systemie nic nie trzeba wyrażać. W drugim równaniu X = y+ 1 zmienna X już wyrażone. Ta zmienna jest równa wyrażeniu y+ 1 . Następnie możesz zastąpić to wyrażenie pierwszym równaniem zamiast zmiennej X

Po podstawieniu wyrażenia y Zamiast tego + 1 do pierwszego równania X, otrzymujemy równanie 25(y+ 1) + 10y= 200 . Jest to równanie liniowe z jedną zmienną. Równanie to jest dość łatwe do rozwiązania:

Znaleźliśmy wartość zmiennej y. Podstawmy teraz tę wartość do jednego z równań i znajdźmy wartość X. W tym celu wygodnie jest użyć drugiego równania X = y+ 1 . Podstawmy do niego wartość y

Oznacza to, że para (6; 5) jest rozwiązaniem układu równań, zgodnie z naszym zamierzeniem. Sprawdzamy i upewniamy się, że para (6; 5) spełnia układ:

Przykład 2

Podstawmy pierwsze równanie X= 2 + y do drugiego równania 3 x− 2y= 9. W pierwszym równaniu zmienna X równe wyrażeniu 2 + y. Zamiast tego podstawmy to wyrażenie do drugiego równania X

Teraz znajdźmy wartość X. Aby to zrobić, podstawimy wartość y do pierwszego równania X= 2 + y

Oznacza to, że rozwiązaniem układu jest wartość pary (5; 3)

Przykład 3. Rozwiąż następujący układ równań metodą podstawieniową:

Tutaj, w przeciwieństwie do poprzednich przykładów, jedna ze zmiennych nie jest wyrażona wprost.

Aby zastąpić jedno równanie drugim, najpierw potrzebujesz .

Wskazane jest wyrażenie zmiennej, która ma współczynnik jeden. Zmienna ma współczynnik jeden X, co jest zawarte w pierwszym równaniu X+ 2y= 11. Wyraźmy tę zmienną.

Po wyrażeniu zmiennym X, nasz system przyjmie następującą postać:

Teraz podstawmy pierwsze równanie do drugiego i znajdźmy wartość y

Zastąpmy y X

Oznacza to, że rozwiązaniem układu jest para wartości (3; 4)

Oczywiście można także wyrazić zmienną y. To nie zmieni korzeni. Ale jeśli wyrazisz y, Rezultatem nie jest bardzo proste równanie, którego rozwiązanie zajmie więcej czasu. Będzie to wyglądać tak:

Widzimy, że w tym przykładzie wyrażamy X o wiele wygodniejsze niż wyrażanie y .

Przykład 4. Rozwiąż następujący układ równań metodą podstawieniową:

Wyraźmy to w pierwszym równaniu X. Wtedy system przyjmie postać:

y

Zastąpmy y do pierwszego równania i znajdź X. Możesz użyć oryginalnego równania 7 X+ 9y= 8, lub użyj równania, w którym wyrażona jest zmienna X. Użyjemy tego równania, ponieważ jest wygodne:

Oznacza to, że rozwiązaniem układu jest para wartości (5; −3)

Metoda dodawania

Metoda dodawania polega na dodawaniu równań zawartych w układzie wyraz po wyrazie. To dodanie skutkuje nowym równaniem z jedną zmienną. Rozwiązanie takiego równania jest dość proste.

Rozwiążmy następujący układ równań:

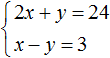
Dodajmy lewą stronę pierwszego równania do lewej strony drugiego równania. I prawa strona pierwszego równania z prawą stroną drugiego równania. Otrzymujemy następującą równość:

Przyjrzyjmy się podobnym terminom:

W rezultacie otrzymaliśmy najprostsze równanie 3 X= 27, którego pierwiastek wynosi 9. Znajomość wartości X możesz znaleźć wartość y. Zastąpmy tę wartość X do drugiego równania x-y= 3 . Otrzymujemy 9 − y= 3 . Stąd y= 6 .

Oznacza to, że rozwiązaniem układu jest para wartości (9; 6)

Przykład 2

Dodajmy lewą stronę pierwszego równania do lewej strony drugiego równania. I prawa strona pierwszego równania z prawą stroną drugiego równania. W powstałej równości przedstawiamy podobne terminy:

W rezultacie otrzymaliśmy najprostsze równanie 5 X= 20, którego pierwiastek wynosi 4. Znajomość wartości X możesz znaleźć wartość y. Zastąpmy tę wartość X do pierwszego równania 2 x+y= 11. Zdobądźmy 8+ y= 11. Stąd y= 3 .

Oznacza to, że rozwiązaniem układu jest para wartości (4;3)

Proces dodawania nie jest szczegółowo opisany. Trzeba to zrobić mentalnie. Podczas dodawania oba równania należy sprowadzić do postaci kanonicznej. To jest do powiedzenia ac + by = c .

Z rozważanych przykładów jasno wynika, że ​​głównym celem dodawania równań jest pozbycie się jednej ze zmiennych. Jednak nie zawsze możliwe jest natychmiastowe rozwiązanie układu równań metodą dodawania. Najczęściej układ najpierw doprowadza się do postaci, w której można dodawać równania zawarte w tym układzie.

Na przykład system można rozwiązać natychmiast dodając. Po dodaniu obu równań terminy y I -y znikną, ponieważ ich suma wynosi zero. W rezultacie powstaje najprostsze równanie 11 X= 22, którego pierwiastek wynosi 2. Będzie można wtedy określić y równa 5.

I układ równań Metody dodawania nie można rozwiązać natychmiast, ponieważ nie doprowadzi to do zniknięcia jednej ze zmiennych. Dodanie da równanie 8 X+ y= 28, co ma nieskończoną liczbę rozwiązań.

Jeśli obie strony równania pomnożymy lub podzielimy przez tę samą liczbę, różną od zera, otrzymamy równanie równoważne podanemu. Zasada ta obowiązuje również w przypadku układu równań liniowych z dwiema zmiennymi. Jedno z równań (lub oba równania) można pomnożyć przez dowolną liczbę. Rezultatem będzie równoważny system, którego korzenie będą pokrywać się z poprzednim.

Wróćmy do pierwszego systemu, który opisywał, ile ciast i filiżanek kawy kupił uczeń. Rozwiązaniem tego układu była para wartości (6; 5).

Pomnóżmy oba równania zawarte w tym układzie przez pewne liczby. Powiedzmy, że mnożymy pierwsze równanie przez 2, a drugie przez 3

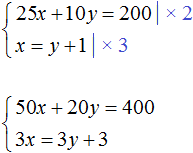
W rezultacie otrzymaliśmy system
Rozwiązaniem tego układu jest nadal para wartości (6; 5)

Oznacza to, że równania zawarte w układzie można sprowadzić do postaci odpowiedniej do zastosowania metody dodawania.

Wróćmy do systemu , którego nie mogliśmy rozwiązać metodą dodawania.

Pomnóż pierwsze równanie przez 6, a drugie przez -2

Otrzymujemy wtedy następujący układ:

Dodajmy równania zawarte w tym układzie. Dodawanie komponentów 12 X i -12 X spowoduje wynik 0, dodanie 18 y i 4 y dam 22 y, a dodanie 108 i -20 daje 88. Następnie otrzymujemy równanie 22 y= 88, stąd y = 4 .

Jeżeli na początku ciężko Ci w głowie dodać równania, to możesz zapisać jak lewa strona pierwszego równania sumuje się z lewą stroną drugiego równania, a prawa strona pierwszego równania z prawą stroną równania drugie równanie:

Wiedząc, że wartość zmiennej y równa się 4, możesz znaleźć wartość X. Zastąpmy y do jednego z równań, na przykład do pierwszego równania 2 X+ 3y= 18. Następnie otrzymujemy równanie z jedną zmienną 2 X+ 12 = 18. Przesuńmy 12 w prawą stronę, zmieniając znak, otrzymamy 2 X= 6, stąd X = 3 .

Przykład 4. Rozwiąż następujący układ równań metodą dodawania:

Pomnóżmy drugie równanie przez -1. Następnie system przyjmie następującą postać:

Dodajmy oba równania. Dodawanie komponentów X I −x spowoduje wynik 0, dodanie 5 y i 3 y dam 8 y, a dodanie 7 i 1 daje 8. Wynikiem jest równanie 8 y= 8, którego pierwiastek wynosi 1. Wiedząc, że wartość y równa się 1, możesz znaleźć wartość X .

Zastąpmy y do pierwszego równania, otrzymujemy X+ 5 = 7, stąd X= 2

Przykład 5. Rozwiąż następujący układ równań metodą dodawania:

Pożądane jest, aby terminy zawierające te same zmienne znajdowały się jeden pod drugim. Dlatego w drugim równaniu wyrazy 5 y i -2 X Zamieńmy się miejscami. W rezultacie system przyjmie postać:

Pomnóżmy drugie równanie przez 3. Wtedy układ przyjmie postać:

Dodajmy teraz oba równania. W wyniku dodawania otrzymujemy równanie 8 y= 16, którego pierwiastek wynosi 2.

Zastąpmy y w pierwszym równaniu otrzymujemy 6 X- 14 = 40. Przesuńmy wyraz -14 na prawą stronę, zmieniając znak i otrzymajmy 6 X= 54 . Stąd X= 9.

Przykład 6. Rozwiąż następujący układ równań metodą dodawania:

Pozbądźmy się ułamków. Pomnóż pierwsze równanie przez 36, a drugie przez 12

W powstałym układzie pierwsze równanie można pomnożyć przez -5, a drugie przez 8

Dodajmy równania w powstałym układzie. Następnie otrzymujemy najprostsze równanie -13 y= −156 . Stąd y= 12. Zastąpmy y do pierwszego równania i znajdź X

Przykład 7. Rozwiąż następujący układ równań metodą dodawania:

Sprowadźmy oba równania do postaci normalnej. Tutaj wygodnie jest zastosować zasadę proporcji w obu równaniach. Jeżeli w pierwszym równaniu prawa strona jest przedstawiona jako , a prawa strona drugiego równania jako , to układ będzie miał postać:

Mamy proporcję. Pomnóżmy jego skrajne i średnie wyrazy. Wtedy system przyjmie postać:

Pomnóżmy pierwsze równanie przez −3 i otwórzmy nawiasy w drugim:

Dodajmy teraz oba równania. W wyniku dodania tych równań otrzymujemy równość z zerem po obu stronach:

Okazuje się, że system ma niezliczoną ilość rozwiązań.

Ale nie możemy po prostu brać dowolnych wartości z nieba X I y. Możemy podać jedną z wartości, a druga zostanie określona w zależności od wartości, którą podamy. Na przykład niech X= 2 . Podstawmy tę wartość do systemu:

W wyniku rozwiązania jednego z równań wartość dla y, co spełni oba równania:

Powstała para wartości (2; −2) spełni wymagania układu:

Znajdźmy inną parę wartości. Pozwalać X= 4. Podstawmy tę wartość do systemu:

Na oko można stwierdzić, że wartość y równa się zeru. Następnie otrzymujemy parę wartości (4; 0) spełniającą nasz system:

Przykład 8. Rozwiąż następujący układ równań metodą dodawania:

Pomnóż pierwsze równanie przez 6, a drugie przez 12

Przepiszmy to, co zostało:

Pomnóżmy pierwsze równanie przez -1. Wtedy system przyjmie postać:

Dodajmy teraz oba równania. W wyniku dodawania powstaje równanie 6 B= 48, którego pierwiastek wynosi 8. Zastąp B do pierwszego równania i znajdź A

Układ równań liniowych z trzema zmiennymi

Równanie liniowe z trzema zmiennymi zawiera trzy zmienne ze współczynnikami, a także wyraz wolny. W formie kanonicznej można to zapisać następująco:

topór + by + cz = re

Równanie to ma niezliczoną ilość rozwiązań. Nadając dwóm zmiennym różne wartości, można znaleźć trzecią wartość. Rozwiązaniem w tym przypadku jest trójka wartości ( X; y; z), co zamienia równanie w tożsamość.

Jeśli zmienne x, y, z są ze sobą powiązane trzema równaniami, wówczas powstaje układ trzech równań liniowych z trzema zmiennymi. Do rozwiązania takiego układu można zastosować te same metody, które obowiązują w przypadku równań liniowych z dwiema zmiennymi: metodę podstawienia i metodę dodawania.

Przykład 1. Rozwiąż następujący układ równań metodą podstawieniową:

Wyraźmy to w trzecim równaniu X. Wtedy system przyjmie postać:

Teraz dokonajmy podstawienia. Zmienny X jest równe wyrażeniu 3 − 2y − 2z . Podstawmy to wyrażenie do pierwszego i drugiego równania:

Otwórzmy nawiasy w obu równaniach i przedstawmy podobne wyrażenia:

Dotarliśmy do układu równań liniowych z dwiema zmiennymi. W takim przypadku wygodnie jest zastosować metodę dodawania. W efekcie zmienna y zniknie i będziemy mogli znaleźć wartość zmiennej z

Teraz znajdźmy wartość y. Aby to zrobić, wygodnie jest użyć równania − y+ z= 4. Zastąp do niego wartość z

Teraz znajdźmy wartość X. Aby to zrobić, wygodnie jest użyć równania X= 3 − 2y − 2z . Podstawmy w nim wartości y I z

Zatem trójka wartości (3; −2; 2) jest rozwiązaniem naszego układu. Sprawdzając upewniamy się, że wartości te spełniają system:

Przykład 2. Rozwiąż układ metodą dodawania

Dodajmy pierwsze równanie do drugiego, pomnożone przez -2.

Jeśli drugie równanie zostanie pomnożone przez -2, przyjmie postać −6X+ 6y- 4z = −4 . Dodajmy to teraz do pierwszego równania:

Widzimy, że w wyniku elementarnych przekształceń została wyznaczona wartość zmiennej X. Jest równy jeden.

Wróćmy do głównego systemu. Dodajmy drugie równanie do trzeciego, pomnożone przez -1. Jeśli trzecie równanie zostanie pomnożone przez -1, przyjmie postać −4X + 5y − 2z = −1 . Dodajmy to teraz do drugiego równania:

Mamy równanie x− 2y= −1 . Podstawmy do niego wartość X które znaleźliśmy wcześniej. Następnie możemy określić wartość y

Teraz znamy znaczenia X I y. Dzięki temu możesz określić wartość z. Skorzystajmy z jednego z równań zawartych w układzie:

Zatem potrójna wartość (1; 1; 1) jest rozwiązaniem naszego układu. Sprawdzając upewniamy się, że wartości te spełniają system:

Zagadnienia tworzenia układów równań liniowych

Zadanie układania układów równań rozwiązuje się poprzez wprowadzenie kilku zmiennych. Następnie zestawiane są równania w oparciu o warunki problemu. Z opracowanych równań tworzą układ i rozwiązują go. Po rozwiązaniu układu należy sprawdzić, czy jego rozwiązanie spełnia warunki zadania.

Problem 1. Samochód Wołga wyjechał z miasta do kołchozu. Wróciła inną drogą, o 5 km krótszą od pierwszej. W sumie samochód przejechał w obie strony 35 km. Ile kilometrów ma długość każdej drogi?

Rozwiązanie

Pozwalać X- długość pierwszej drogi, y- długość drugiej. Jeśli samochód przejechał w obie strony 35 km, pierwsze równanie można zapisać jako X+ y= 35. Równanie to opisuje sumę długości obu dróg.

Mówi się, że samochód wracał drogą o 5 km krótszą od pierwszej. Następnie drugie równanie można zapisać jako X− y= 5. Z tego równania wynika, że ​​różnica długości dróg wynosi 5 km.

Lub drugie równanie można zapisać jako X= y+ 5. Będziemy korzystać z tego równania.

Ponieważ zmienne X I y w obu równaniach oznaczamy tę samą liczbę, to możemy z nich ułożyć układ:

Rozwiążmy ten układ, korzystając z niektórych z wcześniej zbadanych metod. W takim przypadku wygodnie jest zastosować metodę podstawienia, ponieważ w drugim równaniu zmienna X już wyrażone.

Zastąp drugie równanie pierwszym i znajdź y

Zastąpmy znalezioną wartość y w drugim równaniu X= y+ 5 i znajdziemy X

Za pomocą zmiennej wyznaczono długość pierwszej drogi X. Teraz odkryliśmy jego znaczenie. Zmienny X wynosi 20. Oznacza to, że długość pierwszej drogi wynosi 20 km.

A długość drugiej drogi oznaczono y. Wartość tej zmiennej wynosi 15. Oznacza to, że długość drugiej drogi wynosi 15 km.

Sprawdźmy. Najpierw upewnijmy się, że system został rozwiązany poprawnie:

Sprawdźmy teraz, czy rozwiązanie (20; 15) spełnia warunki zadania.

Mówiono, że samochód przejechał w sumie 35 km w obie strony. Dodajemy długości obu dróg i upewniamy się, że rozwiązanie (20; 15) spełnia warunek: 20 km + 15 km = 35 km

Następujący warunek: samochód wrócił inną drogą, krótszą o 5 km od pierwszej . Widzimy, że rozwiązanie (20; 15) również spełnia ten warunek, gdyż 15 km jest krótsze od 20 km o 5 km: 20 km - 15 km = 5 km

Podczas tworzenia układu ważne jest, aby zmienne reprezentowały te same liczby we wszystkich równaniach wchodzących w skład tego układu.

Zatem nasz układ zawiera dwa równania. Równania te z kolei zawierają zmienne X I y, które w obu równaniach reprezentują te same liczby, a mianowicie długości dróg wynoszące 20 km i 15 km.

Problem 2. Na platformę załadowano podkłady dębowe i sosnowe, łącznie 300 podkładów. Wiadomo, że wszystkie podkłady dębowe ważyły ​​o 1 tonę mniej niż wszystkie podkłady sosnowe. Oblicz, ile podkładów dębowych i sosnowych było osobno, jeśli każdy podkład dębowy ważył 46 kg, a każdy podkład sosnowy 28 kg.

Rozwiązanie

Pozwalać X dąb i y Na platformę załadowano podkłady sosnowe. Jeśli w sumie było 300 podkładów, pierwsze równanie można zapisać jako x+y = 300 .

Wszystkie podkłady dębowe ważyły ​​46 X kg, a sosnowe 28 y kg. Ponieważ podkłady dębowe ważyły ​​​​o 1 tonę mniej niż podkłady sosnowe, drugie równanie można zapisać jako 28y- 46X= 1000 . Z równania tego wynika, że ​​różnica mas pomiędzy podkładami dębowymi i sosnowymi wynosi 1000 kg.

Tony przeliczono na kilogramy, ponieważ masę podkładów dębowych i sosnowych mierzono w kilogramach.

W rezultacie otrzymujemy dwa równania tworzące układ

Rozwiążmy ten system. Wyraźmy to w pierwszym równaniu X. Wtedy system przyjmie postać:

Zastąp pierwsze równanie drugim i znajdź y

Zastąpmy y w równanie X= 300 − y i dowiedz się, co to jest X

Oznacza to, że na platformę załadowano 100 podkładów dębowych i 200 sosnowych.

Sprawdźmy, czy rozwiązanie (100; 200) spełnia warunki zadania. Najpierw upewnijmy się, że system został rozwiązany poprawnie:

Mówiono, że łącznie było 300 podkładów. Sumujemy liczbę podkładów dębowych i sosnowych i upewniamy się, że rozwiązanie (100; 200) spełnia warunek: 100 + 200 = 300.

Następujący warunek: wszystkie podkłady dębowe ważyły ​​o 1 tonę mniej niż wszystkie podkłady sosnowe . Widzimy, że rozwiązanie (100; 200) również spełnia ten warunek, ponieważ 46 × 100 kg podkładów dębowych jest lżejsze niż 28 × 200 kg podkładów sosnowych: 5600 kg - 4600 kg = 1000 kg.

Problem 3. Wzięliśmy trzy kawałki stopu miedzi i niklu w proporcjach wagowych 2: 1, 3: 1 i 5: 1. Stopiono z nich kawałek o masie 12 kg, w którym stosunek zawartości miedzi do niklu wynosił 4:1. Znajdź masę każdego pierwotnego kawałka, jeśli masa pierwszego jest dwukrotnie większa od masy drugiego.

Z N nieznany jest układ postaci:

Gdzie ij I b i (i=1,…,m; b=1,…,n)- niektóre znane liczby i x 1 ,…,x n- nieznane numery. W wyznaczaniu współczynników ij indeks I określa numer równania, a drugi J- liczba niewiadomych, przy której znajduje się ten współczynnik.

Układ jednorodny - gdy wszystkie wolne terminy systemu są równe zeru ( b 1 = b 2 = … = b m = 0), jest sytuacja odwrotna system heterogeniczny.

Układ kwadratowy - kiedy numer M równania równają się liczbie N nieznany.

Rozwiązanie systemowe- całość N liczby do 1, do 2, …, do n, takie zastąpienie wszystkiego c ja zamiast x ja w system zamienia wszystkie jego równania w tożsamości.

System połączeń - gdy układ ma co najmniej 1 rozwiązanie, oraz systemie niewspółpracującym gdy układ nie ma rozwiązań.

Układ łączony tego typu (jak podano powyżej, niech będzie (1)) może mieć jedno lub więcej rozwiązań.

Rozwiązania do 1 (1) , do 2 (1) , …, do n (1) I do 1 (2) , do 2 (2) , …, do n (2) będą wspólne systemy typu (1). różny, gdy nawet 1 z równości nie jest spełniona:

do 1 (1) = do 1 (2) , do 2 (1) = do 2 (2) , …, do n (1) = do n (2) .

Będzie to wspólny system typu (1). niektórzy kiedy ma tylko jedno rozwiązanie; gdy system ma co najmniej 2 różne rozwiązania, staje się nieokreślony. Gdy jest więcej równań niż niewiadomych, układ jest przedefiniowany.

Współczynniki niewiadomych zapisuje się w postaci macierzy:

Nazywa się to macierz układu.

Liczby pojawiające się po prawej stronie równań to b 1 ,…,b m Czy wolni członkowie.

Całość N liczby c 1 ,…,c n jest rozwiązaniem tego układu, gdy wszystkie równania układu stają się równe po podstawieniu w nich liczb c 1 ,…,c n zamiast odpowiednich niewiadomych x 1 ,…,x n.

Rozwiązując układ równań liniowych, mogą pojawić się 3 opcje:

1. Układ ma tylko jedno rozwiązanie.

2. Układ ma nieskończoną liczbę rozwiązań. Na przykład, . Rozwiązaniem tego układu będą wszystkie pary liczb różniące się znakiem.

3. Układ nie ma rozwiązań. Na przykład…jeśli istniało rozwiązanie, to wtedy x1 + x2 będzie jednocześnie równe 0 i 1.

Metody rozwiązywania układów równań liniowych.

Metody bezpośrednie podać algorytm, za pomocą którego znajduje się dokładne rozwiązanie SLAU(układy liniowych równań algebraicznych). A gdyby dokładność była absolutna, znaleźliby ją. Prawdziwy komputer elektryczny oczywiście działa z błędem, więc rozwiązanie będzie przybliżone.

§1. Układy równań liniowych.

Zobacz system

zwany systemem M równania liniowe z N nieznany.

Tutaj
- nieznany, - współczynniki dla niewiadomych,
- dowolne wyrazy równań.

Jeżeli wszystkie wolne wyrazy równań są równe zeru, układ nazywa się jednorodny. Decyzją system nazywa się zbiorem liczb
, podstawiając je do układu zamiast niewiadomych, wszystkie równania zamieniają się w tożsamości. System nazywa się wspólny, jeśli ma co najmniej jedno rozwiązanie. System kompatybilny, który ma unikalne rozwiązanie, nazywa się niektórzy. Obydwa systemy nazywane są równowartość, jeśli zbiory ich rozwiązań pokrywają się.

Układ (1) można przedstawić w postaci macierzowej za pomocą równania

(2)

.

§2. Zgodność układów równań liniowych.

Rozszerzoną macierz układu (1) nazwijmy macierzą

Twierdzenie Kroneckera-Capelliego. System (1) jest spójny wtedy i tylko wtedy, gdy stopień macierzy systemu jest równy rządowi macierzy rozszerzonej:

.

§3. Rozwiązanie systemoweN równania liniowe zN nieznany.

Rozważmy system niejednorodny N równania liniowe z N nieznany:

(3)

Twierdzenie Cramera.Jeśli głównym wyznacznikiem systemu (3)
, to układ ma rozwiązanie jednoznaczne, określone wzorami:

te.
,

Gdzie - wyznacznik otrzymany z wyznacznika wymiana kolumnę do kolumny wolnych członków.

Jeśli
i przynajmniej jeden z ≠0, to układ nie ma rozwiązań.

Jeśli
, to układ ma nieskończenie wiele rozwiązań.

Układ (3) można rozwiązać korzystając z jego postaci macierzowej (2). Jeśli ranga macierzy A równa się N, tj.
, następnie macierz A ma odwrotność
. Mnożenie równania macierzowego
do matrixa
po lewej stronie otrzymujemy:

.

Ostatnia równość wyraża sposób rozwiązywania układów równań liniowych za pomocą macierzy odwrotnej.

Przykład. Rozwiąż układ równań za pomocą macierzy odwrotnej.

Rozwiązanie. Matryca
niezdegenerowany, ponieważ
, co oznacza, że ​​istnieje macierz odwrotna. Obliczmy macierz odwrotną:
.

,

Ćwiczenia. Rozwiązać układ metodą Cramera.

§4. Rozwiązywanie dowolnych układów równań liniowych.

Niech dany będzie niejednorodny układ równań liniowych postaci (1).

Załóżmy, że układ jest spójny, tj. spełniony jest warunek twierdzenia Kroneckera-Capelliego:
. Jeśli ranga macierzy
(liczba niewiadomych), to układ ma rozwiązanie unikalne. Jeśli
, to układ ma nieskończenie wiele rozwiązań. Pozwól mi wyjaśnić.

Niech ranga macierzy R(A)= R< N. Ponieważ
, to istnieje jakiś niezerowy drugorzędny rzędu R. Nazwijmy to mollem podstawowym. Niewiadome, których współczynniki tworzą bazę mniejszą, będziemy nazywać zmiennymi podstawowymi. Pozostałe niewiadome nazywamy zmiennymi wolnymi. Przekształćmy równania i przenumerujmy zmienne tak, aby ten element pomocniczy znajdował się w lewym górnym rogu macierzy układu:

.

Pierwszy R linie są liniowo niezależne, reszta jest wyrażona przez nie. Dlatego te linie (równania) można odrzucić. Otrzymujemy:

Nadajmy zmiennym swobodnym dowolne wartości liczbowe: . Zostawmy po lewej stronie tylko zmienne podstawowe, a wolne przesuńmy na prawą stronę.

Mam system R równania liniowe z R nieznane, którego wyznacznik jest różny od 0. Ma unikalne rozwiązanie.

Układ ten nazywany jest ogólnym rozwiązaniem układu równań liniowych (1). Inaczej: nazywa się wyrażanie zmiennych podstawowych poprzez wolne decyzja ogólna systemy. Z niego można uzyskać nieskończoną liczbę rozwiązania prywatne, dając wolnym zmiennym dowolne wartości. Nazywa się rozwiązanie szczególne uzyskane z rozwiązania ogólnego dla zerowych wartości wolnych zmiennych podstawowe rozwiązanie. Liczba różnych rozwiązań podstawowych nie przekracza
. Nazywa się rozwiązanie podstawowe ze składnikami nieujemnymi wspierający rozwiązanie systemowe.

Przykład.

, R=2.

Zmienne
- podstawowy,
- bezpłatny.

Dodajmy równania; wyrażmy
Poprzez
:

- wspólna decyzja.

- prywatne rozwiązanie dla
.

- rozwiązanie podstawowe, odniesienie.

§5. Metoda Gaussa.

Metoda Gaussa jest uniwersalną metodą badania i rozwiązywania dowolnych układów równań liniowych. Polega na sprowadzeniu układu do postaci diagonalnej (lub trójkątnej) poprzez sekwencyjne eliminowanie niewiadomych za pomocą przekształceń elementarnych, które nie naruszają równoważności układów. Zmienną uważa się za wykluczoną, jeśli występuje tylko w jednym równaniu układu o współczynniku 1.

Transformacje elementarne systemy to:

Mnożenie równania przez liczbę inną niż zero;

Dodanie równania pomnożonego przez dowolną liczbę z innym równaniem;

Przestawianie równań;

Odrzucenie równania 0 = 0.

Transformacje elementarne można przeprowadzić nie na równaniach, ale na rozszerzonych macierzach otrzymanych układów równoważnych.

Przykład.

Rozwiązanie. Zapiszmy rozszerzoną macierz układu:

.

Dokonując elementarnych przekształceń, lewą stronę macierzy sprowadzimy do postaci jednostkowej: na głównej przekątnej utworzymy jedynki, a poza nią zera.

Komentarz. Jeżeli podczas wykonywania przekształceń elementarnych otrzyma się równanie postaci 0 = k(Gdzie Do0), wtedy system jest niespójny.

Rozwiązanie układów równań liniowych metodą sekwencyjnej eliminacji niewiadomych można zapisać w postaci stoły.

W lewej kolumnie tabeli znajdują się informacje o zmiennych wyłączonych (podstawowych). Pozostałe kolumny zawierają współczynniki niewiadomych i wolne wyrazy równań.

Rozbudowana macierz systemu jest zapisywana w tabeli źródłowej. Następnie zaczynamy wykonywać przekształcenia Jordana:

1. Wybierz zmienną , które staną się podstawą. Odpowiednia kolumna nazywana jest kolumną kluczową. Wybierz równanie, w którym ta zmienna pozostanie, wykluczona z innych równań. Odpowiedni wiersz tabeli nazywany jest wierszem kluczowym. Współczynnik , stojący na przecięciu wiersza klucza i kolumny klucza, nazywany jest kluczem.

2. Kluczowe elementy ciągu są podzielone na kluczowy element.

3. Kolumna klucza jest wypełniona zerami.

4. Pozostałe elementy obliczamy korzystając z reguły prostokąta. Utwórz prostokąt, którego przeciwległych wierzchołków znajduje się element kluczowy i element przeliczony; od iloczynu elementów znajdujących się na przekątnej prostokąta z elementem kluczowym odejmuje się iloczyn elementów drugiej przekątnej, a powstałą różnicę dzieli się przez element kluczowy.

Przykład. Znajdź rozwiązanie ogólne i rozwiązanie podstawowe układu równań:

Rozwiązanie.

Ogólne rozwiązanie układu:

Podstawowe rozwiązanie:
.

Pojedyncza transformacja podstawieniowa pozwala na przejście z jednej bazy systemu do drugiej: zamiast jednej ze zmiennych głównych do bazy wprowadzana jest jedna ze zmiennych wolnych. W tym celu należy zaznaczyć kluczowy element w kolumnie zmiennej swobodnej i wykonać przekształcenia zgodnie z powyższym algorytmem.

§6. Znalezienie rozwiązań wsparcia

Rozwiązaniem odniesienia układu równań liniowych jest rozwiązanie podstawowe, które nie zawiera składników ujemnych.

Rozwiązania referencyjne układu wyznacza się metodą Gaussa, gdy spełnione są następujące warunki.

1. W pierwotnym systemie wszystkie wolne terminy muszą być nieujemne:
.

2. Spośród dodatnich współczynników wybierany jest element kluczowy.

3. Jeżeli zmienna wprowadzona do bazy ma kilka dodatnich współczynników, to kluczową linią jest ta, w której stosunek wyrazu wolnego do dodatniego współczynnika jest najmniejszy.

Notatka 1. Jeżeli w procesie eliminacji niewiadomych pojawi się równanie, w którym wszystkie współczynniki są dodatnie, a wyraz wolny
, to układ nie ma rozwiązań nieujemnych.

Uwaga 2. Jeżeli w kolumnach współczynników dla zmiennych wolnych nie będzie ani jednego elementu dodatniego, wówczas przejście na inne rozwiązanie referencyjne nie będzie możliwe.

Przykład.

Ogólnie równanie liniowe ma postać:

Równanie ma rozwiązanie: jeśli przynajmniej jeden ze współczynników niewiadomych jest różny od zera. W takim przypadku dowolny wektor wymiarowy nazywany jest rozwiązaniem równania, jeśli po podstawieniu jego współrzędnych równanie staje się tożsamością.

Ogólna charakterystyka rozwiązanego układu równań

Przykład 20.1

Opisz układ równań.

Rozwiązanie:

1. Czy istnieje sprzeczne równanie?(Jeśli współczynniki, w tym przypadku równanie ma postać: i nazywa się kontrowersyjny.)

• Jeśli system zawiera coś sprzecznego, to taki system jest niespójny i nie ma rozwiązania.

2. Znajdź wszystkie dozwolone zmienne. (Nieznane jest nazywanedozwolony dla układu równań, jeżeli jest on uwzględniony w jednym z równań układu o współczynniku +1, ale nie jest uwzględniony w pozostałych równaniach (tj. jest uwzględniony ze współczynnikiem równym zero).

3. Czy układ równań został rozwiązany? (Układ równań nazywa się rozwiązanym, jeśli każde równanie układu zawiera rozwiązaną niewiadomą, wśród której nie ma zbieżnych)

Powstają rozwiązane niewiadome, wzięte po jednej z każdego równania układu pełen zestaw rozwiązanych niewiadomych systemy. (w naszym przykładzie jest to)

Dozwolone niewiadome zawarte w pełnym zestawie są również nazywane podstawowy() i nie są zawarte w zestawie - bezpłatny ().

W ogólnym przypadku rozwiązany układ równań ma postać:

Na tym etapie najważniejsze jest zrozumienie, co to jest rozwiązany nieznany(wliczone w cenę podstawową i bezpłatne).

Ogólne Szczegółowe Rozwiązania podstawowe

Rozwiązanie ogólne rozwiązany układ równań to zbiór wyrażeń rozwiązanych niewiadomych za pomocą wyrazów wolnych i wolnych niewiadomych:

Prywatna decyzja nazywa się rozwiązaniem uzyskanym z rozwiązania ogólnego dla określonych wartości zmiennych wolnych i niewiadomych.

Podstawowe rozwiązanie jest rozwiązaniem szczególnym uzyskanym z rozwiązania ogólnego dla zerowych wartości wolnych zmiennych.

• Rozwiązanie podstawowe (wektor) nazywa się zdegenerowany, jeśli liczba jego niezerowych współrzędnych jest mniejsza niż liczba dozwolonych niewiadomych.
• Rozwiązanie podstawowe nazywa się niezdegenerowany, jeżeli liczba jego niezerowych współrzędnych jest równa liczbie dopuszczalnych niewiadomych układu wchodzących w skład pełnego zbioru.

Twierdzenie (1)

Rozwiązany układ równań jest zawsze spójny(ponieważ ma co najmniej jedno rozwiązanie); Ponadto, jeżeli w układzie nie występują wolne niewiadome,(to znaczy w układzie równań wszystkie dozwolone są uwzględnione w podstawie) wtedy jest to określone(posiada unikalne rozwiązanie); jeśli istnieje przynajmniej jedna zmienna wolna, to układ nie jest zdefiniowany(ma nieskończoną liczbę rozwiązań).

Przykład 1. Znajdź ogólne, podstawowe i dowolne szczególne rozwiązanie układu równań:

Rozwiązanie:

1. Czy sprawdzamy czy system jest autoryzowany?

• Układ jest rozwiązany (ponieważ każde z równań zawiera rozwiązaną niewiadomą)

2. Do zbioru zaliczamy dozwolone niewiadome - po jednej z każdego równania.

3. Zapisujemy rozwiązanie ogólne w zależności od tego, jakie niewiadome uwzględniliśmy w zbiorze.

4. Znalezienie prywatnego rozwiązania. W tym celu przyrównujemy zmienne wolne, których nie uwzględniliśmy w zbiorze, z dowolnymi liczbami.

Odpowiedź: rozwiązanie prywatne(jedna z opcji)

5. Znalezienie podstawowego rozwiązania. Aby to zrobić, przyrównujemy wolne zmienne, których nie uwzględniliśmy w zbiorze, do zera.

Elementarne przekształcenia równań liniowych

Układy równań liniowych są redukowane do równoważnych układów rozwiązanych za pomocą przekształceń elementarnych.

Twierdzenie (2)

Jeśli w ogóle pomnóż równanie układu przez jakąś liczbę różną od zera, a resztę równań pozostaw bez zmian, a następnie . (to znaczy, jeśli pomnożysz lewą i prawą stronę równania przez tę samą liczbę, otrzymasz równanie równoważne temu)

Twierdzenie (3)

Jeśli dodać kolejne do dowolnego równania układu, a następnie pozostaw wszystkie pozostałe równania bez zmian otrzymujemy system równoważny temu. (to znaczy, jeśli dodasz dwa równania (dodając ich lewą i prawą stronę), otrzymasz równanie równoważne danym)

Wniosek z twierdzeń (2 i 3)

Jeśli dodać kolejne równanie do równania pomnożonego przez określoną liczbę i pozostaw wszystkie inne równania bez zmian, wówczas otrzymamy system równoważny temu.

Wzory na przeliczanie współczynników systemowych

Jeśli mamy układ równań i chcemy go przekształcić w rozwiązany układ równań, pomoże nam w tym metoda Jordana-Gaussa.

Transformacja Jordana z elementem rozdzielającym pozwala uzyskać dla układu równań rozwiązaną niewiadomą w równaniu z liczbą . (przykład 2).

Transformacja Jordana składa się z elementarnych transformacji dwóch typów:

Powiedzmy, że chcemy, aby nieznana w dolnym równaniu stała się niewiadomą rozwiązaną. Aby to zrobić, musimy podzielić przez , tak aby suma wynosiła .

Przykład 2 Przeliczmy współczynniki układu

Dzieląc równanie z liczbą przez , jego współczynniki oblicza się ponownie, korzystając ze wzorów:

Aby wykluczyć z równania z liczbą , należy pomnożyć równanie z liczbą przez i dodać do tego równania.

Twierdzenie (4) O zmniejszaniu liczby równań układu.

Jeżeli układ równań zawiera równanie trywialne, to można je wykluczyć z układu i otrzymać układ równoważny pierwotnemu.

Twierdzenie (5) O niezgodności układu równań.

Jeśli układ równań zawiera równanie niespójne, to jest on niespójny.

Algorytm metody Jordana-Gaussa

Algorytm rozwiązywania układów równań metodą Jordana-Gaussa składa się z szeregu podobnych kroków, przy czym na każdym z nich wykonywane są działania w następującej kolejności:

1. Sprawdza, czy system nie jest niespójny. Jeżeli układ zawiera niespójne równanie, to jest on niespójny.
2. Sprawdzana jest możliwość redukcji liczby równań. Jeśli układ zawiera trywialne równanie, jest ono przekreślone.
3. Jeśli układ równań zostanie rozwiązany, zapisz rozwiązanie ogólne układu i, jeśli to konieczne, rozwiązania szczegółowe.
4. Jeżeli układ nie jest rozwiązany, to w równaniu, które nie zawiera rozwiązanej niewiadomej, wybiera się element rozwiązujący i z tym elementem przeprowadza się transformację Jordana.
5. Następnie wróć do punktu 1

Przykład 3 Rozwiąż układ równań metodą Jordana-Gaussa.

Znajdować: dwa rozwiązania ogólne i dwa odpowiadające im rozwiązania podstawowe

Rozwiązanie:

Obliczenia przedstawiono w poniższej tabeli:

Po prawej stronie tabeli znajdują się działania na równaniach. Strzałki wskazują, do którego równania dodawane jest równanie z elementem rozdzielającym, pomnożone przez odpowiedni współczynnik.

Pierwsze trzy wiersze tabeli zawierają współczynniki niewiadomych i prawe strony układu pierwotnego. Wyniki pierwszej transformaty Jordana z elementem rozdzielczym równym jeden podano w wierszach 4, 5, 6. Wyniki drugiej transformaty Jordana z elementem rozdzielczym równym (-1) podano w wierszach 7, 8, 9 Ponieważ trzecie równanie jest trywialne, można je pominąć.

Badanie układu liniowych równań agebraicznych (SLAE) pod kątem spójności oznacza sprawdzenie, czy układ ten ma rozwiązania, czy też ich nie ma. Cóż, jeśli istnieją rozwiązania, wskaż, ile ich jest.

Będziemy potrzebować informacji z tematu „Układ liniowych równań algebraicznych. Pojęcia podstawowe. Macierzowa forma zapisu”. W szczególności potrzebne są pojęcia takie jak macierz układu i macierz układu rozszerzonego, gdyż na nich opiera się sformułowanie twierdzenia Kroneckera-Capelliego. Tradycyjnie będziemy oznaczać macierz systemu literą $A$, a rozszerzoną macierz układu literą $\widetilde(A)$.

Twierdzenie Kroneckera-Capelliego

Układ liniowych równań algebraicznych jest spójny wtedy i tylko wtedy, gdy stopień macierzy układu jest równy rządowi rozszerzonej macierzy układu, tj. $\rang A=\rang\widetilde(A)$.

Przypomnę, że układ nazywamy wspólnym, jeśli ma co najmniej jedno rozwiązanie. Twierdzenie Kroneckera-Capelliego mówi, co następuje: jeśli $\rang A=\rang\widetilde(A)$, to istnieje rozwiązanie; jeśli $\rang A\neq\rang\widetilde(A)$, to ten SLAE nie ma rozwiązań (niespójny). Odpowiedź na pytanie o liczbę tych rozwiązań daje wniosek z twierdzenia Kroneckera-Capelliego. Przy formułowaniu wniosku stosuje się literę $n$, która jest równa liczbie zmiennych danego SLAE.

Wniosek z twierdzenia Kroneckera-Capelliego

1. Jeśli $\rang A\neq\rang\widetilde(A)$, wówczas SLAE jest niespójny (nie ma rozwiązań).
2. Jeśli $\rang A=\rang\widetilde(A)< n$, то СЛАУ является неопределённой (имеет бесконечное количество решений).
3. Jeżeli $\rang A=\rang\widetilde(A) = n$, to SLAE jest określone (ma dokładnie jedno rozwiązanie).

Należy pamiętać, że sformułowane twierdzenie i jego wniosek nie wskazują, jak znaleźć rozwiązanie SLAE. Za ich pomocą można jedynie dowiedzieć się, czy takie rozwiązania istnieją, czy nie, a jeśli istnieją, to ile.

Przykład nr 1

Przeglądaj SLAE $ \left \(\begin(aligned) & -3x_1+9x_2-7x_3=17;\\ & -x_1+2x_2-4x_3=9;\\ & 4x_1-2x_2+19x_3=-42. \end(aligned )\right.$ dla zgodności.Jeśli SLAE jest kompatybilne, wskaż liczbę rozwiązań.

Aby sprawdzić istnienie rozwiązań danego SLAE, korzystamy z twierdzenia Kroneckera-Capelliego. Będziemy potrzebować macierzy układu $A$ i rozszerzonej macierzy układu $\widetilde(A)$, napiszemy je:

$$ A=\left(\begin(tablica) (ccc) -3 i 9 i -7 \\ -1 i 2 i -4 \\ 4 i -2 i 19 \end(array) \right);\; \widetilde(A)=\left(\begin(array) (ccc|c) -3 i 9 &-7 i 17 \\ -1 i 2 i -4 i 9\\ 4 i -2 i 19 i -42 \end(tablica) \right). $$

Musimy znaleźć $\rang A$ i $\rang\widetilde(A)$. Można to zrobić na wiele sposobów, niektóre z nich są wymienione w sekcji Ranking matrycy. Do badania takich układów stosuje się zazwyczaj dwie metody: „Obliczanie rangi macierzy z definicji” lub „Obliczanie rangi macierzy metodą przekształceń elementarnych”.

Metoda numer 1. Obliczanie rang z definicji.

Zgodnie z definicją ranga to najwyższy rząd minorów macierzy, wśród których jest przynajmniej jeden różny od zera. Zwykle badanie rozpoczyna się od nieletnich pierwszego rzędu, ale tutaj wygodniej jest od razu przystąpić do obliczania molla trzeciego rzędu macierzy $A$. Elementy drugorzędne trzeciego rzędu znajdują się na przecięciu trzech wierszy i trzech kolumn omawianej macierzy. Ponieważ macierz $A$ zawiera tylko 3 wiersze i 3 kolumny, to element podrzędny trzeciego rzędu macierzy $A$ jest wyznacznikiem macierzy $A$, tj. $\Delta A$. Do obliczenia wyznacznika stosujemy wzór nr 2 z tematu „Wzory na obliczanie wyznaczników drugiego i trzeciego rzędu”:

$$ \Delta A=\lewo| \begin(tablica) (ccc) -3 i 9 i -7 \\ -1 i 2 i -4 \\ 4 i -2 i 19 \end(tablica) \right|=-21. $$

Zatem istnieje moll trzeciego rzędu macierzy $A$, który nie jest równy zero. Niemożliwe jest skonstruowanie drobnej czwartego rzędu, gdyż wymaga ona 4 wierszy i 4 kolumn, a macierz $A$ ma tylko 3 wiersze i 3 kolumny. Zatem najwyższy rząd nieletnich macierzy $A$, wśród których jest przynajmniej jeden nierówny zero, jest równy 3. Zatem $\rang A=3$.

Musimy także znaleźć $\rang\widetilde(A)$. Przyjrzyjmy się strukturze macierzy $\widetilde(A)$. Do prostej macierzy $\widetilde(A)$ znajdują się elementy macierzy $A$ i okazało się, że $\Delta A\neq 0$. W rezultacie macierz $\widetilde(A)$ ma moll trzeciego rzędu, który nie jest równy zero. Nie możemy skonstruować nieletnich czwartego rzędu macierzy $\widetilde(A)$, więc wnioskujemy: $\rang\widetilde(A)=3$.

Ponieważ $\rang A=\rang\widetilde(A)$, to zgodnie z twierdzeniem Kroneckera-Capelliego układ jest niesprzeczny, tj. ma rozwiązanie (przynajmniej jedno). Aby wskazać liczbę rozwiązań, bierzemy pod uwagę, że nasz SLAE zawiera 3 niewiadome: $x_1$, $x_2$ i $x_3$. Ponieważ liczba niewiadomych wynosi $n=3$, wnioskujemy: $\rang A=\rang\widetilde(A)=n$, zatem zgodnie z wnioskiem z twierdzenia Kroneckera-Capelliego układ jest określony, tj. ma unikalne rozwiązanie.

Problem jest rozwiązany. Jakie wady i zalety ma ta metoda? Najpierw porozmawiajmy o zaletach. Po pierwsze, musieliśmy znaleźć tylko jeden wyznacznik. Następnie od razu wyciągnęliśmy wniosek dotyczący liczby rozwiązań. Zazwyczaj standardowe standardowe obliczenia dają układy równań, które zawierają trzy niewiadome i mają unikalne rozwiązanie. W przypadku takich układów metoda ta jest bardzo wygodna, gdyż z góry wiemy, że istnieje rozwiązanie (w przeciwnym razie przykładu nie byłoby w standardowych obliczeniach). Te. Wystarczy, że w najszybszy sposób pokażemy istnienie rozwiązania. Po drugie, obliczona wartość wyznacznika macierzy układu (tj. $\Delta A$) przyda się później: gdy zaczniemy rozwiązywać dany układ metodą Cramera lub wykorzystując macierz odwrotną.

Jednak metoda obliczania rangi jest z definicji niepożądana, jeśli macierz układu $A$ jest prostokątna. W takim przypadku lepiej zastosować drugą metodę, która zostanie omówiona poniżej. Dodatkowo, jeśli $\Delta A=0$, to nie możemy nic powiedzieć o liczbie rozwiązań danego niejednorodnego SLAE. Być może SLAE ma nieskończoną liczbę rozwiązań, a może nie ma ich wcale. Jeśli $\Delta A=0$, wymagane są dodatkowe badania, co często jest kłopotliwe.

Podsumowując to, co zostało powiedziane, zauważam, że pierwsza metoda jest dobra dla tych SLAE, których macierz systemu jest kwadratowa. Co więcej, sam SLAE zawiera trzy lub cztery niewiadome i jest pobierany ze standardowych standardowych obliczeń lub testów.

Metoda numer 2. Obliczanie rang metodą przekształceń elementarnych.

Metodę tę opisano szczegółowo w odpowiednim temacie. Zaczniemy obliczać rząd macierzy $\widetilde(A)$. Dlaczego macierze $\widetilde(A)$ a nie $A$? Faktem jest, że macierz $A$ jest częścią macierzy $\widetilde(A)$, zatem obliczając rząd macierzy $\widetilde(A)$ jednocześnie znajdziemy rząd macierzy $A$ .

\begin(aligned) &\widetilde(A) =\left(\begin(array) (ccc|c) -3 i 9 &-7 i 17 \\ -1 i 2 i -4 i 9\\ 4 & - 2 i 19 i -42 \end(array) \right) \rightarrow \left|\text(zamień pierwszą i drugą linię)\right| \rightarrow \\ &\rightarrow \left(\begin(array) (ccc|c) -1 i 2 i -4 i 9 \\ -3 i 9 &-7 i 17\\ 4 i -2 i 19 i - 42 \end(array) \right) \begin(array) (l) \phantom(0) \\ r_2-3r_1\\ r_3+4r_1 \end(array) \rightarrow \left(\begin(array) (ccc| c) -1 i 2 i -4 i 9 \\ 0 i 3 i 5 i -10\\ 0 i 6 i 3 i -6 \end(array) \right) \begin(array) (l) \phantom(0 ) \\ \phantom(0)\\ r_3-2r_2 \end(array)\rightarrow\\ &\rightarrow \left(\begin(array) (ccc|c) -1 i 2 & -4 i 9 \\ 0 & 3 &5 & -10\\ 0 & 0 & -7 & 14 \end(array) \right) \end(aligned)

Zredukowaliśmy macierz $\widetilde(A)$ do postaci rzutowej. Otrzymana macierz rzutów ma trzy niezerowe wiersze, więc jej rząd wynosi 3. W związku z tym rząd macierzy $\widetilde(A)$ jest równy 3, tj. $\rang\widetilde(A)=3$. Dokonując przekształceń elementami macierzy $\widetilde(A)$, jednocześnie przekształcaliśmy elementy macierzy $A$ położone do prostej. Macierz $A$ jest również zredukowana do postaci rzutowej: $\left(\begin(array) (ccc) -1 & 2 & -4 \\ 0 & 3 &5 \\ 0 & 0 & -7 \end(array) \prawo)$. Wniosek: rząd macierzy $A$ również wynosi 3, tj. $\zadzwonił A=3$.

Ponieważ $\rang A=\rang\widetilde(A)$, to zgodnie z twierdzeniem Kroneckera-Capelliego układ jest niesprzeczny, tj. ma rozwiązanie. Aby wskazać liczbę rozwiązań, bierzemy pod uwagę, że nasz SLAE zawiera 3 niewiadome: $x_1$, $x_2$ i $x_3$. Ponieważ liczba niewiadomych wynosi $n=3$, wnioskujemy: $\rang A=\rang\widetilde(A)=n$, zatem zgodnie z wnioskiem z twierdzenia Kroneckera-Capelliego układ jest zdefiniowany, tj. ma unikalne rozwiązanie.

Jakie są zalety drugiej metody? Główną zaletą jest jego wszechstronność. Nie ma dla nas znaczenia, czy macierz układu jest kwadratowa, czy nie. Ponadto faktycznie przeprowadziliśmy transformacje do przodu metody Gaussa. Pozostało tylko kilka kroków i moglibyśmy znaleźć rozwiązanie tego SLAE. Szczerze mówiąc, bardziej podoba mi się ta druga metoda niż pierwsza, ale wybór jest kwestią gustu.

Odpowiedź: Podany SLAE jest spójny i zdefiniowany.

Przykład nr 2

Przeglądaj SLAE $ \left\( \begin(aligned) & x_1-x_2+2x_3=-1;\\ & -x_1+2x_2-3x_3=3;\\ & 2x_1-x_2+3x_3=2;\\ & 3x_1- 2x_2+5x_3=1;\\ & 2x_1-3x_2+5x_3=-4.\end(aligned) \right.$ dla zgodności.

Rzędy macierzy układu i macierzy układu rozszerzonego wyznaczymy metodą przekształceń elementarnych. Rozszerzona macierz systemowa: $\widetilde(A)=\left(\begin(array) (ccc|c) 1 i -1 i 2 i -1\\ -1 i 2 i -3 i 3 \\ 2 i -1 & 3 & 2 \\ 3 & -2 & 5 & 1 \\ 2 & -3 & 5 & -4 \end(array) \right)$. Znajdźmy wymagane rangi, przekształcając rozszerzoną macierz układu:

$$ \left(\begin(tablica) (ccc|c) 1 i -1 i 2 i -1\\ -1 i 2 i -3 i 3 \\ 2 i -3 i 5 i -4 \\ 3 & -2 i 5 i 1 \\ 2 i -1 i 3 i 2 \end(array) \right) \begin(array) (l) \phantom(0)\\r_2+r_1\\r_3-2r_1\\ r_4 -3r_1\\r_5-2r_1\end(array)\rightarrow \left(\begin(array) (ccc|c) 1 & -1 & 2 & -1\\ 0 & 1 & -1 & 2 \\ 0 & -1 i 1 i -2 \\ 0 i 1 i -1 i 4 \\ 0 i 1 i -1 i 4 \end(array) \right) \begin(array) (l) \phantom(0)\\ \phantom(0)\\r_3-r_2\\ r_4-r_2\\r_5+r_2\end(array)\rightarrow\\ $$ $$ \rightarrow\left(\begin(array) (ccc|c) 1 & -1 i 2 i -1\\ 0 i 1 i -1 i 2 \\ 0 i 0 i 0 i 2 \\ 0 i 0 i 0 i 2 \\ 0 i 0 i 0 i 0 \end(tablica) \ prawo) \begin(array) (l) \phantom(0)\\\phantom(0)\\\phantom(0)\\ r_4-r_3\\\phantom(0)\end(array)\rightarrow \left (\begin(tablica) (ccc|c) 1 i -1 i 2 i -1\\ 0 i 1 i -1 i 2 \\ 0 i 0 i 0 i 2 \\ 0 i 0 i 0 i 0 \\ 0 i 0 i 0 i 0 \end(array) \right) $$

Rozbudowana macierz układu zostaje zredukowana do postaci schodkowej. Ranga macierzy rzutowej jest równa liczbie jej niezerowych wierszy, więc $\rang\widetilde(A)=3$. Macierz $A$ (do linii) również zostaje sprowadzona do postaci rzutowej, a jej rząd wynosi 2, $\rang(A)=2$.

Ponieważ $\rang A\neq\rang\widetilde(A)$, to zgodnie z twierdzeniem Kroneckera-Capelliego układ jest niespójny (tj. nie ma rozwiązań).

Odpowiedź: System jest niespójny.

Przykład nr 3

Przeglądaj SLAE $ \left\( \begin(aligned) & 2x_1+7x_3-5x_4+11x_5=42;\\ & x_1-2x_2+3x_3+2x_5=17;\\ & -3x_1+9x_2-11x_3-7x_5=-64 ;\\ & -5x_1+17x_2-16x_3-5x_4-4x_5=-90;\\ & 7x_1-17x_2+23x_3+15x_5=132. \end(aligned) \right.$ dla zgodności.

Rozszerzoną macierz układu doprowadzamy do postaci krokowej:

$$ \left(\begin(tablica)(ccccc|c) 2 i 0 i 7 i -5 i 11 i 42\\ 1 i -2 i 3 i 0 i 2 i 17 \\ -3 i 9 i -11 & 0 i -7 i -64 \\ -5 i 17 i -16 i -5 i -4 i -90 \\ 7 i -17 i 23 i 0 i 15 i 132 \end(array) \right) \overset (r_1\leftrightarrow(r_3))(\rightarrow) $$ $$ \rightarrow\left(\begin(array)(ccccc|c) 1 i -2 i 3 i 0 i 2 i 17\\ 2 i 0 i 7 & -5 i 11 i 42\\ -3 i 9 i -11 i 0 i -7 i -64\\ -5 i 17 i -16 i -5 i -4 i -90\\ 7 i -17 i 23 & 0 & 15 & 132 \end(array) \right) \begin(array) (l) \phantom(0)\\ r_2-2r_1 \\r_3+3r_1 \\ r_4+5r_1 \\ r_5-7r_1 \end( tablica) \rightarrow \left(\begin(tablica)(ccccc|c) 1 i -2 i 3 i 0 i 2 i 17\\ 0 i 4 i 1 i -5 i 7 i 8\\ 0 i 3 i - 2 i 0 i -1 i -13\\ 0 i 7 i -1 i -5 i 6 i -5 \\ 0 i -3 i 2 i 0 i 1 i 13 \end(array) \right) \begin( array) (l) \phantom(0)\\ \phantom(0)\\4r_3+3r_2 \\ 4r_4-7r_2 \\ 4r_5+3r_2 \end(array) \rightarrow $$ $$ \rightarrow\left(\begin (tablica)(ccccc|c) 1 i -2 i 3 i 0 i 2 i 17\\ 0 i 4 i 1 i -5 i 7 i 8\\ 0 i 0 i -11 i 15 i -25 i -76 \\ 0 i 0 i -11 i 15 i -25 i -76 \\ 0 i 0 i 11 i -15 i 25 i 76 \end(tablica) \right) \begin(tablica) (l) \phantom(0 )\\ \phantom(0)\\\phantom(0) \\ r_4-r_3 \\ r_5+r_2 \end(array) \rightarrow \left(\begin(array)(ccccc|c) 1 i -2 & 3 i 0 i 2 i 17\\ 0 i 4 i 1 i -5 i 7 i 8\\ 0 i 0 i -11 i 15 i -25 i -76\\ 0 i 0 i 0 i 0 i 0 i 0 \\ 0 i 0 i 0 i 0 i 0 i 0 \end(tablica) \right) $$

Rozszerzoną macierz układu i macierz samego układu doprowadziliśmy do postaci krokowej. Ranga rozszerzonej macierzy układu jest równa trzy, ranga macierzy układu jest również równa trzy. Ponieważ system zawiera $n=5$ niewiadomych, tj. $\rang\widetilde(A)=\rang(A)\lt(n)$, to zgodnie z wnioskiem z twierdzenia Kroneckera-Capelliego układ ten jest nieokreślony, tj. ma nieskończoną liczbę rozwiązań.

Odpowiedź: System jest niepewny.

W drugiej części przeanalizujemy przykłady, które często pojawiają się w standardowych obliczeniach lub testach z matematyki wyższej: badanie spójności i rozwiązanie SLAE w zależności od wartości zawartych w nim parametrów.