Punctele singulare ale unei funcții și clasificarea lor. Puncte singulare izolate. Reziduuri și formule pentru calculul lor

Modele descrise prin sisteme de două ecuații diferențiale autonome.

planul de fază. Portret de fază. metoda izoclinului. izoclinele principale. Stabilitate în stare de echilibru. Sisteme liniare. Tipuri de puncte cheie: nod, șa, focalizare, centru. Exemplu: reacții chimice de ordinul întâi.

Cele mai interesante rezultate privind modelarea calitativă a proprietăților sistemelor biologice au fost obținute pe modele a două ecuații diferențiale, care permit un studiu calitativ folosind metoda planul de fază. Să considerăm un sistem de două ecuații diferențiale ordinare autonome de formă generală

(4.1)

P(x,y), Q(x,y)- funcţii continue definite într-un anumit domeniu G plan euclidian ( X y- coordonate carteziene) şi având în această zonă derivate continue de ordin nu mai mici decât prima.

Regiune G poate fi nelimitat sau limitat. Dacă variabile X y au o semnificație biologică specifică (concentrații de substanțe, abundență de specii), cel mai adesea zona G este cadranul pozitiv al semiplanului drept:

0 £ X< ¥ ,0 £ y< ¥ .

Concentrațiile de substanțe sau abundența speciilor pot fi limitate și de sus de volumul vasului sau de zona habitatului. Atunci intervalul de variabile are forma:

0 £ X< x 0 , 0 £ y< y 0 .

Variabile X y schimbare în timp în conformitate cu sistemul de ecuații (4.1), astfel încât fiecare stare a sistemului să corespundă unei perechi de valori ale variabilelor ( X y).

În schimb, pentru fiecare pereche de variabile ( X y) corespunde unei anumite stări a sistemului.

Luați în considerare un plan cu axe de coordonate pe care sunt trasate valorile variabilelor X y. Fiecare punct M acest plan corespunde unei anumite stări a sistemului. Un astfel de plan se numește plan de fază și descrie totalitatea tuturor stărilor sistemului. Punctul M(x, y) se numește punctul reprezentativ sau reprezentativ.

Lasati la momentul initial t=t 0 reprezentând coordonatele punctului M 0 (X(t 0),y(t 0)). În fiecare moment următor t punctul de reprezentare se va deplasa în funcție de modificările valorilor variabilelor X(t),y(t). Set de puncte M(X(t), YT)) pe planul de fază, a cărui poziţie corespunde stărilor sistemului în procesul de modificare a variabilelor în timp x(t), YT) conform ecuațiilor (4.1), se numește traiectoria fazei.

Setul de traiectorii de fază pentru diferite valori inițiale ale variabilelor oferă un „portret” ușor vizibil al sistemului. Clădire portret de fază vă permite să trageți concluzii despre natura modificărilor variabilelor X y fără a cunoaşte soluţiile analitice ale sistemului original de ecuaţii(4.1).

Pentru a reprezenta un portret de fază, este necesar să se construiască un câmp vectorial de direcții pentru traiectoriile sistemului în fiecare punct al planului de fază. Prin specificarea unui incrementD t>0,obținem incrementele corespunzătoare D Xși D y din expresii:

D x=P(x,y)D t,

D y=Q(x,y)D t.

direcția vectorială dy/dx la un moment dat ( X y) depinde de semnul funcţiilor P(x, y), Q(x, y)și poate fi dat de un tabel:

P(x,y)>0,Q(x,y)>0
P(x,y)<0,Q(x,y)<0
P(x,y)>0,Q(x,y)<0
P(x,y)<0,Q(x,y)>0

.(4.2)

Rezolvarea acestei ecuații y=y(x, c), sau implicit F(X y)=c, Unde Cu este constanta integrării, dă familia curbelor integrale din ecuația (4.2) - traiectorii de fază sistem (4.1) pe plan X y.

Metoda izoclinului

Pentru a construi un portret de fază, se folosește metoda izoclinei - pe planul de fază sunt trasate linii care intersectează curbele integrale la un unghi specific. Ecuația izoclinului este ușor de obținut din (4.2). Sa punem

Unde A– o anumită constantă. Sens A reprezintă tangenta pantei tangentei la traiectoria fazei și poate lua valori din -¥ la + ¥ . Înlocuind în loc de dy/dxîn (4.2) cantitatea A obținem ecuația izoclinului:

.(4.3)

Ecuația (4.3) determină în fiecare punct al planului singura tangentă la curba integrală corespunzătoare, cu excepția punctului în care P(x,y)= 0, Q (X y) = 0 , în care direcția tangentei devine nedefinită, deoarece valoarea derivatei devine nedefinită:

.

Acest punct este punctul de intersecție al tuturor izoclinelor - punct special. Ea dispare simultan derivatele temporale ale variabilelor Xși y.

Astfel, la punctul singular, ratele de modificare a variabilelor sunt egale cu zero. Prin urmare, punctului singular al ecuațiilor diferențiale ale traiectoriilor de fază (4.2) îi corespunde starea staționară a sistemului(4.1), iar coordonatele sale sunt valorile staționare ale variabilelor X y.

De un interes deosebit sunt izoclinele principale:

dy/dx=0, P(X y)=0 – izoclinul tangentelor orizontale și

dy/dx=¥ , Q(X y)=0 – izoclinul tangentelor verticale.

Prin construirea izoclinelor principale și găsirea punctului de intersecție a acestora (X y), ale căror coordonate îndeplinesc condițiile:

vom găsi astfel punctul de intersecție al tuturor izoclinelor planului de fază, la care direcția tangentelor la traiectoriile de fază este nedefinită. Acest - punct singular, care corespunde starea staționară a sistemului(Fig. 4.2).

Sistemul (4.1) are atâtea stări staționare câte puncte de intersecție ale izoclinelor principale sunt pe planul de fază.

Fiecare traiectorie de fază corespunde unui set de mișcări ale unui sistem dinamic care trec prin aceleași stări și care diferă între ele doar prin începutul referinței de timp.

Dacă sunt îndeplinite condițiile teoremei Cauchy, atunci prin fiecare punct al spațiului x, y, t trece printr-o singură curbă integrală. Același lucru este valabil, datorită autonomiei, pentru traiectorii de fază: o traiectorie de fază unică trece prin fiecare punct al planului de fază.

Stabilitate în stare de echilibru

Lăsați sistemul să fie în echilibru.

Atunci punctul reprezentativ este situat la unul dintre punctele singulare ale sistemului, în care, prin definiție:

.

Dacă un punct singular este stabil sau nu este determinat de dacă punctul reprezentativ pleacă sau nu cu o mică abatere de la starea staționară. Așa cum se aplică unui sistem de două ecuații, definiția stabilității în limbaje, ddupă cum urmează.

Starea de echilibru este stabilă dacă pentru orice zonă dată de abateri de la starea de echilibru (e )zona poate fi specificată d (e ), care inconjoara starea de echilibru si avand proprietatea ca nici o traiectorie care incepe in interiorul regiunii d , nu va ajunge niciodată la graniță e . (Fig. 4.4)

Pentru o clasă mare de sisteme - sisteme brute – a cărui natura comportamentului nu se schimbă cu o mică modificare a tipului de ecuații, informații despre tipul de comportament în vecinătatea stării staționare pot fi obținute prin studierea nu a originalului, ci a celor simplificate. liniarizat sistem.

Sisteme liniare.

Luați în considerare un sistem de două ecuații liniare:

.(4.4)

Aici a, b, c, d- constante, X y- Coordonate carteziene pe planul de fază.

Soluția generală va fi căutată sub forma:

.(4.5)

Înlocuiți aceste expresii în (4.4) și reduceți cu e l t:

(4.6)

Sistem algebric de ecuații (4.6) cu necunoscute A, B are o soluție diferită de zero numai dacă determinantul său, compus din coeficienții necunoscutelor, este egal cu zero:

.

Extinderea acestui determinant, obținem ecuația caracteristică a sistemului:

.(4.7)

Rezolvarea acestei ecuații oferă valorile indicatoruluil 1,2 , sub care sunt posibile valori diferite de zero pentru Ași B soluții ale ecuației (4.6). Aceste valori sunt

.(4.8)

Dacă expresia radicală este negativă, atuncil 1,2 numere complexe conjugate. Să presupunem că ambele rădăcini ale ecuației (4.7) au părți reale diferite de zero și că nu există rădăcini multiple. Atunci soluția generală a sistemului (4.4) poate fi reprezentată ca o combinație liniară de exponenți cu exponențil 1 , l 2 :

(4.9)

Pentru a analiza natura traiectoriilor posibile ale sistemului pe planul de fază, folosim transformare liniară de coordonate omogene, care va aduce sistemul la forma canonica:

,(4.10)

ceea ce permite o reprezentare mai convenabilă pe planul de fază comparativ cu sistemul original (4.4). Să introducem coordonate noiξ , η dupa formulele:

(4.1)

Din cursul algebrei liniare se știe că dacă părțile reale nu sunt egale cu zerol 1 , l 2 sistemul original (4.4) cu ajutorul transformărilor (4.11) poate fi întotdeauna transformat în forma canonică (4.10) și poate fi studiat comportamentul său pe planul de fazăξ , η . Luați în considerare diferitele cazuri care se pot prezenta aici.

Rădăcinile λ 1 , λ 2 – valabil și de același semn

În acest caz, coeficienții de transformare sunt reali, ne deplasăm din planul realX yla planul real ξ, η. Împărțind a doua din ecuațiile (4.10) la prima, obținem:

.(4.12)

Integrând această ecuație, găsim:

Unde .(4.13)

Să fim de acord să înțelegem prin λ 2 rădăcina ecuației caracteristice cu un modul mare, care nu încalcă generalitatea raționamentului nostru. Atunci, întrucât în ​​cazul în cauză rădăcinile λ 1 , λ2 – valabil și de același semn,A>1 , și avem de-a face cu curbe integrale de tip parabolic.

Toate curbele integrale (cu excepția axei η , care corespunde ) atingeți la originea axei ξ, care este și o curbă integrală a ecuației (4.11). Originea coordonatelor este un punct singular.

Să aflăm acum direcția de mișcare a punctului reprezentativ de-a lungul traiectoriilor de fază. Dacă λ 1, λ2 sunt negative, deci, după cum se vede din ecuațiile (4.10), |ξ|, |η| scade in timp. Punctul reprezentativ se apropie de origine, dar nu ajunge niciodată la ea. În caz contrar, aceasta ar contrazice teorema lui Cauchy, care afirmă că doar o traiectorie de fază trece prin fiecare punct al planului de fază.

Un astfel de punct singular prin care trec curbele integrale, la fel ca o familie de parabole trece prin origine, se numește nod (Fig. 4.5)

Starea de echilibru de tip nod la λ 1, λ2 < 0 este stabil conform lui Lyapunov, deoarece punctul reprezentativ se deplasează de-a lungul tuturor curbelor integrale către originea coordonatelor. Acest nod stabil. Dacă λ 1, λ2 > 0, atunci |ξ|, |η| crește cu timpul și punctul reprezentativ se îndepărtează de origine. În acest caz, punctul singular– nod instabil .

Pe planul de fază X y caracterul calitativ general al comportarii curbelor integrale va ramane, dar tangentele la curbele integrale nu vor coincide cu axele de coordonate. Unghiul de înclinare al acestor tangente va fi determinat de raportul coeficienților α , β , γ , δ în ecuaţiile (4.11).

Rădăcinile λ 1 , λ 2 sunt valabile și au semne diferite.

Convertiți din coordonate X y la coordonate ξ, η din nou real. Ecuațiile pentru variabilele canonice au din nou forma (4.10), dar acum semnele λ 1, λ2 diferit. Ecuația traiectoriei fazei are forma:

Unde , (4.14)

Integrând (4.14), găsim

(4.15)

Acest ecuația definește o familie de curbe de tip hiperbolic, unde ambele axe de coordonate sunt asimptotele (la A=1 am avea o familie de hiperbole isoscele). Axele de coordonate sunt, de asemenea, curbe integrale în acest caz– acestea vor fi singurele curbe integrale care trec prin origine. Fiecaredintre care constă din traiectorii în trei faze: a două mișcări către o stare de echilibru (sau departe de o stare de echilibru) și dintr-o stare de echilibru. Toate celelalte curbe integrale– sunt hiperbole care nu trec prin origine (Fig. 4.6) Acest punct singular se numește "şa ». Liniile de nivel de lângă șaua de munte se comportă ca traiectorii de fază în vecinătatea șei.

Să luăm în considerare natura mișcării punctului reprezentativ de-a lungul traiectoriilor de fază în apropierea stării de echilibru. Să, de exemplu,λ1 >0, λ2<0 . Apoi punctul reprezentativ plasat pe axă ξ , se va îndepărta de origine și se va plasa pe axă η – se va apropia la infinit de originea coordonatelor, fără a ajunge la el într-un timp finit. Oriunde punctul reprezentativ este în momentul inițial (cu excepția punctului singular și a punctelor de pe asimptotă η =0), se va îndepărta în cele din urmă de starea de echilibru, chiar dacă la început se deplasează de-a lungul uneia dintre curbele integrale către un punct singular.

Este evident că punctul singular de tip șa este întotdeauna instabil . Doar în condiții inițiale special alese pe asimptotăη =0 sistemul se va apropia de o stare de echilibru. Totuși, acest lucru nu contrazice afirmația că sistemul este instabil. Daca numarati, că toate stările inițiale ale sistemului pe planul de fază sunt la fel de probabile, atunci probabilitatea unei astfel de stări inițiale care corespunde mișcării în direcția La punctul singular este egal cu zero. Prin urmare, orice mișcare reală va scoate sistemul din starea de echilibru.Revenind la coordonateX y,obținem aceeași imagine calitativă a naturii mișcării traiectoriilor în jurul originii.

Granița dintre cazurile considerate ale unui nod și o șa este cazul când unul dintre indicatorii caracteristici, de exemplu λ 1 , dispare, ceea ce apare atunci când determinantul sistemului- expresie adbc=0(vezi formula 4.8 ). În acest caz, coeficienții părților din dreapta ale ecuațiilor (4.4) sunt proporționali unul cu celălalt:

iar sistemul are drept stări de echilibru toate punctele dreptei:

Curbele integrale rămase sunt o familie de drepte paralele cu o pantă , de-a lungul căruia punctele reprezentative fie se apropie de starea de echilibru, fie se îndepărtează de aceasta, în funcție de semnul celei de-a doua rădăcini a ecuației caracteristice λ 2 = a+d.(Fig. 4. 7 ) În acest caz, coordonatele stării de echilibru depind de valoarea inițială a variabilelor.

Rădăcinile λ 1 , λ 2 – complexconjuga

În acest caz, pe buneXși y noi vom au conjugate complexe ξ , η (4.10) . Cu toate acestea, prin introducerea unei alte transformări intermediare, este posibil și în acest caz să se reducă considerația la o transformare omogenă liniară reală. Sa punem:

(4.16)

Unde a, b,și u,v – valori reale. Se poate arăta că transformarea dinX y La u,v este, în ipotezele noastre, reală, liniară, omogenă cu un determinant diferit de zero. Datorita ecuatiilor(4.10, 4.16) avem:

Unde

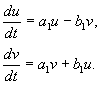(4.17)

Împărțirea celei de-a doua ecuații la prima, primim:

care este mai ușor de integrat, dacă trecem la sistemul de coordonate polare (r, φ ) . După înlocuire ajungem de unde:

.(4.18)

Astfel, pe planul de fazău, vavem de-a face cu o familie de spirale logaritmice, fiecare dintre ele arepunct asimptotic la origine.Punct singular care este punctul asimptotic al tuturor curbelor integrale având forma spiralelor, prieten cuib înprieten, sunat se concentreze ( fig.4.8 ) .

Să luăm în considerare natura mișcării punctului reprezentativ de-a lungul traiectoriilor de fază. Înmulțirea primei ecuații (4.17) cuu, iar al doilea la vși adăugând , obținem:

Unde

Lăsa A 1 < 0 (A 1 = Reλ ) . Punctul reprezentativ se apropie apoi continuu de origine fara a ajunge la ea intr-un timp finit. Aceasta înseamnă că traiectoriile de fază sunt spirale răsucitoare și corespund oscilațiilor amortizate variabile. Acest - focalizare constantă .

În cazul unui focus stabil, ca și în cazul unui nod stabil, nu numai condiția Lyapunov este îndeplinită, ci și o cerință mai strictă. Și anume, pentru orice abateri inițiale, sistemul se va întoarce în cele din urmă cât de aproape se dorește de poziția de echilibru. O astfel de stabilitate, în care abaterile inițiale nu numai că nu cresc, dar decadează, tinde spre zero, se numește stabilitate absolută .

Dacă în formulă (4.18) A 1 >0 , atunci punctul reprezentativ se îndepărtează de origine și avem de-a face focalizare instabilă . Când se deplasează dintr-un avionu,vla planul de fazăX, yspiralele vor rămâne și ele spirale, dar vor fi deformate.

Luați în considerare acum cazul cândA 1 =0 . Traiectorii de fază în avionu, vvor fi cercuri care în avionX yse potrivesc elipselor:

Astfel, laa 1=0 printr-un punct specialx= 0,y= 0 nicio curbă integrală nu trece. Un astfel de punct singular izolat, în apropierea căruia curbele integrale sunt curbe închise, în special, elipse încorporate una în cealaltă și care înglobează punctul singular, se numește centru.

Astfel, sunt posibile șase tipuri de echilibru, în funcție de natura rădăcinilor ecuației caracteristice (4.7). Vedere a traiectoriilor de fază în avion X y pentru aceste șase cazuri este prezentat în Fig. 4.9.

Orez. 4.9.Tipuri de portrete de fază în vecinătatea unei stări staționare pentru sistemul de ecuații liniare (4.4).

Cele cinci tipuri de stări de echilibru sunt brute, natura lor nu se schimbă cu modificări suficient de mici în părțile din dreapta ecuațiilor (4.4). În acest caz, modificările ar trebui să fie mici nu numai în partea dreaptă, ci și în derivatele lor de ordinul întâi. A șasea stare de echilibru - centrul - nu este grosieră. Cu mici modificări ale parametrilor din partea dreaptă a ecuațiilor, se ajunge într-un focus stabil sau instabil.

Diagrama de bifurcație

Să introducem notația:

. (4.11)

Atunci ecuația caracteristică poate fi scrisă sub forma:

. (4.12)

Să considerăm un plan cu coordonate carteziene dreptunghiulare s , D și marcați pe el ariile corespunzătoare unuia sau altui tip de stare de echilibru, care este determinată de natura rădăcinilor ecuației caracteristice

.(4.13)

Condiția pentru stabilitatea stării de echilibru va fi prezența unei părți reale negative a lui yl 1 și l 2 . O condiție necesară și suficientă pentru aceasta este îndeplinirea inegalitățilors > 0, D > 0 . Pe diagrama (4.15), această condiție corespunde punctelor situate în primul sfert al planului parametrilor. Punctul singular va fi focalizarea dacăl 1 și l 2 complex. Această condiție corespunde acelor puncte ale planului pentru care , acestea. puncte dintre două ramuri ale unei paraboles 2 = 4 D. Punctele semiaxelor s = 0, D>0, corespund stărilor de echilibru de tip centru. De asemenea,l 1 și l 2 - semne valide, dar diferite, i.e. un punct singular va fi o şa dacă D<0, etc. Ca rezultat, obținem o diagramă de partiție a planului parametrilor s, D, în regiuni corespunzătoare diferitelor tipuri de stări de echilibru.

Orez. 4.10. Diagrama de bifurcație

pentru sistemul de ecuații liniare 4.4

Dacă coeficienţii sistemului liniar a, b, c, d depinde de un parametru, atunci când acest parametru este modificat, valorile se vor schimba și eles , D . La trecerea granițelor, natura portretului de fază se schimbă calitativ. Prin urmare, astfel de granițe sunt numite granițe de bifurcație - pe părțile opuse ale graniței, sistemul are două portrete de fază topologic diferite și, în consecință, două tipuri diferite de comportament.

Diagrama arată cum pot avea loc astfel de schimbări. Dacă excludem cazurile speciale - originea coordonatelor - atunci este ușor de observat că șaua poate intra într-un nod, stabil sau instabil la traversarea axei y. Un nod stabil se poate muta fie într-o șa, fie într-un focus stabil și așa mai departe. Rețineți că tranzițiile nod stabil-focal stabil și tranzițiile nod instabil-focal instabil nu sunt bifurcaționale, deoarece topologia spațiului de fază nu se schimbă în acest caz. Vom vorbi mai detaliat despre topologia spațiului de fază și a tranzițiilor de bifurcație în Lecția 6.

În tranzițiile de bifurcație, natura stabilității punctului singular se schimbă. De exemplu, o focalizare stabilă prin centru se poate transforma într-o focalizare instabilă. Această bifurcație se numește Bifurcația Andronov-Hopf după numele oamenilor de știință care l-au studiat. Odată cu această bifurcare în sistemele neliniare, se naște un ciclu limită, iar sistemul devine auto-oscilant (vezi prelegerea 8).

Exemplu. Sistem de reacții chimice liniare

Substanţă X curge din exterior cu o viteză constantă, se transformă în substanța Y și cu o viteză proporțională cu concentrația substanței Y, este scos din sfera de reacție. Toate reacțiile sunt de ordinul întâi, cu excepția influxului de materie din exterior, care are ordinul zero. Schema de reacție arată astfel:

(4.14)

și este descris de sistemul de ecuații:

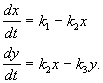(4.15)

Obținem concentrații staționare prin echivalarea părților din dreapta cu zero:

.(4.16)

Luați în considerare portretul de fază al sistemului. Să împărțim a doua ecuație a sistemului (4.16) la prima. Primim:

.(4.17)

Ecuația (4.17) determină comportamentul variabilelor pe planul de fază. Să construim un portret de fază al acestui sistem. Mai întâi, desenăm izoclinele principale pe planul de fază. Ecuația izoclinului tangentelor verticale:

Ecuația pentru izoclinul tangentelor orizontale:

Punctul singular (starea staționară) se află la intersecția izoclinelor principale.

Acum să determinăm în ce unghi axele de coordonate intersectează curbele integrale.

Dacă x= 0, atunci.

Astfel, tangenta pantei tangentei la curbele integrale y=y(x), traversând axa y x=0, este negativă în semiplanul superior (amintim că variabilele X y au valori de concentrație și, prin urmare, ne interesează doar cadranul din dreapta sus al planului de fază). În acest caz, valoarea tangentei unghiului de înclinare al tangentei crește cu distanța de la origine.

Luați în considerare axa y= 0. La intersecția acestei axe, curbele integrale sunt descrise de ecuație

La tangentea pantei curbelor integrale care traversează axa absciselor este pozitivă și crește de la zero la infinit cu creșterea X.

La .

Apoi, cu o creștere suplimentară, tangenta pantei scade în valoare absolută, rămânând negativă și tinde spre -1 la X ® ¥ . Cunoscând direcția tangentelor la curbele integrale pe izoclinele principale și pe axele de coordonate, este ușor să construim întreaga imagine a traiectoriilor de fază.

Natura stabilității punctului singular va fi stabilită prin metoda Lyapunov. Determinantul caracteristic al sistemului are forma:

.

Extinderea determinantului, obținem ecuația caracteristică a sistemului: , adică rădăcinile ecuației caracteristice sunt ambele negative. Prin urmare, starea staționară a sistemului este un nod stabil. În același timp, concentrația substanței X tinde spre o stare staționară întotdeauna monotonă, concentrația substanței Y poate trece prin min sau max. Regimurile oscilatorii într-un astfel de sistem sunt imposibile.

Lăsa zq - punct singular al funcției f(z), t.s. f(z) dar este analitic în acest moment (în special, poate să nu fie definit la acesta). Dacă există o astfel de vecinătate perforată a punctului zq (adică, mulțimea O z - zq f(z) este aliatic, atunci zo numit punct singular izolat funcții f(z). Această definiție este păstrată și în cauză zn = oo, dacă iodul este o vecinătate perforată a unui punct zq = oo intelege multimea z > EU SUNT - apariţia unui cerc centrat la origine. Cu alte cuvinte, punctul singular zq se spune a fi izolat dacă există o vecinătate a acestui punct în care există alte puncte singulare diferite de zq. Peste tot mai jos, luăm în considerare doar puncte singulare ale unui caracter cu o singură valoare (funcția f(z) presupus a fi unic).

În funcţie de comportamentul funcţiei f(z) la z -> zq Există trei tipuri de puncte singulare. Punct singular izolat funcții zq f(z) numit:

1) punct singular detașabil dacă există o limită finită

2) stâlp dacă există o limită

3) punct esential, dacă f(z) nu are nici o limită finită, nici infinită pentru z-> zq.

EXEMPLUL 26.1. Să arătăm că toate cele trei tipuri de puncte singulare sunt realizate. Considera f(z)= punct zq = 0 este izolat

punct singular al acestei funcții. Folosind formula (22.12), obținem expansiunea

din care rezultă că există lim fi(z)= 1. Prin urmare, zq = 0 este

este un punct singular detașabil al funcției fi(z).

Funcţie f'j(z) =--- are un stâlp într-un punct zo= 1 deoarece

2 r" X

Luați în considerare acum funcția )Z Z)= e 1 ^ r și arătați că zo = O este un punct singular esențial al acestei funcții. Când te străduiești z la zero de-a lungul axei reale, limitele stânga și dreapta ale funcției f (z) diferit: lim Cu 1 / 1 = 0,lim cu 1 /* = os. Asta implică,

x->0-0 x->0+0

ce f:i(z) nu are nici o limită finită, nici infinită pentru 2 -> Oh, adică zq = 0 este un punct esenţial singular al acestei funcţii. (Rețineți că așa cum tinde punctul z-iy la zero pe funcția axului imaginar

nu are nicio limită.)

Desigur, există și puncte singulare neizolate. De exemplu. funcția are poli în puncte z n = -, P= ±1, ±2,...

Prin urmare, Zq = 0 este un punct singular neizolat al acestei funcții: în orice vecinătate (arbitrar de mică) a acestui punct există alte puncte singulare g p.

Lăsa zo- punct singular izolat final al unei funcții f(z). Atunci f(z) este asemanator intr-un cartier perforat 0 Zo al punctului zo această vecinătate poate fi privită ca un inel cu raza interioară r = 0. Prin teorema 25.1, în vecinătatea luată în considerare, funcția f(z) poate fi extins într-o serie Laurent (25.2). Vom arăta că comportamentul funcției pentru 2 -> zq (adică tipul punctului singular zo) depinde de forma părții principale a descompunerii (25.2); această împrejurare explică originea termenului „partea principală”.

TEOREMA 2G.2. Un punct singular izolat zo al unei funcții f(z) este detașabil dacă și numai dacă expansiunea Loap într-o vecinătate perforată a acestui punct are oid

acestea. constă doar din partea corectă, iar toți coeficienții părții principale sunt egali cu glonțul.

Dovada. 1. Lasă zo este un punct singular detașabil. Să demonstrăm că expansiunea Laurent a funcției f(z) are forma (26.1). De la punctul singular zo detașabil, atunci există o limită limită finită f(z) = A. Prin urmare, f(z) mărginită într-o vecinătate perforată 0 z - zq a punctului zo, acestea. )(z) pentru toți z din acest cartier. Luați oricare R. U р /?| și folosiți formulele (25.3) pentru coeficienții seriei Laurent:

Pentru coeficienții părții principale a expansiunii n =- 1,-2,... Pentru astfel de valori P noi avem p~n-e 0 la R-> 0. Deoarece valoarea R poate fi ales arbitrar mic, atunci domnule~" poate fi arbitrar mic. Deoarece |c t,| ^ Mr~nși cn nu depind de p, atunci cn = 0 pentru și= - 1, -2,..., ceea ce urma să fie demonstrat.

2. Să presupunem acum că expansiunea Laurent are forma (26.1). Seria (26.1) este o serie de puteri și. prin urmare, converge nu numai în cei perforați, ci și în întregul cartier z-zq inclusiv punctul zo; suma sa S(z) este analitic pentru z și S(z) = )(z) la 0 z - zo R. Prin urmare, există o limită limită finită )(z)\u003d Pm 5 (r) \u003d 5 (r) - Prin urmare, punctul singular zq

Z->Zo Z-*Zo

de unică folosință. Teorema a fost demonstrată.

Cometariu. Din demonstrarea teoremei rezultă că într-o vecinătate perforată 0 z - zo a unui punct singular detașabil, funcția f(z) coincide cu funcția S(r), care este analitică în întreaga vecinătate z - zo . Prin urmare, dacă punem /(th) = S(zq), apoi, fără a modifica valorile funcției f(z)în orice punct al vecinătății perforate, facem această funcție analitică în r, i.e. „eliminați” caracteristica. Aceasta explică termenul de „singularitate amovibilă”. Este firesc să considerăm astfel de puncte ca regulate și nu ca puncte singulare ale funcției f(z).

Luați în considerare, de exemplu, funcția

În exemplul 26.1, s-a arătat că Pm (n) = 1. i.e. punct singular

zq = 0 este detașabil. Setând /i(0) = 1, eliminăm astfel singularitatea și obținem o funcție care este analitică în punctul zq = 0 (și în întregul plan C).

Să caracterizăm acum polii în termeni de expansiuni Laurent.

Teorema 26.3. Un punct singular izolat Zo al unei funcții f(z) este un pol dacă și numai dacă, când partea principală a expansiunii Laurent cu centrul Zq are doar un număr finit de distincte

de la zero coeficienți cu n:

Dovada. 1. Lasă zq - pol, i.e. lim /( z) = oo.

Să demonstrăm că expansiunea Laurent a funcției f(z) are forma (2G.2). Din moment ce lim f(z)= oo. atunci există o vecinătate perforată a punctului

ki zq. în care f(z) este analitic și nu are zerouri. Apoi funcția g(z) = 1 /f(z) va fi, de asemenea, analitic în acest cartier perforat, și lim g(z)= 0. Prin urmare, Zo este de unică folosință *-? *0

punct singular al funcției g(z). Să redefinim g(z) la punct zo, punând g(zo)= 0. Apoi g(z) devine analitic în întreaga vecinătate a punctului (neperforat). z 0 ,și z0 va fi zeroul său izolat. Notează prin N multiplicitatea (ordinea) acestui zero. După cum sa arătat în §23, într-o vecinătate a punctului funcția zq g(z) reprezentabil în formă (vezi (23.2))

și (z$) f 0 și y>(z) este analitic într-o apropiere a punctului zo- pentru că ip(z) continuu la punct zoși g>(zo) F 0" atunci ip(z) nici în apropierea acestui punct nu are zerouri. Prin urmare, funcția 1 /-p(z) va fi, de asemenea, analitic în acest cartier și, prin urmare, se extinde în el într-o serie Taylor:

Extinderea parantezelor și schimbarea denumirilor coeficienților, scriem ultima expansiune sub forma

unde c_jv = 1>o f 0. Astfel, partea principală a expansiunii Laurent a lui f(r) conține doar un număr finit de termeni; am ajuns la egalitatea cerută (26.2).

2. Lăsați într-o vecinătate perforată a unui punct th funcţie )(z) este reprezentată de expansiunea Laurent (26.2) (într-o formă mai extinsă, vezi (26.3)), a cărei parte principală conține doar un număr finit de termeni și Cu- d" f 0. Trebuie să dovedim că Zq - pol de funcție f(z).Înmulțirea egalității (26.3) cu (G - G o) iV , obținem funcția

Seria din (26.4) este o serie de puteri convergentă către o funcție analitică nu numai în zona perforată, ci și în întreaga vecinătate a punctului. Zq. Prin urmare, funcția h(z) devine analitic în acest cartier dacă îl extindem în th prin decor h(zo)= s_dg f 0. Apoi

Astfel, punctul o este un pol și se demonstrează teorema 26.3.

Multiplicitatea (ordinea) funcției zero g(z)= 1//(r) se numește ordinea polului funcția /(r). Dacă N- ordinea stâlpului este atunci g(z)= (r - Zo)N ip(z), si pleaca) F 0 și, așa cum se arată în prima parte a demonstrației teoremei 26.3, expansiunea lui f(r) are forma (26.3), unde c_/v f 0. În schimb, dacă f(r) se extinde în seria (26.3) și e-z F 0, atunci

c.t. N- ordinea polului funcţiei f(r). În acest fel, ordinea polului zq al funcției/(G) este egal cu numărul coeficientului principal diferit de zero al părții principale a expansiunii Laurent în vecinătatea perforată a punctului zq(adică egal cu un astfel de număr N, ce s_dg f 0 și sp= 0 la P > N).

Să demonstrăm următoarea afirmație, care este convenabilă) pentru aplicații.

Corolarul 26.4. Punctul zq este un pol de ordinul N al ficțiunii/(G) dacă și numai dacă/(G) reprezintă sub formă

unde h(z) este o funcție analitică într-o vecinătate a unui punct th și h(zo) f 0.

Dovada. Funcţie cp(z) = l/h(z) este analitică în vreo vecinătate a punctului r. Condiția Corolarului 26.4 este echivalentă cu următoarea:

Asa de zq - multiplicitate zero N funcții g(z).și de aici polul multiplicității N funcții /(2).

Exemplul II 26.5. Găsiți puncte singulare izolate ale unei funcții și determinați tipul lor.

D e u c ţie n. Punctele în care (z 2 + 1 )(z+ H) 2 = 0. Dacă z 2 L- 1 = 0 apoi 2 = ±g dacă (z 4- H) 2 = 0, atunci z= -3. Prin urmare, funcția are trei puncte singulare z= r, 22 = -r, Z3 = - 3. Luați în considerare z:

G - stâlp de ordinul întâi (am folosit Corolarul 26.4). Se poate demonstra în mod similar că 22 = -i tot un stâlp de ordinul întâi. Pentru 2h avem:

Să trecem la considerarea punctelor esențial singulare.

Teorema 26.6. Un punct singular izolat zq al unei funcții f(z) este esențial singular dacă și numai dacă partea principală a expansiunii Laurent centrată pe zq are infinit de diferite de. zero, coeficienți cu p.

Dovada. Teorema 26.6 rezultă direct din teoremele 26.2 și 26.3. Într-adevăr, dacă punctul zq este esențial singular, atunci partea principală a expansiunii Laurent nu poate fi absentă sau nu poate conține un număr finit de termeni (altfel punctul Zq va fi fie detașabil, fie un stâlp). Prin urmare, numărul de termeni din partea principală trebuie să fie infinit.

În schimb, dacă partea principală conține infinit de membri, atunci Zq nu poate fi nici un punct detașabil, nici un stâlp. În consecință, acest punct este esențial singular.

Conform definiției, un punct esențial singular se caracterizează prin faptul că funcția f(2) nu are limită nici finită, nici infinită pentru z ->zq. O idee mai completă despre cât de neregulat este comportamentul unei funcții într-o vecinătate a unui punct esențial singular este dată de următoarea teoremă.

Teorema 26.7 (teorema lui Sochocki). Dacă zq este esențial singular, atunci punctul funcției f(z), apoi pentru orice număr complex L, inclusiv A = oo, există o succesiune de puncte z n astfel încât z n -> zo şi lim f(zn) = A.

n->os

Dovada. Luați în considerare mai întâi cazul A = oo. În prima parte a demonstrației teoremei 2G.2, am stabilit că dacă f(z) este mărginită într-o vecinătate perforată a punctului r0, apoi toți coeficienții c, n = - 1, - 2,... ale părții principale sunt egale cu zero (și, în consecință, singularitatea în th este detașabilă). Deoarece, prin presupunere, r este un punct esențial singular, funcția /(r) este nemărginită în orice vecinătate perforată a punctului r. Să luăm o vecinătate îngustă 0 Z astfel încât f(zi) > 1 (dacă |/(r)| z - zo R/2 există un punct z-2 , unde |/(dd)| > 2 etc.: în cartierul perforat O 71. Este evident că rn -e go și lim /(r«) = oo. Astfel, în cazul A = oo, Teorema 26.7

dovedit.

Lasă acum A f oo. Să presupunem mai întâi că există un cartier perforat 0

= -aa---- va fi analitic în acest cartier perforat și, în consecință,

/(G) - A

în consecință, r este un punct singular izolat al funcției Φ(r). Să arătăm. că r0 este un punct esenţial singular al lui Φ(r). Să fie greșit. Atunci există o limită limită Φ(r), fie finită, fie infinită. pentru că

/(r) = A + , atunci există și Hsh /(r), ceea ce contrazice condiția

F(g) ~ :-*z 0

vedere a teoremei. Astfel r0 este un punct esenţial singular al funcţiei Φ(r). Conform celor demonstrate mai sus, există o succesiune de puncte r n astfel încât r n o și lim Φ(r n) = oo. De aici

Am demonstrat afirmația necesară sub ipoteza că f(r) F Aîntr-o vecinătate perforată a punctului r. Să presupunem acum că acest lucru nu este adevărat, adică. în orice vecinătate perforată în mod arbitrar mică a punctului th există un astfel de punct G", că f(r") = A. Atunci pentru oricare Pîn vecinătatea perforată 0 f(z u) = L. Astfel, afirmaţia cerută este adevărată P-iuo

în toate cazurile, iar teorema 26.7 este demonstrată.

Conform teoremei (Sokhotsky) 26.7, în orice vecinătate (arbitrar de mică) perforată a unui punct esențial singular, funcția f(r) ia valori arbitrar apropiate de orice număr din planul complex extins C.

Pentru a studia puncte singulare izolate, binecunoscutele expansiuni Taylor ale funcțiilor elementare de bază sunt adesea utile.

EXEMPLUL 2G.8. Determinați tipul punctului singular zq = 0 pentru funcție

Rezolvate și e. Extindem numărătorul și numitorul într-o serie Taylor în puteri ale lui r. Înlocuind în (22.11) 3 zîn loc de r și scăderea 1, obținem

Folosind (22.12), obținem extinderea numitorului:

Serii din aceste expansiuni converg în întregul plan complex €. Noi avem

și /2(2) sunt analoge într-o vecinătate a punctului zo = 0 (și chiar în întregul plan) și /2(20) F 0, atunci h(z) este, de asemenea, analitic în apropierea punctului gF 0. Conform Corolarului 26.4, punctul Zo = 0 este polul comenzii N = 4.

Exemplul II 26.9. Găsiți puncte singulare ale unei funcții f(z)= sin j - și determinați tipul lor.

P e în e și e. Funcția are un singur punct singular final zq = 1. În alte puncte din C, funcția w =--- analitic; de unde funcţia păcat w va fi analitic.

Înlocuind în expansiunea sinusului (22.12) - în loc de r, obținem

Am obținut expansiunea funcției sin într-o serie Laurent într-o vecinătate perforată a punctului 20 = 1. Deoarece expansiunea rezultată conține infiniti termeni cu puteri negative (r - 1), atunci zq = 1 este un punct singular esențial (în acest caz, expansiunea Laurent constă numai din partea principală, iar partea corectă lipsește).

De remarcat că în acest caz a fost posibil să se stabilească și natura singularității direct din definiție, fără a recurge la extinderea seriei. Într-adevăr, există secvențe (r") și (2") care converg către zo= 1 și astfel încât f(z" n)= 1, /(2") = 0 (specificați singur astfel de secvențe). Deci, f(z) nu are limită când z -> 1 și de aici și ideea zq - 1 este esențial singular.

Să introducem conceptul de extindere Laurent a unei funcții în vecinătatea unui punct Zq = 00 și luați în considerare legătura dintre expansiune și natura singularității în acest punct. Rețineți că definițiile unui punct singular izolat și tipul acestuia (detașabil, pol sau, în esență, singular) sunt transferate la caz zq = oc neschimbat. Dar teoremele 26.2. 26.3 și 26.6, legate de natura expansiunilor Laurent, trebuie modificate. Ideea este că membrii c n (z - 2o) p. P= -1,-2,..., partea principală, care definește „‘neregularitatea” funcției în apropierea punctului final Zq, deoarece 2 tinde să oo, se vor comporta „corect” (tind spre 0). Dimpotrivă, membrii părții obișnuite cu P= 1,2,... va tinde spre oo; ele determină natura singularităţii în Zq = oo. Prin urmare, partea principală a expansiunii în vecinătatea oo va fi termenii cu puteri pozitive P,și corectă - cu negativ.

Să introducem o nouă variabilă w = 12. Funcţie tv= 1/2, extins astfel încât u(oo) = 0, unu-la-unu și mapează conform vecinătății z > R puncte zq = 00 în vecinătatea lui |w| wq = 0. Dacă funcţia f(z) analitice într-un cartier perforat R z Zq = oc, apoi funcția G(w) = f(l/w) va fi analitic în cartierul galben 0 wo = 0. Deoarece pentru 2 -> oo va fi w-> 0, atunci

Asa de G(w) are la punct wq = 0 este o singularitate de același tip ca f(z) la punct Zq = 00. Să extindem funcția G(w) într-o serie Laurent într-o vecinătate perforată a punctului wo = 0:

Sumele din partea dreaptă a lui (26.5) reprezintă părțile corecte și, respectiv, principale ale expansiunii. Să trecem la variabilă z, substituind w = 1/z:

denotând P\u003d -A *, 6 * \u003d 6_ " \u003d cu pși observând că G(l/z) = f(z), primim

Descompunerea (2G.G) se numește Expansiunea Laurent a funcției f(z) într-o vecinătate perforată a punctului zq= oo. Prima sumă din (2G.6) este numită partea dreaptă, iar a doua sumă este parte principală această descompunere. Deoarece aceste sume corespund părților corecte și principale ale expansiunii (26.5), extinderea (26.6) satisface analogii teoremelor 26.2, 26.3 și 26.6. Astfel, următoarea teoremă este un analog al teoremei 26.2.

Teorema 26.10. Punct singular izolatZq - os (funcții/(G) este detașabil dacă și numai dacă expansiunea Laurent într-o vecinătate perforată a acestui punct are forma

c.t. constă doar din partea corectă.

Punem /(oo) = co. Funcția definită de seria (26.7) convergentă în vecinătate z > R punctele 2o \u003d oc, numite analitic în punctul z o = oo. (Rețineți că această definiție este echivalentă cu analiticitatea funcției G(w) la punct wo = 0.)

Exemplul 26.11. Investigați punctul singular zq = oo al funcției

Din moment ce limita este finită, atunci zo = oo este un punct singular detașabil al funcției f(r). Dacă punem /(oo) = lim J(z)= 0, atunci f(z) va deveni

tic la un moment dat Zo= os. Să arătăm cum să găsim expansiunea corespunzătoare (26.7). Să trecem la variabilă w = 1 fz.Înlocuind z= 1/?e, obținem

(ultima egalitate este valabilă în vecinătatea punctată a punctului ww = 0, dar vom extinde definiția (7(0) = 0). Funcția rezultată are puncte singulare w =±i, w =-1/3, iar la punct Wq = 0 este analitic. Funcția de extindere G(w) treptat w(așa cum sa făcut în Exemplul 25.7) și înlocuind în seria de puteri rezultată w = 1/z se poate obține expansiunea (26.7) a funcției f(z).

Teorema 26.3 pentru caz zo= oo va fi rescris în următoarea formă.

Teorema 26.12. Punct singular izolat du-te = oc funcția f(z) este un pol dacă și numai dacă partea principală a expansiunii Laurent (26.6) are doar un număr finit de coeficienți diferiti de zero Cu":

Aici seria este partea obișnuită, iar polinomul între paranteze este partea principală a expansiunii. Multiplicitatea polului în oc este definită ca multiplicitatea polului wq = 0 funcții G(z). Este ușor de observat că multiplicitatea polului coincide cu numărul Nîn (26,8).

Q p | (i 2 + 1) (z + 3) 2

Sarcină. Arată că funcția f(z) =-- -- are in

punct zo = oo ordinea polului 3.

Teorema 26.6 asupra unui punct singular esențial este rescrisă pentru caz zo= os aproape textual, și nu ne oprim asupra ei în detaliu.

Seria Taylor servește ca un instrument eficient pentru studierea funcțiilor care sunt analitice în cercul zol. Pentru a studia funcțiile care sunt analitice într-o regiune inelară, se dovedește că este posibil să se construiască expansiuni în puteri pozitive și negative (z - zq) ale formă care generalizează expansiunile Taylor. Seria (1), înțeleasă ca suma a două serii, se numește seria Laurent. Este clar că regiunea de convergență a seriei (1) este partea comună a regiunilor de convergență a fiecărei serii (2). Să o găsim. Aria de convergență a primei serii este un cerc a cărui rază este determinată de formula Cauchy-Hadamard În interiorul cercului de convergență, seria (3) converge către o funcție analitică, iar în orice cerc cu rază mai mică, converge absolut si uniform. A doua serie este o serie de puteri în raport cu variabila Seria (5) converge în cadrul cercului său de convergență către funcția analitică a variabilei complexe m-*oo, iar în orice cerc de rază mai mică converge absolut și uniform, ceea ce înseamnă că regiunea de convergență a seriei (4) este aspectul cercului - Dacă atunci există o regiune comună de convergență a seriei (3) și (4) - un inel circular în care seria (1) converge către o funcție analitică. Mai mult, în orice inel, acesta converge absolut și uniform. Exemplul 1. Determinați regiunea de convergență a seriei rad Laurent Puncte singulare izolate și clasificarea lor (z), care este univalorică și apolitică într-un inel circular, pot fi reprezentate în acest inel ca suma unei serii convergente ai cărei coeficienți Cn sunt determinate și calculate în mod unic prin formulele în care 7p este un cerc cu raza m Să fixăm un punct arbitrar z în interiorul inelului R Construim cercuri cu centre in punctul r0 ale caror raze satisfac inegalitatile si consideram un nou inel Conform teoremei integrale a lui Cauchy pentru un domeniu multiconectat, avem Sa transformam fiecare dintre integralele in suma (8) separat. Pentru toate punctele £ de-a lungul cercului 7d*, este îndeplinită relația de sumă a unei serii uniform convergente 1 1. Prin urmare, fracția ^ poate fi reprezentată în vi- /" / Într-un mod oarecum diferit, pentru toate punctele ξ pe cercul ir> avem relația Prin urmare, fracția ^ poate fi reprezentată ca suma unei serii uniform convergente în formulele (10) și (12) sunt funcții analitice într-un inel circular. Prin urmare, prin teorema lui Cauchy, valorile integralelor corespunzătoare nu se schimbă dacă cercurile 7/r și 7r/ sunt înlocuite cu orice cerc. Acest lucru ne permite să combinăm formulele (10) și (12).Înlocuind integralele din partea dreaptă a formulei (8) cu expresiile lor (9) și respectiv (11), obținem expansiunea dorită.Deoarece z este un arbitrar punct al inelului, rezultă că seria ( 14) converge către funcția f(z) peste tot în acest inel, iar în orice inel seria converge către această funcție în mod absolut și uniform. Să demonstrăm acum că descompunerea formei (6) este unică. Să presupunem că are loc încă o descompunere.Atunci, peste tot în interiorul inelului R, avem Pe circumferință, seria (15) converg uniform. Înmulțiți ambele părți ale egalității (unde m este un număr întreg fix și integrați ambele serii termen cu termen. Ca rezultat, ajungem în partea stângă și în partea dreaptă - Csh. Astfel, (4, \u003d St. Deoarece m este un număr arbitrar, atunci ultima serie de egalitate (6), ai cărei coeficienți sunt calculați prin formulele (7), se numește seria Laurent a funcției f(z) din inelul 7) pentru coeficienții seriei Laurent sunt rar utilizate în practică, deoarece, de regulă, necesită calcule greoaie.De obicei, dacă este posibil, se folosesc expansiuni Taylor gata făcute ale funcțiilor elementare.Pe baza unicității expansiunii, orice metodă legitimă duce la același rezultat. Exemplul 2 Luați în considerare expansiunile din seria Laurent ale funcțiilor diferitelor domenii, presupunând că Fuiscija /(z) are două puncte singulare: Prin urmare, există trei domenii de inel şi, centrat în punctul r = 0. în fiecare dintre care funcţia f(r) este analitică: a) cercul este exteriorul cercului (Fig. 27). Să găsim expansiunile Laurent ale funcției /(z) în fiecare dintre aceste regiuni. Reprezentăm /(z) ca sumă de fracții elementare a) Cerc Relația de transformare (16) după cum urmează. Folosind formula pentru suma termenilor unei progresii geometrice, obținem b) Inelul pentru funcția -z rămâne convergent în acest inel, deoarece Seria (19) pentru funcția j^j pentru |z| > 1 diverge. Prin urmare, transformăm funcția /(z) astfel: aplicând din nou formula (19), obținem că Această serie converge pentru. Înlocuind expansiunile (18) și (21) în relația (20), obținem c) Exterioritatea cercului pentru funcția -z cu |z| > 2 diverge, iar seria (21) pentru funcția Să reprezentăm funcția /(z) în următoarea formă: /<*> Folosind formulele (18) și (19), obținem OR 1 Acest exemplu arată că pentru aceeași funcție f(z) expansiunea Laurent, în general, are o formă diferită pentru diferite inele. Exemplul 3. Aflați descompunerea celor 8 serii Laurent ale funcției seria Laurent Puncte singulare izolate și clasificarea lor în regiunea inelară A Folosim reprezentarea funcției f (z) în următoarea formă: și transformăm al doilea termen Folosind formula pentru suma termenilor unei progresii geometrice, obținem Înlocuind expresiile găsite în formula (22), avem Exemplul 4. Extindeți funcția într-o serie Laurent în vecinătatea lui zq subțire = 0. Pentru orice complexă , avem Fie Această expansiune este valabilă pentru orice punct z Ф 0. În acest caz, regiunea inelară este întregul plan complex cu un punct aruncat z - 0. Această regiune poate fi definită prin următoarea relație: Această funcție este analitică în regiune Din formulele (13) pentru coeficienții seriei Laurent, prin același raționament ca în paragraful precedent, se pot obține inegalitățile Kouiw. dacă funcția f(z) este mărginită pe un cerc, unde M este o constantă), atunci puncte singulare izolate Un punct zo se numește punct singular izolat al funcției f(z) dacă există o vecinătate inelară a punctului ( această mulțime se mai numește uneori și o vecinătate perforată a punctului 2o), în care funcția f(z) este cu o singură valoare și analitică. În punctul zo însuși, funcția fie nu este definită, fie nu este cu o singură valoare și analitică. Se disting trei tipuri de puncte singulare în funcție de comportamentul funcției /(z) la apropierea de punctul zo. Se spune că un punct singular izolat este: 1) detașabil dacă există un finit 2) pmusach dacă 3) un punct esențial singular dacă funcția f(z) nu are limită pentru Teorema 16. Un punct singular izolat z0 al unei funcții f(z) este un punct singular detașabil dacă și numai dacă expansiunea Laurent a funcției f(z) într-o vecinătate a punctului zo nu conține o parte principală, adică, are forma Let zo - punct singular amovibil. Atunci există una finită și, prin urmare, funcția f(z) este mărginită într-o vecinătate procologică a punctului r. Am stabilit În virtutea inegalităților Cauchy Deoarece este posibil să alegem ρ cât de mic dorim, atunci toate coeficienții la puteri negative (z - 20) sunt egali cu zero: Dimpotrivă, fie Laurent extinderea funcției /(r) în vecinătatea punctului zq conține doar partea corectă, adică are forma (23) și, prin urmare, este Taylor. Este ușor de observat că pentru z -* z0 funcția /(r) are o valoare limită: Teorema 17. Un punct singular izolat zq al funcției f(z) este detașabil dacă și numai dacă funcția J(z) este delimitat într-o vecinătate perforată a punctului zq, Zgmechai nu. Fie r0 un punct singular detașabil al lui f(r). Presupunând că funcția f(r) este analitică într-un cerc centrat în punctul th. Aceasta definește numele punctului - de unică folosință. Teorema 18. Un punct singular izolat zq al unei funcții f(z) este un pol dacă și numai dacă partea principală a expansiunii Laurent a funcției f(z) într-o vecinătate a punctului conține un număr finit (și pozitiv). de termeni nenuli, adică are forma 4 Fie z0 un pol. De atunci există o vecinătate perforată a punctului z0 în care funcția f(z) este analitică și diferită de zero. Atunci o funcție analitică este definită în această vecinătate și, prin urmare, punctul zq este un punct singular detașabil (zero) al funcției sau unde h(z) este o funcție analitică, h(z0) ∩ 0. este analitic într-o vecinătate a punctului zq, și de aici, de unde obținem că Să presupunem acum că funcția f(z) are o descompunere de forma (24) într-o vecinătate perforată a punctului zo. Aceasta înseamnă că în această vecinătate funcția f(z) este analitică împreună cu funcția. Pentru funcția g(z), expansiunea este valabilă din care este clar că zq este un punct singular detașabil al funcției g(z) și există Atunci funcția tinde la 0 - polul funcției Mai există unul simplu. fapt. Punctul Zq este un pol al funcției f(z) dacă și numai dacă funcția g(z) = y poate fi extinsă la o funcție analitică în vecinătatea punctului zq prin stabilirea g(z0) = 0. Ordinea al polului funcției f(z) se numește ordinul zero al funcției jfa. Teoremele 16 și 18 implică următoarea afirmație. Teorema 19. O subțire singulară izolată este în esență singulară dacă și numai dacă partea principală a expansiunii Laurent într-o vecinătate perforată a acestui punct conține infiniti de termeni nenuli. Exemplul 5. Punctul singular al funcției este zo = 0. Avem Seria Laurent Puncte singulare izolate și clasificarea lor Prin urmare, zo = 0 este un punct singular amovibil. Expansiunea funcției /(z) într-o serie Laurent în vecinătatea punctului zero conține doar partea corectă: Exemplul7. f(z) = Punctul singular al funcției f(z) este zq = 0. Se consideră comportamentul acestei funcții pe axa reală și pe axa imaginară: pe axa reală la x 0, pe axa imaginară Prin urmare, nici finită, nici limita infinită f(z) la z -* 0 nu există. Prin urmare, punctul r0 = 0 este un punct esențial singular al funcției f(z). Să găsim expansiunea Laurent a funcției f(z) într-o vecinătate a punctului zero. Pentru orice complex C avem setat. Atunci expansiunea Laurent conține un număr infinit de termeni cu puteri negative ale lui z.

Definiție. Se numește punctul singular al funcției izolat, dacă într-o vecinătate a acestui punct este o funcție analitică (adică analitică în inel).

Clasificarea punctelor singulare izolate ale unei funcții este legată de comportamentul acestei funcții în vecinătatea unui punct singular.

Definiție. Punctul se numește de unică folosință un punct singular al unei funcţii dacă există o limită finită a acestei funcţii la .

Exemplul 5 Arătați că funcția are o singularitate detașabilă într-un punct.

Soluţie. Reamintind prima limită remarcabilă, calculăm

Aceasta înseamnă că funcția dată are o singularitate detașabilă la punctul respectiv.

Sarcina 4. Arătați că punctul este detașabil pentru .

Definiție. Punctul se numește stâlp funcția , dacă această funcție crește la nesfârșit pentru , adică .

Să fim atenți la legătura dintre conceptele de zero și pol ale unei funcții analitice. Să reprezentăm funcția ca .

Dacă un punct este un zero simplu al unei funcții, atunci funcția are un pol simplu

Dacă punctul este de ordinul zero pentru funcție, atunci pentru funcție este polul Ordin.

Exemplul 6 Arătați că funcția are un pol de ordinul trei într-un punct.

Soluţie. Presupunând că obținem. Deoarece avem tendința de a ajunge la zero, conform oricărei legi, avem . Apoi, și odată cu ea, funcția în sine crește la nesfârșit. Prin urmare, , adică punctul singular este un pol. Pentru o funcție, acest punct este evident un triplu zero. Prin urmare, pentru această funcție, punctul este un pol de ordinul trei.

Sarcina 5. Arătați că punctul are un pol simplu.

Definiție. Punctul se numește în esenţă speciale punct al funcției dacă în acest punct nu există nici o limită finită, nici infinită a funcției (comportamentul funcției nu este definit).

Fie un punct singular esențial al funcției . Apoi, pentru orice număr complex prealocat, există o astfel de secvență de puncte care converg către , de-a lungul căreia valorile tind să: ( teorema lui Sochocki).

Exemplul 7 Arătați că o funcție într-un punct are o singularitate esențială.

Soluţie. Luați în considerare comportamentul unei funcții date în vecinătatea punctului. Căci de-a lungul părții pozitive a axei reale (adică ) avem și ; dacă de-a lungul părții negative a axei reale (adică), atunci și . Deci nu există limită pentru. Prin definiție, o funcție are o singularitate esențială într-un punct.

Să considerăm comportamentul funcției la zero din punctul de vedere al teoremei Sochocki. Fie orice număr complex, altul decât zero și infinit.

Din egalitate găsim . Presupunând , obținem o succesiune de puncte , . Evident, . În fiecare punct al acestei secvențe, funcția este egală cu , și, prin urmare

Sarcina 6. Arătați că funcția are o singularitate esențială într-un punct.

Un punct la infinit este întotdeauna considerat special pentru funcție. Un punct se numește punct singular izolat al unei funcții dacă această funcție nu are alte puncte singulare în afara unui cerc centrat la origine.

Clasificarea punctelor singulare izolate poate fi extinsă și la cazul .

Exemplul 8 Arătați că funcția are un pol dublu la infinit.

Soluţie. Luați în considerare funcția , unde este o funcție analitică într-o vecinătate a punctului și . Aceasta înseamnă că funcția are un zero dublu la infinit, dar atunci pentru funcție punctul este un pol dublu.

Exemplul 9 Arătați că funcția are o singularitate esențială la infinit.

Soluţie. O problemă similară este considerată în pr.7. Luați în considerare comportamentul unei funcții în vecinătatea unui punct infinit îndepărtat. Pentru de-a lungul părții pozitive a axei reale și pentru de-a lungul părții negative a axei reale. Aceasta înseamnă că nu există o limită a funcției la un punct și, în virtutea definiției, acest punct este esențial singular.

Natura singularității unei funcții într-un punct poate fi judecată din parte principală Extindere Laurent într-un cartier din acest punct.

Teorema 1. Pentru ca ideea să fie de unică folosință punct singular al funcției , este necesar și suficient ca expansiunea Laurent corespunzătoare nu conținea partea principală.

Sarcina 6. Folosind expansiunea Taylor a funcției într-o vecinătate a punctului , arătați că are o singularitate detașabilă la zero.

Teorema 2. Pentru ca ideea să fie stâlp funcții , este necesar și suficient pentru ca parte principală expansiunea Laurent corespunzătoare conţinea un număr finit de membri :

Numărul celui mai mare termen negativ determină ordinea polului.

În acest caz, funcția poate fi reprezentată ca

unde este funcția analitică în punctul, , este ordinea polului.

Exemplul 10 Arătați că funcția are poli simpli în puncte.

Soluţie. Să luăm în considerare un punct. Folosim expansiunea Laurent a acestei functii in vecinatatea acestui punct, obtinuta in Exemplul 2:

Deoarece cea mai mare (și singura) putere negativă din partea principală a acestei expansiuni este egală cu unu, punctul este un pol simplu al acestei funcții.

Acest rezultat ar fi putut fi obținut în alt mod. Să reprezentăm în formă și să punem - aceasta este o funcție care este analitică la punctul și . Prin urmare, datorită (8) această funcție are un pol simplu în punct.

O altă modalitate: luați în considerare o funcție care are un zero simplu în punct. Prin urmare, în acest moment are un stâlp simplu.

În mod similar, dacă scriem funcția sub forma , unde este o funcție analitică la punctul și , atunci este imediat clar că punctul este un simplu pol al funcției .

Sarcina 7. Arătați că funcția are un pol de ordinul 2 în punct și un pol de ordinul 4 în punctul .

Teorema 3. Pentru ca ideea să fie în esenţă speciale punct al funcției , este necesar și suficient ca parte principală Extindere Laurent într-un cartier al punctului conţinea un număr infinit de membri .

Exemplul 11. Determinați natura singularității în punctul funcției

Soluţie.În binecunoscuta expansiune a cosinusului, punem în loc de:

Prin urmare, expansiunea Laurent într-o vecinătate a unui punct are forma

Aici partea corectă este un termen. Și partea principală conține un număr infinit de termeni, deci punctul este în esență singular.

Sarcina 8. Arătați că la un moment dat funcția are o singularitate esențială.

Luați în considerare o funcție și notați expansiunea ei Laurent în punctul:

Să facem o înlocuire, în timp ce punctul merge la punct. Acum, în vecinătatea unui punct la infinit, avem

Rămâne să introducem o nouă denumire. Primim

unde este partea principală și este partea regulată a expansiunii Laurent a funcției în vecinătatea unui punct infinit îndepărtat. Astfel, în expansiunea Laurent a unei funcții într-o vecinătate a unui punct, partea principală este o serie în puteri pozitive, în timp ce partea corectă este o serie în puteri negative. Ținând cont de acest lucru

Cu toate acestea, criteriile de mai sus pentru determinarea naturii singularității rămân valabile pentru un punct infinit de îndepărtat.

Exemplul 12. Aflați natura singularității funcției la punct. , apoi la un moment dat se poate dovedi a fi neizolat.

Exemplul 15 Funcția într-un punct infinit depărtat are o singularitate esențială. Arătați că punctul pentru funcție nu este un punct singular izolat.

Soluţie. Funcția are un număr infinit de poli la zerourile numitorului, adică la punctele , . Deoarece , atunci punctul , în orice vecinătate în care există poli , este punctul limită pentru poli.

punct singular

în matematică.

1) Punct singular al curbei dat de ecuația F ( X y) = 0, - punctul M 0 ( x 0, y 0), în care ambele derivate parțiale ale funcției F ( X y) dispar:

Dacă, în plus, nu toate derivatele parțiale a doua ale funcției F ( X y) în punctul M 0 sunt egale cu zero, atunci O. t. se numește dublu. Dacă, odată cu dispariția primelor derivate în punctul M 0, toate derivatele a doua dispar, dar nu toate derivatele a treia sunt egale cu zero, atunci O. t. se numește triplu și așa mai departe. Când se studiază structura unei curbe în apropierea unui dublu O. t., un rol important îl joacă semnul expresiei

Dacă Δ > 0, atunci O. t. se numește izolat; de exemplu, curba y 2 - x 4 + 4x 2= 0 originea este un O. t. izolat (vezi orez. unu ). Dacă Δ x 2 + y 2 + a 2) 2 - 4a 2 x 2 - a 4= 0 originea coordonatelor este nodul O. t. (vezi orez. 2 ). Dacă Δ = 0, atunci curba O. t. este fie izolată, fie caracterizată prin faptul că diferite ramuri ale curbei au o tangentă comună în acest punct, de exemplu: tangentă și formează un punct, ca o curbă y 2 - x 3= 0 (vezi orez. 3 , A); b) cuspid de al 2-lea fel - diferite ramuri ale curbei sunt situate pe aceeași parte a tangentei comune, ca o curbă (y - x 2)2 - x 5= 0 (vezi orez. 3 , b); c) punct de autocontact (pentru o curbă y 2 - x 4= 0 originea este un punct de autocontact; (cm. orez. 3 , v). Alături de O. t. precizat există multe alte O. t. cu nume speciale; de exemplu, un punct asimptotic este vârful unei spirale cu un număr infinit de spire (vezi Fig. orez. 4 ), punct de rupere, punct de colț etc.

2) Un punct singular al unei ecuații diferențiale este un punct în care atât numărătorul, cât și numitorul părții drepte a ecuației diferențiale dispar simultan (vezi Ecuații diferențiale)

unde P și Q sunt funcții diferențiabile continuu. Presupunând O. t. situat la originea coordonatelor și folosind formula Taylor (Vezi formula Taylor), putem reprezenta ecuația (1) sub forma

unde P 1 ( X y) și Q 1 ( X y) sunt infinitezimale în raport cu

Și anume, dacă λ 1 ≠ λ 2 și λ 1 λ 2 > 0 sau λ 1 = λ 2, atunci O. t. este un nod; toate curbele integrale care trec prin puncte dintr-o vecinătate suficient de mică a nodului intră în el. Dacă λ 1 ≠ λ 2 și λ 1 λ 2 i β, α ≠ 0 și β ≠ 0, atunci O. t. este un focar; toate curbele integrale care trec prin puncte într-o vecinătate suficient de mică a focarului sunt spirale cu un număr infinit de spire în orice vecinătate arbitrar mică a focarului. Dacă, în final, λ 1,2 = ± iβ, β ≠ 0, atunci caracterul lui O. t. nu este determinat de termeni liniari în expansiuni ale lui P ( X y) și Q ( X y), așa cum a fost cazul în toate cauzele de mai sus; aici O. t. poate fi un focar sau un centru, sau poate avea un caracter mai complex. În vecinătatea centrului, toate curbele integrale sunt închise și conțin centrul în interiorul lor. Deci, de exemplu, punctul (0, 0) este un nod pentru ecuații la" = 2u/x(λ 1 = 1, λ 2 = 2; vezi orez. 5 , a) și y" = u/x(λ 1 = λ 2 = 1; vezi orez. 5 , b), o șa pentru ecuație y" = -y/x(λ 1 = -1, λ 2 = 1 ; cm. orez. 6 ), focusul pentru ecuație y" =(x + y) / (X y) (λ 1 = 1 - i, λ 2 = 1 + i; cm. orez. 7 ) și centrul ecuației y" = -x / y(λ 1 = -i, λ 2 = i; cm. orez. opt ).

Dacă x, y) și Q ( X y) sunt analitice, vecinătatea unui O. t. de ordin superior poate fi împărțită în regiuni: D 1 - umplut cu curbe integrale, ambele capete fiind incluse în O. t. (regiuni eliptice), D 2 - umplute cu curbe integrale, al căror capăt este inclus în O. t. (regiuni parabolice), și D 3 - regiuni mărginite de două curbe integrale incluse în O. t., între care există curbe integrale de tipul hiperbolelor (regiuni hiperbolice) (vezi. orez. 9 ). Dacă nu există curbe integrale care intră într-un punct O., atunci punctul O. se numește punct de tip stabil. Vecinătatea unui O. t. stabil constă din curbe integrale închise care conțin O. t. în interiorul lor, între care sunt situate spirale (vezi Fig. orez. 10 ).

Studiul ecuațiilor diferențiale O. t., adică, în esență, studiul comportamentului familiilor de curbe integrale într-o vecinătate a lui O. t. M. Lyapunov a, A. Poincaré și alții).

3) Un punct singular al unei funcții analitice cu o singură valoare este un punct în care analiticitatea funcției este încălcată (vezi Funcții analitice). Dacă există un cartier al lui O. t. A, liber de alte O. t., atunci punctul A se numeşte izolat O. t. Dacă A este un O.T izolat și există un O.T finit se numește O.T. amovibil. Prin modificarea adecvată a definiției funcției în punctul a (sau redefinirea acesteia în acest punct, dacă funcția nu este deloc definită), și anume, setarea f(A)= b, este posibil să se realizeze A va deveni un punct obișnuit al funcției corectate. De exemplu, punct z= 0 este un O.T. amovibil pentru funcția f 1 ( z) = f(z), dacă z≠ 0 și f 1(0),=1, punct z= 0 este un punct obișnuit [ f 1 (z) este analitic la punct z= 0]. Dacă A- izolat O. t. și a se numește pol sau punct neesențial singular al funcției f(z), dacă funcționează seria Laurent). f(z) într-o vecinătate a unui O. t. izolat nu conţine puteri negative z - a, dacă A- detașabil O. t., conține un număr finit de puteri negative z - a, dacă A- stâlp (în acest caz, ordinea stâlpului R este definită ca cea mai mare putere a unui - un punct esențial singular. De exemplu, pentru funcție

p = 2, 3, …)

punct z= 0 este polul ordinului R, pentru funcție

punct z= 0 este un punct singular esențial.

La limita cercului de convergență al unei serii de puteri trebuie să existe cel puțin o O. t. a funcției reprezentate în interiorul acestui cerc de seria de puteri dată. Toate punctele limită ale domeniului de existență a unei funcții analitice cu o singură valoare (limită naturală) sunt puncte limită ale acestei funcții. Astfel, toate punctele cercului unitar | z| = 1 sunt speciale pentru funcție

Pentru o funcție analitică cu mai multe valori, conceptul de „O. T." mai dificil. Pe lângă O. t., în foile individuale ale suprafeței Riemann a unei funcții (adică O. t. a elementelor analitice cu o singură valoare), orice punct de ramificare este, de asemenea, un O. t. al funcției. Punctele de ramificație izolate ale unei suprafețe Riemann (adică, punctele de ramificare astfel încât în ​​unele din vecinătățile lor să nu existe alte funcții O.t. în nicio frunză) sunt clasificate după cum urmează. Dacă a este un punct de ramură izolat de ordin finit și există un a finit, se numește pol critic. Dacă A este un punct de ramificație izolat de ordin infinit și a se numește O. t transcendental. Toate celelalte puncte de ramificație izolate sunt numite puncte critice esențial singulare. Exemple: punct z= 0 este un punct critic obișnuit al funcției f ( z) = jurnal zși un punct critic esențial singular al funcției f (z) = sin log z.

Orice O. t., cu excepția uneia detașabile, este un obstacol în calea continuării analitice, adică continuarea analitică de-a lungul unei curbe care trece printr-o O. t. inamovibilă este imposibilă.

Marea Enciclopedie Sovietică. - M.: Enciclopedia Sovietică. 1969-1978 .

Vedeți ce este „Punctul special” în alte dicționare:

Puncte aici. Vezi și punct singular (ecuații diferențiale). O caracteristică sau singularitate în matematică este un punct în care un obiect matematic (de obicei o funcție) nu este definit sau are un comportament neregulat (de exemplu, un punct în care ... ... Wikipedia

O funcție analitică este un punct în care sunt încălcate condițiile de analiticitate. Dacă o funcție analitică f(z) este definită într-o vecinătate a punctului z0 peste tot... Enciclopedia fizică

O funcție analitică este punctul în care analiticitatea unei funcții este încălcată... Dicţionar enciclopedic mare

punct singular- — [Ya.N. Luginsky, M.S. Fezi Zhilinskaya, Yu.S. Kabirov. Dicționar englez rus de inginerie electrică și industria energetică, Moscova, 1999] Subiecte de inginerie electrică, concepte de bază EN punct singular ... Manualul Traducătorului Tehnic

1) Un OT al unei funcții analitice f(z) este un obstacol în calea continuării analitice a unui element al funcției f(z) a unei variabile complexe z de-a lungul unei căi pe planul acestei variabile. Fie ca funcția analitică f(z) să fie definită de niște ... ... Enciclopedie matematică

O funcție analitică, punctul în care analiticitatea funcției este încălcată. * * * PUNCT SINGULAR UN PUNCT SINGULAR al unei funcții analitice, un punct în care analiticitatea funcției este încălcată... Dicţionar enciclopedic

punct singular- ypatingasis taškas statusas T sritis automatika atitikmenys: engl. punct singular vok. singularer Punkt, m rus. punct singular, fpranc. particulă punctiformă, m; point singulier, m … Automatikos terminų žodynas