Mga isahan na punto ng isang function at ang kanilang pag-uuri. Nakahiwalay na mga puntong isahan. Mga nalalabi at mga formula para sa kanilang pagkalkula
Mga modelong inilarawan ng mga sistema ng dalawang autonomous differential equation.
yugto ng eroplano. Larawan ng yugto. paraan ng isocline. pangunahing isocline. Steady State Stability. Mga linear na sistema. Mga uri ng pangunahing punto: node, saddle, focus, center. Halimbawa: unang pagkakasunod-sunod na mga reaksiyong kemikal.
Ang pinaka-kagiliw-giliw na mga resulta sa qualitative modeling ng mga katangian ng biological system ay nakuha sa mga modelo ng dalawang differential equation, na nagpapahintulot sa isang qualitative na pag-aaral gamit ang pamamaraan. yugto ng eroplano. Isaalang-alang ang isang sistema ng dalawang autonomous na ordinaryong differential equation ng pangkalahatang anyo
(4.1)
P(x,y), Q(x,y)- mga tuluy-tuloy na function na tinukoy sa ilang domain G Euclidean plane ( x,y- Cartesian coordinate) at pagkakaroon sa lugar na ito ng tuluy-tuloy na mga derivatives ng order na hindi mas mababa kaysa sa una.
Rehiyon G maaaring maging walang limitasyon o limitado. Kung variable x, y ay may isang tiyak na biological na kahulugan (konsentrasyon ng mga sangkap, kasaganaan ng mga species), kadalasan ang lugar G ay ang positibong kuwadrante ng kanang kalahating eroplano:
0 £ x< ¥ ,0 £ y< ¥ .
Ang mga konsentrasyon ng mga sangkap o ang kasaganaan ng mga species ay maaari ding limitado mula sa itaas ng dami ng sisidlan o ng lugar ng tirahan. Pagkatapos ang hanay ng mga variable ay may anyo:
0 £ x< x 0 , 0 £ y< y 0 .
Mga variable x, y pagbabago sa oras alinsunod sa sistema ng mga equation (4.1), upang ang bawat estado ng system ay tumutugma sa isang pares ng mga halaga ng mga variable ( x, y).
|
|
Sa kabaligtaran, para sa bawat pares ng mga variable ( x, y) ay tumutugma sa isang tiyak na estado ng system.
Isaalang-alang ang isang eroplano na may mga coordinate axes kung saan naka-plot ang mga halaga ng mga variable x,y. Bawat punto M ang eroplanong ito ay tumutugma sa isang tiyak na estado ng system. Ang nasabing eroplano ay tinatawag na phase plane at inilalarawan ang kabuuan ng lahat ng estado ng system. Ang puntong M(x, y) ay tinatawag na naglalarawan o kumakatawan sa punto.
Hayaan sa unang oras t=t 0 na kumakatawan sa mga coordinate ng punto M 0 (x(t 0),y(t 0)). Sa bawat susunod na sandali sa oras t ang naglalarawang punto ay lilipat ayon sa mga pagbabago sa mga halaga ng mga variable x(t),y(t). Set ng mga puntos M(x(t), y(t)) sa phase plane, ang posisyon kung saan tumutugma sa mga estado ng system sa proseso ng pagbabago ng mga variable sa paglipas ng panahon x(t), y(t) ayon sa mga equation (4.1), ay tinatawag na yugto ng tilapon.
Ang hanay ng mga phase trajectories para sa iba't ibang mga paunang halaga ng mga variable ay nagbibigay ng isang madaling nakikitang "portrait" ng system. Gusali phase portrait nagbibigay-daan sa iyo na gumawa ng mga konklusyon tungkol sa likas na katangian ng mga pagbabago sa mga variable x, y nang hindi nalalaman ang mga analytical na solusyon ng orihinal na sistema ng mga equation(4.1).
Upang ilarawan ang isang phase portrait, ito ay kinakailangan upang bumuo ng isang vector field ng mga direksyon para sa mga trajectories ng system sa bawat punto ng phase plane. Sa pamamagitan ng pagtukoy ng pagtaasD t>0,nakukuha namin ang kaukulang mga increment D x at D y mula sa mga expression:
D x=P(x,y)D t,
D y=Q(x,y)D t.
direksyon ng vector dy/dx sa punto ( x, y) depende sa tanda ng mga function P(x, y), Q(x, y) at maaaring ibigay ng isang talahanayan:
|
P(x,y)>0,Q(x,y)>0 |
|
|
P(x,y)<0,Q(x,y)<0 |
|
|
P(x,y)>0,Q(x,y)<0 |
|
|
P(x,y)<0,Q(x,y)>0 |
|
.(4.2)
Solusyon sa equation na ito y=y(x, c), o pahiwatig F(x,y)=c, saan Sa ay ang pare-pareho ng pagsasama, nagbibigay sa pamilya ng integral curves ng equation (4.2) - phase trajectories system (4.1) sa eroplano x, y.
Isocline na pamamaraan
Upang bumuo ng isang phase portrait, ang isa ay gumagamit isocline method - Ang mga linya ay iginuhit sa phase plane na nag-intersect sa integral curves sa isang partikular na anggulo. Ang isocline equation ay madaling makuha mula sa (4.2). Ilagay natin
saan A– isang tiyak na pare-pareho. Ibig sabihin A kumakatawan sa tangent ng slope ng tangent sa phase trajectory at maaaring kumuha ng mga halaga mula sa -¥ sa + ¥ . Pagpapalit sa halip na dy/dx sa (4.2) ang dami A nakukuha namin ang isocline equation:
.(4.3)
Tinutukoy ng equation (4.3) sa bawat punto ng eroplano ang tanging tangent sa katumbas na integral curve, maliban sa punto kung saan P(x,y)= 0, Q (x,y) = 0 , kung saan ang direksyon ng tangent ay nagiging indefinite, dahil ang halaga ng derivative ay nagiging indefinite:
.
Ang puntong ito ay ang intersection point ng lahat ng isoclines - espesyal na punto. Ito ay sabay-sabay na nawawala ang mga derivatives ng oras ng mga variable x at y.
Kaya, sa isahan na punto, ang mga rate ng pagbabago ng mga variable ay katumbas ng zero. Samakatuwid, ang singular na punto ng mga differential equation ng phase trajectories (4.2) ay tumutugma sa nakatigil na estado ng system(4.1), at ang mga coordinate nito ay ang mga nakatigil na halaga ng mga variable x, y.
Ang partikular na interes ay pangunahing isocline:
dy/dx=0, P(x,y)=0 – isocline ng horizontal tangents at
dy/dx=¥ , Q(x,y)=0 – isocline ng vertical tangents.
Sa pamamagitan ng pagbuo ng mga pangunahing isocline at paghahanap ng punto ng kanilang intersection (x, y), ang mga coordinate na nakakatugon sa mga kundisyon:
makikita natin ang punto ng intersection ng lahat ng isoclines ng phase plane, kung saan ang direksyon ng tangents sa phase trajectories ay hindi tiyak. ito - iisang punto, na tumutugma nakatigil na estado ng system(Larawan 4.2).
Ang System (4.1) ay may kasing daming nakatigil na estado gaya ng may mga intersection point ng mga pangunahing isocline sa phase plane.
Ang bawat phase trajectory ay tumutugma sa isang hanay ng mga galaw ng isang dynamical system na dumadaan sa parehong mga estado at naiiba sa isa't isa lamang sa simula ng time reference.
 |
|
Kung ang mga kondisyon ng Cauchy theorem ay nasiyahan, pagkatapos ay sa bawat punto ng espasyo x, y, t dumadaan sa iisang integral curve. Totoo rin ito, salamat sa awtonomiya, para sa mga yugto ng yugto: isang natatanging yugto ng tilapon ang dumadaan sa bawat punto ng yugto ng eroplano.
Steady State Stability
Hayaang nasa ekwilibriyo ang sistema.
Pagkatapos ang kinatawan na punto ay matatagpuan sa isa sa mga isahan na punto ng system, kung saan, sa pamamagitan ng kahulugan:
.
Kung ang isang singular na punto ay stable o hindi ay tinutukoy kung ang kinatawan na punto ay umalis o hindi na may maliit na paglihis mula sa nakatigil na estado. Bilang inilapat sa isang sistema ng dalawang equation, ang kahulugan ng katatagan sa wikae, dtulad ng sumusunod.
Ang estado ng equilibrium ay matatag kung para sa anumang partikular na lugar ng mga paglihis mula sa estado ng balanse (e )maaaring tukuyin ang lugar d (e ), nakapalibot sa estado ng ekwilibriyo at pagkakaroon ng ari-arian na walang tilapon na nagsisimula sa loob ng rehiyon d , ay hindi makakarating sa hangganan e . (Larawan 4.4)
 |
|
Para sa isang malaking klase ng mga sistema - magaspang na sistema – ang likas na katangian ng pag-uugali na kung saan ay hindi nagbabago sa isang maliit na pagbabago sa uri ng mga equation, ang impormasyon tungkol sa uri ng pag-uugali sa paligid ng nakatigil na estado ay maaaring makuha sa pamamagitan ng pag-aaral hindi ang orihinal, ngunit ang pinasimple linearized sistema.
Mga linear na sistema.
Isaalang-alang ang isang sistema ng dalawang linear na equation:
.(4.4)
Dito a B C D- mga pare-pareho, x, y- Cartesian coordinate sa phase plane.
Ang pangkalahatang solusyon ay hahanapin sa form:
.(4.5)
Palitan ang mga ekspresyong ito sa (4.4) at bawasan ng e l t:
(4.6)
Algebraic system ng mga equation (4.6) na may mga hindi alam A, B ay may nonzero na solusyon lamang kung ang determinant nito, na binubuo ng mga coefficient ng mga hindi alam, ay katumbas ng zero:
.
Sa pagpapalawak ng determinant na ito, nakukuha natin ang katangian na equation ng system:
.(4.7)
Ang solusyon ng equation na ito ay nagbibigay ng mga halaga ng indicatorl 1,2 , kung saan posible ang mga hindi zero na halaga A at B mga solusyon ng equation (4.6). Ang mga halagang ito ay
.(4.8)
Kung negatibo ang radikal na pagpapahayag, kung gayonl 1,2 kumplikadong conjugate number. Ipagpalagay na ang parehong mga ugat ng equation (4.7) ay may mga nonzero na tunay na bahagi at na walang maraming mga ugat. Pagkatapos ang pangkalahatang solusyon ng system (4.4) ay maaaring katawanin bilang isang linear na kumbinasyon ng mga exponents na may mga exponentsl 1 , l 2 :
(4.9)
Upang pag-aralan ang likas na katangian ng mga posibleng trajectory ng system sa phase plane, ginagamit namin linear homogenous coordinate na pagbabago, na magdadala sa sistema sa canonical form:
,(4.10)
na nagbibigay-daan sa isang mas maginhawang representasyon sa phase plane kumpara sa orihinal na sistema (4.4). Ipakilala natin ang mga bagong coordinateξ , η ayon sa mga formula:
(4.1)
Ito ay kilala mula sa kurso ng linear algebra na kung ang mga tunay na bahagi ay hindi katumbas ng zerol 1 , l 2 ang orihinal na sistema (4.4) sa tulong ng mga pagbabagong-anyo (4.11) ay maaaring palaging mabago sa canonical form (4.10) at ang pag-uugali nito sa phase plane ay maaaring pag-aralanξ , η . Isaalang-alang ang iba't ibang mga kaso na maaaring magpakita mismo dito.
Mga ugat λ 1 , λ 2 – wasto at may parehong tanda
Sa kasong ito, ang mga koepisyent ng pagbabagong-anyo ay totoo, lumipat tayo mula sa totoong eroplanox,ysa totoong eroplano ξ, η. Hinahati ang pangalawa ng mga equation (4.10) sa una, makuha natin:
.(4.12)
Ang pagsasama ng equation na ito, nakita namin:
Saan .(4.13)
Magkasundo tayo na unawain ni λ 2 ang ugat ng katangiang equation na may malaking modulus, na hindi lumalabag sa pangkalahatan ng ating pangangatwiran. Pagkatapos, dahil sa kaso na isinasaalang-alang ang mga ugat λ 1 , λ2 – wasto at may parehong tanda,a>1 , at kami ay nakikitungo sa mga integral curve ng parabolic type.
Lahat ng integral curve (maliban sa axis η , na tumutugma sa ) hawakan sa pinanggalingan ng axis ξ, na isa ring integral curve ng equation (4.11). Ang pinagmulan ng mga coordinate ay isang isahan na punto.
Alamin natin ngayon ang direksyon ng paggalaw ng kinatawan na punto kasama ang mga yugto ng yugto. Kung λ 1 , λ 2 ay negatibo, kung gayon, gaya ng makikita sa mga equation (4.10), |ξ|, |η| bumababa sa paglipas ng panahon. Ang kinakatawan na punto ay lumalapit sa pinanggalingan, ngunit hindi kailanman umabot dito. Kung hindi, ito ay sasalungat sa teorama ni Cauchy, na nagsasaad na isang yugto lamang ng tilapon ang dumadaan sa bawat punto ng yugto ng eroplano.
Iisang punto kung saan dumadaan ang mga integral curve, tulad ng isang pamilya ng mga parabola 
dumadaan sa pinanggalingan, ay tinatawag na node (Fig. 4.5)
Knot-type equilibrium state sa λ 1 , λ 2 < 0 ay matatag ayon kay Lyapunov, dahil ang kumakatawan sa punto ay gumagalaw kasama ang lahat ng integral curves patungo sa pinanggalingan ng mga coordinate. Ito matatag na buhol. Kung λ 1 , λ 2 > 0, pagkatapos |ξ|, |η| pagtaas sa paglipas ng panahon at ang kinatawan na punto ay lumalayo sa pinanggalingan. Sa kasong ito, ang singular na punto– hindi matatag na node .
Sa phase plane x, y ang pangkalahatang katangian ng husay ng pag-uugali ng mga integral na kurba ay mananatili, ngunit ang mga tangent sa mga integral na kurba ay hindi magkakasabay sa mga coordinate axes. Ang anggulo ng pagkahilig ng mga tangent na ito ay matutukoy ng ratio ng mga coefficient α , β , γ , δ sa mga equation (4.11).
Mga ugat λ 1 , λ 2 ay may bisa at may iba't ibang palatandaan.
I-convert mula sa mga coordinate x,y sa mga coordinate ξ, η muling totoo. Ang mga equation para sa mga canonical variable ay muling may anyo (4.10), ngunit ngayon ang mga palatandaan λ 1 , λ 2 magkaiba. Ang phase trajectory equation ay may anyo:
Saan , (4.14)
Pagsasama-sama (4.14), nakita namin
(4.15)
Ito Ang equation ay tumutukoy sa isang pamilya ng mga kurba ng hyperbolic na uri, kung saan ang parehong coordinate axes ay ang mga asymptotes (sa a=1 magkakaroon tayo ng pamilya ng isosceles hyperbolas). Ang mga coordinate axes ay integral curves din sa kasong ito– ang mga ito lamang ang mga integral na kurba na dumadaan sa pinanggalingan. Bawat isakung saan ay binubuo ng tatlong yugto ng mga trajectory: ng dalawang paggalaw patungo sa isang estado ng ekwilibriyo (o palayo sa isang estado ng ekwilibriyo) at mula sa isang estado ng ekwilibriyo. Lahat ng iba pang integral curves– ay mga hyperbola na hindi dumadaan sa pinanggalingan (Fig. 4.6) Ang natatanging puntong ito ay tinatawag "siya ». Ang mga linya ng antas na malapit sa mountain saddle ay kumikilos tulad ng mga phase trajectories sa paligid ng saddle.
Isaalang-alang natin ang likas na katangian ng paggalaw ng kinatawan na punto kasama ang mga yugto ng tilapon malapit sa estado ng balanse. Hayaan, halimbawa,λ 1 >0 , λ 2<0 . Pagkatapos ang kinatawan na punto ay inilagay sa axis ξ , ay lalayo sa pinanggalingan, at ilalagay sa axis η – ay lalapit nang walang katiyakan sa pinanggalingan ng mga coordinate, nang hindi naaabot sa takdang panahon. Saanman ang kumakatawan na punto ay nasa unang sandali (maliban sa isahan na punto at mga punto sa asymptote η =0), ito ay lalayo sa estado ng ekwilibriyo, kahit na sa simula ay gumagalaw ito sa isa sa mga integral na kurba patungo sa isang isahan na punto.
Obvious naman yun Ang saddle-type na singular point ay palaging hindi matatag . Sa ilalim lamang ng espesyal na piniling mga paunang kondisyon sa asymptoteη =0 lalapit ang sistema sa isang estado ng ekwilibriyo. Gayunpaman, hindi ito sumasalungat sa assertion na ang sistema ay hindi matatag. Kung binibilang mo, na ang lahat ng mga paunang estado ng system sa phase plane ay pantay na posibilidad, pagkatapos ay ang posibilidad ng naturang paunang estado na tumutugma sa paggalaw sa direksyon Upang ang singular point ay katumbas ng zero. Samakatuwid, ang anumang tunay na paggalaw ay mag-aalis ng sistema mula sa estado ng ekwilibriyo.Bumabalik sa mga coordinatex,y,nakukuha natin ang parehong husay na larawan ng kalikasan ng paggalaw ng mga trajectory sa paligid ng pinanggalingan.
Ang hangganan sa pagitan ng mga itinuturing na kaso ng isang node at isang saddle ay ang kaso kailan isa sa mga tagapagpahiwatig ng katangian, halimbawa λ 1 , naglalaho, na nangyayari kapag ang determinant ng system- pagpapahayag adbc=0(tingnan ang formula 4.8 ). Sa kasong ito, ang mga coefficient ng kanang bahagi ng mga equation (4.4) ay proporsyonal sa bawat isa:
at ang sistema ay para sa ekwilibriyo nito ay nagsasaad ng lahat ng mga punto ng linya:
Ang natitirang integral curves ay isang pamilya ng mga parallel na linya na may slope , kung saan ang mga punto ng kinatawan ay maaaring lumalapit sa estado ng ekwilibriyo o lumayo mula dito, depende sa tanda ng pangalawang ugat ng katangian na equation λ 2 = a+d.(Larawan 4. 7 ) Sa kasong ito, ang mga coordinate ng estado ng ekwilibriyo ay nakasalalay sa paunang halaga ng mga variable.
Mga ugat λ 1 , λ 2 – kumplikadoconjugate
Sa kasong ito, para sa totoox at y gagawin natin may mga kumplikadong conjugates ξ , η (4.10) . Gayunpaman, sa pamamagitan ng pagpapakilala ng isa pang intermediate na pagbabago, posible rin sa kasong ito na bawasan ang pagsasaalang-alang sa isang tunay na linear homogenous na pagbabago. Ilagay natin:
(4.16)
saan a, b, at ikaw, v – tunay na mga halaga. Maipapakita na ang pagbabago mula sax,y Upang ikaw, v ay, sa ilalim ng aming mga pagpapalagay, totoo, linear, homogenous na may non-zero determinant. Dahil sa mga equation(4.10, 4.16) mayroon kaming :
saan
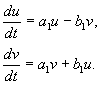(4.17)
Hinahati ang pangalawa ng mga equation sa una, nakukuha natin:
na mas madaling pagsamahin, kung lumipat tayo sa polar coordinate system (r, φ ) . Pagkatapos ng pagpapalit kung saan kami kumukuha:
.(4.18)
Kaya, sa phase planeikaw, vkami ay nakikitungo sa isang pamilya ng logarithmic spiral, bawat isa ay mayasymptotic point sa pinanggalingan.Singular point na siyang asymptotic point ng lahat ng integral curves na may anyo ng mga spiral, nakapugad na kaibigankaibigan, tinawag focus ( fig.4.8 ) .
Isaalang-alang natin ang likas na katangian ng paggalaw ng kinakatawan na punto kasama ang mga tilapon ng phase. Pagpaparami ng una sa mga equation (4.17) sa pamamagitan ngu, at ang pangalawa sa v at pagdaragdag ng , nakukuha namin:
saan
Hayaan a 1 < 0 (a 1 = Reλ ) . Ang kumakatawan na punto pagkatapos ay patuloy na lumalapit sa pinanggalingan nang hindi naaabot ito sa isang takdang panahon. Nangangahulugan ito na ang mga phase trajectories ay twisting spiral at tumutugma sa damped oscillations mga variable. ito - matatag na pokus .
Sa kaso ng isang matatag na pokus, tulad ng sa kaso ng isang matatag na node, hindi lamang ang kondisyon ng Lyapunov ay nasiyahan, kundi pati na rin ang isang mas mahigpit na kinakailangan. Ibig sabihin, para sa anumang mga paunang paglihis, ang sistema ay babalik sa kalaunan nang mas malapit hangga't gusto sa posisyon ng ekwilibriyo. Ang ganitong katatagan, kung saan ang mga paunang paglihis ay hindi lamang tumataas, ngunit ang pagkabulok, na nagiging zero, ay tinatawag ganap na katatagan .
Kung sa formula (4.18) a 1 >0 , pagkatapos ay lumayo ang kumakatawan sa punto mula sa pinanggalingan, at tayo ay nakikitungo sa hindi matatag na pokus . Kapag lumilipat mula sa isang eroplanoikaw, vpapunta sa phase planex, yAng mga spiral ay mananatiling mga spiral, ngunit magiging deformed.
Isaalang-alang ngayon ang kaso kung kailana 1
=0
. Phase trajectories sa eroplanoikaw, vmagkakaroon ng mga bilog 
na nasa eroplanox,ymagkasya ang mga ellipse:
Kaya, saa 1=0 sa pamamagitan ng isang espesyal na puntox= 0,y= 0 walang integral curve pass. Ang nasabing isang nakahiwalay na singular na punto, na malapit sa kung saan ang mga integral na kurba ay saradong mga kurba, lalo na, ang mga ellipse na naka-embed sa bawat isa at nakapaloob ang singular na punto, ay tinatawag na isang sentro.
Kaya, anim na uri ng ekwilibriyo ang posible, depende sa likas na katangian ng mga ugat ng katangiang equation (4.7). View ng phase trajectories sa eroplano x, y para sa anim na kaso na ito ay ipinapakita sa Fig. 4.9.
kanin. 4.9.Mga uri ng mga phase portrait sa kapitbahayan ng isang nakatigil na estado para sa sistema ng mga linear equation (4.4).
Ang limang uri ng mga estado ng ekwilibriyo ay magaspang, ang kanilang kalikasan ay hindi nagbabago na may sapat na maliliit na pagbabago sa kanang bahagi ng mga equation (4.4). Sa kasong ito, ang mga pagbabago ay dapat maliit hindi lamang sa kanang bahagi, kundi pati na rin sa kanilang mga first-order derivatives. Ang ikaanim na estado ng ekwilibriyo - ang sentro - ay hindi magaspang. Sa maliliit na pagbabago sa mga parameter ng kanang bahagi ng mga equation, napupunta ito sa isang matatag o hindi matatag na pokus.
Diagram ng bifurcation
Ipakilala natin ang notasyon:
.
(4.11)
Pagkatapos ang equation ng katangian ay maaaring isulat sa anyo:
.
(4.12)
Isaalang-alang ang isang eroplano na may hugis-parihaba na mga coordinate ng Cartesian s , D at markahan dito ang mga lugar na tumutugma sa isa o ibang uri ng estado ng balanse, na tinutukoy ng likas na katangian ng mga ugat ng katangian na equation
.(4.13)
Ang kundisyon para sa katatagan ng estado ng ekwilibriyo ay ang pagkakaroon ng negatibong tunay na bahagi ng yl 1 at l 2 . Ang isang kinakailangan at sapat na kondisyon para dito ay ang katuparan ng mga hindi pagkakapantay-pantays > 0, D > 0 . Sa diagram (4.15), ang kundisyong ito ay tumutugma sa mga puntos na matatagpuan sa unang quarter ng eroplano ng parameter. Ang singular na punto ang magiging pokus kungl 1 at l 2 kumplikado. Ang kundisyong ito ay tumutugma sa mga puntong iyon ng eroplano kung saan , mga. mga punto sa pagitan ng dalawang sangay ng isang parabolas 2 = 4 D. Mga semiaxis na puntos s = 0, D>0, tumutugma sa mga estado ng equilibrium ng uri ng sentro. Gayundin,l 1 at l 2 - wasto, ngunit iba't ibang mga palatandaan, i.e. ang isang singular na punto ay magiging isang saddle kung D<0, atbp. Bilang resulta, nakakakuha kami ng partition diagram ng parameter plane s, D, sa mga rehiyong naaayon sa iba't ibang uri ng mga estado ng ekwilibriyo.
kanin. 4.10. Diagram ng bifurcation
para sa sistema ng mga linear na equation 4.4
Kung ang mga coefficient ng linear system a B C D depende sa ilang parameter, at kapag binago ang parameter na ito, magbabago din ang mga values , D . Kapag dumadaan sa mga hangganan, ang likas na katangian ng phase portrait ay nagbabago nang husay. Samakatuwid, ang mga naturang hangganan ay tinatawag na mga hangganan ng bifurcation - sa magkabilang panig ng hangganan, ang sistema ay may dalawang topologically different phase portrait at, nang naaayon, dalawang magkaibang uri ng pag-uugali.
Ipinapakita ng diagram kung paano maaaring mangyari ang mga naturang pagbabago. Kung ibubukod namin ang mga espesyal na kaso - ang pinagmulan ng mga coordinate - kung gayon madaling makita na ang saddle ay maaaring pumunta sa isang node, stable o hindi matatag kapag tumatawid sa y-axis. Ang isang stable na node ay maaaring lumipat sa isang saddle o isang stable na focus, at iba pa. Tandaan na ang stable node–stable focus at unstable node–unstable na focus transition ay hindi bifurcational, dahil ang topology ng phase space ay hindi nagbabago sa kasong ito. Pag-uusapan natin nang mas detalyado ang tungkol sa topology ng phase space at bifurcation transition sa Lecture 6.
Sa ilalim ng mga transition ng bifurcation, nagbabago ang likas na katangian ng katatagan ng singular point. Halimbawa, ang isang matatag na pokus sa gitna ay maaaring maging isang hindi matatag na pokus. Ang bifurcation na ito ay tinatawag Andronov-Hopf bifurcation sa mga pangalan ng mga siyentipiko na nag-aral nito. Sa pamamagitan ng bifurcation na ito sa mga nonlinear system, ang isang limit cycle ay ipinanganak, at ang system ay nagiging self-oscillating (tingnan ang lecture 8).
Halimbawa. Sistema ng mga linear na reaksiyong kemikal
sangkap X dumadaloy mula sa labas sa pare-parehong bilis, nagiging substance Y at sa bilis na proporsyonal sa konsentrasyon ng substance Y, ay inalis sa reaction sphere. Ang lahat ng mga reaksyon ay nasa unang pagkakasunud-sunod, maliban sa pag-agos ng bagay mula sa labas, na mayroong zero order. Ang scheme ng reaksyon ay ganito ang hitsura:
(4.14)
at inilalarawan ng sistema ng mga equation:
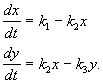(4.15)
Nakukuha namin ang mga nakatigil na konsentrasyon sa pamamagitan ng pag-equate ng kanang bahagi sa zero:
.(4.16)
Isaalang-alang ang phase portrait ng system. Hatiin natin ang pangalawang equation ng system (4.16) sa una. Nakukuha namin:
.(4.17)
Tinutukoy ng equation (4.17) ang pag-uugali ng mga variable sa phase plane. Bumuo tayo ng phase portrait ng system na ito. Una, iginuhit namin ang mga pangunahing isocline sa phase plane. Equation ng isocline ng vertical tangents:
Equation para sa isocline ng horizontal tangents:
Ang singular na punto (nakatigil na estado) ay nasa intersection ng mga pangunahing isocline.
Ngayon, alamin natin kung anong anggulo ang pinagsalubong ng mga coordinate ax sa integral curves.
Kung x= 0, pagkatapos .
Kaya, ang padaplis ng slope ng padaplis sa integral curves y=y(x), tumatawid sa y-axis x=0, ay negatibo sa itaas na kalahating eroplano (tandaan na ang mga variable x, y may mga halaga ng konsentrasyon, at samakatuwid ay interesado lamang kami sa kanang itaas na kuwadrante ng phase plane). Sa kasong ito, ang halaga ng tangent ng anggulo ng pagkahilig ng tangent ay tumataas sa distansya mula sa pinanggalingan.
Isaalang-alang ang axis y= 0. Sa intersection ng axis na ito, ang integral curves ay inilalarawan ng equation
Sa ang padaplis ng slope ng integral curves na tumatawid sa abscissa axis ay positibo at tumataas mula zero hanggang infinity sa pagtaas x.
Sa .
Pagkatapos, sa karagdagang pagtaas, ang tangent ng slope ay bumababa sa ganap na halaga, nananatiling negatibo at may posibilidad na -1 sa x ® ¥ . Ang pag-alam sa direksyon ng mga tangent sa integral curves sa mga pangunahing isocline at sa mga coordinate axes, madaling itayo ang buong larawan ng mga phase trajectories.
 |
|
Ang likas na katangian ng katatagan ng isahan na punto ay itatatag gamit ang pamamaraang Lyapunov. Ang katangian ng determinant ng system ay may anyo:
.
Ang pagpapalawak ng determinant, nakuha namin ang katangian na equation ng system: , ibig sabihin. ang mga ugat ng katangiang equation ay parehong negatibo. Samakatuwid, ang nakatigil na estado ng system ay isang matatag na node. Kasabay nito, ang konsentrasyon ng sangkap X may posibilidad sa isang nakatigil na estado na palaging monotonically, ang konsentrasyon ng substance Y ay maaaring dumaan sa min o max. Ang mga oscillatory regime sa naturang sistema ay imposible.
Hayaan zq - isahan na punto ng function na f(z), t.s. f(z) ngunit ito ay analytic sa puntong ito (sa partikular, maaaring hindi matukoy dito). Kung mayroong tulad ng isang butas na kapitbahayan ng punto zq (ibig sabihin, ang set O z - Ang zq f(z) ay alyatic, kung gayon zo tinawag nakahiwalay na isahan na punto mga function f(z). Ang kahulugan na ito ay napanatili din sa kaso zn = oo, kung ang iodine ay isang butas na kapitbahayan ng isang punto zq = oo unawain ang set z > AKO AY - ang hitsura ng ilang bilog na nakasentro sa pinanggalingan. Sa madaling salita, ang singular na punto Ang zq ay sinasabing isolated kung mayroong isang kapitbahayan ng puntong ito kung saan mayroong iba pang mga singular na punto na naiiba sa zq. Saanman sa ibaba, isinasaalang-alang lamang namin ang mga isahan na punto ng isang karakter na may iisang halaga (ang function f(z) ipinapalagay na kakaiba).
Depende sa pag-uugali ng function f(z) sa z -> zq May tatlong uri ng singular na puntos. Nakahiwalay na puntong isahan zq function f(z) tinatawag na:
1) naaalis na singular na punto kung may hangganan ang hangganan
2) poste kung may limitasyon 
3) mahalagang punto, kung f(z) ay walang hangganan o walang hangganang limitasyon para sa z-> zq.
HALIMBAWA 26.1. Ipakita natin na ang lahat ng tatlong uri ng isahan na mga punto ay naisasakatuparan. Isipin mo f(z)= punto Ang zq = 0 ay nakahiwalay
iisang punto ng function na ito. Gamit ang formula (22.12), nakuha namin ang pagpapalawak
mula sa kung saan ito ay sumusunod na mayroong umiiral na lim fi(z)= 1. Samakatuwid, ang zq = 0 ay
ay isang naaalis na singular na punto ng function fi(z).
Function f'j(z) =--- may poste sa isang punto zo= 1 kasi
2 r“X
Isaalang-alang ngayon ang pag-andar )z(z)= e 1 ^ r at ipakita iyon zo = Ang O ay isang mahalagang isahan na punto ng pagpapaandar na ito. Kapag nagsusumikap z sa zero sa kahabaan ng totoong axis, ang kaliwa at kanang mga limitasyon ng function f (z) iba: lim Sa 1 / 1 = 0,lim may 1 /* = os. Ito ay nagpapahiwatig,
x->0-0 x->0+O
Ano f:i(z) ay walang hangganan o walang hangganang limitasyon para sa 2 ->
Oh, ibig sabihin. Ang zq = 0 ay isang mahalagang isahan na punto ng pagpapaandar na ito. (Tandaan na habang ang punto ay may gawi z-iy sa zero sa imaginary axis function 
walang limitasyon sa lahat.)
Siyempre, mayroon ding mga hindi nakahiwalay na singular na puntos. Halimbawa. Ang function ay may mga pole sa mga punto z n = -, P= ±1, ±2,...
Kaya naman, Ang Zq = 0 ay isang hindi nakahiwalay na singular na punto ng function na ito: sa alinmang (arbitraryong maliit) na kapitbahayan ng puntong ito ay may iba pang mga singular na punto g p.
Hayaan zo- pangwakas na nakahiwalay na singular na punto ng isang function f(z). Pagkatapos f(z) ay katulad sa ilang nabutas na kapitbahayan 0 Zo ng punto zo ang kapitbahayan na ito ay maaaring ituring bilang isang singsing na may panloob na radius r = 0. Sa pamamagitan ng Theorem 25.1, sa kapitbahayan na isinasaalang-alang, ang function f(z) maaaring palawakin sa isang serye ng Laurent (25.2). Ipapakita namin na ang pag-uugali ng function para sa 2 -> zq (i.e. ang uri ng singular point zo) depende sa anyo ng pangunahing bahagi ng agnas (25.2); ipinapaliwanag ng pangyayaring ito ang pinagmulan ng terminong "pangunahing bahagi".
TEOREM 2G.2. Ang isang nakahiwalay na singular point zo ng isang function na f(z) ay naaalis kung at tanging kung ang Lorap expansion sa isang butas na kapitbahayan ng puntong ito ay may oid
mga. binubuo lamang ng tamang bahagi, at ang lahat ng mga coefficient ng pangunahing bahagi ay katumbas ng bala.
Patunay. 1. Hayaan zo ay isang naaalis na singular na punto. Patunayan natin na ang pagpapalawak ng Laurent ng function f(z) ay may anyo (26.1). Dahil ang singular point zo naaalis, pagkatapos ay mayroong isang may hangganang limitasyon lim f(z) = A. Kaya naman, f(z) bounded sa ilang mga butas na kapitbahayan 0 z - zq ng punto zo, mga. )(z) para sa lahat z mula sa kapitbahayan na ito. Kumuha ng kahit ano R. U р /?|, at gamitin ang mga formula (25.3) para sa mga coefficient ng serye ng Laurent:
Para sa mga coefficient ng pangunahing bahagi ng pagpapalawak n =- 1,-2,... Para sa mga naturang halaga P meron kami p~n-e 0 sa R-> 0. Dahil ang halaga R maaaring mapili ng arbitraryong maliit, kung gayon Mr~" maaaring maliit na arbitraryo. Mula noong |c t,| ^ Mr~n at cn ay hindi nakadepende sa p, pagkatapos cn = 0 para sa at= - 1, -2,..., na dapat patunayan.
2. Ipagpalagay natin ngayon na ang pagpapalawak ng Laurent ay may anyo (26.1). Ang Series (26.1) ay isang power series at. samakatuwid, nagtatagpo hindi lamang sa nabutas, kundi pati na rin sa buong kapitbahayan z-zq kasama ang tuldok zo; kabuuan nito S(z) ay analytic para sa z at S(z) = )(z) sa 0 z - zo R. Samakatuwid, mayroong isang finite limit lim )(z)\u003d Pm 5 (r) \u003d 5 (r) - Samakatuwid, ang singular point zq
Z->Zo Z-*Zo
disposable. Napatunayan na ang theorem.
Magkomento. Ito ay sumusunod mula sa patunay ng theorem na sa isang butas na kapitbahayan 0 z - zo ng isang naaalis na singular na punto, ang function f(z) tumutugma sa function na S(r), na analytic sa buong kapitbahayan z - zo . Samakatuwid, kung ilalagay natin ang /(th) = S(zq), pagkatapos, nang hindi binabago ang mga halaga ng pag-andar f(z) sa anumang punto ng nabutas na kapitbahayan, ginagawa naming analytic ang function na ito sa r, i.e. "alisin" ang tampok. Ipinapaliwanag nito ang terminong "naaalis na singularidad". Natural na isaalang-alang ang mga naturang punto bilang regular, at hindi bilang mga isahan na punto ng function f(z).
Isaalang-alang, halimbawa, ang pag-andar
Sa halimbawa 26.1, ipinakita na ang Pm (n) = 1. i.e. iisang punto
zq = 0 ay naaalis. Ang pagtatakda ng /i(0) = 1, sa gayon ay inaalis namin ang singularity at kumuha ng function na analytic sa punto zq = 0 (at sa buong eroplano C).
Ilarawan natin ngayon ang mga pole sa mga tuntunin ng pagpapalawak ni Laurent.
Teorama 26.3. Ang isang nakahiwalay na puntong Zo ng isang function na f(z) ay isang poste kung at kung lamang, kapag ang pangunahing bahagi ng pagpapalawak ng Laurent na may sentrong Zq ay may hangganan lamang na bilang ng mga natatanging
mula sa mga zero coefficient na may n:
Patunay. 1. Hayaan zq - poste, ibig sabihin. lim /( z) = oo.
Patunayan natin na ang pagpapalawak ng Laurent ng function f(z) ay may anyo (2G.2). Since lim f(z)= oo. pagkatapos ay mayroong isang butas na kapitbahayan ng punto
ki zq. kung saan f(z) ay analytic at walang mga zero. Pagkatapos ang pag-andar g(z) = 1 /f(z) ay magiging analytic din sa butas na kapitbahayan na ito, at lim g(z)= 0. Samakatuwid, Zo ay disposable *-? *0
iisang punto ng function g(z). Redefine natin g(z) sa punto zo, paglalagay g(zo)= 0. Pagkatapos g(z) nagiging analytic sa buong kapitbahayan ng (hindi nabutas) na punto z 0 , at z0 ang magiging isolated zero nito. Tukuyin ng N multiplicity (order) ng zero na ito. Gaya ng ipinakita sa §23, sa isang kapitbahayan ng punto zq function g(z) kinakatawan sa anyo (tingnan ang (23.2))
at (z$) f 0 at y>(z) ay analytic sa ilang kapitbahayan ng punto zo- kasi ip(z) tuloy-tuloy sa punto zo at g>(zo) F 0" pagkatapos ip(z) ay walang mga zero sa ilang lugar sa puntong ito. Samakatuwid function 1 /-p(z) ay magiging analytic din sa kapitbahayan na ito at, samakatuwid, lumalawak dito sa isang serye ng Taylor:
Ang pagbubukas ng mga bracket at pagbabago ng mga pagtatalaga ng mga coefficient, isinusulat namin ang huling pagpapalawak sa form
kung saan c_jv = 1>o f 0. Kaya, ang pangunahing bahagi ng Laurent expansion ng f(r) ay naglalaman lamang ng isang may hangganang bilang ng mga termino; nakarating na tayo sa kinakailangang pagkakapantay-pantay (26.2).
2. Hayaan sa isang butas na kapitbahayan ng isang punto ika function )(z) ay kinakatawan ng pagpapalawak ng Laurent (26.2) (sa isang mas pinalawak na anyo, tingnan ang (26.3)), ang pangunahing bahagi nito ay naglalaman lamang ng isang tiyak na bilang ng mga termino, at kasama- d" f 0. Dapat nating patunayan iyon Zq - function na poste f(z). Pagpaparami ng pagkakapantay-pantay (26.3) sa pamamagitan ng (G - G o) iV , nakukuha namin ang function
Ang serye sa (26.4) ay isang serye ng kapangyarihan na nagtatagpo sa isang analytic function hindi lamang sa nabutas, kundi pati na rin sa buong kapitbahayan ng punto Zq. Samakatuwid, ang pag-andar h(z) nagiging analytic sa kapitbahayan na ito kung palawigin natin ito sa pamamagitan ng setting h(zo)= s_dg f 0. Pagkatapos
Kaya ang punto o ay isang poste, at ang Theorem 26.3 ay napatunayan.
Multiplicity (order) ng zeroth function g(z)= 1//(r) ay tinatawag ayos ng poste function /(r). Kung N- ang pagkakasunud-sunod ng poste ay ika, kung gayon g(z)= (r - Zo)N ip(z), at umalis) F 0, at, tulad ng ipinapakita sa unang bahagi ng patunay ng Theorem 26.3, ang pagpapalawak ng f(r) ay may anyo (26.3), kung saan c_/v f 0. Sa kabaligtaran, kung ang f(r) ay lumawak sa serye (26.3) at e-z F 0, pagkatapos
t.s. N- ang pagkakasunud-sunod ng poste ng function na f(r). Sa ganitong paraan, ang pagkakasunud-sunod ng zq pole ng function/(G) ay katumbas ng bilang ng nangungunang nonzero coefficient ng pangunahing bahagi ng pagpapalawak ng Laurent sa nabutas na kapitbahayan ng puntong zq(i.e. katumbas ng naturang numero N, anong s_dg f 0 at sp= 0 sa P > N).
Patunayan natin ang sumusunod na assertion, na maginhawa) para sa mga aplikasyon.
Corollary 26.4. Ang puntong zq ay isang poste ng ayos N ng fiction/(G) kung at kung lamang/(G) kumakatawan sa anyo
kung saan ang h(z) ay isang analytic function sa isang kapitbahayan ng isang punto ika at h(zo) f 0.
Patunay. Function cp(z) = l/h(z) ay analytic sa ilang kapitbahayan ng point r. Ang kondisyon ng Corollary 26.4 ay katumbas ng sumusunod:
Kaya zq - multiplicity zero N mga function g(z). at samakatuwid ang multiplicity pole N function /(2).
II halimbawa 26.5. Maghanap ng mga isolated na singular na punto ng isang function 
at tukuyin ang kanilang uri.
D e u c tio n. Ang mga punto kung saan (z 2 + 1 )(z+ H) 2 = 0. Kung z 2 L- 1 = 0 pagkatapos 2 = ±r kung (z 4- H) 2 = 0, pagkatapos z= -3. Samakatuwid, ang function ay may tatlong isahan na puntos z= r, 22 = -r, Z3 = - 3. Isaalang-alang z:
G - first-order pole (ginamit namin ang Corollary 26.4). Mapapatunayan din na 22 = -i isa ring poste ng unang pagkakasunud-sunod. Para sa 2h mayroon kaming:
Dumaan tayo sa pagsasaalang-alang ng mga mahalagang isahan na mga punto.
Teorama 26.6. Ang isang isolated na singular point zq ng isang function f(z) ay esensyal na isahan kung at kung ang pangunahing bahagi ng Laurent expansion na nakasentro sa zq ay may walang katapusan na maraming pagkakaiba mula sa. zero, mga coefficient na may p.
Patunay. Ang Theorem 26.6 ay direktang sumusunod mula sa Theorems 26.2 at 26.3. Sa katunayan, kung ang punto Ang zq ay mahalagang isahan, kung gayon ang pangunahing bahagi ng pagpapalawak ng Laurent ay hindi maaaring mawala o naglalaman ng isang tiyak na bilang ng mga termino (kung hindi man ang punto Ang Zq ay maaaring naaalis o isang poste). Samakatuwid, ang bilang ng mga termino sa pangunahing bahagi ay dapat na walang hanggan.
Sa kabaligtaran, kung ang pangunahing bahagi ay naglalaman ng walang katapusang maraming miyembro, kung gayon Ang Zq ay hindi maaaring maging isang naaalis na punto o isang poste. Dahil dito, ang puntong ito ay mahalagang isahan.
Ayon sa kahulugan, ang isang mahalagang isahan na punto ay nailalarawan sa pamamagitan ng katotohanan na ang function na f(2) ay walang hangganan o walang hangganang limitasyon para sa z ->zq. Ang isang mas kumpletong ideya kung gaano hindi regular ang pag-uugali ng isang function sa isang kapitbahayan ng isang mahalagang isahan na punto ay ibinibigay ng sumusunod na theorem.
Theorem 26.7 (Sochocki's theorem). Kung ang zq ay mahalagang isahan, kung gayon ang punto ng function na f(z), pagkatapos ay para sa anumang kumplikadong numero L, kasama ang A = oo, mayroong isang pagkakasunod-sunod ng mga puntos z n tulad na z n -> zo at lim f(zn) = A.
n->os
Patunay. Isaalang-alang muna ang kaso A = oo. Sa unang bahagi ng patunay ng Theorem 2G.2, itinatag namin na kung f(z) ay nakatali sa ilang butas na kapitbahayan ng punto r0, pagkatapos ay ang lahat ng mga coefficient c, n = - 1, - 2,... ng pangunahing bahagi ay katumbas ng zero (at, dahil dito, ang singularity sa ika ay naaalis). Dahil sa pamamagitan ng pag-aakalang r0 ay isang mahalagang isahan na punto, ang function na f(r) ay walang hangganan sa anumang nabutas na kapitbahayan ng punto r0. Kunin natin ang ilang makitid na kapitbahayan na 0 Z na ganoon f(zi) > 1 (kung |/(r)| z - zo R/2 may punto z-2 , kung saan |/(dd)| > 2, atbp.: sa nabutas na kapitbahayan O 71. Malinaw na rn -e go at lim /(r«) = oo. Kaya, sa kaso A = oo, Theorem 26.7
napatunayan.
Hayaan mo na A f oo. Ipagpalagay muna na mayroong nabutas na kapitbahayan 0
= -yy---- magiging analytic sa butas na kapitbahayan na ito at, dahil dito,
/(G) - A
dahil dito, ang r ay isang isolated na singular point ng function na Φ(r). Ipakita natin. na ang r0 ay isang mahalagang isahan na punto ng Φ(r). Hayaan itong mali. Pagkatapos ay mayroong isang limitasyon lim Φ(r), maaaring may hangganan o walang katapusan. kasi
/(r) = A + , pagkatapos ay umiiral din ang Hsh /(r), na sumasalungat sa kundisyon
F(g) ~ :-*z 0
view ng theorem. Kaya ang r0 ay isang mahalagang isahan na punto ng function na Φ(r). Ayon sa napatunayan sa itaas, mayroong pagkakasunod-sunod ng mga puntos r n tulad na r n o at lim Φ(r n) = oo. Mula rito
Napatunayan namin ang kinakailangang paninindigan sa ilalim ng pagpapalagay na f(r) F A sa ilang butas na kapitbahayan ng puntong r. Ipagpalagay natin ngayon na hindi ito totoo, i.e. sa anumang di-makatwirang maliit na butas na kapitbahayan ng punto ika mayroong ganoong punto G", na f(r") = A. Pagkatapos ay para sa alinman P sa nabutas na kapitbahayan 0 f(z u) = L. Kaya, ang kinakailangang assertion ay totoo P-yuo
sa lahat ng kaso, at ang Theorem 26.7 ay napatunayan.
Ayon sa (Sokhotsky's) Theorem 26.7, sa alinmang (arbitraryong maliit) na butas na kapitbahayan ng isang mahalagang isahan na punto ang function na f(r) ay kumukuha ng mga halaga na arbitraryong malapit sa anumang numero sa pinahabang kumplikadong eroplano C.
Upang pag-aralan ang mga nakahiwalay na puntong pang-isahan, kadalasang kapaki-pakinabang ang mga kilalang pagpapalawak ng Taylor ng mga pangunahing pag-andar sa elementarya.
HALIMBAWA 2G.8. Tukuyin ang uri ng singular point zq = 0 para sa function
Nalutas at e. Pinapalawak namin ang numerator at denominator sa isang serye ng Taylor sa mga kapangyarihan ng r. Pinapalitan sa (22.11) 3 z sa halip na r at ibawas ang 1, nakukuha natin
Gamit ang (22.12), nakukuha natin ang pagpapalawak ng denominator:
Ang serye sa mga pagpapalawak na ito ay nagtatagpo sa buong kumplikadong eroplano €. Meron kami
at /2(2) ay kahalintulad sa isang kapitbahayan ng punto zo = 0 (at maging sa buong eroplano) at /2(20) F 0, pagkatapos h(z) ay analytic din sa ilang kapitbahayan ng puntong gF 0. Ayon sa Corollary 26.4, ang punto Zo = 0 ang poste ng order N = 4.
II halimbawa 26.9. Maghanap ng Mga Isahan na Punto ng isang Function f(z)= sin j - at tukuyin ang kanilang uri.
P e in e at e. Ang function ay may iisang pangwakas na singular na punto zq = 1. Sa ibang mga punto mula sa C, ang function w =--- analitikal; kaya ang pag-andar ng kasalanan w magiging analitikal.
Ang pagpapalit sa pagpapalawak ng sine (22.12) - sa halip na r, nakukuha natin
Nakuha namin ang pagpapalawak ng function ng kasalanan sa isang serye ng Laurent sa isang butas na kapitbahayan ng punto 20 = 1. Dahil ang resultang pagpapalawak ay naglalaman ng walang katapusang maraming termino na may negatibong kapangyarihan (r - 1), kung gayon Ang zq = 1 ay isang mahalagang isahan na punto (sa kasong ito, ang pagpapalawak ng Laurent ay binubuo lamang ng pangunahing bahagi, at ang tamang bahagi ay wala).
Tandaan na sa kasong ito posible ring itatag ang kalikasan ng singularity nang direkta mula sa kahulugan, nang hindi gumagamit ng pagpapalawak ng serye. Sa katunayan, may mga sequence (r") at (2") na nag-uugnay sa zo= 1, at ganoon f(z" n)= 1, /(2") = 0 (tukuyin ang mga naturang sequence sa iyong sarili). Kaya, f(z) walang limitasyon kung kailan z -> 1 at samakatuwid ang punto Ang zq - 1 ay mahalagang isahan.
Ipakilala natin ang konsepto ng pagpapalawak ng Laurent ng isang function sa isang kapitbahayan ng isang punto Zq = 00 at isaalang-alang ang koneksyon sa pagitan ng pagpapalawak at katangian ng singularity sa puntong ito. Tandaan na ang mga kahulugan ng isang nakahiwalay na singular na punto at ang uri nito (naaalis, poste, o mahalagang isahan) ay dinadala sa case zq = oc hindi nagbabago. Ngunit Theorems 26.2. 26.3 at 26.6, na nauugnay sa likas na katangian ng mga pagpapalawak ng Laurent, ay kailangang baguhin. Ang punto ay ang mga miyembro c n (z - 2o) p. P= -1,-2,..., ang pangunahing bahagi, na tumutukoy sa "'irregularity" ng function malapit sa dulong punto Zq, bilang 2 ay may posibilidad na oo, sila ay kikilos nang "tama" (may posibilidad na 0). Sa kabaligtaran, ang mga miyembro ng regular na bahagi na may P= 1,2,... ay may posibilidad na oo; tinutukoy nila ang katangian ng singularidad sa Zq = oo. Samakatuwid, ang pangunahing bahagi ng pagpapalawak sa kapitbahayan ng oo ay ang mga terminong may positibong kapangyarihan P, at tama - na may negatibo.
Magpakilala tayo ng bagong variable w = 12. Function tv= 1/2, pinalawak upang ang u(oo) = 0, isa-sa-isa at alinsunod na imapa ang kapitbahayan z > R puntos zq = 00 sa kapitbahayan ng |w| wq = 0. Kung ang function f(z) analytics sa isang butas na kapitbahayan R z Zq = oc, pagkatapos ay ang function G(w) = f(l/w) magiging analytic sa yellow neighborhood 0 wo = 0. Since for 2 -> oo magkakaroon w-> 0, pagkatapos
Kaya G(w) ay nasa punto wq = 0 ay isang singularity ng parehong uri bilang f(z) sa punto Zq = 00. Palawakin natin ang function na G(w) sa isang serye ng Laurent sa isang butas na kapitbahayan ng puntong wo = 0:
Ang mga kabuuan sa kanang bahagi ng (26.5) ay kumakatawan sa tama at pangunahing bahagi ng pagpapalawak, ayon sa pagkakabanggit. Lumipat tayo sa variable z, pagpapalit w = 1/z: 
nagsasaad P\u003d -A *, 6 * \u003d 6_ " \u003d may p at mapansin iyon G(l/z) = f(z), nakukuha namin
Ang decomposition (2G.G) ay tinatawag Laurent na pagpapalawak ng function na f(z) sa isang butas na kapitbahayan ng puntong zq= oo. Ang unang kabuuan sa (2G.6) ay tinatawag kanang bahagi, at ang pangalawang kabuuan ay pangunahing bahagi ang agnas na ito. Dahil ang mga kabuuan na ito ay tumutugma sa tama at pangunahing mga bahagi ng pagpapalawak (26.5), ang pagpapalawak (26.6) ay nakakatugon sa mga analogue ng Theorems 26.2, 26.3, at 26.6. Kaya, ang sumusunod na theorem ay isang analogue ng Theorem 26.2.
Teorama 26.10. Nakahiwalay na puntong isahanZq - os (mga function/(G) ay naaalis kung at kung ang pagpapalawak ng Laurent sa isang butas na kapitbahayan ng puntong ito ay may anyo
t.s. binubuo lamang ng tamang bahagi.
Inilagay namin ang /(oo) = co. Ang function na tinukoy ng serye (26.7) na nagtatagpo sa kapitbahayan z > R puntos 2o \u003d oc, tinatawag analitiko sa puntong z o = oo. (Tandaan na ang kahulugang ito ay katumbas ng analyticity ng function G(w) sa punto aba = 0.)
Halimbawa 26.11. Siyasatin ang singular point zq = oo ng function
Dahil ang limitasyon ay may hangganan, kung gayon zo = Ang oo ay isang naaalis na singular na punto ng function na f(r). Kung ilalagay natin ang /(oo) = lim J(z)= 0, pagkatapos f(z) ay magiging
tic sa punto Zo= os. Ipakita natin kung paano hanapin ang kaukulang pagpapalawak (26.7). Lumipat tayo sa variable w = 1 fz. Pagpapalit z= 1 /?e, nakukuha natin
(ang huling pagkakapantay-pantay ay wasto sa nabutas na kapitbahayan ng puntong ww = 0, ngunit palawigin natin ang kahulugan (7(0) = 0). Ang resultang function ay may mga singular na puntos w =± ako, w =-1/3, at sa punto Ang Wq = 0 ay analytic. Pagpapalawak ng function G(w) sa pamamagitan ng grado w(tulad ng ginawa sa Halimbawa 25.7) at pagpapalit sa nagresultang serye ng kapangyarihan w = 1/z maaaring makuha ng isa ang pagpapalawak (26.7) ng function f(z).
Theorem 26.3 para sa kaso zo= oo ay muling isusulat sa sumusunod na anyo.
Teorama 26.12. Nakahiwalay na puntong isahan pumunta = os Ang function na f(z) ay isang poste kung at kung ang pangunahing bahagi ng pagpapalawak ng Laurent (26.6) ay may hangganan lamang na bilang ng mga non-zero coefficient kasama ang":
Narito ang serye ay ang regular na bahagi, at ang parenthesized polynomial ay ang pangunahing bahagi ng pagpapalawak. Ang multiplicity ng pole sa oc ay tinukoy bilang ang multiplicity ng pole wq = 0 function G(z). Madaling makita na ang multiplicity ng poste ay tumutugma sa bilang N sa (26.8).
Q p | (i 2 + 1) (z + 3) 2
Gawain. Ipakita na ang function f(z) =-- -- ay pumasok
punto zo = oo pole order 3.
Ang Theorem 26.6 sa isang mahalagang isahan na punto ay muling isinulat para sa kaso zo= os almost verbatim, at hindi natin ito pinag-uusapan nang detalyado.
Ang serye ng Taylor ay nagsisilbing isang epektibong tool para sa pag-aaral ng mga function na analytic sa bilog zol Upang pag-aralan ang mga function na analytic sa isang annular na rehiyon, lumalabas na posible na bumuo ng mga pagpapalawak sa positibo at negatibong mga kapangyarihan (z - zq) ng form na nag-generalize ng Taylor expansions. Ang serye (1), na nauunawaan bilang kabuuan ng dalawang serye, ay tinatawag na seryeng Laurent. Malinaw na ang rehiyon ng convergence ng serye (1) ay ang karaniwang bahagi ng mga rehiyon ng convergence ng bawat serye (2). Hanapin natin siya. Ang lugar ng convergence ng unang serye ay isang bilog na ang radius ay tinutukoy ng Cauchy-Hadamard formula Sa loob ng bilog ng convergence, ang serye (3) ay nagtatagpo sa isang analytic function, at sa anumang bilog na mas maliit na radius, ito ay ganap na nagtatagpo at pare-pareho. Ang pangalawang serye ay isang serye ng kapangyarihan na may paggalang sa variable. Ang serye (5) ay nagtatagpo sa loob ng bilog ng convergence nito sa analytic function ng complex variable m-*oo, at sa anumang bilog na mas maliit na radius ay ganap at pare-pareho itong nagtatagpo, na nangangahulugan na ang rehiyon ng convergence ng serye (4) ay ang hitsura ng bilog - Kung pagkatapos ay mayroong isang karaniwang rehiyon ng convergence ng serye (3) at (4) - isang pabilog na singsing kung saan ang serye (1) nagtatagpo sa isang analytic function. Bukod dito, sa anumang singsing, ito ay nagtatagpo nang ganap at pantay. Halimbawa 1. Tukuyin ang rehiyon ng convergence ng rad Laurent series Isolated singular points and their classification (z), which is single-valued and apolitical in a circular ring, can represented in this ring, as the sum of a convergent series which coefficients Ang Cn ay katangi-tanging tinutukoy at kinakalkula ng mga formula kung saan ang 7p ay isang bilog na radius m Ayusin natin ang isang di-makatwirang punto z sa loob ng singsing R Bumubuo kami ng mga bilog na may mga sentro sa puntong r na ang radii ay nakakatugon sa mga hindi pagkakapantay-pantay at isinasaalang-alang ang isang bagong singsing. Ayon sa Cauchy integral theorem para sa isang multiply connected domain, mayroon kaming Let us transform each of the integrals in the sum (8) separately. Para sa lahat ng mga puntos £ kasama ang bilog 7d*, ang kaugnayan ng kabuuan ng isang pare-parehong nagtatagpo serye 1 1 ay nasiyahan. Samakatuwid, ang fraction ^ ay maaaring katawanin sa vi- /" / Sa medyo magkaibang paraan, para sa lahat ng mga puntos ξ sa ang bilog ir> mayroon tayong kaugnayan Samakatuwid, ang fraction ^ ay maaaring katawanin bilang ang kabuuan ng isang pare-parehong convergent na serye sa mga formula (10) at (12) ay mga analytic function sa isang pabilog na singsing. Samakatuwid, sa pamamagitan ng teorem ni Cauchy, ang mga halaga ng kaukulang integral ay hindi nagbabago kung ang mga bilog na 7/r at 7r/ ay pinalitan ng anumang bilog. Ito ay nagpapahintulot sa amin na pagsamahin ang mga formula (10) at (12). Ang pagpapalit ng mga integral sa kanang bahagi ng formula (8) ng kanilang mga expression (9) at (11), ayon sa pagkakabanggit, makuha namin ang nais na pagpapalawak. Dahil ang z ay isang arbitrary punto ng singsing, ito ay sumusunod na ang serye ( 14) ay nagtatagpo sa function na f(z) saanman sa singsing na ito, at sa anumang singsing ang serye ay ganap at pare-parehong nagtatagpo sa function na ito. Patunayan natin ngayon na ang agnas ng anyo (6) ay natatangi. Ipagpalagay na ang isa pang agnas ay magaganap. Pagkatapos, saanman sa loob ng singsing R, mayroon tayong Sa circumference, ang serye (15) ay magkakaugnay. I-multiply ang magkabilang panig ng pagkakapantay-pantay (kung saan ang m ay isang nakapirming integer, at isama ang parehong termino ng serye ayon sa termino. Bilang resulta, nakakakuha tayo sa kaliwang bahagi, at sa kanang bahagi - Csh. Kaya, (4, \u003d St. Dahil ang m ay isang arbitrary na numero, kung gayon ang huling serye ng pagkakapantay-pantay (6), na ang mga coefficient ay kinakalkula ng mga formula (7), ay tinatawag na serye ng Laurent ng function na f(z) sa singsing 7) para sa mga coefficient ng serye ng Laurent ay bihirang ginagamit sa pagsasanay, dahil, bilang isang panuntunan, nangangailangan sila ng masalimuot na mga kalkulasyon. Karaniwan, kung maaari, ang mga yari na Taylor expansion ng elementarya ay ginagamit. Batay sa pagiging natatangi ng pagpapalawak, ang anumang lehitimong pamamaraan ay humahantong sa parehong resulta. Halimbawa 2 Isaalang-alang ang mga pagpapalawak ng serye ng Laurent ng mga function ng iba't ibang domain, kung ipagpalagay na ang Fuiscija /(z) ay may dalawang singular na punto: Samakatuwid, mayroong tatlong ring domain at, nakasentro sa punto r = 0. sa bawat isa kung saan ang function na f(r) ay analytic: a) ang bilog ay ang panlabas ng bilog (Larawan 27). Hanapin natin ang mga pagpapalawak ng Laurent ng function /(z) sa bawat isa sa mga rehiyong ito. Kinakatawan namin ang /(z) bilang isang kabuuan ng mga elementarya na praksyon a) Circle Transform relation (16) bilang mga sumusunod Gamit ang formula para sa kabuuan ng mga termino ng isang geometric progression, nakukuha namin b) Ang singsing para sa function -z ay nananatiling convergent sa ring na ito, dahil Serye (19) para sa function na j^j para sa |z| > 1 diverges. Samakatuwid, binabago namin ang function /(z) bilang mga sumusunod: paglalapat muli ng formula (19), nakuha namin na Ang seryeng ito ay nagtatagpo para sa. Ang pagpapalit ng mga pagpapalawak (18) at (21) sa kaugnayan (20), makuha natin ang c) Ang exteriority ng bilog para sa function -z na may |z| > 2 diverges, at serye (21) para sa function Hayaan nating katawanin ang function /(z) sa sumusunod na anyo: /<*> Gamit ang mga formula (18) at (19), nakukuha natin ang OR 1 Ipinapakita ng halimbawang ito na para sa parehong function f(z) ang Laurent expansion, sa pangkalahatan, ay may ibang anyo para sa iba't ibang singsing. Halimbawa 3. Hanapin ang decomposition ng 8 Laurent series ng function Laurent series Isolated singular points and their classification in the annular region A Ginagamit namin ang representasyon ng function f (z) sa sumusunod na anyo: at ibahin ang anyo ng pangalawang termino Gamit ang formula para sa kabuuan ng mga termino ng isang geometric na pag-unlad, nakukuha namin Ang pagpapalit ng mga nahanap na expression sa formula (22), mayroon kaming Halimbawa 4. Palawakin ang function sa isang serye ng Laurent sa kapitbahayan ng manipis na zq = 0. Para sa anumang kumplikado , mayroon kaming Let This expansion was valid for any point z Ф 0. Sa kasong ito, ang annular region ay ang buong complex plane na may isang thrown out point z - 0. Ang rehiyon na ito ay maaaring tukuyin ng sumusunod na relasyon: Ang function na ito ay analytic sa rehiyon Mula sa mga pormula (13) para sa mga coefficient ng serye ng Laurent, sa pamamagitan ng parehong pangangatwiran tulad ng sa nakaraang talata, maaaring makuha ng isa ang hindi pagkakapantay-pantay ng Kouiw. kung ang function na f(z) ay nakatali sa isang bilog, kung saan ang M ay isang pare-pareho), pagkatapos ay nakahiwalay na mga singular na puntos Ang isang point zo ay tinatawag na isang nakahiwalay na punto ng isahan ng function na f(z) kung mayroong isang annular na kapitbahayan ng punto ( Ang hanay na ito ay tinatawag din minsan na isang punctured neighborhood ng punto 2o), kung saan ang function na f(z) ay single-valued at analytic. Sa puntong zo mismo, ang function ay maaaring hindi tinukoy o hindi single-valued at analytic. Tatlong uri ng mga singular na puntos ang nakikilala depende sa pag-uugali ng function /(z) kapag papalapit sa puntong zo. Ang isang nakahiwalay na puntong singular ay sinasabing: 1) naaalis kung mayroong isang may hangganan 2) pmusach kung 3) isang mahalagang puntong isahan kung ang function na f(z) ay walang limitasyon para sa Theorem 16. Ang isang nakahiwalay na singular point z0 ng isang function f(z) ay isang naaalis na singular point kung at kung ang Laurent expansion ng function na f(z) sa isang neighborhood ng point zo ay walang pangunahing bahagi, ibig sabihin, ay may anyo na Let zo - naaalis na isahan na punto. Pagkatapos ay mayroong isang may hangganan, at samakatuwid ang function na f(z) ay nakatali sa isang procological na kapitbahayan ng puntong r. Itinakda namin Sa pamamagitan ng mga hindi pagkakapantay-pantay ng Cauchy Dahil posible na pumili ng ρ bilang maliit hangga't gusto namin, kung gayon ang lahat ng coefficients sa negatibong kapangyarihan (z - 20) ay katumbas ng zero: Sa kabaligtaran, hayaan ang Laurent ang pagpapalawak ng function /(r) sa isang kapitbahayan ng puntong zq ay naglalaman lamang ng tamang bahagi, ibig sabihin, mayroon itong anyo (23) at, samakatuwid, ay si Taylor. Madaling makita na para sa z -* z0 ang function /(r) ay may limitasyon na halaga: Theorem 17. Ang isang nakahiwalay na singular point zq ng function na f(z) ay matatanggal kung at kung ang function na J(z) ay bounded sa ilang mga punctured kapitbahayan ng punto zq, Zgmechai hindi. Hayaang ang r0 ay isang naaalis na singular na punto ng f(r). Ipagpalagay na nakuha natin na ang function na f(r) ay analytic sa ilang bilog na nakasentro sa puntong ika. Tinutukoy nito ang pangalan ng punto - disposable. Theorem 18. Ang isang isolated na singular point zq ng isang function f(z) ay isang poste kung at kung ang pangunahing bahagi ng Laurent expansion ng function na f(z) sa isang neighborhood ng point ay naglalaman ng finite (at positive) number ng mga di-zero na termino, ibig sabihin, ay may anyo 4 Hayaan ang z0 ay isang poste. Mula noon mayroong isang butas na kapitbahayan ng puntong z0 kung saan ang function na f(z) ay analytic at nonzero. Pagkatapos ay tinukoy ang isang analytic function sa kapitbahayan na ito, at Samakatuwid, ang puntong zq ay isang naaalis na singular na punto (zero) ng function o kung saan ang h(z) ay isang analytic function, ang h(z0) ∩ 0. ay analytic sa isang kapitbahayan ng puntong zq, at samakatuwid, kung saan natin makukuha iyon. Nangangahulugan ito na sa lugar na ito ang function na f(z) ay analytic kasama ng function. Para sa function na g(z), valid ang expansion kung saan malinaw na ang zq ay isang naaalis na isahan na punto ng function na g(z) at umiiral Pagkatapos ang function ay may gawi sa 0 - ang pole ng function May isa pang simple. katotohanan. Ang puntong Zq ay isang poste ng function na f(z) kung at kung ang function na g(z) = y ay maaaring i-extend sa isang analytic function sa isang kapitbahayan ng point zq sa pamamagitan ng pagtatakda ng g(z0) = 0. Ang pagkakasunud-sunod ng pole ng function na f(z) ay tinatawag na order ng zero ng function jfa. Ang Theorems 16 at 18 ay nagpapahiwatig ng sumusunod na assertion. Theorem 19. Ang isang nakahiwalay na singular na manipis ay mahalagang isahan kung at kung ang pangunahing bahagi ng pagpapalawak ng Laurent sa isang butas na kapitbahayan ng puntong ito ay naglalaman ng walang katapusang maraming nonzero na termino. Halimbawa 5. Ang singular na punto ng function ay zo = 0. Mayroon kaming Laurent Series Isolated singular points at ang kanilang klasipikasyon Samakatuwid, ang zo = 0 ay isang naaalis na singular na punto. Ang pagpapalawak ng function /(z) sa isang serye ng Laurent sa paligid ng zero point ay naglalaman lamang ng tamang bahagi: Halimbawa7. f(z) = Ang singular na punto ng function na f(z) ay zq = 0. Isaalang-alang ang pag-uugali ng function na ito sa tunay at haka-haka na mga ax: sa totoong axis sa x 0, sa haka-haka na axis Samakatuwid, ni finite o walang katapusang limitasyon f(z) sa z -* 0 ay hindi umiiral. Kaya't ang punto r0 = 0 ay isang mahalagang isahan na punto ng function na f(z). Hanapin natin ang pagpapalawak ng Laurent ng function na f(z) sa isang lugar ng zero point. Para sa anumang kumplikadong C mayroon kaming itinakda namin. Pagkatapos ang pagpapalawak ng Laurent ay naglalaman ng walang katapusang bilang ng mga termino na may negatibong kapangyarihan ng z.
Kahulugan. Tinatawag ang singular na punto ng function nakahiwalay, kung sa ilang kapitbahayan ng puntong ito ay isang analytic function (iyon ay, analytic sa ring).
Ang pag-uuri ng mga nakahiwalay na singular na punto ng isang function ay nauugnay sa pag-uugali ng function na ito sa isang kapitbahayan ng isang singular na punto.
Kahulugan. Tinatawag ang punto disposable isang isahan na punto ng isang function kung mayroong isang finite limit ng function na ito sa .
Halimbawa 5 Ipakita na ang function ay may naaalis na singularity sa isang punto.
Solusyon. Inaalala ang unang kapansin-pansing limitasyon, kinakalkula namin
Nangangahulugan ito na ang ibinigay na function ay may naaalis na singularity sa punto.
Gawain 4. Ipakita na ang punto ay naaalis para sa .
Kahulugan. Tinatawag ang punto poste function , kung ang function na ito ay tataas nang walang katiyakan para sa , iyon ay .
Bigyang-pansin natin ang koneksyon sa pagitan ng mga konsepto ng zero at pole ng isang analytic function. Katawanin natin ang function bilang .
Kung ang isang punto ay isang simpleng zero ng isang function, kung gayon ang function ay may isang simpleng poste
Kung ang punto ay ang order zero para sa function, kung gayon para sa function ito ay ang poste utos.
Halimbawa 6 Ipakita na ang function ay may third-order pole sa isang punto.
Solusyon. Sa pag-aakala, nakukuha namin. Dahil madalas tayong maging zero, ayon sa anumang batas, mayroon tayong . Pagkatapos , at kasama nito ang pag-andar mismo ay tumataas nang walang katiyakan. Samakatuwid, , ibig sabihin, ang singular na punto ay isang poste. Para sa isang function, ang puntong ito ay malinaw na isang triple zero. Samakatuwid, para sa function na ito, ang punto ay isang poste ng ikatlong order.
Gawain 5. Ipakita na ang punto ay may isang simpleng poste.
Kahulugan. Tinatawag ang punto mahalagang espesyal punto ng function kung sa puntong ito ay walang hangganan o walang katapusan na limitasyon ng function (ang pag-uugali ng function ay hindi tinukoy).
Hayaan ang isang mahalagang isahan na punto ng function. Pagkatapos, para sa anumang naitalagang kumplikadong numero mayroong isang pagkakasunud-sunod ng mga puntos na nagtatagpo sa , kung saan ang mga halaga ay may posibilidad na: ( Sochocki's theorem).
Halimbawa 7 Ipakita na ang isang function sa isang punto ay may mahalagang singularity.
Solusyon. Isaalang-alang ang pag-uugali ng isang ibinigay na function sa paligid ng punto. Para sa kahabaan ng positibong bahagi ng totoong axis (i.e. ) mayroon tayo at ; kung kasama ang negatibong bahagi ng tunay na axis (i.e.), kung gayon at . Kaya walang limitasyon para sa . Sa pamamagitan ng kahulugan, ang isang function ay may mahalagang singularity sa isang punto.
Isaalang-alang natin ang pag-uugali ng function sa zero mula sa punto ng view ng Sochocki theorem. Hayaan ang anumang kumplikadong numero maliban sa zero at infinity.
Mula sa pagkakapantay-pantay nakita namin. Sa pag-aakalang , nakakakuha tayo ng pagkakasunod - sunod ng mga puntos , . Malinaw, . Sa bawat punto ng sequence na ito, ang function ay katumbas ng , at samakatuwid
Gawain 6. Ipakita na ang function ay may mahalagang singularity sa isang punto.
Ang isang punto sa infinity ay palaging itinuturing na espesyal para sa function. Ang isang punto ay tinatawag na isang isolated na singular point ng isang function kung ang function na ito ay walang iba pang mga singular na puntos sa labas ng ilang bilog na nakasentro sa pinanggalingan.
Ang pag-uuri ng mga isolated na singular na puntos ay maaari ding palawigin sa kaso.
Halimbawa 8 Ipakita na ang function ay may double pole sa infinity.
Solusyon. Isaalang-alang ang function , kung saan ay isang analytic function sa isang kapitbahayan ng point , at . Nangangahulugan ito na ang function ay may double zero sa infinity, ngunit pagkatapos ay para sa function ang point ay isang double pole.
Halimbawa 9 Ipakita na ang function ay may mahalagang singularity sa infinity.
Solusyon. Ang isang katulad na problema ay isinasaalang-alang sa pr.7. Isaalang-alang ang pag-uugali ng isang function sa kapitbahayan ng isang walang katapusan na malayong punto. Para sa kahabaan ng positibong bahagi ng totoong axis, at para sa kahabaan ng negatibong bahagi ng totoong axis. Nangangahulugan ito na walang limitasyon ng function sa isang punto at, ayon sa kahulugan, ang puntong ito ay mahalagang isahan.
Ang katangian ng singularity ng isang function sa isang punto ay maaaring hatulan mula sa pangunahing bahagi Pagpapalawak ng Laurent sa isang lugar sa puntong ito.
Teorama 1. Para sa punto na disposable singular point ng function , ito ay kinakailangan at sapat na ang kaukulang Laurent expansion hindi naglalaman ng pangunahing bahagi.
Gawain 6. Gamit ang Taylor expansion ng function sa isang neighborhood ng point , ipakita na mayroon itong naaalis na singularity sa zero.
Teorama 2. Para sa punto na poste functions , ay kinakailangan at sapat upang pangunahing bahagi kaukulang pagpapalawak ng Laurent naglalaman ng limitadong bilang ng mga miyembro :
Tinutukoy ng bilang ng pinakamataas na negatibong termino ang pagkakasunud-sunod ng poste.
Sa kasong ito, ang function ay maaaring katawanin bilang
kung saan ang function analytic sa punto, , ay ang pagkakasunud-sunod ng poste.
Halimbawa 10 Ipakita na ang function ay may mga simpleng pole sa mga punto.
Solusyon. Isaalang-alang natin ang isang punto. Ginagamit namin ang pagpapalawak ng Laurent ng function na ito sa paligid ng puntong ito, na nakuha sa Halimbawa 2:
Dahil ang pinakamataas (at tanging) negatibong kapangyarihan sa pangunahing bahagi ng pagpapalawak na ito ay katumbas ng isa, ang punto ay isang simpleng poste ng function na ito.
Ang resultang ito ay maaaring makuha sa ibang paraan. Ipaalam sa amin kumatawan sa form at ilagay - ito ay isang function na analytic sa punto at . Samakatuwid, dahil sa (8) ang function na ito ay may isang simpleng poste sa punto.
Isa pang paraan: isaalang-alang ang isang function na may simpleng zero sa punto. Samakatuwid, sa puntong ito mayroon itong isang simpleng poste.
Katulad nito, kung isusulat natin ang function sa form , kung saan ang isang function na analytic sa punto at , pagkatapos ay agad na malinaw na ang punto ay isang simpleng poste ng function .
Gawain 7. Ipakita na ang function ay may isang poste ng 2nd order sa punto at isang poste ng ika-4 na order sa point .
Teorama 3. Para sa punto na mahalagang espesyal punto ng function , ito ay kinakailangan at sapat na pangunahing bahagi Pagpapalawak ng Laurent sa isang kapitbahayan ng punto naglalaman ng walang katapusang bilang ng mga miyembro .
Halimbawa 11. Tukuyin ang katangian ng singularity sa punto ng function
Solusyon. Sa kilalang pagpapalawak ng cosine, inilalagay namin sa halip na:
Samakatuwid, ang pagpapalawak ng Laurent sa isang kapitbahayan ng isang punto ay may anyo
Narito ang tamang bahagi ay isang termino. At ang pangunahing bahagi ay naglalaman ng isang walang katapusang bilang ng mga termino, kaya ang punto ay mahalagang isahan.
Gawain 8. Ipakita na sa isang punto ang function ay may isang mahalagang singularity.
Isaalang-alang ang ilang function at isulat ang pagpapalawak ng Laurent nito sa puntong:
Gumawa tayo ng kapalit, habang ang punto ay papunta sa punto. Ngayon, sa isang kapitbahayan ng isang punto sa infinity, mayroon kami
Ito ay nananatiling magpakilala ng isang bagong pagtatalaga. Nakukuha namin
kung saan ang pangunahing bahagi, at ang regular na bahagi ng Laurent na pagpapalawak ng function sa paligid ng punto sa infinity. Kaya, sa pagpapalawak ng Laurent ng isang function sa isang kapitbahayan ng isang punto, ang pangunahing bahagi ay isang serye sa mga positibong kapangyarihan, habang ang tamang bahagi ay isang serye sa mga negatibong kapangyarihan. Isinasaalang-alang ito
Gayunpaman, ang mga pamantayan sa itaas para sa pagtukoy ng katangian ng singularity ay nananatiling wasto para sa isang walang katapusan na malayong punto.
Halimbawa 12. Alamin ang katangian ng singularity ng function sa punto. , pagkatapos ay sa isang punto maaari itong lumabas na hindi nakahiwalay.
Halimbawa 15 Ang pag-andar sa isang walang katapusang malayong punto ay may mahalagang singularity. Ipakita na ang punto para sa function ay hindi isang nakahiwalay na puntong isahan.
Solusyon. Ang function ay may walang katapusang bilang ng mga pole sa mga zero ng denominator, iyon ay, sa mga punto , . Dahil , kung gayon ang punto , sa alinmang kapitbahayan kung saan mayroong mga poste , ay ang limitasyon ng punto para sa mga poste.
iisang punto sa matematika. 1) Singular point ng curve na ibinigay ng equation F ( x, y) = 0, - punto M 0 ( x 0 , y 0), kung saan ang parehong partial derivatives ng function F ( x, y) mawala: Kung, bilang karagdagan, hindi lahat ng pangalawang partial derivatives ng function F ( x, y) sa puntong M 0 ay katumbas ng zero, kung gayon ang O. t. ay tinatawag na doble. Kung, kasama ang paglaho ng mga unang derivative sa puntong M 0, ang lahat ng pangalawang derivative ay naglaho, ngunit hindi lahat ng ikatlong derivative ay katumbas ng zero, kung gayon ang O. t. ay tinatawag na triple, at iba pa. Kapag pinag-aaralan ang istraktura ng isang kurba malapit sa isang dobleng O. t., isang mahalagang papel ang ginagampanan ng tanda ng pagpapahayag Kung Δ > 0, kung gayon ang O. t. ay tinatawag na isolated; halimbawa, ang kurba y 2 - x 4 + 4x 2= 0 ang pinagmulan ay isang nakahiwalay na O. t. (tingnan kanin. isa
). Kung Δ x 2 + y 2 + a 2) 2 - 4a 2 x 2 - a 4= 0 ang pinagmulan ng mga coordinate ay ang nodal O. t. (tingnan kanin. 2
). Kung Δ = 0, kung gayon ang O. t. curve ay maaaring nakahiwalay o nailalarawan sa pamamagitan ng katotohanan na ang iba't ibang sangay ng curve ay may isang karaniwang tangent sa puntong ito, halimbawa: tangent at bumubuo ng isang punto, tulad ng isang curve y 2 - x 3= 0 (tingnan kanin. 3
, a); b) cusp ng ika-2 uri - ang iba't ibang mga sanga ng curve ay matatagpuan sa parehong bahagi ng karaniwang tangent, tulad ng isang curve
(y - x 2)2 - x 5= 0 (tingnan kanin. 3
, b); c) punto ng self-contact (para sa isang curve y 2 - x 4= 0 pinanggalingan ay isang punto ng self-contact; (cm. kanin. 3
, v). Kasama ang tinukoy na O. t. mayroong maraming iba pang O. t. na may mga espesyal na pangalan; halimbawa, ang asymptotic point ay ang tuktok ng isang spiral na may walang katapusang bilang ng mga pagliko (tingnan ang Fig. kanin. 4
), break point, corner point, atbp. 2) Ang singular na punto ng differential equation ay isang punto kung saan ang numerator at denominator ng kanang bahagi ng differential equation ay sabay-sabay na nawawala (Tingnan ang Differential Equation) kung saan ang P at Q ay patuloy na naiba-iba na mga function. Ipagpalagay na ang O. t. na matatagpuan sa pinanggalingan ng mga coordinate at gamit ang Taylor formula (Tingnan ang Taylor formula), maaari nating katawanin ang equation (1) sa anyo kung saan ang P 1 ( x, y) at Q 1 ( x, y) ay infinitesimal na may kinalaman sa Ibig sabihin, kung λ 1 ≠ λ 2 at λ 1 λ 2 > 0 o λ 1 = λ 2, kung gayon ang O. t. ay isang node; lahat ng integral curve na dumadaan sa mga punto ng isang sapat na maliit na kapitbahayan ng node ay pumasok dito. Kung λ 1 ≠ λ 2 at λ 1 λ 2 i β, α ≠ 0 at β ≠ 0, kung gayon ang O. t. ay isang pokus; lahat ng integral curve na dumadaan sa mga punto sa isang sapat na maliit na kapitbahayan ng focus ay mga spiral na may walang katapusang bilang ng mga pagliko sa anumang maliit na kapitbahayan ng focus. Kung, sa wakas, λ 1,2 = ± iβ, β ≠ 0, kung gayon ang katangian ng O. t. ay hindi tinutukoy ng mga linear na termino sa mga pagpapalawak ng P ( x, y) at Q ( x, y), tulad ng nangyari sa lahat ng mga kaso sa itaas; dito ang O. t. ay maaaring maging pokus o sentro, o maaari itong magkaroon ng mas kumplikadong karakter. Sa kapitbahayan ng gitna, ang lahat ng integral curve ay sarado at naglalaman ng gitna sa loob ng mga ito. Kaya, halimbawa, ang punto (0, 0) ay isang node para sa mga equation sa" = 2u/x(λ 1 = 1, λ 2 = 2; tingnan kanin. 5
, a) at y" = u/x(λ 1 = λ 2 = 1; tingnan kanin. 5
, b), isang saddle para sa equation y" = -y/x(λ 1 = -1, λ 2 = 1 ; cm. kanin. 6
), ang pokus para sa equation y" =(x + y) /
(x - y) (λ 1 = 1 - i, λ 2 = 1 + i; cm. kanin. 7
) at ang sentro para sa equation y" = -x / y(λ 1 = -i, λ 2 = i; cm. kanin. walo
). Kung x, y) at Q ( x, y) ay analytic, ang kapitbahayan ng isang O. t. ng mas mataas na pagkakasunud-sunod ay maaaring nahahati sa mga rehiyon: D 1 - puno ng integral curves, ang magkabilang dulo nito ay kasama sa O. t. (elliptic na mga rehiyon), D 2 - napuno na may mga integral na kurba, ang isang dulo nito ay kasama sa O. t. (parabolic na mga rehiyon), at D 3 - mga rehiyon na napapalibutan ng dalawang integral na mga kurba na kasama sa O. t., kung saan mayroong mga integral na kurba ng uri ng hyperbolas (hyperbolic na rehiyon) (tingnan. kanin. 9
). Kung walang integral curves na pumapasok sa isang O. point, kung gayon ang O. point ay tinatawag na point of stable type. Ang kapitbahayan ng isang matatag na O. t. ay binubuo ng mga saradong integral na kurba na naglalaman ng O. t. sa loob mismo, sa pagitan ng kung saan matatagpuan ang mga spiral (tingnan ang Fig. kanin. 10
). Ang pag-aaral ng O. t. differential equation, iyon ay, sa esensya, ang pag-aaral ng pag-uugali ng mga pamilya ng integral curves sa isang kapitbahayan ng O. t. M. Lyapunov a, A. Poincaré at iba pa). 3) Ang isang punto ng isang solong-valued analytic function ay isang punto kung saan ang analyticity ng isang function ay nilabag (tingnan ang Analytic function). Kung mayroong isang kapitbahayan ng O. t. a, libre mula sa iba pang O. t., pagkatapos ay ang punto a ay tinatawag na isolated O. t. Kung a ay isang nakahiwalay na O. t. at mayroong isang may hangganan na tinatawag na isang naaalis na O. t. f(a)= b, ito ay posibleng makamit a ay magiging isang ordinaryong punto ng naitama na function. Halimbawa, tuldok z Ang = 0 ay isang naaalis na O.T. para sa function na f 1 ( z) = f(z), kung z≠ 0, at f 1(0),=1, tuldok z= 0 ay isang ordinaryong punto [ f 1 (z) ay analytic sa punto z= 0]. Kung a- isolated O. t. at a ay tinatawag na isang poste o isang inesentially singular point ng function f(z), kung gumagana ang serye ng Laurent f(z) sa isang kapitbahayan ng isang nakahiwalay na O. t. ay hindi naglalaman ng mga negatibong kapangyarihan z - a, kung a- naaalis na O. t., ay naglalaman ng isang may hangganang bilang ng mga negatibong kapangyarihan z - a, kung a- poste (sa kasong ito, ang pagkakasunud-sunod ng poste R ay tinukoy bilang ang pinakamataas na kapangyarihan ng a - isang mahalagang isahan na punto. Halimbawa, para sa function tuldok z= 0 ang poste ng order R, para sa function tuldok z Ang = 0 ay isang mahalagang isahan na punto. Sa hangganan ng bilog ng convergence ng isang serye ng kapangyarihan ay dapat mayroong hindi bababa sa isang O. t. ng function na kinakatawan sa loob ng bilog na ito ng ibinigay na serye ng kapangyarihan. Ang lahat ng boundary point ng domain ng pagkakaroon ng isang single-valued analytic function (natural boundary) ay mga boundary point ng function na ito. Kaya, ang lahat ng mga punto ng bilog ng yunit | z| = 1 ay espesyal sa function Para sa isang multi-valued analytic function, ang konsepto ng "O. T." mas mahirap. Bilang karagdagan sa O. t., sa mga indibidwal na sheet ng Riemann surface ng isang function (iyon ay, ang O. t. ng single-valued analytic elements), ang anumang branch point ay isa ring O. t. ng function. Ang mga nakahiwalay na branch point ng isang Riemann surface (ibig sabihin, mga branch point na sa ilan sa kanilang mga kapitbahayan ay walang ibang O.t. function sa alinmang dahon) ay inuri bilang sumusunod. Kung ang a ay isang nakahiwalay na sangay na punto ng may hangganan na pagkakasunud-sunod at mayroong isang may hangganan na a, ito ay tinatawag na isang kritikal na poste. Kung a ay isang nakahiwalay na punto ng sangay ng walang katapusan na pagkakasunud-sunod at ang a ay tinatawag na isang transendental na O. t. Ang lahat ng iba pang nakahiwalay na mga punto ng sangay ay tinatawag na kritikal na mahalagang isahan na mga punto. Mga halimbawa: tuldok z Ang = 0 ay isang ordinaryong kritikal na punto ng function na f ( z) = log z at isang kritikal na mahalagang isahan na punto ng function f (z) = log ng kasalanan z. Anumang O. t., maliban sa isang naaalis, ay isang balakid sa analytic na pagpapatuloy, ibig sabihin, ang analytic na pagpapatuloy sa isang curve na dumadaan sa isang hindi naaalis na O. t. ay imposible. Great Soviet Encyclopedia. - M.: Encyclopedia ng Sobyet.
1969-1978
.
p = 2, 3, …)
Tingnan kung ano ang "Espesyal na Punto" sa ibang mga diksyunaryo:
Mga puntos dito. Tingnan din ang isahan na punto (differential equation). Ang tampok o singularidad sa matematika ay isang punto kung saan ang isang bagay sa matematika (karaniwang isang function) ay hindi tinukoy o may hindi regular na pag-uugali (halimbawa, isang punto kung saan ... ... Wikipedia
Ang analytic function ay isang punto kung saan nilalabag ang mga kundisyon ng analyticity. Kung ang isang analytic function na f(z) ay tinukoy sa ilang kapitbahayan ng puntong z0 saanman ... Pisikal na Encyclopedia
Ang analytic function ay ang punto kung saan ang analyticity ng isang function ay nilabag ... Malaking Encyclopedic Dictionary
iisang punto- — [Ya.N. Luginsky, M.S. Fezi Zhilinskaya, Yu.S. Kabirov. English Russian Dictionary of Electrical Engineering at Power Industry, Moscow, 1999] Mga paksa sa electrical engineering, mga pangunahing konsepto EN singular point ... Handbook ng Teknikal na Tagasalin
1) Ang isang OT ng isang analytic function na f(z) ay isang hadlang sa analytic na pagpapatuloy ng isang elemento ng function na f(z) ng isang kumplikadong variable z kasama ang ilang landas sa eroplano ng variable na ito. Hayaang tukuyin ang analytic function na f(z) ng ilang ... ... Mathematical Encyclopedia
Isang analytic function, ang punto kung saan nilalabag ang analyticity ng function. * * * SINGULAR POINT ISANG SINGULAR POINT ng analytic function, isang punto kung saan nilalabag ang analyticity ng function ... encyclopedic Dictionary
iisang punto- ypatingasis taškas statusas T sritis automatika atitikmenys: engl. singular point vok. singularer Punkt, m rus. iisang punto, fpranc. punto ng butil, m; point singulier, m … Automatikos terminų žodynas
