1. উপসর্গের ধারণা

ফাংশন গ্রাফ নির্মাণের একটি গুরুত্বপূর্ণ ধাপ হল অ্যাসিম্পটোটস অনুসন্ধান করা। আমরা একাধিকবার উপসর্গের সম্মুখীন হয়েছি: ফাংশনের গ্রাফ তৈরি করার সময়, y=tgx, y=stgx. আমরা সেগুলিকে লাইন হিসাবে সংজ্ঞায়িত করেছি যেগুলি একটি ফাংশনের গ্রাফ "প্রবণ" হয়, কিন্তু কখনই অতিক্রম করে না। উপসর্গের একটি সুনির্দিষ্ট সংজ্ঞা দেওয়ার সময় এসেছে।

তিন ধরনের অ্যাসিম্পটোটস রয়েছে: উল্লম্ব, অনুভূমিক এবং তির্যক। অঙ্কনে, উপসর্গগুলি সাধারণত বিন্দুযুক্ত রেখা দ্বারা চিহ্নিত করা হয়।

আসুন ফাংশনের নিম্নলিখিত কৃত্রিমভাবে নির্মিত গ্রাফটি বিবেচনা করি (চিত্র 16.1), যার একটি উদাহরণ সমস্ত ধরণের অ্যাসিম্পটোটস দেখায়:

আসুন প্রতিটি ধরণের অ্যাসিম্পটোট সংজ্ঞায়িত করি:

1. সরাসরি x=aডাকা উল্লম্ব অ্যাসিম্পটোট ফাংশন যদি.

2. সরাসরি y=cডাকা অনুভূমিক উপসর্গ ফাংশন যদি.

3. সরাসরি y=kx+bডাকা তির্যক অ্যাসিম্পটোট ফাংশন যদি.

জ্যামিতিকভাবে, একটি তির্যক অ্যাসিম্পটোটের সংজ্ঞার অর্থ হল →∞ ফাংশনের গ্রাফটি পছন্দসই একটি সরল রেখার কাছে আসে y=kx+b, অর্থাৎ তারা প্রায় অভিন্ন। কার্যত অভিন্ন অভিব্যক্তির মধ্যে পার্থক্য শূন্যের দিকে থাকে।

উল্লেখ্য যে অনুভূমিক এবং তির্যক উপসর্গগুলি শুধুমাত্র →∞ শর্তের অধীনে বিবেচনা করা হয়। কখনও কখনও এগুলিকে →+∞ এবং →-∞ এ অনুভূমিক এবং তির্যক অ্যাসিম্পটোটে আলাদা করা হয়।

1. উপসর্গ অনুসন্ধানের জন্য অ্যালগরিদম

উপসর্গ খুঁজে পেতে, আপনি নিম্নলিখিত অ্যালগরিদম ব্যবহার করতে পারেন:

এক, একাধিক বা কোন উল্লম্ব উপসর্গ থাকতে পারে।

• যদি c একটি সংখ্যা হয়, তাহলে y=c- অনুভূমিক অ্যাসিম্পটোট;
• যদি c অসীম হয়, তাহলে কোন অনুভূমিক উপসর্গ নেই।

যদি একটি ফাংশন দুটি বহুপদীর অনুপাত হয়, তাহলে ফাংশনে যদি অনুভূমিক অ্যাসিম্পটোট থাকে, তাহলে আমরা তির্যক অ্যাসিম্পটোট খুঁজব না - সেগুলির অস্তিত্ব নেই।

আসুন একটি ফাংশনের উপসর্গ খুঁজে বের করার উদাহরণ দেখি:

উদাহরণ 16.1.বক্ররেখার উপসর্গ খুঁজুন।

সমাধান এক্স-1≠0; এক্স≠1.

লাইন সোজা কিনা চেক করা যাক x= 1 উল্লম্ব অ্যাসিম্পটোট। এটি করার জন্য, আমরা বিন্দুতে ফাংশনের সীমা গণনা করি x= 1: .

x= 1 - উল্লম্ব অ্যাসিম্পটোট।

সঙ্গে= .

সঙ্গে== কারণ সঙ্গে=2 (সংখ্যা), তারপর y=2- অনুভূমিক অ্যাসিম্পটোট।

যেহেতু একটি ফাংশন বহুপদগুলির একটি অনুপাত, যদি অনুভূমিক অ্যাসিম্পটোট থাকে, আমরা দাবি করি যে কোনও তির্যক অ্যাসিম্পটোট নেই।

x= 1 এবং অনুভূমিক অ্যাসিম্পটোট y=2।স্পষ্টতার জন্য, এই ফাংশনের গ্রাফটি চিত্রে উপস্থাপন করা হয়েছে। 16.2।

উদাহরণ 16.2. বক্ররেখার উপসর্গ খুঁজুন।

সমাধান. 1. ফাংশনের সংজ্ঞার ডোমেন খুঁজুন: এক্স-2≠0; এক্স≠2.

লাইন সোজা কিনা চেক করা যাক x= 2 উল্লম্ব অ্যাসিম্পটোট। এটি করার জন্য, আমরা বিন্দুতে ফাংশনের সীমা গণনা করি x= 2: .

আমরা তাই পেয়েছি, x= 2 - উল্লম্ব অ্যাসিম্পটোট।

2. অনুভূমিক উপসর্গ অনুসন্ধান করতে, আমরা খুঁজে পাই: সঙ্গে= .

যেহেতু অনিশ্চয়তা সীমাতে উপস্থিত হয়, আমরা L'Hopital এর নিয়ম ব্যবহার করি: সঙ্গে== কারণ সঙ্গে- অসীম, তাহলে কোন অনুভূমিক উপসর্গ নেই।

3. তির্যক উপসর্গ অনুসন্ধান করতে, আমরা পাই:

আমরা ফর্মের একটি অনিশ্চয়তা পেয়েছি, আসুন L'Hopital এর নিয়মটি ব্যবহার করি: = =1। সুতরাং, 1. আসুন খুঁজে বের করি খসূত্র অনুযায়ী: .

b= = =

বুঝেছি b= 2. তারপর y=kx+b -তির্যক অ্যাসিম্পটোট। আমাদের ক্ষেত্রে এটি এর মত দেখায়: y=x+2।

ভাত। 16.3

সুতরাং, এই ফাংশনের একটি উল্লম্ব অ্যাসিম্পটোট রয়েছে x= 2 এবং তির্যক অ্যাসিম্পটোট y=x+2।স্পষ্টতার জন্য, ফাংশন গ্রাফটি চিত্রে দেখানো হয়েছে। 16.3।

নিয়ন্ত্রণ প্রশ্ন:

লেকচার 17. একটি ফাংশন অধ্যয়ন এবং একটি গ্রাফ নির্মাণের জন্য সাধারণ স্কিম

এই বক্তৃতায় আমরা পূর্বে অধ্যয়ন করা সমস্ত উপাদান সংক্ষিপ্ত করব। আমাদের দীর্ঘ যাত্রার চূড়ান্ত লক্ষ্য হল বিশ্লেষণমূলকভাবে প্রদত্ত যে কোনও ফাংশন পরীক্ষা করতে এবং এর গ্রাফ তৈরি করতে সক্ষম হওয়া। আমাদের গবেষণার গুরুত্বপূর্ণ অংশগুলি হবে এক্সট্রিমার জন্য ফাংশনের অধ্যয়ন, একঘেয়েতার ব্যবধান নির্ধারণ, গ্রাফের উত্তলতা এবং অবতলতা, ইনফ্লেকশন পয়েন্টগুলির অনুসন্ধান এবং ফাংশনের গ্রাফের উপসর্গগুলি।

উপরোক্ত সব দিক বিবেচনা করে আমরা উপস্থাপন করছি একটি ফাংশন অধ্যয়ন এবং একটি গ্রাফ প্লট করার জন্য স্কিম .

1. ফাংশনের সংজ্ঞার ডোমেন খুঁজুন।

2. জোড়-বিজোড় সমতার জন্য ফাংশন পরীক্ষা করুন:

· যদি , তাহলে ফাংশনটি জোড় (একটি জোড় ফাংশনের গ্রাফটি অক্ষ সম্পর্কে প্রতিসম OU);

· যদি , তাহলে ফাংশনটি বিজোড় (একটি বিজোড় ফাংশনের গ্রাফ উৎপত্তির সাপেক্ষে প্রতিসম);

অন্যথায় ফাংশনটি জোড় বা বিজোড়ও নয়।

3. পর্যায়ক্রমিকতার জন্য ফাংশনটি তদন্ত করুন (আমরা যে ফাংশনগুলি অধ্যয়ন করি তার মধ্যে শুধুমাত্র ত্রিকোণমিতিক ফাংশনগুলি পর্যায়ক্রমিক হতে পারে)।

4. স্থানাঙ্ক অক্ষগুলির সাথে ফাংশন গ্রাফের ছেদ বিন্দুগুলি খুঁজুন:

· উহু: এ=0 (আমরা যদি আমাদের পরিচিত পদ্ধতি ব্যবহার করতে পারি তবেই আমরা সমীকরণটি সমাধান করি);

· OU: এক্স=0.

5. ফাংশনের প্রথম ডেরিভেটিভ এবং প্রথম ধরণের ক্রিটিক্যাল পয়েন্ট খুঁজুন।

6. একঘেয়েমি ব্যবধান এবং ফাংশনের চরমতা খুঁজুন।

7. ফাংশনের দ্বিতীয় ডেরিভেটিভ এবং দ্বিতীয় ধরণের সমালোচনামূলক পয়েন্টগুলি খুঁজুন।

8. ফাংশন গ্রাফ এবং ইনফ্লেকশন বিন্দুর উত্তল-অতলতার ব্যবধান খুঁজুন।

9. ফাংশনের গ্রাফের উপসর্গগুলি খুঁজুন।

10. ফাংশনের একটি গ্রাফ তৈরি করুন। নির্মাণ করার সময়, আপনি অ্যাকাউন্টে নিতে হবে উপসর্গের কাছাকাছি গ্রাফের সম্ভাব্য অবস্থানের ক্ষেত্রে :

11. প্রয়োজন হলে, আরো সঠিক নির্মাণের জন্য নিয়ন্ত্রণ পয়েন্ট নির্বাচন করুন।

আসুন একটি ফাংশন অধ্যয়ন এবং নির্দিষ্ট উদাহরণ ব্যবহার করে এর গ্রাফ নির্মাণের জন্য একটি স্কিম বিবেচনা করুন:

উদাহরণ 17.1. ফাংশন গ্রাফ করুন।

সমাধান. 1. এই ফাংশনটি ব্যতীত সমগ্র সংখ্যা লাইনে সংজ্ঞায়িত করা হয়েছে এক্স=3, কারণ এই মুহুর্তে হরটি শূন্যে চলে যায়।

2. একটি ফাংশন জোড় বা বিজোড় কিনা তা নির্ধারণ করতে, আমরা খুঁজে পাই:

আমরা এটি দেখতে পাই এবং তাই, একটি জোড় বা বিজোড় ফাংশন নয়।

3. ফাংশনটি পর্যায়ক্রমিক নয়।

4. স্থানাঙ্ক অক্ষগুলির সাথে ছেদ বিন্দুগুলি খুঁজুন। অক্ষের সাথে ছেদ বিন্দু খুঁজে বের করতে উহুআসুন গ্রহণ করি এ=0 আমরা সমীকরণ পাই: . সুতরাং, বিন্দু (0; 0) হল স্থানাঙ্ক অক্ষগুলির সাথে ছেদ করার বিন্দু।

5. ভগ্নাংশের পার্থক্যের নিয়ম ব্যবহার করে ফাংশনের ডেরিভেটিভ খুঁজে বের করা যাক: = = = = .

সমালোচনামূলক পয়েন্টগুলি খুঁজে বের করার জন্য, আমরা এমন পয়েন্টগুলি খুঁজে পাই যেখানে ফাংশনের ডেরিভেটিভ 0 এর সমান বা বিদ্যমান নেই।

যদি =0, তাই। গুণনীয়কগুলির মধ্যে অন্তত একটি 0 এর সমান হলে গুণফলটি 0 এর সমান হয়: বা।

এক্স-3) 2 সমান 0, অর্থাৎ অস্তিত্ব নেই যখন এক্স=3.

সুতরাং, ফাংশনটির প্রথম ধরণের তিনটি সমালোচনামূলক পয়েন্ট রয়েছে: ; ; .

6. সংখ্যা অক্ষের উপর আমরা প্রথম ধরণের সমালোচনামূলক বিন্দু চিহ্নিত করি এবং বিন্দুটিকে একটি ছিদ্রযুক্ত বিন্দু দিয়ে চিহ্নিত করি, কারণ ফাংশন এটি সংজ্ঞায়িত করা হয় না.

আমরা প্রতিটি ব্যবধানে ডেরিভেটিভ = চিহ্ন রাখি:

t.min

t.max

ব্যবধানে যেখানে , মূল ফাংশন বৃদ্ধি পায় (এতে (-∞;0]), যেখানে - হ্রাস পায় (এতে)।

ডট এক্স=0 হল ফাংশনের সর্বোচ্চ বিন্দু। সর্বাধিক ফাংশন খুঁজে বের করতে, আমরা 0 বিন্দুতে ফাংশনের মান খুঁজে পাই:

ডট এক্স=6 হল ফাংশনের সর্বনিম্ন বিন্দু। ফাংশনের সর্বনিম্ন খুঁজে পেতে, আমরা 6 পয়েন্টে ফাংশনের মান খুঁজে পাই:

গবেষণা ফলাফল একটি টেবিলে প্রবেশ করা যেতে পারে. সারণীতে সারির সংখ্যা স্থির এবং চারটির সমান, এবং কলামের সংখ্যা অধ্যয়ন করা ফাংশনের উপর নির্ভর করে। প্রথম লাইনের কক্ষগুলিতে, ব্যবধানগুলি ক্রমানুসারে প্রবেশ করানো হয় যার মধ্যে সমালোচনামূলক পয়েন্টগুলি ফাংশনের সংজ্ঞার ডোমেনকে বিভক্ত করে, যার মধ্যে গুরুত্বপূর্ণ পয়েন্টগুলিও রয়েছে। সংজ্ঞা ডোমেনের অন্তর্গত নয় এমন পয়েন্টগুলি তৈরি করার সময় ত্রুটিগুলি এড়াতে, আপনি সেগুলিকে টেবিলে অন্তর্ভুক্ত করতে পারবেন না।

টেবিলের দ্বিতীয় লাইনে বিবেচনাধীন প্রতিটি ব্যবধানে ডেরিভেটিভের চিহ্ন এবং গুরুত্বপূর্ণ পয়েন্টে ডেরিভেটিভের মান রয়েছে। ফাংশনের ডেরিভেটিভের লক্ষণ অনুসারে, ফাংশনের বৃদ্ধি, হ্রাস এবং চরমের ব্যবধানগুলি তৃতীয় লাইনে চিহ্নিত করা হয়েছে।

শেষ লাইনটি ফাংশনের সর্বাধিক এবং সর্বনিম্ন নির্দেশ করে।

এক্স	(-∞;0)		(0;3)		(3;6)		(6;+ ∞)
	+		-		-		+
f(x)
উপসংহার		সর্বোচ্চ				মিনিট

7. প্রথম ডেরিভেটিভের ডেরিভেটিভ হিসাবে ফাংশনের দ্বিতীয় ডেরিভেটিভটি খুঁজে বের করা যাক: = =

অংকের মধ্যে রাখি এক্স-3 বন্ধনীর জন্য এবং হ্রাস সম্পাদন করুন:

আসুন আমরা লবের অনুরূপ পদ উপস্থাপন করি: .

আসুন দ্বিতীয় ধরণের সমালোচনামূলক বিন্দুগুলি খুঁজে বের করি: যে পয়েন্টগুলিতে ফাংশনের দ্বিতীয় ডেরিভেটিভটি শূন্যের সমান বা বিদ্যমান নেই।

0 যদি =0। এই ভগ্নাংশটি শূন্যের সমান হতে পারে না, তাই এমন কোন বিন্দু নেই যেখানে ফাংশনের দ্বিতীয় ডেরিভেটিভটি শূন্যের সমান।

হর ( এক্স-3) 3 সমান 0, অর্থাৎ অস্তিত্ব নেই যখন এক্স=3। :উহু , OU, উৎপত্তি, প্রতিটি অক্ষের জন্য পরিমাপের একক।

একটি ফাংশন প্লট করার আগে, আপনাকে করতে হবে:

বিন্দুযুক্ত রেখা দিয়ে অ্যাসিম্পটোটগুলি আঁকুন;

· স্থানাঙ্ক অক্ষের সাথে ছেদ বিন্দু চিহ্নিত করুন;

ভাত। 17.1

ফাংশনের সর্বাধিক এবং সর্বনিম্ন চিহ্নিত করুন, এবং আর্কস সহ অঙ্কনটিতে সরাসরি ফাংশনের সর্বাধিক এবং সর্বনিম্ন নির্দেশ করার পরামর্শ দেওয়া হয়: k বা ;

· বৃদ্ধি, হ্রাস, উত্তল এবং অবতলতার ব্যবধানে প্রাপ্ত ডেটা ব্যবহার করে ফাংশনের একটি গ্রাফ তৈরি করুন। গ্রাফের শাখাগুলি উপসর্গগুলির দিকে "প্রবণ" হওয়া উচিত, তবে তাদের ছেদ করবে না।

· ফাংশনের গ্রাফটি পরিচালিত গবেষণার সাথে সামঞ্জস্যপূর্ণ কিনা তা পরীক্ষা করুন: যদি ফাংশনটি জোড় বা বিজোড় হয়, তাহলে প্রতিসাম্য পরিলক্ষিত হয় কিনা; বৃদ্ধি এবং হ্রাসের ব্যবধান, উত্তল এবং অবতলতা, এবং প্রবর্তন বিন্দুগুলি তাত্ত্বিকভাবে পাওয়া যায়গুলির সাথে মিলে যায়?

11. আরো সঠিক নির্মাণের জন্য, আপনি বেশ কয়েকটি নিয়ন্ত্রণ পয়েন্ট নির্বাচন করতে পারেন। উদাহরণস্বরূপ, আসুন পয়েন্ট -2 এবং 7 এ ফাংশনের মানগুলি খুঁজে বের করি:

আমরা নিয়ন্ত্রণ পয়েন্টগুলি বিবেচনা করে সময়সূচী সামঞ্জস্য করি।

নিয়ন্ত্রণ প্রশ্ন:

1. একটি ফাংশন গ্রাফ করার জন্য অ্যালগরিদম কি?
2. একটি ফাংশন এর সংজ্ঞার ডোমেনের বাইরের পয়েন্টে একটি এক্সট্রিম থাকতে পারে?

অধ্যায় 3. 3. একটি ফাংশনের অখণ্ড ক্যালকুলাস

- (গ্রীক থেকে একটি নেতিবাচক অংশ।, এবং উপসর্গগুলি একসাথে মিলে যায়)। একটি সরল রেখা ক্রমাগত একটি বক্ররেখার কাছে আসছে এবং এটি শুধুমাত্র অসীমে মিলিত হচ্ছে। রাশিয়ান ভাষায় অন্তর্ভুক্ত বিদেশী শব্দের অভিধান। চুদিনভ এ.এন., 1910. অ্যাসিম্পটোট থেকে... ... রাশিয়ান ভাষার বিদেশী শব্দের অভিধান

ASYMPTOTE- (গ্রীক অ্যাসিম্পটোটোস নন-কানসিডিং থেকে), একটি সরল রেখা যেখানে একটি বক্ররেখার একটি অসীম শাখা সীমা ছাড়াই আসে, উদাহরণস্বরূপ একটি হাইপারবোলার অ্যাসিম্পটোট ... আধুনিক বিশ্বকোষ

ASYMPTOTE- (গ্রীক অ্যাসিম্পটোটস নন-কানসিডিং থেকে) একটি অসীম শাখা সহ একটি বক্ররেখা, একটি সরল রেখা যেখানে এই শাখাটি সীমা ছাড়াই আসে, উদাহরণস্বরূপ, একটি হাইপারবোলার অ্যাসিম্পটোট ... বড় বিশ্বকোষীয় অভিধান

উপসর্গ- একটি বক্ররেখা সহ একটি সরল রেখা ধীরে ধীরে এটির কাছে আসছে। অ্যাসিম্পটোট একটি সরল রেখা যার দিকে কিছু ফাংশনের বক্ররেখা, যার একটি অসীম শাখা রয়েছে, প্রবণতা (কখনও এটিতে না পৌঁছে) যখন তার যুক্তি সীমা ছাড়াই বৃদ্ধি পায় বা... প্রযুক্তিগত অনুবাদকের গাইড

অ্যাসিম্পটোট- (গ্রীক অ্যাসিম্পটোটোস নন-কনসিডিং থেকে), একটি সরল রেখা যেখানে একটি বক্ররেখার একটি অসীম শাখা সীমা ছাড়াই আসে, উদাহরণস্বরূপ একটি হাইপারবোলার অ্যাসিম্পটোট। ... সচিত্র বিশ্বকোষীয় অভিধান

ASYMPTOTE- মহিলা, জিওম। একটি সরল রেখা, সর্বদা একটি বক্ররেখার কাছে আসে (হাইপারবোল), কিন্তু কখনই এটির সাথে একত্রিত হয় না। এটি ব্যাখ্যা করার জন্য একটি উদাহরণ: যদি কোনো সংখ্যাকে অর্ধেক ভাগ করা হয়, তবে এটি অসীমে হ্রাস পাবে, কিন্তু কখনই শূন্য হবে না। ডাহলের ব্যাখ্যামূলক অভিধান

উপসর্গ- বিশেষ্য, সমার্থক শব্দের সংখ্যা: 1 লাইন (182) ASIS প্রতিশব্দের অভিধান। ভি.এন. ত্রিশীন। 2013… সমার্থক অভিধান

অ্যাসিম্পটোট- (গ্রীক শব্দ থেকে: a, sun, piptw) অমিল। উপসর্গ দ্বারা এমন একটি রেখাকে বোঝায় যা অনির্দিষ্টকালের জন্য প্রসারিত হয়ে একটি নির্দিষ্ট বাঁকা রেখা বা এর কিছু অংশের কাছে আসে যাতে সাধারণ রেখার মধ্যে দূরত্ব কম হয়ে যায়... ...

অ্যাসিম্পটোট- একটি পৃষ্ঠ হল একটি সরল রেখা যা পৃষ্ঠকে অন্তত দুইটি বিন্দুতে ছেদ করে... Brockhaus এবং Efron এর এনসাইক্লোপিডিয়া

ASYMPTOTE- (অ্যাসিম্পটোট) আর্গুমেন্ট (আর্গুমেন্ট) পরিবর্তন করার সময় এই ফাংশনটি যে মানটির জন্য চেষ্টা করে, কিন্তু আর্গুমেন্টের কোনো চূড়ান্ত মানের জন্য এটি অর্জন করে না। উদাহরণস্বরূপ, যদি আউটপুট x এর মোট খরচ TC=a+bx ফাংশন দ্বারা দেওয়া হয়, যেখানে a এবং b ধ্রুবক... অর্থনৈতিক অভিধান

অ্যাসিম্পটোট- একটি সরল রেখা যার দিকে কিছু ফাংশনের বক্ররেখা থাকে (কখনও এটিতে না পৌঁছায়), একটি অসীম শাখা থাকে, যখন এর যুক্তি সীমা ছাড়াই বৃদ্ধি বা হ্রাস পায়। উদাহরণস্বরূপ, ফাংশনে: y = c + 1/x y এর মান... ... অর্থনৈতিক এবং গাণিতিক অভিধান

একটি ফাংশনের গ্রাফে কয়টি উপসর্গ থাকতে পারে?

এক, এক, দুই, তিন,... বা অসীম বহু নয়। আমরা উদাহরণের জন্য বেশিদূর যাব না; আসুন প্রাথমিক ফাংশনগুলি মনে রাখি। একটি প্যারাবোলা, একটি কিউবিক প্যারাবোলা এবং একটি সাইন ওয়েভের মোটেও উপসর্গ নেই। একটি সূচকীয়, লগারিদমিক ফাংশনের গ্রাফে একটি একক অ্যাসিম্পটোট রয়েছে। arctangent এবং arccotangent তাদের দুটি আছে, এবং স্পর্শক এবং cotangent অসীমভাবে অনেক আছে. একটি গ্রাফে অনুভূমিক এবং উল্লম্ব উভয় উপসর্গ থাকা অস্বাভাবিক নয়। হাইপারবোল, সবসময় তোমাকে ভালবাসবে।

একটি ফাংশনের গ্রাফের উপসর্গ খুঁজে বের করার অর্থ কী?

এর মানে হল তাদের সমীকরণ বের করা, এবং সমস্যার প্রয়োজন হলে সরলরেখা আঁকা। প্রক্রিয়াটির মধ্যে একটি ফাংশনের সীমা খুঁজে পাওয়া জড়িত।

একটি ফাংশনের গ্রাফের উল্লম্ব উপসর্গ

গ্রাফের উল্লম্ব অ্যাসিম্পটোট, একটি নিয়ম হিসাবে, ফাংশনের অসীম বিচ্ছিন্নতার বিন্দুতে অবস্থিত। এটি সহজ: যদি একটি বিন্দুতে ফাংশনটি অসীম বিচ্ছিন্নতা ভোগ করে, তাহলে সমীকরণ দ্বারা নির্দিষ্ট করা সরল রেখাটি গ্রাফের উল্লম্ব অ্যাসিম্পটোট।

দ্রষ্টব্য: দয়া করে মনে রাখবেন যে এন্ট্রি দুটি সম্পূর্ণ ভিন্ন ধারণার উল্লেখ করতে ব্যবহৃত হয়। একটি বিন্দু উহ্য বা একটি রেখার সমীকরণ প্রেক্ষাপটের উপর নির্ভর করে।

সুতরাং, একটি বিন্দুতে একটি উল্লম্ব অ্যাসিম্পটোটের উপস্থিতি প্রতিষ্ঠা করার জন্য, এটি দেখানো যথেষ্ট যে একতরফা সীমাগুলির মধ্যে অন্তত একটি অসীম। প্রায়শই এটি সেই বিন্দু যেখানে ফাংশনের হর শূন্য। মূলত, আমরা ইতিমধ্যেই একটি ফাংশনের ধারাবাহিকতার পাঠের শেষ উদাহরণগুলিতে উল্লম্ব উপসর্গগুলি খুঁজে পেয়েছি। কিন্তু কিছু ক্ষেত্রে শুধুমাত্র একতরফা সীমা আছে, এবং যদি এটি অসীম হয়, তাহলে আবার - উল্লম্ব অ্যাসিম্পটোটকে ভালবাসুন এবং অনুগ্রহ করুন। সহজতম দৃষ্টান্ত: এবং অর্ডিনেট অক্ষ।

উপরের থেকে, একটি সুস্পষ্ট সত্যও অনুসরণ করে: যদি ফাংশনটি ক্রমাগত চালু থাকে, তাহলে কোন উল্লম্ব উপসর্গ নেই। কোনো কারণে একটা প্যারাবোলা মাথায় এল। সত্যিই, আপনি এখানে একটি সরল রেখা কোথায় "লাঠি" করতে পারেন? ...হ্যাঁ... আমি বুঝতে পেরেছি... আঙ্কেল ফ্রয়েডের অনুসারীরা হিস্টিরিয়া হয়ে উঠল =)

কথোপকথন বিবৃতি সাধারণত মিথ্যা: উদাহরণস্বরূপ, ফাংশনটি সম্পূর্ণ সংখ্যা লাইনে সংজ্ঞায়িত করা হয় না, তবে সম্পূর্ণরূপে উপসর্গ থেকে বঞ্চিত হয়।

একটি ফাংশনের গ্রাফের ঢালু উপসর্গ

তির্যক (একটি বিশেষ ক্ষেত্রে - অনুভূমিক) অ্যাসিম্পটোটগুলি আঁকা যেতে পারে যদি ফাংশনের যুক্তি "প্লাস ইনফিনিটি" বা "মাইনাস ইনফিনিটি" এর দিকে থাকে। সুতরাং, একটি ফাংশনের গ্রাফে 2টির বেশি বাঁকযুক্ত অ্যাসিম্পটোট থাকতে পারে না। উদাহরণস্বরূপ, একটি সূচকীয় ফাংশনের গ্রাফটিতে একটি একক অনুভূমিক অ্যাসিম্পটোট রয়েছে এবং তে আর্কটেনজেন্টের গ্রাফটিতে দুটি অনুরূপ অ্যাসিম্পটোট রয়েছে এবং এতে আলাদা আলাদা রয়েছে।

যখন উভয় স্থানে গ্রাফটি একটি একক তির্যক অ্যাসিম্পটোটের কাছে আসে, তখন এটি একটি একক এন্ট্রির অধীনে "অসীম" একত্রিত করার প্রথাগত। উদাহরণস্বরূপ, ...আপনি সঠিকভাবে অনুমান করেছেন: .

একটি ফাংশনের গ্রাফের উপসর্গ

অ্যাসিম্পটোটের ভূতটি দীর্ঘকাল ধরে সাইটের চারপাশে ঘুরে বেড়াচ্ছে অবশেষে একটি পৃথক নিবন্ধে বাস্তবায়িত হতে এবং বিভ্রান্ত পাঠকদের জন্য বিশেষ আনন্দ আনতে ফাংশন সম্পূর্ণ অধ্যয়ন. একটি গ্রাফের উপসর্গ খুঁজে পাওয়া এই কাজের কয়েকটি অংশের মধ্যে একটি যা স্কুল কোর্সে শুধুমাত্র একটি ওভারভিউ পদ্ধতিতে কভার করা হয়, যেহেতু ঘটনাগুলি গণনার চারপাশে আবর্তিত হয় ফাংশন সীমা, কিন্তু তারা এখনও উচ্চতর গণিতের অন্তর্গত। দর্শকদের জন্য যাদের গাণিতিক বিশ্লেষণের সামান্য বোঝাপড়া আছে, আমি মনে করি ইঙ্গিতটি পরিষ্কার ;-) ... থামুন, থামুন, আপনি কোথায় যাচ্ছেন? সীমা- এটি সহজ!

প্রথম পাঠে অবিলম্বে উপসর্গের উদাহরণগুলি পাওয়া গেছে প্রাথমিক ফাংশনের গ্রাফ, এবং বিষয় এখন বিস্তারিত বিবেচনা গ্রহণ করা হয়.

তাই একটি অ্যাসিম্পটোট কি?

কল্পনা করুন পরিবর্তনশীল বিন্দু, যা ফাংশনের গ্রাফ বরাবর "ভ্রমণ" করে। অ্যাসিম্পটোট হল সোজা, যা অনির্দিষ্টভাবে বন্ধএকটি ফাংশনের গ্রাফটি যখন এর পরিবর্তনশীল বিন্দু অসীমতায় চলে যায় তখন তার কাছে আসে।

বিঃদ্রঃ : সংজ্ঞাটি অর্থপূর্ণ, যদি আপনার ক্যালকুলাস স্বরলিপিতে একটি সূত্রের প্রয়োজন হয়, অনুগ্রহ করে পাঠ্যপুস্তকটি পড়ুন।

সমতলে, অ্যাসিম্পটোটগুলি তাদের প্রাকৃতিক অবস্থান অনুসারে শ্রেণিবদ্ধ করা হয়:

1) উল্লম্ব উপসর্গ, যা ফর্মের একটি সমীকরণ দ্বারা দেওয়া হয়, যেখানে "আলফা" একটি বাস্তব সংখ্যা। একটি জনপ্রিয় প্রতিনিধি অর্ডিনেট অক্ষ নিজেই সংজ্ঞায়িত করে,
বমি বমি ভাবের সামান্য অনুভূতির সাথে আমরা হাইপারবোলটি মনে করি।

2) তির্যক উপসর্গঐতিহ্যগতভাবে লিখিত একটি সরল রেখার সমীকরণএকটি কোণ সহগ সহ। কখনও কখনও একটি বিশেষ ক্ষেত্রে একটি পৃথক গ্রুপ হিসাবে চিহ্নিত করা হয় - অনুভূমিক উপসর্গ. উদাহরণস্বরূপ, অ্যাসিম্পটোট সহ একই হাইপারবোলা।

চলুন দ্রুত যাই, মেশিনগানের ফায়ারের সংক্ষিপ্ত বিস্ফোরণ দিয়ে বিষয়টিতে আঘাত করা যাক:

একটি ফাংশনের গ্রাফে কয়টি উপসর্গ থাকতে পারে?

এক, এক, দুই, তিন,... বা অসীম বহু নয়। আমরা উদাহরণের জন্য বেশিদূর যাব না, আসুন মনে রাখি প্রাথমিক ফাংশন. একটি প্যারাবোলা, একটি কিউবিক প্যারাবোলা এবং একটি সাইন ওয়েভের মোটেও উপসর্গ নেই। একটি সূচকীয়, লগারিদমিক ফাংশনের গ্রাফে একটি একক অ্যাসিম্পটোট রয়েছে। arctangent এবং arccotangent তাদের দুটি আছে, এবং স্পর্শক এবং cotangent অসীমভাবে অনেক আছে. একটি গ্রাফে অনুভূমিক এবং উল্লম্ব উভয় উপসর্গ থাকা অস্বাভাবিক নয়। হাইপারবোল, সবসময় তোমাকে ভালবাসবে।

মানে কি?

একটি ফাংশনের গ্রাফের উল্লম্ব উপসর্গ

গ্রাফের উল্লম্ব অ্যাসিম্পটোট সাধারণত অবস্থিত অসীম বিচ্ছিন্নতার বিন্দুতেফাংশন এটি সহজ: যদি একটি বিন্দুতে ফাংশনটি অসীম বিচ্ছিন্নতা ভোগ করে, তাহলে সমীকরণ দ্বারা নির্দিষ্ট করা সরল রেখাটি গ্রাফের উল্লম্ব অ্যাসিম্পটোট।

বিঃদ্রঃ : মনে রাখবেন যে এন্ট্রি দুটি সম্পূর্ণ ভিন্ন ধারণার উল্লেখ করতে ব্যবহৃত হয়। একটি বিন্দু উহ্য বা একটি রেখার সমীকরণ প্রেক্ষাপটের উপর নির্ভর করে।

সুতরাং, একটি বিন্দুতে একটি উল্লম্ব অ্যাসিম্পটোটের উপস্থিতি স্থাপন করার জন্য, এটি দেখানোই যথেষ্ট অন্তত একটাএকতরফা সীমা থেকে অসীম. প্রায়শই এটি সেই বিন্দু যেখানে ফাংশনের হর শূন্য। মূলত, আমরা ইতিমধ্যে পাঠের শেষ উদাহরণগুলিতে উল্লম্ব উপসর্গগুলি খুঁজে পেয়েছি একটি ফাংশনের ধারাবাহিকতার উপর. কিন্তু কিছু ক্ষেত্রে শুধুমাত্র একতরফা সীমা আছে, এবং যদি এটি অসীম হয়, তাহলে আবার - উল্লম্ব অ্যাসিম্পটোটকে ভালবাসুন এবং অনুগ্রহ করুন। সহজতম উদাহরণ: এবং অর্ডিনেট অক্ষ (দেখুন। গ্রাফ এবং প্রাথমিক ফাংশন বৈশিষ্ট্য).

উপরোক্ত থেকে, একটি সুস্পষ্ট সত্য এছাড়াও অনুসরণ করে: যদি ফাংশন ক্রমাগত চালু থাকে, তাহলে কোন উল্লম্ব উপসর্গ নেই. কোনো কারণে একটা প্যারাবোলা মাথায় এল। সত্যিই, আপনি এখানে একটি সরল রেখা কোথায় "লাঠি" করতে পারেন? ...হ্যাঁ... আমি বুঝতে পেরেছি... আঙ্কেল ফ্রয়েডের অনুসারীরা হিস্টিরিয়া হয়ে উঠল =)

কথোপকথন বিবৃতি সাধারণত মিথ্যা: উদাহরণস্বরূপ, ফাংশনটি সম্পূর্ণ সংখ্যা লাইনে সংজ্ঞায়িত করা হয় না, তবে সম্পূর্ণরূপে উপসর্গ থেকে বঞ্চিত হয়।

একটি ফাংশনের গ্রাফের ঢালু উপসর্গ

তির্যক (একটি বিশেষ ক্ষেত্রে - অনুভূমিক) অ্যাসিম্পটোটগুলি আঁকা যেতে পারে যদি ফাংশনের যুক্তি "প্লাস ইনফিনিটি" বা "মাইনাস ইনফিনিটি" এর দিকে থাকে। এই জন্য একটি ফাংশনের গ্রাফে দুটির বেশি তির্যক অ্যাসিম্পটোট থাকতে পারে না. উদাহরণস্বরূপ, একটি সূচকীয় ফাংশনের গ্রাফে একটি একক অনুভূমিক অ্যাসিম্পটোট রয়েছে এবং তে আর্কট্যাঞ্জেন্টের গ্রাফটিতে দুটি অনুভূমিক অ্যাসিম্পটোট রয়েছে এবং এতে আলাদা আলাদা রয়েছে।

যখন উভয় স্থানে গ্রাফ একটি একক তির্যক অ্যাসিম্পটোটের কাছে আসে, তখন "অসীম" সাধারণত একটি একক এন্ট্রির অধীনে একত্রিত হয়। উদাহরণস্বরূপ, ...আপনি সঠিকভাবে অনুমান করেছেন: .

সাধারণ নিয়ম:

যদি দুইটা থাকে চূড়ান্তসীমা , তাহলে সরলরেখা হল তে ফাংশনের গ্রাফের তির্যক অ্যাসিম্পটোট। যদি অন্তত একটাতালিকাভুক্ত সীমার মধ্যে অসীম, তারপর কোন তির্যক অ্যাসিম্পটোট নেই।

বিঃদ্রঃ : সূত্রগুলি বৈধ থাকে যদি "x" শুধুমাত্র "প্লাস ইনফিনিটি" বা শুধুমাত্র "মাইনাস ইনফিনিটি" তে থাকে।

আসুন দেখান যে প্যারাবোলার কোন তির্যক উপসর্গ নেই:

সীমা অসীম, যার মানে কোন তির্যক অ্যাসিম্পটোট নেই। উল্লেখ্য যে সীমা খুঁজে বের করুন উত্তর ইতিমধ্যে প্রাপ্ত হওয়ার পর থেকে প্রয়োজনটি অদৃশ্য হয়ে গেছে।

বিঃদ্রঃ : যদি আপনার প্লাস-মাইনাস, মাইনাস-প্লাস চিহ্নগুলি বুঝতে অসুবিধা হয় (বা থাকবে), অনুগ্রহ করে পাঠের শুরুতে সহায়তাটি দেখুন
অসীম ফাংশন উপর, যেখানে আমি আপনাকে বলেছিলাম কিভাবে এই লক্ষণগুলিকে সঠিকভাবে ব্যাখ্যা করতে হয়।

এটা স্পষ্ট যে কোন দ্বিঘাত, ঘন ফাংশন, 4র্থ এবং উচ্চতর ডিগ্রীর বহুপদীতেও তির্যক উপসর্গ থাকে না।

এখন নিশ্চিত করা যাক যে গ্রাফটিতেও একটি তির্যক অ্যাসিম্পটোট নেই। অনিশ্চয়তা প্রকাশ করতে আমরা ব্যবহার করি হাসপাতালের নিয়ম:
, যা চেক করা প্রয়োজন ছিল.

যখন ফাংশনটি অনির্দিষ্টকালের জন্য বৃদ্ধি পায়, কিন্তু কোন সরল রেখা নেই যেখানে এর গ্রাফটি পৌঁছাবে অসীম বন্ধ.

আসুন পাঠের ব্যবহারিক অংশে এগিয়ে যাই:

একটি ফাংশনের গ্রাফের উপসর্গগুলি কীভাবে খুঁজে পাওয়া যায়?

সাধারণ কাজটি ঠিক এইভাবে তৈরি করা হয় এবং এতে গ্রাফের সমস্ত উপসর্গ (উল্লম্ব, ঝোঁক/অনুভূমিক) খুঁজে বের করা জড়িত। যদিও, প্রশ্নটি উত্থাপনের ক্ষেত্রে আরও সুনির্দিষ্ট হওয়ার জন্য, আমরা অ্যাসিম্পটোটসের উপস্থিতির জন্য গবেষণার কথা বলছি (সর্বশেষে, কোনওটিই নাও হতে পারে)। আসুন সহজ কিছু দিয়ে শুরু করা যাক:

উদাহরণ 1

একটি ফাংশনের গ্রাফের উপসর্গ খুঁজুন

সমাধানএটি দুটি পয়েন্টে বিভক্ত করা সুবিধাজনক:

1) প্রথমে আমরা উল্লম্ব অ্যাসিম্পটোটস আছে কিনা তা পরীক্ষা করি। হরটি শূন্যে যায় এবং এটি অবিলম্বে স্পষ্ট যে এই সময়ে ফাংশনটি ক্ষতিগ্রস্ত হয় অন্তহীন ফাঁক, এবং সমীকরণ দ্বারা প্রদত্ত সরলরেখাটি ফাংশনের গ্রাফের উল্লম্ব অ্যাসিম্পটোট। কিন্তু, এই ধরনের উপসংহার আঁকার আগে, একতরফা সীমা খুঁজে বের করা প্রয়োজন:

আমি আপনাকে গণনার কৌশলটির কথা মনে করিয়ে দিচ্ছি যা আমি একইভাবে নিবন্ধে ফোকাস করেছি ফাংশনের ধারাবাহিকতা। ব্রেক পয়েন্ট. সীমা চিহ্নের অধীনে অভিব্যক্তিতে আমরা প্রতিস্থাপন করি। সংখ্যায় আকর্ষণীয় কিছু নেই:
.

কিন্তু হর মধ্যে এটা সক্রিয় আউট অসীম ঋণাত্মক সংখ্যা:
, এটা সীমা ভাগ্য নির্ধারণ করে.

বাম-হাতের সীমা অসীম, এবং নীতিগতভাবে, একটি উল্লম্ব অ্যাসিম্পটোটের উপস্থিতি সম্পর্কে একটি রায় তৈরি করা ইতিমধ্যেই সম্ভব। কিন্তু একতরফা সীমা শুধু এর জন্যই নয় - তারা বুঝতে সাহায্য করে কিভাবেফাংশনের গ্রাফটি সনাক্ত করুন এবং এটি তৈরি করুন সঠিকভাবে. অতএব, আমাদের অবশ্যই ডান হাতের সীমা গণনা করতে হবে:

উপসংহার: একতরফা সীমা অসীম, যার মানে সরলরেখা হল ফাংশনের গ্রাফের উল্লম্ব অ্যাসিম্পটোট।

প্রথম সীমা সসীম, যার মানে "কথোপকথন চালিয়ে যাওয়া" এবং দ্বিতীয় সীমা খুঁজে বের করা প্রয়োজন:

দ্বিতীয় সীমাও সসীম.

সুতরাং, আমাদের উপসর্গ হল:

উপসংহার: সমীকরণ দ্বারা প্রদত্ত সরলরেখা হল ফাংশনের গ্রাফের অনুভূমিক অ্যাসিম্পটোট।

অনুভূমিক অ্যাসিম্পটোট খুঁজে বের করতে
আপনি একটি সরলীকৃত সূত্র ব্যবহার করতে পারেন:

যদি বিদ্যমান থাকে সসীমসীমা, তাহলে সরলরেখা হল ফাংশনের গ্রাফের অনুভূমিক অ্যাসিম্পটোট।

এটি সহজেই দেখা যায় যে ফাংশনের লব এবং হর বৃদ্ধির একই ক্রম, যার মানে চাওয়া সীমা সীমাবদ্ধ হবে: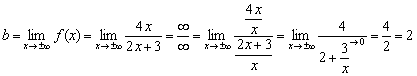

উত্তর:

শর্ত অনুযায়ী, আপনি অঙ্কন সম্পূর্ণ করতে হবে না, কিন্তু যদি পুরো দোলনায় ফাংশন অধ্যয়ন, তারপর খসড়াটিতে আমরা অবিলম্বে একটি স্কেচ তৈরি করি:

তিনটি পাওয়া সীমার উপর ভিত্তি করে, ফাংশনের গ্রাফটি কীভাবে অবস্থিত হতে পারে তা নিজের জন্য খুঁজে বের করার চেষ্টা করুন। এটা কি আদৌ কঠিন? 5-6-7-8 পয়েন্ট খুঁজুন এবং তাদের অঙ্কনে চিহ্নিত করুন। যাইহোক, এই ফাংশনের গ্রাফটি ব্যবহার করে নির্মিত হয় একটি প্রাথমিক ফাংশনের গ্রাফের রূপান্তর, এবং পাঠকরা যারা সাবধানে উপরের নিবন্ধের উদাহরণ 21 পরীক্ষা করেছেন তারা সহজেই অনুমান করতে পারেন এটি কি ধরনের বক্ররেখা।

উদাহরণ 2

একটি ফাংশনের গ্রাফের উপসর্গ খুঁজুন

এটি আপনার নিজের সমাধান করার জন্য একটি উদাহরণ। আমি আপনাকে মনে করিয়ে দিচ্ছি যে প্রক্রিয়াটিকে দুটি পয়েন্টে ভাগ করা সুবিধাজনক - উল্লম্ব অ্যাসিম্পটোটস এবং তির্যক অ্যাসিম্পটোটস৷ নমুনা সমাধানে, একটি সরলীকৃত স্কিম ব্যবহার করে অনুভূমিক অ্যাসিম্পটোট পাওয়া যায়।

অনুশীলনে, ভগ্নাংশ-যুক্তিমূলক ফাংশনগুলি প্রায়শই সম্মুখীন হয় এবং হাইপারবোলাস প্রশিক্ষণের পরে, আমরা কাজটিকে জটিল করব:

উদাহরণ 3

একটি ফাংশনের গ্রাফের উপসর্গ খুঁজুন

সমাধান: এক, দুই এবং সম্পন্ন:

1) উল্লম্ব অ্যাসিম্পটোটস অবস্থিত অসীম বিচ্ছিন্নতার পয়েন্টে, তাই আপনাকে হরটি শূন্যে যায় কিনা তা পরীক্ষা করতে হবে। সিদ্ধান্ত নেওয়া যাক দ্বিঘাত সমীকরণ:

বৈষম্যকারীটি ইতিবাচক, তাই সমীকরণটির দুটি আসল মূল রয়েছে এবং কাজটি উল্লেখযোগ্যভাবে বৃদ্ধি পেয়েছে =)

আরও একতরফা সীমা খুঁজে বের করার জন্য, বর্গাকার ত্রিনমিককে ফ্যাক্টরাইজ করা সুবিধাজনক:
(কম্প্যাক্ট নোটেশনের জন্য, "মাইনাস" প্রথম বন্ধনীতে অন্তর্ভুক্ত ছিল)। নিরাপদে থাকার জন্য, মানসিকভাবে বন্ধনী বা খসড়া খুলে পরীক্ষা করা যাক।

ফর্মে ফাংশনটি আবার লিখি

আসুন বিন্দুতে একতরফা সীমা খুঁজে বের করা যাক:

এবং বিন্দুতে:

সুতরাং, সরলরেখাগুলি হল প্রশ্নে থাকা ফাংশনের গ্রাফের উল্লম্ব উপসর্গ।

2) যদি আপনি ফাংশন তাকান , তাহলে এটা বেশ সুস্পষ্ট যে সীমাটি সসীম হবে এবং আমাদের একটি অনুভূমিক অ্যাসিম্পটোট আছে। আসুন সংক্ষিপ্তভাবে এর উপস্থিতি দেখাই:

সুতরাং, সরলরেখা (অ্যাবসিসা অক্ষ) এই ফাংশনের গ্রাফের অনুভূমিক অ্যাসিম্পটোট।

উত্তর:

পাওয়া সীমা এবং উপসর্গ ফাংশনের গ্রাফ সম্পর্কে অনেক তথ্য প্রদান করে। নিম্নলিখিত তথ্যগুলি বিবেচনায় রেখে অঙ্কনটি মানসিকভাবে কল্পনা করার চেষ্টা করুন:

আপনার খসড়াতে গ্রাফের আপনার সংস্করণ স্কেচ করুন।

অবশ্যই, পাওয়া সীমাগুলি স্পষ্টভাবে গ্রাফের উপস্থিতি নির্ধারণ করে না, এবং আপনি একটি ভুল করতে পারেন, তবে অনুশীলন নিজেই অমূল্য সাহায্য প্রদান করবে সম্পূর্ণ ফাংশন অধ্যয়ন. সঠিক চিত্রটি পাঠের শেষে রয়েছে।

উদাহরণ 4

একটি ফাংশনের গ্রাফের উপসর্গ খুঁজুন

উদাহরণ 5

একটি ফাংশনের গ্রাফের উপসর্গ খুঁজুন

এগুলি স্বাধীন সমাধানের জন্য কাজ। উভয় গ্রাফে আবার অনুভূমিক অ্যাসিম্পটোট রয়েছে, যা অবিলম্বে নিম্নলিখিত বৈশিষ্ট্যগুলির দ্বারা সনাক্ত করা হয়: উদাহরণ 4-এ বৃদ্ধি আদেশহর আরো, লবের বৃদ্ধির ক্রম থেকে, এবং উদাহরণ 5 এ লব এবং হর বৃদ্ধির একই ক্রম. নমুনা সমাধানে, প্রথম ফাংশনটি সম্পূর্ণরূপে তির্যক অ্যাসিম্পটোটের উপস্থিতির জন্য পরীক্ষা করা হয় এবং দ্বিতীয়টি - সীমার মাধ্যমে।

অনুভূমিক অ্যাসিম্পটোটস, আমার বিষয়গত ইমপ্রেশনে, "সত্যিই কাত" হওয়াগুলির তুলনায় লক্ষণীয়ভাবে বেশি সাধারণ। দীর্ঘ প্রতীক্ষিত সাধারণ মামলা:

উদাহরণ 6

একটি ফাংশনের গ্রাফের উপসর্গ খুঁজুন

সমাধান: রীতির ক্লাসিক:

1) যেহেতু হর ধনাত্মক, তাহলে ফাংশন একটানাসমগ্র সংখ্যা রেখা বরাবর, এবং কোন উল্লম্ব উপসর্গ নেই। …এটা কি ভালো? সঠিক শব্দ নয় - চমৎকার! পয়েন্ট নং 1 বন্ধ।

2) আসুন তির্যক উপসর্গের উপস্থিতি পরীক্ষা করি:

প্রথম সীমা সসীম, তাই চলুন চলুন. গণনার সময় দ্বিতীয় সীমা বাদ দিতে হবে অনিশ্চয়তা "অসীম বিয়োগ অসীম"আমরা অভিব্যক্তিটি একটি সাধারণ হরকে নিয়ে আসি:

দ্বিতীয় সীমাও সসীমঅতএব, প্রশ্নে থাকা ফাংশনের গ্রাফটিতে একটি তির্যক অ্যাসিম্পটোট রয়েছে:

উপসংহার:

এইভাবে, যখন ফাংশনের গ্রাফ অসীম বন্ধএকটি সরল রেখার কাছে যায়:

লক্ষ্য করুন যে এটি তার তির্যক অ্যাসিম্পটোটকে উৎপত্তিস্থলে ছেদ করে, এবং এই ধরনের ছেদ বিন্দুগুলি বেশ গ্রহণযোগ্য - এটি গুরুত্বপূর্ণ যে "সবকিছু স্বাভাবিক" অসীমতায় (আসলে, এখানেই আমরা অ্যাসিম্পটোটস সম্পর্কে কথা বলছি)।

উদাহরণ 7

একটি ফাংশনের গ্রাফের উপসর্গ খুঁজুন

সমাধান: মন্তব্য করার জন্য বিশেষ কিছু নেই, তাই আমি একটি পরিষ্কার সমাধানের আনুমানিক উদাহরণ আঁকব:

1) উল্লম্ব উপসর্গ। এর বিন্দু অন্বেষণ করা যাক.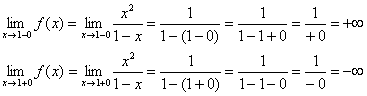

সরলরেখা হল গ্রাফের জন্য উল্লম্ব অ্যাসিম্পটোট।

2) তির্যক উপসর্গ:

সরলরেখা হল গ্রাফের জন্য তির্যক অ্যাসিম্পটোট।

উত্তর:

পাওয়া একতরফা সীমা এবং উপসর্গগুলি আমাদের উচ্চ আত্মবিশ্বাসের সাথে ভবিষ্যদ্বাণী করতে দেয় যে এই ফাংশনের গ্রাফটি কেমন দেখাচ্ছে। পাঠের শেষে সঠিক অঙ্কন।

উদাহরণ 8

একটি ফাংশনের গ্রাফের উপসর্গ খুঁজুন

এটি স্বাধীন সমাধানের একটি উদাহরণ; কিছু সীমা গণনা করার সুবিধার জন্য, আপনি লবটিকে হর পদ দ্বারা পদ দ্বারা ভাগ করতে পারেন। আবার, আপনার ফলাফল বিশ্লেষণ করার সময়, এই ফাংশনের একটি গ্রাফ আঁকার চেষ্টা করুন।

স্পষ্টতই, "বাস্তব" তির্যক অ্যাসিম্পটোটের মালিকরা হল সেই ভগ্নাংশের মূলদ ফাংশনের গ্রাফ যার লবের সর্বোচ্চ ডিগ্রি আরো একটাহর এর সর্বোচ্চ ডিগ্রী। যদি এটি বেশি হয়, কোন তির্যক অ্যাসিম্পটোট থাকবে না (উদাহরণস্বরূপ, )।

কিন্তু অন্যান্য অলৌকিক ঘটনা জীবনে ঘটে:

উদাহরণ 9

উদাহরণ 11

উপসর্গের উপস্থিতির জন্য একটি ফাংশনের গ্রাফ পরীক্ষা করুন

সমাধান: এটা স্পষ্ট যে , তাই আমরা শুধুমাত্র ডান অর্ধ-বিমান বিবেচনা করি, যেখানে ফাংশনের একটি গ্রাফ আছে।

সুতরাং, সরলরেখা (অর্ডিনেট অক্ষ) হল ফাংশনের গ্রাফের জন্য উল্লম্ব অ্যাসিম্পটোট।

2) তির্যক অ্যাসিম্পটোটের উপর অধ্যয়ন সম্পূর্ণ স্কিম অনুসারে করা যেতে পারে তবে নিবন্ধে হাসপাতালের নিয়মআমরা খুঁজে পেয়েছি যে একটি রৈখিক ফাংশন একটি লগারিদমিক তুলনায় উচ্চতর বৃদ্ধির ক্রম আছে, তাই: (একই পাঠের উদাহরণ 1 দেখুন)।

উপসংহার: x-অক্ষ হল তে ফাংশনের গ্রাফের অনুভূমিক অ্যাসিম্পটোট।

উত্তর:
, যদি;
, যদি.

স্পষ্টতার জন্য অঙ্কন:

এটি আকর্ষণীয় যে একটি আপাতদৃষ্টিতে অনুরূপ ফাংশনের কোনও উপসর্গ নেই (যারা চান তারা এটি পরীক্ষা করতে পারেন)।

স্ব-অধ্যয়নের জন্য দুটি চূড়ান্ত উদাহরণ:

উদাহরণ 12

উপসর্গের উপস্থিতির জন্য একটি ফাংশনের গ্রাফ পরীক্ষা করুন

সাধারণ কাজটি ঠিক এইভাবে তৈরি করা হয় এবং এতে গ্রাফের সমস্ত উপসর্গ (উল্লম্ব, ঝোঁক/অনুভূমিক) খুঁজে বের করা জড়িত। যদিও, প্রশ্নটি উত্থাপনের ক্ষেত্রে আরও সুনির্দিষ্ট হওয়ার জন্য, আমরা অ্যাসিম্পটোটসের উপস্থিতির জন্য গবেষণার কথা বলছি (সর্বশেষে, কোনওটিই নাও হতে পারে)।

আসুন সহজ কিছু দিয়ে শুরু করা যাক:

উদাহরণ 1

সমাধান এটি দুটি পয়েন্টে বিভক্ত করা সুবিধাজনক:

1) প্রথমে আমরা উল্লম্ব অ্যাসিম্পটোটস আছে কিনা তা পরীক্ষা করি। হরটি শূন্যে যায় এবং এটি অবিলম্বে স্পষ্ট যে এই সময়ে ফাংশনটি ক্ষতিগ্রস্ত হয় অন্তহীন ফাঁক, এবং সমীকরণ দ্বারা প্রদত্ত সরলরেখাটি ফাংশনের গ্রাফের উল্লম্ব অ্যাসিম্পটোট। কিন্তু, এই ধরনের উপসংহার আঁকার আগে, একতরফা সীমা খুঁজে বের করা প্রয়োজন:

আমি আপনাকে গণনার কৌশলটির কথা মনে করিয়ে দিচ্ছি যা আমি একইভাবে নিবন্ধে ফোকাস করেছি ফাংশনের ধারাবাহিকতা। ব্রেক পয়েন্ট. সীমা চিহ্নের অধীনে অভিব্যক্তিতে আমরা প্রতিস্থাপন করি। সংখ্যায় আকর্ষণীয় কিছু নেই:
.

কিন্তু হর মধ্যে এটা সক্রিয় আউট অসীম ঋণাত্মক সংখ্যা:
, এটা সীমা ভাগ্য নির্ধারণ করে.

বাম-হাতের সীমা অসীম, এবং নীতিগতভাবে, একটি উল্লম্ব অ্যাসিম্পটোটের উপস্থিতি সম্পর্কে একটি রায় তৈরি করা ইতিমধ্যেই সম্ভব। কিন্তু একতরফা সীমা শুধু এর জন্যই নয় - তারা বুঝতে সাহায্য করে কিভাবেফাংশনের গ্রাফটি সনাক্ত করুন এবং এটি তৈরি করুন সঠিকভাবে. অতএব, আমাদের অবশ্যই ডান হাতের সীমা গণনা করতে হবে:

উপসংহার: একতরফা সীমা অসীম, যার মানে সরলরেখা হল ফাংশনের গ্রাফের উল্লম্ব অ্যাসিম্পটোট।

প্রথম সীমা সসীম, যার মানে "কথোপকথন চালিয়ে যাওয়া" এবং দ্বিতীয় সীমা খুঁজে বের করা প্রয়োজন:

দ্বিতীয় সীমাও সসীম.

সুতরাং, আমাদের উপসর্গ হল:

উপসংহার: সমীকরণ দ্বারা প্রদত্ত সরলরেখা হল ফাংশনের গ্রাফের অনুভূমিক অ্যাসিম্পটোট।

অনুভূমিক অ্যাসিম্পটোট খুঁজে বের করতে আপনি একটি সরলীকৃত সূত্র ব্যবহার করতে পারেন:

যদি একটি সসীম সীমা থাকে, তাহলে সরলরেখা হল ফাংশনের গ্রাফের অনুভূমিক অ্যাসিম্পটোট।

এটি সহজেই দেখা যায় যে ফাংশনের লব এবং হর বৃদ্ধির একই ক্রম, যার মানে চাওয়া সীমা সীমাবদ্ধ হবে:

উত্তর:

শর্ত অনুযায়ী, আপনি অঙ্কন সম্পূর্ণ করতে হবে না, কিন্তু যদি পুরো দোলনায় ফাংশন অধ্যয়ন, তারপর খসড়াটিতে আমরা অবিলম্বে একটি স্কেচ তৈরি করি:

তিনটি পাওয়া সীমার উপর ভিত্তি করে, ফাংশনের গ্রাফটি কীভাবে অবস্থিত হতে পারে তা নিজের জন্য খুঁজে বের করার চেষ্টা করুন। এটা কি আদৌ কঠিন? 5-6-7-8 পয়েন্ট খুঁজুন এবং তাদের অঙ্কনে চিহ্নিত করুন। যাইহোক, এই ফাংশনের গ্রাফটি ব্যবহার করে নির্মিত হয় একটি প্রাথমিক ফাংশনের গ্রাফের রূপান্তর, এবং পাঠকরা যারা সাবধানে উপরের নিবন্ধের উদাহরণ 21 পরীক্ষা করেছেন তারা সহজেই অনুমান করতে পারেন এটি কি ধরনের বক্ররেখা।

উদাহরণ 2

একটি ফাংশনের গ্রাফের উপসর্গ খুঁজুন

এটি আপনার নিজের সমাধান করার জন্য একটি উদাহরণ। আমি আপনাকে মনে করিয়ে দিই যে প্রক্রিয়াটি সুবিধাজনকভাবে দুটি পয়েন্টে বিভক্ত - উল্লম্ব অ্যাসিম্পটোটস এবং তির্যক অ্যাসিম্পটোটস৷ নমুনা সমাধানে, একটি সরলীকৃত স্কিম ব্যবহার করে অনুভূমিক অ্যাসিম্পটোট পাওয়া যায়।

অনুশীলনে, ভগ্নাংশ-যুক্তিমূলক ফাংশনগুলি প্রায়শই সম্মুখীন হয় এবং হাইপারবোলাস প্রশিক্ষণের পরে, আমরা কাজটিকে জটিল করব:

উদাহরণ 3

একটি ফাংশনের গ্রাফের উপসর্গ খুঁজুন

সমাধান: এক, দুই এবং সম্পন্ন:

1) উল্লম্ব অ্যাসিম্পটোটস অবস্থিত অসীম বিচ্ছিন্নতার পয়েন্টে, তাই আপনাকে হরটি শূন্যে যায় কিনা তা পরীক্ষা করতে হবে। সিদ্ধান্ত নেওয়া যাক দ্বিঘাত সমীকরণ :

বৈষম্যকারীটি ইতিবাচক, তাই সমীকরণটির দুটি আসল মূল রয়েছে এবং কাজটি উল্লেখযোগ্যভাবে বৃদ্ধি পেয়েছে =)

আরও একতরফা সীমা খুঁজে বের করার জন্য, বর্গাকার ত্রিনমিককে ফ্যাক্টরাইজ করা সুবিধাজনক:
(কম্প্যাক্ট নোটেশনের জন্য, "মাইনাস" প্রথম বন্ধনীতে অন্তর্ভুক্ত ছিল)। নিরাপদে থাকার জন্য, মানসিকভাবে বন্ধনী বা খসড়া খুলে পরীক্ষা করা যাক।

ফর্মে ফাংশনটি আবার লিখি

আসুন বিন্দুতে একতরফা সীমা খুঁজে বের করা যাক:

এবং বিন্দুতে:

সুতরাং, সরলরেখাগুলি হল প্রশ্নে থাকা ফাংশনের গ্রাফের উল্লম্ব উপসর্গ।

2) যদি আপনি ফাংশন তাকান , তাহলে এটা বেশ সুস্পষ্ট যে সীমাটি সসীম হবে এবং আমাদের একটি অনুভূমিক অ্যাসিম্পটোট আছে। আসুন সংক্ষিপ্তভাবে এর উপস্থিতি দেখাই:

সুতরাং, সরলরেখা (অ্যাবসিসা অক্ষ) এই ফাংশনের গ্রাফের অনুভূমিক অ্যাসিম্পটোট।

উত্তর:

পাওয়া সীমা এবং উপসর্গ ফাংশনের গ্রাফ সম্পর্কে অনেক তথ্য প্রদান করে। নিম্নলিখিত তথ্যগুলি বিবেচনায় রেখে অঙ্কনটি মানসিকভাবে কল্পনা করার চেষ্টা করুন:

আপনার খসড়াতে গ্রাফের আপনার সংস্করণ স্কেচ করুন।

অবশ্যই, পাওয়া সীমাগুলি স্পষ্টভাবে গ্রাফের উপস্থিতি নির্ধারণ করে না, এবং আপনি একটি ভুল করতে পারেন, তবে অনুশীলন নিজেই অমূল্য সাহায্য প্রদান করবে সম্পূর্ণ ফাংশন অধ্যয়ন. সঠিক চিত্রটি পাঠের শেষে রয়েছে।

উদাহরণ 4

একটি ফাংশনের গ্রাফের উপসর্গ খুঁজুন

উদাহরণ 5

একটি ফাংশনের গ্রাফের উপসর্গ খুঁজুন

এগুলি স্বাধীন সমাধানের জন্য কাজ। উভয় গ্রাফে আবার অনুভূমিক অ্যাসিম্পটোট রয়েছে, যা অবিলম্বে নিম্নলিখিত বৈশিষ্ট্যগুলির দ্বারা সনাক্ত করা হয়: উদাহরণ 4-এ বৃদ্ধি আদেশহর হল লবের বৃদ্ধির ক্রম থেকে বড়, এবং উদাহরণ 5-এ লব এবং হর বৃদ্ধির একই ক্রম. নমুনা সমাধানে, প্রথম ফাংশনটি সম্পূর্ণরূপে তির্যক অ্যাসিম্পটোটের উপস্থিতির জন্য পরীক্ষা করা হয়, এবং দ্বিতীয়টি - সীমার মাধ্যমে।

অনুভূমিক অ্যাসিম্পটোটস, আমার বিষয়গত ইমপ্রেশনে, "সত্যিই কাত" হওয়াগুলির তুলনায় লক্ষণীয়ভাবে বেশি সাধারণ। দীর্ঘ প্রতীক্ষিত সাধারণ মামলা:

উদাহরণ 6

একটি ফাংশনের গ্রাফের উপসর্গ খুঁজুন

সমাধান: রীতির ক্লাসিক:

1) যেহেতু হর ধনাত্মক, তাহলে ফাংশন একটানাসমগ্র সংখ্যা রেখা বরাবর, এবং কোন উল্লম্ব উপসর্গ নেই। …এটা কি ভালো? সঠিক শব্দ নয় - চমৎকার! পয়েন্ট নং 1 বন্ধ।

2) আসুন তির্যক উপসর্গের উপস্থিতি পরীক্ষা করি:

প্রথম সীমা সসীম, তাই চলুন চলুন. গণনার সময় দ্বিতীয় সীমা বাদ দিতে হবে অনিশ্চয়তা "অসীম বিয়োগ অসীম"আমরা অভিব্যক্তিটি একটি সাধারণ হরকে নিয়ে আসি:

দ্বিতীয় সীমাও সসীমঅতএব, প্রশ্নে থাকা ফাংশনের গ্রাফটিতে একটি তির্যক অ্যাসিম্পটোট রয়েছে:

উপসংহার:

এইভাবে, যখন ফাংশনের গ্রাফ অসীম বন্ধএকটি সরল রেখার কাছে যায়:

লক্ষ্য করুন যে এটি তার তির্যক অ্যাসিম্পটোটকে উৎপত্তিস্থলে ছেদ করে, এবং এই ধরনের ছেদ বিন্দুগুলি বেশ গ্রহণযোগ্য - এটি গুরুত্বপূর্ণ যে "সবকিছু স্বাভাবিক" অসীমতায় (আসলে, এখানেই আমরা অ্যাসিম্পটোটস সম্পর্কে কথা বলছি)।

উদাহরণ 7

একটি ফাংশনের গ্রাফের উপসর্গ খুঁজুন

সমাধান: মন্তব্য করার জন্য বিশেষ কিছু নেই, তাই আমি একটি পরিষ্কার সমাধানের আনুমানিক উদাহরণ আঁকব:

1) উল্লম্ব উপসর্গ। এর বিন্দু অন্বেষণ করা যাক.

সরলরেখা হল গ্রাফের জন্য উল্লম্ব অ্যাসিম্পটোট।

2) তির্যক উপসর্গ:

সরলরেখা হল গ্রাফের জন্য তির্যক অ্যাসিম্পটোট।

উত্তর:

পাওয়া একতরফা সীমা এবং উপসর্গগুলি আমাদের উচ্চ আত্মবিশ্বাসের সাথে ভবিষ্যদ্বাণী করতে দেয় যে এই ফাংশনের গ্রাফটি কেমন দেখাচ্ছে। পাঠের শেষে সঠিক অঙ্কন।

উদাহরণ 8

একটি ফাংশনের গ্রাফের উপসর্গ খুঁজুন

এটি স্বাধীন সমাধানের একটি উদাহরণ; কিছু সীমা গণনা করার সুবিধার জন্য, আপনি লবটিকে হর পদ দ্বারা পদ দ্বারা ভাগ করতে পারেন। আবার, আপনার ফলাফল বিশ্লেষণ করার সময়, এই ফাংশনের একটি গ্রাফ আঁকার চেষ্টা করুন।

স্পষ্টতই, "বাস্তব" তির্যক অ্যাসিম্পটোটের মালিকরা হল সেই ভগ্নাংশের মূলদ ফাংশনের গ্রাফ যার লবের সর্বোচ্চ ডিগ্রি আরো একটাহর এর সর্বোচ্চ ডিগ্রী। যদি এটি বেশি হয়, তাহলে আর একটি তির্যক অ্যাসিম্পটোট থাকবে না (উদাহরণস্বরূপ, )।

কিন্তু অন্যান্য অলৌকিক ঘটনা জীবনে ঘটে:

উদাহরণ 9

সমাধান: ফাংশন একটানাসম্পূর্ণ সংখ্যা রেখায়, যার মানে কোন উল্লম্ব উপসর্গ নেই। কিন্তু ভাল প্রবণ বেশী হতে পারে. আমরা পরীক্ষা করি:

আমার মনে আছে কিভাবে আমি বিশ্ববিদ্যালয়ে একটি অনুরূপ ফাংশনের সম্মুখীন হয়েছিলাম এবং কেবল বিশ্বাস করতে পারিনি যে এটিতে একটি তির্যক অ্যাসিম্পটোট রয়েছে। যতক্ষণ না আমি দ্বিতীয় সীমা গণনা করি:

কঠোরভাবে বলতে গেলে, এখানে দুটি অনিশ্চয়তা রয়েছে: এবং , কিন্তু একটি উপায় বা অন্যভাবে, আপনাকে সমাধান পদ্ধতি ব্যবহার করতে হবে, যা নিবন্ধের 5-6 উদাহরণে আলোচনা করা হয়েছে বর্ধিত জটিলতার সীমা সম্পর্কে. সূত্রটি ব্যবহার করার জন্য আমরা সংযোজিত অভিব্যক্তি দ্বারা গুন এবং ভাগ করি:

উত্তর:

সম্ভবত সবচেয়ে জনপ্রিয় তির্যক অ্যাসিম্পটোট।

এখন অবধি, অসীমকে "একই ব্রাশ দিয়ে কাটা" করা হয়েছে, তবে এটি ঘটে যে ফাংশনের গ্রাফ দুটি ভিন্নতির্যক উপসর্গ এ এবং এ:

উদাহরণ 10

উপসর্গের উপস্থিতির জন্য একটি ফাংশনের গ্রাফ পরীক্ষা করুন

সমাধান: আমূল অভিব্যক্তিটি ইতিবাচক, যার অর্থ ডোমেইন- যে কোনো সংখ্যা বৈধ, এবং উল্লম্ব লাঠি হতে পারে না.

তির্যক উপসর্গ বিদ্যমান কিনা তা পরীক্ষা করা যাক।

যদি "x" থাকে "মাইনাস ইনফিনিটি", তাহলে:
(বর্গমূলের নীচে একটি "X" যোগ করার সময়, আপনাকে অবশ্যই একটি "বিয়োগ" চিহ্ন যোগ করতে হবে যাতে হরটির নেতিবাচকতা হারাতে না পারে)

এটা অস্বাভাবিক দেখায়, কিন্তু এখানে অনিশ্চয়তা হল "ইনফিনিটি মাইনাস ইনফিনিটি।" সংযোজিত রাশি দ্বারা লব এবং হরকে গুণ করুন:

সুতরাং, সরলরেখা হল গ্রাফের তির্যক অ্যাসিম্পটোট।

"প্লাস ইনফিনিটি" সহ সবকিছুই তুচ্ছ:

এবং সরলরেখা হল .

উত্তর:

যদি;
, যদি.

আমি গ্রাফিক ইমেজ প্রতিরোধ করতে পারি না:


এটি একটি শাখা হাইপারবোলস .

প্রাথমিকভাবে উপসর্গের সম্ভাব্য প্রাপ্যতা সীমিত হওয়া অস্বাভাবিক নয় ফাংশনের ডোমেইন:

উদাহরণ 11

উপসর্গের উপস্থিতির জন্য একটি ফাংশনের গ্রাফ পরীক্ষা করুন

সমাধান: এটা স্পষ্ট যে , তাই আমরা শুধুমাত্র ডান অর্ধ-বিমান বিবেচনা করি, যেখানে ফাংশনের একটি গ্রাফ আছে।

1) ফাংশন একটানাব্যবধানে , যার মানে যদি একটি উল্লম্ব অ্যাসিম্পটোট বিদ্যমান থাকে, তাহলে এটি শুধুমাত্র অর্ডিনেট অক্ষ হতে পারে। আসুন পয়েন্টের কাছাকাছি ফাংশনের আচরণ অধ্যয়ন করি ডানে:

বিঃদ্রঃ, এখানে কোন অনিশ্চয়তা নেই(এই ধরনের ক্ষেত্রে নিবন্ধের শুরুতে জোর দেওয়া হয়েছিল সীমা সমাধানের পদ্ধতি).

সুতরাং, সরলরেখা (অর্ডিনেট অক্ষ) হল ফাংশনের গ্রাফের জন্য উল্লম্ব অ্যাসিম্পটোট।

2) তির্যক অ্যাসিম্পটোটের উপর অধ্যয়ন সম্পূর্ণ স্কিম অনুসারে করা যেতে পারে তবে নিবন্ধে হাসপাতালের নিয়মআমরা খুঁজে পেয়েছি যে একটি রৈখিক ফাংশন একটি লগারিদমিক তুলনায় উচ্চতর বৃদ্ধির ক্রম আছে, তাই: (একই পাঠের উদাহরণ 1 দেখুন)।

উপসংহার: x-অক্ষ হল তে ফাংশনের গ্রাফের অনুভূমিক অ্যাসিম্পটোট।

উত্তর:

যদি;
, যদি.

স্পষ্টতার জন্য অঙ্কন:

এটি আকর্ষণীয় যে একটি আপাতদৃষ্টিতে অনুরূপ ফাংশনের কোনও উপসর্গ নেই (যারা চান তারা এটি পরীক্ষা করতে পারেন)।

স্ব-অধ্যয়নের জন্য দুটি চূড়ান্ত উদাহরণ:

উদাহরণ 12

উপসর্গের উপস্থিতির জন্য একটি ফাংশনের গ্রাফ পরীক্ষা করুন

উল্লম্ব অ্যাসিম্পটোটস পরীক্ষা করতে, আপনাকে প্রথমে খুঁজে বের করতে হবে একটি ফাংশনের ডোমেইন, এবং তারপর "সন্দেহজনক" পয়েন্টগুলিতে একতরফা সীমার একটি দম্পতি গণনা করুন৷ তির্যক অ্যাসিম্পটোটগুলিও বাদ দেওয়া হয় না, যেহেতু ফাংশনটি "প্লাস" এবং "বিয়োগ" অনন্তে সংজ্ঞায়িত করা হয়।

উদাহরণ 13

উপসর্গের উপস্থিতির জন্য একটি ফাংশনের গ্রাফ পরীক্ষা করুন

কিন্তু এখানে শুধুমাত্র তির্যক উপসর্গ থাকতে পারে, এবং দিকনির্দেশগুলি আলাদাভাবে বিবেচনা করা উচিত।

আমি আশা করি আপনি সঠিক অ্যাসিম্পটোট খুঁজে পেয়েছেন =)

আমি তোমার সাফল্য কামনা করি!

সমাধান এবং উত্তর:

উদাহরণ 2:সমাধান :
. আসুন একতরফা সীমা খুঁজে বের করা যাক:

সোজা এ ফাংশনের গ্রাফের উল্লম্ব অ্যাসিম্পটোট .
2) তির্যক উপসর্গ।

সোজা .
উত্তর:

অঙ্কন উদাহরণ 3 থেকে:

উদাহরণ 4:সমাধান :
1) উল্লম্ব উপসর্গ। ফাংশন একটি বিন্দুতে একটি অসীম বিরতি ভোগ করে . আসুন একতরফা সীমা গণনা করা যাক:

বিঃদ্রঃ: একটি অসীম ঋণাত্মক সংখ্যা একটি জোড় শক্তির একটি অসীম ধনাত্মক সংখ্যার সমান: .

সোজা ফাংশনের গ্রাফের উল্লম্ব অ্যাসিম্পটোট।
2) তির্যক উপসর্গ।


সোজা (abscissa axis) হল ফাংশনের গ্রাফের অনুভূমিক অ্যাসিম্পটোট .
উত্তর: