রিং বিভাগের জড়তার মুহূর্ত। সরল বিভাগের জড়তার মুহূর্ত। সমকোণী ত্রিভুজের জড়তার অক্ষীয় মুহূর্ত

সংজ্ঞা

জড়তার অক্ষীয় (বা নিরক্ষীয়) মুহূর্তঅক্ষের সাথে সম্পর্কিত বিভাগকে একটি পরিমাণ বলা হয় যা সংজ্ঞায়িত করা হয়:

অভিব্যক্তি (1) এর অর্থ হল জড়তার অক্ষীয় মুহূর্ত গণনা করতে, অসীম ক্ষেত্রগুলির গুণফলের যোগফল () তাদের থেকে ঘূর্ণনের অক্ষ পর্যন্ত দূরত্বের বর্গ দ্বারা গুণিত সমগ্র এলাকা S ধরে নেওয়া হয়:

পারস্পরিক লম্ব অক্ষের (উদাহরণস্বরূপ, কার্টেসিয়ান স্থানাঙ্ক ব্যবস্থায় X এবং Y অক্ষের সাপেক্ষে) বিভাগের জড়তার অক্ষীয় মুহূর্তগুলির সমষ্টি এই অক্ষগুলির ছেদ বিন্দুর সাপেক্ষে জড়তা () এর মেরু মুহূর্ত দেয়:

সংজ্ঞা

পোলার মুহূর্তজড়তাকে কিছু বিন্দুর সাপেক্ষে জড়তা বিভাগের মুহূর্ত বলা হয়।

জড়তার অক্ষীয় মুহূর্তগুলি সর্বদা শূন্যের চেয়ে বেশি, কারণ তাদের সংজ্ঞায় (1) অবিচ্ছেদ্য চিহ্নের অধীনে প্রাথমিক ক্ষেত্রফলের ক্ষেত্রফলের মান রয়েছে (), সর্বদা ধনাত্মক, এবং এই ক্ষেত্র থেকে দূরত্বের বর্গক্ষেত্র অক্ষ

যদি আমরা জটিল আকারের একটি অংশ নিয়ে কাজ করি, তবে প্রায়শই গণনায় আমরা এই সত্যটি ব্যবহার করি যে অক্ষের সাপেক্ষে একটি জটিল বিভাগের জড়তার অক্ষীয় মুহূর্ত এই বিভাগের অংশগুলির জড়তার অক্ষীয় মুহুর্তের সমষ্টির সমান। একই অক্ষের সাথে আপেক্ষিক। যাইহোক, এটা মনে রাখা উচিত যে বিভিন্ন অক্ষ এবং বিন্দুর সাপেক্ষে পাওয়া জড়তার মুহূর্তগুলিকে যোগ করা অসম্ভব।

বিভাগটির মাধ্যাকর্ষণ কেন্দ্রের মধ্য দিয়ে যাওয়া অক্ষের সাপেক্ষে জড়তার অক্ষীয় মুহূর্তটির সমান্তরাল অক্ষগুলির সাপেক্ষে সমস্ত মুহুর্তের মধ্যে সবচেয়ে ছোট মান রয়েছে। যেকোনো অক্ষ সম্পর্কে জড়তার মুহূর্ত () শর্ত থাকে যে এটি মাধ্যাকর্ষণ কেন্দ্রের মধ্য দিয়ে যাওয়া অক্ষের সমান্তরাল হয়:

বিভাগের মাধ্যাকর্ষণ কেন্দ্রের মধ্য দিয়ে যাওয়া অক্ষের সাপেক্ষে বিভাগের জড়তার মুহূর্ত কোথায়; - ক্রস-বিভাগীয় এলাকা; - অক্ষের মধ্যে দূরত্ব।

সমস্যা সমাধানের উদাহরণ

উদাহরণ 1

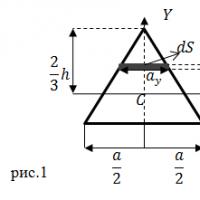
ব্যায়াম	ত্রিভুজের মাধ্যাকর্ষণ () কেন্দ্রের মধ্য দিয়ে যাওয়া Z অক্ষের সাপেক্ষে একটি সমদ্বিবাহু ত্রিভুজাকার ক্রস-সেকশনের জড়তার অক্ষীয় মুহূর্ত কত? ত্রিভুজের উচ্চতা হল।
সমাধান	আসুন একটি ত্রিভুজাকার অংশে একটি আয়তক্ষেত্রাকার প্রাথমিক এলাকা নির্বাচন করুন (চিত্র 1 দেখুন)। এটি ঘূর্ণনের অক্ষ থেকে একটি দূরত্বে অবস্থিত, এক বাহুর দৈর্ঘ্য হল, অন্য দিকে। চিত্র 1 থেকে এটি অনুসরণ করে যে: নির্বাচিত আয়তক্ষেত্রের ক্ষেত্রফল, (1.1) বিবেচনায় নেওয়ার সমান: জড়তার অক্ষীয় মুহূর্ত খুঁজে পেতে, আমরা এর সংজ্ঞাটি আকারে ব্যবহার করি:
উত্তর

উদাহরণ 2

ব্যায়াম	একটি বৃত্তের আকারে একটি বিভাগের লম্ব অক্ষ X এবং Y (চিত্র 2) এর সাপেক্ষে জড়তার অক্ষীয় মুহূর্তগুলি খুঁজুন যার ব্যাস d এর সমান।
সমাধান	সমস্যা সমাধানের জন্য, বিভাগ () এর কেন্দ্রের সাপেক্ষে মেরু মুহূর্তটি খুঁজে বের করে শুরু করা আরও সুবিধাজনক। আসুন আমরা পুরো বিভাগটিকে অসীমভাবে পাতলা বেধের রিংগুলিতে ভাগ করি, যার ব্যাসার্ধটি দ্বারা চিহ্নিত করা হবে। তারপর আমরা প্রাথমিক এলাকা খুঁজে পাই:

সাধারণ বিভাগগুলির জন্য, স্থির মুহূর্ত এবং জড়তার মুহূর্তগুলি একীকরণ ব্যবহার করে সূত্র (2.1)-(2.4) ব্যবহার করে পাওয়া যায়। বিবেচনা করুন, উদাহরণস্বরূপ, জড়তার অক্ষীয় মুহূর্ত গণনা করা জে এক্সচিত্রে দেখানো একটি নির্বিচারে বিভাগের জন্য। 2.9। বিবেচনা করে যে একটি আয়তক্ষেত্রাকার স্থানাঙ্ক সিস্টেমে এলাকা উপাদান dF=dxdy,আমরা পেতে

wherex^(y) এবং x ইন (y) -কিছু নির্দিষ্ট মানের কনট্যুর পয়েন্টের স্থানাঙ্ক u

এক্স এর উপর ইন্টিগ্রেশন সঞ্চালন, আমরা খুঁজে

মাত্রা দ্বারা)স্তরে বিভাগের প্রস্থ প্রতিনিধিত্ব করে এ(চিত্র 2.9 দেখুন), এবং পণ্য b(y)dy = dF -অক্ষের সমান্তরাল ছায়াযুক্ত প্রাথমিক স্ট্রিপের ক্ষেত্র উহু.এটিকে বিবেচনায় নিয়ে, ফর্মুলা ফরম রূপান্তরিত হয়

জড়তার মুহুর্তের জন্য অনুরূপ অভিব্যক্তি পাওয়া যেতে পারে জে.

আয়তক্ষেত্র.আসুন মূল কেন্দ্রীয় অক্ষগুলি সম্পর্কে জড়তার মুহূর্তগুলি খুঁজে বের করি, যা সম্পত্তি 2 (§ 2.5) অনুসারে, আয়তক্ষেত্রের প্রতিসাম্য অক্ষগুলির সাথে মিলে যায় (চিত্র 2.10)। যেহেতু বিভাগের প্রস্থ ধ্রুবক, তারপর সূত্র ব্যবহার করে (2.14) আমরা প্রাপ্ত করি

অক্ষ সম্পর্কে জড়তার মুহূর্ত ওহ x x xআমরা প্রথম সূত্র দ্বারা নির্ধারণ করি (2.6):

জড়তা / এবং জেএকইভাবে পাওয়া যায়। আসুন একটি আয়তক্ষেত্রের জড়তার অক্ষীয় মুহূর্তগুলির জন্য সূত্রগুলি লিখি:

নির্বিচারে ত্রিভুজ।প্রথমে, আসুন অক্ষ সম্পর্কে জড়তার মুহূর্তটি খুঁজে বের করা যাক 0 ( x vত্রিভুজের ভিত্তির মধ্য দিয়ে যাওয়া (চিত্র 2.11)। অংশের প্রস্থ দ্বারা())স্তরে y (ত্রিভুজের মিল থেকে পাওয়া যায়:

এই পরিমাণটিকে সূত্রে প্রতিস্থাপিত করে (2.14) এবং একীকরণ সম্পাদন করে, আমরা পাই

অক্ষ সম্পর্কে মুহূর্ত উহুএবং 0 2 x 2,বেসের সমান্তরাল এবং মাধ্যাকর্ষণ কেন্দ্রের মধ্য দিয়ে এবং ত্রিভুজের শীর্ষবিন্দুর মধ্য দিয়ে যথাক্রমে, আমরা সূত্র ব্যবহার করে দেখতে পাই (2.6):

এসব সূত্রে খ ( =ঘ/ 3 এবং b 2 = -2h/3 - যথাক্রমে, ত্রিভুজের মাধ্যাকর্ষণ কেন্দ্রের অর্ডিনেট সম্পর্কিতসমন্বয় ব্যবস্থায় O x x 1 y 1এবং 0 2 x 2 y t

1°2 r Г*аУ 1

TL P *2

g >4™_ °2 1

D__V_!__*_ / ^ *3

V XV* ;-7^Лт^

U_ У-_XI - UZ__у

সম্পর্কিত,| খ *, 0 b/ b 2 %*1

ভাত। 2.11 ভাত। 2.12

বেসের সমান্তরাল অক্ষগুলির সাপেক্ষে ত্রিভুজের জড়তার অক্ষীয় মুহুর্তগুলির সূত্রগুলি লিখি:

সমদ্বিবাহু এবং সমদ্বিবাহু ত্রিভুজ।একটি সমকোণী ত্রিভুজের জন্য (চিত্র 2.12), আমরা জড়তার কেন্দ্রাতিগ মুহূর্ত নির্ধারণ করি জেকেন্দ্রীয় অক্ষের সাথে আপেক্ষিক উহুএবং OU,পায়ে সমান্তরাল। এটি সূত্র ব্যবহার করে করা যেতে পারে (2.3)। যাইহোক, নিম্নলিখিত কৌশল প্রয়োগ করে সমস্যার সমাধান সহজ করা যেতে পারে। মধ্যমা ব্যবহার করে 0 { 0 3 প্রদত্ত ত্রিভুজটিকে দুটি সমদ্বিবাহু ত্রিভুজে ভাগ করুন 0 ( 0 3 এএবং Ofi 3 বি.অক্ষ 0 3 x 3 এবং 0 3 y 3এই ত্রিভুজগুলির জন্য প্রতিসাম্যের অক্ষ এবং, সম্পত্তি 2 (§ 2.5) এর উপর ভিত্তি করে, পৃথকভাবে তাদের প্রতিটির প্রধান অক্ষ হবে এবং তাই সমগ্র ত্রিভুজের O x AB.অতএব, জড়তার কেন্দ্রাতিগ মুহূর্ত জে=0। সেন্ট্রিফিউজ

অক্ষ সম্পর্কে ত্রিভুজের মুহূর্ত উহুএবং OUআমরা শেষ সূত্র ব্যবহার করে দেখতে পাই (2.6):

আসুন একটি সমকোণী ত্রিভুজের জড়তার মুহূর্তগুলির জন্য সূত্রগুলি লিখি:

প্রতিসাম্যের অক্ষ সম্পর্কে একটি সমদ্বিবাহু ত্রিভুজের জড়তার মুহূর্ত OU(চিত্র 2.13) আমরা সূত্রের চতুর্থ (2.17) ব্যবহার করে, একটি ভিত্তি সহ একটি সমকোণী ত্রিভুজের জড়তার দ্বিগুণ মুহূর্ত হিসাবে সংজ্ঞায়িত করি। জএবং উচ্চতা খ/ 2:

এইভাবে, প্রধান কেন্দ্রীয় অক্ষ সম্পর্কে একটি সমদ্বিবাহু ত্রিভুজের জড়তার মুহূর্ত উহুএবং OUসূত্র দ্বারা নির্ধারিত

বৃত্ত।প্রথমত, পোলার কোঅর্ডিনেট সিস্টেম (চিত্র 2.14) ব্যবহার করে সূত্র (2.4) ব্যবহার করে একটি বৃত্তের জড়তার মেরু মুহূর্ত গণনা করা সুবিধাজনক।

সেই বিবেচনায় dF-rdrdQ,আমরা খুঁজে পাব

যেহেতু (2.4) অনুসারে পোলার মোমেন্ট দুটি অক্ষীয় মুহুর্তের যোগফলের সমান, তাই আমরা পাই

রিং।বলয়ের জড়তার মুহূর্তগুলি (চিত্র 2.15) রেডিআই সহ দুটি বৃত্তের জড়তার মুহূর্তগুলির মধ্যে পার্থক্য হিসাবে পাওয়া যায় আমি 2এবং আর (:

অর্ধবৃত্ত(ভাত। 2.16). অর্ধবৃত্তের সমতলে একটি ক্ষেত্রফল নির্বাচন করা যাক dFমেরু স্থানাঙ্ক সহ জি, 0 এবং কার্টেসিয়ান স্থানাঙ্ক x v y vযার জন্য, চিত্র অনুযায়ী. 2.16 আমাদের আছে:

সূত্র (2.1) এবং (2.5) ব্যবহার করে, আমরা যথাক্রমে অক্ষের সাপেক্ষে অর্ধবৃত্তের স্থির মুহূর্ত খুঁজে পাই 0 ( x (এবং অভিকর্ষের 0 কেন্দ্রে অর্ডিনেট করুন সম্পর্কিতসমন্বয় ব্যবস্থায় 0 ( x ( Uy

অক্ষ 0, x, এবং আপেক্ষিক 0 ( y vযেগুলি অর্ধবৃত্তের প্রধান অক্ষ, জড়তার অক্ষীয় মুহূর্তগুলি বৃত্তের জড়তার অর্ধেক মুহুর্তের সমান:

প্রধান কেন্দ্রীয় অক্ষ সম্পর্কে জড়তার মুহূর্তটি প্রথম সূত্র (2.6) ব্যবহার করে নির্ধারিত হয়:

উপবৃত্ত।অর্ধ-অক্ষ সহ একটি উপবৃত্তের জড়তার অক্ষীয় মুহূর্ত গণনা করতে কএবং খঅক্ষের সাথে আপেক্ষিক উহু(চিত্র 2.17) আমরা নিম্নরূপ এগিয়ে যাই। উপবৃত্তের চারপাশে একটি বৃত্ত আঁকুন এবং প্রস্থের দুটি প্রাথমিক স্ট্রাইপ নির্বাচন করুন dxএবং উচ্চতা 2укবৃত্ত এবং 2 এর জন্য উহএকটি উপবৃত্তের জন্য এই দুটি স্ট্রিপের জড়তার মুহূর্তগুলি একটি আয়তক্ষেত্রের জন্য প্রথম সূত্রের (2.15) দ্বারা নির্ধারণ করা যেতে পারে:

থেকে এই অভিব্যক্তি একত্রিত করা -এআগে ক,আমরা পেতে

ভাত। 2.16

ভাত। 2.17

একটি বৃত্ত এবং একটি উপবৃত্তের সমীকরণ থেকে আমাদের আছে

এটা মাথায় রেখে

অক্ষ সম্পর্কে জড়তার মুহুর্তের জন্য অনুরূপ অভিব্যক্তি পাওয়া যেতে পারে OU.ফলস্বরূপ, উপবৃত্তের জন্য আমাদের কাছে অক্ষীয় মুহূর্তের জন্য নিম্নলিখিত সূত্র থাকবে:

ঘূর্ণিত রড।ঘূর্ণিত রডগুলির (আই-বিম, চ্যানেল, কোণ) বিভাগের জ্যামিতিক বৈশিষ্ট্যগুলি রোলড স্টিলের ভাণ্ডার টেবিলে দেওয়া হয়েছে (পরিশিষ্ট দেখুন)।

মৃতদেহ মিদূরত্ব প্রতি বর্গ dঅক্ষের মধ্যে:

J = J c + m d 2 , (\displaystyle J=J_(c)+md^(2),)

কোথায় মি- মোট শরীরের ওজন।

উদাহরণস্বরূপ, একটি অক্ষের শেষের মধ্য দিয়ে যাওয়া একটি রডের জড়তার মুহূর্ত সমান:

J = J c + m d 2 = 1 12 m l 2 + m (l 2) 2 = 1 3 m l 2। (\displaystyle J=J_(c)+md^(2)=(\frac (1)(12))ml^(2)+m\left((\frac (l)(2))\right)^ (2)=(\frac (1)(3))ml^(2))

কিছু দেহের জড়তার অক্ষীয় মুহূর্ত

জড়তার মুহূর্তঘূর্ণনের নির্দিষ্ট অক্ষের সাপেক্ষে সরল আকারের সমজাতীয় দেহ

শরীর	বর্ণনা	অক্ষ অবস্থান ক	নিষ্ক্রিয়তা মুহূর্ত জে ক
	উপাদান বিন্দু ভর মি	দূরত্বে rএকটি বিন্দু থেকে, স্থির
	ফাঁপা পাতলা দেয়ালের সিলিন্ডার বা ব্যাসার্ধের রিং rএবং ভর মি	সিলিন্ডারের অক্ষ	mr 2 (\displaystyle mr^(2))
	কঠিন সিলিন্ডার বা ব্যাসার্ধ ডিস্ক rএবং ভর মি	সিলিন্ডারের অক্ষ	1 2 m r 2 (\displaystyle (\frac (1)(2))mr^(2))
	ফাঁপা পুরু-প্রাচীরযুক্ত ভর সিলিন্ডার মিবাইরের ব্যাসার্ধ সহ r 2 এবং ভিতরের ব্যাসার্ধ r 1	সিলিন্ডারের অক্ষ	m r 2 2 + r 1 2 2 (\displaystyle m(\frac (r_(2)^(2)+r_(1)^(2))(2)))
	কঠিন সিলিন্ডার দৈর্ঘ্য l, ব্যাসার্ধ rএবং ভর মি		1 4 m ⋅ r 2 + 1 12 m ⋅ l 2 (\displaystyle (1 \over 4)m\cdot r^(2)+(1 \over 12)m\cdot l^(2))
	ফাঁপা পাতলা দেয়ালের সিলিন্ডার (রিং) দৈর্ঘ্য l, ব্যাসার্ধ rএবং ভর মি	অক্ষটি সিলিন্ডারের লম্ব এবং ভরের কেন্দ্রের মধ্য দিয়ে যায়	1 2 m ⋅ r 2 + 1 12 m ⋅ l 2 (\displaystyle (1 \over 2)m\cdot r^(2)+(1 \over 12)m\cdot l^(2))
	সোজা পাতলা দৈর্ঘ্যের রড lএবং ভর মি	অক্ষটি রডের সাথে লম্ব এবং এর ভর কেন্দ্রের মধ্য দিয়ে যায়	1 12 m l 2 (\displaystyle (\frac (1)(12))ml^(2))
	সোজা পাতলা দৈর্ঘ্যের রড lএবং ভর মি	অক্ষটি রডের লম্ব এবং এর শেষের মধ্য দিয়ে যায়	1 3 মি এল 2 (\ ডিসপ্লেস্টাইল (\ frac (1)(3))ml^(2))
	পাতলা দেয়ালযুক্ত ব্যাসার্ধ গোলক rএবং ভর মি	অক্ষটি গোলকের কেন্দ্রের মধ্য দিয়ে যায়	2 3 m r 2 (\displaystyle (\frac (2)(3))mr^(2))
	ব্যাসার্ধ বল rএবং ভর মি	অক্ষটি বলের কেন্দ্রের মধ্য দিয়ে যায়	2 5 mr 2 (\displaystyle (\frac (2)(5))mr^(2))
	ব্যাসার্ধ শঙ্কু rএবং ভর মি	শঙ্কু অক্ষ	3 10 m r 2 (\displaystyle (\frac (3)(10))mr^(2))
	উচ্চতা সহ সমদ্বিবাহু ত্রিভুজ জ, ভিত্তি কএবং ভর মি	অক্ষটি ত্রিভুজের সমতলে লম্ব এবং শীর্ষবিন্দুর মধ্য দিয়ে যায়	1 24 মি (a 2 + 12 h 2) (\displaystyle (\frac (1)(24))m(a^(2)+12h^(2)))
	পাশের সাথে নিয়মিত ত্রিভুজ কএবং ভর মি	অক্ষটি ত্রিভুজের সমতলে লম্ব এবং ভরের কেন্দ্রের মধ্য দিয়ে যায়	1 12 m a 2 (\displaystyle (\frac (1)(12))ma^(2))
	পাশে বর্গক্ষেত্র কএবং ভর মি	অক্ষটি বর্গক্ষেত্রের সমতলে লম্ব এবং ভরের কেন্দ্রের মধ্য দিয়ে যায়	1 6 m a 2 (\ প্রদর্শনশৈলী (\frac (1)(6))ma^(2))
	পাশ দিয়ে আয়তক্ষেত্র কএবং খএবং ভর মি	অক্ষটি আয়তক্ষেত্রের সমতলে লম্ব এবং ভরের কেন্দ্রের মধ্য দিয়ে যায়	1 12 মি (a 2 + b 2) (\displaystyle (\frac (1)(12))m(a^(2)+b^(2)))
	ব্যাসার্ধের নিয়মিত n-গন rএবং ভর মি	অক্ষটি সমতলের লম্ব এবং ভরের কেন্দ্রের মধ্য দিয়ে যায়	mr 2 6 [ 1 + 2 cos ⁡ (π / n) 2 ] (\displaystyle (\frac (mr^(2))(6))\left)
	গাইড বৃত্ত ব্যাসার্ধ সহ টরাস (ফাঁপা) আর, উৎপন্ন বৃত্তের ব্যাসার্ধ rএবং ভর মি	অক্ষটি টরাস গাইড বৃত্তের সমতলে লম্ব এবং ভরের কেন্দ্রের মধ্য দিয়ে যায়	I = m (3 4 r 2 + R 2) (\displaystyle I=m\left((\frac (3)(4))\,r^(2)+R^(2)\right))

সূত্র প্রাপ্ত

পাতলা দেয়ালের সিলিন্ডার (রিং, হুপ)

সূত্রের উৎপত্তি

একটি শরীরের জড়তার মুহূর্ত তার উপাদান অংশের জড়তার মুহূর্তগুলির যোগফলের সমান। আসুন একটি পাতলা দেয়ালের সিলিন্ডারকে ভর সহ উপাদানগুলিতে ভাগ করি dmএবং জড়তা মুহূর্ত dJ i. তারপর

J = ∑ d J i = ∑ R i 2 d m। (1)। (\displaystyle J=\sum dJ_(i)=\sum R_(i)^(2)dm.\qquad (1)

যেহেতু একটি পাতলা-দেয়ালের সিলিন্ডারের সমস্ত উপাদান ঘূর্ণনের অক্ষ থেকে একই দূরত্বে থাকে, সূত্র (1) রূপান্তরিত হয়

J = ∑ R 2 d m = R 2 ∑ d m = m R 2। (\displaystyle J=\sum R^(2)dm=R^(2)\sum dm=mR^(2))

পুরু দেয়ালের সিলিন্ডার (রিং, হুপ)

সূত্রের উৎপত্তি

বাইরের ব্যাসার্ধ সহ একটি সমজাতীয় বলয় থাকতে দিন আর, ভিতরের ব্যাসার্ধ আর 1, পুরু জএবং ঘনত্ব ρ। এর পুরু পাতলা রিং মধ্যে এটি ভাঙ্গা যাক ডাঃ. একটি পাতলা ব্যাসার্ধের বলয়ের জড়তার ভর এবং মুহূর্ত rহবে

d m = ρ d V = ρ ⋅ 2 π r h d r ; d J = r 2 d m = 2 π ρ h r 3 d r। (\displaystyle dm=\rho dV=\rho \cdot 2\pi rhdr;\qquad dJ=r^(2)dm=2\pi \rho hr^(3)dr.)

পুরু বলয়ের জড়তার মুহূর্তটিকে অবিচ্ছেদ্য হিসাবে খুঁজে বের করা যাক

J = ∫ R 1 R d J = 2 π ρ h ∫ R 1 R r 3 d r = (\displaystyle J=\int _(R_(1))^(R)dJ=2\pi \rho h\int _ (R_(1))^(R)r^(3)dr=) = 2 π ρ h r 4 4 | R 1 R = 1 2 π ρ h (R 4 − R 1 4) = 1 2 π ρ h (R 2 − R 1 2) (R 2 + R 1 2)। (\displaystyle =2\pi \rho h\left.(\frac (r^(4))(4))\right|_(R_(1))^(R)=(\frac (1)(2 ))\pi \rho h\left(R^(4)-R_(1)^(4)\right)=(\frac (1)(2))\pi \rho h\left(R^(2) -R_(1)^(2)\ডান)\বাম(R^(2)+R_(1)^(2)\ডান)।

যেহেতু বলয়ের আয়তন এবং ভর সমান

V = π (R 2 − R 1 2) h ; m = ρ V = π ρ (R 2 − R 1 2) h , (\displaystyle V=\pi \left(R^(2)-R_(1)^(2)\right)h;\qquad m= \rho V=\pi \rho \left(R^(2)-R_(1)^(2)\right)h,)

আমরা রিং এর জড়তা মুহূর্ত জন্য চূড়ান্ত সূত্র প্রাপ্ত

J = 1 2 m (R 2 + R 1 2)। (\displaystyle J=(\frac (1)(2))m\left(R^(2)+R_(1)^(2)\right))

সমজাতীয় ডিস্ক (কঠিন সিলিন্ডার)

সূত্রের উৎপত্তি

শূন্য অভ্যন্তরীণ ব্যাসার্ধ সহ একটি রিং হিসাবে একটি সিলিন্ডার (ডিস্ক) বিবেচনা করা ( আর 1 = 0 ), আমরা সিলিন্ডারের (ডিস্ক) জড়তার মুহুর্তের সূত্র পাই:

J = 1 2 m R 2। (\displaystyle J=(\frac (1)(2))mR^(2))

কঠিন শঙ্কু

সূত্রের উৎপত্তি

এর একটি বেধ সঙ্গে পাতলা ডিস্ক মধ্যে শঙ্কু ভাঙ্গা যাক dh, শঙ্কুর অক্ষের লম্ব। এই জাতীয় ডিস্কের ব্যাসার্ধ সমান

r = R h H , (\displaystyle r=(\frac (Rh)(H)),)

কোথায় আর- শঙ্কু বেসের ব্যাসার্ধ, এইচ- শঙ্কুর উচ্চতা, জ- শঙ্কুর শীর্ষ থেকে ডিস্কের দূরত্ব। এই জাতীয় ডিস্কের জড়তার ভর এবং মুহূর্ত হবে

d J = 1 2 r 2 d m = 1 2 π ρ 4 d h = 1 2 π ρ (R h H) 4 d h ; (\displaystyle dJ=(\frac (1)(2))r^(2)dm=(\frac (1)(2))\pi \rho r^(4)dh=(\frac (1)( 2))\pi \rho \left((\frac (Rh)(H))\right)^(4)dh;)

একত্রীকরণ, আমরা পেতে

J = ∫ 0 H d J = 1 2 π ρ (R H) 4 ∫ 0 H h 4 d h = 1 2 π ρ (R H) 4 h 5 5 | 0 H == 1 10 π ρ R 4 H = (ρ ⋅ 1 3 π R 2 H) 3 10 R 2 = 3 10 m R 2 । (\displaystyle (\begin(aligned)J=\int _(0)^(H)dJ=(\frac (1)(2))\pi \rho \left((\frac (R)(H)) \right)^(4)\int _(0)^(H)h^(4)dh=(\frac (1)(2))\pi \rho \left((\frac (R)(H) )\right)^(4)\বাম।(\frac (h^(5))(5))\right|_(0)^(H)==(\frac (1)(10))\pi \rho R^(4)H=\left(\rho \cdot (\frac (1)(3))\pi R^(2)H\right)(\frac (3)(10))R^( 2)=(\frac (3)(10))mR^(2)।\end(সারিবদ্ধ)))

কঠিন সমজাতীয় বল

সূত্রের উৎপত্তি

আসুন বলটিকে পুরুত্বের পাতলা ডিস্কে ভাঙ্গা যাক dh, ঘূর্ণনের অক্ষের লম্ব। উচ্চতায় অবস্থিত এই জাতীয় ডিস্কের ব্যাসার্ধ জগোলকের কেন্দ্র থেকে, আমরা সূত্র ব্যবহার করে এটি খুঁজে পাই

r = R 2 − h 2। (\displaystyle r=(\sqrt (R^(2)-h^(2))))

এই জাতীয় ডিস্কের জড়তার ভর এবং মুহূর্ত হবে

d m = ρ d V = ρ ⋅ π r 2 d h ; (\displaystyle dm=\rho dV=\rho \cdot \pi r^(2)dh;) d J = 1 2 r 2 d m = 1 2 π ρ 4 d h = 1 2 π ρ (R 2 − h 2) 2 d h = 1 2 π ρ (R 4 − 2 R 2 h 2 + h 4) d h . (\displaystyle dJ=(\frac (1)(2))r^(2)dm=(\frac (1)(2))\pi \rho r^(4)dh=(\frac (1)( 2))\pi \rho \left(R^(2)-h^(2)\right)^(2)dh=(\frac (1)(2))\pi \rho \left(R^( 4)-2R^(2)h^(2)+h^(4)\right)dh।)

আমরা একীকরণের মাধ্যমে বলের জড়তার মুহূর্তটি খুঁজে পাই:

J = ∫ − R R d J = 2 ∫ 0 R d J = π ρ ∫ 0 R (R 4 − 2 R 2 h 2 + h 4) d h = = π ρ (R 4 h − 2 3 R 2 h 3 + 1 5 h 5) | 0 R = π ρ (R 5 − 2 3 R 5 + 1 5 R 5) = 8 15 π ρ R 5 = = (4 3 π R 3 ρ) ⋅ 2 5 R 2 = 2 5 m R 2 । (\displaystyle (\begin(aligned)J&=\int _(-R)^(R)dJ=2\int _(0)^(R)dJ=\pi \rho \int _(0)^(R )\left(R^(4)-2R^(2)h^(2)+h^(4)\right)dh=\\&=\pi \rho \left.\left(R^(4) h-(\frac (2)(3))R^(2)h^(3)+(\frac (1)(5))h^(5)\right)\right|_(0)^( R)=\pi \rho \left(R^(5)-(\frac (2)(3))R^(5)+(\frac (1)(5))R^(5)\ডান) =(\frac (8)(15))\pi \rho R^(5)=\\&=\left((\frac (4)(3))\pi R^(3)\rho \ ডান) \cdot (\frac (2)(5))R^(2)=(\frac (2)(5))mR^(2)।\end(সারিবদ্ধ)))

পাতলা দেয়ালযুক্ত গোলক

সূত্রের উৎপত্তি

এটি বের করার জন্য, আমরা ব্যাসার্ধের একটি সমজাতীয় বলের জড়তার মুহুর্তের সূত্রটি ব্যবহার করি আর :

J 0 = 2 5 M R 2 = 8 15 π ρ R 5। (\displaystyle J_(0)=(\frac (2)(5))MR^(2)=(\frac (8)(15))\pi \rho R^(5))

আসুন আমরা হিসাব করি যে বলের জড়তার মুহূর্ত কতটা পরিবর্তিত হবে যদি, একটি ধ্রুবক ঘনত্ব ρ, এর ব্যাসার্ধ একটি অসীম পরিমাণে বৃদ্ধি পায় ডাঃ .

J = d J 0 d R d R = d d R (8 15 π ρ R 5) d R = = 8 3 π ρ R 4 d R = (ρ ⋅ 4 π R 2 d R) 2 3 R 2 = 2 3 m R 2। (\displaystyle (\begin(aligned)J&=(\frac (dJ_(0))(dR))dR=(\frac (d)(dR))\left((\frac (8)(15))\ pi \rho R^(5)\right)dR=\\&=(\frac (8)(3))\pi \rho R^(4)dR=\left(\rho \cdot 4\pi R^ (2)dR\right)(\frac (2)(3))R^(2)=(\frac (2)(3))mR^(2)।\end(সারিবদ্ধ)))

পাতলা রড (অক্ষ কেন্দ্রের মধ্য দিয়ে যায়)

সূত্রের উৎপত্তি

এর রডটি দৈর্ঘ্যের ছোট ছোট টুকরো টুকরো করা যাক ডাঃ. এই ধরনের একটি খণ্ডের জড়তার ভর এবং মুহূর্ত সমান

d m = m d r l ; d J = r 2 d m = m r 2 d r l . (\displaystyle dm=(\frac (mdr)(l));\qquad dJ=r^(2)dm=(\frac (mr^(2)dr)(l)))

একত্রীকরণ, আমরা পেতে

J = ∫ − l / 2 l / 2 d J = 2 ∫ 0 l / 2 d J = 2 m l ∫ 0 l / 2 r 2 d r = 2 m l r 3 3 | 0 l / 2 = 2 m l l 3 24 = 1 12 m l 2 । (\displaystyle J=\int _(-l/2)^(l/2)dJ=2\int _(0)^(l/2)dJ=(\frac (2m)(l))\int _ (0)^(l/2)r^(2)dr=(\frac (2m)(l))\left.(\frac (r^(3))(3))\right|_(0) ^(l/2)=(\frac (2m)(l))(\frac (l^(3))(24))=(\frac (1)(12))ml^(2.)

পাতলা রড (অক্ষ শেষের মধ্য দিয়ে যায়)

সূত্রের উৎপত্তি

ঘূর্ণনের অক্ষ যখন রডের মাঝখান থেকে শেষ পর্যন্ত চলে যায়, তখন রডের মাধ্যাকর্ষণ কেন্দ্রটি অক্ষের সাপেক্ষে দূরত্বে চলে যায়। l ⁄ 2. স্টেইনারের উপপাদ্য অনুসারে, জড়তার নতুন মুহূর্ত সমান হবে

J = J 0 + m r 2 = J 0 + m (l 2) 2 = 1 12 m l 2 + 1 4 m l 2 = 1 3 m l 2 । (\displaystyle J=J_(0)+mr^(2)=J_(0)+m\left((\frac (l)(2))\right)^(2)=(\frac (1)( 12))ml^(2)+(\frac (1)(4))ml^(2)=(\frac (1)(3))ml^(2.)

গ্রহ এবং উপগ্রহের জড়তার মাত্রাহীন মুহূর্ত

গ্রহ এবং তাদের উপগ্রহের অভ্যন্তরীণ গঠন অধ্যয়নের জন্য তাদের জড়তার মাত্রাহীন মুহূর্তগুলি অত্যন্ত গুরুত্বপূর্ণ। ব্যাসার্ধের একটি শরীরের জড়তার মাত্রাহীন মুহূর্ত rএবং ভর মিদূরত্বে অবস্থিত ঘূর্ণনের একটি নির্দিষ্ট অক্ষের সাপেক্ষে একই ভরের একটি বস্তুগত বিন্দুর জড়তার মুহূর্ত এবং ঘূর্ণনের অক্ষের সাথে তার জড়তার মুহুর্তের অনুপাতের সমান r(সমান জনাব 2)। এই মান গভীরতার উপর ভরের বন্টন প্রতিফলিত করে। গ্রহ এবং উপগ্রহের কাছাকাছি এটি পরিমাপ করার পদ্ধতিগুলির মধ্যে একটি হল প্রদত্ত গ্রহ বা উপগ্রহের কাছাকাছি উড়ন্ত একটি AMS দ্বারা প্রেরিত রেডিও সংকেতের ডপলার স্থানান্তর নির্ধারণ করা। একটি পাতলা দেয়ালযুক্ত গোলকের জন্য, জড়তার মাত্রাহীন মুহূর্ত হল 2/3 (~0.67), একটি সমজাতীয় বলের জন্য এটি 0.4 এবং সাধারণভাবে, শরীরের ভর যত ছোট হবে তার কেন্দ্রে ঘনীভূত হবে। উদাহরণস্বরূপ, চাঁদে 0.4 (0.391 এর সমান) এর কাছাকাছি জড়তার একটি মাত্রাহীন মুহূর্ত রয়েছে, তাই এটি অনুমান করা হয় যে এটি তুলনামূলকভাবে সমজাতীয়, এর ঘনত্ব গভীরতার সাথে সামান্য পরিবর্তিত হয়। পৃথিবীর জড়তার মাত্রাহীন মুহূর্ত একটি সমজাতীয় বলের চেয়ে কম (সমান 0.335), যা একটি ঘন কোরের অস্তিত্বের পক্ষে একটি যুক্তি।

জড়তার কেন্দ্রাতিগ মুহূর্ত

একটি আয়তক্ষেত্রাকার কার্টেসিয়ান স্থানাঙ্ক ব্যবস্থার অক্ষের সাথে সম্পর্কিত একটি দেহের জড়তার কেন্দ্রাতিগ মুহূর্তগুলি নিম্নলিখিত পরিমাণগুলি:

J x y = ∫ (m) x y d m = ∫ (V) x y ρ d V , (\displaystyle J_(xy)=\int \সীমা _((m))xydm=\int \সীমা _((V))xy\ rho dV,) J x z = ∫ (m) x z d m = ∫ (V) x z ρ d V , (\displaystyle J_(xz)=\int \সীমা _((m))xzdm=\int \সীমা _((V))xz\ rho dV,) J y z = ∫ (m) y z d m = ∫ (V) y z ρ d V , (\displaystyle J_(yz)=\int \সীমা _((m))yzdm=\int \সীমা _((V))yz\ rho dV,)

কোথায় এক্স , yএবং z- আয়তন সহ একটি ছোট শরীরের উপাদানের স্থানাঙ্ক dV, ঘনত্ব ρ এবং ভর dm .

OX অক্ষ বলা হয় শরীরের জড়তার প্রধান অক্ষ, যদি জড়তা কেন্দ্রাতিগ মুহূর্ত জে xyএবং জে xzএকই সাথে শূন্যের সমান। শরীরের প্রতিটি বিন্দু দিয়ে জড়তার তিনটি প্রধান অক্ষ টানা যায়। এই অক্ষগুলি একে অপরের সাথে পারস্পরিকভাবে লম্ব। শরীরের জড়তা মুহূর্তএকটি নির্বিচারে বিন্দুতে আঁকা জড়তার তিনটি প্রধান অক্ষের সাথে সম্পর্কিত ওমৃতদেহ বলা হয় জড়তার প্রধান মুহূর্তএই শরীরের.

দেহের ভর কেন্দ্রের মধ্য দিয়ে যাওয়া জড়তার প্রধান অক্ষগুলিকে বলা হয় শরীরের জড়তার প্রধান কেন্দ্রীয় অক্ষ, এবং এই অক্ষ সম্পর্কে জড়তা মুহূর্ত হল এটি জড়তার প্রধান কেন্দ্রীয় মুহূর্ত. একটি সমজাতীয় দেহের প্রতিসাম্যের অক্ষ সর্বদা তার জড়তার প্রধান কেন্দ্রীয় অক্ষগুলির মধ্যে একটি।

জড়তার জ্যামিতিক মুহূর্ত

আয়তনের জড়তার জ্যামিতিক মুহূর্ত

J V a = ∫ (V) r 2 d V , (\displaystyle J_(Va)=\int \সীমা _((V))r^(2)dV,)

যেখানে, আগের মতো r- উপাদান থেকে দূরত্ব dVঅক্ষে ক .

এলাকার জড়তার জ্যামিতিক মুহূর্তঅক্ষের সাথে সম্পর্কিত - শরীরের একটি জ্যামিতিক বৈশিষ্ট্য, সূত্র দ্বারা প্রকাশ করা হয়:

J S a = ∫ (S) r 2 d S , (\displaystyle J_(Sa)=\int \সীমা _((S))r^(2)dS,)

যেখানে একীকরণ পৃষ্ঠের উপর সঞ্চালিত হয় এস, ক ডি এস- এই পৃষ্ঠের উপাদান।

মাত্রা জেএসএ- চতুর্থ শক্তি থেকে দৈর্ঘ্য ( d i m J S a = L 4 (\displaystyle \mathrm (dim) J_(Sa)=\mathrm (L^(4)) )), যথাক্রমে, পরিমাপের SI একক হল 4। নির্মাণ গণনা, সাহিত্য এবং ঘূর্ণিত ধাতু ভাণ্ডার মধ্যে, এটি প্রায়ই সেমি 4 নির্দেশিত হয়।

বিভাগের প্রতিরোধের মুহূর্তটি এলাকার জড়তার জ্যামিতিক মুহূর্তের মাধ্যমে প্রকাশ করা হয়:

W = J S a r m a x। (\displaystyle W=(\frac (J_(Sa))(r_(সর্বোচ্চ))))।

এখানে r সর্বোচ্চ- পৃষ্ঠ থেকে অক্ষের সর্বোচ্চ দূরত্ব।

কিছু পরিসংখ্যানের ক্ষেত্রফলের জড়তা জ্যামিতিক মুহূর্ত
আয়তক্ষেত্রের উচ্চতা h (\ প্রদর্শনশৈলী h)এবং প্রস্থ b (\ প্রদর্শনশৈলী খ):	J y = b h 3 12 (\displaystyle J_(y)=(\frac (bh^(3))(12))) J z = h b 3 12 (\displaystyle J_(z)=(\frac (hb^(3))(12)))
বাহ্যিক কনট্যুর বরাবর উচ্চতা এবং প্রস্থ সহ আয়তক্ষেত্রাকার বক্স বিভাগ H (\displaystyle H)এবং বি (\ ডিসপ্লেস্টাইল বি), এবং অভ্যন্তরীণ জন্য h (\ প্রদর্শনশৈলী h)এবং b (\ প্রদর্শনশৈলী খ)যথাক্রমে	J z = B H 3 12 − b h 3 12 = 1 12 (B H 3 − b h 3) (\displaystyle J_(z)=(\frac (BH^(3))(12))-(\frac (bh^( 3))(12))=(\frac (1)(12))(BH^(3)-bh^(3))) J y = H B 3 12 − h b 3 12 = 1 12 (H B 3 − h b 3) (\displaystyle J_(y)=(\frac (HB^(3))(12))-(\frac (hb^( 3))(12))=(\frac (1)(12))(HB^(3)-hb^(3)))
বৃত্তের ব্যাস ডি (\ ডিসপ্লেস্টাইল ডি)	J y = J z = π d 4 64 (\displaystyle J_(y)=J_(z)=(\frac (\pi d^(4))(64)))

সমতল আপেক্ষিক জড়তা মুহূর্ত

একটি নির্দিষ্ট সমতলের সাপেক্ষে একটি অনমনীয় দেহের জড়তার মুহূর্ত হল একটি স্কেলার পরিমাণ যা এই বিন্দু থেকে প্রশ্নে সমতল পর্যন্ত দূরত্বের বর্গ দ্বারা শরীরের প্রতিটি বিন্দুর ভরের গুণফলের সমষ্টির সমান।

যদি একটি নির্বিচারে পয়েন্ট মাধ্যমে O (\displaystyle O)স্থানাঙ্ক অক্ষ আঁকুন x, y, z (\displaystyle x,y,z), তারপর স্থানাঙ্ক সমতল আপেক্ষিক জড়তা মুহূর্ত x O y (\ ডিসপ্লেস্টাইল xOy), y O z (\ ডিসপ্লেস্টাইল yOz)এবং z O x (\ ডিসপ্লেস্টাইল zOx)সূত্র দ্বারা প্রকাশ করা হবে:

J x O y = ∑ i = 1 n m i z i 2 , (\displaystyle J_(xOy)=\sum _(i=1)^(n)m_(i)z_(i)^(2)\ ,) J y O z = ∑ i = 1 n m i x i 2 , (\displaystyle J_(yOz)=\sum _(i=1)^(n)m_(i)x_(i)^(2)\ ,) J z O x = ∑ i = 1 n m i y i 2। (\displaystyle J_(zOx)=\sum _(i=1)^(n)m_(i)y_(i)^(2)\ .)

একটি কঠিন শরীরের ক্ষেত্রে, সমষ্টি একীকরণ দ্বারা প্রতিস্থাপিত হয়।

জড়তার কেন্দ্রীয় মুহূর্ত

জড়তার কেন্দ্রীয় মুহূর্ত (O বিন্দু সম্পর্কে জড়তার মুহূর্ত, মেরু সম্পর্কে জড়তার মুহূর্ত, জড়তার মেরু মুহূর্ত) J O (\ প্রদর্শনশৈলী J_(O))অভিব্যক্তি দ্বারা নির্ধারিত পরিমাণ হল:

J a = ∫ (m) r 2 d m = ∫ (V) ρ r 2 d V , (\displaystyle J_(a)=\int \সীমা _((m))r^(2)dm=\int \সীমা _((V))\rho r^(2)dV,)

জড়তার কেন্দ্রীয় মুহূর্তকে জড়তার প্রধান অক্ষীয় মুহুর্তের পরিপ্রেক্ষিতে প্রকাশ করা যেতে পারে, সেইসাথে সমতল সম্পর্কে জড়তার মুহূর্তগুলির পরিপ্রেক্ষিতে:

J O = 1 2 (J x + J y + J z), (\displaystyle J_(O)=(\frac (1)(2))\left(J_(x)+J_(y)+J_(z) \ঠিক),) J O = J x O y + J y O z + J x O z। (\displaystyle J_(O)=J_(xOy)+J_(yOz)+J_(xOz)।

জড়তার টেনসর এবং জড়তার উপবৃত্তাকার

ভরের কেন্দ্রের মধ্য দিয়ে যাওয়া একটি নির্বিচারে অক্ষের সাপেক্ষে একটি দেহের জড়তার মুহূর্ত এবং ইউনিট ভেক্টর দ্বারা নির্দিষ্ট একটি দিক রয়েছে s → = ‖ s x , s y , s z ‖ T , | s → | = 1 (\displaystyle (\vec(s))=\left\Vert s_(x),s_(y),s_(z)\right\Vert ^(T),\left\vert (\vec(s) )\right\vert =1), একটি চতুর্মুখী (দ্বিলিনিয়ার) আকারে উপস্থাপন করা যেতে পারে:

I s = s → T ⋅ J^ ⋅ s → , (\displaystyle I_(s)=(\vec(s))^(T)\cdot (\hat (J))\cdot (\vec (s)) ,\qquad) (1)

জড়তা টেনসর কোথায়। জড়তা টেনসর ম্যাট্রিক্স প্রতিসম এবং এর মাত্রা রয়েছে 3 × 3 (\displaystyle 3\times 3)এবং কেন্দ্রাতিগ মুহূর্তের উপাদান নিয়ে গঠিত:

J ^ = ‖ J x x − J x y − J x z − J y x J y y − J y z − J z x − J z y J z z ‖ , (\displaystyle (\hat (J))=\left\Vert (\begin(array) )(ccc)J_(xx)&-J_(xy)&-J_(xz)\\-J_(yx)&J_(yy)&-J_(yz)\\-J_(zx)&-J_(zy) &J_(zz)\end(অ্যারে))\right\Vert ,) J x y = J y x , J x z = J z x , J z y = J y z , (\displaystyle J_(xy)=J_(yx), \quad J_(xz)=J_(zx), \quad J_(zy)= J_(yz),\quad )J x x = ∫ (m) (y 2 + z 2) d m , J y y = ∫ (m) (x 2 + z 2) d m , J z z = ∫ (m) (x 2 + y 2) d m। (\displaystyle J_(xx)=\int \সীমা _((m))(y^(2)+z^(2))dm,\quad J_(yy)=\int \সীমা _(m)) (x^(2)+z^(2))dm, \quad J_(zz)=\int \সীমা _((m))(x^(2)+y^(2))dm।)

উপযুক্ত স্থানাঙ্ক ব্যবস্থা নির্বাচন করে, জড়তা টেনসর ম্যাট্রিক্সকে তির্যক আকারে হ্রাস করা যেতে পারে। এটি করার জন্য, আপনাকে টেনসর ম্যাট্রিক্সের জন্য eigenvalue সমস্যাটি সমাধান করতে হবে J ^ (\ ডিসপ্লেস্টাইল (\ হ্যাট (জে))):

J^d = Q ^ T ⋅ J ^ ⋅ Q ^ , (\displaystyle (\hat (J))_(d)=(\hat (Q))^(T)\cdot (\hat (J))\ cdot (\ হ্যাট (Q)),) J^d = ‖ J X 0 0 0 J Y 0 0 J Z ‖ , (\displaystyle (\hat (J))_(d)=\left\Vert (\begin(array)(ccc)J_(X)&0&0\ \0&J_(Y)&0\\0&0&J_(Z)\end(array))\right\Vert ,)

কোথায় Q ^ (\ ডিসপ্লেস্টাইল (\ হ্যাট (Q)))- জড়তা টেনসরের নিজস্ব ভিত্তিতে রূপান্তরের অর্থোগোনাল ম্যাট্রিক্স। সঠিক ভিত্তিতে, স্থানাঙ্ক অক্ষগুলি জড়তা টেনসরের প্রধান অক্ষ বরাবর নির্দেশিত হয় এবং জড়তা টেনসর উপবৃত্তাকার প্রধান আধা-অক্ষগুলির সাথেও মিলিত হয়। পরিমাণ J X , J Y , J Z (\ displaystyle J_(X), J_(Y), J_(Z))- জড়তার প্রধান মুহূর্ত। অভিব্যক্তি (1) এর নিজস্ব স্থানাঙ্ক ব্যবস্থায় ফর্ম রয়েছে:

I s = J X ⋅ s x 2 + J Y ⋅ s y 2 + J Z ⋅ s z 2 , (\displaystyle I_(s)=J_(X)\cdot s_(x)^(2)+J_(Y)\cdot s_(y )^(2)+J_(Z)\cdot s_(z)^(2),)

যেখান থেকে আমরা তার নিজস্ব স্থানাঙ্কে উপবৃত্তাকার সমীকরণ পাই। সমীকরণের উভয় পক্ষকে দ্বারা ভাগ করা আমি (\displaystyle I_(গুলি))

(s x I s) 2 ⋅ J X + (s y I s) 2 ⋅ J Y + (s z I s) 2 ⋅ J Z = 1 (\ displaystyle \left((s_(x) \over (\sqrt (I_(s))) ))\right)^(2)\cdot J_(X)+\left((s_(y)\over (\sqrt (I_(s))))\right)^(2)\cdot J_(Y) +\left((s_(z) \over (\sqrt (I_(s))))\right)^(2)\cdot J_(Z)=1)

এবং প্রতিস্থাপন করা:

ξ = s x I s , η = s y I s , ζ = s z I s , (\displaystyle \xi =(s_(x) \over (\sqrt (I_(s))),\eta =(s_(y) ) \over (\sqrt (I_(s)))), \zeta =(s_(z) \over (\sqrt (I_(s)))),)

আমরা স্থানাঙ্কে উপবৃত্তাকার সমীকরণের ক্যানোনিকাল ফর্ম পাই ξ η ζ (\displaystyle \xi \eta \zeta ):

ξ 2 ⋅ J X + η 2 ⋅ J Y + ζ 2 ⋅ J Z = 1. (\displaystyle \xi ^(2)\cdot J_(X)+\eta ^(2)\cdot J_(Y)+\zeta ^( 2)\cdot J_(Z)=1।)

উপবৃত্তাকার কেন্দ্র থেকে একটি নির্দিষ্ট বিন্দুর দূরত্ব উপবৃত্তাকার কেন্দ্র এবং এই বিন্দুর মধ্য দিয়ে যাওয়া একটি সরল রেখা বরাবর শরীরের জড়তার মুহূর্তের মানের সাথে সম্পর্কিত।

জড়তার অক্ষীয় মুহূর্ত হল প্রাথমিক ক্ষেত্রগুলির পণ্যগুলির সম্পূর্ণ অংশ এবং বিবেচনাধীন বিভাগের সমতলে থাকা একটি নির্দিষ্ট অক্ষের দূরত্বের বর্গক্ষেত্রের সমষ্টি। জড়তার অক্ষীয় মুহূর্তের মাত্রা বাঁকানো বিকৃতি প্রতিরোধ করার মরীচির ক্ষমতাকে চিহ্নিত করে।

J - জড়তার অক্ষীয় মুহূর্ত

জে x =

J y =

প্রতিরোধের অক্ষীয় মুহূর্তনিরপেক্ষ অক্ষ থেকে সবচেয়ে দূরে অংশের তন্তুগুলির দূরত্বের সাথে জড়তার অক্ষীয় মুহুর্তের অনুপাতকে বলা হয়।

W - প্রতিরোধের অক্ষীয় মুহূর্ত।

W x = , W y =

জড়তার পোলার মুহূর্তবলা হয়, পুরো অংশের উপর নেওয়া, বিভাগটির মাধ্যাকর্ষণ কেন্দ্রে তাদের দূরত্বের বর্গ দ্বারা প্রাথমিক এলাকার গুণফলের যোগফল। স্থানাঙ্ক অক্ষ ছেদ না হওয়া পর্যন্ত।

জড়তার মেরু মুহূর্তটি টর্সনাল বিকৃতি প্রতিরোধ করার একটি অংশের ক্ষমতাকে চিহ্নিত করে।

জড়তার মেরু মুহূর্ত।

= .

প্রতিরোধের পোলার মুহূর্তবিবেচনাধীন বিভাগের মাধ্যাকর্ষণ কেন্দ্র থেকে বিভাগের সবচেয়ে দূরবর্তী বিন্দুর দূরত্বের সাথে জড়তার মেরু মুহুর্তের অনুপাত।

প্রতিরোধের পোলার মুহূর্ত

1. আয়তক্ষেত্রাকার বিভাগ।

J y = (mm 4), J x = (mm 4)

W x = (mm 3), W y = (মিমি 3)

2. বৃত্তাকার বিভাগ

J x = J y = (mm 4), = (mm 4)

W y = W x = (মিমি 3), = (মিমি 3)

3. রিং বিভাগ

J x = J y = - = (মিমি 4) , α=d/D

W y = W x = 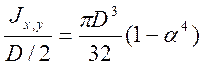(মিমি 3)

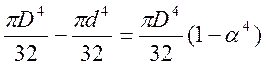= (মিমি 4)

=(মিমি 3)

4. বক্স বিভাগ।

জে x = =(মিমি 4)

J y = =(মিমি 4)

W x = (মিমি 3)

W y = (মিমি 3)

অভিন্ন স্ট্রেস বিতরণ সহ অংশগুলির গণনা।

এই ধরণের অংশগুলির মধ্যে রয়েছে চোখ এবং পিনের সাথে রড, সেইসাথে হাইড্রোলিক এবং বায়ুসংক্রান্ত সিলিন্ডার এবং অন্যান্য চাপের জাহাজ, দ্বিধাতু উপাদান (তাপীয় রিলে)।

ট্র্যাকশন গণনা।

1) রডের উপর প্রসার্য বল F প্রয়োগ করা হয়।

ট্র্যাকশন রড একটি অনুদৈর্ঘ্য লোড উপলব্ধি করে, যার প্রভাবে এটি প্রসারিত হয়। এই ক্ষেত্রে, পরম প্রসারণের মাত্রা প্রসারিত হুকের আইন দ্বারা নির্ধারিত হয়:

σ р =Eε। , σ р =F/A, , σ р =F/A<=[ σ р ]= σ T / n -

প্রসার্য ট্র্যাকশন শক্তি অবস্থা, (A=H*B, A=)।

আঙুলের সাথে মিথস্ক্রিয়া ফলস্বরূপ, লগগুলি যোগাযোগ এলাকার উপর চূর্ণ হয়।

নিষ্পেষণ শক্তি শর্ত:

σ সেমি = F/A<=[σ см ]= 2σ T / n , A=d*b.

চোখের সাথে মিথস্ক্রিয়া থেকে শিয়ারের জন্য আঙ্গুলগুলি গণনা করা হয়:

τ av =F/A<=[τ ср ]= 0,5σ T / n; A=*i, i - количество платежей среза (i=2).

2) কমপ্রেসিভ ফোর্স F2 রডে প্রয়োগ করা হয়।

থ্রাস্ট রড কম্প্রেশনে কাজ করে। পরম সংক্ষিপ্তকরণের মাত্রাও হুকের আইন দ্বারা নির্ধারিত হয়:

σ c =F/A<=[σ с ]=[σ р ]=σ T / n. – Для коротких стержней тяги.

লম্বা রড - যখন দৈর্ঘ্য ক্রস-বিভাগীয় মাত্রার 3 গুণ অতিক্রম করে। এখানে রড রডের তাত্ক্ষণিক বাঁকানোর সম্ভাবনা রয়েছে।

σ с =<=[σ с ]=[σ р ]=σ T / n, φ – коэффициент продольного изгиба, величина табличная – зависит от материала, гибкости стержня и характера закрепления концов стержня.

আইলেট এবং আঙ্গুলগুলি আগের হিসাবের অনুরূপভাবে গণনা করা হয়।

পাতলা দেয়ালযুক্ত পাত্রের গণনা।

পাতলা দেয়ালযুক্ত জাহাজের মধ্যে রয়েছে হাইড্রোলিক এবং বায়ুসংক্রান্ত সিলিন্ডার, রিসিভার, পাইপলাইন ইত্যাদি।

আকৃতির উপর নির্ভর করে, পাত্রগুলি হল:

নলাকার (হাইড্রোলিক এবং বায়ুসংক্রান্ত সিলিন্ডার, কিছু ধরণের রিসিভার, পাইপলাইন);

গোলাকার (কিছু ধরণের রিসিভার, বটম এবং নলাকার জাহাজের কভার, ঝিল্লি ইত্যাদি);

টরাস (পাইপলাইনের বক্ররেখার অংশ, পয়েন্টার প্রেসার গেজের সংবেদনশীল উপাদান)।

সমস্ত জাহাজে, তরল বা গ্যাসের অভ্যন্তরীণ শক্তির প্রভাবে, অনুদৈর্ঘ্য এবং ক্রস বিভাগে দেয়ালে চাপ দেখা দেয়।

নলাকার জাহাজ।

একটি পাতলা নলাকার শেল অভ্যন্তরীণ চাপ P দিয়ে লোড করা হয়। - সিলিন্ডারের ক্রস বিভাগ হিসাবে গণনা করা হয়।

টরাস জাহাজ।

এগুলিকে বাঁকা নলাকার হিসাবে গণনা করা হয়।

15.10.04 তাপমাত্রা পরিবর্তনের সময় উদ্ভূত চাপের গণনা।

যখন তাপমাত্রা ওঠানামা করে, তখন অনমনীয় সমর্থনের মধ্যে স্থির একটি অংশ কম্প্রেসিভ বা প্রসার্য বিকৃতি অনুভব করে। যখন তাপমাত্রা Dt দ্বারা বৃদ্ধি পায় (হ্রাস), রডটি অবশ্যই পরম প্রসারণের পরিমাণ (খাটো করা) দ্বারা দীর্ঘায়িত (খাটো করা) আবশ্যক:

ডিl= কt* l* ডিt, যেখানে a t হল রৈখিক সম্প্রসারণের তাপমাত্রা সহগ (স্টিলের জন্য 12*10 -6 °C -1), তারপর পরম প্রসারণের মান (সংক্ষিপ্তকরণ): Δε t = Δ l টি / l = α টি* ডিt, কিন্তু যেহেতু যদি রডটি কঠোরভাবে স্থির করা হয় তবে এটি দীর্ঘায়িত (খাটো করা যায় না), তাই এর উপাদানগুলিতে কম্প্রেশন (টেনশন) চাপ দেখা দেবে, যার মানগুলি হুকের আইন দ্বারা নির্ধারিত হয়:

σ с,р =E*ε t =E*α t *Δt।

একটি মরীচির অংশের জড়তার মুহূর্তগুলি (বিম, রড), ক্রস-বিভাগীয় এলাকার মতো, শক্তি গণনার সাথে জড়িত উপাদানটির প্রধান জ্যামিতিক বৈশিষ্ট্যগুলির মধ্যে একটি। আমি আপনাকে মনে করিয়ে দিই যে শক্তি উপাদানের শক্তিতে একটি মরীচি এমন একটি উপাদান যার মাত্রাগুলির একটি হল দৈর্ঘ্য...

অন্য দুটি থেকে উল্লেখযোগ্যভাবে বড় - প্রস্থ এবং উচ্চতা। এটি শেষ দুটি সামগ্রিক মাত্রা এবং আকৃতি যা উপাদানের বৈশিষ্ট্য সহ, মরীচির শক্তি বৈশিষ্ট্যকে প্রভাবিত করে।

একটি বিভাগের জড়তার জ্যামিতিক মুহূর্তগুলিকে দেহের জড়তার মুহুর্তগুলির সাথে বিভ্রান্ত করা উচিত নয়, যদিও তাদের অর্থ খুব মিল। একটি নির্দিষ্ট অক্ষের চারপাশে একটি শরীরের জড়তার মুহূর্ত হল পণ্যগুলির যোগফল ভরঅক্ষ থেকে এই বিন্দুতে বর্গ দূরত্ব দ্বারা শরীরের প্রাথমিক "ভলিউম" বিন্দু। একটি বিভাগের জড়তার মুহূর্ত (সমতল চিত্র) হল পণ্যগুলির যোগফল এলাকাএই বিভাগের প্রাথমিক "সমতল" পয়েন্টগুলি বিবেচনাধীন অক্ষ থেকে তাদের থেকে বর্গ দূরত্ব দ্বারা।

জড়তার অক্ষীয় মুহূর্ত, সেইসাথে জড়তার ব্যাসার্ধ এবং প্রায় ত্রিশটি প্রাথমিক পরিসংখ্যানের প্রতিরোধের মুহূর্তগুলি গণনা করার সূত্রগুলি, যেখান থেকে একটি মরীচির যে কোনও ক্রস-সেকশন তৈরি করা যেতে পারে, "উপাদানের প্রতিরোধের উপাদান" বিভাগে নেওয়া যেতে পারে। অধ্যায় নং 1 "সাধারণ প্রযুক্তিগত তথ্য" এর ভলিউম নং 1 "ডিজাইনারস হ্যান্ডবুক" মেকানিক্যাল ইঞ্জিনিয়ার" V.I. অনুরিভ। এই তিন খণ্ডের রেফারেন্স বই, যা যান্ত্রিক প্রকৌশলীদের কয়েক প্রজন্মের জন্য প্রধান রেফারেন্স বই এবং প্রায় দশটি পুনর্মুদ্রণের মধ্য দিয়ে গেছে, এটি আজও চাহিদা এবং প্রাসঙ্গিক হিসাবে অব্যাহত রয়েছে। আমি মনে করি প্রতিটি প্রকৌশলীর এটি থাকা উচিত, বিশেষ করে যেহেতু এটি ইন্টারনেটে খুঁজে পাওয়া কোন সমস্যা নয়। অবশ্যই, আমরা যে সূত্রগুলিতে আগ্রহী তা অন্যান্য রেফারেন্স সাহিত্যে পাওয়া যেতে পারে।

আই-বিম, চ্যানেল, কোণ, পাইপ এবং অন্যান্য ঘূর্ণিত এবং বাঁকানো প্রোফাইলগুলির জন্য, যা যান্ত্রিক প্রকৌশল এবং নির্মাণে ব্যাপকভাবে ব্যবহৃত হয়, জড়তার মুহূর্তগুলি সহ বিভাগগুলির জ্যামিতিক বৈশিষ্ট্যগুলি GOSTs, OSTs এবং অন্যান্য নিয়ন্ত্রক নথিতে পাওয়া যেতে পারে। যা তাদের উৎপাদন নিয়ন্ত্রণ করে।

দুই বা ততোধিক প্রাথমিক প্রোফাইলের সমন্বয়ে গঠিত বিম এবং রডগুলি ওজন এবং মাত্রার ক্ষেত্রে একটি একক প্রোফাইলের সাথে পর্যাপ্ত প্রতিস্থাপনের অনুপস্থিতিতে উপাদানগুলির শক্তি এবং দৃঢ়তা বাড়ানোর জন্য ব্যবহৃত হয়। অনুশীলনে, এগুলি জোড়া কোণ, দুই-শাখা কলাম, একটি শীট ফালা দিয়ে শক্তিশালী করা বেল্ট সহ বিম এবং অন্যান্য ক্ষেত্রে।

একটি যৌগিক বিভাগের জ্যামিতিক বৈশিষ্ট্য। এক্সেলে গণনা।

নিবন্ধে, আমরা একটি উদাহরণ হিসাবে বিবেচনা করেছি একটি যৌগিক চিত্র যা একটি ত্রিভুজ এবং একটি অর্ধবৃত্ত কাটআউট সহ একটি আয়তক্ষেত্র নিয়ে গঠিত। আসুন এই উদাহরণ দিয়ে চালিয়ে যাই। যদিও আপনি সম্ভবত অনুশীলনে এমন উদ্ভট ক্রস-সেকশন সহ একটি রশ্মি দেখতে পাবেন না, তবে এটি খুব জটিল এবং দৃষ্টান্তমূলক উদাহরণের জন্য আমাদের জন্য উপযুক্ত হবে!

MS Excel বা OOo Calc চালু করুন এবং শুরু করুন!

ব্লগ নিবন্ধে ব্যবহৃত স্প্রেডশীট বিন্যাস করার সাধারণ নিয়ম এখানে পাওয়া যাবে।

উপরে উল্লিখিত নিবন্ধ থেকে আমরা ইতিমধ্যেই মাধ্যাকর্ষণ কেন্দ্রগুলির স্থানাঙ্ক, ক্রস-বিভাগীয় উপাদানগুলির ক্ষেত্র এবং সমগ্র যৌগিক বিভাগের ক্ষেত্রফল জানি। এই নিবন্ধে আমরা আমাদের শুরু করা কাজ চালিয়ে যাব এবং অন্যান্য জ্যামিতিক বৈশিষ্ট্যগুলি গণনা করব।

প্রাথমিক তথ্য:

আইটেম 1 , 2 , 3 ফাইল থেকে কপি করুন এবং D3:F6 কোষের পরিসর পূরণ করুন।

4. আসুন তাদের নিজস্ব কেন্দ্রীয় অক্ষের সাথে সম্পর্কিত উপাদানগুলির জড়তার অক্ষীয় এবং কেন্দ্রাতিগ মুহূর্তগুলি গণনা করি Ixi , Iyi , Ixiyi cm4-এ, V.I-এর "মেকানিক্যাল ডিজাইনারদের হ্যান্ডবুক" থেকে সূত্র ব্যবহার করে অনুরিভা

ঘরে D7: =80*40^3/12/10000 =42,667

Ix1 = ক 1 *(খ1 ^3)/12

ঘরে D8: =40*80^3/12/10000 =170,667

Iy1 = b1 *(a1 ^3)/12

ঘরে D9: =0 =0,000

Ix1 y1 = 0 (অক্ষীয় প্রতিসাম্য সহ উপাদান)

ঘরে E7: =24*42^3/36/10000 =4,939

Ix2 = ক 2 *(জ 2 ^3)/36

ঘরে E8: =42*24^3/48/10000 =1,210

আই.ই2 = জ 2 *(ক 2 ^3)/48

ঘরে E9: =0 =0,000

Ix2 y2 = 0 (অক্ষীয় প্রতিসাম্য সহ উপাদান)

সেল F7 এ: =- (PI()/8*26^4-8/9/PI()*26^4)/10000=-5,016

Ix3 =- (π /8)*(r 3 ^4) — (8/(9* π ))*(r 3 ^4)

সেল F8-এ: =-PI()/8*26^4/10000 =-17,945

আই.ই3 =- (π /8)*(r 3 ^4)

ঘরে F9: =0 =0,000

Ix3 y3 = 0 (অক্ষীয় প্রতিসাম্য সহ উপাদান)

তৃতীয় উপাদানের জড়তার অক্ষীয় মুহূর্ত - অর্ধবৃত্ত - নেতিবাচক কারণ এটি একটি আয়তক্ষেত্রে একটি কাটআউট - একটি খালি স্থান!

জ্যামিতিক বৈশিষ্ট্যের গণনা:

আইটেম 5 , 6 , 7 ফাইল থেকে অনুলিপি করুন এবং সম্মিলিত কোষগুলি পূরণ করুন D11E11F11...D15E15F15।

8. আসুন আমরা মাধ্যাকর্ষণ কেন্দ্রের মধ্য দিয়ে আঁকা কেন্দ্রীয় অক্ষ x0 এবং y0 এর সাপেক্ষে বিভাগের জড়তার অক্ষীয় এবং কেন্দ্রাতিগ মুহূর্তগুলি গণনা করি Ix 0 , আই.ই 0 , Ix0 y0 cm4 এ

একত্রিত কক্ষে D16E16F16: =((D5-D15)^2*D6+(E5-D15)^2*E6+(F5-D15)^2*F6)/10000+D7+E7+F7=90,122

Ix0 = Σ ((yci — Yc )^2* ফাই )+ ΣIxi

একত্রিত কক্ষে D17E17F17: =((D4-D14)^2*D6+(E4-D14)^2*E6+(F4-D14)^2*F6)/10000+D8+E8+F8=159,678

আই.ই0 = Σ ((xci — Xc )^2* ফাই )+ ΣIyi

একত্রিত সেল D18E18F18-এ: =((D5-D15)*(D4-D14)*D6+(E5-D15)*(E4-D14)*E6+(F5-D15)*(F4-D14)*F6)/10000+D9+E9+F9=-50,372

Ix0y0 = Σ ((yci -Yc)*(xci -Xc)*Fi )+Σ Ixiyi

9. আসুন বিভাগটির জড়তার প্রধান কেন্দ্রীয় মুহূর্তগুলি গণনা করি IVএবং আইউ cm4 এ

একত্রিত কক্ষে D19E19F19: =($D$16+$D$17)/2+((($D$16-$D$17)/2)^2+$D$18^2)^0.5=186,111

Iv =(Ix0 +Iy0 )/2+(((Ix0 -Iy0 )/2)^2+Ix0y0 ^2)^0.5

একত্রিত কক্ষে D20E20F20: =($D$16+$D$17)/2- ((($D$16-$D$17)/2)^2+$D$18^2)^0.5=63,689

Iu =(Ix0 +Iy0 )/2- (((Ix0 -Iy0 )/2)^2+Ix0y0 ^2)^0.5

10. আসুন মূল অক্ষ v এর কেন্দ্রীয় অক্ষ x0 এর দিকে প্রবণতার কোণটি খুঁজে বের করি α ডিগ্রী মধ্যে

একত্রিত কক্ষে D21E21F21: =ATAN(D18/(D20-D16))/PI()*180=62,311

α =arctg (Ix0y0 /(Iu -Ix0 ))

11. এবং উপসংহারে, আমরা যৌগিক বিভাগের gyration এর রেডিআই গণনা করি ivএবং iuমিমি মধ্যে

মার্জ করা ঘরে D22E22F22: =(D19*10000/D11)^0.5 =26,540

iv =(IV / চ 0 )^0,5

মার্জ করা ঘরে D23E23F23: =(D20*10000/D11)^0.5 =15,526

iu =(আইউ / চ 0 )^0,5

কাজটি সম্পন্ন হয়েছে - তিনটি সাধারণ উপাদানের একটি যৌগিক অংশের জড়তা এবং ব্যাসার্ধের ব্যাসার্ধ গণনা করা হয়েছে! জড়তা উপবৃত্তাকার নির্মাণের জন্য সমস্ত প্রয়োজনীয় তথ্য প্রাপ্ত করা হয়েছে।

একটি গণনা প্রোগ্রাম সহ একটি এক্সেল ফাইল আপনাকে সহজেই দুটি বা তিনটি সাধারণ উপাদান সমন্বিত একটি মরীচির ক্রস বিভাগের জ্যামিতিক বৈশিষ্ট্যগুলির সম্পূর্ণ গণনা করতে দেয়। প্রয়োজনে, গণনা মডিউলের ক্ষমতাগুলিকে আরও বেশি সংখ্যক উপাদানে প্রসারিত করা সহজ।

জন্য গ্রহণ নতুন নিবন্ধ সম্পর্কে তথ্য এবং জন্য কাজের প্রোগ্রাম ফাইল ডাউনলোড করা হচ্ছে অনুগ্রহপূর্বক নিবন্ধন করুন প্রতিটি নিবন্ধের শেষে বা পৃষ্ঠার উপরের উইন্ডোতে অবস্থিত উইন্ডোতে ঘোষণার জন্য।

ভুলে যেও না নিশ্চিত করুন সদস্যতা লিঙ্কে ক্লিক করে একটি চিঠিতে যা অবিলম্বে নির্দিষ্ট মেইলে আপনার কাছে আসবে (ফোল্ডারে আসতে পারে « স্প্যাম » )!!!

আমি আগ্রহের সাথে আপনার মন্তব্য পড়ব, প্রিয় পাঠক!!! আপনার চিন্তা শেয়ার করুন!

আমি অনুরোধ করছি লেখকের কাজকে সম্মান করা গণনা প্রোগ্রামের সাথে ফাইলটি ডাউনলোড করুন সাবস্ক্রিপশনের পরে নিবন্ধ ঘোষণার জন্য!