Функцияның дара нүктелері және олардың классификациясы. Оқшауланған ерекше нүктелер. Қалдықтар және оларды есептеу формулалары

Екі автономды дифференциалдық теңдеулер жүйесімен сипатталған модельдер.

фазалық жазықтық. Фазалық портрет. изоклиндік әдіс. негізгі изоклиндер. Тұрақты күйдегі тұрақтылық. Сызықтық жүйелер. Негізгі нүкте түрлері: түйін, ершік, фокус, орталық. Мысалы: бірінші ретті химиялық реакциялар.

Биологиялық жүйелердің қасиеттерін сапалы модельдеу бойынша ең қызықты нәтижелер екі дифференциалдық теңдеулердің модельдерінде алынды, бұл әдісті пайдалана отырып, сапалы зерттеуге мүмкіндік береді. фазалық жазықтық. Жалпы түрдегі екі автономды қарапайым дифференциалдық теңдеулер жүйесін қарастырайық

(4.1)

P(x,y), Q(x,y)- кейбір облыста анықталған үздіксіз функциялар Гевклидтік жазықтық ( x,y- декарттық координаталар) және осы аймақта біріншіден төмен емес ретті үзіліссіз туындылары бар.

Аймақ Гшектеусіз немесе шектеулі болуы мүмкін. Айнымалылар болса x, yбелгілі бір биологиялық мағынаға ие (заттардың концентрациясы, түрлердің көптігі), көбінесе аумақ Гоң жарты жазықтықтың оң квадранты:

0 £ x< ¥ ,0 £ ж< ¥ .

Заттардың концентрациясы немесе түрлердің көптігі жоғарыдан ыдыстың көлемімен немесе тіршілік ету ортасының ауданымен шектелуі мүмкін. Сонда айнымалылар диапазоны келесі пішінге ие болады:

0 £ x< x 0 , 0 £ ж< y 0 .

Айнымалылар x, y(4.1) теңдеулер жүйесіне сәйкес уақыт бойынша өзгерту, жүйенің әрбір күйі айнымалы мәндер жұбына сәйкес келетіндей ( x, y).

Керісінше, әрбір айнымалы жұп үшін ( x, y) жүйенің белгілі бір күйіне сәйкес келеді.

Айнымалылардың мәндері сызылған координаталық осьтері бар жазықтықты қарастырайық x,y. Әрбір нүкте Мбұл жазықтық жүйенің белгілі бір күйіне сәйкес келеді. Мұндай жазықтық фазалық жазықтық деп аталады және жүйенің барлық күйлерінің жиынтығын бейнелейді. М(х, у) нүктесі бейнелеуші ​​немесе бейнелеуші ​​нүкте деп аталады.

Бастапқы уақытта рұқсат етіңіз t=t 0 нүкте координаталарын білдіреді М 0 (x(т 0), ж(т 0)). Уақыттың әрбір келесі сәтінде тбейнелеу нүктесі айнымалы мәндердегі өзгерістерге сәйкес қозғалады x(т), ж(т). Ұпайлар жинағы М(x(т), ж(т)) уақыт бойынша айнымалылардың өзгеру процесіндегі орны жүйе күйлеріне сәйкес келетін фазалық жазықтықта x(t), у(т)(4.1) теңдеулері бойынша шақырылады фазалық траектория.

Айнымалылардың әртүрлі бастапқы мәндері үшін фазалық траекториялар жиынтығы жүйенің оңай көрінетін «портретін» береді. Ғимарат фазалық портретайнымалылардың өзгеру сипаты туралы қорытынды жасауға мүмкіндік береді x, yбастапқы теңдеулер жүйесінің аналитикалық шешімдерін білмей(4.1).

Фазалық портретті бейнелеу үшін фазалық жазықтықтың әрбір нүктесінде жүйелік траекториялар үшін бағыттардың векторлық өрісін салу қажет. Артықшылықты көрсету арқылыD t>0,сәйкес өсімдерді аламыз D xЖәне D жөрнектерден:

D x=P(x,y)D т,

D y=Q(x,y)D т.

векторлық бағыт dy/dxнүктесінде ( x, y) функциялардың таңбасына байланысты P(x, y), Q(x, y)және кесте арқылы берілуі мүмкін:

P(x,y)>0,Q(x,y)>0
P(x,y)<0,Q(x,y)<0
P(x,y)>0,Q(x,y)<0
P(x,y)<0,Q(x,y)>0

.(4.2)

Осы теңдеудің шешімі y=y(x, c), немесе жанама түрде Ф(x,y)=c,қайда бастапинтегралдау константасы болып табылады, (4.2) - теңдеуінің интегралдық қисықтарының тобын береді. фазалық траекторияларжүйе (4.1) жазықтықта x, y.

Изоклиндік әдіс

Фазалық портретті құру үшін пайдаланылады изоклиндік әдісинтегралдық қисықтарды белгілі бір бұрышпен қиып өтетін фазалық жазықтықта түзулер сызылады. Изоклиндік теңдеуді (4.2) алу оңай. қояйық

қайда БІРАҚ– белгілі бір тұрақты. Мағынасы БІРАҚфазалық траекторияға жанаманың көлбеуінің тангенсін көрсетеді және мынадан мәндерді қабылдай алады -¥ + дейін ¥ . Оның орнына ауыстыру dy/dx(4.2) саны БІРАҚизоклиндік теңдеуін аламыз:

.(4.3)

(4.3) теңдеу жазықтықтың әрбір нүктесінде сәйкес интегралдық қисыққа жалғыз жанаманы анықтайды. P(x,y)= 0, Q (x,y) = 0 , онда жанаманың бағыты белгісіз болады, өйткені туындының мәні белгісіз болады:

.

Бұл нүкте барлық изоклиндердің қиылысу нүктесі - ерекше нүкте.Ол бір уақытта айнымалылардың уақыт бойынша туындыларын жояды xЖәне ж.

Осылайша, сингулярлық нүктеде айнымалылардың өзгеру жылдамдығы нөлге тең болады. Сондықтан фазалық траекториялардың дифференциалдық теңдеулерінің сингулярлық нүктесі (4.2) сәйкес келеді. жүйенің стационарлық жағдайы(4.1) және оның координаталары айнымалылардың стационарлық мәндері болып табылады x, y.

Ерекше қызығушылық тудырады Негізгі изоклиндер:

dy/dx=0, P(x,y)=0 – горизонталь жанамалардың изоклиналы және

dy/dx=¥ , Q(x,y)=0 – тік жанамалардың изоклиналы.

Негізгі изоклинальдарды тұрғызу және олардың қиылысу нүктесін табу арқылы (x,y), координаталары шарттарды қанағаттандырады:

осылайша фазалық траекторияларға жанамалардың бағыты белгісіз болатын фазалық жазықтықтың барлық изоклинальдарының қиылысу нүктесін табамыз. Бұл - дара нүкте, сәйкес келеді жүйенің стационарлық жағдайы(4.2-сурет).

(4.1) жүйеде фазалық жазықтықта бас изоклиндердің қиылысу нүктелері қанша болса, сонша стационарлық күйлер бар.

Әрбір фазалық траектория динамикалық жүйенің бірдей күйлер арқылы өтетін және бір-бірінен тек уақыт анықтамасының басы бойынша ғана ерекшеленетін қозғалыстар жиынтығына сәйкес келеді.

Егер Коши теоремасының шарттары орындалса, онда кеңістіктің әрбір нүктесі арқылы x, y, tбір интегралдық қисық арқылы өтеді. Фазалық траекториялар үшін автономияның арқасында дәл солай: бірегей фазалық траектория фазалық жазықтықтың әрбір нүктесі арқылы өтеді.

Тұрақты күйдегі тұрақтылық

Жүйе тепе-теңдікте болсын.

Сонда өкіл нүкте жүйенің ерекше нүктелерінің бірінде орналасады, онда анықтамасы бойынша:

.

Ерекше нүктенің орнықтылығы немесе тұрақты еместігі бейнелеуші ​​нүктенің стационарлық күйден аздаған ауытқумен кету-кетпеуімен анықталады. Екі теңдеу жүйесіне қолданылғандай тілдегі тұрақтылық анықтамасыe, гкелесідей.

Кез келген берілген аймақ үшін тепе-теңдік күйден ауытқу болса, тепе-теңдік күй тұрақты болады. (e )аумақты белгілеуге болады г (e ), тепе-теңдік күйін қоршап, аймақ ішінде басталатын траектория жоқ қасиеті бар г , ешқашан шекараға жетпейді e . (4.4-сурет)

Жүйелердің үлкен класы үшін - өрескел жүйелер – мінез-құлқының сипаты теңдеу түрінің шамалы өзгеруімен өзгермейтін, стационарлық күйге жақын жерде мінез-құлық түрі туралы ақпаратты түпнұсқаны емес, жеңілдетілгенін зерттеу арқылы алуға болады сызықтықжүйесі.

Сызықтық жүйелер.

Екі сызықтық теңдеулер жүйесін қарастырайық:

.(4.4)

Мұнда а б С Д- тұрақтылар, x, y- фазалық жазықтықтағы декарттық координаталар.

Жалпы шешім келесі түрде ізделеді:

.(4.5)

Бұл өрнектерді (4.4) орнына қойып, азайтыңыз e л т:

(4.6)

(4.6) белгісіздері бар теңдеулер алгебралық жүйесі А, ВБелгісіздердің коэффициенттерінен құралған анықтауышы нөлге тең болса ғана нөлден басқа шешімі болады:

.

Осы анықтауышты кеңейте отырып, жүйенің сипаттамалық теңдеуін аламыз:

.(4.7)

Бұл теңдеудің шешімі көрсеткіштің мәндерін береділ 1,2 , оның астында нөлден басқа мәндер мүмкін АЖәне Б(4.6) теңдеуінің шешімдері. Бұл құндылықтар

.(4.8)

Егер радикалды өрнек теріс болса, ондал 1,2 күрделі конъюгаттық сандар. (4.7) теңдеудің екі түбірінің де нөлден басқа нақты бөліктері бар және көп түбірлері жоқ деп есептейік. Сонда (4.4) жүйенің жалпы шешімін дәрежелермен дәрежелердің сызықтық комбинациясы ретінде көрсетуге болады.л 1 , л 2 :

(4.9)

Фазалық жазықтықта жүйенің мүмкін траекторияларының сипатын талдау үшін біз пайдаланамыз сызықты біртекті координаттарды түрлендіру,бұл жүйені әкеледі канондық формасы:

,(4.10)

бастапқы жүйемен салыстырғанда фазалық жазықтықта ыңғайлырақ бейнелеуге мүмкіндік береді (4.4). Жаңа координаттарды енгізейікξ , η формулалар бойынша:

(4.1)

Нақты бөлшектер нөлге тең болмаса, сызықтық алгебра курсынан белгіліл 1 , л 2 бастапқы жүйені (4.4) түрлендірулер (4.11) көмегімен әрқашан канондық түрге (4.10) түрлендіруге болады және оның фазалық жазықтықтағы тәртібін зерттеуге болады.ξ , η . Мұнда өзін көрсетуі мүмкін әртүрлі жағдайларды қарастырыңыз.

Тамырлар λ 1 , λ 2 – жарамды және бірдей белгі

Бұл жағдайда түрлендіру коэффициенттері нақты, біз нақты жазықтықтан қозғаламызx,yнақты жазықтыққа ξ, η. (4.10) теңдеулердің екіншісін біріншіге бөлсек, аламыз:

.(4.12)

Бұл теңдеуді интегралдасақ, табамыз:

Мұнда .(4.13)

λ арқылы түсінуге келістік 2 біздің пайымдауымыздың жалпылығын бұзбайтын үлкен модульді сипаттамалық теңдеудің түбірі. Сонда қарастырылып отырған жағдайда түбірлер λ болғандықтан 1 , λ2 – жарамды және бір белгі,а>1 , ал біз параболалық типті интегралдық қисықтармен айналысамыз.

Барлық интегралдық қисықтар (осьтен басқа η , сәйкес келеді ) осьтің басына түртіңіз ξ, ол да (4.11) теңдеуінің интегралдық қисығы болып табылады. Координаталар басы жеке нүкте болып табылады.

Енді өкіл нүктенің фазалық траекториялар бойымен қозғалыс бағытын анықтайық. Егер λ 1 , λ 2 теріс болса, (4.10), |ξ|, |η| теңдеулерінен көрініп тұрғандай. уақыт өте азаяды. Көрсеткіш нүкте бастапқы нүктеге жақындайды, бірақ оған ешқашан жетпейді. Әйтпесе, бұл фазалық жазықтықтың әрбір нүктесі арқылы тек бір фазалық траектория өтетінін көрсететін Коши теоремасына қайшы келеді.

Параболалар тобы сияқты интегралдық қисық сызықтар өтетін мұндай ерекше нүкте басынан өтеді, түйін деп аталады (сур. 4.5)

λ кезіндегі түйін типті тепе-теңдік күйі 1 , λ 2 < 0 Ляпунов бойынша тұрақты, өйткені өкіл нүкте барлық интегралдық қисықтардың бойымен координаталар басына қарай жылжиды. Бұл тұрақты түйін. Егер λ 1 , λ 2 > 0, содан кейін |ξ|, |η| уақыт өткен сайын ұлғаяды және өкіл нүкте координаттық нүктеден алыстайды. Бұл жағдайда сингулярлық нүкте– тұрақсыз түйін .

Фазалық жазықтықта x, y интегралдық қисықтардың мінез-құлқының жалпы сапалық сипаты сақталады, бірақ интегралдық қисықтардың жанамалары координаталық осьтермен сәйкес келмейді. Бұл жанамалардың көлбеу бұрышы коэффициенттердің қатынасымен анықталады α , β , γ , δ (4.11) теңдеулерде.

Тамырлар λ 1 , λ 2 жарамды және әртүрлі белгілері бар.

Қайдан түрлендірукоординаттар x,y координаттарға ξ, η қайтадан шынайы. Канондық айнымалылар үшін теңдеулер қайтадан (4.10) пішініне ие, бірақ енді λ белгілері 1 , λ 2 әртүрлі. Фазалық траектория теңдеуі нысаны бар:

Мұнда ,(4.14)

(4.14) интегралдасақ, табамыз

(4.15)

Бұл теңдеу екі координат осьтері де гиперболалық типті қисықтардың тобын анықтайдыасимптоталар болып табылады (ат а=1 бізде тең қабырғалы гиперболалар отбасы болар еді). Координаталық осьтер де бұл жағдайда интегралдық қисықтар болып табылады– бұлар координат басынан өтетін жалғыз интегралдық қисықтар болады. Әрбіроның ішінде үш фазалық траекториядан тұрады: тепе-теңдік күйіне қарай (немесе тепе-теңдік күйден алыс) және тепе-теңдік күйден екі қозғалыстың. Барлық басқа интегралдық қисықтар– басынан өтпейтін гиперболалар (Cурет 2). 4.6) Бұл ерекше нүкте деп аталады «ер-тоқым ». Тау седласының жанындағы деңгей сызықтары ершікті маңайдағы фазалық траекториялар сияқты әрекет етеді.

Өкіл нүктенің тепе-теңдік күйге жақын фазалық траекториялар бойымен қозғалысының сипатын қарастырайық. Мысалы,λ 1 >0 , λ 2<0 . Содан кейін оське орналастырылған өкілдік нүкте ξ , бастапқыдан алыстап, оське орналасады η – координаталар басына шексіз жақындайды, оған шекті уақытта жетпейді. Бейнелеуші ​​нүкте бастапқы сәтте қай жерде болса да (сингулярлық нүкте мен асимптотадағы нүктелерді қоспағанда) η =0), ол бастапқыда интегралдық қисықтардың бірі бойымен сингулярлық нүктеге қарай жылжыса да, ақырында тепе-теңдік күйден алыстайды.

Ол анық седла типті сингулярлық нүкте әрқашан тұрақсыз . Асимптотада арнайы таңдалған бастапқы шарттарда ғанаη =0 жүйе тепе-теңдік күйіне жақындайды. Дегенмен, бұл жүйе тұрақсыз деген тұжырымға қайшы келмейді. Егер санасаңыз, жүйенің фазалық жазықтықтағы барлық бастапқы күйлері бірдей ықтимал болса, онда бағыттағы қозғалысқа сәйкес келетін осындай бастапқы күйдің ықтималдығыдейін сингулярлық нүкте нөлге тең. Демек, кез келген нақты қозғалыс жүйені тепе-теңдік күйінен алып тастайды.Координаттар дегенге қайта келуx,y,траекториялардың координаттың басы айналасындағы қозғалысының сипатының бірдей сапалық бейнесін аламыз.

Түйін мен ершіктің қарастырылатын жағдайлары арасындағы шекара жағдай болып табыладықашан сипаттамалық көрсеткіштердің бірі, мысалы λ 1 , жоғалады, ол жүйенің детерминанты болған кезде пайда болады- өрнек adbc=0(4.8 формуланы қараңыз ). Бұл жағдайда (4.4) теңдеулердің оң жақтарының коэффициенттері өзара пропорционал болады.:

және жүйе өзінің тепе-теңдігі үшін түзудің барлық нүктелерін көрсетеді:

Қалған интегралдық қисықтар еңісі бар параллель түзулер тобы болып табылады , оның бойында λ сипаттамалық теңдеудің екінші түбірінің белгісіне байланысты өкіл нүктелер тепе-теңдік күйге жақындайды немесе одан алыстайды. 2 = a+d.(Cурет 4. 7 ) Бұл жағдайда тепе-теңдік күйінің координаталары айнымалылардың бастапқы мәніне тәуелді болады.

Тамырлар λ 1 , λ 2 – кешенконъюгат

Бұл жағдайда, шын мәніндеxЖәне жБіз боламыз күрделі конъюгаттар бар ξ , η (4.10) . Дегенмен, тағы бір аралық түрлендіруді енгізу арқылы бұл жағдайда нақты сызықтық біртекті түрлендіруге қарауды азайтуға болады. қояйық:

(4.16)

қайда a, b,Және u,v – нақты құндылықтар. бастап түрлендіруді көрсетуге боладыx,yдейін u, v біздің болжамдарымыз бойынша, нақты, сызықтық, нөлге тең емес анықтауышпен біртекті. Теңдеулердің арқасында(4.10, 4.16) бізде:

қайда

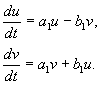(4.17)

Теңдеулердің екіншісін біріншіге бөлу, Біз алып жатырмыз:

біріктіру оңайырақ, полярлық координаталар жүйесіне ауыссақ (r, φ ) . Ауыстырудан кейінбіз қайдан аламыз:

.(4.18)

Осылайша, фазалық жазықтықтаu, vбіз әрқайсысында бар логарифмдік спиральдар отбасымен айналысамызбасындағы асимптотикалық нүкте.Спираль тәрізді барлық интегралдық қисықтардың асимптотикалық нүктесі болып табылатын сингулярлық нүкте, кірген досдосым, шақырды назар аудару ( 4.8-сурет ) .

Көрсеткіш нүктенің фазалық траекториялар бойымен қозғалысының сипатын қарастырайық. (4.17) теңдеулерінің біріншісін көбейтуu, ал екіншісі - vжәне қосу арқылы біз мынаны аламыз:

Қайда

Болсын а 1 < 0 (а 1 = Reλ ) . Одан кейін бейнелеу нүктесі ақырғы уақытта оған жетпей, басына үздіксіз жақындайды. Бұл фазалық траекториялардың бұралмалы спираль болып табылатынын және сөнген тербелістерге сәйкес келетінін білдіреді.айнымалылар. Бұл - тұрақты фокус .

Тұрақты фокус жағдайында, тұрақты түйін жағдайындағы сияқты, тек Ляпунов шарты ғана емес, сонымен қатар одан да қатаң талап орындалады. Атап айтқанда, кез келген бастапқы ауытқулар үшін жүйе ақыр соңында тепе-теңдік жағдайына қалағандай жақын оралады. Мұндай тұрақтылық деп аталады, онда бастапқы ауытқулар өспейді, бірақ нөлге бейім ыдырауы. абсолютті тұрақтылық .

Формулада болса (4.18) а 1 >0 , содан кейін бейнелеуші ​​нүкте координаттық нүктеден алыстайды және біз онымен айналысамыз тұрақсыз фокус . Ұшақтан қозғалғандаu,vфазалық жазықтыққаx, жспиральдар да спираль болып қалады, бірақ деформацияланады.

Енді қашан болған жағдайды қарастырайықа 1 =0 . Жазықтықтағы фазалық траекторияларu, vшеңберлер болады ол ұшақтаx,yэллипстерге сәйкес келеді:

Осылайша, сағата 1=0 арнайы нүкте арқылыx= 0,y= 0 интегралдық қисық өтпейді. Жанында интегралдық қисықтар тұйық қисық сызықтар, атап айтқанда, бір-біріне енгізілген және сингулярлық нүктені қоршап тұрған эллипстер болатын мұндай оқшауланған ерекше нүкте центр деп аталады.

Сонымен, (4.7) сипаттамалық теңдеудің түбірлерінің табиғатына байланысты тепе-теңдіктің алты түрі мүмкін. Жазықтықтағы фазалық траекториялардың көрінісі x, yосы алты жағдай үшін суретте көрсетілген. 4.9.

Күріш. 4.9.Сызықтық теңдеулер жүйесі үшін стационарлық күйдің маңайындағы фазалық портреттердің түрлері (4.4).

Тепе-теңдік күйлерінің бес түрі өрескел, олардың табиғаты (4.4) теңдеулердің оң жақтарында жеткілікті аз өзгерістермен өзгермейді. Бұл жағдайда өзгерістер тек оң жақта ғана емес, сонымен қатар олардың бірінші ретті туындыларында да аз болуы керек. Алтыншы тепе-теңдік күйі – орталық – өрескел емес. Теңдеулердің оң жағындағы параметрлердің аздаған өзгерістерімен ол тұрақты немесе тұрақсыз фокусқа өтеді.

Бифуркация диаграммасы

Белгілеуді енгізейік:

. (4.11)

Сонда сипаттамалық теңдеуді келесі түрде жазуға болады:

. (4.12)

Тік бұрышты декарттық координаталары бар жазықтықты қарастырайық с , D және оған сипаттамалық теңдеудің түбірлерінің табиғатымен анықталатын тепе-теңдік күйдің сол немесе басқа түріне сәйкес аймақтарды белгілеңіз.

.(4.13)

Тепе-теңдік күйінің тұрақтылығының шарты у-ның теріс нақты бөлігінің болуы боладыл 1 және л 2 . Бұл үшін қажетті және жеткілікті шарт теңсіздіктердің орындалуы болып табыладыс > 0, D > 0 . (4.15) диаграммада бұл шарт параметр жазықтығының бірінші ширегінде орналасқан нүктелерге сәйкес келеді. Ерекше нүкте фокус болады, егерл 1 және л 2 кешен. Бұл шарт жазықтықтың сол нүктелеріне сәйкес келеді , анау. параболаның екі тармағының арасындағы нүктелерс 2 = 4 D. Жартылай ось нүктелері с = 0, D>0, орталық типті тепе-теңдік күйлеріне сәйкес келеді. Сияқты,л 1 және л 2 - жарамды, бірақ әртүрлі белгілер, яғни. сингулярлық нүкте ершік болады, егер D<0, және т.б. Нәтижесінде біз параметр жазықтығын бөлу диаграммасын аламыз с, D, тепе-теңдік күйлерінің әртүрлі түрлеріне сәйкес аймақтарға.

Күріш. 4.10.Бифуркация диаграммасы

сызықтық теңдеулер жүйесі үшін 4.4

Сызықтық жүйенің коэффициенттері болса а б С Дқандай да бір параметрге байланысты, содан кейін бұл параметр өзгертілгенде, мәндер де өзгередіс , D . Шекаралардан өткенде фазалық портреттің сипаты сапалы түрде өзгереді. Сондықтан мұндай шекаралар бифуркациялық шекаралар деп аталады - шекараның қарама-қарсы жағында жүйеде топологиялық жағынан әртүрлі екі фазалық портрет және сәйкесінше екі түрлі мінез-құлық түрі болады.

Диаграмма мұндай өзгерістердің қалай болатынын көрсетеді. Егер ерекше жағдайларды - координаттардың шығу тегін алып тастасақ, онда седла y осін кесіп өткенде тұрақты немесе тұрақсыз түйінге кіре алатынын оңай байқауға болады. Тұрақты түйін не седлаға, не тұрақты фокусқа ауыса алады және т.б. Тұрақты түйін – тұрақты фокус және тұрақсыз түйін – тұрақсыз фокус ауысулары бифуркациялық емес екенін ескеріңіз, өйткені бұл жағдайда фазалық кеңістіктің топологиясы өзгермейді. Фазалық кеңістіктің топологиясы мен бифуркациялық ауысулар туралы толығырақ 6-дәрісте айтатын боламыз.

Бифуркациялық ауысулар кезінде сингулярлық нүктенің тұрақтылық сипаты өзгереді. Мысалы, орталық арқылы тұрақты фокус тұрақсыз фокусқа айналуы мүмкін. Бұл бифуркация деп аталады Андронов-Хопф бифуркациясызерттеген ғалымдардың атымен. Сызықты емес жүйелерде бұл бифуркация кезінде шекті цикл туады және жүйе өздігінен тербеліске айналады (8-дәрісті қараңыз).

Мысал. Сызықтық химиялық реакциялар жүйесі

Зат Xсырттан тұрақты жылдамдықпен ағып, У затына айналады және заттың концентрациясына пропорционал жылдамдықпен Ы, реакция сферасынан алынады. Барлық реакциялар бірінші ретті, тек нөлдік ретті заттың сырттан келуін қоспағанда. Реакция схемасы келесідей көрінеді:

(4.14)

және теңдеулер жүйесімен сипатталады:

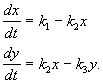(4.15)

Оң жақтарын нөлге теңестіру арқылы стационарлық концентрацияларды аламыз:

.(4.16)

Жүйенің фазалық портретін қарастырайық. (4.16) жүйенің екінші теңдеуін біріншіге бөлейік. Біз алып жатырмыз:

.(4.17)

(4.17) теңдеу фазалық жазықтықтағы айнымалылардың әрекетін анықтайды. Осы жүйенің фазалық портретін салайық. Алдымен фазалық жазықтықта негізгі изоклинальдарды саламыз. Тік жанамалардың изоклиналы теңдеуі:

Көлденең жанамалардың изоклиналы теңдеуі:

Сингулярлық нүкте (стационар күй) бас изоклиндердің қиылысында жатыр.

Енді координат осьтері интегралдық қисықтарды қандай бұрышта қиып өтетінін анықтайық.

Егер x= 0, содан кейін .

Осылайша, интегралдық қисықтарға жанаманың көлбеуінің тангенсі y=y(x),у осін кесіп өту x=0, жоғарғы жарты жазықтықта теріс (айнымалылар екенін еске түсіріңіз x, yконцентрация мәндері бар, сондықтан бізді тек фазалық жазықтықтың жоғарғы оң квадранты қызықтырады). Бұл жағдайда жанаманың көлбеу бұрышының тангенсінің мәні басынан қашықтығына қарай артады.

Осьті қарастырыңыз у= 0. Осы осьтің қиылысында интегралдық қисықтар теңдеу арқылы сипатталады

Сағат абсцисса осін қиып өтетін интегралдық қисықтардың көлбеуінің тангенсі оң болады және өскен сайын нөлден шексіздікке дейін өседі x.

Сағат.

Содан кейін, одан әрі өсумен еңістің тангенсі абсолютті мәнде төмендейді, теріс болып қалады және -1-ге ұмтылады. x ® ¥ . Негізгі изоклиналдардағы және координат осьтеріндегі интегралдық қисық сызықтарға жанамалардың бағытын біле отырып, фазалық траекториялардың бүкіл суретін салу оңай.

Дара нүктенің орнықтылығының сипаты Ляпунов әдісі арқылы белгіленеді. Жүйенің сипаттамалық детерминанты мына түрде болады:

.

Анықтаушыны кеңейте отырып, жүйенің сипаттамалық теңдеуін аламыз: , яғни. сипаттамалық теңдеудің түбірлері де теріс. Демек, жүйенің стационарлық күйі тұрақты түйін болып табылады. Бұл ретте заттың концентрациясы Xстационарлық күйге әрқашан монотонды түрде ұмтылады, У затының концентрациясы min немесе макс арқылы өтуі мүмкін. Мұндай жүйеде тербелмелі режимдер мүмкін емес.

Болсын zq – f(z) функциясының дара нүктесі, t.s. f(z)бірақ осы сәтте аналитикалық болып табылады (атап айтқанда, онда анықталмауы мүмкін). Егер нүктенің осындай тесілген төңірегі бар болса zq (яғни, O z - жиыны zq f(z) алиат болып табылады zoшақырды оқшауланған сингулярлық нүктефункциялары f(z).Бұл анықтама жағдайда да сақталған zn = oo, егер йод нүктенің тесілген маңы болса zq = oo жиынды түсініңіз z > I - бастапқыда центрленген қандай да бір шеңбердің пайда болуы. Басқаша айтқанда, сингулярлық нүкте zq оқшауланған деп аталады, егер осы нүктенің көршілестігі бар болса, онда басқа ерекше нүктелер бар. zq. Төмендегі барлық жерде біз бір мәнді таңбаның ерекше нүктелерін ғана қарастырамыз (функция f(z)бірегей деп есептеледі).

Функцияның әрекетіне байланысты f(z)сағ z -> zqБірыңғай нүктелердің үш түрі бар. Оқшауланған сингулярлық нүкте zq функциялары f(z)шақырды:

1) алынбалы сингулярлы нүктеегер шекті шектеу болса

2) полюсшектеу болса

3) маңызды нүкте,егер f(z) үшін шекті де, шексіз де шек жоқ z-> zq.

МЫСАЛ 26.1. Бірегей нүктелердің үш түрі де жүзеге асатынын көрсетейік. Қарастырыңыз f(z)= нүкте zq = 0 оқшауланған

осы функцияның жеке нүктесі. (22.12) формуланы пайдаланып, кеңейтуді аламыз

одан лим бар деген қорытынды шығады fi(z)= 1. Демек, zq = 0 болады

функцияның алынбалы сингулярлық нүктесі болып табылады fi(z).

Функция f'j(z) =--- нүктесінде полюсі бар zo= 1 себебі

2 r«X

Енді функцияны қарастырыңыз )z(z)= e 1 ^ r және оны көрсетіңіз zo = O - бұл функцияның маңызды сингулярлық нүктесі. Талпынған кезде zнақты ось бойымен нөлге, f функциясының сол және оң шектері (z)әртүрлі: лим бастап 1 / 1 = 0,лим 1 /* = арқылы os. Бұл білдіреді,

x->0-0 x->0+0

не f:i(z) 2 үшін шекті де, шексіз де шек жоқ -> О, яғни. zq = 0 – бұл функцияның мәні бойынша ерекше нүктесі. (Нәтижеге байланысты екенін ескеріңіз z-iyойша ось функциясы бойынша нөлге дейін

шектеуі жоқ.)

Әрине, оқшауланбаған ерекше нүктелер де бар. Мысалға. функцияның нүктелерінде полюстері бар z n = -, П= ±1, ±2,...

Демек, Zq = 0 - бұл функцияның оқшауланбаған сингулярлық нүктесі: осы нүктенің кез келген (еркін шағын) маңайында басқа ерекше нүктелер бар. g б.

Болсын зо-функцияның соңғы оқшауланған сингулярлық нүктесі f(z).Содан кейін f(z)нүктенің кейбір тесілген маңайында 0 Zo ұқсас zoбұл төңіректі ішкі радиусы r = 0 сақина ретінде қарастыруға болады. 25.1 теоремасы бойынша қарастырылып отырған көршілестікте функция f(z)Лоран сериясында кеңейтілуі мүмкін (25.2). Біз 2 үшін функцияның әрекетін көрсетеміз -> zq (яғни дара нүктенің түрі zo)ыдыраудың негізгі бөлігінің формасына байланысты (25.2); бұл жағдай «негізгі бөлім» терминінің шығуын түсіндіреді.

ТЕОРЕМА 2G.2. f(z) функциясының оқшауланған сингулярлық zo нүктесі, егер осы нүктенің тесілген төңірегіндегі Лорап кеңеюінде оид болса ғана алынуы мүмкін.

анау. тек дұрыс бөліктен тұрады, ал негізгі бөліктің барлық коэффициенттері оққа тең.

Дәлелдеу. 1. рұқсат етіңіз zoалынбалы ерекше нүкте болып табылады. Функцияның Лоран кеңеюі екенін дәлелдейік f(z)(26.1) нысаны бар. Бірегей нүктеден бастап zoалынбалы, онда шекті шекті лим бар f(z) = A.Демек, f(z)нүктенің 0 z - zq кейбір тесілген төңірегінде шектелген зо,анау. )(z) барлығы үшін zосы маңайдан. Кез келгенін алыңыз Р. U р /?|, және Лоран қатарының коэффициенттері үшін (25.3) формулаларды қолданыңыз:

Кеңейтудің негізгі бөлігінің коэффициенттері үшін n =- 1,-2,... Мұндай мәндер үшін ПБізде бар p~n-e 0 кезінде Р-> 0. Мәннен бастап Ронда ерікті түрде шағын таңдауға болады мырза~"ерікті түрде аз болуы мүмкін. |c t,| болғандықтан ^ мырза~нжәне cn p-ге тәуелді емес, онда cn = 0 үшін Және= - 1, -2,..., ол дәлелдеуге тиіс болды.

2. Енді Лоран кеңеюінің (26.1) формасы бар деп есептейік. Серия (26.1) - қуатты қатар және. сондықтан тек тесілген жерде ғана емес, сонымен бірге бүкіл маңайда жақындайды z-zq оның ішінде нүкте zo;оның мөлшері S(z)үшін аналитикалық болып табылады z және S(z) = )(z) 0 z кезінде - zoР.Демек, шекті лим бар )(z)\u003d Pm 5 (r) \u003d 5 (r) - Демек, жеке нүкте zq

Z->Zo Z-*Zo

бір реттік. Теорема дәлелденді.

Пікір. Теореманы дәлелдеуден шығатыны, тесілген маңайда 0 z - zo алынбалы сингулярлық нүктенің функциясы f(z)бүкіл көршілестікте аналитикалық болып табылатын S(r) функциясымен сәйкес келеді z - zo . Сондықтан, егер /(th) = қойсақ S(zq), содан кейін функцияның мәндерін өзгертпей f(z)тесілген маңайдың кез келген нүктесінде біз бұл функцияны r-де аналитикалық жасаймыз, яғни. мүмкіндікті «жою». Бұл «алынбалы ерекшелік» терминін түсіндіреді. Мұндай нүктелерді функцияның жеке нүктелері ретінде емес, тұрақты деп қарастыру заңды f(z).

Мысалы, функцияны қарастырайық

26.1 мысалында Pm (n) = 1 болатыны көрсетілген. дара нүкте

zq = 0 алынбалы. /i(0) = 1 параметрін орнату, осылайша біз ерекшелікті жоямыз және нүктеде аналитикалық функцияны аламыз. zq = 0 (және бүкіл С жазықтығында).

Енді полюстерді Лоранның кеңеюі бойынша сипаттайық.

26.3 теорема. f(z) функциясының оқшауланған сингулярлық Zo нүктесі полюс болып табылады, егер және егер, Zq центрі бар Лоран кеңеюінің негізгі бөлігінде тек шектеулі санды ерекшеленген кезде

n болатын нөлдік коэффициенттерден:

Дәлелдеу. 1. рұқсат етіңіз zq - полюс, яғни. лим /( z) = oo.

Функцияның Лоран кеңеюі екенін дәлелдейік f(z)(2G.2) нысаны бар. Лимнен бері f(z)= oo. онда нүктенің тесілген төңірегі бар

ки zq. онда f(z)аналитикалық және нөлдері жоқ. Содан кейін функция g(z) = 1 /f(z)Сондай-ақ осы тесілген төңіректе аналитикалық болады және лим g(z)= 0. Сондықтан, Зобір реттік *-? *0

функцияның дара нүктесі g(z).Қайта анықтайық g(z)нүктесінде zo, қою g(zo)= 0. Содан кейін g(z)(тесілмеген) нүктенің бүкіл маңайында аналитикалық болады z 0,және z0оның оқшауланған нөлі болады. арқылы белгілеңіз Носы нөлдің еселігі (тәртібі). §23-те көрсетілгендей, нүктенің маңында zq функциясы g(z)түрінде ұсынылуы мүмкін ((23.2) қараңыз)

және (z$) f 0 және y>(z)нүктенің кейбір төңірегінде аналитикалық болып табылады зо-Өйткені ip(z)нүктесінде үздіксіз zoЖәне g>(zo) F 0" содан кейін ip(z)осы нүктенің кейбір төңірегінде де нөл жоқ. Сондықтан 1-функция /-p(z)Сондай-ақ осы төңіректе аналитикалық болады, сондықтан оны Тейлор сериясында кеңейтеді:

Жақшаларды ашып, коэффициенттердің белгілерін өзгерте отырып, біз соңғы кеңейтуді пішінге жазамыз

мұндағы c_jv = 1>o f 0. Осылайша, f(r) Лоран кеңеюінің негізгі бөлігі терминдердің шектеулі санын ғана қамтиды; қажетті теңдікке жеттік (26.2).

2. Нүктенің тесілген маңайында болсын thфункциясы )(z)Лоран кеңеюімен (26.2) ұсынылған (кеңейтілген түрде, қараңыз (26.3)), оның негізгі бөлігі терминдердің шектеулі санын ғана қамтиды және бастап- d» f 0. Біз мұны дәлелдеуіміз керек Zq – функция полюсі f(z).(26.3) теңдігін көбейту (Г - Г o) iV , функциясын аламыз

(26.4) қатары тек тесілген жерде ғана емес, сонымен қатар нүктенің бүкіл маңайында аналитикалық функцияға жинақталатын дәрежелік қатар. Zq. Демек, функция h(z)Егер біз оны орнату арқылы кеңейтсек, осы маңайда аналитикалық болады h(zo)= s_dg f 0. Содан кейін

Осылайша o нүктесі полюс болып табылады және 26.3 теоремасы дәлелденді.

Нөлдік функцияның еселігі (тәртібі). g(z)= 1//(r) деп аталады полюс тәртібіфункциясы /(r). Егер N-полюстің реті th, онда g(z)= (r - Zo)N ip(z),және (бару) Ф 0, және 26.3 теоремасының дәлелдеуінің бірінші бөлігінде көрсетілгендей, f(r) кеңеюі (26.3) түрінде болады, мұндағы c_/v f 0. Керісінше, егер f(r) (26.3) және қатарға кеңейсе e-z F 0, содан кейін

т.с. N- f(r) функциясының полюсінің реті. Осылайша, функцияның zq полюсінің реті/(G) zq нүктесінің тесілген төңірегіндегі Лоран кеңеюінің негізгі бөлігінің жетекші нөлдік емес коэффициентінің санына тең.(яғни осындай санға тең N,қандай s_dg f 0 және sp= 0 кезінде П > N).

Қолданбалар үшін ыңғайлы) келесі бекітуді дәлелдейміз.

Қорытынды 26.4. zq нүктесі көркем шығарманың N ретті полюсі болып табылады/(G) егер және тек егер/(G) түрінде көрсетеді

мұндағы h(z) – нүктенің маңайындағы аналитикалық функция th және h(zo) f 0.

Дәлелдеу. Функция cp(z) = л/сағ(z) r нүктесінің кейбір маңайында аналитикалық болып табылады.Қорытынды 26.4 шарты келесіге эквивалентті:

Сондықтан zq - еселік нөл Нфункциялары g(z).демек, еселік полюсі Нфункциялары /(2).

II мысал 26.5. Функцияның оқшауланған дара нүктелерін табыңыз және олардың түрін анықтайды.

D e u c tio n. Қандай нүктелер (з 2 + 1 )(z+ H) 2 = 0. Егер z 2 L- 1 = 0, содан кейін 2 = ±gегер (з 4- H) 2 = 0, сонда z= -3. Демек, функцияның үш ерекше нүктесі бар z= r, 22 = -r, З3 = - 3. Қарастырыңыз z:

G -бірінші ретті полюс (қорытынды 26.4 қолдандық). 22 = екенін дәл осылай дәлелдеуге болады -ісонымен қатар бірінші ретті полюс. 2 сағат ішінде бізде:

Мәні бойынша ерекше нүктелерді қарастыруға көшейік.

26.6 теорема. f(z) функциясының оқшауланған zq сингулярлық нүктесі, егер центрінде zq орналасқан Лоран кеңеюінің негізгі бөлігінің шексіз көп айырмашылығы бар болса ғана, мәні бойынша сингулярлық болады. нөл, коэффициенттері p.

Дәлелдеу. 26.6 теоремасы 26.2 және 26.3 теоремаларынан тікелей шығады. Шынында да, егер нүкте zq мәні бойынша сингуляр болса, онда Лоран кеңеюінің негізгі бөлігі жоқ болуы немесе терминдердің шектеулі санын қамтуы мүмкін емес (әйтпесе нүкте Zq алынбалы немесе тірек болады). Сондықтан негізгі бөліктегі мүшелер саны шексіз болуы керек.

Керісінше, негізгі бөлікте шексіз көп мүшелер болса, онда Zq алынбалы нүкте де, полюс те бола алмайды. Демек, бұл нүкте шын мәнінде ерекше.

Анықтамаға сәйкес, мәнді сингулярлық нүкте f(2) функциясының шекті де, шексіз де шегі болмайтындығымен сипатталады. z ->zq. Функцияның мәнді сингулярлық нүктенің маңайындағы әрекетінің қаншалықты ретсіз екендігі туралы толық түсінік келесі теорема арқылы берілген.

26.7 теоремасы (Сочокки теоремасы). Егер zq мәні жеке болса, онда f(z) функциясының нүктесі), кез келген күрделі сан үшін L, оның ішінде A = oo, z n -> zo және болатындай z n нүктелерінің тізбегі барлим f(zn) = БІРАҚ.

n->os

Дәлелдеу. Алдымен жағдайды қарастырыңыз A = oo. 2G.2 теоремасын дәлелдеудің бірінші бөлігінде біз егер f(z) r0 нүктесінің кейбір тесілген төңірегінде шектелген болса, онда барлық коэффициенттер c, n = -Негізгі бөліктің 1, - 2,... нөлге тең (демек, th-дегі ерекшелік жойылады). Болжам бойынша r0 мәні бойынша ерекше нүкте болғандықтан, f(r) функциясы r0 нүктесінің кез келген тесілген маңайында шектелмеген. Кейбір тар 0 Z төңірегін алайық f(zi) > 1 (егер |/(r)| z - zo R/2 нүкте бар z-2 , мұндағы |/(dd)| > 2 және т.б.: тесілген маңайда О 71. rn -e go және lim /(r«) = oo болатыны анық. Сонымен, A = oo жағдайда, 26.7 теоремасы

дәлелденген.

Енді рұқсат етіңіз A f oo. Алдымен тесілген 0 маңы бар деп есептейік

= -жж---- осы тесілген төңіректе аналитикалық болады және, демек,

/(G) - БІРАҚ

демек, r – Φ(r) функциясының оқшауланған сингулярлық нүктесі. көрсетейік. бұл r0 Φ(r) мәні бойынша ерекше нүкте болып табылады. Қате болсын. Сонда шекті lim Φ(r) бар, не ақырлы, не шексіз. Өйткені

/(r) = A + , онда Hsh /(r) да бар, бұл шартқа қайшы келеді

F(g) ~ :-*z 0

теореманың көрінісі. Осылайша, r0 Φ(r) функциясының мәні бойынша ерекше нүктесі болып табылады. Жоғарыда дәлелденгенге сәйкес, r n o және lim Φ(r n) = oo болатындай r n нүктелерінің тізбегі бар. Осы жерден

Біз f(r) деген болжам бойынша қажетті бекітуді дәлелдедік. Ф А r нүктесінің кейбір тесілген төңірегінде.Енді бұл дұрыс емес деп есептейік, яғни. th нүктесінің кез келген ерікті шағын тесілген төңірегінде мұндай нүкте бар G»,бұл f(r") = A. Сонда кез келген үшін Птесілген төңіректе 0 f(z u) = L. Осылайша, қажетті бекіту ақиқат П-юо

барлық жағдайларда және 26.7 теоремасы дәлелденді.

(Сохотский) 26.7 теоремасына сәйкес, мәнді бір нүктенің кез келген (еркін шағын) тесілген төңірегінде f(r) функциясы кеңейтілген күрделі С жазықтығындағы кез келген санға ерікті түрде жақын мәндерді қабылдайды.

Оқшауланған сингулярлық нүктелерді зерттеу үшін негізгі элементар функциялардың әйгілі Тейлор кеңейтімдері жиі пайдалы.

МЫСАЛ 2G.8. Функция үшін zq = 0 дара нүктенің түрін анықтаңыз

Шешілген және e. Тейлор қатарындағы алым мен бөлгішті r дәрежесінде кеңейтеміз. (22.11) 3-ке ауыстырамыз. z r және 1-ді шегерудің орнына аламыз

(22.12) көмегімен бөлгіштің кеңеюін аламыз:

Бұл кеңейтімдердегі қатарлар бүкіл күрделі жазықтықта € жақындайды. Бізде бар

және /2(2) нүктенің маңайында ұқсас zo = 0 (тіпті бүкіл жазықтықта) және /2(20) Ф 0, содан кейін h(z) gF 0 нүктесінің кейбір маңайында да аналитикалық болып табылады. Қорытынды 26.4 сәйкес нүкте Zo = 0 - тапсырыстың полюсі N = 4.

II мысал 26.9. Функцияның дара нүктелерін табыңыз f(z)= sin j - және олардың түрін анықтаңыз.

P e in e және e. Функцияның жалғыз соңғы сингулярлық нүктесі бар zq = 1. С-дан басқа нүктелерде функция w =--- аналитикалық; сондықтан күнә функциясы wаналитикалық болады.

Синустың кеңеюінде алмастыру (22.12) - r орнына, біз аламыз

Біз 20 = 1 нүктесінің тесілген төңірегінде Лоран қатарындағы sin функциясының кеңеюін алдық. Алынған кеңеюде теріс дәрежелері бар шексіз көп мүшелер (r - 1) болғандықтан, онда zq = 1 маңызды сингулярлық нүкте (бұл жағдайда Лоран кеңеюі тек негізгі бөліктен тұрады, ал дұрыс бөлік жоқ).

Айта кетейік, бұл жағдайда қатарды кеңейтуге жүгінбей-ақ, сингулярлық сипатын анықтаудан тікелей анықтауға болады. Шынында да, (r") және (2") жинақталатын тізбектер бар zo= 1 және осылайша f(z" n)= 1, /(2") = 0 (мұндай тізбектерді өзіңіз көрсетіңіз). Сонымен, f(z)қашан шектеу жоқ z -> 1 және сондықтан нүкте zq - 1 мәні бойынша сингулярлы.

Функцияның нүктенің маңайындағы Лоран кеңеюі ұғымын енгізейік Zq = 00 және осы нүктедегі ерекшеліктің кеңеюі мен табиғаты арасындағы байланысты қарастырыңыз. Оқшауланған сингулярлық нүктенің және оның түрінің (алынбалы, полюсті немесе шын мәнінде сингулярлы) анықтамалары іске қосылатынын ескеріңіз. zq = oc өзгермеген. Бірақ 26.2 теоремалар. Лоран кеңейтімдерінің сипатына қатысты 26.3 және 26.6 өзгерту қажет. Мәселе мынада, мүшелер c n (z - 2o) б. П= -1,-2,..., соңғы нүктеге жақын функцияның "‘дұрыссыздығын" анықтайтын негізгі бөлік Zq, 2 oo-ға бейім болғандықтан, олар «дұрыс» әрекет етеді (0-ге бейім). Керісінше, тұрақты бөліктің мүшелері -мен П= 1,2,... oo-ға бейім болады; олардағы даралықтың сипатын анықтайды Zq = oo. Сондықтан oo төңірегінде кеңейтудің негізгі бөлігі оң өкілеттіктері бар терминдер болады P,және дұрыс - теріс.

Жаңа айнымалыны енгізейік w = 12. Функция tv= 1/2, u(oo) = 0 болатындай кеңейтілген, бір-біріне және көршілес аумақты конформды түрде картаға түсіреді z > Rұпай |w| маңайында zq = 00 wq = 0. Егер функция f(z)тесілген төңіректегі аналитика Р z Zq = oc, содан кейін функция G(w) = f(l/w)сары төңіректе аналитикалық болады 0 wo = 0. Өйткені 2 үшін -> oo болады w-> 0, содан кейін

Сондықтан G(w)нүктесінде бар wq = 0 - ұқсас түрдегі ерекшелік f(z)нүктесінде Zq = 00. Лоран қатарындағы G(w) функциясын wo = 0 нүктесінің тесілген маңайында кеңейтейік:

(26.5) оң жағындағы қосындылар сәйкесінше кеңейтудің дұрыс және негізгі бөліктерін білдіреді. Айнымалыға көшейік z,алмастыру w = 1/z:

белгілеу П\u003d -A *, 6 * \u003d 6_ " \u003d бжәне мұны байқайды G(л/з) = f(z), Біз алып жатырмыз

ыдырау (2G.G) деп аталады f(z) функциясының zq нүктесінің тесілген маңайындағы Лоран кеңеюі= oo. (2G.6) бірінші қосынды деп аталады оң жақ бөлігі, ал екінші қосынды негізгі бөлігібұл ыдырау. Бұл қосындылар кеңейтудің (26.5) дұрыс және негізгі бөліктеріне сәйкес болғандықтан, кеңейту (26.6) 26.2, 26.3 және 26.6 теоремаларының аналогтарын қанағаттандырады. Осылайша, келесі теорема 26.2 теоремасының аналогы болып табылады.

26.10 теорема. Оқшауланған сингулярлық нүктеZq - os (функциялар/(G) осы нүктенің тесілген төңірегіндегі Лоран кеңеюінің пішіні болған жағдайда ғана алынуы мүмкін.

т.с. тек дұрыс бөліктен тұрады.

Біз /(oo) = қоямыз ко.(26.7) қатармен анықталатын функция көршілестікте жинақталады z > Rнүктелер 2o \u003d oc, деп аталады z нүктесінде аналитикалық o = oo. (Бұл анықтама функцияның аналитикалықтығына баламалы екенін ескеріңіз G(w) нүктесінде во = 0.)

26.11 мысал. Функцияның zq = oo ерекше нүктесін зерттеңіз

Шек шекті болғандықтан, онда zo = oo - f(r) функциясының алынбалы сингулярлық нүктесі. Егер /(oo) = lim қойсақ J(z)= 0, онда f(z)айналады

нүктесінде тик Зо= os. Сәйкес кеңейтуді қалай табуға болатынын көрсетейік (26.7). Айнымалыға көшейік w = 1 fz.Ауыстыру z= 1 /?e, аламыз

(соңғы теңдік ww = 0 нүктесінің тесілген маңайында жарамды, бірақ біз анықтаманы кеңейтеміз (7(0) = 0). Алынған функцияның жеке нүктелері бар. w =±i, w =-1/3 және нүктеде Wq = 0 аналитикалық болып табылады. Кеңейту функциясы G(w)дәрежелер бойынша w(25.7-мысалда жасалғандай) және алынған дәрежелік қатарға ауыстыру w = 1/zфункцияның кеңеюін (26.7) алуға болады f(z).

Жағдай үшін 26.3 теоремасы zo= oo келесі пішінде қайта жазылады.

26.12 теорема. Оқшауланған сингулярлық нүктебару = ок f(z) функциясы полюс болып табылады, егер Лоран кеңеюінің негізгі бөлігі болса ғана (26.6) нөлдік емес коэффициенттердің шектеулі саны ғана барбастап":

Мұнда қатар тұрақты бөлік, ал жақшадағы көпмүше кеңейтудің негізгі бөлігі болып табылады. Полюстің oc-тегі еселігі полюстің еселігі ретінде анықталады wq = 0 функция G(z).Полюстің еселігі санмен сәйкес келетінін байқау қиын емес Н(26.8) ішінде.

Q p | (i 2 + 1) (z + 3) 2

Тапсырма. Функция екенін көрсетіңіз f(z) =-- -- бар

нүкте zo = oo полюс тәртібі 3.

Жағдай үшін маңызды ерекше нүкте туралы 26.6 теоремасы қайта жазылады zo= os сөзбе-сөз, және біз оған егжей-тегжейлі тоқталмаймыз.

Тейлор қатары zol шеңберінде аналитикалық болатын функцияларды зерттеудің тиімді құралы ретінде қызмет етеді. Сақиналық аймақта аналитикалық болатын функцияларды зерттеу үшін оң және теріс дәрежедегі (z - zq) кеңейтулерді құруға болатыны белгілі болды. Тейлор кеңейтімдерін жалпылайтын пішін. Екі қатардың қосындысы ретінде түсінілетін қатар (1) Лоран қатары деп аталады. (1) қатарларының жинақтылық облысы әрбір (2) қатарының жинақтылық облыстарының ортақ бөлігі екені анық. Оны тауып алайық. Бірінші қатардың жинақталу ауданы деп радиусы Коши-Хадамард формуласымен анықталатын шеңберді айтамыз Жиналу шеңберінің ішінде (3) қатар аналитикалық функцияға жинақталады, ал кез келген кіші радиусы бар шеңберде абсолютті жинақталады. және біркелкі. Екінші қатар айнымалыға қатысты дәрежелі қатар болып табылады.(5) қатар өзінің жинақтылық шеңбері шегінде күрделі айнымалы m-*oo аналитикалық функциясына жинақталады, ал кез келген кіші радиусы шеңберде ол абсолютті және біркелкі жинақталады, бұл (4) қатардың жинақтылық облысы шеңбердің пайда болуы дегенді білдіреді - Егер онда (3) және (4) қатарының жинақтылығының ортақ облысы бар болса - (1) қатары болатын дөңгелек сақина. аналитикалық функцияға жинақталады. Оның үстіне, кез келген сақинада ол абсолютті және біркелкі жиналады. Мысал 1. Рад Лоран қатарының жинақтылық аймағын анықтаңыз Оқшауланған сингулярлық нүктелер және олардың классификациясы (z), ол дөңгелек сақинада бірмәнді және аполитикалық болып табылады, бұл сақинада коэффициенттері жинақталған қатардың қосындысы ретінде ұсынылуы мүмкін. Cn бірегей түрде анықталады және формулалар бойынша есептеледі, мұнда 7p радиусы m шеңбер болып табылады. R сақинасының ішіндегі ерікті z нүктесін бекітейік. Радиустары теңсіздіктерді қанағаттандыратын r нүктесінде центрлері бар шеңберлер тұрғызып, жаңа сақинаны қарастырамыз.Көбейткіш байланысқан облыс үшін Коши интегралдық теоремасы бойынша бізде (8) қосындысындағы интегралдардың әрқайсысын бөлек түрлендірейік. 7d* шеңбері бойындағы барлық £ нүктелері үшін біркелкі жинақталған қатардың 1 1 қосындысының қатынасы орындалады. Сондықтан ^ бөлігін vi- /" түрінде көрсетуге болады / Біршама басқаша, барлық ξ нүктелері үшін шеңбер ir> бізде қатынас бар Сондықтан ^ бөлігін (10) және (12) формулалардағы біркелкі жинақталған қатардың қосындысы ретінде көрсетуге болады, дөңгелек сақинадағы аналитикалық функциялар. Демек, Коши теоремасы бойынша 7/r және 7r/ шеңберлері кез келген шеңбермен ауыстырылса, сәйкес интегралдардың мәндері өзгермейді. Бұл (10) және (12) формулаларын біріктіруге мүмкіндік береді.(8) формуланың оң жағындағы интегралдарды олардың сәйкесінше (9) және (11) өрнектерімен ауыстырсақ, біз қажетті кеңейтуді аламыз.Себебі z ерікті. сақина нүктесінде ( 14) қатары осы сақинаның барлық жерінде f(z) функциясына жинақталады, ал кез келген сақинада қатар бұл функцияға абсолютті және біркелкі жинақталады. Енді (6) түрінің ыдырауы бірегей екенін дәлелдеп көрейік. Тағы бір ыдырау орын алады деп есептейік.Одан кейін R сақинасының барлық жерінде бізде шеңбер бойынша қатар (15) біркелкі жинақталады. Теңдіктің екі жағын да көбейтіңіз (мұндағы m - тұрақты бүтін сан, және екі қатарды да мүше бойынша интегралдаңыз. Нәтижесінде біз сол жақта, ал оң жағында - Csh. Осылайша, (4, \u003d St. m ерікті сан болғандықтан, коэффициенттері (7) формулалармен есептелетін соңғы теңдік қатары (6) Лоран қатарының коэффициенттері үшін 7) сақинадағы f(z) функциясының Лоран қатары деп аталады. практикада сирек қолданылады, өйткені, әдетте, олар күрделі есептеулерді қажет етеді.Әдетте, мүмкін болса, қарапайым функциялардың дайын Тейлор кеңейтімдері қолданылады.Кеңейтудің бірегейлігіне негізделген кез келген заңды әдіс бірдей нәтижеге әкеледі. 2-мысал Фуисций /(r) екі сингулярлық нүктесі бар деп есептей отырып, әртүрлі облыстардың функцияларының Лоран сериясының кеңеюін қарастырайық: Демек, үш сақина облысы бар. және центрі r = 0 нүктесінде орналасқан. Олардың әрқайсысында f(r) функциясы аналитикалық болып табылады: а) шеңбер шеңбердің сыртқы көрінісі болып табылады (27-сурет). Осы аймақтардың әрқайсысында /(z) функциясының Лоран кеңейтімдерін табайық. /(z) элементар бөлшектердің қосындысы ретінде көрсетеміз a) Шеңберді түрлендіру қатынасы (16) Геометриялық прогрессияның мүшелерінің қосындысының формуласын пайдаланып, аламыз. b) -z функциясына арналған сақина осы сақинада жинақты болып қалады, өйткені |z| үшін j^j функциясына арналған (19) сериясы > 1 айырмашылығы бар. Сондықтан, /(z) функциясын келесідей түрлендіреміз: (19) формуласын қайта қолданып, Бұл қатар үшін жинақталатынын аламыз. (18) және (21) кеңейтімдерін (20) қатынасына қойып, в) -z функциясы үшін шеңбердің сыртқы көрінісін |z| > 2 ажыратылады және функциясы үшін (21) қатары /(z) функциясын келесі түрде көрсетейік: /<*> (18) және (19) формулаларын пайдаланып, НЕМЕСЕ 1 мәнін аламыз Бұл мысал бірдей f(z) функциясы үшін Лоран кеңеюінің, жалпы айтқанда, әртүрлі сақиналар үшін басқа пішінге ие екенін көрсетеді. Мысал 3. Лоран қатары функциясының 8 Лоран қатарының ыдырауын табыңыз Оқшауланған дара нүктелер және олардың сақиналы А аймағындағы жіктелуі f (z) функциясының көрінісін келесі түрде қолданамыз: және екінші мүшесін түрлендіру геометриялық прогрессияның мүшелерінің қосындысының формуласын аламыз Табылған өрнектерді (22) формулаға қойып, бізде 4-мысал бар. Лоран қатарындағы функцияны жұқа zq = 0 маңайында кеңейтіңіз. Кез келген комплекс үшін , бізде Let Бұл кеңею кез келген z Ф 0 нүктесі үшін жарамды. Бұл жағдайда сақиналы аймақ бір лақтырылған z - 0 нүктесі бар бүкіл кешенді жазықтық болып табылады. Бұл аймақты келесі қатынас арқылы анықтауға болады: Бұл функция аналитикалық болып табылады. аймақта Лоран қатарының коэффициенттері үшін формулалардан (13) алдыңғы абзацтағыдай дәлелдеу арқылы Kouiw теңсіздіктерін алуға болады. егер f(z) функциясы шеңбермен шектелген болса, мұндағы M тұрақты), онда оқшауланған ерекше нүктелер zo нүктесі f(z) функциясының оқшауланған сингулярлық нүктесі деп аталады, егер нүктенің сақиналы маңайы бар болса. бұл жиынды кейде 2o нүктесінің тесілген маңайы деп те атайды, мұнда f(z) функциясы бірмәнді және аналитикалық болады. zo нүктесінің өзінде функция анықталмаған немесе бір мәнді және аналитикалық емес. zo нүктесіне жақындаған кезде /(z) функциясының әрекетіне байланысты ерекше нүктелердің үш түрі ажыратылады. Оқшауланған сингулярлық нүкте деп аталады: 1) егер ақырғы бар болса, алынбалы 2) егер pmusach болса, 3) f(z) функциясының шегі болмаса, мәнді сингулярлы нүкте. Теорема 16. f(z) функциясының оқшауланған z0 сингулярлық нүктесі, егер zo нүктесінің маңайындағы f(z) функциясының Лоран кеңеюі негізгі бөлікті қамтымаса ғана, алынбалы сингулярлық нүкте болып табылады, яғни, Let zo пішіні бар - алынбалы сингулярлық нүкте. Сонда ақырлысы бар, демек, f(z) функциясы r нүктесінің прокологиялық маңайында шектелген. Коши теңсіздіктерінің арқасында орнатамыз. Өйткені ρ-ті өзіміз қалағандай кіші етіп таңдауға болатындықтан, онда барлық Теріс дәрежелердегі коэффициенттер (z - 20) нөлге тең: Керісінше, Лоранның /(r) функциясының zq нүктесінің маңайындағы кеңеюі тек дұрыс бөлікті қамтысын, яғни оның (23) түрі бар. сондықтан ол Тейлор. z -* z0 үшін /(r) функциясының шекті мәні бар екенін көру оңай: Теорема 17. f(z) функциясының оқшауланған zq сингулярлық нүктесі J(z) функциясы болған жағдайда ғана алынып тасталуы мүмкін. zq нүктесінің кейбір тесілген төңірегінде шектелген, Zgmechai емес. r0 f(r)-ның алынбалы сингулярлық нүктесі болсын. Егер f(r) функциясы th нүктесінде центрленген қандай да бір шеңберде аналитикалық болады деп есептейміз. Бұл нүктенің атауын анықтайды - бір реттік. Теорема 18. f(z) функциясының оқшауланған zq нүктесі полюс болып табылады, егер f(z) функциясының Лоран кеңеюінің нүктенің маңайындағы негізгі бөлігі соңғы (және оң) санды қамтитын болса ғана. нөлдік емес мүшелердің, яғни 4 түрі бар z0 полюс болсын. Содан бері f(z) функциясы аналитикалық және нөлге тең емес z0 нүктесінің тесілген маңайы бар. Содан кейін осы маңайда аналитикалық функция анықталады және Демек, zq нүктесі функцияның алынбалы сингулярлық нүктесі (нөл) болып табылады немесе мұндағы h(z) аналитикалық функция, h(z0) ∩ 0. маңайында аналитикалық болады. zq нүктесі, демек, біз оны қайдан аламыз Енді f(z) функциясының zo нүктесінің тесілген маңайында (24) түрінің ыдырауы бар деп есептейік. Бұл осы маңайда f(z) функциясы функциямен бірге аналитикалық екенін білдіреді. g(z) функциясы үшін кеңейту жарамды, одан zq g(z) функциясының алынбалы сингулярлық нүктесі және бар екені анық. Сонда функция 0-ге ұмтылады - функцияның полюсі Тағы бір қарапайым бар. факт. Zq нүктесі f(z) функциясының полюсі болып табылады, егер g(z) = y функциясын g(z0) = 0 орнату арқылы zq нүктесінің маңайындағы аналитикалық функцияға кеңейту мүмкін болса ғана. f(z) функциясының полюсі jfa функциясының нөлдік реті деп аталады. 16 және 18 теоремалар келесі бекітуді білдіреді. Теорема 19. Оқшауланған сингулярлық жіңішке, егер осы нүктенің тесілген төңірегінде Лоран кеңеюінің негізгі бөлігі шексіз көп нөлден басқа мүшелерден тұратын болса ғана, мәні бойынша сингулярлы болады. Мысал 5. Функцияның сингулярлық нүктесі zo = 0. Бізде Лоран сериясының оқшауланған сингулярлық нүктелері бар және олардың классификациясы Сондықтан zo = 0 алынбалы сингулярлық нүкте болып табылады. Лоран қатарындағы /(z) функциясының нөлдік нүктеге жақын жерде кеңеюі тек дұрыс бөлікті қамтиды: 7-мысал. f(z) = f(z) функциясының сингулярлық нүктесі zq = 0. Бұл функцияның нақты және жорамал осьтердегі әрекетін қарастырайық: x 0 нүктесіндегі нақты осьте, елестету осінде Сондықтан ақырлы да, z -* 0 кезінде f(z) шексіз шегі жоқ. Демек, r0 = 0 нүктесі f(z) функциясының мәні бойынша дара нүктесі болып табылады. f(z) функциясының нөлдік нүктенің маңайындағы Лоран кеңеюін табайық. Кез келген С кешені үшін біз орнаттық. Сонда Лоранның кеңеюі z-дің теріс дәрежелері бар шексіз көп мүшелерден тұрады.

Анықтама.Функцияның сингулярлық нүктесі деп аталады оқшауланған, егер бұл нүктенің кейбір маңайында аналитикалық функция болса (яғни сақинадағы аналитикалық).

Функцияның оқшауланған дара нүктелерінің классификациясы осы функцияның дара нүктенің маңайындағы әрекетімен байланысты.

Анықтама.Нүкте деп аталады бір реттік функцияның сингулярлық нүктесі, егер бұл функцияның соңғы шегі -де болса.

5-мысалФункцияның нүктеде алынбалы сингулярлығы бар екенін көрсетіңіз.

Шешім.Бірінші керемет шекті еске түсіре отырып, біз есептейміз

Бұл берілген функцияның нүктеде алынбалы сингулярлық бар екенін білдіреді.

4-тапсырма.Нүкте үшін алынбалы екенін көрсетіңіз.

Анықтама.Нүкте деп аталады полюс функциясы, егер бұл функция үшін шексіз артады, яғни.

Аналитикалық функцияның нөл және полюсі ұғымдарының байланысына назар аударайық. Функцияны ретінде көрсетейік.

Егер нүкте функцияның қарапайым нөлі болса, онда функцияның жай полюсі болады

Егер нүкте функция үшін нөл реті болса, онда функция үшін ол полюс болады тапсырыс.

6-мысалФункцияның нүктеде үшінші ретті полюсі бар екенін көрсетіңіз.

Шешім.Десек, аламыз. Біз нөлге бейім болғандықтан, кез келген заңға сәйкес бізде . Сонда , және онымен бірге функцияның өзі шексіз өседі. Демек, , яғни дара нүкте полюс болып табылады. Функция үшін бұл нүкте үш есе нөл екені анық. Демек, бұл функция үшін нүкте үшінші ретті полюс болып табылады.

5-тапсырма.Нүктенің жай полюсі бар екенін көрсетіңіз.

Анықтама.Нүкте деп аталады негізінен ерекше функцияның нүктесі, егер бұл нүктеде функцияның ақырғы да, шексіз де шегі болмаса (функцияның әрекеті анықталмаған).

Функцияның маңызды сингулярлық нүктесі болсын . Содан кейін кез келген алдын ала тағайындалған күрделі сан үшін мәндер тенденцияға сәйкес келетін нүктелердің тізбегі бар: ( Сочокки теоремасы).

7-мысалНүктедегі функцияның маңызды ерекшелікке ие екенін көрсетіңіз.

Шешім.Берілген функцияның нүктеге жақын жерде әрекетін қарастырайық . Өйткені нақты осьтің оң бөлігінің бойымен (яғни ) бізде және ; егер нақты осьтің теріс бөлігінің бойымен (яғни), онда және . Сондықтан шектеу жоқ. Анықтау бойынша функция нүктеде маңызды ерекшелікке ие.

Функцияның нөлдегі әрекетін Сочокки теоремасы тұрғысынан қарастырайық. Нөл мен шексіздіктен басқа кез келген күрделі сан болсын.

Теңдіктен табамыз. Десек, нүктелер тізбегін аламыз, . Әлбетте, . Бұл тізбектің әрбір нүктесінде функция -ге тең, демек

6-тапсырма.Функцияның нүктеде маңызды ерекшелік бар екенін көрсетіңіз.

Шексіздік нүктесі әрқашан функция үшін арнайы болып саналады. Нүкте функцияның оқшауланған сингулярлық нүктесі деп аталады, егер бұл функцияның басында центрде орналасқан қандай да бір шеңберден тыс басқа ерекше нүктелер болмаса.

Оқшауланған сингулярлық нүктелердің жіктелуін жағдайға да кеңейтуге болады .

8-мысалФункцияның шексіздікте қос полюсі бар екенін көрсетіңіз.

Шешім.Функцияны қарастырайық, мұндағы аналитикалық функция нүктенің маңайында және . Бұл функция шексіздікте қос нөлге ие екенін білдіреді, бірақ функция үшін нүкте қос полюс болып табылады.

9-мысалФункцияның шексіздікте маңызды сингулярлылығы бар екенін көрсетіңіз.

Шешім.Ұқсас мәселе 7-бапта қарастырылған. Шексіз алыс нүкте маңындағы функцияның әрекетін қарастырайық. Нақты осьтің оң бөлігінің бойымен, ал нақты осьтің теріс бөлігінің бойымен. Бұл нүктеде функцияның шегі жоқ екенін және анықтаманың күші бойынша бұл нүкте мәні бойынша ерекше екенін білдіреді.

Нүктедегі функцияның сингулярлылығының табиғатын анықтауға болады негізгі бөлігі Осы нүктенің төңірегінде Лоран кеңеюі.

Теорема 1.Мәселе болу үшін бір реттік функциясының сингулярлық нүктесі , сәйкес Лоран кеңеюі қажет және жеткілікті негізгі бөлігін қамтыған жоқ.

6-тапсырма.Функцияның Тейлор кеңеюін нүктенің маңайында пайдаланып, оның нөлде алынбалы сингулярлығы бар екенін көрсетіңіз.

2-теорема.Мәселе болу үшін полюс функциялары қажет және жеткілікті негізгі бөлігі сәйкес Лоран кеңеюі мүшелерінің шектеулі санын қамтиды :

Ең жоғары теріс мүшенің саны полюстің ретін анықтайды.

Бұл жағдайда функцияны келесідей көрсетуге болады

мұндағы нүктедегі аналитикалық функция, , полюстің реті.

10-мысалФункцияның нүктелерінде қарапайым полюстері бар екенін көрсетіңіз.

Шешім.Бір нүктені қарастырайық. Біз 2-мысалда алынған осы нүктеге жақын жерде осы функцияның Лоран кеңеюін қолданамыз:

Бұл кеңейтудің негізгі бөлігіндегі ең жоғары (және жалғыз) теріс қуат біреуге тең болғандықтан, нүкте бұл функцияның қарапайым полюсі болып табылады.

Бұл нәтижені басқа жолмен алуға болатын еді. Пішінде көрсетейік және қоямыз - бұл және нүктесінде аналитикалық болатын функция. Демек, (8)-ге байланысты бұл функция нүктеде қарапайым полюске ие.

Басқа әдіс: нүктесінде қарапайым нөлі бар функцияны қарастырыңыз. Демек, бұл кезде оның қарапайым полюсі бар.

Сол сияқты функцияны , мұндағы және нүктесінде аналитикалық болатын функция түрінде жазсақ, онда нүкте функцияның қарапайым полюсі екені бірден түсінікті болады.

7-тапсырма.Функцияның нүктесінде 2-ші ретті полюсі және нүктесінде 4-ші ретті полюсі бар екенін көрсетіңіз.

Теорема 3.Мәселе болу үшін негізінен ерекше функциясының нүктесі, бұл қажет және жеткілікті негізгі бөлігі Лоранның кеңеюі нүктенің төңірегінде мүшелердің шексіз санын қамтиды .

11-мысал.Функция нүктесіндегі даралықтың сипатын анықтаңыз

Шешім.Косинустың белгілі кеңеюінде біз оның орнына қоямыз:

Демек, нүктенің маңайындағы Лоран кеңеюі пішінге ие

Мұнда дұрыс бөлік бір термин. Ал негізгі бөлікте шексіз көп терминдер бар, сондықтан нүкте мәні бойынша дара.

8-тапсырма.Бір нүктеде функцияның маңызды ерекшелікке ие екенін көрсетіңіз.

Кейбір функцияларды қарастырыңыз және оның Лоран кеңеюін мына нүктеге жазыңыз:

Нүкте нүктеге барғанша алмастырайық . Енді бізде шексіздік нүктесінің маңайында бар

Жаңа белгілеуді енгізу қалды. Біз алып жатырмыз

мұндағы негізгі бөлік және шексіздіктегі нүктенің маңындағы функцияның Лоран кеңеюінің тұрақты бөлігі. Сонымен, функцияның нүктенің маңайындағы Лоран кеңеюінде негізгі бөлік оң дәрежелердегі қатар, ал дұрыс бөлік теріс дәрежелердегі қатар болып табылады. Осыны ескере отырып

Дегенмен, даралықтың табиғатын анықтаудың жоғарыдағы критерийлері шексіз алыс нүкте үшін жарамды болып қалады.

12-мысал.Нүктедегі функцияның даралығының табиғатын табыңыз. , содан кейін ол бір сәтте оқшауланбаған болып шығуы мүмкін.

15-мысалШексіз алыс нүктедегі функция маңызды ерекшелікке ие. Функцияның нүктесі оқшауланған сингулярлық нүкте емес екенін көрсетіңіз.

Шешім.Функция азайғыштың нөлдерінде, яғни , нүктелерінде шексіз полюстерге ие. Өйткені, кез келген маңайында полюстері бар нүкте полюстер үшін шекті нүкте болып табылады.

дара нүкте

математикада.

1) F ( теңдеуімен берілген қисық сызықтың ерекше нүктесі x, y) = 0, - нүктесі M 0 ( x 0 , y 0), онда F функциясының екі жеке туындысы да ( x, y) жоғалады:

Егер қосымша F функциясының барлық екінші дербес туындылары болмаса x, y) нүктесінде М 0 нөлге тең болса, онда О. т. қос деп аталады. Егер М 0 нүктесінде бірінші туындылардың жойылуымен қатар барлық екінші туындылар жойылып кетсе, бірақ үшінші туындылардың барлығы нөлге тең болмаса, онда О. т. үштік деп аталады және т.б. Қос О.т маңындағы қисық құрылымын зерттегенде өрнек белгісі маңызды рөл атқарады.

Егер Δ > 0 болса, онда O. т. оқшауланған деп аталады; мысалы, қисық y 2 - x 4 + 4x 2= 0 басы оқшауланған O. t. (қараңыз күріш. бір ). Егер Δ x 2 + y 2 + a 2) 2 - 4a 2 x 2 - a 4= 0 координаталар басы - түйіндік O. t. (қараңыз күріш. 2 ). Егер Δ = 0 болса, онда O. t. қисығы не оқшауланған, не қисық сызықтың әртүрлі тармақтарының осы нүктеде ортақ жанама болуымен сипатталады, мысалы: жанама және қисық тәрізді нүктені құрайды. y 2 - x 3= 0 (қараңыз күріш. 3 , а); б) 2-ші текті төбе – қисық тәрізді қисық сызықтың әртүрлі тармақтары ортақ жанаманың бір жағында орналасқан. (y - x 2)2 - x 5= 0 (қараңыз күріш. 3 , b); в) өздігінен жанасу нүктесі (қисық үшін y 2 - x 4= 0 басы - өздігінен жанасу нүктесі; (см. күріш. 3 , ішінде). Көрсетілген О. т.-мен қатар ерекше атаулары бар басқа да көптеген О. т. мысалы, асимптотикалық нүкте - айналуларының шексіз саны бар спиральдың шыңы (суретті қараңыз). күріш. 4 ), үзіліс нүктесі, бұрыш нүктесі және т.б.

2) Дифференциалдық теңдеудің сингулярлық нүктесі – дифференциалдық теңдеудің оң жақ бөлігінің алымы мен бөлімі бір уақытта жойылатын нүкте (Дифференциалдық теңдеулерді қараңыз)

мұндағы P және Q үздіксіз дифференциалданатын функциялар. О.т координаталар басында орналасқан деп есептеп және Тейлор формуласын қолданып (Тейлор формуласын қараңыз), біз (1) теңдеуді формада көрсете аламыз.

мұндағы P 1 ( x, y) және Q 1 ( x, y) қатысты шексіз аз

Атап айтқанда, егер λ 1 ≠ λ 2 және λ 1 λ 2 > 0 немесе λ 1 = λ 2 болса, онда O. t. түйін болып табылады; түйіннің жеткілікті шағын маңайындағы нүктелер арқылы өтетін барлық интегралдық қисық сызықтар оған енеді. Егер λ 1 ≠ λ 2 және λ 1 λ 2 i β, α ≠ 0 және β ≠ 0 болса, онда O. t. фокус; фокустың жеткілікті шағын төңірегінде нүктелер арқылы өтетін барлық интегралдық қисықтар фокустың кез келген ерікті шағын маңайындағы бұрылыстарының шексіз саны бар спиральдар болып табылады. Егер, ақырында, λ 1,2 = ± менβ, β ≠ 0, онда O. t. сипаты P кеңейтулерінде сызықтық мүшелермен анықталмайды ( x, y) және Q ( x, y), жоғарыда аталған барлық жағдайларда болғандай; мұндағы O. т. фокус немесе орталық болуы мүмкін немесе күрделірек сипатқа ие болуы мүмкін. Орталықтың маңайында барлық интегралдық қисық сызықтар тұйықталған және олардың ішінде орталықты қамтиды. Сонымен, мысалы, (0, 0) нүктесі теңдеулер үшін түйін болып табылады сағ" = 2u/x(λ 1 = 1, λ 2 = 2; қараңыз күріш. бес , а) және ж" = u/x(λ 1 = λ 2 = 1; қараңыз күріш. бес , b) теңдеу үшін ершік y" = -y/x(λ 1 = -1, λ 2 = 1 ; см. күріш. 6 ), теңдеу үшін фокус y" =(x + y) / (x - y) (λ 1 = 1 - мен, λ 2 = 1 + мен; см. күріш. 7 ) және теңдеудің центрі y" = -x / y(λ 1 = -і, λ 2 = мен; см. күріш. 8 ).

Егер x, y) және Q ( x, y) аналитикалық болып табылады, жоғары ретті О. т.-ның көршілестігін аймақтарға бөлуге болады: D 1 - интегралдық қисықтармен толтырылған, олардың екі ұшы О. т.-ға (эллиптикалық аймақтар), D 2 - толтырылған. интегралдық қисықтары бар, оның бір ұшы О.т.-ға кіреді (параболалық облыстар) және D 3 - О.т.-ға кіретін екі интегралдық қисықпен шектелген облыстар, олардың арасында гиперболалар типінің интегралдық қисықтары бар. (гиперболалық аймақтар) (қараңыз. күріш. тоғыз ). Егер О нүктесіне кіретін интегралдық қисық сызықтар болмаса, онда О нүктесі тұрақты типті нүкте деп аталады. Орнықты О.т.-ның маңайы олардың арасында спиральдар орналасқан, ішінде O.-ты қамтитын тұйық интегралдық қисықтардан тұрады (суретті қараңыз). күріш. 10 ).

О.т дифференциалдық теңдеулерін зерттеу, яғни мәні бойынша О.т.М.Ляпунов а, А.Пуанкаре және т.б. маңайындағы интегралдық қисықтардың отбасыларының мінез-құлқын зерттеу).

3) Бір мәнді аналитикалық функцияның дара нүктесі деп функцияның аналитикалық қасиеті бұзылатын нүктені айтады (Аналитикалық функцияларды қараңыз). Егер О. т маңайында болса. а, басқа O. т.-дан бос, содан кейін нүкте бірақоқшауланған O. t деп аталады.Егер бірақоқшауланған O. т. болып табылады және бар шектеулі a алынбалы O. t деп аталады. f(а)= b, қол жеткізуге болады атүзетілген функцияның кәдімгі нүктесі болады. Мысалы, нүкте z= 0 - f 1 (функциясы үшін алынбалы О.Т. z) = f(z), егер z≠ 0, және f 1(0),=1, нүкте z= 0 қарапайым нүкте [ f 1 (z) нүктесінде аналитикалық болып табылады z= 0]. Егер бірақ- оқшауланған O. t. және a полюсі немесе функцияның мәнсіз дара нүктесі деп аталады. f(z), егер Лоран сериясы) қызмет атқарса f(z) оңашаланған О.т маңайында теріс күштер жоқ z - а, егер бірақ- алынбалы O. т., теріс қуаттардың шектеулі санын қамтиды z - а, егер бірақ- полюс (бұл жағдайда полюстің реті Р a-ның ең жоғары дәрежесі ретінде анықталады - мәні бойынша ерекше нүкте. Мысалы, функция үшін

p = 2, 3, …)

нүкте z= 0 - тапсырыстың полюсі Р, функциясы үшін

нүкте z= 0 маңызды ерекше нүкте болып табылады.

Дәрежелік қатардың жинақтылық шеңберінің шекарасында берілген дәрежелік қатармен осы шеңбер ішінде бейнеленген функцияның кем дегенде бір О.м болуы керек. Бір мәнді аналитикалық функцияның өмір сүру облысының барлық шекаралық нүктелері (табиғи шекара) осы функцияның шекаралық нүктелері болып табылады. Сонымен бірлік шеңбердің барлық нүктелері | z| = 1 функция үшін ерекше

Көп мәнді аналитикалық функция үшін «О. Т.» қиынырақ. Функцияның Риман бетінің бөлек парақтарында (яғни, бір мәнді аналитикалық элементтердің О. т.) О. т.-дан басқа кез келген тармақталған нүкте де функцияның О. т.-сы болып табылады. Риман бетінің оқшауланған тармақтары (яғни, олардың кейбір маңайларында ешбір жапырақта басқа О.т. функциялары жоқ болатын тармақ нүктелері) келесідей жіктеледі. Егер а ақырлы ретті оқшауланған тармақталған нүкте болса және ақырғы а бар болса, оны критикалық полюс деп атайды. Егер бірақШексіз ретті оқшауланған тармақталған нүкте және a трансцендентальды O. t деп аталады. Барлық қалған оқшауланған тармақталған нүктелер сыни мәнді жеке нүктелер деп аталады. Мысалдар: нүкте z= 0 - f функциясының кәдімгі критикалық нүктесі ( z) = журнал zжәне функцияның маңызды маңызды сингулярлық нүктесі f (z) = күнә журналы z.

Алынбалыдан басқа кез келген О.т. аналитикалық жалғасуға кедергі болып табылады, яғни алынбайтын О. т. арқылы өтетін қисық бойымен аналитикалық жалғасу мүмкін емес.

Ұлы Совет энциклопедиясы. - М.: Совет энциклопедиясы. 1969-1978 .

Басқа сөздіктерде «Арнайы нүкте» не екенін қараңыз:

Мұнда ұпайлар. Сондай-ақ сингулярлық нүктені (дифференциалдық теңдеулер) қараңыз. Математикадағы ерекшелік немесе ерекшелік – математикалық объектінің (әдетте функция) анықталмаған немесе тұрақты емес әрекетке ие болатын нүктесі (мысалы, ... ... Wikipedia

Аналитикалық функция - аналитикалық шарттар бұзылатын нүкте. Егер f(z) аналитикалық функциясы барлық жерде z0 нүктесінің кейбір маңайында анықталған болса ... Физикалық энциклопедия

Аналитикалық функция - бұл функцияның аналитикалықтығы бұзылатын нүкте ... Үлкен энциклопедиялық сөздік

дара нүкте- — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Электротехника және энергетикалық өнеркәсібінің ағылшынша орысша сөздігі, Мәскеу, 1999] Электротехника тақырыптары, негізгі ұғымдар EN сингулярлық нүкте ... Техникалық аудармашының анықтамалығы

1) f(z) аналитикалық функциясының ОТ – бұл айнымалының жазықтығындағы қандай да бір жол бойымен z күрделі айнымалысының f(z) функциясының элементінің аналитикалық жалғасуына кедергі. f(z) аналитикалық функциясы кейбір ... ... арқылы анықталсын. Математикалық энциклопедия

Аналитикалық функция, функцияның аналитикалық қасиеті бұзылатын нүкте. * * * ЖЕКЕ НҮКТЕГЕ аналитикалық функцияның ЖЕКЕ НҮКТЕГІ, функцияның аналитикалық қасиеті бұзылатын нүкте ... энциклопедиялық сөздік

дара нүкте- ypatingasis taškas statusas T sritis automatika atitikmenys: ағылшын. сингулярлық нүкте вок. сингулярлық Punkt, m rus. сингулярлық нүкте, fpranc. нүктелік бөлшек, м; нүкте сингулиер, м … Automatikos терминų žodynas