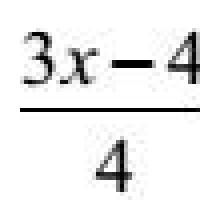Математическая статистика и ее методы. Математическая статистика для специалистов различных областей. Вариационный ряд для виборки имеет вид

Методы математической статистики

1. Введение

Математической статистикой называется наука, занимающаяся разработкой методов получения, описания и обработки опытных данных с целью изучения закономерностей случайных массовых явлений.

В математической статистике можно выделить два направления: описательную статистику и индуктивную статистику (статистический вывод). Описательная статистика занимается накоплением, систематизацией и представлением опытных данных в удобной форме. Индуктивная статистика на основе этих данных позволяет сделать определенные выводы относительно объектов, о которых собраны данные, или оценки их параметров.

Типичными направлениями математической статистики являются:

1) теория выборок;

2) теория оценок;

3) проверка статистических гипотез;

4) регрессионный анализ;

5) дисперсионный анализ.

В основе математической статистики лежит ряд исходных понятий без которых невозможно изучение современных методов обработки опытных данных. В ряд первых из них можно поставить понятие генеральной совокупности и выборки.

При массовом промышленном производстве часто нужно без проверки каждого выпускаемого изделия установить, соответствует ли качество продукции стандартам. Так как количество выпускаемой продукции очень велико или проверка продукции связана с приведением ее в негодность, то проверяется небольшое количество изделий. На основе этой проверки нужно дать заключение о всей серии изделий. Конечно нельзя утверждать, что все транзисторы из партии в 1 млн. штук годны или негодны, проверив один из них. С другой стороны, поскольку процесс отбора образцов для испытаний и сами испытания могут оказаться длительными по времени и привести к большим затратам, то объем проверки изделий должен быть таким, чтобы он смог дать достоверное представление о всей партии изделий, будучи минимальных размеров. С этой целью введем ряд понятий.

Вся совокупность изучаемых объектов или экспериментальных данных называется генеральной совокупностью. Будем обозначать через N число объектов или количество данных, составляющих генеральную совокупность. Величину N называют объемом генеральной совокупности. Если N>>1, то есть N очень велико, то обычно считают N = ¥.

Случайной выборкой или просто выборкой называют часть генеральной совокупности, наугад отобранную из нее. Слово "наугад" означает, что вероятности выбора любого объекта из генеральной совокупности одинакова. Это важное предположение, однако, часто трудно это проверить на практике.

Объемом выборки называют число объектов или количество данных, составляющих выборку, и обозначают n . В дальнейшем будем считать, что элементам выборки можно приписать соответственно числовые значения х 1 , х 2 , ... х n . Например, в процессе контроля качества производимых биполярных транзисторов это могут быть измерения их коэффициента усиления по постоянному току.

2. Числовые характеристики выборки

2.1 Выборочное среднее

Для конкретной выборки объема n ее выборочное среднее

определяется соотношением

где х i – значение элементов выборки. Обычно требуется описать статистические свойства произвольных случайных выборок, а не одной из них. Это значит, что рассматривается математическая модель, которая предполагает достаточно большое количество выборок объема n. В этом случае элементы выборки рассматриваются как случайные величины Х i , принимающие значения х i с плотностью вероятностей f(x), являющейся плотностью вероятностей генеральной совокупности. Тогда выборочное среднее также является случайной величиной

равной

Как и ранее будем обозначать случайные величины прописными буквами, а значения случайных величин – строчными.

Среднее значение генеральной совокупности, из которой производится выборка, будем называть генеральным средним и обозначать m x . Можно ожидать, что если объем выборки значителен, то выборочное среднее не будет заметно отличаться от генерального среднего. Поскольку выборочное среднее является случайной величиной, для нее можно найти математическое ожидание:

Таким образом, математическое ожидание выборочного среднего равно генеральному среднему. В этом случае говорят, что выборочное среднее является несмещенной оценкой генерального среднего. В дальнейшем мы вернемся к этому термину. Так как выборочное среднее является случайной величиной, флуктуирующей вокруг генерального среднего, то желательно оценить эту флуктуацию с помощью дисперсии выборочного среднего. Рассмотрим выборку, объем которой n значительно меньше объема генеральной совокупности N (n << N). Предположим, что при формировании выборки характеристики генеральной совокупности не меняются, что эквивалентно предположению N = ¥. Тогда

Случайные величины Х i и X j (i¹j) можно считать независимыми, следовательно,

Подставим полученный результат в формулу для дисперсии:

где s 2 – дисперсия генеральной совокупности.

Из этой формулы следует, что с увеличением объема выборки флуктуации среднего выборочного около среднего генерального уменьшаются как s 2 /n. Проиллюстрируем сказанное примером. Пусть имеется случайный сигнал с математическим ожиданием и дисперсией соответственно равными m x = 10, s 2 = 9.

Отсчеты сигнала берутся в равноотстоящие моменты времени t 1 , t 2 , ... ,

X(t)
X 1

t 1 t 2 . . . t n t

Так как отсчеты являются случайными величинами, то будем их обозначать X(t 1), X(t 2), . . . , X(t n).

Определим количество отсчетов, чтобы среднее квадратическое отклонение оценки математического ожидания сигнала не превысило 1% его математического ожидания. Поскольку m x = 10, то нужно, чтобы

С другой стороны поэтому или Отсюда получаем, что n ³ 900 отсчетов.

2.2 Выборочная дисперсия

По выборочным данным важно знать не только выборочное среднее, но и разброс выборочных значений около выборочного среднего. Если выборочное среднее является оценкой генерального среднего, то выборочная дисперсия должна быть оценкой генеральной дисперсии. Выборочная дисперсия

для выборки, состоящей из случайных величин определяется следующим образом

Используя это представление выборочной дисперсии, найдем ее математическое ожидание

(Е.П. Врублевский, О.Е. Лихачев, Л.Г. Врублевская)

Применяя в исследовании те или иные методы, в конечном итоге экспериментатор получает большую или мень­шую совокупность различных числовых показателей, призванных характеризовать изучаемое явление. Но без систематизации и надлежащей обработки полученных результатов, без глубокого и всестороннего анализа фактов не удается извлечь заключенную в них информацию, от­крыть закономерности, сделать обоснованные выводы. Приведенные в тексте самые элементарные и вполне доступные для каждого студента приемы матема­тической обработки результатов носят демонстрационный характер. Это означает, что примеры иллюстрируют применение того или иного математико-статистического метода, а не дают его развернутую интерпретацию.

Средние величины и показатели вариации .Прежде чем говорить о более существенных вещах, необходимо уяснить такие статистические понятия, как генеральная и выборочная совокупности. Группа чисел, объединяемых каким-либо признаком, называется совокупностью. Наблюдения, проводимые над какими-то объектами, могут охватывать всех членов изучаемой совокупности без исключения или ограничиваться обследованием лишь некоторой ее части. В первом случае наблюде­ние будет называться сплошным, или полным,во втором - частичным, или выборочным. Сплошное обследование проводится очень редко, так как в силу ряда причин оно практически либо невыполни­мо, либо нецелесообразно. Так, невозможно, например, об­следовать всех мастеров спорта по легкой атлетике. Поэтому в подавля­ющем большинстве случаев вместо сплошного наблюдения изучению подвергают какую-то часть обследуемой совокупности, по которой и судят о ее состоянии в целом.

Совокупность, из которой отбирается часть ее членов для совместного изучения, называется генеральной,а ото­бранная тем или иным способом часть данной совокупности получила название выборочнойсовокупности или просто выборкой. Следует уточнить, что понятие генеральной совокупности является относительным. В одном случае это все спортсмены, а в дру­гом - города, вуза. Так, например, генеральной совокупностью могут быть все студенты вуза, а выборкой - студенты специализации футбола. Число объектов в любой совокупности называется объемом (объем генеральной совокупности обозначается N, а объем выборки n).

Предполагается, что выборка с должной достоверностью представляет генеральную совокупность только в том случае, если ее элементы избраны из генеральной нетенденциозно. Для этого существует несколько путей: отбор выборки в соответствии с таблицей случайных чисел, разделение генеральной совокуп­ности на ряд непересекающихся групп, когда из каждой выбирается определенное количество объектов, и др.

Что касается объема выборки, то в соответствии с основными положениями математической статистики выборки тем представительнее (репрезентативнее), чем она полнее. Исследователь, стремясь к рентабельности своей работы, заинтересован в минимальном объеме выборки, и в такой ситуации количество объектов, отбираемых в вы­борку, является результатом компромиссного решения. Чтобы знать, насколько выборка достаточно достоверно представляет генеральную совокупность, необходимо оп­ределить ряд показателей (параметров).

Вычисление средней арифметической величины .Средняя арифметическая величина выборки характеризует сред­ний уровень значений изучаемой случайной величины в наблюдавшихся случаях и вычисляется путем деления сум­мы отдельных величин исследуемого признака на общее число наблюдений:

, (1)

где х i - вариант ряда;

п -объем совокупности.

Суммой Σпринято обозначать суммирование тех данных, ко­торые стоят справа от него. Нижние и верхние показатели Σ ука­зывают, с какого числа следует начать сложение и какими показателями его закончить. Так, обозначает, что необходимо сложить все х, имеющие порядковые номера от 1 до п . Знак показывает суммирование всех х от первого до последнего показателя.

Таким образом, вычисления по формуле (1) предполагают следующий порядок действий:

1. Суммируют все полученные х i , т. е. ,

2. Найденную сумму - делят на объем совокупности п.

Для удобства и наглядности работы с показателями необходимо составить таблицу, так как сложению подлежат x i , перебираемые от первого до последнего числа.

Например, средняя арифметическая определяется по формуле:

Результаты измерений приведены в таблице 1.

Таблица 1

Результаты тестирования спортсменов

Данным, полученным в результате эксперимента, свойственна изменчивость, которая может быть вызвана случайной ошибкой: погрешностью измерительного прибора, неоднородностью образцов и т.д. После проведения большого количества однородных данных экспериментатору необходимо их обработать для извлечения как можно более точной информации о рассматриваемой величине. Для обработки больших массивов данных измерений, наблюдений и т.п., которые могут быть получены при проведении эксперимента, удобно применять методы математической статистики .

Математическая статистика неразрывно связана с теорией вероятностей, но между этими науками есть существенное различие. Теория вероятностей использует уже известные распределения случайных величин , на основе которых рассчитываются вероятности событий, математическое ожидание т.д. Задача математической статистики – получить как можно более достоверную информацию о распределении случайной величины на основе экспериментальных данных.

Типичные направления математической статистики:

• теория выборок;
• теория оценок;
• проверка статистических гипотез;
• регрессионный анализ;
• дисперсионный анализ.

Методы математической статистики

Методы оценки и проверки гипотез основываются на вероятностных и гиперслучайных моделях происхождения данных.

Математическая статистика оценивает параметры и функции от них, которые представляют важные характеристики распределений (медиану, математическое ожидание, стандартное отклонение, квантили и др.), плотности и функции распределения и пр. Используются точечные и интервальные оценки.

Современная математическая статистика содержит большой раздел – статистический последовательный анализ , в котором допускается формирование массива наблюдений по одному массиву.

Математическая статистика также содержит общую теорию проверки гипотез и большое количество методов для проверки конкретных гипотез (например, о симметрии распределения, о значениях параметров и характеристик, о согласии эмпирической функции распределения с заданной функцией распределения, гипотеза проверки однородности (совпадение характеристик или функций распределения в двух выборках) и др.).

Проведением выборочных обследований , связанных с построением адекватных методов оценки и проверки гипотез, со свойствами разных схем организации выборок, занимается раздел математической статистики, имеющий большое значение. Методы математической статистики непосредственно использует следующие основные понятия.

Выборка

Определение 1

Выборкой называются данные, которые получены при проведении эксперимента.

Например, результаты дальности полета пули при выстреле одного и того же или группы однотипных орудий.

Эмпирическая функция распределения

Замечание 1

Функция распределения дает возможность выразить все важнейшие характеристики случайной величины.

В математической стаитистике существует понятие теоретической (заранее не известной) и эмпирической функции распределения.

Эмпирическая функция определяется по данным опыта (эмпирические данные), т.е. по выборке.

Гистограмма

Гистограммы используются для наглядного, но довольно приближенного, представления о неизвестном распределении.

Гистограмма представляет собой графическое изображение распределения данных.

Для получения качественной гистограммы придерживаются следующих правил :

• Количество элементов выборки должно быть существенно меньше объема выборки.
• Интервалы разбиения должны содержать достаточное число элементов выборки.

Если выборка очень большая зачастую интервал элементов выборки разбивают на одинаковые части.

Выборочное среднее и выборочная дисперсия

С помощью данных понятий можно получить оценку необходимых числовых характеристик неизвестного распределения, не прибегая к построению функции распределения, гистограммы и т.п.

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ЗАКОНЫ ИХ РАСПРЕДЕЛЕНИЯ.

Случайной называют такую величину, которая принимает значения в зависимости от стечения случайных обстоятельств. Различают дискретные и случайные непрерывные величины.

Дискретной называют величину, если она принимает счетное множество значений. (Пример: число пациентов на приеме у врача, число букв на странице, число молекул в заданном объеме).

Непрерывной называют величину, которая может принимать значения внутри некоторого интервала. (Пример: температура воздуха, масса тела, рост человека и т.д.)

Законом распределения случайной величины называется совокупность возможных значений этой величины и, соответствующих этим значениям, вероятностей (или частот встречаемости).

П р и м е р:

x	x 1	x 2	x 3	x 4	...	x n
p	р 1	р 2	р 3	р 4	...	p n

x	x 1	x 2	x 3	x 4	...	x n
m	m 1	m 2	m 3	m 4	...	m n

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН.

Во многих случаях наряду с распределением случайной величины или вместо него информацию об этих величинах могут дать числовые параметры, получившие название числовых характеристик случайной величины . Наиболее употребительные из них:

1 .Математическое ожидание - (среднее значение) случайной величины есть сумма произведений всех возможных ее значений на вероятности этих значений:

2 .Дисперсия случайной величины:

3 .Среднее квадратичное отклонение :

Правило “ТРЕХ СИГМ” - если случайная величина распределена по нормальному закону, то отклонение этой величины от среднего значения по абсолютной величине не превосходит утроенного среднего квадратичного отклонения

ЗАОН ГАУССА – НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ

Часто встречаются величины, распределенные по нормальному закону (закон Гаусса). Главная особенность : он является предельным законом, к которому приближаются другие законы распределения.

Случайная величина распределена по нормальному закону, если ее плотность вероятности имеет вид:

M(X) - математическое ожидание случайной величины;

s - среднее квадратичное отклонение.

Плотность вероятности (функция распределения) показывает, как меняется вероятность, отнесенная к интервалу dx случайной величины, в зависимости от значения самой величины:

ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

Математическая статистика - раздел прикладной математики, непосредственно примыкающий к теории вероятностей. Основное отличие математической статистики от теории вероятностей состоит в том, что в математической статистике рассматриваются не действия над законами распределения и числовыми характеристиками случайных величин, а приближенные методы отыскания этих законов и числовых характеристик по результатам экспериментов.

Основными понятиями математической статистики являются:

1. Генеральная совокупность;

2. выборка;

3. вариационный ряд;

4. мода;

5. медиана;

6. процентиль,

7. полигон частот,

8. гистограмма.

Генеральная совокупность - большая статистическая совокупность, из которой отбирается часть объектов для исследования

(Пример: все население области, студенты вузов данного города и т.д.)

Выборка (выборочная совокупность) - множество объектов, отобранных из генеральной совокупности.

Вариационный ряд - статистическое распределение, состоящее из вариант (значений случайной величины) и соответствующих им частот.

Пример:

X,кг

m

x - значение случайной величины (масса девочек в возрасте 10 лет);

m - частота встречаемости.

Мода – значение случайной величины, которому соответствует наибольшая частота встречаемости. (В приведенном выше примере моде соответствует значение 24 кг, оно встречается чаще других: m = 20).

Медиана – значение случайной величины, которое делит распределение пополам: половина значений расположена правее медианы, половина (не больше) – левее.

Пример:

1, 1, 1, 1, 1. 1, 2, 2, 2, 3 , 3, 4, 4, 5, 5, 5, 5, 6, 6, 7 , 7, 7, 7, 7, 7, 8, 8, 8, 8, 8 , 8, 9, 9, 9, 10, 10, 10, 10, 10, 10

В примере мы наблюдаем 40 значений случайной величины. Все значения расположены в порядке возрастания с учетом частоты их встречаемости. Видно, что справа от выделенного значения 7 расположены 20 (половина) из 40 значений. Стало быть, 7 – это медиана.

Для характеристики разброса найдем значения, не выше которых оказалось 25 и 75% результатов измерения. Эти величины называются 25-м и 75-м процентилями . Если медиана делит распределение пополам, то 25-й и 75-й процентили отсекают от него по четвертушке. (Саму медиану, кстати, можно считать 50-м процентилем.) Как видно из примера, 25-й и 75-й процентили равны соответственно 3 и 8.

Используют дискретное (точечное) статистическое распределение инепрерывное (интервальное) статистическое распределение.

Для наглядности статистические распределения изображают графически в виде полигона частот или - гистограммы .

Полигон частот - ломаная линия, отрезки которой соединяют точки с координатами (x 1 ,m 1 ), (x 2 ,m 2 ), ..., или для полигона относительных частот – с координатами (x 1 ,р * 1 ), (x 2 ,р * 2 ), ...(Рис.1).

m m i /n f(x)

Рис.1 Рис.2

Гистограмма частот - совокупность смежных прямоугольников, построенных на одной прямой линии (Рис.2), основания прямоугольников одинаковы и равны dx , а высоты равны отношению частоты к dx , или р * к dx (плотность вероятности).

Пример:

х, кг	2,7	2,8	2,9	3,0	3,1	3,2	3,3	3,4	3,5	3,6	3,7	3,8	3,9	4,0	4,1	4,2	4,3	4,4
m

Полигон частот

Отношение относительной частоты к ширине интервала носит название плотности вероятности f(x)=m i / n dx = p* i / dx

Пример построения гистограммы .

Воспользуемся данными предыдущего примера.

1. Расчет количества классовых интервалов

гдеn - число наблюдений. В нашем случае n = 100 . Следовательно:

2. Расчет ширины интервала dх :

,

3. Составление интервального ряда:

dх	2.7-2.9	2.9-3.1	3.1-3.3	3.3-3.5	3.5-3.7	3.7-3.9	3.9-4.1	4.1-4.3	4.3-4.5
m
f(x)	0.3	0.75	1.25	0.85	0.55	0.6	0.4	0.25	0.05

Гистограмма

Методы математической статистики применяются, как правило, на всех этапах анализа исследовательских материалов для выбора стратегии решения задач по конкретным выборочным данным, оценивания полученных результатов. Для обработки материала использовались методы математической статистики. Математическая обработка материалов позволяет со всей четкостью выделить и оценить количественные параметры объективной информации, проанализировать и представить их в различных соотношениях и зависимостях. Они позволяют определить меру варьирования величин в собранных материалах, содержащих количественную информацию о некотором множестве случаев, часть из которых подтверждает предполагаемые связи, а часть не выявляет их, вычислить достоверность количественных различий между выделенными совокупностями случаев, получить другие математические характеристики, необходимые для верного истолкования фактов. Достоверность различий полученных в ходе исследования определялась по t-критерию Стьюдента.

Рассчитывались следующие величины.

1. Среднее арифметическое значение выборки.

Характеризует среднее значение рассматриваемой совокупности. Обозначим результаты измерений. Тогда:

где У- сумма всех значений, когда текущий индекс i изменяется от 1 до n.

2. Среднее квадратическое отклонение (стандартное отклонение) , характеризующее рассеивание, разбросанность рассматриваемой совокупности относительно среднего арифметического значения.

= (x max - x min)/ k

где - среднее квадратическое отклонение

хmaх - максимальное значение таблицы;

хmin - минимальное значение таблицы;

k - коэффициент

3. Стандартная ошибка средней арифметической или ошибка репрезентативности (m). Стандартная ошибка средней арифметической характеризует степень отклонения выборочной средней арифметической от средней арифметической генеральной совокупности.

Стандартная ошибка средней арифметической вычисляется по формуле:

где у - стандартное отклонение результатов измерений,

n - объем выборки. Чем меньше m тем выше стабильность, устойчивость результатов.

4. Критерий Стьюдента.

(в числителе - разность средних значений двух групп, в знаменателе - квадратный корень из суммы квадратов стандартных ошибок этих средних).

При обработке полеченных результатов исследования использовали компьютерную программу с пакетом Excel.

Организация исследования

Исследование проводилось нами по общепринятым правилам, и осуществлялось в 3 этапа.

На первом этапе был собран и проанализирован полученный материал по рассматриваемой проблеме исследования. Формировался предмет научного исследования. Проведенный анализ литературы на данном этапе позволил конкретизировать цель и задачи исследования. Проведено первичное тестирование техники бега на 30 м.<... class="gads_sm">

На третьем этапе был систематизирован полученный в результате научного исследования материал, обобщена вся имеющаяся информация по проблеме исследования.

Экспериментальное исследование проводилось на базе ГУО «Ляховичская средняя школа», в общей сложности выборка составила 20 учащихся 6 классов (11-12 лет).

Глава 3. Анализ результатов исследования

В результате педагогического эксперимента нами были выявлен исходный уровень техники бега на 30 м учащихся в контрольной и экспериментальной группах (Приложения 1-2). Статистическая обработка полученных результатов позволила получить следующие данные (таблица 6).

Таблица 6. Исходный уровень качества бега

Как видно из таблицы 6 среднее количество баллов у спортсменов контрольной и экспериментальной группы статистически не отличаются, в экспериментальной группе средний бал составил 3,6 балла, а в контрольной 3,7 балла. T-критерий в обеих группах tэмп=0,3; Р?0,05, при tкрит=2,1; Результаты исходного тестирования показали, что показатели не зависят от обученности и носят случайный характер. По первоначальному тестированию показатели качества бега у контрольной группы немного превышали показатели экспериментальной группы. Но не было выявлено статистически достоверных различий в группах, что является доказательством идентичности учащихся контрольной и экспериментальной групп по технике бега 30м.

За время эксперимента в обеих группах улучшились показатели, характеризующие эффективность техники бега. Однако это улучшение в разных группах участников эксперимента носило разный характер. В результате обучения выявлен закономерный небольшой прирост показателей в контрольной группе (3,8 балла). Как видно из Приложения 2 в экспериментальной группе был выявлен большой прирост показателей. Учащиеся занимались по предложенной нами программе, что достоверно улучшило показатели.

Таблица 7. Изменения качества бега у испытуемых экспериментальной группы

В ходе эксперимента мы установили, что повышенные нагрузки в экспериментальной группе дали значительные улучшения развития быстроты, нежели в контрольной группе.

В подростковом возрасте целесообразно развивать быстроту путем преимущественного использования средств физического воспитания, направленных на повышение частоты движений. В возрасте 12-15 лет повышаются скоростные способности, в результате применения главным образом скоростно-силовых и силовых упражнений которые использованы нами в процессе проведения уроков физической культуры и внеклассных занятий спортивной секции баскетбола и лёгкой атлетики.

При проведении занятий в экспериментальной группе велась строгая этапность усложнения и двигательного опыта. Своевременно велась работа над ошибками. Как показал анализ фактических данных, экспериментальная методика обучения оказало существенное изменение на качество выполнения техники бега (tэмп=2,4). Анализ полученных результатов в экспериментальной группе и сравнение их с данными, полученными в контрольной группе при использовании общепринятой методики обучения, дают основание утверждать, что предложенная нами методика повысит эффективность обучения.

Таким образом, на этапе совершенствования методики бега 30м в школе мы выявили динамику изменения показателей тестирования в экспериментальной и контрольной группе. После проведенного эксперимента качество выполнение приема повысилась в экспериментальной группе до 4,9 баллов (t=3,3; Р?0,05). К концу эксперимента качество владения техникой бега в экспериментальной группе оказалось выше, чем в контрольной группе.