Punkty osobliwe funkcji i ich klasyfikacja. Pojedyncze pojedyncze punkty. Reszty i wzory do ich obliczania
Modele opisane układami dwóch autonomicznych równań różniczkowych.
płaszczyzna fazy. Portret fazowy. metoda izokliny. główne izokliny. Stabilność stanu ustalonego. Systemy liniowe. Kluczowe typy punktów: węzeł, siodło, skupienie, centrum. Przykład: reakcje chemiczne pierwszego rzędu.
Najciekawsze wyniki dotyczące jakościowego modelowania właściwości układów biologicznych uzyskano na modelach dwóch równań różniczkowych, które pozwalają na jakościowe badanie metodą płaszczyzna fazy. Rozważ układ dwóch autonomicznych równań różniczkowych zwyczajnych o ogólnej postaci
(4.1)
P(x,y), Q(x,y)- funkcje ciągłe zdefiniowane w jakiejś dziedzinie g płaszczyzna euklidesowa ( x,y- współrzędne kartezjańskie) i mające w tym obszarze ciągłe pochodne rzędu nie mniejszego niż pierwszy.
Region g może być nieograniczony lub ograniczony. Jeśli zmienne x, y mają określone znaczenie biologiczne (stężenia substancji, liczebność gatunków), najczęściej obszar g jest dodatnim kwadrantem prawej półpłaszczyzny:
0 £ x< ¥ ,0 £ tak< ¥ .
Stężenia substancji lub liczebność gatunków można również ograniczać od góry objętością statku lub powierzchnią siedliska. Wtedy zakres zmiennych ma postać:
0 £ x< x 0 , 0 £ tak< y 0 .
Zmienne x, y zmiana w czasie zgodnie z układem równań (4.1), tak aby każdemu stanowi układu odpowiadała para wartości zmiennych ( x, y).
|
|
I odwrotnie, dla każdej pary zmiennych ( x, y) odpowiada pewnemu stanowi systemu.
Rozważ płaszczyznę z osiami współrzędnych, na której wykreślane są wartości zmiennych x,y. Każdy punkt m płaszczyzna ta odpowiada pewnemu stanowi układu. Płaszczyzna taka nazywana jest płaszczyzną fazową i przedstawia całość wszystkich stanów układu. Punkt M(x, y) nazywany jest punktem przedstawiającym lub reprezentującym.
Niech na początku t=t 0 reprezentujące współrzędne punktu m 0 (x(T 0)tak(T 0)). W każdej następnej chwili w czasie T punkt przedstawiający będzie się poruszał zgodnie ze zmianami wartości zmiennych x(T)tak(T). Zestaw punktów m(x(T), y(t)) na płaszczyźnie fazowej, której położenie odpowiada stanom układu w procesie zmiany zmiennych w czasie x(t), t(t) zgodnie z równaniami (4.1) nazywa się trajektoria faz.
Zestaw trajektorii fazowych dla różnych wartości początkowych zmiennych daje łatwo widoczny „portret” układu. Budynek portret fazowy pozwala wyciągać wnioski na temat charakteru zmian zmiennych x, y bez znajomości rozwiązań analitycznych pierwotnego układu równań(4.1).
W celu zobrazowania portretu fazowego konieczne jest skonstruowanie pola wektorowego kierunków trajektorii układu w każdym punkcie płaszczyzny fazowej. Określając przyrostD t>0,otrzymujemy odpowiednie przyrosty D x I D tak z wyrażeń:
D x=P(x,y)D T,
D y=Q(x,y)D T.
kierunek wektora dy/dx W punkcie ( x, y) zależy od znaku funkcji P(x, y), Q(x, y) i może być podany w tabeli:
|
P(x,y)>0,Q(x,y)>0 |
|
|
P(x,y)<0,Q(x,y)<0 |
|
|
P(x,y)>0,Q(x,y)<0 |
|
|
P(x,y)<0,Q(x,y)>0 |
|
.(4.2)
Rozwiązanie tego równania y=y(x, c), lub domyślnie F(x,y)=c, gdzie od jest stałą całkowania, daje rodzinę krzywych całkowych równania (4.2) - trajektorie faz system (4.1) w samolocie x, y.
Metoda izoklinowa
Do skonstruowania portretu fazowego używa się metoda izoklinowa - linie są rysowane na płaszczyźnie fazowej, które przecinają krzywe całkowe pod jednym określonym kątem. Równanie izokliny jest łatwe do uzyskania z (4.2). Włóżmy
gdzie ALE– pewna stała. Oznaczający ALE reprezentuje tangens nachylenia stycznej do trajektorii fazy i może przyjmować wartości od -¥ do + ¥ . Zastępowanie zamiast dy/dx w (4.2) ilość ALE otrzymujemy równanie izokliny:
.(4.3)
Równanie (4.3) określa w każdym punkcie płaszczyzny jedyną styczną do odpowiedniej krzywej całkowej, z wyjątkiem punktu, w którym P(x,y)= 0, Q (x,y) = 0 , w którym kierunek stycznej staje się nieokreślony, ponieważ wartość pochodnej staje się nieokreślona:
.
Ten punkt jest punktem przecięcia wszystkich izolinii - specjalny punkt. Jednocześnie znika pochodne czasowe zmiennych x I tak.
Zatem w punkcie osobliwym szybkości zmian zmiennych są równe zeru. Dlatego punkt osobliwy równań różniczkowych trajektorii fazowych (4.2) odpowiada stan stacjonarny układu(4.1), a jego współrzędne są stacjonarnymi wartościami zmiennych x, y.
Szczególnie interesujące są główne izokliny:
dy/dx=0, P(x,y)=0 – izoklina stycznych poziomych i
dy/dx=¥ , Q(x,y)=0 – izoklina stycznych pionowych.
Konstruując główne izokliny i znajdując punkt ich przecięcia (x,y), którego współrzędne spełniają warunki:
znajdziemy w ten sposób punkt przecięcia wszystkich izolinii płaszczyzny fazowej, w którym kierunek stycznych do trajektorii fazowych jest nieokreślony. Ten - punkt osobliwy, co odpowiada stan stacjonarny układu(rys. 4.2).
Układ (4.1) ma tyle stanów stacjonarnych, ile jest punktów przecięcia głównych izolinii na płaszczyźnie fazowej.
Każda trajektoria fazowa odpowiada zestawowi ruchów układu dynamicznego przechodzącego przez te same stany i różniących się od siebie jedynie początkiem odniesienia czasu.
 |
|
Jeżeli warunki twierdzenia Cauchy'ego są spełnione, to przez każdy punkt przestrzeni x, y, t przechodzi przez pojedynczą krzywą całkową. To samo jest prawdą, dzięki autonomii, dla trajektorii fazowych: unikalna trajektoria fazowa przechodzi przez każdy punkt płaszczyzny fazowej.
Stabilność stanu ustalonego
Niech system będzie w równowadze.
Wówczas punkt reprezentatywny znajduje się w jednym z osobliwych punktów układu, w którym z definicji:
.
To, czy punkt osobliwy jest stabilny, czy nie, zależy od tego, czy punkt reprezentatywny odchodzi z niewielkim odchyleniem od stanu stacjonarnego. W odniesieniu do układu dwóch równań definicja stabilności w językumi, Dnastępująco.
Stan równowagi jest stabilny, jeśli dla dowolnego obszaru odchyleń od stanu równowagi (mi )obszar można określić D (mi ), otaczający stan równowagi i mający właściwość, że nie ma trajektorii rozpoczynającej się w regionie D , nigdy nie dotrze do granicy mi . (Rys. 4.4)
 |
|
Dla dużej klasy systemów - szorstkie systemy – charakter zachowania się nie zmienia przy niewielkiej zmianie typu równań, informacje o rodzaju zachowania w sąsiedztwie stanu stacjonarnego można uzyskać badając nie oryginał, ale uproszczony zlinearyzowany system.
Systemy liniowe.
Rozważ układ dwóch równań liniowych:
.(4.4)
Tutaj a, b, c, d- stałe, x, y- Współrzędne kartezjańskie na płaszczyźnie fazowej.
Ogólnego rozwiązania będzie szukać w postaci:
.(4.5)
Zastąp te wyrażenia w (4.4) i zmniejsz o mi ja T:
(4.6)
Algebraiczny układ równań (4.6) z niewiadomymi A, B ma rozwiązanie niezerowe tylko wtedy, gdy jego wyznacznik, złożony ze współczynników niewiadomych, jest równy zero:
.
Rozwijając ten wyznacznik otrzymujemy równanie charakterystyczne układu:
.(4.7)
Rozwiązanie tego równania daje wartości wskaźnikaja 1,2 , pod którym możliwe są wartości niezerowe dla A I b rozwiązania równania (4.6). Te wartości są
.(4.8)
Jeśli radykalne wyrażenie jest negatywne, toja 1,2 złożone liczby sprzężone. Załóżmy, że oba pierwiastki równania (4.7) mają niezerowe części rzeczywiste i nie ma pierwiastków wielokrotnych. Wtedy rozwiązanie ogólne systemu (4.4) można przedstawić jako liniową kombinację wykładników z wykładnikamija 1 , ja 2 :
(4.9)
Aby przeanalizować charakter możliwych trajektorii układu na płaszczyźnie fazowej, używamy liniowa jednorodna transformacja współrzędnych, co doprowadzi system do Forma kanoniczna:
,(4.10)
co pozwala na wygodniejszą reprezentację na płaszczyźnie fazowej w porównaniu z oryginalnym systemem (4.4). Wprowadźmy nowe współrzędneξ , η według wzorów:
(4.1)
Z przebiegu algebry liniowej wiadomo, że jeśli części rzeczywiste nie są równe zeruja 1 , ja 2 oryginalny system (4.4) za pomocą przekształceń (4.11) można zawsze przekształcić do postaci kanonicznej (4.10), a jego zachowanie na płaszczyźnie fazowej można badaćξ , η . Rozważ różne przypadki, które mogą się tutaj pojawić.
Korzenie λ 1 , λ 2 – ważny i tego samego znaku
W tym przypadku współczynniki transformacji są rzeczywiste, oddalamy się od rzeczywistej płaszczyznyx,ydo rzeczywistego samolotu ξ, η. Dzieląc drugie z równań (4.10) przez pierwsze otrzymujemy:
.(4.12)
Całkując to równanie, znajdujemy:
Gdzie .(4.13)
Zgódźmy się rozumieć przez λ 2 pierwiastek równania charakterystycznego o dużym module, który nie narusza ogólności naszego rozumowania. Następnie, ponieważ w rozpatrywanym przypadku pierwiastki λ 1 , λ2 – ważny i tego samego znaku,a>1 , a mamy do czynienia z krzywymi całkowymi typu parabolicznego.
Wszystkie krzywe całkowe (z wyjątkiem osi η , co odpowiada ) dotknij początku osi ξ, która jest również krzywą całkową równania (4.11). Początek współrzędnych jest pojedynczym punktem.
Ustalmy teraz kierunek ruchu reprezentatywnego punktu wzdłuż trajektorii fazowych. Jeśli λ 1 , λ 2 są więc ujemne, jak wynika z równań (4.10), |ξ|, |η| zmniejszać się z czasem. Punkt reprezentujący zbliża się do początku, ale nigdy go nie osiąga. W przeciwnym razie byłoby to sprzeczne z twierdzeniem Cauchy'ego, które mówi, że tylko jedna trajektoria fazowa przechodzi przez każdy punkt płaszczyzny fazowej.
Taki punkt osobliwy, przez który przechodzą krzywe całkowe, podobnie jak rodzina parabol 
przechodzi przez początek, nazywa się węzłem (ryc. 4.5)
Stan równowagi typu węzeł przy λ 1 , λ 2 < 0 jest stabilna według Lapunowa, ponieważ reprezentujący punkt porusza się wzdłuż wszystkich krzywych integralnych w kierunku początku współrzędnych. Ten stabilny węzeł. Jeśli λ 1 , λ 2 > 0, to |ξ|, |η| wraz z upływem czasu rośnie, a punkt reprezentatywny oddala się od początku. W tym przypadku punkt osobliwy– niestabilny węzeł .
Na płaszczyźnie fazowej x, y ogólny jakościowy charakter zachowania krzywych całkowych pozostanie, ale styczne do krzywych całkowych nie będą pokrywać się z osiami współrzędnych. Kąt nachylenia tych stycznych będzie określony przez stosunek współczynników α , β , γ , δ w równaniach (4.11).
Korzenie λ 1 , λ 2 są ważne i mają różne znaki.
Konwertuj z współrzędne x,y do współrzędnych ξ, η znowu prawdziwe. Równania dla zmiennych kanonicznych ponownie mają postać (4.10), ale teraz znaki λ 1 , λ 2 inny; różny. Równanie trajektorii fazowej ma postać:
Gdzie , (4.14)
Integrując (4.14), znajdujemy
(4.15)
Ten równanie definiuje rodzinę krzywych typu hiperbolicznego, gdzie obie osie współrzędnych są asymptoty (w a=1 mielibyśmy rodzinę hiperbol równoramiennych). W tym przypadku osie współrzędnych są również krzywymi integralnymi– będą to jedyne krzywe całkowe przechodzące przez początek. Każdyz czego składa się z trajektorii trójfazowych: dwóch ruchów w kierunku stanu równowagi (lub odejścia od stanu równowagi) i ze stanu równowagi. Wszystkie inne krzywe całkowe– to hiperbole, które nie przechodzą przez początek (ryc. 4.6) Ten pojedynczy punkt nazywa się "siodło ». Linie poziomu w pobliżu siodła górskiego zachowują się jak trajektorie fazowe w pobliżu siodła.
Rozważmy naturę ruchu punktu reprezentatywnego wzdłuż trajektorii fazowych w pobliżu stanu równowagi. Niech na przykładλ 1 > 0 , λ 2<0 . Następnie reprezentatywny punkt umieszczony na osi ξ , odsunie się od początku i zostanie umieszczony na osi η – zbliży się w nieskończoność do początku współrzędnych, bez osiągnięcia tego w skończonym czasie. Wszędzie tam, gdzie w chwili początkowej znajduje się punkt reprezentujący (z wyjątkiem punktu osobliwego i punktów na asymptocie η =0), w końcu odejdzie od stanu równowagi, nawet jeśli na początku porusza się wzdłuż jednej z krzywych całkowych w kierunku punktu osobliwego.
To oczywiste, że punkt osobliwy typu siodłowego jest zawsze niestabilny . Tylko w specjalnie dobranych warunkach początkowych na asymptocieη =0 system zbliży się do stanu równowagi. Nie jest to jednak sprzeczne z twierdzeniem, że system jest niestabilny. Jeśli liczysz, że wszystkie stany początkowe układu na płaszczyźnie fazowej są jednakowo prawdopodobne, to prawdopodobieństwo takiego stanu początkowego, który odpowiada ruchowi w kierunku do punkt osobliwy jest równy zero. Dlatego każdy rzeczywisty ruch wyprowadzi system ze stanu równowagi.Wracając do współrzędnychx,y,otrzymujemy ten sam jakościowy obraz natury ruchu trajektorii wokół początku.
Granicą pomiędzy rozpatrywanymi przypadkami węzła i siodła jest przypadek gdy na przykład jeden z charakterystycznych wskaźników λ 1 , znika, co ma miejsce, gdy wyznacznik systemu- wyrażenie adbc=0(patrz wzór 4.8 ). W tym przypadku współczynniki prawych stron równań (4.4) są do siebie proporcjonalne:
a układ ma za stan równowagi wszystkie punkty linii:
Pozostałe krzywe całkowe to rodzina linii równoległych o nachyleniu , wzdłuż którego punkty reprezentatywne albo zbliżają się do stanu równowagi, albo od niego oddalają, w zależności od znaku drugiego pierwiastka równania charakterystycznego λ 2 = a+d.(Rys. 4. 7 ) W tym przypadku współrzędne stanu równowagi zależą od początkowej wartości zmiennych.
Korzenie λ 1 , λ 2 – złożonysprzężony
W tym przypadku naprawdęx I tak będziemy mają złożone koniugaty ξ , η (4.10) . Jednak wprowadzając jeszcze jedną transformację pośrednią, możliwe jest również w tym przypadku zredukowanie rozważania do rzeczywistej liniowej transformacji jednorodnej. Włóżmy:
(4.16)
gdzie a, b, I ty, v – prawdziwe wartości. Można wykazać, że transformacja zx,y do ty, v jest, zgodnie z naszymi założeniami, rzeczywista, liniowa, jednorodna z niezerowym wyznacznikiem. Ze względu na równania(4.10, 4.16) mamy :
gdzie
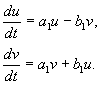(4.17)
Dzielenie drugiego z równań przez pierwsze, otrzymujemy:
co jest łatwiejsze do zintegrowania, jeśli przełączymy się na biegunowy układ współrzędnych (r, φ ) . Po podstawieniu otrzymujemy skąd:
.(4.18)
Tak więc na płaszczyźnie fazowejty, vmamy do czynienia z rodziną spiral logarytmicznych, z których każda maasymptotyczny punkt na początku.Punkt osobliwy będący punktem asymptotycznym wszystkich krzywych integralnych mających postać spiral, zagnieżdżony przyjaciel wprzyjaciel, zwany Centrum ( rys.4.8 ) .
Rozważmy naturę ruchu punktu reprezentującego wzdłuż trajektorii fazowych. Mnożenie pierwszego z równań (4.17) przezty, a drugi do v i dodając , otrzymujemy:
Gdzie
Zostawiać a 1 < 0 (a 1 = Odnośnieλ ) . Punkt reprezentujący następnie stale zbliża się do początku, nie osiągając go w skończonym czasie. Oznacza to, że trajektorie faz są skręcanymi spiralami i odpowiadają drganiom tłumionym zmienne. Ten - stałe skupienie .
W przypadku stabilnego ogniskowania, podobnie jak w przypadku stabilnego węzła, spełniony jest nie tylko warunek Lapunowa, ale także bardziej rygorystyczny wymóg. Mianowicie, w przypadku jakichkolwiek początkowych odchyleń, system ostatecznie powróci tak blisko, jak to pożądane, do pozycji równowagi. Taka stabilność, w której początkowe odchylenia nie tylko nie rosną, ale zanikają, dążąc do zera, nazywa się absolutna stabilność .
Jeśli we wzorze (4.18) a 1 >0 , wtedy reprezentujący punkt oddala się od początku i mamy do czynienia z niestabilna ostrość . Wysiadając z samolotuty, vdo płaszczyzny fazowejx, takspirale również pozostaną spiralami, ale zostaną zdeformowane.
Rozważmy teraz przypadek, kiedya 1
=0
. Trajektorie fazowe na samolociety, vbędą kręgi 
który w samolociex,ydopasuj elipsy:
Tak więc, w1=0 przez specjalny punktx= 0,y= 0 nie przechodzi żadna integralna krzywa. Taki izolowany punkt osobliwy, w pobliżu którego krzywe całkowe są krzywymi zamkniętymi, w szczególności elipsami zatopionymi w sobie i obejmującymi punkt osobliwy, nazywa się środkiem.
Możliwych jest zatem sześć typów równowagi, w zależności od charakteru pierwiastków równania charakterystycznego (4.7). Widok trajektorii faz na samolocie x, y dla tych sześciu przypadków pokazano na ryc. 4.9.
Ryż. 4.9.Rodzaje portretów fazowych w sąsiedztwie stanu stacjonarnego dla układu równań liniowych (4.4).
Pięć typów stanów równowagi jest przybliżonych, ich natura nie zmienia się przy wystarczająco małych zmianach po prawej stronie równań (4.4). W tym przypadku zmiany powinny być niewielkie nie tylko po prawej stronie, ale także w ich pochodnych pierwszego rzędu. Szósty stan równowagi – centrum – nie jest grubiański. Przy niewielkich zmianach parametrów prawej strony równań przechodzi w stabilne lub niestabilne ogniskowanie.
Schemat bifurkacji
Wprowadźmy notację:
.
(4.11)
Wtedy równanie charakterystyczne można zapisać w postaci:
.
(4.12)
Rozważ płaszczyznę o prostokątnych współrzędnych kartezjańskich s , D i zaznacz na nim obszary odpowiadające temu lub innemu rodzajowi stanu równowagi, który jest określony przez naturę pierwiastków równania charakterystycznego
.(4.13)
Warunkiem stabilności stanu równowagi będzie obecność ujemnej części rzeczywistej yja 1 i ja 2 . Warunkiem koniecznym i wystarczającym do tego jest spełnienie nierównościs > 0, D > 0 . Na wykresie (4.15) warunek ten odpowiada punktom znajdującym się w pierwszej ćwiartce płaszczyzny parametrów. Pojedynczy punkt będzie w centrum uwagi, jeślija 1 i ja 2 złożony. Warunek ten odpowiada tym punktom płaszczyzny, dla których , tych. punkty między dwoma gałęziami parabolis 2 = 4 D. Punkty półosi s = 0, D>0, odpowiadają stanom równowagi typu centrum. Podobnie,ja 1 i ja 2 - ważne, ale różne znaki, tj. pojedynczy punkt będzie siodłem, jeśli D<0, itp. W rezultacie otrzymujemy diagram podziału płaszczyzny parametrów s, D, na regiony odpowiadające różnym typom stanów równowagi.
Ryż. 4.10. Schemat bifurkacji
dla układu równań liniowych 4.4
Jeżeli współczynniki układu liniowego a, b, c, d zależą od jakiegoś parametru, to gdy ten parametr zostanie zmieniony, wartości również się zmieniąs , D . Podczas przekraczania granic charakter portretu fazowego zmienia się jakościowo. Dlatego takie granice nazywane są granicami bifurkacyjnymi - po przeciwnych stronach granicy system ma dwa topologicznie różne portrety fazowe i odpowiednio dwa różne typy zachowań.
Diagram pokazuje, jak takie zmiany mogą mieć miejsce. Jeśli wykluczymy przypadki szczególne – początek współrzędnych – to łatwo zauważyć, że siodełko może przejść do węzła stabilnego lub niestabilnego podczas przekraczania osi y. Stabilny węzeł może albo przejść do siodła, albo do stabilnego skupienia i tak dalej. Należy zauważyć, że stabilne przejścia ogniskowania między węzłem a niestabilnym węzłem nie są bifurkacyjne, ponieważ topologia przestrzeni fazowej nie zmienia się w tym przypadku. Bardziej szczegółowo o topologii przestrzeni fazowej i przejść bifurkacyjnych omówimy w Wykładzie 6.
W przypadku przejść bifurkacyjnych zmienia się charakter stabilności punktu osobliwego. Na przykład stabilna ostrość przez środek może zmienić się w niestabilną ostrość. Ta bifurkacja nazywa się Bifurkacja Andronowa-Hopfa nazwiskami naukowców, którzy ją badali. Wraz z tą bifurkacją w układach nieliniowych rodzi się cykl graniczny i układ staje się samooscylujący (patrz wykład 8).
Przykład. Układ liniowych reakcji chemicznych
Substancja x napływa z zewnątrz w stałym tempie, zamienia się w substancję Y i w tempie proporcjonalnym do stężenia substancji Y, jest wyjęty ze sfery reakcyjnej. Wszystkie reakcje są pierwszego rzędu, z wyjątkiem napływu materii z zewnątrz, który ma zerowy rząd. Schemat reakcji wygląda następująco:
(4.14)
i jest opisana układem równań:
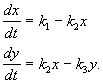(4.15)
Stężenia stacjonarne otrzymujemy, przyrównując prawe strony do zera:
.(4.16)
Rozważ portret fazowy systemu. Podzielmy drugie równanie układu (4.16) przez pierwsze. Otrzymujemy:
.(4.17)
Równanie (4.17) określa zachowanie zmiennych na płaszczyźnie fazowej. Zbudujmy portret fazowy tego układu. Najpierw rysujemy główne izokliny na płaszczyźnie fazowej. Równanie izokliny stycznych pionowych:
Równanie na izoklinę stycznych poziomych:
Punkt osobliwy (stan stacjonarny) leży na przecięciu głównych izoklin.
Teraz określmy, pod jakim kątem osie współrzędnych przecinają krzywe całkowe.
Jeśli x= 0, to .
Zatem styczna nachylenia stycznej do krzywych całkowych y=y(x), przekroczenie osi y x=0, jest ujemna w górnej połowie płaszczyzny (przypomnijmy, że zmienne x, y mają wartości koncentracji i dlatego interesuje nas tylko prawy górny kwadrant płaszczyzny fazowej). W tym przypadku wartość stycznej kąta nachylenia stycznej wzrasta wraz z odległością od początku.
Rozważ oś y= 0. Na przecięciu tej osi krzywe całkowe są opisane równaniem
Na tangens nachylenia krzywych całkowych przecinających oś odciętych jest dodatni i rośnie od zera do nieskończoności wraz ze wzrostem x.
Na .
Następnie, przy dalszym wzroście, styczna spadku maleje w wartości bezwzględnej, pozostając ujemną i dąży do -1 przy x ® ¥ . Znając kierunek stycznych do krzywych całkowych na głównych izoklinach i na osiach współrzędnych, łatwo jest skonstruować cały obraz trajektorii fazowych.
 |
|
Charakter stabilności punktu osobliwego zostanie ustalony za pomocą metody Lapunowa. Charakterystyczny wyznacznik systemu ma postać:
.
Rozszerzając wyznacznik otrzymujemy równanie charakterystyczne układu: , tj. oba pierwiastki równania charakterystycznego są ujemne. Dlatego stan stacjonarny systemu jest stabilnym węzłem. Jednocześnie stężenie substancji x dąży do stanu stacjonarnego zawsze monotonicznie, stężenie substancji Y może przejść przez min lub max. Reżimy oscylacyjne w takim systemie są niemożliwe.
Zostawiać zq - punkt osobliwy funkcji f(z), t.s. F z) ale jest analityczny w tym momencie (w szczególności nie może być w tym zdefiniowany). Jeśli istnieje takie przebite sąsiedztwo punktu zq (tj. zbiór O z - zq f(z) jest aliasem, to Zo nazywa się izolowany punkt osobliwy Funkcje F z). Ta definicja jest również zachowana w przypadku zn = oo, jeśli jod to przebite sąsiedztwo punktu zq = oo zrozum zbiór z > i - pojawienie się jakiegoś okręgu wyśrodkowanego na początku. Innymi słowy, punkt osobliwy zq mówi się, że jest izolowany, jeśli istnieje sąsiedztwo tego punktu, w którym znajdują się inne punkty osobliwe różne od zq. Wszędzie poniżej rozważamy tylko punkty osobliwe znaku jednowartościowego (funkcja F z) zakłada się, że jest unikalny).
W zależności od zachowania funkcji F z) w z -> zq Istnieją trzy rodzaje punktów osobliwych. Izolowany pojedynczy punkt funkcje zq F z) nazywa się:
1) zdejmowany pojedynczy punkt jeśli istnieje skończona granica
2) Polak jeśli istnieje limit 
3) istotny punkt, Jeśli F z) nie ma ani skończonej, ani nieskończonej granicy dla z-> zq.
PRZYKŁAD 26.1. Pokażmy, że realizowane są wszystkie trzy rodzaje punktów osobliwych. Rozważać F(z)= punkt zq = 0 jest izolowane
punkt osobliwy tej funkcji. Korzystając ze wzoru (22.12), otrzymujemy rozwinięcie
z czego wynika, że istnieje lim fi(z)= 1. Zatem zq = 0 to
jest usuwalnym pojedynczym punktem funkcji fi(z).
Funkcjonować f'j(z) =--- ma w punkcie słupek Zo= 1 ponieważ
2 r" X
Rozważ teraz funkcję )z(z)= e 1 ^ r i pokaż, że zo = O jest istotnym punktem osobliwym tej funkcji. Kiedy starasz się z do zera wzdłuż osi rzeczywistej, lewa i prawa granica funkcji f (z) inny: lim od 1 / 1 = 0, lim z 1 /* = os. Oznacza to,
x->0-0 x->0+O
Co f:i(z) nie ma ani skończonej, ani nieskończonej granicy dla 2 ->
Och, czyli zq = 0 jest w zasadzie pojedynczym punktem tej funkcji. (Zauważ, że ponieważ punkt ma tendencję z-iy do zera na funkcji osi urojonej 
nie ma żadnych ograniczeń.)
Oczywiście istnieją również nieizolowane punkty osobliwe. Na przykład. funkcja ma bieguny w punktach z n = -, P= ±1, ±2,...
W konsekwencji, Zq = 0 jest nieizolowanym punktem osobliwym tej funkcji: w dowolnym (dowolnym małym) sąsiedztwie tego punktu znajdują się inne punkty osobliwe gp.
Zostawiać zo- końcowy izolowany punkt osobliwy funkcji F z). Następnie F z) jest podobny w jakimś przebitym sąsiedztwie 0 Zo punktu Zo to sąsiedztwo można traktować jako pierścień o promieniu wewnętrznym r = 0. Z Twierdzenia 25.1 w rozważanym sąsiedztwie funkcja F z) można rozszerzyć w serii Laurent (25.2). Pokażemy, że zachowanie funkcji dla 2 -> zq (czyli rodzaj punktu osobliwego zo) zależy od postaci głównej części rozkładu (25.2); ta okoliczność wyjaśnia pochodzenie terminu „część główna”.
TWIERDZENIE 2G.2. Izolowany punkt osobliwy zo funkcji f(z) jest usuwalny wtedy i tylko wtedy, gdy rozwinięcie Lorapa w przebitym sąsiedztwie tego punktu ma oid
tych. składa się tylko z właściwej części, a wszystkie współczynniki części głównej są równe pociskowi.
Dowód. 1. Niech Zo jest usuwalnym pojedynczym punktem. Udowodnijmy, że rozwinięcie funkcji Laurenta F z) ma postać (26.1). Od pojedynczego punktu Zo zdejmowany, wtedy istnieje skończony limit limit f(z) = A. W konsekwencji, F z) ograniczone w jakimś przebitym sąsiedztwie 0 z - zq punktu z oo, tych. )(z) dla wszystkich z z tej okolicy. Weź którąś R. U р /?| i użyj wzorów (25.3) dla współczynników szeregu Laurenta:
Dla współczynników głównej części rozwinięcia n =- 1,-2,... Dla takich wartości P mamy p~n-e 0 w r-> 0. Od wartości r można wybrać dowolnie małe, a następnie Pan~" może być dowolnie mały. Ponieważ |c t,| ^ Pan~n a cn nie zależą od p, to cn = 0 dla I= - 1, -2,..., co miało być udowodnione.
2. Załóżmy teraz, że rozwinięcie Laurenta ma postać (26.1). Seria (26.1) to seria potęgowa i. dlatego zbiega się nie tylko w przebitej, ale i w całym sąsiedztwie z-zq w tym kropka z oo; jego suma S(z) jest analityczny dla z i S(z) = )(z) o 0 zł - Zo R. Dlatego istnieje skończony limit granic )(z)\u003d Pm 5 (r) \u003d 5 (r) - Dlatego punkt osobliwy zq
Z->Zo Z-*Zo
jednorazowy. Twierdzenie zostało udowodnione.
Komentarz. Z dowodu twierdzenia wynika, że w przebitym sąsiedztwie 0 z - zo usuwalnego punktu osobliwego funkcja F z) pokrywa się z funkcją S(r), która jest analityczna w całym sąsiedztwie z - z oo . Dlatego jeśli postawimy /(th) = S(zq), następnie bez zmiany wartości funkcji F z) w dowolnym punkcie przebitego sąsiedztwa wykonujemy tę funkcję analityczną w r, tj. „usuń” funkcję. To wyjaśnia termin „usuwalna osobliwość”. Naturalne jest traktowanie takich punktów jako regularnych, a nie osobliwych punktów funkcji F z).
Rozważmy na przykład funkcję
W przykładzie 26.1 pokazano, że Pm (n) = 1. tj. punkt osobliwy
zq = 0 jest usuwalny. Ustawiając /i(0) = 1, eliminujemy w ten sposób osobliwość i uzyskujemy funkcję analityczną w punkcie zq = 0 (i w całej płaszczyźnie C).
Scharakteryzujmy teraz bieguny pod kątem rozszerzeń Laurenta.
Twierdzenie 26.3. Izolowany punkt osobliwy Zo funkcji f(z) jest biegunem wtedy i tylko wtedy, gdy, gdy główna część ekspansji Laurenta z centrum Zq ma tylko skończoną liczbę odrębnych
od zerowych współczynników z n:
Dowód. 1. Niech zq - biegun, czyli lim /( z) = oo.
Udowodnijmy, że rozwinięcie funkcji Laurenta F z) ma postać (2G.2). Od lim F z)= oo. wtedy istnieje przebite sąsiedztwo punktu
Ki zq. w której F z) jest analityczny i nie zawiera zer. Następnie funkcja g(z) = 1 /F z) będzie również analityczny w tej przebitej okolicy, a lim g(z)= 0. Dlatego Zo jest jednorazowy *-? *0
punkt osobliwy funkcji g(z). Zdefiniujmy na nowo g(z) w punkcie Zo, oddanie g(zo)= 0. Wtedy g(z) staje się analityczny w całym sąsiedztwie (nieprzebitego) punktu z 0 , oraz z0 będzie jego izolowanym zerem. Oznacz przez n krotność (kolejność) tego zera. Jak pokazano w §23, w sąsiedztwie punktu funkcja zq g(z) reprezentowalne w formie (patrz (23.2))
oraz (z$) f 0 i y>(z) jest analityczny w jakimś sąsiedztwie punktu zo- Dlatego ip(z) ciągły w punkcie Zo I g>(zo) F 0" to ip(z) również nie ma zer w niektórych okolicach tego punktu. Dlatego funkcja 1 /-p(z) będzie również analityczny w tym sąsiedztwie i dlatego rozwija się w nim w szereg Taylora:
Otwierając nawiasy i zmieniając oznaczenia współczynników wpisujemy ostatnie rozwinięcie w formularzu
gdzie c_jv = 1>o f 0. Zatem główna część rozwinięcia Laurenta f(r) zawiera tylko skończoną liczbę termów; osiągnęliśmy wymaganą równość (26.2).
2. Wpuść przebite sąsiedztwo punktu ten funkcjonować )(z) jest reprezentowana przez rozwinięcie Laurenta (26.2) (w bardziej rozwiniętej formie, patrz (26.3)), którego główna część zawiera tylko skończoną liczbę wyrazów, oraz od- D" F 0. Musimy to udowodnić Zq - funkcja biegun F z). Mnożenie równości (26,3) przez (G - g o) iV , otrzymujemy funkcję
Szereg w (26.4) jest szeregiem potęgowym zbieżnym do funkcji analitycznej nie tylko w przebitym, ale również w całym sąsiedztwie punktu Zq. Dlatego funkcja h(z) staje się analityczny w tym sąsiedztwie, jeśli rozszerzymy go w th przez ustawienie h(zo)= s_dg F 0. Wtedy
Zatem punkt o jest biegunem, a Twierdzenie 26.3 jest udowodnione.
Wielokrotność (kolejność) funkcji zerowej g(z)= 1//(r) nazywa się biegun porządku funkcja /(r). Jeśli N- rząd bieguna to th, to g(z)= (r - Zo)N ip(z), i idź) F 0 i, jak pokazano w pierwszej części dowodu Twierdzenia 26.3, rozwinięcie f(r) ma postać (26.3), gdzie c_/v F 0. I odwrotnie, jeśli f(r) rozwija się w szereg (26,3) i e-z F 0, to
p.p. N- rząd bieguna funkcji f(r). W ten sposób, rząd bieguna zq funkcji/(G) jest równa liczbie wiodącego niezerowego współczynnika głównej części rozwinięcia Laurenta w przebitym sąsiedztwie punktu zq(tj. równa takiej liczbie N, co s_dg F 0 i sp= 0 w P > N).
Udowodnijmy następujące twierdzenie, które jest wygodne) dla aplikacji.
Wniosek 26.4. Punkt zq jest biegunem rzędu N fikcji/(G) wtedy i tylko wtedy gdy/(G) reprezentować w formie
gdzie h(z) jest funkcją analityczną w sąsiedztwie punktu ten i h(zo) f 0.
Dowód. Funkcjonować cp(z) = l/h(z) jest analityczny w pewnym sąsiedztwie punktu r. Warunek z wniosku 26.4 jest równoważny z następującym:
Dlatego zq - krotność zero n Funkcje g(z). i stąd biegun wielokrotności n funkcje /(2).
II przykład 26.5. Znajdź izolowane punkty osobliwe funkcji 
i określić ich rodzaj.
D e u k cja. Punkty, w których (z 2 + 1 )(z+ H) 2 = 0. Jeśli z 2 L- 1 = 0 następnie 2 = ±r Jeśli (z 4- H) 2 = 0, to z= -3. Dlatego funkcja ma trzy punkty osobliwe z= r, 22 = -r, Z3 = - 3. Rozważ z:
G - słup pierwszego rzędu (użyliśmy Corollary 26,4). Podobnie można wykazać, że 22 = -i także słup pierwszego rzędu. Na 2h mamy:
Przejdźmy do rozważenia kwestii zasadniczo pojedynczych.
Twierdzenie 26.6. Izolowany punkt osobliwy zq funkcji f(z) jest zasadniczo osobliwy wtedy i tylko wtedy, gdy główna część rozwinięcia Laurenta wyśrodkowana na zq ma nieskończenie wiele różnych od. zero, współczynniki z p.
Dowód. Twierdzenie 26.6 wynika bezpośrednio z Twierdzeń 26.2 i 26,3. Rzeczywiście, jeśli punkt zq jest w zasadzie liczba pojedyncza, to główna część rozwinięcia Laurenta nie może być nieobecna ani zawierać skończonej liczby wyrazów (w przeciwnym razie punkt Zq będzie albo zdejmowany, albo słupek). Dlatego liczba terminów w części głównej musi być nieskończona.
I odwrotnie, jeśli główna część zawiera nieskończenie wiele członków, to Zq nie może być ani punktem zdejmowanym, ani biegunem. W konsekwencji ten punkt jest zasadniczo pojedynczy.
Zgodnie z definicją punkt zasadniczo osobliwy charakteryzuje się tym, że funkcja f(2) nie ma ani skończonej, ani nieskończonej granicy dla z ->zq. Pełniejsze wyobrażenie o tym, jak nieregularne jest zachowanie funkcji w sąsiedztwie zasadniczo osobliwego punktu, daje następujące twierdzenie.
Twierdzenie 26,7 (twierdzenie Sochockiego). Jeżeli zq jest w istocie liczbą pojedynczą, to punkt funkcji f(z), to dla dowolnej liczby zespolonej L, w tym A = oo, istnieje ciąg punktów z n taki, że z n -> zo i Lim f(zł) = ALE.
n->os
Dowód. Rozważ najpierw sprawę A = z oo. W pierwszej części dowodu Twierdzenia 2G.2 ustaliliśmy, że if F z) jest ograniczony w jakimś przebitym sąsiedztwie punktu r0, to wszystkie współczynniki c, n = - 1, - 2,... części głównej są równe zeru (w konsekwencji osobliwość w th jest usuwalna). Ponieważ z założenia r0 jest zasadniczo osobliwym punktem, funkcja f(r) jest nieograniczona w każdym przebitym sąsiedztwie punktu r0. Weźmy jakieś wąskie sąsiedztwo 0 Z takie, że f(zi) > 1 (jeśli |/(r)| z - zo R/2 jest punkt z-2 , gdzie |/(dd)| > 2 itd.: w przebitej okolicy O 71. Jest oczywiste, że rn -e go i lim /(r«) = oo. Zatem w przypadku A = oo Twierdzenie 26,7
udowodniony.
Niech teraz f z oo. Załóżmy najpierw, że jest przebita okolica 0
= -rr---- będzie analityczny w tym przebitym sąsiedztwie, a w konsekwencji
/(G) - ALE
w konsekwencji r jest izolowanym punktem osobliwym funkcji Φ(r). Pokażmy. że r0 jest zasadniczo pojedynczym punktem Φ(r). Niech będzie źle. Wtedy istnieje granica lim Φ(r), skończona lub nieskończona. Dlatego
/(r) = A + , to Hsh /(r) również istnieje, co jest sprzeczne z warunkiem
F(g) ~ :-*z 0
widok twierdzenia. Zatem r0 jest zasadniczo osobliwym punktem funkcji Φ(r). Zgodnie z tym, co zostało udowodnione powyżej, istnieje ciąg punktów r n taki, że r n o i lim Φ(r n) = oo. Stąd
Udowodniliśmy wymagane twierdzenie przy założeniu, że f(r) F A w jakimś przebitym sąsiedztwie punktu r. Załóżmy teraz, że to nieprawda, tj. w dowolnym dowolnie małym przebitym sąsiedztwie punktu th taki punkt znajduje się G",że f(r") = A. Wtedy dla dowolnego P w przebitym sąsiedztwie 0 f(zu) = L. Zatem wymagane twierdzenie jest prawdziwe P-ty
we wszystkich przypadkach i twierdzenie 26.7 jest udowodnione.
Zgodnie z Twierdzeniem (Sokhotsky'ego) 26.7, w dowolnym (arbitralnie małym) przebitym sąsiedztwie zasadniczo osobliwego punktu funkcja f(r) przyjmuje wartości arbitralnie zbliżone do dowolnej liczby w rozszerzonej płaszczyźnie zespolonej C.
Do badania izolowanych punktów osobliwych często przydatne są dobrze znane rozwinięcia Taylora podstawowych funkcji elementarnych.
PRZYKŁAD 2G.8. Określ typ punktu osobliwego zq = 0 dla funkcji
Rozwiązany i e. Rozszerzamy licznik i mianownik w szeregu Taylora w potęgach r. Podstawianie do (22.11) 3 z zamiast r i odejmowania 1 otrzymujemy
Używając (22.12) otrzymujemy rozwinięcie mianownika:
Serie w tych rozszerzeniach zbiegają się w całej złożonej płaszczyźnie €. Mamy
i /2(2) są analogiczne w sąsiedztwie punktu zo = 0 (a nawet w całej płaszczyźnie) i /2(20) F 0, to h(z) jest również analityczny w pewnym sąsiedztwie punktu gF 0. Zgodnie z wnioskiem 26.4 punkt Zo = 0 jest biegunem porządku N = 4.
II przykład 26.9. Znajdź punkty osobliwe funkcji F z)= sin j - i określ ich rodzaj.
P e in e i e. Funkcja ma jeden końcowy punkt osobliwy zq = 1. W innych punktach z C funkcja w =--- analityczne; stąd funkcja grzechu w będzie analityczny.
Podstawiając w rozwinięciu sinusa (22.12) - zamiast r otrzymujemy
Otrzymaliśmy rozwinięcie funkcji sin w szeregu Laurenta w przebitym sąsiedztwie punktu 20 = 1. Ponieważ wynikowe rozwinięcie zawiera nieskończenie wiele wyrazów o ujemnych potęgach (r - 1), to zq = 1 jest zasadniczym punktem osobliwym (w tym przypadku rozwinięcie Laurenta składa się tylko z części głównej i brakuje właściwej części).
Należy zauważyć, że w tym przypadku również możliwe było ustalenie charakteru osobliwości bezpośrednio z definicji, bez uciekania się do rozszerzania serii. Rzeczywiście, istnieją sekwencje (r") i (2") zbieżne do Zo= 1 i takie, że f(z" n)= 1, /(2") = 0 (określ takie sekwencje samodzielnie). F z) nie ma limitu, kiedy z -> 1 i stąd punkt zq - 1 jest zasadniczo liczbą pojedynczą.
Wprowadźmy pojęcie rozwinięcia Laurenta funkcji w sąsiedztwie punktu Zq = 00 i rozważ związek między rozwinięciem a naturą osobliwości w tym punkcie. Zauważ, że definicje izolowanego punktu osobliwego i jego typ (zdejmowany, biegunowy lub zasadniczo osobliwy) przenoszą się do przypadku zq = oc bez zmian. Ale twierdzenia 26.2. 26,3 i 26.6, związane z charakterem rozszerzeń Laurenta, muszą zostać zmienione. Chodzi o to, że członkowie c n (z - 2o) pkt. P= -1,-2,..., część główna, określająca „nieregularność” funkcji w pobliżu punktu końcowego Zq, ponieważ 2 ma tendencję do oo, będą się zachowywać „poprawnie” (z tendencją do 0). Wręcz przeciwnie, członkowie regularnej części z P= 1,2,... będzie dążyć do oo; określają charakter osobliwości w Zq = oo. Dlatego główną częścią ekspansji w sąsiedztwie oo będą terminy o pozytywnych mocach P, i poprawny - z negatywem.
Wprowadźmy nową zmienną w = 12. Funkcjonować telewizor= 1/2, rozszerzone tak, że u(oo) = 0, jeden do jednego i konformalnie odwzorowuje sąsiedztwo z > R zwrotnica zq = 00 w sąsiedztwie |w| wq = 0. Jeśli funkcja F z) analityka w przebitej okolicy r z Zq = oc, to funkcja G(w) = f(l/w) będzie analityczne w żółtym sąsiedztwie 0 wo = 0. Ponieważ dla 2 -> oo będzie w-> 0, to
Dlatego G(w) ma w punkcie wq = 0 jest osobliwością tego samego typu co F z) w punkcie Zq = 00. Rozwińmy funkcję G(w) w szeregu Laurenta w przebitym sąsiedztwie punktu wo = 0:
Sumy po prawej stronie (26,5) reprezentują odpowiednio właściwą i główną część rozwinięcia. Przejdźmy do zmiennej z, zastępowanie w = 1/z: 
oznaczający P\u003d -A *, 6 * \u003d 6_ ” \u003d z i zauważając, że G(l/z) = F z), otrzymujemy
Rozkład (2G.G) nazywa się Rozwinięcie Laurenta funkcji f(z) w przebitym sąsiedztwie punktu zq= oo. Pierwsza suma w (2G.6) nazywa się prawa część, a druga suma to Głównym elementem ten rozkład. Ponieważ te sumy odpowiadają poprawnym i głównym częściom rozwinięcia (26,5), rozwinięcie (26.6) spełnia analogie twierdzeń 26,2, 26,3 i 26,6. Zatem następujące twierdzenie jest analogiem twierdzenia 26.2.
Twierdzenie 26.10. Izolowany pojedynczy punktZq - os (Funkcje/(G) jest usuwalny wtedy i tylko wtedy, gdy rozwinięcie Laurenta w przebitym sąsiedztwie tego punktu ma postać
p.p. składa się tylko z właściwej części.
Wstawiamy /(oo) = współ. Funkcja określona szeregiem (26,7) zbieżnym w sąsiedztwie z > R punkty 2o \u003d oc, zwane analityczny w punkcie z o = oo. (Zauważ, że ta definicja jest równoważna analityczności funkcji G(w) w punkcie nie = 0.)
Przykład 26.11. Zbadaj punkt osobliwy zq = oo funkcji
Ponieważ granica jest skończona, więc zo = oo jest usuwalnym punktem osobliwym funkcji f(r). Jeśli postawimy /(oo) = lim J z)= 0, to F z) stanie się
tik w punkcie Zo= os. Pokażmy, jak znaleźć odpowiednie rozwinięcie (26.7). Przejdźmy do zmiennej w = 1 F z. Zastępowanie z= 1 /?e, otrzymujemy
(ostatnia równość obowiązuje w przebitym sąsiedztwie punktu ww = 0, ale rozszerzymy definicję (7(0) = 0). Wynikowa funkcja ma punkty osobliwe w =± ja, w =-1/3 i w punkcie Wq = 0 jest analityczne. Rozszerzenie funkcji G(w) przez stopnie w(jak zrobiono w Przykładzie 25.7) i podstawiając do wynikowego szeregu potęgowego w = 1/z można uzyskać rozwinięcie (26,7) funkcji F z).
Twierdzenie 26.3 dla przypadku Zo= oo zostanie przepisane w następującej formie.
Twierdzenie 26.12. Izolowany pojedynczy punkt idź = os funkcja f(z) jest biegunem wtedy i tylko wtedy, gdy główna część rozwinięcia Laurenta (26.6) ma tylko skończoną liczbę niezerowych współczynników od":
Tutaj seria jest częścią regularną, a wielomian w nawiasie jest główną częścią rozszerzenia. Wielokrotność bieguna w oc jest zdefiniowana jako krotność bieguna wq = 0 funkcji G(z).Łatwo zauważyć, że krotność bieguna pokrywa się z liczbą n w (26,8).
Qp | (i 2 + 1) (z + 3) 2
Zadanie. Pokaż, że funkcja F z) =-- -- ma w
punkt zo = oo słup zamów 3.
Twierdzenie 26.6 o zasadniczym punkcie osobliwym jest przepisywane dla przypadku Zo= os prawie dosłownie i nie rozwodzimy się nad tym szczegółowo.
Szeregi Taylora służą jako efektywne narzędzie do badania funkcji analitycznych w okręgu zol W badaniu funkcji analitycznych w obszarze pierścieniowym okazuje się, że możliwe jest konstruowanie rozwinięć w dodatnich i ujemnych potęgach (z - zq) forma, która uogólnia rozwinięcia Taylora. Szereg (1), rozumiany jako suma dwóch szeregów, nazywamy szeregiem Laurenta. Jest oczywiste, że obszar zbieżności szeregu (1) jest wspólną częścią obszarów zbieżności każdego z szeregu (2). Znajdźmy ją. Obszar zbieżności pierwszego szeregu to okrąg, którego promień jest określony wzorem Cauchy-Hadamarda Wewnątrz okręgu zbieżności szereg (3) zbiega się do funkcji analitycznej, a w dowolnym okręgu o mniejszym promieniu jest zbieżny bezwzględnie i jednolicie. Szereg drugi jest szeregiem potęgowym względem zmiennej Szereg (5) jest zbieżny w swoim okręgu zbieżności do funkcji analitycznej zmiennej zespolonej m-*oo, a w dowolnym okręgu o mniejszym promieniu jest zbieżny bezwzględnie i jednostajnie, co oznacza, że obszar zbieżności szeregu (4) jest wyglądem okręgu - Jeżeli wtedy istnieje wspólny obszar zbieżności szeregu (3) i (4) - kołowy pierścień, w którym szereg (1) zbiega się do funkcji analitycznej. Co więcej, w każdym pierścieniu zbiega się absolutnie i jednorodnie. Przykład 1. Wyznacz obszar zbieżności szeregu rad Laurenta Pojedyncze punkty osobliwe i ich klasyfikacja (z), która jest jednowartościowa i apolityczna w pierścieniu kołowym, można przedstawić w tym pierścieniu jako sumę szeregu zbieżnego, którego współczynniki Cn są jednoznacznie określone i obliczone za pomocą wzorów gdzie 7p jest okręgiem o promieniu m Ustalmy dowolny punkt z wewnątrz pierścienia R Konstruujemy okręgi o środkach w punkcie r, których promienie spełniają nierówności i rozważamy nowy pierścień.Zgodnie z twierdzeniem Cauchy'ego dla dziedziny wielokrotnie połączonej mamy Przekształćmy osobno każdą z całek w sumie (8). Dla wszystkich punktów £ na okręgu 7d* zachowana jest zależność de suma jednostajnie zbieżnego szeregu 1 1. Dlatego ułamek ^ można przedstawić w vi- /" / W nieco inny sposób dla wszystkich punktów ξ na koło ir> mamy zależność Dlatego ułamek ^ można przedstawić jako sumę jednostajnie zbieżnego szeregu we wzorach (10) i (12) są funkcjami analitycznymi w pierścieniu kołowym. Dlatego, zgodnie z twierdzeniem Cauchy'ego, wartości odpowiednich całek nie zmieniają się, jeśli okręgi 7/r i 7r/ zostaną zastąpione dowolnym okręgiem. To pozwala nam łączyć wzory (10) i (12).Zastępując całki po prawej stronie wzoru (8) odpowiednio ich wyrażeniami (9) i (11), otrzymujemy pożądane rozwinięcie.Ponieważ z jest arbitralne punktu pierścienia, wynika z tego, że szereg (14) jest zbieżny do funkcji f(z) wszędzie w tym pierścieniu, aw każdym pierścieniu szereg jest zbieżny do tej funkcji absolutnie i jednostajnie. Wykażmy teraz, że dekompozycja postaci (6) jest wyjątkowa. Załóżmy, że zachodzi jeszcze jeden rozkład.Wtedy wszędzie wewnątrz pierścienia R mamy Na obwodzie szeregi (15) zbiegają się jednostajnie. Pomnóż obie strony równości (gdzie m jest stałą liczbą całkowitą i integruj obie serie termin po terminie. W rezultacie otrzymujemy lewą stronę, a po prawej - Csh. Tak więc (4, \u003d St. Ponieważ m jest dowolną liczbą, to ostatnia seria równości (6), której współczynniki są obliczane ze wzorów (7), nazywana jest szeregiem Laurenta funkcji f(z) w pierścieniu 7) dla współczynników szeregu Laurenta są rzadko stosowane w praktyce, ponieważ z reguły wymagają kłopotliwych obliczeń.Zazwyczaj, jeśli to możliwe, stosuje się gotowe rozwinięcia Taylora funkcji elementarnych.Ze względu na unikalność rozwinięcia, każdy słuszny sposób prowadzi do tego samego rezultatu. Przykład 2 Rozważ rozwinięcia funkcji różnych dziedzin w szereg Laurenta, zakładając, że Fuiscius /(r) ma dwa punkty osobliwe: Zatem istnieją trzy dziedziny pierścieniowe i wyśrodkowany w punkcie r = 0, w którym funkcja f(r) jest analityczna: a) okrąg jest zewnętrzną stroną okręgu (ryc. 27). Znajdźmy rozwinięcia Laurenta funkcji /(z) w każdym z tych regionów. Reprezentujemy /(z) jako sumę ułamków elementarnych a) Relacja przekształcenia koła (16) w następujący sposób Korzystając ze wzoru na sumę członów postępu geometrycznego, otrzymujemy b) Pierścień dla funkcji -z pozostaje zbieżny w tym pierścieniu, ponieważ Szereg (19) dla funkcji j^j dla |z| > 1 odbiega. Dlatego przekształcamy funkcję /(z) w następujący sposób: stosując ponownie wzór (19) otrzymujemy, że Ten szereg jest zbieżny dla. Podstawiając rozwinięcia (18) i (21) do zależności (20), otrzymujemy c) Zewnętrzność okręgu dla funkcji -z przy |z| > 2 rozbieżności i szereg (21) dla funkcji Reprezentujmy funkcję /(z) w postaci: /<*> Używając wzorów (18) i (19), otrzymujemy OR 1 Ten przykład pokazuje, że dla tej samej funkcji f(z) rozwinięcie Laurenta, ogólnie mówiąc, ma różną postać dla różnych pierścieni. Przykład 3. Znajdź rozkład 8 szeregu Laurenta funkcji szereg Laurenta Odosobnione punkty osobliwe i ich klasyfikacja w obszarze pierścieniowym A Reprezentację funkcji f (z) wykorzystujemy w postaci: i transformujemy drugi wyraz wzór na sumę wyrazów postępu geometrycznego, otrzymujemy Podstawiając znalezione wyrażenia do wzoru (22), mamy Przykład 4. Rozwiń funkcję w szeregu Laurenta w sąsiedztwie cienkiego zq = 0. Dla dowolnego złożonego , mamy Niech To rozwinięcie obowiązuje dla dowolnego punktu z Ф 0. W tym przypadku obszar pierścieniowy jest całą płaszczyzną zespoloną z jednym odrzuconym punktem z - 0. Obszar ten można zdefiniować za pomocą następującej zależności: Ta funkcja jest analityczna w rejonie Ze wzorów (13) na współczynniki szeregu Laurenta, analogicznie jak w poprzednim akapicie, można otrzymać nierówności Kouiwa. jeśli funkcja f(z) jest ograniczona na okręgu, gdzie M jest stałą), to punkty osobliwe izolowane Punkt zo nazywamy izolowanym punktem osobliwym funkcji f(z), jeśli istnieje pierścieniowe sąsiedztwo punktu ( zbiór ten bywa też nazywany przebitym sąsiedztwem punktu 2o), w którym funkcja f(z) jest jednowartościowa i analityczna. W samym punkcie zo funkcja albo nie jest zdefiniowana, albo nie jest jednowartościowa i analityczna. Rozróżnia się trzy typy punktów osobliwych w zależności od zachowania funkcji /(z) przy zbliżaniu się do punktu zo. Mówi się, że izolowany punkt osobliwy jest: 1) usuwalny, jeśli istnieje skończony 2) pmusach, jeśli 3) zasadniczo osobliwym punktem, jeśli funkcja f(z) nie ma granic dla Twierdzenie 16. Izolowany punkt osobliwy z0 funkcji f(z) jest usuwalnym punktem osobliwym wtedy i tylko wtedy, gdy rozwinięcie Laurenta funkcji f(z) w sąsiedztwie punktu zo nie zawiera części głównej, tj. ma postać Let zo - zdejmowany punkt osobliwy. Wtedy istnieje jedynka skończona, a więc funkcja f(z) jest ograniczona w prokologicznym sąsiedztwie punktu r. Wyznaczamy na mocy nierówności Cauchy'ego Ponieważ można wybrać ρ tak małą, jak nam się podoba, to wszystkie współczynniki przy ujemnych potęgach (z - 20) są równe zeru: Odwrotnie, niech rozwinięcie funkcji /(r) w sąsiedztwie punktu zq zawiera tylko poprawną część, czyli ma postać (23) a zatem jest Taylorem. Łatwo zauważyć, że dla z -* z0 funkcja /(r) ma wartość graniczną: Twierdzenie 17. Izolowany punkt osobliwy zq funkcji f(z) jest usuwalny wtedy i tylko wtedy, gdy funkcja J(z) jest ograniczony w jakimś przebitym sąsiedztwie punktu zq, Zgmechai nie. Niech r0 będzie usuwalnym punktem osobliwym f(r). Zakładając, że otrzymujemy, że funkcja f(r) jest analityczna w jakimś okręgu o środku w punkcie th. To określa nazwę punktu - jednorazowy. Twierdzenie 18. Izolowany punkt osobliwy zq funkcji f(z) jest biegunem wtedy i tylko wtedy, gdy główna część rozwinięcia Laurenta funkcji f(z) w sąsiedztwie punktu zawiera liczbę skończoną (i dodatnią) niezerowych wyrazów, czyli ma postać 4 Niech z0 będzie biegunem. Od tego czasu istnieje przebite sąsiedztwo punktu z0, w którym funkcja f(z) jest analityczna i niezerowa. Wtedy funkcja analityczna jest zdefiniowana w tym otoczeniu i stąd punkt zq jest usuwalnym punktem osobliwym (zero) funkcji lub gdzie h(z) jest funkcją analityczną, h(z0) ∩ 0. jest analitycznym w otoczeniu punkt zq, a więc skąd to otrzymujemy Załóżmy teraz, że funkcja f(z) ma rozkład postaci (24) w przebitym sąsiedztwie punktu zo. Oznacza to, że w tym sąsiedztwie funkcja f(z) jest analityczna razem z funkcją. Dla funkcji g(z) obowiązuje rozwinięcie, z którego jasno wynika, że zq jest usuwalnym punktem osobliwym funkcji g(z) i istnieje Następnie funkcja dąży do 0 - bieguna funkcji Jest jeszcze jeden prosty fakt. Punkt Zq jest biegunem funkcji f(z) wtedy i tylko wtedy, gdy funkcję g(z) = y można rozszerzyć do funkcji analitycznej w sąsiedztwie punktu zq przez ustawienie g(z0) = 0. bieguna funkcji f(z) nazywamy rzędem zera funkcji jfa. Twierdzenia 16 i 18 implikują następujące twierdzenie. Twierdzenie 19. Izolowana osobliwa cienka jest zasadniczo osobliwa wtedy i tylko wtedy, gdy główna część rozwinięcia Laurenta w przebitym sąsiedztwie tego punktu zawiera nieskończenie wiele niezerowych członów. Przykład 5. Punktem osobliwym funkcji jest zo = 0. Mamy odosobnione punkty osobliwe serii Laurenta i ich klasyfikacja Dlatego zo = 0 jest usuwalnym punktem osobliwym. Rozwinięcie funkcji /(z) w szeregu Laurenta w pobliżu punktu zerowego zawiera tylko poprawną część: Przykład7. f(z) = Punktem osobliwym funkcji f(z) jest zq = 0. Rozważ zachowanie tej funkcji na osi rzeczywistej i urojonej: na osi rzeczywistej w punkcie x 0, na osi urojonej Dlatego ani skończone, ani nieskończona granica f(z) przy z -* 0 nie istnieje. Stąd punkt r0 = 0 jest zasadniczo osobliwym punktem funkcji f(z). Znajdźmy rozwinięcie Laurenta funkcji f(z) w sąsiedztwie punktu zerowego. Dla dowolnego kompleksu C mamy ustalone. Następnie rozszerzenie Laurenta zawiera nieskończoną liczbę wyrazów o ujemnych potęgach z.
Definicja. Punkt osobliwy funkcji nazywa się odosobniony, jeśli w jakimś sąsiedztwie tego punktu znajduje się funkcja analityczna (czyli analityczna w pierścieniu).
Klasyfikacja izolowanych punktów osobliwych funkcji jest związana z zachowaniem tej funkcji w sąsiedztwie punktu osobliwego.
Definicja. Punkt nazywa się jednorazowy punkt osobliwy funkcji, jeśli istnieje skończona granica tej funkcji w .
Przykład 5 Pokaż, że funkcja ma w punkcie usuwalną osobliwość.
Rozwiązanie. Przypominając pierwszą godną uwagi granicę, obliczamy
Oznacza to, że dana funkcja ma w punkcie usuwalną osobliwość.
Zadanie 4. Pokaż, że punkt jest usuwalny dla .
Definicja. Punkt nazywa się Polak funkcja , jeśli ta funkcja rośnie w nieskończoność dla , to znaczy .
Zwróćmy uwagę na związek między pojęciami zera i bieguna funkcji analitycznej. Reprezentujmy funkcję jako .
Jeśli punkt jest prostym zerem funkcji, to funkcja ma prosty biegun
Jeżeli punkt jest porządkiem zero dla funkcji, to dla funkcji jest to biegun zamówienie.
Przykład 6 Pokaż, że funkcja ma w punkcie biegun trzeciego rzędu.
Rozwiązanie. Zakładając , że otrzymamy . Ponieważ dążymy do zera, zgodnie z jakimkolwiek prawem, mamy . Następnie , a wraz z nim sama funkcja rośnie w nieskończoność. Dlatego , czyli punkt osobliwy jest biegunem. Dla funkcji ten punkt jest oczywiście potrójnym zerem. Stąd dla tej funkcji punkt jest biegunem trzeciego rzędu.
Zadanie 5. Pokaż, że punkt ma prosty biegun.
Definicja. Punkt nazywa się zasadniczo wyjątkowy punktu funkcji, jeśli w tym punkcie nie ma ani skończonej, ani nieskończonej granicy funkcji (zachowanie funkcji nie jest zdefiniowane).
Niech będzie istotnym punktem osobliwym funkcji . Następnie dla dowolnej wcześniej przypisanej liczby zespolonej istnieje taki ciąg punktów zbieżnych do , wzdłuż którego wartości mają tendencję do : ( Twierdzenie Sochockiego).
Przykład 7 Pokaż, że funkcja w punkcie ma zasadniczą osobliwość.
Rozwiązanie. Rozważ zachowanie danej funkcji w pobliżu punktu. Bo wzdłuż dodatniej części osi rzeczywistej (tj.) mamy i ; jeśli wzdłuż ujemnej części osi rzeczywistej (tj.), to i . Więc nie ma ograniczeń dla . Z definicji funkcja ma w pewnym momencie istotną osobliwość.
Rozważmy zachowanie funkcji w punkcie zero z punktu widzenia twierdzenia Sochockiego. Niech będzie dowolną liczbą zespoloną inną niż zero i nieskończoność.
Od równości znajdujemy . Zakładając , otrzymujemy ciąg punktów , . Oczywiście, . W każdym punkcie tej sekwencji funkcja jest równa , a zatem
Zadanie 6. Pokaż, że funkcja ma w pewnym momencie istotną osobliwość.
Punkt w nieskończoności jest zawsze uważany za specjalny dla funkcji. Punkt nazywany jest izolowanym punktem osobliwym funkcji, jeśli ta funkcja nie ma innych punktów osobliwych poza pewnym okręgiem, którego środek znajduje się w punkcie początkowym.
Klasyfikację pojedynczych punktów osobliwych można również rozszerzyć na przypadek.
Przykład 8 Pokaż, że funkcja ma podwójny biegun w nieskończoności.
Rozwiązanie. Rozważmy funkcję , gdzie jest funkcją analityczną w sąsiedztwie punktu , oraz . Oznacza to, że funkcja ma podwójne zero w nieskończoności, ale wtedy dla funkcji punkt jest biegunem podwójnym.
Przykład 9 Pokaż, że funkcja ma istotną osobliwość w nieskończoności.
Rozwiązanie. Podobny problem jest rozważany w pr.7. Rozważ zachowanie funkcji w sąsiedztwie nieskończenie odległego punktu. Wzdłuż dodatniej części osi rzeczywistej i wzdłuż ujemnej części osi rzeczywistej. Oznacza to, że w punkcie nie ma granic funkcji i, z definicji, punkt ten jest w zasadzie pojedynczy.
Charakter osobliwości funkcji w punkcie można ocenić na podstawie Głównym elementem Ekspansja Laurenta w sąsiedztwie tego punktu.
Twierdzenie 1. Aby punkt był jednorazowy punkt osobliwy funkcji , konieczne i wystarczające jest, aby odpowiednie rozwinięcie Laurenta nie zawierał głównej części.
Zadanie 6. Korzystając z rozwinięcia Taylora funkcji w sąsiedztwie punktu , pokaż, że ma ona usuwalną osobliwość w punkcie zero.
Twierdzenie 2. Aby punkt był Polak funkcje , jest konieczne i wystarczające, aby Głównym elementem odpowiednia ekspansja Laurenta zawierał skończoną liczbę członków :
Liczba najwyższego składnika ujemnego określa kolejność bieguna.
W tym przypadku funkcję można przedstawić jako
gdzie jest funkcją analityczną w punkcie , jest rząd bieguna.
Przykład 10 Pokaż, że funkcja ma w punktach proste bieguny.
Rozwiązanie. Rozważmy punkt. Korzystamy z rozwinięcia Laurenta tej funkcji w pobliżu tego punktu, uzyskanego w Przykładzie 2:
Ponieważ najwyższa (i jedyna) ujemna moc w głównej części tego rozwinięcia jest równa jeden, punkt jest prostym biegunem tej funkcji.
Ten wynik można było uzyskać w inny sposób. Reprezentujmy w formie i wstawmy - jest to funkcja analityczna w punkcie i . Stąd, ze względu na (8) funkcja ta ma w punkcie prosty biegun.
Inny sposób: rozważ funkcję, która ma w punkcie proste zero. Stąd w tym momencie ma prosty słup.
Podobnie, jeśli napiszemy funkcję w postaci , gdzie jest funkcją analityczną w punkcie i , to od razu widać, że punkt jest prostym biegunem funkcji .
Zadanie 7. Pokaż, że funkcja ma biegun drugiego rzędu w punkcie i biegun czwartego rzędu w punkcie .
Twierdzenie 3. Aby punkt był zasadniczo wyjątkowy punktu funkcji , konieczne i wystarczające jest, aby Głównym elementem Ekspansja Laurenta w sąsiedztwie punktu zawierał nieskończoną liczbę członków .
Przykład 11. Określ charakter osobliwości w punkcie funkcji
Rozwiązanie. W dobrze znanym rozszerzeniu cosinusa wstawiamy zamiast:
Stąd rozwinięcie Laurenta w sąsiedztwie punktu ma postać
Tutaj właściwa część to jeden termin. A główna część zawiera nieskończoną liczbę terminów, więc punkt jest zasadniczo pojedynczy.
Zadanie 8. Pokaż, że w pewnym momencie funkcja ma zasadniczą osobliwość.
Rozważ jakąś funkcję i zapisz jej rozwinięcie Laurenta w punkcie :
Zróbmy zamianę , podczas gdy punkt idzie do punktu . Teraz, w sąsiedztwie punktu w nieskończoności, mamy
Pozostaje wprowadzić nowe oznaczenie. dostajemy
gdzie jest główną częścią i jest regularną częścią rozwinięcia funkcji Laurenta w sąsiedztwie nieskończenie odległego punktu. Tak więc w rozwinięciu Laurenta funkcji w sąsiedztwie punktu, główna część jest szeregiem w potęgach dodatnich, podczas gdy poprawna część jest szeregiem w potęgach ujemnych. Biorąc to pod uwagę
Powyższe kryteria określania natury osobliwości pozostają jednak aktualne dla nieskończenie odległego punktu.
Przykład 12. Poznaj naturę osobliwości funkcji w punkcie. , to w pewnym momencie może okazać się, że nie jest izolowany.
Przykład 15 Funkcja w nieskończenie odległym punkcie ma zasadniczą osobliwość. Pokaż, że punkt funkcji nie jest izolowanym punktem osobliwym.
Rozwiązanie. Funkcja ma nieskończoną liczbę biegunów w zerach mianownika, czyli w punktach , . Ponieważ , to punkt , w jakimkolwiek sąsiedztwie, w którym znajdują się bieguny , jest punktem granicznym dla biegunów.
punkt osobliwy w matematyce. 1) Punkt osobliwy krzywej dany równaniem F ( x, y) = 0, - punkt M 0 ( x 0 , y 0), w którym obie pochodne cząstkowe funkcji F ( x, y) znikają: Jeżeli dodatkowo nie wszystkie drugie pochodne cząstkowe funkcji F ( x, y) w punkcie M 0 są równe zeru, to O. t. nazywa się podwójnym. Jeśli wraz z zanikiem pierwszych pochodnych w punkcie M 0 znikają wszystkie drugie pochodne, ale nie wszystkie trzecie pochodne są równe zeru, to O. t. nazywamy potrójnym i tak dalej. Przy badaniu struktury krzywej w pobliżu podwójnego O. t. ważną rolę odgrywa znak wyrażenia Jeśli Δ > 0, to O. t. nazywamy izolowanym; na przykład krzywa y 2 - x 4 + 4x 2= 0 pochodzenie jest izolowanym O. t. (patrz Ryż. jeden
). Jeśli Δ x 2 + y 2 + a 2) 2 - 4a 2x2 - a 4= 0 początek współrzędnych jest węzłem O. t. (patrz Ryż. 2
). Jeśli Δ = 0, to krzywa O. t. jest albo izolowana, albo charakteryzuje się tym, że różne gałęzie krzywej mają w tym punkcie wspólną styczną, na przykład: styczną i tworzą punkt, jak krzywa y 2 - x 3= 0 (patrz Ryż. 3
, a); b) wierzchołek II rodzaju - różne gałęzie łuku znajdują się po tej samej stronie wspólnej stycznej, podobnie jak łuk
(y - x 2)2 - x 5= 0 (patrz Ryż. 3
, b); c) punkt kontaktu własnego (dla krzywej y 2 - x 4= 0 początek jest punktem kontaktu z samym sobą; (cm. Ryż. 3
, w). Wraz z określonym O. t. istnieje wiele innych O. t. o specjalnych nazwach; na przykład punktem asymptotycznym jest wierzchołek spirali o nieskończonej liczbie zwojów (patrz ryc. Ryż. 4
), punkt przerwania, punkt narożny itp. 2) Punkt osobliwy równania różniczkowego to punkt, w którym zarówno licznik, jak i mianownik z prawej strony równania różniczkowego znikają jednocześnie (patrz Równania różniczkowe) gdzie P i Q są funkcjami ciągle różniczkowanymi. Zakładając, że O. t. znajduje się w początku współrzędnych i korzystając ze wzoru Taylora (Patrz wzór Taylora), możemy przedstawić równanie (1) w postaci gdzie P 1 ( x, y) i Q1 ( x, y) są nieskończenie małe w stosunku do Mianowicie, jeśli λ 1 ≠ λ 2 i λ 1 λ 2 > 0 lub λ 1 = λ 2, to O. t. jest węzłem; wchodzą do niego wszystkie krzywe całkowe przechodzące przez punkty odpowiednio małego sąsiedztwa węzła. Jeżeli λ 1 ≠ λ 2 i λ 1 λ 2 i β, α ≠ 0 i β ≠ 0, to O. t. jest ogniskiem; wszystkie krzywe całkowe przechodzące przez punkty w wystarczająco małym sąsiedztwie ogniska są spiralami o nieskończonej liczbie zwojów w dowolnym dowolnie małym sąsiedztwie ogniska. Jeżeli ostatecznie λ 1,2 = ± iβ, β ≠ 0, to charakter O. t. nie jest określony przez wyrażenia liniowe w rozwinięciach P ( x, y) i Q ( x, y), podobnie jak we wszystkich powyższych przypadkach; tutaj O. t. może być ogniskiem lub centrum, albo może mieć bardziej złożony charakter. W sąsiedztwie środka wszystkie krzywe całkowe są zamknięte i zawierają środek wewnątrz siebie. Na przykład punkt (0, 0) jest węzłem dla równań w" = 2u/x(λ 1 = 1, λ 2 = 2; patrz Ryż. pięć
, a) i tak" = u/x(λ 1 = λ 2 = 1; patrz Ryż. pięć
, b), siodło do równania y" = -y/x(λ 1 = -1, λ 2 = 1 ; cm. Ryż. 6
), skupienie na równaniu y” =(x + y) /
(x - y) (λ 1 = 1 - i, λ 2 = 1 + i; cm. Ryż. 7
) i środek równania y" = -x / y(λ 1 = -i, λ 2 = i; cm. Ryż. 8
). Jeśli x, y) i Q ( x, y) są analityczne, sąsiedztwo O. t. wyższego rzędu można podzielić na obszary: D 1 - wypełnione krzywymi całkowitymi, których oba końce są zawarte w O. t. (regiony eliptyczne), D 2 - wypełnione z krzywymi całkowitymi, których jeden koniec jest zawarty w O. t. (regiony paraboliczne), a D 3 - regiony ograniczone dwiema krzywymi całkowitymi zawartymi w O. t., pomiędzy którymi znajdują się krzywe całkowe typu hiperboli (regiony hiperboliczne) (zob. Ryż. dziewięć
). Jeśli nie ma krzywych całkowych wchodzących w punkt O., to punkt O. nazywany jest punktem typu stabilnego. Sąsiedztwo stabilnego O. t. składa się z zamkniętych krzywych integralnych zawierających O. t. wewnątrz siebie, pomiędzy którymi znajdują się spirale (patrz ryc. Ryż. 10
). Badanie równań różniczkowych O. t., czyli w istocie badanie zachowania rodzin krzywych całkowych w sąsiedztwie O. t. M. Lyapunowa, A. Poincaré i innych). 3) Punktem osobliwym jednowartościowej funkcji analitycznej jest punkt, w którym naruszona jest analityczność funkcji (patrz Funkcje analityczne). Jeśli istnieje sąsiedztwo O. t. a, wolny od innych O. t., to punkt ale nazywa się izolowanym O. t. If ale jest izolowanym O. t. i istnieje skończone a nazywa się usuwalnym O. t. F(a)= b, jest to możliwe do osiągnięcia a stanie się zwykłym punktem korygowanej funkcji. Na przykład kropka z= 0 jest zdejmowanym OT dla funkcji f 1 ( z) = F(z), Jeśli z≠ 0 i F 1(0),=1, kropka z= 0 to zwykły punkt [ F 1 (z) jest analityczny w punkcie z= 0]. Jeśli ale- izolowane O. t. i a nazywamy biegunem lub nieistotnie osobliwym punktem funkcji F(z), jeśli działa seria Laurenta) F(z) w sąsiedztwie izolowanego O. t. nie zawiera potęg ujemnych z - a, Jeśli ale- wymienny O. t., zawiera skończoną liczbę ujemnych potęg z - a, Jeśli ale- słup (w tym przypadku kolejność słupa) r jest definiowany jako najwyższa potęga a - zasadniczo pojedynczy punkt. Na przykład dla funkcji kropka z= 0 to biegun rzędu r, dla funkcji kropka z= 0 jest podstawowym punktem osobliwym. Na granicy okręgu zbieżności szeregu potęgowego musi znajdować się co najmniej jeden mb funkcji reprezentowanej wewnątrz tego okręgu przez dany szereg potęgowy. Wszystkie punkty brzegowe dziedziny istnienia jednowartościowej funkcji analitycznej (granica naturalna) są punktami brzegowymi tej funkcji. Zatem wszystkie punkty okręgu jednostkowego | z| = 1 są specjalne dla funkcji W przypadku wielowartościowej funkcji analitycznej pojęcie „O. T." trudniejsze. Oprócz O. t. w oddzielnych arkuszach powierzchni Riemanna funkcji (to znaczy O. t. jednowartościowych elementów analitycznych), każdy punkt rozgałęzienia jest również O. t. funkcji. Izolowane rozgałęzienia powierzchni Riemanna (tj. rozgałęzienia takie, że w niektórych z ich sąsiedztw nie ma innych funkcji O.t. w żadnym liściu) są klasyfikowane w następujący sposób. Jeżeli a jest izolowanym punktem rozgałęzienia o skończonym porządku i istnieje skończone a, nazywamy to biegunem krytycznym. Jeśli ale jest izolowanym punktem rozgałęzienia nieskończonego porządku, a a nazywa się transcendentalnym O. t. Wszystkie inne izolowane punkty rozgałęzienia nazywane są krytycznymi zasadniczo pojedynczymi punktami. Przykłady: kropka z= 0 jest zwykłym punktem krytycznym funkcji f ( z) = log z i krytyczny istotny punkt osobliwy funkcji F (z) = log grzechu z. Każde O. t., z wyjątkiem usuwalnego, stanowi przeszkodę dla kontynuacji analitycznej, tj. kontynuacja analityczna wzdłuż krzywej przechodzącej przez nieusuwalne O. t. jest niemożliwa. Wielka radziecka encyklopedia. - M.: Encyklopedia radziecka.
1969-1978
.
p = 2, 3, …)
Zobacz, co „Punkt specjalny” znajduje się w innych słownikach:
Punkty tutaj. Zobacz także punkt osobliwy (równania różniczkowe). Cecha lub osobliwość w matematyce to punkt, w którym obiekt matematyczny (zwykle funkcja) nie jest zdefiniowany lub zachowuje się nieregularnie (na przykład punkt, w którym ... ... Wikipedia
Funkcja analityczna to punkt, w którym naruszane są warunki analityczności. Jeżeli funkcja analityczna f(z) jest zdefiniowana w jakimś sąsiedztwie punktu z0 wszędzie… Encyklopedia fizyczna
Funkcja analityczna to punkt, w którym zostaje naruszona analityczność funkcji ... Wielki słownik encyklopedyczny
punkt osobliwy- — [Ja.N. Ługiński, MS Fezi Zhilinskaya, Yu.S. Kabirov. Angielsko-rosyjski słownik elektrotechniki i energetyki, Moskwa, 1999] Tematy elektrotechniki, podstawowe pojęcia EN punkt osobliwy ... Podręcznik tłumacza technicznego
1) OT funkcji analitycznej f(z) jest przeszkodą w kontynuacji analitycznej elementu funkcji f(z) zmiennej zespolonej z wzdłuż pewnej ścieżki na płaszczyźnie tej zmiennej. Niech funkcja analityczna f(z) będzie określona przez jakiś ... ... Encyklopedia matematyczna
Funkcja analityczna, punkt, w którym zostaje naruszona analityczność funkcji. * * * PUNKT POJEDYNCZY PUNKT POJEDYNCZY funkcji analitycznej, punkt, w którym zostaje naruszona analityczność funkcji ... słownik encyklopedyczny
punkt osobliwy- ypatingasis taškas statusas T sritis automatika atitikmenys: engl. osobliwy punkt vok. osobliwy punkt, m rus. punkt osobliwy, fpranc. cząstka punktowa, m; point singulier, m … Automatikos terminų žodynas
