Геометрично или геометрично. Геометрична прогресия. Изчерпателно ръководство с примери (2020 г.). Защо е необходима геометричната прогресия и нейната история?

Нека разгледаме определена серия.

7 28 112 448 1792...

Абсолютно ясно е, че стойността на всеки от неговите елементи е точно четири пъти по-голяма от предишната. Това означава, че тази серия е прогресия.

Геометричната прогресия е безкрайна последователност от числа, чиято основна характеристика е, че следващото число се получава от предишното чрез умножаване по определено число. Това се изразява със следната формула.

a z +1 =a z ·q, където z е номерът на избрания елемент.

Съответно z ∈ N.

Периодът, в който се изучава геометрична прогресия в училище, е 9 клас. Примерите ще ви помогнат да разберете концепцията:

0.25 0.125 0.0625...

Въз основа на тази формула знаменателят на прогресията може да се намери, както следва:

Нито q, нито b z могат да бъдат нула. Освен това всеки от елементите на прогресията не трябва да е равен на нула.

Съответно, за да разберете следващото число в поредица, трябва да умножите последното по q.

За да зададете тази прогресия, трябва да посочите нейния първи елемент и знаменател. След това е възможно да се намери всеки от следващите членове и тяхната сума.

Разновидности

В зависимост от q и a 1 тази прогресия се разделя на няколко вида:

• Ако и 1, и q са по-големи от едно, тогава такава последователност е геометрична прогресия, нарастваща с всеки следващ елемент. Пример за това е представен по-долу.

Пример: a 1 =3, q=2 - и двата параметъра са по-големи от единица.

Тогава числовата последователност може да бъде записана така:

3 6 12 24 48 ...

• Ако |q| е по-малко от едно, тоест умножението по него е еквивалентно на деление, тогава прогресия с подобни условия е намаляваща геометрична прогресия. Пример за това е представен по-долу.

Пример: a 1 =6, q=1/3 - a 1 е по-голямо от едно, q е по-малко.

Тогава числовата последователност може да бъде записана по следния начин:

6 2 2/3 ... - всеки елемент е 3 пъти по-голям от елемента след него.

• Променлив знак. Ако q<0, то знаки у чисел последовательности постоянно чередуются вне зависимости от a 1 , а элементы ни возрастают, ни убывают.

Пример: a 1 = -3, q = -2 - и двата параметъра са по-малки от нула.

Тогава числовата последователност може да бъде записана така:

3, 6, -12, 24,...

Формули

Има много формули за удобно използване на геометричните прогресии:

• Z-членна формула. Позволява ви да изчислите елемент под определено число, без да изчислявате предишни числа.

Пример:р = 3, а 1 = 4. Изисква се да се преброи четвъртият елемент от прогресията.

Решение:а 4 = 4 · 3 4-1 = 4 · 3 3 = 4 · 27 = 108.

• Сумата от първите елементи, чието количество е равно на z. Позволява ви да изчислите сумата от всички елементи на последователност доa zвключително.

Тъй като (1-р) е в знаменателя, тогава (1 - q)≠ 0, следователно q не е равно на 1.

Забележка: ако q=1, тогава прогресията ще бъде поредица от безкрайно повтарящи се числа.

Сума от геометрична прогресия, примери:а 1 = 2, р= -2. Изчислете S5.

Решение:С 5 = 22 - изчисление по формулата.

• Сума, ако |р| < 1 и если z стремится к бесконечности.

Пример:а 1 = 2 , р= 0,5. Намерете сумата.

Решение:S z = 2 · = 4

S z = 2 + 1 + 0.5 + 0.25 + 0.125 + 0.0625 = 3.9375 4

Някои свойства:

• Характерно свойство. Ако е налице следното условие работи за всякаквиz, тогава дадената редица от числа е геометрична прогресия:

a z 2 = a z -1 · аz+1

• Също така, квадратът на което и да е число в геометрична прогресия се намира чрез добавяне на квадратите на всеки две други числа в дадена серия, ако те са на еднакво разстояние от този елемент.

a z 2 = a z - T 2 + a z + T 2 , КъдетоT- разстоянието между тези числа.

• Елементиразличават се по qведнъж.
• Логаритмите на елементите на една прогресия също образуват прогресия, но аритметична, тоест всеки от тях е по-голям от предходния с определено число.

Примери за някои класически задачи

За да разберете по-добре какво е геометрична прогресия, примерите с решения за клас 9 могат да помогнат.

• Условия:а 1 = 3, а 3 = 48. Намеретер.

Решение: всеки следващ елемент е по-голям от предишния вр веднъж.Необходимо е да се изразят някои елементи по отношение на други, като се използва знаменател.

следователноа 3 = р 2 · а 1

При заместванер= 4

• Условия:а 2 = 6, а 3 = 12. Изчислете S 6.

Решение:За да направите това, просто намерете q, първия елемент и го заменете във формулата.

а 3 = р· а 2 , следователно,р= 2

a 2 = q · 1,Ето защо a 1 = 3

S 6 = 189

• · а 1 = 10, р= -2. Намерете четвъртия елемент от прогресията.

Решение: за да направите това, достатъчно е да изразите четвъртия елемент през първия и през знаменателя.

a 4 = q 3· a 1 = -80

Пример за приложение:

• Банков клиент направи депозит в размер на 10 000 рубли, при условията на който всяка година клиентът ще има 6% от тях, добавени към главницата. Колко пари ще има в сметката след 4 години?

Решение: Първоначалната сума е 10 хиляди рубли. Това означава, че една година след инвестицията в сметката ще има сума равна на 10 000 + 10 000 · 0,06 = 10000 1,06

Съответно сумата в сметката след още една година ще бъде изразена, както следва:

(10000 · 1,06) · 0,06 + 10000 · 1,06 = 1,06 · 1,06 · 10000

Тоест всяка година сумата се увеличава с 1,06 пъти. Това означава, че за да се намери сумата на средствата в сметката след 4 години, е достатъчно да се намери четвъртият елемент от прогресията, който се дава от първия елемент, равен на 10 хиляди, и знаменателят, равен на 1,06.

S = 1,06 1,06 1,06 1,06 10000 = 12625

Примери за задачи за изчисляване на суми:

Геометричната прогресия се използва в различни задачи. Пример за намиране на сумата може да бъде даден по следния начин:

а 1 = 4, р= 2, изчислиS 5.

Решение: всички данни, необходими за изчислението, са известни, просто трябва да ги замените във формулата.

С 5 = 124

• а 2 = 6, а 3 = 18. Изчислете сбора на първите шест елемента.

Решение:

В геом. прогресия, всеки следващ елемент е q пъти по-голям от предходния, тоест, за да изчислите сумата, трябва да знаете елементаа 1 и знаменателр.

а 2 · р = а 3

р = 3

По същия начин трябва да намеритеа 1 , знаейкиа 2 Ир.

а 1 · р = а 2

a 1 =2

С 6 = 728.

Урок по темата „Безкрайно намаляваща геометрична прогресия“

Целта на урока:запознаване на учениците с нов тип редица - безкрайно намаляваща геометрична прогресия.

Задачи:

формулиране на първоначална идея за границата на числова последователност; запознаване с друг начин за преобразуване на безкрайни периодични дроби в обикновени по формулата за сумата на безкрайно намаляваща геометрична прогресия;

развитие на интелектуалните качества на личността на учениците като логическо мислене, способност за извършване на оценъчни действия и обобщение;

насърчаване на активност, взаимопомощ, колективизъм и интерес към предмета.

Оборудване:компютърен клас, проектор, екран.

Тип урок:урок - изучаване на нова тема.

По време на часовете

аз . орг. момент. Посочете темата и целта на урока.

II . Актуализиране на знанията на учениците.1. Проверка на домашните.

1) Проверка на основни формули, свързани с аритметична и геометрична прогресия. Двама ученици подготвят бележки по формули на дъската.

2) Останалите ученици го правят математическа диктовка по темата „Формули на сбора“.

Задачи:

№1. Намерете сумата от първите пет члена на аритметична прогресия, ако нейният първи член е 6 (1-ви вариант), -20 (2-ри вариант), а петият член е -6 (1-ви вариант), 20 (2-ри вариант).

№2. Намерете сумата от първите пет члена на аритметична прогресия, ако нейният първи член е -20 (1-ви вариант), 6 (2-ри вариант), а разликата е 10 (1-ви вариант), -3 (2-ри вариант).

№3. Намерете сумата от първите пет члена на геометрична прогресия, ако нейният първи член е равен на 1 (1-ви вариант), -1 (2-ри вариант), а знаменателят е -2 (1-ви вариант), 2 (2-ри вариант).

В края на диктовката работата на двама ученици се проверява селективно за оценка, останалите извършват самопроверка, като използват готови решения, написани върху капаците на дъската.

Решения:

Задачи

1. Аритметичната прогресия се дава от формулата а н = 7 – 4 н. намирам а 10 . (-33)

2. В аритметична прогресия а 3 = 7 И а 5 = 1 . намирам а 4 . (4)

3. В аритметична прогресия а 3 = 7 И а 5 = 1 . намирам а 17 . (-35)

4. В аритметична прогресия а 3 = 7 И а 5 = 1 . намирам С 17 . (-187)

5. За геометрична прогресия
намерете петия член.

6. За геометрична прогресия
намирам нти член.

7. Експоненциално b 3 = 8 И b 5 = 2 . намирам b 4 . (4)

8. Експоненциално b 3 = 8 И b 5 = 2 . намирам b 1 И р .

9. Експоненциално b 3 = 8 И b 5 = 2 . намирам С 5 . (62)

III . Учене на нова тема(демонстрация на презентация).

Да разгледаме квадрат със страна, равна на 1. Нека начертаем друг квадрат, чиято страна е половината от размера на първия квадрат, след това друг, чиято страна е половината от втория, след това следващия и т.н. Всеки път страната на новия квадрат е равна на половината от предишния.

В резултат на това получихме поредица от страни на квадрати образувайки геометрична прогресия със знаменателя .

И което е много важно, колкото повече изграждаме такива квадрати, толкова по-малка ще бъде страната на квадрата. Например,

Тези. С нарастването на числото n членовете на прогресията се доближават до нула.

Използвайки тази фигура, можете да разгледате друга последователност.

Например последователността от области на квадрати:

. И отново, ако ннараства безкрайно, след което областта се доближава до нула толкова близо, колкото искате.

Нека да разгледаме друг пример. Равностранен триъгълник със страни равни на 1 cm. Нека построим следния триъгълник с върховете в средините на страните на 1-вия триъгълник, съгласно теоремата за средната линия на триъгълника - страната на 2-рия е равна на половината от страната на първия, страната на 3-тия е равно на половината от страната на 2-ра и т.н. Отново получаваме последователност от дължини на страните на триъгълници.

при
.

Ако разгледаме геометрична прогресия с отрицателен знаменател.

След това отново с нарастващи числа нусловията на прогресията се доближават до нула.

Нека обърнем внимание на знаменателите на тези последователности. Навсякъде знаменателите бяха по-малки от 1 по абсолютна стойност.

Можем да заключим: една геометрична прогресия ще бъде безкрайно намаляваща, ако модулът на нейния знаменател е по-малък от 1.

Фронтална работа.

определение:

Геометричната прогресия се нарича безкрайно намаляваща, ако модулът на нейния знаменател е по-малък от единица.
.

Използвайки определението, можете да решите дали една геометрична прогресия е безкрайно намаляваща или не.

Задача

Дали последователността е безкрайно намаляваща геометрична прогресия, ако е дадена по формулата:

;
.

Решение:

. Ще намерим р .

;
;
;
.

тази геометрична прогресия безкрайно намалява.

б)тази последователност не е безкрайно намаляваща геометрична прогресия.

Помислете за квадрат със страна, равна на 1. Разделете го наполовина, една от половините наполовина и т.н. Площите на всички получени правоъгълници образуват безкрайно намаляваща геометрична прогресия:

Сумата от площите на всички правоъгълници, получени по този начин, ще бъде равна на площта на 1-ви квадрат и равна на 1.

Но от лявата страна на това равенство е сумата от безкраен брой членове.

Нека разгледаме сумата от първите n члена.

Според формулата за сумата от първите n членове на геометрична прогресия, тя е равна на .

Ако ннараства неограничено, тогава

или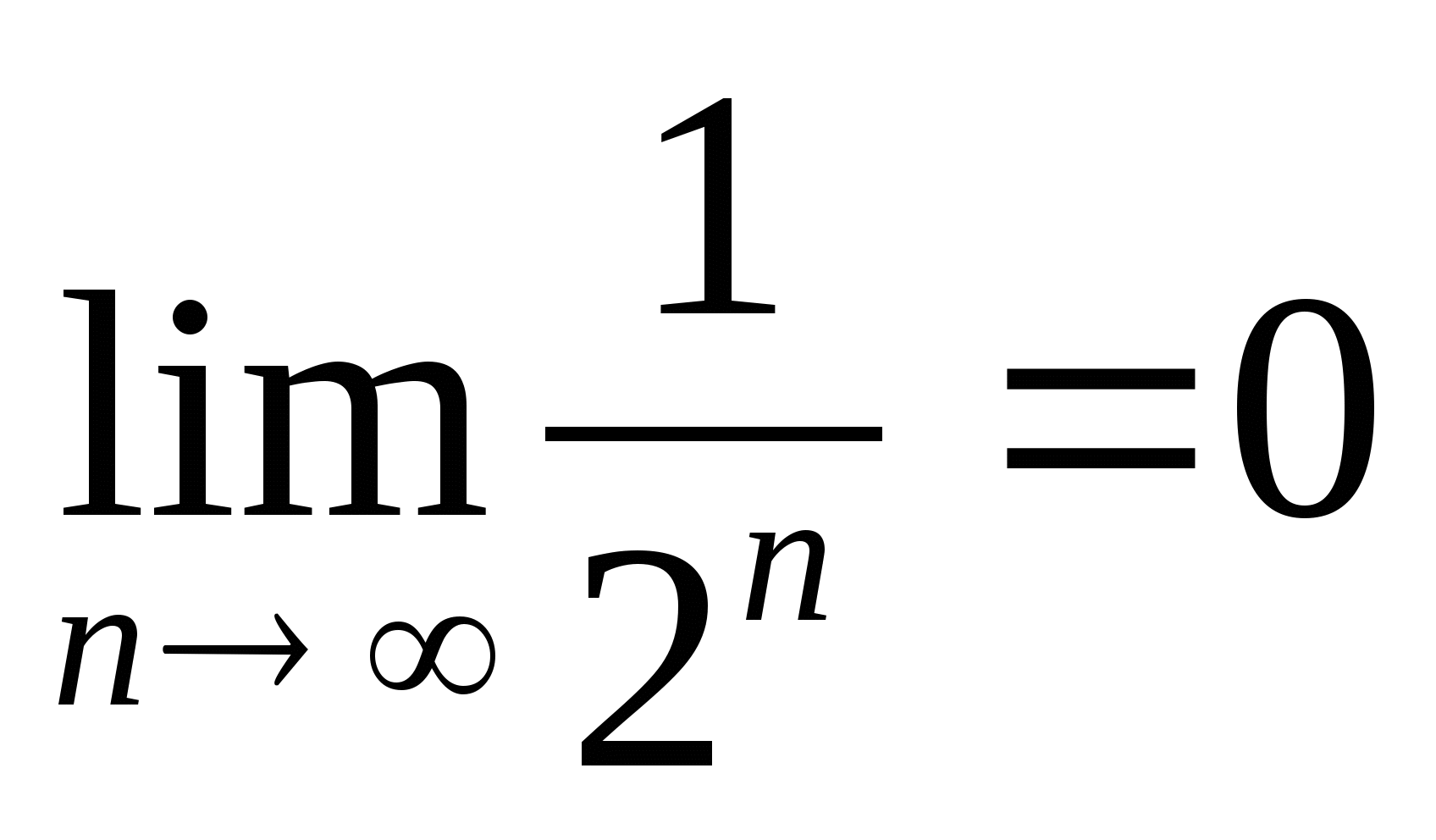
. Ето защо
, т.е.
.

Сума от безкрайно намаляваща геометрична прогресияима ограничение на последователността С 1 , С 2 , С 3 , …, С н , … .

Например за прогресия
,

защото

Сумата от безкрайно намаляваща геометрична прогресияможе да се намери с помощта на формулата
.

III . Разбиране и консолидация(завършване на задачи).

Задача No2. Намерете сумата на безкрайно намаляваща геометрична прогресия, като първият член е 3, а вторият е 0,3.

Решение:

Задача No3. учебник, стр. 160, № 433(1)

Намерете сумата от безкрайно намаляваща геометрична прогресия:

Решение:

Задача No4. Запишете безкрайната периодична десетична дроб 0,(5) като обикновена дроб.

1-ви метод. Нека x=0,(5)= 0,555... / 10 2-ри метод. 0,(5)=0,555...=

Задача No5. учебник, стр. 162, № 445(3) (самостоятелно решение)

Запишете безкрайната периодична десетична дроб 0,(12) като обикновена дроб.

Отговор: 0,(12)= 4/33.

IV . Обобщаване.

С каква последователност се запознахте днес?

Дефинирайте безкрайно намаляваща геометрична прогресия.

Как да докажем, че една геометрична прогресия е безкрайно намаляваща?

Дайте формулата за сумата на безкрайно намаляваща геометрична прогресия.

V . Домашна работа.

Геометричната прогресия е числова последователност, чийто първи член е различен от нула, а всеки следващ член е равен на предишния член, умножен по същото ненулево число. Геометричната прогресия се обозначава с b1,b2,b3, …, bn, …

Свойства на геометричната прогресия

Съотношението на който и да е член на геометричната грешка към предишния му член е равно на същото число, тоест b2/b1 = b3/b2 = b4/b3 = ... = bn/b(n-1) = b( n+1)/bn = …. Това следва пряко от определението за аритметична прогресия. Това число се нарича знаменател на геометрична прогресия. Обикновено знаменателят на геометричната прогресия се обозначава с буквата q.

Един от начините за уточняване на геометрична прогресия е да се уточни нейният първи член b1 и знаменателят на геометричната грешка q. Например b1=4, q=-2. Тези две условия определят геометричната прогресия 4, -8, 16, -32, ….

Ако q>0 (q не е равно на 1), тогава прогресията е монотонна последователност. Например последователността 2, 4,8,16,32, ... е монотонно нарастваща последователност (b1=2, q=2).

Ако знаменателят в геометричната грешка е q=1, тогава всички членове на геометричната прогресия ще бъдат равни един на друг. В такива случаи се казва, че прогресията е постоянна последователност.

Формула за n-тия член на прогресията

За да бъде числова редица (bn) геометрична прогресия, е необходимо всеки от нейните членове, започвайки от втория, да е средно геометрично на съседни членове. Тоест, необходимо е да се изпълни следното уравнение - (b(n+1))^2 = bn * b(n+2), за всяко n>0, където n принадлежи към набора от естествени числа N.

Формулата за n-тия член на геометричната прогресия е:

bn=b1*q^(n-1), където n принадлежи към набора от естествени числа N.

Нека да разгледаме един прост пример:

В геометрична прогресия b1=6, q=3, n=8 намерете bn.

Нека използваме формулата за n-тия член на геометрична прогресия.

Геометричната прогресия е нов вид числова редица, с която предстои да се запознаем. За успешни запознанства не пречи поне да знаете и разбирате. Тогава няма да има проблеми с геометричната прогресия.)

Какво е геометрична прогресия? Концепцията за геометрична прогресия.

Започваме обиколката, както обикновено, с основите. Пиша незавършена редица от числа:

1, 10, 100, 1000, 10000, …

Можете ли да забележите модела и да кажете кои числа ще дойдат следващите? Пиперът е ясен, след това ще последват числата 100 000, 1 000 000 и т.н. Дори без много умствени усилия всичко е ясно, нали?)

ДОБРЕ. Друг пример. Пиша тази последователност:

1, 2, 4, 8, 16, …

Можете ли да кажете кои числа ще дойдат след числото 16 и името осмочлен на последователността? Ако сте разбрали, че това ще бъде числото 128, тогава много добре. Така че половината битка е в разбирането смисълИ ключови точкивече е направена геометрична прогресия. Можете да растете допълнително.)

И сега отново преминаваме от усещанията към строгата математика.

Ключови точки на геометричната прогресия.

Ключова точка #1

Геометричната прогресия е последователност от числа.Така е и с прогресията. Нищо изискано. Само тази последователност е подредена различно.Следователно, естествено, има друго име, да...

Ключов момент #2

С втората ключова точка въпросът ще бъде по-сложен. Нека се върнем малко назад и си припомним ключовото свойство на аритметичната прогресия. Ето го: всеки член е различен от предишния със същата сума.

Възможно ли е да се формулира подобно ключово свойство за геометрична прогресия? Помислете малко... Разгледайте по-отблизо дадените примери. Познахте ли? да В геометричната прогресия (всяка!) всеки от нейните членове се различава от предходния същия брой пъти.Винаги!

В първия пример това число е десет. Който и член от редицата да вземете, той е по-голям от предишния десет пъти.

Във втория пример е две: всеки член е по-голям от предишния два пъти.

Това е ключов момент, по който геометричната прогресия се различава от аритметичната прогресия. В аритметична прогресия се получава всеки следващ член добавяйкисъщата стойност спрямо предишния член. И тук - умножениепредходния срок със същата сума. Това е цялата разлика.)

Ключова точка #3

Тази ключова точка е напълно идентична с тази за аритметична прогресия. а именно: Всеки член на геометрична прогресия стои на своето място.Всичко е абсолютно същото като в аритметичната прогресия и коментарите според мен са излишни. Има първия член, има сто и първия и т.н. Нека разменим поне два члена – моделът (а с него и геометричната прогресия) ще изчезнат. Това, което ще остане, е просто последователност от числа без никаква логика.

Това е всичко. Това е целият смисъл на геометричната прогресия.

Термини и обозначения.

Но сега, след като разбрахме значението и ключовите точки на геометричната прогресия, можем да преминем към теорията. Иначе какво е теория без разбиране на смисъла, нали?

Как да обозначим геометричната прогресия?

Как се записва геометричната прогресия в общ вид? Няма проблем! Всеки член от прогресията също е написан като буква. Само за аритметична прогресия обикновено се използва буквата "А", за геометрични – букв "б". Членски номер, както обикновено, е посочено индекс долу вдясно. Ние просто изброяваме самите членове на прогресията, разделени със запетаи или точка и запетая.

Като този:

b 1,b 2 , b 3 , b 4 , b 5 , b 6 , …

Накратко, тази прогресия се записва така: (b n) .

Или така, за крайни прогресии:

b 1, b 2, b 3, b 4, b 5, b 6.

b 1, b 2, …, b 29, b 30.

Или накратко:

(b n), н=30 .

Това всъщност е цялото обозначение. Всичко е същото, само буквата е различна, да.) И сега преминаваме директно към определението.

Дефиниция на геометричната прогресия.

Геометричната прогресия е числова последователност, в която първият член е различен от нула, а всеки следващ член е равен на предишния член, умножен по същото ненулево число.

Това е цялото определение. Повечето думи и фрази са ви ясни и познати. Ако, разбира се, разбирате значението на геометричната прогресия „на пръсти“ и като цяло. Но има и няколко нови фрази, на които бих искал да обърна специално внимание.

Първо, думите: „първият член на който ненулев".

Това ограничение на първия срок не е въведено случайно. Какво мислите, че ще се случи, ако първият член b 1 ще бъде равно на нула? На какво ще бъде равен вторият член, ако всеки член е по-голям от предходния? същия брой пъти?Да кажем три пъти? Да видим... Умножете първия член (т.е. 0) по 3 и получете... нула! Ами третият член? Също нула! И четвъртият член също е нула! И така нататък…

Просто получаваме торба гевреци, поредица от нули:

0, 0, 0, 0, …

Разбира се, такава последователност има право на живот, но не представлява практически интерес. Всичко е чисто. Всеки член от него е нула. Сборът от произволен брой членове също е нула... Какви интересни неща можете да правите с него? Нищо…

Следните ключови думи: "умножено по същото ненулево число."

Същият този номер има и свое специално име - знаменател на геометричната прогресия. Нека започнем да се запознаваме.)

Знаменател на геометрична прогресия.

Всичко е просто като белене на круши.

Знаменателят на геометрична прогресия е ненулево число (или количество), което показваколко пътивсеки термин от прогресията повече от предишния.

Отново, подобно на аритметичната прогресия, ключовата дума, която трябва да търсите в това определение, е думата "Повече ▼". Това означава, че всеки член на геометричната прогресия е получен умножениеточно към този знаменател предишен член.

Нека обясня.

Да изчислим, да речем второпишка, трябва да вземеш първичлен и умножават сего към знаменателя. За изчисление десетипишка, трябва да вземеш деветичлен и умножават сего към знаменателя.

Знаменателят на самата геометрична прогресия може да бъде всичко. Абсолютно всеки! Цяло, дробно, положително, отрицателно, ирационално - всичко. Освен нула. Това ни казва думата „не-нула“ в дефиницията. Защо тази дума е необходима тук - повече за това по-късно.

Знаменател на геометричната прогресиянай-често се обозначава с буквата р.

Как да го намерите р? Няма проблем! Трябва да вземем всеки термин от прогресията и разделете на предишния член. Разделението е фракция. Оттук и името - „знаменател на прогресията“. Знаменателят, той обикновено се намира в дроб, да...) Въпреки че, логично, стойността ртрябва да се нарече частенгеометрична прогресия, подобно на разликаза аритметична прогресия. Но се разбрахме да се обадим знаменател. И ние също няма да преоткриваме колелото.)

Нека да дефинираме например количеството рза тази геометрична прогресия:

2, 6, 18, 54, …

Всичко е елементарно. Да вземем всякаквипореден номер. Взимаме каквото си поискаме. С изключение на първия. Например 18. И разделете на предишен номер. Тоест на 6.

Получаваме:

р = 18/6 = 3

Това е всичко. Това е правилният отговор. За тази геометрична прогресия знаменателят е три.

Нека сега намерим знаменателя рза друга геометрична прогресия. Например този:

1, -2, 4, -8, 16, …

Все същото. Без значение какви признаци имат самите членове, ние все още приемаме всякаквиномер на последователността (например 16) и разделете на предишен номер(т.е. -8).

Получаваме:

д = 16/(-8) = -2

И това е.) Този път знаменателят на прогресията се оказа отрицателен. Минус две. Случва се.)

Нека сега вземем тази прогресия:

1, 1/3, 1/9, 1/27, …

И отново, независимо от вида на числата в редицата (дали цели числа, дори дроби, дори отрицателни, дори ирационални), ние вземаме произволно число (например 1/9) и разделяме на предишното число (1/3). Според правилата за работа с дроби, разбира се.

Получаваме:

Това е всичко.) Тук знаменателят се оказа дробен: р = 1/3.

Какво мислите за тази "прогресия"?

3, 3, 3, 3, 3, …

Очевидно тук р = 1 . Формално това също е геометрична прогресия, само с идентични членове.) Но такива прогресии не са интересни за изучаване и практическо приложение. Същото като прогресиите с плътни нули. Затова няма да ги разглеждаме.

Както можете да видите, знаменателят на прогресията може да бъде всичко - цяло число, дроб, положително, отрицателно - всичко! Не може просто да е нула. Не можете да познаете защо?

Добре, нека използваме конкретен пример, за да видим какво ще се случи, ако вземем за знаменател рнула.) Нека например имаме b 1 = 2 , А р = 0 . Тогава на какво ще бъде равен вторият член?

Ние броим:

b 2 = b 1 · р= 2 0 = 0

Ами третият член?

b 3 = b 2 · р= 0 0 = 0

Видове и поведение на геометричните прогресии.

Всичко беше повече или по-малко ясно: ако прогресията е разлика де положителен, тогава прогресията се увеличава. Ако разликата е отрицателна, тогава прогресията намалява. Има само два варианта. Няма трето.)

Но с поведението на геометричната прогресия всичко ще бъде много по-интересно и разнообразно!)

Без значение как се държат условията тук: те се увеличават, намаляват и безкрайно се приближават до нула и дори променят знаците, последователно се хвърлят в „плюс“ и след това в „минус“! И в цялото това многообразие трябва да можеш да разбираш добре, да...

Нека да го разберем?) Нека започнем с най-простия случай.

Знаменателят е положителен ( р >0)

С положителен знаменател, първо, членовете на геометричната прогресия могат да влязат в него плюс безкрайност(т.е. увеличаване без ограничение) и може да влезе в минус безкрайност(т.е. намаляване без ограничение). Вече сме свикнали с това поведение на прогресиите.

Например:

(b n): 1, 2, 4, 8, 16, …

Тук всичко е просто. Получава се всеки член на прогресията повече от предишния. Освен това всеки термин се оказва умножениепредишен член на положителенчисло +2 (т.е. р = 2 ). Поведението на такава прогресия е очевидно: всички членове на прогресията растат неограничено, отивайки в космоса. Плюс безкрайност...

А сега ето прогресията:

(b n): -1, -2, -4, -8, -16, …

Тук също се получава всеки член на прогресията умножениепредишен член на положителенчисло +2. Но поведението на такава прогресия е точно обратното: всеки член на прогресията се получава по-малко от предишния, и всички негови членове намаляват неограничено, отивайки до минус безкрайност.

Сега нека помислим: какво е общото между тези две прогресии? Точно така, знаменател! Тук-там р = +2 . Положително число.две. И тук поведениеТези две прогресии са фундаментално различни! Не можете да познаете защо? да Всичко е за първи член!Той, както се казва, е този, който нарича мелодията.) Вижте сами.

В първия случай, първият член на прогресията положителен(+1) и следователно всички следващи членове, получени чрез умножаване по положителензнаменател р = +2 , също ще бъде положителен.

Но във втория случай, първият срок отрицателен(-1). Следователно всички следващи членове на прогресията, получени чрез умножаване по положителен р = +2 , също ще бъдат получени отрицателен.Защото „минус“ към „плюс“ винаги дава „минус“, да.)

Както можете да видите, за разлика от аритметичната прогресия, геометричната прогресия може да се държи напълно различно не само в зависимост от знаменателяр, но и в зависимост от първия член, да.)

Запомнете: поведението на геометрична прогресия се определя еднозначно от нейния първи член b 1 и знаменателр .

И сега започваме да анализираме по-малко познати, но много по-интересни случаи!

Да вземем например тази последователност:

(b n): 1, 1/2, 1/4, 1/8, 1/16, …

Тази последователност също е геометрична прогресия! Всеки член от тази прогресия също се оказва умножениепредишния член, със същия номер. Това е просто число - дробен: р = +1/2 . Или +0,5 . Освен това (важно!) числото по-малко от едно:р = 1/2<1.

Защо тази геометрична прогресия е интересна? Накъде се насочват нейните членове? Нека да разгледаме:

1/2 = 0,5;

1/4 = 0,25;

1/8 = 0,125;

1/16 = 0,0625;

…….

Какви интересни неща можете да забележите тук? Първо, спадът по отношение на прогресията се забелязва веднага: всеки от нейните членове по-малкопредишния точно 2 пъти.Или, според дефиницията на геометрична прогресия, всеки член Повече ▼предишен 1/2 пъти, защото знаменател на прогресията р = 1/2 . И когато се умножи по положително число, по-малко от едно, резултатът обикновено намалява, да...

Какво Повече ▼може да се види в поведението на тази прогресия? Намаляват ли членовете му? неограничен, отивайки към минус безкрайност? Не! Те изчезват по особен начин. Отначало намаляват доста бързо, а след това все по-бавно. И докато остава през цялото време положителен. Макар и много, много малък. И към какво се стремят самите те? Не се ли досетихте? да Те се стремят към нула!) Освен това, обърнете внимание, членовете на нашата прогресия са от нула никога не достигайте!само приближавайки го безкрайно близо. Много е важно.)

Подобна ситуация ще възникне в следната прогресия:

(b n): -1, -1/2, -1/4, -1/8, -1/16, …

Тук b 1 = -1 , А р = 1/2 . Всичко е същото, само сега условията ще се доближат до нулата от другата страна, отдолу. Оставайки през цялото време отрицателен.)

Такава геометрична прогресия, членовете на която приближаване до нула без ограничение(без значение от положителната или отрицателната страна), в математиката има специално име - безкрайно намаляваща геометрична прогресия.Тази прогресия е толкова интересна и необичайна, че дори ще бъде обсъждана отделен урок .)

И така, разгледахме всички възможни положителензнаменателите са както големи, така и по-малки. Ние не считаме самата единица за знаменател поради посочените по-горе причини (помнете примера с поредица от тройки...)

Нека обобщим:

положителенИ повече от един (р>1), тогава условията на прогресията:

а) увеличаване без ограничение (акоb 1 >0);

б) намалява неограничено (акоb 1 <0).

Ако знаменателят на геометричната прогресия положителен И по-малко от едно (0< р<1), то члены прогрессии:

а) безкрайно близо до нула по-горе(Акоb 1 >0);

б) приближаващи се безкрайно близо до нула отдолу(Акоb 1 <0).

Сега остава да разгледаме случая отрицателен знаменател.

Знаменателят е отрицателен ( р <0)

Няма да отиваме далеч за пример. Защо точно рошава баба?!) Нека например първият член на прогресията е b 1 = 1 и нека вземем знаменателя q = -2.

Получаваме следната последователност:

(b n): 1, -2, 4, -8, 16, …

И така нататък.) Получава се всеки член на прогресията умножениепредишен член на отрицателно число-2. В този случай всички членове, стоящи на нечетни места (първо, трето, пето и т.н.), ще бъдат положителен, а на четни места (второ, четвърто и т.н.) – отрицателен.Знаците се редуват строго. Плюс-минус-плюс-минус... Тази геометрична прогресия се нарича - нарастващ знак редуващ се.

Накъде се насочват нейните членове? Но никъде.) Да, в абсолютна стойност (т.е. по модул)членовете на нашата прогресия се увеличават неограничено (оттук и името „увеличаване“). Но в същото време всеки член на прогресията последователно ви хвърля в жегата, после в студа. Или „плюс“, или „минус“. Нашата прогресия се колебае... Освен това обхватът на колебанията нараства бързо с всяка стъпка, да.) Следователно стремежите на членовете на прогресията отиват нанякъде специалноТук Не.Нито до плюс безкрайност, нито до минус безкрайност, нито до нула – никъде.

Нека сега разгледаме някакъв дробен знаменател между нула и минус едно.

Например, нека бъде b 1 = 1 , А q = -1/2.

Тогава получаваме прогресията:

(b n): 1, -1/2, 1/4, -1/8, 1/16, …

И отново имаме редуване на знаци! Но за разлика от предишния пример, тук вече има ясна тенденция членовете да се доближават до нула.) Само че този път нашите условия се доближават до нула не строго отгоре или отдолу, а отново колебае се. Алтернативно приемане на положителни и отрицателни стойности. Но в същото време те модулисе доближават все повече и повече до заветната нула.)

Тази геометрична прогресия се нарича безкрайно намаляващ знак, редуващ се.

Защо тези два примера са интересни? И фактът, че и в двата случая се провежда редуване на знаци!Този трик е типичен само за прогресии с отрицателен знаменател, да.) Следователно, ако в някоя задача видите геометрична прогресия с редуващи се членове, вече ще знаете със сигурност, че знаменателят й е 100% отрицателен и няма да сгрешите в знака.)

Между другото, в случай на отрицателен знаменател, знакът на първия член изобщо не влияе на поведението на самата прогресия. Независимо от знака на първия член на прогресията, във всеки случай знакът на членовете ще бъде спазен. Единственият въпрос е, на какви места(четни или нечетни) ще има членове със специфични знаци.

Помня:

Ако знаменателят на геометричната прогресия отрицателен , тогава признаците на условията на прогресията са винаги редуват се.

В същото време самите членове:

а) увеличаване без ограничениепо модул, Акор<-1;

б) се приближава до нула безкрайно, ако -1< р<0 (прогрессия бесконечно убывающая).

Това е всичко. Всички типични случаи са анализирани.)

В процеса на анализиране на различни примери за геометрични прогресии периодично използвах думите: "клони към нула", "клони към плюс безкрайност", "клони към минус безкрайност"... Всичко е наред.) Тези фигури на речта (и конкретни примери) са само първоначално въведение в поведениеразнообразие от числови последователности. Използвайки примера на геометричната прогресия.

Защо изобщо трябва да знаем поведението на прогресията? Какво значение има къде отива? Към нула, до плюс безкрайност, до минус безкрайност... Какво ни прави това?

Работата е там, че още в университета, в курса по висша математика, ще ви е необходима способност да работите с голямо разнообразие от числови последователности (с всякакви, не само прогресии!) и способността да си представите как точно тази или онази последователност се държи - дали нараства, дали намалява неограничено, дали клони към определено число (и не непременно към нула), или дори изобщо не клони към нищо... Цял раздел е посветен на тази тема в курса по математика анализ - теория на границите.И малко по-конкретно – концепцията ограничение на числовата последователност.Много интересна тема! Има смисъл да отидеш в колеж и да го разбереш.)

Някои примери от този раздел (последователности с ограничение) и по-специално, безкрайно намаляваща геометрична прогресияТе започват да свикват с това в училище. Свикваме.)

Освен това способността да изучавате добре поведението на последователностите ще ви бъде от голяма полза в бъдеще и ще бъде много полезна в функционално изследване.Най-разнообразни. Но способността да работите компетентно с функции (изчислявате производни, изучавате ги изцяло, изграждате техните графики) вече драстично повишава вашето математическо ниво! Имате ли съмнения? Няма нужда. Запомнете и думите ми.)

Нека да разгледаме геометричната прогресия в живота?

В живота около нас много, много често се сблъскваме с геометричната прогресия. Дори без дори да го знае.)

Например различни микроорганизми, които ни заобикалят навсякъде в огромни количества и които дори не можем да видим без микроскоп, се размножават точно в геометрична прогресия.

Да кажем, че една бактерия се възпроизвежда чрез разделяне наполовина, давайки потомство на 2 бактерии. На свой ред всеки от тях, когато се размножава, също се разделя наполовина, давайки общо потомство от 4 бактерии. Следващото поколение ще произведе 8 бактерии, след това 16 бактерии, 32, 64 и така нататък. С всяко следващо поколение броят на бактериите се удвоява. Типичен пример за геометрична прогресия.)

Освен това някои насекоми – листни въшки и мухи – се размножават експоненциално. А понякога и зайци, между другото.)

Друг пример за геометрична прогресия, по-близо до ежедневието, е т.нар сложна лихва.Това интересно явление често се среща в банковите депозити и се нарича капитализация на лихвата.Какво е?

Вие самият сте още, разбира се, млади. Учите в училище, не ходите в банки. Но вашите родители вече са възрастни и независими хора. Те ходят на работа, печелят пари за ежедневния си хляб и влагат част от парите в банката, правейки спестявания.)

Да приемем, че вашият баща иска да спести определена сума пари за семейна ваканция в Турция и поставя 50 000 рубли в банката при 10% годишно за период от три години с капитализация на годишната лихва.Освен това през целия този период нищо не може да се направи с депозита. Не можете нито да попълвате депозита, нито да теглите пари от сметката. Колко печалба ще направи след тези три години?

Е, първо, трябва да разберем какво представляват 10% годишно. Означава, че след годинаБанката ще добави 10% към сумата на първоначалния депозит. От това, което? Разбира се, от първоначална сума на депозита.

Изчисляваме размера на сметката след една година. Ако първоначалната сума на депозита е била 50 000 рубли (т.е. 100%), тогава след една година колко лихва ще има по сметката? Точно така, 110%! От 50 000 рубли.

Така че изчисляваме 110% от 50 000 рубли:

50000·1,1 = 55000 рубли.

Надявам се разбирате, че намирането на 110% от дадена стойност означава умножаване на тази стойност по числото 1,1? Ако не разбирате защо е така, спомнете си пети и шести клас. А именно – връзка между проценти и дроби и части.)

Така увеличението за първата година ще бъде 5000 рубли.

Колко пари ще има в сметката след две години? 60 000 рубли? За съжаление (или по-скоро за щастие), всичко не е толкова просто. Целият трик на капитализацията на лихвите е, че при всяко ново начисляване на лихви, същите тези лихви вече ще се вземат предвид от новата сума!От този, който вечее по сметката В момента.А начислената лихва за предходния период се добавя към първоначалната сума на депозита и по този начин сама участва в изчисляването на новата лихва! Тоест стават пълноценна част от общата сметка. Или общо капитал.Оттук и името - капитализация на лихвата.

Това е в икономиката. И в математиката такива проценти се наричат сложна лихва.Или процент лихва.) Номерът им е, че при последователно изчисляване процентите се изчисляват всеки път от новата стойност.И то не от оригинала...

Следователно, за да се изчисли сумата чрез две години, трябва да изчислим 110% от сумата, която ще бъде в сметката след година.Тоест вече от 55 000 рубли.

Ние броим 110% от 55 000 рубли:

55000·1,1 = 60500 рубли.

Това означава, че процентното увеличение за втората година ще бъде 5500 рубли, а за две години - 10 500 рубли.

Вече можете да познаете, че след три години сумата в сметката ще бъде 110% от 60 500 рубли. Това отново е 110% от предишната (миналата година)суми.

Тук мислим:

60500·1,1 = 66550 рубли.

Сега подреждаме нашите парични суми по години в последователност:

50000;

55000 = 50000 1,1;

60500 = 55000·1,1 = (50000·1,1)·1,1;

66550 = 60500 1,1 = ((50000 1,1) 1,1) 1,1

Е, как е? Защо не геометрична прогресия? Първи член b 1 = 50000 , и знаменателят р = 1,1 . Всеки член е строго 1,1 пъти по-голям от предходния. Всичко е в строго съответствие с определението.)

И колко допълнителни лихвени бонуси ще „натрупа“ вашият баща, докато неговите 50 000 рубли лежат в банковата му сметка от три години?

Ние броим:

66550 – 50000 = 16550 рубли

Не много, разбира се. Но това е, ако първоначалната сума на депозита е малка. Ами ако има повече? Да речем, не 50, а 200 хиляди рубли? Тогава увеличението за три години ще бъде 66 200 рубли (ако направите сметката). Което вече е много добре.) Ами ако приносът е още по-голям? Това е...

Извод: колкото по-висок е първоначалният депозит, толкова по-изгодна става капитализацията на лихвата. Ето защо депозитите с лихвена капитализация се предоставят от банките за дълги периоди. Да кажем за пет години.

Освен това всякакви лоши болести като грип, морбили и още по-ужасни болести (същата SARS в началото на 2000-те или чумата през Средновековието) обичат да се разпространяват експоненциално. Оттук и мащабът на епидемиите, да...) И всичко това се дължи на факта, че геометричната прогресия с цял положителен знаменател (р>1) – нещо, което расте много бързо! Спомнете си размножаването на бактериите: от една бактерия се получават две, от две - четири, от четири - осем и така нататък... Същото е и с разпространението на всяка инфекция.)

Най-простите задачи на геометричната прогресия.

Нека започнем, както винаги, с един прост проблем. Чисто за да се разбере смисъла.

1. Известно е, че вторият член на геометричната прогресия е 6, а знаменателят е -0,5. Намерете първия, третия и четвъртия член.

Така ни е дадено безкраенгеометрична прогресия, но известна втори сроктази прогресия:

b 2 = 6

Освен това ние също знаем знаменател на прогресията:

q = -0,5

И трябва да намерите първо, третоИ четвърточленове на тази прогресия.

Така че действаме. Записваме последователността според условията на задачата. Директно в обща форма, където вторият член е шест:

b 1, 6,b 3 , b 4 , …

Сега да започнем да търсим. Започваме, както винаги, с най-простото. Можете да изчислите например третия член б 3? Мога! Вие и аз вече знаем (директно в смисъла на геометричната прогресия), че третият член (b 3)повече от второто (b 2 ) V "q"веднъж!

Така че ние пишем:

b 3 =b 2 · р

Вместо това заместваме шест в този израз б 2и -0,5 вместо това ри ние броим. Не пренебрегваме и минуса, разбира се...

b 3 = 6·(-0,5) = -3

Като този. Третият член се оказа отрицателен. Нищо чудно: нашият знаменател р– отрицателен. И умножаването на плюс по минус, разбира се, ще бъде минус.)

Сега отчитаме следващия, четвърти член на прогресията:

b 4 =b 3 · р

b 4 = -3·(-0,5) = 1,5

Четвъртият мандат отново е с плюс. Петият член отново ще бъде минус, шестият ще бъде плюс и т.н. Знаците се редуват!

И така, бяха намерени третият и четвъртият член. Резултатът е следната последователност:

b 1; 6; -3; 1,5; ...

Сега остава само да намерим първия член b 1според известното второ. За целта стъпваме в другата посока, наляво. Това означава, че в този случай не е необходимо да умножаваме втория член на прогресията по знаменателя, а разделям.

Разделяме и получаваме:

Това е всичко.) Отговорът на проблема ще бъде така:

-12; 6; -3; 1,5; …

Както можете да видите, принципът на решение е същият като в . Ние знаем всякаквичлен и знаменателгеометрична прогресия - можем да намерим всеки друг член от нея. Ще намерим този, който искаме.) Единствената разлика е, че събирането/изваждането се заменя с умножение/деление.

Запомнете: ако знаем поне един член и знаменател на геометрична прогресия, тогава винаги можем да намерим всеки друг член на тази прогресия.

Следният проблем, според традицията, е от реална версия на OGE:

2.

...; 150; Х; 6; 1.2; ...

Е, как е? Този път няма първи член, няма знаменател р, просто е дадена поредица от числа... Нещо вече познато, нали? да Подобна задача вече е решена в аритметична прогресия!

Така че не ни е страх. Все същото. Да обърнем глава и да си припомним елементарния смисъл на геометричната прогресия. Разглеждаме внимателно нашата последователност и разбираме кои параметри от геометричната прогресия на трите основни (първи член, знаменател, номер на член) са скрити в нея.

Членски номера? Няма членски номера, да... Но са четирима последователенчисла. Не виждам смисъл да обяснявам какво означава тази дума на този етап.) Има ли две съседни известни числа?Яжте! Това са 6 и 1.2. Така че можем да намерим знаменател на прогресията.Взимаме числото 1,2 и го делим към предишния номер.До шест.

Получаваме:

Получаваме:

х= 150·0,2 = 30

Отговор: х = 30 .

Както можете да видите, всичко е съвсем просто. Основната трудност е само в изчисленията. Особено трудно е в случай на отрицателни и дробни знаменатели. Така че тези, които имат проблеми, повтарят аритметиката! Как се работи с дроби, как се работи с отрицателни числа и така нататък... В противен случай тук ще се забавите безмилостно.

Сега нека модифицираме малко проблема. Сега ще стане интересно! Нека премахнем последното число 1.2 от него. Сега нека разрешим този проблем:

3. Изписани са няколко последователни члена на геометричната прогресия:

...; 150; Х; 6; ...

Намерете члена на прогресията, обозначен с буквата x.

Всичко е същото, само две съседни известенСега нямаме членове на прогресията. Това е основният проблем. Тъй като величината рчрез два съседни члена можем лесно да определим ние не можем.Имаме ли шанс да се справим със задачата? Със сигурност!

Нека запишем неизвестния член " х"директно по смисъла на геометричната прогресия! В общи линии.

Да да! Точно с неизвестен знаменател!

От една страна, за X можем да запишем следното отношение:

х= 150 ·р

От друга страна, имаме пълното право да опишем същото това X чрез следващиячлен, през шест! Разделете шест на знаменателя.

Като този:

х = 6/ р

Очевидно сега можем да приравним и двете съотношения. Тъй като ние изразяваме същотовеличина (x), но две различни начини.

Получаваме уравнението:

Умножавайки всичко по р, опростявайки и съкращавайки, получаваме уравнението:

q2 = 1/25

Решаваме и получаваме:

q = ±1/5 = ±0,2

Опа! Знаменателят се оказа двоен! +0,2 и -0,2. И кой да изберете? Задънен край?

Спокоен! Да, проблема наистина го има две решения!Нищо лошо в това. Случва се.) Не се изненадвате, когато например получите два корена при решаване на обичайната задача? Тук е същата история.)

За q = +0,2ще получим:

X = 150 0,2 = 30

И за р = -0,2 ще:

X = 150·(-0,2) = -30

Получаваме двоен отговор: х = 30; х = -30.

Какво означава този интересен факт? И какво съществува две прогресии, отговарящи на условията на задачата!

Като тези:

…; 150; 30; 6; …

…; 150; -30; 6; …

И двете са подходящи.) Защо мислите, че имахме разделение в отговорите? Само заради елиминирането на определен член от прогресията (1,2), идващ след шест. И знаейки само предишния (n-1)-ти и следващите (n+1)-ти член на геометричната прогресия, вече не можем да кажем нищо еднозначно за n-тия член, стоящ между тях. Вариантите са два – с плюс и с минус.

Но няма проблем. По правило в задачите за геометрична прогресия има допълнителна информация, която дава недвусмислен отговор. Да кажем думите: "променлива прогресия"или "прогресия с положителен знаменател"и така нататък... Именно тези думи трябва да служат като подсказка кой знак, плюс или минус, трябва да се избере при подготовката на окончателния отговор. Ако няма такава информация, тогава да, задачата ще има две решения.)

Сега решаваме сами.

4. Определете дали числото 20 е член на геометрична прогресия:

4 ; 6; 9; …

5. Знакът на променлива геометрична прогресия е даден:

…; 5; х ; 45; …

Намерете термина на прогресията, посочен с буквата х .

6. Намерете четвъртия положителен член на геометричната прогресия:

625; -250; 100; …

7. Вторият член на геометричната прогресия е равен на -360, а петият му член е равен на 23,04. Намерете първия член на тази прогресия.

Отговори (в безпорядък): -15; 900; Не; 2.56.

Поздравления, ако всичко се получи!

Нещо не пасва? Някъде имаше двоен отговор? Прочетете внимателно условията на заданието!

Последният проблем не работи? Там няма нищо сложно.) Ние работим директно според значението на геометричната прогресия. Е, можете да нарисувате картина. Помага.)

Както можете да видите, всичко е елементарно. Ако прогресията е кратка. Ами ако е дълго? Или броят на необходимия член е много голям? Бих искал, по аналогия с аритметичната прогресия, по някакъв начин да получа удобна формула, която улеснява намирането всякаквичлен на всяка геометрична прогресия по неговия номер.Без да умножавам много, много пъти по р. И има такава формула!) Подробностите са в следващия урок.

Геометричната прогресия е числова последователност, чийто първи член е различен от нула, а всеки следващ член е равен на предишния член, умножен по същото ненулево число.

Означава се геометрична прогресия b1,b2,b3, …, bn, ….

Съотношението на който и да е член на геометричната грешка към предишния му член е равно на същото число, тоест b2/b1 = b3/b2 = b4/b3 = ... = bn/b(n-1) = b( n+1)/bn = …. Това следва пряко от определението за аритметична прогресия. Това число се нарича знаменател на геометрична прогресия. Обикновено знаменателят на геометричната прогресия се обозначава с буквата q.

Монотонна и постоянна последователност

Един от начините за уточняване на геометрична прогресия е да се уточни нейният първи член b1 и знаменателят на геометричната грешка q. Например b1=4, q=-2. Тези две условия определят геометричната прогресия 4, -8, 16, -32, ….

Ако q>0 (q не е равно на 1), тогава прогресията е монотонна последователност.Например последователността 2, 4,8,16,32, ... е монотонно нарастваща последователност (b1=2, q=2).

Ако знаменателят в геометричната грешка е q=1, тогава всички членове на геометричната прогресия ще бъдат равни един на друг. В такива случаи казват, че има прогресия постоянна последователност.

Формула за n-тия член на геометрична прогресия

За да бъде числова редица (bn) геометрична прогресия, е необходимо всеки от нейните членове, започвайки от втория, да е средно геометрично на съседни членове. Тоест, необходимо е да се изпълни следното уравнение
(b(n+1))^2 = bn * b(n+2), за всяко n>0, където n принадлежи към набора от естествени числа N.

Формулата за n-тия член на геометричната прогресия е:

bn=b1*q^(n-1),

където n принадлежи на множеството от естествени числа N.

Формула за сумата от първите n члена на геометрична прогресия

Формулата за сумата от първите n члена на геометрична прогресия има формата:

Sn = (bn*q - b1)/(q-1), където q не е равно на 1.

Нека да разгледаме един прост пример:

В геометрична прогресия b1=6, q=3, n=8 намерете Sn.

За да намерим S8, използваме формулата за сумата от първите n члена на геометрична прогресия.

S8= (6*(3^8 -1))/(3-1) = 19 680.