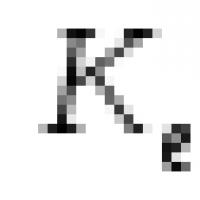সাবস্পেসের রৈখিক স্বাধীনতা। রৈখিক স্থানের সাবস্পেস। বৈশিষ্ট্য. সাবস্পেসের যোগফল এবং ছেদ। রৈখিক স্থানগুলির আইসোমরফিজম

সংজ্ঞা। রৈখিক স্থানসংখ্যা ক্ষেত্রের উপরে প্রতিএকটি সেট বলা হয় আর উপাদান, যাকে আমরা ভেক্টর বলব এবং বোঝাব ,, এবং তাই, যদি:

এই স্বতঃসিদ্ধ থেকে এটি অনুসরণ করে যে:

রৈখিক শাঁস

সংজ্ঞা।রৈখিক শেলভেক্টরের পরিবার হল রৈখিক স্থানে তাদের সম্ভাব্য সমস্ত রৈখিক সংমিশ্রণের সেট এল.

রৈখিক হুলটি একটি রৈখিক স্থান কিনা তা পরীক্ষা করা সহজ এল.

রৈখিক শেল এটিকে ভেক্টর দ্বারা বিস্তৃত একটি সাবস্পেসও বলা হয় বা একটি পরিবারের ভেক্টর দ্বারা উত্পন্ন হয় এল, সব ধারণকারী পদমর্যাদাভেক্টরের পরিবারকে এর রৈখিক স্প্যানের মাত্রা বলা হয়।

ভিত্তির প্রথম বৈশিষ্ট্যগত বৈশিষ্ট্য: এর রৈখিক শেল সবকিছুর সাথে মিলে যায়এল.

সাবস্পেস

সংজ্ঞা। লিনিয়ার সাবস্পেস বা ভেক্টর সাবস্পেসএকটি অ-খালি সেট কে রৈখিক স্থান এল যেমন যে কে সংজ্ঞায়িত করা সাপেক্ষে নিজেই একটি রৈখিক স্থান এল একটি স্কেলার দ্বারা যোগ এবং গুণের ক্রিয়াকলাপ। সমস্ত সাবস্পেসের সেট হিসাবে চিহ্নিত করা হয় ল্যাট ( এল ) . একটি উপসেট একটি সাবস্পেস হওয়ার জন্য এটি প্রয়োজনীয় এবং যথেষ্ট

শেষ দুটি বিবৃতি নিম্নলিখিতগুলির সমতুল্য:

বিশেষ করে, একটি উপাদান নিয়ে গঠিত একটি স্থান হল যেকোনো স্থানের একটি সাবস্পেস; যেকোন স্থান নিজেই একটি সাবস্পেস। এই দুটির সাথে মিলে না এমন সাবস্পেসকে বলা হয় নিজস্ববা অ তুচ্ছ

সাবস্পেসের বৈশিষ্ট্য

অসীম-মাত্রিক স্থানগুলিতে কার্যকরী বিশ্লেষণে, বিশেষ জোর দেওয়া হয় বন্ধ সাবস্পেস।

ভেক্টরের রৈখিক নির্ভরতা

সংজ্ঞা।ভেক্টরের একটি পরিবারকে রৈখিক বলা হয় স্বাধীন, যদি কোন অ-তুচ্ছ রৈখিক সমন্বয় শূন্যের সমান না হয়, অর্থাৎ থেকে

এটি অনুসরণ করে যে সবকিছু = 0। অন্যথায় এটিকে রৈখিক বলা হয় নির্ভরশীল. পরিবারের রৈখিক স্বাধীনতা মানে শূন্য ভেক্টরটি পারিবারিক উপাদানগুলির একটি রৈখিক সংমিশ্রণ হিসাবে অনন্যভাবে উপস্থাপিত হয়।তারপর অন্য কোনো ভেক্টর হয় একটি একক প্রতিনিধিত্ব বা কোনোটি নেই। প্রকৃতপক্ষে, দুটি উপস্থাপনা তুলনা

এটি ভিত্তিটির দ্বিতীয় বৈশিষ্ট্যগত বৈশিষ্ট্যকে বোঝায়: এর উপাদানগুলি রৈখিকভাবে স্বাধীন।এই দুটি বৈশিষ্ট্যের সংজ্ঞা ভিত্তির প্রাথমিক সংজ্ঞার সমতুল্য।

লক্ষ্য করুন ভেক্টরের একটি পরিবার রৈখিকভাবে স্বাধীন হয় যদি এবং শুধুমাত্র যদি এটি তার রৈখিক স্প্যানের ভিত্তি তৈরি করে।

শূন্য বা দুটি অভিন্ন ভেক্টর থাকলে একটি পরিবার স্পষ্টতই রৈখিকভাবে নির্ভরশীল।

লেম্মা ঘ.ভেক্টরের একটি পরিবার রৈখিকভাবে নির্ভরশীল যদি এবং শুধুমাত্র যদি অন্তত একটি ভেক্টর অন্যদের একটি রৈখিক সমন্বয় হয়।

প্রমাণ।

যদি

বিপরীতভাবে, যদি, তাহলে

লেমা 2।রৈখিকভাবে নির্ভরশীল, তারপর এটি একটি রৈখিক সংমিশ্রণ।

প্রমাণ।

যদি তারা সমান না হয়, তাহলে তাদের অবশ্যই হতে হবে, অন্যথায় আমরা তাই এর মধ্যে একটি অ-তুচ্ছ নির্ভরতা পেতে পারি

রৈখিক (ভেক্টর)একটি স্থান হল ভেক্টর নামক নির্বিচারে উপাদানগুলির একটি সেট V, যেখানে ভেক্টর যোগ করার এবং একটি ভেক্টরকে একটি সংখ্যা দ্বারা গুণ করার কাজগুলি সংজ্ঞায়িত করা হয়, যেমন যে কোন দুটি ভেক্টর \mathbf(u) এবং (\mathbf(v)) একটি ভেক্টর বরাদ্দ করা হয় \mathbf(u)+\mathbf(v), ভেক্টরের সমষ্টিকে বলা হয় \mathbf(u) এবং (\mathbf(v)), যেকোনো ভেক্টর (\mathbf(v)) এবং যেকোন সংখ্যা \lambda বাস্তব সংখ্যার ক্ষেত্র থেকে \mathbb(R) একটি ভেক্টরের সাথে যুক্ত। \lambda\mathbf(v), ভেক্টরের গুণফলকে বলা হয় \mathbf(v) সংখ্যা দ্বারা \lambda ; তাই নিম্নলিখিত শর্ত পূরণ করা হয়:

1. গণিত(সংযোজনের commutativity);
2. \mathbf(u)+(\mathbf(v)+\mathbf(w))=(\mathbf(u)+\mathbf(v))+\mathbf(w)\,~\forall \mathbf(u), \mathbf(v),\mathbf(w)\ in V(সংযোজনের সহযোগীতা);
3. V তে একটি মৌল \mathbf(o)\ আছে, যাকে শূন্য ভেক্টর বলা হয়, যেমন \mathbf(v)+\mathbf(o)=\mathbf(v)\,~\forall \mathbf(v)\ in V;
4. প্রতিটি ভেক্টরের (\mathbf(v)) ভেক্টরের বিপরীতে একটি ভেক্টর থাকে যাকে বলা হয় \mathbf(v)+(-\mathbf(v))=\mathbf(o);
5. \lambda(\mathbf(u)+\mathbf(v))=\lambda \mathbf(u)+\lambda \mathbf(v)\, ~\forall \mathbf(u),\mathbf(v)\ in V ,~\forall \lambda\in \mathbb(R);
6. (\lambda+\mu)\mathbf(v)=\lambda \mathbf(v)+\mu \mathbf(v)\,~ \forall \mathbf(v)\in V,~\forall \lambda,\mu\ ইন\mathbb(R);
7. \lambda(\mu \mathbf(v))=(\lambda\mu)\mathbf(v)\, ~ \forall \mathbf(v)\in V, ~\forall \lambda,\mu\in \mathbb( আর);
8. 1\cdot \mathbf(v)=\mathbf(v)\, ~\forall \mathbf(v)\ in V.

শর্ত 1-8 বলা হয় রৈখিক স্থানের স্বতঃসিদ্ধ. ভেক্টরগুলির মধ্যে স্থাপন করা সমান চিহ্নের অর্থ হল সমতার বাম এবং ডান দিকগুলি V সেটের একই উপাদানকে সমান বলে।

রৈখিক স্থানের সংজ্ঞায়, একটি ভেক্টরকে একটি সংখ্যা দ্বারা গুণ করার কাজটি বাস্তব সংখ্যার জন্য চালু করা হয়। এমন স্থানকে বলা হয় বাস্তব সংখ্যার ক্ষেত্রের উপর রৈখিক স্থান, বা, সংক্ষেপে, বাস্তব রৈখিক স্থান. যদি সংজ্ঞায়, বাস্তব সংখ্যার ক্ষেত্রে \mathbb(R) এর পরিবর্তে, আমরা জটিল সংখ্যা \mathbb(C) এর ক্ষেত্র নিই, তাহলে আমরা পাব জটিল সংখ্যার ক্ষেত্রের উপর রৈখিক স্থান, বা, সংক্ষেপে, জটিল রৈখিক স্থান. একটি সংখ্যা ক্ষেত্র হিসাবে, আমরা মূলদ সংখ্যার ক্ষেত্র \mathbb(Q) চয়ন করতে পারি এবং এই ক্ষেত্রে আমরা মূলদ সংখ্যার ক্ষেত্রের উপর একটি রৈখিক স্থান পাই। পরবর্তীতে, অন্যথায় বলা না হলে, বাস্তব রৈখিক স্থান বিবেচনা করা হবে। কিছু ক্ষেত্রে, সংক্ষিপ্ততার জন্য, আমরা রৈখিক শব্দটি বাদ দিয়ে স্থান সম্পর্কে কথা বলব, যেহেতু নীচে আলোচনা করা সমস্ত স্থান রৈখিক।

নোট 8.1

1. স্বতঃসিদ্ধ 1-4 দেখায় যে একটি রৈখিক স্থান সংযোজন ক্রিয়াকলাপের ক্ষেত্রে একটি পরিবর্তনশীল গোষ্ঠী।

2. স্বতঃসিদ্ধ 5 এবং 6 ভেক্টর যোগ করার ক্রিয়াকলাপ (স্বতঃসিদ্ধ 5) বা সংখ্যা যোগ করার ক্রিয়াকলাপের সাথে (স্বতত 6) একটি সংখ্যা দ্বারা একটি ভেক্টরকে গুণ করার ক্রিয়াকলাপের বন্টন নির্ধারণ করে। Axiom 7, কখনও কখনও একটি সংখ্যা দ্বারা গুণের সহযোগীতার আইন বলা হয়, দুটি ভিন্ন ক্রিয়াকলাপের মধ্যে সংযোগ প্রকাশ করে: একটি ভেক্টরকে একটি সংখ্যা দ্বারা গুণ করা এবং সংখ্যাগুলিকে গুণ করা। Axiom 8 দ্বারা সংজ্ঞায়িত সম্পত্তিকে একটি ভেক্টরকে একটি সংখ্যা দ্বারা গুণ করার অপারেশনের এককতা বলা হয়।

3. রৈখিক স্থান হল একটি অ-খালি সেট, যেহেতু এটি অগত্যা একটি শূন্য ভেক্টর ধারণ করে।

4. ভেক্টর যোগ করা এবং একটি ভেক্টরকে একটি সংখ্যা দ্বারা গুণ করার ক্রিয়াকলাপকে ভেক্টরের রৈখিক ক্রিয়াকলাপ বলা হয়।

5. ভেক্টর \mathbf(u) এবং \mathbf(v) ভেক্টরের মধ্যে পার্থক্য হল বিপরীত ভেক্টর (-\mathbf(v)) এর সাথে ভেক্টর \mathbf(u) এর যোগফল এবং চিহ্নিত করা হয়: \mathbf(u)-\mathbf(v)=\mathbf(u)+(-\mathbf(v)).

6. দুটি নন-জিরো ভেক্টর \mathbf(u) এবং \mathbf(v) কে সমরেখা (আনুপাতিক) বলা হয় যদি একটি সংখ্যা \lambda থাকে \mathbf(v)=\lambda \mathbf(u). সমকোনতার ধারণাটি যেকোন সীমিত সংখ্যক ভেক্টর পর্যন্ত প্রসারিত। শূন্য ভেক্টর \mathbf(o) যেকোন ভেক্টরের সাথে সমান্তরাল বলে বিবেচিত হয়।

রৈখিক স্থান স্বতঃসিদ্ধের সমষ্টি

1. লিনিয়ার স্পেসে একটি মাত্র শূন্য ভেক্টর আছে।

2. রৈখিক স্থানে, যেকোনো ভেক্টর \mathbf(v)\V-এর জন্য একটি অনন্য বিপরীত ভেক্টর রয়েছে (-\mathbf(v))\in ভি.

3. একটি নির্বিচারে স্থান ভেক্টরের গুণফল এবং শূন্য সংখ্যাটি শূন্য ভেক্টরের সমান, অর্থাৎ 0\cdot \mathbf(v)=\mathbf(o)\, ~\forall \mathbf(v)\ in V.

4. যেকোনো সংখ্যা দ্বারা একটি শূন্য ভেক্টরের গুণফল একটি শূন্য ভেক্টরের সমান, যে কোনো সংখ্যা \lambda-এর জন্য।

5. একটি প্রদত্ত ভেক্টরের বিপরীত ভেক্টরটি সংখ্যা (-1) দ্বারা এই ভেক্টরের গুণফলের সমান, অর্থাৎ (-\mathbf(v))=(-1)\mathbf(v)\,~\forall \mathbf(v)\ in V.

6. ফর্মের অভিব্যক্তিতে \mathbf(a+b+\ldots+z)(একটি সীমিত সংখ্যক ভেক্টরের যোগফল) বা \alpha\cdot\beta\cdot\ldots\cdot\omega\cdot \mathbf(v)(একটি ভেক্টরের গুণফল এবং একটি সীমিত সংখ্যক ফ্যাক্টর) আপনি বন্ধনীগুলিকে যে কোনও ক্রমে রাখতে পারেন বা সেগুলি নির্দিষ্ট করতে পারবেন না।

উদাহরণস্বরূপ, প্রথম দুটি বৈশিষ্ট্য প্রমাণ করা যাক। শূন্য ভেক্টরের স্বতন্ত্রতা। যদি \mathbf(o) এবং \mathbf(o)" দুটি শূন্য ভেক্টর হয়, তাহলে Axiom 3 দ্বারা আমরা দুটি সমতা পাই: \mathbf(o)"+\mathbf(o)=\mathbf(o)"বা \mathbf(o)+\mathbf(o)"=\mathbf(o), যার বাম দিকগুলি Axiom 1 অনুসারে সমান। ফলস্বরূপ, ডান দিকগুলিও সমান, অর্থাৎ \mathbf(o)=\mathbf(o)". বিপরীত ভেক্টরের স্বতন্ত্রতা। যদি ভেক্টর \mathbf(v)\V এর দুটি বিপরীত ভেক্টর থাকে (-\mathbf(v)) এবং (-\mathbf(v))", তাহলে স্বতঃসিদ্ধ 2, 3,4 দ্বারা আমরা তাদের সমতা পাই:

(-\mathbf(v))"=(-\mathbf(v))"+\underbrace(\mathbf(v)+(-\mathbf(v)))_(\mathbf(o))= \ underbrace( (-\mathbf(v))"+\mathbf(v))_(\mathbf(o))+(-\mathbf(v))=(-\mathbf(v))।

অবশিষ্ট বৈশিষ্ট্য একইভাবে প্রমাণিত হয়।

রৈখিক স্থানের উদাহরণ

1. আসুন বোঝাই \(\mathbf(o)\) - অপারেশন সহ একটি শূন্য ভেক্টর সম্বলিত একটি সেট \mathbf(o)+ \mathbf(o)=\mathbf(o)এবং \lambda \mathbf(o)=\mathbf(o). নির্দেশিত ক্রিয়াকলাপের জন্য, স্বতঃসিদ্ধ 1-8 সন্তুষ্ট। ফলস্বরূপ, সেট \(\mathbf(o)\) যেকোন সংখ্যা ক্ষেত্রের উপর একটি রৈখিক স্থান। এই রৈখিক স্থানকে নাল বলা হয়।

2. আসুন V_1,\,V_2,\,V_3 বোঝাই - ভেক্টরের সেট (নির্দেশিত সেগমেন্ট) একটি সরলরেখায়, একটি সমতলে, মহাকাশে, যথাক্রমে, ভেক্টর যোগ করার এবং একটি সংখ্যা দ্বারা ভেক্টরকে গুণ করার স্বাভাবিক ক্রিয়াকলাপের সাথে। রৈখিক স্থানের স্বতঃসিদ্ধ 1-8 এর পূর্ণতা প্রাথমিক জ্যামিতি থেকে অনুসরণ করে। ফলস্বরূপ, V_1,\,V_2,\,V_3 সেটগুলি বাস্তব রৈখিক স্থান। মুক্ত ভেক্টরের পরিবর্তে, আমরা ব্যাসার্ধ ভেক্টরের সংশ্লিষ্ট সেটগুলি বিবেচনা করতে পারি। উদাহরণস্বরূপ, একটি সমতলে ভেক্টরের একটি সেট যার একটি সাধারণ উত্স রয়েছে, যেমন সমতলের একটি নির্দিষ্ট বিন্দু থেকে প্লট করা একটি বাস্তব রৈখিক স্থান। একক দৈর্ঘ্যের ব্যাসার্ধ ভেক্টরের সেট একটি রৈখিক স্থান গঠন করে না, কারণ এই ভেক্টরগুলির যেকোনো একটির জন্য যোগফল \mathbf(v)+\mathbf(v)বিবেচনাধীন সেটের অন্তর্গত নয়।

3. আসুন বোঝাই \mathbb(R)^n - ম্যাট্রিক্স-কলামের একটি সেট n\times1 আকারের ম্যাট্রিক্স যোগ করার এবং ম্যাট্রিক্সকে একটি সংখ্যা দ্বারা গুণ করার কাজগুলির সাথে। রৈখিক স্থানের স্বতঃসিদ্ধ 1-8 এই সেটের জন্য সন্তুষ্ট। এই সেটের শূন্য ভেক্টর হল শূন্য কলাম o=\begin(pmatrix)0&\cdots&0\end(pmatrix)^T. ফলস্বরূপ, সেট \mathbb(R)^n একটি বাস্তব রৈখিক স্থান। একইভাবে, জটিল উপাদান সহ n\times1 আকারের কলামগুলির একটি সেট \mathbb(C)^n হল একটি জটিল রৈখিক স্থান। বিপরীতে, অ-নেতিবাচক বাস্তব উপাদান সহ কলাম ম্যাট্রিক্সের সেটটি একটি রৈখিক স্থান নয়, কারণ এতে বিপরীত ভেক্টর থাকে না।

4. আসুন বোঝাই \(Ax=o\) - একটি সমজাতীয় সিস্টেম Ax=o এর রৈখিক বীজগণিত সমীকরণের সমাধানের সেট এবং অজানা (যেখানে A হল সিস্টেমের আসল ম্যাট্রিক্স), এর কলামগুলির একটি সেট হিসাবে বিবেচিত মাপ n\times1 ম্যাট্রিক্স যোগ করার ক্রিয়াকলাপ এবং একটি সংখ্যা দ্বারা ম্যাট্রিক্সকে গুণ করে। মনে রাখবেন যে এই অপারেশনগুলি প্রকৃতপক্ষে সেটে সংজ্ঞায়িত করা হয়েছে \(Ax=o\)। একটি সমজাতীয় সিস্টেমের সমাধানের বৈশিষ্ট্য 1 থেকে (বিভাগ 5.5 দেখুন) এটি অনুসরণ করে যে একটি সমজাতীয় সিস্টেমের দুটি সমাধানের যোগফল এবং একটি সংখ্যা দ্বারা তার সমাধানের গুণফলও একটি সমজাতীয় সিস্টেমের সমাধান, যেমন সেট \(Ax=o\) এর অন্তর্গত। কলামের জন্য রৈখিক স্থানের স্বতঃসিদ্ধ (রৈখিক স্থানের উদাহরণে পয়েন্ট 3 দেখুন)। অতএব, একটি সমজাতীয় সিস্টেমের সমাধানের সেট একটি বাস্তব রৈখিক স্থান।

একজাতীয় সিস্টেমের সমাধানগুলির সেট \(Ax=b\) Ax=b, ~b\ne o , বিপরীতে, একটি রৈখিক স্থান নয়, যদি শুধুমাত্র এটিতে একটি শূন্য উপাদান না থাকে (x=o হল একজাতীয় সিস্টেমের সমাধান নয়)।

5. আসুন M_(m\times n) বোঝাই - ম্যাট্রিক্স যোগ করা এবং ম্যাট্রিক্সকে একটি সংখ্যা দ্বারা গুণ করার ক্রিয়াকলাপের সাথে m\times n আকারের ম্যাট্রিকের একটি সেট। রৈখিক স্থানের স্বতঃসিদ্ধ 1-8 এই সেটের জন্য সন্তুষ্ট। শূন্য ভেক্টর হল উপযুক্ত মাপের একটি শূন্য ম্যাট্রিক্স O। অতএব, সেট M_(m\times n) একটি রৈখিক স্থান।

6. আসুন P(\mathbb(C))-কে বোঝাই - জটিল সহগ সহ একটি চলকের বহুপদীর সেট। ডিগ্রী শূন্যের বহুপদ হিসাবে বিবেচিত একটি সংখ্যা দ্বারা বহুপদকে গুণ করার ক্রিয়াকলাপগুলি সংজ্ঞায়িত করা হয় এবং স্বতঃসিদ্ধ 1-8 (বিশেষত, একটি শূন্য ভেক্টর একটি বহুপদ যা একইভাবে শূন্যের সমান)। অতএব, সেট P(\mathbb(C)) হল জটিল সংখ্যার ক্ষেত্রের উপর একটি রৈখিক স্থান। বাস্তব সহগ সহ বহুপদগুলির P(\mathbb(R)) সেটটিও একটি রৈখিক স্থান (তবে অবশ্যই, বাস্তব সংখ্যার ক্ষেত্রের উপরে)। বাস্তব সহগ সহ সর্বাধিক n ডিগ্রি বহুপদীর P_n(\mathbb(R)) সেটটিও একটি বাস্তব রৈখিক স্থান। মনে রাখবেন যে এই সেটটিতে অনেকগুলি পদ যোগ করার ক্রিয়াকলাপ সংজ্ঞায়িত করা হয়েছে, যেহেতু বহুপদীর যোগফলের ডিগ্রি পদগুলির ডিগ্রির বেশি হয় না।

ডিগ্রী n এর বহুপদীর সেটটি একটি রৈখিক স্থান নয়, যেহেতু এই জাতীয় বহুপদীর যোগফল নিম্ন ডিগ্রির বহুপদী হতে পারে যা বিবেচনাধীন সেটের অন্তর্গত নয়। ধনাত্মক সহগ সহ n-এর চেয়ে বেশি ডিগ্রির সমস্ত বহুপদীর সেটটিও একটি রৈখিক স্থান নয়, কারণ এই ধরনের বহুপদকে একটি ঋণাত্মক সংখ্যা দ্বারা গুণ করলে একটি বহুপদী হবে যা এই সেটের অন্তর্গত নয়।

7. আসুন C(\mathbb(R))-কে বোঝাই - \mathbb(R) এ সংজ্ঞায়িত এবং অবিচ্ছিন্ন বাস্তব ফাংশনের সেট। f,g ফাংশনের যোগফল (f+g) এবং f ফাংশনের গুণফল \lambda f এবং বাস্তব সংখ্যা \lambda সমতা দ্বারা সংজ্ঞায়িত করা হয়:

(f+g)(x)=f(x)+g(x),\quad (\lambda f)(x)=\lambda\cdot f(x)সকল x\in \mathbb(R) এর জন্য

এই ক্রিয়াকলাপগুলি প্রকৃতপক্ষে C(\mathbb(R)) তে সংজ্ঞায়িত করা হয়েছে যেহেতু অবিচ্ছিন্ন ফাংশনের যোগফল এবং একটি অবিচ্ছিন্ন ফাংশনের গুণফল এবং একটি সংখ্যা অবিচ্ছিন্ন ফাংশন, যেমন C(\mathbb(R)) এর উপাদান। রৈখিক স্থানের স্বতঃসিদ্ধতা পরীক্ষা করা যাক। যেহেতু বাস্তব সংখ্যার যোগ কম্যুটেটিভ, তাই এটি সমতা অনুসরণ করে f(x)+g(x)=g(x)+f(x)যেকোনো x\in \mathbb(R) এর জন্য। অতএব f+g=g+f, i.e. স্বতঃসিদ্ধ 1 সন্তুষ্ট। স্বতঃসিদ্ধ 2 যোগের সহযোগীতা থেকে একইভাবে অনুসরণ করে। শূন্য ভেক্টর হল ফাংশন o(x), একইভাবে শূন্যের সমান, যা অবশ্যই অবিচ্ছিন্ন। যে কোনো ফাংশনের জন্য f সমতা f(x)+o(x)=f(x) ধরে, যেমন Axiom 3 সত্য হল f ভেক্টরের বিপরীত ভেক্টরটি হবে ফাংশন (-f)(x)=-f(x)। তারপর f+(-f)=o (স্বতঃসিদ্ধ 4 সত্য)। স্বতঃসিদ্ধ 5, 6 বাস্তব সংখ্যার যোগ এবং গুণনের ক্রিয়াকলাপের বণ্টন থেকে অনুসরণ করে এবং স্বতঃসিদ্ধ 7 - সংখ্যার গুণনের সহযোগীতা থেকে। শেষ স্বতঃসিদ্ধটি সন্তুষ্ট, যেহেতু একটি দ্বারা গুণ করলে ফাংশনটি পরিবর্তন হয় না: 1\cdot f(x)=f(x) যেকোনো x\in \mathbb(R), অর্থাৎ 1\cdot f=f। সুতরাং, প্রবর্তিত ক্রিয়াকলাপগুলির সাথে বিবেচনা করা সেট C(\mathbb(R)) হল একটি বাস্তব রৈখিক স্থান। একইভাবে, এটি প্রমাণিত হয় C^1(\mathbb(R)), C^2(\mathbb(R)), \ldots, C^m(\mathbb(R))- প্রথম, দ্বিতীয়, ইত্যাদির ক্রমাগত ডেরিভেটিভ আছে এমন ফাংশনের সেট। অর্ডার, যথাক্রমে, এছাড়াও রৈখিক স্থান.

আসুন বাস্তব সহগ সহ ত্রিকোণমিতিক দ্বিপদ (প্রায়শই \omega\ne0 ) সেট বোঝাই, যেমন ফর্মের অনেক ফাংশন f(t)=a\sin\omega t+b\cos\omega t, কোথায় a\in \mathbb(R), ~b\in \mathbb(R). এই ধরনের দ্বিপদগুলির যোগফল এবং একটি বাস্তব সংখ্যা দ্বারা দ্বিপদীর গুণফল হল ত্রিকোণমিতিক দ্বিপদ। বিবেচনাধীন সেটের জন্য রৈখিক স্থান স্বতঃসিদ্ধ সন্তুষ্ট (যেহেতু T_(\omega)(\mathbb(R))\subset C(\mathbb(R))) অতএব, অনেক T_(\ওমেগা)(\mathbb(R))ফাংশনের জন্য একটি সংখ্যা দ্বারা যোগ এবং গুণের স্বাভাবিক ক্রিয়াকলাপ সহ, এটি একটি বাস্তব রৈখিক স্থান। শূন্য উপাদান দ্বিপদ o(t)=0\cdot\sin\omega t+0\cdot\cos\omega t, একইভাবে শূন্যের সমান।

\mathbb(R) তে সংজ্ঞায়িত বাস্তব ফাংশন এবং একঘেয়েমি একটি রৈখিক স্থান নয়, যেহেতু দুটি একঘেয়ে ফাংশনের পার্থক্য একটি নন-মোনোটোন ফাংশন হতে পারে।

8. আসুন বোঝাই \mathbb(R)^X - ক্রিয়াকলাপ সহ X সেটে সংজ্ঞায়িত বাস্তব ফাংশনের সেট:

(f+g)(x)=f(x)+g(x),\quad (\lambda f)(x)=\lambda\cdot f(x)\quad \forall x\in X

এটি একটি বাস্তব রৈখিক স্থান (প্রমাণটি আগের উদাহরণের মতোই)। এই ক্ষেত্রে, সেট X নির্বিচারে নির্বাচন করা যেতে পারে। বিশেষ করে, যদি X=\(1,2,\ldots,n\), তারপর f(X) হল সংখ্যার একটি ক্রমকৃত সেট f_1,f_2,\ldots,f_n, কোথায় f_i=f(i),~i=1,\ldots,nএই ধরনের সেটকে n\times1 মাত্রার একটি ম্যাট্রিক্স-কলাম হিসাবে বিবেচনা করা যেতে পারে, যেমন একটি গুচ্ছ \mathbb(R)^(\(1,2,\ldots,n\))সেট \mathbb(R)^n এর সাথে মিলে যায় (রৈখিক স্থানের উদাহরণের জন্য পয়েন্ট 3 দেখুন)। যদি X=\mathbb(N) (মনে করুন যে \mathbb(N) হল প্রাকৃতিক সংখ্যার সেট), তাহলে আমরা একটি রৈখিক স্থান পাই \mathbb(R)^(\mathbb(N))- অনেক সংখ্যা ক্রম \(f(i)\)_(i=1)^(\infty). বিশেষ করে, অভিসারী সংখ্যা ক্রমগুলির সেটটিও একটি রৈখিক স্থান গঠন করে, যেহেতু দুটি অভিসারী ক্রমগুলির যোগফল একত্রিত হয় এবং যখন একটি অভিসারী ক্রমটির সমস্ত পদকে একটি সংখ্যা দ্বারা গুণ করা হয়, তখন আমরা একটি অভিসারী ক্রম পাই। বিপরীতে, বিবর্তিত ক্রমগুলির সেটটি একটি রৈখিক স্থান নয়, কারণ, উদাহরণস্বরূপ, ভিন্ন ভিন্ন অনুক্রমের যোগফলের একটি সীমা থাকতে পারে।

9. আসুন বোঝাই \mathbb(R)^(+) - ধনাত্মক বাস্তব সংখ্যার সেট যার সমষ্টি a\oplus b এবং গুণফল \lambda\ast a (এই উদাহরণের স্বরলিপিগুলি সাধারণ সংখ্যা থেকে আলাদা) সমতা দ্বারা সংজ্ঞায়িত: a\oplus b=ab,~ \lambda\ast a=a^(\lambda), অন্য কথায়, উপাদানগুলির যোগফলকে সংখ্যার গুণফল হিসাবে বোঝা যায়, এবং একটি সংখ্যা দ্বারা একটি উপাদানের গুণকে একটি শক্তি বৃদ্ধি হিসাবে বোঝা হয়। উভয় ক্রিয়াকলাপই প্রকৃতপক্ষে \mathbb(R)^(+) সেটে সংজ্ঞায়িত করা হয়েছে, যেহেতু ধনাত্মক সংখ্যার গুণফল একটি ধনাত্মক সংখ্যা এবং একটি ধনাত্মক সংখ্যার যেকোন প্রকৃত শক্তি একটি ধনাত্মক সংখ্যা। আসুন স্বতঃসিদ্ধের বৈধতা পরীক্ষা করি। সমতা

a\oplus b=ab=ba=b\oplus a,\quad a\oplus(b\oplus c)=a(bc)=(ab)c=(a\oplus b)\oplus c

দেখান যে স্বতঃসিদ্ধ 1 এবং 2 সন্তুষ্ট। এই সেটের শূন্য ভেক্টর এক, যেহেতু a\oplus1=a\cdot1=a, অর্থাৎ o=1। a এর বিপরীত ভেক্টর হল ভেক্টর \frac(1)(a), যা a\ne o থেকে সংজ্ঞায়িত করা হয়েছে। প্রকৃতপক্ষে, a\oplus\frac(1)(a)=a\cdot\frac(1)(a)=1=o. আসুন স্বতঃসিদ্ধ 5, 6,7,8 এর পূর্ণতা পরীক্ষা করি:

\begin(একত্রিত) \mathsf(5))\quad \lambda\ast(a\oplus b)=(a\cdot b)^(\lambda)= a^(\lambda)\cdot b^(\lambda) = \lambda\ast a\oplus \lambda\ast b\,;\hfill\\ \mathsf(6))\quad (\lambda+ \mu)\ast a=a^(\lambda+\mu)=a^( \lambda)\cdot a^(\mu)=\lambda\ast a\oplus\mu\ast a\,;\hfill\\ \mathsf(7)) \quad \lambda\ast(\mu\ast a) =(a^(\mu))^(\lambda)=a^(\lambda\mu)=(\lambda\cdot \mu)\ast a\,;\hfill\\ \mathsf(8))\quad 1\ast a=a^1=a\,.\hfill \end(সংগৃহীত)

সমস্ত স্বতঃসিদ্ধ সন্তুষ্ট. ফলস্বরূপ, বিবেচনাধীন সেটটি একটি বাস্তব রৈখিক স্থান।

10. যাক V একটি বাস্তব রৈখিক স্থান। আসুন আমরা V-তে সংজ্ঞায়িত রৈখিক স্কেলার ফাংশনের সেট বিবেচনা করি, অর্থাৎ ফাংশন f\colon V\to \mathbb(R), বাস্তব মান গ্রহণ করা এবং শর্তগুলি সন্তুষ্ট করা:

f(\mathbf(u)+\mathbf(v))=f(u)+f(v)~~ \forall u,v\in V(সংযোজন);

f(\lambda v)=\lambda\cdot f(v)~~ \forall v\in V,~ \forall \lambda\in \mathbb(R)(সমজাতীয়তা)।

রৈখিক ফাংশনগুলিতে রৈখিক ক্রিয়াকলাপগুলি রৈখিক স্থানগুলির উদাহরণের অনুচ্ছেদ 8-এর মতো একইভাবে নির্দিষ্ট করা হয়েছে। যোগফল f+g এবং গুণফল \lambda\cdot f সমতা দ্বারা সংজ্ঞায়িত করা হয়েছে:

(f+g)(v)=f(v)+g(v)\quad \forall v\in V;\qquad (\lambda f)(v)=\lambda f(v)\quad \forall v\ V-এ, ~ \forall \lambda\in \mathbb(R)।

রৈখিক স্থান স্বতঃসিদ্ধের পূর্ণতা অনুচ্ছেদ 8 এর মতো একইভাবে নিশ্চিত করা হয়েছে। তাই, রৈখিক স্থান V-তে সংজ্ঞায়িত রৈখিক ফাংশনগুলির সেটটি একটি রৈখিক স্থান। এই স্থানটিকে V মহাকাশের সাথে সংযুক্ত করা হয় এবং V^(\ast) দ্বারা চিহ্নিত করা হয়। এর উপাদানগুলোকে বলা হয় কভেক্টর।

উদাহরণস্বরূপ, ভেক্টর আর্গুমেন্টের স্কেলার ফাংশনের সেট হিসাবে বিবেচিত n ভেরিয়েবলের রৈখিক ফর্মগুলির সেটটি হল স্পেস \mathbb(R)^n এর সাথে রৈখিক স্থান সংযোজিত।

আপনি যদি একটি ত্রুটি লক্ষ্য করেন, টাইপো বা কোন পরামর্শ আছে, মন্তব্য লিখুন.

http://matworld.ru/linear-algebra/linear-space/linear-subspace.php

দিন এলএবং এম- মহাশূন্যের দুটি উপ-স্থান আর.

পরিমাণ এল+এমএকে ভেক্টরের সেট বলা হয় x+y, কোথায় এক্স∈এলএবং y∈এম. স্পষ্টতই, থেকে ভেক্টরের কোনো রৈখিক সংমিশ্রণ L+Mঅন্তর্গত L+M, তাই L+Mমহাকাশের একটি সাবস্পেস আর(স্থানের সাথে মিলিত হতে পারে আর).

পার হয়ে এল∩এমসাবস্পেস এলএবং এমএকই সাথে সাবস্পেসের অন্তর্গত ভেক্টরের সেট এলএবং এম(শুধুমাত্র একটি শূন্য ভেক্টর গঠিত হতে পারে)।

উপপাদ্য 6.1।নির্বিচার সাবস্পেসের মাত্রার যোগফল এলএবং এমসসীম-মাত্রিক রৈখিক স্থান আরএই সাবস্পেসগুলির যোগফলের মাত্রা এবং এই সাবস্পেসগুলির ছেদগুলির মাত্রার সমান:

dim L+dim M=dim(L+M)+dim(L∩M)।

প্রমাণ। এর উল্লেখ করা যাক F=L+Mএবং G=L∩M. দিন ছ ছ-মাত্রিক সাবস্পেস। এর একটি ভিত্তি বেছে নেওয়া যাক। কারণ জি⊂এলএবং জি⊂এমতাই ভিত্তি জিভিত্তি যোগ করা যেতে পারে এলএবং বেস পর্যন্ত এম. যাক সাবস্পেস ভিত্তি এলএবং সাবস্পেস ভিত্তি যাক এম. আসুন ভেক্টর দেখাই

সাবস্পেসের অন্তর্গত G=L∩M. অন্যদিকে, ভেক্টর vসাবস্পেসের ভিত্তি ভেক্টরগুলির একটি রৈখিক সংমিশ্রণ দ্বারা প্রতিনিধিত্ব করা যেতে পারে জি:

সাবস্পেসের ভিত্তির রৈখিক স্বাধীনতার কারণে এলআমাদের আছে:

রৈখিকভাবে স্বাধীন। কিন্তু কোনো ভেক্টর zথেকে চ(সাবস্পেসের যোগফলের সংজ্ঞা অনুসারে) যোগফল দ্বারা প্রতিনিধিত্ব করা যেতে পারে x+y, কোথায় x∈L, y∈M. তার পালা এক্সভেক্টরের একটি রৈখিক সংমিশ্রণ দ্বারা উপস্থাপিত a y- ভেক্টরের রৈখিক সংমিশ্রণ। ফলস্বরূপ, ভেক্টর (6.10) সাবস্পেস তৈরি করে চ. আমরা দেখতে পেয়েছি যে ভেক্টর (6.10) একটি ভিত্তি তৈরি করে F=L+M.

সাবস্পেস বেস অধ্যয়নরত এলএবং এমএবং সাবস্পেস ভিত্তি F=L+M(6.10), আমাদের আছে: ম্লান L=g+l, dim M=g+m, dim (L+M)=g+l+m. তাই:

dim L+dim M−dim(L∩M)=dim(L+M)। ■

2. একটি রৈখিক অপারেটরের আইজেনভেক্টর এবং আইজেন ভ্যালু।

http://www.studfiles.ru/preview/6144691/page:4/

ভেক্টর X ≠ 0 বলা হয় eigenvectorম্যাট্রিক্স A সহ রৈখিক অপারেটর, যদি l সংখ্যা থাকে যেমন AX = lX।

এই ক্ষেত্রে, l নম্বরটি বলা হয় eigenvalueঅপারেটর (ম্যাট্রিক্স A) ভেক্টর x এর সাথে সম্পর্কিত।

অন্য কথায়, একটি eigenvector হল একটি ভেক্টর যা একটি রৈখিক অপারেটরের ক্রিয়াকলাপের অধীনে একটি সমরেখা ভেক্টরে রূপান্তরিত হয়, যেমন শুধু কিছু সংখ্যা দিয়ে গুণ করুন। বিপরীতে, অনুপযুক্ত ভেক্টরগুলি রূপান্তর করা আরও জটিল।

আসুন সমীকরণের একটি সিস্টেম আকারে একটি eigenvector এর সংজ্ঞা লিখি:

চলুন সব পদ বাম দিকে সরানো যাক:

পরবর্তী সিস্টেমটি নিম্নরূপ ম্যাট্রিক্স আকারে লেখা যেতে পারে:

(A - lE) X = O

ফলস্বরূপ সিস্টেমে সর্বদা একটি শূন্য সমাধান থাকে X = O। এই ধরনের সিস্টেমে যে সমস্ত মুক্ত পদ শূন্যের সমান হয় তাকে বলা হয় সমজাতীয়. যদি এই ধরনের সিস্টেমের ম্যাট্রিক্স বর্গাকার হয় এবং এর নির্ধারক শূন্যের সমান না হয়, তাহলে ক্র্যামারের সূত্র ব্যবহার করে আমরা সর্বদা একটি অনন্য সমাধান পাব - শূন্য। এটি প্রমাণিত হতে পারে যে একটি সিস্টেমের অ-শূন্য সমাধান আছে যদি এবং শুধুমাত্র যদি এই ম্যাট্রিক্সের নির্ধারক শূন্যের সমান হয়, অর্থাৎ

|A - lE| = = 0

একটি অজানা সঙ্গে এই সমীকরণ বলা হয় চরিত্রগত সমীকরণ(চরিত্রগত বহুপদ) ম্যাট্রিক্স A (লিনিয়ার অপারেটর)।

এটি প্রমাণ করা যেতে পারে যে একটি রৈখিক অপারেটরের বৈশিষ্ট্যগত বহুপদ ভিত্তি পছন্দের উপর নির্ভর করে না।

উদাহরণস্বরূপ, আসুন ম্যাট্রিক্স A = দ্বারা সংজ্ঞায়িত লিনিয়ার অপারেটরের eigenvalues ​​এবং eigenvectors খুঁজে বের করি।

এটি করার জন্য, আসুন একটি চরিত্রগত সমীকরণ তৈরি করি |A - lE| = = (1 -l) 2 – 36 = 1 – 2l+l 2 - 36 =l 2 – 2l- 35; D = 4 + 140 = 144; eigenvaluesl 1 = (2 - 12)/2 = -5;l 2 = (2 + 12)/2 = 7।

eigenvectors খুঁজে বের করার জন্য, আমরা সমীকরণের দুটি সিস্টেম সমাধান করি

(A + 5E)X = O

(A - 7E)X = O

তাদের প্রথমটির জন্য, প্রসারিত ম্যাট্রিক্স ফর্ম নেয়

,

যেখান থেকে x 2 = c, x 1 + (2/3)c = 0; x 1 = -(2/3)s, i.e. X (1) = (-(2/3)s; s)।

তাদের দ্বিতীয়টির জন্য, প্রসারিত ম্যাট্রিক্স ফর্ম নেয়

,

যেখান থেকে x 2 = c 1, x 1 - (2/3)c 1 = 0; x 1 = (2/3)s 1, অর্থাৎ X(2) = ((2/3)s 1; s 1)।

সুতরাং, এই রৈখিক অপারেটরের eigenvectors হল eigenvalue (-5) সহ (-(2/3)с; с) ফর্মের সমস্ত ভেক্টর এবং (2/3)с 1 ; с 1) ফর্মের সমস্ত ভেক্টর eigenvalue 7।

এটি প্রমাণ করা যেতে পারে যে অপারেটর A এর eigenvectors এর ভিত্তিতে গঠিত ম্যাট্রিক্সটি তির্যক এবং এর ফর্ম রয়েছে:

,

যেখানে আমি এই ম্যাট্রিক্সের eigenvalues.

কথোপকথনটিও সত্য: যদি কোনো ভিত্তিতে ম্যাট্রিক্স A তির্যক হয়, তাহলে এই ভিত্তির সমস্ত ভেক্টর এই ম্যাট্রিক্সের ইজেনভেক্টর হবে।

এটিও প্রমাণিত হতে পারে যে যদি একটি রৈখিক অপারেটরের n জোড়ভিত্তিক স্বতন্ত্র ইজেনভ্যালু থাকে, তবে সংশ্লিষ্ট আইজেনভেক্টরগুলি রৈখিকভাবে স্বাধীন, এবং সংশ্লিষ্ট ভিত্তিতে এই অপারেটরের ম্যাট্রিক্সের একটি তির্যক রূপ রয়েছে।

এর আগের উদাহরণ দিয়ে এটি ব্যাখ্যা করা যাক। ধরা যাক নির্বিচারে অ-শূন্য মান c এবং c 1, কিন্তু এমন যে ভেক্টর X (1) এবং X (2) রৈখিকভাবে স্বাধীন, যেমন একটি ভিত্তি গঠন করবে। উদাহরণস্বরূপ, ধরুন c = c 1 = 3, তারপর X (1) = (-2; 3), X (2) = (2; 3)। আসুন আমরা এই ভেক্টরগুলির রৈখিক স্বাধীনতা যাচাই করি:

12 ≠ 0. এই নতুন ভিত্তিতে, ম্যাট্রিক্স A রূপ নেবে A * =।

এটি যাচাই করতে, আসুন A * = C -1 AC সূত্রটি ব্যবহার করি। প্রথমে C-1 বের করা যাক।

গ -1 = ;

পরীক্ষার টিকিট নং 11

1. রৈখিক স্থান একটি নতুন বেস রূপান্তর. ট্রানজিশন ম্যাট্রিক্স।

http://www.studfiles.ru/preview/6144772/page:3/

একটি নতুন ভিত্তি পরিবর্তন

R মহাকাশে দুটি ঘাঁটি রয়েছে: পুরানোটি e l , e 2 ,...e n এবং নতুনটি e l * , e 2 * , ...e n * । যেকোন নতুন ভিত্তি ভেক্টরকে পুরানো ভিত্তি ভেক্টরের রৈখিক সংমিশ্রণ হিসাবে উপস্থাপন করা যেতে পারে:

পুরাতন ভিত্তি থেকে নতুন একটি রূপান্তর নির্দিষ্ট করা যেতে পারে রূপান্তর ম্যাট্রিক্স

মনে রাখবেন যে পুরানো ভিত্তির উপর নতুন ভিত্তি ভেক্টরের গুণন সহগগুলি এই ম্যাট্রিক্সের সারি নয়, কলাম তৈরি করে।

ম্যাট্রিক্স A অ-একবচন, কারণ অন্যথায় এর কলামগুলি (এবং সেই কারণে ভিত্তি ভেক্টর) রৈখিকভাবে নির্ভরশীল হবে। অতএব, এটির একটি বিপরীত ম্যাট্রিক্স A -1 রয়েছে।

ভেক্টর X-এর স্থানাঙ্ক (x l, x 2,... x n) আছে পুরানো ভিত্তি এবং স্থানাঙ্কগুলি (x l *, x 2 *,... x n *) নতুন ভিত্তির সাপেক্ষে, যেমন Х = x l e l + x 2 e 2 +... x n e n = x l * e l * + x 2 * e 2 * + ... x n * e n * ।

আসুন এই সমীকরণে পূর্ববর্তী সিস্টেম থেকে e l * , e 2 * , ...e n * মানগুলি প্রতিস্থাপন করি:

x l e l + x 2 e 2 + ... x n e n = x l * (a 11 e l + a 12 e 2 + … + a 1n e n) + x 2 * (a 21 e l + a 22 e 2 + … + + a 2n e n) +... x n * (a n1 e l + a n2 e 2 + … + a nn e n)

0 = e l (x l * a 11 + x 2 * a 21 + … + x n * a n1 - x l) + e 2 (x l * a 12 + x 2 * a 22 + … + x n * a n2 – x 2) + + … + e n (x l * a 1n + x 2 * a 2n + … + x n * a nn – x n)

e l, e 2,...e n ভেক্টরগুলির রৈখিক স্বাধীনতার কারণে, শেষ সমীকরণে তাদের জন্য সমস্ত সহগ অবশ্যই শূন্যের সমান হতে হবে। এখান থেকে:

অথবা ম্যাট্রিক্স আকারে

উভয় পক্ষকে A -1 দ্বারা গুণ করুন, আমরা পাই:

উদাহরণস্বরূপ, বেসিস e l , e 2 , e 3 ভেক্টর দেওয়া যাক a 1 = (1, 1, 0), এবং 2 = (1, -1, 1), এবং 3 = (-3, 5, -6) ) এবং b = (4; -4; 5)। দেখান যে a l, a 2 এবং 3 ভেক্টরগুলিও একটি ভিত্তি তৈরি করে এবং এই ভিত্তিতে ভেক্টর b প্রকাশ করে।

দেখা যাক যে ভেক্টর a l, a 2, এবং 3 রৈখিকভাবে স্বাধীন। এটি করার জন্য, আমরা নিশ্চিত করি যে তাদের দ্বারা গঠিত ম্যাট্রিক্সের র্যাঙ্ক তিনটির সমান:

লক্ষ্য করুন যে মূল ম্যাট্রিক্সটি ট্রানজিশন ম্যাট্রিক্স A এর চেয়ে বেশি কিছু নয়। আসলে, বেস el, e 2, e 3 এবং a l, a 2, এবং 3 এর মধ্যে সংযোগ সিস্টেম দ্বারা প্রকাশ করা যেতে পারে:

A -1 হিসাব করি।

= 6 + 0 - 3 – 0 – 5 + 6 = 4

অর্থাৎ, ভিত্তিতে a l, a 2, a 3 ভেক্টর b = (0.5; 2; -0.5)।

2 ইউক্লিডীয় স্থানের ভেক্টরের মধ্যে ভেক্টরের দৈর্ঘ্য এবং কোণ।

http://mathhelpplanet.com/static.php?p=evklidovy-prostranstva

ধরুন এবং একটি রৈখিক স্থানের সাবস্পেস হবে।

সাবস্পেস অতিক্রম করে এবং একে ভেক্টরের একটি সেট বলা হয়, যার প্রত্যেকটি একই সাথে এবং একই সাথে, অর্থাৎ সাবস্পেসের ছেদকে দুটি সেটের সাধারণ ছেদ হিসাবে সংজ্ঞায়িত করা হয়।

সাবস্পেসের বীজগাণিতিক যোগফল এবং ফর্মের ভেক্টরের একটি সেট বলা হয়, যেখানে সাবস্পেসের বীজগাণিতিক যোগফল (সংক্ষেপে, শুধু যোগফল) বোঝানো হয়

ফর্মে একটি ভেক্টরের প্রতিনিধিত্ব , যেখানে , বলা হয় ভেক্টর পচন কোন সাবস্পেস নেই এবং .

নোট 8.8

1. সাবস্পেসের ছেদ একটি সাবস্পেস। অতএব, মাত্রা, ভিত্তি, ইত্যাদি ধারণা। ছেদগুলিতে প্রয়োগ করুন।

2. সাবস্পেসের যোগফল হল একটি সাবস্পেস। অতএব, মাত্রা, ভিত্তি, ইত্যাদি ধারণা। পরিমাণে প্রযোজ্য।

প্রকৃতপক্ষে, সেটে রৈখিক ক্রিয়াকলাপগুলির বন্ধত্ব দেখানো প্রয়োজন। ধরুন দুটি ভেক্টর যোগফলের অন্তর্গত, অর্থাৎ তাদের প্রতিটি সাবস্পেসে পচে যায়:

আসুন যোগফল খুঁজে বের করা যাক: . তারপর থেকে, এবং তারপর। ফলস্বরূপ, সংযোজন পরিচালনার ক্ষেত্রে সেটটি বন্ধ রয়েছে। চলুন কাজ খুঁজে বের করা যাক:. যেহেতু, a, তারপর। ফলস্বরূপ, একটি সংখ্যা দ্বারা গুণের ক্রিয়াকলাপের ক্ষেত্রে সেটটি বন্ধ হয়ে যায়। সুতরাং, একটি রৈখিক সাবস্পেস।

3. একটি রৈখিক স্থানের সমস্ত সাবস্পেসের সেটে ইন্টারসেকশনের ক্রিয়াকলাপ সংজ্ঞায়িত করা হয়। এটি পরিবর্তনশীল এবং সহযোগী। সাবস্পেস V-এর যেকোন পরিবারের ছেদ হল একটি রৈখিক সাবস্পেস, এবং অভিব্যক্তিতে বন্ধনীগুলি - ইচ্ছামত স্থাপন করা যেতে পারে বা একেবারেই নয়।

4. ন্যূনতম রৈখিক সাবস্পেস একটি সসীম-মাত্রিক রৈখিক স্থানের একটি উপসেট ধারণ করা হল সমস্ত সাবস্পেসের ছেদ, অর্থাৎ . যদি , তাহলে নির্দিষ্ট ছেদটি নাল সাবস্পেসের সাথে মিলে যায়, যেহেতু এটি যেকোনো সাবস্পেসের মধ্যে থাকে। যদি একটি রৈখিক সাবস্পেস হয়, তাহলে নির্দেশিত ছেদটি এর সাথে মিলে যায়, যেহেতু এটি প্রতিটি ছেদকারী সাবস্পেসের মধ্যে থাকে (এবং তাদের মধ্যে একটি: )।

লিনিয়ার শেলের ন্যূনতম সম্পত্তি: রৈখিক শেল কোনো উপসেট সসীম-মাত্রিক রৈখিক স্থান ন্যূনতম রৈখিক সাবস্পেস ধারণকারী , অর্থাৎ .

প্রকৃতপক্ষে, আমাদের বোঝানো যাক . দুটি সেটের সমতা প্রমাণ করা প্রয়োজন: . যেহেতু (মন্তব্য 8.7 এর অনুচ্ছেদ 6 দেখুন), তারপর। আমাদের অন্তর্ভুক্তি প্রমাণ করা যাক. একটি নির্বিচারে উপাদান ফর্ম আছে, যেখানে. কোন সাবস্পেস ধারণকারী হতে দিন. এটিতে সমস্ত ভেক্টর এবং তাদের যেকোনো রৈখিক সংমিশ্রণ রয়েছে (রিমার্কস 8.7 এর অনুচ্ছেদ 7 দেখুন), বিশেষ করে, ভেক্টর। অতএব, ভেক্টর যে কোন সাবস্পেস ধারণকারী। এর মানে হল যে এটি এই জাতীয় সাবস্পেসগুলির ছেদগুলির অন্তর্গত৷ এইভাবে, . সমতা দুটি অন্তর্ভুক্তি থেকে অনুসরণ করে।

5. একটি রৈখিক স্থানের সমস্ত সাবস্পেসের সেটে সাবস্পেস সংযোজনের ক্রিয়াকলাপ সংজ্ঞায়িত করা হয়। এটি পরিবর্তনশীল এবং সহযোগী। অতএব, সীমিত সংখ্যক সাবস্পেসের সমষ্টিতে, বন্ধনীগুলিকে ইচ্ছামত স্থাপন করা যেতে পারে বা একেবারেই না।

6. আমরা সাবস্পেসের মিলনকে ভেক্টরের একটি সেট হিসাবে সংজ্ঞায়িত করতে পারি, যার প্রতিটি একটি স্পেস বা স্পেস (বা উভয় সাবস্পেস) এর অন্তর্গত। যাইহোক, সাধারণ ক্ষেত্রে সাবস্পেসের মিলন একটি সাবস্পেস নয় (এটি শুধুমাত্র অতিরিক্ত শর্তের অধীনে একটি সাবস্পেস হবে বা )।

7. সাবস্পেসের যোগফল তাদের মিলনের রৈখিক স্প্যানের সাথে মিলে যায়। প্রকৃতপক্ষে, সংজ্ঞা থেকে অন্তর্ভুক্তি অনুসরণ করে। সেটের যেকোনো উপাদানের ফর্ম আছে, যেমন সেট থেকে দুটি ভেক্টরের একটি রৈখিক সমন্বয়। আসুন বিপরীত অন্তর্ভুক্তি প্রমাণ করি। যে কোন উপাদানের ফর্ম আছে , কোথায় . আসুন এই যোগফলটিকে দুই ভাগে ভাগ করি, প্রথম যোগফলের জন্য সমস্ত পদ বরাদ্দ করি। অবশিষ্ট পদগুলি দ্বিতীয় যোগফল তৈরি করবে:

প্রথম যোগফল কিছু ভেক্টর, দ্বিতীয় যোগফল কিছু ভেক্টর। তাই, . মানে, . ফলস্বরূপ দুটি অন্তর্ভুক্তি বিবেচনাধীন সেটগুলির সমতা নির্দেশ করে।

উপপাদ্য 8.4 সাবস্পেসের যোগফলের মাত্রার উপর। যদি এবং একটি সসীম-মাত্রিক রৈখিক স্থানের সাবস্পেস , তাহলে সাবস্পেসের যোগফলের মাত্রা তাদের ছেদ করার মাত্রা ছাড়াই তাদের মাত্রার যোগফলের সমান (গ্রাসম্যানের সূত্র ):

আসলে, ছেদ ভিত্তি হতে দিন. সাবস্পেসের ভিত্তি পর্যন্ত ভেক্টরের একটি ক্রমযুক্ত সেট এবং সাবস্পেসের ভিত্তি পর্যন্ত ভেক্টরের একটি ক্রমযুক্ত সেট দিয়ে এটিকে সম্পূরক করি। উপপাদ্য 8.2 দ্বারা এই ধরনের একটি সংযোজন সম্ভব। উপরের তিনটি ভেক্টরের সেট থেকে আমরা একটি অর্ডারকৃত সেট তৈরি করি ভেক্টর আসুন দেখাই যে এই ভেক্টরগুলি স্থানের জেনারেটর। প্রকৃতপক্ষে, এই স্থানের যেকোন ভেক্টরকে একটি অর্ডারকৃত সেট থেকে ভেক্টরগুলির একটি রৈখিক সংমিশ্রণ হিসাবে উপস্থাপন করা হয়

তাই, . আসুন প্রমাণ করি যে জেনারেটর রৈখিকভাবে স্বাধীন এবং তাই তারা স্থানের ভিত্তি। প্রকৃতপক্ষে, আসুন এই ভেক্টরগুলির একটি রৈখিক সংমিশ্রণ তৈরি করি এবং এটিকে শূন্য ভেক্টরের সাথে সমান করি:

প্রথম দুটি যোগফল বোঝানো যাক - এটি থেকে কিছু ভেক্টর, শেষ যোগফলটি বোঝানো যাক - এটি থেকে কিছু ভেক্টর। সমতা (8.14): মানে ভেক্টরটিও স্থানের অন্তর্গত। মানে, . ভিত্তিতে এই ভেক্টর প্রসারিত, আমরা খুঁজে . (8.14) এ এই ভেক্টরের সম্প্রসারণ বিবেচনা করে, আমরা পাই

সাবস্পেসের ভিত্তির পরিপ্রেক্ষিতে শেষ সমতাকে শূন্য ভেক্টরের প্রসারণ হিসাবে বিবেচনা করা যেতে পারে। এই সম্প্রসারণের সমস্ত সহগ শূন্য: এবং . (8.14) মধ্যে প্রতিস্থাপন, আমরা পেতে. এটি শুধুমাত্র তুচ্ছ ক্ষেত্রেই সম্ভব এবং , যেহেতু ভেক্টরের সিস্টেমটি রৈখিকভাবে স্বাধীন (এটি সাবস্পেসের ভিত্তি)। এইভাবে, সমতা (8.14) শুধুমাত্র তুচ্ছ ক্ষেত্রে সন্তুষ্ট হয় যখন সমস্ত সহগ একই সময়ে শূন্যের সমান হয়। অতএব, ভেক্টর সেট রৈখিকভাবে স্বাধীন, যেমন স্থানের ভিত্তি। সাবস্পেসের যোগফলের মাত্রা গণনা করা যাক:

Q.E.D.

উদাহরণ 8.6।একটি বিন্দুতে একটি সাধারণ উৎপত্তি সহ ব্যাসার্ধ ভেক্টরের স্থানটিতে, নিম্নলিখিত সাবস্পেসগুলি দেওয়া হয়: এবং - একটি বিন্দুতে ছেদকারী সরল রেখার অন্তর্গত ব্যাসার্ধ ভেক্টরের তিনটি সেট এবং যথাক্রমে; এবং যথাক্রমে ছেদকারী সমতলগুলির অন্তর্গত ব্যাসার্ধ ভেক্টরের দুটি সেট এবং; সরলরেখা, সমতলের অন্তর্গত, সরলরেখা সমতলের অন্তর্গত, সমতল এবং একটি সরলরেখায় ছেদ করে (চিত্র 8.2)। নির্দেশিত পাঁচটি উপস্থানের প্রতিটি দুটির যোগফল এবং ছেদগুলি খুঁজুন।

সমাধান। যোগফল খুঁজে বের করা যাক। এবং যথাক্রমে দুটি ভেক্টর যুক্ত করলে আমরা সমতলের সাথে সম্পর্কিত একটি ভেক্টর পাই। বিপরীতে, যেকোন ভেক্টর (চিত্র 8.2 দেখুন) এর অন্তর্গত, যথাক্রমে লাইনের উপর প্রজেকশন এবং ভেক্টর নির্মাণ করে ফর্মে উপস্থাপন করা যেতে পারে। এর মানে হল যে প্লেনের যেকোন ব্যাসার্ধ ভেক্টরকে সাবস্পেসগুলিতে প্রসারিত করা যেতে পারে এবং , যেমন . একইভাবে, আমরা দেখতে পাই যে, a হল সমতলের অন্তর্গত ব্যাসার্ধ ভেক্টরের সেট এবং লাইনগুলির মধ্য দিয়ে যায়।

যোগফল খুঁজে বের করা যাক। স্থানের যেকোনো ভেক্টরকে সাবস্পেস এবং . প্রকৃতপক্ষে, ব্যাসার্ধ ভেক্টরের শেষে আমরা সরলরেখার সমান্তরাল একটি সরল রেখা আঁকি (চিত্র 8.2 দেখুন), অর্থাৎ আমরা সমতলে ভেক্টরের অভিক্ষেপ তৈরি করি। তারপর আমরা ভেক্টর স্থগিত করি যাতে . তাই, . তখন থেকে. একইভাবে আমরা যে প্রাপ্ত. অবশিষ্ট পরিমাণ সহজভাবে পাওয়া যায়: . লক্ষ্য করুন .

উপপাদ্য 8.4 ব্যবহার করে, আসুন আমরা পরীক্ষা করি, উদাহরণস্বরূপ, মাত্রায় সমতা। প্রতিস্থাপন এবং Grassmann সূত্রে, আমরা প্রাপ্ত, প্রত্যাশিত হিসাবে, থেকে.

আমরা চিত্র থেকে সাবস্পেসের ছেদ খুঁজে পাই। 8.2, জ্যামিতিক আকারের ছেদ হিসাবে:

শূন্য ব্যাসার্ধ ভেক্টর কোথায়।

স্থানের সমষ্টি মাত্র। সরাসরি যোগফলের মানদণ্ড।

রৈখিক স্থান একটি সেট বলা হয় এল , যেখানে একটি সংখ্যা দ্বারা যোগ এবং গুণের ক্রিয়াকলাপ সংজ্ঞায়িত করা হয়, যেমন উপাদান প্রতিটি জোড়া জন্য ক, খএল এখানে কিছু গএল , যাকে বলা হয় তাদের যোগফল, এবং কোনো উপাদানের জন্য কএল এবং যেকোনো সংখ্যা R বিদ্যমান খএল দ্বারা  এর গুণফল বলা হয় ক. রৈখিক স্থানের উপাদানগুলিকে বলা হয় ভেক্টর . একটি সংখ্যা দ্বারা যোগ এবং গুণের ক্রিয়াকলাপগুলি নিম্নলিখিত স্বতঃসিদ্ধগুলিকে সন্তুষ্ট করে।

সংযোজনের স্বতঃসিদ্ধ:  a, b, c  এল

a+b = b+a -পরিবর্তনশীলতা

(a+b) + c = a + (b+c) -সহযোগীতা

মহাকাশে একটি উপাদান আছে যাকে বলা হয় নাল ভেক্টর এবং মনোনীত করা হয় 0 , যা কোনো যোগ করে কথেকে এল একই উপাদান দেয় একটি,সেগুলো.  0এল:  a এল 0 + a = a.

সকলের জন্যে কথেকে এল বিদ্যমান বিপরীত উপাদান , নির্দেশিত -ক, যেমন যে (-a) + a = 0

( a এল  (-ক) এল: (-a) + a = 0)

সংযোজন স্বতঃসিদ্ধ থেকে সমষ্টি:

1. নাল ভেক্টর অনন্য, যেমন অন্তত একটি জন্য যদি a এল এটা ন্যায্য যে b + a = a, যে b = 0.

2. যেকোনো ভেক্টরের জন্য কএল বিপরীত উপাদান অনন্য, যেমন b + a = 0  b = (-a)

গুণের স্বতঃসিদ্ধ:  ,   R  ক, খ  এল

 (ক) = ()ক

(a+b) =a +খ -বন্টন (ভেক্টর দ্বারা)

(+)a =a +একটি -বন্টন (সংখ্যা দ্বারা)

1a = ক

গুণন স্বতঃসিদ্ধ থেকে সমষ্টি:  ক এল    আর

 0 = 0

0 a = 0

(-ক) = (-1) ক
^

2.1 রৈখিক স্থানের উদাহরণ

1. স্থান কে n উচ্চতার কলাম n. এই স্থানের উপাদানগুলি হল n বাস্তব সংখ্যা সম্বলিত কলাম, যেখানে একটি সংখ্যা দ্বারা উপাদান অনুসারে যোগ এবং উপাদান অনুসারে গুণের ক্রিয়াকলাপ রয়েছে। এই জাতীয় স্থানের একটি নাল ভেক্টর হল n শূন্য সমন্বিত একটি কলাম।

2. ত্রিমাত্রিক স্থানের সাধারণ ভেক্টর আর 3 যোগ ক্রিয়াকলাপ "সমান্তরালগ্রাম নিয়ম অনুসারে" এবং গুণ-প্রসারণ সহ। ধারণা করা হয় যে সমস্ত ভেক্টরের শুরু স্থানাঙ্কের উৎপত্তিস্থলে, একটি নাল ভেক্টর হল একটি ভেক্টর যা স্থানাঙ্কের উৎপত্তিস্থলে শেষ হয়

3. একটি চলক 1-এ ডিগ্রী n-এর বহুপদ হল ফাংশন

পি এন ( এক্স ) =  n এক্স +  n-1 এক্স n n-1 + … +  1 এক্স +  0 এবং  n  0

অনেক বহুপদ ডিগ্রী উচ্চতর নয় n, একটি সংখ্যা দ্বারা যোগ এবং গুণের স্বাভাবিক ক্রিয়াকলাপের সাথে, একটি রৈখিক স্থান গঠন করে। উল্লেখ্য যে ডিগ্রী n এর বহুপদীর সেট একটি রৈখিক স্থান গঠন করে না। আসল বিষয়টি হ'ল ডিগ্রির দুটি বহুপদীর যোগফল, উদাহরণস্বরূপ, 3, ডিগ্রী 2 এর বহুপদ হতে পারে (উদাহরণস্বরূপ, ( এক্স 3 + 3) + (– এক্স 3 – 2এক্স 2 + 7) = – 2এক্স 2 + 10 ডিগ্রী 2 এর একটি বহুপদ)। যাইহোক, বহুপদী সংযোজনের ক্রিয়াকলাপ ডিগ্রী কমাতে পারে, কিন্তু বাড়াতে পারে না, তাই n-এর চেয়ে বেশি নয় ডিগ্রির বহুপদীর সেট যোগের অধীনে বন্ধ হয়ে যায় (অর্থাৎ, n-এর চেয়ে বেশি নয় ডিগ্রির দুটি বহুপদীর যোগফল সর্বদা a ডিগ্রীর বহুপদ n এর চেয়ে বেশি নয়) এবং একটি রৈখিক স্থান গঠন করে।
^

2.2 মাত্রা, ভিত্তি, স্থানাঙ্ক।

রৈখিক সংমিশ্রণ ভেক্টর ( e 1 , ই 2 , …ই n )  রাশি বলা হয়  1 e 1 +  2 e 2 + … n e n = সুতরাং একটি রৈখিক সংমিশ্রণ কেবলমাত্র সংখ্যাগত সহগ সহ ভেক্টরের সমষ্টি। যদি সমস্ত সহগ  i 0 এর সমান, একটি রৈখিক সমন্বয় বলা হয় নগণ্য .

2টি ভেক্টরের সিস্টেমকে বলা হয় রৈখিকভাবে নির্ভরশীল , যদি এই ভেক্টরগুলির সমান একটি নন-তুচ্ছ রৈখিক সমন্বয় থাকে 0 . অন্য কথায়, যদি n সংখ্যা থাকে  R যেমন সবগুলি শূন্যের সমান নয়, এবং সহগ সহ ভেক্টরগুলির রৈখিক সমন্বয় নাল ভেক্টরের সমান:

অন্যথায় ভেক্টর বলা হয় রৈখিকভাবে স্বাধীন . অন্য কথায়, ভেক্টর বলা হয় রৈখিকভাবে স্বাধীন , যদি
 1 থেকে e 1 +  2 e 2 + …+ n e n = 0 অনুসরণ করে  1 =  2 = …= n = 0, অর্থাৎ যদি নাল ভেক্টরের সমান এই ভেক্টরগুলির কোনো রৈখিক সংমিশ্রণ তুচ্ছ।

পচন ভেক্টর কভেক্টর সিস্টেম অনুযায়ী ( e i)কে প্রতিনিধিত্ব বলা হয় কভেক্টরের রৈখিক সংমিশ্রণ হিসাবে ( e i) অন্য কথায়, ছড়িয়ে পড়ে ভেক্টর কভেক্টর দ্বারা ( e i) মানে সংখ্যা বের করা  i এরকম যে

a = 1 e 1 +  2 e 2 + … k e k

উল্লেখ্য যে ভেক্টরের স্বাধীনতার সংজ্ঞা নিম্নলিখিত রূপ দেওয়া যেতে পারে: ভেক্টর স্বাধীন হয় যদি এবং শুধুমাত্র যদি সম্প্রসারণ হয় 0 একা তাদের মতে।

রৈখিক স্থান বলা হয় সসীম-মাত্রিক , যদি একটি পূর্ণসংখ্যা n থাকে যাতে এই স্থানের ভেক্টরগুলির সমস্ত স্বাধীন সিস্টেমে সর্বাধিক n উপাদান থাকে।

মাত্রা সসীম-মাত্রিক রৈখিক স্থান এল রৈখিকভাবে স্বাধীন ভেক্টরের সর্বাধিক সম্ভাব্য সংখ্যা (dim দ্বারা চিহ্নিত করা হয় এল বা আবছা এল ) অন্য কথায়, একটি রৈখিক স্থান বলা হয় n-মাত্রিক , যদি:

1. মহাকাশে n ভেক্টর নিয়ে গঠিত একটি স্বাধীন সিস্টেম আছে;

2. n +1 ভেক্টর সমন্বিত যে কোনো সিস্টেম রৈখিকভাবে নির্ভরশীল।

ভিত্তি রৈখিক স্থান এল nভেক্টরের যে কোনও স্বাধীন সিস্টেমকে বলা হয়, যার উপাদানগুলির সংখ্যা স্থানের মাত্রার সমান।

উপপাদ্য ঘ.ভেক্টরের যে কোনো স্বাধীন সিস্টেম একটি ভিত্তির পরিপূরক হতে পারে। অর্থাৎ, যদি সিস্টেম  এল kস্বাধীন এবং স্থানের মাত্রার চেয়ে কম ভেক্টর রয়েছে (n  এল k, যে ভেক্টরের মিলিত সেট ( e 1 ,e 2 ,…ই n, চ 1 ,চ 2 ,…চ k-n) স্বাধীন, k ভেক্টর ধারণ করে এবং তাই একটি ভিত্তি তৈরি করে এল k. ▄ এইভাবে, যেকোন রৈখিক স্থানে অনেকগুলি (আসলে, অসীম অনেকগুলি) বেস থাকে।

ভেক্টর সিস্টেম বলা হয় সম্পূর্ণ , যদি কোন কএল সিস্টেমের ভেক্টরগুলিতে প্রসারিত করা যেতে পারে (এটি সম্ভব যে সম্প্রসারণটি অনন্য নয়)।

বিপরীতে, একটি স্বাধীন সিস্টেমে যেকোনো ভেক্টরের প্রসারণ সর্বদা অনন্য (কিন্তু সর্বদা বিদ্যমান নয়)। সেগুলো.

উপপাদ্য 2রৈখিক স্থানের ভিত্তিতে যে কোনো ভেক্টরের পচন সর্বদাবিদ্যমান এবং অনন্য। অর্থাৎ ভিত্তি হল একটি স্বাধীন ও সম্পূর্ণ ব্যবস্থা। সহগ  i ভিত্তি অনুসারে ভেক্টর সম্প্রসারণের ( e i) ডাকল স্থানাঙ্ক ভিত্তিতে ভেক্টর ( e i }.▄

নাল ভেক্টরের সমস্ত স্থানাঙ্ক যেকোনো ভিত্তিতে 0 এর সমান।

2.3 উদাহরণ

1. স্থান আর 3 - স্কুল কোর্স থেকে পরিচিত ভেক্টরগুলির একটি ত্রিমাত্রিক স্থান - "নির্দেশিত অংশগুলি" যোগ করার স্বাভাবিক ক্রিয়াকলাপ "সমান্তরালগ্রাম নিয়ম অনুসারে" এবং একটি সংখ্যা দ্বারা গুণ। স্ট্যান্ডার্ড ভিত্তি তিনটি স্থানাঙ্ক অক্ষ বরাবর নির্দেশিত তিনটি পারস্পরিক লম্ব ভেক্টর গঠন করে; তারা অক্ষর দ্বারা মনোনীত করা হয় i , jএবং k.

2. স্থান কে n উচ্চতা n এর কলামের মাত্রা n আছে। স্ট্যান্ডার্ড ভিত্তি কলামের স্পেসে তারা ভেক্টর গঠন করে - এগুলি এমন কলাম যেখানে i-th অবস্থানে রয়েছে এবং অবশিষ্ট উপাদানগুলি শূন্য:

প্রকৃতপক্ষে, এটি দেখতে সহজ যে যে কোনও কলাম একটি অনন্য উপায়ে ভেক্টরগুলির একটি সিস্টেমে পচনশীল হয়, যথা: , অর্থাৎ, যে কোনও কলামের সম্প্রসারণ সহগ এই কলামের সংশ্লিষ্ট উপাদানগুলির সমান।

3. n এর চেয়ে বেশি নয় ডিগ্রির বহুপদীর স্থানটির n+1 মাত্রা রয়েছে। স্ট্যান্ডার্ড ভিত্তি এই স্থানটিতে:

()। প্রকৃতপক্ষে, ডিগ্রী n-এর বহুপদীর সংজ্ঞা থেকে এটা স্পষ্ট যে n-এর চেয়ে বেশি নয় এমন ডিগ্রীর বহুপদকে স্বতন্ত্রভাবে ভেক্টরের রৈখিক সংমিশ্রণ হিসাবে উপস্থাপন করা হয় এবং রৈখিক সংমিশ্রণের সহগগুলি কেবল বহুপদীর সহগ (যদি বহুপদী k-এর ডিগ্রি n-এর চেয়ে কম, তারপর শেষ n-k সহগগুলি 0 এর সমান)।
^

2.4 রৈখিক স্থানগুলির আইসোমরফিজম

ভিত্তি হতে দিন এল n . তারপর সবাই কএল n n সংখ্যার একটি সেটের সাথে এক থেকে এক চিঠিপত্র – ভেক্টর স্থানাঙ্ক কভিত্তিতে অতএব, সবাই কএল n কলাম স্পেস থেকে কেউ এক-একটি ভেক্টর ম্যাপ করতে পারে কে n - কলাম, যা ভেক্টরের স্থানাঙ্ক থেকে গঠিত হয় ক. ভিত্তি যেমন একটি সংজ্ঞায়িত চিঠিপত্র সঙ্গে, থেকে আদর্শ ভিত্তি কে n . 4

ভেক্টরের সমষ্টি পরীক্ষা করা সহজ এল n ভিত্তির মধ্যে সংশ্লিষ্ট স্থানাঙ্কগুলির সমষ্টির দিকে নিয়ে যায়; মানে ভেক্টরের সমষ্টি এল n আমাদের চিঠিপত্রের সাথে সংশ্লিষ্ট কলামের যোগফলের সাথে মিলে যায় কে n ; একটি অনুরূপ নিয়ম একটি সংখ্যা দ্বারা গুণ প্রযোজ্য.

এই স্পেসগুলিতে প্রবর্তিত ক্রিয়াকলাপগুলি সংরক্ষণ করে দুটি স্থানের উপাদানগুলির মধ্যে এক-একটি চিঠিপত্র বলা হয় আইসোমরফিজম . আইসোমরফিজম, সমতার মতো, একটি ট্রানজিটিভ (ট্রানজিটিভ) সম্পত্তি: যদি স্থান এল n আইসোমরফিক কে n , এবং স্থান কে n কিছু স্থানের জন্য আইসোমরফিক এম n , তারপর এল n আইসোমরফিক এম n .

উপপাদ্য 3. n মাত্রার প্রতিটি রৈখিক স্থান আইসোমরফিক কে n, তাই, ট্রানজিটিভিটির কারণে, n মাত্রার সমস্ত রৈখিক স্থান একে অপরের সাথে আইসোমরফিক। ▄

গণিতের দৃষ্টিকোণ থেকে আইসোমরফিক বস্তুগুলি মূলত একটি বস্তুর ভিন্ন ভিন্ন "অবতার" (উপলব্ধি) এবং একটি নির্দিষ্ট স্থানের জন্য প্রমাণিত যে কোনো সত্য প্রথম থেকে অন্য কোনো স্থানের জন্যও সত্য।

2.5 সাবস্পেস

সাবস্পেস স্থান এল একটি উপসেট বলা হয় এম এল , একটি সংখ্যা দ্বারা যোগ এবং গুণের ক্রিয়াকলাপের অধীনে বন্ধ, যেমন x,y

এম 

স্পষ্টতই, 0 এম , যদি এম - সাবস্পেস এল , অর্থাৎ, নাল ভেক্টর যেকোনো সাবস্পেস 5 এর অন্তর্গত।

রৈখিক স্থানের প্রতিটি সাবস্পেস নিজেই একটি রৈখিক স্থান। একগুচ্ছ ( 0 ) হল একটি সাবস্পেস (একটি রৈখিক স্থানের সমস্ত স্বতঃসিদ্ধ যদি স্থানটি একটি একক উপাদান নিয়ে গঠিত - নাল ভেক্টর) 6।

প্রতিটি রৈখিক স্থান দুটি ধারণ করে নগণ্য সাবস্পেস: স্পেস নিজেই এবং শূন্য সাবস্পেস ( 0 ); অন্যান্য সাবস্পেস বলা হয় অ তুচ্ছ .

দুটি সাবস্পেসের ছেদ একটি সাবস্পেস। দুটি সাবস্পেসের মিলন সাধারণত একটি সাবস্পেস নয়; উদাহরণস্বরূপ, মূলের মধ্য দিয়ে যাওয়া দুটি লাইনের মিলনে বিভিন্ন রেখার সাথে যুক্ত ভেক্টরের যোগফল থাকে না (যেমন রেখাগুলির মধ্যে থাকে) 7।

যাক, n এল k . তারপর এই ভেক্টরগুলির সমস্ত রৈখিক সংমিশ্রণের সেট, অর্থাৎ ফর্মের সমস্ত ভেক্টরের সেট

ক =  1 চ 1 +  2 চ 2 + … n চ n

একটি এন-ডাইমেনশনাল সাবস্পেস গঠন করে জি {চ 1 , চ 2 ,…চ n ), যাকে বলা হয় রৈখিক শেল ভেক্টর ( চ 1 , চ 2 ,…চ n)।

উপপাদ্য 4.যে কোনো সাবস্পেসের ভিত্তি সমগ্র স্থানের ভিত্তিতে পরিপূরক হতে পারে। সেগুলো. দিন এম n এল k সাবস্পেস, মাত্রা n – ভিত্তিতে এম n . তারপর ইন এল k এই ধরনের ভেক্টরের একটি সেট আছে  এল k , যে ভেক্টর সিস্টেম ( চ 1 , চ 2 …চ n , ছ 1 , ছ 2 , …g k-n) 8 রৈখিকভাবে স্বাধীন এবং এতে k উপাদান রয়েছে, তাই এটি একটি ভিত্তি তৈরি করে। ▄
^

2.6 সাবস্পেসের উদাহরণ।

1. খ আর 3 স্থানাঙ্কের উত্সের মধ্য দিয়ে যাওয়া প্রতিটি সমতল একটি দ্বি-মাত্রিক উপ-স্থান গঠন করে এবং স্থানাঙ্কগুলির উত্সের মধ্য দিয়ে যাওয়া প্রতিটি লাইন একটি এক-মাত্রিক উপ-স্থান গঠন করে (বিমান এবং রেখা নেই 0 , সাবস্পেস হতে পারে না), এবং অন্যান্য সাবস্পেস এর মধ্যে আর 3 না.

2. কলাম স্পেসে কে 3 ফর্মের কলাম, যেমন যে কলামগুলির তৃতীয় স্থানাঙ্ক 0 হয় একটি সাবস্পেস তৈরি করে যা স্পষ্টতই স্পেসের আইসোমরফিক কে 2 কলাম, উচ্চতা 2।

3. মহাকাশে পৃ n বহুপদ, ডিগ্রী n এর চেয়ে বেশি নয়, বহুপদী, ডিগ্রী 2 এর বেশি নয়, ফর্ম ত্রিমাত্রিকসাবস্পেস (তাদের তিনটি সহগ আছে)।

4. ত্রিমাত্রিক স্থান পৃ 2 ডিগ্রীর বহুপদী 2-এর বেশি নয়, বহুপদ যেগুলি একটি নির্দিষ্ট বিন্দুতে অদৃশ্য হয়ে যায় x 0 একটি দ্বি-মাত্রিক সাবস্পেস গঠন করে (এটি প্রমাণ করুন!)

5. টাস্ক।স্থান কে 4 একটি গুচ্ছ এম কলামগুলি নিয়ে গঠিত যার স্থানাঙ্কগুলি শর্ত পূরণ করে: 1 2 2 + 3 =0 (*)। প্রমাণ কর যে এম ত্রিমাত্রিক সাবস্পেস কে 4 .

সমাধান. আসুন প্রমাণ করি এম সাবস্পেস প্রকৃতপক্ষে, যাক ক এম , খ এম , যার অর্থ a 1 2a 2 + a 3 =0, b 1 2b 2 + b 3 =0। কিন্তু ভেক্টর যোগের নিয়ম অনুযায়ী ( ক + খ) i= ক i+খ i. এটি অনুসরণ করে যে যদি ভেক্টরের জন্য কএবং খশর্ত (*) সন্তুষ্ট, তারপর জন্য ক + খএই শর্ত পূরণ করা হয়. এটাও স্পষ্ট যে যদি একটি কলামের জন্য কশর্ত (*) সন্তুষ্ট, তারপর এটি কলামের জন্যও সন্তুষ্ট ক.এবং অবশেষে, সেটের নাল ভেক্টর এম অন্তর্গত সুতরাং এটি প্রমাণিত হয় এম সাবস্পেস আসুন প্রমাণ করি যে এটি ত্রিমাত্রিক। উল্লেখ্য যে কোন ভেক্টর ক এম অবস্থার কারণে (*) স্থানাঙ্ক (**) আছে। দিন মি 1 = , মি 2 =, ক জ 4 = আসুন দেখান যে ভেক্টর সিস্টেম ( মি 1 , মি 2 , জ 4 ) একটি ভিত্তি গঠন করে এম . চলুন একটি রৈখিক সংমিশ্রণ করা যাক 1 মি 1 + 2 মি 2 +জ 4 = নির্বিচারে সহগ সহ। স্পষ্টতই, কোন ভেক্টর কথেকে এম (দেখুন (**)) সেট অনুযায়ী পচে যায় ( মি 1 , মি 2 , জ 4 ); এটি করার জন্য, 1 = a 1, 2 = a 2, 4 = a 4 ভেক্টরের স্থানাঙ্কগুলিকে সম্প্রসারণ সহগ হিসাবে বেছে নেওয়া যথেষ্ট মি 1 , মি 2 , জ 4 , নাল ভেক্টরের সমান, শূন্য সহগ সহ একটি সমন্বয়: 1 = 0, 2 = 0, 4 = 0। নাল ভেক্টর সম্প্রসারণের অনন্যতা থেকে এটি অনুসরণ করে যে ( মি 1 , মি 2 , জ 4 ) ভেক্টরের স্বাধীন সিস্টেম। এবং এই ঘটনা থেকে সবাই ক এম সিস্টেম অনুযায়ী প্রসারিত হয় ( মি 1 , মি 2 , জ 4 ), এটি অনুসরণ করে যে এই সিস্টেমটি সম্পূর্ণ। একটি সম্পূর্ণ এবং স্বাধীন সিস্টেম সাবস্পেসে একটি ভিত্তি তৈরি করে এম . যেহেতু এই ভিত্তিতে তিনটি ভেক্টর রয়েছে, তাহলে এম ত্রিমাত্রিক সাবস্পেস।