Eksponentiškai arba eksponentiškai. Geometrinė progresija. Išsamus vadovas su pavyzdžiais (2020). Kodėl mums reikia geometrinės progresijos ir jos istorijos

Panagrinėkime seriją.

7 28 112 448 1792...

Visiškai aišku, kad bet kurio jo elemento vertė yra lygiai keturis kartus didesnė nei ankstesnio. Taigi ši serija yra progresas.

Geometrinė progresija – tai begalinė skaičių seka, kurios pagrindinė ypatybė yra ta, kad kitas skaičius gaunamas iš ankstesnio, padauginus iš kokio nors konkretaus skaičiaus. Tai išreiškiama tokia formule.

a z +1 =a z q, kur z yra pasirinkto elemento skaičius.

Atitinkamai, z ∈ N.

Laikotarpis, kai mokykloje mokomasi geometrinės progresijos, yra 9 klasė. Pavyzdžiai padės suprasti sąvoką:

0.25 0.125 0.0625...

Remiantis šia formule, progreso vardiklį galima rasti taip:

Nei q, nei b z negali būti lygūs nuliui. Be to, kiekvienas progresavimo elementas neturėtų būti lygus nuliui.

Atitinkamai, norėdami sužinoti kitą serijos skaičių, turite padauginti paskutinį iš q.

Norėdami nurodyti šią eigą, turite nurodyti pirmąjį jo elementą ir vardiklį. Po to galima rasti bet kurį iš vėlesnių terminų ir jų sumą.

Veislės

Priklausomai nuo q ir a 1, ši progresija skirstoma į keletą tipų:

• Jei ir a 1, ir q yra didesni už vieną, tai tokia seka yra geometrinė progresija, didėjanti su kiekvienu sekančiu elementu. Tokio pavyzdys pateikiamas žemiau.

Pavyzdys: a 1 =3, q=2 – abu parametrai yra didesni už vieną.

Tada skaitinę seką galima parašyti taip:

3 6 12 24 48 ...

• Jei |q| mažiau nei vienas, tai yra, daugyba iš jo yra lygi dalybai, tada progresija su panašiomis sąlygomis yra mažėjanti geometrinė progresija. Tokio pavyzdys pateikiamas žemiau.

Pavyzdys: a 1 = 6, q = 1/3 – a 1 yra didesnis už vieną, q yra mažesnis.

Tada skaitinę seką galima parašyti taip:

6 2 2/3 ... - bet kuris elementas yra 3 kartus didesnis nei po jo einantis elementas.

• Ženklas-kintamasis. Jei q<0, то знаки у чисел последовательности постоянно чередуются вне зависимости от a 1 , а элементы ни возрастают, ни убывают.

Pavyzdys: a 1 = -3 , q = -2 – abu parametrai yra mažesni už nulį.

Tada seką galima parašyti taip:

3, 6, -12, 24,...

Formulės

Norint patogiai naudoti geometrines progresijas, yra daug formulių:

• z-tojo nario formulė. Leidžia apskaičiuoti elementą pagal tam tikrą skaičių, neskaičiuojant ankstesnių skaičių.

Pavyzdys:q = 3, a 1 = 4. Reikia apskaičiuoti ketvirtąjį progresijos elementą.

Sprendimas:a 4 = 4 · 3 4-1 = 4 · 3 3 = 4 · 27 = 108.

• Pirmųjų elementų, kurių skaičius yra, suma z. Leidžia apskaičiuoti visų sekos elementų sumą ikia zimtinai.

Nuo (1-q) yra vardiklyje, tada (1 - q)≠ 0, taigi q nėra lygus 1.

Pastaba: jei q = 1, progresija būtų be galo pasikartojančio skaičiaus serija.

Geometrinės progresijos suma, pavyzdžiai:a 1 = 2, q= -2. Apskaičiuokite S 5 .

Sprendimas:S 5 = 22 - skaičiavimas pagal formulę.

• Suma, jei |q| < 1 и если z стремится к бесконечности.

Pavyzdys:a 1 = 2 , q= 0,5. Raskite sumą.

Sprendimas:Sz = 2 · = 4

Sz = 2 + 1 + 0.5 + 0.25 + 0.125 + 0.0625 = 3.9375 4

Kai kurios savybės:

• būdinga savybė. Jei tokia sąlyga atlikta bet kuriaiz, tada duotoji skaičių serija yra geometrinė progresija:

a z 2 = a z -1 · az+1

• Be to, bet kurio geometrinės progresijos skaičiaus kvadratas randamas pridedant bet kurių kitų dviejų skaičių kvadratus tam tikroje eilutėje, jei jie yra vienodu atstumu nuo šio elemento.

a z 2 = a z - t 2 + a z + t 2 , Kurtyra atstumas tarp šių skaičių.

• Elementaiskiriasi qkartą.
• Progresijos elementų logaritmai taip pat sudaro progresiją, bet jau aritmetinę, tai yra, kiekvienas iš jų yra didesnis už ankstesnį tam tikru skaičiumi.

Kai kurių klasikinių problemų pavyzdžiai

Norint geriau suprasti, kas yra geometrinė progresija, gali padėti pavyzdžiai su 9 klasės sprendimu.

• Sąlygos:a 1 = 3, a 3 = 48. Rastiq.

Sprendimas: kiekvienas paskesnis elementas yra didesnis nei ankstesnisq kartą.Vienus elementus būtina išreikšti per kitus, naudojant vardiklį.

Vadinasi,a 3 = q 2 · a 1

Keičiantq= 4

• Sąlygos:a 2 = 6, a 3 = 12. Apskaičiuokite S 6 .

Sprendimas:Norėdami tai padaryti, pakanka rasti q, pirmąjį elementą, ir pakeisti jį į formulę.

a 3 = q· a 2 , vadinasi,q= 2

a 2 = q a 1,Štai kodėl a 1 = 3

S 6 = 189

• · a 1 = 10, q= -2. Raskite ketvirtąjį progresijos elementą.

Sprendimas: tam pakanka ketvirtąjį elementą išreikšti per pirmąjį ir per vardiklį.

a 4 = q 3· a 1 = -80

Taikymo pavyzdys:

• Banko klientas įnešė 10 000 rublių indėlį, pagal kurį kiekvienais metais klientas prie pagrindinės sumos pridės 6% jo. Kiek pinigų bus sąskaitoje po 4 metų?

Sprendimas: pradinė suma yra 10 tūkstančių rublių. Taigi, praėjus metams po investicijos, sąskaitoje bus suma lygi 10 000 + 10 000 · 0,06 = 10 000 1,06

Atitinkamai, suma sąskaitoje po kitų metų bus išreikšta taip:

(10 000 1,06) 0,06 + 10 000 1,06 = 1,06 1,06 10 000

Tai yra, kiekvienais metais suma padidėja 1,06 karto. Tai reiškia, kad norint rasti lėšų sumą sąskaitoje po 4 metų, pakanka rasti ketvirtąjį progresijos elementą, kurį suteikia pirmasis elementas lygus 10 tūkst., o vardiklis lygus 1,06.

S = 1,06 1,06 1,06 1,06 10 000 = 12 625

Sumos apskaičiavimo užduočių pavyzdžiai:

Įvairiose problemose naudojama geometrinė progresija. Sumos nustatymo pavyzdys gali būti pateiktas taip:

a 1 = 4, q= 2, apskaičiuokiteS5.

Sprendimas: visi skaičiavimui reikalingi duomenys yra žinomi, tereikia juos pakeisti formulėje.

S 5 = 124

• a 2 = 6, a 3 = 18. Apskaičiuokite pirmųjų šešių elementų sumą.

Sprendimas:

Geom. progresija, kiekvienas kitas elementas yra q kartų didesnis už ankstesnį, tai yra, norint apskaičiuoti sumą, reikia žinoti elementąa 1 ir vardiklisq.

a 2 · q = a 3

q = 3

Panašiai mes turime rastia 1 , žinanta 2 Irq.

a 1 · q = a 2

a 1 =2

S 6 = 728.

Susijusi pamoka „Be galo mažėjanti geometrinė progresija“

Pamokos tikslas: supažindinantis mokinius su naujos rūšies seka – be galo mažėjančia geometrine progresija.

Užduotys:

pradinės skaitmeninės sekos ribos idėjos formulavimas; supažindinimas su kitu būdu begalines periodines trupmenas paversti paprastosiomis, naudojant be galo mažėjančios geometrinės progresijos sumos formulę;

mokinių asmenybės intelektinių savybių, tokių kaip loginis mąstymas, gebėjimas atlikti vertinamuosius veiksmus, apibendrinimas, ugdymas;

aktyvumo ugdymas, savitarpio pagalba, kolektyvizmas, domėjimasis dalyku.

Įranga: kompiuterių klasė, projektorius, ekranas.

Pamokos tipas: Pamoka – naujos temos įsisavinimas.

Per užsiėmimus

aš . Org. momentas. Pranešimas apie pamokos temą ir tikslą.

II . Mokinių žinių atnaujinimas.1. Namų darbų tikrinimas.

1) Pagrindinių formulių, susijusių su aritmetine ir geometrine progresija, patikrinimas. Du mokiniai užrašo formules prie lentos.

2) Likę mokiniai tai daro matematinis diktantas tema „Suminės formulės“.

Užduotys:

№1. Raskite pirmųjų penkių aritmetinės progresijos narių sumą, jei jos pirmasis narys yra 6 (1 variantas), -20 (2 variantas), o penktasis narys yra -6 (1 variantas), 20 (2 variantas).

№2. Raskite pirmųjų penkių aritmetinės progresijos narių sumą, jei pirmasis jos narys yra -20 (1 variantas), 6 (2 variantas), o skirtumas yra 10 (1 variantas), -3 (2 variantas).

№3. Raskite pirmųjų penkių geometrinės progresijos narių sumą, jei pirmasis jos narys yra 1 (1 variantas), -1 (2 variantas), o vardiklis yra -2 (1 variantas), 2 (2 variantas).

Pasibaigus diktantui, pasirinktinai, įvertinimui tikrinami dviejų mokinių darbai, likusieji atlieka savikontrolę pagal lentos atlapuose užrašytus paruoštus sprendimus.

Sprendimai:

Užduotys

1. Aritmetinė progresija pateikiama formule a n = 7 – 4 n. Rasti a 10 . (-33)

2. Aritmetinė progresija a 3 = 7 Ir a 5 = 1 . Rasti a 4 . (4)

3. Aritmetinė progresija a 3 = 7 Ir a 5 = 1 . Rasti a 17 . (-35)

4. Aritmetinė progresija a 3 = 7 Ir a 5 = 1 . Rasti S 17 . (-187)

5. Geometrinei progresijai
rasti penktą terminą.

6. Geometrinei progresijai
rasti n– narys.

7. Eksponentiškai b 3 = 8 Ir b 5 = 2 . Rasti b 4 . (4)

8. Eksponentiškai b 3 = 8 Ir b 5 = 2 . Rasti b 1 Ir q .

9. Eksponentiškai b 3 = 8 Ir b 5 = 2 . Rasti S 5 . (62)

III . Naujos temos tyrinėjimas(demonstracinis pristatymas).

Apsvarstykite kvadratą, kurio kraštinė lygi 1. Nubraižykime kitą kvadratą, kurio kraštinė yra pusė pirmojo kvadrato, tada dar vieną, kurio kraštinė yra pusė antrojo, tada kitą ir tt. Kiekvieną kartą naujo kvadrato kraštinė yra pusė ankstesnės.

Dėl to gavome kvadratų kraštinių seką formuojant geometrinę progresiją su vardikliu .

Ir, kas labai svarbu, kuo daugiau statysime tokių aikščių, tuo mažesnė bus aikštės pusė. Pavyzdžiui,

Tie. didėjant skaičiui n, progresijos nariai artėja prie nulio.

Remiantis šia figūra, galima apsvarstyti dar vieną seką.

Pavyzdžiui, kvadratų sričių seka:

. Ir vėl, jei n didėja neribotą laiką, tada plotas savavališkai artėja prie nulio.

Panagrinėkime dar vieną pavyzdį. Lygiakraštis trikampis, kurio kraštinė yra 1 cm. Pastatykime kitą trikampį, kurio viršūnės yra 1-ojo trikampio kraštinių vidurio taškuose, pagal trikampio vidurio linijos teoremą - 2-ojo kraštinė lygi pusei pirmojo kraštinės, 3-iojo kraštinė yra pusė trikampio kraštinės. 2-oji ir kt. Vėl gauname trikampių kraštinių ilgių seką.

adresu
.

Jei nagrinėsime geometrinę progresiją su neigiamu vardikliu.

Tada vėl didėjant skaičiui n progresijos sąlygos artėja prie nulio.

Atkreipkime dėmesį į šių sekų vardiklius. Visur vardikliai buvo mažesni nei 1 modulis.

Galime daryti išvadą: geometrinė progresija be galo mažės, jei jos vardiklio modulis yra mažesnis už 1.

Darbas priekyje.

Apibrėžimas:

Sakoma, kad geometrinė progresija be galo mažėja, jei jos vardiklio modulis yra mažesnis už vieną.
.

Apibrėžimo pagalba galima išspręsti klausimą, ar geometrinė progresija be galo mažėja, ar ne.

Užduotis

Ar seka yra be galo mažėjanti geometrinė progresija, jei ji pateikiama pagal formulę:

;
.

Sprendimas:

. Raskime q .

;
;
;
.

ši geometrinė progresija be galo mažėja.

b)ši seka nėra be galo mažėjanti geometrinė progresija.

Apsvarstykite kvadratą, kurio kraštinė lygi 1. Padalinkite jį per pusę, vieną iš pusių vėl per pusę ir pan. visų gautų stačiakampių plotai sudaro be galo mažėjančią geometrinę progresiją:

Visų tokiu būdu gautų stačiakampių plotų suma bus lygi 1 kvadrato plotui ir lygi 1.

Tačiau kairėje šios lygybės pusėje yra begalinio skaičiaus terminų suma.

Apsvarstykite pirmųjų n narių sumą.

Pagal geometrinės progresijos pirmųjų n narių sumos formulę lygi .

Jeigu n tada didėja neribotą laiką

arba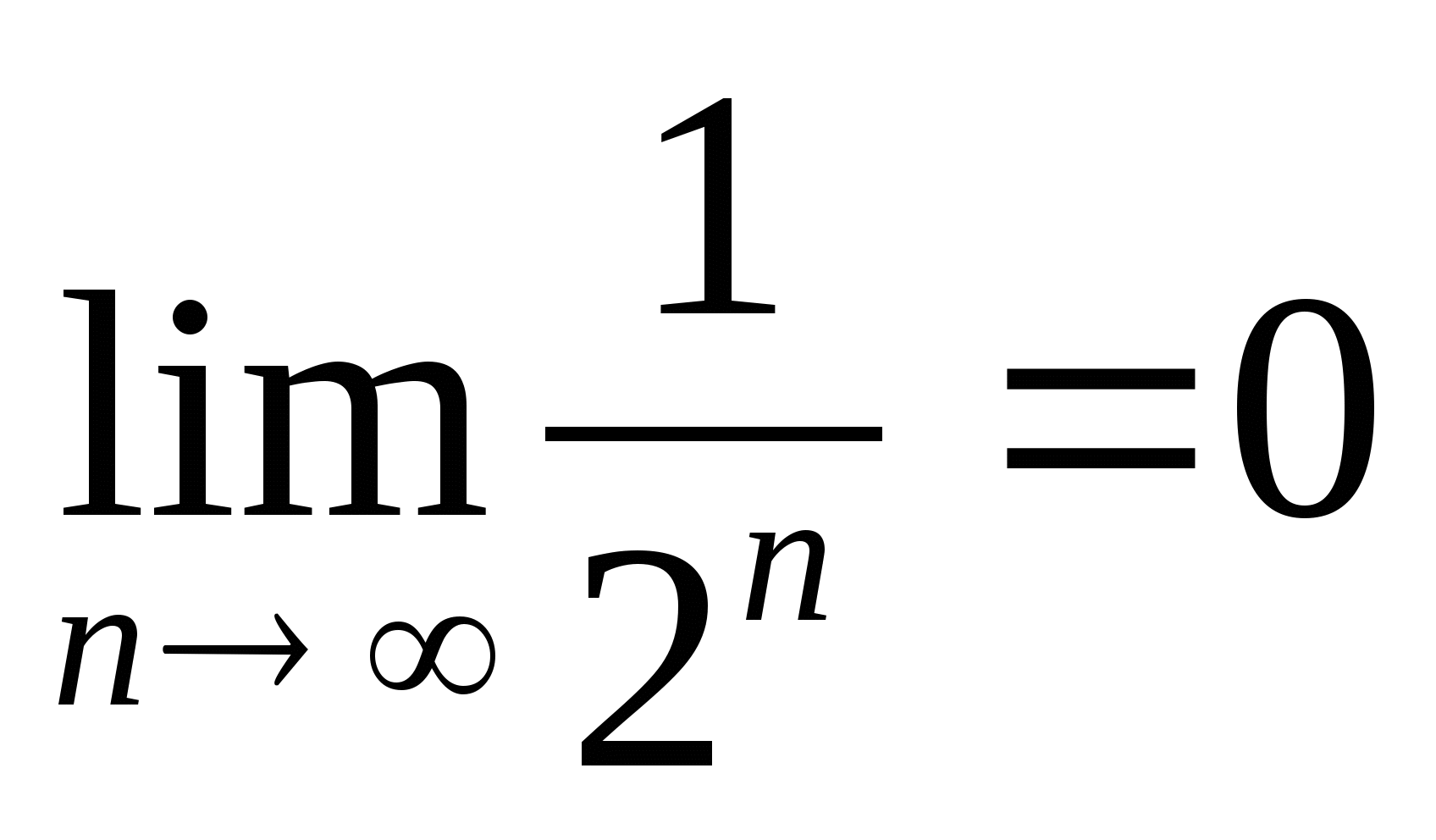
. Štai kodėl
, t.y.
.

Be galo mažėjančios geometrinės progresijos suma yra sekos riba S 1 , S 2 , S 3 , …, S n , … .

Pavyzdžiui, dėl progresavimo
,

Nes

Be galo mažėjančios geometrinės progresijos suma galima rasti naudojant formulę
.

III . Apmąstymas ir konsolidacija(užduočių atlikimas).

Užduotis numeris 2. Raskite be galo mažėjančios geometrinės progresijos sumą, kurios pirmasis narys yra 3, antrasis – 0,3.

Sprendimas:

Užduotis numeris 3. vadovėlis, p. 160, Nr.433(1)

Raskite be galo mažėjančios geometrinės progresijos sumą:

Sprendimas:

Užduotis numeris 4. Parašykite begalinę periodinę dešimtainę trupmeną 0,(5) kaip bendrąją trupmeną.

1-as būdas. Tegu x = 0, (5) = 0,555 ... / 10 2-as metodas. 0,(5)=0,555…=

Užduotis numeris 5. vadovėlis, p.162, Nr.445(3) (savarankiškas sprendimas)

Parašykite begalinę periodinę dešimtainę trupmeną 0,(12) kaip bendrąją trupmeną.

Atsakymas: 0,(12)=4/33.

IV . Apibendrinant.

Kokią seką sutikote šiandien?

Apibrėžkite be galo mažėjančią geometrinę progresiją.

Kaip įrodyti, kad geometrinė progresija be galo mažėja?

Pateikite be galo mažėjančios geometrinės progresijos sumos formulę.

V . Namų darbai.

Geometrinė progresija yra skaitinė seka, kurios pirmasis narys yra ne nulis, o kiekvienas kitas narys yra lygus ankstesniam nariui, padaugintam iš to paties nulinio skaičiaus. Geometrinė progresija žymima b1,b2,b3, …, bn, …

Geometrinės progresijos savybės

Bet kurio geometrinės paklaidos nario santykis su ankstesniu jos nariu yra lygus tam pačiam skaičiui, ty b2/b1 = b3/b2 = b4/b3 = … = bn/b(n-1) = b(n+ 1)/bn = …. Tai tiesiogiai išplaukia iš aritmetinės progresijos apibrėžimo. Šis skaičius vadinamas geometrinės progresijos vardikliu. Dažniausiai geometrinės progresijos vardiklis žymimas raide q.

Vienas iš būdų nustatyti geometrinę progresiją yra nustatyti pirmąjį jos narį b1 ir geometrinės paklaidos q vardiklį. Pavyzdžiui, b1=4, q=-2. Šios dvi sąlygos suteikia geometrinę progresiją 4, -8, 16, -32, … .

Jei q>0 (q nelygu 1), tai progresija yra monotoniška seka. Pavyzdžiui, seka, 2, 4,8,16,32, ... yra monotoniškai didėjanti seka (b1=2, q=2).

Jei geometrinėje paklaidoje vardiklis q=1, tai visi geometrinės progresijos nariai bus lygūs vienas kitam. Tokiais atvejais sakoma, kad progresas yra pastovi seka.

N-ojo progresijos nario formulė

Kad skaitinė seka (bn) būtų geometrinė progresija, būtina, kad kiekvienas jos narys, pradedant nuo antrojo, būtų gretimų narių geometrinis vidurkis. Tai yra, būtina įvykdyti tokią lygtį - (b(n+1))^2 = bn * b(n+2), esant bet kuriam n>0, kur n priklauso natūraliųjų skaičių aibei N.

Geometrinės progresijos n-ojo nario formulė yra tokia:

bn=b1*q^(n-1), kur n priklauso natūraliųjų skaičių aibei N.

Apsvarstykite paprastą pavyzdį:

Geometrinėje progresijoje b1=6, q=3, n=8 raskite bn.

Naudokime geometrinės progresijos n-ojo nario formulę.

Geometrinė progresija yra naujos rūšies skaičių seka, su kuria turime susipažinti. Sėkmingai pažinčiai nekenkia bent jau pažinti ir suprasti. Tada nebus jokių problemų dėl geometrinės progresijos.)

Kas yra geometrinė progresija? Geometrinės progresijos samprata.

Ekskursiją, kaip įprasta, pradedame nuo pradinukų. Rašau nebaigtą skaičių seką:

1, 10, 100, 1000, 10000, …

Ar galite pagauti modelį ir pasakyti, kurie skaičiai bus toliau? Pipiras skaidrus, skaičiai 100000, 1000000 ir pan. Net ir be didelio psichinio streso viskas aišku, tiesa?)

GERAI. Kitas pavyzdys. Rašau tokia seka:

1, 2, 4, 8, 16, …

Ar galite pasakyti, kurie skaičiai eis toliau, vadovaudamiesi numeriu 16 ir vardu aštunta sekos narys? Jei supratote, kad tai bus skaičius 128, tada labai gerai. Taigi, pusė mūšio yra supratimas prasmė Ir Pagrindiniai klausimai geometrinė progresija jau atlikta. Galite augti toliau.)

O dabar nuo pojūčių vėl pereiname prie griežtos matematikos.

Pagrindiniai geometrinės progresijos momentai.

Pagrindinis momentas Nr. 1

Geometrinė progresija yra skaičių seka. Kaip ir progresas. Nieko sudėtingo. Ką tik sutvarkiau šią seką kitaip. Taigi, žinoma, jis turi kitą pavadinimą, taip ...

Pagrindinis momentas #2

Dėl antrojo pagrindinio punkto klausimas bus sudėtingesnis. Grįžkime šiek tiek atgal ir prisiminkime pagrindinę aritmetinės progresijos savybę. Štai jis: kiekvienas narys skiriasi nuo ankstesnio ta pačia suma.

Ar įmanoma suformuluoti panašią pagrindinę geometrinės progresijos savybę? Truputį pagalvokite... Pažvelkite į pateiktus pavyzdžius. Atspėjote? Taip! Geometrine progresija (bet kokia!) kiekvienas jos narys skiriasi nuo ankstesnio tiek pat kartų. Visada!

Pirmajame pavyzdyje šis skaičius yra dešimt. Kad ir kurį sekos terminą imtumėte, jis didesnis nei ankstesnis dešimt kartų.

Antrame pavyzdyje tai yra du: kiekvienas narys yra didesnis nei ankstesnis. du kartus.

Būtent šiuo pagrindiniu tašku geometrinė progresija skiriasi nuo aritmetinės. Aritmetinėje progresijoje gaunamas kiekvienas kitas narys pridedant tos pačios vertės nei ankstesnis terminas. Ir čia - daugyba ankstesnę kadenciją ta pačia suma. Štai ir skirtumas.)

Pagrindinis momentas #3

Šis pagrindinis taškas yra visiškai identiškas aritmetinės progresijos taškui. Būtent: kiekvienas geometrinės progresijos narys yra savo vietoje. Viskas lygiai taip pat kaip aritmetinėje progresijoje ir komentarai, manau, nereikalingi. Yra pirmas terminas, yra šimtas pirmas ir t.t. Pertvarkykime bent du narius – raštas (o kartu su juo ir geometrinė progresija) išnyks. Lieka tik skaičių seka be jokios logikos.

Tai viskas. Tai yra visa geometrinės progresijos esmė.

Terminai ir pavadinimai.

O dabar, išnagrinėję geometrinės progresijos reikšmę ir pagrindinius taškus, galime pereiti prie teorijos. Priešingu atveju, kas yra teorija nesuvokiant prasmės, tiesa?

Kas yra geometrinė progresija?

Kaip bendrais bruožais rašoma geometrinė progresija? Jokiu problemu! Kiekvienas progreso narys taip pat rašomas kaip raidė. Tik aritmetinei progresijai dažniausiai naudojama raidė "A", geometrinei - raidė "b". Nario numeris, kaip įprasta, yra nurodyta apatinis dešinysis indeksas. Patys progresijos nariai yra tiesiog išvardyti, atskirti kableliais arba kabliataškiais.

Kaip šitas:

b1,b 2 , b 3 , b 4 , b 5 , b 6 , …

Trumpai tokia progresija parašyta taip: (b n) .

Arba taip, jei norite baigtinio progreso:

b 1 , b 2 , b 3 , b 4 , b 5 , b 6 .

b 1 , b 2 , ..., b 29 , b 30 .

Arba trumpai:

(b n), n=30 .

Tiesą sakant, tai yra visi pavadinimai. Viskas tas pats, tik raidė skiriasi, taip.) O dabar mes einame tiesiai prie apibrėžimo.

Geometrinės progresijos apibrėžimas.

Geometrinė progresija yra skaitinė seka, kurios pirmasis narys yra ne nulis, o kiekvienas paskesnis narys yra lygus ankstesniam nariui, padaugintam iš to paties skaičiaus, kuris skiriasi nuo nulio.

Tai yra visas apibrėžimas. Dauguma žodžių ir frazių jums yra aiškūs ir žinomi. Nebent, žinoma, supranti geometrinės progresijos reikšmę „ant pirštų“ ir apskritai. Tačiau yra ir keletas naujų frazių, į kurias norėčiau atkreipti ypatingą dėmesį.

Pirma, žodžiai: „kurios pirmoji kadencija skiriasi nuo nulio".

Šis pirmosios kadencijos apribojimas nebuvo įvestas atsitiktinai. Kaip manote, kas atsitiks, jei pirmą kadenciją b 1 pasirodo nulis? Koks bus antrasis terminas, jei kiekvienas terminas yra didesnis nei ankstesnis tiek pat kartų? Tarkim tris kartus? Pažiūrėkime... Pirmąjį narį (t.y. 0) padauginkite iš 3 ir gaukite... nulį! O trečias narys? Taip pat nulis! Ir ketvirtas terminas taip pat yra nulis! Ir taip toliau…

Mes gauname tik maišelį beigelių nulių seka:

0, 0, 0, 0, …

Žinoma, tokia seka turi teisę į gyvybę, bet tai nėra praktinio intereso. Viskas taip aišku. Bet kuris jo narys yra nulis. Bet kokio narių skaičiaus suma taip pat lygi nuliui... Ką įdomaus galite padaryti su juo? Nieko…

Šie raktiniai žodžiai: "padaugintas iš to paties skaičiaus, kuris skiriasi nuo nulio".

Tas pats numeris taip pat turi savo specialų pavadinimą - geometrinės progresijos vardiklis. Pradėkime susitikinėti.)

Geometrinės progresijos vardiklis.

Viskas paprasta.

Geometrinės progresijos vardiklis yra ne nulis skaičius (arba reikšmė), nurodantis kiek kartųkiekvienas progresijos narys daugiau nei ankstesnis.

Vėlgi, pagal analogiją su aritmetine progresija, pagrindinis žodis, į kurį reikia atkreipti dėmesį šiame apibrėžime, yra žodis "daugiau". Tai reiškia, kad gaunamas kiekvienas geometrinės progresijos narys daugyba iki šio vardiklio ankstesnis narys.

paaiškinu.

Norėdami apskaičiuoti, tarkime antra narys pasiimti Pirmas narys ir padauginti tai į vardiklį. Skaičiavimui dešimtas narys pasiimti devintas narys ir padauginti tai į vardiklį.

Pačios geometrinės progresijos vardiklis gali būti bet koks. Visiškai bet kas! Sveikasis skaičius, trupmeninis, teigiamas, neigiamas, neracionalus – visi. Išskyrus nulį. Apie tai kalba apibrėžime esantis žodis „ne nulis“. Kam čia reikalingas šis žodis – apie tai vėliau.

Geometrinės progresijos vardiklis dažniausiai žymimas raide q.

Kaip rasti šį q? Jokiu problemu! Turime priimti bet kurį progresavimo terminą ir padalinti iš ankstesnio termino. Skyrius yra trupmena. Iš čia ir kilo pavadinimas – „progresavimo vardiklis“. Vardiklis, jis paprastai sėdi trupmenoje, taip...) Nors, logiškai mąstant, vertė q reikėtų skambinti privatus geometrinė progresija, panaši į skirtumas aritmetinei progresijai. Bet sutiko paskambinti vardiklis. Ir dviračio taip pat neišradinėsime iš naujo.)

Apibrėžkime, pavyzdžiui, vertę qšiai geometrinei progresijai:

2, 6, 18, 54, …

Viskas elementaru. Mes imame bet koks eilės numeris. Ko mes norime, tą ir imamės. Išskyrus patį pirmąjį. Pavyzdžiui, 18. Ir padalinti iš ankstesnis numeris. Tai yra, 6 val.

Mes gauname:

q = 18/6 = 3

Tai viskas. Tai teisingas atsakymas. Tam tikros geometrinės progresijos vardiklis yra trys.

Raskime vardiklį q kitai geometrinei progresijai. Pavyzdžiui, taip:

1, -2, 4, -8, 16, …

Visi vienodi. Kad ir kokius ženklus turėtų patys nariai, mes vis tiek imamės bet koks eilės numerį (pavyzdžiui, 16) ir padalykite iš ankstesnis numeris(t.y. -8).

Mes gauname:

d = 16/(-8) = -2

Ir viskas.) Šį kartą progresijos vardiklis pasirodė neigiamas. Minus du. Atsitinka.)

Paimkime šią progresą:

1, 1/3, 1/9, 1/27, …

Ir vėlgi, nepriklausomai nuo sekos skaičių tipo (lyginiai sveikieji skaičiai, net trupmeniniai, net neigiami, net neracionalūs), imame bet kurį skaičių (pavyzdžiui, 1/9) ir padalijame iš ankstesnio skaičiaus (1/3). Žinoma, pagal operacijų su trupmenomis taisykles.

Mes gauname:

Tai viskas.) Čia vardiklis pasirodė trupmeninis: q = 1/3.

Bet toks "progresas" kaip tu?

3, 3, 3, 3, 3, …

Aišku čia q = 1 . Formaliai tai irgi geometrinė progresija, tik su tie patys nariai.) Tačiau tokia pažanga nėra įdomi studijoms ir praktiniam pritaikymui. Lygiai taip pat kaip progresija su vientisaisiais nuliais. Todėl mes jų nenagrinėsime.

Kaip matote, progresijos vardiklis gali būti bet kas – sveikasis skaičius, trupmena, teigiamas, neigiamas – bet kas! Tai negali būti tik nulis. Neatspėjote kodėl?

Na, pažiūrėkime į konkretų pavyzdį, kas atsitiks, jei paimsime vardiklį q nulis.) Pavyzdžiui, turėkime b 1 = 2 , A q = 0 . Kokia tada bus antroji kadencija?

Mes tikime:

b 2 = b 1 · q= 2 0 = 0

O trečias narys?

b 3 = b 2 · q= 0 0 = 0

Geometrinių progresijų tipai ir elgsena.

Su viskuo buvo daugiau ar mažiau aišku: jei progreso skirtumas d yra teigiamas, progresas didėja. Jei skirtumas yra neigiamas, progresija mažėja. Yra tik du variantai. Trečio nėra.)

Tačiau naudojant geometrinę progresiją viskas bus daug įdomiau ir įvairiau!)

Kai tik nariai čia elgiasi: didėja ir mažėja, ir be galo artėja prie nulio, ir net keičia ženklus, pakaitomis veržiasi arba į „pliusą“, arba į „minusą“! Ir visą šią įvairovę reikia mokėti gerai suprasti, taip...

Mes suprantame?) Pradėkime nuo paprasčiausio atvejo.

Vardiklis yra teigiamas ( q >0)

Turint teigiamą vardiklį, pirmiausia gali patekti geometrinės progresijos nariai plius begalybė(t. y. didinti neribotą laiką) ir gali eiti į minus begalybė(t.y. mažėti neribotą laiką). Prie tokio progresavimo elgesio jau pripratome.

Pavyzdžiui:

(b n): 1, 2, 4, 8, 16, …

Čia viskas paprasta. Kiekvienas progresijos narys yra daugiau nei ankstesnis. Ir kiekvienas narys gauna daugyba ankstesnis narys įjungtas teigiamas skaičius +2 (t.y. q = 2 ). Tokios progresijos elgesys akivaizdus: visi progresijos nariai auga neribotai, eidami į erdvę. Plius begalybė...

Štai progresas:

(b n): -1, -2, -4, -8, -16, …

Čia taip pat gaunamas kiekvienas progresijos narys daugyba ankstesnis narys įjungtas teigiamas numeris +2. Bet tokios progresijos elgesys jau yra tiesiogiai priešingas: gaunamas kiekvienas progresijos narys mažiau nei ankstesnis, o visi jo terminai mažėja neribotai, eidami į minus begalybę.

Dabar pagalvokime: ką bendro turi šios dvi pažangos? Teisingai, vardiklis! Čia ir ten q = +2 . Teigiamas skaičius. Deuce. Ir čia elgesįŠios dvi pažangos iš esmės skiriasi! Neatspėjote kodėl? Taip! Viskas apie pirmasis narys! Tai jis, kaip sakoma, užsako muziką.) Pažiūrėkite patys.

Pirmuoju atveju pirmasis progresavimo terminas teigiamas(+1), taigi ir visi tolesni terminai, gauti padauginus iš teigiamas vardiklis q = +2 , taip pat teigiamas.

Bet antruoju atveju – pirmasis terminas neigiamas(-1). Todėl visi tolesni progresijos nariai gaunami padauginus iš teigiamas q = +2 , taip pat bus gauta neigiamas. Jei „minusas“ yra „pliusas“, visada nurodo „minusą“, taip.)

Kaip matote, skirtingai nei aritmetinė progresija, geometrinė progresija gali veikti visiškai skirtingai, ne tik priklausomai nuo nuo vardiklioq, bet ir priklausomai nuo nuo pirmojo nario, Taip.)

Atminkite: geometrinės progresijos elgesį vienareikšmiškai lemia pirmasis jos narys b 1 ir vardiklisq .

O dabar pradedame mažiau žinomų, bet daug įdomesnių atvejų analizę!

Paimkite, pavyzdžiui, tokią seką:

(b n): 1, 1/2, 1/4, 1/8, 1/16, …

Ši seka taip pat yra geometrinė progresija! Taip pat gaunamas kiekvienas šios progresijos narys daugyba ankstesnį terminą, tuo pačiu numeriu. Tik numeris yra trupmeninis: q = +1/2 . Arba +0,5 . Ir (svarbu!) skaičius, mažesnis:q = 1/2<1.

Kuo įdomi ši geometrinė progresija? Kur keliauja jos nariai? Pažiūrėkime:

1/2 = 0,5;

1/4 = 0,25;

1/8 = 0,125;

1/16 = 0,0625;

…….

Kas čia įdomaus? Pirma, iš karto į akis krenta progresijos narių mažėjimas: kiekvienas jos narys mažiau tiksliai ankstesnis 2 kartus. Arba, pagal geometrinės progresijos apibrėžimą, kiekvienas terminas daugiau ankstesnis 1/2 karto, nes progresijos vardiklis q = 1/2 . O padauginus iš teigiamo skaičiaus, mažesnio už vieną, rezultatas paprastai mažėja, taip ...

Ką daugiau galima pastebėti šios progresijos elgesyje? Ar jos nariai išnyksta? neribotas, eiti į minus begalybę? Ne! Jie išnyksta ypatingu būdu. Iš pradžių jie mažėja gana greitai, o vėliau vis lėčiau. Ir visą laiką būnant teigiamas. Nors labai, labai mažas. Ir ko jie siekia? Neatspėjote? Taip! Jie linkę į nulį!) Ir, atkreipkite dėmesį, mūsų progreso nariai niekada nepasieksi! Tik be galo arti jo. Tai labai svarbu.)

Panaši situacija bus tokia progresija:

(b n): -1, -1/2, -1/4, -1/8, -1/16, …

Čia b 1 = -1 , A q = 1/2 . Viskas taip pat, tik dabar nariai priartės prie nulio iš kitos pusės, iš apačios. Visą laiką buvimas neigiamas.)

Tokia geometrinė progresija, kurios nariai artėja prie nulio neribotą laiką.(nesvarbu, iš teigiamos ar neigiamos pusės), matematikoje jis turi specialų pavadinimą - be galo mažėjanti geometrinė progresija.Ši pažanga tokia įdomi ir neįprasta, kad net bus atskira pamoka .)

Taigi, mes apsvarstėme viską, kas įmanoma teigiamas vardikliai yra ir dideli, ir mažesni. Mes nelaikome paties vardiklio dėl aukščiau nurodytų priežasčių (prisiminkite pavyzdį su trigubų seka ...)

Apibendrinti:

teigiamasIr daugiau nei vienas (q>1), tada progreso nariai:

a) didinti neribotą laiką (jeib 1 >0);

b) mažėti neribotą laiką (jeib 1 <0).

Jei geometrinės progresijos vardiklis teigiamas Ir mažiau nei vienas (0< q<1), то члены прогрессии:

a) be galo artimas nuliui aukščiau(Jeib 1 >0);

b) be galo artimas nuliui iš apačios(Jeib 1 <0).

Dabar belieka išnagrinėti bylą neigiamas vardiklis.

Vardiklis yra neigiamas ( q <0)

Pavyzdžiu toli nenueisime. Kodėl, tiesą sakant, pasišiaušusi močiutė?!) Tegul, pavyzdžiui, pirmasis progreso narys b 1 = 1 , ir paimkite vardiklį q = -2.

Gauname tokią seką:

(b n): 1, -2, 4, -8, 16, …

Ir taip toliau.) Kiekvienas progresijos narys gaunamas daugyba ankstesnis narys įjungtas neigiamas skaičius-2. Tokiu atveju bus visi nariai nelyginėse vietose (pirmoje, trečioje, penktoje ir kt.). teigiamas, o lygiose vietose (antra, ketvirta ir kt.) - neigiamas.Ženklai yra griežtai tarpusavyje. Pliusas-minusas-pliusas-minusas... Tokia geometrinė progresija vadinama - didėjantis ženklas kaitaliojamas.

Kur keliauja jos nariai? Ir niekur.) Taip, absoliučia verte (ty modulo) mūsų progresavimo terminai didėja neribotai (iš čia ir pavadinimas „didėja“). Bet tuo pačiu metu kiekvienas progreso narys pakaitomis meta jį į karštį, paskui į šaltį. Arba pliusas arba minusas. Mūsų progresija svyruoja... Be to, svyravimų diapazonas sparčiai auga su kiekvienu žingsniu, taip.) Todėl progresijos narių siekiai kažkur eiti konkrečiaiČia Nr. Nei į pliusinę begalybę, nei iki minus begalybės, nei iki nulio – niekur.

Dabar apsvarstykite trupmeninį vardiklį tarp nulio ir minus vieno.

Pavyzdžiui, tegul būna b 1 = 1 , A q = -1/2.

Tada gauname progresą:

(b n): 1, -1/2, 1/4, -1/8, 1/16, …

Ir vėl turime ženklų kaitą! Tačiau, skirtingai nei ankstesniame pavyzdyje, čia jau pastebima tendencija, kad terminai artėja prie nulio.) Tik šį kartą mūsų terminai artėja prie nulio ne griežtai iš viršaus ar apačios, o vėlgi. dvejodama. Pakaitomis imkite teigiamas arba neigiamas vertes. Bet tuo pačiu jie moduliai vis labiau artėja prie branginamo nulio.)

Ši geometrinė progresija vadinama be galo mažėjantis kintamasis ženklas.

Kodėl šie du pavyzdžiai yra įdomūs? Ir tai, kad abiem atvejais vyksta kintamieji simboliai! Toks lustas būdingas tik progresijoms su neigiamu vardikliu, taip.) Todėl jei kurioje nors užduotyje matote geometrinę progresiją su besikeičiančiais nariais, tuomet jau tvirtai žinosite, kad jos vardiklis yra 100% neigiamas ir nesuklysite ženkle.)

Beje, esant neigiamam vardikliui, pirmojo nario ženklas visiškai neįtakoja pačios progresijos elgesio. Kad ir koks būtų pirmojo progreso nario ženklas, bet kuriuo atveju bus stebimas narių kaitos ženklas. Visas klausimas yra tiesiog kokiose vietose(lyginis ar nelyginis) bus nariai su konkrečiais ženklais.

Prisiminti:

Jei geometrinės progresijos vardiklis neigiamas , tada progresijos terminų ženklai visada yra Alternatyva.

Tuo pačiu metu patys nariai:

a) didėti neribotą laikąmodulo, Jeiq<-1;

b) be galo artėti prie nulio, jei -1< q<0 (прогрессия бесконечно убывающая).

Tai viskas. Analizuojami visi tipiniai atvejai.)

Analizuodamas įvairius geometrinių progresijų pavyzdžius, aš periodiškai vartodavau žodžius: "linkęs į nulį", "linkęs į plius begalybę", linkęs į minus begalybę... Viskas gerai.) Šie kalbos posūkiai (ir konkretūs pavyzdžiai) yra tik pradinė pažintis su elgesįįvairios skaičių sekos. Geometrinės progresijos pavyzdys.

Kodėl mes netgi turime žinoti progresavimo elgesį? Koks skirtumas, kur ji eina? Iki nulio, iki plius begalybės, iki minus begalybės... Kas mums tai rūpi?

Reikalas tas, kad jau universitete, studijuojant aukštąją matematiką, reikės gebėjimo dirbti su įvairiomis skaitinėmis sekomis (su bet kokiomis, ne tik progresijomis!) Ir gebėjimo tiksliai įsivaizduoti, kaip ta ar kita seka elgiasi. - ar jis neribotai didėja, ar mažėja, ar linkęs į konkretų skaičių (ir nebūtinai iki nulio), ar net visai nelinkęs į nieką... Šiai temai matematikos eigoje yra skirtas visas skyrius analizė - ribos teorija.Šiek tiek konkrečiau, koncepcija skaičių sekos riba. Labai įdomi tema! Prasminga eiti į koledžą ir išsiaiškinti.)

Kai kurie pavyzdžiai iš šio skyriaus (sekos, kurios turi apribojimą) ir ypač be galo mažėjanti geometrinė progresija pradėti mokytis mokykloje. Priprasti.)

Be to, gebėjimas gerai ištirti sekų elgesį ateityje bus labai naudingas ir bus labai naudingas funkcijų tyrimas. Patys įvairiausi. Tačiau gebėjimas kompetentingai dirbti su funkcijomis (skaičiuoti išvestis, jas išnagrinėti iki galo, sudaryti jų grafikus) jau labai padidina jūsų matematinį lygį! Abejoti? Nereikia. Taip pat atsiminkite mano žodžius.)

Pažiūrėkime į geometrinę progresiją gyvenime?

Gyvenime aplink mus labai, labai dažnai susiduriame su eksponentine progresija. Net to nežinodamas.)

Pavyzdžiui, įvairūs mikroorganizmai, kurie mus supa visur didžiuliais kiekiais ir kurių net nematome be mikroskopo, dauginasi tiksliai geometrine progresija.

Tarkime, viena bakterija dauginasi dalindamasi per pusę, palikuonių susilaukdama 2 bakterijos. Savo ruožtu kiekvienas iš jų, daugindamasis, taip pat dalijasi per pusę, suteikdamas bendrą 4 bakterijų palikuonį. Kita karta duos 8 bakterijas, tada 16 bakterijų, 32, 64 ir pan. Su kiekviena sekančia karta bakterijų skaičius padvigubėja. Tipiškas geometrinės progresijos pavyzdys.)

Taip pat kai kurie vabzdžiai – amarai, musės – dauginasi eksponentiškai. Ir kartais, beje, triušiai.)

Kitas geometrinės progresijos pavyzdys, artimesnis kasdieniam gyvenimui, yra vadinamasis sudėtinės palūkanos. Toks įdomus reiškinys dažnai aptinkamas bankų indėliuose ir vadinamas palūkanų kapitalizacija. Kas tai yra?

Jūs pats, žinoma, dar jaunas. Mokate mokykloje, į bankus nesikreipiate. Tačiau jūsų tėvai yra suaugę ir nepriklausomi žmonės. Jie eina į darbą, užsidirba pinigų kasdienei duonai, o dalį pinigų deda į banką, taupydami.)

Tarkime, jūsų tėtis nori sutaupyti tam tikrą pinigų sumą šeimos atostogoms Turkijoje ir įdėti 50 000 rublių į banką po 10% per metus trejiems metams. su metine palūkanų kapitalizacija. Be to, per visą šį laikotarpį su užstatu nieko negalima daryti. Negalite nei papildyti indėlio, nei išsiimti pinigų iš sąskaitos. Kokį pelną jis uždirbs per šiuos trejus metus?

Na, pirmiausia reikia išsiaiškinti, kas yra 10% per metus. Tai reiškia kad per metus Prie pradinės indėlio sumos bankas pridės 10 proc. Nuo ko? Žinoma, nuo pradinė indėlio suma.

Apskaičiuokite sąskaitos sumą per metus. Jei pradinė indėlio suma buvo 50 000 rublių (t.y. 100%), tai kiek palūkanų sąskaitoje bus per metus? Teisingai, 110%! Nuo 50 000 rublių.

Taigi mes laikome 110% iš 50 000 rublių:

50 000 1,1 \u003d 55 000 rublių.

Tikiuosi, suprantate, kad 110% vertės radimas reiškia šią reikšmę padauginti iš skaičiaus 1,1? Jei nesuprantate, kodėl taip yra, prisiminkite penktą ir šeštą klases. Būtent - procentų santykis su trupmenomis ir dalimis.)

Taigi, pirmųjų metų padidėjimas bus 5000 rublių.

Kiek pinigų bus sąskaitoje po dvejų metų? 60 000 rublių? Deja (tiksliau, laimei), tai nėra taip paprasta. Visa palūkanų kapitalizavimo gudrybė yra ta, kad su kiekvienu nauju palūkanų kaupimu į tas pačias palūkanas jau bus atsižvelgta nuo naujos sumos! Nuo to, kuris jau yra sąskaitoje Šiuo metu. O už praėjusį terminą sukauptos palūkanos pridedamos prie pradinės indėlio sumos ir taip jie patys dalyvauja skaičiuojant naujas palūkanas! Tai yra, jie tampa visa bendros sąskaitos dalimi. arba bendras kapitalo. Iš čia ir pavadinimas - palūkanų kapitalizacija.

Tai yra ekonomikoje. O matematikoje tokie procentai vadinami sudėtinės palūkanos. Arba procentų procentų.) Jų gudrybė ta, kad atliekant nuoseklųjį skaičiavimą procentai skaičiuojami kiekvieną kartą nuo naujos vertės. Ne is originalo...

Todėl, norint apskaičiuoti sumą per dvejus metus, turime apskaičiuoti 110% sumos, kuri bus sąskaitoje per metus. Tai yra, jau nuo 55 000 rublių.

Mes laikome 110% iš 55 000 rublių:

55 000 1,1 \u003d 60 500 rublių.

Tai reiškia, kad antrus metus procentinis padidėjimas jau bus 5500 rublių, o dvejus metus - 10 500 rublių.

Dabar jau galite spėti, kad po trejų metų suma sąskaitoje bus 110% 60 500 rublių. Tai vėlgi 110 proc. iš praėjusių (praėjusių metų) sumos.

Čia mes svarstome:

60500 1,1 \u003d 66550 rublių.

Ir dabar mes kuriame savo pinigines sumas pagal metus iš eilės:

50000;

55 000 = 50 000 1,1;

60500 = 55000 1,1 = (50000 1,1) 1,1;

66550 = 60500 1,1 = ((50000 1,1) 1,1) 1,1

Taigi kaip yra? Kodėl gi ne geometrinė progresija? Pirmasis narys b 1 = 50000 , ir vardiklis q = 1,1 . Kiekvienas terminas yra griežtai 1,1 karto didesnis nei ankstesnis. Viskas griežtai atitinka apibrėžimą.)

O kiek papildomų procentinių premijų „įkris“ jūsų tėtis, kol jo 50 000 rublių banko sąskaitoje buvo trejus metus?

Mes tikime:

66550 - 50000 = 16550 rublių

Tai, žinoma, blogai. Bet tai yra, jei pradinė įnašo suma yra nedidelė. O jei yra daugiau? Sakyk, ne 50, o 200 tūkstančių rublių? Tada trejų metų padidėjimas jau bus 66 200 rublių (jei skaičiuosite). Kas jau labai gerai.) O jei indėlis dar didesnis? Tai štai kas...

Išvada: kuo didesnis pradinis įnašas, tuo pelningesnė tampa palūkanų kapitalizacija. Būtent todėl indėlius su palūkanų kapitalizacija bankai teikia ilgam laikui. Tarkime, penkeri metai.

Be to, eksponentiškai mėgsta plisti visokios blogos ligos, tokios kaip gripas, tymai ir dar baisesnės ligos (tas pats SARS 2000-ųjų pradžioje arba maras viduramžiais). Taigi epidemijų mastas, taip ...) Ir viskas dėl to, kad geometrinė progresija su visas teigiamas vardiklis (q>1) - dalykas, kuris auga labai greitai! Prisiminkite bakterijų dauginimąsi: iš vienos bakterijos gaunamos dvi, iš dviejų – keturios, iš keturių – aštuonios ir taip toliau... Plintant bet kokiai infekcijai viskas yra taip pat.)

Paprasčiausi geometrinės progresijos uždaviniai.

Pradėkime, kaip visada, nuo paprastos problemos. Tik tam, kad suprastum prasmę.

1. Žinoma, kad antrasis geometrinės progresijos narys yra 6, o vardiklis -0,5. Raskite pirmą, trečią ir ketvirtą terminus.

Taigi mums duota begalinis Gerai žinoma geometrinė progresija antrasis narysši progresija:

b2 = 6

Be to, mes taip pat žinome progresijos vardiklis:

q = -0,5

Ir reikia rasti pirmas, trečias Ir ketvirtašios progresijos nariai.

Čia mes veikiame. Užrašome seką pagal uždavinio sąlygą. Tiesiogiai bendrai, kai antrasis narys yra šeši:

b1,6,b 3 , b 4 , …

Dabar pradėkime ieškoti. Pradedame, kaip visada, nuo paprasčiausio. Galite apskaičiuoti, pavyzdžiui, trečiąjį terminą b 3? Gali! Jau žinome (tiesiogiai geometrinės progresijos prasme), kad trečiasis narys (b 3) daugiau nei sekundę (b 2 ) V "q" kartą!

Taigi rašome:

b 3 =b 2 · q

Vietoj šios išraiškos pakeičiame šešis b 2 ir vietoj -0,5 q ir manome. Ir minusas, žinoma, taip pat nėra ignoruojamas ...

b 3 \u003d 6 (-0,5) \u003d -3

Kaip šitas. Trečioji kadencija pasirodė neigiama. Nenuostabu: mūsų vardiklis q- neigiamas. Ir pliusą padauginus iš minuso, tai, žinoma, bus minusas.)

Dabar mes svarstome kitą, ketvirtą progresavimo terminą:

b 4 =b 3 · q

b 4 \u003d -3 (-0,5) \u003d 1,5

Ketvirtasis narys vėl su pliusu. Penktasis terminas vėl bus su minusu, šeštas su pliusu ir t.t. Ženklai – pakaitiniai!

Taigi trečiasis ir ketvirtasis nariai buvo rasti. Rezultatas yra tokia seka:

b1; 6; -3; 1,5; …

Dabar belieka rasti pirmąjį terminą b 1 pagal gerai žinomą antrąjį. Norėdami tai padaryti, žengiame kita kryptimi, į kairę. Tai reiškia, kad šiuo atveju nereikia dauginti antrojo progresijos nario iš vardiklio, o Dalintis.

Padalijame ir gauname:

Tai viskas.) Atsakymas į problemą bus toks:

-12; 6; -3; 1,5; …

Kaip matote, sprendimo principas yra toks pat kaip ir . Mes žinome bet koks narys ir vardiklis geometrinė progresija – galime rasti bet kurį kitą terminą. Ko tik norime, tą rasime.) Skirtumas tik tas, kad sudėjimas/atimtis pakeičiamas daugyba/dalyba.

Atminkite: jei žinome bent vieną geometrinės progresijos narį ir vardiklį, visada galime rasti bet kurį kitą šios progresijos narį.

Ši užduotis, remiantis tradicija, yra iš tikrosios OGE versijos:

2.

…; 150; X; 6; 1,2; …

Taigi kaip yra? Šį kartą nėra pirmojo termino, vardiklio q, pateikiama tik skaičių seka... Jau kažkas pažįstamo, tiesa? Taip! Panaši problema jau buvo išspręsta aritmetinėje progresijoje!

Čia mes nebijome. Visi vienodi. Pasukite galvą ir prisiminkite elementarią geometrinės progresijos reikšmę. Atidžiai žiūrime į savo seką ir išsiaiškiname, kurie trijų pagrindinių geometrinės progresijos parametrai (pirmasis narys, vardiklis, nario numeris) joje paslėpti.

Narių numeriai? Narių numerių nėra, taip... Bet yra keturi paeiliui numeriai. Ką reiškia šis žodis, šiame etape nematau prasmės aiškinti.) Ar yra du kaimyniniai žinomi numeriai? Valgyk! Tai yra 6 ir 1,2. Taigi galime rasti progresijos vardiklis. Taigi paimame skaičių 1,2 ir padalijame į ankstesnį numerį.Šešiems.

Mes gauname:

Mes gauname:

x= 150 0,2 = 30

Atsakymas: x = 30 .

Kaip matote, viskas yra gana paprasta. Pagrindinis sunkumas slypi tik skaičiavimuose. Tai ypač sudėtinga, kai yra neigiami ir trupmeniniai vardikliai. Taigi tie, kurie turi problemų, pakartokite aritmetiką! Kaip dirbti su trupmenomis, kaip dirbti su neigiamais skaičiais ir taip toliau... Kitaip čia negailestingai sulėtinsi tempą.

Dabar šiek tiek pakeiskime problemą. Dabar bus įdomu! Išimkime paskutinį skaičių 1.2. Išspręskime šią problemą dabar:

3. Išrašomi keli iš eilės geometrinės progresijos nariai:

…; 150; X; 6; …

Raskite progresijos terminą, pažymėtą raide x.

Viskas tas pats, tik du kaimynai garsus progresijos narių nebeturime. Tai yra pagrindinė problema. Kadangi dydis q per du gretimus terminus jau galime nesunkiai nustatyti mes negalime. Ar turime galimybę priimti iššūkį? tikrai!

Parašykime nežinomą terminą x"Tiesiogiai geometrinės progresijos prasme! Apskritai.

Taip taip! Tiesiogiai su nežinomu vardikliu!

Viena vertus, x galime parašyti tokį santykį:

x= 150q

Kita vertus, mes turime visas teises nupiešti tą patį X per Kitas narys, per šešis! Padalinkite šešis iš vardiklio.

Kaip šitas:

x = 6/ q

Akivaizdu, kad dabar galime sulyginti abu šiuos santykius. Kadangi mes išreiškiame tas pats reikšmė (x), bet du Skirtingi keliai.

Gauname lygtį:

Viską padauginus iš q, supaprastindami, sumažindami, gauname lygtį:

q 2 \u003d 1/25

Mes išsprendžiame ir gauname:

q = ±1/5 = ±0,2

Oi! Vardiklis dvigubas! +0,2 ir -0,2. Ir kurį pasirinkti? Aklavietė?

Ramus! Taip, problema tikrai yra du sprendimai! Nieko blogo tame. Būna.) Nenustebate, kai, pavyzdžiui, išspręsdami įprastą gaunate dvi šaknis? Čia ta pati istorija.)

Dėl q = +0,2 mes gausime:

X \u003d 150 0,2 \u003d 30

Ir už q = -0,2 bus:

X = 150 (-0,2) = -30

Gauname dvigubą atsakymą: x = 30; x = -30.

Ką reiškia šis įdomus faktas? Ir kas egzistuoja dvi progresijos, atitinkanti problemos sąlygą!

Kaip šie:

…; 150; 30; 6; …

…; 150; -30; 6; …

Tinka ir vienas, ir kitas.) Kokia, jūsų nuomone, yra atsakymų išsiskirstymo priežastis? Vien dėl konkretaus progresijos nario pašalinimo (1,2), ateinančio po šešių. O žinodami tik ankstesnius (n-1) ir vėlesnius (n+1) geometrinės progresijos narius, jau negalime nieko vienareikšmiškai pasakyti apie tarp jų stovintį n-tąjį narį. Yra du variantai – pliusas ir minusas.

Bet tai nesvarbu. Paprastai geometrinės progresijos užduotyse yra papildomos informacijos, kuri suteikia nedviprasmišką atsakymą. Tarkime žodžius: "ženklų kintamoji progresija" arba "progresas su teigiamu vardikliu" ir taip toliau... Būtent šie žodžiai turėtų pasitarnauti kaip užuomina, kurį ženklą, pliusą ar minusą, reikėtų pasirinkti pateikiant galutinį atsakymą. Jei tokios informacijos nėra, tada – taip, užduotis turės du sprendimai.)

O dabar sprendžiame patys.

4. Nustatykite, ar skaičius 20 bus geometrinės progresijos narys:

4 ; 6; 9; …

5. Pateikiama kintamoji geometrinė progresija:

…; 5; x ; 45; …

Raskite raide nurodytą progresijos terminą x .

6. Raskite ketvirtąjį teigiamą geometrinės progresijos narį:

625; -250; 100; …

7. Antrasis geometrinės progresijos narys yra -360, o penktasis jos narys yra 23,04. Raskite pirmąjį šios progresijos terminą.

Atsakymai (netvarkingai): -15; 900; Ne; 2.56.

Sveikiname, jei viskas pavyko!

Kažkas netinka? Ar kažkur yra dvigubas atsakymas? Atidžiai perskaitome užduoties sąlygas!

Paskutinis galvosūkis neveikia? Nieko ten sudėtinga.) Dirbame tiesiogiai pagal geometrinės progresijos reikšmę. Na, jūs galite piešti paveikslėlį. Tai padeda.)

Kaip matote, viskas yra elementaru. Jei progresas trumpas. O jei ilgas? O gal norimo nario skaičius labai didelis? Norėčiau, pagal analogiją su aritmetine progresija, kaip nors gauti patogią formulę, kurią būtų lengva rasti bet koks bet kurios geometrinės progresijos narys pagal jo numerį. Daug daug kartų nedauginant iš q. Ir yra tokia formulė!) Išsami informacija – kitoje pamokoje.

Geometrinė progresija yra skaitinė seka, kurios pirmasis narys yra ne nulis, o kiekvienas kitas narys yra lygus ankstesniam nariui, padaugintam iš to paties nulinio skaičiaus.

Pažymima geometrinė progresija b1,b2,b3, …, bn, … .

Bet kurio geometrinės paklaidos nario santykis su ankstesniu jos nariu yra lygus tam pačiam skaičiui, ty b2/b1 = b3/b2 = b4/b3 = … = bn/b(n-1) = b(n+ 1)/bn = …. Tai tiesiogiai išplaukia iš aritmetinės progresijos apibrėžimo. Šis skaičius vadinamas geometrinės progresijos vardikliu. Dažniausiai geometrinės progresijos vardiklis žymimas raide q.

Monotoniška ir pastovi seka

Vienas iš būdų nustatyti geometrinę progresiją yra nustatyti pirmąjį jos narį b1 ir geometrinės paklaidos q vardiklį. Pavyzdžiui, b1=4, q=-2. Šios dvi sąlygos suteikia geometrinę progresiją 4, -8, 16, -32, … .

Jei q>0 (q nelygu 1), tai progresija yra monotoniška seka. Pavyzdžiui, seka, 2, 4,8,16,32, ... yra monotoniškai didėjanti seka (b1=2, q=2).

Jei geometrinėje paklaidoje vardiklis q=1, tai visi geometrinės progresijos nariai bus lygūs vienas kitam. Tokiais atvejais sakoma, kad progresas yra pastovi seka.

Geometrinės progresijos n-ojo nario formulė

Kad skaitinė seka (bn) būtų geometrinė progresija, būtina, kad kiekvienas jos narys, pradedant nuo antrojo, būtų gretimų narių geometrinis vidurkis. Tai yra, būtina įvykdyti šią lygtį
(b(n+1))^2 = bn * b(n+2), esant bet kuriam n>0, kur n priklauso natūraliųjų skaičių aibei N.

Geometrinės progresijos n-ojo nario formulė yra tokia:

bn=b1*q^(n-1),

kur n priklauso natūraliųjų skaičių aibei N.

Geometrinės progresijos pirmųjų n narių sumos formulė

Pirmųjų n geometrinės progresijos narių sumos formulė yra tokia:

Sn = (bn*q – b1)/(q-1), kur q nelygus 1.

Apsvarstykite paprastą pavyzdį:

Geometrinėje progresijoje b1=6, q=3, n=8 raskite Sn.

Norėdami rasti S8, naudojame geometrinės progresijos pirmųjų n narių sumos formulę.

S8= (6*(3^8 -1))/(3-1) = 19680 m.