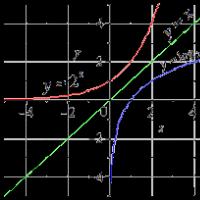
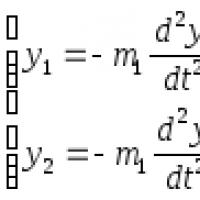İki serbestlik dereceli bir sistemin serbest titreşimleri. İki serbestlik dereceli sistemlerin serbest titreşimleri Temel koordinatlara geçiş

İki serbestlik dereceli sistemler, birkaç serbestlik dereceli sistemlerin özel bir durumudur. Ancak bu sistemler en basit sistemlerdir ve titreşim frekanslarını, genliklerini ve dinamik sapmaları belirlemek için hesaplama formüllerinin nihai biçimde elde edilmesine olanak tanır.

yEylemsizlik kuvvetleri nedeniyle ışın sapmaları:

P2 =1 (1)

(1) numaralı ifadedeki (-) işaretler eylemsizlik kuvvetleri ve birimlerinden kaynaklanmaktadır. hareketler ters yöndedir.

Kütle titreşimlerinin harmonik kanuna göre meydana geldiğine inanıyoruz:

(2)

Kütle hareketinin ivmesini bulalım:

(3)

(2) ve (3) ifadelerini denklem (1)'de değiştirerek şunu elde ederiz:

(5)

A 1 ve A 2 salınımlarının genliklerinin bilinmediğini düşünüyoruz ve denklemleri dönüştürüyoruz:

(6)

A 1 = A 2 =0 homojen denklem sisteminin çözümü bize uymuyor; sıfır olmayan bir çözüm elde etmek için sistemin (6) determinantlarını sıfıra eşitliyoruz:

(7)

Doğal salınımların  bilinmeyen dairesel frekansını dikkate alarak denklemi (8) dönüştürelim:

Denklem (9), iki serbestlik derecesine sahip sistemlerin serbest salınımlarının biharmonik denklemi olarak adlandırılır.

 2 =Z değişkenini değiştirerek şunu elde ederiz:

buradan Z 1 ve Z 2'yi belirliyoruz.

Sonuç olarak, aşağıdaki sonuçlar çıkarılabilir:

1. İki serbestlik derecesine sahip sistemlerin serbest titreşimleri  1 ve  2 olmak üzere iki frekansta meydana gelir. Düşük frekans  1 temel veya temel ton olarak adlandırılır, daha yüksek frekans  2 ise ikinci frekans veya üst ton olarak adlandırılır.

N serbestlik derecesine sahip sistemlerin serbest titreşimleri n tonlu olup, n serbest titreşimlerden oluşur.

2. m1 ve m2 kütlelerinin hareketleri aşağıdaki formüllerle ifade edilir:

yani, eğer salınımlar  1 frekansında meydana geliyorsa, o zaman herhangi bir anda kütle hareketleri aynı işaretlere sahiptir.

Salınımlar yalnızca  2 frekansında meydana gelirse, o zaman kütle hareketleri herhangi bir zamanda zıt işaretlere sahiptir.

 1 ve  2 frekanslı kütlelerin eşzamanlı salınımlarıyla, sistem esas olarak  1 frekansında salınır ve  2 frekanslı bir üst ton bu salınımlara uyar.

İki serbestlik dereceli bir sistem  frekanslı bir itici kuvvete maruz kalıyorsa, o zaman aşağıdakiler gereklidir:

  0,7  1 .

Ders 9

Sonsuz sayıda serbestlik derecesine sahip sistemlerin salınımları.

Mekanik titreşim teorisinin teknolojinin hemen hemen tüm alanlarında çok sayıda ve çok çeşitli uygulamaları vardır. Çeşitli mekanik sistemlerin amacı ve tasarım çözümü ne olursa olsun, bunların titreşimleri, elastik sistemlerin titreşim teorisinin konusu olan aynı fiziksel yasalara tabidir. Doğrusal salınım teorisi en eksiksiz şekilde geliştirilmiştir. Çeşitli serbestlik derecelerine sahip sistemlerin salınımları teorisi, 18. yüzyılda Lagrange tarafından klasik eseri Analitik Mekanik'te ortaya atıldı.

Joseph Louis Lagrange (1736 - 1813) - 19 yaşından itibaren Torino'da matematik profesörü. 1759'dan beri - Berlin Bilimler Akademisi'nin üyesi ve 1766'dan beri - başkanı; 1787'den itibaren Paris'te yaşadı. 1776'da St. Petersburg Bilimler Akademisi'nin fahri yabancı üyesi seçildi.

19. yüzyılın sonunda Rayleigh, sonsuz serbestlik derecesine sahip (yani, deforme olabilen sistemin tüm hacmi boyunca sürekli bir kütle dağılımına sahip) sistemlerin doğrusal salınım teorisinin temellerini attı. 20. yüzyılda doğrusal teorinin tamamlandığı söylenebilir (ardışık yaklaşımlar kullanılarak daha yüksek salınım frekanslarının belirlenmesini de mümkün kılan Bubnov-Galerkin yöntemi).

John William Strett (Lord Rayleigh) (1842 - 1919) - İngiliz fizikçi, salınım teorisi üzerine bir dizi eserin yazarı.

Ivan Grigorievich Bubnov (1872 - 1919) - gemi yapı mekaniğinin kurucularından biri. 1910'dan beri St. Petersburg Politeknik Enstitüsü'nde profesör - Denizcilik Akademisi'nde.

Boris Grigorievich Galerkin (1871-1945) - Leningrad Politeknik Enstitüsü'nde profesör.

Rayleigh formülü, elastik sistemlerin titreşimleri ve kararlılığı teorisinde en popüler olanıdır. Rayleigh formülünün türetilmesinin altında yatan fikir şuna iniyor.  frekansına sahip elastik bir sistemin monoharmonik (tek tonlu) serbest salınımları ile noktalarının hareketleri harmonik yasaya göre zaman içinde meydana gelir:

burada  1 (x,y,z),  2 (x,y,z),  3 (x,y,z), söz konusu salınım şeklini (genlik) belirleyen noktanın uzaysal koordinatlarının fonksiyonlarıdır.

Bu fonksiyonlar biliniyorsa, cismin kinetik ve potansiyel enerjisinin toplamının sabit olması koşulundan serbest titreşimlerin frekansı  bulunabilir. Bu durum yalnızca bir bilinmeyen miktar içeren bir denkleme yol açar.

Ancak bu işlevler önceden bilinmemektedir. Rayleigh yönteminin yol gösterici fikri, bu fonksiyonların seçimlerini sınır koşulları ve titreşimlerin beklenen şekliyle eşleştirerek belirlemektir.

Bu fikrin bir çubuğun düzlemsel bükülme titreşimleri için uygulanmasını daha ayrıntılı olarak ele alalım; titreşimlerin şekli =(x) fonksiyonu ile tanımlanır. Serbest salınımlar bağımlılıkla tanımlanır

bükülmüş bir çubuğun potansiyel enerjisi

(2)

kinetik enerji

(3)

Nerede ben- çubuğun uzunluğu, m=m(x) çubuğun dağıtılmış kütlesinin yoğunluğu;

Çubuğun kavisli ekseninin eğriliği - enine titreşimlerin hızı;

Verilen (1)

.

(4)

(5)

Zamanla bu miktarların her biri sürekli olarak değişir, ancak enerjinin korunumu yasasına göre toplamları sabit kalır, yani.

veya (4), (5) ifadelerini burada değiştirerek

(7)

Bu Rayleigh'in formülüne yol açar:

(8)

M i kütleli konsantre yükler, dağıtılmış kütlesi m olan bir çubukla ilişkilendirilirse Rayleigh formülü şu şekli alır:

(9)

Türetmenin tüm süreci, kabul edilen varsayımlar çerçevesinde (çubukların bükülmesine ilişkin teknik teorinin geçerliliği, elastik olmayan direncin yokluğu), eğer (x) titreşimlerin gerçek biçimi ise bu formülün doğru olduğunu göstermektedir. . Ancak (x) fonksiyonu önceden bilinmemektedir. Rayleigh formülünün pratik önemi, titreşim şekli (x) verildiğinde doğal frekansı  bulmak için kullanılabilmesidir. Aynı zamanda karara az çok ciddi bir yakınlık unsuru da dahil ediliyor. Bu nedenle Rayleigh formülüne bazen yaklaşık formül denir.

m=cosnt Problemin kinematik sınır koşullarını sağlayan (x)=ax 2 fonksiyonunun titreşimini alalım.

Tanımlıyoruz:

Formül (8)'e göre

Bu sonuç kesin olandan önemli ölçüde farklı

Henüz Rayleigh formülü kadar popüler olmayan Grammel formülü daha doğrudur (belki de göreceli "gençliği" nedeniyle - 1939'da önerilmiştir).

Çubuğun serbest bükülme titreşimleriyle ilgili aynı sorun üzerinde tekrar duralım.

Çubuğun serbest salınımlarının belirtilen biçimi (x) olsun. Daha sonra maksimum eylemsizlik kuvvetlerinin yoğunluğu m 2  ifadesiyle belirlenir; burada daha önce olduğu gibi m=m(x) çubuğun dağıtılmış kütlesinin yoğunluğudur;  2 doğal frekansın karesidir. Bu kuvvetler, sapmaların maksimum olduğu anda belirlenen değere ulaşır; (x) fonksiyonu tarafından belirlenir.

Maksimum atalet kuvvetlerinin neden olduğu bükülme momentleri cinsinden en yüksek potansiyel bükülme enerjisinin ifadesini yazalım:

. (10)

Burada - m 2  yükünün neden olduğu eğilme momentleri. Koşullu yük m'nin neden olduğu bükülme momentini gösterelim, yani.  Atalet kuvvetinden 2 kat daha az.

, (11)

ve ifade (10) şu şekilde yazılabilir:

. (12)

Yukarıdakiyle aynı en yüksek kinetik enerji

. (13)

(12) ve (13) numaralı ifadeleri eşitleyerek Grammel formülüne ulaşırız:

(14)

Bu formülü kullanarak hesaplama yapmak için öncelikle uygun bir (x) fonksiyonunu belirtmeniz gerekir. Daha sonra m=m(x)(x) koşullu yükü belirlenerek m koşullu yükünün neden olduğu ifadeler yazılır. Formül (14) kullanılarak sistemin doğal salınım frekansı belirlenir.

Örnek: (bir öncekini düşünün)

sen

m(x)·(x)=maks 2

TEORİK MEKANİK

UDC 531.8:621.8

D.M.Kobylyansky, V.F.Gorbunov, V.A.

BİR SERBESTLİK DERECESİNDEKİ CİSİMLERİN DÖNME VE TİTREŞİMLERİNİN UYUMLULUĞU

Şekil 1a'da gösterildiği gibi, üzerine üç ideal kısıtlamanın uygulandığı ve yalnızca vücudun tüm yönlerdeki hareketini engelleyen düz bir T gövdesini ele alalım. Bağlantılar eşkenar üçgenin köşelerinde bulunan A, B, C noktalarıdır. Merkezi üçgenin merkeziyle çakışacak ve onunla aynı hizada olacak şekilde bir koordinat sistemi seçtikten sonra (Şekil 1a), bağların koordinatlarını elde ederiz: A(0;R), B(^l/3 /2 ; -R/2), C^-Ld/e/2; -I/2), burada I üçgenin merkezinden köşelerine kadar olan mesafedir, yani A, B, C noktalarından geçen dairenin yarıçapıdır. Bu pozisyonda cisim bir serbestlik derecesine sahip olacaktır. ancak A, B, C noktalarındaki sınırının normalleri, hızların anlık merkezi olacak bir noktada kesişirse. Aksi takdirde cismin serbestlik derecesi sıfır olur ve öteleme hareketinin yanı sıra dönme hareketi de yapamaz. Bir cisim bir serbestlik derecesine sahip olduğunda, yukarıdaki normallerin kesişim noktasında anlık dönme merkezi ile dönmeye başlayabilir. Bu nokta koordinatların orijini, O noktası olsun. Eğer anlık dönme merkezi konumunu değiştirmezse, o zaman T cisminin mümkün olan tek şekli, merkezi O noktasında olan R yarıçaplı bir dairedir.

Sorun ortaya çıkıyor: Vücudun herhangi bir hareket merkezine göre dönmesine izin veren başka vücut biçimleri var mı?

vücudun vücudu bu bağlantıları koparmadan sürekli olarak A, B, C üç noktasından mı geçti? Bildiğimiz literatürde böyle bir sorun dikkate alınmamıştır ve görünüşe göre ilk kez çözülmektedir.

Bu sorunu çözmek için öncelikle ABC üçgeninin, T cismine bağlı X1O1Y1 koordinat sistemine göre hareketini katı bir cisim olarak ele alıyoruz (Şekil 1b). Daha sonra, üçgenin hareketi, üçgenin 360° tam dönüşü sırasında köşeleri sürekli olarak gövdenin sınırında kalacak şekilde meydana gelirse, gövde de gerekli hareketi sabite göre ters yönde gerçekleştirecektir. ABC üçgeni ve ilgili XOU koordinat sistemi.

ABC üçgeninin hareketini O merkezine göre bir dönme ve O merkezinin ОіХі ekseni boyunca /(g), ОіУі ekseni boyunca g(t) hareketi olarak tanımlarız. O zaman A noktasının yörüngesinin parametrik denklemi şu şekilde olacaktır: x = ryaSh +/(r); уі=г-єо,?ґ +g(t), ґє (1)

g=0'da O noktasının O1 noktasıyla çakışması gerektiğinden, /(0)= g(0)=0 koşulunun karşılanması gerekir. r = 2n/3 açısıyla döndürüldüğünde A noktasının B1 noktasıyla, B noktasının C noktasıyla ve C noktasıyla çakışmasını istiyoruz.

A1 noktasıyla. r = 4n/3 açısıyla dönerken A noktası C1 noktasına, B noktası A1 noktasına ve C noktası B1 noktasına gitmelidir. Üçgenin köşelerinin hareketi için bu gereklilikleri birleştirmek, dönme merkezini hareket ettirme fonksiyonlarının değerleri için koşullara yol açar /(0)=/(2 p/3)=/(4 p/3)= 0; g0)=g(2l/3)=g(4l/3)=0 . (2) Koşullar (2), geniş bir fonksiyon sınıfı, özellikle m'nin bir tamsayı olduğu sin(3mt/2) formundaki fonksiyonlar ve bunların genel olarak değişken katsayılı formun doğrusal kombinasyonları tarafından karşılanır:

H (g) = ^ bt (g) 8Іп(3тґ / 2)

Ayrıca,

Şekil 1. Hesaplama şeması: a) - sabit gövdenin konumu ve XOU sistemindeki bağlantıları; b) - gövdeyle ilişkili sabit sistem X1O1U1'in ve ABC üçgeniyle ilişkili hareketli sistem XOU'nun konumu

Teorik mekanik

İncir. 2. Gövde şekilleri ve dönme merkezlerinin hareket yörüngeleri

Pirinç. 3. Bir açıyla dönerken gövdenin konumu ve dönme merkezinin buna karşılık gelen hareket yörüngesi

yer değiştirme fonksiyonları, sikloidler, trokoidler, lemniskatlar gibi kapalı eğrileri tanımlayan fonksiyonlar (2) koşuluna göre uygun parametrelerle alınabilir. Bu durumda tüm olası fonksiyonlar 2n/3 periyotlu periyodik olmalıdır.

Böylece, /(^, g(t) (2) veya formlarındaki (3) değerlerine ilişkin koşullara sahip parametrik denklemler sistemi (1), T gövdesinin sınırı için istenen denklemi verir. Şekil 2, görev koşullarını karşılayan olası gövde şekillerinin örneklerini göstermektedir. Her şeklin merkezinde, O1 dönme merkezinin yörüngesi gösterilmiştir ve A, B, C nokta bağlantıları, daha iyi görselleştirilmeleri için genişletilmiştir. ifade (3) ile tanımlanan sınıftan sabit katsayılı basit fonksiyon türlerinin bile, dönmeye maruz kalan cisimlerin sınırlarını tanımlayan oldukça geniş bir eğri kümesine sahip olduğumuzu gösterin ve

Sadece bir serbestlik derecesi ile aynı anda salınımlar. Şekil 2'deki sınır eğrileri a), c), dönme merkezinin yalnızca yatay eksen boyunca hareketine karşılık gelir

Harmonik yasaya göre ОіХі, görülebileceği gibi, iki simetri eksenine sahiptir ve tamamen dışbükey, oval (Şekil 2a) olabilir veya dışbükeyliği içbükeylikle birleştirebilir (Şekil 2b). Dönme merkezinin aynı genliğe sahip dikey ve yatay harmonik yasası ile sınır eğrileri simetrilerini kaybeder (Şekil 2 c, d). Harmonik titreşimlerin frekansının bir cismin sınır eğrisinin şekli üzerindeki önemli etkisi, Şekil 2 d, f'de gösterilmektedir. Genlik ve frekansın sınırın şekli ve geometrik özellikleri üzerindeki etkisinin tam bir analizi yapılmadan. Bu çalışmadaki eğriler hakkında, Şekil 2'de sunulan örneklerin zaten istenen şekli seçerken teknik sorunları çözme yeteneğini gösterdiğini belirtmek isterim.

dönme hareketini dönme düzlemindeki salınımlarla birleştirmek için gövde.

Şimdi cismin ABC üçgeniyle ilişkili sabit koordinat sistemi XOU'ya göre hareketini göz önünde bulundurarak, yani X1O1U1 koordinat sisteminden XOU koordinat sistemine hareket ederek, cismin sınır eğrisinin aşağıdaki parametrik denklemlerini elde ederiz. verilen dönme açısı p x = cosp-

Cosp(4)

veya denklemler (1) dikkate alındığında, denklemler (4) x = cosp- formunu alır.

- [ R cos(t) + g (t) - g (p)] sin p, y = sin p +

Çünkü s.

Denklemler (5), vücudun herhangi bir noktasının yörüngesini, verilen kutuplara göre tanımlamayı mümkün kılar.

t-g.i m*4<. п-і

t-ÍLÍtWM. d-0

Pirinç. 4. Gövdelerin dönme ve titreşim uyumluluğunu sağlayan, farklı sayıda bağlantıya sahip gövde şekilleri çeşitleri

son koordinatlar R,t. Özellikle, R=0, t=0'da, Ob koordinatlarının kökenine, yani dönme merkezine denk gelen bir noktaya sahibiz; söz konusu şemada yörüngesi (5)'ten sonraki denklemlerle açıklanmaktadır. :

*0 = -f (ph) cos ph + g (ph) sin ph, y0 = - f (ph) sin ph- g (ph) cos r.

Şekil 3, φ açısıyla döndürüldüğünde vücut konumlarının bir örneğini (Şekil 2b) göstermektedir ve her şeklin merkezinde, dönme merkezinin yörüngesi gösterilmektedir.

Oi, vücudun bu açıyla dönmesine karşılık gelir. Animasyon yapmak teknik olarak zor değil

Şekil 3'te gösterilen vücut hareketinin fiziksel bir model yerine kullanılmasına rağmen, bir dergi makalesinin çerçevesi buna yalnızca elektronik versiyonda izin verebilir. Gösterilen örnek hala

Ele alınan problemin bir genellemesi, normal bir üçgenin köşelerinde bulunan noktalar biçimindeki n ideal bağlantıdan oluşan ve yalnızca vücudun öteleme hareketlerini önleyen bir sistemdir. Bu nedenle, üçgende olduğu gibi, gövde, bağlantı noktalarında normallerin gövde sınırıyla kesiştiği nokta olan dönme merkezine göre dönmeye başlayabilir. Bu durumda, OU ekseni üzerinde bulunan ve dönme merkezinden H mesafesinde bulunan A gövdesinin bir noktasının yörüngesinin denklemi (1) ile aynı forma sahip olacaktır. Bu durumda dönme merkezini (2) hareket ettirme fonksiyonlarının değerlerinin koşulları

Kobylyansky Gorbunov

Dmitri Mihayloviç Valery Fedorovich

Bölümün yüksek lisans öğrencisi. sabit ve - belge. teknoloji. bilimler, prof. departman yüz

taşıma araçları, sabit ve taşıma araçları

f(2kp/p)=g(2kp/p)=0. (7)

Koşul (7), periyodu 2n/n olan, örneğin 8m(n-m4/2) periyodik fonksiyonlara ve ayrıca bunların form (3)'ün doğrusal kombinasyonlarına ve kapalı eğrileri tanımlayan diğer fonksiyonlara karşılık gelir. Yukarıda bahsedilene benzer bir akıl yürütme, aynı denklemlere (4-6) yol açar; bu, vücudun şeklini, dönüş sırasındaki konumunu ve dönüş merkezinin yörüngesini, gövdenin dönüşle tutarlı salınımlarıyla hesaplamayı mümkün kılar. . Bu tür hesaplamaların bir örneği Şekil 4'tür; burada noktalı çizgi gövdelerin başlangıç ​​konumunu gösterir, düz çizgi gövdelerin l/3 açısı boyunca dönerken konumunu gösterir ve her şeklin merkezinde Vücudun tam dönüşü sırasında dönme merkezinin tam yörüngesi. Ve bu örnekte, bir n-gon'un merkezi olarak yalnızca O dönme merkezinin yatay hareketi dikkate alınsa da, elde edilen sonuçlar, dönme hareketini birleştiren, bir serbestlik derecesine sahip bir cismin çok çeşitli olası şekillerini gösterir. dört, beş ve altı bağlantının varlığında salınımlarla.

Bir serbestlik derecesine sahip cisimlerin dönme ve salınım hareketlerinin uyumluluğunu hesaplamak için elde edilen yöntem, üçüncü koordinat boyunca hareketlerin ve diğer koordinat düzlemlerinde dönmelerin yasak olduğu uzaysal cisimler için herhangi bir ekleme yapılmadan da kullanılabilir.

Gogolin Vyacheslav Anatolyevich

Dr. teknoloji. bilimler, prof. departman uygulamalı matematikçi ve

İki serbestlik derecesine sahip bir sistem verilmiş olsun ve bunlar genelleştirilmiş koordinatlardır. Sistemin kinetik ve potansiyel enerjisi formüller (10.2) ile verilir:

T ve P fonksiyonları kesinlikle pozitiftir ve bu nedenle:

(10.2)'yi (10.12)'ye değiştirerek, iki serbestlik derecesine sahip bir sistemin küçük salınımları için diferansiyel denklemler elde ederiz:

Sistemin, kararlı bir denge konumuna karşılık gelen sıfır çözümü A=B=0 vardır. Sıfır olmayan çözümler için (10.15)'ten aşağıdaki ilişkiyi oluşturuyoruz:

Kararlılık eşitsizlikleri nedeniyle, ikinci dereceden denklem (10.18'e göre) iki pozitif gerçek köke sahiptir. Bunları artan sırada sıralayalım:

İkinci ana titreşim için:

(10.21)

Ana titreşimler harmonik titreşimlerdir.

(10.16)'da ve yerine koyarak, ana titreşimlerde A ve B genlikleri arasındaki bağlantıları buluruz: . Faktörlere özform katsayıları (genlik dağılım katsayıları) denir. Hem olumlu hem de olumsuz olabilirler. Ana salınımdaki her iki koordinat aynı fazda olduğunda; antifazda.

Her koordinat boyunca ortaya çıkan hareket, iki ana salınımın toplamı olacaktır:

(10.22)

burada - başlangıç ​​koşullarına bağlıdır, - başlangıç ​​koşullarına bağlı değildir ve salınım sisteminin kendisinin parametreleri tarafından belirlenir. Genel durumda, frekanslar kıyaslanamaz ve bu nedenle ortaya çıkan hareket periyodik olmayacaktır.

1. Eşit m kütleli iki maddesel nokta ve her biri uzunlukta iki çubuktan oluşan çift matematiksel sarkacın doğal frekanslarını ve doğal titreşim modlarını (küçük) belirleyin.

Genel biçimde benzer bir sistem Örnek 2'de (§34) ele alınmıştır. Orada elde edilen (2) ve (3) formüllerini kullanalım.

Ne zaman şunu elde ederiz:

Salınımlar küçük olduğundan, ikinci dereceden küçük salınımlara kadar:

(3)

(1)'den (3)'ü hesaba katarak şunu not ediyoruz:

(4)

(4) ve (2)'yi karşılaştırdığımızda şunu fark ediyoruz:

Frekansların denklemini (7.52) genişleterek şunu elde ederiz:

(9.50)'den dağılım katsayılarını buluyoruz: .

İlk büyük salınım:

Fazda hareket - her anda çubuklar bir yönde döner.

İkinci ana tereddüt:

Antifazda hareket - her anda çubuklar tam olarak zıt yönlerde döner.

Titreşim modları Şekil 2'de gösterilmektedir. 50. İkinci ana titreşimde hareketsiz kalan özel bir F noktası vardır. Bu tür noktalara düğüm adı verilir. O bitiş noktası bir düğüm değildir.

2. Kütleli iki katı cisim ve katı iki yay, düzgün bir yatay düzlem üzerinde yer alan ve küçük doğrusal salınımlar gerçekleştirebilen bir sistem halinde birleştirilir.

İlk büyük salınım:

Cisimler sağa ya da sola doğru aynı fazda hareket eder. İkinci cismin salınım genliği 1,62 kat daha fazladır.

İkinci ana tereddüt:

Cisimler antifazda hareket eder: ya birbirlerine doğru, düğüme doğru ya da düğümden uzaklaşırlar. İkinci cismin salınımlarının genliği birincinin genliğinin 0,62'sidir.

Muhafazakar bir mekanik sistemin kararlı bir denge konumu etrafındaki hareket denklemlerinden

iki serbestlik derecesi durumunda:

(1)

(Sylvester'ın kriterine göre:

(1) kararlı bir denge konumuna yakın iki serbestlik derecesine sahip bir mekanik sistemin küçük serbest salınımlarının diferansiyel denklemleri sistemi. Çözümü şu şekilde aranır:

(2)

Bu çözümü küçük titreşimlerin diferansiyel denklemleri sistemine koyarsak:

(3)

A ve B'ye göre bu bir homojen cebirsel denklem sistemidir. Sistemin determinantı sıfır olduğunda önemsiz olmayan bir çözümü vardır:

(4)

Bu iki ikinci dereceden denklem, frekans denklemi olarak adlandırılır; küçük salınımların diferansiyel denklem sisteminin iki çözümüne karşılık gelen iki pozitif kökü vardır:

Böylece, her genelleştirilmiş koordinat, farklı frekanslardaki iki salınımın toplamı olarak bulunur. ana dalgalanmalar . Bu durumda sistem (3)'ten de anlaşılacağı üzere ana titreşimlerin genlikleri birbirleriyle şu şekilde ilişkilidir:

(5)

Nerede - Biçim faktörleri ana dalgalanmalar.

Sonuç olarak, serbest titreşim denklemlerinin (1) çözümü nihayet şu şekli alır:

(6)

Gelen Kutusu(6) genlikler ve başlangıç ​​aşamaları, Titreşimler başlangıç ​​koşullarından belirlenir.

İki serbestlik dereceli mekanik sistemlerin zorlanmış titreşimleri. Dinamik titreşim sönümleyici

Mekanik sistemlerde istenmeyen titreşimlerin ortadan kaldırılmasına denir titreşim koruması (sönümleme). Bu durumda kullanılan teknik cihazlara denir. titreşim sönümleyiciler (damperler).

Dinamik bir sönümleyicinin çalışma prensibi, bir koordinata karşılık gelen periyodik olarak değişen rahatsız edici genelleştirilmiş kuvvetin eyleminin, başka bir koordinata karşılık gelen potansiyel bir genelleştirilmiş kuvvetin eylemiyle nötrleştirildiği anti-rezonans olgusunun kullanımına dayanmaktadır.

Mekanik bir sistemin, korunumlu kuvvetlere ek olarak, harmonik yasaya göre zamanla değişen bozucu bir kuvvete de maruz kalmasına izin verin.

Bu durumda mekanik sistemin diferansiyel hareket denklemleri şu şekildedir:

İki çözümün toplamı olarak doğrusal diferansiyel homojen olmayan denklemler sistemine (bu durumda) genel bir çözüm arıyoruz: - homojen diferansiyel denklemler sistemine genel bir çözüm; -homojen olmayan diferansiyel denklemler sisteminin özel çözümü.

Rahatsız edici kuvvetin zamana bağlılığı dikkate alınarak, formda özel bir çözüm aranır.

Bunu diferansiyel denklemler sistemine koymak şunu verir:

Bu sistemi Cramer kuralını kullanarak çözersek şunu elde ederiz:

Frekans denkleminin sol tarafına denk gelip ortadan kaybolduğu için

rahatsız edici kuvvetin frekansı doğal frekanslardan biriyle çakıştığında

salınımlar veya A ve B katsayıları bu durumda sonsuza döner. Böylece, iki serbestlik derecesine sahip bir sistemin salınımı durumunda, iki rezonans frekansı

Zorunlu diferansiyel denklem sisteminin genel çözümü

titreşimler şu forma sahiptir:

Görülebileceği gibi, bir salınımlı sistemin parametrelerini seçerek örneğin A = 0 koşulunun yerine getirilmesi mümkündür, yani birinci genelleştirilmiş koordinata karşılık gelen zorlanmış salınımların genliği sıfır olur.

Bu olaya antirezonans denir.

Söz konusu durumda bu durum şu durumlarda meydana gelir:

Etki teorisinin temel kavramları ve hipotezleri. Etki teorisinin temel denklemi

Kısa bir süre içinde meydana gelen bir fenomen, yani. Maddi nesnelerin noktalarının hızları neredeyse anında sonlu değerlere değişir. üflemek .

Çarpma sırasında hızdaki son değişiklik çok kısa bir sürede meydana geldiğinden, çok büyük ivmelenmeler ve dolayısıyla çok büyük kuvvetler ortaya çıkar. Bu kuvvetler çok kısa bir süre boyunca etki eder, ancak bu süre içindeki itkileri sonlu niceliklerdir.

Kısa bir süre boyunca bir çarpışma sırasında ortaya çıkan, ancak aynı zamanda büyük bir değere ulaşan, dolayısıyla bu süre içindeki darbeleri sonlu değerler olan kuvvetlere denir. şok kuvvetleri .

Darbenin devam ettiği kısa süreye denir etki süresi. Çarpma sırasında darbe kuvvetlerinin darbelerine denir. şok darbeleri .

Sıradan (şoksuz) bir kuvvetin etkisi altında hareket eden m kütlesinin MT'si verilsin. Dikkate alınan MT'nin bir hızı olduğu anda - çarpışmadan önceki hız, darbe kuvveti onun üzerinde hareket etmeye başlar ve eylemi o anda durur. MT'nin kuvvetlerin etkisi altında ve çarpma süresindeki hareketini belirleyelim.

Teoremi bir noktanın momentumundaki değişime uygulayarak şunu elde ederiz:

,

Çarpmadan sonraki andaki noktanın hızı nerede?

Belirli bir integralin ortalama değerine ilişkin teoremi kullanarak şunu yazabiliriz:

,

kuvvetlerin ortalama değerleri nerede ve belirli bir süre içinde. Üstelik sonlu bir niceliktir; Çarpma sırasındaki darbe kuvveti çok büyük bir değere ulaşır (sırasıyla). Bu nedenle ürün, sonlu bir miktar olan ürüne kıyasla ihmal edilebilir olacaktır.

Potansiyel bir alanın kuvvetlerine ve zaman içinde periyodik olarak değişen kuvvetlere maruz kalan, iki serbestlik derecesine sahip bir sistemin küçük salınımlarını ele alalım. Sistemin sonuçta ortaya çıkan hareketlerine zorlanmış salınımlar denir.

Rahatsız edici genelleştirilmiş kuvvetlerin zamanla uyumlu bir yasaya göre, eşit periyotlara ve başlangıç ​​fazına sahip olarak değişmesine izin verin. O zaman söz konusu sistemin hareket denklemleri şu şekilde olacaktır:

Söz konusu durumdaki hareket denklemleri, sabit katsayılı ve sağ tarafı olan doğrusal ikinci dereceden diferansiyel denklemler sistemidir.

Ana koordinatlara git

Hareket denklemlerini incelemeyi kolaylaştırmak için sistemin ana koordinatlarına geçelim. Koordinatlar arasındaki ilişki formun önceki paragrafındaki formüllerle belirlenir:

Normal koordinatlara karşılık gelen genelleştirilmiş kuvvetleri uygun şekilde gösterelim. Genelleştirilmiş kuvvetler, sisteme etki eden kuvvetlerin temel çalışmasının ifadesindeki genelleştirilmiş koordinatların karşılık gelen değişimlerinin katsayılarını temsil ettiğinden, o zaman.

Buradan:

Böylece asal koordinatlardaki hareket denklemleri şu şekli alır:

Normal koordinatlarda iki serbestlik derecesine sahip bir sistemin zorlanmış salınım denklemleri birbirinden bağımsızdır ve ayrı ayrı entegre edilebilir.

Rahatsız edici kuvvetin kritik frekansları

Normal koordinatlardaki değişimin salınımlı doğasını belirleyen veya belirleyen denklem, diferansiyel hareket denklemleri her iki durumda da aynı olduğundan, bir noktanın düz bir çizgi boyunca zorlanmış salınımı dikkate alındığında ayrıntılı olarak incelenir. Özellikle, bozucu kuvvetin frekansı, sistemin doğal salınımlarından birinin frekansına eşitse, o zaman çözüm, faktör olarak t süresini içerecektir. Sonuç olarak, yeterince büyük bir t için normal genelleştirilmiş koordinatlardan biri keyfi olarak büyük olacaktır veya rezonans olgusunu yaşarız.