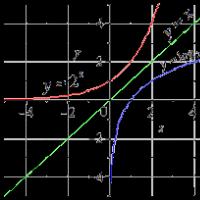
Verilen y 2x'in ters fonksiyonu. Fonksiyon türleri. Ters fonksiyon. Bir fonksiyonun tanım alanı ve değer alanı. Ters Fonksiyonu Bulma

Belirli bir f fonksiyonu ve argümanının belirli bir değeri verildiğinde, bu noktada fonksiyonun değerini hesaplamanın gerekli olduğu bir problemle zaten karşılaştık. Ancak bazen ters problemle yüzleşmeniz gerekir: bilinen bir f fonksiyonu ve onun belirli değeri y olduğunda, fonksiyonun belirli bir y değerini aldığı argümanın değerini bulmak.

Her değerini kendi tanım kümesindeki tek bir noktada alan fonksiyona tersinir fonksiyon denir. Örneğin, doğrusal bir fonksiyon şöyle olabilir: tersinir fonksiyon. Ancak ikinci dereceden fonksiyon veya sinüs fonksiyonu tersinir fonksiyonlar olmayacaktır. Çünkü bir fonksiyon aynı değeri farklı argümanlarla alabilir.

Ters fonksiyon

F'nin keyfi bir tersinir fonksiyon olduğunu varsayalım. Kendi y0 değerlerinin tanım kümesindeki her sayı, x0 tanım kümesinden yalnızca bir sayıya karşılık gelir, öyle ki f(x0) = y0.

Şimdi her x0 değerini bir y0 değeriyle ilişkilendirirsek yeni bir fonksiyon elde ederiz. Örneğin, f(x) = k * x + b doğrusal fonksiyonu için g(x) = (x - b)/k fonksiyonu bunun tersi olacaktır.

Eğer bazı işlevler G her noktada X Ters çevrilebilir fonksiyonun değer aralığı f, f(y) = x olacak şekilde bir değer alırsa, o zaman fonksiyon deriz G- f'nin ters bir fonksiyonu vardır.

Bize ters çevrilebilir bir f fonksiyonunun grafiği verilirse, o zaman ters fonksiyonun bir grafiğini oluşturmak için aşağıdaki ifadeyi kullanabiliriz: f fonksiyonunun grafiği ve onun ters fonksiyonu g, düzlüğe göre simetrik olacaktır. y = x denklemiyle belirtilen çizgi.

Eğer bir g fonksiyonu bir f fonksiyonunun tersi ise, o zaman g fonksiyonu tersinir bir fonksiyon olacaktır. Ve f fonksiyonu g fonksiyonunun tersi olacaktır. Genellikle iki fonksiyonun f ve g'nin karşılıklı olarak birbirinin tersi olduğu söylenir.

Aşağıdaki şekil f ve g fonksiyonlarının karşılıklı olarak birbirine ters grafiklerini göstermektedir.

Aşağıdaki teoremi türetelim: Eğer bir f fonksiyonu belirli bir A aralığında artarsa ​​(veya azalırsa), o zaman tersinirdir. F fonksiyonunun değer aralığında tanımlanan ters g fonksiyonu aynı zamanda artan (veya buna uygun olarak azalan) bir fonksiyondur. Bu teorem denir ters fonksiyon teoremi.

Tam anlamıyla monoton (azalan veya artan) ve x ∈ a tanım bölgesinde sürekli olan belirli bir y = f(x) fonksiyonuna sahip olduğumuzu varsayalım; B ; değer aralığı y ∈ c ; d ve c aralığında; d bu durumda a değerleri aralığına sahip x = g (y) tanımlı bir fonksiyona sahip olacağız; B. İkinci fonksiyon da sürekli ve kesinlikle monoton olacaktır. Y = f(x)'e göre bu ters bir fonksiyon olacaktır. Yani, y = f(x)'in belirli bir aralıkta azalacağı veya artacağı durumda x = g(y)'nin ters fonksiyonundan bahsedebiliriz.

Bu iki fonksiyon, f ve g, karşılıklı olarak ters olacaktır.

Ters fonksiyon kavramına neden ihtiyacımız var?

Bu ifadeler kullanılarak tam olarak yazılan y = f(x) denklemlerini çözmek için buna ihtiyacımız var.

Diyelim ki cos (x) = 1 3 denklemine bir çözüm bulmamız gerekiyor. Çözümleri tüm noktalar olacaktır: x = ± a rc c o s 1 3 + 2 π · k, k ∈ Z

Örneğin ters kosinüs ve kosinüs fonksiyonları birbirine ters olacaktır.

Verilenlerin tersi olan fonksiyonları bulmak için çeşitli problemlere bakalım.

örnek 1

Durum: y = 3 x + 2'nin ters fonksiyonu nedir?

Çözüm

Koşulda belirtilen fonksiyonun tanım alanı ve değer aralığı tüm gerçek sayılar kümesidir. Bu denklemi x üzerinden yani x'i y'ye ifade ederek çözmeye çalışalım.

x = 1 3 y - 2 3 elde ederiz. İhtiyacımız olan ters fonksiyon bu, ama burada argüman y olacak ve fonksiyon da x olacak. Daha tanıdık bir gösterim elde etmek için bunları yeniden düzenleyelim:

Cevap: y = 1 3 x - 2 3 fonksiyonu y = 3 x + 2'nin tersi olacaktır.

Her iki karşılıklı ters fonksiyon aşağıdaki gibi çizilebilir:

Her iki grafiğin de y = x'e göre simetrisini görüyoruz. Bu çizgi birinci ve üçüncü çeyreğin açıortayıdır. Sonuç, daha sonra tartışacağımız karşılıklı ters fonksiyonların özelliklerinden birinin kanıtıdır.

Belirli bir üstel fonksiyonun tersi olan logaritmik fonksiyonu bulmamız gereken bir örneği ele alalım.

Örnek 2

Durum: y = 2 x için hangi fonksiyonun tersi olacağını belirleyin.

Çözüm

Belirli bir fonksiyon için tanım alanı tamamen gerçek sayılardır. Değer aralığı 0 aralığındadır; + ∞ . Şimdi x'i y cinsinden ifade etmemiz, yani belirtilen denklemi x cinsinden çözmemiz gerekiyor. X = log 2 y'yi elde ederiz. Değişkenleri yeniden düzenleyelim ve y = log 2 x elde edelim.

Sonuç olarak tüm tanım kümesi boyunca birbirine ters olacak üstel ve logaritmik fonksiyonlar elde ettik.

Cevap: y = log 2 x .

Grafikte her iki fonksiyon da şöyle görünecek:

Karşılıklı ters fonksiyonların temel özellikleri

Bu paragrafta karşılıklı olarak ters olan y = f (x) ve x = g (y) fonksiyonlarının ana özelliklerini listeliyoruz.

Tanım 1

1. İlk özelliği daha önce zaten türetmiştik: y = f (g (y)) ve x = g (f (x)).
2. İkinci özellik birinciden gelir: y = f (x) tanım alanı, ters x = g (y) fonksiyonunun değer aralığıyla çakışacaktır ve bunun tersi de geçerlidir.
3. Ters olan fonksiyonların grafikleri y = x'e göre simetrik olacaktır.
4. Eğer y = f(x) artıyorsa x = g(y) artacaktır, eğer y = f(x) azalıyorsa x = g(y) de azalacaktır.

Fonksiyonların tanım alanı ve anlam alanı kavramlarına çok dikkat etmenizi ve asla karıştırmamanızı tavsiye ederiz. Diyelim ki karşılıklı olarak ters iki fonksiyonumuz var: y = f (x) = a x ve x = g (y) = log a y. Birinci özelliğe göre, y = f (g (y)) = a log a y. Bu eşitlik yalnızca y'nin pozitif değerleri durumunda geçerli olacaktır ve negatif değerler için logaritma tanımlanmamıştır, bu nedenle log a y = y olduğunu yazmak için acele etmeyin. Bunun yalnızca y pozitif olduğunda doğru olduğunu kontrol edip eklediğinizden emin olun.

Ancak x = f (g (x)) = log a a x = x eşitliği, x'in herhangi bir gerçek değeri için doğru olacaktır.

Özellikle trigonometrik ve ters trigonometrik fonksiyonlarla çalışmanız gerekiyorsa bu noktayı unutmayın. Yani, ark sin sin 7 π 3 ≠ 7 π 3, çünkü arksinüs aralığı π 2'dir; π 2 ve 7 π 3 buna dahil değildir. Doğru giriş şu şekilde olacaktır:

a r c günah günah 7 π 3 = a r c günah günah 2 π + π 3 = = a r c günah günah π 3 = π 3

Ancak sin a r c sin 1 3 = 1 3 doğru bir eşitliktir, yani. x ∈ - 1 için sin (a r c sin x) = x; 1 ve a r c sin (sin x) = x için x ∈ - π 2 ; π 2. Ters fonksiyonların aralığına ve kapsamına daima dikkat edin!

• Temel karşılıklı ters fonksiyonlar: kuvvet fonksiyonları

Eğer bir y = x a kuvvet fonksiyonumuz varsa, o zaman x > 0 için x = y 1 a kuvvet fonksiyonu da bunun tersi olacaktır. Harfleri değiştirip sırasıyla y = x a ve x = y 1 a elde edelim.

Grafikte şöyle görünecekler (pozitif ve negatif katsayılı durumlar):

• Temel karşılıklı ters fonksiyonlar: üstel ve logaritmik

1'e eşit olmayan pozitif bir sayı olacak a'yı alalım.

> 1 ve a olan fonksiyonların grafikleri< 1 будут выглядеть так:

• Temel karşılıklı ters fonksiyonlar: trigonometrik ve ters trigonometrik

Eğer sinüs ve arksinüsün ana dalını çizmek isteseydik, şöyle görünürdü (vurgulanan ışık alanı olarak gösterilir).

Dersin Hedefleri:

Eğitici:

• program materyaline uygun olarak yeni bir konu hakkında bilgi geliştirmek;
• bir fonksiyonun tersinirlik özelliğini incelemek ve belirli bir fonksiyonun ters fonksiyonunun nasıl bulunacağını öğretmek;

Gelişimsel:

• öz kontrol becerilerini ve anlamlı konuşmayı geliştirmek;
• ters fonksiyon kavramında uzmanlaşın ve ters fonksiyonu bulma yöntemlerini öğrenin;

Eğitimsel: İletişimsel yeterliliği geliştirmek.

Teçhizat: bilgisayar, projektör, ekran, interaktif beyaz tahta SMART Board, grup çalışması için çalışma notları (bağımsız çalışma).

Dersler sırasında.

1. Organizasyon anı.

Hedef – öğrencileri sınıfta çalışmaya hazırlamak:

Devamsızların tanımı,

Öğrencileri çalışma havasına sokmak, dikkati düzenlemek;

Dersin konusunu ve amacını belirtin.

2. Öğrencilerin temel bilgilerinin güncellenmesi.Ön anket.

Hedef - Çalışılan teorik materyalin doğruluğunu ve farkındalığını, kapsanan materyalin tekrarını oluşturmak.<Приложение 1 >

Öğrencilere yönelik interaktif beyaz tahtada bir fonksiyonun grafiği gösterilir. Öğretmen bir görev formüle eder - bir fonksiyonun grafiğini düşünün ve fonksiyonun incelenen özelliklerini listeleyin. Öğrenciler araştırma tasarımına uygun olarak bir fonksiyonun özelliklerini listelerler. Fonksiyonun grafiğinin sağında öğretmen, isimlendirilen özellikleri etkileşimli tahtaya bir işaretleyici ile yazar.

Fonksiyon özellikleri:

Çalışmanın sonunda öğretmen bugün derste bir fonksiyonun başka bir özelliği olan tersinirlik hakkında bilgi sahibi olacaklarını bildirdi. Yeni materyali anlamlı bir şekilde incelemek için öğretmen çocukları dersin sonunda öğrencilerin cevaplaması gereken ana soruları tanımaya davet eder. Sorular normal bir tahtaya yazılır ve her öğrenciye dağıtılır (dersten önce dağıtılır).

1. Hangi fonksiyona tersinir denir?
2. Herhangi bir fonksiyon tersine çevrilebilir mi?
3. Bir verinin tersi hangi fonksiyona denir?
4. Bir fonksiyonun tanım alanı ile değer kümesi ve bunun tersi nasıl ilişkilidir?
5. Bir fonksiyon analitik olarak veriliyorsa, ters fonksiyon bir formülle nasıl tanımlanabilir?
6. Bir fonksiyon grafiksel olarak verilmişse, ters fonksiyonunun grafiği nasıl çizilir?

3. Yeni materyalin açıklanması.

Hedef - program materyaline uygun olarak yeni bir konu hakkında bilgi üretmek; bir fonksiyonun tersinirlik özelliğini incelemek ve belirli bir fonksiyonun ters fonksiyonunun nasıl bulunacağını öğretmek; anlamlı konuşma geliştirin.

Öğretmen paragraftaki materyale uygun olarak materyali sunar. Etkileşimli beyaz tahtada öğretmen, tanım alanları ve değer kümeleri aynı olan ancak fonksiyonlardan biri monoton olan ve diğeri olmayan iki fonksiyonun grafiklerini karşılaştırır ve böylece öğrencilere tersinir fonksiyon kavramını tanıtır. .

Öğretmen daha sonra tersinir bir fonksiyonun tanımını formüle eder ve interaktif beyaz tahtada monoton bir fonksiyonun grafiğini kullanarak tersinir fonksiyon teoreminin bir kanıtını yapar.

Tanım 1: y=f(x), x X fonksiyonu çağrılır geri dönüşümlü değerlerinden herhangi birini X kümesinin yalnızca bir noktasında alıyorsa.

Teorem: Eğer bir y=f(x) fonksiyonu bir X kümesi üzerinde monoton ise, o zaman tersinirdir.

Kanıt:

1. Fonksiyona izin ver y=f(x) kadar artar X bırak gitsin x 1 ≠x 2- setin iki noktası X.
2. Spesifik olmak gerekirse, izin ver x 1< x 2.
   O zaman gerçeğinden yola çıkarak x 1< x 2 bunu takip ediyor f(x1) < f(x2).
3. Dolayısıyla argümanın farklı değerleri, fonksiyonun farklı değerlerine karşılık gelir; fonksiyon tersinirdir.

(Teoremin ispatı ilerledikçe öğretmen çizim üzerinde gerekli tüm açıklamaları yapmak için keçeli kalem kullanır)

Ters fonksiyonun tanımını formüle etmeden önce öğretmen öğrencilerden önerilen fonksiyonlardan hangisinin tersinir olduğunu belirlemelerini ister. İnteraktif beyaz tahta, fonksiyonların grafiklerini gösterir ve analitik olarak tanımlanmış birçok fonksiyonu yazar:

B)

G) y = 2x + 5

D) y = -x 2 + 7

Öğretmen ters fonksiyonun tanımını tanıtır.

Tanım 2: Tersine çevrilebilir fonksiyon olsun y=f(x) sette tanımlanmış X Ve E(f)=Y. Her birini eşleştirelim sen itibaren e tek anlamı bu X, hangi f(x)=y. Daha sonra üzerinde tanımlanan bir fonksiyon elde ederiz. e, A X– fonksiyon aralığı

Bu işlev belirlenmiş x=f -1 (y) ve fonksiyonun tersi denir y=f(x).

Öğrencilerden ters fonksiyonların tanım alanı ile değer kümesi arasındaki bağlantı hakkında bir sonuç çıkarmaları istenir.

Belirli bir fonksiyonun tersinin nasıl bulunacağı sorusunu düşünmek için öğretmen iki öğrenciyi yanına çekti. Bir gün önce çocuklara, belirli bir fonksiyonun ters fonksiyonunu bulmanın analitik ve grafiksel yöntemlerini bağımsız olarak analiz etmeleri için öğretmenden bir görev verildi. Öğretmen öğrencilerin derse hazırlanmasında danışmanlık yaptı.

İlk öğrenciden mesaj.

Not: fonksiyonun monotonluğu yeterli Ters fonksiyonun varlığı için koşul. Ama o değil gerekli bir koşul.

Öğrenci, bir fonksiyonun monoton değil de tersinir olduğu, bir fonksiyonun monoton olmadığı ve tersinir olmadığı, monoton ve tersinir olduğu çeşitli durumlara örnekler verdi.

Öğrenci daha sonra öğrencilere analitik olarak verilen ters fonksiyonu bulma yöntemini tanıtır.

Algoritma bulma

1. Fonksiyonun monoton olduğundan emin olun.
2. X değişkenini y cinsinden ifade edin.
3. Değişkenleri yeniden adlandırın. x=f -1 (y) yerine y=f -1 (x) yazın

Daha sonra verilen bir fonksiyonun ters fonksiyonunu bulmak için iki örneği çözer.

Örnek 1: y=5x-3 fonksiyonu için ters bir fonksiyonun olduğunu gösterin ve analitik ifadesini bulun.

Çözüm. Doğrusal fonksiyon y=5x-3 R üzerinde tanımlanır, R üzerinde artar ve değer aralığı R'dir. Bu, ters fonksiyonun R üzerinde mevcut olduğu anlamına gelir. Analitik ifadesini bulmak için y=5x- denklemini çözün. x için 3; Bu gerekli ters fonksiyondur. R üzerinde tanımlıdır ve artmaktadır.

Örnek 2: y=x 2, x≤0 fonksiyonu için ters bir fonksiyonun olduğunu gösterin ve analitik ifadesini bulun.

Fonksiyon süreklidir, tanım alanında monotondur, dolayısıyla tersinirdir. Fonksiyonun tanım alanlarını ve değer kümelerini analiz ettikten sonra, ters fonksiyonun analitik ifadesi hakkında karşılık gelen bir sonuca varılır.

İkinci öğrenci konuyla ilgili bir sunum yapar. grafik Ters fonksiyonu bulma yöntemi. Açıklama sırasında öğrenci etkileşimli tahtanın olanaklarından yararlanır.

y=f -1 (x) fonksiyonunun y=f(x) fonksiyonunun tersi olan bir grafiğini elde etmek için, y=f(x) fonksiyonunun grafiğini düz çizgiye göre simetrik olarak dönüştürmek gerekir. y=x.

İnteraktif beyaz tahtada anlatım sırasında aşağıdaki görev gerçekleştirilir:

Aynı koordinat sisteminde bir fonksiyonun grafiğini ve ters fonksiyonunun grafiğini oluşturun. Ters fonksiyon için analitik bir ifade yazın.

4. Yeni malzemenin birincil konsolidasyonu.

Hedef - Çalışılan materyalin anlaşılmasının doğruluğunu ve farkındalığını oluşturmak, materyalin temel anlayışındaki boşlukları tespit etmek ve bunları düzeltmek.

Öğrenciler çiftlere ayrılır. Onlara işi çiftler halinde yapacakları görev sayfaları verilir. İşin tamamlanma süresi sınırlıdır (5-7 dakika). Bir çift öğrenci bilgisayarda çalışıyor, bu süre zarfında projektör kapanıyor ve geri kalan çocuklar öğrencilerin bilgisayarda nasıl çalıştıklarını göremiyor.

Süre sonunda (öğrencilerin çoğunluğunun çalışmayı tamamladığı varsayılır) öğrencilerin çalışmaları interaktif tahtada gösterilir (projektör tekrar açılır), burada görevin yapılıp yapılmadığı kontrol sırasında belirlenir. çiftler halinde doğru bir şekilde tamamlandı. Öğretmen gerekirse düzeltici ve açıklayıcı çalışmalar yapar.

Çiftler halinde bağımsız çalışma<Ek 2 >

5. Ders özeti. Ders öncesi sorulan sorulara gelince. Ders notlarının ilanı.

Ödev §10. 10.6(a,c) 10.8-10.9(b) 10.12 (b)

Cebir ve analizin başlangıcı. 10. Sınıf Genel eğitim kurumları için 2 bölüm halinde (profil düzeyi) / A.G. Mordkovich, L.O. Denishcheva, T.A. Koreshkova, vb.; ed. A.G. Mordkovich, M: Mnemosyne, 2007

Ters fonksiyonun tanımı ve özellikleri: Direkt ve ters fonksiyonların karşılıklı monotonluğuna ilişkin lemma; doğrudan ve ters fonksiyonların grafiklerinin simetrisi; Bir parça, aralık ve yarım aralıkta kesinlikle monoton olan bir fonksiyon için ters fonksiyonun varlığı ve sürekliliğine ilişkin teoremler. Ters fonksiyon örnekleri. Bir problemin çözümüne bir örnek. Özelliklerin kanıtları ve teoremler.

İçerik

Ayrıca bakınız: Fonksiyonun tanımı, üst ve alt sınırlar, monotonik fonksiyon.

Tanım ve özellikler

Ters fonksiyonun tanımı
Bir fonksiyonun X tanım alanına ve Y değerlerine sahip olmasına izin verin. Ve şu özelliğe sahip olmasına izin verin:
hepsi için .
O zaman Y kümesindeki herhangi bir öğe için X kümesinin yalnızca bir öğesi ilişkilendirilebilir. Bu yazışma, adı verilen bir işlevi tanımlar. ters fonksiyonİle . Ters fonksiyon şu şekilde gösterilir:
.

Tanımdan şu sonuç çıkıyor
;
hepsi için ;
hepsi için .

Doğrudan ve ters fonksiyonların grafiklerinin simetrisinin özelliği
Doğrudan ve ters fonksiyonların grafikleri düz çizgiye göre simetriktir.

Bir aralıkta ters fonksiyonun varlığı ve sürekliliğine ilişkin teorem
Fonksiyonun segment üzerinde sürekli ve kesinlikle artan (azalan) olmasına izin verin. Daha sonra ters fonksiyon tanımlanır ve kesinlikle artan (azalan) segment üzerinde süreklidir.

Artan bir fonksiyon için. Azaltmak için - .

Bir aralıkta ters fonksiyonun varlığı ve sürekliliğine ilişkin teorem
Fonksiyonun açık sonlu veya sonsuz bir aralıkta sürekli ve kesinlikle artan (azalan) olmasına izin verin. Daha sonra ters fonksiyon tanımlanır ve aralıkta süreklidir, bu kesinlikle artar (azalır).

Artan bir fonksiyon için.
Azaltmak için: .

Benzer şekilde ters fonksiyonun yarı aralıkta varlığı ve sürekliliğine ilişkin teoremi de formüle edebiliriz.

Fonksiyon sürekli ise ve yarı aralıkta veya kesinlikle artarsa ​​(azalırsa), o zaman yarı aralıkta veya ters fonksiyon tanımlanır, bu da kesinlikle artar (azalır). Burada .

Kesinlikle artıyorsa, aralıklar ve aralıklara karşılık gelir ve . Kesinlikle azalıyorsa, aralıklar ve aralıklara karşılık gelir ve .
Bu teorem, bir aralıkta ters fonksiyonun varlığı ve sürekliliğine ilişkin teoremle aynı şekilde kanıtlanır.

Ters fonksiyon örnekleri

arksinüs

Grafikler y = günah x ve ters fonksiyon y = ark sin x.

Trigonometrik fonksiyonu düşünün sinüs: . Argümanın tüm değerleri için tanımlanmış ve süreklidir ancak monoton değildir. Ancak tanımın kapsamını daraltırsanız monoton alanları tespit edebilirsiniz. Yani segmentte fonksiyon tanımlanır, süreklidir, kesin olarak artar ve değerleri alır. -1 önce +1 . Bu nedenle üzerinde arksinüs adı verilen ters bir fonksiyon vardır. Arsinüsün bir alanı ve bir dizi değeri vardır.

Logaritma

Grafikler y = 2 kere ve ters fonksiyon y = günlük 2 x.

Üstel fonksiyon, argümanın tüm değerleri için tanımlanmış, sürekli ve kesinlikle artan bir fonksiyondur. Değer kümesi açık bir aralıktır. Ters fonksiyon, iki tabanının logaritmasıdır. Bir tanım alanına ve bir dizi anlamlara sahiptir.

Kare kök

Grafikler y = x 2 ve ters fonksiyon.

Güç fonksiyonu herkes için tanımlanmış ve süreklidir. Değerlerinin kümesi yarım aralıktır. Ancak argümanın tüm değerleri için monoton değildir. Ancak yarı aralıkta süreklidir ve kesinlikle monoton bir şekilde artar. Dolayısıyla kümeyi tanım kümesi olarak alırsak, karekök adı verilen ters bir fonksiyon vardır. Ters fonksiyonun bir etki alanı ve bir dizi değeri vardır.

Örnek. N dereceli bir kökün varlığının ve benzersizliğinin kanıtı

n'nin bir doğal sayı olduğu denklemin, negatif olmayan gerçek bir sayı olduğunu, gerçek sayılar kümesi üzerinde tek bir çözüme sahip olduğunu kanıtlayın. Bu çözüme a'nın n kökü denir. Yani, negatif olmayan herhangi bir sayının n dereceli benzersiz bir kökü olduğunu göstermeniz gerekir.

x değişkeninin bir fonksiyonunu düşünün:
(P1) .

Sürekli olduğunu kanıtlayalım.
Süreklilik tanımını kullanarak şunu gösteriyoruz:
.
Newton'un binom formülünü uyguluyoruz:
(P2)
.
Fonksiyon limitlerinin aritmetik özelliklerini uygulayalım. olduğundan, yalnızca ilk terim sıfırdan farklıdır:
.
Süreklilik kanıtlanmıştır.

(A1) fonksiyonunun kesinlikle olarak arttığını kanıtlayalım.
Eşitsizliklerle birbirine bağlanan rastgele sayıları alalım:
, , .
Bunu göstermemiz gerekiyor. Değişkenleri tanıtalım. Daha sonra . O zamandan beri (A2)'den açıktır ki . Veya
.
Kesin artış kanıtlanmıştır.

Fonksiyonun değer kümesini bulalım.
Noktada , .
Limitini bulalım.
Bunu yapmak için Bernoulli eşitsizliğini uyguluyoruz. Sahip olduğumuzda:
.
O zamandan beri ve .
Eşitsizlik özelliğini sonsuz büyük fonksiyonlara uyguladığımızda şunu buluruz:
Böylece, , .

Ters fonksiyon teoremine göre ters fonksiyon tanımlıdır ve bir aralıkta süreklidir. Yani herkes için denklemi karşılayan benzersiz bir tane vardır. elimizde olduğundan, bu, herhangi biri için denklemin, x sayısının n derecesinin kökü olarak adlandırılan benzersiz bir çözümü olduğu anlamına gelir:
.

Özelliklerin ve teoremlerin kanıtları

Doğrudan ve ters fonksiyonların karşılıklı monotonluğuna ilişkin lemmanın kanıtı

Bir fonksiyonun X tanım alanına ve Y değerlerine sahip olmasına izin verin. Ters fonksiyona sahip olduğunu kanıtlayalım. dayanarak bunu kanıtlamamız gerekiyor
hepsi için .

Tam tersini varsayalım. Sayılar olsun, öyle olsun. Öyle olsun.
Aksi takdirde, gösterimi şu şekilde değiştirelim. O halde f'nin katı monotonluğu nedeniyle eşitsizliklerden birinin sağlanması gerekir:
f kesinlikle artıyorsa;
f kesinlikle azalıyorsa.

Yani . Bir çelişki ortaya çıktı. Bu nedenle ters fonksiyonu vardır.
Fonksiyon kesinlikle artan olsun. Ters fonksiyonun da tam olarak arttığını kanıtlayalım. Aşağıdaki gösterimi tanıtalım:

. Yani, eğer , o zaman olduğunu kanıtlamamız gerekiyor.

Tam tersini varsayalım. Olsun ama.

Eğer öyleyse. Bu durum ortadan kalkar.

İzin vermek . Daha sonra, , veya fonksiyonunun kesin artışı nedeniyle. Bir çelişki ortaya çıktı. Bu nedenle yalnızca şans mümkündür.

Lemmanın tam olarak artan bir fonksiyon olduğu kanıtlanmıştır. Bu lemma tam olarak azalan bir fonksiyon için benzer şekilde kanıtlanabilir.

Doğrudan ve ters fonksiyonların grafiklerinin simetrisi ile ilgili özelliğin kanıtı
(2.1) .
Doğrudan bir fonksiyonun grafiğinde rastgele bir nokta olsun:
.
Düz bir çizgiye göre A noktasına simetrik bir noktanın ters fonksiyonun grafiğine ait olduğunu gösterelim:
(2.2) .
Ters fonksiyonun tanımından şu sonuç çıkar:

Bu nedenle (2.2)’yi göstermemiz gerekiyor. Ters fonksiyonun grafiği y = f-1(x) y = f doğrudan fonksiyonunun grafiğine simetriktir(X)

y = x düz çizgisine göre.
, .

A ve S noktalarından dik açıları koordinat eksenine indiriyoruz. Daha sonra

A noktasından doğruya dik bir çizgi çiziyoruz. Doğruların C noktasında kesişmesine izin verin. Düz bir çizgi üzerinde bir S noktası oluşturuyoruz, öyle ki. O halde S noktası, düz çizgiye göre A noktasına simetrik olacaktır.
.

Üçgenleri düşünün ve . Eşit uzunlukta iki kenarları vardır: ve ve aralarında eşit açılar vardır: . Bu nedenle uyumludurlar. Daha sonra
.
Bir üçgen düşünün. O zamandan beri
.
Aynı şey üçgen için de geçerlidir:
.

Daha sonra
;
.

Şimdi buluyoruz ve:
(2.2)
Yani, denklem (2.2):
(2.1) .

sağlanır, çünkü , ve (2.1) sağlanır:
Bir fonksiyonun grafiğindeki düz çizgiye göre simetrik olarak yansıtılan tüm noktalar, ters fonksiyonun grafiğine aittir.
Daha sonra yerleri değiştirebiliriz. Sonuç olarak bunu anlıyoruz
Bir fonksiyonun grafiğinin düz bir çizgiye göre simetrik olarak yansıtılan tüm noktaları fonksiyonun grafiğine aittir.
Bundan, fonksiyonların grafiklerinin düz çizgiye göre simetrik olduğu sonucu çıkar.

Özelliği kanıtlanmıştır.

Bir aralıkta ters fonksiyonun varlığı ve sürekliliğine ilişkin teoremin kanıtı

Fonksiyonun tanım alanını - segmenti - gösterelim.

1. Fonksiyon değerleri kümesinin segment olduğunu gösterelim:
,
Nerede .

Aslında fonksiyon segment üzerinde sürekli olduğundan Weierstrass teoremine göre minimum ve maksimuma ulaşır. Daha sonra Bolzano-Cauchy teoremine göre fonksiyon segmentteki tüm değerleri alır. Yani, var olan herkes için, bunun için. Bir minimum ve bir maksimum olduğundan, işlev kümeden yalnızca segmentin değerlerini alır.

2. Fonksiyon kesinlikle monoton olduğundan, yukarıdakilere göre ters bir fonksiyon vardır ve bu da kesinlikle monotondur (artırırsa artar; azalırsa azalır). Ters fonksiyonun alanı kümedir ve değerler kümesi kümedir.

3. Şimdi ters fonksiyonun sürekli olduğunu kanıtlıyoruz.

3.1. Parçanın keyfi bir iç noktası olsun: . Bu noktada ters fonksiyonun sürekli olduğunu kanıtlayalım.

Noktanın buna karşılık gelmesine izin verin. Ters fonksiyon kesinlikle monoton olduğundan, yani parçanın iç noktası olduğundan:
.
Sürekliliğin tanımına göre, herhangi biri için öyle bir fonksiyonun olduğunu kanıtlamamız gerekir:
(3.1) hepsi için .

İstediğimiz kadar küçük alabileceğimizi unutmayın. Aslında, eşitsizliklerin (3.1) yeterince küçük değerler için karşılandığı bir fonksiyon bulursak, o zaman eşitsizlikleri (3.1) koyarsak, herhangi bir büyük değer için otomatik olarak karşılanacaktır.

Noktaları ve noktaları segmente ait olacak kadar küçük alalım:
.
Gösterimi tanıtalım ve düzenleyelim:



.

İlk eşitsizliği (3.1) dönüştürelim:
(3.1) hepsi için .
;
;
;
(3.2) .
Kesinlikle monoton olduğundan şu sonuca varılır:
(3.3.1) artarsa;
(3.3.2) eğer azalırsa.
Ters fonksiyon da kesinlikle monoton olduğundan, eşitsizlikler (3.3) eşitsizlikleri (3.2) ima eder.

Herhangi bir ε için > 0 δ var, yani |f -1 (y) - f -1 (y 0) |< ε hepsi için |y - y 0 | < δ .

Eşitsizlikler (3.3), uçları noktadan mesafelerde uzakta olan açık bir aralığı tanımlar. Bu uzaklıkların en küçüğü olsun:
.
, , 'nin katı monotonluğu nedeniyle. Bu yüzden . O zaman aralık eşitsizlikler (3.3) tarafından tanımlanan aralıkta yer alacaktır. Ve ona ait tüm değerler için eşitsizlikler (3.2) sağlanacaktır.

Yeterince küçük olması için şunu bulduk:
.
Şimdi gösterimi değiştirelim.
Yeterince küçük için böyle bir şey var, yani
.
Bu, ters fonksiyonun iç noktalarda sürekli olduğu anlamına gelir.

3.2. Şimdi tanım alanının uçlarını düşünün. Burada tüm mantık aynı kalıyor. Bu noktaların tek taraflı komşuluklarını dikkate almanız yeterli. Nokta yerine veya, nokta yerine - veya olacaktır.

Yani artan bir fonksiyon için .
.
Ters fonksiyon bu noktada süreklidir, çünkü yeterince küçük herhangi bir tane için vardır, böylece
.

Azalan bir fonksiyon için, .
Ters fonksiyon bu noktada süreklidir, çünkü yeterince küçük herhangi bir tane için vardır, böylece
.
Ters fonksiyon bu noktada süreklidir, çünkü yeterince küçük herhangi bir tane için vardır, böylece
.

Teorem kanıtlandı.

Bir aralıkta ters fonksiyonun varlığı ve sürekliliğine ilişkin teoremin kanıtı

Fonksiyonun tanım alanını - açık bir aralık - gösterelim. değerlerinin kümesi olsun. Yukarıdakilere göre, bir tanım alanına, bir değerler kümesine sahip ve kesinlikle monoton olan (artırırsa artar, azalırsa azalır) ters bir fonksiyon vardır. Bunu kanıtlamak bize kalıyor
1) küme açık bir aralıktır ve bu
2) Ters fonksiyon üzerinde süreklidir.
Burada .

1. Fonksiyon değerleri kümesinin açık bir aralık olduğunu gösterelim:
.

Elemanları karşılaştırma işlemi olan herhangi bir boş olmayan küme gibi, fonksiyon değerleri kümesinin de alt ve üst sınırları vardır:
.
Burada ve sonlu sayılar veya semboller olabilir ve .

1.1. ve noktalarının fonksiyon değerleri kümesine ait olmadığını gösterelim. Yani bir değerler kümesi segment olamaz.

Eğer veya öyle ise sonsuzluğa işaret: veya , o zaman böyle bir nokta kümenin bir elemanı değildir. Bu nedenle birden fazla değere ait olamaz.

(veya) sonlu bir sayı olsun. Tam tersini varsayalım. (veya) noktasının fonksiyon değerleri kümesine ait olmasına izin verin. Yani, (veya) böyle bir şey var. Puanları alalım ve eşitsizlikleri giderelim:
.
Fonksiyon kesinlikle monoton olduğundan, o zaman
f artarsa;
f azalıyorsa.
Yani fonksiyon değerinin küçük (büyük) olduğu bir nokta bulduk. Ancak bu, alt (üst) sınırın tanımıyla çelişmektedir; buna göre
hepsi için .
Bu nedenle noktalar fonksiyon değerleri kümesine ait olamaz.

1.2. Şimdi değerler kümesinin bir aralık olduğunu, aralıkların ve noktaların birleşimi olmadığını göstereceğiz. Yani, herhangi bir nokta için , bunun için .

Infimum ve supremum tanımlarına göre, noktaların herhangi bir komşuluğu ve kümesinin en az bir elemanını içerir. Aralığa ait rastgele bir sayı olsun: . O zaman bir mahalle için var, bunun için
.
Bir mahalle için , bunun için
.

O zamandan beri ve , o zaman . Daha sonra
(4.1.1) artarsa;
(4.1.2) eğer azalırsa.
Eşitsizliklerin (4.1) çelişkiyle kanıtlanması kolaydır. Ancak sette, artarsa ​​kesinlikle artan, azalırsa kesinlikle azalan ters bir fonksiyon olduğunu kullanabilirsiniz. Daha sonra hemen eşitsizlikleri (4.1) elde ederiz.

Yani artarsa;
eğer azalırsa.
Segmentin uçlarında fonksiyon ve değerlerini alır. Çünkü Bolzano-Cauchy teoremine göre bunun bir anlamı var.

O zamandan beri, herhangi biri için var olduğunu göstermiş olduk. Bu, fonksiyonun değer kümesinin açık bir aralık olduğu anlamına gelir.

2. Şimdi ters fonksiyonun aralıktaki herhangi bir noktada sürekli olduğunu göstereceğiz: . Bunu yapmak için segmente başvurun. Çünkü ters fonksiyon nokta dahil doğru parçası üzerinde süreklidir.

Teorem kanıtlandı.

Referanslar:
O.I. Besov. Matematiksel analiz üzerine dersler. Bölüm 1. Moskova, 2004.
SANTİMETRE. Nikolsky. Matematiksel analiz dersi. Cilt 1. Moskova, 1983.

Ayrıca bakınız:

$X$ ve $Y$ kümeleri reel sayılar kümesine dahil edilsin. Tersinir fonksiyon kavramını tanıtalım.

Tanım 1

Bir $X$ kümesini bir $Y$ kümesine eşleyen $f:X\to Y$ fonksiyonuna, herhangi bir $x_1,x_2\in X$ öğesi için, bunun $x_1\ne x_2$ takip etmesinden dolayı tersinir denir. bu $f(x_1 )\ne f(x_2)$.

Artık ters fonksiyon kavramını tanıtabiliriz.

Tanım 2

$f:X\to Y$ fonksiyonunun, $X$ kümesini $Y$ kümesine eşlemesinin tersinir olmasına izin verin. Daha sonra $f^(-1):Y\to X$ işlevi, $Y$ kümesini $f^(-1)\left(y\right)=x$ koşuluyla tanımlanan $X$ kümesine eşler: $f( x)$'ın tersi denir.

Teoremi formüle edelim:

Teorem 1

$y=f(x)$ fonksiyonunun monoton olarak artan (azalan) ve belirli bir $X$ aralığında sürekli olarak tanımlandığını varsayalım. Daha sonra bu fonksiyonun değerlerinin karşılık gelen $Y$ aralığında, aynı zamanda monoton olarak artan (azalan) ve $Y$ aralığında sürekli olan ters bir fonksiyona sahiptir.

Şimdi doğrudan karşılıklı ters fonksiyonlar kavramını tanıtalım.

Tanım 3

Tanım 2 çerçevesinde $f(x)$ ve $f^(-1)\left(y\right)$ fonksiyonlarına karşılıklı ters fonksiyonlar adı verilir.

Karşılıklı ters fonksiyonların özellikleri

$y=f(x)$ ve $x=g(y)$ fonksiyonlarının karşılıklı olarak tersi olsun, o zaman

$y=f(g\left(y\right))$ ve $x=g(f(x))$

$y=f(x)$ fonksiyonunun tanım alanı, $\ x=g(y)$ fonksiyonunun değer alanına eşittir. Ve $x=g(y)$ fonksiyonunun tanım alanı, $\ y=f(x)$ fonksiyonunun değer alanına eşittir.

$y=f(x)$ ve $x=g(y)$ fonksiyonlarının grafikleri $y=x$ düz çizgisine göre simetriktir.

Fonksiyonlardan biri artarsa ​​(azalırsa), diğer fonksiyon artar (azalır).

Ters Fonksiyonu Bulma

$y=f(x)$ denklemi $x$ değişkenine göre çözülür.

Elde edilen köklerden $X$ aralığına ait olanlar bulunur.

Bulunan $x$, $y$ sayısıyla eşleştirilir.

örnek 1

$y=x^2$ fonksiyonunun $X=[-1,0]$ aralığında ters fonksiyonunu bulun

Bu fonksiyon $X$ aralığında azalan ve sürekli olduğundan, o zaman $Y=$ aralığında da azalan ve süreklidir (Teorem 1).

$x$'ı hesaplayalım:

\ \

Uygun $x$'ı seçin:

Cevap: ters fonksiyon $y=-\sqrt(x)$.

Ters fonksiyonları bulma problemleri

Bu bölümde bazı temel fonksiyonlar için ters fonksiyonları ele alacağız. Sorunları yukarıda verilen şemaya göre çözeceğiz.

Örnek 2

$y=x+4$ fonksiyonu için ters fonksiyonu bulun

$y=x+4$ denkleminden $x$'ı bulalım:

Örnek 3

$y=x^3$ fonksiyonu için ters fonksiyonu bulun

Çözüm.

Fonksiyon tüm tanım kümesi boyunca artan ve sürekli olduğundan, Teorem 1'e göre üzerinde ters sürekli ve artan bir fonksiyon bulunur.

$y=x^3$ denkleminden $x$'ı bulalım:

$x$'ın uygun değerlerini bulma

Değer bizim durumumuza uygundur (çünkü tanım alanı tüm sayılardır)

Değişkenleri yeniden tanımlayalım, ters fonksiyonun şu şekilde olduğunu elde edelim:

Örnek 4

$$ aralığında $y=cosx$ fonksiyonunun ters fonksiyonunu bulun

Çözüm.

$X=\left$ kümesinde $y=cosx$ fonksiyonunu düşünün. $X$ kümesinde süreklidir ve azalmaktadır ve $X=\left$ kümesini $Y=[-1,1]$ kümesine eşler, dolayısıyla ters sürekli monoton fonksiyonun varlığına ilişkin teoreme göre, $y=cosx$ fonksiyonu $ Y$ kümesinde bir ters fonksiyon vardır, bu da $Y=[-1,1]$ kümesinde sürekli ve artandır ve $[-1,1]$ kümesini eşler $\left$ kümesine.

$y=cosx$ denkleminden $x$'yi bulalım:

$x$'ın uygun değerlerini bulma

Değişkenleri yeniden tanımlayalım, ters fonksiyonun şu şekilde olduğunu elde edelim:

Örnek 5

$y=tgx$ fonksiyonunun $\left(-\frac(\pi )(2),\frac(\pi )(2)\right)$ aralığında ters fonksiyonunu bulun.

Çözüm.

$X=\left(-\frac(\pi )(2),\frac(\pi )(2)\right)$ kümesindeki $y=tgx$ fonksiyonunu düşünün. $X$ kümesinde süreklidir ve artmaktadır ve $X=\left(-\frac(\pi )(2),\frac(\pi )(2)\right)$ kümesini $Y kümesine eşler =R$, bu nedenle, ters sürekli monoton fonksiyonun varlığına ilişkin teoreme göre, $Y$ kümesindeki $y=tgx$ işlevi, $Y$ kümesinde de sürekli ve artan bir ters fonksiyona sahiptir. $ ve $R$ kümesini $\left(- \frac(\pi )(2),\frac(\pi )(2)\right)$ kümesine eşler

$y=tgx$ denkleminden $x$'yi bulalım:

$x$'ın uygun değerlerini bulma

Değişkenleri yeniden tanımlayalım, ters fonksiyonun şu şekilde olduğunu elde edelim: