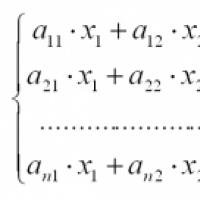Gauss yöntemi açıklamasını kullanarak bir matris çözme. Gauss yöntemi. Gauss yöntemini kullanarak çamuru çözme örnekleri

Bugün doğrusal cebirsel denklem sistemlerini çözmek için Gauss yöntemini inceliyoruz. Cramer yöntemini kullanarak aynı SLAE'leri çözmeye ayrılmış önceki makalede bu sistemlerin ne olduğunu okuyabilirsiniz. Gauss yöntemi herhangi bir özel bilgi gerektirmez, yalnızca dikkat ve tutarlılığa ihtiyacınız vardır. Matematiksel açıdan okul eğitiminin bunu uygulamak için yeterli olmasına rağmen, öğrenciler genellikle bu yönteme hakim olmakta zorlanırlar. Bu yazıda bunları hiçliğe indirmeye çalışacağız!

Gauss yöntemi

M Gauss yöntemi– SLAE'leri çözmek için en evrensel yöntem (çok büyük sistemler hariç). Daha önce tartışılanlardan farklı olarak Cramer'in yöntemi sadece tek çözümü olan sistemler için değil aynı zamanda sonsuz sayıda çözümü olan sistemler için de uygundur. Burada üç olası seçenek var.

1. Sistemin benzersiz bir çözümü vardır (sistemin ana matrisinin determinantı sıfıra eşit değildir);
2. Sistemin sonsuz sayıda çözümü vardır;
3. Çözüm yok, sistem uyumsuz.

Yani bir sistemimiz var (bir çözümü olsun) ve onu Gauss yöntemini kullanarak çözeceğiz. Nasıl çalışır?

Gauss yöntemi ileri ve ters olmak üzere iki aşamadan oluşur.

Gauss yönteminin doğrudan vuruşu

Öncelikle sistemin genişletilmiş matrisini yazalım. Bunu yapmak için ana matrise serbest üyelerden oluşan bir sütun ekleyin.

Gauss yönteminin tüm özü, bu matrisi temel dönüşümler yoluyla kademeli (veya aynı zamanda üçgen şeklinde) bir forma getirmektir. Bu formda, matrisin ana köşegeninin altında (veya üstünde) yalnızca sıfırlar bulunmalıdır.

Ne yapabilirsin:

1. Matrisin satırlarını yeniden düzenleyebilirsiniz;
2. Bir matriste eşit (veya orantılı) satırlar varsa, bunlardan biri hariç tümünü kaldırabilirsiniz;
3. Bir dizeyi herhangi bir sayıyla (sıfır hariç) çarpabilir veya bölebilirsiniz;
4. Boş satırlar kaldırıldı;
5. Bir dizeye sıfırdan farklı bir sayıyla çarpılan bir dize ekleyebilirsiniz.

Ters Gauss Yöntemi

Sistemi bu şekilde dönüştürdükten sonra bilinmeyen bir Xn bilinir hale gelir ve geri kalan tüm bilinmeyenleri, zaten bilinen x'leri sistemin denklemlerinde birinciye kadar değiştirerek ters sırada bulabilirsiniz.

İnternet her zaman elinizin altında olduğunda, Gauss yöntemini kullanarak bir denklem sistemini çözebilirsiniz. çevrimiçi. Katsayıları çevrimiçi hesap makinesine girmeniz yeterlidir. Ancak kabul etmelisiniz ki, örneğin bir bilgisayar programı tarafından değil, kendi beyniniz tarafından çözüldüğünü fark etmek çok daha keyifli.

Gauss yöntemini kullanarak bir denklem sistemini çözme örneği

Ve şimdi - her şeyin net ve anlaşılır hale gelmesi için bir örnek. Bir doğrusal denklem sistemi verilse, bunu Gauss yöntemini kullanarak çözmeniz gerekir:

Öncelikle genişletilmiş matrisi yazalım:

Şimdi dönüşümleri yapalım. Matrisin üçgen görünümünü elde etmemiz gerektiğini hatırlıyoruz. 1. satırı (3) ile çarpalım. 2. satırı (-1) ile çarpın. 2. satırı 1. satıra ekleyin ve şunu elde edin:

Daha sonra 3. satırı (-1) ile çarpın. 3. satırı 2. satıra ekleyelim:

1. satırı (6) ile çarpalım. 2. satırı (13) ile çarpalım. 2. satırı 1. satıra ekleyelim:

Voila - sistem uygun forma getirildi. Bilinmeyenleri bulmak için kalır:

Bu örnekteki sistemin benzersiz bir çözümü var. Sonsuz sayıda çözümü olan sistemleri çözmeyi ayrı bir makalede ele alacağız. Belki ilk başta matrisi dönüştürmeye nereden başlayacağınızı bilemeyeceksiniz, ancak uygun uygulamadan sonra alışacaksınız ve SLAE'leri Gauss yöntemini kullanarak fındık gibi kıracaksınız. Ve aniden kırılması çok zor olan bir SLAE ile karşılaşırsanız yazarlarımızla iletişime geçin! Yazışma Ofisine bir talep bırakarak ucuz bir makale sipariş edebilirsiniz. Birlikte her sorunu çözeceğiz!

Bilinmeyenleri içeren bir doğrusal cebirsel denklem sistemi (SLAE) verilmiştir. Bu sistemi çözmek gerekiyor: kaç çözümü olduğunu (hiç, bir veya sonsuz sayıda) belirlemek ve en az bir çözümü varsa bunlardan herhangi birini bulmak.

Resmi olarak Sorun şu şekilde ifade ediliyor: sistemi çözün:

katsayılar nerede ve biliniyor ve değişkenler - istenen bilinmeyenler.

Bu problemin matris gösterimi uygundur:

katsayılardan oluşan bir matris ve yüksekliğin sütun vektörleridir.

SLAE'nin gerçek sayılar alanı üzerinde değil, alan üzerinde olabileceğini belirtmekte fayda var. modulo herhangi bir sayı, yani:

— Gauss algoritması bu tür sistemler için de çalışır (ancak bu durum aşağıda ayrı bir bölümde tartışılacaktır).

Gauss algoritması

Açıkça konuşursak, aşağıda açıklanan yönteme doğru bir şekilde "Gauss-Jordan eleme" yöntemi adı verilir, çünkü bu, araştırmacı Wilhelm Jordan tarafından 1887'de açıklanan Gauss yönteminin bir varyasyonudur (Wilhelm Jordan'ın her ikisinin de yazarı olmadığını belirtmekte fayda var). Ürdün teoremi eğrileri veya Ürdün cebiri - bunların hepsi aynı adı taşıyan üç farklı bilim adamıdır; ayrıca görünüşe göre "Ürdün" transkripsiyonu daha doğrudur, ancak "Ürdün" yazımı Rus literatüründe zaten oluşturulmuştur). Jordan'la eş zamanlı olarak (ve hatta bazı verilere göre ondan önce) bu algoritmanın B.-I. Clasen tarafından icat edildiğini belirtmek de ilginçtir.

Temel şema

Kısaca konuşursak, algoritma tutarlı dışlama Her denklemde yalnızca bir değişken kalana kadar her denklemdeki değişkenler. Eğer , o zaman Gauss-Jordan algoritmasının sistem matrisini birim matrise indirgemeye çalıştığını söyleyebiliriz - sonuçta, matris birim matris haline geldikten sonra sistemin çözümü açıktır - çözüm benzersizdir ve verilmiştir elde edilen katsayılara göre.

Bu durumda, algoritma sistemin iki basit eşdeğer dönüşümüne dayanır: birincisi, iki denklem değiştirilebilir ve ikinci olarak, herhangi bir denklem, bu satırın (sıfır olmayan katsayılı) doğrusal bir kombinasyonu ile değiştirilebilir ve diğer satırlar (keyfi katsayılarla).

İlk adımda Gauss-Jordan algoritması ilk satırı bir katsayıya böler. Daha sonra algoritma, ilk satırı, ilk sütundaki katsayıları sıfıra dönecek şekilde katsayılarla kalan satırlara ekler - bunun için, açıkçası, ilk satırı -'inci satıra eklerken, onu ile çarpmanız gerekir. Bir matrisle yapılan her işlem için (bir sayıya bölme, bir satıra başka bir tane ekleme), karşılık gelen işlemler vektörle gerçekleştirilir; bir bakıma matrisin inci sütunu gibi davranıyor.

Sonuç olarak, ilk adımın sonunda, matrisin ilk sütunu bir olacak (yani, ilk satırda bir ve geri kalanında sıfırlar içerecek).

Algoritmanın ikinci adımı da benzer şekilde gerçekleştirilir, yalnızca şimdi ikinci sütun ve ikinci satır dikkate alınır: önce ikinci satır bölünür ve ardından matrisin ikinci sütununu sıfırlayacak katsayılarla diğer tüm satırlardan çıkarılır. .

Dönen arama

Elbette yukarıda açıklanan diyagram eksiktir. Yalnızca her -'inci adımda öğe sıfırdan farklıysa işe yarar - aksi halde mevcut sütunda kalan katsayıların -'inci satırı ekleyerek sıfırlanmasını sağlayamayız.

Bu gibi durumlarda algoritmanın çalışmasını sağlamak için tam olarak bir süreç vardır. bir referans elemanı seçme(İngilizce'de buna tek kelimeyle "dönme" denir). İstenilen öğenin sıfırdan farklı bir sayı içermesi için matrisin satırlarının ve/veya sütunlarının yeniden düzenlenmesinden oluşur.

Bilgisayarda satırları yeniden düzenlemenin, sütunları yeniden düzenlemeye göre çok daha kolay olduğunu unutmayın: Sonuçta, iki sütunu değiştirirken, bu iki değişkenin yer değiştirdiğini hatırlamanız gerekir, böylece daha sonra yanıtı geri yüklerken hangi yanıtı doğru bir şekilde geri yükleyebilirsiniz. hangi değişkene aittir? Satırları yeniden düzenlerken bu tür ek eylemlerin gerçekleştirilmesine gerek yoktur.

Neyse ki, yöntemin doğru olması için satır değişimleri tek başına yeterlidir (hem satırlar hem de sütunlar değiştirildiğinde "tam dönme" yerine "kısmi dönme" adı verilir). Peki takas için hangi diziyi seçmelisiniz? Ve referans eleman aramasının yalnızca mevcut eleman sıfır olduğunda yapılması gerektiği doğru mu?

Bu sorunun genel bir cevabı yok. Çeşitli buluşsal yöntemler vardır ancak bunlardan (basitlik ve etki açısından) en etkili olanı şudur: sezgisel: Modülü en büyük olan eleman referans eleman olarak alınmalı ve referans elemanın aranıp onunla değiştirilmesi gerekmektedir. Her zaman ve yalnızca gerektiğinde değil (yani yalnızca olduğunda değil).

Başka bir deyişle, Gauss-Jordan algoritmasının . aşamasını kısmi dönme sezgiseli ile yürütmeden önce, . sütunda indeksleri maksimum moduloya kadar olan elemanlar arasından bulmak ve bu elemanla olan satırı th ile değiştirmek gerekir. sıra.

İlk olarak, bu buluşsal yöntem, çözüm sırasında element olsa bile SLAE'yi çözmenize izin verecektir. İkinci olarak ve oldukça önemlisi, bu buluşsal yöntem, sayısal kararlılık Gauss-Jordan algoritması.

Bu buluşsal yöntem olmadan, sistem her aşamada Gauss-Jordan algoritmasının çalışacağı şekilde olsa bile, sonuçta biriken hata o kadar büyük olabilir ki, hata boyutundaki matrisler için bile hatanın kendisi cevabı aşabilir. .

Dejenere vakalar

Dolayısıyla, kısmi dönmeli Gauss-Jordan algoritmasında durursak, o zaman sistemin dejenere olmaması (yani sıfırdan farklı bir determinantı olması, yani benzersiz bir çözümü olması) durumunda algoritmanın tartışılacağı ileri sürülür. yukarıda anlatılanlar tam olarak çalışacak ve birim matrise gelecektir (bunun kanıtı yani her zaman sıfır olmayan bir destek elemanının bulunacağının kanıtı burada verilmemiştir).

Şimdi düşünelim Genel dava- ne zaman ve mutlaka eşit değildir. 3. adımda destek elemanının bulunmadığını varsayalım. Bu, inci sütunda mevcut satırdan başlayan tüm satırların sıfır içerdiği anlamına gelir. Bu durumda bu değişkenin tanımlanamayacağı ve bağımsız değişken(herhangi bir değeri alabilir). Gauss-Jordan algoritmasının sonraki tüm değişkenler için çalışmaya devam edebilmesi için, böyle bir durumda mevcut satırın sayısını artırmadan mevcut -'inci sütunu atlamanız yeterlidir (sanal olarak -'yi kaldırdığımızı söyleyebiliriz). matrisin inci sütunu).

Yani algoritmanın çalışması sırasında bazı değişkenlerin bağımsız olduğu ortaya çıkabilmektedir. Değişken sayısı denklem sayısından büyük olduğunda en azından değişkenlerin bağımsız bulunacağı açıktır.

Genel olarak, eğer en az bir bağımsız değişken bulunursa, o zaman isteğe bağlı bir değer alabilir, geri kalan (bağımlı) değişkenler ise onun aracılığıyla ifade edilecektir. Bu, reel sayılar alanında çalıştığımızda sistemin potansiyel olarak sahip olduğu anlamına gelir. sonsuz sayıda çözüm(Eğer bir SLAE modülünü dikkate alırsak, o zaman çözümlerin sayısı bu modülün bağımsız değişken sayısının kuvvetine eşit olacaktır). Ancak dikkatli olunmalıdır: bağımsız değişkenler keşfedilse bile yine de SLAE'nin hiçbir çözümü olmayabilir. Bu, kalan işlenmemiş denklemlerin (Gauss-Jordan algoritmasının ulaşamadığı denklemler, yani bunlar yalnızca bağımsız değişkenlerin kaldığı denklemler) sıfır olmayan en az bir serbest terime sahip olması durumunda gerçekleşir.

Ancak bulunan çözümü açıkça değiştirerek bunu kontrol etmek daha kolaydır: tüm bağımsız değişkenlere sıfır değerler atayın, bulunan değerleri bağımlı değişkenlere atayın ve bu çözümü mevcut SLAE'ye değiştirin.

Uygulama

Burada Gauss-Jordan algoritmasının kısmi dönme buluşsal yöntemiyle (sütundaki maksimum olarak bir referans elemanı seçerek) bir uygulamasını sunuyoruz.

Sistem matrisinin kendisi fonksiyon girişine iletilir. Matrisin son sütunu, eski gösterimimizde, serbest katsayılar sütunudur (bu, programlamaya kolaylık sağlamak için yapıldı - çünkü algoritmanın kendisinde, serbest katsayılarla yapılan tüm işlemler, matrisle işlemleri tekrarlar).

İşlev, çözümlerin sayısını sisteme (, veya) döndürür (sonsuzluk, kodda herhangi bir büyük değere ayarlanabilecek özel bir sabitle gösterilir). En az bir çözüm varsa, o zaman vektörde döndürülür.

int gauss (vektör< vector< double >> a, vektör< double >& ans) ( int n = (int ) a.size () ; int m = (int ) a[ 0 ] .size () - 1 ; vektör< int >< m && row< n; ++ col) { int sel = row; for (int i= row; i< n; ++ i) if (abs (a[ i] [ col] ) >abs (a[ sel] [ sütun] ) ) sel = i; if (abs (a[ sel] [ sütun] )< EPS) continue ; for (int i= col; i<= m; ++ i) swap (a[ sel] [ i] , a[ row] [ i] ) ; where[ col] = row; for (int i= 0 ; i< n; ++ i) if (i ! = row) { double c = a[ i] [ col] / a[ row] [ col] ; for (int j= col; j<= m; ++ j) a[ i] [ j] - = a[ row] [ j] * c; } ++ row; } ans.assign (m, 0 ) ; for (int i= 0 ; i< m; ++ i) if (where[ i] ! = - 1 ) ans[ i] = a[ where[ i] ] [ m] / a[ where[ i] ] [ i] ; for (int i= 0 ; i< n; ++ i) { double sum = 0 ; for (int j= 0 ; j< m; ++ j) sum + = ans[ j] * a[ i] [ j] ; if (abs (sum - a[ i] [ m] ) >EPS) dönüş 0 ; ) for (int i= 0 ; i< m; ++ i) if (where[ i] == - 1 ) return INF; return 1 ; }

İşlev, geçerli sütuna ve geçerli satıra yönelik iki işaretçiyi destekler.

Ayrıca her değişken için hangi satırda yer alması gerektiğinin yazıldığı bir vektör oluşturulur (yani her sütun için bu sütunun sıfırdan farklı olduğu satırın numarası yazılır). Bu vektör gereklidir çünkü bazı değişkenler çözüm sırasında "tanımlanmamış" olabilir (yani bunlar isteğe bağlı bir değer atanabilen bağımsız değişkenlerdir - örneğin yukarıdaki uygulamada bunlar sıfırdır).

Uygulama kısmi döndürme tekniğini kullanır, maksimum modül elemanına sahip satırı arar ve ardından bu satırı konumuna göre yeniden düzenler (her ne kadar açık satır yeniden düzenlemesi bazı dizilerde iki endeksin değiştirilmesiyle değiştirilebilirse de, pratikte bu gerçek bir kazanç sağlamayacaktır) , çünkü değişim işlemleri boşa gider).

Uygulamada, basitlik adına, mevcut satır baş elemana bölünmez - böylece algoritmanın sonunda matris birim yerine köşegen olur (ancak görünüşe göre satırı şu şekilde böler: öncü unsur, ortaya çıkan hataları bir miktar azaltmamıza olanak tanır).

Bir çözüm bulunduğunda, sistemin en az bir çözümü olup olmadığını kontrol etmek için matrise geri eklenir. Bulunan çözümün doğrulanması başarılıysa, işlev en az bir bağımsız değişkenin olup olmadığına bağlı olarak veya - değerini döndürür.

Asimptotikler

Ortaya çıkan algoritmanın asimptotik davranışını tahmin edelim. Algoritma, her birinde aşağıdakilerin gerçekleştiği aşamalardan oluşur:

Açıkçası, ilk nokta ikinciden daha küçük bir asimptotik davranışa sahiptir. Ayrıca ikinci noktanın birden fazla kez (SLAE'de bağımlı değişkenlerin olabileceği sayıda) gerçekleştirilmediğini unutmayın.

Böylece, son asimptotikler algoritma şeklini alır.

Bu tahmin dönüştüğünde .

SLAE gerçek sayılar alanında değil, modülo iki alanında dikkate alındığında, sistemin çok daha hızlı çözülebileceğini unutmayın - buna aşağıdaki "SLAE modulo çözme" bölümünde bakın.

Eylem sayısının daha doğru tahmini

Zaten bildiğimiz gibi, tüm algoritmanın çalışma süresi aslında mevcut denklemin geri kalanından çıkarılması için harcanan süre ile belirlenir.

Bu, mevcut denklemin diğerlerine eklenmesiyle adımların her birinde gerçekleşebilir. Ekleme sırasında iş, mevcut olandan başlayarak yalnızca sütunlarla yapılır. Yani toplam işlemlerdir.

Eklentiler

Algoritmanın hızlandırılması: ileri ve geri vuruşlara bölünmesi

Algoritmanın ileri ve geri aşamalara bölündüğü, daha klasik olan başka bir versiyonunu dikkate alarak algoritmanın iki kat hızlanmasını sağlayabilirsiniz.

Genel olarak, yukarıda açıklanan algoritmanın aksine, matrisi köşegen forma değil, şu şekle indirgemek mümkündür: üçgen görünüm- ana köşegenin kesinlikle altındaki tüm öğeler sıfıra eşit olduğunda.

Üçgen matrisli bir sistem önemsiz bir şekilde çözülür - ilk önce, son değişkenin değeri hemen son denklemden bulunur, daha sonra bulunan değer sondan bir önceki denklemde değiştirilir ve sondan bir önceki değişkenin değeri bulunur ve böylece Açık. Bu süreç denir geri viteste Gauss algoritması.

Düz vuruş Gauss algoritması, bir istisna dışında yukarıda açıklanan Gauss-Jordan algoritmasına benzer bir algoritmadır: mevcut değişken tüm denklemlerden hariç tutulmaz, yalnızca mevcut değişkenden sonraki denklemlerden çıkarılır. Bunun sonucu aslında köşegen değil, üçgen bir matristir.

Aradaki fark ileri vuruşun işe yaramasıdır Daha hızlı Gauss-Jordan algoritması - ortalama olarak bir denklemin diğerine yarısı kadar ekleme yaptığı için. Ters vuruş, her durumda ileri vuruştan asimptotik olarak daha hızlıdır.

Böylece, eğer , o zaman bu algoritma zaten işlemleri gerçekleştirecektir - bu da Gauss-Jordan algoritmasının yarısı kadardır.

SLAE modülünün çözümü

Modulo SLAE'leri çözmek için yukarıda açıklanan algoritmayı kullanabilirsiniz; algoritma doğruluğunu korur.

Elbette artık bir referans elemanı seçmek için herhangi bir karmaşık teknik kullanmak gereksiz hale geliyor; mevcut sütunda sıfır olmayan herhangi bir elemanı bulmak yeterlidir.

Modül basitse, hiçbir zorluk ortaya çıkmaz - Gauss algoritmasının çalışması sırasında meydana gelen bölünmeler herhangi bir özel sorun yaratmaz.

Özellikle dikkat çekici ikiye eşit modül: Onun için matrisle yapılan tüm işlemler çok verimli bir şekilde gerçekleştirilebiliyor. Örneğin, bir diziyi diğer modülo ikiden çıkarmak aslında onların simetrik farkıdır (“xor”). Böylece, tüm matrisin bit maskeleri halinde sıkıştırılması ve yalnızca bunlarla çalışılmasıyla algoritmanın tamamı önemli ölçüde hızlandırılabilir. Gauss-Jordan algoritmasının ana bölümünün standart C++ "bitset" kapsayıcısını kullanan yeni bir uygulaması:

int gauss (vektör< bitset< N>> a, int n, int m, bit kümesi< N>& cevap) (vektör< int >burada (m, -1 ) ; for (int sütun= 0, satır= 0; sütun< m && row< n; ++ col) { for (int i= row; i< n; ++ i) if (a[ i] [ col] ) { swap (a[ i] , a[ row] ) ; break ; } if (! a[ row] [ col] ) continue ; where[ col] = row; for (int i= 0 ; i< n; ++ i) if (i ! = row && a[ i] [ col] ) a[ i] ^ = a[ row] ; ++ row; }

Gördüğünüz gibi, eski uygulamadan çok daha hızlı olmasına rağmen, yani bit sıkıştırması nedeniyle birkaç kat daha hızlı olmasına rağmen uygulama biraz daha kısa hale geldi. Ayrıca, modülo iki sistem çözümünün pratikte çok hızlı çalıştığına da dikkat edilmelidir, çünkü bir satırdan diğerini çıkarmanın gerekli olduğu durumlar oldukça nadiren meydana gelir (seyrek matrislerde, bu algoritma, kare sırasına göre bir zamanda çalışabilir). küp yerine boyut).

Eğer modül keyfi(mutlaka basit olması gerekmez), o zaman her şey biraz daha karmaşık hale gelir. Çin kalan teoremini kullanarak, rastgele bir modülle ilgili sorunu yalnızca "asallık derecesi" biçimindeki modüllere indirgeyeceğimiz açıktır. [daha fazla metin gizlendi çünkü Bu doğrulanmamış bir bilgidir - belki de çözmenin yanlış yolu ]

Son olarak soruya bakalım SLAE çözümlerinin sayısı modulo. Bunun cevabı oldukça basit: çözüm sayısı eşittir, burada modül ve bağımsız değişken sayısıdır.

Bir destek elemanı seçmenin farklı yolları hakkında biraz

Yukarıda da belirttiğimiz gibi bu sorunun net bir cevabı yok.

Geçerli sütundaki maksimum öğeyi bulmayı içeren "kısmi dönme" buluşsal yöntemi pratikte oldukça iyi çalışıyor. Ayrıca, pivot elemanı mevcut satırdan ve mevcut sütundan başlayarak tüm alt matrisin elemanları arasında arandığında "tam dönme" ile neredeyse aynı sonucu verdiği ortaya çıktı.

Ancak bu maksimum öğe buluşsal yöntemlerinin her ikisinin de aslında orijinal denklemlerin nasıl ölçeklendirildiğine oldukça bağlı olduğunu belirtmek ilginçtir. Örneğin sistemin denklemlerinden biri bir milyonla çarpılırsa, ilk adımda bu denklem neredeyse kesinlikle önde gelen denklem olarak seçilecektir. Bu oldukça garip görünüyor, bu yüzden biraz daha karmaşık bir buluşsal yönteme geçmek mantıklıdır - sözde "örtük dönme".

Örtük dönmenin buluşsal yöntemi, farklı satırların öğelerinin, sanki her iki satır, içlerindeki maksimum öğe bire eşit olacak şekilde normalleştirilmiş gibi karşılaştırılmasıdır. Bu tekniği uygulamak için, her satırdaki mevcut maksimum değeri korumanız yeterlidir (veya her satırı, içindeki maksimum mutlak değerde bire eşit olacak şekilde koruyun, ancak bu, birikmiş hatanın artmasına neden olabilir).

Bulunan yanıtın iyileştirilmesi

Çünkü, çeşitli buluşsal yöntemlere rağmen, Gauss-Jordan algoritması - mertebesinde boyutlarda bile özel matrislerde hala büyük hatalara yol açabilir.

Bu bağlamda, Gauss-Jordan algoritması tarafından elde edilen cevap, buna bazı basit sayısal yöntemlerin (örneğin, basit yineleme yöntemi) uygulanmasıyla geliştirilebilir.

Böylece çözüm iki adımlı bir çözüme dönüşür: önce Gauss-Jordan algoritması çalıştırılır, ardından ilk adımda elde edilen çözüm başlangıç ​​verisi olarak alınarak bazı sayısal yöntemler gerçekleştirilir.

Bu teknik, Gauss-Jordan algoritması tarafından çözülen problemler kümesini kabul edilebilir bir hatayla bir miktar genişletmemize olanak tanır.

Edebiyat

• William H. Press, Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery. Sayısal Tarifler: Bilimsel Hesaplama Sanatı
• Anthony Ralston, Philip Rabinowitz. Sayısal analizde ilk ders

Carl Friedrich Gauss - Alman matematikçi, aynı isimli SLAE'leri çözme yönteminin kurucusu

Carl Friedrich Gauss ünlü bir büyük matematikçiydi ve bir zamanlar “Matematiğin Kralı” olarak tanındı. Her ne kadar "Gauss'un yöntemi" adı genel olarak kabul edilse de, Gauss onun yazarı değildir: Gauss'un yöntemi ondan çok önce biliniyordu. İlk tanımı 2. yüzyıl arasında derlenen “Dokuz Kitapta Matematik” adlı Çin eserinde yer almaktadır. M.Ö e. ve ben yüzyıl. N. e. ve 10. yüzyıl civarında yazılmış eski eserlerin bir derlemesidir. M.Ö e.

– bilinmeyenlerin tutarlı bir şekilde hariç tutulması. Bu yöntem ikinci dereceden doğrusal cebirsel denklem sistemlerini çözmek için kullanılır. Denklemler Gauss yöntemi kullanılarak kolayca çözülebilse de öğrenciler çoğu zaman işaretler (artı ve eksiler) konusunda kafaları karıştığı için doğru çözümü bulamazlar. Bu nedenle SLAE'leri çözerken son derece dikkatli olmanız gerekir ve ancak o zaman en karmaşık denklemi bile kolayca, hızlı ve doğru bir şekilde çözebilirsiniz.

Doğrusal cebirsel denklem sistemlerinin çeşitli avantajları vardır: Denklemin önceden tutarlı olması gerekmez; denklem sayısının bilinmeyen değişkenlerin sayısıyla çakışmadığı veya ana matrisin determinantının sıfıra eşit olduğu denklem sistemlerini çözmek mümkündür; Nispeten az sayıda hesaplama işlemiyle sonuçlara ulaşmak için Gauss yöntemini kullanmak mümkündür.

Daha önce de belirtildiği gibi Gauss yöntemi öğrenciler için bazı zorluklara neden olmaktadır. Ancak yöntemi ve çözüm algoritmasını öğrenirseniz çözümün inceliklerini hemen anlayacaksınız.

Öncelikle doğrusal denklem sistemleri hakkındaki bilgileri sistematize edelim.

Not!

Bir SLAE, unsurlarına bağlı olarak aşağıdakilere sahip olabilir:

1. Bir çözüm;
2. birçok çözüm;
3. hiçbir çözümü yok.

İlk iki durumda SLAE uyumlu, üçüncü durumda ise uyumsuz olarak adlandırılır. Bir sistemin tek çözümü varsa kesin, birden fazla çözümü varsa belirsiz olarak adlandırılır.

Gauss yöntemi - teorem, çözüm örnekleri güncellenme tarihi: 22 Kasım 2019: Bilimsel Makaleler.Ru

Doğrusal denklem sistemlerini dikkate almaya devam ediyoruz. Bu ders konuyla ilgili üçüncü derstir. Genel olarak doğrusal denklem sisteminin ne olduğuna dair belirsiz bir fikriniz varsa, kendinizi çaydanlık gibi hissediyorsanız, o zaman Sonraki sayfasındaki temel bilgilerle başlamanızı öneririm, dersi incelemenizde fayda var.

Gauss yöntemi kolaydır! Neden? Ünlü Alman matematikçi Johann Carl Friedrich Gauss, yaşamı boyunca tüm zamanların en büyük matematikçisi, bir dahi olarak tanındı ve hatta “Matematiğin Kralı” lakabını aldı. Ve bildiğiniz gibi ustaca olan her şey basit! Bu arada, sadece enayiler değil, dahiler de para kazanıyor - Gauss'un portresi 10 Alman Markı banknotun üzerindeydi (euro'nun piyasaya sürülmesinden önce) ve Gauss hala sıradan posta pullarından Almanlara gizemli bir şekilde gülümsüyor.

Gauss yöntemi basittir, çünkü BEŞİNCİ SINIF ÖĞRENCİSİNİN BİLGİSİ bu konuda uzmanlaşmak için YETERLİDİR. Toplama ve çarpmayı bilmelisiniz!Öğretmenlerin okul matematik seçmeli derslerinde bilinmeyenleri sıralı olarak hariç tutma yöntemini sıklıkla düşünmeleri tesadüf değildir. Bu bir paradoks ama öğrenciler Gauss metodunu en zor buluyorlar. Şaşırtıcı bir şey yok - her şey metodolojiyle ilgili ve yöntemin algoritması hakkında erişilebilir bir biçimde konuşmaya çalışacağım.

Öncelikle doğrusal denklem sistemleri hakkında biraz bilgi verelim. Bir doğrusal denklem sistemi şunları yapabilir:

1) Benzersiz bir çözüme sahip olun. 2) Sonsuz sayıda çözümü var. 3) Çözümünüz yok (olun) ortak olmayan).

Gauss yöntemi çözüm bulmak için en güçlü ve evrensel araçtır herhangi Doğrusal denklem sistemleri. Hatırladığımız kadarıyla, Cramer kuralı ve matris yöntemi sistemin sonsuz sayıda çözümü olduğu veya tutarsız olduğu durumlarda uygun değildir. Ve bilinmeyenlerin sıralı olarak ortadan kaldırılması yöntemi Her neyse bizi cevaba götürecek! Bu dersimizde yine 1 numaralı durum (sistemin tek çözümü) için Gauss yöntemini ele alacağız, 2-3 numaralı noktaların durumlarına bir makale ayrılmıştır. Yöntemin algoritmasının her üç durumda da aynı şekilde çalıştığını not ediyorum.

Dersten en basit sisteme dönelim Doğrusal denklem sistemi nasıl çözülür? Gauss metodunu kullanarak çözelim.

İlk adım yazmaktır genişletilmiş sistem matrisi: . Katsayıların hangi prensibe göre yazıldığını sanırım herkes görebilir. Matrisin içindeki dikey çizginin herhangi bir matematiksel anlamı yoktur; bu sadece tasarım kolaylığı için üstü çizili bir çizgidir.

Referans : hatırlamanı tavsiye ederim şartlar lineer Cebir. Sistem Matrisi yalnızca bilinmeyenlerin katsayılarından oluşan bir matristir; bu örnekte sistemin matrisi: . Genişletilmiş Sistem Matrisi – bu, sistemin aynı matrisi artı serbest terimlerin bir sütunudur, bu durumda: . Kısaca belirtmek gerekirse, matrislerden herhangi birine basitçe matris adı verilebilir.

Genişletilmiş sistem matrisi yazıldıktan sonra onunla bazı eylemlerin gerçekleştirilmesi gerekir. temel dönüşümler.

Aşağıdaki temel dönüşümler mevcuttur:

1) Teller matrisler Olabilmek yeniden düzenlemek bazı yerlerde. Örneğin, söz konusu matriste birinci ve ikinci satırları ağrısız bir şekilde yeniden düzenleyebilirsiniz:

2) Matriste orantılı (özel bir durum olarak - aynı) satırlar varsa (veya ortaya çıkmışsa), o zaman şunları yapmalısınız: silmek matristen biri hariç tüm bu satırlar. Örneğin matrisi düşünün . Bu matriste son üç satır orantılı olduğundan yalnızca birini bırakmak yeterlidir: .

3) Dönüşümler sırasında matriste sıfır satır görünüyorsa, o zaman aynı zamanda silmek. Tabii ki çizmeyeceğim, sıfır çizgisi hangi çizgidir? hepsi sıfır.

4) Matris satırı şu şekilde olabilir: çarpmak (bölmek) herhangi bir numaraya sıfır olmayan. Örneğin matrisi düşünün. Burada ilk satırı –3'e bölmeniz ve ikinci satırı 2 ile çarpmanız önerilir: . Bu eylem çok faydalıdır çünkü matrisin daha sonraki dönüşümlerini basitleştirir.

5) Bu dönüşüm en çok zorluğa neden olur, ancak aslında karmaşık bir şey de yoktur. Bir matrisin bir satırına şunları yapabilirsiniz: bir sayıyla çarpılan başka bir dize ekle, sıfırdan farklı. Pratik bir örnekten matrisimize bakalım: . İlk önce dönüşümü çok detaylı bir şekilde anlatacağım. İlk satırı –2 ile çarpın: , Ve ikinci satıra ilk satırı -2 ile çarparak ekliyoruz: . Artık ilk satır “geriye” –2 ile bölünebilir: . Gördüğünüz gibi EKLENEN satır LI – değişmedi. Her zaman EKLENEN satır değişir UT.

Pratikte elbette bu kadar ayrıntılı yazmıyorlar, kısaca yazıyorlar: Bir kez daha: ikinci satıra ilk satırı –2 ile çarparak ekledim. Bir satır genellikle sözlü olarak veya taslak üzerinde çarpılır ve zihinsel hesaplama süreci şöyle olur:

“Matrisi yeniden yazıyorum ve ilk satırı yeniden yazıyorum: »

"İlk sütun. En altta sıfır almam gerekiyor. Bu nedenle üsttekini -2: ile çarpıyorum ve ilkini ikinci satıra ekliyorum: 2 + (–2) = 0. Sonucu ikinci satıra yazıyorum: »

“Şimdi ikinci sütun. En üstte -1 ile -2'yi çarpıyorum: . İlkini ikinci satıra ekliyorum: 1 + 2 = 3. Sonucu ikinci satıra yazıyorum: »

“Ve üçüncü sütun. En üstte -5 ile -2'yi çarpıyorum: . İlkini ikinci satıra ekliyorum: –7 + 10 = 3. Sonucu ikinci satıra yazıyorum: »

Lütfen bu örneği dikkatlice anlayın ve sıralı hesaplama algoritmasını anlayın, bunu anlarsanız Gauss yöntemi pratik olarak cebinizde. Ama elbette bu dönüşüm üzerinde çalışmaya devam edeceğiz.

Temel dönüşümler denklem sisteminin çözümünü değiştirmez

! DİKKAT: dikkate alınan manipülasyonlar kullanılamaz, matrislerin "kendi başlarına" verildiği bir görev teklif edilirse. Örneğin “klasik” matrislerle işlemler Hiçbir durumda matrislerin içindeki hiçbir şeyi yeniden düzenlememelisiniz! Sistemimize dönelim. Pratik olarak parçalara ayrılır.

Sistemin genişletilmiş matrisini yazalım ve temel dönüşümleri kullanarak onu şuna indirelim: kademeli görünüm:

(1) Birinci satır ikinci satıra –2 ile çarpılarak eklendi. Ve yine: neden ilk satırı –2 ile çarpıyoruz? Altta sıfır elde etmek için bu, ikinci satırda bir değişkenden kurtulmak anlamına gelir.

(2) İkinci satırı 3'e bölün.

Temel dönüşümlerin amacı – matrisi aşamalı forma indirgeyin: . Görevin tasarımında, sadece "merdivenleri" basit bir kalemle işaretliyorlar ve ayrıca "basamaklarda" bulunan sayıları da daire içine alıyorlar. "Adımlı görünüm" terimi bilimsel ve eğitimsel literatürde tamamen teorik değildir; yamuk görünüm veya üçgen görünüm.

Temel dönüşümler sonucunda elde ettik eş değer orijinal denklem sistemi:

Şimdi sistemin ters yönde "çözülmesi" gerekiyor - aşağıdan yukarıya doğru bu işleme denir Gauss yönteminin tersi.

Alt denklemde zaten hazır bir sonucumuz var: .

Sistemin ilk denklemini ele alalım ve zaten bilinen “y” değerini onun içine koyalım:

Gauss yönteminin üç bilinmeyenli üç doğrusal denklemden oluşan bir sistemin çözülmesini gerektirdiği en yaygın durumu ele alalım.

örnek 1

Denklem sistemini Gauss yöntemini kullanarak çözün:

Sistemin genişletilmiş matrisini yazalım:

Şimdi çözüm sırasında ulaşacağımız sonucu hemen çizeceğim: Tekrar ediyorum, amacımız temel dönüşümleri kullanarak matrisi adım adım forma getirmektir. Nereden başlamalı?

İlk önce sol üstteki numaraya bakın: Neredeyse her zaman burada olmalı birim. Genel olarak konuşursak, -1 (ve bazen diğer sayılar) işe yarar, ancak bir şekilde geleneksel olarak bir genellikle oraya yerleştirilir. Bir birim nasıl organize edilir? İlk sütuna bakıyoruz - bitmiş bir birimimiz var! Birinci dönüşüm: birinci ve üçüncü satırları değiştirin:

Artık ilk satır çözümün sonuna kadar değişmeden kalacak. Şimdi iyi.

Sol üst köşedeki ünite düzenlenmiştir. Şimdi bu yerlerde sıfır almanız gerekiyor:

Sıfırları “zor” bir dönüşüm kullanarak elde ederiz. İlk önce ikinci satırla ilgileniyoruz (2, –1, 3, 13). İlk pozisyonda sıfır almak için ne yapılması gerekiyor? Gerekiyor ikinci satıra ilk satırı –2 ile çarparak ekleyin. Zihinsel olarak veya taslakta ilk satırı –2 ile çarpın: (–2, –4, 2, –18). Ve sürekli olarak (yine zihinsel olarak veya taslak üzerinde) ekleme yapıyoruz, ikinci satıra zaten –2 ile çarpılmış olan ilk satırı ekliyoruz:

Sonucu ikinci satıra yazıyoruz:

Üçüncü satırı da aynı şekilde ele alıyoruz (3, 2, –5, –1). İlk pozisyonda sıfır almak için ihtiyacınız olan üçüncü satıra ilk satırı –3 ile çarparak ekleyin. Zihinsel olarak veya taslakta ilk satırı –3 ile çarpın: (–3, –6, 3, –27). VE üçüncü satıra ilk satırı –3 ile çarparak ekliyoruz:

Sonucu üçüncü satıra yazıyoruz:

Uygulamada bu eylemler genellikle sözlü olarak gerçekleştirilir ve tek adımda yazılır:

Her şeyi aynı anda ve aynı anda saymaya gerek yok. Hesaplamaların sırası ve sonuçların “girilmesi” tutarlı ve genellikle şu şekildedir: önce ilk satırı yeniden yazarız ve yavaşça kendimize üfleriz - SÜREKLİ ve DİKKATLİCE:
Yukarıda hesaplamaların zihinsel sürecini zaten tartışmıştım.

Bu örnekte bunu yapmak kolaydır; ikinci satırı –5'e böleriz (çünkü oradaki tüm sayılar 5'e kalansız bölünebilir). Aynı zamanda üçüncü satırı -2'ye bölüyoruz çünkü sayılar ne kadar küçük olursa çözüm o kadar basit olur:

Temel dönüşümlerin son aşamasında, burada bir sıfır daha almanız gerekir:

Bunun için üçüncü satıra ikinci satırı –2 ile çarparak ekliyoruz:
Bu eylemi kendiniz anlamaya çalışın - ikinci satırı zihinsel olarak –2 ile çarpın ve ekleme işlemini gerçekleştirin.

Gerçekleştirilen son eylem, sonucun saç modelidir, üçüncü satırı 3'e bölün.

Temel dönüşümler sonucunda eşdeğer bir doğrusal denklem sistemi elde edildi: Serin.

Şimdi Gauss yönteminin tersi devreye giriyor. Denklemler aşağıdan yukarıya doğru “gevşemektedir”.

Üçüncü denklemde zaten hazır bir sonucumuz var:

İkinci denkleme bakalım: . "Zet"in anlamı zaten bilinmektedir, dolayısıyla:

Ve son olarak ilk denklem: . "Igrek" ve "zet" biliniyor, bu sadece küçük şeyler meselesi:

Cevap:

Tekrar tekrar belirtildiği gibi, herhangi bir denklem sistemi için bulunan çözümü kontrol etmek mümkün ve gereklidir, neyse ki bu kolay ve hızlıdır.

Örnek 2

Bu, bağımsız bir çözüm örneği, nihai tasarımın bir örneği ve dersin sonunda bir cevaptır.

Şunu belirtmek gerekir ki kararın ilerlemesi karar sürecimle örtüşmeyebilir, ve bu Gauss yönteminin bir özelliğidir. Ama cevaplar aynı olmalı!

Örnek 3

Gauss yöntemini kullanarak bir doğrusal denklem sistemini çözme

Sol üstteki “adıma” bakıyoruz. Orada bir birimimiz olmalı. Sorun şu ki, ilk sütunda hiç birim yok, dolayısıyla satırları yeniden düzenlemek hiçbir şeyi çözmeyecek. Bu gibi durumlarda ünitenin temel bir dönüşüm kullanılarak düzenlenmesi gerekir. Bu genellikle birkaç yolla yapılabilir. Bunu yaptım: (1) İlk satıra ikinci satırı -1 ile çarparak ekliyoruz. Yani ikinci satırı zihinsel olarak –1 ile çarpıp birinci ve ikinci satırları ekledik, ikinci satır değişmedi.

Şimdi sol üstte “eksi bir” var ki bu da bize çok yakışıyor. +1 almak isteyen herkes ek bir hareket yapabilir: İlk satırı –1 ile çarpın (işaretini değiştirin).

(2) Birinci satırın 5 ile çarpılması ikinci satıra eklendi. İlk satırın 3 ile çarpılması üçüncü satıra eklendi.

(3) İlk satır -1 ile çarpılmıştır, prensip olarak bu güzellik içindir. Üçüncü satırın işareti de değiştirilerek ikinci sıraya taşındı, böylece ikinci “adım”da gerekli üniteye sahip olduk.

(4) İkinci satır üçüncü satıra 2 ile çarpılarak eklendi.

(5) Üçüncü satır 3'e bölündü.

Hesaplamalarda bir hata olduğunu (daha nadiren bir yazım hatası) gösteren kötü bir işaret, "kötü" bir sonuçtur. Yani, eğer aşağıda , gibi bir şey varsa ve buna göre, , o zaman yüksek bir olasılıkla temel dönüşümler sırasında bir hata yapıldığını söyleyebiliriz.

Biz bunun tersini uyguluyoruz, örneklerin tasarımında genellikle sistemin kendisini yeniden yazmıyorlar, ancak denklemler "doğrudan verilen matristen alınıyor." Size hatırlatırım, ters vuruş aşağıdan yukarıya doğru çalışır. Evet, işte bir hediye:

Cevap: .

Örnek 4

Gauss yöntemini kullanarak bir doğrusal denklem sistemini çözme

Bu kendi başınıza çözebileceğiniz bir örnektir, biraz daha karmaşıktır. Birisinin kafası karışırsa sorun olmaz. Dersin sonunda tam çözüm ve örnek tasarım. Sizin çözümünüz benim çözümümden farklı olabilir.

Son bölümde Gauss algoritmasının bazı özelliklerine bakacağız. İlk özellik bazen sistem denklemlerinde bazı değişkenlerin eksik olmasıdır, örneğin: Genişletilmiş sistem matrisi nasıl doğru şekilde yazılır? Derste bu noktadan zaten bahsetmiştim. Cramer kuralı. Matris yöntemi. Sistemin genişletilmiş matrisinde eksik değişkenlerin yerine sıfırları koyarız: Bu arada, bu oldukça kolay bir örnek, çünkü ilk sütunda zaten bir sıfır var ve gerçekleştirilecek daha az temel dönüşüm var.

İkinci özellik şudur. Ele alınan tüm örneklerde “adımlara” –1 veya +1 yerleştirdik. Orada başka numaralar olabilir mi? Bazı durumlarda bunu yapabilirler. Sistemi düşünün: .

Burada sol üst “adım”da iki tane var. Ancak ilk sütundaki tüm sayıların 2'ye kalansız bölünebildiğini, diğerinin ise iki ve altı olduğunu fark ediyoruz. Ve sol üstteki ikisi bize yakışacak! İlk adımda aşağıdaki dönüşümleri yapmanız gerekir: ilk satırı –1 ile çarparak ikinci satıra ekleyin; üçüncü satıra ilk satırı –3 ile çarparak ekleyin. Bu şekilde ilk sütunda gerekli sıfırları alacağız.

Veya başka bir geleneksel örnek: . Burada ikinci “adım”daki üç de bize uyar, çünkü 12 (sıfır almamız gereken yer) 3'e kalansız bölünebilir. Aşağıdaki dönüşümü gerçekleştirmek gerekir: ikinci satırı üçüncü satıra -4 ile çarparak ekleyin, bunun sonucunda ihtiyacımız olan sıfır elde edilecektir.

Gauss'un yöntemi evrenseldir ancak bir özelliği vardır. Sistemleri tam anlamıyla ilk seferde diğer yöntemleri (Cramer yöntemi, matris yöntemi) kullanarak çözmeyi güvenle öğrenebilirsiniz - çok katı bir algoritmaları vardır. Ancak Gauss yöntemine güvenebilmek için en az 5-10 onlu sistemi “işe sokmalı” ve çözmelisiniz. Bu nedenle ilk başta hesaplamalarda karışıklıklar ve hatalar olabilir ve bunda olağandışı veya trajik bir şey yoktur.

Pencerenin dışında yağmurlu bir sonbahar havası... Bu nedenle, kendi başına çözmek için daha karmaşık bir örnek isteyen herkes için:

Örnek 5

Dört bilinmeyenli 4 doğrusal denklem sistemini Gauss yöntemini kullanarak çözün.

Böyle bir görev pratikte o kadar da nadir değildir. Bu sayfayı iyice inceleyen bir çaydanlığın bile böyle bir sistemi sezgisel olarak çözme algoritmasını anlayacağını düşünüyorum. Temelde her şey aynı; yalnızca daha fazla eylem var.

Sistemin çözümünün olmadığı (tutarsız) veya sonsuz sayıda çözümün olduğu durumlar derste tartışılmaktadır. Uyumsuz sistemler ve ortak bir çözüme sahip sistemler. Burada Gauss yönteminin dikkate alınan algoritmasını düzeltebilirsiniz.

Sana başarılar diliyorum!

Çözümler ve cevaplar:

Örnek 2: Çözüm : Sistemin genişletilmiş matrisini yazalım ve temel dönüşümleri kullanarak onu adım adım forma getirelim.
Gerçekleştirilen temel dönüşümler: (1) Birinci satır ikinci satıra –2 ile çarpılarak eklendi. Birinci satır üçüncü satıra -1 ile çarpılarak eklendi. Dikkat! Burada birinciyi üçüncü satırdan çıkarmak isteyebilirsiniz; bunu çıkarmamanızı şiddetle tavsiye ederim - hata riski büyük ölçüde artar. Sadece katlayın! (2) İkinci satırın işareti değiştirildi (-1 ile çarpıldı). İkinci ve üçüncü satırlar değiştirildi. Not , "adımlarda" sadece bir tanesinden değil, aynı zamanda -1'den de memnunuz ki bu daha da uygun. (3) İkinci satır üçüncü satıra 5 ile çarpılarak eklendi. (4) İkinci satırın işareti değiştirildi (-1 ile çarpıldı). Üçüncü satır 14'e bölündü.

Tersi:

Cevap : .

Örnek 4: Çözüm : Sistemin genişletilmiş matrisini yazalım ve temel dönüşümleri kullanarak onu adım adım forma getirelim:

Gerçekleştirilen dönüşümler: (1) Birinci satıra ikinci satır eklendi. Böylece sol üstteki “basamak”ta istenilen ünite düzenlenmiştir. (2) İlk satırın 7 ile çarpılması ikinci satıra eklendi. İlk satırın 6 ile çarpılması üçüncü satıra eklendi.

İkinci “adım”la her şey daha da kötüye gidiyor , bunun için "adaylar" 17 ve 23 sayılarıdır ve bizim ya bir ya da -1'e ihtiyacımız var. Dönüşümler (3) ve (4) istenen birimin elde edilmesini amaçlayacaktır. (3) Üçüncü satıra ikinci satır -1 ile çarpılarak eklendi. (4) Üçüncü satır, ikinci satıra -3 ile çarpılarak eklendi. İkinci adımda gerekli öğe alındı. . (5) İkinci satır üçüncü satıra 6 ile çarpılarak eklendi. (6) İkinci satır -1 ile çarpılır, üçüncü satır -83'e bölünür.

Tersi:

Cevap :

Örnek 5: Çözüm : Sistemin matrisini yazalım ve temel dönüşümleri kullanarak onu aşamalı bir forma getirelim:

Gerçekleştirilen dönüşümler: (1) Birinci ve ikinci satırlar değiştirildi. (2) Birinci satır ikinci satıra –2 ile çarpılarak eklendi. İlk satır -2 ile çarpılarak üçüncü satıra eklendi. Birinci satır dördüncü satıra -3 ile çarpılarak eklendi. (3) İkinci satır üçüncü satıra 4 ile çarpılarak eklenir. İkinci satır ise –1 ile çarpılarak dördüncü satıra eklenir. (4) İkinci satırın işareti değiştirildi. Dördüncü satır 3'e bölünerek üçüncü satırın yerine yerleştirildi. (5) Üçüncü satır dördüncü satıra –5 ile çarpılarak eklenir.

Tersi:

Cevap :

Bugün doğrusal cebirsel denklem sistemlerini çözmek için Gauss yöntemini inceliyoruz. Cramer yöntemini kullanarak aynı SLAE'leri çözmeye ayrılmış önceki makalede bu sistemlerin ne olduğunu okuyabilirsiniz. Gauss yöntemi herhangi bir özel bilgi gerektirmez, yalnızca dikkat ve tutarlılığa ihtiyacınız vardır. Matematiksel açıdan okul eğitiminin bunu uygulamak için yeterli olmasına rağmen, öğrenciler genellikle bu yönteme hakim olmakta zorlanırlar. Bu yazıda bunları hiçliğe indirmeye çalışacağız!

Gauss yöntemi

M Gauss yöntemi– SLAE'leri çözmek için en evrensel yöntem (çok büyük sistemler hariç). Daha önce tartışılanın aksine sadece tek çözümü olan sistemler için değil aynı zamanda sonsuz sayıda çözümü olan sistemler için de uygundur. Burada üç olası seçenek var.

1. Sistemin benzersiz bir çözümü vardır (sistemin ana matrisinin determinantı sıfıra eşit değildir);
2. Sistemin sonsuz sayıda çözümü vardır;
3. Çözüm yok, sistem uyumsuz.

Yani bir sistemimiz var (bir çözümü olsun) ve onu Gauss yöntemini kullanarak çözeceğiz. Nasıl çalışır?

Gauss yöntemi ileri ve ters olmak üzere iki aşamadan oluşur.

Gauss yönteminin doğrudan vuruşu

Öncelikle sistemin genişletilmiş matrisini yazalım. Bunu yapmak için ana matrise serbest üyelerden oluşan bir sütun ekleyin.

Gauss yönteminin tüm özü, bu matrisi temel dönüşümler yoluyla kademeli (veya aynı zamanda üçgen şeklinde) bir forma getirmektir. Bu formda, matrisin ana köşegeninin altında (veya üstünde) yalnızca sıfırlar bulunmalıdır.

Ne yapabilirsin:

1. Matrisin satırlarını yeniden düzenleyebilirsiniz;
2. Bir matriste eşit (veya orantılı) satırlar varsa, bunlardan biri hariç tümünü kaldırabilirsiniz;
3. Bir dizeyi herhangi bir sayıyla (sıfır hariç) çarpabilir veya bölebilirsiniz;
4. Boş satırlar kaldırıldı;
5. Bir dizeye sıfırdan farklı bir sayıyla çarpılan bir dize ekleyebilirsiniz.

Ters Gauss Yöntemi

Sistemi bu şekilde dönüştürdükten sonra bilinmeyen bir Xn bilinir hale gelir ve geri kalan tüm bilinmeyenleri, zaten bilinen x'leri sistemin denklemlerinde birinciye kadar değiştirerek ters sırada bulabilirsiniz.

İnternet her zaman elinizin altında olduğunda, Gauss yöntemini kullanarak bir denklem sistemini çözebilirsiniz. çevrimiçi. Katsayıları çevrimiçi hesap makinesine girmeniz yeterlidir. Ancak kabul etmelisiniz ki, örneğin bir bilgisayar programı tarafından değil, kendi beyniniz tarafından çözüldüğünü fark etmek çok daha keyifli.

Gauss yöntemini kullanarak bir denklem sistemini çözme örneği

Ve şimdi - her şeyin net ve anlaşılır hale gelmesi için bir örnek. Bir doğrusal denklem sistemi verilse, bunu Gauss yöntemini kullanarak çözmeniz gerekir:

Öncelikle genişletilmiş matrisi yazalım:

Şimdi dönüşümleri yapalım. Matrisin üçgen görünümünü elde etmemiz gerektiğini hatırlıyoruz. 1. satırı (3) ile çarpalım. 2. satırı (-1) ile çarpın. 2. satırı 1. satıra ekleyin ve şunu elde edin:

Daha sonra 3. satırı (-1) ile çarpın. 3. satırı 2. satıra ekleyelim:

1. satırı (6) ile çarpalım. 2. satırı (13) ile çarpalım. 2. satırı 1. satıra ekleyelim:

Voila - sistem uygun forma getirildi. Bilinmeyenleri bulmak için kalır:

Bu örnekteki sistemin benzersiz bir çözümü var. Sonsuz sayıda çözümü olan sistemleri çözmeyi ayrı bir makalede ele alacağız. Belki ilk başta matrisi dönüştürmeye nereden başlayacağınızı bilemeyeceksiniz, ancak uygun uygulamadan sonra alışacaksınız ve SLAE'leri Gauss yöntemini kullanarak fındık gibi kıracaksınız. Ve aniden kırılması çok zor olan bir SLAE ile karşılaşırsanız yazarlarımızla iletişime geçin! Yazışma Bürosuna bir talep bırakarak bunu yapabilirsiniz. Birlikte her sorunu çözeceğiz!