هندسيا أو هندسيا. المتوالية الهندسية. الدليل الشامل مع الأمثلة (2020). لماذا هناك حاجة للتقدم الهندسي وتاريخه؟

دعونا نفكر في سلسلة معينة.

7 28 112 448 1792...

ومن الواضح تمامًا أن قيمة أي عنصر من عناصره أكبر بأربع مرات تمامًا من العنصر السابق. هذا يعني أن هذه السلسلة عبارة عن تقدم.

التقدم الهندسي هو تسلسل لا نهائي من الأرقام، السمة الرئيسية له هي أن الرقم التالي يتم الحصول عليه من الرقم السابق عن طريق الضرب برقم محدد. يتم التعبير عن ذلك من خلال الصيغة التالية.

a z +1 =a z ·q، حيث z هو رقم العنصر المحدد.

وفقا لذلك، ض ∈ ن.

الفترة التي يتم فيها دراسة التقدم الهندسي في المدرسة هي الصف التاسع. ستساعدك الأمثلة على فهم المفهوم:

0.25 0.125 0.0625...

وبناء على هذه الصيغة يمكن إيجاد مقام التقدم على النحو التالي:

لا يمكن أن يكون q أو b z صفرًا. كما أن كل عنصر من عناصر التقدم يجب ألا يساوي الصفر.

وفقًا لذلك، لمعرفة الرقم التالي في السلسلة، عليك ضرب الرقم الأخير بـ q.

لتعيين هذا التقدم، يجب عليك تحديد العنصر الأول والمقام. بعد ذلك، من الممكن العثور على أي من الحدود اللاحقة ومجموعها.

أصناف

اعتمادًا على q وa 1، ينقسم هذا التقدم إلى عدة أنواع:

• إذا كان كل من 1 و q أكبر من واحد، فإن هذا التسلسل هو تقدم هندسي يتزايد مع كل عنصر لاحق. ويرد أدناه مثال على ذلك.

مثال: أ 1 =3، ف=2 - كلا المعلمتين أكبر من واحد.

ومن ثم يمكن كتابة التسلسل الرقمي على النحو التالي:

3 6 12 24 48 ...

• إذا |ف| أقل من واحد، أي أن الضرب به يعادل القسمة، فإن المتوالية ذات الشروط المماثلة تكون متوالية هندسية تناقصية. ويرد أدناه مثال على ذلك.

مثال: أ 1 =6، ف=1/3 - أ 1 أكبر من واحد، ف أقل.

ومن ثم يمكن كتابة التسلسل الرقمي على النحو التالي:

6 2 2/3 ... - أي عنصر أكبر بثلاث مرات من العنصر الذي يليه.

• علامة بالتناوب. إذا س<0, то знаки у чисел последовательности постоянно чередуются вне зависимости от a 1 , а элементы ни возрастают, ни убывают.

مثال: أ 1 = -3، ف = -2 - كلا المعلمتين أقل من الصفر.

ومن ثم يمكن كتابة التسلسل الرقمي على النحو التالي:

3, 6, -12, 24,...

الصيغ

هناك العديد من الصيغ للاستخدام المريح للتقدم الهندسي:

• صيغة المصطلح Z. يسمح لك بحساب عنصر تحت رقم محدد دون حساب الأرقام السابقة.

مثال:س = 3, أ 1 = 4. مطلوب حساب العنصر الرابع من التقدم.

حل:أ 4 = 4 · 3 4-1 = 4 · 3 3 = 4 · 27 = 108.

• مجموع العناصر الأولى التي تساوي كميتها ض. يسمح لك بحساب مجموع كل عناصر التسلسل حتىأ ضشامل.

منذ (1-س) في المقام، ثم (1 - ف)≠ 0، وبالتالي فإن q لا تساوي 1.

ملاحظة: إذا كانت q=1، فسيكون التقدم عبارة عن سلسلة من الأرقام المتكررة بلا حدود.

مجموع التقدم الهندسي، أمثلة:أ 1 = 2, س= -2. احسب S5.

حل:س 5 = 22- الحساب باستخدام الصيغة.

• المبلغ إذا |س| < 1 и если z стремится к бесконечности.

مثال:أ 1 = 2 , س= 0.5. العثور على المبلغ.

حل:سز = 2 · = 4

سز = 2 + 1 + 0.5 + 0.25 + 0.125 + 0.0625 = 3.9375 4

بعض الخصائص:

• خاصية مميزة. إذا كان الشرط التالي يعمل لأيض، فإن سلسلة الأرقام المعطاة هي تقدم هندسي:

أ ض 2 = أ ض -1 · أض+1

• أيضًا، يمكن العثور على مربع أي رقم في متوالية هندسية عن طريق إضافة مربعي أي رقمين آخرين في سلسلة معينة، إذا كانا على مسافة متساوية من هذا العنصر.

أ ض 2 = أ ض - ر 2 + أ ض + ر 2 ، أينر- المسافة بين هذه الأرقام.

• عناصرتختلف في سمرة واحدة.
• وتشكل لوغاريتمات عناصر التقدم أيضًا تقدمًا، ولكنها حسابية، أي أن كل منها أكبر من السابق برقم معين.

أمثلة على بعض المشاكل الكلاسيكية

لفهم ما هو التقدم الهندسي بشكل أفضل، يمكن أن تساعد الأمثلة مع الحلول للفئة 9.

• شروط:أ 1 = 3, أ 3 = 48. البحثس.

الحل: كل عنصر لاحق أكبر من العنصر الذي قبلهس مرة واحدة.من الضروري التعبير عن بعض العناصر بدلالة عناصر أخرى باستخدام المقام.

لذلك،أ 3 = س 2 · أ 1

عند الاستبدالس= 4

• شروط:أ 2 = 6, أ 3 = 12. احسب S 6.

حل:للقيام بذلك، ما عليك سوى العثور على q، العنصر الأول واستبداله في الصيغة.

أ 3 = س· أ 2 ، لذلك،س= 2

أ 2 = ف · أ 1،لهذا أ 1 = 3

س6= 189

• · أ 1 = 10, س= -2. ابحث عن العنصر الرابع للتقدم.

الحل: للقيام بذلك يكفي التعبير عن العنصر الرابع من خلال الأول ومن خلال المقام.

أ 4 = س 3· أ 1 = -80

مثال تطبيقى:

• قام أحد عملاء البنك بإيداع مبلغ قدره 10000 روبل، وبموجب شروطه، سيضيف العميل كل عام 6٪ منه إلى المبلغ الأصلي. كم سيكون المبلغ في الحساب بعد 4 سنوات؟

الحل: المبلغ الأولي هو 10 آلاف روبل. وهذا يعني أنه بعد سنة من الاستثمار سيكون لدى الحساب مبلغ يساوي 10,000 + 10,000 · 0.06 = 10000 1.06

وعليه فإن المبلغ الموجود في الحساب بعد سنة أخرى سيتم التعبير عنه على النحو التالي:

(10000 · 1.06) · 0.06 + 10000 · 1.06 = 1.06 · 1.06 · 10000

أي أن المبلغ يزيد كل عام بمقدار 1.06 مرة. وهذا يعني أنه للعثور على مقدار الأموال في الحساب بعد 4 سنوات، يكفي العثور على العنصر الرابع من التقدم، والذي يعطى بالعنصر الأول يساوي 10 آلاف والمقام يساوي 1.06.

س = 1.06 1.06 1.06 1.06 10000 = 12625

أمثلة على مسائل حساب المجموع:

يستخدم التقدم الهندسي في مختلف المشاكل. يمكن إعطاء مثال للعثور على المبلغ على النحو التالي:

أ 1 = 4, س= 2، احسبس 5.

الحل: جميع البيانات اللازمة للحساب معروفة، ما عليك سوى استبدالها في الصيغة.

س 5 = 124

• أ 2 = 6, أ 3 = 18. احسب مجموع العناصر الستة الأولى.

حل:

في جيوم. التقدم، كل عنصر تالٍ أكبر بمقدار q من العنصر السابق، أي لحساب المجموع الذي تحتاج إلى معرفة العنصرأ 1 والقاسمس.

أ 2 · س = أ 3

س = 3

وبالمثل، تحتاج إلى العثور عليهاأ 1 ، معرفةأ 2 وس.

أ 1 · س = أ 2

أ 1 =2

س 6 = 728.

الدرس حول هذا الموضوع "تناقص التقدم الهندسي بشكل لا نهائي"

الغرض من الدرس:تعريف الطلاب بنوع جديد من التسلسل - وهو تقدم هندسي متناقص بشكل لا نهائي.

مهام:

صياغة فكرة أولية عن حد التسلسل العددي؛ التعرف على طريقة أخرى لتحويل الكسور الدورية اللانهائية إلى كسور عادية باستخدام صيغة مجموع التقدم الهندسي المتناقص بشكل لا نهائي؛

تنمية الصفات الفكرية لشخصية تلاميذ المدارس مثل التفكير المنطقي والقدرة على القيام بإجراءات تقييمية والتعميم؛

تعزيز النشاط والمساعدة المتبادلة والجماعية والاهتمام بالموضوع.

معدات:فئة الكمبيوتر، جهاز العرض، الشاشة.

نوع الدرس:الدرس - تعلم موضوع جديد.

خلال الفصول الدراسية

أنا . منظمة. لحظة. اذكر موضوع الدرس والغرض منه.

ثانيا . تحديث معارف الطلاب.1. التحقق من الواجبات المنزلية.

1) التحقق من الصيغ الأساسية المتعلقة بالمتتابعات الحسابية والهندسية. يقوم طالبان بإعداد ملاحظات حول الصيغ على السبورة.

2) يفعله باقي الطلاب الإملاء الرياضي حول موضوع "مجموع الصيغ".

مهام:

№1. أوجد مجموع الحدود الخمسة الأولى للتقدم الحسابي إذا كان حدها الأول هو 6 (الخيار الأول)، -20 (الخيار الثاني)، والحد الخامس هو -6 (الخيار الأول)، 20 (الخيار الثاني).

№2. أوجد مجموع الحدود الخمسة الأولى للتقدم الحسابي إذا كان حدها الأول هو -20 (الخيار الأول)، و6 (الخيار الثاني)، والفرق هو 10 (الخيار الأول)، و-3 (الخيار الثاني).

№3. أوجد مجموع الحدود الخمسة الأولى للمتتالية الهندسية إذا كان حدها الأول يساوي 1 (الخيار الأول)، -1 (الخيار الثاني)، والمقام هو -2 (الخيار الأول)، 2 (الخيار الثاني).

في نهاية الإملاء، يتم فحص عمل اثنين من الطلاب بشكل انتقائي للتقييم، بينما يقوم الباقي بإجراء اختبار ذاتي باستخدام الحلول الجاهزة المكتوبة على لوحات السبورة.

حلول:

مهام

1. يتم إعطاء التقدم الحسابي من خلال الصيغة أ ن = 7 – 4 ن. يجد أ 10 . (-33)

2. في التقدم الحسابي أ 3 = 7 و أ 5 = 1 . يجد أ 4 . (4)

3. في التقدم الحسابي أ 3 = 7 و أ 5 = 1 . يجد أ 17 . (-35)

4. في التقدم الحسابي أ 3 = 7 و أ 5 = 1 . يجد س 17 . (-187)

5. للتقدم الهندسي
العثور على الحد الخامس.

6. للتقدم الهندسي
يجد نالعضو ال.

7. أضعافا مضاعفة ب 3 = 8 و ب 5 = 2 . يجد ب 4 . (4)

8. أضعافا مضاعفة ب 3 = 8 و ب 5 = 2 . يجد ب 1 و س .

9. أضعافا مضاعفة ب 3 = 8 و ب 5 = 2 . يجد س 5 . (62)

ثالثا . تعلم موضوع جديد(مظاهرة العرض).

لنفترض مربعًا طول ضلعه 1. لنرسم مربعًا آخر طول ضلعه نصف حجم المربع الأول، ثم مربعًا آخر طول ضلعه نصف الثاني، ثم المربع الذي يليه، وما إلى ذلك. في كل مرة يساوي جانب المربع الجديد نصف المربع السابق.

ونتيجة لذلك، حصلنا على سلسلة من جوانب المربعات تشكيل متوالية هندسية مع المقام .

والأهم من ذلك، أنه كلما قمنا ببناء مثل هذه المربعات، كلما كان جانب المربع أصغر. على سبيل المثال,

أولئك. ومع زيادة العدد n، تقترب شروط التقدم من الصفر.

باستخدام هذا الرقم، يمكنك التفكير في تسلسل آخر.

على سبيل المثال، تسلسل مساحات المربعات:

. ومرة أخرى، إذا نتزداد إلى أجل غير مسمى، ثم تقترب المساحة من الصفر إلى أقرب ما تريد.

دعونا ننظر إلى مثال آخر. مثلث متساوي الأضلاع طول أضلاعه 1 سم. لنقم ببناء المثلث التالي بحيث تكون رءوسه في منتصف أضلاع المثلث الأول، وفقًا لنظرية خط الوسط للمثلث - ضلع الثاني يساوي نصف ضلع الأول، وضلع الثالث يساوي نصف الجانب الثاني، الخ. مرة أخرى نحصل على سلسلة من أطوال أضلاع المثلثات.

في
.

إذا اعتبرنا تقدمًا هندسيًا بمقام سلبي.

ثم، مرة أخرى، بأعداد متزايدة نشروط التقدم تقترب من الصفر.

دعونا ننتبه إلى قواسم هذه المتتابعات. في كل مكان كانت القواسم أقل من 1 في القيمة المطلقة.

يمكننا أن نستنتج أن المتتابعة الهندسية سوف تتناقص بشكل لا نهائي إذا كان معامل مقامها أقل من 1.

العمل الأمامي.

تعريف:

يقال إن المتوالية الهندسية تتناقص بشكل لا نهائي إذا كان معامل مقامها أقل من واحد.
.

باستخدام التعريف، يمكنك أن تقرر ما إذا كان التقدم الهندسي يتناقص بشكل لا نهائي أم لا.

مهمة

هل المتوالية عبارة عن متوالية هندسية متناقصة بشكل لا نهائي إذا كانت معطاة بالصيغة:

;
.

حل:

. سوف نجد س .

;
;
;
.

هذا التقدم الهندسي يتناقص بلا حدود.

ب)هذا التسلسل ليس تقدمًا هندسيًا متناقصًا بشكل لا نهائي.

خذ بعين الاعتبار مربعًا طول ضلعه يساوي 1. اقسمه إلى نصفين، أي نصفين إلى نصفين، وما إلى ذلك. تشكل مساحات جميع المستطيلات الناتجة متوالية هندسية متناقصة بشكل لا نهائي:

مجموع مساحات جميع المستطيلات التي تم الحصول عليها بهذه الطريقة سيكون مساوياً لمساحة المربع الأول ويساوي 1.

لكن على الجانب الأيسر من هذه المساواة يوجد مجموع عدد لا نهائي من الحدود.

لنفكر في مجموع حدود n الأولى.

وفقًا لصيغة مجموع الحدود n الأولى للتقدم الهندسي، فهي تساوي .

لو نيزيد بلا حدود إذن

أو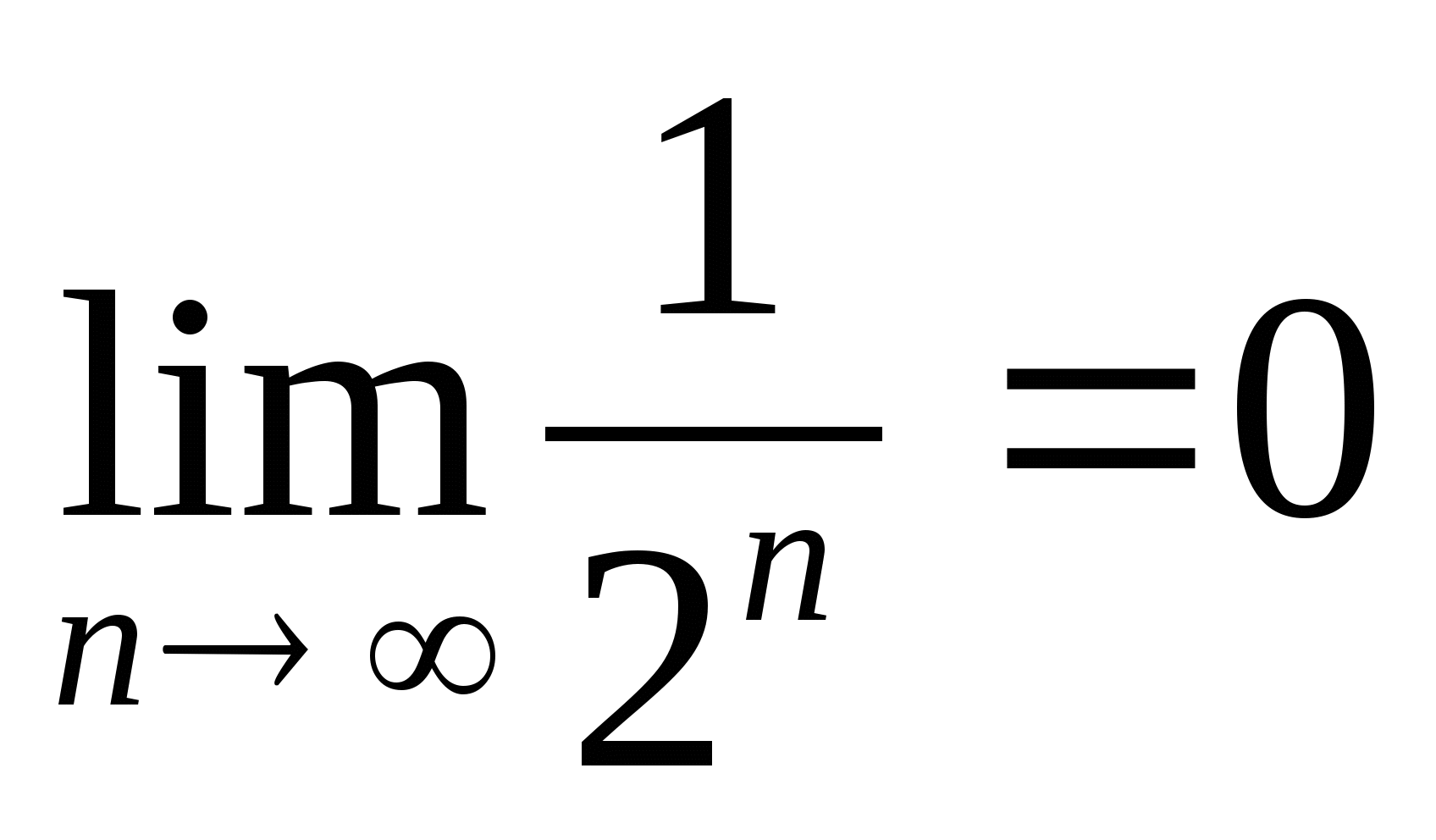
. لهذا
، أي.
.

مجموع متوالية هندسية متناقصة بشكل لا نهائيهناك حد التسلسل س 1 , س 2 , س 3 , …, س ن , … .

على سبيل المثال، للتقدم
,

لأن

مجموع متوالية هندسية متناقصة بشكل لا نهائييمكن العثور عليها باستخدام الصيغة
.

ثالثا . الفهم والتوحيد(استكمال المهام).

المهمة رقم 2. أوجد مجموع متوالية هندسية متناقصة بشكل لا نهائي حيث يكون الحد الأول 3 والحد الثاني 0.3.

حل:

المهمة رقم 3. الكتاب المدرسي ص 160 رقم 433(1)

أوجد مجموع المتوالية الهندسية المتناقصة بلا حدود:

حل:

المهمة رقم 4. اكتب الكسر العشري الدوري اللانهائي 0,(5) ككسر عادي.

الطريقة الأولى. دع x=0,(5)= 0.555... / 10 الطريقة الثانية. 0,(5)=0.555…=

المهمة رقم 5. الكتاب المدرسي ص 162 رقم 445(3) (الحل المستقل)

اكتب الكسر العشري الدوري اللانهائي 0,(12) ككسر عادي.

الجواب: 0,(12)= 4/33.

رابعا . تلخيص.

ما هو التسلسل الذي تعرفت عليه اليوم؟

تحديد متوالية هندسية متناقصة بشكل لا نهائي.

كيف نثبت أن التقدم الهندسي يتناقص بشكل لا نهائي؟

أعط صيغة مجموع المتوالية الهندسية المتناقصة بشكل لا نهائي.

الخامس . العمل في المنزل.

المتوالية الهندسية هي متوالية عددية حدها الأول غير الصفر، وكل حد لاحق يساوي الحد السابق مضروبا في نفس العدد غير الصفر. يُشار إلى التقدم الهندسي بـ b1، b2، b3، …، bn، …

خصائص التقدم الهندسي

نسبة أي حد من الخطأ الهندسي إلى حده السابق تساوي نفس العدد، أي b2/b1 = b3/b2 = b4/b3 = ... = bn/b(n-1) = b( ن+1)/مليار = … . وهذا يتبع مباشرة من تعريف التقدم الحسابي. ويسمى هذا الرقم مقام التقدم الهندسي. عادةً ما يُشار إلى مقام التقدم الهندسي بالحرف q.

إحدى طرق تحديد المتوالية الهندسية هي تحديد حدها الأول b1 ومقام الخطأ الهندسي q. على سبيل المثال، ب1=4، س=-2. يحدد هذان الشرطان التقدم الهندسي 4، -8، 16، -32، ….

إذا كانت q>0 (q لا تساوي 1)، فإن التقدم يكون تسلسلًا رتيبًا. على سبيل المثال، المتتابعة 2، 4،8،16،32، ... هي متوالية متزايدة بشكل رتيب (b1=2، q=2).

إذا كان المقام في الخطأ الهندسي هو q=1، فإن جميع حدود المتوالية الهندسية ستكون متساوية مع بعضها البعض. في مثل هذه الحالات، يقال إن التقدم هو تسلسل ثابت.

صيغة للفصل التاسع من التقدم

لكي تكون المتوالية العددية (bn) متتابعة هندسية، يجب أن يكون كل عضو من أعضائها، بدءاً من الثاني، هو الوسط الهندسي للأعضاء المجاورة. أي أنه من الضروري تحقيق المعادلة التالية - (b(n+1))^2 = bn * b(n+2)، لأي n>0، حيث n ينتمي إلى مجموعة الأعداد الطبيعية N.

صيغة الحد n من التقدم الهندسي هي:

bn=b1*q^(n-1)، حيث تنتمي n إلى مجموعة الأعداد الطبيعية N.

دعونا نلقي نظرة على مثال بسيط:

في التقدم الهندسي b1=6, q=3, n=8 ابحث عن bn.

دعونا نستخدم صيغة الحد n من المتوالية الهندسية.

التقدم الهندسي هو نوع جديد من التسلسل الرقمي الذي نحن على وشك التعرف عليه. من أجل المواعدة الناجحة، لا يضر أن تعرف وتفهم على الأقل. ثم لن تكون هناك مشاكل مع التقدم الهندسي.)

ما هو التقدم الهندسي؟ مفهوم التقدم الهندسي.

نبدأ الجولة كالعادة بالأساسيات. أكتب سلسلة غير مكتملة من الأرقام:

1, 10, 100, 1000, 10000, …

هل يمكنك اكتشاف النمط ومعرفة الأرقام التي ستأتي بعد ذلك؟ الفلفل واضح، ثم تأتي الأرقام 100000، 1000000 وهكذا. حتى بدون الكثير من الجهد العقلي، كل شيء واضح، أليس كذلك؟)

نعم. مثال آخر. أنا أكتب هذا التسلسل:

1, 2, 4, 8, 16, …

هل يمكنك معرفة الأرقام التي ستأتي بعد الرقم 16 والاسم؟ ثامنعضو تسلسلي؟ إذا عرفت أنه سيكون الرقم 128، فهذا جيد جدًا. لذا فإن نصف المعركة تكمن في الفهم حاسةو النقاط الرئيسيةلقد تم بالفعل تحقيق التقدم الهندسي. يمكنك أن تنمو أكثر.)

والآن ننتقل مرة أخرى من الأحاسيس إلى الرياضيات الصارمة.

النقاط الرئيسية للتقدم الهندسي.

النقطة الرئيسية رقم 1

التقدم الهندسي هو تسلسل الأرقام.وكذلك التقدم. لا شيء يتوهم. يتم ترتيب هذا التسلسل فقط بشكل مختلف.ومن الطبيعي أن يكون له اسم مختلف، نعم.

النقطة الرئيسية رقم 2

مع النقطة الرئيسية الثانية، سيكون السؤال أصعب. دعونا نعود قليلاً ونتذكر الخاصية الأساسية للتقدم الحسابي. ها هو: كل عضو يختلف عن سابقه بنفس المبلغ.

هل من الممكن صياغة خاصية رئيسية مماثلة للتقدم الهندسي؟ فكر قليلاً... ألق نظرة فاحصة على الأمثلة المقدمة. هل خمنت ذلك؟ نعم! في التقدم الهندسي (أي!) يختلف كل عضو من أعضائه عن العضو السابق نفس العدد من المرات.دائماً!

في المثال الأول، هذا الرقم هو عشرة. أيًا كان عضو التسلسل الذي تأخذه، فهو أكبر من العضو السابق عشرة مرات.

وفي المثال الثاني هو اثنان: كل حد أكبر من الذي قبله مرتين.

وهذه هي النقطة الأساسية التي يختلف بها التقدم الهندسي عن التقدم الحسابي. في التقدم الحسابي، يتم الحصول على كل حد لاحق بإضافةنفس القيمة للفترة السابقة. و هنا - عمليه الضربالمدة السابقة بنفس المقدار. هذا هو الفرق كله.)

النقطة الرئيسية رقم 3

هذه النقطة الأساسية مطابقة تمامًا لتلك الخاصة بالتقدم الحسابي. يسمى: كل عضو في التقدم الهندسي يقف في مكانه.كل شيء هو نفسه تمامًا كما هو الحال في التقدم الحسابي والتعليقات، كما أعتقد، غير ضرورية. هناك الحد الأول، وهناك الحد المائة والأول، وما إلى ذلك. دعونا نتبادل حدين على الأقل - سيختفي النمط (ومعه التقدم الهندسي). ما سيبقى هو مجرد سلسلة من الأرقام دون أي منطق.

هذا كل شئ. هذا هو بيت القصيد من التقدم الهندسي.

المصطلحات والتسميات.

لكن الآن، بعد أن فهمنا المعنى والنقاط الرئيسية للتقدم الهندسي، يمكننا الانتقال إلى النظرية. وإلا فما هي النظرية دون فهم المعنى، أليس كذلك؟

كيفية الإشارة إلى التقدم الهندسي؟

كيف تتم كتابة التقدم الهندسي بشكل عام؟ لا مشكلة! تتم كتابة كل مصطلح من التقدم أيضًا كرسالة. فقط للتقدم الحسابي، عادة ما يتم استخدام الحرف "أ"، للحرف الهندسي "ب". رقم عضوية، كالعادة، يشار الفهرس في أسفل اليمين. نحن ببساطة ندرج أعضاء التقدم أنفسهم، مفصولين بفواصل أو فواصل منقوطة.

مثله:

ب 1,ب 2 , ب 3 , ب 4 , ب 5 , ب 6 , …

باختصار، تتم كتابة هذا التقدم على النحو التالي: (ب ن) .

أو هكذا، للتقدم المحدود:

ب 1، ب 2، ب 3، ب 4، ب 5، ب 6.

ب 1، ب 2، …، ب 29، ب 30.

أو باختصار:

(ب ن), ن=30 .

وهذا، في الواقع، هو كل التعيين. كل شيء هو نفسه، فقط الحرف مختلف، نعم.) والآن ننتقل مباشرة إلى التعريف.

تعريف التقدم الهندسي.

المتوالية الهندسية هي تسلسل رقمي يكون فيه الحد الأول غير صفر، وكل حد لاحق يساوي الحد السابق مضروبًا في نفس العدد غير الصفري.

هذا هو التعريف كله. معظم الكلمات والعبارات واضحة ومألوفة بالنسبة لك. إذا فهمت بالطبع معنى التقدم الهندسي "على أصابعك" وبشكل عام. ولكن هناك أيضًا بعض العبارات الجديدة التي أود أن أوليها اهتمامًا خاصًا.

أولا الكلمات : "العضو الأول فيه غير صفرية".

لم يتم تقديم هذا القيد على الفصل الأول عن طريق الصدفة. ما رأيك سيحدث إذا كان العضو الأول ب 1 سوف تكون مساوية للصفر؟ ما قيمة الحد الثاني إذا كان كل حد أكبر من الحد الذي قبله؟ نفس العدد من المرات؟دعنا نقول ثلاث مرات؟ دعونا نرى... اضرب الحد الأول (أي 0) في 3 واحصل على... صفر! ماذا عن العضو الثالث؟ صفر أيضاً! والحد الرابع أيضًا صفر! وما إلى ذلك وهلم جرا…

لقد حصلنا للتو على كيس من الخبز، سلسلة من الأصفار:

0, 0, 0, 0, …

بالطبع، مثل هذا التسلسل له الحق في الحياة، لكنه ليس له أي فائدة عملية. كل شيء واضح. وأي عضو فيه صفر. مجموع أي عدد من الحدود هو أيضًا صفر... ما الأشياء المثيرة للاهتمام التي يمكنك القيام بها بها؟ لا شئ…

الكلمات الرئيسية التالية: "مضروبة بنفس الرقم غير الصفر."

هذا الرقم نفسه له أيضًا اسم خاص به - مقام التقدم الهندسي. لنبدأ بالتعرف.)

مقام التقدم الهندسي.

كل شيء بسيط مثل قصف الكمثرى.

مقام التقدم الهندسي هو رقم (أو كمية) غير الصفر يشير إلىكم مرةكل فترة من التقدم أكثر من السابق.

مرة أخرى، على غرار التقدم الحسابي، الكلمة الأساسية التي يجب البحث عنها في هذا التعريف هي الكلمة "أكثر". وهذا يعني أنه يتم الحصول على كل مصطلح من التقدم الهندسي عمليه الضربإلى هذا القاسم بالذات العضو السابق.

دعني أشرح.

لحساب، دعنا نقول ثانيةديك، بحاجة إلى أن تأخذ أولاًعضو و تتضاعفذلك إلى القاسم. للحساب العاشرديك، بحاجة إلى أن تأخذ تاسععضو و تتضاعفذلك إلى القاسم.

يمكن أن يكون مقام التقدم الهندسي نفسه أي شيء. على الاطلاق أي شخص! كامل، كسري، إيجابي، سلبي، غير عقلاني - كل شيء. باستثناء الصفر. هذا ما تخبرنا به كلمة "غير الصفر" في التعريف. لماذا هناك حاجة لهذه الكلمة هنا - المزيد عن ذلك لاحقًا.

مقام التقدم الهندسيفي أغلب الأحيان يشار إليه بالحرف س.

كيفية العثور عليه س؟ لا مشكلة! يجب أن نأخذ أي مصطلح للتقدم و القسمة على المصطلح السابق. القسمة هي جزء. ومن هنا الاسم - "قاسم التقدم". المقام، عادة ما يكون في جزء، نعم...) على الرغم من أن القيمة منطقية سينبغي أن يسمى خاصالتقدم الهندسي، على غرار اختلافللتقدم الحسابي. لكننا اتفقنا على الاتصال المقام - صفة مشتركة - حالة. ولن نعيد اختراع العجلة أيضًا.)

دعونا نحدد، على سبيل المثال، الكمية سلهذا التقدم الهندسي:

2, 6, 18, 54, …

كل شيء أساسي. دعونا أعتبر أيرقم التسلسل. نحن نأخذ ما نريد. باستثناء أول واحد. على سبيل المثال، 18. والقسمة على الرقم السابق. يعني في الساعة 6.

نحن نحصل:

س = 18/6 = 3

هذا كل شئ. هذا هو الجواب الصحيح. في هذه المتوالية الهندسية، المقام هو ثلاثة.

دعونا الآن نجد المقام سلتقدم هندسي آخر. على سبيل المثال، هذا:

1, -2, 4, -8, 16, …

كل نفس. بغض النظر عن العلامات التي يمتلكها الأعضاء أنفسهم، ما زلنا نأخذها أيرقم التسلسل (على سبيل المثال، 16) والقسمة عليه الرقم السابق(أي -8).

نحن نحصل:

د = 16/(-8) = -2

وهذا كل شيء.) هذه المرة تبين أن قاسم التقدم سلبي. ناقص اثنين. يحدث.)

لنأخذ الآن هذا التقدم:

1, 1/3, 1/9, 1/27, …

ومرة أخرى، بغض النظر عن نوع الأرقام في التسلسل (سواء كانت أعداد صحيحة، أو حتى كسور، أو حتى سلبية، أو حتى غير عقلانية)، فإننا نأخذ أي رقم (على سبيل المثال، 1/9) ونقسمه على الرقم السابق (1/3). حسب قواعد العمل مع الكسور بالطبع.

نحن نحصل:

هذا كل شيء.) هنا تبين أن المقام كسري: س = 1/3.

ما رأيك في هذا "التقدم"؟

3, 3, 3, 3, 3, …

من الواضح هنا س = 1 . رسميًا، هذا أيضًا تقدم هندسي، فقط مع أعضاء متطابقين.) لكن مثل هذه التطورات ليست مثيرة للاهتمام للدراسة والتطبيق العملي. نفس التقدم مع الأصفار الصلبة. ولذلك، فإننا لن ننظر فيها.

كما ترون، يمكن أن يكون قاسم التقدم أي شيء - عدد صحيح، كسري، إيجابي، سلبي - أي شيء! لا يمكن أن يكون مجرد صفر. لا أستطيع التخمين لماذا؟

حسنًا، دعونا نستخدم بعض الأمثلة المحددة لنرى ما سيحدث إذا أخذنا المقام على أنه المقام سصفر.) دعونا، على سبيل المثال، لدينا ب 1 = 2 ، أ س = 0 . إذن ماذا سيكون الحد الثاني مساويًا؟

نحن نعد:

ب 2 = ب 1 · س= 2 0 = 0

ماذا عن العضو الثالث؟

ب 3 = ب 2 · س= 0 0 = 0

أنواع وسلوك التقدم الهندسي.

كان كل شيء أكثر أو أقل وضوحًا: إذا كان هناك اختلاف في التقدم دإيجابية، ثم يزداد التقدم. إذا كان الفرق سلبيا، فإن التقدم يتناقص. هناك خياران فقط. لا يوجد ثالث.)

ولكن مع سلوك التقدم الهندسي، سيكون كل شيء أكثر إثارة للاهتمام وتنوعًا!)

بغض النظر عن كيفية تصرف المصطلحات هنا: فهي تزيد، وتنقص، وتقترب من الصفر إلى أجل غير مسمى، بل وتتغير العلامات، وترمي نفسها بالتناوب في "زائد" ثم في "ناقص"! وفي كل هذا التنوع عليك أن تكون قادرًا على الفهم جيدًا، نعم...

دعونا نكتشف ذلك؟) لنبدأ بأبسط حالة.

القاسم موجب ( س >0)

مع القاسم الإيجابي، أولا، يمكن الدخول في شروط التقدم الهندسي بالإضافة إلى اللانهاية(أي: الزيادة بلا حد) ويمكن الدخول فيها ناقص اللانهاية(أي: النقصان بلا حدود). لقد اعتدنا بالفعل على سلوك التقدم هذا.

على سبيل المثال:

(ب ن): 1, 2, 4, 8, 16, …

كل شيء بسيط هنا. يتم الحصول على كل مصطلح من التقدم أكثر من السابق. علاوة على ذلك، يظهر كل مصطلح عمليه الضربالعضو السابق على إيجابيالرقم +2 (أي س = 2 ). إن سلوك مثل هذا التقدم واضح: جميع أعضاء التقدم ينموون بلا حدود، ويذهبون إلى الفضاء. بالإضافة إلى اللانهاية...

والآن إليكم التقدم:

(ب ن): -1, -2, -4, -8, -16, …

هنا أيضًا يتم الحصول على كل مصطلح من التقدم عمليه الضربالعضو السابق على إيجابيرقم +2. لكن سلوك مثل هذا التقدم هو عكس ذلك تمامًا: يتم الحصول على كل حد من التقدم أقل من السابق، وكل حدودها تتناقص بلا حدود، إلى سالب ما لا نهاية.

الآن دعونا نفكر: ما هو القاسم المشترك بين هذين التقدمين؟ هذا صحيح، القاسم! هنا وهناك س = +2 . رقم موجب، عدد إيجابي.اثنين. و هنا سلوكهذين التقدمين مختلفان بشكل أساسي! لا أستطيع التخمين لماذا؟ نعم! انها كل شيء عن العضو الأول!إنه، كما يقولون، هو الذي يعزف اللحن.) انظر بنفسك.

في الحالة الأولى، الفصل الأول من التقدم إيجابي(+1)، وبالتالي، يتم الحصول على جميع الحدود اللاحقة عن طريق الضرب في إيجابيالمقام - صفة مشتركة - حالة س = +2 ، سيكون أيضا إيجابي.

لكن في الحالة الثانية، الفصل الأول سلبي(-1). لذلك، يتم الحصول على جميع الحدود اللاحقة للتقدم عن طريق الضرب بـ إيجابي س = +2 ، سيتم الحصول عليها أيضًا سلبي.لأن "ناقص" إلى "زائد" يعطي دائمًا "ناقص"، نعم.)

كما ترون، على عكس التقدم الحسابي، يمكن أن يتصرف التقدم الهندسي بشكل مختلف تمامًا وليس اعتمادًا فقط من القاسمس، ولكن أيضا اعتمادا من العضو الأول، نعم.)

تذكر: يتم تحديد سلوك التقدم الهندسي بشكل فريد من خلال مصطلحه الأول ب 1 والقاسمس .

والآن نبدأ في تحليل الحالات الأقل شهرة، ولكنها أكثر إثارة للاهتمام!

لنأخذ على سبيل المثال هذا التسلسل:

(ب ن): 1, 1/2, 1/4, 1/8, 1/16, …

هذا التسلسل هو أيضًا تقدم هندسي! يظهر أيضًا كل مصطلح من هذا التقدم عمليه الضربالعضو السابق بنفس الرقم . إنه مجرد رقم - كسري: س = +1/2 . أو +0,5 . علاوة على ذلك (مهم!) الرقم أقل من واحد:س = 1/2<1.

لماذا هذا التقدم الهندسي مثير للاهتمام؟ وإلى أين يتجه أعضاؤها؟ دعونا نلقي نظرة:

1/2 = 0,5;

1/4 = 0,25;

1/8 = 0,125;

1/16 = 0,0625;

…….

ما هي الأشياء المثيرة للاهتمام التي يمكنك ملاحظتها هنا؟ أولا، الانخفاض من حيث التقدم ملحوظ على الفور: كل عضو من أعضائه أقلالسابق بالضبط 2 مرات.أو حسب تعريف المتوالية الهندسية كل حد أكثرسابق 1/2 مرة، لأن قاسم التقدم س = 1/2 . وعند الضرب بعدد موجب أقل من واحد، عادة ما تنخفض النتيجة، نعم...

ماذا أكثريمكن أن ينظر إليه في سلوك هذا التقدم؟ هل يتضاءل أعضاؤها؟ غير محدود، الذهاب إلى ناقص اللانهاية؟ لا! يختفون بطريقة خاصة. في البداية، تنخفض بسرعة كبيرة، ثم ببطء أكثر فأكثر. وبينما تبقى في كل وقت إيجابي. وإن كانت صغيرة جدًا جدًا. وما الذي يسعون إليه هم أنفسهم؟ لم تخمن؟ نعم! إنهم يسعون جاهدين نحو الصفر!) علاوة على ذلك، انتبه، فإن أعضاء تقدمنا ​​هم من الصفر لا تصل أبدا!فقط يقترب منه إلى ما لا نهاية. انها مهمة جدا.)

سيحدث موقف مماثل في التقدم التالي:

(ب ن): -1, -1/2, -1/4, -1/8, -1/16, …

هنا ب 1 = -1 ، أ س = 1/2 . كل شيء هو نفسه، فقط الآن ستقترب الحدود من الصفر من الجانب الآخر، من الأسفل. البقاء في كل وقت سلبي.)

مثل هذا التقدم الهندسي، شروطه يقترب من الصفر بلا حدود(سواء كان من الجانب الإيجابي أو السلبي)، في الرياضيات له اسم خاص - تناقص التقدم الهندسي بشكل لا نهائي.هذا التقدم مثير للاهتمام وغير عادي لدرجة أنه سيتم مناقشته درس منفصل .)

لذلك، أخذنا في الاعتبار كل ما هو ممكن إيجابيالقواسم كبيرة وصغيرة. نحن لا نعتبر الوحدة نفسها مقامًا للأسباب المذكورة أعلاه (تذكر المثال الذي يتضمن سلسلة من ثلاثة توائم...)

دعونا نلخص:

إيجابيو أكثر من واحد (س>1)، ثم شروط التقدم:

أ) زيادة بلا حدود (إذاب 1 >0);

ب) النقصان بلا حدود (إذاب 1 <0).

إذا كان قاسم التقدم الهندسي إيجابي و أقل من واحد (0< س<1), то члены прогрессии:

أ) قريبة بلا حدود من الصفر فوق(لوب 1 >0);

ب) يقترب إلى ما لا نهاية من الصفر من الأسفل(لوب 1 <0).

يبقى الآن للنظر في هذه القضية القاسم السلبي.

المقام سلبي ( س <0)

لن نذهب بعيداً للحصول على مثال. لماذا بالضبط الجدة الأشعث؟!) فليكن مثلا الفصل الأول من التقدم ب 1 = 1 ودعنا نأخذ المقام س = -2.

نحصل على التسلسل التالي:

(ب ن): 1, -2, 4, -8, 16, …

وهكذا.) يتم الحصول على كل مصطلح من التقدم عمليه الضربالعضو السابق على رقم سلبي-2. في هذه الحالة، جميع الأعضاء الذين يقفون في الأماكن الفردية (الأول، الثالث، الخامس، الخ) سيكونون كذلك إيجابي، وفي الأماكن الزوجية (الثاني والرابع وما إلى ذلك) - سلبي.العلامات تتناوب بشكل صارم. زائد ناقص زائد ناقص... هذا التقدم الهندسي يسمى - زيادة علامة بالتناوب.

وإلى أين يتجه أعضاؤها؟ ولكن ليس في أي مكان.) نعم، بالقيمة المطلقة (أي modulo)أعضاء تقدمنا ​​يتزايدون بلا حدود (ومن هنا جاء اسم "تزايد"). ولكن في الوقت نفسه، يرميك كل عضو في التقدم بالتناوب في الحرارة، ثم في البرد. إما "زائد" أو "ناقص". إن تقدمنا ​​يتذبذب... علاوة على ذلك، فإن نطاق التقلبات يتزايد بسرعة مع كل خطوة، نعم.) لذلك فإن تطلعات أعضاء التقدم تسير في مكان ما خاصةهنا لا.لا إلى زائد اللانهاية، ولا إلى ناقص اللانهاية، ولا إلى الصفر - في أي مكان.

لنفكر الآن في المقام الكسري بين صفر وسالب واحد.

على سبيل المثال، فليكن ب 1 = 1 ، أ ف = -1/2.

ثم نحصل على التقدم:

(ب ن): 1, -1/2, 1/4, -1/8, 1/16, …

ومرة أخرى لدينا تناوب العلامات! ولكن، على عكس المثال السابق، يوجد هنا بالفعل ميل واضح لأن تقترب الحدود من الصفر.) هذه المرة فقط تقترب حدودنا من الصفر ليس من الأعلى أو الأسفل بشكل صارم، ولكن مرة أخرى متردد. أخذ القيم الإيجابية والسلبية بالتناوب. لكنهم في نفس الوقت وحداتيقتربون أكثر فأكثر من الصفر العزيز.)

ويسمى هذا التقدم الهندسي علامة تناقص لا نهائية، بالتناوب.

لماذا هذين المثالين مثيران للاهتمام؟ وحقيقة أنه في كلتا الحالتين يحدث تناوب العلامات!هذه الحيلة نموذجية فقط للتقدم ذي المقام السلبي، نعم.) لذلك، إذا رأيت في بعض المهام تقدمًا هندسيًا بشروط متناوبة، فستعرف بالفعل على وجه اليقين أن مقامه سلبي بنسبة 100٪ ولن ترتكب أي خطأ في الإشارة.)

بالمناسبة، في حالة وجود مقام سلبي، فإن علامة الحد الأول لا تؤثر على الإطلاق على سلوك التقدم نفسه. وبغض النظر عن علامة الحد الأول من التتابع، ففي كل الأحوال ستلاحظ علامة الحدود. والسؤال الوحيد هو، في أي الأماكن(زوجي أو فردي) سيكون هناك أعضاء بعلامات محددة.

يتذكر:

إذا كان قاسم التقدم الهندسي سلبي ، فعلامات شروط التقدم تكون دائمًا البديل.

وفي نفس الوقت فإن الأعضاء أنفسهم:

أ) الزيادة بلا حدودmodulo، لوس<-1;

ب) يقترب من الصفر إلى ما لا نهاية إذا كان -1< س<0 (прогрессия бесконечно убывающая).

هذا كل شئ. تم تحليل جميع الحالات النموذجية.)

في عملية تحليل مجموعة متنوعة من الأمثلة على التقدم الهندسي، كنت أستخدم الكلمات بشكل دوري: "يميل إلى الصفر", "يميل إلى زائد اللانهاية", "يميل إلى ناقص اللانهاية"... لا بأس.) هذه الصور الكلامية (والأمثلة المحددة) هي مجرد مقدمة أولية لـ سلوكمجموعة متنوعة من تسلسل الأرقام. باستخدام مثال التقدم الهندسي.

لماذا نحتاج حتى إلى معرفة سلوك التقدم؟ ما الفرق الذي يحدثه أين تذهب؟ نحو الصفر، إلى زائد اللانهاية، إلى ناقص اللانهاية... ماذا يفعل ذلك بنا؟

الشيء هو أنه بالفعل في الجامعة، في دورة الرياضيات العليا، ستحتاج إلى القدرة على العمل مع مجموعة واسعة من التسلسلات الرقمية (مع أي، وليس فقط التقدم!) والقدرة على تخيل بالضبط كيف هذا التسلسل أو ذاك يتصرف - سواء كان يزيد، أو يتناقص بشكل غير محدود، أو يميل إلى رقم معين (وليس بالضرورة إلى الصفر)، أو حتى لا يميل إلى أي شيء على الإطلاق... تم تخصيص قسم كامل لهذا الموضوع في سياق الرياضيات تحليل - نظرية الحدود.وبشكل أكثر تحديدًا - المفهوم حد التسلسل الرقميموضوع مثير جدا للاهتمام! من المنطقي أن تذهب إلى الكلية وتكتشف ذلك.)

بعض الأمثلة من هذا القسم (التسلسلات ذات الحد) وعلى وجه الخصوص، تناقص التقدم الهندسي بشكل لا نهائييبدأون في التعود عليها في المدرسة. لقد اعتدنا على ذلك.)

علاوة على ذلك، فإن القدرة على دراسة سلوك التسلسلات جيدًا ستفيدك كثيرًا في المستقبل وستكون مفيدة جدًا في ذلك البحوث الوظيفية.الأكثر تنوعا. لكن القدرة على العمل بكفاءة مع الوظائف (حساب المشتقات، ودراستها بالكامل، وبناء الرسوم البيانية الخاصة بها) تزيد بشكل كبير من مستواك الرياضي! هل لديك أي شكوك؟ لا حاجة. تذكر أيضًا كلامي.)

دعونا ننظر إلى التقدم الهندسي في الحياة؟

في الحياة من حولنا، نواجه تقدمًا هندسيًا في كثير من الأحيان. حتى دون أن يعرفوا ذلك.)

على سبيل المثال، تتكاثر الكائنات الحية الدقيقة المختلفة التي تحيط بنا في كل مكان بكميات هائلة والتي لا يمكننا حتى رؤيتها بدون مجهر، بدقة في تقدم هندسي.

لنفترض أن إحدى البكتيريا تتكاثر عن طريق الانقسام إلى نصفين، مما يؤدي إلى إنتاج ذرية إلى نوعين من البكتيريا. بدوره، كل واحد منهم، عند التكاثر، ينقسم أيضًا إلى النصف، مما ينتج عنه ذرية مشتركة مكونة من 4 بكتيريا. الجيل القادم سينتج 8 بكتيريا، ثم 16 بكتيريا، 32، 64 وهكذا. ومع كل جيل لاحق، يتضاعف عدد البكتيريا. مثال نموذجي للتقدم الهندسي.)

كما أن بعض الحشرات – مثل المن والذباب – تتكاثر بشكل كبير. بالمناسبة، وأحيانًا الأرانب أيضًا.)

مثال آخر على التقدم الهندسي، الأقرب إلى الحياة اليومية، هو ما يسمى الفائدة المركبة.غالبًا ما توجد هذه الظاهرة المثيرة للاهتمام في الودائع المصرفية وتسمى رسملة الفائدة.ما هو؟

أنت نفسك لا تزال شابًا بالطبع. أنت تدرس في المدرسة، ولا تذهب إلى البنوك. لكن والديك أصبحا بالفعل بالغين وأشخاصًا مستقلين. يذهبون إلى العمل، ويكسبون المال من أجل خبزهم اليومي، ويضعون جزءًا من المال في البنك، ويدخرون.)

لنفترض أن والدك يريد توفير مبلغ معين من المال لقضاء إجازة عائلية في تركيا ويضع 50000 روبل في البنك بفائدة 10% سنويًا لمدة ثلاث سنوات مع رسملة الفائدة السنوية.علاوة على ذلك، خلال هذه الفترة بأكملها، لا يمكن فعل أي شيء بالوديعة. لا يمكنك تجديد الوديعة أو سحب الأموال من الحساب. ما مقدار الربح الذي سيحققه بعد هذه السنوات الثلاث؟

حسنًا، أولاً وقبل كل شيء، نحتاج إلى معرفة ما هي نسبة 10% سنويًا. هذا يعني انه في سنةسيقوم البنك بإضافة 10% إلى مبلغ الوديعة الأولية. من ماذا؟ بالطبع من مبلغ الإيداع الأولي.

نحسب حجم الحساب بعد سنة. إذا كان مبلغ الإيداع الأولي 50000 روبل (أي 100٪)، فبعد عام سيكون هناك مقدار الفائدة على الحساب؟ هذا صحيح، 110٪! من 50000 روبل.

لذلك نحسب 110٪ من 50000 روبل:

50000·1.1 = 55000 روبل.

أتمنى أن تفهم أن العثور على 110% من القيمة يعني ضرب تلك القيمة في الرقم 1.1؟ إذا كنت لا تفهم سبب ذلك، فتذكر الصفين الخامس والسادس. يسمى - العلاقة بين النسب المئوية والكسور والأجزاء.)

وبالتالي فإن الزيادة في السنة الأولى ستكون 5000 روبل.

كم من المال سيكون في الحساب خلال عامين؟ 60.000 روبل؟ لسوء الحظ (أو بالأحرى، لحسن الحظ)، كل شيء ليس بهذه البساطة. إن الحيلة الكاملة لرسملة الفائدة هي أنه مع كل فائدة جديدة متراكمة، سيتم أخذ هذه المصالح نفسها في الاعتبار بالفعل من المبلغ الجديد!من الذي بالفعلموجود على الحساب في اللحظة.ويتم إضافة الفائدة المستحقة عن الفترة السابقة إلى مبلغ الوديعة الأصلي، وبالتالي تشارك نفسها في حساب الفائدة الجديدة! أي أنها تصبح جزءًا كاملاً من الحساب الإجمالي. أو عامة عاصمة.ومن هنا الاسم - رسملة الفائدة.

إنه في الاقتصاد. وفي الرياضيات تسمى هذه النسب الفائدة المركبة.أو نسبة الفائدة.) حيلتهم هي أنه عند الحساب بشكل تسلسلي، يتم حساب النسب المئوية في كل مرة من القيمة الجديدة.وليس من الأصل..

لذلك، لحساب المبلغ من خلال سنتان، نحتاج إلى حساب 110% من المبلغ الذي سيكون في الحساب في سنة.وهذا هو بالفعل من 55000 روبل.

نحن نعول 110٪ من 55000 روبل:

55000·1.1 = 60500 روبل.

وهذا يعني أن نسبة الزيادة للسنة الثانية ستكون 5500 روبل، ولمدة عامين – 10500 روبل.

الآن يمكنك بالفعل تخمين أنه بعد ثلاث سنوات سيكون المبلغ الموجود في الحساب 110٪ من 60500 روبل. وهذا مرة أخرى 110% من العام السابق (العام الماضي)كميات.

وهنا نعتقد:

60500·1.1 = 66550 روبل.

الآن نقوم بترتيب مبالغنا النقدية حسب السنة بالتسلسل:

50000;

55000 = 50000 1.1;

60500 = 55000 1.1 = (50000 1.1) 1.1؛

66550 = 60500 1.1 = ((50000 1.1) 1.1) 1.1

اذا كيف كانت؟ لماذا لا يكون التقدم الهندسي؟ العضو الأول ب 1 = 50000 ، والقاسم س = 1,1 . كل مصطلح أكبر بدقة 1.1 مرة من المصطلح السابق. كل شيء يتوافق تمامًا مع التعريف.)

وكم عدد مكافآت الفائدة الإضافية التي "سيجمعها" والدك بينما كان مبلغ 50 ألف روبل موجودًا في حسابه المصرفي لمدة ثلاث سنوات؟

نحن نعد:

66550 – 50000 = 16550 روبل

ليس كثيرًا بالطبع. ولكن هذا إذا كان مبلغ الإيداع الأولي صغيرًا. ماذا لو كان هناك المزيد؟ لنفترض، ليس 50، ولكن 200 ألف روبل؟ ثم ستكون الزيادة على مدى ثلاث سنوات 66200 روبل (إذا قمت بالحسابات). وهو أمر جيد جدًا بالفعل.) ماذا لو كانت المساهمة أكبر؟ هذا كل شيء...

الخلاصة: كلما ارتفع الإيداع الأولي، كلما أصبحت رسملة الفائدة أكثر ربحية. ولهذا السبب توفر البنوك الودائع برسملة الفائدة لفترات طويلة. لنفترض لمدة خمس سنوات.

أيضًا، جميع أنواع الأمراض السيئة مثل الأنفلونزا والحصبة وحتى الأمراض الأكثر فظاعة (نفس السارس في أوائل العقد الأول من القرن الحادي والعشرين أو الطاعون في العصور الوسطى) تحب الانتشار بشكل كبير. ومن هنا حجم الأوبئة، نعم...) وكل ذلك يرجع إلى حقيقة التقدم الهندسي مع القاسم الإيجابي كله (س>1) - الشيء الذي ينمو بسرعة كبيرة! تذكر تكاثر البكتيريا: من بكتيريا واحدة يتم الحصول على اثنتين، ومن اثنين إلى أربعة، ومن أربعة إلى ثمانية، وهكذا... الأمر نفسه مع انتشار أي عدوى.)

أبسط المسائل على التقدم الهندسي.

لنبدأ، كما هو الحال دائمًا، بمشكلة بسيطة. بحتة لفهم المعنى.

1. من المعروف أن الحد الثاني للمتتابعة الهندسية هو 6، والمقام هو -0.5. أوجد الحدود الأولى والثالثة والرابعة.

لذلك أعطيت لنا بلا نهايةالتقدم الهندسي، ولكن معروف الفصل الثانيهذا التقدم:

ب 2 = 6

وبالإضافة إلى ذلك، نحن نعرف أيضا قاسم التقدم:

ف = -0.5

وتحتاج إلى العثور عليها الاول الثالثو الرابعأعضاء هذا التقدم.

لذلك نحن نتصرف. نكتب التسلسل حسب ظروف المشكلة. مباشرة في الصورة العامة حيث الحد الثاني هو ستة:

ب 1، 6،ب 3 , ب 4 , …

الآن لنبدأ بالبحث. نبدأ، كما هو الحال دائمًا، بالأبسط. يمكنك حساب الحد الثالث على سبيل المثال ب 3؟ يستطيع! أنا وأنت نعرف بالفعل (مباشرة بمعنى التقدم الهندسي) أن الحد الثالث (ب3)أكثر من الثانية (ب 2 ) الخامس "ف"مرة واحدة!

لذلك نكتب:

ب 3 =ب 2 · س

نعوض بستة في هذا التعبير بدلًا من ب 2و -0.5 بدلاً من ذلك سونحن نحسب. ولا نتجاهل الناقص أيضاً بالطبع..

ب 3 = 6·(-0.5) = -3

مثله. وتبين أن الفصل الثالث سلبي. ولا عجب: قاسمنا س- سلبي. وضرب الموجب في الناقص سيكون بالطبع ناقصًا.)

الآن نحسب الفصل الرابع التالي من التقدم:

ب 4 =ب 3 · س

ب 4 = -3·(-0.5) = 1.5

الفصل الرابع مرة أخرى مع علامة زائد. وسيكون الحد الخامس سالبًا مرة أخرى، وسيكون الحد السادس زائدًا، وهكذا. العلامات تتناوب!

وهكذا تم العثور على الحدين الثالث والرابع. والنتيجة هي التسلسل التالي:

ب 1 ؛ 6؛ -3؛ 1.5؛ ...

الآن كل ما تبقى هو إيجاد الحد الأول ب 1على قول الثاني المشهور. للقيام بذلك، نخطو في الاتجاه الآخر، إلى اليسار. وهذا يعني أننا في هذه الحالة لا نحتاج إلى ضرب الحد الثاني من التقدم في المقام، ولكن يقسم.

نقسم ونحصل على:

هذا كل شيء.) ستكون الإجابة على المشكلة كما يلي:

-12; 6; -3; 1,5; …

كما ترون، مبدأ الحل هو نفسه كما في . نعلم أيعضو و المقام - صفة مشتركة - حالةالتقدم الهندسي - يمكننا أن نجد أي عضو آخر فيه. سنجد ما نريده.) والفرق الوحيد هو أن الجمع/الطرح يتم استبداله بالضرب/القسمة.

تذكر: إذا كنا نعرف عضوًا ومقامًا واحدًا على الأقل للتقدم الهندسي، فيمكننا دائمًا العثور على أي عضو آخر في هذا التقدم.

المشكلة التالية، وفقًا للتقاليد، هي من نسخة حقيقية من OGE:

2.

...; 150؛ العاشر؛ 6؛ 1.2؛ ...

اذا كيف كانت؟ هذه المرة لا يوجد مصطلح أول ولا مقام س، يتم إعطاء مجرد تسلسل من الأرقام... شيء مألوف بالفعل، أليس كذلك؟ نعم! لقد تم بالفعل حل مشكلة مماثلة في التقدم الحسابي!

لذلك نحن لسنا خائفين. كل نفس. دعونا ندير رؤوسنا ونتذكر المعنى الأولي للتقدم الهندسي. نحن ننظر بعناية إلى تسلسلنا ونكتشف معلمات التقدم الهندسي للعناصر الرئيسية الثلاثة (الفصل الأول، المقام، رقم الفصل) المخفية فيه.

أرقام الأعضاء؟ لا يوجد أرقام عضوية، نعم... ولكن هناك أربعة متتابعأعداد. لا أرى أي فائدة في شرح معنى هذه الكلمة في هذه المرحلة.) هل هناك اثنان الأرقام المعروفة المجاورة؟يأكل! هذه هي 6 و 1.2. حتى نتمكن من العثور عليها قاسم التقدم.لذلك نأخذ الرقم 1.2 ونقسمه إلى الرقم السابق.إلى ستة.

نحن نحصل:

نحن نحصل:

س= 150·0.2 = 30

إجابة: س = 30 .

كما ترون، كل شيء بسيط للغاية. الصعوبة الرئيسية تكمن فقط في الحسابات. إنه صعب بشكل خاص في حالة القواسم السالبة والكسرية. لذلك أولئك الذين لديهم مشاكل، كرر العملية الحسابية! كيفية التعامل مع الكسور، وكيفية التعامل مع الأرقام السالبة، وما إلى ذلك... وإلا فسوف تتباطأ هنا بلا رحمة.

الآن دعونا نعدل المشكلة قليلاً. الآن سيصبح الأمر مثيرًا للاهتمام! دعونا نزيل الرقم الأخير 1.2 منه. الآن دعونا نحل هذه المشكلة:

3. تمت كتابة عدة مصطلحات متتالية للتقدم الهندسي:

...; 150؛ العاشر؛ 6؛ ...

ابحث عن مدة التقدم المشار إليها بالحرف x.

كل شيء هو نفسه، اثنان فقط متجاوران مشهورليس لدينا الآن أي أعضاء في التقدم. هذه هي المشكلة الرئيسية. لأن الضخامة سمن خلال مصطلحين متجاورين يمكننا تحديدهما بسهولة لا نستطيع.هل لدينا فرصة للتعامل مع هذه المهمة؟ بالتأكيد!

دعونا نكتب المصطلح المجهول " س"مباشرة بمعنى التقدم الهندسي! بشكل عام.

نعم نعم! الحق مع قاسم غير معروف!

من ناحية، بالنسبة لـ X يمكننا كتابة النسبة التالية:

س= 150·س

ومن ناحية أخرى، لدينا كل الحق في وصف نفس X من خلاله التاليعضوا، من خلال الستة! اقسم ستة على المقام.

مثله:

س = 6/ س

ومن الواضح أنه يمكننا الآن مساواة هاتين النسبتين. وبما أننا نعرب نفس الشيءالحجم (x) ولكن اثنين طرق مختلفة.

نحصل على المعادلة:

مضاعفة كل شيء سوبالتبسيط والاختصار نحصل على المعادلة:

س2 = 1/25

نحن نحل ونحصل على:

ف = ±1/5 = ±0.2

أُووبس! تبين أن القاسم مزدوج! +0.2 و -0.2. وأي واحد يجب أن تختار؟ نهاية؟

هادئ! نعم، المشكلة حقا حلين!لا حرج في ذلك. يحدث ذلك.) ألا تتفاجأ عندما تحصل، على سبيل المثال، على جذرين عند حل المشكلة المعتادة؟ إنها نفس القصة هنا.)

ل ف = +0.2سوف نحصل على:

س = 150 0.2 = 30

ولل س = -0,2 سوف:

س = 150·(-0.2) = -30

نحصل على إجابة مزدوجة: س = 30; س = -30.

ماذا تعني هذه الحقيقة المثيرة للاهتمام؟ وما هو موجود تقدمين، تلبية شروط المشكلة!

مثل هؤلاء:

…; 150; 30; 6; …

…; 150; -30; 6; …

كلاهما مناسب.) لماذا تعتقد أننا انقسمنا في الإجابات؟ فقط بسبب القضاء على عضو معين من التقدم (1،2)، يأتي بعد ستة. ومعرفة الحدين السابقين (n-1) واللاحقين (n+1) فقط من المتوالية الهندسية، لم يعد بإمكاننا قول أي شيء بشكل لا لبس فيه حول الحد n الذي يقع بينهما. هناك خياران - مع علامة زائد ومع ناقص.

لكن لا مشكلة. كقاعدة عامة، في مهام التقدم الهندسي هناك معلومات إضافية تعطي إجابة لا لبس فيها. دعنا نقول الكلمات: "التقدم بالتناوب"أو "التقدم ذو قاسم إيجابي"وما إلى ذلك... هذه الكلمات هي التي يجب أن تكون بمثابة دليل حول العلامة التي يجب اختيارها، زائد أو ناقص، عند إعداد الإجابة النهائية. إذا لم يكن هناك مثل هذه المعلومات، فنعم، ستكون المهمة حلين.)

الآن نقرر بأنفسنا.

4. تحديد ما إذا كان الرقم 20 عضوًا في متوالية هندسية:

4 ; 6; 9; …

5. يتم إعطاء علامة التقدم الهندسي المتناوب:

…; 5; س ; 45; …

ابحث عن مدة التقدم المشار إليها بالحرف س .

6. أوجد الحد الموجب الرابع للمتتالية الهندسية:

625; -250; 100; …

7. الحد الثاني للمتتابعة الهندسية يساوي -360، والحد الخامس له يساوي 23.04. أوجد الحد الأول من هذا التقدم.

الإجابات (في اضطراب): -15؛ 900؛ لا؛ 2.56.

تهانينا إذا نجح كل شيء!

شيء لا يصلح؟ في مكان ما كان هناك إجابة مزدوجة؟ اقرأ شروط المهمة بعناية!

المشكلة الأخيرة لا تعمل؟ لا يوجد شيء معقد هناك.) نحن نعمل مباشرة وفقًا لمعنى التقدم الهندسي. حسنا، يمكنك رسم صورة. تساعد.)

كما ترون، كل شيء أساسي. إذا كان التقدم قصيرا. ماذا لو كان طويلا؟ أم أن عدد العضو المطلوب كبير جداً؟ أود، عن طريق القياس مع التقدم الحسابي، الحصول بطريقة أو بأخرى على صيغة ملائمة تجعل من السهل العثور عليها أيمصطلح أي تقدم هندسي برقمه.دون أن تتضاعف عدة مرات س. وهناك مثل هذه الصيغة!) التفاصيل في الدرس التالي.

المتوالية الهندسية هي متوالية عددية حدها الأول غير الصفر، وكل حد لاحق يساوي الحد السابق مضروبا في نفس العدد غير الصفر.

ويشار إلى التقدم الهندسيب1،ب2،ب3، …، مليار، … .

نسبة أي حد من الخطأ الهندسي إلى حده السابق تساوي نفس العدد، أي b2/b1 = b3/b2 = b4/b3 = ... = bn/b(n-1) = b( ن+1)/مليار = … . وهذا يتبع مباشرة من تعريف التقدم الحسابي. ويسمى هذا الرقم مقام التقدم الهندسي. عادةً ما يُشار إلى مقام التقدم الهندسي بالحرف q.

تسلسل رتيب وثابت

إحدى طرق تحديد المتوالية الهندسية هي تحديد حدها الأول b1 ومقام الخطأ الهندسي q. على سبيل المثال، ب1=4، س=-2. يحدد هذان الشرطان التقدم الهندسي 4، -8، 16، -32، ….

إذا كانت q>0 (q لا تساوي 1)، فإن التقدم يكون تسلسل رتيب.على سبيل المثال، المتتابعة 2، 4،8،16،32، ... هي متوالية متزايدة بشكل رتيب (b1=2، q=2).

إذا كان المقام في الخطأ الهندسي هو q=1، فإن جميع حدود المتوالية الهندسية ستكون متساوية مع بعضها البعض. في مثل هذه الحالات يقولون أن التقدم هو تسلسل ثابت.

صيغة الحد n من التقدم الهندسي

لكي تكون المتوالية العددية (bn) متتابعة هندسية، يجب أن يكون كل عضو من أعضائها، بدءاً من الثاني، هو الوسط الهندسي للأعضاء المجاورة. أي أنه من الضروري تحقيق المعادلة التالية
(b(n+1))^2 = bn * b(n+2)، لأي n>0، حيث n ينتمي إلى مجموعة الأعداد الطبيعية N.

صيغة الحد n من التقدم الهندسي هي:

مليار = b1 * ف ^ (ن-1)،

حيث n ينتمي إلى مجموعة الأعداد الطبيعية N

صيغة لمجموع الحدود n الأولى للتقدم الهندسي

صيغة مجموع الحدود n الأولى للتقدم الهندسي لها الشكل:

Sn = (bn*q - b1)/(q-1)، حيث q لا تساوي 1.

دعونا نلقي نظرة على مثال بسيط:

في المتوالية الهندسية b1=6, q=3, n=8 ابحث عن Sn.

للعثور على S8، نستخدم صيغة مجموع الحدود n الأولى للتقدم الهندسي.

S8= (6*(3^8 -1))/(3-1) = 19,680.