Тригонометрични неравенства. Най-прости и сложни тригонометрични неравенства. Уравнения, еднородни по отношение на
Най-просто решение тригонометрични уравнения
Като начало нека си припомним формулите за решаване на най-простите тригонометрични уравнения.
- $ sinx \u003d a $
- $ cosx \u003d a $
- $ tgx \u003d a $
- $ ctgx \u003d a $
Решение на най-простите тригонометрични неравенства.
За да решим най-простите тригонометрични неравенства, първо трябва да решим съответното уравнение и след това, използвайки тригонометричния кръг, да намерим решението на неравенството. Нека разгледаме решенията на най-простите тригонометрични неравенства чрез примери.
Пример 1
$ sinx \\ ge \\ frac (1) (2) $
Нека намерим решението на тригонометричното неравенство $ sinx \u003d \\ frac (1) (2) $
\ \
Фигура 1. Решение на неравенството $ sinx \\ ge \\ frac (1) (2) $.
Тъй като неравенството има знака „по-голямо или равно на“, решението лежи върху горната дъга на окръжността (спрямо решението на уравнението).
Отговор: $ \\ left [\\ frac (\\ pi) (6) +2 \\ pi n, \\ frac (5 \\ pi) (6) +2 \\ pi n \\ right] $.
Пример 2
Намерете решението на тригонометричното неравенство $ cosx \u003d \\ frac (\\ sqrt (3)) (2) $
\ \
Нека маркираме решението върху тригонометричния кръг
Тъй като неравенството има знак „по-малко“, решението лежи върху дъгата на окръжността, разположена вляво (по отношение на решението на уравнението).
Отговор: $ \\ left (\\ frac (\\ pi) (6) +2 \\ pi n, \\ frac (11 \\ pi) (6) +2 \\ pi n \\ right) $.
Пример 3
$ tgx \\ le \\ frac (\\ sqrt (3)) (3) $
Нека намерим решението на тригонометричното неравенство $ tgx \u003d \\ frac (\\ sqrt (3)) (3) $
\ \
Тук се нуждаем и от домейн. Както си спомняме, допирателната функция $ x \\ ne \\ frac (\\ pi) (2) + \\ pi n, n \\ в Z $
Нека маркираме решението върху тригонометричния кръг
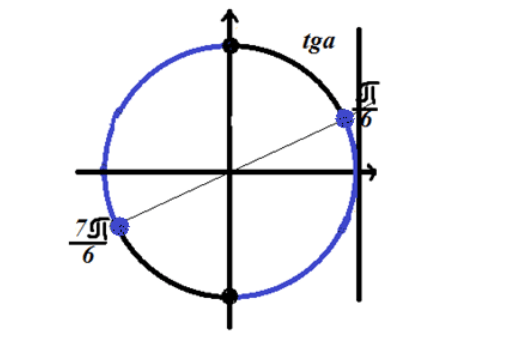
Фигура 3. Решение на неравенството $ tgx \\ le \\ frac (\\ sqrt (3)) (3) $.
Тъй като неравенството има знак по-малко или равно, решението лежи върху кръговите дъги, маркирани в синьо на фигура 3.
Отговор: $ \\ \\ ляво (- \\ frac (\\ pi) (2) +2 \\ pi n \\ дясно., \\ Ляво. \\ Frac (\\ pi) (6) +2 \\ pi n \\ дясно] \\ cup \\ ляво (\\ frac (\\ pi) (2) +2 \\ pi n, \\ дясно. \\ ляво. \\ frac (7 \\ pi) (6) +2 \\ pi n \\ дясно] $
Пример 4
Нека намерим решението на тригонометричното неравенство $ ctgx \u003d \\ sqrt (3) $
\ \
Тук се нуждаем и от домейн. Както си спомняме, допирателната функция $ x \\ ne \\ pi n, n \\ в Z $
Нека маркираме решението върху тригонометричния кръг
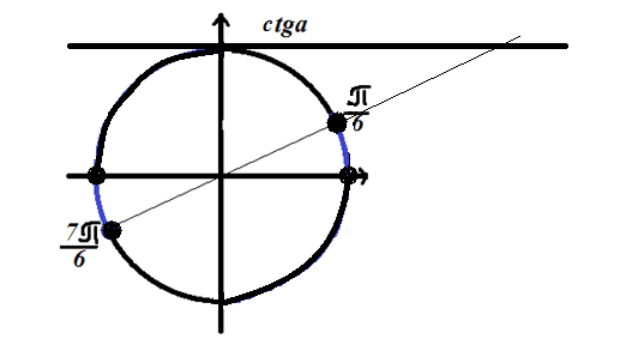
Фигура 4. Решение на неравенството $ ctgx \\ le \\ sqrt (3) $.
Тъй като неравенството има знак "по-голямо от", решението лежи върху кръговите дъги, маркирани в синьо на фигура 4.
Отговор: $ \\ \\ ляво (2 \\ pi n, \\ frac (\\ pi) (6) +2 \\ pi n \\ дясно) \\ cup \\ ляво (\\ pi +2 \\ pi n, \\ frac (7 \\ pi) ( 6) +2 \\ pi n \\ вдясно) $
Проект по алгебра "Решаване на тригонометрични неравенства" Изпълнено от ученик от 10 "Б" клас Казачкова Юлия Ръководител: учител по математика Кочакова Н.Н.
Цел Да се \u200b\u200bконсолидира материалът по темата „Разрешаване на тригонометрични неравенства“ и да се създаде бележка за учениците за подготовка за предстоящия изпит.
Цели Да обобщим материала по тази тема. Организирайте получената информация. Помислете за тази тема в изпита.
Уместност Уместността на избраната от мен тема е, че задачите по темата „Разрешаване на тригонометрични неравенства“ са включени в задачите на изпита.
Тригонометрични неравенства Неравенството е отношение, свързващо две числа или изрази, използващи един от знаците: (по-голямо от); ≥ (по-голямо или равно). Тригонометричното неравенство е неравенство, което съдържа тригонометрични функции.
Тригонометрични неравенства Решението на неравенства, съдържащи тригонометрични функции, се свежда, като правило, до решението на най-простите неравенства от вида: sin x\u003e a, sin x a, cos x a, tg x a, ctg x
Алгоритъм за решаване на тригонометрични неравенства На оста, съответстваща на дадена тригонометрична функция, маркирайте дадената цифрова стойност на тази функция. Начертайте права линия през маркираната точка, която пресича единичния кръг. Изберете точките на пресичане на линията и окръжността, като вземете предвид строгия или не стриктен знак за неравенство. Изберете дъгата на окръжността, върху която се намират решенията на неравенството. Определете стойностите на ъглите в началната и крайната точка на кръговата дъга. Запишете решението на неравенството, като вземете предвид периодичността на дадената тригонометрична функция.
Формули за решаване на тригонометрични неравенства sinx\u003e a; x (arcsin a + 2πn; π- arcsin a + 2πn). sinx а; x (- arccos a + 2πn; arccos a + 2πn). cosxа; x (арктан a + πn; + πn). tgx а; x (πn; арктан + πn). ctgx
Графично решение на основните тригонометрични неравенства sinx\u003e a
Графично решение на основните тригонометрични неравенства sinx Графично решение на основните тригонометрични неравенства cosx\u003e a Графично решение на основните тригонометрични неравенства cosx Графично решение на основните тригонометрични неравенства tgx\u003e a Графично решение на основните тригонометрични неравенства tgx Графично решение на основните тригонометрични неравенства ctgx\u003e a
Неравенствата са отношения на формата a ›b, където a и b са изрази, съдържащи поне една променлива. Неравенствата могат да бъдат строги - ‹,› и не стриктни - ≥, ≤.
Тригонометричните неравенства са изрази с формата: F (x) ›a, F (x)‹ a, F (x) ≤ a, F (x) ≥ a, при което F (x) е представена от една или повече тригонометрични функции.
Пример за най-простото тригонометрично неравенство е: sin x ‹1/2. Прието е тези проблеми да се решават графично; за това са разработени два метода.
Метод 1 - Решаване на неравенства чрез начертаване на функция
За да намерите интервала, удовлетворяващ условията на неравенството sin x ‹1/2, трябва да изпълните следните стъпки:
- На координатната ос изградете синусоида y \u003d sin x.
- Начертайте на същата ос графиката на числовия аргумент на неравенството, т.е. правата линия, преминаваща през точката ½ на ординатата OY.
- Маркирайте точки на пресичане на две графики.
- Засенчете сегмента, който е решението на примера.
Когато в израза присъстват силни знаци, пресечните точки не са решения. Тъй като най-малкият положителен период на синусоидата е 2π, ние пишем отговора по следния начин:
Ако знаците на израза не са строги, тогава интервалът от решения трябва да бъде заграден в квадратни скоби -. Отговорът на проблема може да се запише и като друго неравенство: 
Метод 2 - Решаване на тригонометрични неравенства с помощта на единичната окръжност
Подобни задачи могат лесно да бъдат решени с помощта на тригонометричната окръжност. Алгоритъмът за намиране на отговори е много прост:
- Първо нарисувайте единичен кръг.
- След това е необходимо да се отбележи стойността на дъговата функция на аргумента от дясната страна на неравенството върху дъгата на окръжността.
- Необходимо е да се начертае права линия, минаваща през стойността на дъговата функция, успоредна на оста на абсцисата (OX).
- След това остава само да се избере дъгата на окръжността, която е съвкупността от решения на тригонометричното неравенство.
- Запишете отговора в необходимата форма.
Нека анализираме стъпките на решението, като използваме примера на неравенството sin x ›1/2. Точките α и β са маркирани върху кръга - стойности
Точките на дъгата, разположени над α и β, са интервалът за решаване на даденото неравенство.
Ако трябва да решите примера за cos, тогава дъгата от отговори ще бъде разположена симетрично на оста OX, а не OY. За да разгледате разликата между интервалите на решенията за греха и cos, можете да използвате диаграмите по-долу в текста.
Графичните решения за допирателни и котангенсни неравенства ще се различават както от синус, така и от косинус. Това се дължи на свойствата на функциите.
Тангенсът на дъгата и котангенсът на дъгата са допирателни към тригонометричния кръг и минималният положителен период за двете функции е π. За да използвате бързо и правилно втория метод, трябва да запомните на коя ос са нанесени стойностите на sin, cos, tg и ctg.
Допирателната допирателна върви успоредно на оста OY. Ако поставите стойността на arctan a върху единичната окръжност, тогава втората необходима точка ще бъде разположена в диагоналната четвърт. Ъгли
Дали са точките на прекъсване за функцията, тъй като графиката има тенденция, но никога не достига.
В случай на котангенс, тангенсът протича успоредно на оста OX и функцията се прекъсва в точки π и 2π.
Сложни тригонометрични неравенства
Ако аргументът на функция за неравенство е представен не просто от променлива, а от цял \u200b\u200bизраз, съдържащ неизвестно, тогава вече говорим за сложно неравенство. Курсът и редът на неговото решение са малко по-различни от методите, описани по-горе. Да предположим, че е необходимо да се намери решение на следното неравенство:
Графичното решение предвижда изграждането на обикновена синусоида y \u003d sin x чрез произволно избрани стойности на x. Нека изчислим таблица с координати за опорните точки на графиката:
Резултатът трябва да бъде хубава крива.
За по-лесно намиране на решение заменете аргумента на сложната функция
Пресичането на две графики ви позволява да определите площта на желаните стойности, при които е изпълнено условието за неравенство.
Намереният сегмент е решението за променливата t:
Целта на задачата обаче е да се намерят всички възможни варианти на неизвестния x:
Решаването на двойното неравенство е съвсем просто, трябва да преместите π / 3 до крайните части на уравнението и да извършите необходимите изчисления:
Отговор на задачата ще изглежда като интервал за строго неравенство:
Такива задачи ще изискват опит и умение на учениците при работа с тригонометрични функции. Колкото повече учебни задачи ще бъдат решени в процеса на подготовка, толкова по-лесно и по-бързо студентът ще намери отговора на тестовия въпрос на USE.
МЕТОДИ ЗА РЕШЯВАНЕ НА ТРИГОНОМЕТРИЧНИ НЕРАВНОВОДСТВА
Уместност. Исторически на тригонометричните уравнения и неравенства е отделено специално място в училищния курс. Можем да кажем, че тригонометрията е един от най-важните раздели на училищния курс и на цялата математическа наука като цяло.
Тригонометричните уравнения и неравенства заемат едно от централните места в хода на математическата гимназия, както в съдържанието на учебния материал, така и в методите на учебно-познавателната дейност, които могат и трябва да се формират по време на тяхното изучаване и се прилагат за решаване на голям брой проблеми от теоретичен и приложен характер. ...
Решаването на тригонометрични уравнения и неравенства създава предпоставките за систематизиране на знанията на учениците, свързани с целия учебен материал по тригонометрия (например свойствата на тригонометричните функции, методи за преобразуване на тригонометрични изрази и др.) И дава възможност за установяване на ефективни връзки с изучавания материал по алгебра (уравнения, еквивалентност на уравнения, неравенства, идентични трансформации алгебрични изрази и др.).
С други думи, разглеждането на методи за решаване на тригонометрични уравнения и неравенства предполага един вид прехвърляне на тези умения в ново съдържание.
Важността на теорията и многобройните й приложения са доказателство за уместността на избраната тема. Това от своя страна ви позволява да определите целите, задачите и предмета на изследване на курсовата работа.
Цел на изследването: да се обобщят наличните видове тригонометрични неравенства, основните и специални методи за тяхното решаване, да се избере набор от задачи за решаване на тригонометрични неравенства от ученици.
Изследователски цели:
1. Въз основа на анализа на наличната литература по темата за изследване, систематизирайте материала.
2. Дайте набор от задачи, необходими за консолидиране на темата „Тригонометрични неравенства“.
Обект на изследване са тригонометрични неравенства в училищния курс по математика.
Предмет на изследване: видове тригонометрични неравенства и методи за тяхното решаване.
Теоретично значение е да организираме материала.
Практическо значение: прилагане на теоретични знания при решаване на проблеми; анализ на основните често срещани методи за решаване на тригонометрични неравенства.
Изследователски методи : анализ на научна литература, синтез и обобщение на получените знания, анализ на решаване на проблеми, търсене на оптимални методи за решаване на неравенства.
§1. Видове тригонометрични неравенства и основни методи за тяхното решаване
1.1. Най-прости тригонометрични неравенства
Две тригонометрични изразисвързани със знак или\u003e се наричат \u200b\u200bтригонометрични неравенства.
Решаването на тригонометрично неравенство означава да се намери набор от стойности на неизвестните, включени в неравенството, за които неравенството е удовлетворено.
Основната част от тригонометричните неравенства се решава чрез тяхното свеждане до решаване на най-простите:
Това може да бъде метод за факторинг, заместващ променливата ( 
, 
и т.н.), където първо се решава обичайното неравенство, а след това неравенството на формата 
и др., или други начини.
Най-простите неравенства могат да бъдат решени по два начина: с помощта на единичната окръжност или графично.
Нека бъдеf (x
- една от основните тригонометрични функции. За решаване на неравенството 
достатъчно е да се намери решението му за един период, т.е. на всеки сегмент, чиято дължина е равна на периода на функциятае
х
... Тогава ще бъде намерено решението на първоначалното неравенствох
, както и тези стойности, които се различават от тези, открити от произволен брой периоди на функциите. В този случай е удобно да се използва графичният метод.
Нека дадем пример за алгоритъм за решаване на неравенствата 
(
) и 
.
Алгоритъм за решаване на неравенството (
).
1. Формулирайте дефиницията на синуса на числох върху единичния кръг.
3. На оста на ординатата маркирайте точката с координататаа .
4. Начертайте права линия през тази точка, успоредна на оста OX и маркирайте точките на нейното пресичане с окръжността.
5. Изберете дъга на окръжност, всички точки на която имат ордината по-малка ота .
6. Посочете посоката на байпаса (обратно на часовниковата стрелка) и запишете отговора, като добавите към краищата на интервала периода на функцията2πn
,
.
Алгоритъм за решаване на неравенството .
1. Формулирайте дефиницията на тангента на числох върху единичния кръг.
2. Начертайте единичен кръг.
3. Начертайте линия на допирателните и маркирайте точка с ордината върху неяа .
4. Свържете тази точка с начало и маркирайте пресечната точка на получения отсечка линия с единичния кръг.
5. Изберете дъга от окръжност, всички точки на която имат ордината на допирателната линия, по-малка ота .
6. Посочете посоката на байпаса и запишете отговора, като вземете предвид обхвата на функцията, като добавите точкаπn
,
(числото вляво в записа винаги е по-малко от числото вдясно).
Графичната интерпретация на решенията на най-простите уравнения и формули за решаване на неравенства в общ вид са посочени в Приложението (Приложения 1 и 2).
Пример 1.
Решаване на неравенството 
.
Начертайте права линия на единичния кръг 
която пресича окръжността в точки A и B.
Всички ценностиу
на интервала NM повече
, всички точки на дъгата AMB удовлетворяват това неравенство. При всички ъгли на въртене, големи 
но по-малък 
,
ще приеме стойности по-големи от
(но не повече от един).
Фиг. 1
По този начин решението на неравенството ще бъдат всички стойности на интервала 
, т.е. 
... За да се получат всички решения на това неравенство, е достатъчно да се добавят в краищата на този интервал 
където 
, т.е. 
,
.
Имайте предвид, че стойностите 
и 
са корените на уравнението 
,
тези. 
;
.
Отговор: 
, .
1.2. Графичен метод
На практика често е полезен графичен метод за решаване на тригонометрични неравенства. Нека разгледаме същността на метода, като използваме примера за неравенство 
:
1. Ако аргументът е сложен (различен отх ), след това го заменяме ст .
2. Изграждаме в една координатна равнинаиграчка
графики на функциите 
и 
.
3. Ние откриваме такивадве съседни точки на пресичане на графикимежду коитосинусоида разположенпо-горе
прав ... Намерете абсцисите на тези точки.
4. Записваме двойното неравенство за аргументат имайки предвид косинусния период (т ще бъде между намерените абсциси).
5. Направете обратната подмяна (връщане към първоначалния аргумент) и изразете стойносттах от двойното неравенство пишем отговора под формата на числов интервал.
Пример 2. Решаване на неравенството :.
При решаване на неравенства по графичен метод е необходимо да се начертаят графиките на функциите възможно най-точно. Преобразуваме неравенството във формата:
Нека да изградим в една координатна система графиките на функциите 
и 
(фиг. 2).
Фиг. 2
Графиките на функциите се пресичат в точкаИ
с координати 
; 
... Между 
графични точки 
под точките на графиката 
... И когато стойностите на функциите са еднакви. Следователно в 
.
Отговор: 
.
1.3. Алгебричен метод
Доста често първоначалното тригонометрично неравенство може да бъде сведено до алгебрично (рационално или ирационално) неравенство чрез добре подбрана подмяна. Този метод включва трансформиране на неравенство, въвеждане на заместване или заместване на променлива.
Нека разгледаме конкретни примери за приложението на този метод.
Пример 3.
Намаляване до най-простата форма 
.
(фиг. 3)
Фиг. 3
, 
.
Отговор: 
,
Пример 4. Решаване на неравенството:
ODZ: 
, 
.
Използване на формули: 
, 
пишем неравенството под формата: 
.
Или ако приемем 
след прости трансформации получаваме
,
,
.
Решавайки последното неравенство по метода на интервалите, получаваме:
Фиг. 4
, съответно 
... Тогава от фиг. 4 следва 
където 
.
Фиг. 5
Отговор: 
, 
.
1.4. Метод на разстоянието
Обща схема за решаване на тригонометрични неравенства по интервален метод:
През тригонометрични формули фактор.
Намерете точките на прекъсване и нулите на функцията, поставете ги върху кръга.
Вземете всяка точкаДА СЕ (но не е намерен по-рано) и разберете знака на произведението. Ако произведението е положително, поставете точка зад единичната окръжност на лъча, съответстваща на ъгъла. В противен случай поставете точката вътре в кръга.
Ако дадена точка възникне четен брой пъти, ние я наричаме точка с четна кратност, ако нечетен брой пъти, точка с нечетна кратност. Начертайте дъги, както следва: започнете от точкаДА СЕ , ако следващата точка на нечетна кратност, тогава дъгата пресича окръжността в тази точка, ако точката на четна кратност, тогава тя не се пресича.
Дъгите извън кръга са положителни разстояния; вътре в кръга са отрицателни интервали.
Пример 5. Решаване на неравенството
, 
.
Точки от първата поредица: 
.
Точки от втората поредица: 
.
Всяка точка възниква нечетен брой пъти, т.е. всички точки с нечетна множественост.
Нека разберем знака на продукта на адрес 
:. Нека маркираме всички точки на единичния кръг (фиг. 6):
Фигура: 6
Отговор: 
, 
; 
, 
; 
, 
.
Пример 6 ... Решаване на неравенството.
Решение:
Намерете нулите на израза .
Получавайтеаем :
,
;
, 
;
, 
;
, 
;
На единичната окръжност серийните стойностих
1
представени с точки 
... Сериях
2
дава точки 
... Поредицах
3
получаваме две точки 
... И накрая, поредицатах
4
ще представлява точки 
... Нека поставим всички тези точки върху единичния кръг, като посочим неговата множественост в скоби до всяка от тях.
Сега оставете номера 
ще бъде равно. Правим оценка по знака:
Така че въпросътA
трябва да бъде избран на лъч, образуващ ъгъл 
с гредаО,
извън единичния кръг. (Обърнете внимание, че спомагателният лъчОТНОСНО
A
изобщо не е необходимо да се изобразява на снимката. ТочкаA
е избрано приблизително.)
Сега от точкатаA
чертаем вълнообразна непрекъсната линия последователно към всички маркирани точки. Освен това в точки нашата линия преминава от една област в друга: ако е била извън единичния кръг, тогава тя отива вътре в нея. Стигайки до точката 
, линията се връща във вътрешната област, тъй като множествеността на тази точка е четна. По същия начин в точката 
(с равномерна кратност) линията трябва да бъде обърната към външния регион. И така, нарисувахме определена картина, показана на фиг. 7. Помага за избора на необходимите области от единичния кръг. Те са маркирани със знак "+".
Фиг. 7
Окончателен отговор:
Забележка. Ако вълнообразната линия, след като заобиколи всички точки, отбелязани на единичния кръг, не може да бъде върната към точкатаA , не пресичане на кръга на „незаконното“ място, това означава, че е имало грешка в решението, а именно липсвали нечетен брой корени.
Отговор: .
§2. Комплекс от задачи за решаване на тригонометрични неравенства
В процеса на развиване на уменията на учениците за решаване на тригонометрични неравенства също могат да бъдат разграничени 3 етапа.
1. подготвителен,
2. формирането на умения за решаване на най-простите тригонометрични неравенства;
3. въвеждане на тригонометрични неравенства от други видове.
Целта на подготвителния етап е, че е необходимо да се формира у учениците способността да се използва тригонометричен кръг или графика за решаване на неравенства, а именно:
Способност за решаване на най-простите неравенства на формата ,
, ,
,
използване на свойствата на функциите на синус и косинус;
Възможност за съставяне на двойни неравенства за дъги на числов кръг или за дъги от графики на функции;
Възможност за извършване на различни трансформации на тригонометрични изрази.
Препоръчва се този етап да се приложи в процеса на систематизиране на знанията на учениците за свойствата на тригонометричните функции. Основният инструмент може да бъде задачи, предлагани на ученици и изпълнявани или под ръководството на учител, или самостоятелно, както и умения, придобити при решаване на тригонометрични уравнения.
Ето примери за такива задачи:
1
... Маркирайте точка върху единичната окръжност 
, ако
.
2.
В коя четвърт от координатната равнина е точката , ако 
по равно: 
3.
Маркирайте точки върху тригонометричния кръг , ако:
4. Намалете израза до тригонометрични функцииАз четвъртинки.
и) 
,
б) 
,
в) 
5. Дадена е дъгата.М - среднаАз-то тримесечие,R - среднаIIпетото тримесечие. Гранична стойност на променливатат за: (съставят двойно неравенство) а) дъга MP; б) дъги RM.
6. Запишете двойно неравенство за избраните раздели на графиката:
Фигура: 1
7.
Решаване на неравенства 
, 
, 
, 
.
8. Преобразуване на израз .
На втория етап на преподаване на решението на тригонометричните неравенства могат да бъдат предложени следните препоръки, свързани с методологията за организиране на дейностите на учениците. В този случай трябва да се съсредоточите върху уменията, които учениците вече трябва да работят с тригонометричен кръг или графика, формирани по време на решението на най-простите тригонометрични уравнения.
Първо, възможно е да се мотивира целесъобразността на получаването на общ метод за решаване на най-простите тригонометрични неравенства, като се позовава например на неравенство на формата 
.
Използвайки знанията и уменията, придобити на подготвителния етап, учениците ще внесат предложеното неравенство във формата 
, но може да е трудно да се намери набор от решения за произтичащото неравенство, тъй като невъзможно е да се реши само с помощта на свойствата на синусоидната функция. Тази трудност може да бъде избегната чрез позоваване на съответната илюстрация (решаване на уравнението графично или използване на единичната окръжност).
На второ място, учителят трябва да насочи вниманието на учениците към различните начини за изпълнение на заданието, да даде подходящ пример за решаване на неравенства както графично, така и с помощта на тригонометричния кръг.
Помислете за такива варианти за решаване на неравенството .
1. Решаване на неравенството с помощта на единичната окръжност.
В първия урок за решаване на тригонометрични неравенства ще предложим на учениците подробен алгоритъм за решение, който в поетапно представяне отразява всички основни умения, необходими за решаване на неравенството.
Етап 1. Нека нарисуваме единичен кръг, маркираме точката на оста на ординатите 
и изчертайте права линия през него, успоредна на оста на абсцисата. Тази линия ще пресича единичната окръжност в две точки. Всяка от тези точки представлява числа, чийто синус е .
Стъпка 2. Тази права линия е разделила кръга на две дъги. Нека да изберем този, на който са изобразени числа със синус, по-голям от ... Естествено, тази дъга се намира над изтеглената линия.
Фигура: 2
Стъпка 3.Нека да изберем един от краищата на маркираната дъга. Нека запишем едно от числата, което е представено от тази точка на единичната окръжност 
.
Стъпка 4. За да изберете числото, съответстващо на втория край на избраната дъга, ние ще „ходим“ по тази дъга от посочения край до другия. В същото време припомняме, че когато се движим обратно на часовниковата стрелка, числата, през които ще преминем, се увеличават (ако се движим в обратна посока, числата ще намаляват). Записваме числото, което е изобразено на единичния кръг до втория край на маркираната дъга 
.
По този начин виждаме, че неравенството удовлетворяват числата, за които неравенството 
... Решихме неравенството за числа, разположени в същия период на синусоидната функция. Следователно всички решения на неравенството могат да бъдат написани във формата 
Студентите трябва да бъдат помолени внимателно да разгледат чертежа и да разберат защо са налице всички решения на неравенството може да се запише като 
, 
.
Фигура: 3
Необходимо е да се обърне внимание на учениците върху факта, че когато решаваме неравенства за косинусовата функция, чертаем права линия, успоредна на оста на ординатите.
Графичен начин за решаване на неравенството.
Изграждаме диаграми 
и 
като се има предвид това 
.
Фигура: 4
След това пишем уравнението 
и неговото решение 
, 
, 
намерени с помощта на формули 
, 
, 
.
(Даванен
стойности 0, 1, 2, намираме три корена на уравнението). Стойностите 
са три последователни абсциси на пресечните точки на графиките и ... Очевидно винаги на интервала 
важи неравенството 
, и на интервала 
- неравенство 
... Ние се интересуваме от първия случай и след това, добавяйки кратно на синусовия период в краищата на този интервал, получаваме решение на неравенството като: 
, .
Фигура: пет
Обобщете. За решаване на неравенството , е необходимо да се състави съответното уравнение и да се реши. Намерете корените от получената формула 
и 
и напишете отговора на неравенството във формата: , .
Трето, фактът за множеството корени на съответното тригонометрично неравенство се потвърждава много ясно при графичното му решаване.
Фигура: 6
Необходимо е да се покаже на учениците, че цикълът, който е решението на неравенството, се повтаря след същия интервал, равен на периода на тригонометричната функция. Можете също така да разгледате подобна илюстрация за графиката на функцията синус.
Четвърто, препоръчително е да се извърши работа по актуализиране на методите на учениците за преобразуване на сумата (разликата) на тригонометричните функции в продукт, за да се привлече вниманието на учениците към ролята на тези методи при решаването на тригонометрични неравенства.
Такава работа може да бъде организирана чрез самостоятелно изпълнение на предложените от учителя задачи на учениците, сред които ще отделим следното:
Пето, от учениците трябва да се илюстрира решението на всяко най-просто тригонометрично неравенство, като се използва графика или тригонометричен кръг. Наложително е да се обърне внимание на неговата целесъобразност, по-специално на използването на окръжност, тъй като при решаване на тригонометрични неравенства, съответната илюстрация служи като много удобно средство за фиксиране на множеството от решения на това неравенство
Препоръчително е да запознаете учениците с техниките за решаване на тригонометрични неравенства, които не са най-простите по следната схема: позоваване на конкретно тригонометрично неравенство, отнасящо се до съответното тригонометрично уравнение съвместно търсене (учител - ученици) за техника на решение; независимо прехвърляне на намерената техника към други неравенства от същия тип.
За да систематизирате знанията на учениците по тригонометрия, препоръчваме да изберете конкретно такива неравенства, решението на които изисква различни трансформации, които могат да бъдат приложени в процеса на решаването му, и да съсредоточите вниманието на учениците върху техните характеристики.
Като такива продуктивни неравенства можем да предложим например следното:
В заключение даваме пример за набор от задачи за решаване на тригонометрични неравенства.
1. Решаване на неравенствата:
2. Решаване на неравенствата: 3. Намерете всички решения на неравенствата: 4. Намерете всички решения на неравенствата:и) 
удовлетворяващо условието 
;
б) 
удовлетворяващо условието 
.
5. Намерете всички решения на неравенствата:
и) ;
б) ;
в) 
;
д) 
;
д) 
.
6. Решаване на неравенствата:
и) ;
б) ;
при);
д) 
;
д);
д);
ж) 
.
7. Решаване на неравенствата:
и) 
;
б) ;
при);
д).
8. Решаване на неравенствата:
и) ;
б) ;
при);
д) 
;
д) 
;
д);
ж) 
;
з).
Препоръчително е да предложите задачи 6 и 7 на ученици, изучаващи математика на напреднало ниво, задача 8 на ученици от класове с напреднало изучаване на математика.
§3. Специални методи за решаване на тригонометрични неравенства
Специални методи за решаване на тригонометрични уравнения - тоест тези методи, които могат да се използват само за решаване на тригонометрични уравнения. Тези методи се основават на използването на свойства на тригонометрични функции, както и на използването на различни тригонометрични формули и идентичности.
3.1. Секторен метод
Помислете за секторния метод за решаване на тригонометрични неравенства. Решение на неравенствата на формата 
къдетоP
(
х
)
иВъпрос:
(
х
)
- рационални тригонометрични функции (в тях рационално се включват синуси, косинуси, допирателни и котангенти), подобни на решението на рационални неравенства. Рационални неравенства удобно е да се решава по метода на интервалите по числовата ос. Неговият аналог при решаването на рационални тригонометрични неравенства е методът на секторите в тригонометричния кръг, заsinx
иcosx
(
) или тригонометричен полукръг заtgx
иctgx
(
).
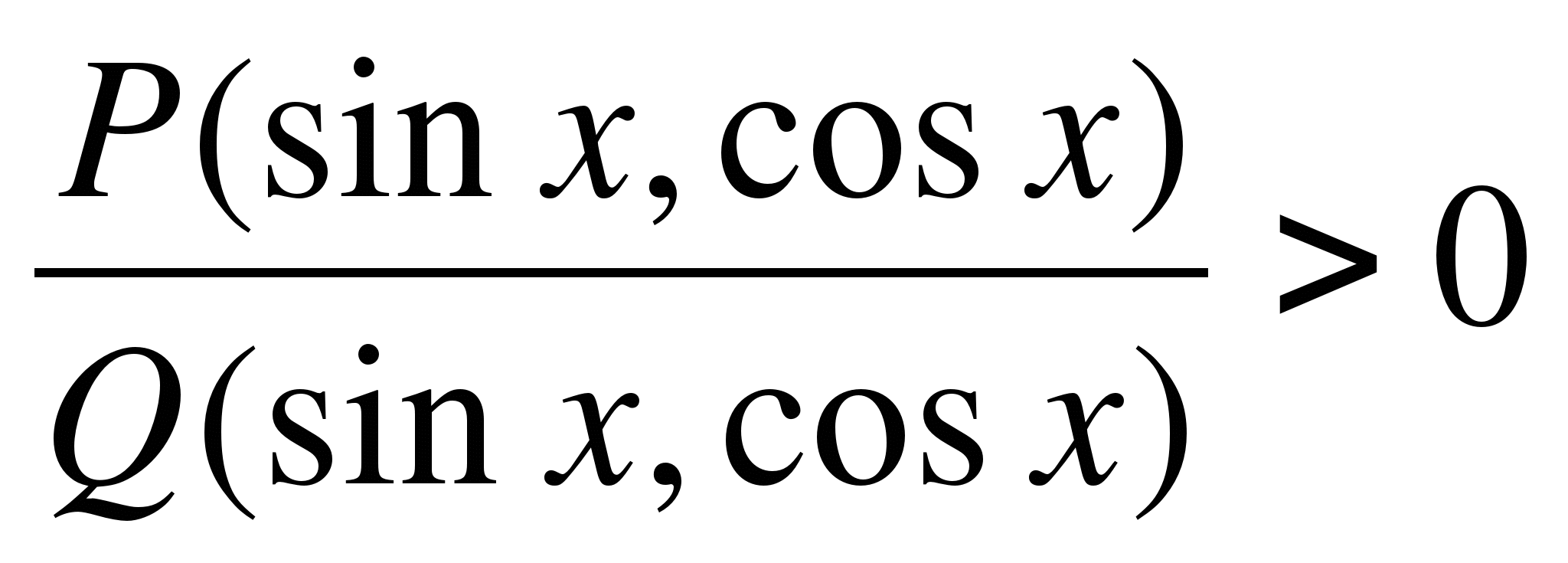
В метода на интервалите всеки линеен коефициент на числителя и знаменателя на формата 
на числовата ос има точка 
, и при преминаване през тази точка променя знака. В секторния метод всеки фактор на формуляра 
където 
- една от функциитеsinx
илиcosx
и 
, в тригонометричния кръг съответстват два ъгъла 
и 
които разделят кръга на два сектора. При преминаване през и функция променя знака.
Запомнете следното:
а) Фактори на формата 
и 
където 
, запазете знака за всички ценности 
... Такива фактори на числителя и знаменателя се отхвърлят, променяйки се (ако 
) за всеки такъв спад знакът на неравенството към обратното.
б) Фактори на формата 
и 
също се изхвърлят. Освен това, ако това са фактори на знаменателя, тогава неравенствата на формата се добавят към еквивалентната система от неравенства 
и 
... Ако това са факторите на числителя, то в еквивалентната система от ограничения те съответстват на неравенствата и в случай на строго първоначално неравенство и равенство 
и 
в случай на слабо начално неравенство. При изхвърляне на множителя 
или 
знакът за неравенство е обърнат.
Пример 1.
Решаване на неравенства: а) 
, б) 
.
имаме функция, б). Решете неравенството, което имаме,
3.2. Метод с концентричен кръг
Този метод е аналогичен на метода на паралелните числови оси при решаване на системи от рационални неравенства.
Да разгледаме пример за система от неравенства.
Пример 5.
Решете системата от най-простите тригонометрични неравенства 
Първо, нека решим всяко неравенство поотделно (Фигура 5). В горния десен ъгъл на фигурата ще посочим за кой аргумент се разглежда тригонометричната окръжност.
Фиг. 5
След това конструираме система от концентрични кръгове за аргументах ... Изчертаваме кръг и го засенчваме според решението на първото неравенство, след това чертаем кръг с по-голям радиус и го засенчваме според решението на второто, след това чертаем кръг за третото неравенство и основен кръг. Черпим лъчи от центъра на системата през краищата на дъгите, така че да пресичат всички кръгове. Оформяме решение върху основния кръг (Фигура 6).
Фиг. 6
Отговор:
, 
.
Заключение
Всички цели на курсовото проучване бяха изпълнени. Теоретичният материал е систематизиран: дадени са основните видове тригонометрични неравенства и основните методи за тяхното решаване (графичен, алгебричен, метод на интервали, сектори и метод на концентрични кръгове). За всеки метод е даден пример за решаване на неравенство. Теоретичната част беше последвана от практическата. Той съдържа набор от задачи за решаване на тригонометрични неравенства.
Тази курсова работа може да се използва от студентите за самостоятелна работа. Учениците могат да контролират нивото на овладяване на тази тема, да се упражняват в изпълнението на задачи с различна сложност.
След като разгледахме съответната литература по този въпрос, очевидно е, че можем да заключим, че способността и уменията за решаване на тригонометрични неравенства в училищния курс по алгебра и принципите на анализа са много важни, развитието на които изисква значителни усилия от страна на учителя по математика.
Следователно тази работа ще бъде полезна за учителите по математика, тъй като дава възможност за ефективно организиране на обучението на учениците по темата „Тригонометрични неравенства“.
Проучването може да продължи, като го разшири до окончателната квалификационна работа.
Списък на използваната литература
Богомолов, Н.В. Сборник с задачи по математика [Текст] / Н.В. Богомолов. - М.: Дрофа, 2009. - 206 с.
Вигодски, М. Я. Наръчник по елементарна математика [Текст] / М.Я. Вигодски. - М.: Дрофа, 2006. - 509 с.
Журбенко, Л.Н. Математика в примери и задачи [Текст] / Л.Н. Журбенко. - М.: Инфра-М, 2009. - 373 с.
Иванов, О. А. Елементарна математика за ученици, студенти и учители [Текст] / О.А. Иванов. - М.: МЦНМО, 2009. - 384 с.
Карп, А.П. Задачи по алгебра и началото на анализа за организиране на окончателното повторение и сертифициране в клас 11 [Текст] / А.П. Шаран. - М.: Образование, 2005. - 79 с.
Куланин, Е. Д. 3000 Състезателни проблеми по математика [Текст] / E.D. Куланин. - М.: Ayris-press, 2007. - 624 с.
Leibson, K.L. Сборник с практически задачи по математика [Текст] / К.Л. Лайбсън. - М.: Дрофа, 2010. - 182 с.
Локот, В.В. Задачи с параметри и тяхното решение. Тригонометрия: уравнения, неравенства, системи. 10 клас [Текст] / В.В. Лакът. - М.: ARKTI, 2008. - 64 с.
Манова, А.Н. Математика. Експресен преподавател за подготовка за изпита: учебник. надбавка [Текст] / А.Н. Манова. - Ростов на Дон: Феникс, 2012. - 541 с.
Мордкович, А.Г. Алгебра и начало на математическия анализ. 10-11 клас. Учебник за студенти от образователни институции [Текст] / А.Г. Мордкович. - М.: Airis-press, 2009. - 201 с.
Новиков, А.И. Тригонометрични функции, уравнения и неравенства [Текст] / А.И. Новиков. - М.: FIZMATLIT, 2010. - 260 с.
Оганесян, В.А. Методи на преподаване на математика в средното училище: Обща методика. Учебник. наръчник за студенти нац. - мат. фак. пед. ин-тов. [Текст] / В.А. Ованесян. - М.: Образование, 2006. - 368 с.
Олехник, С.Н. Уравнения и неравенства. Нестандартни методи за решение [Текст] / S.N. Олечник. - М.: Издателство Факториал, 1997. - 219 с.
Севрюков, П.Ф. Тригонометрични, експоненциални и логаритмични уравнения и неравенства [Текст] / P.F. Севрюков. - М.: Народно образование, 2008. - 352 с.
Сергеев, И.Н. Унифициран държавен изпит: 1000 задачи с отговори и решения по математика. Всички задачи на група C [Текст] / IN. Сергеев. - М.: Изпит, 2012. - 301 с.
Соболев, А.Б. Елементарна математика [Текст] / A.B. Соболев. - Екатеринбург: GOU VPO USTU-UPI, 2005. - 81 с.
Фенко, Л.М. Метод на интервали при решаване на неравенства и изучаване на функции [Текст] / Л.М. Фенко. - М.: Дрофа, 2005. - 124 с.
Фридман, Л.М. Теоретични основи на методите на преподаване по математика [Текст] / Л.М. Фридман. - М.: Книжарница „ЛИБРОКОМ”, 2009. - 248 с.
Приложение 1
Графична интерпретация на решения за най-простите неравенства
Фигура: 1
Фигура: 2
Фиг. 3
Фиг. 4
Фиг. 5
Фиг. 6
Фиг. 7
Фиг. 8
Приложение 2
Решения за най-простите неравенства
В практически урок ще разгледаме основните видове задачи от темата „Тригонометрия“, допълнително ще анализираме задачи с повишена сложност и ще разгледаме примери за решаване на различни тригонометрични неравенства и техните системи.
Този урок ще ви помогне да се подготвите за един от видовете задачи B5, B7, C1 и C3.
Нека започнем с повтаряне на основните типове задачи, които обсъдихме в темата „Тригонометрия“ и ще решим няколко нестандартни задачи.
Проблем номер 1... Преобразуване на ъгли в радиани и градуси: а); б).
а) Нека използваме формулата за преобразуване на градусите в радиани
Нека заместим посочената стойност в него.
б) Приложете формулата за преобразуване на радиани в градуси
Да извършим заместването 
.
Отговор. и) ; б).
Проблем номер 2... Изчислете: а); б).
а) Тъй като ъгълът е далеч над табличния, ще го намалим, като извадим синусовия период. Защото ъгълът е посочен в радиани, тогава периодът ще се счита за.
б) В този случай ситуацията е подобна. Тъй като ъгълът е посочен в градуси, тогава периодът на допирателната ще се счита за.
Полученият ъгъл, макар и по-малък от периода, е по-голям, което означава, че вече не се отнася към основната, а към разширената част на таблицата. За да не тренираме отново паметта си, като запомним разширена таблица със стойности на триъгълната функция, изваждаме периода на допирателната отново:
Използвахме странността на допирателната функция.
Отговор. а) 1; б).
Проблем номер 3... Изчисли 
, ако.
Довеждаме целия израз до допирателни, разделяйки числителя и знаменателя на фракцията на. В същото време не можем да се страхуваме от това, защото в този случай стойността на допирателната няма да съществува.
Проблем номер 4... Опростете израза.
Посочените изрази се преобразуват с помощта на формули за гласове. Те са просто необичайно написани с използване на градуси. Първият израз обикновено е число. Нека опростим всички триг функции на свой ред:
Защото , тогава функцията се променя на кофункция, т.е. към котангенса, а ъгълът пада във втората четвърт, в която първоначалната тангенса има отрицателен знак.
По същите причини, както в предишния израз, функцията се променя на кофункция, т.е. върху котангенса, а ъгълът попада в първата четвърт, в която първоначалната тангенса има положителен знак.
Нека включим всичко в опростен израз:
Проблем номер 5... Опростете израза.
Нека напишем тангента на двойния ъгъл съгласно съответната формула и опростим израза:
Последната идентичност е една от универсалните формули за заместване на косинуса.
Проблем номер 6... Изчисли.
Основното нещо е да не допускате стандартна грешка и да не давате отговор, че изразът е равен. Не можете да използвате основното свойство на арктангента, стига до него да има множител под формата на две. За да се отървем от него, ще напишем израза според формулата за тангента на двоен ъгъл, като същевременно го третираме като обикновен аргумент.
Сега можете да използвате основното свойство на арктангенса, не забравяйте, че няма ограничения за числения му резултат.
Проблем номер 7... Решете уравнението.
Когато се решава дробно уравнение, което се равнява на нула, винаги се посочва, че числителят е нула, а знаменателят не, тъй като Не можете да разделите на нула.
Първото уравнение е частен случай на най-простото уравнение, което се решава с помощта на тригонометричен кръг. Запомнете това решение сами. Второто неравенство се решава като най-простото уравнение съгласно общата формула за корените на допирателната, но само със знака не е равно.
Както можете да видите, едно семейство корени изключва друго семейство корени, които не удовлетворяват уравнението на точно същата форма. Тези. без корени.
Отговор. Без корени.
Проблем номер 8... Решете уравнението.
Веднага отбелязваме, че можете да извадите общия фактор и да го направите:
Уравнението е намалено до една от стандартните форми, когато произведението на няколко фактора е нула. Вече знаем, че в този случай или единият от тях е нула, или другият, или третият. Нека напишем това под формата на набор от уравнения:
Първите две уравнения са специални случаи на най-простите, вече сме срещали подобни уравнения много пъти, така че веднага ще посочим техните решения. Нека да намалим третото уравнение до една функция, използвайки формулата за двоен ъгъл на синус.
Нека решим последното уравнение отделно:
Това уравнение няма корени, тъй като синусоидната стойност не може да излиза извън границите 
.
По този начин решението е само първите две семейства корени, те могат да бъдат комбинирани в едно, което може лесно да бъде показано на тригонометричния кръг:
 |
Това е семейство от всички половинки, т.е.
Нека да преминем към решаване на тригонометрични неравенства. Първо, ще анализираме подхода за решаване на пример, без да използваме формули за общи решения, а с помощта на тригонометрична окръжност.
Проблем номер 9... Решаване на неравенството.
Начертайте на тригонометричния кръг помощна линия, съответстваща на синусоидната стойност, равна на, и покажете интервала от ъгли, удовлетворяващи неравенството.
 |
Много е важно да се разбере как точно да се посочи полученият диапазон от ъгли, т.е. какво е нейното начало и какъв е неговият край. Началото на пролуката ще бъде ъгълът, съответстващ на точката, в която ще влезем в самото начало на пролуката, ако се движим обратно на часовниковата стрелка. В нашия случай това е точката отляво, защото движейки се обратно на часовниковата стрелка и преминавайки правилната точка, напротив, оставяме необходимия диапазон от ъгли. Следователно точката вдясно ще съответства на края на празнината.
Сега е необходимо да разберем стойностите на ъглите на началото и края на нашия интервал от решения на неравенството. Типична грешка - това е да се покаже веднага, че дясната точка съответства на ъгъла, лявата и да се даде отговор. Това не е вярно! Имайте предвид, че току-що посочихме празнината, съответстваща на горната част на окръжността, въпреки че се интересуваме от долната, с други думи смесихме началото и края на интервала от нужни ни решения.
За да започне интервал в ъгъла на дясната точка и да завърши в ъгъла на лявата точка, първият посочен ъгъл трябва да е по-малък от втория. За да направим това, ще трябва да измерим ъгъла на дясната точка в отрицателната посока на референцията, т.е. по посока на часовниковата стрелка и ще бъде равно. След това, започвайки от него в положителната посока по посока на часовниковата стрелка, ще стигнем до дясната точка след лявата точка и ще получим стойността на ъгъла за нея. Сега началото на интервала от ъгли е по-малко от края и можем да напишем интервала от решения, без да отчитаме периода:
Като се има предвид, че такива интервали ще се повтарят безкрайно много пъти след произволен брой обороти, получаваме общо решение, вземащо предвид синусовия период:
Поставяме скоби поради факта, че неравенството е строго, и издълбаваме точките на окръжността, които съответстват на краищата на интервала.
Сравнете този отговор с общата формула на решението, която представихме в лекцията.
Отговор. 
.
Този метод е добър за разбиране откъде идват формулите за общите решения на най-простите тригонекви. Освен това е полезно за тези, които са мързеливи да научат всички тези тромави формули. Самият метод обаче също не е лесен, изберете кой подход към решението е най-удобен за вас.
За да разрешите тригонометрични неравенства, можете също да използвате графики на функции, върху които помощната линия е изградена по подобен начин на метода, показан с помощта на единичната окръжност. Ако се интересувате, опитайте се сами да разберете този подход. По-нататък ще използваме общи формули за решаване на най-простите тригонометрични неравенства.
Проблем номер 10... Решаване на неравенството.
Нека използваме формулата за общото решение, като вземем предвид, че неравенството не е строго:
Получаваме в нашия случай:
Отговор. 
Проблем номер 11... Решаване на неравенството.
Ще използваме общата формула на решението за съответното строго неравенство:
Отговор. 
.
Проблем номер 12... Решаване на неравенства: а); б).
При тези неравенства не бива да се бърза да се използват формули за общи решения или тригонометричен кръг, достатъчно е само да запомните за диапазона от стойности на синус и косинус.
а) Тъй като 
, тогава неравенството е безсмислено. Следователно няма решения.
б) Защото по същия начин синусът на всеки аргумент винаги удовлетворява неравенството, посочено в условието. Следователно всички реални стойности на аргумента задоволяват неравенството.
Отговор. а) няма решения; б).
Задание 13... Решаване на неравенството 
.
