Функции. Основните видове, графици, методи за възлагане. Майсторски клас "Производна на функция в изпита" материал за подготовка за изпита (gia) по алгебра (клас 11) по темата Задачи за графиките на производната на изпита

Общинска образователна институция

„Средно училище„ Салтиковская “

Ртищевски район на Саратовска област "

Майсторски клас по математика

в 11 клас

по тази тема

"ПРОИЗВОДНА ФУНКЦИЯ

В ЗАДАЧИТЕ НА УПОТРЕБАТА "

Провежда се от учител по математика

Белоглазова Л.С.

2012-2013 академична година

Целта на майсторския клас : да развие уменията на учениците за прилагане на теоретични знания по темата „Производно на функция“ за решаване на проблемите на единния държавен изпит.

Задачи

Образователни: обобщават и систематизират знанията на учениците по темата

„Производно на функцията“, разгледайте прототипите на USE проблемите по тази тема, предоставете на учениците възможност да тестват знанията си при самостоятелно решаване на проблеми.

Разработване: насърчават развитието на паметта, вниманието, самочувствието и уменията за самоконтрол; формирането на основни ключови компетенции (сравнение, съпоставяне, класификация на обекти, определяне на адекватни начини за решаване на образователен проблем въз основа на определени алгоритми, способност да действат самостоятелно в ситуация на несигурност, да контролират и оценяват дейността си, да откриват и отстраняват причините за възникнали трудности).

Образователни: насърчаване:

насърчаване на отговорно отношение към ученето сред учениците;

развиване на устойчив интерес към математиката;

създаване на положителна вътрешна мотивация за изучаване на математика.

Технология: индивидуално диференцирано обучение, ИКТ.

Методи на преподаване: словесно, визуално, практично, проблематично.

Форми на работа:индивидуално, фронтално, по двойки.

Оборудване и материали за урока: проектор, екран, компютър за всеки ученик, симулатор (Приложение 1),презентация за урока (Приложение № 2),индивидуално - диференцирани карти за самостоятелна работа по двойки (Приложение № 3),списък с интернет сайтове, индивидуално диференцирана домашна работа (Приложение № 4).

Обяснение за майсторския клас. Този майсторски клас се провежда в 11 клас с цел подготовка за изпита. Цели прилагането на теоретичен материал по темата "Производно на функция" при решаване на изпитни задачи.

Продължителност на майсторския клас - 30 минути.

Структура на майсторския клас

I. Организационен момент -1 мин.

II. Комуникация на темата, целите на майсторския клас, мотивация на образователните дейности - 1 мин.

III. Фронтална работа. Обучение "Задачи В8 ЕГЭ". Анализ на работата със симулатора - 6 мин.

IV. Индивидуално - диференцирана работа по двойки. Независимо решаване на проблеми В14. Взаимна проверка - 7 мин.

V. Проверка на индивидуална домашна работа. Проблем с параметър C5 на изпита

3 мин.

VI. Онлайн тестване. Анализ на резултатите от теста - 9 минути.

Vii. Индивидуално - диференцирана домашна работа -1 мин.

VIII. Оценки на урок - 1 мин.

IX. Обобщение на урока. Отражение -1 мин.

Напредък в майсторския клас

Аз .Организиращо време.

II Комуникация на темата, целите на майсторския клас, мотивация на образователните дейности.

(Слайдове 1-2, приложение № 2)

Темата на нашия урок е „Производната на функция в задачи на изпита". Всеки знае поговорката „Малка макара, но скъпа“. Производният е една от тези „макари“ в математиката. Производното се използва при решаване на много практически задачи по математика, физика, химия, икономика и други дисциплини. Позволява ви да решавате проблеми просто, красиво и интересно.

Темата „Производно“ е представена в задачите на част Б (В8, В14) от единния държавен изпит. Някои задачи от C5 също могат да бъдат решени с помощта на производна. Но решаването на тези проблеми изисква добра математическа подготовка и нестандартно мислене.

Работили сте с документи, регулиращи структурата и съдържанието на контролни измервателни материали от единния държавен изпит по математика 2013 г. Направете заключение, чекакви знания и умения са ви необходими, за да решите успешно проблемите на USE по темата "Производно".

(Слайдове 3-4, приложение № 2)

ние учил "Кодификатор съдържателни елементи в MATH за подготовка на контролни измервателни материали за единния държавен изпит ",

"Кодификатор на изискванията за нивото на обучение на завършилите", "Спецификация контролни измервателни материали ","Опция за демонстрацияконтролни измервателни материали от единния държавен изпит 2013 "иоткрих какви знания и умения за функцията и нейната производна са необходими за успешно решаване на задачи по темата „Производно“.

Необходимо е

• ЗНАЯ

p правила за изчисляване на производни;

производни на основни елементарни функции;

геометричното и физическо значение на производното;
уравнение на допирателната към графиката на функцията;
изследване на функция с помощта на производна.

Да може

изпълнявайте действия с функции (опишете поведението и свойствата на функция според графиката, намерете нейните максимални и минимални стойности).

ИЗПОЛЗВАЙТЕ

придобити знания и умения в практиката и ежедневието.

Имате теоретични познания по темата за производни. Днес ще го направимНАУЧЕТЕ СЕ ЗА ПРИЛАГАНЕ НА ЗНАНИЯТА ЗА ДЕРИВАТИВНАТА ФУНКЦИЯ ЗА РЕШАВАНЕ НА ПРОБЛЕМИТЕ ЗА ИЗПОЛЗВАНЕ. ( Слайд 4, Приложение # 2)

Не е за нищо Аристотел каза това „УМЪТ НЕ Е САМО В ЗНАНИЯ, НО И В СПОСОБНОСТТА ДА ПРИЛОЖИ ЗНАНИЯТА НА ПРАКТИКА( Слайд 5, Приложение № 2)

В края на урока ще се върнем към целта на нашия урок и ще разберем дали сме го постигнали?

III ... Фронтална работа. Обучение "Задачи B8 USE" (Приложение 1) . Анализ на работата със симулатора.

Изберете верния отговор от четирите предложени.

Каква, според вас, е трудността при изпълнението на задача B8?

Какво мислиш типични грешки да приемат завършили на изпита, когато решават този проблем?

Когато отговаряте на въпроси на задача B8, трябва да можете да опишете поведението и свойствата на функцията от графиката на производната, а от графиката на функцията - поведението и свойствата на производната на функцията. И това изисква добри теоретични познания по следните теми: „Геометрично и механично значение на производното. Допирателната към графиката на функцията. Приложение на производната за изследване на функции ”.

Анализирайте какви задачи ви създадоха затруднения?

Какви теоретични въпроси трябва да знаете?

IV. Индивидуално - диференцирана работа по двойки. Независимо решаване на проблеми В14. Взаимна проверка. (Приложение № 3)

Запомнете алгоритъма за решаване на задачи (B14 USE) за намиране на екстремни точки, екстремуми на функция, най-големите и най-малките стойности на функция на интервал, използвайки производната.

Решаване на проблеми с помощта на производната.

Студентите са изправени пред проблем:

„Помислете, възможно ли е да решим някои проблеми В14 по различен начин, без да използваме производно?“

1 чифт(Лукянова Д., Гаврюшина Д.)

1) B14. Намерете минималната точка на функцията y \u003d 10x-ln (x + 9) +6

2) B14. Намерете най-голямата стойност на функциятау =

- Опитайте се да разрешите втория проблем по два начина.

2 чифта(Санинская Т., Сазанов А.)

1) B14. Намерете най-малката стойност на функцията y \u003d (x-10) върху сегмента

2) B14. Намерете максималната точка на функцията y \u003d -

(Учениците защитават своето решение, като записват основните етапи от решаването на задачи на дъската. Студенти 1 чифт (Лукянова Д., Гаврюшина Д.) предоставят два начина за решаване на проблем №2).

Решение на проблем. Заключение за студенти:

„Някои проблеми на B14 USE за намиране на най-малката и най-голямата стойност на функция могат да бъдат решени, без да се използва производната, въз основа на свойствата на функциите.“

Анализирайте каква грешка сте допуснали в задачата?

Какви теоретични въпроси трябва да повторите?

V. Проверка на индивидуална домашна работа. Проблем с параметър C5 (USE) ( Слайдове 7-8, Приложение No2)

Лукянова К. получи индивидуална домашна работа: от ръководствата за подготовка за изпита изберете проблем с параметър (C5) и го решете с помощта на производната.

(Студентът дава решение на проблема, разчитайки на функционално-графичния метод, като един от методите за решаване на C5 USE проблемите, и дава кратко обяснение на този метод).

Какви познания за функцията и нейната производна са необходими при решаването на C5 USE проблемите?

V I. Он-лайн тестване на задачи B8, B14. Анализ на резултатите от теста.

Сайт за тестване в урока:

Кой не е допускал грешки?

Кой изпитва трудности при тестване? Защо?

В какви задачи са допуснати грешки?

Заключение: какви теоретични въпроси трябва да знаете?

VI I. Индивидуално - диференцирана домашна работа

(Слайд 9, Приложение No2), (Приложение № 4).

Подготвил съм списък със сайтове в Интернет, за да се подготвя за изпита. Можете също да отидете на тези сайтове зан – линия тестване. До следващия урок трябва да: 1) прегледате теоретичния материал по темата „Производно на функция“;

2) на сайта "Отворена банка от задачи по математика" ( ) намира прототипи на задачи B8 и B14 и решава поне 10 задачи;

3) Лукянова К., Гаврюшина Д. за решаване на задачи с параметри. Останалите ученици решават задачи 1-8 (вариант 1).

VI II. Оценки на урока.

Как бихте оценили себе си за урок?

Мислите ли, че бихте могли да се справите по-добре в клас?

IX. Обобщение на урока. Отражение

Нека обобщим нашата работа. Каква беше целта на урока? Смятате ли, че е постигнато?

Погледнете дъската и в едно изречение, като изберете началото на фразата, продължете изречението, което ви подхожда най-добре.

Почувствах…

Научих…

Успях ...

Имах възможност ...

Ще опитам …

Бях изненадан от това …

Исках…

Можете ли да кажете, че по време на урока е имало обогатяване на вашия запас от знания?

Така че повторихте теоретичните въпроси за производната на функция, приложиха своите знания при решаването на прототипите на USE задачите (B8, B14), а К. Лукянова изпълни задача C5 с параметър, който е задача с повишена сложност.

Беше удоволствие да работя с теб и надявам се, че ще успеете успешно да приложите знанията, получени в уроците по математика, не само при полагане на изпита, но и при по-нататъшното си обучение.

Бих искал да завърша урока с думите на италиански философ Тома Аквински „Знанието е толкова ценно нещо, че не е срамно да го получиш от който и да е източник“ (Слайд 10, Приложение №2).

Желая ви успех в подготовката ви за изпита!

Първо, опитайте се да намерите обхвата на функцията:

Успяхте ли? Нека сравним отговорите:

Вярно ли е? Много добре!

Сега нека се опитаме да намерим диапазона от стойности на функцията:

Намерени? Сравнете:

Събра ли се? Много добре!

Нека отново да работим с графиките, само че сега е малко по-трудно - да намерим както домейна на функцията, така и диапазона от стойности на функцията.

Как да намерите домейна и домейна на функция (разширено)

Ето какво се случи:

С графиките мисля, че разбрахте. Сега нека се опитаме да намерим обхвата на дефиницията на функцията според формулите (ако не знаете как да направите това, прочетете раздела за):

Успяхте ли? Да проверим отговорите:

1. , тъй като радикалният израз трябва да бъде по-голям или равен на нула.
2. , тъй като не можете да разделите на нула и радикалният израз не може да бъде отрицателен.
3. , тъй като съответно за всички.
4. , тъй като не можете да разделите на нула.

Все пак имаме още един не анализиран момент ...

Ще повторя определението отново и ще го подчертая:

Забеляза ли? Думата „само“ е много, много важен елемент от нашето определение. Ще се опитам да ви го обясня на пръсти.

Да приемем, че имаме функция, дадена от права линия. ... Когато заместваме тази стойност в нашето "правило" и получаваме това. Една стойност съответства на една стойност. Можем дори да създадем таблица с различни стойности и да изобразим тази функция, за да се уверим в това.

"Виж! - казвате, - "" се случва два пъти! " Така че може би параболата не е функция? Не, то е!

Фактът, че "" се случва два пъти, не е причина да обвиняваме параболата за неяснота!

Факт е, че при изчисляване на, имаме една игра. И когато изчисляваме с, имаме една игра. Така че е така, параболата е функция. Погледнете графиката:

Разбрах? Ако не, ето ви пример от реалния живот, толкова далеч от математиката!

Да приемем, че имаме група кандидати, които се срещнаха при подаване на документи, всеки от които каза в разговор къде живее:

Съгласете се, напълно възможно е няколко момчета да живеят в един град, но е невъзможно един човек да живее в няколко града едновременно. Това е като логично представяне на нашата "парабола" - няколко различни X отговарят на една и съща игра.

Сега нека измислим пример, при който зависимостта не е функция. Да кажем, че същите момчета разказаха за какви специалности са кандидатствали:

Тук имаме съвсем различна ситуация: един човек може лесно да подаде документи както за една, така и за няколко посоки. Т.е. един елемент задават се набори множество елементи комплекти. Съответно, не е функция.

Нека проверим вашите знания на практика.

Определете от снимките кое е функция и кое не:

Разбрах? Идва отговорите:

• Функцията е - B, E.
• Функцията не е - A, B, D, D.

Питате защо? Ето защо:

Във всички цифри с изключение на AT) и Д) има няколко за един!

Сигурен съм, че сега можете лесно да разграничите функция от не-функция, ще кажете какво е аргумент и какво е зависима променлива, както и да определите обхвата на валидните стойности на аргумента и обхвата на дефиниция на функцията. Преминавайки към следващия раздел, как определяте функция?

Начини за задаване на функция

Какво според вас означават думите „Задаване на функция“? Точно така, това означава да обясним на всички за каква функция в този случай става дума. И обяснете така, че всички да ви разберат правилно и графиките на функциите, съставени от хората според вашето обяснение, да са еднакви.

Как мога да направя това? Как да задам функция? Най-простият метод, който вече е използван повече от веднъж в тази статия, е използвайки формулата. Пишем формула и като заместваме стойност в нея, изчисляваме стойността. И както си спомняте, формулата е закон, правило, според което на нас и на друг човек става ясно как X се превръща в игра.

Обикновено това е точно това, което те правят - в задачите виждаме готови функции, дефинирани от формули, но има и други начини за задаване на функция, които всички забравят, във връзка с които се задава въпросът "как иначе можете да зададете функция?" прегради. Нека да разберем по ред и да започнем с аналитичния метод.

Аналитичен начин за дефиниране на функция

Аналитичният начин е да се определи функция с помощта на формула. Това е най-универсалният и изчерпателен и недвусмислен начин. Ако имате формула, тогава знаете абсолютно всичко за дадена функция - можете да съставите таблица със стойности, използвайки я, можете да изградите графика, да определите къде функцията се увеличава и къде намалява, като цяло я изследвайте изцяло.

Нека разгледаме функция. Какво значение има?

"Какво означава?" - ти питаш. Ще обясня сега.

Нека ви напомня, че в нотацията израз в скоби се нарича аргумент. И този аргумент може да бъде всеки израз, не непременно само. Съответно, какъвто и да е аргументът (израз в скоби), ние ще го запишем вместо в израза.

В нашия пример ще изглежда така:

Нека разгледаме друга задача, свързана с аналитичния начин за задаване на функция, която ще имате на изпита.

Намерете стойността на израза когато.

Сигурен съм, че първоначално сте се уплашили, когато сте видели такъв израз, но в него няма абсолютно нищо лошо!

Всичко е същото като в предишния пример: какъвто и да е аргументът (израз в скоби), ние ще го запишем вместо в израза. Например за функция.

Какво трябва да се направи в нашия пример? Вместо това трябва да пишете и вместо -:

съкратете получения израз:

Това е всичко!

Самостоятелна работа

Сега се опитайте сами да намерите значението на следните изрази:

1. , ако
2. , ако

Успяхте ли? Нека сравним нашите отговори: Свикнали сме с функция, която има формата

Дори в нашите примери ние дефинираме функция точно по този начин, но аналитично можете да определите функция имплицитно, например.

Опитайте се да изградите тази функция сами.

Успяхте ли?

Ето как го изградих.

Какво уравнение изведохме в крайна сметка?

Нали! Линеен, което означава, че графиката ще бъде права линия. Нека направим плоча, за да определим кои точки принадлежат на нашата линия:

Точно за това говорихме ... Един отговаря на няколко.

Нека се опитаме да нарисуваме какво се е случило:

Това, което имаме, има ли функция?

Точно така, не! Защо? Опитайте се да отговорите на този въпрос със снимка. Какво ти се е случило?

„Защото на една стойност отговарят няколко стойности!“

Какъв извод можем да направим от това?

Точно така, функцията не винаги може да бъде изразена изрично и не винаги това, което е „прикрито“ като функция, е функция!

Табличен начин за дефиниране на функция

Както подсказва името, този метод е прост знак. Да да. Като тази, която аз и ти вече сме измислили. Например:

Тук веднага забелязахте модел - играта е три пъти повече от X. И сега задачата за „мислене много добре“: мислите ли, че функция, дадена под формата на таблица, е еквивалентна на функция?

Няма да спорим дълго, но ще теглим!

Така. Изчертаваме функция, определена от тапета, по следните начини:

Виждате ли разликата? Въобще не става въпрос за маркираните точки! Погледни отблизо:

Видя ли го сега? Когато зададем функцията по табличен начин, ние отразяваме на диаграмата само онези точки, които имаме в таблицата и линията (както в нашия случай) минава само през тях. Когато дефинираме функция аналитично, можем да вземем всякакви точки и нашата функция не се ограничава до тях. Ето такава функция. Помня!

Графичен начин за изграждане на функция

Графичният начин за конструиране на функция е също толкова удобен. Изчертаваме нашата функция и друг заинтересован човек може да намери на какво е равна играта при определен х и т.н. Графичните и аналитичните методи са сред най-често срещаните.

Тук обаче трябва да си спомните за какво говорихме в самото начало - не всяка „извивка“, изчертана в координатната система, е функция! Помня? За всеки случай ще копирам дефиницията тук за това какво е функция:

По правило хората обикновено назовават точно тези три начина за дефиниране на функция, които сме анализирали - аналитичен (с помощта на формула), табличен и графичен, като напълно забравят, че функцията може да бъде описана устно. Като този? Това е много просто!

Функционално описание

Как описвате устно функцията? Да вземем нашия скорошен пример -. Тази функция може да бъде описана като „всяка реална стойност на x съответства на нейната тройна стойност“. Това е всичко. Нищо сложно. Вие, разбира се, ще възразите - „има толкова много сложни функции, което е просто невъзможно да се попита устно! " Да, има някои, но има функции, които е по-лесно да се опишат устно, отколкото да се използва формула. Например: "всяка естествена стойност на x съответства на разликата между цифрите, от които се състои, докато най-голямата цифра, съдържаща се в числовия запис, се приема като намалена." Сега нека видим как нашето словесно описание на функцията се прилага на практика:

Най-голямата цифра в дадено число е съответно намаляващата, след това:

Основни видове функции

Сега да преминем към най-интересното - ще разгледаме основните видове функции, с които сте работили / работите и ще работите в хода на училищната и колежната математика, тоест ще ги опознаем, така да се каже, и ще им дадем кратко описание Прочетете повече за всяка функция в съответния раздел.

Линейна функция

Функция на формата, където са реални числа.

Графиката на тази функция е права линия, така че конструкцията на линейна функция се свежда до намиране на координатите на две точки.

Положението на правата линия на координатната равнина зависи от наклона.

Обхватът на функцията (известен още като обхват на валидни стойности на аргументи) е.

Диапазон от стойности -.

Квадратична функция

Функция на формуляра, където

Графиката на функцията е парабола, когато клоновете на параболата са насочени надолу, когато - нагоре.

Много свойства на квадратна функция зависят от стойността на дискриминанта. Дискриминантът се изчислява по формулата

Положението на параболата върху координатната равнина спрямо стойността и коефициента е показано на фигурата:

Домейн

Обхватът на стойностите зависи от екстремума на дадената функция (върховата точка на параболата) и коефициента (посоката на разклоненията на параболата)

Обратна пропорция

Функция, дадена от формулата, където

Числото се нарича фактор на обратната пропорционалност. В зависимост от това каква стойност клоновете на хиперболата са на различни квадрати:

Домейн -.

Диапазон от стойности -.

РЕЗЮМЕ И ОСНОВНИ ФОРМУЛИ

1. Функцията е правило, според което всеки елемент от даден набор е свързан с един елемент от множеството.

• е формула, която обозначава функция, тоест зависимостта на една променлива от друга;
• - променлива или аргумент;
• - зависима величина - променя се, когато аргументът се промени, т.е. според определена формула, отразяваща зависимостта на една величина от друга.

2. Разрешени стойности на аргументи, или домейнът на функция е този, който е свързан с възможното, в което функцията има смисъл.

3. Диапазон от стойности на функцията - това е стойността, която приема, предвид приемливите стойности.

4. Има 4 начина за дефиниране на функция:

• аналитичен (използвайки формули);
• табличен;
• графичен
• словесно описание.

5. Основните видове функции:

• :, където, - реални числа;
• :, където;
• :, където.

Цели на урока:

Образователни: Да се \u200b\u200bнаправи преглед на теоретична информация по темата „Приложение на производно“, за да се обобщят, консолидират и подобрят знанията по тази тема.

Да научи как да прилага получените теоретични знания при решаване на различни видове математически задачи.

Помислете за методите за решаване на USE задачи, свързани с концепцията за производно на основните и повишените нива на сложност.

Образователни:

Обучение на умения: планиране на дейности, работа с оптимално темпо, работа в група, обобщаване.

Да развият способността да оценяват своите способности, способността да общуват с приятели.

Да насърчава чувството за отговорност и съпричастност, да способства за способността за работа в екип; умения .. се отнася до мнението на съучениците.

Развиване: Умейте да формулирате ключовите концепции на темата, която се изучава. Развийте умения за работа в екип.

Тип на урока: комбиниран:

Обобщение, консолидиране на умения, прилагане на свойства на елементарни функции, прилагане на вече формирани знания, умения и умения, прилагане на производна в нестандартни ситуации.

Оборудване: компютър, проектор, екран, раздаващ материал.

План на урока:

1. Организационни дейности

Отражение на настроението

2. Актуализиране на знанията на учениците

3. Устна работа

4. Самостоятелна работа в групи

5. Защита на завършената работа

6. Самостоятелна работа

7. Домашна работа

8. Резюме на урока

9. Отражение на настроението

По време на занятията

1. Отражение на настроението.

Момчета, добро утро. Дойдох на вашия урок с такова настроение (показвайки снимка на слънцето)!

Какво е вашето настроение?

На вашата маса имате карти с изображения на слънцето, слънцето зад облаците и облаците.Покажете какво е настроението ви.

2. Анализирайки резултатите от фалшивите изпити, както и резултатите от окончателното сертифициране от последните години, можем да заключим, че не повече от 30% -35% от завършилите се справят със задачите по математически анализ от работата на изпита. не всички от тях правилно извършват диагностична работа. Това е причината за избора ни. Ще упражним умението да използваме производната при решаване на проблемите с USE.

В допълнение към проблемите на окончателното сертифициране възникват въпроси и съмнения доколко знанията, придобити в тази област, могат и ще бъдат търсени в бъдеще, колко оправдани са както времевите, така и здравните разходи за изучаване на тази тема.

За какво е производното? Къде срещаме производната и я използваме? Възможно ли е без него по математика и не само?

Студентско съобщение 3 минути -

3. Устна работа.

4. Самостоятелна работа в групи (3 групи)

Задача от група 1

) Какво е геометричното значение на производната?

2) а) Фигурата показва графиката на функцията y \u003d f (x) и допирателната към тази графика, нарисувана в точката с абсцисата x0. Намерете стойността на производната на функцията f (x) в точката x0.

б) Фигурата показва графиката на функцията y \u003d f (x) и допирателната към тази графика, изчертана в точка с абсцисата x0. Намерете стойността на производната на функцията f (x) в точката x0.

Отговор от група 1:

1) Стойността на производната на функцията в точката x \u003d x0 е равна на условния коефициент на допирателната, изчертана към графиката на тази функция в точката с абсцисата x0. Нулевият коефициент е равен на допирателната на ъгъла на наклона на допирателната (или, с други думи) на допирателната на ъгъла, образуван от тангенсата и .. x

2) A) f1 (x) \u003d 4/2 \u003d 2

3) B) f1 (x) \u003d - 4/2 \u003d -2

Задача от група 2

1) Какво е физическото значение на производното?

2) Материалната точка се движи по права линия според закона
x (t) \u003d - t2 + 8t-21, където x е разстоянието от референтната точка в метри, t е времето в секунди, измерено от началото на движението. Намерете скоростта му (в метри в секунда) в момент t \u003d 3 s.

3) Материалната точка се движи по права линия според закона
x (t) \u003d ½ * t2-t-4, където x е разстоянието от референтната точка в метри, t е времето в секунди, измерено от началото на движението. В кой момент от времето (в секунди) скоростта му е била равна на 6 m / s?

Отговор от група 2:

1) Физическото (механично) значение на производното е следното.

Ако S (t) е законът на праволинейното движение на тялото, тогава производната изразява моментната скорост в момент t:

V (t) \u003d - x (t) \u003d - 2t \u003d 8 \u003d -2 * 3 + 8 \u003d 2

3) X (t) \u003d 1 / 2t ^ 2-t-4

Задача от група 3

1) Правата y \u003d 3x-5 е успоредна на допирателната към графиката на функцията y \u003d x2 + 2x-7. Намерете абсцисата на точката на допир.

2) Фигурата показва графиката на функцията y \u003d f (x), дефинирана на интервала (-9; 8). Определете броя на целочислените точки на този интервал, в който производната на функцията f (x) е положителна.

Отговор от група 3:

1) Тъй като правата линия y \u003d 3x-5 е успоредна на допирателната, наклонът на допирателната е равен на наклона на правата линия y \u003d 3x-5, т.е. k \u003d 3.

Y1 (x) \u003d 3, y1 \u003d (x ^ 2 + 2x-7) 1 \u003d 2x \u003d 2 2x + 2 \u003d 3

2) Целочислени точки са точки с целочислени абсцисни стойности.

Производната на функцията f (x) е положителна, ако функцията се увеличава.

Въпрос: Какво можете да кажете за производната на функцията, която се описва с поговорката "Колкото по-навътре в гората, толкова повече дърва за огрев"

Отговор: Производната е положителна в цялата област на дефиниция, тъй като тази функция се увеличава монотонно

6. Самостоятелна работа (за 6 варианта)

7. Домашна работа.

Учебна работа Отговори:

Обобщение на урока.

„Музиката може да повдигне или успокои душата, живописта може да угоди на окото, поезията може да събуди чувства, философията да задоволи нуждите на ума, инженерството да подобри материалната страна на живота на хората. Но математиката може да постигне всички тези цели. "

Така каза американският математик Морис Клайн.

Благодаря за вашата работа!

В задача номер 13 на USE по математика от основно ниво ще трябва да демонстрирате уменията и знанията на една от концепциите за поведението на дадена функция: производни в дадена точка или темпове на нарастване или намаляване. Теорията ще бъде добавена към тази задача малко по-късно, но това не ни пречи да разгледаме подробно няколко типични варианта.

Анализ на типичните варианти за задания № 14 на USE по математика от основно ниво

Вариант 14MB1

Графиката показва зависимостта на температурата от времето по време на загряването на двигателя на автомобила. Хоризонталната ос показва времето в минути от пускането на двигателя; вертикалната ос е температурата на двигателя в градуси по Целзий.

Използвайки графиката, задайте на всеки интервал от време характеристиката на процеса на загряване на двигателя в този интервал.

В таблицата под всяка буква посочете съответния номер.

Алгоритъм за изпълнение:

1. Изберете интервала от време, през който температурата е спаднала.
2. Нанесете владетел до 30 ° C и определете интервала от време, през който температурата е била под 30 ° C.

Решение:

Нека да изберем интервала от време, през който температурата е спаднала. Тази област се вижда с невъоръжено око, тя започва 8 минути от момента на стартиране на двигателя.

Нанесете линийка до 30 ° C и определете интервала от време, при който температурата е била под 30 ° C.

Под линийката ще има секция, съответстваща на интервала от време 0 - 1 мин.

С помощта на молив и владетел откриваме през какъв интервал от време температурата е била в диапазона от 40 ° C до 80 ° C.

Нека пропуснем перпендикулярите от точките, съответстващи на 40 ° C и 80 ° C на графиката, а от получените точки ще пропуснем перпендикулярите към оста на времето.

Виждаме, че този температурен интервал съответства на времеви интервал от 3 - 6,5 минути. Тоест от дадените в условието 3 - 6 минути.

Използваме метода за отстраняване, за да изберем липсващия отговор.

Вариант 14MB2

Решение:

Нека анализираме графиката на функция А. Ако функцията се увеличи, тогава производната е положителна и обратно. Производната на функцията е равна на нула в екстремните точки.

Първо, функцията А се увеличава, т.е. производната е положителна. Това съответства на графиките на производни 2 и 3. В максималната точка на функцията x \u003d -2, т.е. в тази точка производната трябва да бъде равна на нула. Това условие е изпълнено от графика номер 3.

Първо, функция B намалява, т.е. производната е отрицателна. На това отговарят графиките на производни 1 и 4. Максималната точка на функцията е x \u003d -2, тоест в този момент производната трябва да е равна на нула. Това условие е изпълнено от графика номер 4.

Първо, функция B се увеличава, т.е. производната е положителна. На това отговарят графиките на производни 2 и 3. Максималната точка на функцията x \u003d 1, т.е. в тази точка производната трябва да е равна на нула. Това условие е изпълнено от графика номер 2.

Чрез метода на елиминиране можем да определим, че графиката на функцията Γ съответства на графиката на производната под номер 1.

Отговор: 3421.

Вариант 14MB3

Алгоритъм на изпълнение за всяка от функциите:

1. Определете интервалите на увеличаване и намаляване на функциите.
2. Определете максималните и минималните точки на функциите.
3. Направете заключения, съобразете предложените графици.

Решение:

Нека анализираме графиката на функцията А.

Ако функцията се увеличава, тогава производната е положителна и обратно. Производната на функцията е равна на нула в екстремните точки.

Екстремната точка е точката, в която се достига максималната или минималната стойност на дадена функция.

Първо, функцията А се увеличава, т.е. производната е положителна. Това съответства на графиките на производни 3 и 4. В максималната точка на функцията x \u003d 0, т.е. в тази точка производната трябва да бъде равна на нула. Това условие е изпълнено от графика номер 4.

Нека анализираме графиката на функцията B.

Първо, функция B намалява, т.е. производната е отрицателна. Това съответства на графиките на производни 1 и 2. Минималната точка на функцията x \u003d -1, т.е. в тази точка производната трябва да е нула. Това условие е изпълнено от графика номер 2.

Нека анализираме графиката на функцията B.

Първо, функцията B намалява, т.е. производната е отрицателна. Това съответства на графиките на производни 1 и 2. Минималната точка на функцията x \u003d 0, т.е. в тази точка производната трябва да е нула. Това условие е изпълнено от графика номер 1.

Чрез метода на елиминиране можем да определим, че графиката на функцията Γ съответства на графиката на производната под номер 3.

Отговор: 4213.

Вариант 14MB4

Фигурата показва графиката на функцията и допирателните към нея в точки с абсциси A, B, C и D.В дясната колона са показани стойностите на производната в точки A, B, C и D. Използвайки графиката, присвойте на всяка точка стойността на производната на функцията в нея.

ТОЧКИ
И
AT
ОТ
д

СТОЙНОСТИТЕ НА ДЕРИВАТА
1) –4
2) 3
3) 2/3
4) -1/2

Нека си припомним какво означава производното, а именно неговата стойност в точката - стойността на производната функция в дадена точка е равна на допирателната на наклона (коефициента) на допирателната.

В отговорите имаме две положителни и две отрицателни възможности. Както си спомняме, ако коефициентът на права линия (графика y \u003d kx + b) положителен - тогава правата линия се увеличава, ако е отрицателна, тогава правата намалява.

Имаме две възходящи прави линии - в точки A и D. Сега нека си припомним какво означава стойността на коефициента k?

Коефициентът k показва колко бързо функцията се увеличава или намалява (всъщност самият коефициент k е производната на функцията y \u003d kx + b).

Следователно k \u003d 2/3 съответства на по-плоска линия - D, а k \u003d 3 - A.

По същия начин, в случай на отрицателни стойности: точка B съответства на по-стръмна права линия с k \u003d - 4, а точка C - -1/2.

Вариант 14MB5

На фигурата точките показват месечните продажби на нагреватели в магазина за уреди. Месеците са показани хоризонтално, а броят на нагревателите, продадени вертикално. За по-голяма яснота точките са свързани с линия.

Използвайки фигурата, съпоставете всеки от посочените периоди от време с характеристиките на продажбите на нагревателите.

Алгоритъм на изпълнение

Анализираме частите на графиката, съответстващи на различни сезони. Формулираме ситуациите, показани на диаграмата. Ние намираме най-подходящите варианти за отговори за тях.

Решение:

През зимата броят на продажбите надвишаваше 120 бр / месец и непрекъснато се увеличаваше. Тази ситуация отговаря на отговор номер 3. Тези. получаваме: А - 3.

През пролетта продажбите постепенно спаднаха от 120 нагревателя на месец на 50. Вариант 2 е най-близо до тази формулировка. Ние имаме: Б - 2.

През лятото броят на продажбите не се промени и беше минимален. Втората част от тази формулировка не е отразена в отговорите и само № 4 е подходяща за първата. Следователно имаме: В 4.

През есента продажбите нараснаха, но броят им през нито един от месеците не надхвърли 100 бройки. Тази ситуация е описана във вариант №1. Получаваме: G - 1.

Вариант 14MB6

Графиката показва зависимостта на скоростта на редовен автобус от времето. Вертикалната ос показва скоростта на автобуса в км / ч, а хоризонталната - времето в минути от началото на движението на автобуса.

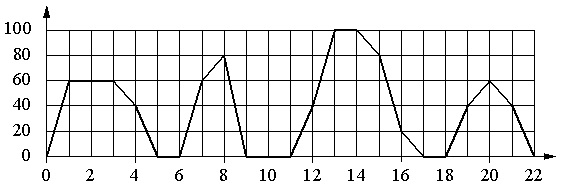
Използвайки графиката, задайте на всеки интервал от време характеристиката на движението на шината в този интервал.

Алгоритъм на изпълнение

1. Определете цената на разделяне на хоризонтална и вертикална скала.
2. Анализираме на свой ред предложените твърдения 1–4 от дясната колона („Характеристики“). Сравняваме ги с интервалите от време в лявата колона на таблицата, намираме двойките „буква-номер“ за отговора.

Решение:

Разделението на хоризонталната скала е 1 s, а вертикалната скала е 20 km / h.

1. Когато автобусът спре, скоростта му е 0. В продължение на 2 минути подред автобусът е имал нулева скорост само от 9-та до 11-та минута. Това време попада в интервала от 8–12 минути. И така, имаме двойка за отговор: Б - 1.
2. Автобусът имаше скорост от 20 км / ч и повече за няколко интервала от време. Освен това вариант А не е подходящ тук, тъй като например в 7-та минута скоростта е била 60 км / ч, вариант Б - защото вече е приложен, вариант Г - защото в началото и края на интервала автобусът е имал нулева скорост ... В този случай е подходящ вариант Б (12–16 минути); на този интервал автобусът започва да се движи със скорост 40 km / h, след това ускорява до 100 km / m и след това постепенно намалява скоростта до 20 km / h. И така, имаме: В 2.
3. Ограничението на скоростта е зададено тук. Ние не разглеждаме варианти Б и В. Останалите интервали A и D са подходящи. Следователно би било правилно първо да разгледате 4-та опция и след това да се върнете отново към 3-та.
4. От двата останали интервала само 4–8 минути са подходящи за характеристика № 4, тъй като в този интервал имаше спиране (на 6-та минута). Нямаше спирки в интервала от 18-22 минути. Получаваме: А - 4... Оттук следва, че за характеристика No 3 е необходимо да се вземе интервалът Г, т.е. оказва се двойка G - 3.

Вариант 14MB7

Фигурата на точки показва ръста на населението на Китай от 2004 до 2013 г. Хоризонтално показва годината, вертикално - ръст на населението в проценти (увеличение на населението спрямо миналата година). За по-голяма яснота точките са свързани с линия.

Използвайки фигурата, съпоставете всеки от посочените периоди от време с характеристиките на растежа на населението на Китай през този период..

Алгоритъм на изпълнение

1. Определете цената на разделяне на вертикалната скала на картината. Намира се като разлика между двойка съседни стойности на скалата, разделена на 2 (тъй като има две разделения между две съседни стойности).
2. Анализираме последователно характеристиките 1–4, дадени в условието (лява колона на таблицата). Сравняваме всеки от тях с определен период от време (дясна колона на таблицата).

Решение:

Разделението на вертикалната скала е 0,01%.

1. Спадът в растежа продължи непрекъснато от 2004 до 2010 г. През 2010–2011 г. растежът беше стабилно минимален и от 2012 г. започна да се увеличава. Тези. растежът спря през 2010г. Тази година е в периода 2009–2011. Съответно имаме: В 1.
2. Най-стръмната падаща линия на графиката на фигурата трябва да се счита за най-големия спад в растежа. Попада в периода 2006-2007. и е 0,04% годишно (0,59-0,56 \u003d 0,04% през 2006 г. и 0,56-0,52 \u003d 0,04% през 2007 г.). От тук получаваме: А - 2.
3. Растежът, посочен в характеристика № 3, започна през 2007 г., продължи през 2008 г. и завърши през 2009 г. Това съответства на период от време B, т.е. ние имаме: Б - 3.
4. Ръстът на населението започва да се увеличава след 2011 г., т.е. през 2012–2013 Следователно получаваме: G-4.

Вариант 14MB8

Фигурата показва графика на функция и допирателни към нея в точки с абсциси A, B, C и D.

В дясната колона са показани стойностите на производната на функцията в точки A, B, C и D. Използвайки графиката, присвойте на всяка точка стойността на производната на функцията в нея.

Алгоритъм на изпълнение

1. Да разгледаме двойка допирателни, имащи остър ъгъл с положителната посока на оста на абсцисата. Сравняваме ги, намираме съвпадение между двойката съответстващи стойности на производни.
2. Помислете за двойка допирателни, образуващи тъп ъгъл с положителната посока на оста на абсцисата. Сравняваме ги в абсолютна стойност, определяме съответствието им със стойностите на дериватите между двете останали в дясната колона.

Решение:

Остър ъгъл с положителната посока на оста на абсцисата се образува от производни в точка В и точка С. Тези производни имат положителни стойности. Следователно тук трябва да избирате между стойностите No 1 и 3. Прилагайки правилото, че ако ъгълът е по-малък от 45 0, тогава производната е по-малка от 1, а ако е по-голяма, тогава е по-голяма от 1, заключаваме: в точка Б производната по модул е \u200b\u200bпо-голяма от 1 в точка С - по-малко от 1. Това означава, че можете да направите двойки за отговора: В 3 и С - 1.

Производните в точка А и точка D образуват тъп ъгъл с положителната посока на абсцисата. И тук прилагаме същото правило, парафразирайки го малко: колкото повече допирателната в дадена точка е „притисната“ към линията на абсцисата (към нейната отрицателна посока), толкова по-голяма е тя в абсолютна стойност. Тогава получаваме: производната в точка А е по-малка по абсолютна стойност от производната в точка D. Следователно имаме двойки за отговор: А - 2 и D - 4.

Вариант 14MB9

Фигурата показва средната дневна температура на въздуха в Москва през януари 2011 г. Хоризонтално показва датата на месеца, вертикално - температурата в градуси по Целзий. За по-голяма яснота точките са свързани с линия.

Използвайки фигурата, съобразете характеристиката на температурната промяна с всеки от посочените периоди от време.

Алгоритъм на изпълнение

Анализираме последователно характеристики 1-4 (дясна колона), като използваме графиката на фигурата. Поставяме всеки от тях в кореспонденция с определен период от време (лява колона).

Решение:

1. Повишаване на температурата се наблюдава едва в края на периода на 22–28 януари. Тук на 27-ми и 28-ми се увеличи съответно с 1 и 2 градуса. В края на периода на 1–7 януари температурата е била стабилна (–10 градуса), в края на 8–14 и 15–21 януари е намалявала (съответно от –1 до –2 и от –11 до –12 градуса). Следователно получаваме: G - 1.
2. Тъй като всеки период от време обхваща 7 дни, температурата трябва да се анализира, започвайки от 4-ия ден на всеки период. Температурата остана непроменена в продължение на 3-4 дни само от 4 до 7 януари. Следователно получаваме отговора: А - 2.
3. Месечната минимална температура се наблюдава на 17 януари. Този брой е между 15 и 21 януари. Следователно имаме двойка: В 3.
4. Температурният максимум падна на 10 януари и възлезе на +1 градуса. Тази дата попада в периода 8-14 януари. Следователно имаме: Б - 4.

Вариант 14MB10

Алгоритъм на изпълнение

1. Стойността на функцията в дадена точка е положителна, ако тази точка се намира над оста Ox.
2. Производната в точка е по-голяма от нула, ако допирателната към тази точка образува остър ъгъл с положителната посока на оста Ox.

Решение:

Точка А. Той се намира под оста Ox, така че стойността на функцията в него е отрицателна. Ако нарисуваме тангенс в него, тогава ъгълът между него и положителната посока Ox ще бъде около 90 0, т.е. образува остър ъгъл. Така че, в този случай характеристика номер 3 е подходяща. Тези. ние имаме: А - 3.

Точка Б. Намира се над оста Вол, т.е. точка има положителна стойност на функцията. Допирателната линия в тази точка ще бъде доста близо до оста на абсцисата, образувайки тъп ъгъл (малко по-малък от 180 0) с положителната си посока. Съответно производната в този момент е отрицателна. По този начин тук е подходяща характеристика 1. Получаваме отговора: В 1.

Точка С. Точката се намира под оста Ox, допирателната в нея образува голям тъп ъгъл с положителната посока на оста на абсцисата. Тези. в точка С стойността както на функцията, така и на производната е отрицателна, което съответства на характеристика No2. Отговор: С - 2.

Точка D. Точката е над оста Ox и допирателната в нея образува остър ъгъл с положителната посока на оста. Това предполага, че и стойността на функцията, и стойността на производната тук са по-големи от нула. Отговор: D - 4.

Вариант 14MB11

На фигурата точките показват месечните продажби на хладилници в магазина за домакински уреди. Месеците се показват хоризонтално, а броят на хладилниците, продадени вертикално. За по-голяма яснота точките са свързани с линия.

Използвайки картината, съпоставете всеки от посочените периоди от време с характеристиките на продажбите на хладилниците.

Правата y \u003d 3x + 2 е допирателна към графиката на функцията y \u003d -12x ^ 2 + bx-10. Намерете b, като се има предвид, че абсцисата на точката на допир е по-малка от нула.

Покажи решение

Решение

Нека x_0 е абсцисата на точката на графиката на функцията y \u003d -12x ^ 2 + bx-10, през която преминава допирателната към тази графика.

Стойността на производната в точката x_0 е равна на наклона на допирателната, тоест y "(x_0) \u003d - 24x_0 + b \u003d 3. От друга страна, допирателната точка принадлежи както на графиката на функцията, така и на допирателната, т.е. 3x_0 + 2. Получаваме системата от уравнения \\ begin (случаи) -24x_0 + b \u003d 3, \\\\ - 12x_0 ^ 2 + bx_0-10 \u003d 3x_0 + 2. \\ край (случаи)

Решавайки тази система, получаваме x_0 ^ 2 \u003d 1, което означава или x_0 \u003d -1, или x_0 \u003d 1. Според условието абсцисата на точката на допир е по-малка от нула, следователно x_0 \u003d -1, тогава b \u003d 3 + 24x_0 \u003d -21.

Отговор

Състояние

Фигурата показва графиката на функцията y \u003d f (x) (която е прекъсната линия, съставена от три отсечки с права линия). Използвайки фигурата, изчислете F (9) -F (5), където F (x) е един от антидеривативите на функцията f (x).

Покажи решение

Решение

Според формулата на Нютон-Лайбниц разликата F (9) -F (5), където F (x) е един от антидеривативите на функцията f (x), е равна на площта на криволинейния трапец, ограничен от графиката на функцията y \u003d f (x), от правите линии y \u003d 0 , x \u003d 9 и x \u003d 5. Според графиката определяме, че посоченият извит трапец е трапец с основи, равни на 4 и 3 и височина 3.

Площта му е \\ frac (4 + 3) (2) \\ cdot 3 \u003d 10.5.

Отговор

Източник: „Математика. Подготовка за изпита-2017. Профилно ниво". Изд. Ф. Ф. Лисенко, С. Ю. Кулабухова.

Състояние

Фигурата показва графиката на y \u003d f "(x) - производната на функцията f (x), дефинирана на интервала (-4; 10). Намерете интервалите на намаляване на функцията f (x). В отговора посочете дължината на най-големия от тях.

Покажи решение

Решение

Както знаете, функцията f (x) намалява на тези интервали, във всяка точка, от които производната f "(x) е по-малка от нула. Като се има предвид, че е необходимо да се намери дължината на най-големия от тях, три такива интервала естествено се различават от фигурата: (-4; -2) ; (0; 3); (5; 9).

Дължината на най-големия от тях - (5; 9) е равна на 4.

Отговор

Източник: „Математика. Подготовка за изпита-2017. Профилно ниво ". Изд. Ф. Ф. Лисенко, С. Ю. Кулабухова.

Състояние

Фигурата показва графиката y \u003d f "(x) - производната на функцията f (x), дефинирана на интервала (-8; 7). Намерете броя на максималните точки на функцията f (x), принадлежащи към интервала [-6; -2].

Покажи решение

Решение

Графиката показва, че производната f "(x) на функцията f (x) променя знака от плюс към минус (в такива точки ще има максимум) в точно една точка (между -5 и -4) от интервала [-6; -2 Следователно има точно една максимална точка на интервала [-6; -2].

Отговор

Източник: „Математика. Подготовка за изпита-2017. Профилно ниво ". Изд. Ф. Ф. Лисенко, С. Ю. Кулабухова.

Състояние

Фигурата показва графика на функцията y \u003d f (x), дефинирана на интервала (-2; 8). Определете броя точки, в които производната на функцията f (x) е 0.

Покажи решение

Решение

Равенство на нула на производната в дадена точка означава, че допирателната към графиката на функцията, нарисувана в тази точка, е успоредна на оста Ox. Следователно намираме точки, в които допирателната към графиката на функцията е успоредна на оста Ox. На тази диаграма такива точки са екстремни точки (точки от максимум или минимум). Както можете да видите, има 5 екстремни точки.

Отговор

Източник: „Математика. Подготовка за изпита-2017. Профилно ниво ". Изд. Ф. Ф. Лисенко, С. Ю. Кулабухова.

Състояние

Правата y \u003d -3x + 4 е успоредна на допирателната към графиката на функцията y \u003d -x ^ 2 + 5x-7. Намерете абсцисата на точката на допир.

Покажи решение

Решение

Наклонът на правата линия към графиката на функцията y \u003d -x ^ 2 + 5x-7 в произволна точка x_0 е равен на y "(x_0). Но y" \u003d - 2x + 5, така че y "(x_0) \u003d - 2x_0 + 5. посоченият в условието коефициент на права линия y \u003d -3x + 4 е -3. Паралелните линии имат същия наклон. Следователно намираме такава стойност на x_0, че \u003d -2x_0 + 5 \u003d -3.

Получаваме: x_0 \u003d 4.

Отговор

Източник: „Математика. Подготовка за изпита-2017. Профилно ниво ". Изд. Ф. Ф. Лисенко, С. Ю. Кулабухова.

Състояние

Фигурата показва графиката на функцията y \u003d f (x) и точките -6, -1, 1, 4 са маркирани на оста на абсцисата. В коя от тези точки стойността на производната е най-малка? Посочете тази точка във вашия отговор.