ფუნქციის სინგულარული წერტილები და მათი კლასიფიკაცია. იზოლირებული სინგულარული წერტილები. ნარჩენები და მათი გამოთვლის ფორმულები

ორი ავტონომიური დიფერენციალური განტოლების სისტემებით აღწერილი მოდელები.

ფაზის თვითმფრინავი. ფაზის პორტრეტი. იზოკლინის მეთოდი. მთავარი იზოკლინები. სტაბილური მდგომარეობის სტაბილურობა. ხაზოვანი სისტემები. საკვანძო წერტილების ტიპები: კვანძი, უნაგირი, ფოკუსი, ცენტრი. მაგალითი: პირველი რიგის ქიმიური რეაქციები.

ბიოლოგიური სისტემების თვისებების ხარისხობრივი მოდელირების ყველაზე საინტერესო შედეგები მიღებულ იქნა ორი დიფერენციალური განტოლების მოდელებზე, რაც საშუალებას იძლევა ხარისხობრივი შესწავლა მეთოდის გამოყენებით. ფაზის თვითმფრინავი. განვიხილოთ ზოგადი ფორმის ორი ავტონომიური ჩვეულებრივი დიფერენციალური განტოლების სისტემა

(4.1)

P(x,y), Q(x,y)- უწყვეტი ფუნქციები განსაზღვრულია ზოგიერთ დომენში გევკლიდეს სიბრტყე ( x, y- დეკარტის კოორდინატები) და აქვს ამ არეალში რიგის უწყვეტი წარმოებულები არანაკლებ პირველზე.

რეგიონი გშეიძლება იყოს შეუზღუდავი ან შეზღუდული. თუ ცვლადები x, yაქვთ სპეციფიკური ბიოლოგიური მნიშვნელობა (ნივთიერებების კონცენტრაცია, სახეობების სიმრავლე), ყველაზე ხშირად ტერიტორია გარის მარჯვენა ნახევარსიბრტყის დადებითი კვადრატი:

0 £ x< ¥ ,0 £ წ< ¥ .

ნივთიერებების კონცენტრაცია ან სახეობების სიმრავლე ასევე შეიძლება შეიზღუდოს ზემოდან გემის მოცულობით ან ჰაბიტატის ფართობით. შემდეგ ცვლადების დიაპაზონს აქვს ფორმა:

0 £ x< x 0 , 0 £ წ< y 0 .

ცვლადები x, yდროში ცვლილება განტოლებათა სისტემის შესაბამისად (4.1), ისე, რომ სისტემის თითოეული მდგომარეობა შეესაბამება ცვლადების მნიშვნელობების წყვილს ( x, y).

პირიქით, თითოეული წყვილი ცვლადი ( x, y) შეესაბამება სისტემის გარკვეულ მდგომარეობას.

განვიხილოთ სიბრტყე კოორდინატთა ღერძებით, რომელზედაც გამოსახულია ცვლადების მნიშვნელობები x, y. ყოველი წერტილი მეს სიბრტყე შეესაბამება სისტემის გარკვეულ მდგომარეობას. ასეთ სიბრტყეს ეწოდება ფაზის სიბრტყე და ასახავს სისტემის ყველა მდგომარეობის მთლიანობას. წერტილს M(x, y) ეწოდება გამომსახველი ან გამომსახველი წერტილი.

ნება საწყის დროს t=t 0 წარმოადგენს წერტილის კოორდინატებს მ 0 (x(ტ 0),ი(ტ 0)). დროის ყოველ მომდევნო მომენტში ტგამოსახული წერტილი გადაადგილდება ცვლადების მნიშვნელობების ცვლილების მიხედვით x(ტ),ი(ტ). ქულების ნაკრები მ(x(ტ), y(t)) ფაზის სიბრტყეზე, რომლის პოზიცია შეესაბამება სისტემის მდგომარეობებს დროთა განმავლობაში ცვლადების შეცვლის პროცესში x(t), y(t)(4.1) განტოლებების მიხედვით, ეწოდება ფაზის ტრაექტორია.

ფაზის ტრაექტორიების ნაკრები ცვლადების სხვადასხვა საწყისი მნიშვნელობებისთვის იძლევა სისტემის ადვილად თვალსაჩინო "პორტრეტს". Შენობა ფაზის პორტრეტისაშუალებას გაძლევთ გამოიტანოთ დასკვნები ცვლადების ცვლილებების ხასიათის შესახებ x, yგანტოლებათა თავდაპირველი სისტემის ანალიტიკური ამონახსნების ცოდნის გარეშე(4.1).

ფაზის პორტრეტის გამოსახატავად აუცილებელია ფაზის სიბრტყის თითოეულ წერტილში სისტემის ტრაექტორიების მიმართულებების ვექტორული ველის აგება. ნამატის მითითებითდ t>0,ვიღებთ შესაბამის ნამატებს დ xდა დ წგამონათქვამებიდან:

დ x=P(x,y)დ ტ,

დ y=Q(x,y)დ ტ.

ვექტორის მიმართულება dy/dxწერტილში ( x, y) დამოკიდებულია ფუნქციების ნიშანზე P(x, y), Q(x, y)და შეიძლება წარმოდგენილი იყოს ცხრილით:

P(x,y)>0,Q(x,y)>0
P(x,y)<0,Q(x,y)<0
P(x,y)>0,Q(x,y)<0
P(x,y)<0,Q(x,y)>0

.(4.2)

ამ განტოლების ამოხსნა y=y(x, გ), ან ირიბად ფ(x, y)=c,სადაც თანარის ინტეგრაციის მუდმივი, იძლევა განტოლების ინტეგრალური მრუდების ოჯახს (4.2) - ფაზის ტრაექტორიებისისტემა (4.1) თვითმფრინავზე x, y.

იზოკლინის მეთოდი

ფაზური პორტრეტის შესაქმნელად გამოიყენება იზოკლინის მეთოდი -ფაზურ სიბრტყეზე დახაზულია ხაზები, რომლებიც კვეთენ ინტეგრალურ მოსახვევებს ერთი კონკრეტული კუთხით. იზოკლინის განტოლების მიღება ადვილია (4.2). დავსვათ

სადაც ა– გარკვეული მუდმივი. მნიშვნელობა აწარმოადგენს ტანგენსის ფერდობის ტანგენტს ფაზის ტრაექტორიაზე და შეუძლია მიიღოს მნიშვნელობები -¥ +-მდე ¥ . ჩანაცვლება ნაცვლად dy/dx(4.2) რაოდენობაში ავიღებთ იზოკლინის განტოლებას:

.(4.3)

განტოლება (4.3) განსაზღვრავს სიბრტყის თითოეულ წერტილში ერთადერთ ტანგენტს შესაბამის ინტეგრალურ მრუდზე, გარდა იმ წერტილისა, სადაც P(x,y)= 0, Q (x, y) = 0 , რომელშიც ტანგენტის მიმართულება ხდება განუსაზღვრელი, ვინაიდან წარმოებულის მნიშვნელობა ხდება განუსაზღვრელი:

.

ეს წერტილი არის ყველა იზოკლინების გადაკვეთის წერტილი - სპეციალური წერტილი.ის ერთდროულად ქრება ცვლადების დროის წარმოებულებს xდა წ.

ამრიგად, სინგულარულ წერტილში ცვლადების ცვლილების ტემპები ნულის ტოლია. მაშასადამე, ფაზური ტრაექტორიების დიფერენციალური განტოლებების სინგულარული წერტილი (4.2) შეესაბამება სისტემის სტაციონარული მდგომარეობა(4.1) და მისი კოორდინატები არის ცვლადების სტაციონარული მნიშვნელობები x, y.

განსაკუთრებით საინტერესოა ძირითადი იზოკლინები:

dy/dx=0, P(x, y)=0 – ჰორიზონტალური ტანგენტების იზოკლინი და

dy/dx=¥ , ქ(x, y)=0 – ვერტიკალური ტანგენტების იზოკლინი.

მთავარი იზოკლინების აგებით და მათი გადაკვეთის წერტილის მოძიებით (x,y), რომლის კოორდინატები აკმაყოფილებს პირობებს:

ამრიგად, ჩვენ ვიპოვით ფაზის სიბრტყის ყველა იზოკლინის გადაკვეთის წერტილს, სადაც ტანგენტების მიმართულება ფაზის ტრაექტორიებზე განუსაზღვრელია. ეს - ცალკეული წერტილი, რაც შეესაბამება სისტემის სტაციონარული მდგომარეობა(ნახ. 4.2).

სისტემას (4.1) აქვს იმდენი სტაციონარული მდგომარეობა, რამდენიც არის მთავარი იზოკლინების გადაკვეთის წერტილები ფაზის სიბრტყეზე.

თითოეული ფაზის ტრაექტორია შეესაბამება დინამიკური სისტემის მოძრაობათა ერთობლიობას, რომელიც გადის იმავე მდგომარეობებში და განსხვავდება ერთმანეთისგან მხოლოდ დროის მითითების დასაწყისით.

თუ კოშის თეორემის პირობები დაკმაყოფილებულია, მაშინ სივრცის თითოეული წერტილის გავლით x, y, tგადის ერთი ინტეგრალური მრუდი. იგივე ითქმის, ავტონომიის წყალობით, ფაზის ტრაექტორიებისთვის: ფაზის სიბრტყის თითოეულ წერტილში გადის უნიკალური ფაზის ტრაექტორია.

სტაბილური მდგომარეობის სტაბილურობა

დაე, სისტემა იყოს წონასწორობაში.

მაშინ წარმომადგენლობითი წერტილი მდებარეობს სისტემის ერთ-ერთ სინგულარულ წერტილში, რომელშიც, განსაზღვრებით:

.

სინგულარული წერტილი სტაბილურია თუ არა, განისაზღვრება იმით, ტოვებს თუ არა წარმომადგენლობითი წერტილი სტაციონარული მდგომარეობიდან მცირე გადახრით. როგორც გამოიყენება ორი განტოლების სისტემაზე, ენაში სტაბილურობის განმარტებაე, დშემდეგნაირად.

წონასწორობის მდგომარეობა სტაბილურია, თუ წონასწორობის მდგომარეობიდან გადახრების რომელიმე მოცემული ზონისთვის (ე )ფართობი შეიძლება დაზუსტდეს დ (ე ), ირგვლივ წონასწორობის მდგომარეობას და აქვს ისეთი თვისება, რომ არ აქვს ტრაექტორია, რომელიც იწყება რეგიონის შიგნით დ , არასოდეს მიაღწევს საზღვარს ე . (ნახ. 4.4)

სისტემების დიდი კლასისთვის - უხეში სისტემები – რომლის ქცევის ბუნება არ იცვლება განტოლებების ტიპის მცირე ცვლილებით, ინფორმაცია სტაციონარული მდგომარეობის სიახლოვეს ქცევის ტიპის შესახებ შეგიძლიათ მიიღოთ არა ორიგინალის, არამედ გამარტივებულის შესწავლით. ხაზოვანისისტემა.

ხაზოვანი სისტემები.

განვიხილოთ ორი წრფივი განტოლების სისტემა:

.(4.4)

Აქ ა ბ გ დ- მუდმივები, x, y- დეკარტის კოორდინატები ფაზის სიბრტყეზე.

ზოგადი გამოსავალი მოიძებნება შემდეგნაირად:

.(4.5)

ჩაანაცვლეთ ეს გამონათქვამები (4.4) და შეამცირეთ ე ლ ტ:

(4.6)

განტოლებათა ალგებრული სისტემა (4.6) უცნობებთან A, Bაქვს არანულოვანი ამონახსნი მხოლოდ იმ შემთხვევაში, თუ მისი განმსაზღვრელი, რომელიც შედგება უცნობის კოეფიციენტებისგან, ნულის ტოლია:

.

ამ დეტერმინანტის გაფართოებით, ჩვენ ვიღებთ სისტემის დამახასიათებელ განტოლებას:

.(4.7)

ამ განტოლების ამოხსნა იძლევა ინდიკატორის მნიშვნელობებსლ 1,2 , რომლის მიხედვითაც შესაძლებელია არანულოვანი მნიშვნელობები ადა ბ(4.6) განტოლების ამონახსნები. ეს ღირებულებებია

.(4.8)

თუ რადიკალური გამოხატულება უარყოფითია, მაშინლ 1,2 რთული კონიუგირებული რიცხვები. დავუშვათ, რომ განტოლების (4.7) ორივე ფესვს აქვს არანულოვანი რეალური ნაწილები და რომ არ არსებობს მრავალი ფესვი. მაშინ სისტემის ზოგადი ამონახსნები (4.4) შეიძლება წარმოდგენილი იყოს მაჩვენებლების წრფივი კომბინაცია ექსპონენტებთან.ლ 1 , ლ 2 :

(4.9)

სისტემის შესაძლო ტრაექტორიების ბუნების გასაანალიზებლად ფაზურ სიბრტყეზე ვიყენებთ წრფივი ჰომოგენური კოორდინატების ტრანსფორმაცია,რაც სისტემას მოუტანს კანონიკური ფორმა:

,(4.10)

რაც იძლევა უფრო მოხერხებულ წარმოდგენას ფაზის სიბრტყეზე თავდაპირველ სისტემასთან შედარებით (4.4). შემოვიტანოთ ახალი კოორდინატებიξ , η ფორმულების მიხედვით:

(4.1)

წრფივი ალგებრის კურსიდან ცნობილია, რომ თუ რეალური ნაწილები ნულის ტოლი არ არისლ 1 , ლ 2 ორიგინალური სისტემა (4.4) გარდაქმნების დახმარებით (4.11) ყოველთვის შეიძლება გარდაიქმნას კანონიკურ ფორმაში (4.10) და მისი ქცევის შესწავლა ფაზის სიბრტყეზე.ξ , η . განვიხილოთ სხვადასხვა შემთხვევები, რომლებიც შეიძლება წარმოაჩინოს აქ.

ფესვები λ 1 , λ 2 - მოქმედი და იგივე ნიშნის

ამ შემთხვევაში ტრანსფორმაციის კოეფიციენტები რეალურია, ჩვენ გადავდივართ რეალური სიბრტყიდანx, yრეალურ სიბრტყემდე ξ, η. განტოლების (4.10) მეორეს პირველზე გაყოფით მივიღებთ:

.(4.12)

ამ განტოლების ინტეგრირებით, ჩვენ ვხვდებით:

სად .(4.13)

მოდით შევთანხმდეთ გავიგოთ λ 2 დამახასიათებელი განტოლების ფესვი დიდი მოდულით, რომელიც არ არღვევს ჩვენი მსჯელობის ზოგადობას. მაშინ, ვინაიდან განსახილველ შემთხვევაში ფესვები λ 1 , λ2 - მოქმედი და იგივე ნიშნის,ა>1 , და საქმე გვაქვს პარაბოლური ტიპის ინტეგრალურ მრუდებთან.

ყველა ინტეგრალური მრუდი (ღერძის გარდა η , რომელიც შეესაბამება ) შეხება ღერძის საწყისთან ξ, რომელიც ასევე არის განტოლების (4.11) ინტეგრალური მრუდი. კოორდინატების წარმოშობა არის სინგულარული წერტილი.

ახლა გავარკვიოთ წარმომადგენლობითი წერტილის მოძრაობის მიმართულება ფაზის ტრაექტორიების გასწვრივ. თუ ლ 1, λ 2 უარყოფითია, მაშ, როგორც ჩანს განტოლებებიდან (4.10), |ξ|, |η| დროთა განმავლობაში მცირდება. გამომსახველი წერტილი უახლოვდება საწყისს, მაგრამ არასოდეს აღწევს მას. წინააღმდეგ შემთხვევაში, ეს ეწინააღმდეგება კოშის თეორემას, რომელიც ამბობს, რომ ფაზის სიბრტყის თითოეულ წერტილში მხოლოდ ერთი ფაზის ტრაექტორია გადის.

ისეთი სინგულარული წერტილი, რომელშიც ინტეგრალური მრუდები გადის, ისევე როგორც პარაბოლების ოჯახი გადის საწყისში, ეწოდება კვანძი (ნახ. 4.5)

კვანძის ტიპის წონასწორობის მდგომარეობა λ 1, λ 2 < 0 ლიაპუნოვის მიხედვით სტაბილურია, ვინაიდან გამომსახველი წერტილი ყველა ინტეგრალური მრუდის გასწვრივ მოძრაობს კოორდინატების საწყისისკენ. ეს სტაბილური კვანძი. თუ ლ 1, λ 2 > 0, მაშინ |ξ|, |ი| დროთა განმავლობაში იზრდება და წარმომადგენლობითი წერტილი შორდება საწყისს. ამ შემთხვევაში, სინგულარული წერტილი– არასტაბილური კვანძი .

ფაზის სიბრტყეზე x, y დარჩება ინტეგრალური მრუდების ქცევის ზოგადი ხარისხობრივი ხასიათი, მაგრამ ინტეგრალური მრუდების ტანგენტები არ დაემთხვევა კოორდინატთა ღერძებს. ამ ტანგენტების დახრის კუთხე განისაზღვრება კოეფიციენტების შეფარდებით α , β , γ , δ განტოლებებში (4.11).

ფესვები λ 1 , λ 2 მოქმედებს და აქვთ სხვადასხვა ნიშნები.

კონვერტაცია საწყისიკოორდინატები x, y კოორდინატებს ξ, η ისევ რეალური. კანონიკური ცვლადების განტოლებებს კვლავ აქვთ ფორმა (4.10), მაგრამ ახლა ნიშნები λ. 1, λ 2 განსხვავებული. ფაზის ტრაექტორიის განტოლებას აქვს ფორმა:

სად, (4.14)

ინტეგრირება (4.14), ჩვენ ვხვდებით

(4.15)

ეს განტოლება განსაზღვრავს ჰიპერბოლური ტიპის მრუდების ოჯახს, სადაც ორივე კოორდინატი ღერძიაარის ასიმპტოტები (ზე ა=1 ჩვენ გვექნებოდა ტოლფერდა ჰიპერბოლების ოჯახი). კოორდინატთა ღერძები ასევე განუყოფელი მრუდებია ამ შემთხვევაში– ეს იქნება ერთადერთი ინტეგრალური მრუდი, რომელიც გადის საწყისზე. თითოეულირომელთაგან შედგება სამი ფაზის ტრაექტორია: ორი მოძრაობა წონასწორობის მდგომარეობისკენ (ან წონასწორობის მდგომარეობიდან დაშორებით) და წონასწორობის მდგომარეობიდან. ყველა სხვა ინტეგრალური მრუდი– არის ჰიპერბოლები, რომლებიც არ გადიან საწყისს (ნახ. 4.6) ეს სინგულარული წერტილი ე.წ "უნაგირს ». მთის უნაგირის მახლობლად დონის ხაზები ფაზური ტრაექტორიების მსგავსად იქცევა უნაგრის სიახლოვეს.

განვიხილოთ წარმომადგენლობითი წერტილის მოძრაობის ბუნება წონასწორობის მდგომარეობის მახლობლად ფაზის ტრაექტორიების გასწვრივ. მოდით, მაგალითად,λ 1 >0, λ 2<0 . შემდეგ ღერძზე განთავსებული წარმომადგენლობითი წერტილი ξ , დაშორდება საწყისს და განთავსდება ღერძზე η – განუსაზღვრელი ვადით მიუახლოვდება კოორდინატების წარმოშობას, სასრულ დროში მიღწევის გარეშე. სადაც არ უნდა იყოს გამომსახველი წერტილი საწყის მომენტში (გამონაკლისია სინგულარული წერტილისა და ასიმპტოტის წერტილები η =0), ის საბოლოოდ დაშორდება წონასწორობის მდგომარეობას, მაშინაც კი, თუ დასაწყისში ის მოძრაობს ერთ-ერთი ინტეგრალური მრუდის გასწვრივ სინგულარული წერტილისკენ.

აშკარაა რომ უნაგირის ტიპის სინგულარული წერტილი ყოველთვის არასტაბილურია . მხოლოდ სპეციალურად შერჩეულ საწყის პირობებში ასიმპტოტზეη =0 სისტემა მიუახლოვდება წონასწორობის მდგომარეობას. თუმცა, ეს არ ეწინააღმდეგება მტკიცებას, რომ სისტემა არასტაბილურია. თუ ითვლი, რომ ფაზის სიბრტყეზე სისტემის ყველა საწყისი მდგომარეობა თანაბრად სავარაუდოა, მაშინ ასეთი საწყისი მდგომარეობის ალბათობა, რომელიც შეესაბამება მიმართულებით მოძრაობასრომ სინგულარული წერტილი ნულის ტოლია. აქედან გამომდინარე, ნებისმიერი რეალური მოძრაობა ამოიღებს სისტემას წონასწორობის მდგომარეობიდან.კოორდინატებზე დაბრუნებაx, y,ჩვენ ვიღებთ იგივე ხარისხობრივ სურათს საწყისების ირგვლივ ტრაექტორიების მოძრაობის ბუნების შესახებ.

კვანძისა და უნაგირების განხილულ შემთხვევებს შორის საზღვარი არის შემთხვევაროდესაც ერთ-ერთი დამახასიათებელი მაჩვენებელი, მაგალითად λ 1 , ქრება, რაც ხდება მაშინ, როდესაც სისტემის განმსაზღვრელი- გამოხატვა adbc=0(იხ. ფორმულა 4.8 ). ამ შემთხვევაში (4.4) განტოლებების მარჯვენა მხარის კოეფიციენტები ერთმანეთის პროპორციულია.:

და სისტემას აქვს თავისი წონასწორობის მდგომარეობა წრფის ყველა წერტილი:

დარჩენილი ინტეგრალური მრუდები არის პარალელური ხაზების ოჯახი დახრილობით , რომლის გასწვრივ წარმომადგენლობითი წერტილები ან უახლოვდებიან წონასწორობის მდგომარეობას ან შორდებიან მისგან, λ დამახასიათებელი განტოლების მეორე ფესვის ნიშნის მიხედვით. 2 = ა+დ.(ნახ.4. 7 ) ამ შემთხვევაში წონასწორობის მდგომარეობის კოორდინატები დამოკიდებულია ცვლადების საწყის მნიშვნელობაზე.

ფესვები λ 1 , λ 2 – კომპლექსიკონიუგატი

ამ შემთხვევაში, რეალურადxდა წჩვენ აქვს რთული კონიუგატები ξ , η (4.10) . თუმცა, კიდევ ერთი შუალედური ტრანსფორმაციის შემოღებით, ამ შემთხვევაშიც შესაძლებელია განხილვის დაყვანა რეალურ ხაზოვან ჰომოგენურ ტრანსფორმაციამდე. დავსვათ:

(4.16)

სადაც ა, ბ,და u,v – რეალური ღირებულებები. შეიძლება ნაჩვენები იყოს, რომ ტრანსფორმაციაx, yრომ u,v არის, ჩვენი დაშვებით, რეალური, წრფივი, ერთგვაროვანი არანულოვანი დეტერმინანტით. განტოლებების გამო(4.10, 4.16) გვაქვს:

სადაც

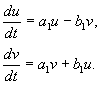(4.17)

განტოლებიდან მეორის გაყოფა პირველზე, ვიღებთ:

რომლის ინტეგრირება უფრო ადვილია, თუ გადავალთ პოლარულ კოორდინატულ სისტემაზე (r, φ ) . ჩანაცვლების შემდეგვიღებთ საიდან:

.(4.18)

ამრიგად, ფაზის სიბრტყეზეu, vსაქმე გვაქვს ლოგარითმული სპირალების ოჯახთან, რომელთაგან თითოეულს აქვსწარმოშობის ასიმპტომური წერტილი.სინგულარული წერტილი, რომელიც არის სპირალის ფორმის ყველა ინტეგრალური მრუდის ასიმპტომური წერტილი, ჩაბუდებული მეგობარიმეგობარი, დაურეკა ფოკუსირება ( ნახ.4.8 ) .

განვიხილოთ წარმომადგენლობითი წერტილის მოძრაობის ბუნება ფაზის ტრაექტორიების გასწვრივ. (4.17) განტოლების პირველის გამრავლებაuდა მეორე ვდა დავამატებთ, მივიღებთ:

სად

დაე ა 1 < 0 (ა 1 = რეλ ) . შემდეგ წარმომადგენლობითი წერტილი განუწყვეტლივ უახლოვდება საწყისს სასრულ დროში მისვლის გარეშე. ეს ნიშნავს, რომ ფაზის ტრაექტორიები არის გრეხილი სპირალები და შეესაბამება დამსხვრეულ რხევებს.ცვლადები. ეს - სტაბილური ფოკუსირება .

სტაბილური ფოკუსის შემთხვევაში, ისევე როგორც სტაბილური კვანძის შემთხვევაში, დაკმაყოფილებულია არა მხოლოდ ლიაპუნოვის მდგომარეობა, არამედ უფრო მკაცრი მოთხოვნაც. კერძოდ, ნებისმიერი საწყისი გადახრის შემთხვევაში, სისტემა საბოლოოდ დაუბრუნდება წონასწორობის პოზიციას მაქსიმალურად ახლოს. ისეთ სტაბილურობას, რომლის დროსაც საწყისი გადახრები არა მხოლოდ არ იზრდება, არამედ იშლება, ნულამდე მიდრეკილებით, ე.წ. აბსოლუტური სტაბილურობა .

თუ ფორმულაში (4.18) ა 1 >0 , მაშინ გამომსახველი წერტილი შორდება საწყისს და საქმე გვაქვს არასტაბილური ფოკუსი . თვითმფრინავიდან გადაადგილებისასu,vფაზის სიბრტყემდეx, წსპირალები ასევე სპირალად დარჩება, მაგრამ დეფორმირებული იქნება.

განვიხილოთ ახლა შემთხვევა, როდესაცა 1 =0 . ფაზის ტრაექტორიები თვითმფრინავზეu, vიქნება წრეები რომელიც თვითმფრინავშიx, yმორგებული ელიფსები:

ამრიგად, ზეa 1=0 სპეციალური წერტილის მეშვეობითx= 0,y= 0 არ გადის ინტეგრალური მრუდი. ასეთ იზოლირებულ სინგულურ წერტილს, რომლის მახლობლად ინტეგრალური მრუდები არის დახურული მრუდები, კერძოდ, ელიფსები, რომლებიც ერთმანეთშია ჩასმული და ერთობიან წერტილს, ეწოდება ცენტრი.

ამრიგად, შესაძლებელია წონასწორობის ექვსი ტიპი, რაც დამოკიდებულია დამახასიათებელი განტოლების ფესვების ბუნებაზე (4.7). ფაზის ტრაექტორიების ხედი თვითმფრინავზე x, yამ ექვსი შემთხვევისთვის ნაჩვენებია ნახ. 4.9.

ბრინჯი. 4.9.ხაზოვანი განტოლებათა სისტემისთვის სტაციონარული მდგომარეობის მიმდებარედ ფაზური პორტრეტების ტიპები (4.4).

წონასწორობის მდგომარეობის ხუთი ტიპი უხეშია, მათი ბუნება არ იცვლება განტოლებების (4.4) მარჯვენა მხარეს საკმარისად მცირე ცვლილებებით. ამ შემთხვევაში ცვლილებები მცირე უნდა იყოს არა მხოლოდ მარჯვენა მხარეს, არამედ მათ პირველი რიგის წარმოებულებშიც. წონასწორობის მეექვსე მდგომარეობა - ცენტრი - არ არის უხეში. განტოლებების მარჯვენა მხარის პარამეტრებში მცირე ცვლილებებით, ის გადადის სტაბილურ ან არასტაბილურ ფოკუსში.

ბიფურკაციის დიაგრამა

შემოვიღოთ აღნიშვნა:

. (4.11)

შემდეგ დამახასიათებელი განტოლება შეიძლება დაიწეროს სახით:

. (4.12)

განვიხილოთ თვითმფრინავი მართკუთხა დეკარტის კოორდინატებით ს , დ და მონიშნეთ მასზე არეები, რომლებიც შეესაბამება ამა თუ იმ ტიპის წონასწორობის მდგომარეობას, რომელიც განისაზღვრება დამახასიათებელი განტოლების ფესვების ბუნებით.

.(4.13)

წონასწორული მდგომარეობის სტაბილურობის პირობა იქნება y-ის უარყოფითი რეალური ნაწილის არსებობალ 1 და ლ 2 . ამისათვის აუცილებელი და საკმარისი პირობაა უთანასწორობების შესრულებას > 0, დ > 0 . დიაგრამაზე (4.15) ეს მდგომარეობა შეესაბამება პარამეტრის სიბრტყის პირველ მეოთხედში მდებარე წერტილებს. ცალკეული წერტილი იქნება აქცენტი თულ 1 და ლ 2 კომპლექსი. ეს მდგომარეობა შეესაბამება სიბრტყის იმ წერტილებს, რომლებისთვისაც , იმათ. წერტილები პარაბოლის ორ ტოტს შორისს 2 = 4 დ. ნახევრადღერძული წერტილები ს = 0, დ>0, შეესაბამება ცენტრის ტიპის წონასწორობის მდგომარეობებს. ანალოგიურად,ლ 1 და ლ 2 - მოქმედებს, მაგრამ განსხვავებული ნიშნები, ე.ი. სინგულარული წერტილი იქნება უნაგირ თუ დ<0, და ა.შ. შედეგად, ვიღებთ პარამეტრის სიბრტყის დანაყოფის დიაგრამას ს, დ, სხვადასხვა ტიპის წონასწორობის მდგომარეობების შესაბამისი რეგიონებში.

ბრინჯი. 4.10.ბიფურკაციის დიაგრამა

წრფივი განტოლებათა სისტემისათვის 4.4

თუ წრფივი სისტემის კოეფიციენტები ა ბ გ დდამოკიდებულია ზოგიერთ პარამეტრზე, მაშინ როდესაც ეს პარამეტრი შეიცვლება, მნიშვნელობებიც შეიცვლებას , დ . საზღვრების გავლისას ფაზის პორტრეტის ბუნება თვისობრივად იცვლება. ამიტომ, ასეთ საზღვრებს ბიფურკაციის საზღვრები ეწოდება - საზღვრის მოპირდაპირე მხარეს სისტემას აქვს ორი ტოპოლოგიურად განსხვავებული ფაზის პორტრეტი და, შესაბამისად, ქცევის ორი განსხვავებული ტიპი.

დიაგრამა გვიჩვენებს, თუ როგორ შეიძლება მოხდეს ასეთი ცვლილებები. თუ გამოვრიცხავთ განსაკუთრებულ შემთხვევებს - კოორდინატების წარმოშობას - მაშინ ადვილი მისახვედრია, რომ უნაგირი y-ღერძის გადაკვეთისას სტაბილურად ან არასტაბილურ კვანძში შეიძლება შევიდეს. სტაბილურ კვანძს შეუძლია გადავიდეს უნაგირზე ან სტაბილურ ფოკუსზე და ა.შ. გაითვალისწინეთ, რომ სტაბილური კვანძი-სტაბილური ფოკუსი და არასტაბილური კვანძი-არასტაბილური ფოკუსის გადასვლები არ არის ორმხრივი, რადგან ფაზის სივრცის ტოპოლოგია ამ შემთხვევაში არ იცვლება. მე-6 ლექციაში უფრო დეტალურად ვისაუბრებთ ფაზური სივრცის ტოპოლოგიასა და ბიფურკაციის გადასვლებზე.

ბიფურკაციის გადასვლების დროს იცვლება სინგულარული წერტილის სტაბილურობის ბუნება. მაგალითად, ცენტრიდან სტაბილური ფოკუსი შეიძლება გადაიქცეს არასტაბილურ ფოკუსად. ამ ბიფურკაციას ე.წ ანდრონოვი-ჰოპფის ბიფურკაციაიმ მეცნიერთა სახელებით, რომლებმაც ის შეისწავლეს. არაწრფივ სისტემებში ამ ბიფურკაციის დროს იბადება ზღვრული ციკლი და სისტემა ხდება თვითრხევადი (იხ. ლექცია 8).

მაგალითი. ხაზოვანი ქიმიური რეაქციების სისტემა

ნივთიერება Xშემოედინება გარედან მუდმივი სიჩქარით, გადაიქცევა Y ნივთიერებად და ნივთიერების კონცენტრაციის პროპორციული სიჩქარით ი, ამოღებულია რეაქციის სფეროდან. ყველა რეაქცია არის პირველი რიგის, გარდა მატერიის გარედან შემოდინებისა, რომელსაც აქვს ნულოვანი რიგი. რეაქციის სქემა ასე გამოიყურება:

(4.14)

და აღწერილია განტოლებათა სისტემით:

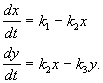(4.15)

ჩვენ ვიღებთ სტაციონარულ კონცენტრაციებს მარჯვენა მხარის ნულთან გათანაბრებით:

.(4.16)

განვიხილოთ სისტემის ფაზის პორტრეტი. სისტემის მეორე განტოლება (4.16) გავყოთ პირველზე. ჩვენ ვიღებთ:

.(4.17)

განტოლება (4.17) განსაზღვრავს ცვლადების ქცევას ფაზის სიბრტყეზე. მოდით ავაშენოთ ამ სისტემის ფაზური პორტრეტი. პირველ რიგში, ჩვენ ვხატავთ მთავარ იზოკლინებს ფაზის სიბრტყეზე. ვერტიკალური ტანგენტების იზოკლინის განტოლება:

ჰორიზონტალური ტანგენტების იზოკლინის განტოლება:

სინგულარული წერტილი (სტაციონარული მდგომარეობა) მდებარეობს ძირითადი იზოკლინების გადაკვეთაზე.

ახლა განვსაზღვროთ, რა კუთხით კვეთენ კოორდინატთა ღერძები ინტეგრალურ მრუდებს.

თუ x= 0, შემდეგ.

ამრიგად, ტანგენსი დახრილობის ტანგენსი ინტეგრალურ მოსახვევებზე y=y(x), y-ღერძის გადაკვეთა x=0, უარყოფითია ზედა ნახევარ სიბრტყეში (შეგახსენებთ, რომ ცვლადები x, yაქვს კონცენტრაციის მნიშვნელობები და ამიტომ ჩვენ გვაინტერესებს მხოლოდ ფაზის სიბრტყის ზედა მარჯვენა კვადრატი). ამ შემთხვევაში, ტანგენტის დახრილობის კუთხის ტანგენტის მნიშვნელობა იზრდება საწყისიდან დაშორებით.

განვიხილოთ ღერძი y= 0. ამ ღერძის გადაკვეთაზე ინტეგრალური მრუდები აღწერილია განტოლებით

ზე აბსცისის ღერძის გადაკვეთის ინტეგრალური მრუდების დახრილობის ტანგენსი დადებითია და იზრდება ნულიდან უსასრულობამდე x.

ზე.

შემდეგ, შემდგომი ზრდით, ფერდობის ტანგენსი მცირდება აბსოლუტურ მნიშვნელობაში, რჩება უარყოფითი და მიდრეკილია -1-მდე x ® ¥ . ძირითადი იზოკლინების და კოორდინატთა ღერძების ინტეგრალური მრუდების მიმართ ტანგენტების ცოდნით, ადვილია ფაზური ტრაექტორიების მთლიანი სურათის აგება.

სინგულარული წერტილის სტაბილურობის ბუნება დადგინდება ლიაპუნოვის მეთოდის გამოყენებით. სისტემის დამახასიათებელ განმსაზღვრელს აქვს ფორმა:

.

განმსაზღვრელი გაფართოებით, ვიღებთ სისტემის დამახასიათებელ განტოლებას: , ე.ი. დამახასიათებელი განტოლების ფესვები ორივე უარყოფითია. ამრიგად, სისტემის სტაციონარული მდგომარეობა არის სტაბილური კვანძი. ამავე დროს, ნივთიერების კონცენტრაცია Xმიდრეკილია სტაციონარული მდგომარეობისკენ ყოველთვის მონოტონურად, Y ნივთიერების კონცენტრაცია შეიძლება გაიაროს min ან max. ასეთ სისტემაში ოსცილატორული რეჟიმები შეუძლებელია.

დაე zq - f(z) ფუნქციის ცალმხრივი წერტილი, t.s. f(z)მაგრამ ამ ეტაპზე ანალიტიკურია (კერძოდ, მასში შეიძლება არ იყოს განსაზღვრული). თუ არსებობს წერტილის ასეთი პუნქციური მეზობლობა zq (ანუ ნაკრები O z - zq f(z) არის ალიატი, მაშინ ზოდაურეკა იზოლირებული სინგულარული წერტილიფუნქციები ვ(ზ).ეს განმარტება შენარჩუნებულია საქმეშიც zn =ოო, თუ იოდი არის წერტილის პუნქცია zq = oo მესმის სიმრავლე z >ᲛᲔ ᲕᲐᲠ - საწყისზე ორიენტირებული რაღაც წრის გამოჩენა. სხვა სიტყვებით რომ ვთქვათ, ცალკეული წერტილი zq იზოლირებულია, თუ არსებობს ამ წერტილის სამეზობლო, რომელშიც არის სხვა ცალკეული წერტილები, რომლებიც განსხვავდება zq. ყველგან ქვემოთ, ჩვენ განვიხილავთ მხოლოდ ერთმნიშვნელოვანი სიმბოლოს ცალკეულ წერტილებს (ფუნქცია f(z)ითვლება უნიკალური).

ფუნქციის ქცევიდან გამომდინარე f(z)ზე z -> zqარსებობს სამი სახის სინგულარული წერტილი. იზოლირებული სინგულარული წერტილი zq ფუნქციები f(z)მოუწოდა:

1) მოსახსნელი სინგულარული წერტილითუ არსებობს სასრული ზღვარი

2) ბოძითუ არის ლიმიტი

3) არსებითი წერტილი,თუ f(z) არ აქვს არც სასრული და არც უსასრულო ზღვარი ზ-> zq.

მაგალითი 26.1. ვაჩვენოთ, რომ სამივე ტიპის სინგულარული წერტილი არის რეალიზებული. განიხილეთ ვ(z)= წერტილი zq = 0 იზოლირებულია

ამ ფუნქციის ცალკეული წერტილი. ფორმულის გამოყენებით (22.12) ვიღებთ გაფართოებას

საიდანაც გამომდინარეობს, რომ არსებობს ლიმი ფი(ზ)= 1. ამიტომ, zq = 0 არის

არის ფუნქციის მოსახსნელი სინგულარული წერტილი ფი (ზ).

ფუნქცია f'j(z) =--- აქვს ბოძი ერთ წერტილში ზო= 1 იმიტომ

2 რ„X

ახლა განიხილეთ ფუნქცია )z(z)= e 1 ^ r და აჩვენე რომ ზო = O არის ამ ფუნქციის არსებითი სინგულარული წერტილი. როცა ისწრაფვის ზნულამდე რეალური ღერძის გასწვრივ, f ფუნქციის მარცხენა და მარჯვენა ზღვრები (z)განსხვავებული: ლიმ თან 1 / 1 = 0, ლიმ 1 /* =-ით os. ეს გულისხმობს,

x->0-0 x->0+0

რა f:i(z)არ აქვს არც სასრული და არც უსასრულო ზღვარი 2-ისთვის -> ოჰ, ე.ი. zq = 0 არის ამ ფუნქციის არსებითად სინგულარული წერტილი. (გაითვალისწინეთ, რომ როგორც წერტილი მიდრეკილია z-iyნულამდე წარმოსახვითი ღერძის ფუნქციაზე

არანაირი შეზღუდვა არ აქვს.)

რა თქმა უნდა, არის არაიზოლირებული სინგულარული წერტილებიც. Მაგალითად. ფუნქციას აქვს პოლუსები წერტილებში z n = -, პ= ±1, ±2,...

აქედან გამომდინარე, Zq = 0 არის ამ ფუნქციის არაიზოლირებული სინგულარული წერტილი: ამ წერტილის ნებისმიერ (თვითნებურად მცირე) სამეზობლოში არის სხვა სინგულარული წერტილები. გ გვ.

დაე ზო-ფუნქციის საბოლოო იზოლირებული სინგულარული წერტილი ვ(ზ).მერე f(z)მსგავსია ზოგიერთ პუნქციურ უბანში წერტილის 0 Zo ზოეს სამეზობლო შეიძლება ჩაითვალოს რგოლად შიდა რადიუსით r = 0. თეორემა 25.1-ით განსახილველ უბანში ფუნქცია f(z)შეიძლება გაფართოვდეს Laurent სერიაში (25.2). ჩვენ ვაჩვენებთ, რომ ფუნქციის ქცევა 2-ისთვის -> zq (ანუ სინგულარული წერტილის ტიპი ზო)დამოკიდებულია დაშლის ძირითადი ნაწილის ფორმაზე (25.2); ეს გარემოება ხსნის ტერმინის „მთავარი ნაწილის“ წარმოშობას.

თეორემა 2G.2. f(z) ფუნქციის იზოლირებული სინგულარული წერტილი zo არის ამოღებული, თუ და მხოლოდ იმ შემთხვევაში, თუ ლორაპის გაფართოებას ამ წერტილის პუნქციას აქვს ოიდი.

იმათ. შედგება მხოლოდ სწორი ნაწილისგან, ხოლო ძირითადი ნაწილის ყველა კოეფიციენტი ტოლია ტყვიის.

მტკიცებულება. 1. მოდით ზოარის მოსახსნელი სინგულარული წერტილი. დავამტკიცოთ, რომ Laurent-ის ფუნქციის გაფართოება f(z)აქვს ფორმა (26.1). ვინაიდან სინგულარული წერტილიდან ზომოსახსნელი, მაშინ არის სასრული ლიმიტი f(z) = A.აქედან გამომდინარე, f(z)შემოსაზღვრულია ზოგიერთ პუნქციურ უბანში 0 z - zq წერტილი ზო,იმათ. )(z) ყველასთვის ზამ უბნიდან. მიიღეთ ნებისმიერი რ. U р /?| და გამოიყენეთ ფორმულები (25.3) ლორანის სერიის კოეფიციენტებისთვის:

გაფართოების ძირითადი ნაწილის კოეფიციენტებისთვის n =- 1,-2,... ასეთი მნიშვნელობებისთვის პჩვენ გვაქვს p~n-e 0 at რ-> 0. მნიშვნელობიდან გამომდინარე რშეიძლება აირჩეს თვითნებურად პატარა, მაშინ ბატონო~"შეიძლება იყოს თვითნებურად მცირე. ვინაიდან |c t,| ^ ბატონოდა cn არ არის დამოკიდებული p-ზე, მაშინ cn = 0 for და= - 1, -2,..., რაც დასამტკიცებელი იყო.

2. ახლა დავუშვათ, რომ Laurent-ის გაფართოებას აქვს ფორმა (26.1). სერია (26.1) არის სიმძლავრის სერია და. შესაბამისად, თავსდება არა მხოლოდ პუნქციურ, არამედ მთელ სამეზობლოში z-zq წერტილის ჩათვლით ზო;მისი ჯამი S(z)არის ანალიტიკური ამისთვის z და S(z) = )(ზ) 0 z-ზე - ზორ.აქედან გამომდინარე, არსებობს სასრული ლიმიტი )(ზ)\u003d Pm 5 (r) \u003d 5 (r) - მაშასადამე, სინგულარული წერტილი zq

ზ->ზო ზ-*ზო

ერთჯერადი. თეორემა დადასტურდა.

კომენტარი. თეორემის დადასტურებიდან გამომდინარეობს, რომ პუნქციაში მოხსნადი სინგულარული წერტილის 0 z - zo, ფუნქცია f(z)ემთხვევა S(r) ფუნქციას, რომელიც ანალიტიკურია მთელ სამეზობლოში ზ - ზო . ამიტომ, თუ დავსვამთ /(th) = S(zq), შემდეგ, ფუნქციის მნიშვნელობების შეცვლის გარეშე f(z)პუნქციური უბნის ნებისმიერ წერტილში ამ ფუნქციას ვაკეთებთ ანალიტიკურ r-ში, ე.ი. "ამოშალე" ფუნქცია. ეს განმარტავს ტერმინს "მოხსნადი სინგულარობა". ბუნებრივია, რომ ასეთი წერტილები რეგულარულად მივიჩნიოთ და არა ფუნქციის ცალკეულ წერტილებად ვ(ზ).

განვიხილოთ, მაგალითად, ფუნქცია

მაგალითში 26.1 ნაჩვენები იყო, რომ Pm (n) = 1. ე.ი. ცალკეული წერტილი

zq = 0 არის მოსახსნელი. დააყენეთ /i(0) = 1, ამით ჩვენ აღმოვფხვრით სინგულარულობას და ვიღებთ ფუნქციას, რომელიც ანალიტიკურია იმ წერტილში. zq = 0 (და მთელ სიბრტყეში C).

ახლა დავახასიათოთ პოლუსები ლორანის გაფართოებების თვალსაზრისით.

თეორემა 26.3. f(z) ფუნქციის იზოლირებული მხოლობითი წერტილი Zo არის პოლუსი, თუ და მხოლოდ თუ, როდესაც ლორანის გაფართოების ძირითად ნაწილს Zq ცენტრით აქვს მხოლოდ სასრული რაოდენობის განსხვავებული

ნულოვანი კოეფიციენტებიდან n-ით:

მტკიცებულება. 1. მოდით zq - პოლუსი, ე.ი. ლიმი /( ზ) = ოო.

დავამტკიცოთ, რომ Laurent-ის ფუნქციის გაფართოება f(z)აქვს ფორმა (2G.2). მას შემდეგ, რაც ლიმ f(z)= ოო. მაშინ არსებობს წერტილის პუნქცია

კი zq. სადაც f(z)არის ანალიტიკური და არ აქვს ნულები. შემდეგ ფუნქცია გ(ზ) = 1 /f(z)ასევე ანალიტიკური იქნება ამ პუნქციურ უბანში და ლიმ გ(ზ)= 0. ამიტომ, ზოარის ერთჯერადი *-? *0

ფუნქციის ცალკეული წერტილი გ(ზ).ხელახლა განვსაზღვროთ გ(ზ)წერტილში ზო, აყენებს გ(ზო)= 0. მაშინ გ(ზ)ხდება ანალიტიკური (არა პუნქცია) წერტილის მთელ მიმდებარედ z 0,და z0იქნება მისი იზოლირებული ნული. აღნიშნეთ მიერ ნამ ნულის სიმრავლე (წესრიგი). როგორც ნაჩვენებია §23-ში, წერტილის მიმდებარე ტერიტორიაზე zq ფუნქცია გ(ზ)წარმოდგენილია ფორმით (იხ. (23.2))

და (z$) ვ 0 და y>(z)არის ანალიტიკური წერტილის ზოგიერთ მიდამოში ზო-იმიტომ რომ IP(z)უწყვეტი წერტილში ზოდა გ>(ზო) ფ 0" მაშინ IP(z)არ აქვს ნულები ამ წერტილის ზოგიერთ უბანშიც. ამიტომ ფუნქცია 1 /-p(z)ასევე იქნება ანალიტიკური ამ სამეზობლოში და, შესაბამისად, გაფართოვდება მასში ტეილორის სერიაში:

ფრჩხილების გახსნით და კოეფიციენტების აღნიშვნების შეცვლით, ჩვენ ვწერთ ბოლო გაფართოებას ფორმაში

სადაც c_jv = 1>o ვ 0. ამრიგად, f(r)-ის ლორანის გაფართოების ძირითადი ნაწილი შეიცავს მხოლოდ სასრულ რაოდენობას; ჩვენ მივედით საჭირო თანასწორობამდე (26.2).

2. შეუშვით წერტილის პუნქციურ მიმდებარედ ეფუნქცია )(ზ)წარმოდგენილია ლორანის გაფართოებით (26.2) (უფრო გაფართოებული სახით, იხ. (26.3)), რომლის ძირითადი ნაწილი შეიცავს მხოლოდ სასრულ რაოდენობას და თან-დ" ვ 0. ეს უნდა დავამტკიცოთ Zq - ფუნქციის პოლუსი ვ(ზ).ტოლობის (26.3) გამრავლება (გ - გპ) iV , ვიღებთ ფუნქციას

სერია (26.4) არის სიმძლავრის სერია, რომელიც აერთიანებს ანალიტიკურ ფუნქციას არა მხოლოდ პუნქციაში, არამედ წერტილის მთელ მიმდებარე ტერიტორიაზე. ზქ. ამიტომ ფუნქცია თ(ზ)ხდება ანალიტიკური ამ სამეზობლოში, თუ ჩვენ გავაფართოვებთ მას პარამეტრით h(zo)= s_dg ვ 0. მაშინ

ამრიგად, o წერტილი არის პოლუსი და დადასტურებულია თეორემა 26.3.

ნულოვანი ფუნქციის სიმრავლე (წესრიგი). გ(ზ)= 1//(r) ეწოდება ბოძების ორდერიფუნქცია /(r). თუ N-პოლუსის რიგი არის ე, მაშინ გ(ზ)= (r - Zo)N ip(z),და წადი) ფ 0 და, როგორც ნაჩვენებია თეორემა 26.3-ის დადასტურების პირველ ნაწილში, f(r)-ის გაფართოებას აქვს ფორმა (26.3), სადაც c_/v ვ 0. პირიქით, თუ f(r) გაფართოვდება სერიაში (26.3) და ე-ზ ფ 0, მაშინ

თ.ს. N- f(r) ფუნქციის პოლუსის რიგი. Ამგვარად, ფუნქციის zq პოლუსის რიგი/(G) უდრის ლორანის გაფართოების ძირითადი ნაწილის წამყვანი არანულოვანი კოეფიციენტის რიცხვს zq წერტილის პუნქციასთან.(ანუ ასეთი რიცხვის ტოლია N,რა ს_დგ ვ 0 და sp= 0 at პ > ნ).

მოდით დავამტკიცოთ შემდეგი მტკიცება, რომელიც მოსახერხებელია) აპლიკაციებისთვის.

დასკვნა 26.4. წერტილი zq არის მხატვრული ლიტერატურის N რიგის პოლუსი/(G) თუ და მხოლოდ თუ/(G) წარმოადგინოს სახით

სადაც h(z) არის ანალიტიკური ფუნქცია წერტილის სამეზობლოშიე და ჰ(ზო) ვ 0.

მტკიცებულება. ფუნქცია cp(z) = l/h(z)ანალიტიკურია r წერტილის ზოგიერთ მიმდებარედ. დასკვნის 26.4 პირობა უდრის შემდეგს:

Ისე zq - სიმრავლე ნული ნფუნქციები გ(ზ).და აქედან გამომდინარე, სიმრავლის პოლუსი ნფუნქციები /(2).

II მაგალითი 26.5. იპოვნეთ ფუნქციის იზოლირებული სინგულარული წერტილები და დაადგინეთ მათი ტიპი.

D e u c tio n. წერტილები, რომლებზეც (ზ 2 + 1 ) (ზ+ H) 2 = 0. თუ ზ 2 L- 1 = 0 შემდეგ 2 = ±რთუ (ზ 4- H) 2 = 0, მაშინ ზ= -3. ამრიგად, ფუნქციას აქვს სამი სინგულარული წერტილი ზ= r, 22 = -r, ზ3 = - 3. განიხილეთ ზ:

G -პირველი რიგის ბოძი (გამოვიყენეთ დასკვნა 26.4). ანალოგიურად შეიძლება დადასტურდეს, რომ 22 = -მეასევე პირველი რიგის ბოძი. 2 საათის განმავლობაში გვაქვს:

მოდით გადავიდეთ არსებითად ცალკეული პუნქტების განხილვაზე.

თეორემა 26.6. f(z) ფუნქციის იზოლირებული სინგულარული წერტილი zq არსებითად სინგულარულია, თუ და მხოლოდ იმ შემთხვევაში, თუ zq-ზე ორიენტირებული Laurent-ის გაფართოების ძირითად ნაწილს უსასრულოდ ბევრი განსხვავებული აქვს. ნული, კოეფიციენტები პ.

მტკიცებულება. თეორემა 26.6 პირდაპირ გამომდინარეობს 26.2 და 26.3 თეორემებიდან. მართლაც, თუ წერტილი zq არსებითად სინგულარულია, მაშინ ლორანის გაფართოების ძირითადი ნაწილი არ შეიძლება არ იყოს ან შეიცავდეს ტერმინების სასრულ რაოდენობას (წინააღმდეგ შემთხვევაში წერტილი Zq იქნება ან მოსახსნელი ან ბოძი). ამიტომ ძირითად ნაწილში ტერმინების რაოდენობა უსასრულო უნდა იყოს.

პირიქით, თუ ძირითადი ნაწილი შეიცავს უსასრულოდ ბევრ წევრს, მაშინ Zq არ შეიძლება იყოს არც მოსახსნელი წერტილი და არც პოლუსი. შესაბამისად, ეს წერტილი არსებითად სინგულარულია.

განმარტების მიხედვით, არსებითად სინგულარული წერტილი ხასიათდება იმით, რომ ფუნქციას f(2) არ აქვს არც სასრული და არც უსასრულო ზღვარი. z ->zq. უფრო სრულყოფილი წარმოდგენა იმის შესახებ, თუ რამდენად არარეგულარულია ფუნქციის ქცევა არსებითად სინგულარული წერტილის სიახლოვეს მოცემულია შემდეგი თეორემით.

თეორემა 26.7 (სოჩოცკის თეორემა). თუ zq არსებითად სინგულარულია, მაშინ ფუნქციის წერტილი f(z), შემდეგ ნებისმიერი რთული რიცხვისთვის L, მათ შორის A =ოო, არის z n წერტილების თანმიმდევრობა, რომ z n -> zo დალიმი f(zn) = ა.

ნ->ოს

მტკიცებულება. ჯერ საქმე განიხილეთ A =ოო. თეორემა 2G.2-ის დამტკიცების პირველ ნაწილში დავადგინეთ, რომ თუ f(z)შემოსაზღვრულია r0 წერტილის ზოგიერთ პუნქციურ მიდამოში, შემდეგ ყველა კოეფიციენტი c, n = -ძირითადი ნაწილის 1, - 2,... ტოლია ნულის (და, შესაბამისად, სინგულარობა th-ში მოსახსნელია). ვინაიდან დაშვებით r0 არის არსებითად სინგულარული წერტილი, ფუნქცია f(r) შეუზღუდავია r0 წერტილის ნებისმიერ პუნქციასთან. ავიღოთ ვიწრო უბნები 0 Z ისეთი, რომ ვ(ზი) > 1 (თუ |/(r)| z - zo R/2 არის წერტილი z-2 , სადაც |/(dd)| > 2 და ა.შ.: პუნქციურ უბანში ო 71. აშკარაა, რომ rn -e go და lim /(r«) = oo. ამრიგად, A = oo შემთხვევაში, თეორემა 26.7

დადასტურებული.

მოდით ახლა ფოო. ჯერ დავუშვათ, რომ არის პუნქცია 0

= -წ---- იქნება ანალიტიკური ამ პუნქციურ უბანში და, შესაბამისად,

/(G) - ა

შესაბამისად, r არის Φ(r) ფუნქციის იზოლირებული სინგულარული წერტილი. ვაჩვენოთ. რომ r0 არის Φ(r) არსებითად სინგულარული წერტილი. დაე, არასწორი იყოს. მაშინ არსებობს ლიმიტი lim Φ(r), სასრული ან უსასრულო. იმიტომ რომ

/(r) = A + , მაშინ Hsh /(r) ასევე არსებობს, რაც ეწინააღმდეგება პირობას

ფ(გ) ~ :-*z 0

თეორემის ხედვა. ამრიგად, r0 არის Φ(r) ფუნქციის არსებითად სინგულარული წერტილი. იმის მიხედვით, რაც ზემოთ დადასტურდა, არსებობს r n წერტილების თანმიმდევრობა ისეთი, რომ r n o და lim Φ(r n) = oo. აქედან

ჩვენ დავამტკიცეთ საჭირო მტკიცება იმ ვარაუდით, რომ f(r) ფ არ წერტილის რომელიღაც პუნქციურ უბანში, ახლა ვივარაუდოთ, რომ ეს სიმართლეს არ შეესაბამება, ე.ი. წერტილის ნებისმიერ თვითნებურად მცირე პუნქციურ უბანში არის ასეთი წერტილი G",რომ f(r") = A. შემდეგ ნებისმიერი პპუნქციურ უბანში 0 f(z u) = L. ამრიგად, საჭირო მტკიცება მართალია პ-იუო

ყველა შემთხვევაში და დადასტურებულია თეორემა 26.7.

(სოხოცკის) თეორემის 26.7-ის მიხედვით, არსებითად სინგულარული წერტილის ნებისმიერ (თვითნებურად მცირე) პუნქციურ მიმდებარე ტერიტორიაზე, ფუნქცია f(r) იღებს მნიშვნელობებს თვითნებურად ახლოს ნებისმიერ რიცხვთან გაფართოებულ C სიბრტყეში.

იზოლირებული სინგულარული წერტილების შესასწავლად ხშირად სასარგებლოა ძირითადი ელემენტარული ფუნქციების ცნობილი ტეილორის გაფართოებები.

მაგალითი 2G.8. განვსაზღვროთ სინგულარული წერტილის ტიპი zq = 0 ფუნქციისთვის

ამოხსნილია და ე. ჩვენ გავაფართოვებთ მრიცხველს და მნიშვნელს ტეილორის სერიებში r-ის ხარისხებში. ჩანაცვლება (22.11) 3-ში ზნაცვლად r და გამოვაკლოთ 1, მივიღებთ

(22.12) გამოყენებით ვიღებთ მნიშვნელის გაფართოებას:

ამ გაფართოებების სერიები ემთხვევა მთელ კომპლექსურ სიბრტყეში €. Ჩვენ გვაქვს

და /2(2) ანალოგიურია წერტილის სამეზობლოში ზო = 0 (და თუნდაც მთელ სიბრტყეში) და /2(20) ფ 0, მაშინ თ(ზ)ასევე ანალიტიკურია gF 0 წერტილის ზოგიერთ სიახლოვეს. დასკვნის 26.4 მიხედვით, წერტილი ზო = 0 არის შეკვეთის პოლუსი N = 4.

II მაგალითი 26.9. იპოვნეთ ფუნქციის სინგულარული წერტილები f(z)= sin j - და დაადგინეთ მათი ტიპი.

P e in e და e. ფუნქციას აქვს ერთი ბოლო სინგულარული წერტილი zq = 1. C-დან სხვა წერტილებში ფუნქცია w =--- ანალიტიკური; აქედან გამომდინარე ცოდვის ფუნქცია ვიქნება ანალიტიკური.

ჩანაცვლება სინუსის გაფართოებაში (22.12) - r-ის ნაცვლად ვიღებთ

ჩვენ მივიღეთ ცოდვის ფუნქციის გაფართოება ლორანის სერიებში 20 = 1 წერტილის პუნქციურ სამეზობლოში. ვინაიდან შედეგად მიღებული გაფართოება შეიცავს უსასრულოდ ბევრ ტერმინს უარყოფითი ძალებით (r - 1), მაშინ zq = 1 არის არსებითი სინგულარული წერტილი (ამ შემთხვევაში, Laurent-ის გაფართოება შედგება მხოლოდ ძირითადი ნაწილისგან, ხოლო სწორი ნაწილი აკლია).

გაითვალისწინეთ, რომ ამ შემთხვევაში ასევე შესაძლებელი იყო სინგულარობის ბუნების დადგენა პირდაპირ განმარტებიდან, სერიის გაფართოების გარეშე. მართლაც, არის თანმიმდევრობები (r") და (2") თანხვედრაში ზო= 1 და ისეთი, რომ f(z" n)= 1, /(2") = 0 (თქვენ თვითონ მიუთითეთ ასეთი თანმიმდევრობები). f(z)არ აქვს ლიმიტი როდის z -> 1 და აქედან გამომდინარე zq - 1 არსებითად მხოლობითია.

მოდით წარმოვიდგინოთ ფუნქციის ლორანის გაფართოების კონცეფცია წერტილის მიმდებარედ Zq = 00 და განიხილეთ კავშირი გაფართოებასა და სინგულარობის ბუნებას შორის ამ ეტაპზე. გაითვალისწინეთ, რომ იზოლირებული სინგულარული წერტილის განმარტებები და მისი ტიპი (მოხსნადი, პოლუსი ან არსებითად სინგულარული) გადადის საქმეზე zq = oc უცვლელი. მაგრამ თეორემები 26.2. 26.3 და 26.6, რომლებიც დაკავშირებულია ლორანის გაფართოებების ბუნებასთან, უნდა შეიცვალოს. საქმე იმაშია, რომ წევრები c n (z - 2o) გვ. პ= -1,-2,..., ძირითადი ნაწილი, რომელიც განსაზღვრავს ფუნქციის "არარეგულარობას" ბოლო წერტილთან ახლოს. Zq, რადგან 2 მიდრეკილია oo-სკენ, ისინი მოიქცევიან „სწორად“ (0-ისკენ მიდრეკილება). პირიქით, რეგულარული ნაწილის წევრები პ= 1,2,... მიდრეკილია oo-სკენ; ისინი განსაზღვრავენ სინგულარობის ბუნებას Zq = oo. მაშასადამე, oo-ს მეზობლად გაფართოების ძირითადი ნაწილი იქნება პოზიტიური უფლებამოსილების მქონე პირობები P,და სწორი - უარყოფითით.

შემოვიტანოთ ახალი ცვლადი w = 12. ფუნქცია ტელევიზორი = 1/2, გაფართოებული ისე, რომ u(oo) = 0, ერთი-ერთზე და კონფორმულად ასახავს სამეზობლოს z > რქულები zq = 00 |w|-ის მიმდებარედ wq = 0. თუ ფუნქცია f(z)ანალიტიკა პუნქციურ უბანში რ z Zq = oc, შემდეგ ფუნქცია G(w) = f(l/w)ანალიტიკური იქნება ყვითელ სამეზობლოში 0 wo = 0. ვინაიდან 2 -> oo იქნება ვ-> 0, მაშინ

Ისე G(w)აქვს წერტილში wq = 0 არის იგივე ტიპის სინგულარობა f(z)წერტილში Zq = 00. მოდით გავაფართოვოთ ფუნქცია G(w) ლორანის სერიაში wo = 0 წერტილის პუნქციურ მიმდებარე ტერიტორიაზე:

(26.5) მარჯვენა მხარეს ჯამები წარმოადგენს გაფართოების სწორ და ძირითად ნაწილებს, შესაბამისად. მოდით გადავიდეთ ცვლადზე z,ჩანაცვლება w = 1/z:

აღმნიშვნელი პ\u003d -A *, 6 * \u003d 6_ " \u003d ერთად გვდა ამის შემჩნევა G(l/z) = f(z), ვიღებთ

დაშლა (2G.G) ე.წ f(z) ფუნქციის ლორენტული გაფართოება zq წერტილის პუნქციურ მიმდებარე ტერიტორიაზე= ოო. პირველი ჯამი (2G.6) ე.წ მარჯვენა ნაწილიდა მეორე ჯამი არის მთავარი ნაწილიეს დაშლა. ვინაიდან ეს ჯამები შეესაბამება გაფართოების სწორ და ძირითად ნაწილებს (26.5), გაფართოება (26.6) აკმაყოფილებს თეორემების 26.2, 26.3 და 26.6 ანალოგებს. ამრიგად, შემდეგი თეორემა არის თეორემა 26.2-ის ანალოგი.

თეორემა 26.10. იზოლირებული სინგულარული წერტილიზქ - os (ფუნქციები/(G) მოსახსნელია, თუ და მხოლოდ იმ შემთხვევაში, თუ ლორანის გაფართოებას ამ წერტილის პუნქციურ უბანში აქვს ფორმა

თ.ს. შედგება მხოლოდ სწორი ნაწილისგან.

ჩვენ დავაყენეთ /(ოო) = თანა.სამეზობლოში (26.7) კონვერტაციის სერიით განსაზღვრული ფუნქცია z > რწერტილები 2o \u003d oc, ე.წ ანალიტიკური z წერტილშიო = ოო. (გაითვალისწინეთ, რომ ეს განმარტება უდრის ფუნქციის ანალიტიკურობას G(w) წერტილში ვაი = 0.)

მაგალითი 26.11. გამოიკვლიეთ ფუნქციის სინგულარული წერტილი zq = oo

ვინაიდან ზღვარი სასრულია, მაშ ზო = oo არის f(r) ფუნქციის მოსახსნელი სინგულარული წერტილი. თუ დავსვამთ /(ოო) = ლიმ J(z)= 0, მაშინ f(z)გახდება

ტიკ წერტილში ზო= os. მოდით ვაჩვენოთ, თუ როგორ უნდა ვიპოვოთ შესაბამისი გაფართოება (26.7). მოდით გადავიდეთ ცვლადზე ვ = 1 fz.ჩანაცვლება ზ= 1 /?e, ვიღებთ

(ბოლო ტოლობა მოქმედებს ww = 0 წერტილის პუნქციურ სამეზობლოში, მაგრამ ჩვენ განვავრცობთ განმარტებას (7(0) = 0). შედეგად ფუნქციას აქვს სინგულარული წერტილები. w =± მე, w =-1/3 და წერტილში Wq = 0 არის ანალიტიკური. გაფართოების ფუნქცია G(w)გრადუსით ვ(როგორც გაკეთდა მაგალითში 25.7) და ჩანაცვლება მიღებული სიმძლავრის სერიაში w = 1/zშეიძლება მივიღოთ ფუნქციის გაფართოება (26.7). ვ(ზ).

თეორემა 26.3 შემთხვევისთვის ზო= oo გადაიწერება შემდეგი ფორმით.

თეორემა 26.12. იზოლირებული სინგულარული წერტილიწადი = oc ფუნქცია f(z) არის პოლუსი, თუ და მხოლოდ იმ შემთხვევაში, თუ ლორანის გაფართოების ძირითადი ნაწილია (26.6) აქვს არანულოვანი კოეფიციენტების მხოლოდ სასრული რაოდენობათან":

აქ სერია არის რეგულარული ნაწილი, ხოლო ფრჩხილებში ჩასმული მრავალწევრი არის გაფართოების ძირითადი ნაწილი. ბოძების სიმრავლე oc-ში განისაზღვრება, როგორც პოლუსის სიმრავლე wq = 0 ფუნქცია გ(ზ).ადვილი მისახვედრია, რომ პოლუსის სიმრავლე რიცხვს ემთხვევა ნ(26.8)-ში.

Q p | (i 2 + 1) (z + 3) 2

დავალება. აჩვენე რომ ფუნქცია f(z) =-- -- აქვს

წერტილი ზო =ოო ბოძების შეკვეთა 3.

თეორემა 26.6 არსებითი სინგულარული წერტილის შესახებ გადაწერილია შემთხვევისთვის ზო= os თითქმის სიტყვასიტყვით და მასზე დეტალურად არ ვჩერდებით.

ტეილორის სერიები ემსახურება როგორც ეფექტურ ინსტრუმენტს ფუნქციების შესასწავლად, რომლებიც ანალიტიკურია ზოლში წრეში ანალიტიკური ფუნქციების შესასწავლად, აღმოჩნდება, რომ შესაძლებელია გაფართოებების აგება დადებითი და უარყოფითი ძალებით (z - zq). ფორმა, რომელიც აზოგადებს ტეილორის გაფართოებებს. სერია (1), გაგებული, როგორც ორი სერიის ჯამი, ეწოდება Laurent სერია. ცხადია, რომ (1) სერიის დაახლოების რეგიონი არის თითოეული სერიის (2) დაახლოების რეგიონების საერთო ნაწილი. მოდი ვიპოვოთ იგი. პირველი სერიის კონვერგენციის არე არის წრე, რომლის რადიუსი განისაზღვრება კოში-ჰადამარის ფორმულით. კონვერგენციის წრის შიგნით სერია (3) უახლოვდება ანალიტიკურ ფუნქციას, ხოლო უფრო მცირე რადიუსის ნებისმიერ წრეში ის აბსოლუტურად იყრის თავს. და ერთნაირად. მეორე სერია არის სიმძლავრის სერია ცვლადის მიმართ. სერია (5) კონვერგენციის წრეში ხვდება კომპლექსური ცვლადის m-*oo ანალიტიკურ ფუნქციას, ხოლო მცირე რადიუსის ნებისმიერ წრეში ის აბსოლიტურად და თანაბრად იყრის თავს. რაც ნიშნავს, რომ (4) სერიების კონვერგენციის რეგიონი არის წრის გარეგნობა - თუ მაშინ არის (3) და (4) სერიების დაახლოების საერთო რეგიონი - წრიული რგოლი, რომელშიც სერია (1) უახლოვდება ანალიტიკურ ფუნქციას. უფრო მეტიც, ნებისმიერ რგოლში ის აბსოლიტურად და ერთნაირად იყრის თავს. მაგალითი 1. დაადგინეთ რადი ლორანის სერიის კონვერგენციის რეგიონი. იზოლირებული სინგულარული წერტილები და მათი კლასიფიკაცია (z), რომელიც არის ერთმნიშვნელოვანი და აპოლიტიკური წრიულ რგოლში, შეიძლება წარმოდგენილი იყოს ამ რგოლში, როგორც კონვერგენციული სერიის ჯამი, რომლის კოეფიციენტები Cn ცალსახად განისაზღვრება და გამოითვლება ფორმულებით, სადაც 7p არის m რადიუსის წრე. მოდით დავაფიქსიროთ თვითნებური z წერტილი R რგოლში. ვაშენებთ წრეებს r0 წერტილში ცენტრებით, რომელთა რადიუსი აკმაყოფილებს უტოლობებს და განვიხილავთ ახალ რგოლს, კოშის ინტეგრალური თეორემის მიხედვით, გამრავლებული დაკავშირებული დომენის მიხედვით, გვაქვს ცალ-ცალკე გარდაქმნას თითოეული ინტეგრალი ჯამში (8). ყველა £ წერტილისთვის 7d* წრის გასწვრივ, თანაბრად კონვერგენტული სერიის ჯამის კავშირი 1 1 დაკმაყოფილებულია. ამიტომ, ^ წილადი შეიძლება წარმოდგენილი იყოს vi- /" / ყველა £ წერტილისთვის წრეზე ir> მიმართებაში. დაკმაყოფილებულია მაშასადამე, წილადი ^ შეიძლება წარმოდგენილი იყოს, როგორც ერთნაირად კონვერგენტული სერიების ჯამი ფორმულებში (10) და (12) არის ანალიტიკური ფუნქციები წრიულ რგოლში. მაშასადამე, კოშის თეორემით, შესაბამისი ინტეგრალების მნიშვნელობები არ იცვლება, თუ წრეები 7/r და 7r/ შეიცვლება რომელიმე წრით. ეს საშუალებას გვაძლევს გავაერთიანოთ ფორმულები (10) და (12).(8) ფორმულის მარჯვენა მხარეს ინტეგრალების ჩანაცვლებით მათი გამოსახულებებით (9) და (11), შესაბამისად, მივიღებთ სასურველ გაფართოებას. ვინაიდან z არის თვითნებური. რგოლის წერტილიდან გამომდინარეობს, რომ სერია (14) იკრიბება f(z) ფუნქციასთან ყველგან ამ რგოლში და ნებისმიერ რგოლში სერია ამ ფუნქციასთან აბსოლიტურად და ერთგვაროვნად იყრის თავს. ახლა დავამტკიცოთ, რომ ფორმის (6) დაშლა უნიკალურია. დავუშვათ, რომ კიდევ ერთი დაშლა ხდება.მაშინ, ყველგან R რგოლის შიგნით გვაქვს წრეწირზე, სერიები (15) ერთნაირად იყრის თავს. გავამრავლოთ ტოლობის ორივე მხარე (სადაც m არის ფიქსირებული მთელი რიცხვი და გავაერთიანოთ ორივე სერიები ტერმინით. შედეგად ვიღებთ მარცხენა მხარეს, ხოლო მარჯვენა მხარეს - Csh. ამრიგად, (4, \u003d St. ვინაიდან m არის თვითნებური რიცხვი, მაშინ ბოლო ტოლობის სერია (6), რომლის კოეფიციენტები გამოითვლება ფორმულებით (7), ეწოდება f(z) ფუნქციის Laurent სერია რგოლში 7) კოეფიციენტებისთვის. Laurent სერიები იშვიათად გამოიყენება პრაქტიკაში, რადგან, როგორც წესი, ისინი საჭიროებენ რთულ გამოთვლებს. ჩვეულებრივ, თუ შესაძლებელია, გამოიყენება ელემენტარული ფუნქციების მზა ტეილორის გაფართოებები. გაფართოების უნიკალურობიდან გამომდინარე, ნებისმიერი ლეგიტიმური მეთოდი იწვევს იმავეს. შედეგი მაგალითი 2 განვიხილოთ Laurent-ის სერიის გაფართოებები სხვადასხვა დომენების ფუნქციების, თუ დავუშვებთ, რომ Fuiscija /(z)-ს აქვს ორი სინგულარული წერტილი: მაშასადამე, არსებობს სამი რგოლის დომენი. და ცენტრით r = 0 წერტილში. თითოეულში f(r) ფუნქცია ანალიტიკურია: ა) წრე არის წრის გარე მხარე (სურ. 27). მოდით ვიპოვოთ /(z) ფუნქციის Laurent გაფართოებები თითოეულ ამ რეგიონში. ჩვენ წარმოვადგენთ /(z) ელემენტარული წილადების ჯამს ა) წრეწირის გარდაქმნის კავშირს (16) შემდეგნაირად გეომეტრიული პროგრესიის წევრთა ჯამის ფორმულის გამოყენებით ვიღებთ ბ) -z ფუნქციის რგოლი კონვერგენტული რჩება ამ რგოლში, ვინაიდან სერია (19) j^j ფუნქციისთვის |z| > 1 განსხვავდება. მაშასადამე, ჩვენ გარდაქმნით /(z) ფუნქციას შემდეგნაირად: ფორმულის (19) ხელახლა გამოყენებით მივიღებთ, რომ ეს სერია ერთვის. (18) და (21) გაფართოებების (20) მიმართებით ჩანაცვლებით მივიღებთ გ) -z ფუნქციის წრის გარეგნობას |z| > 2 განსხვავდება და სერია (21) ფუნქციისთვის მოდით წარმოვადგინოთ ფუნქცია /(z) შემდეგი სახით: /<*> (18) და (19) ფორმულების გამოყენებით ვიღებთ OR 1-ს ეს მაგალითი გვიჩვენებს, რომ იგივე ფუნქციისთვის f(z) Laurent გაფართოებას, ზოგადად რომ ვთქვათ, აქვს განსხვავებული ფორმა სხვადასხვა რგოლებისთვის. მაგალითი 3. იპოვეთ ლორანის ფუნქციის 8 ლორანის სერიის დაშლა იზოლირებული სინგულარული წერტილები და მათი კლასიფიკაცია რგოლურ არეში A ვიყენებთ f (z) ფუნქციის გამოსახულებას შემდეგი ფორმით: და გარდაქმნით მეორე წევრის გამოყენებით გეომეტრიული პროგრესიის ტერმინების ჯამის ფორმულა ვიღებთ ნაპოვნი გამონათქვამების ჩანაცვლებით ფორმულაში (22), გვაქვს მაგალითი 4. გააფართოვეთ ფუნქცია ლორანის სერიებში თხელი zq = 0-ის სიახლოვეს. ნებისმიერი რთულისთვის. , გვაქვს Let ეს გაფართოება მოქმედებს ნებისმიერი z Ф 0 წერტილისთვის. ამ შემთხვევაში, რგოლის უბანი არის მთელი რთული სიბრტყე ერთი გამოგდებული წერტილით z - 0. ეს რეგიონი შეიძლება განისაზღვროს შემდეგი მიმართებით: ეს ფუნქცია არის ანალიტიკური. რეგიონში ლორანის სერიის კოეფიციენტების ფორმულებიდან (13), იგივე დასაბუთებით, როგორც წინა აბზაცში, შეიძლება მივიღოთ Kouiw უტოლობა. თუ ფუნქცია f(z) შემოიფარგლება წრეზე, სადაც M არის მუდმივი), მაშინ იზოლირებული სინგულარული წერტილები A zo წერტილს ეწოდება f(z) ფუნქციის იზოლირებული სინგულარული წერტილი, თუ არსებობს წერტილის რგოლური მეზობლობა ( ამ სიმრავლეს ზოგჯერ ასევე უწოდებენ 2o წერტილის პუნქციას, სადაც ფუნქცია f(z) არის ერთმნიშვნელოვანი და ანალიტიკური. თავად zo წერტილში ფუნქცია ან არ არის განსაზღვრული, ან არ არის ერთმნიშვნელოვანი და ანალიტიკური. ზო წერტილის მიახლოებისას /(z) ფუნქციის ქცევის მიხედვით გამოირჩევა სინგულარული წერტილების სამი ტიპი. იზოლირებულ სინგულურ წერტილს ამბობენ, რომ არის: 1) მოსახსნელი, თუ არსებობს სასრული 2) pmusach თუ 3) არსებითად სინგულარული წერტილი, თუ ფუნქციას f(z) არ აქვს ლიმიტი თეორემა 16. f(z) ფუნქციის იზოლირებული მხოლობითი წერტილი z0 არის ამოსახსნელი სინგულარული წერტილი, თუ და მხოლოდ იმ შემთხვევაში, თუ f(z) ფუნქციის ლორენტური გაფართოება zo წერტილის სამეზობლოში არ შეიცავს ძირითად ნაწილს, ე.ი. აქვს ფორმა Let zo - მოსახსნელი სინგულარული წერტილი. მაშინ არსებობს სასრული და, შესაბამისად, ფუნქცია f(z) შემოსაზღვრულია r წერტილის პროკოლოგიურ სამეზობლოში. ჩვენ დავაყენეთ კოშის უტოლობების საფუძველზე, ვინაიდან შესაძლებელია ავირჩიოთ ρ, როგორც ჩვენ გვსურს, მაშინ ყველა კოეფიციენტები უარყოფით სიმძლავრეებზე (z - 20) უდრის ნულს: პირიქით, მოდით Laurent ფუნქციის /(r) გაფართოება zq წერტილის სამეზობლოში შეიცავს მხოლოდ სწორ ნაწილს, ანუ აქვს ფორმა (23) და, შესაბამისად, არის ტეილორი. ადვილი მისახვედრია, რომ z -* z0-სთვის /(r) ფუნქციას აქვს ზღვრული მნიშვნელობა: თეორემა 17. f(z) ფუნქციის zq იზოლირებული ცალმხრივი წერტილი არის ამოღებული, თუ და მხოლოდ იმ შემთხვევაში, თუ ფუნქცია J(z) არის. შემოსაზღვრულია ზქ წერტილის რომელიღაც პუნქციურ უბანში, ზღმეჩაი არა. მოდით r0 იყოს f(r-ის) მოხსნადი სინგულარული წერტილი. თუ დავუშვებთ, რომ f(r) ფუნქცია არის ანალიტიკური რაღაც წრეში, რომელიც ორიენტირებულია th წერტილში. ეს განსაზღვრავს წერტილის სახელს - ერთჯერადი. თეორემა 18. f(z) ფუნქციის zq იზოლირებული სინგულარული წერტილი არის პოლუსი, თუ და მხოლოდ იმ შემთხვევაში, თუ f(z) ფუნქციის ლორანის გაფართოების ძირითადი ნაწილი წერტილის სამეზობლოში შეიცავს სასრულ (და დადებით) რიცხვს. არანულოვანი წევრებისგან, ანუ აქვს ფორმა 4. მოდით, z0 იყოს პოლუსი. მას შემდეგ არსებობს z0 წერტილის პუნქციური მეზობლობა, რომელშიც ფუნქცია f(z) არის ანალიტიკური და არანულოვანი. შემდეგ ანალიტიკური ფუნქცია განისაზღვრება ამ სამეზობლოში, და აქედან გამომდინარე, zq წერტილი არის ფუნქციის ამოსახსნელი სინგულარული წერტილი (ნული), ან სადაც h(z) არის ანალიტიკური ფუნქცია, h(z0) ∩ 0. არის ანალიტიკური სამეზობლოში. zq წერტილის და აქედან გამომდინარე, საიდანაც მივიღებთ, რომ ახლა დავუშვათ, რომ f(z) ფუნქციას აქვს (24) ფორმის დაშლა zo წერტილის პუნქციასთან. ეს ნიშნავს, რომ ამ სამეზობლოში ფუნქცია f(z) ანალიტიკურია ფუნქციასთან ერთად. g(z) ფუნქციისთვის მოქმედებს გაფართოება, საიდანაც ირკვევა, რომ zq არის g(z) ფუნქციის მოხსნადი სინგულარული წერტილი და არსებობს, შემდეგ ფუნქცია მიდრეკილია 0-ზე - ფუნქციის პოლუსი არის კიდევ ერთი მარტივი. ფაქტი. წერტილი Zq არის f(z) ფუნქციის პოლუსი, თუ და მხოლოდ იმ შემთხვევაში, თუ ფუნქცია g(z) = y შეიძლება გაფართოვდეს ანალიზურ ფუნქციაზე zq წერტილის სამეზობლოში g(z0) = 0-ის დაყენებით. f(z) ფუნქციის პოლუსს ეწოდება jfa ფუნქციის ნულის რიგი. მე-16 და მე-18 თეორემები გულისხმობს შემდეგ მტკიცებას. თეორემა 19. იზოლირებული სინგულარული თხელი არსებითად სინგულარულია, თუ და მხოლოდ იმ შემთხვევაში, თუ ლორანის გაფართოების ძირითადი ნაწილი ამ წერტილის პუნქციურ სამეზობლოში შეიცავს უსასრულოდ ბევრ არანულოვან წევრს. მაგალითი 5. ფუნქციის სინგულარული წერტილია zo = 0. ჩვენ გვაქვს Laurent Series იზოლირებული სინგულარული წერტილები და მათი კლასიფიკაცია ამიტომ, zo = 0 არის ამოსახსნელი სინგულარული წერტილი. /(z) ფუნქციის გაფართოება ლორანის სერიაში ნულოვანი წერტილის სიახლოვეს შეიცავს მხოლოდ სწორ ნაწილს: მაგალითი7. f(z) = f(z) ფუნქციის სინგულარული წერტილი არის zq = 0. განვიხილოთ ამ ფუნქციის ქცევა რეალურ და წარმოსახვით ღერძებზე: რეალურ ღერძზე x 0-ზე, წარმოსახვით ღერძზე ამიტომ, არც სასრული და არც უსასრულო ზღვარი f(z) z -* 0-ზე არ არსებობს. აქედან გამომდინარე, წერტილი r0 = 0 არის f(z) ფუნქციის არსებითად სინგულარული წერტილი. ვიპოვოთ f(z) ფუნქციის Laurent-ის გაფართოება ნულოვანი წერტილის სამეზობლოში. ნებისმიერი კომპლექსისთვის C ჩვენ გვაქვს დავაყენეთ. შემდეგ ლორანის გაფართოება შეიცავს უსასრულო რაოდენობის წევრებს z-ის უარყოფითი ძალებით.

განმარტება.ფუნქციის სინგულარული წერტილი ეწოდება იზოლირებული, თუ ამ წერტილის რომელიმე სამეზობლოში არის ანალიტიკური ფუნქცია (ანუ ანალიტიკური რგოლში).

ფუნქციის იზოლირებული სინგულარული წერტილების კლასიფიკაცია დაკავშირებულია ამ ფუნქციის ქცევასთან სინგულარული წერტილის სიახლოვეს.

განმარტება.წერტილი ე.წ ერთჯერადი ფუნქციის სინგულარული წერტილი, თუ არსებობს ამ ფუნქციის სასრული ზღვარი.

მაგალითი 5აჩვენეთ, რომ ფუნქციას აქვს მოხსნადი სინგულარობა წერტილში.

გამოსავალი.პირველი მნიშვნელოვანი ლიმიტის გახსენებით, ჩვენ ვიანგარიშებთ

ეს ნიშნავს, რომ მოცემულ ფუნქციას აქვს მოხსნადი სინგულარობა წერტილში.

დავალება 4.აჩვენეთ, რომ წერტილი არის მოსახსნელი .

განმარტება.წერტილი ე.წ ბოძი ფუნქცია, თუ ეს ფუნქცია იზრდება განუსაზღვრელი ვადით, ეს არის.

ყურადღება მივაქციოთ კავშირს ანალიტიკური ფუნქციის ნულისა და პოლუსის ცნებებს შორის. მოდით წარმოვადგინოთ ფუნქცია როგორც .

თუ წერტილი არის ფუნქციის მარტივი ნული, მაშინ ფუნქციას აქვს მარტივი პოლუსი

თუ წერტილი არის ფუნქციის ნულის რიგი, მაშინ ფუნქციისთვის ის არის პოლუსი შეკვეთა.

მაგალითი 6აჩვენეთ, რომ ფუნქციას აქვს მესამე რიგის პოლუსი ერთ წერტილში.

გამოსავალი.ვივარაუდოთ , მივიღებთ . როგორც ჩვენ მიდრეკილნი ვართ ნულისკენ, ნებისმიერი კანონის მიხედვით, გვაქვს . შემდეგ და მასთან ერთად ფუნქცია იზრდება განუსაზღვრელი ვადით. მაშასადამე, , ანუ სინგულარული წერტილი არის პოლუსი. ფუნქციისთვის, ეს წერტილი აშკარად არის სამმაგი ნული. აქედან გამომდინარე, ამ ფუნქციისთვის წერტილი არის მესამე რიგის პოლუსი.

დავალება 5.აჩვენეთ, რომ წერტილს აქვს მარტივი პოლუსი.

განმარტება.წერტილი ე.წ არსებითად განსაკუთრებული ფუნქციის წერტილი თუ ამ მომენტში არ არის ფუნქციის არც სასრული და არც უსასრულო ზღვარი (ფუნქციის ქცევა არ არის განსაზღვრული).

მოდით იყოს ფუნქციის არსებითი სინგულარული წერტილი. შემდეგ ნებისმიერი წინასწარ მინიჭებული კომპლექსური რიცხვისთვის არის წერტილების ისეთი თანმიმდევრობა, რომელიც კონვერგირდება, რომლის გასწვრივ მნიშვნელობები მიდრეკილია: ( სოჭოკის თეორემა).

მაგალითი 7აჩვენეთ, რომ ფუნქციას აქვს არსებითი სინგულარობა.

გამოსავალი.განვიხილოთ მოცემული ფუნქციის ქცევა წერტილის სიახლოვეს . რადგან რეალური ღერძის (ე.ი.) დადებითი ნაწილის გასწვრივ გვაქვს და ; თუ რეალური ღერძის უარყოფითი ნაწილის გასწვრივ (ე.ი.), მაშინ და . ასე რომ, არ არსებობს ლიმიტი. განმარტებით, ფუნქციას აქვს არსებითი სინგულარობა წერტილში.

განვიხილოთ ფუნქციის ქცევა ნულზე სოჭოკის თეორემის თვალსაზრისით. მოდით იყოს ნებისმიერი რთული რიცხვი ნულისა და უსასრულობის გარდა.

თანასწორობიდან ვპოულობთ. ვივარაუდოთ, რომ მივიღებთ წერტილების თანმიმდევრობას, . ცხადია,. ამ მიმდევრობის თითოეულ წერტილში ფუნქცია უდრის და ამიტომ

დავალება 6.აჩვენეთ, რომ ფუნქციას აქვს არსებითი სინგულარობა წერტილში.

უსასრულობის წერტილი ყოველთვის განიხილება განსაკუთრებული ფუნქციისთვის. წერტილს ეწოდება ფუნქციის იზოლირებული სინგულარული წერტილი, თუ ამ ფუნქციას არ აქვს სხვა სინგულარული წერტილები საწყისზე ორიენტირებული წრის გარეთ.

იზოლირებული სინგულარული წერტილების კლასიფიკაცია ასევე შეიძლება გავრცელდეს შემთხვევაზე.

მაგალითი 8აჩვენეთ, რომ ფუნქციას აქვს ორმაგი პოლუსი უსასრულობაში.

გამოსავალი.განვიხილოთ ფუნქცია , სადაც არის ანალიტიკური ფუნქცია წერტილის სამეზობლოში და . ეს ნიშნავს, რომ ფუნქციას აქვს ორმაგი ნული უსასრულობაში, მაგრამ შემდეგ ფუნქციისთვის წერტილი არის ორმაგი პოლუსი.

მაგალითი 9აჩვენეთ, რომ ფუნქციას აქვს არსებითი სინგულარობა უსასრულობაში.

გამოსავალი.მსგავსი პრობლემა განიხილება პრ.7-ში. განვიხილოთ ფუნქციის ქცევა უსასრულოდ შორეული წერტილის სიახლოვეს. რეალური ღერძის დადებითი ნაწილისთვის და რეალური ღერძის უარყოფითი ნაწილისთვის. ეს ნიშნავს, რომ არ არსებობს ფუნქციის ლიმიტი წერტილში და, განმარტების ძალით, ეს წერტილი არსებითად სინგულარულია.

ფუნქციის სინგულარობის ბუნება წერტილში შეიძლება შეფასდეს მთავარი ნაწილი ლორანის გაფართოება ამ წერტილის მიმდებარე ტერიტორიაზე.

თეორემა 1.იმისთვის, რომ წერტილი იყოს ერთჯერადი ფუნქციის სინგულარული წერტილი, აუცილებელია და საკმარისია შესაბამისი ლორანის გაფართოება არ შეიცავდა ძირითად ნაწილს.

დავალება 6.ფუნქციის ტეილორის გაფართოების გამოყენებით წერტილის სამეზობლოში აჩვენეთ, რომ მას აქვს მოხსნადი სინგულარობა ნულზე.

თეორემა 2.იმისთვის, რომ წერტილი იყოს ბოძი ფუნქციონირებს, აუცილებელია და საკმარისი იმისათვის, რომ მთავარი ნაწილი Laurent-ის შესაბამისი გაფართოება შეიცავდა წევრების სასრულ რაოდენობას :

ყველაზე მაღალი უარყოფითი წევრის რიცხვი განსაზღვრავს პოლუსის რიგითობას.

ამ შემთხვევაში ფუნქცია შეიძლება წარმოდგენილი იყოს როგორც

სადაც არის ფუნქცია ანალიტიკური წერტილში, , არის პოლუსის რიგი.

მაგალითი 10აჩვენეთ, რომ ფუნქციას აქვს მარტივი პოლუსები წერტილებში.

გამოსავალი.განვიხილოთ ერთი წერტილი. ჩვენ ვიყენებთ ამ ფუნქციის Laurent-ის გაფართოებას ამ წერტილის სიახლოვეს, მიღებული მაგალითში 2:

ვინაიდან ამ გაფართოების ძირითად ნაწილში ყველაზე მაღალი (და ერთადერთი) უარყოფითი ძალა უდრის ერთს, წერტილი არის ამ ფუნქციის მარტივი პოლუსი.

ამ შედეგის მიღება სხვა გზით შეიძლებოდა. მოდით წარმოვადგინოთ ფორმაში და დავაყენოთ - ეს არის ფუნქცია, რომელიც ანალიტიკურია წერტილში და . აქედან გამომდინარე, (8)-ის გამო ამ ფუნქციას აქვს მარტივი პოლუსი წერტილში.

სხვა გზა: განიხილეთ ფუნქცია, რომელსაც აქვს მარტივი ნული წერტილში. აქედან გამომდინარე, ამ ეტაპზე მას აქვს მარტივი ბოძი.

ანალოგიურად, თუ ფუნქციას დავწერთ ფორმაში, სადაც არის ფუნქცია ანალიტიკური წერტილში და, მაშინვე ცხადი ხდება, რომ წერტილი არის ფუნქციის მარტივი პოლუსი.

დავალება 7.აჩვენეთ, რომ ფუნქციას აქვს მე-2 რიგის პოლუსი წერტილში და მე-4 რიგის პოლუსი წერტილში.

თეორემა 3.იმისთვის, რომ წერტილი იყოს არსებითად განსაკუთრებული ფუნქციის წერტილი, აუცილებელია და საკმარისია, რომ მთავარი ნაწილი ლორანის გაფართოება წერტილის მიმდებარე ტერიტორიაზე შეიცავდა წევრთა უსასრულო რაოდენობას .

მაგალითი 11.განსაზღვრეთ სინგულარობის ბუნება ფუნქციის წერტილში

გამოსავალი.კოსინუსის ცნობილ გაფართოებაში ჩვენ ვსვამთ ნაცვლად:

მაშასადამე, ლორანის გაფართოებას წერტილის მიმდებარედ აქვს ფორმა

აქ სწორი ნაწილი არის ერთი ტერმინი. და მთავარი ნაწილი შეიცავს უსასრულო რაოდენობის ტერმინებს, ამიტომ წერტილი არსებითად სინგულარულია.

დავალება 8.აჩვენეთ, რომ ერთ წერტილში ფუნქციას აქვს არსებითი სინგულარობა.

განვიხილოთ ზოგიერთი ფუნქცია და ჩაწერეთ მისი Laurent გაფართოება წერტილში:

მოდით გავაკეთოთ ჩანაცვლება, სანამ წერტილი მიდის წერტილამდე. ახლა, უსასრულობის წერტილის სამეზობლოში, გვაქვს

რჩება ახალი აღნიშვნის შემოღება. ვიღებთ

სადაც არის ძირითადი ნაწილი და არის ფუნქციის ლორანის გაფართოების რეგულარული ნაწილი უსასრულოდ შორეული წერტილის მიმდებარედ. ამრიგად, ლორენტის გაფართოებაში ფუნქციის წერტილის სამეზობლოში, ძირითადი ნაწილი არის სერია დადებითი ძალებით, ხოლო სწორი ნაწილი არის სერია უარყოფითი ძალებით. ამის გათვალისწინებით

თუმცა, ზემოხსენებული კრიტერიუმები სინგულარობის ბუნების დასადგენად ძალაში რჩება უსასრულოდ შორეულ წერტილში.

მაგალითი 12.გაარკვიეთ ფუნქციის სინგულარობის ბუნება წერტილში. , მაშინ გარკვეულ მომენტში ის შეიძლება აღმოჩნდეს არაიზოლირებული.

მაგალითი 15ფუნქციას უსასრულოდ შორეულ წერტილში აქვს არსებითი სინგულარობა. აჩვენეთ, რომ ფუნქციის წერტილი არ არის იზოლირებული სინგულარული წერტილი.

გამოსავალი.ფუნქციას აქვს პოლუსების უსასრულო რაოდენობა მნიშვნელის ნულებთან, ანუ წერტილებზე , . ვინაიდან , მაშინ წერტილი , რომლის ნებისმიერ სამეზობლოში არის ბოძები , არის ბოძების ზღვრული წერტილი.

ცალკეული წერტილი

მათემატიკაში.

1) მრუდის სინგულარული წერტილი, რომელიც მოცემულია განტოლებით F ( x, y) = 0, - წერტილი M 0 ( x 0, y 0), რომელშიც F ფუნქციის ორივე ნაწილობრივი წარმოებული ( x, y) გაქრება:

თუ დამატებით F ფუნქციის ყველა მეორე ნაწილობრივი წარმოებული არ არის ( x, y) წერტილში M 0 უდრის ნულს, მაშინ O.t-ს ორმაგი ეწოდება. თუ M 0 წერტილში პირველი წარმოებულების გაქრობასთან ერთად ქრება ყველა მეორე წარმოებული, მაგრამ ყველა მესამე წარმოებული არ არის ნულის ტოლი, მაშინ O.t-ს ეწოდება სამმაგი და ა.შ. ორმაგი O.t.-ის მახლობლად მრუდის სტრუქტურის შესწავლისას მნიშვნელოვან როლს ასრულებს გამოხატვის ნიშანი.

თუ Δ > 0, მაშინ O.t.-ს ეწოდება იზოლირებული; მაგალითად, მრუდი y 2 - x 4 + 4x 2= 0 საწყისი არის იზოლირებული O.t. (იხ ბრინჯი. ერთი ). თუ Δ x 2 + y 2 + a 2) 2 - 4a 2 x 2 - a 4= 0 კოორდინატების საწყისი არის კვანძოვანი O.t. (იხ ბრინჯი. 2 ). თუ Δ = 0, მაშინ O.t. მრუდი ან იზოლირებულია ან ხასიათდება იმით, რომ მრუდის სხვადასხვა ტოტებს აქვთ საერთო ტანგენსი ამ წერტილში, მაგალითად: ტანგენსი და ქმნიან წერტილს, როგორც მრუდი. y 2 - x 3= 0 (იხ ბრინჯი. 3 , ა); ბ) მე-2 სახის კუსპი - მრუდის სხვადასხვა ტოტები განლაგებულია საერთო ტანგენსის ერთ მხარეს, მრუდის მსგავსად. (y - x 2)2 - x 5= 0 (იხ ბრინჯი. 3 , ბ); გ) თვითკონტაქტის წერტილი (მრუდისთვის y 2 - x 4= 0 საწყისი არის თვითკონტაქტის წერტილი; (სმ. ბრინჯი. 3 , ვ). მითითებულ O.t.-თან ერთად არის მრავალი სხვა O. t. განსაკუთრებული სახელწოდებით; მაგალითად, ასიმპტომური წერტილი არის სპირალის მწვერვალი უსასრულო რაოდენობის ბრუნვით (იხ. ბრინჯი. 4 ), შესვენების წერტილი, კუთხის წერტილი და ა.შ.

2) დიფერენციალური განტოლების სინგულარული წერტილი არის წერტილი, სადაც დიფერენციალური განტოლების მარჯვენა მხარის მრიცხველიც და მნიშვნელიც ერთდროულად ქრება (იხილეთ დიფერენციალური განტოლებები)

სადაც P და Q განუწყვეტლივ დიფერენცირებადი ფუნქციებია. ვივარაუდოთ, რომ O.t მდებარეობს კოორდინატების სათავეში და ტეილორის ფორმულის გამოყენებით (იხ. ტეილორის ფორმულა), ჩვენ შეგვიძლია წარმოვადგინოთ განტოლება (1) სახით.

სადაც P 1 ( x, y) და Q 1 ( x, y) უსასრულოდ მცირეა

კერძოდ, თუ λ 1 ≠ λ 2 და λ 1 λ 2 > 0 ან λ 1 = λ 2, მაშინ O.t არის კვანძი; მასში შედის ყველა ინტეგრალური მრუდი, რომელიც გადის კვანძის საკმარისად მცირე უბნის წერტილებში. თუ λ 1 ≠ λ 2 და λ 1 λ 2 i β, α ≠ 0 და β ≠ 0, მაშინ O.t არის ფოკუსი; ყველა ინტეგრალური მრუდი, რომელიც გადის წერტილებს ფოკუსის საკმარისად მცირე სამეზობლოში, არის სპირალები უსასრულო რაოდენობის ბრუნვით ფოკუსის ნებისმიერ თვითნებურად მცირე სამეზობლოში. თუ საბოლოოდ, λ 1,2 = ± მეβ, β ≠ 0, მაშინ O.t-ის ხასიათი არ არის განსაზღვრული წრფივი ტერმინებით P-ის გაფართოებებში ( x, y) და Q ( x, y), როგორც ეს იყო ყველა ზემოაღნიშნულ შემთხვევაში; აქ O.t. შეიძლება იყოს ფოკუსი ან ცენტრი, ან შეიძლება ჰქონდეს უფრო რთული ხასიათი. ცენტრის მახლობლად, ყველა ინტეგრალური მრუდი დახურულია და შეიცავს ცენტრს მათ შიგნით. მაგალითად, წერტილი (0, 0) არის კვანძი განტოლებისთვის ზე" = 2u/x(λ 1 = 1, λ 2 = 2; იხ ბრინჯი. 5 , ა) და წ" = u/x(λ 1 = λ 2 = 1; იხ ბრინჯი. 5 , ბ), უნაგირს განტოლებისთვის y" = -y/x(λ 1 = -1, λ 2 = 1 ; სმ. ბრინჯი. 6 ), ფოკუსი განტოლებისთვის y" =(x + y) / (x - y) (λ 1 = 1 - მე, λ 2 = 1 + მე; სმ. ბრინჯი. 7 ) და განტოლების ცენტრი y" = -x / y(λ 1 = -მე, λ 2 = მე; სმ. ბრინჯი. რვა ).

თუ x, y) და Q ( x, y) არის ანალიტიკური, უმაღლესი რიგის O.t-ის სამეზობლო შეიძლება დაიყოს რეგიონებად: D 1 - ივსება ინტეგრალური მრუდებით, ორივე ბოლო შედის O.t.-ში (ელიფსური რეგიონები), D 2 - ივსება ინტეგრალური მრუდებით, ერთი ბოლო შედის O.t.-ში (პარაბოლური რეგიონები) და D 3 - რეგიონები, რომლებიც შემოსაზღვრულია O.t-ში შემავალი ორი ინტეგრალური მრუდით, რომელთა შორის არის ჰიპერბოლების (ჰიპერბოლური რეგიონები) ტიპის ინტეგრალური მრუდები (იხ. ბრინჯი. 9 ). თუ არ არის ინტეგრალური მრუდები, რომლებიც შედის O. წერტილში, მაშინ O. წერტილს ეწოდება სტაბილური ტიპის წერტილი. სტაბილური O.t.-ის სამეზობლო შედგება დახურული ინტეგრალური მოსახვევებისგან, რომლებიც შეიცავს O.t.-ს შიგნით, რომელთა შორის არის სპირალები (იხ. ბრინჯი. 10 ).

O.t. დიფერენციალური განტოლებების შესწავლა, ანუ, არსებითად, ინტეგრალური მრუდების ოჯახების ქცევის შესწავლა O.t. M. Lyapunov a, A. Poincaré და სხვათა სამეზობლოში).

3) ერთმნიშვნელოვანი ანალიტიკური ფუნქციის სინგულარული წერტილი არის წერტილი, რომელშიც ირღვევა ფუნქციის ანალიტიურობა (იხ. ანალიტიკური ფუნქციები). თუ არის ო.ტ. ა, თავისუფალი სხვა O. t., მაშინ წერტილი აეწოდება იზოლირებული O.t. თუ აარის იზოლირებული O. t. და არსებობს სასრული a ეწოდება მოსახსნელი O. t. ვ(ა)= ბ, შესაძლებელია მიღწევა აგახდება შესწორებული ფუნქციის ჩვეულებრივი წერტილი. მაგალითად, წერტილი ზ= 0 არის მოსახსნელი O.T. ფუნქციისთვის f 1 ( ზ) = ვ(ზ), თუ ზ≠ 0 და ვ 1 (0), = 1, წერტილი ზ= 0 არის ჩვეულებრივი წერტილი [ ვ 1 (ზ) არის ანალიტიკური წერტილი ზ= 0]. თუ ა- იზოლირებული O.t. და a-ს ეწოდება ფუნქციის პოლუსი ან არსებითად სინგულარული წერტილი ვ(ზ), თუ Laurent სერია) ფუნქციონირებს ვ(ზ) იზოლირებული ო.ტ-ის მიმდებარე ტერიტორიაზე არ შეიცავს უარყოფით ძალას ზ - ა, თუ ა- მოსახსნელი O.t., შეიცავს უარყოფით ძალების სასრულ რაოდენობას ზ - ა, თუ ა- ბოძი (ამ შემთხვევაში, ბოძის რიგი რგანისაზღვრება, როგორც a-ს უმაღლესი ძალა - არსებითად სინგულარული წერტილი. მაგალითად, ფუნქციისთვის

p = 2, 3, ...)

წერტილი ზ= 0 არის რიგის პოლუსი რ, ფუნქციისთვის

წერტილი ზ= 0 არის არსებითი სინგულარული წერტილი.

სიმძლავრის სერიის კონვერგენციის წრის საზღვარზე უნდა იყოს ფუნქციის მინიმუმ ერთი O.t, რომელიც წარმოდგენილია ამ წრის შიგნით მოცემული სიმძლავრის სერიით. ერთმნიშვნელოვანი ანალიტიკური ფუნქციის (ბუნებრივი საზღვარი) არსებობის დომენის ყველა სასაზღვრო წერტილი ამ ფუნქციის სასაზღვრო წერტილებია. ამრიგად, ერთეული წრის ყველა წერტილი | ზ| = 1 არის სპეციალური ფუნქციისთვის

მრავალმნიშვნელოვანი ანალიტიკური ფუნქციისთვის, კონცეფცია „O. თ." უფრო რთული. O.t-ის გარდა, ფუნქციის რიმანის ზედაპირის ცალკეულ ფურცლებში (ანუ ერთმნიშვნელოვანი ანალიტიკური ელემენტების O. t.), ნებისმიერი განშტოების წერტილი ასევე არის ფუნქციის O. t.. რიმანის ზედაპირის იზოლირებული განშტოების წერტილები (ანუ განშტოების წერტილები ისეთი, რომ ზოგიერთ მათ უბნებში არ არის სხვა O.t. ფუნქცია რომელიმე ფოთოლში) კლასიფიცირებულია შემდეგნაირად. თუ a არის სასრული რიგის იზოლირებული განშტოების წერტილი და არსებობს სასრული a, მას კრიტიკული პოლუსი ეწოდება. თუ აარის უსასრულო რიგის იზოლირებული განშტოების წერტილი და a-ს ეწოდება ტრანსცენდენტული O. t. ყველა სხვა იზოლირებულ განშტოებას ეწოდება კრიტიკული არსებითად სინგულარული წერტილები. მაგალითები: წერტილი ზ= 0 არის f ფუნქციის ჩვეულებრივი კრიტიკული წერტილი ( ზ) = ჟურნალი ზდა ფუნქციის კრიტიკული არსებითი სინგულარული წერტილი ვ (ზ) = ცოდვის ჟურნალი ზ.

ნებისმიერი O. t., გარდა მოსახსნელი, არის დაბრკოლება ანალიტიკური გაგრძელებისთვის, ანუ შეუძლებელია ანალიზური გაგრძელება მრუდის გასწვრივ, რომელიც გადის მოუხსნელ O. t.-ზე.

დიდი საბჭოთა ენციკლოპედია. - მ.: საბჭოთა ენციკლოპედია. 1969-1978 .

ნახეთ, რა არის "სპეციალური წერტილი" სხვა ლექსიკონებში:

ქულები აქ. აგრეთვე სინგულარული წერტილი (დიფერენციალური განტოლებები). თვისება ან სინგულარობა მათემატიკაში არის წერტილი, სადაც მათემატიკური ობიექტი (ჩვეულებრივ ფუნქცია) არ არის განსაზღვრული ან აქვს არარეგულარული ქცევა (მაგალითად, წერტილი, სადაც ... ... ვიკიპედია

ანალიტიკური ფუნქცია არის წერტილი, რომელშიც ირღვევა ანალიტიკურობის პირობები. თუ ანალიტიკური ფუნქცია f(z) განისაზღვრება z0 წერტილის რომელიმე მიმდებარე ტერიტორიაზე ყველგან… ფიზიკური ენციკლოპედია

ანალიტიკური ფუნქცია არის წერტილი, როდესაც ფუნქციის ანალიტიურობა ირღვევა ... დიდი ენციკლოპედიური ლექსიკონი

ცალკეული წერტილი- — [Ya.N. Luginsky, M.S. Fezi Zhilinskaya, Yu.S. Kabirov. English Russian Dictionary of Electrical Engineering and Power Industry, მოსკოვი, 1999] ელექტროტექნიკის თემები, ძირითადი ცნებები EN სინგულარული წერტილი ... ტექნიკური მთარგმნელის სახელმძღვანელო

1) ანალიტიკური f(z) ფუნქციის OT არის დაბრკოლება z რთული ცვლადის f(z) ფუნქციის ელემენტის ანალიტიკური გაგრძელებისთვის ამ ცვლადის სიბრტყის რომელიმე ბილიკის გასწვრივ. ანალიტიკური ფუნქცია f(z) განისაზღვროს ზოგიერთი ... ... მათემატიკური ენციკლოპედია

ანალიტიკური ფუნქცია, წერტილი, როდესაც ირღვევა ფუნქციის ანალიტიურობა. * * * სინგულარული წერტილი ანალიტიკური ფუნქციის სინგულარული წერტილი, წერტილი, რომელშიც ფუნქციის ანალიტიურობა ირღვევა ... ენციკლოპედიური ლექსიკონი

ცალკეული წერტილი- ypatingasis taškas statusas T sritis automatika atitikmenys: ინგლ. სინგულარული წერტილი vok. singularer Punkt, m rus. სინგულარული წერტილი, fpranc. წერტილოვანი ნაწილაკი, მ; წერტილი singulier, m … ავტომატური ტერმინალი