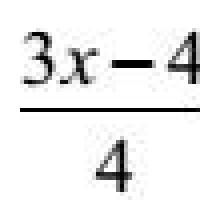Paprastų tiesinių lygčių sprendimas. Tiesinės lygtys. Sprendimas, pavyzdžiai Kaip išspręsti padalijimo lygtis

Lygtis su vienu nežinomuoju, kuri, atidarius skliaustus ir suvedus panašius terminus, įgauna formą

ax + b = 0, kur a ir b yra savavališki skaičiai, vadinamas tiesinė lygtis su vienu nepažįstamu. Šiandien išsiaiškinsime, kaip išspręsti šias tiesines lygtis.

Pavyzdžiui, visos lygtys:

2x + 3= 7 – 0,5x; 0,3x = 0; x/2 + 3 = 1/2 (x – 2) – tiesinis.

Nežinomo reikšmė, kuri lygtį paverčia tikrąja lygybe, vadinama sprendimą arba lygties šaknis .

Pavyzdžiui, jei lygtyje 3x + 7 = 13 vietoj nežinomo x pakeičiame skaičių 2, gauname teisingą lygybę 3 2 +7 = 13. Tai reiškia, kad reikšmė x = 2 yra sprendinys arba šaknis lygties.

O reikšmė x = 3 nepaverčia lygties 3x + 7 = 13 tikrąja lygybe, nes 3 2 +7 ≠ 13. Tai reiškia, kad reikšmė x = 3 nėra lygties sprendinys ar šaknis.

Bet kokių tiesinių lygčių sprendimas redukuojasi iki formos lygčių sprendimo

ax + b = 0.

Perkelkime laisvąjį terminą iš kairės lygties pusės į dešinę, pakeitę ženklą priešais b į priešingą, gausime

Jei a ≠ 0, tai x = ‒ b/a .

1 pavyzdys. Išspręskite lygtį 3x + 2 =11.

Perkelkime 2 iš kairės lygties pusės į dešinę, pakeitę ženklą priešais 2 į priešingą, gausime
3x = 11–2.

Tada atlikime atimtį
3x = 9.

Norėdami rasti x, turite padalyti sandaugą iš žinomo koeficiento, ty
x = 9:3.

Tai reiškia, kad reikšmė x = 3 yra lygties sprendimas arba šaknis.

Atsakymas: x = 3.

Jei a = 0 ir b = 0, tada gauname lygtį 0x = 0. Ši lygtis turi be galo daug sprendinių, nes bet kurį skaičių padauginus iš 0 gauname 0, bet b taip pat lygus 0. Šios lygties sprendimas yra bet koks skaičius.

2 pavyzdys. Išspręskite lygtį 5 (x – 3) + 2 = 3 (x – 4) + 2x ‒ 1.

Išplėskime skliaustus:
5x – 15 + 2 = 3x – 12 + 2x ‒ 1.

5x – 3x ‒ 2x = – 12 ‒ 1 + 15 ‒ 2.

Štai keletas panašių terminų:
0x = 0.

Atsakymas: x – bet koks skaičius.

Jei a = 0 ir b ≠ 0, tada gauname lygtį 0х = - b. Ši lygtis neturi sprendinių, nes bet kurį skaičių padauginus iš 0 gauname 0, bet b ≠ 0.

3 pavyzdys. Išspręskite lygtį x + 8 = x + 5.

Sugrupuokime terminus, kurių kairėje pusėje yra nežinomųjų, o dešinėje – laisvus terminus:
x – x = 5 – 8.

Štai keletas panašių terminų:
0х = ‒ 3.

Atsakymas: nėra sprendimų.

Įjungta figūra 1 parodyta tiesinės lygties sprendimo schema

Paruoškime bendrą lygčių su vienu kintamuoju sprendimo schemą. Panagrinėkime 4 pavyzdžio sprendimą.

4 pavyzdys. Tarkime, kad turime išspręsti lygtį

1) Padauginkite visus lygties narius iš mažiausio bendro vardiklių kartotinio, lygaus 12.

2) Sumažinus gauname
4 (x – 4) + 3 2 (x + 1) ‒ 12 = 6 5 (x – 3) + 24x – 2 (11x + 43)

3) Norėdami atskirti terminus, kuriuose yra nežinomų ir laisvų terminų, atidarykite skliaustus:
4x - 16 + 6x + 6 - 12 = 30x - 90 + 24x - 22x - 86.

4) Vienoje dalyje sugrupuokime terminus, kuriuose yra nežinomųjų, o kitoje - laisvuosius:
4x + 6x - 30x - 24x + 22x = ‒ 90 - 86 + 16 - 6 + 12.

5) Pateiksime panašius terminus:
- 22х = -154.

6) Padalinkite iš – 22, gauname
x = 7.

Kaip matote, lygties šaknis yra septyni.

Paprastai tokie lygtis galima išspręsti naudojant šią schemą:

a) perkelkite lygtį į sveikąjį skaičių;

b) atidarykite skliaustus;

c) sugrupuokite terminus, kuriuose yra nežinomasis vienoje lygties dalyje, o laisvuosius – kitoje;

d) atsivesti panašius narius;

e) išspręskite aх = b formos lygtį, kuri gauta atvedus panašius dėmenis.

Tačiau ši schema nėra būtina kiekvienai lygčiai. Sprendžiant daug paprastesnių lygčių, reikia pradėti ne nuo pirmos, o nuo antrosios ( Pavyzdys. 2), trečias ( Pavyzdys. 13) ir net nuo penktojo etapo, kaip nurodyta 5 pavyzdyje.

5 pavyzdys. Išspręskite lygtį 2x = 1/4.

Raskite nežinomą x = 1/4: 2,
x = 1/8 .

Pažiūrėkime, kaip išspręsti kai kurias tiesines lygtis, rastas pagrindiniame valstybiniame egzamine.

6 pavyzdys. Išspręskite lygtį 2 (x + 3) = 5 – 6x.

2x + 6 = 5 - 6x

2x + 6x = 5-6

Atsakymas: - 0,125

7 pavyzdys. Išspręskite lygtį – 6 (5 – 3x) = 8x – 7.

– 30 + 18x = 8x – 7

18x – 8x = – 7 +30

Atsakymas: 2.3

8 pavyzdys. Išspręskite lygtį

3 (3x – 4) = 4 7x + 24

9x – 12 = 28x + 24

9x – 28x = 24 + 12

9 pavyzdys. Raskite f(6), jei f (x + 2) = 3 7

Sprendimas

Kadangi turime rasti f (6), ir mes žinome f (x + 2),
tada x + 2 = 6.

Išsprendžiame tiesinę lygtį x + 2 = 6,
gauname x = 6 – 2, x = 4.

Jei x = 4, tada
f(6) = 3 7-4 = 3 3 = 27

Atsakymas: 27.

Jei vis dar turite klausimų ar norite nuodugniau suprasti lygčių sprendimą, užsiregistruokite į mano pamokas TVARKARAŠYBĖJE. Mielai jums padėsiu!

„TutorOnline“ taip pat rekomenduoja žiūrėti naują vaizdo įrašą, kurį parašė mūsų dėstytojas Olga Aleksandrovna, kuri padės suprasti tiek tiesines lygtis, tiek kitas.

svetainėje, kopijuojant visą medžiagą ar jos dalį, būtina nuoroda į šaltinį.

Šiame vaizdo įraše analizuosime visą rinkinį tiesinių lygčių, kurios išsprendžiamos naudojant tą patį algoritmą – todėl jos vadinamos paprasčiausiomis.

Pirmiausia apibrėžkime: kas yra tiesinė lygtis ir kuri vadinama paprasčiausia?

Tiesinė lygtis yra ta, kurioje yra tik vienas kintamasis ir tik iki pirmojo laipsnio.

Paprasčiausia lygtis reiškia konstrukciją:

Visos kitos tiesinės lygtys sumažinamos iki paprasčiausių naudojant algoritmą:

1. Išskleiskite skliaustus, jei tokių yra;
2. Perkelkite terminus su kintamuoju į vieną lygybės ženklo pusę, o terminus be kintamojo į kitą;
3. Lygybės ženklo kairėje ir dešinėje nurodykite panašius terminus;
4. Gautą lygtį padalinkite iš kintamojo $x$ koeficiento.

Žinoma, šis algoritmas ne visada padeda. Faktas yra tas, kad kartais po visų šių machinacijų kintamojo $x$ koeficientas pasirodo lygus nuliui. Šiuo atveju galimi du variantai:

1. Lygtis apskritai neturi sprendinių. Pavyzdžiui, kai pasirodo kažkas panašaus į $0\cdot x=8$, t.y. kairėje yra nulis, o dešinėje yra skaičius, kuris nėra nulis. Žemiau esančiame vaizdo įraše apžvelgsime keletą priežasčių, kodėl tokia situacija yra įmanoma.
2. Sprendimas yra visi skaičiai. Vienintelis atvejis, kai tai įmanoma, yra tada, kai lygtis sumažinta iki konstrukcijos $0\cdot x=0$. Visai logiška, kad kad ir kokius $x$ pakeistume, vis tiek išeis „nulis lygus nuliui“, t.y. teisinga skaitinė lygybė.

Dabar pažiūrėkime, kaip visa tai veikia, naudodamiesi realaus gyvenimo pavyzdžiais.

Lygčių sprendimo pavyzdžiai

Šiandien mes susiduriame su tiesinėmis lygtimis ir tik pačiomis paprasčiausiomis. Apskritai tiesinė lygtis reiškia bet kokią lygybę, kurioje yra tiksliai vienas kintamasis, ir ji eina tik iki pirmojo laipsnio.

Tokios konstrukcijos sprendžiamos maždaug tokiu pačiu būdu:

1. Visų pirma, reikia išplėsti skliaustus, jei tokių yra (kaip mūsų paskutiniame pavyzdyje);
2. Tada derinkite panašius
3. Galiausiai išskirkite kintamąjį, t.y. perkelkite viską, kas susiję su kintamuoju – terminus, kuriuose jis yra – į vieną pusę, o viską, kas lieka be jo, perkelkite į kitą pusę.

Tada, kaip taisyklė, reikia atvesti panašius iš kiekvienos gautos lygybės pusės, o po to belieka padalyti iš koeficiento „x“, ir mes gausime galutinį atsakymą.

Teoriškai tai atrodo gražiai ir paprastai, tačiau praktiškai net patyrę aukštųjų mokyklų studentai gali padaryti įžeidžiančių klaidų gana paprastose tiesinėse lygtyse. Paprastai klaidos daromos atidarant skliaustus arba skaičiuojant „pliusus“ ir „minusus“.

Be to, pasitaiko, kad tiesinė lygtis apskritai neturi sprendinių arba sprendinys yra visa skaičių tiesė, t.y. bet koks skaičius. Šios subtilybės apžvelgsime šios dienos pamokoje. Bet pradėsime, kaip jau supratote, nuo paprasčiausių užduočių.

Paprastų tiesinių lygčių sprendimo schema

Pirmiausia leiskite man dar kartą parašyti visą paprasčiausių tiesinių lygčių sprendimo schemą:

1. Išplėskite skliaustus, jei tokių yra.
2. Išskiriame kintamuosius, t.y. Viską, kur yra „X“, perkeliame į vieną pusę, o viską be „X“ – į kitą.
3. Pateikiame panašias sąlygas.
4. Viską padaliname iš koeficiento „x“.

Žinoma, ši schema ne visada veikia, joje yra tam tikrų subtilybių ir gudrybių, ir dabar mes su jais susipažinsime.

Realių paprastų tiesinių lygčių pavyzdžių sprendimas

Užduotis Nr.1

Pirmas žingsnis reikalauja, kad atidarytume skliaustus. Tačiau šiame pavyzdyje jų nėra, todėl šį žingsnį praleidžiame. Antrame etape turime išskirti kintamuosius. Atkreipkite dėmesį: mes kalbame tik apie atskiras sąlygas. Užsirašykime:

Kairėje ir dešinėje pateikiame panašius terminus, tačiau tai jau buvo padaryta čia. Todėl pereiname prie ketvirto žingsnio: padalinkite iš koeficiento:

\[\frac(6x)(6)=-\frac(72)(6)\]

Taigi mes gavome atsakymą.

2 užduotis

Šioje užduotyje matome skliaustus, todėl išplėskime juos:

Ir kairėje, ir dešinėje matome maždaug vienodą dizainą, bet veikime pagal algoritmą, t.y. atskiriant kintamuosius:

Štai keletas panašių:

Kokiomis šaknimis tai veikia? Atsakymas: bet kokiam. Todėl galime parašyti, kad $x$ yra bet koks skaičius.

Užduotis Nr.3

Trečioji tiesinė lygtis įdomesnė:

\[\left(6-x \right)+\left(12+x \right)-\left(3-2x \right)=15\]

Čia yra keli skliaustai, bet jie iš nieko nepadauginami, tiesiog prieš juos yra skirtingi ženklai. Išskaidykime juos:

Atliekame antrą mums jau žinomą žingsnį:

\[-x+x+2x=15-6-12+3\]

Paskaičiuokime:

Atliekame paskutinį žingsnį - viską padaliname iš koeficiento „x“:

\[\frac(2x)(x)=\frac(0)(2)\]

Ką reikia atsiminti sprendžiant tiesines lygtis

Jei ignoruosime pernelyg paprastas užduotis, norėčiau pasakyti:

• Kaip sakiau aukščiau, ne kiekviena tiesinė lygtis turi sprendimą – kartais tiesiog nėra šaknų;
• Net jei yra šaknų, tarp jų gali būti nulis – nieko blogo.

Nulis yra toks pat skaičius, kaip ir kiti, jokiu būdu neturėtumėte jo diskriminuoti arba manyti, kad jei gaunate nulį, padarėte kažką ne taip.

Kitas bruožas yra susijęs su skliaustų atidarymu. Atkreipkite dėmesį: kai prieš juos yra „minusas“, mes jį pašaliname, bet skliausteliuose keičiame ženklus į priešingas. Ir tada galime jį atidaryti naudodami standartinius algoritmus: gausime tai, ką matėme atlikdami aukščiau pateiktus skaičiavimus.

Šio paprasto fakto supratimas padės išvengti kvailų ir skaudžių klaidų vidurinėje mokykloje, kai tokie dalykai laikomi savaime suprantamu dalyku.

Sudėtingų tiesinių lygčių sprendimas

Pereikime prie sudėtingesnių lygčių. Dabar konstrukcijos taps sudėtingesnės ir atliekant įvairias transformacijas atsiras kvadratinė funkcija. Tačiau neturėtume to bijoti, nes jei pagal autoriaus planą sprendžiame tiesinę lygtį, tada transformacijos metu visi monomai, turintys kvadratinę funkciją, tikrai bus panaikinti.

1 pavyzdys

Akivaizdu, kad pirmas žingsnis yra atidaryti skliaustus. Padarykime tai labai atsargiai:

Dabar pažvelkime į privatumą:

\[-x+6((x)^(2))-6((x)^(2))+x=-12\]

Štai keletas panašių:

Akivaizdu, kad ši lygtis neturi sprendimų, todėl atsakyme parašysime tai:

\[\varnothing\]

arba nėra šaknų.

2 pavyzdys

Atliekame tuos pačius veiksmus. Pirmas žingsnis:

Viską perkelkime su kintamuoju į kairę, o be jo - į dešinę:

Štai keletas panašių:

Akivaizdu, kad ši tiesinė lygtis neturi sprendimo, todėl ją parašysime taip:

\[\varnothing\],

arba nėra šaknų.

Sprendimo niuansai

Abi lygtys yra visiškai išspręstos. Panaudoję šias dvi išraiškas kaip pavyzdį, dar kartą įsitikinome, kad net paprasčiausiose tiesinėse lygtyse viskas gali būti ne taip paprasta: gali būti arba viena, arba jų nėra, arba be galo daug šaknų. Mūsų atveju mes nagrinėjome dvi lygtis, abi tiesiog neturi šaknų.

Tačiau norėčiau atkreipti jūsų dėmesį į kitą faktą: kaip dirbti su skliaustais ir kaip juos atidaryti, jei prieš juos yra minuso ženklas. Apsvarstykite šią išraišką:

Prieš atidarydami, turite viską padauginti iš „X“. Atkreipkite dėmesį: dauginasi kiekvienas atskiras terminas. Viduje yra du terminai - atitinkamai du terminai ir padauginti.

Ir tik baigus šias iš pažiūros elementarias, bet labai svarbias ir pavojingas transformacijas, galima atversti skliaustą iš to, kad po jo yra minuso ženklas. Taip, taip: tik dabar, kai transformacijos baigtos, prisimename, kad prieš skliaustus yra minuso ženklas, o tai reiškia, kad viskas žemiau tiesiog keičia ženklus. Tuo pačiu metu dingsta patys laikikliai ir, svarbiausia, dingsta ir priekinis „minusas“.

Tą patį darome su antrąja lygtimi:

Neatsitiktinai atkreipiu dėmesį į šiuos mažus, atrodytų, nereikšmingus faktus. Nes lygčių sprendimas visada yra elementarių transformacijų seka, kai nesugebėjimas aiškiai ir kompetentingai atlikti nesudėtingų veiksmų lemia tai, kad pas mane ateina gimnazistai ir vėl mokosi spręsti tokias paprastas lygtis.

Žinoma, ateis diena, kai šiuos įgūdžius ištobulinsite iki automatizavimo. Jums nebereikės kaskart atlikti tiek daug transformacijų, viską surašysite vienoje eilutėje. Bet kol jūs tik mokotės, kiekvieną veiksmą turite parašyti atskirai.

Dar sudėtingesnių tiesinių lygčių sprendimas

Tai, ką dabar spręsime, vargu ar galima pavadinti paprasčiausia užduotimi, tačiau prasmė išlieka ta pati.

Užduotis Nr.1

\[\left(7x+1 \right)\left(3x-1 \right)-21((x)^(2))=3\]

Padauginkime visus pirmosios dalies elementus:

Pasirūpinkime privatumu:

Štai keletas panašių:

Užbaikime paskutinį žingsnį:

\[\frac(-4x)(4)=\frac(4)(-4)\]

Štai mūsų galutinis atsakymas. Ir nepaisant to, kad spręsdami turėjome koeficientus su kvadratine funkcija, jie vienas kitą panaikino, todėl lygtis yra tiesinė, o ne kvadratinė.

2 užduotis

\[\left(1-4x \right)\left(1-3x \right)=6x\left(2x-1 \right)\]

Atsargiai atlikime pirmąjį veiksmą: padauginkite kiekvieną elementą iš pirmojo skliausto iš kiekvieno elemento iš antrojo. Po pakeitimų iš viso turėtų būti keturi nauji terminai:

Dabar atidžiai padauginkime kiekvieną terminą:

Perkelkime terminus su "X" į kairę, o tuos, kurių nėra - į dešinę:

\[-3x-4x+12((x)^(2))-12((x)^(2))+6x=-1\]

Čia yra panašūs terminai:

Dar kartą gavome galutinį atsakymą.

Sprendimo niuansai

Svarbiausia pastaba apie šias dvi lygtis yra tokia: kai tik pradedame dauginti skliaustus, kuriuose yra daugiau nei vienas narys, tai daroma pagal tokią taisyklę: paimame pirmąjį narį iš pirmojo ir padauginame iš kiekvieno elemento iš Antras; tada paimame antrą elementą iš pirmojo ir panašiai padauginame su kiekvienu elementu iš antrojo. Dėl to turėsime keturias kadencijas.

Apie algebrinę sumą

Šiuo paskutiniu pavyzdžiu norėčiau priminti mokiniams, kas yra algebrinė suma. Klasikinėje matematikoje 1–7 USD turime omenyje paprastą konstrukciją: iš vieno atimti septynis. Algebroje tai reiškia: prie skaičiaus „vienas“ pridedame kitą skaičių, būtent „minus septyni“. Taip algebrinė suma skiriasi nuo įprastos aritmetinės sumos.

Kai tik atlikdami visas transformacijas, kiekvieną sudėjimą ir dauginimą pradėsite matyti konstrukcijas, panašias į aukščiau aprašytas, tiesiog neturėsite problemų algebroje dirbdami su daugianariais ir lygtimis.

Galiausiai pažvelkime į dar keletą pavyzdžių, kurie bus dar sudėtingesni nei tie, kuriuos ką tik pažvelgėme, ir norėdami juos išspręsti, turėsime šiek tiek išplėsti standartinį algoritmą.

Lygčių su trupmenomis sprendimas

Norėdami išspręsti tokias užduotis, prie algoritmo turėsime pridėti dar vieną žingsnį. Bet pirmiausia leiskite jums priminti mūsų algoritmą:

1. Atidarykite skliaustus.
2. Atskiri kintamieji.
3. Atsineškite panašių.
4. Padalinkite iš santykio.

Deja, šis nuostabus algoritmas, nepaisant viso savo efektyvumo, pasirodo ne visai tinkamas, kai prieš mus yra trupmenos. Ir tai, ką matysime toliau, abiejose lygtyse turime trupmeną tiek kairėje, tiek dešinėje.

Kaip tokiu atveju dirbti? Taip, tai labai paprasta! Norėdami tai padaryti, prie algoritmo turite pridėti dar vieną žingsnį, kurį galima atlikti tiek prieš, tiek po pirmojo veiksmo, būtent, atsikratyti trupmenų. Taigi algoritmas bus toks:

1. Atsikratykite frakcijų.
2. Atidarykite skliaustus.
3. Atskiri kintamieji.
4. Atsineškite panašių.
5. Padalinkite iš santykio.

Ką reiškia „atsikratyti trupmenų“? Ir kodėl tai galima padaryti ir po pirmojo standartinio žingsnio, ir prieš jį? Tiesą sakant, mūsų atveju visos trupmenos yra skaitinės savo vardikliu, t.y. Visur vardiklis yra tik skaičius. Todėl, padauginus abi lygties puses iš šio skaičiaus, atsikratysime trupmenų.

1 pavyzdys

\[\frac(\left(2x+1 \right)\left(2x-3 \right))(4)=((x)^(2))-1\]

Atsikratykime šios lygties trupmenų:

\[\frac(\left(2x+1 \right)\left(2x-3 \right)\cdot 4)(4)=\left(((x)^(2))-1 \right)\cdot 4\]

Atkreipkite dėmesį: viskas padauginama iš „keturių“ vieną kartą, t.y. vien todėl, kad turite du skliaustus, nereiškia, kad turite padauginti kiekvieną iš „keturių“. Užsirašykime:

\[\left(2x+1 \right)\left(2x-3 \right)=\left(((x)^(2))-1 \right)\cdot 4\]

Dabar išplėskime:

Išskiriame kintamąjį:

Atliekame panašių terminų sumažinimą:

\[-4x = -1\left| :\kairė(-4 \dešinė) \dešinė.\]

\[\frac(-4x)(-4)=\frac(-1)(-4)\]

Gavome galutinį sprendimą, pereikime prie antrosios lygties.

2 pavyzdys

\[\frac(\left(1-x \right)\left(1+5x \right))(5)+((x)^(2))=1\]

Čia atliekame visus tuos pačius veiksmus:

\[\frac(\left(1-x \right)\left(1+5x \right)\cdot 5)(5)+((x)^(2))\cdot 5=5\]

\[\frac(4x)(4)=\frac(4)(4)\]

Problema išspręsta.

Tiesą sakant, tai yra viskas, ką šiandien norėjau jums pasakyti.

Pagrindiniai klausimai

Pagrindinės išvados yra šios:

• Žinoti tiesinių lygčių sprendimo algoritmą.
• Galimybė atidaryti skliaustus.
• Nesijaudinkite, jei kur nors turite kvadratinių funkcijų, tolimesnių transformacijų metu jos bus sumažintos.
• Tiesinėse lygtyse yra trijų tipų šaknys, net ir pačios paprasčiausios: viena šaknis, visa skaičių eilutė yra šaknis, o šaknų visai nėra.

Tikiuosi, kad ši pamoka padės jums įsisavinti paprastą, bet labai svarbią temą, kad galėtumėte geriau suprasti visą matematiką. Jei kažkas neaišku, eikite į svetainę ir išspręskite ten pateiktus pavyzdžius. Sekite naujienas, jūsų laukia dar daug įdomių dalykų!

Sprendimą už akių, be išimtinių įstatyme numatytų sprendimo būdų, atsakovo prašymu gali panaikinti tas pats teismas, atnaujinęs bylos nagrinėjimą iš esmės, jeigu jis gali įrodyti, kad jo neatvykimas į teismo posėdį buvo nulemtas svarbių priežasčių.

Peržiūrėti įsiteisėjusį sprendimą kasacine tvarka galima, jeigu teismas atnaujino dėl svarbios priežasties praleistą kasacijos terminą.

Išskirtinumas:

Išskirtinumo savybė – tai negalėjimas pakartotinai kreiptis į teismą su ieškiniu, skundu, pareiškimu byloje tarp tų pačių šalių ar jų teisių perėmėjų, dėl to paties dalyko ir remiantis tomis pačiomis aplinkybėmis (ieškinio pagrindu). jeigu yra įsiteisėjęs sprendimas.

Jeigu įsiteisėjus sprendimui, kuriuo iš atsakovo išieškomos periodinės išmokos, pasikeičia aplinkybės, turinčios įtakos įmokų dydžiui ar jų trukmei nustatyti, tai kiekviena šalis, pareikšdama naują ieškinį, turi teisę reikalauti, kad 2013 m. mokėjimų sumos ir laiko pasikeitimas.

Tokiu atveju nauji reikalavimai tampa teismo nagrinėjimo dalyku, priimamas naujas sprendimas, kuris pagal bendrąsias taisykles įsiteisėja.

Taip pat nepriimtinas identiško prašymo pateikimas nagrinėti, kai pirminio svarstymo metu šalių ginčas galutinai išspręstas nutartimi dėl taikos sutarties patvirtinimo arba dėl pareiškėjo reikalavimų atsisakymo. Antras skundas teismui neleidžiamas, jei procesas nutraukiamas.

Privalomas turtas:

Privalomas reiškia, kad valdžios institucijos, pareigūnai, organizacijos ir piliečiai privalo savo veiklą pajungti sprendimo turiniui.

Civilinio proceso kodekse pabrėžiama, kad sprendimas yra privalomas visoje Rusijos Federacijos teritorijoje, o įstatymų numatytais atvejais Rusijos Federacijos teismai gali kreiptis į užsienio teismus su prašymu vykdyti sprendimus.

Valstybės įstaigos ir pareigūnai įpareigoti imtis reikiamų veiksmų, kad būtų įformintos ir įregistruotos įsiteisėjusiu teismo sprendimu nustatytos teisės.

Įsigaliojusį teismo sprendimą privalo vykdyti įpareigoti asmenys savo noru, o būtinais atvejais – priverstinai – vykdomieji organai.

Būtinybė įgyvendinti sprendime numatytus veiksmus vadinamas sprendimų vykdytinumu.

Tai yra neatskiriama prievolės dalis. Prievolės sąvoka yra platesnė už vykdytinumą, ji apima ir visų asmenų ir organizacijų, neturinčių tiesioginio teisinio suinteresuotumo konkrečioje byloje, pareigą atsižvelgti į teismo sprendimo autoritetą ir prisidėti prie jo įgyvendinimo.

Sprendimai visais atvejais yra privalomi, tačiau ne visus juos reikia vykdyti, nes jie negali būti vykdomi. Pavyzdžiui, priimant sprendimus dėl reikalavimų pripažinti nereikalaujama konkrečių veiksmų, kad būtų apginta atsakovo ginčijama teisė. Kad jie būtų privalomi, pakanka, kad teismas pripažintų tam tikras aplinkybes ar teisinius santykius (pvz.: tėvystės nustatymas, autorystės teisės pripažinimas ir pan.).

Sprendimai dėl ieškinio pripažinimo gali turėti žalingą poveikį byloje dėl reikalavimo priteisti. Pavyzdžiui, sprendimas nustatyti tėvystę turi prejudicinę reikšmę ieškinio dėl alimentų išieškojimo atvejui. Taip pat sprendimas pripažinti autorystės teisę yra privalomas teismui renkant autorinį atlyginimą iš leidyklos.

Rusijos Federacijos Šeimos kodeksas, be šeimos teisės klausimų, nustato keletą procesinių taisyklių dėl teismo veiksmų (pareigų) po sprendimo priėmimo. Pavyzdžiui, IC nurodo, kad teismas privalo per 3 dienas nuo teismo sprendimo dėl santuokos nutraukimo įsiteisėjimo dienos išsiųsti šio sprendimo išrašą civilinės metrikacijos įstaigai, esanti valstybės registravimo vietoje. santuoka.

Šeimos teisė reikalauja, kad teismas, siekdamas įvykdyti sprendimą, atliktų tam tikrus veiksmus. Įsigalioję teismų sprendimai įgyja nuosavybės, kilusios iš teisinės galios esmės, prejudiciškumo (predecision) kokybės.

Prejudiciškumas reiškia, kad teismo nustatyti ir sprendime užfiksuoti santykiai ir faktai negali būti paneigti teisminėms ir administracinėms institucijoms atliekant antrinį jų tyrimą.

Prietarai priklauso nuo taisyklių:

1. Teismas, administracijos organai, veikdami kaip jurisdikciniai organai, iš naujo visiškai ar iš dalies išanalizuodami faktus ir santykius, kurių turinį teismas nustatė įsiteisėjusiu sprendimu, privalo pagrįsti savo sprendimus dėl šių faktų ir santykių ta pačia forma, kuria jie buvo nustatyti, tai yra, teismo sprendime jau nustatyti faktai dar kartą neįrodinėjami.

2. Šalis, savo reikalavimus grindžianti teisiniais santykiais, dėl kurių visiškai ar iš dalies buvo priimtas įsiteisėjęs teismo sprendimas, neprivalo pakartotinai įrodinėti šių teisinių santykių egzistavimo, jų sudedamųjų dalių turinio, t. taip pat juridiniai faktai, kuriais grindžiami šalių reikalavimai.

Santykiai ir faktai laikomi galiojančiais ir neįrodinėjami tol, kol galioja sprendimo teisinė galia, ty iki sprendimo panaikinimo. Kita šalis, nesutikdama su pareiškėjo prašymu, negali pateikti įrodymų, paneigiančių anksčiau teismo nustatytus faktus ir aplinkybes, taip pat reikalauti, kad teismas juos ištirtų ir pridėtų prie bylos.

3. Jeigu tyrimo objektas yra santykiai, kurių turinys nustatytas įsiteisėjusiu sprendimu, tai išankstinis nustatymas, tai yra prejudiciškumas, taikomas teisiniams santykiams visa apimtimi bet kurioje jo dalyje tokia forma, kokia ji yra. buvo teisminio tyrimo objektas.

Įsiteisėjęs sprendimas turi prejudicinę reikšmę nagrinėjant baudžiamąją bylą. Įsiteisėjęs nuosprendis baudžiamojoje byloje yra privalomas bylą nagrinėjančiam teismui dėl asmens, dėl kurio buvo priimtas teismo nuosprendis, veiksmų civilinių teisinių pasekmių klausimais, ar šis veiksmas buvo atliktas ir ar tai padarė šis asmuo.

Tiesinės lygtys. Sprendimas, pavyzdžiai.

Dėmesio!
Yra papildomų
Specialiajame 555 skyriuje nurodytos medžiagos.
Tiems, kurie labai „nelabai...“
Ir tiems, kurie „labai...“)

Tiesinės lygtys.

Tiesinės lygtys nėra pati sunkiausia mokyklinės matematikos tema. Tačiau yra keletas gudrybių, kurios gali sugluminti net apmokytą studentą. Išsiaiškinkime?)

Paprastai tiesinė lygtis apibrėžiama kaip formos lygtis:

kirvis + b = 0 Kur a ir b– bet kokie skaičiai.

2x + 7 = 0. Čia a = 2, b=7

0,1x - 2,3 = 0 Čia a = 0,1, b=-2,3

12x + 1/2 = 0 Čia a = 12, b = 1/2

Nieko sudėtingo, tiesa? Ypač jei nepastebite žodžių: "kur a ir b yra bet kokie skaičiai"... O jei pastebėsi ir nerūpestingai pagalvoji?) Juk jeigu a=0, b = 0(galimi bet kokie skaičiai?), tada gauname juokingą išraišką:

Bet tai dar ne viskas! Jei, tarkim, a=0, A b = 5, Pasirodo, tai kažkas visiškai neįprasto:

Kas erzina ir menkina pasitikėjimą matematika, taip...) Ypač per egzaminus. Tačiau iš šių keistų posakių taip pat reikia rasti X! Kurios iš viso nėra. Ir, stebėtinai, šį X labai lengva rasti. Mes išmoksime tai padaryti. Šioje pamokoje.

Kaip atpažinti tiesinę lygtį pagal jos išvaizdą? Tai priklauso nuo išvaizdos.) Apgaulė ta, kad tiesinės lygtys nėra tik formos lygtys kirvis + b = 0 , bet ir bet kokias lygtis, kurias galima redukuoti į šią formą transformuojant ir supaprastinant. Ir kas žino, ar jis nusileis, ar ne?)

Kai kuriais atvejais galima aiškiai atpažinti tiesinę lygtį. Tarkime, jei turime lygtį, kurioje yra tik pirmojo laipsnio nežinomieji ir skaičiai. Ir lygtyje nėra trupmenos padalytos iš nežinomas , svarbu! Ir padalijimas pagal numeris, arba skaitinė trupmena – sveikintina! Pavyzdžiui:

Tai tiesinė lygtis. Čia yra trupmenos, bet nėra x kvadrate, kube ir pan., o vardikliuose nėra x, t.y. Nr padalijimas iš x. Ir čia yra lygtis

negali būti vadinamas linijiniu. Čia X yra pirmojo laipsnio, bet yra dalyba iš išraiškos su x. Po supaprastinimų ir transformacijų galite gauti tiesinę lygtį, kvadratinę lygtį arba bet ką, ko norite.

Pasirodo, kad sudėtingame pavyzdyje tiesinės lygties neįmanoma atpažinti tol, kol jos beveik neišspręsi. Tai erzina. Tačiau užduotyse, kaip taisyklė, jie neklausia apie lygties formą, tiesa? Užduotys reikalauja lygčių nuspręsti. Tai mane džiugina.)

Tiesinių lygčių sprendimas. Pavyzdžiai.

Visas tiesinių lygčių sprendimas susideda iš identiškų lygčių transformacijų. Beje, šios transformacijos (jų dvi!) yra sprendimų pagrindas visos matematikos lygtys. Kitaip tariant, sprendimas bet koks lygtis prasideda būtent nuo šių transformacijų. Tiesinių lygčių atveju jis (sprendinys) yra pagrįstas šiomis transformacijomis ir baigiasi išsamiu atsakymu. Prasminga sekti nuorodą, tiesa?) Be to, yra ir tiesinių lygčių sprendimo pavyzdžių.

Pirmiausia pažvelkime į paprasčiausią pavyzdį. Be jokių spąstų. Tarkime, kad turime išspręsti šią lygtį.

x - 3 = 2 - 4x

Tai tiesinė lygtis. X yra pirmoje galioje, nėra skirstymo iš X. Bet iš tikrųjų mums nesvarbu, kokia tai lygtis. Turime tai išspręsti. Schema čia paprasta. Surinkite viską su X kairėje lygties pusėje, viską be X (skaičių) dešinėje.

Norėdami tai padaryti, turite perkelti - 4x į kairę pusę, su ženklo pakeitimu, žinoma, ir - 3 - į dešinę. Beje, tai yra pirmoji identiška lygčių transformacija. Nustebino? Tai reiškia, kad nesekėte nuorodos, bet veltui...) Gauname:

x + 4x = 2 + 3

Čia yra panašūs, mes svarstome:

Ko mums reikia pilnai laimei? Taip, kad kairėje būtų grynas X! Penki yra kelyje. Atsikratyti penkių su pagalba antroji identiška lygčių transformacija. Būtent, mes padalijame abi lygties puses iš 5. Gauname paruoštą atsakymą:

Žinoma, elementarus pavyzdys. Tai apšilimui.) Nelabai aišku, kodėl čia prisiminiau identiškas transformacijas? GERAI. Paimkime jautį už ragų.) Nuspręskime ką nors solidesnio.

Pavyzdžiui, čia yra lygtis:

Nuo ko pradėti? Su X – į kairę, be X – į dešinę? Gali buti taip. Maži žingsneliai ilgame kelyje. Arba galite tai padaryti iš karto, universaliai ir galingai. Jei, žinoma, jūsų arsenale yra identiškų lygčių transformacijų.

Aš užduodu jums pagrindinį klausimą: Kas jums labiausiai nepatinka šioje lygtyje?

95 iš 100 žmonių atsakys: trupmenomis ! Atsakymas teisingas. Taigi atsikratykime jų. Todėl iš karto pradedame nuo antroji tapatybės transformacija. Ko reikia, norint padauginti kairėje esančią trupmeną, kad vardiklis visiškai sumažėtų? Teisingai, ties 3. O dešinėje? Iš 4. Tačiau matematika leidžia padauginti abi puses iš tas pats numeris. Kaip mes galime išeiti? Padauginkime abi puses iš 12! Tie. į bendrą vardiklį. Tada ir trys, ir keturi bus sumažinti. Nepamirškite, kad kiekvieną dalį reikia padauginti visiškai. Štai kaip atrodo pirmasis žingsnis:

Išplečiant skliaustus:

Pastaba! Skaitiklis (x+2) Aš dedu jį į skliaustus! Taip yra todėl, kad dauginant trupmenas padauginamas visas skaitiklis! Dabar galite sumažinti trupmenas:

Išplėskite likusius skliaustus:

Ne pavyzdys, o grynas malonumas!) Dabar prisiminkime burtažodį iš pradinės mokyklos: su X - į kairę, be X - į dešinę! Ir pritaikykite šią transformaciją:

Štai keletas panašių:

Ir padalykite abi dalis iš 25, t.y. dar kartą pritaikykite antrąją transformaciją:

Tai viskas. Atsakymas: X=0,16

Atkreipkite dėmesį: norėdami originalią painią lygtį paversti gražia forma, panaudojome dvi (tik dvi!) tapatybės transformacijos– vertimas į kairę į dešinę su ženklo pakeitimu ir lygties daugyba-dalyba iš to paties skaičiaus. Tai universalus metodas! Taip dirbsime su bet koks lygtys! Visiškai bet kas. Štai kodėl aš nuolat nuobodžiai kartoju apie šias identiškas transformacijas.)

Kaip matote, tiesinių lygčių sprendimo principas yra paprastas. Mes paimame lygtį ir supaprastiname ją naudodami identiškas transformacijas, kol gausime atsakymą. Pagrindinės problemos čia yra skaičiavimuose, o ne sprendimo principe.

Bet... Elementariausių tiesinių lygčių sprendimo procese būna tokių netikėtumų, kad gali įvaryti į stiprų stuporą...) Laimei, tokių netikėtumų gali būti tik du. Pavadinkime juos ypatingais atvejais.

Ypatingi atvejai sprendžiant tiesines lygtis.

Pirma staigmena.

Tarkime, kad susiduriate su labai paprasta lygtimi, panašiai kaip:

2x+3=5x+5 – 3x – 2

Šiek tiek atsibodus, perkeliame su X į kairę, be X - į dešinę... Pakeitus ženklą viskas puiku... Gauname:

2x-5x+3x=5-2-3

Skaičiuojame, ir... oi!!! Mes gauname:

Ši lygybė pati savaime nėra smerktina. Nulis tikrai yra nulis. Bet X trūksta! Ir mes turime įrašyti atsakyme, kam x lygus? Priešingu atveju sprendimas nesiskaito, tiesa...) Aklavietė?

Ramus! Tokiais abejotinais atvejais jus išgelbės pačios bendriausios taisyklės. Kaip išspręsti lygtis? Ką reiškia išspręsti lygtį? Tai reiškia, Raskite visas x reikšmes, kurios, pakeistos į pradinę lygtį, suteiks mums teisingą lygybę.

Bet mes turime tikrą lygybę jauįvyko! 0=0, kiek tiksliau?! Belieka išsiaiškinti, ties kokiu x tai atsitinka. Kokiomis X reikšmėmis galima pakeisti originalus lygtis, jei šie x ar jie vis tiek bus sumažinti iki nulio? Nagi?)

Taip!!! X gali būti pakeistas bet koks! Kokių tu nori? Mažiausiai 5, mažiausiai 0,05, mažiausiai -220. Jie vis tiek susitrauks. Jei netikite manimi, galite tai patikrinti.) Pakeiskite bet kokias X reikšmes originalus lygtį ir apskaičiuokite. Visą laiką gausite gryną tiesą: 0=0, 2=2, -7,1=-7,1 ir pan.

Štai jūsų atsakymas: x – bet koks skaičius.

Atsakymas gali būti parašytas skirtingais matematiniais simboliais, esmė nesikeičia. Tai visiškai teisingas ir išsamus atsakymas.

Antra staigmena.

Paimkime tą pačią elementariąją tiesinę lygtį ir pakeiskime joje tik vieną skaičių. Štai ką mes nuspręsime:

2x+1=5x+5 – 3x – 2

Po tų pačių identiškų transformacijų gauname kažką intriguojančio:

Kaip šitas. Išsprendėme tiesinę lygtį ir gavome keistą lygybę. Matematine prasme gavome klaidinga lygybė. Tačiau paprastai tai netiesa. Rave. Tačiau nepaisant to, ši nesąmonė yra labai gera priežastis teisingam lygties sprendimui.)

Vėlgi, mes galvojame remdamiesi bendromis taisyklėmis. Ką x, pakeistas į pradinę lygtį, duos mums tiesa lygybe? Taip, jokios! Tokių X nėra. Kad ir ką įdėtum, viskas sumažės, liks tik nesąmonė.)

Štai jūsų atsakymas: sprendimų nėra.

Tai taip pat visiškai išsamus atsakymas. Matematikoje tokių atsakymų randama dažnai.

Kaip šitas. Dabar, tikiuosi, X išnykimas sprendžiant bet kokią (ne tik tiesinę) lygtį jūsų visiškai nesupainios. Tai jau pažįstamas dalykas.)

Dabar, kai išsprendėme visas tiesinių lygčių spąstus, prasminga jas išspręsti.

Jei jums patinka ši svetainė...

Beje, turiu jums dar keletą įdomių svetainių.)

Galite praktikuotis spręsdami pavyzdžius ir sužinoti savo lygį. Testavimas su momentiniu patvirtinimu. Mokykimės – su susidomėjimu!)

Galite susipažinti su funkcijomis ir išvestinėmis.