Еднини точки на функција и нивна класификација. Изолирани еднини точки. Остатоци и формули за нивна пресметка
Модели опишани со системи на две автономни диференцијални равенки.
фазна рамнина. Фазен портрет. изоклина метода. главни изоклинини. Стабилна состојба. Линеарни системи. Видови клучни точки: јазол, седло, фокус, центар. Пример: хемиски реакции од прв ред.
Најинтересните резултати за квалитативното моделирање на својствата на биолошките системи се добиени на модели на две диференцијални равенки, кои овозможуваат квалитативно проучување со користење на методот фазна рамнина. Размислете за систем од две автономни обични диференцијални равенки од општата форма
(4.1)
P(x,y), Q(x,y)- континуирани функции дефинирани во некој домен ГЕвклидска рамнина ( x, y- Декартови координати) и имајќи во оваа област континуирани деривати од ред не пониски од првиот.
Регионот Гможе да биде или неограничен или ограничен. Доколку променливите x, yимаат специфично биолошко значење (концентрации на супстанции, изобилство на видови), најчесто областа Ге позитивниот квадрант на десната полурамнина:
0 £ x< ¥ ,0 £ y< ¥ .
Концентрациите на супстанции или изобилството на видови, исто така, може да се ограничат одозгора со волуменот на садот или од областа на живеалиштето. Тогаш опсегот на променливи има форма:
0 £ x< x 0 , 0 £ y< y 0 .
Променливи x, yпромена во времето во согласност со системот на равенки (4.1), така што секоја состојба на системот одговара на пар вредности на променливи ( x, y).
|
|
Спротивно на тоа, за секој пар на променливи ( x, y) одговара на одредена состојба на системот.
Размислете за рамнина со координатни оски на кои се нацртани вредностите на променливите x, y. Секоја точка Моваа рамнина одговара на одредена состојба на системот. Таквата рамнина се нарекува фазна рамнина и ја прикажува севкупноста на сите состојби на системот. Точката M(x, y) се нарекува точка која прикажува или претставува.
Нека во почетното време t=t 0 претставува координати на точки М 0 (x(т 0), y(т 0)). Во секој следен момент во времето тточката на прикажување ќе се движи според промените во вредностите на променливите x(т), y(т). Збир на поени М(x(т), y(t)) на фазна рамнина, чија положба одговара на состојбите на системот во процесот на менување на променливите со текот на времето x(t), y(t)според равенките (4.1), се нарекува фаза на траекторија.
Збирот на фазни траектории за различни почетни вредности на променливите дава лесно видлив „портрет“ на системот. Зграда фазен портретви овозможува да извлечете заклучоци за природата на промените во променливите x, yбез да се знаат аналитичките решенија на првобитниот систем на равенки(4.1).
За да се прикаже фазен портрет, неопходно е да се конструира векторско поле на насоки за системските траектории во секоја точка од фазната рамнина. Со одредување на прирастД t>0,ги добиваме соодветните зголемувања Д xи Д yод изразите:
Д x=P(x,y)Д т,
Д y=Q(x,y)Д т.
векторска насока dy/dxво точка ( x, y) зависи од знакот на функциите P(x, y), Q(x, y)и може да се даде со табела:
|
P(x,y)>0,Q(x,y)>0 |
|
|
P(x,y)<0,Q(x,y)<0 |
|
|
P(x,y)>0,Q(x,y)<0 |
|
|
P(x,y)<0,Q(x,y)>0 |
|
.(4.2)
Решение на оваа равенка y=y(x, c), или имплицитно Ф(x, y)=c,каде Сое константа на интеграција, ја дава фамилијата на интегрални криви на равенката (4.2) - фазни траекториисистем (4.1) во авионот x, y.
Изоклин метод
За да се изгради фазен портрет, се користи изоклина метода -на фазната рамнина се исцртуваат линии кои ги сечат интегралните кривини под еден специфичен агол. Лесно се добива изоклина равенка од (4.2). Да ставиме
каде А– одредена константа. Значење Аја претставува тангентата на наклонот на тангентата на траекторијата на фазата и може да зема вредности од -¥ до + ¥ . Замена наместо dy/dxво (4.2) количината Аја добиваме изоклинската равенка:
.(4.3)
Равенката (4.3) ја одредува во секоја точка од рамнината единствената тангента на соодветната интегрална крива, освен точката каде што P(x,y)= 0, П (x, y) = 0 , во која насоката на тангентата станува неодредена, бидејќи вредноста на изводот станува неопределена:
.
Оваа точка е пресечна точка на сите изоклинини - посебна точка.Истовремено ги исчезнува временските деривати на променливите xи y.
Така, во еднината точка, стапките на промена на променливите се еднакви на нула. Според тоа, единствената точка на диференцијалните равенки на фазните траектории (4.2) одговара на стационарна состојба на системот(4.1), а неговите координати се стационарни вредности на променливите x, y.
Од особен интерес се главни изоклинини:
dy/dx=0, П(x, y)=0 – изоклина на хоризонтални тангенти и
dy/dx=¥ , П(x, y)=0 – изоклина на вертикални тангенти.
Со конструирање на главните рамноправни и пронаоѓање на точката на нивното вкрстување (x,y), чии координати ги задоволуваат условите:
така ќе ја најдеме точката на пресек на сите изоклинини на фазната рамнина, на која правецот на тангентите кон фазните траектории е неопределен. Ова - единствена точка, што одговара стационарна состојба на системот(Сл. 4.2).
Системот (4.1) има онолку стационарни состојби колку што има пресечни точки на главните рамнини на фазната рамнина.
Секоја фазна траекторија одговара на збир на движења на динамички систем кои минуваат низ истите состојби и се разликуваат едни од други само со почетокот на временската референца.
 |
|
Ако условите на теоремата на Коши се задоволени, тогаш низ секоја точка од просторот x, y, tпоминува низ една интегрална крива. Истото важи, благодарение на автономијата, за фазните траектории: единствена фазна траекторија поминува низ секоја точка од фазната рамнина.
Стабилна состојба
Нека системот е во рамнотежа.
Тогаш репрезентативната точка се наоѓа на една од еднините точки на системот, во која, по дефиниција:
.
Дали една точка е стабилна или не, се одредува со тоа дали репрезентативната точка заминува или не со мало отстапување од стационарната состојба. Како што се применува на систем од две равенки, дефиницијата за стабилност во јазикотд, гкако што следи.
Состојбата на рамнотежа е стабилна ако за која било дадена област на отстапувања од состојбата на рамнотежа (д )област може да се определи г (д ), опкружувајќи ја состојбата на рамнотежа и имаат својство дека нема траекторија што започнува во регионот г , никогаш нема да стигне до граница д . (Сл. 4.4)
 |
|
За голема класа системи - груби системи – чиешто однесување не се менува со мала промена во видот на равенките, информации за типот на однесување во близина на стационарната состојба може да се добијат со проучување не на оригиналот, туку на поедноставениот линеаризирансистем.
Линеарни системи.
Размислете за систем од две линеарни равенки:
.(4.4)
Еве а бе це де- константи, x, y- Декартови координати на фазната рамнина.
Општото решение ќе се бара во форма:
.(4.5)
Заменете ги овие изрази во (4.4) и намалете за д л т:
(4.6)
Алгебарски систем на равенки (4.6) со непознати А, Бима ненула решение само ако нејзината детерминанта, составена од коефициентите на непознатите, е еднаква на нула:
.
Проширувајќи ја оваа детерминанта, ја добиваме карактеристичната равенка на системот:
.(4.7)
Решението на оваа равенка ги дава вредностите на индикаторотл 1,2 , под кои се можни ненулти вредности за Аи Брешенија на равенката (4.6). Овие вредности се
.(4.8)
Ако радикалниот израз е негативен, тогашл 1,2 сложени конјугирани броеви. Да претпоставиме дека двата корени на равенката (4.7) имаат ненула реални делови и дека нема повеќе корени. Тогаш општото решение на системот (4.4) може да се претстави како линеарна комбинација на експоненти со експонентил 1 , л 2 :
(4.9)
За да ја анализираме природата на можните траектории на системот на фазната рамнина, користиме линеарна хомогена координатна трансформација,што ќе го доведе системот до канонска форма:
,(4.10)
што овозможува поудобно претставување на фазната рамнина во споредба со оригиналниот систем (4.4). Ајде да воведеме нови координатиξ , η според формулите:
(4.1)
Од текот на линеарната алгебра се знае дека ако реалните делови не се еднакви на нулал 1 , л 2 оригиналниот систем (4.4) со помош на трансформации (4.11) секогаш може да се трансформира во канонска форма (4.10) и да се проучи неговото однесување на фазната рамнинаξ , η . Размислете за различните случаи што може да се појават овде.
Корени λ 1 , λ 2 – важечки и со ист знак
Во овој случај, коефициентите на трансформација се реални, се движиме од реалната рамнинаx, yдо вистинската рамнина ξ, η. Поделувајќи ја втората од равенките (4.10) со првата, добиваме:
.(4.12)
Интегрирајќи ја оваа равенка, наоѓаме:
Каде .(4.13)
Да се согласиме да разбереме со λ 2 коренот на карактеристичната равенка со голем модул, што не ја нарушува општоста на нашето расудување. Потоа, бидејќи во случајот што се разгледува корените λ 1 , λ2 - важечки и со ист знак,а>1 , а имаме работа со интегрални криви од параболичен тип.
Сите интегрални кривини (освен оската η , што одговара на ) допир на почетокот на оската ξ, што е и интегрална крива на равенката (4.11). Потеклото на координатите е единствена точка.
Сега да ја дознаеме насоката на движење на репрезентативната точка долж фазните траектории. Ако λ 1, λ 2 се негативни, тогаш, како што може да се види од равенките (4.10), |ξ|, |η| се намалуваат со текот на времето. Репрезентативната точка се приближува до потеклото, но никогаш не го достигнува. Во спротивно, ова би било во спротивност со теоремата на Коши, која вели дека само една фаза траекторија минува низ секоја точка на фазната рамнина.
Таква единствена точка низ која минуваат интегралните кривини, исто како фамилија на параболи 
поминува низ потеклото, се нарекува јазол (Сл. 4.5)
Рамнотежна состојба од типот на јазол на λ 1, λ 2 < 0 е стабилна според Љапунов, бидејќи претставувачката точка се движи по сите интегрални кривини кон потеклото на координатите. Ова стабилен јазол. Ако λ 1, λ 2 > 0, тогаш |ξ|, |η| се зголемува со текот на времето и репрезентативната точка се оддалечува од потеклото. Во овој случај, единствената точка– нестабилен јазол .
На фазна рамнина x, y ќе остане општиот квалитативен карактер на однесувањето на интегралните криви, но тангентите на интегралните криви нема да се совпаѓаат со координатните оски. Аголот на наклонетост на овие тангенти ќе се определи со односот на коефициентите α , β , γ , δ во равенките (4.11).
Корени λ 1 , λ 2 се валидни и имаат различни знаци.
Конвертирај одкоординати x, y до координати ξ, η повторно вистински. Равенките за канонските променливи повторно ја имаат формата (4.10), но сега знаците λ 1, λ 2 различни. Равенката на фазна траекторија има форма:
Каде, (4.14)
Интегрирајќи (4.14), наоѓаме
(4.15)
Ова равенката дефинира фамилија на криви од хиперболичен тип, каде што двете координатни оскисе асимптоти (на а=1 би имале семејство на рамнокраки хиперболи). Координатните оски се исто така интегрални криви во овој случај– ова ќе бидат единствените интегрални кривини кои минуваат низ потеклото. Секојод кои се состои од три фазни траектории: на две движења кон состојба на рамнотежа (или далеку од состојба на рамнотежа) и од состојба на рамнотежа. Сите други интегрални кривини– се хиперболи кои не минуваат низ потеклото (Сл. 4.6) Оваа единствена точка се нарекува „седло ». Нивоените линии во близина на планинското седло се однесуваат како фазни траектории во близина на седлото.
Да ја разгледаме природата на движењето на репрезентативната точка долж фазните траектории во близина на состојбата на рамнотежа. Нека, на пример,λ 1 >0 , λ 2<0 . Потоа репрезентативната точка поставена на оската ξ , ќе се оддалечи од потеклото и ќе се постави на оската η – неодредено ќе се приближува до потеклото на координатите, без да го достигнеме во конечно време. Секаде каде што претставува точката е во почетниот момент (со исклучок на еднината точка и точките на асимптотата η =0), на крајот ќе се оддалечи од состојбата на рамнотежа, дури и ако на почетокот се движи по една од интегралните кривини кон еднина точка.
Очигледно е дека Единствена точка од типот на седло е секогаш нестабилна . Само под специјално избрани почетни услови на асимптотаη =0 системот ќе се приближи до состојба на рамнотежа. Сепак, ова не е во спротивност со тврдењето дека системот е нестабилен. Ако сметате, дека сите почетни состојби на системот на фазната рамнина се подеднакво веројатни, тогаш веројатноста за таква почетна состојба што одговара на движењето во насокаДо еднина точка е еднаква на нула. Затоа, секое вистинско движење ќе го отстрани системот од состојбата на рамнотежа.Враќање на координатитеx, y,ја добиваме истата квалитативна слика за природата на движењето на траекториите околу потеклото.
Границата помеѓу разгледуваните случаи на јазол и седло е случајкога еден од карактеристичните показатели, на пример λ 1 , исчезнува, што настанува кога детерминантата на системот- изразување adbc=0(види формула 4.8 ). Во овој случај, коефициентите на десните страни на равенките (4.4) се пропорционални еден на друг:
а системот за своите рамнотежни состојби ги има сите точки на правата:
Останатите интегрални кривини се фамилија на паралелни прави со наклон , по кои репрезентативните точки или се приближуваат до состојбата на рамнотежа или се оддалечуваат од неа, во зависност од знакот на вториот корен на карактеристичната равенка λ 2 = a+d.(Сл.4. 7 ) Во овој случај, координатите на рамнотежната состојба зависат од почетната вредност на променливите.
Корени λ 1 , λ 2 – комплексконјугираат
Во овој случај, навистинаxи yние ќе имаат сложени конјугати ξ , η (4.10) . Меѓутоа, со воведување на уште една средна трансформација, исто така е можно во овој случај разгледувањето да се сведе на вистинска линеарна хомогена трансформација. Да ставиме:
(4.16)
каде а, б,и u, v – реални вредности. Може да се покаже дека трансформацијата одx, yДо u, v е, според нашите претпоставки, реална, линеарна, хомогена со ненулта детерминанта. Поради равенките(4.10, 4.16) имаме:
каде
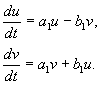(4.17)
Поделба на втората од равенките со првата, добиваме:
што е полесно да се интегрира, ако се префрлиме на поларниот координатен систем (r, φ ) . По заменатадобиваме од каде:
.(4.18)
Така, на фазната рамнинаu, vимаме работа со фамилија на логаритамски спирали, од кои секоја имаасимптотична точка на потеклото.Еднина точка која е асимптотична точка на сите интегрални криви кои имаат форма на спирали, вгнезден пријател вопријател, повикан фокус ( сл.4.8 ) .
Да ја разгледаме природата на движењето на репрезентативната точка по должината на фазните траектории. Множење на првата од равенките (4.17) соu, а вториот до vи додавајќи, добиваме:
Каде
Нека а 1 < 0 (а 1 = Одгλ ) . Претставувачката точка потоа континуирано се приближува до потеклото без да го достигне во одредено време. Ова значи дека фазните траектории се извртувачки спирали и одговараат на пригушени осцилациипроменливи. Ова - стабилен фокус .
Во случај на стабилен фокус, како и во случај на стабилен јазол, не е задоволен само условот на Љапунов, туку и построг услов. Имено, за какви било почетни отстапувања, системот на крајот ќе се врати колку што сакате поблиску до положбата на рамнотежа. Таквата стабилност, во која почетните отстапувања не само што не се зголемуваат, туку се распаѓаат, со тенденција на нула, се нарекува апсолутна стабилност .
Ако во формулата (4.18) а 1 >0 , тогаш претставувачката точка се оддалечува од потеклото, а ние се занимаваме со нестабилен фокус . При движење од авионu, vдо фазната рамнинаx, yспиралите исто така ќе останат спирали, но ќе се деформираат.
Размислете сега за случајот когаа 1
=0
. Фазни траектории на авионотu, vќе има кругови 
кои во авионотx, yфит елипсови:
Така, воа 1=0 преку посебна точкаx= 0,y= 0 не поминува интегрална крива. Таквата изолирана единствена точка, во близина на која интегралните криви се затворени кривини, особено елипсите вградени една во друга и ја опфаќаат еднината точка, се нарекува центар.
Така, можни се шест типа на рамнотежа, во зависност од природата на корените на карактеристичната равенка (4.7). Поглед на фазните траектории на авионот x, yза овие шест случаи е прикажано на сл. 4.9.
Ориз. 4.9.Видови фазни портрети во соседството на стационарна состојба за системот на линеарни равенки (4.4).
Петте типови на рамнотежни состојби се груби, нивната природа не се менува со доволно мали промени во десната страна на равенките (4.4). Во овој случај, промените треба да бидат мали не само во десните страни, туку и во нивните деривати од прв ред. Шестата состојба на рамнотежа - центарот - не е груба. Со мали промени во параметрите на десната страна на равенките, тој оди во стабилен или нестабилен фокус.
Дијаграм на бифуркација
Да ја воведеме ознаката:
.
(4.11)
Тогаш карактеристичната равенка може да се запише во форма:
.
(4.12)
Размислете за рамнина со правоаголни Декартови координати с , Д и означете ги на него областите што одговараат на еден или друг вид на рамнотежна состојба, што се одредува според природата на корените на карактеристичната равенка
.(4.13)
Услов за стабилност на рамнотежната состојба ќе биде присуството на негативен реален дел од yл 1 и л 2 . Неопходен и доволен услов за тоа е исполнувањето на нееднаквоститес > 0, Д > 0 . На дијаграмот (4.15), оваа состојба одговара на точките лоцирани во првата четвртина од рамнината на параметарот. Единствената точка ќе биде фокусот акол 1 и л 2 комплекс. Оваа состојба одговара на оние точки на рамнината за кои , тие. точки помеѓу две гранки на параболатас 2 = 4 Д. Полуоски точки с = 0, Д>0, одговараат на состојбите на рамнотежа од типот на центарот. Исто така,л 1 и л 2 - валидни, но различни знаци, т.е. единствена точка ќе биде седло ако Д<0, итн. Како резултат на тоа, добиваме дијаграм за поделба на рамнината на параметарот с, Д, во региони што одговараат на различни типови на рамнотежни состојби.
Ориз. 4.10.Дијаграм на бифуркација
за системот линеарни равенки 4.4
Ако коефициентите на линеарниот систем а бе це дезависат од некој параметар, тогаш кога ќе се смени овој параметар, ќе се променат и вредноститес , Д . При минување низ границите, природата на фазниот портрет квалитативно се менува. Затоа, таквите граници се нарекуваат граници на бифуркација - на спротивните страни на границата, системот има два тополошки различни фазни портрети и, соодветно, два различни типа на однесување.
Дијаграмот покажува како може да се случат такви промени. Ако ги исклучиме посебните случаи - потеклото на координатите - тогаш лесно може да се види дека седлото може да оди во јазол, стабилен или нестабилен при преминување на y-оската. Стабилен јазол може или да се премести во седло или стабилен фокус, итн. Забележете дека транзициите на стабилен јазол-стабилен фокус и нестабилен јазол-нестабилен фокус не се бифуркационални, бидејќи топологијата на фазниот простор не се менува во овој случај. Подетално за топологијата на фазниот простор и бифуркационите транзиции ќе зборуваме во Предавање 6.
При бифуркациски транзиции, природата на стабилноста на еднината точка се менува. На пример, стабилен фокус низ центарот може да се претвори во нестабилен фокус. Оваа бифуркација се нарекува Бифуркација Андронов-Хопфсо имињата на научниците кои го проучувале. Со оваа бифуркација во нелинеарни системи, се раѓа граничен циклус и системот станува самоосцилирачки (види предавање 8).
Пример. Систем на линеарни хемиски реакции
Супстанција Xвлева однадвор со константна брзина, се претвора во супстанција Y и со брзина пропорционална на концентрацијата на супстанцијата Y, се вади од реакциската сфера. Сите реакции се од прв ред, со исклучок на приливот на материја однадвор, кој има нула ред. Шемата за реакција изгледа вака:
(4.14)
и е опишан со системот на равенки:
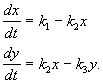(4.15)
Добиваме стационарни концентрации со изедначување на десните страни на нула:
.(4.16)
Размислете за фазен портрет на системот. Да ја поделиме втората равенка на системот (4.16) со првата. Добиваме:
.(4.17)
Равенката (4.17) го одредува однесувањето на променливите на фазната рамнина. Дозволете ни да изградиме фазен портрет на овој систем. Прво, ги цртаме главните изоклинини на фазната рамнина. Равенка на изоклина на вертикални тангенти:
Равенка за изоклина на хоризонтални тангенти:
Единечната точка (стационарна состојба) лежи на пресекот на главните изоклинини.
Сега да одредиме под кој агол координатните оски ги сечат интегралните криви.
Ако x= 0, тогаш.
Така, тангентата на наклонот на тангентата на интегралните кривини y=y(x),преминување на y-оската x=0, е негативен во горната полурамнина (да потсетиме дека променливите x, yимаат концентрациони вредности и затоа нè интересира само горниот десен квадрант на фазната рамнина). Во овој случај, вредноста на тангентата на аголот на наклонетост на тангентата се зголемува со растојанието од потеклото.
Размислете за оската y= 0. На пресекот на оваа оска, интегралните криви се опишани со равенката
На тангентата на наклонот на интегралните криви што ја преминуваат оската на апсцисата е позитивна и се зголемува од нула до бесконечност со зголемување x.
Во .
Потоа, со дополнително зголемување, тангентата на наклонот се намалува во апсолутна вредност, останувајќи негативна и се стреми кон -1 при x ® ¥ . Знаејќи го правецот на тангентите на интегралните кривини на главните изоклинини и на координатните оски, лесно е да се конструира целата слика на фазните траектории.
 |
|
Природата на стабилноста на единствената точка ќе се утврди со помош на методот Љапунов. Карактеристичната детерминанта на системот има форма:
.
Проширувајќи ја детерминантата, ја добиваме карактеристичната равенка на системот: , т.е. корените на карактеристичната равенка се и негативни. Затоа, стационарната состојба на системот е стабилен јазол. Во исто време, концентрацијата на супстанцијата Xтежнее кон стационарна состојба секогаш монотоно, концентрацијата на супстанцијата Y може да помине низ min или max. Осцилаторните режими во таков систем се невозможни.
Нека zq - еднина точка на функцијата f(z), т.с. f(z)но е аналитички во овој момент (особено, може да не се дефинира во него). Ако постои такво дупнато соседство на точката zq (т.е., множеството O z - zq f(z) е алијатичен, тогаш зоповикани изолирана единствена точкафункции f(z).Оваа дефиниција е зачувана и во случајот zn =оо, ако јодот е дупнато соседство на точка zq = oo разбирам множеството z >ЈАС СУМ - појавата на некој круг центриран на потеклото. Со други зборови, единствената точка zq се вели дека е изолиран ако постои соседство на оваа точка во која има други еднини точки различни од zq. Насекаде подолу, ги разгледуваме само еднините точки од карактер со една вредност (функцијата f(z)се претпоставува дека е единствен).
Во зависност од однесувањето на функцијата f(z)на z -> zqПостојат три типа на еднини точки. Изолирана единствена точка zq функции f(z)наречен:
1) отстранлива единствена точкаако има конечна граница
2) столбако има ограничување 
3) суштинска точка,ако f(z) нема ниту конечна ниту бесконечна граница за z-> zq.
ПРИМЕР 26.1. Да покажеме дека се реализирани сите три типа на еднини точки. Да се разгледа ѓ(з)= точка zq = 0 е изолиран
единствена точка на оваа функција. Користејќи ја формулата (22.12), го добиваме проширувањето
од што произлегува дека постои лим fi(z)= 1. Затоа, zq = 0 е
е отстранлива еднина точка на функцијата fi(z).
Функција f'j(z) =--- има столб во една точка зо= 1 затоа што
2 р„Х
Размислете сега за функцијата )z(z)= e 1 ^ r и покажете дека зо =О е суштинска еднина точка на оваа функција. Кога се стремиме zна нула по реалната оска, левата и десната граница на функцијата f (з)различни: лим Со 1 / 1 = 0, лим со 1 /* =ос. Ова имплицира,
x->0-0 x->0+O
што f:i(z)нема ниту конечна ниту бесконечна граница за 2 ->
О, т.е. zq = 0 е суштински единствена точка на оваа функција. (Забележете дека како што се стреми поентата z-iyдо нула на функцијата замислена оска 
нема ограничување.)
Се разбира, има и неизолирани еднини точки. На пример. функцијата има полови во точките z n = -, П= ±1, ±2,...
Оттука, Zq = 0 е неизолирана еднина точка на оваа функција: во кое било (произволно мало) соседство на оваа точка има други еднини точки g стр.
Нека зо-конечна изолирана еднина точка на функцијата f(z).Потоа f(z)е сличен во некое дупнато маало 0 Зо на точката зоова соседство може да се смета како прстен со внатрешен радиус r = 0. Според теорема 25.1, во соседството што се разгледува, функцијата f(z)може да се прошири во серијата Laurent (25.2). Ќе покажеме дека однесувањето на функцијата за 2 -> zq (т.е. типот на еднина точка зо)зависи од формата на главниот дел од распаѓањето (25.2); оваа околност го објаснува потеклото на поимот „главен дел“.
ТЕОРЕМА 2Г.2. Изолирана еднина точка zo од функцијата f(z) е отстранлива ако и само ако Lorap експанзијата во пробиено соседство на оваа точка има оид
тие. се состои само од правилниот дел, а сите коефициенти на главниот дел се еднакви на куршумот.
Доказ. 1. Нека зое отстранлива единствена точка. Да докажеме дека Лорентовото проширување на функцијата f(z)ја има формата (26.1). Од еднина точка зоотстранлив, тогаш постои конечна граница lim f(z) = А.Оттука, f(z)ограничена во некое дупнато маало 0 z - zq од точката зо,тие. )(z) за сите zод оваа населба. Земете било кој Р. U р /?|, и користете ги формулите (25.3) за коефициентите од серијата Laurent:
За коефициентите на главниот дел од проширувањето n =- 1,-2,... За такви вредности Пние имаме p~n-e 0 во Р-> 0. Бидејќи вредноста Рможе да се избере произволно мали, тогаш г-дин ~"може да биде произволно мал. Бидејќи |c t,| ^ Mr~nи cn не зависат од p, тогаш cn = 0 за и= - 1, -2,..., што требаше да се докаже.
2. Сега да претпоставиме дека проширувањето на Лорен ја има формата (26.1). Серијата (26.1) е моќна серија и. затоа, конвергира не само во дупнато, туку и во целото соседство z-zq вклучувајќи ја и точката зо;нејзиниот износ S(z)е аналитички за z и S(z) = )(з)во 0 з - зоР.Затоа, постои конечна граница )(з)\u003d Pm 5 (r) \u003d 5 (r) - Затоа, еднината точка zq
З->Зо З-*Зо
за еднократна употреба. Теоремата е докажана.
Коментар. Од доказот на теоремата произлегува дека во дупната населба 0 z - zo на отстранлива еднина точка функцијата f(z)се совпаѓа со функцијата S(r), која е аналитичка во целото соседство z - зо . Затоа, ако ставиме /(th) = S(zq), потоа, без промена на вредностите на функцијата f(z)во која било точка од пробиеното соседство, оваа функција ја правиме аналитичка во r, т.е. „отстранете ја“ функцијата. Ова го објаснува терминот „отстранлива сингуларност“. Природно е таквите точки да се сметаат за правилни, а не како еднини точки на функцијата f(z).
Размислете, на пример, функцијата
Во примерот 26.1, се покажа дека Pm (n) = 1. т.е. единствена точка
zq = 0 е отстранлив. Поставувајќи /i(0) = 1, со тоа ја елиминираме сингуларноста и добиваме функција која е аналитичка во точката zq = 0 (и во целата рамнина C).
Сега да ги окарактеризираме половите во однос на Лореновите проширувања.
Теорема 26.3. Изолирана еднина точка Zo од функција f(z) е пол ако и само ако, кога главниот дел од проширувањето на Лорент со центар Zq има само конечен број на различни
од нула коефициенти со n:
Доказ. 1. Нека zq - столб, т.е. lim /( z) = оо.
Да докажеме дека Лорентовото проширување на функцијата f(z)ја има формата (2Г.2). Бидејќи лим f(z)= оо. тогаш постои дупнато соседство на точката
ки zq. при што f(z)е аналитичка и нема нули. Потоа функцијата g(z) = 1 /f(z)ќе бидат и аналитички во оваа дупната населба, а лим g(z)= 0. Затоа, Зодали е за еднократна употреба *-? *0
единствена точка на функцијата g(z).Ајде да редефинираме g(z)во точката зо, ставање g(zo)= 0. Потоа g(z)станува аналитички во целото соседство на (непродупчената) точка z 0,и z0ќе биде неговата изолирана нула. Означи со Нмножина (ред) на оваа нула. Како што беше прикажано во §23, во соседството на точката zq функција g(z)може да се претстави во форма (види (23.2))
и (z$) f 0 и y>(z)е аналитички во некое соседство на точката зо-Бидејќи IP(z)континуирано во точка зои g>(зо) Ф 0" тогаш IP(z)нема ниту нули во некое соседство на оваа точка. Затоа функцијата 1 /-p(z)исто така ќе биде аналитички во ова соседство и, според тоа, ќе се прошири во него во серија на Тејлор:
Отворајќи ги заградите и менувајќи ги ознаките на коефициентите, го пишуваме последното проширување во форма
каде c_jv = 1>о ѓ 0. Така, главниот дел од Лорентовото проширување на f(r) содржи само конечен број членови; дојдовме до потребната еднаквост (26.2).
2. Пушти во дупната населба на точка тифункција )(з)е претставена со проширувањето на Лорен (26.2) (во попроширена форма, видете (26.3)), чиј главен дел содржи само конечен број членови, и со-г" ѓ 0. Тоа мора да го докажеме Zq - функционален пол f(z).Множење на еднаквоста (26.3) со (Г - Г o) iV , ја добиваме функцијата
Серијата во (26.4) е серија на моќност која конвергира кон аналитичка функција не само во пробиената, туку и во целото соседство на точката Zq. Затоа, функцијата h(z)станува аналитички во ова соседство ако го прошириме во ти со поставување ч(зо)= s_dg ѓ 0. Потоа
Така точката o е пол, а теоремата 26.3 е докажана.
Множество (ред) на нултата функција g(z)= 1//(r) се нарекува поредокфункција /(r). Ако N-редоследот на полот е ти, тогаш g(z)= (р - Zo)N ip(z),и (оди) Ф 0, и, како што е прикажано во првиот дел од доказот на теоремата 26.3, проширувањето на f(r) има форма (26.3), каде што c_/v ѓ 0. Спротивно на тоа, ако f(r) се прошири во серијата (26.3) и е-з Ф 0, тогаш
т.с. N-редоследот на полот на функцијата f(r). На овој начин, редоследот на zq полот на функцијата/(Г) е еднаков на бројот на водечкиот ненулти коефициент на главниот дел од проширувањето на Лорент во пробиеното соседство на точката zq(т.е. еднаков на таков број N,што s_dg ѓ 0 и сп= 0 во П > N).
Дозволете ни да го докажеме следното тврдење, што е погодно) за апликации.
Заклучок 26.4. Точката zq е пол од редот N на фикцијата/(Г) ако и само ако/(Г) претставуваат во форма
каде што h(z) е аналитичка функција во соседство на точкати и h(zo) f 0.
Доказ. Функција cp(z) = l/h(z)е аналитичка во некое соседство на точката r. Условот од заклучокот 26.4 е еквивалентен на следново:
Значи zq - мноштво нула Нфункции g(z).а оттука и полот на мноштво Нфункции /(2).
II пример 26.5. Најдете изолирани еднини точки на функција 
и да го определи нивниот тип.
D e u c tio n Точките на кои (з 2 + 1 ) (з+ H) 2 = 0. Ако z 2 L- 1 = 0 потоа 2 = ± rако (з 4- H) 2 = 0, тогаш z= -3. Според тоа, функцијата има три еднини точки z= r, 22 = -r, З3 = - 3. Размислете z:
Г -столб од прв ред (користевме заклучок 26.4). Слично може да се докаже дека 22 = - јасисто така столб од прв ред. За 2 часа имаме:
Да преминеме на разгледување на суштински еднина точки.
Теорема 26.6. Изолирана еднина точка zq од функцијата f(z) е суштински еднина ако и само ако главниот дел од Лорентовото проширување со центар на zq има бесконечно многу различни од. нула, коефициенти со стр.
Доказ. Теоремата 26.6 следи директно од теоремите 26.2 и 26.3. Навистина, ако поентата zq е суштински еднина, тогаш главниот дел од проширувањето на Лорент не може да отсуствува или да содржи конечен број членови (инаку точката Zq ќе биде или отстранлив или столб). Затоа, бројот на членовите во главниот дел мора да биде бесконечен.
Спротивно на тоа, ако главниот дел содржи бесконечно многу членови, тогаш Zq не може да биде ниту отстранлива точка ниту столб. Следствено, оваа точка е суштински единствена.
Според дефиницијата, суштински еднина точка се карактеризира со тоа што функцијата f(2) нема ниту конечна ниту бесконечна граница за z ->zq. Поцелосна идеја за тоа колку е неправилно однесувањето на функцијата во соседството на суштински еднина точка е дадена со следнава теорема.
Теорема 26.7 (теорема на Сочоцки). Ако zq е суштински еднина, тогаш точката на функцијата f(z), тогаш за кој било сложен број L, вклучувајќи A =оо, постои низа точки z n таква што z n -> zo илим f(zn) = А.
n->os
Доказ. Размислете прво за случајот A =оо. Во првиот дел од докажувањето на теоремата 2G.2, утврдивме дека ако f(z)е ограничена во некое пробиено соседство на точката r0, тогаш сите коефициенти c, n = - 1, - 2,... од главниот дел се еднакви на нула (и, следствено, сингуларноста во ти е отстранлива). Бидејќи според претпоставката r0 е суштински еднина точка, функцијата f(r) е неограничена во кое било пробиено соседство на точката r0. Да земеме некое тесно соседство 0 Z такво што f(zi) > 1 (ако |/(r)| z - zo R/2 има точка z-2 , каде |/(дд)| > 2 и сл.: во дупната населба О 71. Очигледно е дека rn -e go и lim /(r«) = oo. Така, во случајот A = oo, теорема 26.7
докажано.
Нека сега А ѓоо. Прво да претпоставиме дека има пробиено соседство 0
= -гг---- ќе биде аналитички во оваа пробиена населба и, следствено,
/(Г) - А
следствено, r е изолирана еднина точка на функцијата Φ(r). Ајде да покажеме. дека r0 е суштински еднина точка на Φ(r). Нека е погрешно. Тогаш постои граница lim Φ(r), или конечна или бесконечна. Бидејќи
/(r) = A + , тогаш Hsh /(r) исто така постои, што е во спротивност со условот
F(g) ~ :-*z 0
поглед на теоремата. Така, r0 е суштински единствена точка на функцијата Φ(r). Според она што беше докажано погоре, постои низа од точки r n таква што r n o и lim Φ(r n) = oo. Од тука
Го докажавме потребното тврдење под претпоставка дека f(r) Ф Аво некое дупнато маало на точката р Сега да претпоставиме дека тоа не е точно т.е. во секое произволно мало продупчено соседство на точката има таква точка Г",дека f(r") = A. Потоа за било кој Пво пробиеното соседство 0 f(z u) = L. Така, бараното тврдење е точно П-јуо
во сите случаи, а теоремата 26.7 е докажана.
Според (Сохоцки) теорема 26.7, во кое било (произволно мало) пробиено соседство на суштински еднина точка, функцијата f(r) зема вредности произволно блиску до кој било број во проширената сложена рамнина C.
За проучување на изолирани еднини точки, често се корисни добро познатите Тејлорови проширувања на основните елементарни функции.
ПРИМЕР 2Г.8. Определи го типот на еднина точка zq = 0 за функцијата
Решени и д. Ги прошируваме броителот и именителот во тејлоровата серија во моќност на r. Заменувајќи ги во (22.11) 3 zнаместо r и одземање 1, добиваме
Користејќи го (22.12), го добиваме проширувањето на именителот:
Сериите во овие проширувања се спојуваат во целата комплексна рамнина €. Ние имаме
и /2(2) се аналогни во соседството на точката зо = 0 (па дури и во целата рамнина) и /2 (20) Ф 0, тогаш h(z)е аналитичка и во некое соседство на точката gF 0. Според заклучокот 26.4, точката Зо = 0 е пол на редот N = 4.
II пример 26.9. Најдете еднини точки на функција f(z)= sin j - и определи го нивниот тип.
P e во e и e. Функцијата има една завршна еднина точка zq = 1. Во други точки од C, функцијата w =--- аналитички; па оттука и функцијата грев wќе бидат аналитички.
Замена во проширувањето на синусот (22.12) - наместо r, добиваме
Го добивме проширувањето на функцијата грев во серија на Лорент во пробиено соседство на точката 20 = 1. Бидејќи добиеното проширување содржи бесконечно многу членови со негативни моќи (r - 1), тогаш zq = 1 е суштинска еднина точка (во овој случај, проширувањето на Лорент се состои само од главниот дел, а точниот дел недостасува).
Забележете дека во овој случај, исто така беше можно да се утврди природата на сингуларноста директно од дефиницијата, без прибегнување кон проширување на серијата. Навистина, постојат низи (r") и (2") кои се спојуваат кон зо= 1, и така што f(z" n)= 1, /(2") = 0 (само наведете ги таквите секвенци). f(z)нема ограничување кога z -> 1 и оттука поентата zq - 1 е суштински еднина.
Да го воведеме концептот на Лорентно проширување на функција во соседство на точка Zq = 00 и разгледајте ја врската помеѓу проширувањето и природата на сингуларноста во оваа точка. Забележете дека дефинициите за изолирана единствена точка и нејзиниот тип (отстранлив, пол или суштински еднина) се пренесуваат на случајот zq = oc непроменет. Но, теоремите 26.2. 26.3 и 26.6, поврзани со природата на проширувањата на Лорен, треба да се променат. Поентата е дека членовите c n (z - 2o) стр. П= -1,-2,..., главниот дел, дефинирајќи ја „„неправилноста“ на функцијата во близина на крајната точка Zq, бидејќи 2 има тенденција да oo, тие ќе се однесуваат „правилно“ (наклонуваат кон 0). Напротив, членовите на регуларниот дел со П= 1,2,... ќе има тенденција да oo; тие ја одредуваат природата на сингуларноста во Zq = oo. Затоа, главен дел од проширувањето во соседството на оо ќе бидат термините со позитивни моќи П,и точно - со негативно.
Ајде да воведеме нова променлива w = 12. Функција ТВ= 1/2, продолжен така што u(oo) = 0, еден на еден и конформално го мапира соседството z > Рпоени zq = 00 во соседството на |w| wq = 0. Ако функцијата f(z)аналитика во дупната населба Р z Zq = oc, потоа функцијата G(w) = f(l/w)ќе биде аналитички во жолтото соседство 0 wo = 0. Бидејќи за 2 -> оо ќе има w-> 0, тогаш
Значи G(w)има во точката wq = 0 е сингуларитет од ист тип како f(z)во точката Zq = 00. Дозволете ни да ја прошириме функцијата G(w) во серија на Laurent во продупчено соседство на точката wo = 0:
Збировите на десната страна на (26.5) ги претставуваат точните и главните делови на проширувањето, соодветно. Ајде да преминеме на променливата z,замена w = 1/z: 
означувајќи П\u003d -A *, 6 * \u003d 6_ " \u003d со стри забележувајќи го тоа G(l/z) = f(z), добиваме
Распаѓањето (2G.G) се нарекува Лорентно проширување на функцијата f(z) во пробиено соседство на точката zq= оо. Првата сума во (2G.6) се нарекува десен дел, а втората сума е главен делова распаѓање. Бидејќи овие збирови одговараат на точните и главни делови на проширувањето (26.5), проширувањето (26.6) ги задоволува аналозите на теоремите 26.2, 26.3 и 26.6. Така, следната теорема е аналог на теоремата 26.2.
Теорема 26.10. Изолирана единствена точкаZq - ос (функции/(Г) е отстранлив ако и само ако Лорентната експанзија во продупченото соседство на оваа точка ја има формата
т.с. се состои само од правилниот дел.
Ставивме /(оо) = ко.Функцијата дефинирана со серијата (26.7) која се спојува во соседството z > Рточки 2o \u003d oc, повикани аналитички во точката zо = оо. (Забележете дека оваа дефиниција е еквивалентна на аналитичноста на функцијата Г(в) во точката леле = 0.)
Пример 26.11. Истражете ја еднината точка zq = oo на функцијата
Затоа што границата е конечна зо = oo е отстранлива еднина точка на функцијата f(r). Ако ставиме /(оо) = лим J(z)= 0, тогаш f(z)ќе стане
тик во точка Зо= ос. Дозволете ни да покажеме како да го најдеме соодветното проширување (26.7). Ајде да преминеме на променливата w = 1 fz.Замена z= 1 /?е, добиваме
(последната еднаквост важи во пробиеното соседство на точката ww = 0, но ние ќе ја прошириме дефиницијата (7(0) = 0). Резултирачката функција има еднини точки w =± јас, w =-1/3, а во точката Wq = 0 е аналитичка. Функција за проширување G(w)по степени w(како што беше направено во Пример 25.7) и замена во добиената серија на моќност w = 1/zможе да се добие проширувањето (26.7) на функцијата f(z).
Теорема 26.3 за случајот зо= oo ќе се препише во следната форма.
Теорема 26.12. Изолирана единствена точкаоди = ок Функцијата f(z) е пол ако и само ако главниот дел од проширувањето на Лорен (26.6) има само конечен број ненулти коефициентиСо":
Овде серијата е правилен дел, а полиномот заграден е главниот дел од проширувањето. Мноштвото на полот во oc се дефинира како множина на полот wq = 0 функции G(z).Лесно е да се види дека мноштвото на полот се совпаѓа со бројот Нво (26.8).
П стр | (i 2 + 1) (z + 3) 2
Задача. Покажете дека функцијата f(z) =-- -- има внатре
точка зо = oo пол ред 3.
Теоремата 26.6 за суштинска еднина точка е препишана за случајот зо= os речиси дословно, и не се задржуваме подетално на тоа.
Сериите Тејлор служат како ефикасна алатка за проучување на функции кои се аналитички во кругот zol За проучување на функциите кои се аналитички во прстенест регион, излегува дека е можно да се конструираат проширувања во позитивни и негативни сили (z - zq) на форма која ги генерализира Тејлоровите проширувања. Серијата (1), сфатена како збир од две серии, се нарекува серија Лоран. Јасно е дека регионот на конвергенција на серијата (1) е заедничкиот дел од регионите на конвергенција на секоја од сериите (2). Ајде да ја најдеме. Областа на конвергенција на првата серија е круг чиј радиус е одреден со формулата Коши-Хадамард Внатре во кругот на конвергенција, серијата (3) конвергира до аналитичка функција, а во секој круг со помал радиус, таа апсолутно конвергира и рамномерно. Втората серија е серија на моќност во однос на променливата.Серијата (5) конвергира во рамките на својот круг на конвергенција до аналитичката функција на сложената променлива m-*oo, а во кој било круг со помал радиус таа конвергира апсолутно и рамномерно, што значи дека регионот на конвергенција на серијата (4) е изгледот на кругот - Ако тогаш постои заедничка област на конвергенција на серијата (3) и (4) - кружен прстен во кој се конвергира серијата (1). на аналитичка функција. Покрај тоа, во кој било прстен, тој се спојува апсолутно и рамномерно. Пример 1. Определете го регионот на конвергенција на рад Лоренвата серија Изолирани еднини точки и нивната класификација (z), која е едновредносна и аполитична во кружен прстен, може да се претстави во овој прстен како збир на конвергентна серија чии коефициенти Cn се уникатно определени и пресметани со формулите каде што 7p е круг со радиус m Дозволете ни да поправиме произволна точка z внатре во прстенот R Конструираме кругови со центри во точката r0 чии радиуси ги задоволуваат неравенките и разгледуваме нов прстен.Според интегралната теорема на Коши за множи поврзан домен, имаме Дозволете да го трансформираме секој од интегралите во збирот (8) посебно. За сите точки £ по должината на кружницата 7d*, релацијата de збирот на рамномерно конвергентна серија 1 1 е задоволена. Затоа, дропката ^ може да се претстави во vi- /" / За сите точки £ на кружницата ir> релацијата е задоволна Затоа, дропот ^ може да се претстави како збир на рамномерно конвергентна серија во формулите (10) и (12) се аналитички функции во кружен прстен. Според тоа, според теоремата на Коши, вредностите на соодветните интеграли не се менуваат ако круговите 7/r и 7r/ се заменат со кој било круг. Ова ни овозможува да ги комбинираме формулите (10) и (12). Заменувајќи ги интегралите од десната страна на формулата (8) со нивните изрази (9) и (11), соодветно, го добиваме саканото проширување. Бидејќи z е произволно точка на прстенот, следува дека серијата (14) конвергира кон функцијата f(z) насекаде во овој прстен, а во кој било прстен серијата се конвергира кон оваа функција апсолутно и рамномерно. Сега да докажеме дека разложувањето на формата (6) е единствено. Да претпоставиме дека се случува уште едно разложување.Тогаш, насекаде во прстенот R, имаме На обемот, серијата (15) се спојува рамномерно. Помножете ги двете страни на еднаквоста (каде m е фиксен цел број и интегрирајте ги двете серии член по член. Како резултат на тоа, добиваме на левата страна, а на десната страна - Csh. Така, (4, \u003d St. Бидејќи m е произволен број, тогаш последната серија на еднаквост (6), чии коефициенти се пресметуваат со формулите (7), се нарекува Лорентна серија на функцијата f(z) во прстенот 7) за коефициентите на Laurent сериите ретко се користат во пракса, бидејќи, по правило, бараат незгодни пресметки. Обично, ако е можно, се користат готови Тејлор проширувања на елементарните функции. Врз основа на уникатноста на проширувањето, секој легитимен метод води кон истото Пример 2 Разгледајте ги проширувањата на серијата Лорент на функциите на различни домени, под претпоставка дека Fuiscija /(z) има две еднини точки: Затоа, постојат три домени на прстенот и центрирано во точката r = 0. во секоја од нив функцијата f(r) е аналитичка: а) кругот е надворешноста на кругот (сл. 27). Да ги најдеме Лорентовите проширувања на функцијата /(z) во секој од овие региони. /(z) го претставуваме како збир на елементарни дропки а) Релација за трансформација на круг (16) на следниов начин Користејќи ја формулата за збир на членовите на геометриска прогресија, добиваме б) Прстенот за функцијата -z останува конвергентен во овој прстен, бидејќи серијата (19) за функцијата j^j за |z| > 1 се разминува. Затоа, ја трансформираме функцијата /(z) на следниов начин: применувајќи ја формулата (19) повторно, добиваме дека Оваа серија конвергира за. Заменувајќи ги проширувањата (18) и (21) во релацијата (20), добиваме в) Надворешноста на кружницата за функцијата -z со |z| > 2 дивергира и серијата (21) за функцијата Да ја претставиме функцијата /(z) во следнава форма: /<*> Користејќи ги формулите (18) и (19), добиваме ИЛИ 1 Овој пример покажува дека за иста функција f(z) Лорентовото проширување, генерално земено, има различна форма за различни прстени. Пример 3. Најдете го разложувањето на 8-те Лоренови серии на функцијата серија Лорент Изолирани еднини точки и нивната класификација во прстенестиот регион A Го користиме претставувањето на функцијата f (z) во следнава форма: и го трансформираме вториот член Користејќи го формула за збир на членовите на геометриска прогресија, добиваме Со замена на пронајдените изрази во формулата (22), имаме пример 4. Проширете ја функцијата во серија на Лорен во соседството на тенок zq = 0. За која било сложена , имаме Нека Ова проширување важи за која било точка z Ф 0. Во овој случај, прстенестиот регион е целата сложена рамнина со една точка z исфрлена - 0. Овој регион може да се дефинира со следнава врска: Оваа функција е аналитичка во регионот Од формулите (13) за коефициентите на серијата Лоран, со истото резонирање како и во претходниот став, може да се добијат Kouiw неравенките. ако функцијата f(z) е ограничена на круг, каде што M е константа), тогаш изолираните еднини точки Точката zo се нарекува изолирана еднина точка на функцијата f(z) ако постои прстенесто соседство на точката ( ова множество понекогаш се нарекува и прободено соседство на точката 2o), каде што функцијата f(z) е единечна и аналитичка. Во самата точка zo, функцијата или не е дефинирана или не е едновредносна и аналитичка. Се разликуваат три типа на еднини точки во зависност од однесувањето на функцијата /(z) при приближување до точката zo. Изолирана еднина точка се нарекува: 1) отстранлива ако постои конечна 2) pmusach ако 3) суштински еднина точка ако функцијата f(z) нема ограничување за Теорема 16. Изолирана еднина точка z0 од функцијата f(z) е отстранлива еднина точка ако и само ако Лорентовото проширување на функцијата f(z) во соседството на точката zo не содржи главен дел, т.е. има форма Let zo - отстранлива еднина точка. Тогаш постои конечна, па оттука функцијата f(z) е ограничена во проколошко соседство на точката r. Ние ги поставивме врз основа на неравенките на Коши Бидејќи е можно да се избере p како произволно мали, тогаш сите коефициенти се негативни моќите (z - 20) се еднакви на нула: обратно, нека Laurent проширувањето на функцијата /(r) во соседството на точката zq го содржи само точниот дел, т.е. ја има формата (23) и затоа , е Тејлор. Лесно е да се види дека за z -* z0 функцијата /(r) има гранична вредност: Теорема 17. Изолирана еднина точка zq од функцијата f(z) може да се отстрани ако и само ако функцијата J(z) е ограничена во некоја дупната населба на точката zq, Zgmechai не. Нека r0 е отстранлива еднина точка од f(r). Претпоставувајќи дека добиваме дека функцијата f(r) е аналитичка во некој круг центриран во точката th. Ова го дефинира името на точката - за еднократна употреба. Теорема 18. Изолирана еднина точка zq од функцијата f(z) е пол ако и само ако главниот дел од Лорентовото проширување на функцијата f(z) во соседството на точката содржи конечен (и позитивен) број од ненула членови, т.е. има форма 4 Нека z0 е пол. Оттогаш постои пробиено соседство на точката z0 во која функцијата f(z) е аналитичка и ненула. Тогаш во ова соседство се дефинира аналитичка функција, па оттука, точката zq е отстранлива еднина точка (нула) на функцијата или каде што h(z) е аналитичка функција, h(z0) ∩ 0. е аналитичка во соседството на точката zq, и оттука, од каде добиваме дека Сега да претпоставиме дека функцијата f(z) има распаѓање на формата (24) во пробиено соседство на точката zo. Тоа значи дека во ова соседство функцијата f(z) е аналитичка заедно со функцијата. За функцијата g(z) важи проширувањето од кое е јасно дека zq е отстранлива еднина точка на функцијата g(z) и постои. Тогаш функцијата се стреми кон 0 - полот на функцијата Има уште една едноставна факт. Точката Zq е пол на функцијата f(z) ако и само ако функцијата g(z) = y може да се прошири на аналитичка функција во соседството на точката zq со поставување g(z0) = 0. Редоследот на полот на функцијата f(z) се вика редот на нула на функцијата jfa. Теоремите 16 и 18 го подразбираат следното тврдење. Теорема 19. Изолирана еднина тенка е суштински еднина ако и само ако главниот дел од Лорентовото проширување во пробиеното соседство на оваа точка содржи бесконечно многу ненула членови. Пример 5. Еднина точка на функцијата е zo = 0. Имаме изолирани еднини точки од Laurent Series и нивна класификација Затоа, zo = 0 е отстранлива еднина точка. Проширувањето на функцијата /(z) во серија на Лоран во близина на нултата точка го содржи само правилниот дел: Пример7. f(z) = Еднина точка на функцијата f(z) е zq = 0. Да го разгледаме однесувањето на оваа функција на реалната и имагинарната оска: на реалната оска на x 0, на имагинарната оска Затоа, ниту конечни ниту бесконечна граница f(z) при z -* 0 не постои. Оттука точката r0 = 0 е суштински еднина точка на функцијата f(z). Да го најдеме Лорентовото проширување на функцијата f(z) во соседството на нултата точка. За секој комплекс C имаме Поставивме. Тогаш Лорентската експанзија содржи бесконечен број членови со негативни сили од z.
Дефиниција.Се нарекува еднина точка на функцијата изолирани, ако во некое соседство на оваа точка е аналитичка функција (односно аналитичка во прстенот).
Класификацијата на изолираните еднини точки на функцијата е поврзана со однесувањето на оваа функција во соседството на еднина точка.
Дефиниција.Точката се нарекува за еднократна употреба еднина точка на функција ако постои конечна граница на оваа функција во .
Пример 5Покажете дека функцијата има отстранлива сингуларност во точка.
Решение.Потсетувајќи се на првата извонредна граница, ние пресметуваме
Ова значи дека дадената функција има отстранлива сингуларитет во точката.
Задача 4.Покажете дека точката е отстранлива за .
Дефиниција.Точката се нарекува столб функција , ако оваа функција се зголемува на неодредено време за , тоа е .
Да обрнеме внимание на врската помеѓу концептите нула и пол на аналитичка функција. Да ја претставиме функцијата како .
Ако точката е едноставна нула на функцијата, тогаш функцијата има едноставен пол
Ако точката е редот нула за функцијата, тогаш за функцијата тоа е полот со цел.
Пример 6Покажете дека функцијата има пол од трет ред во точка.
Решение.Претпоставувајќи , добиваме . Како што се стремиме кон нула, според кој било закон, имаме . Потоа, а со тоа и самата функција се зголемува на неодредено време. Затоа, , односно, еднината точка е пол. За функција, оваа точка е очигледно тројна нула. Оттука, за оваа функција, точката е пол од трет ред.
Задача 5.Покажете дека точката има едноставен пол.
Дефиниција.Точката се нарекува во суштина посебен точка на функцијата ако во оваа точка нема ниту конечна ниту бесконечна граница на функцијата (однесувањето на функцијата не е дефинирано).
Нека е суштинска еднина точка на функцијата. Потоа, за секој претходно доделен комплексен број постои таква низа точки што се конвергираат во , по која вредностите имаат тенденција да: ( Сочочка теорема).
Пример 7Покажете дека функцијата во точка има суштинска сингуларност.
Решение.Да го разгледаме однесувањето на дадена функција во близина на точката. За по позитивниот дел од реалната оска (т.е. ) имаме и ; ако по негативниот дел од реалната оска (т.е.), тогаш и . Значи, нема ограничување за. По дефиниција, функцијата има суштинска сингуларност во точка.
Да го разгледаме однесувањето на функцијата на нула од гледна точка на теоремата на Сочоки. Нека е кој било комплексен број различен од нула и бесконечност.
Од еднаквоста наоѓаме . Претпоставувајќи , добиваме низа од точки , . Очигледно,. Во секоја точка од оваа низа, функцијата е еднаква на , и затоа
Задача 6.Покажете дека функцијата има суштинска сингуларност во точка.
Точката во бесконечност секогаш се смета за посебна за функцијата. Точката се нарекува изолирана еднина точка на функцијата ако оваа функција нема други еднини точки надвор од кругот центриран на почетокот.
Класификацијата на изолирани еднини точки може да се прошири и на случајот.
Пример 8Покажете дека функцијата има двоен пол на бесконечност.
Решение.Размислете за функцијата , каде што е аналитичка функција во соседството на точката , и . Тоа значи дека функцијата има двојна нула на бесконечност, но тогаш за функцијата точката е двоен пол.
Пример 9Покажете дека функцијата има суштинска сингуларност во бесконечноста.
Решение.Сличен проблем се разгледува и во пр.7. Размислете за однесувањето на функцијата во соседството на бесконечно оддалечена точка. За по позитивниот дел од реалната оска, и за по негативниот дел од реалната оска. Ова значи дека не постои ограничување на функцијата во точка и, врз основа на дефиницијата, оваа точка е суштински еднина.
Природата на сингуларноста на функцијата во точка може да се процени од главен дел Лорентна експанзија во соседството на оваа точка.
Теорема 1.За поентата да биде за еднократна употреба единствена точка на функцијата , потребно е и доволно соодветното Лорентно проширување не го содржеше главниот дел.
Задача 6.Користејќи го Тејлоровото проширување на функцијата во соседството на точката, покажете дека има отстранлива сингуларитет на нула.
Теорема 2.За поентата да биде столб функции , е неопходен и доволен за да главен дел соодветната Лорентна експанзија содржеше конечен број членови :
Бројот на највисокиот негативен член го одредува редоследот на полот.
Во овој случај, функцијата може да се претстави како
каде е функцијата аналитичка во точката, , е редот на полот.
Пример 10Покажете дека функцијата има едноставни полови во точките.
Решение.Ајде да разгледаме една точка. Го користиме Лорентното проширување на оваа функција во близина на оваа точка, добиено во Пример 2:
Бидејќи највисоката (и единствена) негативна моќност во главниот дел од оваа експанзија е еднаква на една, поентата е едноставен пол на оваа функција.
Овој резултат можеше да се добие на друг начин. Да претставиме во форма и да ставиме - ова е функција која е аналитичка во точката и . Оттука, поради (8) оваа функција има едноставен пол во точката.
Друг начин: разгледајте функција која има едноставна нула во точката. Оттука, во овој момент има едноставен столб.
Слично на тоа, ако ја напишеме функцијата во форма , каде е аналитичка на функција во точката и , тогаш веднаш е јасно дека точката е едноставен пол на функцијата.
Задача 7.Покажете дека функцијата има пол од втор ред во точката и пол од 4 ред во точката.
Теорема 3.За поентата да биде во суштина посебен точка на функцијата , потребно е и доволно тоа главен дел Лорентна експанзија во соседството на точката содржеше бесконечен број членови .
Пример 11.Определи ја природата на сингуларноста на точката на функцијата
Решение.Во добро познатото проширување на косинус, ставаме наместо:
Оттука, проширувањето на Лорент во соседство на точка ја има формата
Овде правилниот дел е еден термин. А главниот дел содржи бесконечен број поими, така што поентата е суштински еднина.
Задача 8.Покажете дека во одредена точка функцијата има суштинска сингуларност.
Размислете за некоја функција и запишете ја нејзината Laurent проширување на точката:
Ајде да направиме замена, додека поентата оди на поентата. Сега, во соседството на точка на бесконечност, имаме
Останува да се воведе нова ознака. Добиваме
каде што е главниот дел, а е правилниот дел од Лореновото проширување на функцијата во соседството на бескрајно оддалечена точка. Така, во Лореновото проширување на функција во соседство на точка, главниот дел е серија во позитивни моќи, додека правилниот дел е серија во негативни моќи. Земајќи го предвид ова
Меѓутоа, горенаведените критериуми за одредување на природата на сингуларноста остануваат валидни за бескрајно далечна точка.
Пример 12.Откријте ја природата на сингуларноста на функцијата во точката. , тогаш во одреден момент може да испадне дека е неизолиран.
Пример 15Функцијата на бесконечно оддалечена точка има суштинска сингуларност. Покажете дека точката за функцијата не е изолирана еднина точка.
Решение.Функцијата има бесконечен број на полови на нулите на именителот, односно во точките , . Бидејќи , тогаш точката , во која било населба од која има столбови , е граничната точка за половите.
единствена точка по математика. 1) Единствена точка на кривата дадена со равенката F ( x, y) = 0, - точка М 0 ( x 0, y 0), во која двата парцијални изводи на функцијата F ( x, y) исчезнат: Ако, дополнително, не сите втори парцијални изводи на функцијата F ( x, y) во точката M 0 се еднакви на нула, тогаш O. t се нарекува двојно. Ако, заедно со исчезнувањето на првите изводи во точката M 0, исчезнат сите втори изводи, но не сите трети изводи се еднакви на нула, тогаш O. t. се нарекува тројно, итн. При проучување на структурата на кривата во близина на двојна О.т., важна улога игра знакот на изразот Ако Δ > 0, тогаш O. t се нарекува изолиран; на пример, кривата y 2 - x 4 + 4x 2= 0 потеклото е изолиран O. t. (види оризот. еден
). Ако Δ x 2 + y 2 + a 2) 2 - 4a 2 x 2 - a 4= 0 потеклото на координатите е нодалот O. t. (види оризот. 2
). Ако Δ = 0, тогаш кривата O. t. е или изолирана или се карактеризира со фактот дека различни гранки на кривата имаат заедничка тангента во оваа точка, на пример: тангента и формираат точка, како крива y 2 - x 3= 0 (види оризот. 3
, А); б) врв од втор вид - различни гранки на кривата се наоѓаат на иста страна од заедничката тангента, како крива
(y - x 2)2 - x 5= 0 (види оризот. 3
, б); в) точка на само-контакт (за крива y 2 - x 4= 0 потекло е точка на самоконтакт; (цм. оризот. 3
, v). Заедно со наведениот O. t. има и многу други O. t. со посебни имиња; на пример, асимптотична точка е врв на спирала со бесконечен број вртења (види Сл. оризот. 4
), точка на прекин, аголна точка итн. 2) Единствена точка на диференцијалната равенка е точка во која истовремено исчезнуваат и броителот и именителот на десната страна на диференцијалната равенка (Види Диференцијални равенки) каде што P и Q се континуирано диференцијабилни функции. Претпоставувајќи O. t. лоциран на потеклото на координатите и користејќи ја формулата на Тејлор (Види ја формулата на Тејлор), можеме да ја претставиме равенката (1) во форма каде P 1 ( x, y) и Q 1 ( x, y) се бесконечно мали во однос на Имено, ако λ 1 ≠ λ 2 и λ 1 λ 2 > 0 или λ 1 = λ 2, тогаш O. t е јазол; во него влегуваат сите интегрални криви што минуваат низ точки на доволно мало соседство на јазолот. Ако λ 1 ≠ λ 2 и λ 1 λ 2 i β, α ≠ 0 и β ≠ 0, тогаш O. t. е фокус; сите интегрални криви што минуваат низ точките во доволно мало соседство на фокусот се спирали со бесконечен број на вртења во кое било произволно мало соседство на фокусот. Ако, конечно, λ 1,2 = ± јасβ, β ≠ 0, тогаш карактерот на O. t. не е одреден со линеарни членови во проширувања на P ( x, y) и П ( x, y), како што беше случај во сите горенаведени случаи; овде O. t. може да биде фокус или центар, или може да има покомплексен карактер. Во соседството на центарот, сите интегрални кривини се затворени и го содржат центарот внатре во нив. Така, на пример, точката (0, 0) е јазол за равенките на" = 2u/x(λ 1 = 1, λ 2 = 2; види оризот. 5
, а) и y" = u/x(λ 1 = λ 2 = 1; види оризот. 5
, б), седло за равенката y" = -y/x(λ 1 = -1, λ 2 = 1 ; цм. оризот. 6
), фокусот за равенката y" =(x + y) /
(x - y) (λ 1 = 1 - јас, λ 2 = 1 + јас; цм. оризот. 7
) и центарот за равенката y" = -x / y(λ 1 = - јас, λ 2 = јас; цм. оризот. осум
). Ако x, y) и Q ( x, y) се аналитички, соседството на O. t. од повисок ред може да се подели на региони: D 1 - исполнето со интегрални криви, чии двата краја се вклучени во O. t. (елиптични региони), D 2 - исполнети со интегрални криви, чиј еден крај е вклучен во O. t. (параболични региони), и D 3 - региони ограничени со две интегрални криви вклучени во O. t., меѓу кои има интегрални криви од типот на хиперболи (хиперболични региони) (види. оризот. 9
). Ако нема интегрални криви кои влегуваат во O. точка, тогаш O. точката се нарекува точка од стабилен тип. Соседството на стабилна O. t. се состои од затворени интегрални кривини кои содржат O. t. внатре во себе, меѓу кои се наоѓаат спирали (види Сл. оризот. 10
). Проучување на диференцијалните равенки на O. t., односно, во суштина, проучување на однесувањето на семејствата на интегрални криви во соседството на O. t. M. Lyapunov a, A. Poincaré и други). 3) Единствена точка на аналитичка функција со една вредност е точка во која е нарушена аналитичноста на функцијата (види Аналитички функции). Ако има маало на О.т. а, ослободени од други О. т., потоа точката асе нарекува изолиран O. t. Ако ае изолиран O.T. и постои конечен O.T. се нарекува отстранлив O.T. Со соодветно менување на дефиницијата на функцијата во точката a (или редефинирање во овој момент, ако функцијата воопшто не е дефинирана во неа), имено, поставување ѓ(а)= б, можно е да се постигне аќе стане обична точка на поправената функција. На пример, точка z= 0 е отстранлив O.T. за функцијата f 1 ( z) = ѓ(z), ако z≠ 0, и ѓ 1 (0), = 1, точка z= 0 е обична точка [ ѓ 1 (z) е аналитички во точката z= 0]. Ако а- изолиран O. t. а a се нарекува пол или несуштинска еднина точка на функцијата ѓ(z), ако серијата Laurent) функционира ѓ(z) во соседство на изолиран О.т не содржи негативни овластувања z - a, ако а- отстранлив O. t., содржи конечен број негативни моќи z - a, ако а- столб (во овој случај, редоследот на столбот Рсе дефинира како највисока моќност на a - суштински еднина точка. На пример, за функцијата точка z= 0 е пол на редот Р, за функцијата точка z= 0 е суштинска еднина точка. На границата на кругот на конвергенција на сериите на моќност мора да има најмалку еден O. t. од функцијата претставена во оваа кружница со дадената серија на моќност. Сите гранични точки од доменот на постоење на една вредносна аналитичка функција (природна граница) се гранични точки на оваа функција. Така, сите точки на единечниот круг | z| = 1 се посебни за функцијата За повеќевредносна аналитичка функција, концептот на „О. Т." потешко. Покрај O. t., во поединечните листови на Римановата површина на функцијата (односно, O. t. на аналитички елементи со една вредност), која било точка на разгранување е исто така O. t. на функцијата. Изолираните точки на разгранување на Римановата површина (т.е., точките на разгранување такви што во некои од нивните соседства нема други O.t. функции во ниту еден лист) се класифицирани на следниов начин. Ако a е изолирана разгранета точка со конечен ред и постои конечна a, таа се нарекува критичен пол. Ако ае изолирана разгранета точка од бесконечен ред, а a се нарекува трансцендентална O. t. Сите други изолирани точки на разгранување се нарекуваат критични суштински еднина точки. Примери: точка z= 0 е обична критична точка на функцијата f ( z) = дневник zи критична суштинска единствена точка на функцијата ѓ (z) = дневник за гревови z. Секој O. t., освен отстранлив, е пречка за аналитичко продолжување, т.е. аналитичкото продолжение по крива што минува низ неотстранлив O. t. е невозможно. Голема советска енциклопедија. - М.: Советска енциклопедија.
1969-1978
.
p = 2, 3, ...)
Погледнете што е „Специјална точка“ во другите речници:
Поени овде. Видете исто така еднина точка (диференцијални равенки). Карактеристика или сингуларност во математиката е точка во која математички објект (обично функција) не е дефиниран или има неправилно однесување (на пример, точка во која ... ... Википедија
Аналитичка функција е точка во која се нарушуваат условите на аналитичност. Ако аналитичката функција f(z) е дефинирана во некое соседство на точката z0 насекаде… Физичка енциклопедија
Аналитичка функција е точката во која е нарушена аналитичноста на функцијата ... Голем енциклопедиски речник
единствена точка- - [Ја.Н. Лугински, М.С. Фези Жилинскаја, Ју.С. Кабиров. Англиски руски речник на електротехниката и електроенергетската индустрија, Москва, 1999] Теми од електротехниката, основни концепти EN еднина точка ... Прирачник за технички преведувач
1) ОТ на аналитичка функција f(z) е пречка за аналитичко продолжение на елемент од функцијата f(z) од сложена променлива z по некоја патека на рамнината на оваа променлива. Нека аналитичката функција f(z) е дефинирана со некои ... ... Математичка енциклопедија
Аналитичка функција, точка во која е нарушена аналитичноста на функцијата. * * * ЕДИНСТВЕНА ТОЧКА ЕДИНСТВЕНА ТОЧКА на аналитичка функција, точка во која се нарушува аналитичноста на функцијата ... енциклопедиски речник
единствена точка- ypatingasis taškas statusas T sritis automatika atitikmenys: engl. еднина точка vok. единствена Punkt, m rus. единствена точка, fpranc. точка честичка, m; единствена точка, m …
