Düzlemdeki herhangi bir noktanın hızı nasıl belirlenir? Hız yönünde. Düzlem hareket denklemleri

Keyfi bir noktanın hızı Mşekli, kutup ve kutup etrafındaki dönme hareketi ile birlikte öteleme hareketi sırasında noktanın aldığı hızların toplamı olarak tanımlarız.

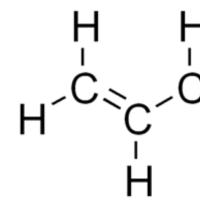
Noktanın konumunu hayal edelim M(Şekil 1.6) gibi.

Bu ifadeyi zamana göre farklılaştırdığımızda şunu elde ederiz:

, Çünkü

.

Aynı zamanda hız v MA. hangi nokta M bir figürün bir direğin etrafında döndürülmesiyle elde edilir A, ifadesinden belirlenecek

v MA=ω · M.A.,

Nerede ω - düz bir şeklin açısal hızı.

Herhangi bir noktanın hızı M düz şekil geometrik olarak noktanın hızının toplamıdır A, kutup olarak alınır ve hız, nokta M bir figür bir direğin etrafında döndüğünde. Bu hızın hızının büyüklüğü ve yönü, hızların paralelkenarının oluşturulmasıyla bulunur.

Sorun 1

Bir noktanın hızını belirleme A, Merdanenin merkez hızı 5 m/s ise merdanenin açısal hızı . Silindir yarıçapı r=0,2m, köşe . Silindir kaymadan yuvarlanır.

Cisim düzleme paralel hareket yaptığı için noktanın hızı A kutup hızından oluşacaktır (nokta İLE) ve noktanın aldığı hız A bir direğin etrafında dönerken İLE.

,

Cevap:

Düzlem paralel hareket eden bir cismin iki noktasının hızlarının izdüşümü üzerine teorem

Bazı iki noktayı ele alalım A Ve İÇİNDE düz figür. Bir noktaya değinmek A kutup başına (Şekil 1.7), şunu elde ederiz:

.

Bu nedenle eşitliğin her iki tarafının da yönlendirilen eksene yansıtılması AB ve vektörün dik olduğu göz önüne alındığında AB, bulduk

vB· cosβ=v bir· cosα+ v V A· cos90°.

Çünkü vVA· cos90°=0şunu elde ederiz: katı bir cismin iki noktasının hızlarının bu noktalardan geçen eksene izdüşümleri eşittir.

Sorun 1

Çekirdek AB pürüzsüz bir duvardan ve pürüzsüz bir zeminden aşağı kayar, nokta hızı A V A =5m/s, zemin ve çubuk arasındaki açı AB eşittir 30 0 . Bir noktanın hızını belirleme İÇİNDE.

Anlık hız merkezini kullanarak düzlemsel bir şekil üzerindeki noktaların hızlarını belirleme

Düz bir şeklin noktalarının hızlarını direğin hızına göre belirlerken, direğin hızı ile direğin etrafındaki dönme hareketinin hızı büyüklük olarak eşit ve zıt yönde olabilir ve hızı 1/2 olan bir P noktası vardır. zamanda belirli bir an sıfırdır buna hızların anlık merkezi adını verin.

Anlık hız merkezi zamanın belirli bir anında hızı sıfır olan bir düzlem şekliyle ilişkili bir noktadır.

Düz bir şeklin noktalarının hızları, zamanın belirli bir anında, sanki şeklin hareketi, hızların anlık merkezinden geçen bir eksen etrafında anında dönüyormuş gibi belirlenir (Şekil 1.8).

v bir=ω · PA; ().

Çünkü vB=ω · P.B.; (), O w=vB/P.B.=v bir/PA

Düz bir şeklin noktalarının hızları, bu noktalardan anlık hız merkezine olan en kısa mesafelerle orantılıdır.

Elde edilen sonuçlar aşağıdaki sonuçlara yol açmaktadır:

1) Anlık hız merkezinin konumunu belirlemek için hızın büyüklüğünü, yönünü ve herhangi iki noktanın hızının yönünü bilmeniz gerekir. A Ve İÇİNDE düz şekil; anlık hız merkezi P noktalardan oluşturulan dikmelerin kesişme noktasında bulunur A Ve İÇİNDE bu noktaların hızlarına;

2) açısal hız ω Belirli bir andaki düz şekil, hızın anlık merkeze olan mesafeye oranına eşittir R hızlar: ω =v bir/PA;

3) Noktanın anlık hız merkezine (P) göre hızı, açısal hızın (w) yönünü gösterecektir.

4) Bir noktanın hızı, o noktaya olan en kısa mesafeyle doğru orantılıdır İÇİNDE anlık hız merkezine R v A = ω·BP

Sorun 1

Krank OA uzunluk 0,2 m açısal hızla düzgün bir şekilde döner ω=8 rad/s. Bağlantı çubuğuna AB noktada İLE biyel menteşelidir CD. Mekanizmanın belirli bir konumu için noktanın hızını belirleyin D açı ise kaydırıcı.

Nokta hareketi İÇİNDE yatay kılavuzlarla sınırlanan kaydırıcı yalnızca yatay kılavuzlar boyunca öteleme hareketi yapabilir. Nokta hızı İÇİNDE ile aynı yöne yönlendirilir. Biyel kolunun iki noktası aynı yönde hızlara sahip olduğundan gövde anlık öteleme hareketi yapar ve biyel kolunun tüm noktalarının hızları aynı yön ve değerde olur.

RİJİT BİR CİSİMİN DÜZLEMSEL HAREKETİ

Çalışma soruları:

1.Rijit bir cismin düzlemsel hareket denklemleri.

2. Düzlemsel bir figürün noktalarının hızı

3. Anlık hız merkezi

4. Düzlemsel bir figürün noktalarının hızlanması

1. Rijit bir cismin düzlemsel hareket denklemleri

Katı bir cismin düzlemsel hareketibuna diyorlarBir cismin tüm kesit noktalarının kendi düzleminde hareket ettiği hareket.

Sert gövdeye izin ver 1 düz bir hareket yapar.

Sekant uçak vücutta 1 sekant düzleminde hareket eden bir P bölümü oluşturur .

Düzleme paralel ise vücudun diğer bölümlerini, örneğin noktalardan gerçekleştirin
vb. bölümlere aynı dik olarak uzanırsa, tüm bu noktalar ve vücudun tüm bölümleri eşit olarak hareket edecektir.

Sonuç olarak, bu durumda vücudun hareketi tamamen bölümlerinden birinin paralel düzlemlerden herhangi birinde hareketi ile belirlenir ve bölümün konumu, örneğin bu bölümün iki noktasının konumu ile belirlenir. A Ve İÇİNDE.

Bölüm konumu P uçakta Ohoo segmentin konumuna göre belirlenir AB, bu bölümde gerçekleştirilir. Düzlemde iki noktanın konumu A(
) Ve İÇİNDE(
) bir sınırlamaya tabi olan dört parametre (koordinat) ile karakterize edilir - segmentin uzunluğu biçimindeki bağlantı denklemi AB:

Bu nedenle P bölümünün düzlemdeki konumu belirtilebilir. üç bağımsız parametre - koordinatlar
puanA ve açı, bu bir segment oluşturur AB akslı Ah. Tam durak A, P bölümünün konumunu belirlemek için seçilene ne ad verilir? KUTUP.

Bir gövde bölümü hareket ettiğinde kinematik parametreleri zamanın fonksiyonudur

Denklemler katı bir cismin düzlemsel (düzlem-paralel) hareketinin kinematik denklemleridir. Şimdi elde edilen denklemlere göre düzlemsel hareket halindeki bir cismin öteleme ve dönme hareketi yaptığını göstereceğiz. Şekil 2'ye izin verin. bir parça tarafından belirtilen bir gövdenin bölümü
koordinat sisteminde Ah, başlangıç ​​konumundan taşındı 1 son pozisyona 2.

Bir cismin belirli bir konumdan olası hareketinin iki yolunu göstereceğiz. 1 2. konuma getirin.

İlk yol. Noktayı kutup olarak ele alalım .Segmenti taşı
kendine paralel, yani bir rota boyunca giderek ,noktalar birleştirilene kadar Ve . Segmentin konumunu alıyoruz . bir açıyla ve düz şeklin segment tarafından belirtilen son konumunu elde ederiz
.

İkinci yol. Noktayı kutup olarak ele alalım . Segmenti taşıma
kendine paralel, yani yörünge boyunca giderek
noktalar birleştirilene kadar Ve .Segmentin konumunu alın
. Daha sonra bu parçayı direğin etrafında döndürüyoruz Açık köşe ve düz şeklin segment tarafından belirtilen son konumunu elde ederiz
.

Aşağıdaki sonuçları çıkaralım.

1. Düzlemsel hareket, denklemlere tam uygun olarak öteleme ve dönme hareketlerinin birleşimidir ve bir cismin düzlemsel hareketi modeli, cismin kutbu ve dönüşüyle ​​birlikte cismin tüm noktalarının öteleme hareketi olarak düşünülebilir. vücut direğe göre.

2. Bir cismin öteleme hareketinin yörüngesi kutup seçimine bağlıdır . İncirde. Şekil 13.3'te ele alınan durumda, ilk hareket yönteminde, bir noktanın kutup olarak alındığı durumda şunu görüyoruz: öteleme hareketinin yörüngesi yörüngeden önemli ölçüde farklı
diğer kutup için İÇİNDE.

3. Gövdenin dönüşü direk seçimine bağlı değildir. Köşe Vücudun dönüşünün büyüklüğü ve dönüş yönü sabit kalır . Her iki durumda da Şekil 2'de ele alınmıştır. 13.3'te dönüş saat yönünün tersine gerçekleşti.

Düzlemsel hareket halindeki bir cismin temel özellikleri şunlardır: direğin yörüngesi, cismin kutup etrafında dönme açısı, direğin hızı ve ivmesi, cismin açısal hızı ve açısal ivmesi. Ek eksenler
öteleme hareketi sırasında kutupla birlikte hareket ederler A ana eksenlere paralel Ohoo direğin yörüngesi boyunca.

Bir düzlem şeklinin kutbunun hızı, aşağıdaki denklemlerden zaman türevleri kullanılarak belirlenebilir:

Vücudun açısal özellikleri de benzer şekilde belirlenir: açısal hız
;

açısal ivme

.

İncirde. kutupta A hız vektörünün projeksiyonları gösterilmiştir eksende Ah, ah. Gövde dönüş açısı , açısal hız ve açısal ivme bir noktanın etrafındaki yay oklarıyla gösterilir A. Hareketin dönme özelliklerinin kutup seçiminden bağımsız olması nedeniyle açısal özellikler ,,Yay oklarıyla düz bir şeklin herhangi bir noktasında gösterilebilir, örneğin B noktasında.

Düzlem bir şekil üzerindeki noktaların hızlarını belirleme

Düz bir şeklin hareketinin, şeklin tüm noktalarının hızla hareket ettiği öteleme hareketinden oluştuğu düşünülebilir. direkler A ve bu kutup etrafındaki dönme hareketinden. Herhangi bir noktanın hızının olduğunu gösterelim. MŞekil, bu hareketlerin her birinde noktanın aldığı hızlardan geometrik olarak oluşturulmuştur.

Aslında herhangi bir noktanın konumu M rakamlar eksenlere göre tanımlanır Ohoo yarıçap vektörü(Şekil 3), burada - direğin yarıçap vektörü A , - noktanın konumunu tanımlayan vektör M eksenlere göre, direkle birlikte hareket etmek Aöteleme (şeklin bu eksenlere göre hareketi kutup etrafında bir dönüştür) A). Daha sonra

Ortaya çıkan eşitlikte miktardireğin hızıdır A; aynı beden hıza eşit , hangi nokta Mşu saatte alır:yani eksenlere göreveya başka bir deyişle bir figür bir direğin etrafında döndüğünde A. Dolayısıyla önceki eşitlikten şu sonuç çıkıyor:

Hız , hangi nokta M bir figürün bir direğin etrafında döndürülmesiyle elde edilir A :

nerede - şeklin açısal hızı.

Böylece herhangi bir noktanın hızı M düz şekil geometrik olarak başka bir noktanın hızının toplamıdır A, kutup olarak alınır ve noktanın hızı MŞeklin bu direğin etrafında döndürülmesiyle elde edilir. Modül ve hız yönükarşılık gelen paralelkenarın oluşturulmasıyla bulunur (Şekil 4).

Şekil 3 Şekil 4

Bir cisim üzerindeki iki noktanın hızlarının izdüşümü üzerine teorem

Düzlemsel bir şeklin (veya düzleme paralel hareket eden bir cismin) noktalarının hızlarının belirlenmesi genellikle oldukça karmaşık hesaplamalar içerir. Bununla birlikte, bir şeklin (veya cismin) noktalarının hızlarını belirlemek için pratik olarak daha uygun ve daha basit bir dizi başka yöntem elde etmek mümkündür.

Şekil 5

Bu yöntemlerden biri şu teoremle verilmektedir: Rijit bir cismin iki noktasının hızlarının bu noktalardan geçen bir eksene izdüşümleri birbirine eşittir. Bazı iki noktayı ele alalım A Ve İÇİNDE düz şekil (veya gövde). Bir noktaya değinmek A kutup başına (Şekil 5), şunu elde ederiz:. Dolayısıyla eşitliğin her iki tarafının da yönlendirilen eksene yansıtılması AB ve vektör verildiğindedik AB, bulduk

ve teorem kanıtlanmıştır.

Anlık hız merkezini kullanarak düzlemsel bir şekil üzerindeki noktaların hızlarının belirlenmesi.

Düz bir şeklin (veya düzlemsel hareket halindeki bir cismin) noktalarının hızlarını belirlemeye yönelik başka bir basit ve görsel yöntem, anlık hız merkezi kavramına dayanır.

Anlık hız merkezi zamanın belirli bir anında hızı sıfır olan düz bir şeklin noktasıdır.

Şekil hareket ederse bunu doğrulamak kolaydır ilerlemeyen bir şekilde, o zaman zamanın her anında böyle bir nokta Tvar ve üstelik tektir. Bir anda izin ver T puan A Ve İÇİNDE düz figürlerin hızları vardır Ve , birbirine paralel değil (Şek. 6). Sonra işaret et R, dik doğruların kesişme noktasında yer alan ah vektöre Ve İÇİNDE B vektöre ve anlık hız merkezi olacaktır.. Aslında bunu varsayarsak, daha sonra hız projeksiyon teoremine göre vektörhem dik olmalı hem de AR(Çünkü) Ve Sanal Gerçeklik(Çünkü), ki bu imkansızdır. Aynı teoremden, şeklin başka hiçbir noktasının zamanın bu anında sıfıra eşit bir hıza sahip olamayacağı açıktır.

Şekil 6

Eğer şimdi, şu anda konuyu ele alırsak R direğin ötesinde, ardından noktanın hızı A irade

Çünkü . Şeklin herhangi bir diğer noktası için de benzer bir sonuç elde edilir. Sonuç olarak, düz bir şeklin noktalarının hızları, sanki şeklin hareketi anlık hız merkezi etrafında bir dönüşmüş gibi, zamanın belirli bir anında belirlenir. burada

Eşitliklerden şu da çıkıyor:Düz bir şeklin noktaları MCS'ye olan mesafeleriyle orantılıdır.

Elde edilen sonuçlar aşağıdaki sonuçlara yol açmaktadır.

1. Hızların anlık merkezini belirlemek için yalnızca hızların yönlerini bilmeniz yeterlidir. Ve bazı iki nokta A Ve İÇİNDE düz bir şekil (veya bu noktaların yörüngesi); anlık hızların merkezi, noktalardan oluşturulan dik doğruların kesişme noktasında bulunur. A Ve İÇİNDE bu noktaların hızlarına (veya yörüngelere olan teğetlere).

2. Düz bir şekil üzerindeki herhangi bir noktanın hızını belirlemek için herhangi bir noktanın hızının büyüklüğünü ve yönünü bilmeniz gerekir. Aşekli ve diğer noktasının hızının yönü İÇİNDE. Daha sonra noktalardan geri yükleme A Ve İÇİNDE dik olarak Ve anlık hız merkezini oluşturalım R ve yöndeŞeklin dönme yönünü belirleyelim. Bundan sonra bilerek, hızı bulalımHerhangi bir nokta M düz figür. Yönlendirilmiş vektördik RMşeklin dönme yönünde.

3. Açısal hızDüz bir şeklin belirli bir anında şeklin herhangi bir noktasının hızının, anlık hız merkezine olan uzaklığına oranına eşittir. R :

Anlık hız merkezini belirlemenin bazı özel durumlarını ele alalım.

a) Düzlemsel paralel hareket, bir silindirik cismin diğer bir sabit cismin yüzeyi boyunca kaymadan yuvarlanması ile gerçekleştiriliyorsa, o zaman nokta R belirli bir anda sabit bir yüzeye temas eden yuvarlanan bir cismin (Şekil 7), kaymanın olmaması nedeniyle sıfıra eşit bir hıza sahiptir (), ve dolayısıyla hızların anlık merkezidir. Bir örnek, ray üzerinde yuvarlanan bir tekerlektir.

b) Noktaların hızları ise A Ve İÇİNDE Düz şekiller birbirine paraleldir ve çizgi AB dik değil(Şekil 8, a), o zaman anlık hızların merkezi sonsuzda yer alır ve tüm noktaların hızları paraleldir. Üstelik hız projeksiyonları teoreminden şu sonuç çıkıyor: yani. ; diğer tüm noktalar için de benzer bir sonuç elde edilir. Sonuç olarak, söz konusu durumda, şeklin tüm noktalarının belirli bir andaki hızları hem büyüklük hem de yön bakımından birbirine eşittir; şekil, hızların anlık öteleme dağılımına sahiptir (vücudun bu hareket durumuna aynı zamanda anlık öteleme de denir). Açısal hızŞu anda vücut görünüşe göre sıfıra eşit.

Şekil 7

Şekil 8

c) Noktaların hızları ise A Ve İÇİNDE düz şekiller birbirine paraleldir ve aynı zamanda çizgidir AB dik, daha sonra anlık hız merkezi RŞekil 8'de gösterilen yapı ile belirlenir, b. Yapıların adilliği orandan kaynaklanmaktadır. Bu durumda öncekilerden farklı olarak merkezi bulmak R Talimatlara ek olarak hız modüllerini de bilmeniz gerekir.

d) Hız vektörü biliniyorsabir nokta İÇİNDEşekil ve açısal hızı, daha sonra anlık hız merkezinin konumu R, dik olarak uzanan(Şekil 8, b), şu şekilde bulunabilir:.

Hızın belirlenmesi ile ilgili problemlerin çözümü.

Gerekli kinematik özellikleri (bir cismin açısal hızı veya noktalarının hızları) belirlemek için, herhangi bir noktanın hızının büyüklüğünü ve yönünü, diğer bir kesit noktasının hızının yönünü bilmek gerekir. bu vücut. Çözüm, problem verilerine dayanarak bu özelliklerin belirlenmesiyle başlamalıdır.

Hareketi incelenen mekanizma, çizimde ilgili özelliklerin belirlenmesinin gerekli olduğu konumda gösterilmelidir. Hesaplarken, anlık hız merkezi kavramının belirli bir katı cisim için geçerli olduğu unutulmamalıdır. Birkaç cisimden oluşan bir mekanizmada, her öteleme dışı hareket eden cisim, zamanın belirli bir anında kendi anlık hız merkezine sahiptir. R ve açısal hızı.

Örnek 1.Bobin şeklinde bir gövde, orta silindiri sabit bir düzlem boyunca yuvarlanacak şekilde yuvarlanır.(santimetre). Silindir yarıçapı:R= 4 kitle iletişim araçları R= 2 cm (Şek. 9). .

Şekil 9

Çözüm.Noktaların hızını belirleyelim A, B Ve İLE.

Anlık hızların merkezi, bobinin düzlemle temas ettiği noktada bulunur.

Hız direği İLE .

Bobin açısal hızı

Nokta hızları A Ve İÇİNDE Bu noktaları anlık hız merkezine bağlayan düz parçalara dik olarak yönlendirilir. Hızlar:

Örnek 2.Yarıçap tekerleği R= Yolun düz bir bölümü boyunca kaymadan 0,6 m yuvarlanma (Şekil 9.1); C merkezinin hızı sabit ve eşittirvc = 12 m/sn. Tekerleğin açısal hızını ve uçlarının hızını bulun M 1 , M 2 , M 3 , M 4 dikey ve yatay tekerlek çapı.

Şekil 9.1

Çözüm. Tekerlek düzlemsel paralel hareket gerçekleştirir. Tekerlek hızının anlık merkezi, yatay düzlemle temas noktası olan M1 noktasında bulunur;

Tekerlek açısal hızı

M2, M3 ve M4 noktalarının hızlarını bulun

Örnek3 . Yarıçaplı araba tahrik tekerleği R= Otoyolun düz bir bölümü boyunca kayan (kaymalı) 0,5 m yuvarlanma; merkezinin hızı İLE sabit ve eşittirvc = 4 m/sn. Tekerlek hızlarının anlık merkezi şu noktadadır: R mesafeli H = Dönen düzlemden 0,3 m uzakta. Tekerleğin açısal hızını ve noktaların hızını bulun A Ve İÇİNDE dikey çapı.

Şekil 9.2

Çözüm.Tekerlek açısal hızı

Noktaların hızlarını bulma A Ve İÇİNDE

Örnek 4.Biyel kolunun açısal hızını bulun AB ve noktaların hızı İÇİNDE ve krank mekanizmasının C'si (Şek. 9.3, A). Krankın açısal hızı verilir O.A. ve boyutları: ω OA = 2 sn -1, O.A. =AB = 0,36m, AC= 0,18 m.

A) B)

Şekil 9.3

Çözüm. Krank O.A.dönme hareketi yapar, biyel kolu AB- düzlem paralel hareket (Şekil 9.3, B).

Noktanın hızını bulma A bağlantı O.A.

Nokta hızı İÇİNDE yatay olarak yönlendirilir. Noktaların hızlarının yönünü bilmek A Ve İÇİNDE Bağlantı Çubuğu AB, anlık hız merkezi noktasının konumunu belirleyin RAV.

Bağlantı açısal hızı AB ve noktaların hızı İÇİNDE ve C:

Örnek 5.Çekirdek AB uçlarını karşılıklı dik düz çizgiler boyunca kaydırır, böylece bir açıyla hız (Şekil 10). Çubuk uzunluğu AB = ben. Sonun hızını belirleyelim A ve çubuğun açısal hızı.

Şekil 10

Çözüm.Bir noktanın hız vektörünün yönünü belirlemek zor değildir A dikey bir düz çizgi boyunca kayar. Daha sonradik doğruların kesişme noktasındadır ve (Şekil 10).

Açısal hız

Nokta hızı A :

Ve çubuğun merkezinin hızı İLEörneğin dikey olarak yönlendirilmiş eşittir:

Hız planı.

Bir cismin düz bir bölümünün çeşitli noktalarının hızlarının bilinmesine izin verin (Şekil 11). Bu hızlar belirli bir noktadan itibaren bir ölçekte çizilirse HAKKINDA ve uçlarını düz çizgilerle birleştirdiğinizde hız planı adı verilen bir resim elde edersiniz. (Resmin üzerinde) .

Şekil 11

Hız planı özellikleri.

a) Hız planındaki üçgenlerin kenarları diktir ilgili doğrudan vücut düzleminde.

Gerçekten mi, . Ama hız açısından. Araç Ve dik AB, Öyleyse.Tam olarak aynı.

b) Hız planının kenarları, vücut düzlemindeki karşılık gelen düz bölümlerle orantılıdır.

Çünkü, hız planının kenarlarının vücut düzlemindeki düz bölümlerle orantılı olduğu sonucu çıkar.

Bu özellikleri birleştirerek, hız planının karşılık gelen vücut şekline benzer olduğu ve ona göre dönme yönünde 90˚ döndürüldüğü sonucuna varabiliriz. Hız planının bu özellikleri, vücut noktalarının hızlarını grafiksel olarak belirlemenize olanak tanır.

Örnek 6.Şekil 12 ölçeklendirme mekanizmasını göstermektedir. Bilinen açısal hız bağlantı OA.

Şekil 12

Çözüm.Hız planının oluşturulabilmesi için bir noktanın hızının ve en azından diğer bir noktanın hız vektörünün yönünün bilinmesi gerekir. Örneğimizde noktanın hızını belirleyebiliriz. A : ve vektörünün yönü.

Şekil 13

(Şek. 13) noktasından kenara koyun. Ö derecelendirmekKaydırıcı hız vektörünün yönü bilinmektedir İÇİNDE– yatay. Hız planını noktadan itibaren çiziyoruz HAKKINDA doğrudanBENhız yönündenoktanın bulunması gereken yerBbu noktanın hızını belirleyen İÇİNDE. Hız planının kenarları mekanizmanın karşılık gelen bağlantılarına dik olduğundan, o zaman noktadan itibaren A dik olarak düz bir çizgi çizin AB düz çizgiyle kesişmeden önce BEN. Kesişme noktası noktayı belirleyecektirBve dolayısıyla noktanın hızı İÇİNDE : . Hız planının ikinci özelliğine göre kenarları bir mekanizmanın bağlantılarına benzer. Nokta İLE böler AB yarı yarıya yani İle paylaşmalı A Byarısında. Nokta İle Hız planında hızın büyüklüğünü ve yönünü belirleyecek(Eğer İle noktaya bağlan HAKKINDA).

Hız noktaları e sıfıra eşittir, yani nokta e hız planındaki nokta ile örtüşüyor HAKKINDA.

Sonraki olmalı. Ve . Bu çizgileri çizip kesişme noktalarını buluyoruzD.Çizgi segmenti Ö D hız vektörünü belirleyecek.

Örnek 7.Eklemli olarak dört bağlantılıOABC tahrik krankO.A.cm bir eksen etrafında düzgün bir şekilde döner HAKKINDA açısal hız ileω = 4 s -1 ve biyel kolu kullanma AB= 20 cm krankın dönmesine neden olur Güneş eksen etrafında İLE(Şekil 13.1, A). Noktaların hızını belirleme A Ve İÇİNDE, ve biyel kolunun açısal hızları AB ve krank Güneş.

A) B)

Şekil 13.1

Çözüm.Nokta hızı A krank O.A.

Bir noktaya değinmek A direğin arkasında bir vektör denklemi oluşturalım

Nerede

Bu denklemin grafiksel çözümü Şekil 13.1'de verilmiştir. ,B(hız planı).

Aldığımız hız planını kullanarak

Biyel kolunun açısal hızı AB

Nokta hızı İÇİNDE Vücudun iki noktasının hızlarının onları birleştiren düz çizgiye izdüşümleri üzerine teorem kullanılarak bulunabilir.

B ve krankın açısal hızı kuzeydoğu

Bir düzlem şeklinin noktalarının ivmelerinin belirlenmesi

Herhangi bir noktanın ivmesinin olduğunu gösterelim. M Düz bir şeklin hızı (ve hızı), bu şeklin öteleme ve dönme hareketleri sırasında noktanın aldığı ivmelerden oluşur. Nokta konumu M eksenlerle ilgili olarak HAKKINDA xy (bkz. Şekil 30) belirlenir yarıçap vektörü- vektör arasındaki açıve bir bölüm yüksek lisans(Şekil 14).

Böylece herhangi bir noktanın ivmesi M düz şekil geometrik olarak başka bir noktanın ivmesinden oluşur A kutup olarak alınan ve nokta olan ivme MŞeklin bu direğin etrafında döndürülmesiyle elde edilir. Modül ve ivmenin yönü, karşılık gelen paralelkenarın oluşturulmasıyla bulunur (Şekil 23).

Ancak hesaplama ve hızlanma bir nokta Aşu an bu rakam; 2) başka bir noktanın yörüngesi İÇİNDE rakamlar. Bazı durumlarda şeklin ikinci noktasının yörüngesi yerine anlık hız merkezinin konumunu bilmek yeterlidir.

Problemleri çözerken, gövde (veya mekanizma), ilgili noktanın ivmesinin belirlenmesinin gerekli olduğu konumda tasvir edilmelidir. Hesaplama, problem verilerine göre kutup olarak alınan noktanın hızının ve ivmesinin belirlenmesiyle başlar.

Çözüm planı (Düz bir şeklin bir noktasının hız ve ivmesi ile şeklin başka bir noktasının hız ve ivme yönü verilmişse):

1) Düz bir şeklin iki noktasının hızlarına dikler çizerek anlık hız merkezini bulun.

2) Şeklin anlık açısal hızını belirleyin.

3) Kutup çevresindeki bir noktanın merkezcil ivmesini, tüm ivme terimlerinin bilinen ivme yönüne dik eksen üzerindeki izdüşümlerinin toplamını sıfıra eşitleyerek belirleriz.

4) Tüm ivme terimlerinin bilinen ivme yönüne dik eksen üzerindeki izdüşümlerinin toplamını sıfıra eşitleyerek dönme ivmesinin modülünü bulun.

5) Bulunan dönme ivmesinden düz bir şeklin anlık açısal ivmesini belirleyin.

6) İvme dağılım formülünü kullanarak düz bir şekil üzerindeki bir noktanın ivmesini bulun.

Problemleri çözerken, “kesinlikle katı bir cismin iki noktasının ivme vektörlerinin izdüşümü üzerine teoremi” uygulayabilirsiniz:

“Düzlemsel paralel hareket gerçekleştiren mutlak rijit bir cismin iki noktasının, bu cismin hareket düzleminde belirli bir açıyla bu iki noktadan geçen düz çizgiye göre döndürülmüş bir düz çizgi üzerindeki ivme vektörlerinin izdüşümleriaçısal ivme yönünde eşittir.”

Bu teoremin, mutlak katı bir cismin yalnızca iki noktasının ivmesi hem büyüklük hem de yön olarak biliniyorsa, yalnızca bu cismin diğer noktalarının ivme vektörlerinin yönleri biliniyorsa (cismin geometrik boyutları) uygulanması uygundur. bilinmiyor), bilinmiyor Ve - buna göre, bu cismin açısal hız ve açısal ivme vektörlerinin hareket düzlemine dik eksene izdüşümleri, bu cismin noktalarının hızları bilinmemektedir.

Düz bir şeklin noktalarının ivmesini belirlemenin bilinen 3 yolu daha vardır:

1) Yöntem, mutlak katı bir cismin düzlemsel paralel hareket yasalarının zaman içinde iki kez farklılaşmasına dayanmaktadır.

2) Yöntem, mutlak katı bir cismin anlık ivme merkezinin kullanılmasına dayanmaktadır (mutlak katı bir cismin anlık ivme merkezi aşağıda tartışılacaktır).

3) Yöntem, kesinlikle katı bir cisim için bir ivme planının kullanılmasına dayanmaktadır.

Düzlem hareket denklemleri.

Ana teorem

Düz bir figürün kendi düzlemindeki hareketi iki hareketten oluşur: keyfi olarak seçilen bir nokta (kutup) boyunca öteleme ve bu kutbun etrafında dönme.

Düz bir şeklin bir düzlem üzerindeki konumu, seçilen direğin konumu ve bu direğin etrafındaki dönme açısı ile belirlenir, dolayısıyla düzlemin hareketi üç denklemle tanımlanır:

İlk iki denklem (Şekil 5), şu durumda şeklin yapacağı hareketi belirler: φ = sabit, figürün tüm noktalarının direk ile aynı şekilde hareket edeceği bu hareketin öteleme olacağı açıktır. A.

Üçüncü denklem, şeklin yapacağı hareketi belirler. x A = sabit Ve y A = sabit, onlar. direk ne zaman A hareketsiz olacak; bu hareket figürün direğin etrafında dönmesi olacaktır A.

Bu durumda dönme hareketi kutup seçimine bağlı değildir ve öteleme hareketi direğin hareketi ile karakterize edilir.

Bir düzlem şeklinin iki noktasının hızları arasındaki ilişki.

Bir düzlem şeklinin A ve B gibi iki noktasını düşünün. Nokta konumu İÇİNDE sabit koordinat sistemine göre Oxy yarıçap vektörü tarafından belirlenir r B (Şekil 5):

r B = r A + ρ,

Nerede r bir - bir noktanın yarıçap vektörü A, ρ = AB

bir noktanın konumunu tanımlayan vektör İÇİNDE

hareketli eksenlere göre Ah 1 ve 1, direk ile ötelemeli olarak hareket ediyor A sabit eksenlere paralel Ohoo.

Daha sonra noktanın hızı İÇİNDE eşit olacak

.

Ortaya çıkan eşitlikte miktar direğin hızıdır A.

Değer noktanın hızına eşittir İÇİNDE='a ulaşır yapı, onlar. eksenlere göre Ah 1 ve 1 bir figür bir direğin etrafında döndüğünde A. Bu hızın gösterimini tanıtalım:

Buradan,

İÇİNDE

Düz bir şeklin herhangi bir B noktasının hızı, seçilen A kutbunun V A hızı ile kutup etrafında dönme hareketi yapan noktanın VBA hızının geometrik toplamına eşittir. (Şekil 6):

Noktanın dönme hareketinin hızı segmente dik olarak yönlendirilir AB ve eşittir

B noktasının hızının büyüklüğü ve yönü, karşılık gelen paralelkenarın oluşturulmasıyla bulunur.(Şekil 6).

Örnek 1. C tekerleğinin merkezinin hızı V C'ye eşitse, düz bir ray üzerinde kaymadan yuvarlanan bir tekerleğin jantının A, B ve D noktalarının hızlarını bulun.

Çözüm. Direk için hızı bilinen C noktasını seçiyoruz. O zaman A noktasının hızı

nerede ve modulo.

ω açısal hızının değerini, noktanın olması koşulundan buluruz. R tekerlek ray üzerinde kaymıyor ve bu nedenle şu anda sıfırdır VP = 0.

Şu anda noktanın hızı R eşittir

O zamandan beri R hızlar ve karşıt taraflar tek bir düz çizgide yönlendirilir ve VP = 0, O VPC = VC, bunu nereden alıyoruz ω = V C . /R, buradan, V AC = ω R = V C .

Nokta hızı A modülleri eşit olan karşılıklı dik vektörler üzerine kurulmuş bir karenin köşegenidir, bu nedenle

D noktasının hızı da benzer şekilde belirlenir.

Bu durumda hızlar büyüklük bakımından eşit ve aynı doğru doğrultusundadır; dolayısıyla VB = 2VC .

Çekirdek AB Yer çekimi etkisi ve ağırlık merkezi etrafında dönme etkisi altında başlangıç ​​hızı olmadan düşme olarak temsil edilebilecek düzlemsel bir hareket gerçekleştirir. İLE sabit açısal hızla.

Bir noktanın hareket denklemlerini belirleme İÇİNDE, eğer ilk anda çubuk AB yataydı ve nokta İÇİNDE sağdaydı. Yerçekimi ivmesi Q. Çubuk uzunluğu 2 litre. Başlangıç ​​noktası konumu İLE Koordinatların orijini olarak alın ve koordinat eksenlerini şekilde gösterildiği gibi yönlendirin.

İlişkiler (2) ve (3)'e dayanarak, denklemler (1) şu şekli alacaktır:

Entegrasyonun gerçekleştirilmesi ve bunu ilk anda fark edilmesi t=0, x B =l Ve y B =0 noktanın koordinatlarını alıyoruz İÇİNDE aşağıdaki formda.

Düz bir şeklin hareketi, şeklin tüm noktalarının direğin hızında hareket ettiği öteleme hareketinden oluşur. A ve bu kutbun etrafındaki dönme hareketinden (Şekil 3.4). Herhangi bir noktanın hızı Mşekil geometrik olarak noktanın bu hareketlerin her birinde aldığı hızlardan oluşur.

Şekil 3.4

Aslında noktanın konumu M eksenlerle ilgili olarak Ahsen yarıçap tarafından belirlenir - vektör
, Nerede - direğin yarıçap vektörü A,=
- noktanın konumunu tanımlayan yarıçap vektörü M nispeten
, direkle birlikte hareket etmek A giderek. Daha sonra

.

direğin hızıdır A,hıza eşit
, hangi nokta Mşu saatte alır:
yani eksenlere göre
veya başka bir deyişle bir figür bir direğin etrafında döndüğünde A. Böylece şu sonuç çıkıyor

Nerede ω – şeklin açısal hızı.

Şekil 3.5

Böylece, Düz bir şeklin herhangi bir M noktasının hızı, kutup olarak alınan başka bir A noktasının hızı ile şekil bu kutup etrafında döndüğünde M noktasının aldığı hızın geometrik olarak toplamıdır. Modül ve hız yönü karşılık gelen paralelkenarın oluşturulmasıyla bulunur (Şekil 3.5).

10.3. Bir cisim üzerindeki iki noktanın hızlarının izdüşümü üzerine teorem

Düzlemsel bir şeklin (veya düzleme paralel hareket eden bir cismin) noktalarının hızlarını belirlemenin basit yollarından biri teoremdir: katı bir cismin iki noktasının hızlarının bu noktalardan geçen bir eksene izdüşümleri birbirine eşittir.

Şekil 3.6

Bazı iki noktayı ele alalım A Ve İÇİNDE düz şekil (veya gövde) (Şekil 3.6). Bir noktaya değinmek A direk için bunu alıyoruz
. Bu nedenle eşitliğin her iki tarafının da yönlendirilen eksene yansıtılması AB ve vektör verildiğinde
dik AB, bulduk

,

ve teorem kanıtlanmıştır. Bu sonucun tamamen fiziksel değerlendirmelerden de açıkça anlaşıldığına dikkat edin: eğer eşitlik
yerine getirilmeyecek, o zaman noktalar arasındaki mesafeyi hareket ettirirken A Ve İÇİNDE değişmesi gerekir ki bu imkansızdır; vücut kesinlikle sağlamdır. Dolayısıyla bu eşitlik yalnızca düzlemsel paralel hareket için değil aynı zamanda katı bir cismin herhangi bir hareketi için de geçerlidir.

10.4. Anlık hız merkezini kullanarak düzlemsel bir şekil üzerindeki noktaların hızlarını belirleme

Düz bir şeklin (veya düzlemsel hareket halindeki bir cismin) noktalarının hızlarını belirlemeye yönelik başka bir basit ve görsel yöntem, anlık hız merkezi kavramına dayanır.

Anlık hız merkezi (IVC), zamanın belirli bir anında hızı sıfır olan düz bir şeklin noktasıdır.

Bir şekil ilerici olmayan bir şekilde hareket ediyorsa, o zaman zamanın her anında böyle bir nokta T var ve üstelik tektir. Bir anda izin ver T puan A Ve İÇİNDEşeklin düzlemleri hızlara sahiptir Ve , birbirine paralel değildir (Şekil 3.7.). Sonra işaret et R, dik doğruların kesişme noktasında yer alan ah vektöre Ve İÇİNDEB vektöre ve hızların anlık merkezi olacaktır, çünkü
.

Şekil 3.7

Aslında eğer
, daha sonra hız projeksiyon teoremine göre vektör hem dik olmalı hem de AR(Çünkü
), Ve Sanal Gerçeklik(Çünkü
), ki bu imkansızdır. Aynı teoremden, şeklin başka hiçbir noktasının zamanın bu anında sıfıra eşit bir hıza sahip olamayacağı açıktır.

Eğer şimdi şu anda T bir noktaya değin R direğin arkasında. Daha sonra noktanın hızı A irade

,

Çünkü =0. Şeklin herhangi bir diğer noktası için de aynı sonuç elde edilir. Daha sonra, Düz bir şeklin noktalarının hızları, sanki şeklin hareketi anlık hız merkezi etrafında bir dönüşmüş gibi, zamanın belirli bir anında belirlenir. burada

( ); ( )

ve bu şekilde şeklin herhangi bir noktası için devam eder.

Bundan da şu sonuç çıkıyor
Ve
, Daha sonra

=,

onlar. Ne Düz bir şeklin noktalarının hızları, anlık hız merkezine olan mesafeleriyle orantılıdır.

Elde edilen sonuçlar aşağıdaki sonuçlara yol açmaktadır:

1. Hızların anlık merkezini belirlemek için yalnızca hızların yönlerini bilmeniz gerekir; örneğin,VeBir düzlem şeklinin A ve B gibi iki noktası.

2. Düz bir şeklin herhangi bir noktasının hızını belirlemek için, şeklin herhangi bir A noktasının hızının büyüklüğünü ve yönünü, diğer B noktasının hızının yönünü bilmeniz gerekir.

3. Açısal hızDüz bir şeklin hızı, zamanın her anında, şeklin herhangi bir noktasının hızının, P hızlarının anlık merkezine olan uzaklığına oranına eşittir:

.

için başka bir ifade bulalım ω eşitliklerden
Ve

bunu takip ediyor
Ve
, Neresi

.

Teorik mekaniği çözmeye yardımcı olacak MCS'yi tanımlamanın bazı özel durumlarını ele alalım.

1. Düzlemsel paralel hareket, bir silindirik cismin diğer bir sabit cismin yüzeyi boyunca kaymadan yuvarlanması ile gerçekleştiriliyorsa, o zaman nokta R Sabit bir yüzeye temas eden yuvarlanan bir cismin (Şekil 3.8), belirli bir anda, kaymanın olmaması nedeniyle sıfıra eşit bir hıza sahiptir (
) ve dolayısıyla hızların anlık merkezidir.

Şekil 3.8

2. Noktaların hızı A Ve İÇİNDE Düz şekiller birbirine paraleldir ve çizgi AB dik değil (Şekil 3.9, a), o zaman anlık hızların merkezi sonsuza uzanır ve tüm noktaların hızları // . Üstelik hız projeksiyonları teoreminden şu sonuç çıkıyor:
yani
, bu durumda şekil anlık bir öteleme hareketine sahiptir.

3. Hız noktaları varsa A Ve İÇİNDE düz şekil // birbirine ve aynı zamanda bir çizgiye AB dik , daha sonra anlık hız merkezi R yapıya göre belirlenir (Şekil 3.9,b).

Şekil 3.9

Yapının geçerliliği şu şekildedir:
. Bu durumda öncekilerden farklı olarak merkezi bulmak R Talimatlara ek olarak hız modüllerini de bilmeniz gerekir Ve .

4. Hız vektörü biliniyorsa bir nokta İÇİNDEşekil ve açısal hızı ω , daha sonra anlık hız merkezinin konumu R, dik olarak uzanan (bkz. Şekil?), eşitlikten bulunabilir
hangi verir
.