Üstel veya üstel olarak. Geometrik ilerleme. Örneklerle kapsamlı rehber (2020). Neden geometrik bir ilerlemeye ve onun tarihine ihtiyacımız var?

Bir dizi düşünelim.

7 28 112 448 1792...

Öğelerinden herhangi birinin değerinin bir öncekinden tam olarak dört kat daha fazla olduğu kesinlikle açıktır. Yani bu seri bir ilerlemedir.

Geometrik bir ilerleme, ana özelliği, bir sonraki sayının bir öncekinden belirli bir sayı ile çarpılarak elde edilmesi olan sonsuz bir sayı dizisidir. Bu, aşağıdaki formülle ifade edilir.

a z +1 =a z q, burada z, seçilen öğenin sayısıdır.

Buna göre, z ∈ N.

Okulda geometrik bir dizinin çalışıldığı dönem 9. sınıftır. Örnekler, kavramı anlamanıza yardımcı olacaktır:

0.25 0.125 0.0625...

Bu formüle dayanarak, ilerlemenin paydası aşağıdaki gibi bulunabilir:

Ne q ne de b z sıfır olamaz. Ayrıca, ilerlemenin öğelerinin her biri sıfıra eşit olmamalıdır.

Buna göre dizideki bir sonraki sayıyı bulmak için son sayıyı q ile çarpmanız gerekir.

Bu ilerlemeyi belirtmek için, ilk öğesini ve paydasını belirtmeniz gerekir. Bundan sonra, sonraki terimlerden herhangi birini ve toplamlarını bulmak mümkündür.

Çeşitler

q ve a 1'e bağlı olarak, bu ilerleme birkaç türe ayrılır:

• Hem a 1 hem de q birden büyükse, böyle bir dizi sonraki her elemanla artan geometrik bir dizidir. Bunun bir örneği aşağıda sunulmuştur.

Örnek: a 1 =3, q=2 - her iki parametre de birden büyüktür.

Daha sonra sayısal dizi şu şekilde yazılabilir:

3 6 12 24 48 ...

• eğer |q| birden az, yani onunla çarpma bölmeye eşdeğerdir, o zaman benzer koşullara sahip bir dizi, azalan bir geometrik dizidir. Bunun bir örneği aşağıda sunulmuştur.

Örnek: a 1 =6, q=1/3 - a 1 birden büyüktür, q küçüktür.

O zaman sayısal dizi aşağıdaki gibi yazılabilir:

6 2 2/3 ... - herhangi bir eleman, onu takip eden elemandan 3 kat daha büyüktür.

• İşaret değişkeni. eğer q<0, то знаки у чисел последовательности постоянно чередуются вне зависимости от a 1 , а элементы ни возрастают, ни убывают.

Örnek: a 1 = -3 , q = -2 - her iki parametre de sıfırdan küçüktür.

O zaman dizi şu şekilde yazılabilir:

3, 6, -12, 24,...

formüller

Geometrik ilerlemelerin rahat kullanımı için birçok formül vardır:

• z'inci üyenin formülü. Önceki sayıları hesaplamadan belirli bir sayının altındaki öğeyi hesaplamanıza olanak tanır.

Örnek:Q = 3, A 1 = 4. Dizinin dördüncü elemanının hesaplanması gerekmektedir.

Çözüm:A 4 = 4 · 3 4-1 = 4 · 3 3 = 4 · 27 = 108.

• sayısı olan ilk elemanların toplamı z. Bir dizinin tüm öğelerinin toplamını hesaplamanıza izin verir.bir zdahil.

beri (1-Q) paydada ise (1 - q)≠ 0, dolayısıyla q 1'e eşit değildir.

Not: q=1 ise, ilerleme sonsuz tekrar eden bir sayı dizisi olacaktır.

Geometrik ilerlemenin toplamı, örnekler:A 1 = 2, Q= -2. S5'i hesaplayın.

Çözüm:S 5 = 22 - formüle göre hesaplama.

• tutar eğer |Q| < 1 и если z стремится к бесконечности.

Örnek:A 1 = 2 , Q= 0.5 Miktarı bulun.

Çözüm:Sz = 2 · = 4

Sz = 2 + 1 + 0.5 + 0.25 + 0.125 + 0.0625 = 3.9375 4

Bazı özellikler:

• karakteristik özellik. Aşağıdaki koşul ise herhangi biri için gerçekleştirilenz, o zaman verilen sayı serisi geometrik bir ilerlemedir:

bir z 2 = bir z -1 · Az+1

• Ayrıca, herhangi bir sayıdaki geometrik dizinin karesi, bu elemandan eşit uzaklıktalarsa, belirli bir dizideki diğer iki sayının kareleri toplanarak bulunur.

bir z 2 = bir z - T 2 + bir z + T 2 , NeredeTbu sayılar arasındaki mesafedir.

• Elementlerq'da farklılıkbir kere.
• İlerleme öğelerinin logaritmaları da bir ilerleme oluşturur, ancak zaten aritmetiktir, yani her biri bir öncekinden belirli bir sayı daha fazladır.

Bazı klasik problemlere örnekler

Geometrik ilerlemenin ne olduğunu daha iyi anlamak için 9. sınıf için çözümlü örnekler yardımcı olabilir.

• Koşullar:A 1 = 3, A 3 = 48. BulQ.

Çözüm: Sonraki her eleman bir öncekinden daha büyüktür.Q bir kere.Bir payda kullanarak bazı unsurları diğerleri aracılığıyla ifade etmek gerekir.

Buradan,A 3 = Q 2 · A 1

ikame ederkenQ= 4

• Koşullar:A 2 = 6, A 3 = 12. S 6'yı hesaplayın.

Çözüm:Bunun için ilk eleman olan q'yu bulup formülde yerine koymak yeterlidir.

A 3 = Q· A 2 , buradan,Q= 2

bir 2 = q bir 1 ,Bu yüzden bir 1 = 3

Ö 6 = 189

• · A 1 = 10, Q= -2. İlerlemenin dördüncü öğesini bulun.

Çözüm: Bunu yapmak için dördüncü öğeyi birinci ve payda üzerinden ifade etmek yeterlidir.

bir 4 = q 3· 1 = -80

Uygulama örneği:

• Bankanın müşterisi 10.000 ruble tutarında bir depozito yatırdı ve bu şartlara göre müşteri her yıl bunun% 6'sını anapara miktarına ekleyecek. 4 yıl sonra hesapta ne kadar para olur?

Çözüm: İlk miktar 10 bin ruble. Yani, yatırımdan bir yıl sonra, hesap 10.000 + 10.000'e eşit bir tutara sahip olacaktır. · 0,06 = 10000 1,06

Buna göre bir yıl sonra hesaptaki tutar aşağıdaki gibi ifade edilecektir:

(10000 1,06) 0,06 + 10000 1,06 = 1,06 1,06 10000

Yani her yıl miktar 1,06 kat artıyor. Bu, 4 yıl sonra hesaptaki fon miktarını bulmak için, ilk öğenin 10 bine eşit olduğu ve paydanın 1,06'ya eşit olduğu ilerlemenin dördüncü öğesini bulmak için yeterli olduğu anlamına gelir.

S = 1,06 1,06 1,06 1,06 10000 = 12625

Toplamı hesaplamak için görev örnekleri:

Çeşitli problemlerde geometrik ilerleme kullanılır. Toplamı bulmak için bir örnek şu şekilde verilebilir:

A 1 = 4, Q= 2, hesaplaS5.

Çözüm: Hesaplama için gerekli tüm veriler biliniyor, bunları formülde yerine koymanız yeterli.

S 5 = 124

• A 2 = 6, A 3 = 18. İlk altı elemanın toplamını hesaplayın.

Çözüm:

Geom. ilerleme, sonraki her öğe bir öncekinden q kat daha büyüktür, yani toplamı hesaplamak için öğeyi bilmeniz gerekirA 1 ve paydaQ.

A 2 · Q = A 3

Q = 3

Benzer şekilde, bulmamız gerekiyorA 1 , bilmekA 2 VeQ.

A 1 · Q = A 2

bir 1 =2

S 6 = 728.

ilgili ders “Sonsuz azalan geometrik ilerleme”

Dersin amacı:öğrencileri yeni bir dizi dizisiyle tanıştırmak - sonsuz azalan bir geometrik ilerleme.

Görevler:

sayısal dizinin limitinin ilk fikrinin formülasyonu; sonsuz azalan geometrik ilerlemenin toplamı formülünü kullanarak sonsuz periyodik kesirleri sıradan kesirlere dönüştürmenin başka bir yolunu tanıma;

mantıksal düşünme, değerlendirme eylemleri yeteneği, genelleme gibi okul çocuklarının kişiliğinin entelektüel niteliklerinin gelişimi;

faaliyet eğitimi, karşılıklı yardımlaşma, kolektivizm, konuya ilgi.

Teçhizat: bilgisayar sınıfı, projektör, perde.

ders türü: Ders - yeni bir konuya hakim olmak.

dersler sırasında

BEN . Org. an. Dersin konusu ve amacı hakkında mesaj.

III . Öğrencilerin bilgilerini güncellemek.1. Ödevi kontrol etmek.

1) Aritmetik ve geometrik ilerlemelerle ilgili temel formüllerin doğrulanması. İki öğrenci tahtaya formüller yazar.

2) Öğrencilerin geri kalanı "Toplam Formülleri" konulu matematiksel dikte.

Görevler:

№1. Bir aritmetik dizinin ilk üyesi 6 (1. seçenek), -20 (2. seçenek) ve beşinci üye -6 (1. seçenek), 20 (2. seçenek) ise, ilk beş üyesinin toplamını bulun.

№2. Bir aritmetik dizinin ilk terimi -20(1. seçenek), 6(2. seçenek) ve fark 10(1. seçenek), -3(2. seçenek) ise ilk beş teriminin toplamını bulun.

№3. İlk terimi 1(1. seçenek), -1 (2. seçenek) ve paydası -2(1. seçenek), 2(2. seçenek) olan bir geometrik dizinin ilk beş teriminin toplamını bulun.

Dikte sonunda seçmeli olarak iki öğrencinin çalışmaları değerlendirme için kontrol edilir, geri kalanlar tahtanın yakalarına yazılan hazır çözümlere göre kendi kendini inceler.

Çözümler:

Görevler

1. Aritmetik ilerleme formülle verilir A N = 7 – 4 N. Bulmak A 10 . (-33)

2. Aritmetik ilerleme A 3 = 7 Ve A 5 = 1 . Bulmak A 4 . (4)

3. Aritmetik ilerleme A 3 = 7 Ve A 5 = 1 . Bulmak A 17 . (-35)

4. Aritmetik ilerleme A 3 = 7 Ve A 5 = 1 . Bulmak S 17 . (-187)

5. Geometrik ilerleme için
beşinci terimi bulunuz.

6. Geometrik ilerleme için
bulmak N-inci üye.

7. Katlanarak B 3 = 8 Ve B 5 = 2 . Bulmak B 4 . (4)

8. Katlanarak B 3 = 8 Ve B 5 = 2 . Bulmak B 1 Ve Q .

9. Katlanarak B 3 = 8 Ve B 5 = 2 . Bulmak S 5 . (62)

III . Yeni bir konu keşfetmek(gösteri sunumu).

Bir kenarı 1'e eşit olan bir kareyi ele alalım. Bir kenarı birinci karenin yarısı olan başka bir kare çizelim, sonra bir kenarı saniyenin yarısı olan başka bir kare çizelim, sonra bir sonraki kareyi çizelim. Her seferinde yeni karenin kenarı bir öncekinin yarısı kadardır.

Sonuç olarak, karelerin bir kenar dizisini elde ettik. payda ile geometrik bir dizi oluşturma.

Ve çok önemli olan, bu tür kareleri ne kadar çok inşa edersek, karenin kenarı o kadar küçük olacaktır. Örneğin,

Onlar. n sayısı arttıkça ilerleme terimleri sıfıra yaklaşır.

Bu şekil yardımıyla bir dizi daha düşünülebilir.

Örneğin, karelerin alanlarının sırası:

. Ve yine, eğer N süresiz olarak artar, sonra alan keyfi olarak sıfıra yaklaşır.

Bir örnek daha ele alalım. Bir kenarı 1 cm olan eşkenar üçgen. Üçgen orta çizgi teoremine göre, köşeleri 1. üçgenin kenarlarının orta noktalarında olacak şekilde bir sonraki üçgeni oluşturalım - 2.'nin kenarı birincinin kenarının yarısına eşittir, 3.'ün kenarı da 2. vb. Yine üçgenlerin kenar uzunluklarının bir dizisini elde ederiz.

de
.

Negatif paydalı geometrik bir ilerlemeyi düşünürsek.

Sonra yine artan sayılarla Nİlerleme koşulları sıfıra yaklaşıyor.

Bu dizilerin paydalarına dikkat edelim. Her yerde paydalar 1 modulodan azdı.

Şu sonuca varabiliriz: paydasının modülü 1'den küçükse, geometrik bir ilerleme sonsuz azalacaktır.

Ön çalışma.

Tanım:

Paydasının modülü birden küçükse, bir geometrik ilerlemenin sonsuz azalan olduğu söylenir.
.

Tanım yardımıyla, bir geometrik dizinin sonsuz azalıp azalmadığı sorusunu çözmek mümkündür.

Görev

Aşağıdaki formülle verilirse, dizi sonsuz azalan bir geometrik ilerleme midir?

;
.

Çözüm:

. Bulalım Q .

;
;
;
.

bu geometrik ilerleme sonsuz bir şekilde azalmaktadır.

B) bu dizi sonsuz azalan bir geometrik dizi değildir.

Bir kenarı 1'e eşit olan bir kare düşünün. Onu ikiye bölün, yarılardan biri tekrar ikiye bölün ve böyle devam edin. ortaya çıkan tüm dikdörtgenlerin alanları, sonsuz azalan bir geometrik ilerleme oluşturur:

Bu şekilde elde edilen tüm dikdörtgenlerin alanlarının toplamı 1.karenin alanına eşit olacak ve 1'e eşit olacaktır.

Ama bu eşitliğin sol tarafında sonsuz sayıda terimin toplamı var.

İlk n terimin toplamını düşünün.

Bir geometrik dizinin ilk n teriminin toplamı formülüne göre, şuna eşittir: .

Eğer N süresiz olarak artar, o zaman

veya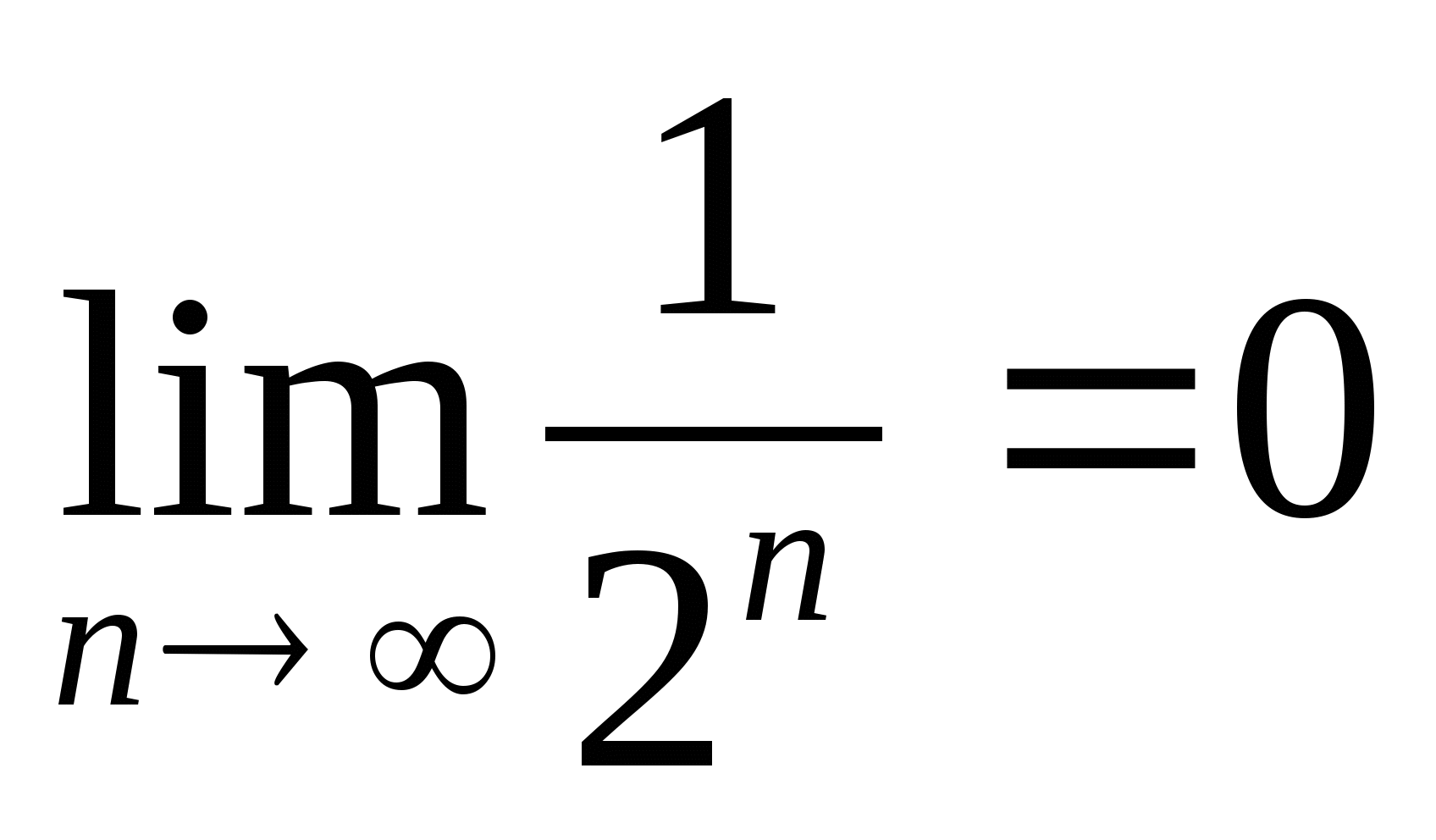
. Bu yüzden
, yani
.

Sonsuz azalan geometrik ilerlemenin toplamı sıralama sınırı var S 1 , S 2 , S 3 , …, S N , … .

Örneğin, bir ilerleme için
,

Çünkü

Sonsuz azalan geometrik ilerlemenin toplamı formül kullanılarak bulunabilir
.

III . Yansıma ve Konsolidasyon(görevlerin tamamlanması).

Görev numarası 2. Birinci terim 3, ikinci terim 0,3 ile sonsuz azalan geometrik ilerlemenin toplamını bulun.

Çözüm:

Görev numarası 3. ders kitabı, s. 160, sayı 433(1)

Sonsuz azalan bir geometrik ilerlemenin toplamını bulun:

Çözüm:

Görev numarası 4. Sonsuz periyodik ondalık kesri 0,(5) ortak bir kesir olarak yazın.

1. yol x = 0, (5) = 0,555 ... / 10 2. yöntem olsun. 0,(5)=0,555…=

Görev numarası 5. ders kitabı, s. 162, No. 445(3) (bağımsız karar)

Sonsuz periyodik ondalık kesir 0,(12)'yi ortak bir kesir olarak yazın.

Cevap: 0,(12)=4/33.

IV . Özetleme.

Bugün hangi sırayla tanıştınız?

Sonsuz azalan bir geometrik ilerleme tanımlayın.

Geometrik bir ilerlemenin sonsuza kadar azaldığı nasıl kanıtlanır?

Sonsuz azalan bir geometrik ilerlemenin toplamı için formülü verin.

V . Ev ödevi.

Geometrik ilerleme, ilk terimi sıfır olmayan ve sonraki her terim önceki terimin sıfır olmayan aynı sayı ile çarpımına eşit olan sayısal bir dizidir. Geometrik ilerleme b1,b2,b3, …, bn, … ile gösterilir.

Geometrik ilerlemenin özellikleri

Geometrik hatanın herhangi bir teriminin önceki terimine oranı aynı sayıya eşittir, yani b2/b1 = b3/b2 = b4/b3 = … = bn/b(n-1) = b(n+ 1)/bn = …. Bu, doğrudan bir aritmetik ilerlemenin tanımından kaynaklanır. Bu sayıya geometrik ilerlemenin paydası denir. Genellikle geometrik bir ilerlemenin paydası q harfi ile gösterilir.

Bir geometrik ilerleme belirlemenin bir yolu, ilk terimini b1 ve geometrik hata q'nun paydasını ayarlamaktır. Örneğin, b1=4, q=-2. Bu iki koşul 4, -8, 16, -32, … şeklinde bir geometrik dizi verir.

q>0 ise (q 1'e eşit değildir), o zaman ilerleme monoton bir dizidir. Örneğin, 2, 4,8,16,32, ... dizisi monoton artan bir dizidir (b1=2, q=2).

Geometrik hatada payda q=1 ise, geometrik dizinin tüm üyeleri birbirine eşit olacaktır. Bu gibi durumlarda, ilerlemenin sabit bir dizi olduğu söylenir.

İlerlemenin n'inci üyesinin formülü

Sayısal dizinin (bn) geometrik bir ilerleme olması için, ikinciden başlayarak her bir üyesinin, komşu üyelerin geometrik ortalaması olması gerekir. Yani, n'nin N doğal sayılar kümesine ait olduğu herhangi bir n>0 için (b(n+1))^2 = bn * b(n+2) denklemini yerine getirmek gerekir.

Bir geometrik dizinin n'inci üyesi için formül şöyledir:

bn=b1*q^(n-1), burada n, N doğal sayılar kümesine aittir.

Basit bir örnek düşünün:

Geometrik dizide b1=6, q=3, n=8 bn'yi bulun.

Bir geometrik dizinin n'inci üyesinin formülünü kullanalım.

Geometrik ilerleme, tanımamız gereken yeni bir tür sayı dizisidir. Başarılı bir tanışma için en azından bilmek ve anlamaktan zarar gelmez. O zaman geometrik ilerlemede sorun olmaz.)

Geometrik ilerleme nedir? Geometrik ilerleme kavramı.

Tura her zamanki gibi temel ile başlıyoruz. Bitmemiş bir sayı dizisi yazıyorum:

1, 10, 100, 1000, 10000, …

Bir örüntü yakalayıp bir sonraki sayının hangisi olacağını söyleyebilir misiniz? Biber temiz, 100000, 1000000 ve benzeri sayılar daha da ileri gidecek. Çok fazla zihinsel stres olmadan bile, her şey açık, değil mi?)

TAMAM. Başka bir örnek. Aşağıdaki sırayı yazıyorum:

1, 2, 4, 8, 16, …

16 numara ve isimden sonra hangi numaraların geleceğini söyleyebilir misiniz? sekizinci sıra üyesi? 128 rakamı olacağını anladıysanız, o zaman çok iyi. Yani, savaşın yarısı anlayışta Anlam Ve anahtar noktaları Geometrik ilerleme zaten yapıldı. Daha da büyüyebilirsin.)

Ve şimdi tekrar duyumlardan titiz matematiğe dönüyoruz.

Geometrik bir ilerlemenin kilit anları.

Anahtar an #1

Geometrik ilerleme sayı dizisi.İlerleme gibi. Zor bir şey yok. Bu diziyi yeni düzenledim farklı. Bu nedenle, elbette, başka bir adı var, evet ...

Anahtar an #2

İkinci kilit nokta ile, soru daha yanıltıcı olacaktır. Biraz geriye gidelim ve aritmetik ilerlemenin temel özelliğini hatırlayalım. İşte burada: her üye bir öncekinden farklıdır aynı miktarda.

Geometrik bir ilerleme için benzer bir anahtar özelliği formüle etmek mümkün mü? Biraz düşünün... Verilen örneklere bir bakın. Tahmin mi ettin? Evet! Geometrik bir ilerlemede (herhangi biri!), üyelerinin her biri bir öncekinden farklıdır aynı sayıda. Her zaman!

İlk örnekte bu sayı ondur. Dizinin hangi terimini alırsanız alın bir öncekinden büyüktür on kere.

İkinci örnekte, bu bir ikidir: her üye bir öncekinden daha büyüktür. iki kere.

Geometrik ilerlemenin aritmetik olandan farkı işte bu kilit noktadadır. Aritmetik ilerlemede, sonraki her terim elde edilir eklemeönceki terimle aynı değerdedir. Ve burada - çarpma işlemiönceki dönem aynı miktarda. Fark bu.)

Anahtar an #3

Bu kilit nokta, bir aritmetik ilerleme için olanla tamamen aynıdır. Yani: geometrik ilerlemenin her üyesi kendi yerindedir. Her şey aritmetik ilerlemede olduğu gibi tamamen aynı ve bence yorumlar gereksiz. Birinci terim var, yüz birinci terim var, vb. En az iki üyeyi yeniden düzenleyelim - desen (ve onunla birlikte geometrik ilerleme) kaybolacaktır. Geriye mantıksız bir sayı dizisi kalıyor.

Bu kadar. Geometrik ilerlemenin tüm amacı budur.

Terimler ve atamalar.

Ve şimdi, geometrik ilerlemenin anlamını ve kilit noktalarını ele aldıktan sonra, teoriye geçebiliriz. Aksi takdirde, anlamını anlamadan bir teori nedir, değil mi?

Geometrik ilerleme nedir?

Genel anlamda bir geometrik ilerleme nasıl yazılır? Sorun değil! İlerlemenin her üyesi ayrıca bir harf olarak yazılır. Yalnızca aritmetik ilerleme için harf genellikle kullanılır "A", geometrik - harf için "B". Üye numarası, her zamanki gibi, belirtilir sağ alt dizin. İlerlemenin üyeleri, basitçe virgül veya noktalı virgülle ayrılmış olarak listelenir.

Bunun gibi:

b1,B 2 , B 3 , B 4 , B 5 , B 6 , …

Kısaca, böyle bir ilerleme aşağıdaki gibi yazılır: (bn) .

Veya bunun gibi, sonlu ilerlemeler için:

b1 , b2 , b3 , b4 , b5 , b6 .

b 1 , b 2 , ..., b 29 , b 30 .

Veya kısaca:

(bn), N=30 .

Aslında, tüm atamalar budur. Her şey aynı, sadece harf farklı, evet.) Ve şimdi doğrudan tanıma geçiyoruz.

Geometrik ilerlemenin tanımı.

Geometrik ilerleme, ilk terimi sıfır olmayan ve sonraki her terim önceki terimin sıfır olmayan aynı sayı ile çarpımına eşit olan sayısal bir dizidir.

Bütün tanım bu. Kelimelerin ve ifadelerin çoğu açık ve size tanıdık geliyor. Tabii "parmaklarda" ve genel olarak geometrik bir ilerlemenin anlamını anlamadığınız sürece. Ancak özellikle dikkat çekmek istediğim birkaç yeni kelime öbeği de var.

İlk olarak, kelimeler: "ilk dönem olan sıfırdan farklı".

İlk dönem üzerindeki bu kısıtlama tesadüfen getirilmemiştir. İlk dönem olursa ne olur sizce? B 1 sıfır mı çıkıyor Her terim bir öncekinden büyükse ikinci terim ne olur? aynı sayıda mı?Üç kez diyelim mi? Bakalım... İlk terimi (yani 0) 3 ile çarpın ve... sıfır elde edin! Ve üçüncü üye? Sıfır da! Ve dördüncü terim de sıfır! Ve benzeri…

Sadece bir torba simit alıyoruz, bir dizi sıfır:

0, 0, 0, 0, …

Tabii ki, böyle bir sekansın yaşam hakkı vardır, ancak pratikte hiçbir önemi yoktur. Her şey çok açık. Üyelerinden herhangi biri sıfırdır. Herhangi bir sayıda üyenin toplamı da sıfırdır ... Bununla ne gibi ilginç şeyler yapabilirsiniz? Hiç bir şey…

Aşağıdaki anahtar kelimeler: "sıfır olmayan aynı sayı ile çarpılır".

Aynı numaranın kendi özel adı da vardır - geometrik ilerlemenin paydası. Çıkmaya başlayalım.)

Geometrik ilerlemenin paydası.

Her şey basit.

Geometrik ilerlemenin paydası, sıfır olmayan bir sayıdır (veya değerdir). kaç seferilerlemenin her üyesi öncekinden daha fazla.

Yine aritmetik diziye benzeterek bu tanımda dikkat edilmesi gereken anahtar kelime kelimedir. "Daha". Bu, bir geometrik ilerlemenin her teriminin elde edildiği anlamına gelir. çarpma işlemi tam da bu paydaya önceki üye

Açıklarım.

Hesaplamak için diyelim ikinci alınacak üye Birinciüye ve çarpmak paydaya kadar. hesaplama için onuncu alınacak üye dokuzuncuüye ve çarpmak paydaya kadar.

Geometrik ilerlemenin kendisinin paydası herhangi bir şey olabilir. Kesinlikle herkes! Tamsayı, kesirli, pozitif, negatif, irrasyonel - herkes. Sıfır hariç. Tanımdaki "sıfır olmayan" kelimesinin bize anlattığı şey budur. Bu kelimeye neden burada ihtiyaç duyulduğu - daha sonra daha fazlası.

Geometrik ilerlemenin paydası genellikle bir harfle gösterilir Q.

Bunu nasıl bulabilirim Q? Sorun değil! İlerlemenin herhangi bir dönemini almalıyız ve önceki terime bölmek. Bölüm kesir. Dolayısıyla adı - "ilerlemenin paydası". Payda, genellikle bir kesirde bulunur, evet ...) Her ne kadar mantıksal olarak değer Qçağrılmalı özel geometrik ilerleme, benzer fark aritmetik ilerleme için. Ama aramayı kabul etti payda. Tekerleği de yeniden icat etmeyeceğiz.)

Örneğin, değeri tanımlayalım Q bu geometrik ilerleme için:

2, 6, 18, 54, …

Her şey basit. biz alırız herhangi Sıra numarası. Ne istiyorsak onu alıyoruz. İlki hariç. Örneğin, 18. Ve şuna bölün: önceki numara. Yani, 6'da.

Biz:

Q = 18/6 = 3

Bu kadar. Bu doğru cevap. Belirli bir geometrik ilerleme için payda üçtür.

paydayı bulalım Q başka bir geometrik ilerleme için. Örneğin, bunun gibi:

1, -2, 4, -8, 16, …

Hepsi aynı. Üyelerin sahip oldukları işaretler ne olursa olsun, biz hala alıyoruz herhangi sıra numarası (örneğin, 16) ve şuna bölün: önceki numara(yani -8).

Biz:

D = 16/(-8) = -2

Ve bu kadar.) Bu sefer ilerlemenin paydası negatif çıktı. Eksi iki. Olur.)

Bu ilerlemeyi ele alalım:

1, 1/3, 1/9, 1/27, …

Ve yine, dizideki sayıların türünden bağımsız olarak (çift tamsayılar, hatta kesirli, hatta negatif, hatta irrasyonel), herhangi bir sayıyı (örneğin, 1/9) alır ve bir önceki sayıya (1/3) böleriz. Elbette kesirler ile işlem kurallarına göre.

Biz:

Hepsi bu kadar.) Burada paydanın kesirli olduğu ortaya çıktı: Q = 1/3.

Ama senin gibi bir "ilerleme"?

3, 3, 3, 3, 3, …

Açıkçası burada Q = 1 . Resmi olarak, bu aynı zamanda geometrik bir ilerlemedir, yalnızca aynı üyeler.) Ancak bu tür ilerlemeler, çalışma ve pratik uygulama için ilginç değildir. Tıpkı katı sıfırlı ilerlemeler gibi. Bu nedenle, onları dikkate almayacağız.

Gördüğünüz gibi, ilerlemenin paydası herhangi bir şey olabilir - tamsayı, kesirli, pozitif, negatif - herhangi bir şey! Sadece sıfır olamaz. Nedenini tahmin edemedin mi?

Pekala, belirli bir örneğe bakalım, payda olarak alırsak ne olur? Q sıfır.) Örneğin, B 1 = 2 , A Q = 0 . O zaman ikinci dönem ne olacak?

İnanıyoruz:

B 2 = B 1 · Q= 2 0 = 0

Ve üçüncü üye?

B 3 = B 2 · Q= 0 0 = 0

Geometrik dizilerin türleri ve davranışları.

Her şey az ya da çok açıktı: eğer ilerlemedeki fark D olumlu, ilerleme artıyor. Fark negatifse, ilerleme azalır. Sadece iki seçenek var. Üçüncüsü yok.)

Ancak geometrik bir ilerlemenin davranışıyla her şey çok daha ilginç ve çeşitli olacak!)

Üyeler burada davranır davranmaz: artarlar ve azalırlar ve süresiz olarak sıfıra yaklaşırlar ve hatta dönüşümlü olarak "artı" veya "eksi" ye koşarak işaretleri değiştirirler! Ve bütün bu çeşitlilik içinde insan iyi anlayabilmeli, evet...

Anladık mı?) En basit durumla başlayalım.

Payda pozitiftir ( Q >0)

Pozitif bir payda ile, ilk olarak, bir geometrik ilerlemenin üyeleri artı sonsuzluk(yani süresiz olarak artar) ve içine girebilir eksi sonsuzluk(yani süresiz olarak azaltın). İlerlemelerin bu tür davranışlarına zaten alıştık.

Örneğin:

(bn): 1, 2, 4, 8, 16, …

Burada her şey basit. İlerlemenin her üyesi öncekinden daha fazla. Ve her üye alır çarpma işlemiönceki üye pozitif+2 sayısı (yani Q = 2 ). Böyle bir ilerlemenin davranışı açıktır: ilerlemenin tüm üyeleri uzaya girerek süresiz olarak büyür. artı sonsuzluk...

Şimdi ilerleme şöyle:

(bn): -1, -2, -4, -8, -16, …

Burada da ilerlemenin her terimi elde edilir. çarpma işlemiönceki üye pozitif+2 numara. Ancak böyle bir ilerlemenin davranışı zaten tam tersidir: ilerlemenin her üyesi elde edilir öncekinden daha az ve tüm terimleri sonsuza kadar azalarak eksi sonsuza gider.

Şimdi düşünelim: Bu iki ilerlemenin ortak noktası nedir? Bu doğru, payda! Burada ve orada Q = +2 . Pozitif sayı. ikili. Ve burada davranış Bu iki ilerleme temelde farklıdır! Nedenini tahmin edemedin mi? Evet! Her şey hakkında ilk üye! Müziği sipariş eden, dedikleri gibi.) Kendiniz görün.

İlk durumda, ilerlemenin ilk terimi pozitif(+1) ve dolayısıyla, ile çarpılarak elde edilen sonraki tüm terimler pozitif payda Q = +2 , Ayrıca olacak pozitif.

Ancak ikinci durumda, birinci terim olumsuz(-1). Bu nedenle, ile çarpılarak elde edilen ilerlemenin sonraki tüm üyeleri pozitif Q = +2 , ayrıca elde edilecek olumsuz."Eksi" için "artı" her zaman "eksi" verir, evet.)

Gördüğünüz gibi, aritmetik bir diziden farklı olarak, geometrik bir dizi tamamen farklı şekillerde davranabilir; paydadanQ, ama aynı zamanda bağlı olarak ilk üyeden, Evet.)

Unutmayın: Bir geometrik ilerlemenin davranışı, ilk üyesi tarafından benzersiz bir şekilde belirlenir. B 1 ve paydaQ .

Ve şimdi daha az tanıdık ama çok daha ilginç vakaların analizine başlıyoruz!

Örneğin, aşağıdaki diziyi ele alalım:

(bn): 1, 1/2, 1/4, 1/8, 1/16, …

Bu dizi aynı zamanda geometrik bir dizidir! Bu ilerlemenin her üyesi ayrıca elde edilir çarpma işlemiönceki terim, aynı sayı ile. sadece numara kesirli: Q = +1/2 . Veya +0,5 . Ve (önemli!) sayı, daha küçük olan:Q = 1/2<1.

Bu geometrik ilerlemede ilginç olan nedir? Üyeleri nereye gidiyor? Bir göz atalım:

1/2 = 0,5;

1/4 = 0,25;

1/8 = 0,125;

1/16 = 0,0625;

…….

Burada ilginç olan nedir? İlk olarak, ilerlemenin üyelerindeki azalma hemen dikkat çekicidir: üyelerinin her biri azönceki tam olarak 2 kez. Ya da geometrik ilerlemenin tanımına göre, her terim Dahaöncesi 1/2 kez, Çünkü ilerleme paydası Q = 1/2 . Ve birden küçük pozitif bir sayı ile çarpıldığında, sonuç genellikle azalır, evet ...

Ne Daha Bu ilerlemenin davranışında görülebilir mi? Üyeleri kayboluyor mu? sınırsız, eksi sonsuza mı gidiyor? HAYIR! Özel bir şekilde kaybolurlar. İlk başta oldukça hızlı bir şekilde azalırlar ve sonra giderek daha yavaş bir şekilde azalırlar. Ve tüm kalırken pozitif. Çok, çok küçük olmasına rağmen. Ve ne için çabalıyorlar? Tahmin etmedin mi? Evet! Sıfıra meyilliler!) Ve dikkat edin, ilerlememizin üyeleri asla ulaşma! Sadece ona sonsuz yakın. Bu çok önemli.)

Benzer bir durum böyle bir ilerlemede olacaktır:

(bn): -1, -1/2, -1/4, -1/8, -1/16, …

Burada B 1 = -1 , A Q = 1/2 . Her şey aynı, ancak şimdi üyeler diğer taraftan sıfıra aşağıdan yaklaşacaklar. her zaman kalmak olumsuz.)

Üyeleri olan böyle bir geometrik ilerleme sonsuza kadar sıfıra yaklaşıyor.(olumlu veya olumsuz fark etmez), matematikte özel bir adı vardır - sonsuz azalan geometrik ilerleme. Bu ilerleme o kadar ilginç ve sıra dışı ki, ayrı ders .)

Yani, mümkün olan her şeyi düşündük pozitif paydalar hem büyük hem de daha küçüktür. Yukarıda belirtilen nedenlerden dolayı birin kendisini payda olarak görmüyoruz (üçlü dizili örneği hatırlayın ...)

Özetlemek:

pozitifVe birden fazla (Q>1), ardından ilerlemenin üyeleri:

A) süresiz olarak artar (eğerB 1 >0);

b) süresiz olarak azaltmak (eğerB 1 <0).

Geometrik ilerlemenin paydası ise pozitif Ve birden az (0< Q<1), то члены прогрессии:

a) sıfıra sonsuz yakın üstünde(EğerB 1 >0);

b) sıfıra sonsuz yakın aşağıdan(EğerB 1 <0).

Şimdi davayı düşünmek kalır negatif payda.

Payda negatiftir ( Q <0)

Bir örnek için uzağa gitmeyeceğiz. Aslında neden tüylü büyükanne?!) Örneğin, ilerlemenin ilk üyesi olsun B 1 = 1 ve paydayı alın q = -2.

Aşağıdaki sırayı elde ederiz:

(bn): 1, -2, 4, -8, 16, …

Ve böyle devam eder.) İlerlemenin her terimi elde edilir çarpma işlemiönceki üye negatif bir sayı-2. Bu durumda tek sıradaki (birinci, üçüncü, beşinci vb.) tüm üyeler pozitif ve çift yerlerde (ikinci, dördüncü vb.) - olumsuz.İşaretler kesinlikle serpiştirilmiştir. Artı-eksi-artı-eksi ... Böyle bir geometrik ilerleme denir - artan işaret dönüşümlü.

Üyeleri nereye gidiyor? Ve hiçbir yerde.) Evet, mutlak değerde (yani modulo) ilerlememizin koşulları sonsuza kadar artar (dolayısıyla "artan" adı). Ancak aynı zamanda, ilerlemenin her üyesi dönüşümlü olarak onu sıcağa, sonra soğuğa atar. Ya artı ya da eksi. İlerlememiz dalgalanıyor... Üstelik dalgalanmaların aralığı her adımda hızla artıyor, evet.) Bu nedenle ilerleme üyelerinin bir yere gitme özlemleri özellikle Burada HAYIR. Ne artı sonsuza, ne eksi sonsuza, ne de sıfıra - hiçbir yere.

Şimdi sıfır ile eksi bir arasında bir kesirli payda düşünün.

Olsun mesela B 1 = 1 , A q = -1/2.

Ardından ilerlemeyi elde ederiz:

(bn): 1, -1/2, 1/4, -1/8, 1/16, …

Ve yine bir dizi işaretimiz var! Ancak, önceki örnekten farklı olarak, burada zaten terimlerin sıfıra yaklaşma eğilimi vardır.) Ancak bu sefer terimlerimiz sıfıra tam olarak yukarıdan veya aşağıdan değil, yine sıfıra yaklaşıyor. tereddüt. Dönüşümlü olarak pozitif veya negatif değerler alarak. Ama aynı zamanda onlar modüller değer verilen sıfıra gittikçe yaklaşıyor.)

Bu geometrik diziye denir sonsuz azalan alternatif işaret.

Bu iki örnek neden ilginç? Ve her iki durumda da gerçekleştiği gerçeği alternatif karakterler! Böyle bir çip, yalnızca negatif paydalı ilerlemeler için tipiktir, evet.) Bu nedenle, bazı görevlerde değişen üyelerle geometrik bir ilerleme görürseniz, paydasının% 100 negatif olduğunu zaten kesin olarak bileceksiniz ve yanılmayacaksınız. tabelada.)

Bu arada, negatif bir payda durumunda, ilk terimin işareti, ilerlemenin davranışını hiç etkilemez. Sıralamanın ilk üyesinin işareti ne olursa olsun, her halükarda üyelerin münavebesinin işareti gözlenecektir. Bütün soru sadece hangi yerlerde(çift veya tek) belirli işaretlere sahip üyeler olacaktır.

Hatırlamak:

Geometrik ilerlemenin paydası ise olumsuz , o zaman ilerleme terimlerinin işaretleri her zaman alternatif.

Aynı zamanda, üyelerin kendileri:

a) sonsuza kadar artmakmodulo, EğerQ<-1;

b) -1 ise sıfıra sonsuz yaklaşır< Q<0 (прогрессия бесконечно убывающая).

Bu kadar. Tüm tipik durumlar analiz edilir.)

Çeşitli geometrik ilerleme örneklerini ayrıştırma sürecinde, periyodik olarak şu kelimeleri kullandım: "sıfır eğilimindedir", "artı sonsuza eğilimlidir", eksi sonsuza eğilimlidir... Sorun değil.) Bu konuşma sıraları (ve belirli örnekler), yalnızca davranışçeşitli sayı dizileri. Geometrik ilerlemeye bir örnek.

İlerleme davranışını neden bilmemiz gerekiyor? Nereye gittiğinin ne önemi var? Sıfıra, artı sonsuza, eksi sonsuza... Bu bizi ne ilgilendiriyor?

Mesele şu ki, zaten üniversitede, yüksek matematik dersinde, çeşitli sayısal dizilerle (sadece ilerlemelerle değil, herhangi biriyle!) Çalışma yeteneğine ve bunun veya bu dizinin tam olarak nasıl davrandığını hayal etme yeteneğine ihtiyacınız olacak. - sınırsız artar mı, azalır mı, belirli bir sayıya mı eğilimlidir (ve sıfıra olması gerekmez) veya hatta hiçbir şeye eğilimlidir ... Matematik dersinde bu konuya bütün bir bölüm ayrılmıştır. analiz - limit teorisi. Biraz daha spesifik olarak, konsept sayı dizisinin sınırı.Çok ilginç bir konu! Üniversiteye gidip bunu çözmek mantıklı.)

Bu bölümden bazı örnekler (sınırlı diziler) ve özellikle, sonsuz azalan geometrik ilerleme okulda öğrenmeye başlayın. Alışmak.)

Dahası, gelecekte dizilerin davranışını iyi bir şekilde inceleme yeteneği büyük ölçüde işe yarayacak ve fonksiyon araştırması En çeşitli. Ancak işlevlerle yetkin bir şekilde çalışma yeteneği (türevleri hesaplayın, tam olarak keşfedin, grafiklerini oluşturun) zaten matematiksel seviyenizi önemli ölçüde artırıyor! Şüphe? Gerek yok. Sözlerimi de unutma.)

Hayattaki geometrik bir ilerlemeye bakalım mı?

Etrafımızdaki yaşamda, üstel ilerlemeyle çok, çok sık karşılaşıyoruz. Farkında olmadan.)

Örneğin, bizi her yerde büyük miktarlarda çevreleyen ve mikroskopsuz bile göremediğimiz çeşitli mikroorganizmalar, tam olarak geometrik bir dizide çoğalırlar.

Diyelim ki bir bakteri ikiye bölünerek çoğalıyor ve 2 bakteride yavru veriyor. Sırayla, her biri çoğalarak ikiye bölünür ve 4 bakterinin ortak yavrularını verir. Bir sonraki nesil 8 bakteri verecek, sonra 16 bakteri, 32, 64 vb. Birbirini takip eden her nesilde, bakteri sayısı iki katına çıkar. Tipik bir geometrik ilerleme örneği.)

Ayrıca bazı böcekler - yaprak bitleri, sinekler - katlanarak çoğalır. Ve bu arada bazen tavşanlar da.)

Günlük hayata daha yakın bir geometrik ilerlemenin başka bir örneği, sözde bileşik faiz. Böyle ilginç bir fenomen genellikle banka mevduatlarında bulunur ve buna denir. faiz kapitalizasyonu. Ne olduğunu?

Sen kendin, elbette, hala gençsin. Okulda okuyorsun, bankalara başvurmuyorsun. Ama ailen yetişkin ve bağımsız insanlar. İşe giderler, günlük ekmek için para kazanırlar ve paranın bir kısmını bankaya yatırarak birikim yaparlar.)

Diyelim ki babanız Türkiye'de bir aile tatili için belirli bir miktar para biriktirmek istiyor ve bankaya üç yıllık bir süre için yıllık %10 faizle 50.000 ruble yatırmak istiyor. yıllık faiz kapitalizasyonu ile. Ayrıca, tüm bu süre boyunca depozito ile hiçbir şey yapılamaz. Depozitoyu yenileyemez veya hesaptan para çekemezsiniz. Bu üç yılda ne kadar kar edecek?

Öncelikle, yıllık %10'un ne olduğunu bulmanız gerekiyor. Bu demektir bir yıl içinde Banka tarafından ilk depozito miktarına %10 eklenecektir. Neyden? tabii ki, dan ilk depozito miktarı.

Bir yıldaki hesabın miktarını hesaplayın. Depozitonun ilk tutarı 50.000 ruble (yani %100) ise, o zaman bir yılda hesaptaki faiz ne kadar olacak? Bu doğru, %110! 50.000 ruble'den.

Bu yüzden 50.000 ruble'nin %110'unu dikkate alıyoruz:

50.000 1,1 \u003d 55.000 ruble.

Değerin %110'unu bulmanın bu değeri 1.1 sayısıyla çarpmak anlamına geldiğini anlamışsınızdır umarım? Bunun neden böyle olduğunu anlamadıysanız, beşinci ve altıncı sınıfları hatırlayın. Yani - yüzdelerin kesirler ve kısımlarla ilişkisi.)

Böylece ilk yıl için artış 5000 ruble olacak.

İki yıl sonra hesapta ne kadar para olacak? 60.000 ruble mi? Ne yazık ki (veya daha doğrusu, neyse ki), o kadar basit değil. Faiz kapitalizasyonunun tüm hilesi, her yeni faiz tahakkukunda, bu aynı faizlerin halihazırda dikkate alınacak olmasıdır. yeni miktardan! Kimden çoktan hesapta Şu anda. Ve bir önceki dönem için tahakkuk eden faiz, mevduatın ilk tutarına eklenir ve böylece yeni faiz hesaplamasına kendileri katılırlar! Yani, toplam hesabın tam bir parçası haline gelirler. veya genel başkent. Dolayısıyla adı - faiz kapitalizasyonu.

Ekonomide. Ve matematikte bu tür yüzdelere denir bileşik faiz. Veya yüzde yüzde.) Onların hilesi, sıralı hesaplamada, yüzdelerin her seferinde hesaplanmasıdır. yeni değerden. orjinalinden değil...

Bu nedenle, toplamı hesaplamak için iki yıl, hesapta olacak miktarın% 110'unu hesaplamamız gerekiyor bir yıl içinde. Yani, zaten 55.000 ruble.

55.000 ruble'nin %110'unu dikkate alıyoruz:

55000 1,1 \u003d 60500 ruble.

Bu, ikinci yıl için yüzde artışının zaten 5.500 ruble ve iki yıl için - 10.500 ruble olacağı anlamına gelir.

Şimdi, üç yıl içinde hesaptaki miktarın 60.500 rublenin% 110'u olacağını tahmin edebilirsiniz. Bu yine %110 öncekinden (geçen yıl) tutarlar.

Burada şunları düşünüyoruz:

60500 1,1 \u003d 66550 ruble.

Ve şimdi parasal tutarlarımızı yıllara göre sırayla oluşturuyoruz:

50000;

55000 = 50000 1.1;

60500 = 55000 1,1 = (50000 1,1) 1,1;

66550 = 60500 1,1 = ((50000 1,1) 1,1) 1,1

Peki nasıl? Neden geometrik bir ilerleme olmasın? ilk üye B 1 = 50000 ve payda Q = 1,1 . Her terim kesinlikle bir öncekinden 1.1 kat daha fazladır. Her şey tam anlamıyla tanıma uygundur.)

Ve babanız, 50.000 rublesi üç yıl boyunca banka hesabındayken, ek yüzde kaç ikramiye "katılacak"?

İnanıyoruz:

66550 - 50000 = 16550 ruble

Tabii ki kötü. Ancak bu, katkının başlangıç ​​​​miktarının küçük olması durumundadır. Ya daha fazlası varsa? Diyelim ki 50 değil, 200 bin ruble? O zaman üç yıllık artış zaten 66.200 ruble olacak (eğer sayarsanız). Hangisi zaten çok iyi.) Ve eğer katkı daha da büyükse? İşte bu...

Sonuç: İlk katkı ne kadar yüksek olursa, faiz kapitalizasyonu o kadar karlı olur. Bu nedenle faiz kapitalizasyonlu mevduat bankalar tarafından uzun vadeli olarak sağlanmaktadır. Beş yıl diyelim.

Ayrıca grip, kızamık ve hatta daha korkunç hastalıklar (2000'lerin başındaki aynı SARS veya Orta Çağ'daki veba) gibi her türlü kötü hastalık katlanarak yayılmayı sever. Dolayısıyla salgınların ölçeği, evet ...) Ve bunların hepsi, geometrik bir ilerlemenin tüm pozitif payda (Q>1) - çok hızlı büyüyen bir şey! Bakterilerin üremesini hatırlayın: bir bakteriden iki, ikiden dört, dörtten sekiz vb. Elde edilir ... Herhangi bir enfeksiyonun yayılmasıyla her şey aynıdır.)

Geometrik ilerlemedeki en basit problemler.

Her zamanki gibi basit bir problemle başlayalım. Tamamen anlamını anlamak için.

1. Geometrik dizinin ikinci teriminin 6, paydasının -0,5 olduğu bilinmektedir. Birinci, üçüncü ve dördüncü terimleri bulun.

Yani bize verildi sonsuz iyi bilinen geometrik ilerleme ikinci dönem bu ilerleme:

b2 = 6

Ayrıca, biz de biliyoruz ilerleme paydası:

q = -0,5

Ve bulmalısın Ilk üçüncüsü Ve dördüncü bu ilerlemenin üyeleri.

İşte oynuyoruz. Sıralamayı problemin durumuna göre yazıyoruz. Doğrudan genel anlamda, ikinci üyenin altı olduğu durumlarda:

b1,6,B 3 , B 4 , …

Şimdi aramaya başlayalım. Her zamanki gibi en basitinden başlıyoruz. Örneğin, üçüncü terimi hesaplayabilirsiniz. b3? Olabilmek! Üçüncü terimin (doğrudan bir geometrik ilerleme anlamında) zaten biliyoruz ki (b 3) bir saniyeden fazla (B 2 ) V "Q" bir kere!

Öyleyse yazıyoruz:

b3 =B 2 · Q

Bu ifadede altı yerine yerine koyarız. b2 ve bunun yerine -0,5 Q ve düşünüyoruz. Ve eksi de göz ardı edilmiyor elbette ...

b3 \u003d 6 (-0,5) \u003d -3

Bunun gibi. Üçüncü dönem olumsuz çıktı. Şaşılacak bir şey yok: paydamız Q- olumsuz. Ve artı eksi ile çarpıldığında, elbette eksi olacaktır.)

Şimdi ilerlemenin bir sonraki, dördüncü dönemini ele alıyoruz:

4 =B 3 · Q

b 4 \u003d -3 (-0,5) \u003d 1,5

Dördüncü üye yine artı ile. Beşinci terim yine eksi ile, altıncı artı ile vb. Olacaktır. İşaretler - alternatif!

Böylece üçüncü ve dördüncü üyeler bulundu. Sonuç aşağıdaki sıradır:

b1; 6; -3; 1.5; …

Şimdi geriye ilk terimi bulmak kalıyor b 1 iyi bilinen saniyeye göre. Bunu yapmak için diğer yöne, sola doğru adım atıyoruz. Bu, bu durumda, ilerlemenin ikinci terimini payda ile çarpmamız gerekmediği, ancak paylaşmak.

Bölüyoruz ve alıyoruz:

Hepsi bu kadar.) Sorunun cevabı şu şekilde olacaktır:

-12; 6; -3; 1,5; …

Gördüğünüz gibi, çözüm ilkesi . Biliyoruz herhangiüye ve payda geometrik ilerleme - başka herhangi bir terim bulabiliriz. Ne istersek onu buluruz.) Tek fark, toplama/çıkarmanın yerini çarpma/bölmeye bırakmasıdır.

Unutmayın: Bir geometrik dizinin en az bir üyesini ve paydasını biliyorsak, bu dizinin başka herhangi bir üyesini her zaman bulabiliriz.

Geleneğe göre aşağıdaki görev, OGE'nin gerçek versiyonundandır:

2.

…; 150; X; 6; 1.2; …

Peki nasıl? Bu sefer ilk terim yok, payda yok Q, sadece bir sayı dizisi verilir ... Zaten tanıdık bir şey, değil mi? Evet! Aritmetik ilerlemede benzer bir problem zaten ele alındı!

Burada korkmuyoruz. Hepsi aynı. Başınızı çevirin ve geometrik bir ilerlemenin temel anlamını hatırlayın. Dizimize dikkatlice bakarız ve üç ana geometrik dizinin (ilk üye, payda, üye sayısı) hangi parametrelerinin içinde gizlendiğini buluruz.

Üye numaraları? Üye sayısı yok evet... Ama dört tane var. ardışık sayılar. Bu kelimenin ne anlama geldiğini, bu aşamada açıklamanın anlamını görmüyorum.) İki tane var mı? komşu bilinen numaralar? Yemek yemek! Bunlar 6 ve 1.2'dir. böylece bulabiliriz ilerleme paydası. Bu yüzden 1.2 sayısını alıyoruz ve bölüyoruz önceki numaraya Altı için.

Biz:

Biz:

X= 150 0,2 = 30

Cevap: X = 30 .

Gördüğünüz gibi, her şey oldukça basit. Ana zorluk sadece hesaplamalarda yatmaktadır. Negatif ve kesirli paydalar söz konusu olduğunda özellikle zordur. Yani sorunu olanlar aritmetiği tekrar etsin! Kesirlerle nasıl çalışılır, negatif sayılarla nasıl çalışılır vs... Aksi takdirde burada acımasızca yavaşlarsınız.

Şimdi sorunu biraz değiştirelim. Şimdi ilginç olacak! İçindeki son 1.2 sayısını çıkaralım. Şimdi bu sorunu çözelim:

3. Bir geometrik ilerlemenin birkaç ardışık terimi yazılır:

…; 150; X; 6; …

X harfi ile gösterilen ilerlemenin terimini bulun.

Her şey aynı, sadece iki komşu ünlü artık ilerleme üyelerimiz yok. Bu ana sorundur. Çünkü büyüklük Q iki komşu terim aracılığıyla, zaten kolayca belirleyebiliriz yapamayız Meydan okumayla karşılaşma şansımız var mı? Kesinlikle!

Bilinmeyen terimi yazalım" X"Doğrudan geometrik bir ilerleme anlamında! Genel anlamda.

Evet evet! Doğrudan bilinmeyen bir payda ile!

Bir yandan x için şu oranı yazabiliriz:

X= 150Q

Öte yandan, aynı X'i boyamaya hakkımız var. Sonrakiüye, altı aracılığıyla! Altıyı paydaya böl.

Bunun gibi:

X = 6/ Q

Açıkçası, şimdi bu oranların her ikisini de eşitleyebiliriz. ifade ettiğimiz için aynısı değer (x), ancak iki Farklı yollar.

Denklemi elde ederiz:

Her şeyi ile çarpmak Q, basitleştirme, azaltma, denklemi elde ederiz:

q 2 \u003d 1/25

Çözüyoruz ve alıyoruz:

q = ±1/5 = ±0,2

Hata! Payda çifttir! +0,2 ve -0,2. Ve hangisini seçmeli? Çıkmaz sokak?

Sakinlik! evet sorun gerçekten iki çözüm! Bunda yanlış bir şey yok. Olur.) Örneğin, her zamanki gibi çözerek iki kök elde ettiğinizde şaşırmaz mısınız? Burada da aynı hikaye var.)

İçin q = +0,2 alacağız:

X \u003d 150 0,2 \u003d 30

Ve için Q = -0,2 irade:

X = 150 (-0,2) = -30

İkili bir cevap alıyoruz: X = 30; X = -30.

Bu ilginç gerçek ne anlama geliyor? Ve var olan iki ilerleme, sorunun koşulunu yerine getiriyor!

Bunlar gibi:

…; 150; 30; 6; …

…; 150; -30; 6; …

Her ikisi de uygundur.) Sizce cevapların ikiye ayrılmasının nedeni nedir? Sırf ilerlemenin belirli bir üyesinin elenmesi nedeniyle (1,2), altıdan sonra geliyor. Ve geometrik dizinin yalnızca önceki (n-1)-inci ve sonraki (n+1)-inci üyelerini bildiğimize göre, aralarında duran n-inci üye hakkında artık kesin olarak hiçbir şey söyleyemeyiz. İki seçenek vardır - artı ve eksi.

Ama önemli değil. Kural olarak, geometrik ilerleme görevlerinde, kesin bir cevap veren ek bilgiler vardır. Sözleri söyleyelim: "işaret dönüşümlü ilerleme" veya "pozitif bir payda ile ilerleme" vb... Son cevabı verirken artı veya eksi hangi işaretin seçilmesi gerektiğine dair ipucu görevi görmesi gereken bu kelimelerdir. Böyle bir bilgi yoksa, o zaman - evet, görev iki çözüm.)

Ve artık kendimiz karar veriyoruz.

4. 20 sayısının bir geometrik dizinin üyesi olup olmayacağını belirleyin:

4 ; 6; 9; …

5. Alternatif bir geometrik ilerleme verilir:

…; 5; X ; 45; …

Harf ile gösterilen ilerlemenin terimini bulun X .

6. Geometrik dizinin dördüncü pozitif terimini bulun:

625; -250; 100; …

7. Geometrik dizinin ikinci terimi -360, beşinci terimi 23.04'tür. Bu ilerlemenin ilk terimini bulun.

Cevaplar (dağınık): -15; 900; HAYIR; 2.56.

Her şey yolunda gittiyse tebrikler!

Bir şey uymuyor mu? Bir yerde çift cevap var mı? Görevlendirme şartlarını dikkatle okuyoruz!

Son bulmaca çalışmıyor mu? Orada karmaşık bir şey yok.) Doğrudan geometrik bir ilerlemenin anlamına göre çalışıyoruz. Peki, bir resim çizebilirsin. Yardımcı olur.)

Gördüğünüz gibi, her şey basit. İlerleme kısaysa. Ya uzunsa? Yoksa istenilen üye sayısı çok mu fazla? Aritmetik ilerlemeye benzeterek, bulmayı kolaylaştıran uygun bir formül elde etmek istiyorum. herhangi herhangi bir geometrik ilerlemenin üyesi onun numarasına göre. Defalarca çarpmadan Q. Ve böyle bir formül var!) Ayrıntılar - bir sonraki derste.

Geometrik ilerleme, ilk terimi sıfır olmayan ve sonraki her terim önceki terimin sıfır olmayan aynı sayı ile çarpımına eşit olan sayısal bir dizidir.

Geometrik ilerleme gösterilir b1,b2,b3, …, milyar, … .

Geometrik hatanın herhangi bir teriminin önceki terimine oranı aynı sayıya eşittir, yani b2/b1 = b3/b2 = b4/b3 = … = bn/b(n-1) = b(n+ 1)/bn = …. Bu, doğrudan bir aritmetik ilerlemenin tanımından kaynaklanır. Bu sayıya geometrik ilerlemenin paydası denir. Genellikle geometrik bir ilerlemenin paydası q harfi ile gösterilir.

Monoton ve sabit dizi

Bir geometrik ilerleme belirlemenin bir yolu, ilk terimini b1 ve geometrik hata q'nun paydasını ayarlamaktır. Örneğin, b1=4, q=-2. Bu iki koşul 4, -8, 16, -32, … şeklinde bir geometrik dizi verir.

q>0 ise (q 1'e eşit değildir), o zaman ilerleme şu şekildedir: monoton sıra.Örneğin, 2, 4,8,16,32, ... dizisi monoton artan bir dizidir (b1=2, q=2).

Geometrik hatada payda q=1 ise, geometrik dizinin tüm üyeleri birbirine eşit olacaktır. Bu gibi durumlarda, ilerleme olduğu söylenir sabit sıra.

Geometrik ilerlemenin n'inci üyesinin formülü

Sayısal dizinin (bn) geometrik bir ilerleme olması için, ikinciden başlayarak her bir üyesinin, komşu üyelerin geometrik ortalaması olması gerekir. Yani, aşağıdaki denklemi yerine getirmek gerekir
(b(n+1))^2 = bn * b(n+2), herhangi bir n>0 için, burada n, N doğal sayılar kümesine aittir.

Bir geometrik dizinin n'inci üyesi için formül şöyledir:

bn=b1*q^(n-1),

burada n, N doğal sayılar kümesine aittir.

Bir geometrik dizinin ilk n teriminin toplamı için formül

Bir geometrik dizinin ilk n teriminin toplamı için formül şöyledir:

Sn = (bn*q - b1)/(q-1) burada q, 1'e eşit değildir.

Basit bir örnek düşünün:

Geometrik dizide b1=6, q=3, n=8 Sn'yi bulun.

S8'i bulmak için, bir geometrik ilerlemenin ilk n teriminin toplamı formülünü kullanırız.

Ö8= (6*(3^8 -1))/(3-1) = 19680.