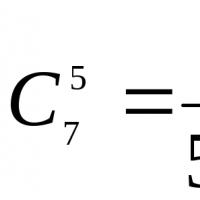Kombinatoriklerin temel formülleri. Kombinatorik problemleri çözme yöntemleri Temel kombinatorik
Malzemede gezinmeyi kolaylaştırmak için bu konunun içeriğini ekleyeceğim:
Giriiş. Setler ve seçimler.
Bu konuda kombinatoriğin temel kavramlarına bakacağız: permütasyonlar, kombinasyonlar ve yerleştirmeler. Miktarlarını bulabileceğiniz özlerini ve formüllerini öğrenelim.
Çalışmak için bazı yardımcı bilgilere ihtiyacımız var. Küme gibi temel bir matematik kavramıyla başlayalım. Küme kavramı "Küme kavramı. Kümeleri tanımlama yöntemleri" başlığında detaylı olarak tartışılmıştır.
Kalabalıklar hakkında çok kısa bir hikaye: göster\gizle
Kısaca: Bir küme nesnelerin bir koleksiyonudur. Kümeleri süslü parantez içinde yazın. Öğelerin yazılma sırası önemli değildir; öğelerin tekrarına izin verilmez. Örneğin, 11115555999 sayısının rakam kümesi şöyle olacaktır: $\(1,5,9\)$. "Kaplan yavrusu" sözcüğündeki ünsüz harfler kümesi şöyledir: $\(t, g, r, n, k\)$. $5\in A$ gösterimi, 5. elemanın $A=\(1,5,9 \)$ kümesine ait olduğu anlamına gelir. Sonlu bir kümedeki eleman sayısına denir güç bu kümenin bir tanesidir ve $|A|$'ı belirtir. Örneğin, 3 öğe içeren bir $A=\(1,5,9 \)$ kümesi için şunu elde ederiz: $|A|=3$.
Kardinalitesi $n$, $|U|=n$ (yani, $U$ kümesinin $n$ öğeleri vardır) olan, boş olmayan belirli bir sonlu $U$ kümesini düşünün. Şöyle bir kavram tanıtalım örnek(bazı yazarlar buna tuple diyor). $n$ öğelerinden ($(n,k)$-sample olarak kısaltılır) $k$ hacminin bir örneğiyle, $(a_1, a_2,\ldots, a_k)$ öğelerinin bir kümesini kastediyoruz, burada $a_i\in ABD doları. Elemanlarının sırası belirtilmişse seçime sıralı seçim denir. Yalnızca elemanların sırası farklı olan iki sıralı örnek farklıdır. Örnek elemanlarının sırası önemli değilse, örnek sırasız olarak adlandırılır.
Bir seçimin tanımının öğe tekrarları hakkında hiçbir şey söylemediğini unutmayın. Set elemanlarının aksine seçim elemanları tekrarlanabilir.
Örneğin, $U=\(a,b,c,d,e\)$ kümesini düşünün. $U$ kümesi 5 öğe içerir; $|U|=5$. Tekrarsız bir örnek şu şekilde olabilir: $(a,b,c)$. Bu seçim 3 öğe içerir; bu örneğin boyutu 3'tür. Yani $(5,3)$-örneğidir.
Tekrarlı bir örnek şu şekilde olabilir: $(a,a,a,a,a,c,c,d)$. 8 element içerir, yani. hacmi 8'dir. Yani bu bir $(5,8)$-örneğidir.
İki $(5,3)$-örneği daha ele alalım: $(a,b,b)$ ve $(b,a,b)$. Örneklerimizin sırasız olduğunu varsayarsak, o zaman $(a,b,b)$ örneği $(b,a,b)$ örneğine eşittir, yani. $(a,b,b)=(b,a,b)$. Örneklerimizin sıralandığını varsayarsak $(a,b,b)\neq(b,a,b)$ olur.
Biraz daha az soyut başka bir örneğe bakalım:) Diyelim ki bir sepette altı şeker var ve hepsi farklı. İlk şekeri 1 rakamıyla, ikinci şekeri 2 rakamıyla vb. ilişkilendirirsek, o zaman şu set sepetteki şekerlerle ilişkilendirilebilir: $U=\(1,2,3,4, 5,6\)$. Üç şekeri çıkarmak için elimizi rastgele bir sepete koyduğumuzu hayal edin. Çıkarılan şekerler seçimdir. 6 şekerden 3'ünü aldığımız için (6,3)-örneği elde ederiz. Şekerlerin avuç içine yerleştirilme sırası tamamen önemsizdir, dolayısıyla bu örnek sırasızdır. Peki, tüm şekerler farklı olduğundan seçim tekrarlanmadan yapılır. Yani bu durumda tekrarsız, sırasız (6,3) bir örnekten bahsediyoruz.
Şimdi diğer taraftan yaklaşalım. Bir şeker üretim fabrikasında olduğumuzu ve bu fabrikada dört çeşit şeker ürettiğimizi düşünelim. Bu durumda $U$ kümesi şu şekildedir: $U=\(1,2,3,4 \)$ (her sayı kendi şeker türünden sorumludur). Şimdi tüm şekerlerin, yanında durduğumuz tek bir kanala döküldüğünü hayal edelim. Ve avuçlarımızı yerleştirerek bu akıştan 20 şeker seçiyoruz. Bir avuç şeker buna örnektir. Şekerlerin yerleştirildiği sıra bir avuç kadar önemli mi? Doğal olarak hayır, yani numune sırasız. Sadece 4 çeşit şeker var ve genel akıştan yirmi adet seçiyoruz - çeşitlerin tekrarı kaçınılmazdır. Aynı zamanda numuneler çok farklı olabilir; hatta tüm şekerlerimiz aynı türden olabilir. Dolayısıyla bu durumda tekrarlı, sırasız (4,20) bir örnekle karşı karşıyayız.
Birkaç örneğe daha bakalım. Küplerin üzerine 7 farklı harf yazılsın: k, o, n, f, e, t, a. Bu harfler $U=\(k,o,n,f,e,t,a\)$ kümesini oluşturur. Diyelim ki bu küplerden 5 harften oluşan “kelimeler” yapmak istiyoruz. Bu kelimelerin harfleri (örneğin “konfe”, “tenko” vb.) (7,5) seçimlerini oluşturur: $(k,o,n,f,e)$, $(t,e,n) ,k ,o)$, vb. Böyle bir örnekte harflerin sırasının önemli olduğu açıktır. Örneğin “nokft” ve “kfton” kelimeleri farklıdır (her ne kadar aynı harflerden oluşsalar da), çünkü içlerindeki harflerin sırası eşleşmemektedir. Bu tür “kelimelerde” harflerin tekrarı yoktur çünkü sadece yedi küp vardır. Yani, her kelimenin harf kümesi, tekrarsız, sıralı (7,5) bir örnektir.
Başka bir örnek: 1, 5, 7, 8 rakamlarından oluşan dört basamaklı her türlü sekiz basamaklı sayıyı yapıyoruz. Örneğin 11111111, 15518877, 88881111 vb. $U$ kümesi şu şekildedir: $U=\(1,5,7,8\)$. Oluşturulan her sayının rakamları bir (4,8) örneği oluşturur. Bir sayıdaki rakamların sırası önemlidir; numune sipariş edilir. Tekrarlara izin verilir, dolayısıyla burada tekrarlı sıralı (4,8)-örnekle uğraşıyoruz.
$n$ öğelerinin $k$ kadar tekrarı olmayan yerleşimler
$n$ öğelerinin $k$ tarafından tekrarlanmadan yerleştirilmesi - sıralı $(n,k)$-selection tekrarsız.
Söz konusu örnekteki öğeler tekrarlanamayacağından, örneğe orijinal kümedekinden daha fazla öğe seçemeyiz. Dolayısıyla bu tür örnekler için şu eşitsizlik doğrudur: $n≥ k$. $n$ öğelerinin $k$ kadar tekrarı olmayan yerleşimlerin sayısı aşağıdaki formülle belirlenir:
\begin(equation)A_(n)^(k)=\frac(n{(n-k)!} \end{equation} !}
"!" işareti ne anlama geliyor?: göster\gizle
"N!" Kaydediliyor ("en faktöriyel" olarak okuyun), 1'den n'ye kadar tüm sayıların çarpımını belirtir;
$$ n!=1\cdot2\cdot 3\cdot \ldots\cdot n $$
Tanım gereği $0!=1!=1$ olduğu varsayılır. Örneğin 5!'i bulalım:
$$ 5!=1\cdot 2\cdot 3\cdot 4\cdot 5=120. $$
Örnek No.1
Alfabe bir dizi sembolden oluşur $E=\(+,*,0,1,f\)$. Bu alfabede tekrar eden harf içermeyen üç harfli kelimelerin sayısını belirleyelim.
Üç karakterli kelimelerle “+*0” veya “0f1” gibi ifadeleri kastediyoruz. $E$ kümesinin beş öğesi vardır, dolayısıyla üç karakterli kelimelerin harfleri (5,3) seçimlerini oluşturur. İlk soru şu: Bu numuneler sipariş edildi mi, edilmedi mi? Yalnızca harf sıraları farklı olan kelimeler farklı kabul edilir, bu nedenle örnekteki öğelerin sırası önemlidir. Bu, numunenin sipariş edildiği anlamına gelir. İkinci soru: Tekrarlara izin veriliyor mu, izin verilmiyor mu? Bu sorunun cevabı şu koşulla verilmektedir: kelimeler tekrar eden harfler içermemelidir. Özetlemek gerekirse: problemin koşullarını sağlayan her kelimenin harfleri, tekrarsız, sıralı (5,3) bir örnek oluşturur. Yani her kelimenin harfleri 3'ün 5'i tekrarlanmadan bir yerleşim oluşturur. Bu yerleşimlere örnekler aşağıda verilmiştir:
$$ (+,*,f), \; (*,+,f), \; (1,+,0) $$
Bu yerleşimlerin toplam sayısıyla ilgileniyoruz. Formül (1)'e göre 3'ün 5 unsurunun tekrarı olmadan yerleştirme sayısı şu şekilde olacaktır:
$$ A_(5)^(3)=\frac(5{(5-3)!}=\frac{5!}{2!}=60. $$ !}
Onlar. Harfleri tekrarlanmayacak 60 adet üç karakterli kelime oluşturabilirsiniz.
Cevap: 60.
$k$ öğesinin $n$ öğelerinin tekrarına sahip yerleşimler
$n$ öğelerinin $k$ kadar tekrarlarıyla yerleştirme - sıralı tekrarlı $(n,k)$-selection.
$k$'ın $n$ öğelerinin tekrarına sahip yerleşimlerin sayısı aşağıdaki formülle belirlenir:
\begin(equation)\bar(A)_(n)^(k)=n^k \end(denklem)
Örnek No.2
$\(5,7,2\)$ rakam kümesinden kaç tane beş basamaklı sayı yapılabilir?
Bu sayı kümesinden beş basamaklı 55555, 75222 vb. sayıları yapabilirsiniz. Bu tür sayıların her birinin rakamları bir (3,5)-örneği oluşturur: $(5,5,5,5,5)$, $(7,5,2,2,2)$. Kendimize soralım: Bunlar ne tür örnekler? Birincisi, sayılardaki rakamlar tekrarlanabildiği için tekrarlı örneklerle uğraşıyoruz. İkinci olarak bir sayıdaki rakamların sırası önemlidir. Örneğin 27755 ile 77255 farklı sayılardır. Sonuç olarak, tekrarlı sıralı (3,5) örnekleriyle uğraşıyoruz. Bu tür örneklerin toplam sayısını (yani gerekli beş basamaklı sayıların toplam sayısını) formül (2)'yi kullanarak buluyoruz:
$$ \bar(A)_(3)^(5)=3^5=243. $$
Buna göre verilen rakamlardan 243 adet beş basamaklı sayı oluşturulabilir.
Cevap: 243.
$n$ öğelerinin tekrarı olmayan permütasyonlar
$n$ öğelerinin tekrarı olmayan bir permütasyon, tekrarsız, sıralı bir $(n,n)$-seçimidir.
Özünde, tekrarsız permütasyon, numune boyutunun orijinal kümenin önem derecesine eşit olduğu, tekrarsız yerleştirmenin özel bir durumudur. $n$ öğelerinin tekrarı olmadan permütasyonların sayısı aşağıdaki formülle belirlenir:
\begin(denklem)P_(n)=n! \end(denklem)
Bu arada, $P_n=A_(n)^(n)$ olduğunu düşünürseniz bu formülü elde etmek kolaydır. Sonra şunu elde ederiz:
$$ P_n=A_(n)^(n)=\frac(n{(n-n)!}=\frac{n!}{0!}=\frac{n!}{1}=n! $$ !}
Örnek No.3
Dondurucuda farklı firmalara ait beş porsiyon dondurma bulunmaktadır. Yiyeceklerin yenilme sırasını kaç farklı şekilde seçebilirsiniz?
1 rakamının ilk dondurmaya, 2 rakamının ikinciye vb. karşılık gelmesine izin verin. Dondurucunun içeriğini temsil edecek $U=\(1,2,3,4,5\)$ kümesini alacağız. Yemek yeme sırası şu şekilde olabilir: $(2,1,3,5,4)$ veya şu şekilde olabilir: $(5,4,3,1,2)$. Bu tür kümelerin her biri bir (5,5)-örneğidir. Düzenli ve tekrarsız olacaktır. Başka bir deyişle, bu tür her örnek, orijinal kümenin 5 öğesinin bir permütasyonudur. Formül (3)'e göre, bu permütasyonların toplam sayısı:
$$ P_5=5!=120. $$
Sonuç olarak, yeme sırasını seçmek için 120 sipariş vardır.
Cevap: 120.
Tekrarlı permütasyonlar
Tekrarlı permütasyon, tekrarlı sıralı bir $(n,k)$-örneğidir; burada $a_1$ öğesi $k_1$ kez tekrarlanır, $a_2$ $k_2$ kez tekrarlanır ve bu şekilde son $ öğesine kadar devam eder. a_r$, $ k_r$ kez tekrarlanır. Bu durumda, $k_1+k_2+\ldots+k_r=k$.
Tekrarlı permütasyonların toplam sayısı aşağıdaki formülle belirlenir:
\begin(denklem)P_(k)(k_1,k_2,\ldots,k_r)=\frac(k{k_1!\cdot k_2!\cdot \ldots \cdot k_r!} \end{equation} !}
Örnek No. 4
Kelimeler $U=\(a,b,d\)$ alfabesine göre oluşturulur. Bu kelimelerde “a” harfinin 2 kez tekrarlanması gerekiyorsa, yedi karakterden kaç farklı kelime oluşabilir; "b" harfi - 1 kez ve "d" harfi - 4 kez mi?
Arama kelimelerinin örnekleri şunlardır: "aabdddd", "daddabd" vb. Her kelimenin harfleri tekrarlarla bir (3,7) örneği oluşturur: $(a,a,b,d,d,d,d)$, $(d,a,d,d,a,b,d) )$ vb. Bu tür numunelerin her biri iki "a" öğesi, bir "b" öğesi ve dört "d" öğesinden oluşur. Başka bir deyişle, $k_1=2$, $k_2=1$, $k_3=4$. Tüm sembollerin toplam tekrar sayısı doğal olarak örneklem büyüklüğüne eşittir; $k=k_1+k_2+k_3=7$. Bu verileri formül (4)'te yerine koyarsak:
$$ P_7(2,1,4)=\frac(7{2!\cdot 1!\cdot 4!}=105. $$ !}
Dolayısıyla toplam arama kelimesi sayısı 105'tir.
Cevap: 105.
Her biri $k$ değerindeki $n$ öğelerinin tekrarı olmayan kombinasyonlar
$n$ öğelerinin $k$ kadar tekrarı olmayan bir kombinasyon, tekrarsız, sırasız bir $(n,k)$-örneğidir.
$k$'ın $n$ öğelerinin tekrarı olmadan toplam kombinasyon sayısı aşağıdaki formülle belirlenir:
\begin(denklem)C_(n)^(k)=\frac(n{(n-k)!\cdot k!} \end{equation} !}
Örnek No. 5
Sepetin içerisinde üzerinde 1'den 10'a kadar tam sayıların yazılı olduğu kartlar bulunmaktadır. Sepetten 4 adet kart alınıp üzerlerine yazılan sayılar toplanır. Sepetten kaç farklı kart seti çekilebilir?
Yani bu problemde başlangıç kümesi şöyledir: $U=\(1,2,3,4,5,6,7,8,9,10\)$. Bu setten dört öğe seçiyoruz (yani sepetten dört kart). Dışarı çekilen elemanların sayıları bir (10,4)-seçimi oluşturur. Tüm kartların numaraları farklı olduğundan bu seçimde tekrarlara izin verilmez. Soru şu: Kartların seçilme sırası önemli mi, değil mi? Yani, örneğin $(1,2,7,10)$ ve $(10,2,1,7)$ örnekleri eşit mi, eşit değil mi? Burada sorunun koşullarına dönmeniz gerekiyor. Daha sonra elemanların toplamını bulmak için kartlar çıkarılır. Bu, terimlerin yerlerinin değiştirilmesi toplamı değiştirmeyeceğinden kartların sırasının önemli olmadığı anlamına gelir. Örneğin, $(1,2,7,10)$ örneği ve $(10,2,1,7)$ örneği aynı $1+2+7+10=10+2+1+ sayısına karşılık gelecektir. 7= 20 dolar. Sonuç: Sorunun koşullarından, sırasız örneklerle uğraştığımız anlaşılmaktadır. Onlar. tekrarsız sırasız (10,4) örneklerin toplam sayısını bulmamız gerekiyor. Yani 10 elementin 4'lü kombinasyon sayısını bulmamız gerekiyor. Bunun için formül (5)'i kullanıyoruz:
$$ C_(10)^(4)=\frac(10{(10-4)!\cdot 4!}=\frac{10!}{6!\cdot 4!}=210. $$ !}
Bu nedenle toplam aranan set sayısı 210'dur.
Cevap: 210.
Her biri $k$ değerindeki $n$ öğelerinin tekrarlarıyla kombinasyonlar
$k$'ın $n$ öğelerinin tekrarlarından oluşan bir kombinasyon, tekrarları olan sırasız bir $(n,k)$-örneğidir.
$k$'ın $n$ öğelerinin tekrarlarından oluşan toplam kombinasyon sayısı aşağıdaki formülle belirlenir:
\begin(denklem)\bar(C)_(n)^(k)=\frac((n+k-1){(n-1)!\cdot k!} \end{equation} !}
Örnek No. 6
Dört çeşit şekerin hareket ettiği bir konveyörün hemen yanında bir şeker fabrikasında olduğumuzu hayal edin. Elimizi bu dereye sokup yirmi parça çıkarıyoruz. Bir avuç dolusu kaç farklı "şeker kombinasyonu" olabilir?
İlk türün 1 sayısına, ikinci türün 2 sayısına vb. karşılık geldiğini varsayarsak, problemimizin ilk kümesi şu şekilde olur: $U=\(1,2,3,4\) $. Bu setten 20 element seçiyoruz (yani montaj hattından gelen aynı 20 şeker). Bir avuç şeker bir (4,20)-örneği oluşturur. Doğal olarak çeşitlerin tekrarları olacaktır. Soru şu: Örnekteki öğelerin sırası önemli mi, değil mi? Sorunun koşullarından, elemanların düzenlenme sırasının önemli olmadığı sonucu çıkar. Bir avuç dolusunun önce 15 lolipop, sonra 4 çikolatalı şeker ya da önce 4 çikolatalı şeker, sonra 15 lolipop içermesi bizim için hiç fark etmez. Yani tekrarlı, sırasız (4,20) bir örnekle uğraşıyoruz. Bu örneklerin toplam sayısını bulmak için formül (6) kullanıyoruz:
$$ \bar(C)_(4)^(20)=\frac((4+20-1){(4-1)!\cdot 20!}=\frac{23!}{3!\cdot 20!}=1771. $$ !}
Dolayısıyla toplam aranan kombinasyon sayısı 1771'dir.
Konuyla ilgili özet:
10. sınıf öğrencisi “B” tarafından tamamlandı
53 numaralı ortaokul
Glukhov Mihail Aleksandroviç
Naberezhnye Chelny
2002
İçerik
| Kombinatorik tarihinden_______________________________________________ | 3 |
| Toplama kuralı_________________________________________________________ | 4 |
| - | |
| Ürün kuralı_____________________________________________ | 4 |
| Görev örnekleri__________________________________________________________ | - |
| Kesişen kümeler_______________________________________________ | 5 |
| Görev örnekleri__________________________________________________________ | - |
| Euler çevreleri______________________________________________________________ | - |
| Tekrarı olmayan yerleştirmeler_____________________________________________ | 6 |
| Görev örnekleri__________________________________________________________ | - |
| Tekrarsız permütasyonlar________________________________________________ | 7 |
| Görev örnekleri__________________________________________________________ | - |
| Tekrarı olmayan kombinasyonlar_______________________________________________ | 8 |
| Görev örnekleri__________________________________________________________ | - |
| Tekrarı olmayan yerleşimler ve kombinasyonlar______________________________ | 9 |
| Görev örnekleri__________________________________________________________ | - |
| Tekrarlı permütasyonlar________________________________________________ | 9 |
| Görev örnekleri__________________________________________________________ | - |
| Bağımsız çözüme yönelik problemler________________________________ | 10 |
| Kaynakça___________________________________ | 11 |
Kombinatorik tarihinden
Kombinatorik, sonlu bir kümenin elemanlarından oluşturulabilen çeşitli bileşik türleriyle ilgilenir. Kombinatoriklerin bazı unsurları Hindistan'da 2. yüzyılın başlarında biliniyordu. M.Ö e. Nydia'lılar artık "kombinasyon" olarak adlandırılan sayıların nasıl hesaplanacağını biliyorlardı. 12. yüzyılda Bhaskara bazı kombinasyon ve permütasyon türlerini hesapladı. Hintli bilim adamlarının bileşikleri şiirsel kullanımları, şiir yapısının incelenmesi ve şiirsel eserlerle bağlantılı olarak incelediklerine inanılıyor. Örneğin, n heceden oluşan bir ayağın vurgulu (uzun) ve vurgusuz (kısa) hecelerinin olası kombinasyonlarının hesaplanmasıyla bağlantılı olarak. Bilimsel bir disiplin olarak kombinatorik 17. yüzyılda kuruldu. Fransız yazar A., “Aritmetiğin Teorisi ve Uygulaması” (1656) kitabında da bir bölümün tamamını kombinasyonlara ve permütasyonlara ayırmıştır.
B. Pascal, “Aritmetik Üçgen Üzerine İnceleme” ve “Sayısal Düzenler Üzerine İnceleme” (1665) adlı eserinde, binom katsayıları doktrininin ana hatlarını çizdi. P. Fermat, matematiksel kareler ve figürlü sayılar arasındaki bağlantıları bileşikler teorisiyle biliyordu. Kombinatorik terimi, Leibniz'in 1665 yılında kombinasyon ve permütasyon teorisine ilk kez bilimsel bir temel sağlayan "Kombinasyon Sanatı Üzerine Söylem" adlı eserini yayınlamasından sonra kullanılmaya başlandı. J. Bernoulli yerleştirmeleri ilk kez 1713 yılında “Ars conjectandi” (tahmin sanatı) kitabının ikinci bölümünde inceledi. Kombinasyonların modern sembolizmi, çeşitli eğitim kılavuzları yazarları tarafından ancak 19. yüzyılda önerildi.
Kombinatoryal formüllerin tamamı sonlu kümelerle ilgili iki temel ifadeden türetilebilir: toplam kuralı ve çarpım kuralı.
Toplama Kuralı
Sonlu kümeler kesişmiyorsa, X U Y'nin (veya) eleman sayısı, X kümesinin eleman sayısı ile Y kümesinin eleman sayısının toplamına eşittir.
Yani birinci rafta X kitap, ikinci rafta Y kitap varsa birinci veya ikinci raftan X+Y yollarıyla kitap seçebilirsiniz.
Sorun örnekleri
Öğrencinin matematikteki pratik çalışmaları tamamlaması gerekir. Kendisine cebirde 17 konu ve geometride 13 konu seçeneği sunuldu. Pratik çalışması için bir konuyu kaç farklı şekilde seçebilir?
Çözüm: X=17, Y=13
Toplama kuralına göre X U Y=17+13=30 konu.
Nakit piyango için 5, spor piyangosu için 6, araba piyangosu için 10 bilet bulunmaktadır. Bir spor lotosundan veya oto piyangodan bir bileti kaç farklı şekilde seçebilirsiniz?
Çözüm: Nakit ve giyim piyangosunun seçime dahil olmaması nedeniyle sadece 6 + 10 = 16 seçenek bulunmaktadır.
Ürün kuralı
Eğer X elemanı k farklı şekilde, Y elemanı ise m farklı şekilde seçilebiliyorsa, (X,Y) çifti k*m farklı şekilde seçilebilir.
Yani birinci rafta 5, ikinci rafta 10 kitap varsa birinci raftan bir, ikinci raftan bir kitap 5 * 10 = 50 şekilde seçebilirsiniz.
Sorun örnekleri
Bir ciltçinin 12 farklı kitabı kırmızı, yeşil ve kahverengi ciltlerle ciltlemesi gerekir. Bunu kaç farklı şekilde yapabilir?
Çözüm: 12 kitap ve 3 renk vardır yani çarpım kuralına göre 12*3=36 cilt seçeneği mümkündür.
Soldan sağa ve sağdan sola aynı okunan beş basamaklı kaç sayı vardır?
Çözüm: Bu tür sayılarda son rakam birinciyle, sondan bir önceki rakam da ikinciyle aynı olacaktır. Üçüncü rakam herhangi bir şey olacaktır. Bu formda temsil edilebilir XYZYX, burada Y ve Z herhangi bir sayıdır ve X sıfır değildir. Yani çarpım kuralına göre hem soldan sağa hem de sağdan sola eşit olarak okunabilecek rakam sayısı 9*10*10=900 seçenektir.
Kesişen kümeler
Ancak X ve Y kümeleri kesiştiğinde aşağıdaki formülü kullanırlar:
X ve Y'nin küme olduğu ve kesişim alanıdır. Sorun örnekleri20 kişi İngilizce, 10 kişi Almanca biliyor, bunlardan 5'i hem İngilizce hem de Almanca biliyor. Toplamda kaç kişi var?
Cevap: 10+20-5=25 kişi.
Sorunu görsel olarak çözmek için Euler çemberleri de sıklıkla kullanılır. Örneğin:
Yurt dışına seyahate çıkan 100 turistten 30'u Almanca, 28'i İngilizce, 42'si Fransızca, 8'i İngilizce ve Almanca, 10'u İngilizce ve Fransızca, 5'i Almanca ve Fransızca, 3'ü de üçü birden konuşmaktadır. diller. turistler herhangi bir dil konuşmuyor mu?Çözüm: Bu problemin durumunu grafiksel olarak ifade edelim. İngilizce bilenleri bir daireyle, Fransızca bilenleri bir başka daireyle, Almanca bilenleri üçüncü bir daireyle gösterelim.
Üç turist üç dili de konuşuyor, bu da çevrelerin genel kısmında 3 numaraya girdiğimiz anlamına geliyor. 10 kişi İngilizce ve Fransızca konuşuyor, 3'ü de Almanca konuşuyor. Sonuç olarak 10-3=7 kişi sadece İngilizce ve Fransızca konuşmaktadır.Benzer şekilde 8-3 = 5 kişinin sadece İngilizce ve Almanca konuştuğunu, 5-3 = 2 turistin ise Almanca ve Fransızca konuştuğunu görüyoruz. Bu verileri uygun kısımlara giriyoruz.
Şimdi kaç kişinin listelenen dillerden yalnızca birini konuştuğunu belirleyelim. 30 kişi Almanca biliyor ama 5+3+2=10 kişi başka dil konuşuyor, dolayısıyla sadece 20 kişi Almanca biliyor. Benzer şekilde 13 kişinin yalnızca İngilizce konuştuğunu ve 30 kişinin yalnızca Fransızca konuştuğunu görüyoruz.Soruna göre sadece 100 turist var. 20+13+30+5+7+2+3=80 turist en az bir dil biliyor, dolayısıyla 20 kişi bu dillerden hiçbirini konuşmuyor.
Tekrarı olmayan yerleşimler.
Her biri 6 rakamdan oluşan ve tüm rakamları farklı olmak üzere kaç telefon numarası oluşturulabilir?
Bu, tekrarı olmayan bir yerleştirme probleminin bir örneğidir. Buraya 6'lı 10 sayı yerleştirilmiştir ve aynı sayıların farklı sıralarda olduğu seçenekler farklı kabul edilir.
n elemandan oluşan bir X kümesi, m≤n ise, X kümesinin n elemanlarının tekrarsız olarak m'ye düzenlenmesine m eleman içeren sıralı X kümesi denir.
N elemanın m ile tüm düzenlemelerinin sayısı şu şekilde gösterilir:
N! - n-faktöriyel (faktöriyel faktör), 1'den herhangi bir n sayısına kadar doğal serideki sayıların çarpımıdır. Görev
4 erkek 6 kızdan 4'ünü dansa kaldırmayı kaç farklı şekilde isteyebilir?
Çözüm: İki erkek aynı anda aynı kızı davet edemez. Aynı kızların farklı erkeklerle dans ettiği seçenekler de farklı kabul ediliyor, bu nedenle:
360 seçenek mümkündür.
Tekrarı olmayan permütasyonlar
n=m durumunda (tekrarsız yerleştirmelere bakınız), m'nin n elemanının x kümesinin permütasyonu denir.
N elemanın tüm permütasyonlarının sayısı P n ile gösterilir.
n=m için geçerlidir:
Sorun örnekleri
0, 1, 2, 3, 4,5 rakamlarından tekrarlanmadığı takdirde kaç farklı altı basamaklı sayı oluşturulabilir?
1) Bu sayılardan tüm permütasyonların sayısını bulun: P 6 =6!=720
2) 0 bir sayının önünde olamaz, dolayısıyla 0'ın önünde olduğu permütasyonların sayısı bu sayıdan çıkarılmalıdır. Ve bu P 5 =5!=120'dir.
P 6 -P 5 =720-120=600
Yaramaz Maymun
Evet çarpık ayaklı Mishka
Dörtlü çalmaya başladık
Durun kardeşlerim, durun! –
Maymun bağırıyor - bekle!
Müzik nasıl gitmeli?
Sonuçta böyle oturmuyorsun...
Ve bu şekilde koltuk değiştirdiler; müzik yine pek iyi gitmiyor.
Belirli bir kümedeki örneklerin sayısını genel biçimde sayma problemini ele alalım. Biraz set olsun N, oluşan N elementler. Aşağıdakilerden oluşan herhangi bir alt küme M öğeler, sıraları dikkate alınmadan veya dikkate alınmadan dikkate alınabilir; sırayı değiştirirken diğerine geç M– örnekleme.
Aşağıdaki tanımları formüle edelim:
Tekrarı olmayan yerleşimler
Tekrarlamadan yerleştirmeN tarafından elemanlarM NkapsamakMçeşitli unsurlar.
Tanımdan, öğeler aynı olsa bile, iki düzenlemenin hem öğeleri hem de sıraları bakımından birbirinden farklı olduğu sonucu çıkar.
Teorem 3. Tekrarsız yerleşim sayısı ürüne eşittir M en büyüğü sayı olan faktörler N . Yazın:
Tekrarı olmayan permütasyonlar
PermütasyonlarN elemanlara bir kümenin farklı sıralamaları denirN.
Bu tanımdan, iki permütasyonun yalnızca elemanların sırasına göre farklılık gösterdiği ve bunların özel bir yerleştirme durumu olarak değerlendirilebileceği sonucu çıkmaktadır.
Teorem 4. Tekrarsız farklı permütasyonların sayısı aşağıdaki formülle hesaplanır:
Tekrarsız kombinasyonlar
Tekrarlanmayan bir kombinasyonN tarafından elemanlarM Bir kümenin herhangi bir sırasız alt kümesine denirNkapsamakM çeşitli unsurlar.
Tanımdan, iki kombinasyonun yalnızca öğeler açısından farklı olduğu sonucu çıkar; sıra önemli değildir.
Teorem 5. Tekrarsız kombinasyon sayısı aşağıdaki formüllerden biri kullanılarak hesaplanır:
örnek 1. Odada 5 sandalye var. Bunları üzerlerine kaç farklı şekilde yerleştirebilirsiniz?
a) 7 kişi; b) 5 kişi; c) 3 kişi mi?
Çözüm: a) Öncelikle sandalyelere oturacak 7 kişiden 5'ini seçmeniz gerekiyor. Yapılabilir  yol. Belirli bir beşin her seçimiyle şunları üretebilirsiniz:
yol. Belirli bir beşin her seçimiyle şunları üretebilirsiniz:  yeniden düzenlemeler. Çarpma teoremine göre gerekli iniş yöntemi sayısı eşittir.
yeniden düzenlemeler. Çarpma teoremine göre gerekli iniş yöntemi sayısı eşittir.
Yorum: Sorun yalnızca çarpım teoremi kullanılarak çözülebilir ve şu mantık yürütülebilir: 1. sandalyeye oturmak için 7 seçenek vardır, 2. sandalyeye oturmak için 6 seçenek vardır, 3. sandalyede -5, 4. -4 ve 5-. inci -3. Bu durumda 7 kişiyi 5 sandalyeye oturtma yollarının sayısı. Her iki yöntemin çözümleri tutarlıdır, çünkü

b) Çözüm açıktır - 
V)  - işgal edilen sandalyelerin seçim sayısı.
- işgal edilen sandalyelerin seçim sayısı.
 - seçilen üç sandalyede üç kişilik koltuk sayısı.
- seçilen üç sandalyede üç kişilik koltuk sayısı.
Toplam seçim sayısı.
Formülleri kontrol etmek zor değil  ;
;
 ;
;
Aşağıdakilerden oluşan bir kümenin tüm alt kümelerinin sayısı N elementler.
Yerleşimleri tekrarla
Tekrarlayarak yerleştirerekN tarafından elemanlarM Bir kümenin her sıralı alt kümesine denirN, oluşanM Böylece bu alt kümeye 1'den 1'e kadar herhangi bir öğe dahil edilebilir.Mya da tamamen yok olmak.
Tekrarlı yerleşimlerin sayısı şu şekilde gösterilir:  ve çarpma teoreminin bir sonucu olan formül kullanılarak hesaplanır:
ve çarpma teoreminin bir sonucu olan formül kullanılarak hesaplanır:

Örnek 2. N = (a, b, c) üç harften oluşan bir küme olsun. Bu kümeye dahil olan herhangi bir harf kümesine kelime diyelim. Bu harflerden oluşturulabilecek uzunluğu 2 olan kelime sayısını bulun:  .
.
Yorum: Açıkçası, tekrarlı yerleşimler de şu durumlarda dikkate alınabilir:  .
.
Örnek 3. Uzunluğu 3 olan tüm olası kelimeleri oluşturmak için (a, b) harflerini kullanmanız gerekir. Bu kaç farklı şekilde yapılabilir?
Cevap:

Ders 2
Klasik tanıma göre, A olayının olasılığını hesaplamak, onun lehine olan sonuçların sayısını saymak anlamına gelir. Bu genellikle kombinatoryal yöntemler kullanılarak yapılır.
Kombinatorik, belirli bir kümeden elemanların seçilmesi ve bunların belirli kurallara göre gruplar halinde düzenlenmesi, özellikle de belirli bir sonlu kümenin elemanlarından elde edilen kombinasyonların (örneklerin) sayısının sayılması problemlerini inceleyen bir matematik dalıdır. Her biri, belirli bir eylemi gerçekleştirmek için olası seçeneklerin sayısını saymayı ve "kaç şekilde?" sorusunu yanıtlamayı gerektirir.
Pek çok kombinatoryal problem, sırasıyla çarpma ve toplama kuralları olarak adlandırılan aşağıdaki iki önemli kural kullanılarak çözülebilir.
Çarpma kuralı(temel prensip): Eğer sonlu bir kümeden ilk nesne (x öğesi) n yolla seçilebiliyorsa ve bu tür her seçimden sonra ikinci nesne (y öğesi) m yolla seçilebiliyorsa, o zaman her iki nesne (x ve y) belirtilen sırada n ve m şekillerde seçilebilir.
Bu prensip açıkça üç veya daha fazla nesnenin durumunu da kapsar.
Örnek 1. 1, 2, 3, 4, 5 sayılarından kaç tane üç basamaklı sayı oluşturulabilir?
a) sayılar tekrarlanmıyor mu?
b) Sayılar tekrarlanabilir mi?
İlk sıradaki numarayı seçmenin 5 farklı yolu vardır (solda üç haneli bir sayı). Birinci sırayı örneğin 2 rakamı doldurduktan sonra ikinci sırayı dolduracak dört rakam kalıyor. Üçüncü sırayı doldurmak için üç sayı seçeneği bulunmaktadır. Dolayısıyla çarpma kuralına göre sayıları sıralamanın 5 × 4 × 3 = 60 yolu vardır, yani üç basamaklı sayıların gerekli sayısı 60’tır. (Bu sayılardan bazıları: 243, 541, 514, 132, ...) Eğer sayılar tekrarlanabiliyorsa 5×5×5= 125 adet üç basamaklı sayının olduğu açıktır (Bunlardan bazıları: 255, 333, 414, 111, 122, .. .)
Toplama kuralı. Eğer bir x nesnesi n farklı şekilde seçilebiliyorsa ve bir y nesnesi m farklı şekilde seçilebiliyorsa ve birinci ve ikinci yöntemler kesişmiyorsa, belirtilen nesnelerden herhangi biri (x veya y) n+m olarak seçilebilir. yollar.
Bu kural herhangi bir sonlu sayıda nesne için geçerlidir.
Örnek 2.Öğrenci grubunda 14 kız ve 6 erkek bulunmaktadır. Aynı cinsiyetten iki öğrenci farklı görevleri tamamlamak üzere kaç farklı şekilde seçilebilir?
Çarpma kuralına göre iki kız 14×13=182 şekilde, iki erkek çocuk ise 6×5=30 şekilde seçilebilir. Aynı cinsiyetten iki öğrenci seçmelisiniz: iki kız öğrenci veya iki erkek öğrenci. Bu tür seçim yöntemlerinin eklenmesi kuralına göre 182 + 30 = 212 olacaktır.
Kombinatoryal formüller kullanırsanız olasılıksal (ve diğer) problemleri çözmek genellikle daha kolaydır. Bunların her biri, söz konusu kümenin n farklı öğesinden rastgele m öğenin seçilmesinden oluşan bir deneydeki (deney) olası sonuçların sayısını belirler.
m elemanın seçilmesi için iki şema vardır (0< m £ n) из исходного множества: iade yok(tekrar yok) ve tekrar hoşgeldiniz(tekrarlamayla). İlk durumda seçilen öğeler döndürülmez; Tüm m öğelerini aynı anda veya sırayla tek tek seçebilirsiniz. İkinci şemada seçim, her adımda seçilen öğenin zorunlu olarak geri getirilmesiyle öğe öğe gerçekleştirilir.
İadesiz seçim şeması
Bize n farklı elemandan oluşan bir küme verilsin.
Konaklama n öğeden, her biri m öğeden (0< m £ n) называется любое упорядоченное подмножество данного множества, содержащее m элементов.
Tanımdan, yerleştirmelerin, elemanların bileşimi veya düzenlenme sırası bakımından birbirinden farklı olan m elemandan oluşan seçimler (kombinasyonlar) olduğu anlaşılmaktadır.
N elemanın m elemana göre yerleşim sayısı sembolüyle gösterilir (“A'dan ene em”) ve aşağıdaki formülle hesaplanır:
Bir düzenleme oluşturmak için, n öğeli bir kümeden m öğe seçip bunları düzenlemeniz, yani m yeri kümenin öğeleriyle doldurmanız gerekir. İlk eleman n farklı şekilde seçilebilir, yani n elemandan herhangi biri ilk sıraya yerleştirilebilir. İkinci eleman daha sonra geri kalan n-1 eleman arasından n-1 yolla seçilebilir. Üçüncü elemanı seçmenin n-2 yolu vardır, dördüncüyü seçmenin n-3 yolu vardır ve son olarak son m'inci eleman için (n-(m-1)) yolu vardır. Dolayısıyla, çarpma kuralına göre, verilen n elemandan m elemanı seçmenin n(n-1)(n-2)...(n-(m-1)) yolu vardır, yani .
Örnek 3. D = (a, b, c) kümesindeki 2 elemanın farklı düzenlemelerini yapın; onların sayısını sayın.
Üç elementten iki elementin aşağıdaki düzenlemeleri oluşturulabilir: (a, b), (b, a), (a, c), (c, a), (b, c), (c, b). Formül (1)'e göre sayıları: = 3×2 = 6'dır.
Yeniden düzenleme n elemanın n elemanın n elemana göre düzenlenmesidir.
Tanımdan permütasyonların n öğeden oluşan ve yalnızca öğelerin sırasına göre farklılık gösteren seçimler (kombinasyonlar) olduğu anlaşılmaktadır. N elemanın permütasyon sayısı P n ("en'den pe") sembolüyle gösterilir ve aşağıdaki formülle hesaplanır:
Formül (3) permütasyon tanımından çıkar:
Örnek 4. E = (2, 7, 8) kümesinin elemanlarından çeşitli permütasyonlar oluşturun; onların sayısını sayın.
Bu kümenin elemanlarından aşağıdaki permütasyonlar yapılabilir: (2,7,8); (2,8,7); (7,2,8); (7,8,2); (8,2,7); (8,7,2). Formül (3)'e göre elimizde: P 3 = 3! = 1×2×3 = 6.
Örnek 5. 5 farklı kitap bir rafa kaç farklı şekilde sıralanabilir?
Gerekli yol sayısı, 5 öğenin (kitapların) permütasyon sayısına eşittir, yani.
P 5 =5!=1×2×3×4×5 = 120.
Kombinasyon her biri m'nin n elemanından (0< m £ n) элементов называется любое подмножество, которое содержит m элементов данного множества.
Tanımdan, kombinasyonların, her biri verilen n elementten alınan m elementten oluşan ve birbirinden en az bir elementle farklı olan, yani sadece elementlerin bileşiminde farklılık gösteren örnekler (kombinasyonlar) olduğu anlaşılmaktadır.
n elementin m elemente göre kombinasyonlarının sayısı sembolüyle gösterilir (“en'den em'e kadar”) ve aşağıdaki formülle hesaplanır:
n elemanın m elemana göre diziliş sayısı şu şekilde bulunabilir: n eleman içeren bir kümeden m eleman seçin (bu çeşitli şekillerde yapılabilir); daha sonra ortaya çıkan kombinasyonların (alt kümelerin) her birinde, alt kümeleri sıralamak için tüm permütasyonları yapın (bu, P m yollarıyla yapılabilir). Bu nedenle çarpma kuralına göre şunu yazabiliriz:
Buradan veya
Formüllerin geçerli olduğu gösterilebilir:
Örnek 5. D - (a, b, c) kümesindeki 2 elemanın farklı kombinasyonlarını oluşturun; onların sayısını sayın.
Üç elementten iki elementin aşağıdaki kombinasyonları oluşturulabilir: (a, b); (AC); (M.Ö). Sayıları: (formül (4)).
Örnek 6. 10 kırmızı ve 4 pembe karanfil içeren bir vazodan 3 çiçek kaç farklı şekilde seçilebilir? 1 kırmızı karanfil ve 2 pembe karanfil seçersen ne olur?
Çiçeklerin seçilme sırası önemli olmadığı için 14 karanfil içeren bir vazodan 3 çiçek seçmenin birkaç yolu vardır. Formül (4)'ü kullanarak şunu buluruz: . Sonraki: Kırmızı karanfili farklı şekillerde seçebilirsiniz. Mevcut dört karanfilden iki pembe karanfili seçmenin birkaç yolu vardır. Bu nedenle çarpma kuralına göre farklı şekillerde bir kırmızı ve iki pembe karanfilden oluşan bir buket oluşturulabilir.
Geri dönüşlü seçim şeması
N'den m eleman seçildikten sonra elemanlar döndürülür ve sıralanırsa buna denir. tekrarlı yerleşimler.
Tekrarlı yerleştirmeler; elemanları, sıraları ve tekrar sayıları bakımından birbirinden farklılık gösterebilir. Her biri m tekrarlı olan n elemanın tüm yerleşimlerinin sayısı bir sembolle gösterilir ve formül (6) kullanılarak hesaplanır.
Örnek 7. 3 element a, b, c'den iki elementin tüm yerleşimlerini tekrarlarla oluşturur.
Formül (1.12)'ye göre tekrarlı ikililer halinde yerleştirme sayısı eşittir. Bunlar: (a,a), (a,b), (a,c), (b,b), (b,a), (b,c), (c,c), (c,a) , (c, b)
Örnek 8. Rakamlar kullanılarak kaç tane beş basamaklı sayı oluşturulabilir:
a) 2, 5, 7, 8 sayılarından oluşan beş basamaklı sayıların tümü, göründükleri sırayla (örneğin, 25558 ve 52855) veya sayıların kendisinde (örneğin, 52788) birbirinden farklıdır. ve 78888). Bu nedenle, 5'in 4 öğesinin tekrarlı düzenlemeleridir, yani. . Bu nedenle beş basamaklı sayıların gerekli sayısı . Çarpma kuralı kullanılarak da aynı sonuç elde edilebilir: Beş basamaklı bir sayının soldan ilk rakamı dört şekilde, ikincisi dört şekilde, üçüncüsü dörtte, dördüncüsü dörtte ve beşincisi dört şekilde seçilebilir. dört. Toplamda 4×4×4×4×4=1024 beş basamaklı sayı elde ederiz.
b) Beş basamaklı sayılar 0, 1, 9 rakamlarından oluşuyorsa soldaki ilk rakam iki şekilde seçilebilir (0 ilk rakamı işgal edemez), geri kalan dört rakamın her biri üç şekilde seçilebilir. yollar. Çarpma kuralına göre 2×3×3×3×3=162 gibi sayılar çıkacaktır. (Aksi takdirde: .)
N elemandan m eleman seçildiğinde, elemanlar başka bir sıralamaya gerek kalmadan döndürülürse buna denir. tekrarlı kombinasyonlar.
m'nin n elemanının tekrarlı tüm kombinasyonlarının sayısı bir sembolle gösterilir ve formülle hesaplanır
Örnek 9.Üç element a, b, c'den, iki elementin tüm kombinasyonlarını tekrarlarla oluşturur.
Formül (7)'ye göre ikilinin tekrarlı kombinasyon sayısı eşittir. Bu kombinasyonları tekrarlarla yapıyoruz: (a, a), (a.b), (a, c), (b,b), (b, c), (c, c).
Örnek 10.Üç çeşit çiçek varsa, 5 çiçekten oluşan bir buket kaç farklı şekilde yapılabilir?
Söz konusu set üç farklı elementten oluşmakta olup, numunelerin hacmi 5'e eşittir. Buketteki çiçeklerin sırası önemli olmadığından gerekli buket sayısı, üç elementin tekrarı olan kombinasyon sayısına eşittir. her biri 5 adet. Formül (7)'ye göre elimizde
N elemanlı bir kümenin k farklı elemanı olsun, 1. eleman n 1 defa tekrarlansın, 2. eleman n 2 defa..., k'inci eleman n k defa tekrarlansın ve n 1 +n 2 +... +n k =n .
Belirli bir kümenin n elemanının permütasyonlarına denir tekrarlı permütasyonlar n elementten oluşan.
N elemanın tekrarı ile permütasyonların sayısı sembolü ile gösterilir
Р n (n 1, n 2, …, n k) ve formülle hesaplanır
Örnek 11. 3, 3, 5, 5, 8 sayılarından kaç farklı beş basamaklı sayı oluşturulabilir?
Formül (8)'i uygulayalım. Burada n=5, n 1 =2, n 2 =2, n 3 = 1. 3, 5 ve 8 sayılarını içeren beş basamaklı farklı sayıların sayısı eşittir
Plan:
1. Kombinatorik elemanları.
2. Kombinatoriğin genel kuralları.
4. Kombinatoryal problemlerin çözümünde grafiklerin (şemaların) uygulanması.
1. Kombinatorik ve kökenleri.Kombinatorik Belirli bir kümeye ait elemanlardan belirli koşullara bağlı olarak kaç farklı kombinasyonun yapılabileceğine ilişkin soruların incelendiği matematik alanıdır.
Kombinatorik 16. yüzyılda ortaya çıktı. O dönemde toplumun ayrıcalıklı katmanlarının hayatında kumar (kartlar, zarlar) büyük bir yer tutuyordu. Piyangolar yaygındı. Başlangıçta, kombinatoryal problemler esas olarak kumarla ilgiliydi: 2 veya 3 zar atarak belirli sayıda puanı kaç farklı yoldan alabiliriz veya belirli bir kart oyununda 2 papazı kaç farklı yoldan alabiliriz. Bunlar ve kumarla ilgili diğer sorunlar, kombinatoriklerin geliştirilmesinde ve ayrıca olasılık teorisinin geliştirilmesinde itici güç olmuştur.
Zar oynarken farklı kombinasyonların sayısını ilk sayanlardan biri İtalyan matematikçi Tartaglia'ydı. Tabloları derledi (r zarında k puan almanın yollarının sayısı). Ancak aynı miktarda puanın farklı şekillerde düşebileceğini hesaba katmadığı için tabloları çok sayıda hata içeriyordu.
Kombinatorik konularının teorik çalışması 17. yüzyılda Fransız matematikçiler Blaise Pascal ve Fermat tarafından üstlenildi. Araştırmalarının çıkış noktası da kumar sorunlarıydı.
Kombinatoriklerin daha da geliştirilmesi J. Bernoulli, G. Leibniz, L. Euler'in isimleriyle ilişkilidir. Ancak çalışmalarında çeşitli oyunlara yapılan uygulamalar büyük rol oynadı.
Günümüzde ulaştırma problemlerini, özellikle de çizelgeleme problemlerini çözmek, üretim ve satış planlarını hazırlamak vb. için kombinatoryal yöntemler kullanılmaktadır.
2. Kombinatoriğin genel kuralları.Toplama kuralı: Eğer bir A nesnesi m yolla ve bir B nesnesi k yolla seçilebiliyorsa, o zaman "ya A ya da B" nesnesi m + k yolla seçilebilir.
Örnekler:
1. Bir kutuda n farklı renkte top olduğunu varsayalım. 1 top rastgele kaldırılıyor. Bu kaç farklı şekilde yapılabilir?
Cevap: n yol.
Bu n topu iki kutuya dağıtalım: birincisinde m tane top var, ikincisinde k tane top var. Rastgele seçilen bir kutudan rastgele 1 top çekiliyor. Bu kaç farklı şekilde yapılabilir?
Çözüm: Top birinci kutudan m farklı şekilde, ikinci kutudan ise k farklı şekilde çıkarılabilir. Bu durumda toplam yol sayısı m+k=n olur.
2. Deniz semaforu.Denizcilik semaforunda alfabenin her harfi, iki bayrağın işaretçinin vücuduna göre belirli bir konumuna karşılık gelir. Bu türden kaç tane sinyal olabilir?
Çözüm: Toplam sayı, her iki bayrak da işaretçinin vücudunun karşıt taraflarında bulunduğunda konumların ve işaretçinin vücudunun aynı tarafında bulunduğunda konumların toplamıdır. Olası pozisyonların sayısını sayarken toplam kuralı uygulanır.
Ürün kuralı: A nesnesi m şekilde seçilebiliyorsa ve bu tür her seçimden sonra başka bir B nesnesi (A nesnesinin seçimine bakılmaksızın) k şekilde seçilebiliyorsa, o zaman “A ve B” nesne çiftleri m * k cinsinden seçilebilir. yollar.
Örnekler:
1. Kaç tane iki basamaklı sayı var?Çözüm: Onlar sayısı 1'den 9'a kadar herhangi bir sayı ile gösterilebilir. Birler sayısı 0'dan 9'a kadar herhangi bir sayı ile gösterilebilir. Onlar sayısı 1 ise, birler sayısı herhangi bir sayı olabilir (0'dan itibaren) 9'a kadar). Böylece, onlar sayısı 1 olan 10 adet iki basamaklı sayı vardır. Diğer herhangi bir onluk sayı için de benzer şekilde mantık yürütürüz. O zaman 9 tane olduğunu hesaplayabiliriz. *10 = 90 adet iki basamaklı sayı.
2. 2 adet çekmece bulunmaktadır. Birinde m adet çok renkli küp, diğerinde ise k adet çok renkli top bulunmaktadır. “Küp-Top” çiftini kaç farklı şekilde seçebilirsiniz?
Çözüm: Top seçimi küp seçimine bağlı değildir ve bunun tersi de geçerlidir. Bu nedenle belirli bir çiftin seçilebileceği yolların sayısı m *k'dir.
3. Tekrarsız popülasyon ve tekrarsız örnek.Tekrarlanmayan nüfus a 1, a 2, a 3, ..., a n gibi sonlu sayıda farklı elemandan oluşan bir kümedir.
Örnek: N kümesi çok renkli parçalar.
Örnekleme hacmik (kN) belirli bir popülasyonun m elementinden oluşan bir gruptur.
Örnek: Verilen m'den seçilen çok renkli parçalardan dikilmiş rengârenk bir şerit n .
Gönderen gönderilerher biri n elemank bu tür örneklere, genel popülasyonun verilen n elementi arasından tekrar edilmeden seçilen, her biri k element içeren ve elementlerin bileşimi veya diziliş sırası bakımından birbirinden farklı olan örnekler denir.
- yerleşim sayısı n'ye göre k.
Yerleşim sayısı n'ye göre k şu şekilde belirlenebilir: ilk seçim nesnesi seçilebilir N yollar, ardından ikinci nesne seçilebilir n -1 yolu vb.
Bu formülü dönüştürdüğümüzde:
Unutulmamalıdır ki 0!=1.
Örnekler:
1. Futbol şampiyonasının A sınıfı 1. grubunda 17 takım yer alıyor. Madalyalar verilir: altın, gümüş ve bronz. Kaç farklı şekilde oynanabilir?
Çözüm:Kazanan takım kombinasyonları, unsurların bileşimi ve sırası bakımından birbirinden farklılık gösterir; 17'den 3'e kadar olan yerleşimlerdir.
2. Bilim topluluğu 25 kişiden oluşur. Dernek başkanı, başkan yardımcısı, bilimsel sekreter ve sayman seçmek gerekir. Bu kaç farklı şekilde yapılabilir?
Çözüm:Şirketin yönetim kombinasyonları, unsurların bileşimi ve sırası bakımından birbirinden farklılık gösterir; 25'ten 4'e kadar yerleşimlerdir.
Tekrarı olmayan permütasyonlar Nelementlertekrarı olmayan yerleşimler denir n'nin n elemanı yani yerleşimler birbirinden yalnızca öğelerin sırasına göre farklılık gösterir.
Permütasyon sayısı.
Örnekler:
1. 1, 2, 3, 4, 5 rakamlarından farklı rakamlardan oluşmak şartıyla kaç farklı beş basamaklı sayı oluşturulabilir?
Çözüm:5 elementin permütasyonları var.2. 6 adet çok renkli parçayı renkli bir kurdele halinde kaç farklı şekilde bir araya getirebilirsiniz?Çözüm:6 elementin permütasyonları var.
Tekrarı olmayan kombinasyonlar Ntarafından elemanlark bu tür örneklere, her biri k element içeren, genel popülasyonun verilen n elementi arasından tekrar edilmeden seçilen ve yalnızca elementlerin bileşimi bakımından birbirinden farklı olan örnekler denir.
- kombinasyon sayısı n'ye göre k
Her birinin elemanlarıkombinasyonlar düzenlenebiliryollar. Daha sonraÖrnekler:1. Bir satranç şampiyonasında yarı finale 20 kişi katılırsa ve sadece üç kişi finale çıkarsa, bu üç kişi kaç farklı şekilde belirlenebilir?
Çözüm:Bu durumda bu üçlünün yer alma sırasının bir önemi yoktur. Bu nedenle finale kalan üçlüler 20'ye 3'lü kombinasyonlardır.
2. Bir konferans için on kişiden üç delegeyi kaç farklı şekilde seçebilirsiniz?Çözüm:Bu durumda bu üçlünün yer alma sırasının bir önemi yoktur. Bu nedenle, üçlü delegeler 10'a 3'ün birleşimidir.
Soyut:
4.Birleşimsel problemlerin çözümünde grafiklerin (şemaların) kullanılması.
Her adımdaki olası seçimlerin sayısının hangi öğelerin daha önce seçildiğine bağlı olması durumunda, kombinasyon oluşturma süreci bir “ağaç” olarak gösterilebilir. İlk olarak, ilk adımda yapılabilecek farklı seçimler olduğu için bir noktadan o kadar çok parça çizilir. Her parçanın sonundan, eğer bu öğe ilk adımda seçilmişse, vb. ikinci adımda seçilebildiği kadar çok parça çizin.
Görev:
Uzay aracının komutları derlenirken seyahat katılımcılarının psikolojik uyumu konusu da dikkate alınıyor. 3 kişilik bir uzay gemisi mürettebatı oluşturmak gerekiyor: bir komutan, bir mühendis ve bir doktor. Komutanlık pozisyonu için 4 aday var: bir 1, bir 2, bir 3, bir 4 .Mühendis 3'ün yerine:b 1, b 2, b 3. Doktor yeri için - 3: c 1, c 2, c 3. Denetim şunu gösterdi: Komutana 1 psikolojik olarak mühendisler b 1 ve b 3 ile uyumludur ve doktorlar c 1 ve c 3. Komutan a 2 - mühendislerle birlikte b 1 ve b 2. ve tüm doktorlar. Komutana 3 - mühendislerleb 1 ve b 2 ve doktorlarc1 ve c3. Komutan a 4 - tüm mühendisler ve doktorla birlikte c2. Ayrıca mühendisb 1 doktorla uyumlu değil c 3, b 2 - doktorla c 1 ve b 3 - doktorla c 2. Bu koşullar altında gemi mürettebatı kaç farklı şekilde oluşturulabilir?
Çözüm:
İlgili “ağacı” oluşturalım.

Cevap: 10 kombinasyon.
Böyle bir ağaç bir grafiktir ve kombinatoryal problemleri çözmek için kullanılır.