Взяття логарифма. Що таке логарифм? Рішення логарифмів. Приклади. Властивості логарифмів. Приклади розв'язання логарифмів на підставі формул

логарифмом числа N по підставі а називається показник ступеня х , В яку потрібно звести а , Щоб отримати число N

За умови, що
,
,

З визначення логарифма випливає, що
, Тобто
- це рівність є основним логарифмическим тотожністю.

Логарифми по підставі 10 називаються десятковими логарифмами. замість
пишуть
.

Логарифми по підставі e називаються натуральними і позначаються
.

Основні властивості логарифмів.

Логарифм одиниці при будь-якій підставі дорівнює нулю

Логарифм добутку дорівнює сумі логарифмів співмножників.

3) Логарифм приватного дорівнює різниці логарифмів

множник
називається модулем переходу від логарифмів при підставі a до логарифмам при підставі b .

За допомогою властивостей 2-5 часто вдається звести логарифм складного виразу до результату простих арифметичних дій над логарифмами.

наприклад,

Такі перетворення логарифма називаються логарифмування. Перетворення зворотні логарифмуванню називаються потенцированием.

Глава 2. Елементи вищої математики.

1. Межі

межею функції
є кінцеве число А, якщо при прагненні xx 0 для кожного наперед заданого
, Знайдеться таке число
, Що як тільки
, то
.

Функція, що має межу, відрізняється від нього на нескінченно малу величину:
, Где- Б.М.В., тобто
.

Приклад. Розглянемо функцію
.

при прагненні
, функція y прямує до нуля:

1.1. Основні теореми про границі.

Межа постійної величини дорівнює цій постійній величині

.

Межа суми (різниці) кінцевого числа функцій дорівнює сумі (різниці) меж цих функцій.

Межа твори кінцевого числа функцій дорівнює добутку меж цих функцій.

Межа приватного двох функцій дорівнює приватному меж цих функцій, якщо межа знаменника не дорівнює нулю.

чудові межі

,
, де

1.2. Приклади обчислення меж

Однак, не всі межі обчислюються так просто. Найчастіше обчислення межі зводиться до розкриття невизначеності типу: або.

.

2. Похідна функції

Нехай ми маємо функцію
, Безперервну на відрізку
.

аргумент дістав сяке-таке збільшення
. Тоді і функція одержить збільшення
.

значенню аргументу відповідає значення функції
.

значенню аргументу
відповідає значення функції.

Отже,.

Знайдемо межа цього відношення при
. Якщо ця межа існує, то він називається похідною даної функції.

Визначення 3Проізводной даної функції
по аргументу називається границя відношення приросту функції до приросту аргументу, коли приріст аргументу довільним чином прямує до нуля.

Похідна функції
може бути позначена в такий спосіб:

; ; ; .

Визначення 4Операція знаходження похідної від функції називається дифференцированием.

2.1. Механічний зміст похідної.

Розглянемо прямолінійний рух деякого твердого тіла або матеріальної точки.

Нехай в деякий момент часу рухається точка
перебувала на відстані від початкового положення
.

Через деякий проміжок часу
вона перемістилася на відстань
. ставлення =- середня швидкість матеріальної точки
. Знайдемо межа цього відношення, враховуючи що
.

Отже, визначення миттєвої швидкості руху матеріальної точки зводиться до знаходження похідної від шляху за часом.

2.2. Геометричне значення похідної

Нехай у нас є графічно задана деяка функція
.

Мал. 1. Геометричний зміст похідної

якщо
, То точка
, Буде переміщатися по кривій, наближаючись до точки
.

отже
, Тобто значення похідної при даному значенні аргументу чисельно дорівнює тангенсу кута утвореного дотичною в даній точці з позитивним напрямком осі
.

2.3. Таблиця основних формул диференціювання.

Степенева функція

показова функція

логарифмічна функція

Тригонометрична функція

Зворотній тригонометрическая функція

2.4. Правила диференціювання.

похідна від

Похідна суми (різниці) функцій

Похідна добутку двох функцій

Похідна частки двох функцій

2.5. похідна від складної функції.

Нехай дана функція
така, що її можна представити у вигляді

і
, Де змінна є проміжним аргументом, тоді

Похідна складної функції дорівнює добутку похідної даної функції по проміжному аргументу на похідну проміжного аргументу по x.

Приклад 1.

Приклад 2.

3. Диференціал функції.

нехай є
, Дифференцируемая на деякому відрізку
і нехай у цієї функції є похідна

,

тоді можна записати

(1),

де - нескінченно мала величина,

так як при

Помноживши всі члени рівності (1) на
маємо:

де
- Б.М.В. вищого порядку.

величина
називається диференціалом функції
і позначається

.

3.1. Геометричне значення диференціала.

Нехай дана функція
.

Рис.2. Геометричний сенс диференціала.

.

Очевидно, що диференціал функції
дорівнює збільшенню ординати дотичної в цій точці.

3.2. Похідні і диференціали різних порядків.

Якщо є
, тоді
називається першою похідною.

Похідна від першої похідної називається похідною другого порядку і записується
.

Похідною n-го порядку від функції
називається похідна (n-1) -го порядку і записується:

.

Диференціал від диференціала функції називається другим диференціалом або диференціалом другого порядку.

.

.

3.3 Рішення біологічних задач із застосуванням диференціювання.

Задача1. Дослідження показали, що зростання колонії мікроорганізмів підкоряється закону
, де N - чисельність мікроорганізмів (в тис.), t -час (дні).

б) Чи буде в цей період чисельність колонії збільшуватися або зменшуватися?

Відповідь. Чисельність колонії буде збільшуватися.

Завдання 2. Вода в озері періодично тестується для контролю вмісту хвороботворних бактерій. через t днів після тестування концентрація бактерій визначається співвідношенням

.

Коли в озері настане мінімальна концентрація бактерій і можна буде в ньому купатися?

РешеніеФункція досягає max або min, коли її похідна дорівнює нулю.

,

Визначимо max або min буде через 6 днів. Для цього візьмемо другу похідну.

Відповідь: Через 6 днів буде мінімальна концентрація бактерій.

Як відомо, при перемножуванні виразів зі ступенями їх показники завжди складаються (a b * a c \u003d a b + c). Цей математичний закон був виведений Архімедом, а пізніше, в VIII столітті, математик Вірасен створив таблицю цілих показників. Саме вони послужили для подальшого відкриття логарифмів. Приклади використання цієї функції можна зустріти практично скрізь, де потрібно спростити громіздке множення на просте додавання. Якщо ви витратите хвилин 10 на прочитання цієї статті, ми вам пояснимо, що таке логарифми і як з ними працювати. Простою і доступною мовою.

Визначення в математиці

Логарифмом називається вираз такого вигляду: log ab \u003d c, тобто логарифмом будь-якого невід'ємного числа (тобто будь-якого позитивного) "b" по його підставі "a" вважається ступінь "c", в яку необхідно звести підставу "a", щоб в результаті отримати значення "b". Розберемо логарифм на прикладах, припустимо, є вираз log 2 8. Як знайти відповідь? Дуже просто, потрібно знайти таку ступінь, щоб з 2 в бажаного ступеня отримати 8. Проробивши в розумі деякі розрахунки, отримуємо число 3! І справді, адже 2 певною мірою 3 дає у відповіді число 8.

різновиди логарифмів

Для багатьох учнів і студентів ця тема здається складною та незрозумілою, однак насправді логарифми не так страшні, головне - зрозуміти загальний їх зміст і запам'ятати їх свойст і деякі правила. Існує три окремих види логарифмічних виразів:

1. Натуральний логарифм ln a, де підставою є число Ейлера (e \u003d 2,7).
2. Десятковий a, де підставою служить число 10.
3. Логарифм будь-якого числа b по підставі a\u003e 1.

Кожен з них вирішується стандартним способом, що включає в себе спрощення, скорочення і наступне приведення до одного логарифму за допомогою логарифмічних теорем. Для отримання вірних значень логарифмів слід запам'ятати їх властивості та черговість дій при їх рішеннях.

Правила і деякі обмеження

У математиці існує кілька правил-обмежень, які приймаються як аксіома, тобто не підлягають обговоренню і є істиною. Наприклад, не можна числа ділити на нуль, а ще неможливо витягти корінь парного степеня з негативних чисел. Логарифми також мають свої правила, дотримуючись яких можна з легкістю навчитися працювати навіть з довгими і ємними логарифмічними виразами:

• підставу "a" завжди повинно бути більше нуля, і при цьому не бути рівним 1, інакше вираз втратить свій сенс, адже "1" і "0" в будь-якого ступеня завжди рівні своїм значенням;
• якщо а\u003e 0, то і а b\u003e 0, виходить, що і "з" має бути більше нуля.

Як вирішувати логарифми?

Наприклад, дано завдання знайти відповідь рівняння 10 х \u003d 100. Це дуже легко, потрібно підібрати такий ступінь, звівши в яку число десять, ми отримаємо 100. Це, звичайно ж, 10 2 \u003d 100.

А тепер давайте уявимо даний вираз у вигляді логарифмічного. Отримаємо log 10 100 \u003d 2. При вирішенні логарифмів всі дії практично сходяться до того, щоб знайти ту ступінь, в яку необхідно ввести підставу логарифма, щоб отримати заданий число.

Для безпомилкового визначення значення невідомої ступеня необхідно навчитися працювати з таблицею ступенів. Виглядає вона наступним чином:

Як бачите, деякі показники ступеня можна вгадати інтуїтивно, якщо є технічний склад розуму і знання таблиці множення. Однак для великих значень потрібно таблиця ступенів. Нею можуть користуватися навіть ті, хто зовсім нічого не тямить в складних математичних темах. У лівому стовпчику вказані числа (підстава a), верхній ряд чисел - це значення ступеня c, в яку зводиться число a. На перетині в осередках визначені значення чисел, які є відповіддю (a c \u003d b). Візьмемо, наприклад, найпершу осередок з числом 10 і зведемо її в квадрат, отримаємо значення 100, яке зазначено на перетині двох наших осередків. Все так просто і легко, що зрозуміє навіть справжнісінький гуманітарій!

Рівняння і нерівності

Виходить, що за певних умов показник ступеня - це і є логарифм. Отже, будь-які математичні чисельні вираження можна записати у вигляді логарифмічного рівності. Наприклад, 3 4 \u003d 81 можна записати у вигляді логарифма числа 81 по підставі 3, рівному чотирьом (log 3 81 \u003d 4). Для негативних ступенів правила такі ж: 2 -5 \u003d 1/32 запишемо у вигляді логарифма, отримаємо log 2 (1/32) \u003d -5. Однією з найбільш захоплюючих розділів математики є тема "логарифми". Приклади і рішення рівнянь ми розглянемо трохи нижче, відразу ж після вивчення їх властивостей. А зараз давайте розберемо, як виглядають нерівності і як їх відрізнити від рівнянь.

Дано вираз такого вигляду: log 2 (x-1)\u003e 3 - воно є логарифмическим нерівністю, Так як невідоме значення "х" знаходиться під знаком логарифма. А також в вираженні порівнюються дві величини: логарифм шуканого числа за основою два більше, ніж число три.

Найголовніша відмінність між логарифмічними рівняннями і нерівностями полягає в тому, що рівняння з логарифмами (приклад - логарифм 2 x \u003d √9) мають на увазі у відповіді одне або кілька певних числових значень, тоді як при вирішенні нерівності визначаються як область допустимих значень, так і точки розриву цієї функції. Як наслідок, у відповіді виходить не просте безліч окремих чисел як у відповіді рівняння, а а безперервний ряд або набір чисел.

Основні теореми про логарифми

При вирішенні примітивних завдань по знаходженню значень логарифма, його властивості можна і не знати. Однак коли мова заходить про логарифмічних рівняннях або нерівностях, в першу чергу, необхідно чітко розуміти і застосовувати на практиці всі основні властивості логарифмів. З прикладами рівнянь ми познайомимося пізніше, давайте спочатку розберемо кожне властивість більш докладно.

1. Основне тотожність виглядає так: а logaB \u003d B. Воно застосовується лише за умови, коли а більше 0, не дорівнює одиниці і B більше нуля.
2. Логарифм твори можна уявити в такій формулі: log d (s 1 * s 2) \u003d log d s 1 + log d s 2. При цьому обов'язковою умовою є: d, s 1 і s 2\u003e 0; а ≠ 1. Можна навести доказ для цієї формули логарифмів, з прикладами і рішенням. Нехай log as 1 \u003d f 1 і log as 2 \u003d f 2, тоді a f1 \u003d s 1, a f2 \u003d s 2. Отримуємо, що s 1 * s 2 \u003d a f1 * a f2 \u003d a f1 + f2 (властивості ступенів ), а далі по визначенню: log a (s 1 * s 2) \u003d f 1 + f 2 \u003d log a s1 + log as 2, що й треба було довести.
3. Логарифм приватного виглядає так: log a (s 1 / s 2) \u003d log a s 1 - log a s 2.
4. Теорема у вигляді формули набуває такого вигляду: log a q b n \u003d n / q log a b.

Називається ця формула "властивістю ступеня логарифма". Вона нагадує собою властивості звичайних ступенів, і не дивно, адже вся математика тримається на закономірних постулатах. Давайте подивимося на доказ.

Нехай log a b \u003d t, виходить a t \u003d b. Якщо звести обидві частини в ступінь m: a tn \u003d b n;

але так як a tn \u003d (a q) nt / q \u003d b n, отже log a q b n \u003d (n * t) / t, тоді log a q b n \u003d n / q log a b. Теорема доведена.

Приклади завдань і нерівностей

Найпоширеніші типи завдань на тему логарифмів - приклади рівнянь і нерівностей. Вони зустрічаються практично у всіх задачниках, а також входять в обов'язкову частину іспитів з математики. Для вступу до університету або здачі вступних випробувань з математики необхідно знати, як правильно вирішувати подібні завдання.

На жаль, єдиного плану або схеми за рішенням і визначенням невідомого значення логарифма не існує, проте до кожного математичного нерівності або логарифмическому рівняння можна застосувати певні правила. Перш за все слід з'ясувати, чи можна спростити вираз або привести до загального вигляду. Спрощувати довгі логарифмічні вирази можна, якщо правильно використовувати їх властивості. Давайте швидше з ними познайомимося.

При вирішенні ж логарифмічних рівнянь, слід визначити, який перед нами вид логарифма: приклад вираження може містити натуральний логарифм або ж десятковий.

Ось приклади ln100, ln1026. Їх рішення зводиться до того, що потрібно визначити ту ступінь, в якій підставу 10 дорівнюватиме 100 і 1 026 відповідно. Для рішень же натуральних логарифмів потрібно застосувати логарифмічні тотожності або ж їх властивості. Давайте на прикладах розглянемо рішення логарифмічних завдань різного типу.

Як використовувати формули логарифмів: з прикладами і рішеннями

Отже, розглянемо приклади використання основних теорем про логарифми.

1. Властивість логарифма твори можна застосовувати в завданнях, де необхідно розкласти велике значення числа b на більш прості множники. Наприклад, log 2 4 + log 2 128 \u003d log 2 (4 * 128) \u003d log 2 512. Відповідь дорівнює 9.
2. log 4 8 \u003d log 2 2 2 3 \u003d 3/2 log 2 + 2 \u003d 1,5 - як бачите, застосовуючи четверте властивість ступеня логарифма, вдалося вирішити на перший погляд складне і нерозв'язних вираз. Необхідно всього лише розкласти підставу на множники і потім винести значення ступеня з знака логарифма.

Завдання з ЄДІ

Логарифми часто зустрічаються на вступних іспитах, особливо багато логарифмічних завдань в ЄДІ (державний іспит для всіх випускників шкіл). Зазвичай ці завдання присутні не тільки в частині А (найлегша тестова частина іспиту), але і в частині С (найскладніші і об'ємні завдання). Іспит на увазі точне і ідеальне знання теми "Натуральні логарифми".

Приклади і рішення задач взяті з офіційних варіантів ЄДІ. Давайте подивимося, як вирішуються такі завдання.

Дано log 2 (2x-1) \u003d 4. Рішення:
перепишемо вираз, трохи його спростивши log 2 (2x-1) \u003d 2 2, за визначенням логарифма отримаємо, що 2x-1 \u003d 2 4, отже 2x \u003d 17; x \u003d 8,5.

• Все логарифми найкраще приводити до одного основи, щоб рішення не було громіздким і заплутаним.
• Всі вираз, що стоять під знаком логарифма, вказуються як позитивні, тому при винесенні множником показника ступеня вираження, який стоїть під знаком логарифма і як його заснування, залишається під логарифмом вираз має бути позитивно.

У міру розвитку суспільства, ускладнення виробництва розвивалася і математика. Рух від простого до складного. Від звичайного обліку методом додавання і віднімання, при їх багаторазовому повторенні, прийшли до поняття множення і ділення. Скорочення багаторазово повторюваною операції множення стало поняттям зведення в ступінь. Перші таблиці залежності чисел від заснування і числа зведення в ступінь були складені ще в VIII столітті індійським математиком Варас. З них і можна відраховувати час виникнення логарифмів.

історичний нарис

Відродження Європи в XVI столітті стимулювало і розвиток механіки. Т ребовался великий обсяг обчислення, Пов'язаних з множенням і діленням багатозначних чисел. Стародавні таблиці надали велику послугу. Вони дозволяли замінювати складні операції на більш прості - додавання і віднімання. Великим кроком вперед стала робота математика Міхаеля Штіфеля, опублікована в 1544 році, в якій він реалізував ідею багатьох математиків. Що дозволило використовувати таблиці не тільки для ступенів у вигляді простих чисел, але і для довільних раціональних.

1614 року шотландець Джон Непер, розвиваючи ці ідеї, вперше ввів новий термін «логарифм числа». Були складені нові складні таблиці для розрахунку логарифмів синусів і косинусів, а також тангенсов. Це сильно скоротило працю астрономів.

Стали з'являтися нові таблиці, які успішно використовувалися вченими протягом трьох століть. Минуло чимало часу, перш ніж нова операція в алгебрі придбала свій завершений вигляд. Було дано визначення логарифма, і його властивості були вивчені.

Тільки в XX столітті з появою калькулятора і комп'ютера людство відмовилося від древніх таблиць, успішно працювали протягом XIII століть.

Сьогодні ми називаємо логарифмом b по підставі a число x, яке є ступенем числа а, щоб вийшло число b. У вигляді формули це записується: x \u003d log a (b).

Наприклад, log 3 (9) буде дорівнює 2. Це очевидно, якщо йти за визначенням. Якщо 3 звести в ступінь 2, то отримаємо 9.

Так, сформульоване визначення ставить тільки одне обмеження, числа a і b повинні бути речовими.

різновиди логарифмів

Класичне визначення носить назву речовинний логарифм і фактично є рішенням рівняння a x \u003d b. Варіант a \u003d 1 є прикордонним і не представляє інтересу. Увага: 1 в будь-якого ступеня дорівнює 1.

Речовий значення логарифма визначено тільки при підставі і аргументі більше 0, при цьому основа не повинна дорівнювати 1.

Особливе місце в області математики грають логарифми, які будуть називатися залежно від величини їх підстави:

Правила та обмеження

Основоположним властивістю логарифмів є правило: логарифм добутку дорівнює логарифмічною сумі. log abp \u003d lоg a (b) + log a (p).

Як варіант цього твердження буде: log з (b / p) \u003d lоg з (b) - log з (p), функція приватного дорівнює різниці функцій.

З попередніх двох правил легко видно, що: lоg a (b p) \u003d p * log a (b).

Серед інших властивостей можна виділити:

Зауваження. Не треба робити поширену помилку - логарифм суми не дорівнює сумі логарифмів.

Багато століть операція пошуку логарифма була досить трудомісткою завданням. Математики користувалися відомою формулою логарифмічною теорії розкладання на многочлен:

ln (1 + x) \u003d x - (x ^ 2) / 2 + (x ^ 3) / 3 - (x ^ 4) / 4 + ... + ((-1) ^ (n + 1)) * (( x ^ n) / n), де n - натуральне число більше 1, що визначає точність обчислення.

Логарифми з іншими підставами обчислювалися, використовуючи теорему про перехід від одного підстави до іншого і властивості логарифма твори.

Так як цей спосіб дуже трудомісткий і при вирішенні практичних завдань трудноосуществім, то використовували заздалегідь складені таблиці логарифмів, що значно прискорювало всю роботу.

У деяких випадках використовували спеціально складені графіки логарифмів, що давало меншу точність, але значно прискорювало пошук потрібного значення. Крива функції y \u003d log a (x), побудована за декількома точками, дозволяє за допомогою звичайної лінійки знаходити значення функції в будь-якій точці. Інженери тривалий час для цих цілей використовували так звану міліметровий папір.

У XVII столітті з'явилися перші допоміжні аналогові обчислювальні умови, які до XIX століття набули закінченого вигляду. Найбільш вдале пристрій одержав назву логарифмічна лінійка. При всій простоті пристрою, її поява значно прискорило процес всіх інженерних розрахунків, і це переоцінити важко. В даний час вже мало хто знайомий з цим пристроєм.

Поява калькуляторів і комп'ютерів зробило безглуздим використання будь-яких інших пристроїв.

Рівняння і нерівності

Для вирішення різних рівнянь і нерівностей з використанням логарифмів застосовуються такі формули:

• Перехід від одного підстави до іншого: lоg a (b) \u003d log c (b) / log c (a);
• Як наслідок попереднього варіанту: lоg a (b) \u003d 1 / log b (a).

Для вирішення нерівностей корисно знати:

• Значення логарифма буде позитивним тільки в тому випадку, коли підстава і аргумент одночасно більше або менше одиниці; якщо хоча б одна умова порушено, значення логарифма буде негативним.
• Якщо функція логарифма застосовується до правої і лівої частини нерівності, і підстава логарифма більше одиниці, то знак нерівності зберігається; в іншому випадку він змінюється.

приклади завдань

Розглянемо кілька варіантів застосування логарифмів і їх властивості. Приклади з рішенням рівнянь:

Розглянемо варіант розміщення логарифма в ступеня:

• Завдання 3. Обчислити 25 ^ log 5 (3). Рішення: в умовах завдання запис аналогічна наступної (5 ^ 2) ^ log5 (3) або 5 ^ (2 * log 5 (3)). Запишемо по-іншому: 5 ^ log 5 (3 * 2), або квадрат числа в якості аргументу функції можна записати як квадрат самої функції (5 ^ log 5 (3)) ^ 2. Використовуючи властивості логарифмів, цей вислів одно 3 ^ 2. Відповідь: в результаті обчислення отримуємо 9.

Практичне застосування

Будучи виключно математичним інструментом, здається далеким від реального життя, що логарифм несподівано придбав велике значення для опису об'єктів реального світу. Важко знайти науку, де його не застосовують. Це в повній мірі відноситься не тільки до природних, а й гуманітарних галузей знань.

логарифмічні залежності

Наведемо кілька прикладів числових залежностей:

Механіка і фізика

Історично механіка і фізика завжди розвивалися з використанням математичних методів дослідження і одночасно служили стимулом для розвитку математики, в тому числі логарифмів. Теорія більшості законів фізики написана мовою математики. Наведемо лише два приклади опису фізичних законів з використанням логарифма.

Вирішувати завдання розрахунку такої складної величини як швидкість ракети можна, застосовуючи формулу Ціолковського, яка поклала початок теорії освоєння космосу:

V \u003d I * ln (M1 / M2), де

• V - кінцева швидкість літального апарату.
• I - питома імпульс двигуна.
• M 1 - початкова маса ракети.
• M 2 - кінцева маса.

Інший важливий приклад - це використання у формулі іншого великого вченого Макса Планка, яка служить для оцінки рівноважного стану в термодинаміки.

S \u003d k * ln (Ω), де

• S - термодинамічна властивість.
• k - постійна Больцмана.
• Ω - статистичний вага різних станів.

хімія

Менш очевидним буде використання формул в хімії, що містять відношення логарифмів. Наведемо теж тільки два приклади:

• Рівняння Нернста, умова окислювально-відновного потенціалу середовища по відношенню до активності речовин і константою рівноваги.
• Розрахунок таких констант, як показник автопроліза і кислотність розчину теж не обходяться без нашої функції.

Психологія і біологія

І вже зовсім незрозуміло до чого тут психологія. Виявляється, сила відчуття добре описується цією функцією як зворотне відношення значення інтенсивності подразника до нижнього значення інтенсивності.

Після вищенаведених прикладів вже не дивує, що і в біології широко використовується тема логарифмів. Про біологічні форми, відповідні логарифмическим спіралям, можна писати цілі томи.

інші області

Здається, неможливо існування світу без зв'язку з цією функцією, і вона править усіма законами. Особливо, коли закони природи пов'язані з геометричною прогресією. Варто звернутися до сайту МатПрофі, і таких прикладів знайдеться безліч в наступних сферах діяльності:

Список може бути нескінченним. Освоївши основні закономірності цієї функції, можна зануритися в світ нескінченної мудрості.

(Від грецького λόγος - «слово», «ставлення» і ἀριθμός - «число») числа b по підставі a (Log α b) Називається таке число c, і b= a c, Тобто записи log α b=c і b \u003d a c еквівалентні. Логарифм має сенс, якщо a\u003e 0, а ≠ 1, b\u003e 0.

Говорячи іншими словами логарифм числа b по підставі аформулюється як показник ступеня, в яку треба звести число a, Щоб отримати число b(Логарифм існує тільки у позитивних чисел).

З цього формулювання випливає, що обчислення x \u003d log α b, Рівнозначно рішенням рівняння a x \u003d b.

наприклад:

log 2 8 \u003d 3 тому, що 8 \u003d 2 3.

Виділимо, що зазначена формулювання логарифма дає можливість відразу визначити значення логарифма, Коли число під знаком логарифма виступає деяким ступенем підстави. І в правду, формулювання логарифма дає можливість обґрунтувати, що якщо b \u003d a з, То логарифм числа b по підставі a дорівнює з. Також ясно, що тема логарифмирования тісно взаємопов'язана з темою ступеня числа.

Обчислення логарифма називають логарифмування. Логарифмування - це математична операція взяття логарифма. При логарифмування, твори співмножників трансформується в суми членів.

потенціювання - це математична операція зворотна логарифмуванню. При потенціюванні заданий підставу зводиться до степеня вираження, над яким виконується потенцирование. При цьому суми членів трансформуються в твір співмножників.

Досить часто використовуються речові логарифми з підставами 2 (двійковий), е число Ейлера e ≈ 2,718 (натуральний логарифм) і 10 (десятковий).

На даному етапі доцільно розглянути зразки логарифмівlog 7 2 , ln √ 5, lg0.0001.

А записи lg (-3), log -3 3.2, log -1 -4.3 не мають сенсу, так як в першій з них під знаком логарифма поміщено негативне число, в другій - негативне число в підставі, а в третій - і негативне число під знаком логарифма і одиниця в підставі.

Умови визначення логарифма.

Варто окремо розглянути умови a\u003e 0, a ≠ 1, b\u003e 0.прі яких дається визначення логарифма. Розглянемо, чому взяті ці обмеження. У цей нам допоможе рівність виду x \u003d log α b , Зване основним логарифмическим тотожністю, яке безпосередньо випливає з даного вище визначення логарифма.

візьмемо умова a ≠ 1. Оскільки одиниця в будь-якого ступеня дорівнює одиниці, то рівність x \u003d log α b може існувати лише при b \u003d 1, Але при цьому log 1 + 1 буде будь-яким дійсним числом. Для виключення цієї неоднозначності і береться a ≠ 1.

Доведемо необхідність умови a\u003e 0. при a \u003d 0 за формулюванням логарифма може існувати тільки при b \u003d 0. І відповідно тоді log 0 0може бути будь-яким відмінним від нуля дійсним числом, так як нуль в будь-який відмінною від нуля ступеня є нуль. Виключити цю неоднозначність дає умова a ≠ 0. А при a<0 нам би довелося відкинути розбір раціональних і ірраціональних значень логарифма, оскільки ступінь з раціональним і ірраціональним показником визначена лише для невід'ємних підстав. Саме з цієї причини і обумовлено умова a\u003e 0.

І остання умова b\u003e 0 випливає з нерівності a\u003e 0, Оскільки x \u003d log α b, А значення ступеня з позитивним підставою a завжди позитивно.

Особливості логарифмів.

логарифми характеризуються відмінними особливостями, Які зумовили їх повсюдне вживання для значного полегшення кропітких розрахунків. При переході «в світ логарифмів» множення трансформується на значно більш легке складання, розподіл - на віднімання, а зведення в ступінь і добування кореня трансформуються відповідне в множення і ділення на показник ступеня.

Формулювання логарифмів і таблицю їх значень (для тригонометричних функцій) Вперше видав в 1614 році шотландський математик Джон Непер. Логарифмічні таблиці, збільшені і деталізовані іншими вченими, широко використовувалися при виконанні наукових і інженерних обчислень, і залишалися актуальними поки не стали застосовуватися електронні калькулятори і комп'ютери.

логарифмом позитивного числаN за основою( b> 0, b1 ) називається показник ступеняx , В яку потрібно звести b, щоб отримати N .

Позначення логарифма:

Ця запис рівнозначна наступною:b x \u003d N .

П р и м і р и: log 3 81 \u003d 4, так, як 3 4 \u003d 81;

Log 1/3 27 \u003d – 3, так як (1/3) - 3 \u003d 3 3 \u003d 27.

Вищенаведене визначення логарифма можна записати у вигляді тотожності:

Основні властивості логарифмів.

1) log b= 1 , так як b 1 \u003d B.

b

2) log 1 = 0 , так як b 0 = 1 .

b

3) Логарифм добутку дорівнює сумі логарифмів співмножників:

log ( ab) \u003d Log a+ log b.

4) Логарифм приватного дорівнює різниці логарифмів діленого і дільника:

log ( a/ b) \u003d Log a- log b.

5) Логарифм ступеня дорівнює добутку показника степеня на логарифм її заснування:

log ( b k ) = k · log b.

Наслідком цієї властивості є наступне:логарифм кореня дорівнює логарифму подкоренного числа, діленому на ступінь кореня:

6) Якщо в підставі логарифма знаходиться ступінь, то величину, зворотний показнику ступеня, можна винести за знак балкирима:

Два останніх властивості можна об'єднати в одне:

7) Формула модуля переходу (т.e . переходу від однієї підстави логарифма до іншого основи):

В окремому випадку при N \u003d a маємо:

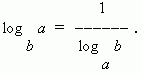
десятковим логарифмом називається логарифм по підставі10. Він позначається lg, тобто log 10 N = lg N . Логарифми чисел 10, 100, 1000, ... p авни відповідно 1, 2, 3, ...,тобто мають стільки позитивних

одиниць, скільки нулів стоїть в логаріфміруемом числі після одиниці. Логарифми чисел 0.1, 0.01, 0.001, ...p авни відповідно -1, –2, -3, ..., тобто мають стільки негативних одиниць, скільки нулів стоїть в логаріфміруемом числі перед одиницею ( вважаючи і нуль цілих). логарифми інших чисел мають дробову частину, яка називається мантиссой. цілачастина логарифма називається характеристикою. Для практичного притрансформаційних змін десяткові логарифми найбільш зручні.

натуральним логарифмом називається логарифм по підставі е. він позначається ln, тобто log eN = ln N. число е є ірраціональним, йогонаближене значення 2.718281828.воно є межею, до якого прагне число(1 + 1 / n) n при необмеженому зростанні n (Див. перший чудовий межа ).
Як це не здасться дивним, натуральні логарифми виявилися дуже зручними при проведенні різного роду операцій, пов'язаних з аналізом функцій.Обчислення логарифмів за основою ездійснюється набагато швидше, ніж по будь-якій іншій підставі.