ما هي النقطة الدنيا للدالة؟ المادة النظرية. نواصل البحث عن القيم القصوى للدالة معًا

النقطة القصوى للدالة هي النقطة في مجال تعريف الدالة التي تأخذ فيها قيمة الدالة قيمة دنيا أو قصوى. تسمى قيم الوظيفة عند هذه النقاط الحدود القصوى (الحد الأدنى والحد الأقصى) للوظيفة.

تعريف. نقطة س1 مجال الوظيفة F(س) يسمى أقصى نقطة للوظيفة ، إذا كانت قيمة الدالة عند هذه النقطة أكبر من قيم الدالة عند نقاط قريبة بدرجة كافية منها، وتقع على يمينها ويسارها (أي أن التباين يحمل F(س0 ) > F(س 0 + Δ س) س1 أقصى.

تعريف. نقطة س2 مجال الوظيفة F(س) يسمى النقطة الدنيا للوظيفة، إذا كانت قيمة الدالة عند هذه النقطة أقل من قيم الدالة عند نقاط قريبة بدرجة كافية منها، وتقع على يمينها ويسارها (أي أن التباين يحمل F(س0 ) < F(س 0 + Δ س) ). في هذه الحالة نقول أن الدالة عند هذه النقطة س2 الحد الأدنى.

دعنا نقول نقطة س1 - النقطة القصوى للوظيفة F(س) . ثم في الفاصل الزمني حتى س1 تزيد الوظيفة، وبالتالي فإن مشتقة الدالة أكبر من الصفر ( F "(س) > 0)، وفي الفاصل الزمني بعد ذلك س1 تنخفض الدالة وبالتالي مشتق من وظيفةأقل من الصفر ( F "(س) < 0 ). Тогда в точке س1

دعونا نفترض أيضا أن هذه النقطة س2 - النقطة الدنيا للوظيفة F(س) . ثم في الفاصل الزمني حتى س2 الدالة تتناقص، ومشتقة الدالة أقل من الصفر ( F "(س) < 0 ), а в интервале после س2 الدالة متزايدة، ومشتقة الدالة أكبر من الصفر ( F "(س)> 0). في هذه الحالة أيضا عند هذه النقطة س2 مشتق الدالة صفر أو غير موجود.

نظرية فيرما (علامة ضرورية على وجود الحد الأقصى للدالة). إذا كانت النقطة س0 - النقطة القصوى للوظيفة F(س) ، عند هذه النقطة يكون مشتق الدالة يساوي صفر ( F "(س) = 0) أو غير موجود.

تعريف. تسمى النقاط التي يكون فيها مشتق الدالة صفراً أو غير موجود نقاط حرجة .

مثال 1.دعونا نفكر في الوظيفة.

عند هذه النقطة س= 0 مشتقة الدالة هي صفر، وبالتالي النقطة س= 0 هي النقطة الحرجة. ومع ذلك، كما يمكن أن نرى في الرسم البياني للدالة، فإنه يزيد في جميع أنحاء مجال التعريف بأكمله، وبالتالي فإن النقطة س= 0 ليست النقطة القصوى لهذه الدالة.

وبالتالي فإن الشروط التي تكون مشتقة الدالة عند نقطة ما تساوي صفرًا أو غير موجودة هي شروط ضرورية لحد أقصى، ولكنها ليست كافية، حيث يمكن إعطاء أمثلة أخرى لدوال تتوفر فيها هذه الشروط، ولكن الدالة لا يوجد حد أقصى عند النقطة المقابلة. لهذا يجب أن يكون هناك أدلة كافية، مما يسمح للمرء بالحكم على ما إذا كان هناك حد متطرف عند نقطة حرجة معينة ونوع الحد الأقصى هو - الحد الأقصى أو الحد الأدنى.

النظرية (أول علامة كافية على وجود الحد الأقصى للدالة).نقطة حرجة س0 F(س) إذا تغيرت إشارة مشتق الدالة عند المرور بهذه النقطة، وإذا تغيرت الإشارة من "زائد" إلى "ناقص"، فهي نقطة عظمى، وإذا كانت من "ناقص" إلى "زائد"، إذن إنها نقطة الحد الأدنى.

إذا كان بالقرب من هذه النقطة س0 ، إلى اليسار واليمين منه، يحتفظ المشتق بعلامته، وهذا يعني أن الدالة إما تتناقص فقط أو تزيد فقط في منطقة معينة من النقطة س0 . في هذه الحالة، عند هذه النقطة س0 ليس هناك المدقع.

لذا، لتحديد النقاط القصوى للوظيفة، عليك القيام بما يلي :

1. العثور على مشتق من وظيفة.
2. مساواة المشتقة بالصفر وتحديد النقاط الحرجة.
3. حدد النقاط الحرجة على خط الأعداد عقليًا أو على الورق وحدد علامات مشتق الدالة في الفترات الناتجة. إذا تغيرت إشارة المشتقة من "موجب" إلى "ناقص"، فإن النقطة الحرجة هي النقطة القصوى، وإذا كانت من "ناقص" إلى "موجب"، فإن النقطة الحرجة هي النقطة الصغرى.
4. احسب قيمة الدالة عند النقاط القصوى.

مثال 2.أوجد الحد الأقصى للدالة .

حل. لنجد مشتقة الدالة:

دعونا نساوي المشتقة بالصفر للعثور على النقاط الحرجة:

.

نظرًا لأن أي قيم لـ "x" لا يساوي المقام صفرًا، فإننا نساوي البسط بالصفر:

حصلت على نقطة حرجة واحدة س= 3 . دعونا نحدد إشارة المشتقة في الفترات المحددة بهذه النقطة:

في الفترة من ناقص اللانهاية إلى 3 - علامة ناقص، أي أن الدالة تتناقص،

في الفترة من 3 إلى زائد اللانهاية هناك علامة زائد، أي أن الدالة تزداد.

وهذا هو، الفترة س= 3 هي النقطة الدنيا.

لنجد قيمة الدالة عند النقطة الصغرى:

وبذلك يتم إيجاد النقطة القصوى للدالة: (3؛ 0)، وهي النقطة الصغرى.

النظرية (العلامة الكافية الثانية لوجود الحد الأقصى للدالة).نقطة حرجة س0 هي النقطة القصوى للوظيفة F(س) إذا كان المشتق الثاني للدالة عند هذه النقطة لا يساوي الصفر ( F ""(س) ≠ 0) وإذا كانت المشتقة الثانية أكبر من الصفر ( F ""(س) > 0)، فالنقطة القصوى، وإذا كانت المشتقة الثانية أقل من الصفر ( F ""(س) < 0 ), то точкой минимума.

ملاحظة 1. إذا كان عند هذه النقطة س0 فإذا اختفت المشتقتان الأولى والثانية، فإنه في هذه المرحلة لا يمكن الحكم على وجود الحد الأقصى بناء على المعيار الكافي الثاني. في هذه الحالة، تحتاج إلى استخدام المعيار الكافي الأول للحد الأقصى للدالة.

الملاحظة 2. المعيار الكافي الثاني للحد الأقصى للدالة لا ينطبق حتى عندما لا يكون المشتق الأول موجودًا عند نقطة ثابتة (ثم لا يكون المشتق الثاني موجودًا أيضًا). في هذه الحالة، تحتاج أيضًا إلى استخدام الإشارة الكافية الأولى للقيمة القصوى للدالة.

الطبيعة المحلية للدالة القصوى

يترتب على التعريفات المذكورة أعلاه أن الحد الأقصى للدالة محلي بطبيعته - فهو أكبر وأصغر قيمة للدالة مقارنة بالقيم القريبة.

لنفترض أنك تنظر إلى أرباحك على مدار عام واحد. إذا كسبت 45000 روبل في شهر مايو، وفي أبريل 42000 روبل وفي يونيو 39000 روبل، فإن أرباح شهر مايو هي الحد الأقصى لدالة الأرباح مقارنة بالقيم القريبة. لكن في أكتوبر كسبت 71000 روبل، وفي سبتمبر 75000 روبل، وفي نوفمبر 74000 روبل، لذا فإن أرباح شهر أكتوبر هي الحد الأدنى لدالة الأرباح مقارنة بالقيم القريبة. ويمكنك أن ترى بسهولة أن الحد الأقصى بين قيم أبريل ومايو ويونيو أقل من الحد الأدنى لشهر سبتمبر وأكتوبر ونوفمبر.

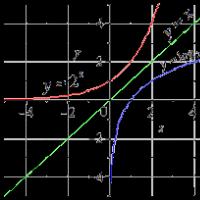
بشكل عام، يمكن أن يكون للدالة في فترة ما عدة نقاط متطرفة، وقد يتبين أن قيمة صغرى معينة للدالة أكبر من أي قيمة عظمى. لذلك، بالنسبة للوظيفة الموضحة في الشكل أعلاه، .

وهذا يعني أنه لا ينبغي للمرء أن يعتقد أن الحد الأقصى والحد الأدنى للدالة هما، على التوالي، أكبر وأصغر قيمها في المقطع بأكمله قيد النظر. عند النقطة القصوى تكون للدالة أكبر قيمة فقط بالمقارنة مع تلك القيم التي تكون عند جميع النقاط قريبة بما فيه الكفاية من النقطة القصوى، وعند النقطة الدنيا تكون لها أصغر قيمة فقط بالمقارنة مع تلك القيم ​​​​أنها قريبة بما فيه الكفاية في جميع النقاط من النقطة الدنيا.

لذلك، يمكننا توضيح المفهوم أعلاه للنقاط القصوى للدالة ونسمي الحد الأدنى من النقاط المحلية، والحد الأقصى من النقاط المحلية.

نحن نبحث عن الحد الأقصى للدالة معًا

مثال 3.

الحل: الدالة معرفة ومستمرة على خط الأعداد بأكمله. مشتق منه موجود أيضًا على خط الأعداد بأكمله. لذلك، في هذه الحالة، النقاط الحرجة هي فقط تلك التي، أي. ، من أين و . النقاط الحرجة وتقسيم مجال تعريف الدالة بأكمله إلى ثلاث فترات من الرتابة: . دعونا نختار نقطة تحكم واحدة في كل منها ونوجد إشارة المشتقة عند هذه النقطة.

بالنسبة للفاصل الزمني، يمكن أن تكون نقطة التحكم: العثور على. بأخذ نقطة في الفترة نحصل عليها، وبأخذ نقطة في الفترة نحصل عليها. لذلك، في الفترات و ، وفي الفاصل الزمني. وفقًا للمعيار الكافي الأول للحد الأقصى، لا يوجد حد أقصى عند النقطة (نظرًا لأن المشتق يحتفظ بإشارته في الفترة)، وعند النقطة يكون للدالة حد أدنى (نظرًا لأن علامة المشتقة تتغير من ناقص إلى زائد عند المرور من خلال هذه النقطة). لنجد القيم المقابلة للدالة: , a . في هذه الفترة تقل الدالة، لأنه في هذه الفترة، وفي هذه الفترة تزيد، لأنه في هذه الفترة.

لتوضيح بناء الرسم البياني نجد نقاط تقاطعه مع محاور الإحداثيات. عندما نحصل على معادلة جذورها و، أي تم العثور على نقطتين (0؛ 0) و (4؛ 0) من الرسم البياني للدالة. باستخدام جميع المعلومات الواردة، نقوم ببناء رسم بياني (انظر بداية المثال).

للتحقق الذاتي أثناء العمليات الحسابية، يمكنك استخدام آلة حاسبة مشتقة على الانترنت .

مثال 4.أوجد الحد الأقصى للدالة وقم ببناء الرسم البياني الخاص بها.

مجال تعريف الدالة هو خط الأعداد بأكمله، باستثناء النقطة، أي. .

لتقصير الدراسة، يمكنك استخدام حقيقة أن هذه الوظيفة حتى، منذ ذلك الحين . ولذلك، فإن الرسم البياني له متماثل حول المحور أويولا يمكن إجراء الدراسة إلا خلال هذه الفترة.

العثور على المشتقة والنقاط الحرجة للوظيفة:

1) ;

2) ,

لكن الدالة تعاني من انقطاع عند هذه النقطة، لذا لا يمكن أن تكون نقطة متطرفة.

وبالتالي، فإن الدالة المعطاة لها نقطتان حاسمتان: و . مع الأخذ بعين الاعتبار تكافؤ الدالة، سوف نتحقق فقط من النقطة باستخدام المعيار الثاني الكافي للقيمة القصوى. للقيام بذلك، نجد المشتقة الثانية ونحدد علامتها في : نحصل . بما أن و، فهي النقطة الدنيا للدالة، و .

للحصول على صورة أكثر اكتمالا للرسم البياني للدالة، دعونا نتعرف على سلوكها عند حدود مجال التعريف:

(هنا يشير الرمز إلى الرغبة سإلى الصفر من اليمين، و سيظل إيجابيا؛ وبالمثل يعني الطموح سإلى الصفر من اليسار، و سيبقى سلبيا). وهكذا إذاً . التالي نجد

,

أولئك. اذا ثم .

الرسم البياني للدالة لا يحتوي على نقاط تقاطع مع المحاور. الصورة في بداية المثال.

للتحقق الذاتي أثناء العمليات الحسابية، يمكنك استخدام آلة حاسبة مشتقة على الانترنت .

نواصل البحث عن القيم القصوى للدالة معًا

مثال 8.أوجد الحد الأقصى للدالة.

حل. دعونا نجد مجال تعريف الوظيفة. وبما أنه يجب استيفاء عدم المساواة، فإننا نحصل عليها من .

دعونا نجد المشتقة الأولى للدالة.

الحد الأقصى هو أعلى رقم أو أعلى حد يمكن الوصول إليه. والحد الأدنى، كما نعلم جميعا جيدا، هو العكس المباشر للحد الأقصى، أي. هذا هو العدد الأصغر والحد الأصغر. وتوجد كلمتا الحد الأدنى والحد الأقصى ومشتقاتهما في ألفاظ وعبارات مثل:

احصل على أقصى استفادة من التواصل.

لتتعلم قصيدة تحتاج إلى قراءتها 3-4 مرات على الأقل.

أقصى ما يمكنه فعله هو...

لديهم على الأقل صديقان مشتركان.

حصل على الحد الأقصى من الدرجات.

الاستفادة القصوى من الفرص المتاحة لك!

هذا هو الحد الأدنى الذي تحتاج إلى معرفته.

أجر المعيشة.

الحد الأدنى من الضغط الجوي.

الحد الأدنى/الحد الأقصى للطقس البارد لمدة ….. سنوات.

ستحتاج إلى بضع ساعات على الأقل لإكمال هذه المهمة.

يمكن أيضًا العثور على مفاهيم مثل الحد الأقصى والحد الأدنى في مصطلحات علمية خاصة. على سبيل المثال، في الرياضيات هناك مفهوم مثل الحد الأقصى والحد الأدنى للدالة.

وهكذا، في الرياضيات تسمى القيمة القصوى للدالة بالحد الأقصى. في هذه الحالة، تكون القيمة القصوى للدالة أكبر من جميع القيم المجاورة لها. الحد الأقصى للدالة هو قيمتها عندما تزداد القيمة أولا ثم تبدأ فورا في النقصان، بينما يكون لها الحد الأقصى في المكان الذي تنتقل فيه زيادة الدالة ونقصانها من واحدة إلى أخرى. وبالتالي فإن الحد الأدنى للدالة هو أصغر قيمة للدالة.

يمكن اعتبار المشتقة الأولى للدالة موجبة إذا ارتفعت عند زيادة المتغير، فيمكن اعتبار الدالة موجبة. إذا انخفض المتغير الأول مع زيادة المشتق، فيجب اعتبار الدالة سالبة.

المشتق هو القيمة الأساسية المستخدمة في الحسابات التفاضلية (دراسة المشتقات والتفاضلات التي تساعد على دراسة الدوال الرياضية)، ويمكن فهمه على أنه معدل تغير الدالة عند نقطة محددة. كلما زادت السرعة، كلما تغيرت الدالة بشكل أقل، وكلما كانت أبطأ (ومع ذلك، هذا صحيح فقط إذا كانت الدالة موجبة). وبالتالي فإن معدل تغير الدالة عند نقطة معينة هو الذي يحدد ميلها وتحدبها. المتغير هو الكمية التي يمكن أن تغير قيمتها. ويشار إليه بـ x أو الوقت.

يمكن اعتبار المتغير سمة للنظام (المادي والمجرد) يمكنه تغيير قيمته. بمعنى أكثر عالمية، يمكن تسمية المتغير بالوقت، ودرجة الحرارة، وبشكل عام، الحياة بأكملها (يمكن أن تتغير). يحتوي المتغير على العديد من القيم التي يمكن أن يأخذها. يمكننا أن نفترض أن هذه المجموعة متغيرة.

أما بالنسبة للدالة نفسها، فيجب أن تنتقل من القيمة الموجبة إلى القيمة السالبة حتى الصفر. وبالتالي، عند قيمة المتغير الذي يتوافق مع الحد الأقصى للدالة، فإن مشتقتها ستكون مساوية للصفر. هذه الخاصية للدالة هي التي تسمح لنا بتحديد قيم x التي تصل عندها الدالة إلى الحد الأقصى. ومع ذلك، إذا قمنا بزيادة المتغير، وفي الوقت نفسه، زادت الدالة أولاً ثم انخفضت، فإن الدالة، عند التغيير من قيمة سالبة إلى قيمة موجبة (المرور بالصفر)، لن تصل إلى الحد الأقصى، ولكن، على العكس من ذلك، الحد الأدنى للقيمة. على الرغم من أنه من الممكن منطقيًا اعتبار هذه القيمة القصوى (فهي تقع في أعلى نقطة من الوظيفة).

تسمى النقاط القصوى والدنيا للدالة أيضًا بالنقاط القصوى.

وهكذا، سواء في الحياة العادية أو في الرياضيات، فإن الحد الأقصى والحد الأدنى هما متضادان متطرفان يعنيان شيئًا أكبر وشيئًا أصغر.

قيم الوظائف والحد الأقصى والحد الأدنى من النقاط

أكبر قيمة دالة

أصغر قيمة دالة

وكما قال العراب: "لا شيء شخصي". المشتقات فقط!

تعتبر المهمة الإحصائية 12 صعبة للغاية، وكل ذلك لأن الرجال لم يقرؤوا هذه المقالة (نكتة). في معظم الحالات، يقع اللوم على الإهمال.

12 مهمة تأتي على نوعين:

1. ابحث عن النقطة القصوى/الدنيا (اطلب العثور على قيم "x").
2. ابحث عن أكبر/أصغر قيمة للدالة (اطلب العثور على قيم "y").

كيف تتصرف في هذه الحالات؟

العثور على الحد الأقصى/الحد الأدنى للنقطة

1. يساويها بالصفر.
2. سيكون "x" الذي تم العثور عليه أو العثور عليه هو الحد الأدنى أو الأقصى للنقاط.
3. حدد العلامات باستخدام طريقة الفاصل الزمني وحدد النقطة المطلوبة في المهمة.

مهام امتحان الدولة الموحدة:

أوجد النقطة القصوى للدالة

• نأخذ المشتقة:

هذا صحيح، أولاً تزيد الدالة، ثم تنخفض - هذه هي النقطة القصوى!
الجواب: -15

أوجد النقطة الدنيا للدالة

• دعونا نحول ونأخذ المشتق:

• عظيم! أولاً تتناقص الدالة، ثم تزيد - هذه هي النقطة الدنيا!

الجواب: -2

أوجد أكبر/أصغر قيمة للدالة

1. خذ مشتقة الدالة المقترحة.
   
2. يساويها بالصفر.
   
3. ستكون "x" التي تم العثور عليها هي النقطة الدنيا أو القصوى.
   
4. حدد العلامات باستخدام طريقة الفاصل الزمني وحدد النقطة المطلوبة في المهمة.
5. في مثل هذه المهام، يتم دائمًا تحديد فجوة: يجب تضمين علامة X الموجودة في الخطوة 3 في هذه الفجوة.
6. عوض بالنقطة العظمى أو الصغرى الناتجة في المعادلة الأصلية، وسنحصل على القيمة الأكبر أو الأصغر للدالة.

مهام امتحان الدولة الموحدة:

أوجد القيمة الأكبر للدالة في الفترة [−4; −1]

الجواب: -6

أوجد أكبر قيمة للدالة على القطعة

• أكبر قيمة للدالة هي "11" عند النقطة القصوى (في هذا الجزء) "0".

الجواب: 11

الاستنتاجات:

1. 70٪ من الأخطاء ترجع إلى أن الرجال لا يتذكرون الرد عليها يجب كتابة القيمة الأكبر/الأصغر للدالة "y"، و على اكتب الحد الأقصى/الحد الأدنى للنقطة "x".
2. لا يوجد حل للمشتقة عند إيجاد قيم الدالة؟لا مشكلة، استبدل النقاط المتطرفة للفجوة!
3. يمكن دائمًا كتابة الإجابة كرقم أو علامة عشرية.لا؟ ثم أعد التفكير في المثال.
4. في معظم المهام، سنحصل على نقطة واحدة وسيكون كسلنا في التحقق من الحد الأقصى أو الأدنى مبررًا. لقد حصلنا على نقطة واحدة - يمكنك الرد بأمان.
5. و هنا لا ينبغي عليك فعل ذلك عند البحث عن قيمة دالة!تأكد من أن هذه هي النقطة الصحيحة، وإلا فإن القيم المتطرفة للفجوة قد تكون أكبر أو أصغر.

خوارزمية بسيطة للعثور على الحدود القصوى.

• إيجاد مشتقة الدالة
• نحن نساوي هذه المشتقة بالصفر
• نجد قيم متغير التعبير الناتج (قيم المتغير الذي يتم عنده تحويل المشتق إلى صفر)
• باستخدام هذه القيم، نقوم بتقسيم خط الإحداثيات إلى فترات (لا ننسى نقاط التوقف، والتي يجب أيضًا رسمها على الخط)، كل هذه النقاط تسمى نقاط "مشبوهة" للحد الأقصى
• نحسب أيًا من هذه الفترات ستكون المشتقة موجبة وأيها ستكون سالبة. للقيام بذلك، عليك استبدال القيمة من الفاصل الزمني بالمشتقة.

من النقاط المشبوهة لأقصى الحدود، فمن الضروري العثور عليها . للقيام بذلك، ننظر إلى الفواصل الزمنية الموجودة على الخط الإحداثي. إذا تغيرت إشارة المشتق عند المرور بنقطة ما من موجب إلى ناقص، فستكون هذه النقطة أقصى، وإذا كان من ناقص إلى زائد، ثم الحد الأدنى.

للعثور على القيم الأكبر والأصغر للدالة، تحتاج إلى حساب قيمة الدالة في نهايات المقطع وفي النقاط القصوى. ثم حدد القيمة الأكبر والأصغر.

لنلقي نظرة على مثال
أوجد المشتقة وساويها بالصفر:

نرسم قيم المتغيرات التي تم الحصول عليها على خط الإحداثيات ونحسب إشارة المشتق في كل فترة من الفترات. حسنًا، على سبيل المثال، لنأخذ الأمر الأول-2 ، فإن المشتقة ستكون متساوية-0,24 ، للثانية سنأخذها0 ، فإن المشتق سيكون2 وللثالث نأخذ2 ، فإن المشتق سيكون-0.24. نضع العلامات المناسبة.

نرى أنه عند المرور بالنقطة -1، تتغير إشارة المشتقة من ناقص إلى زائد، أي أن هذه ستكون النقطة الدنيا، وعند المرور بالنقطة 1، ستتغير الإشارة من زائد إلى ناقص، على التوالي، ستكون هذه هي النقطة النقطة القصوى.

تحتل الدالة ودراسة خصائصها أحد الفصول الرئيسية في الرياضيات الحديثة. المكون الرئيسي لأي وظيفة هو الرسوم البيانية التي تصور ليس فقط خصائصها، ولكن أيضا معلمات مشتق هذه الوظيفة. دعونا نفهم هذا الموضوع الصعب. إذن ما هي أفضل طريقة للعثور على النقاط القصوى والدنيا للدالة؟

الوظيفة: التعريف

أي متغير يعتمد بطريقة ما على قيم كمية أخرى يمكن أن يسمى دالة. على سبيل المثال، الدالة f(x 2) هي دالة تربيعية وتحدد قيم المجموعة x بأكملها. لنفترض أن x = 9، فإن قيمة الدالة ستكون 9 2 = 81.

تأتي الوظائف في أنواع مختلفة: منطقية، متجهة، لوغاريتمية، مثلثية، رقمية وغيرها. لقد تمت دراستهم من قبل عقول بارزة مثل لاكروا ولاغرانج ولايبنيز وبرنولي. تعتبر أعمالهم بمثابة الدعامة الأساسية في الطرق الحديثة لدراسة الوظائف. قبل العثور على الحد الأدنى من النقاط، من المهم جدًا فهم معنى الدالة ومشتقتها.

المشتقة ودورها

تعتمد جميع الدوال على متغيراتها، مما يعني أنها يمكن أن تغير قيمتها في أي وقت. على الرسم البياني، سيتم تصوير ذلك على أنه منحنى إما أن ينخفض ​​أو يرتفع على طول المحور الإحداثي (هذه هي المجموعة الكاملة من أرقام "y" على طول الرسم البياني الرأسي). لذا، فإن تحديد النقاط القصوى والدنيا للدالة يرتبط بدقة بهذه "التذبذبات". دعونا نوضح ما هي هذه العلاقة.

يتم رسم مشتق أي دالة بيانيا من أجل دراسة خصائصها الأساسية وحساب مدى سرعة تغير الدالة (أي تغير قيمتها اعتمادا على المتغير "x"). في اللحظة التي تزيد فيها الوظيفة، سيزداد الرسم البياني لمشتقتها أيضًا، ولكن في أي ثانية يمكن أن تبدأ الدالة في الانخفاض، ثم سينخفض ​​الرسم البياني للمشتقة. تسمى تلك النقاط التي يتغير فيها المشتق من علامة الطرح إلى علامة الجمع نقاط الحد الأدنى. من أجل معرفة كيفية العثور على الحد الأدنى من النقاط، يجب أن تفهم بشكل أفضل

كيفية حساب المشتقة؟

يتضمن التعريف والوظائف عدة مفاهيم بشكل عام، يمكن التعبير عن تعريف المشتق على النحو التالي: هذه هي الكمية التي توضح معدل تغير الوظيفة.

تبدو الطريقة الرياضية لتحديدها معقدة بالنسبة للعديد من الطلاب، ولكن في الواقع كل شيء أبسط بكثير. كل ما عليك فعله هو اتباع الخطة القياسية للعثور على مشتق أي دالة. نوضح أدناه كيف يمكنك العثور على النقطة الدنيا للدالة دون تطبيق قواعد التفاضل ودون حفظ جدول المشتقات.

1. يمكنك حساب مشتق دالة باستخدام الرسم البياني. للقيام بذلك، تحتاج إلى تصوير الوظيفة نفسها، ثم خذ نقطة واحدة عليها (النقطة أ في الشكل) ارسم خطًا عموديًا لأسفل حتى محور الإحداثي السيني (النقطة × 0)، وعند النقطة أ ارسم مماسًا للخط. الرسم البياني للوظيفة. يشكل المحور السيني والمماس زاوية معينة أ. لحساب قيمة مدى سرعة زيادة الدالة، تحتاج إلى حساب ظل هذه الزاوية أ.
2. وتبين أن ظل الزاوية بين المماس واتجاه المحور x هو مشتق الدالة في مساحة صغيرة ذات النقطة A. وتعتبر هذه الطريقة طريقة هندسية لتحديد المشتق.

طرق دراسة الوظيفة

في منهج الرياضيات المدرسي، من الممكن العثور على الحد الأدنى لنقطة دالة بطريقتين. لقد ناقشنا بالفعل الطريقة الأولى باستخدام الرسم البياني، ولكن كيف يمكننا تحديد القيمة العددية للمشتقة؟ للقيام بذلك، ستحتاج إلى تعلم العديد من الصيغ التي تصف خصائص المشتق وتساعد في تحويل المتغيرات مثل "x" إلى أرقام. الطريقة التالية عالمية، لذا يمكن تطبيقها على جميع أنواع الوظائف تقريبًا (سواء الهندسية أو اللوغاريتمية).

1. من الضروري مساواة الدالة بالدالة المشتقة، ثم تبسيط التعبير باستخدام قواعد التمايز.
2. في بعض الحالات، عند إعطاء دالة يكون فيها المتغير "x" في المقسوم عليه، فمن الضروري تحديد نطاق القيم المقبولة، باستثناء النقطة "0" منها (لسبب بسيط وهو أنه في الرياضيات لا ينبغي أبدًا اقسم على صفر).
3. بعد ذلك، عليك تحويل الشكل الأصلي للدالة إلى معادلة بسيطة، تساوي التعبير بأكمله بالصفر. على سبيل المثال، إذا كانت الدالة تبدو كما يلي: f(x) = 2x 3 +38x، فوفقًا لقواعد التفاضل يكون مشتقها يساوي f"(x) = 3x 2 +1. ثم نقوم بتحويل هذا التعبير إلى معادلة بالشكل التالي: 3x 2 +1 = 0 .
4. بعد حل المعادلة وإيجاد النقاط "x"، يجب عليك رسمها على المحور السيني وتحديد ما إذا كان المشتق في هذه الأقسام بين النقاط المحددة موجبًا أم سالبًا. بعد التعيين، سيصبح من الواضح عند أي نقطة تبدأ الوظيفة في الانخفاض، أي تغيير الإشارة من ناقص إلى العكس. وبهذه الطريقة يمكنك العثور على الحد الأدنى والحد الأقصى للنقاط.

قواعد التمايز

إن العنصر الأساسي في دراسة الدالة ومشتقاتها هو معرفة قواعد التفاضل. فقط بمساعدتهم يمكنك تحويل التعبيرات المرهقة والوظائف المعقدة الكبيرة. دعونا نتعرف عليهم، هناك الكثير منهم، لكنهم جميعا بسيطون للغاية بسبب الخصائص الطبيعية لكل من وظائف الطاقة واللوغاريتمية.

1. مشتقة أي ثابت تساوي الصفر (f(x) = 0). أي أن المشتقة f(x) = x 5 + x - 160 ستأخذ الصيغة التالية: f" (x) = 5x 4 +1.
2. مشتق من مجموع الحدين: (f+w)" = f"w + fw".
3. مشتق من دالة لوغاريتمية: (log a d)" = d/ln a*d. تنطبق هذه الصيغة على جميع أنواع اللوغاريتمات.
4. مشتقة القوة: (x n)"= n*x n-1. على سبيل المثال، (9x 2)" = 9*2x = 18x.
5. مشتقة الدالة الجيبية: (sin a)" = cos a. إذا كان sin الزاوية a يساوي 0.5، فإن مشتقتها هي √3/2.

النقاط القصوى

لقد ناقشنا بالفعل كيفية العثور على الحد الأدنى من النقاط، ولكن هناك أيضًا مفهوم الحد الأقصى من النقاط للدالة. إذا كان الحد الأدنى يشير إلى تلك النقاط التي تتغير عندها الدالة من علامة الطرح إلى علامة الجمع، فإن النقاط القصوى هي تلك النقاط الموجودة على المحور السيني التي يتغير عندها مشتق الدالة من علامة الزائد إلى العكس - ناقص.

يمكنك العثور عليها باستخدام الطريقة الموضحة أعلاه، ولكن يجب أن تأخذ في الاعتبار أنها تشير إلى تلك المناطق التي تبدأ فيها الدالة في الانخفاض، أي أن المشتق سيكون أقل من الصفر.

في الرياضيات، من المعتاد تعميم كلا المفهومين، واستبدالهما بعبارة "النقاط القصوى". عندما تطلب منك المهمة تحديد هذه النقاط، فهذا يعني أنك بحاجة إلى حساب مشتق دالة معينة والعثور على الحد الأدنى والحد الأقصى للنقاط.