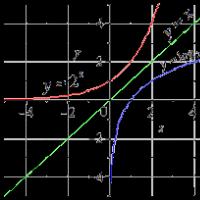
الدالة العكسية لـ y 2x المعطاة. أنواع الوظائف. وظيفة عكسية. مجال التعريف ومجال قيمة الوظيفة. إيجاد الدالة العكسية

لقد واجهنا بالفعل مشكلة حيث أنه، بالنظر إلى دالة معينة f وقيمة معينة للوسيط الخاص بها، كان من الضروري حساب قيمة الدالة عند هذه النقطة. لكن في بعض الأحيان يتعين عليك مواجهة المشكلة العكسية: للعثور على قيمة الوسيطة التي تأخذ فيها الدالة قيمة معينة y، بالنظر إلى دالة معروفة f وقيمتها المحددة y.

تسمى الوظيفة التي تأخذ كل من قيمها عند نقطة واحدة في مجال تعريفها بالدالة العكسية. على سبيل المثال، ستكون الدالة الخطية وظيفة عكسية. لكن الدالة التربيعية أو دالة الجيب لن تكون دوالًا قابلة للعكس. بما أن الدالة يمكن أن تأخذ نفس القيمة مع وسائط مختلفة.

وظيفة عكسية

لنفترض أن f هي دالة اعتباطية قابلة للعكس. كل رقم من مجال قيمه y0 يقابل رقم واحد فقط من مجال التعريف x0، بحيث f(x0) = y0.

إذا قمنا الآن بربط كل قيمة x0 بقيمة y0، فسنحصل على دالة جديدة. على سبيل المثال، بالنسبة للدالة الخطية f(x) = k * x + b، فإن الدالة g(x) = (x - b)/k ستكون معكوسها.

إذا كانت بعض الوظائف زفي كل نقطة Xنطاق قيم الدالة المعكوسة f يأخذ قيمة بحيث f(y) = x، فنقول أن الدالة ز- هناك دالة عكسية لـ f .

إذا حصلنا على رسم بياني لبعض الوظائف المعكوسة f، فمن أجل إنشاء رسم بياني للدالة العكسية، يمكننا استخدام العبارة التالية: الرسم البياني للدالة f ووظيفتها العكسية g سيكونان متماثلين بالنسبة للمستقيم الخط المحدد بالمعادلة y = x.

إذا كانت الدالة g هي معكوس الدالة f، فإن الدالة g ستكون دالة قابلة للعكس. والدالة f ستكون معكوس الدالة g. يُقال عادةً أن الوظيفتين f وg معكوستان لبعضهما البعض.

يوضح الشكل التالي الرسوم البيانية للوظائف f و g معكوسة لبعضها البعض.

دعونا نستنتج النظرية التالية: إذا كانت الدالة f تزيد (أو تنقص) في فترة معينة A، فهي قابلة للعكس. الدالة العكسية g، المحددة في نطاق قيم الدالة f، هي أيضًا دالة متزايدة (أو متناقصة بالمثل). وتسمى هذه النظرية نظرية الدالة العكسية.

لنفترض أن لدينا دالة معينة y = f (x)، وهي رتيبة تمامًا (تناقصية أو متزايدة) ومستمرة في مجال التعريف x ∈ a؛ ب ؛ نطاق قيمه y ∈ c ; د، وعلى الفاصل الزمني ج؛ d في هذه الحالة سيكون لدينا دالة محددة x = g (y) مع نطاق من القيم a ; ب. ستكون الوظيفة الثانية أيضًا مستمرة ورتيبة تمامًا. فيما يتعلق بـ y = f (x) ستكون دالة عكسية. بمعنى أنه يمكننا التحدث عن الدالة العكسية x = g (y) عندما تنخفض y = f (x) أو تزيد خلال فترة زمنية معينة.

هاتان الوظيفتان f وg ستكونان معكوستين بشكل متبادل.

لماذا نحتاج حتى إلى مفهوم الدوال العكسية؟

نحن بحاجة إلى ذلك لحل المعادلات y = f (x)، والتي يتم كتابتها بدقة باستخدام هذه التعبيرات.

لنفترض أننا بحاجة إلى إيجاد حل للمعادلة cos (x) = 1 3 . حلولها ستكون جميع النقاط: x = ± a rc c o s 1 3 + 2 π · k, k ∈ Z

على سبيل المثال، ستكون وظائف جيب التمام وجيب التمام العكسية معكوسة لبعضها البعض.

دعونا نلقي نظرة على العديد من المسائل للعثور على الدوال التي تتعارض مع الدوال المعطاة.

مثال 1

حالة:ما هي الدالة العكسية لـ y = 3 x + 2؟

حل

مجال التعريفات ونطاق قيم الدالة المحددة في الشرط هو مجموعة جميع الأعداد الحقيقية. لنحاول حل هذه المعادلة من خلال x، أي بالتعبير عن x من خلال y.

نحصل على x = 1 3 y - 2 3 . هذه هي الدالة العكسية التي نحتاجها، لكن y ستكون الوسيطة هنا، وx ستكون الدالة. دعونا نعيد ترتيبها للحصول على تدوين مألوف أكثر:

إجابة:الدالة y = 1 3 x - 2 3 ستكون معكوس y = 3 x + 2.

يمكن رسم كلا الدالتين العكسيتين على النحو التالي:

نرى التماثل بين كلا الرسمين البيانيين فيما يتعلق بـ y = x. هذا الخط هو منصف الربعين الأول والثالث. لقد حصلنا على برهان لإحدى خواص الدوال المتبادلة، وهو ما سنتحدث عنه لاحقا.

لنأخذ مثالًا نحتاج فيه إلى إيجاد الدالة اللوغاريتمية التي تمثل معكوس دالة أسية معينة.

مثال 2

حالة:حدد الدالة التي ستكون معكوسًا لـ y = 2 x.

حل

بالنسبة لدالة معينة، مجال التعريف هو كل الأعداد الحقيقية. يقع نطاق القيم في الفاصل الزمني 0؛ + ∞ . الآن نحن بحاجة إلى التعبير عن x بدلالة y، أي حل المعادلة المحددة بدلالة x. نحصل على x = log 2 y. دعونا نعيد ترتيب المتغيرات ونحصل على y = log 2 x.

ونتيجة لذلك، حصلنا على الدوال الأسية واللوغاريتمية، والتي ستكون عكسية لبعضها البعض في جميع أنحاء مجال التعريف بأكمله.

إجابة:ص = سجل 2 س .

على الرسم البياني، ستبدو كلتا الدالتين كما يلي:

الخصائص الأساسية للوظائف العكسية المتبادلة

ندرج في هذه الفقرة الخصائص الرئيسية للدالتين y = f (x) وx = g (y)، وهي معكوسة بشكل متبادل.

التعريف 1

1. لقد اشتقنا بالفعل الخاصية الأولى سابقًا: y = f (g (y)) و x = g (f (x)).
2. الخاصية الثانية تتبع من الأولى: مجال التعريف y = f (x) سيتزامن مع نطاق قيم الدالة العكسية x = g (y)، والعكس صحيح.
3. ستكون الرسوم البيانية للدوال المعكوسة متماثلة بالنسبة إلى y = x.
4. إذا كانت y = f (x) في ازدياد، فإن x = g (y) ستزداد، وإذا كانت y = f (x) تتناقص، فإن x = g (y) ستنخفض أيضًا.

ننصحك بالاهتمام الشديد بمفاهيم مجال التعريف ومجال معنى الوظائف وعدم الخلط بينهما أبدًا. لنفترض أن لدينا وظيفتين معكوستين y = f (x) = a x و x = g (y) = log a y. وفقًا للخاصية الأولى، y = f (g (y)) = a log a y. هذه المساواة لن تكون صحيحة إلا في حالة القيم الموجبة لـ y، وبالنسبة للقيم السالبة لم يتم تعريف اللوغاريتم، لذلك لا تتعجل في تدوين ذلك السجل a y = y. تأكد من التحقق وإضافة أن هذا صحيح فقط عندما تكون y موجبة.

لكن المساواة x = f (g (x)) = log a a x = x ستكون صحيحة لأي قيم حقيقية لـ x.

لا تنس هذه النقطة، خاصة إذا كان عليك التعامل مع الدوال المثلثية والعكسية. لذا، a r c sin sin 7 π 3 ≠ 7 π 3، لأن مدى قوس الجيب هو π 2؛ π 2 و 7 π 3 غير متضمنة فيه. الإدخال الصحيح سيكون

أ r c sin sin 7 π 3 = a r c sin sin 2 π + π 3 = = a r c sin sin π 3 = π 3

لكن sin a r c sin 1 3 = 1 3 هي مساواة صحيحة، أي. الخطيئة (أ ر ج الخطيئة س) = س ل س ∈ - 1 ; 1 و a r c sin (sin x) = x for x ∈ - π 2 ; بي 2. كن حذرًا دائمًا فيما يتعلق بنطاق ونطاق الوظائف العكسية!

• الدوال الأساسية المتبادلة: دوال القدرة

إذا كانت لدينا دالة قوة y = x a ، فبالنسبة لـ x > 0 فإن دالة الطاقة x = y 1 a ستكون أيضًا معكوسها. دعونا نستبدل الحروف ونحصل على y = x a و x = y 1 a على التوالي.

على الرسم البياني سوف تبدو كما يلي (الحالات ذات المعامل الموجب والسالب أ):

• الدوال الأساسية المتبادلة: الأسية واللوغاريتمية

لنأخذ a، والذي سيكون رقمًا موجبًا لا يساوي 1.

الرسوم البيانية للوظائف مع > 1 وa< 1 будут выглядеть так:

• الدوال الأساسية المتبادلة: حساب المثلثات والمثلثية العكسية

إذا أردنا رسم الفرع الرئيسي للجيب وقوس الجيب، فسيبدو هكذا (كما هو موضح في منطقة الضوء المميزة).

أهداف الدرس:

التعليمية:

• تطوير المعرفة حول موضوع جديد وفقا لمواد البرنامج؛
• دراسة خاصية انعكاس الوظيفة وتعليم كيفية العثور على الوظيفة العكسية لوظيفة معينة؛

التنموية:

• تطوير مهارات ضبط النفس، والكلام الموضوعي؛
• إتقان مفهوم الدالة العكسية وتعلم طرق العثور على الدالة العكسية؛

التعليمية: لتطوير الكفاءة التواصلية.

معدات:كمبيوتر، جهاز عرض، شاشة، سبورة بيضاء تفاعلية، SMART Board، نشرات (عمل مستقل) للعمل الجماعي.

خلال الفصول الدراسية.

1. اللحظة التنظيمية.

هدف – إعداد الطلاب للعمل داخل الفصل:

تعريف الغائبين

تهيئة الطلاب للمزاج المناسب للعمل، وتنظيم الاهتمام؛

اذكر موضوع الدرس والغرض منه.

2. تحديث المعرفة الأساسية لدى الطلاب.مسح أمامي.

هدف - إثبات صحة ووعي المادة النظرية المدروسة، وتكرار المادة المغطاة.<Приложение 1 >

يتم عرض رسم بياني للوظيفة على السبورة التفاعلية للطلاب. يقوم المعلم بصياغة مهمة - النظر في الرسم البياني للدالة وسرد الخصائص المدروسة للوظيفة. يسرد الطلاب خصائص الوظيفة وفقًا لتصميم البحث. يقوم المعلم، على يمين الرسم البياني للدالة، بكتابة الخصائص المسماة بعلامة على السبورة التفاعلية.

خصائص الوظيفة:

في نهاية الدراسة، يذكر المعلم أنهم اليوم في الدرس سوف يتعرفون على خاصية أخرى للوظيفة - الانعكاس. لدراسة المواد الجديدة بشكل هادف، يدعو المعلم الأطفال للتعرف على الأسئلة الرئيسية التي يجب على الطلاب الإجابة عليها في نهاية الدرس. تتم كتابة الأسئلة على لوحة عادية ويحصل عليها كل طالب على شكل نشرات (يتم توزيعها قبل الدرس)

1. ما هي الوظيفة التي تسمى عكسية؟
2. هل أي وظيفة قابلة للعكس؟
3. ما هي الوظيفة التي تسمى معكوس المسند؟
4. كيف يرتبط مجال التعريف ومجموعة قيم الدالة وعكسها؟
5. إذا تم إعطاء دالة تحليليا، فكيف يمكن تحديد الدالة العكسية من خلال صيغة؟
6. إذا تم إعطاء دالة بيانيا، فكيف يمكن رسم دالتها العكسية؟

3. شرح المواد الجديدة.

هدف - توليد المعرفة حول موضوع جديد وفقا لمواد البرنامج؛ دراسة خاصية انعكاس الوظيفة وتعليم كيفية العثور على الوظيفة العكسية لوظيفة معينة؛ تطوير خطاب موضوعي.

يعرض المعلم المادة وفقًا للمادة الواردة في الفقرة. على السبورة التفاعلية، يقارن المعلم الرسوم البيانية لوظيفتين تتشابه مجالات تعريفهما ومجموعات القيم، ولكن إحدى الوظائف رتيبة والأخرى ليست كذلك، وبالتالي تعريف الطلاب بمفهوم الدالة المعكوسة .

يقوم المعلم بعد ذلك بصياغة تعريف الدالة القابلة للعكس وإجراء برهان على نظرية الدالة القابلة للعكس باستخدام الرسم البياني للدالة الرتيبة على السبورة التفاعلية.

التعريف 1: يتم استدعاء الدالة y=f(x), x X تفريغ، إذا أخذت أيًا من قيمها فقط عند نقطة واحدة من المجموعة X.

النظرية: إذا كانت الدالة y=f(x) رتيبة في المجموعة X، فهي قابلة للعكس.

دليل:

1. دع الوظيفة ص = و (س)يزيد بنسبة Xدعها تذهب × 1 ≠ × 2- نقطتان من المجموعة X.
2. على وجه التحديد، اسمحوا × 1< × 2.
   ثم من حقيقة ذلك × 1< × 2يتبع ذلك و (× 1) < و(× 2).
3. وبالتالي، فإن القيم المختلفة للوسيطة تتوافق مع قيم مختلفة للدالة، أي. الوظيفة قابلة للعكس.

(مع تقدم إثبات النظرية، يستخدم المعلم قلم التحديد لتقديم جميع الشروحات اللازمة على الرسم)

قبل صياغة تعريف الدالة العكسية، يطلب المعلم من الطلاب تحديد أي من الدوال المقترحة قابلة للعكس؟ تعرض السبورة التفاعلية رسومًا بيانية للوظائف وتكتب العديد من الوظائف المحددة تحليليًا:

ب)

ز) ص = 2س + 5

د) ص = -س 2 + 7

يقدم المعلم تعريف الدالة العكسية.

التعريف 2: دع الوظيفة المعكوسة ص = و (س)محددة على المجموعة Xو ه(و)=ص. دعونا نطابق كل واحد ذمن يهذا هو المعنى الوحيد X، الذي و(س)=ص.ثم نحصل على وظيفة تم تعريفها ي، أ X- نطاق الوظيفة

تم تعيين هذه الوظيفة س=و -1 (ص)ويسمى معكوس الدالة ص = و (س).

يُطلب من الطلاب استخلاص استنتاج حول العلاقة بين مجال التعريف ومجموعة قيم الدوال العكسية.

للنظر في مسألة كيفية العثور على معكوس دالة معينة، قام المعلم بجذب طالبين. في اليوم السابق، تلقى الأطفال مهمة من المعلم لتحليل الأساليب التحليلية والرسومية بشكل مستقل للعثور على الوظيفة العكسية لوظيفة معينة. يقوم المعلم بدور المستشار في إعداد الطلاب للدرس.

رسالة من الطالب الأول .

ملحوظة: رتابة الوظيفة هي كافٍشرط وجود الدالة العكسية لكنه ليسشرط ضروري.

أعطى الطالب أمثلة لمواقف مختلفة عندما تكون الدالة غير رتيبة ولكنها قابلة للعكس، وعندما تكون الدالة غير رتيبة وغير قابلة للعكس، وعندما تكون رتيبة وقابلة للعكس

ثم يعرّف الطالب الطلاب على طريقة لإيجاد الدالة العكسية المعطاة تحليليًا.

العثور على خوارزمية

1. تأكد من أن الوظيفة رتيبة.
2. عبر عن المتغير x بدلالة y .
3. إعادة تسمية المتغيرات. بدلاً من x=f -1 (y) اكتب y=f -1 (x)

ثم يحل مثالين لإيجاد الدالة العكسية لأحد الأمثلة.

مثال 1:وضح أنه بالنسبة للدالة y=5x-3 توجد دالة عكسية وأوجد تعبيرها التحليلي.

حل. يتم تعريف الدالة الخطية y=5x-3 على R، وتزيد على R، ونطاق قيمها هو R. وهذا يعني أن الدالة العكسية موجودة على R. للعثور على تعبيرها التحليلي، قم بحل المعادلة y=5x- 3 ل س؛ نحصل على هذه هي الدالة العكسية المطلوبة. يتم تعريفه وزيادة على R.

مثال 2:بيّن أنه بالنسبة للدالة y=x 2, x≥0 هناك دالة عكسية، وأوجد تعبيرها التحليلي.

الدالة مستمرة ورتيبة في مجال تعريفها، وبالتالي فهي قابلة للعكس. بعد تحليل مجالات التعريف ومجموعات قيم الوظيفة، يتم التوصل إلى استنتاج مماثل حول التعبير التحليلي للدالة العكسية.

يقوم الطالب الثاني بعمل عرض تقديمي عن رسم بيانيطريقة إيجاد الدالة العكسية ويستخدم الطالب خلال شرحه إمكانيات السبورة التفاعلية.

للحصول على رسم بياني للدالة y=f -1 (x)، معكوسًا للدالة y=f(x)، من الضروري تحويل الرسم البياني للدالة y=f(x) بشكل متماثل فيما يتعلق بالخط المستقيم ص=س.

أثناء الشرح على السبورة التفاعلية يتم تنفيذ المهمة التالية:

أنشئ رسمًا بيانيًا للدالة ورسمًا بيانيًا لدالتها العكسية في نفس نظام الإحداثيات. اكتب عبارة تحليلية للدالة العكسية.

4. الدمج الأولي للمواد الجديدة.

هدف - إثبات صحة ووعي فهم المادة المدروسة، وتحديد الثغرات في الفهم الأولي للمادة، وتصحيحها.

يتم تقسيم الطلاب إلى أزواج. يتم إعطاؤهم أوراقًا من المهام، حيث يقومون بالعمل في أزواج. الوقت اللازم لإكمال العمل محدود (5-7 دقائق). يعمل زوج واحد من الطلاب على الكمبيوتر، ويتم إيقاف تشغيل جهاز العرض خلال هذا الوقت ولا يستطيع بقية الأطفال رؤية كيفية عمل الطلاب على الكمبيوتر.

في نهاية الوقت (من المفترض أن غالبية الطلاب قد أكملوا العمل)، يتم عرض عمل الطلاب على اللوحة التفاعلية (يتم تشغيل جهاز العرض مرة أخرى)، حيث يتم تحديد أثناء التحقق مما إذا كانت المهمة أم لا تم إكماله بشكل صحيح في أزواج. إذا لزم الأمر، يقوم المعلم بالعمل التصحيحي والتوضيحي.

العمل المستقل في أزواج<الملحق 2 >

5. ملخص الدرس.بخصوص الأسئلة التي تم طرحها قبل المحاضرة. إعلان درجات الدرس.

الواجب المنزلي §10. رقم 10.6(أ،ج) 10.8-10.9(ب) 10.12(ب)

الجبر وبدايات التحليل. الصف العاشر في جزأين لمؤسسات التعليم العام (المستوى الشخصي) / A. G. Mordkovich، L.O Denishcheva، T.A Koreshkova، إلخ؛ حررت بواسطة أ.ج. موردكوفيتش، م: منيموسين، 2007

تعريف الدالة العكسية وخصائصها: نقاش حول الرتابة المتبادلة للدوال المباشرة والعكسية؛ تماثل الرسوم البيانية للوظائف المباشرة والعكسية؛ نظريات حول وجود واستمرارية الدالة العكسية لدالة رتيبة تمامًا على مقطع وفاصل ونصف فاصل. أمثلة على الوظائف العكسية. مثال على حل مشكلة. البراهين من الخصائص والنظريات.

محتوى

أنظر أيضا: تعريف الدالة، الحدود العلوية والسفلية، الدالة الرتيبة.

التعريف والخصائص

تعريف الدالة العكسية
دع الوظيفة لها مجال التعريف X ومجموعة القيم Y. وليكن لها الخاصية:
للجميع.
ثم بالنسبة لأي عنصر من المجموعة Y، يمكن ربط عنصر واحد فقط من المجموعة X به. تحدد هذه المراسلات وظيفة تسمى وظيفة عكسيةل . تتم الإشارة إلى الدالة العكسية على النحو التالي:
.

ويترتب على ذلك من التعريف
;
للجميع؛
للجميع.

خاصية تماثل الرسوم البيانية للوظائف المباشرة والعكسية
الرسوم البيانية للوظائف المباشرة والعكسية متناظرة بالنسبة للخط المستقيم.

نظرية وجود واستمرارية دالة عكسية على فترة
لتكن الدالة مستمرة ومتزايدة (تناقصية) بشكل صارم على القطعة. ثم يتم تعريف الدالة العكسية والمستمرة على القطعة، والتي تزيد (تتناقص) بشكل صارم.

لوظيفة متزايدة. للتناقص - .

نظرية وجود واستمرارية دالة عكسية على فترة
دع الدالة تكون مستمرة ومتزايدة (تناقصية) بشكل صارم على فترة محدودة أو لا نهائية مفتوحة. ثم يتم تعريف الدالة العكسية ومستمرة على الفاصل الزمني، الذي يزيد (يتناقص) بشكل صارم.

لوظيفة متزايدة.
للتناقص : .

وبطريقة مماثلة، يمكننا صياغة نظرية وجود واستمرارية الدالة العكسية على نصف فترة.

إذا كانت الوظيفة مستمرة وتزيد (تتناقص) بشكل صارم على نصف الفاصل الزمني أو ، فسيتم تحديد الدالة العكسية على نصف الفاصل الزمني أو العكسي، والتي تزيد (تتناقص) بشكل صارم. هنا .

إذا زادت بشكل صارم، فإن الفواصل الزمنية وتتوافق مع الفواصل الزمنية و . إذا كانت تتناقص بشكل صارم، فإن الفواصل الزمنية وتتوافق مع الفواصل الزمنية و .
تم إثبات هذه النظرية بنفس طريقة إثبات نظرية وجود واستمرارية دالة عكسية على فترة.

أمثلة على الوظائف العكسية

أركسين

الرسوم البيانية ص = الخطيئة سوالدالة العكسية y = أرسين x.

خذ بعين الاعتبار الدالة المثلثية التجويف: . وهي محددة ومستمرة لجميع قيم الوسيطة، ولكنها ليست رتيبة. ومع ذلك، إذا قمت بتضييق نطاق التعريف، يمكنك تحديد المناطق الرتيبة. لذلك، في المقطع، يتم تعريف الدالة، ومستمرة، ومتزايدة بشكل صارم، وتأخذ القيم منها -1 قبل +1 . ولذلك، فإن لها دالة عكسية عليها، تسمى قوس الجيب. يحتوي arcsine على مجال تعريف ومجموعة من القيم.

اللوغاريتم

الرسوم البيانية ص = 2 ×والدالة العكسية y = سجل 2 ×.

الدالة الأسية محددة ومستمرة ومتزايدة بشكل صارم لجميع قيم الوسيطة. مجموعة القيمة الخاصة بها هي فترة مفتوحة. الدالة العكسية هي اللوغاريتم للأساس الثاني. ولها مجال تعريف ومجموعة من المعاني.

الجذر التربيعي

الرسوم البيانية ص = س 2 والدالة العكسية.

وظيفة الطاقة محددة ومستمرة للجميع. مجموعة قيمها هي نصف الفاصل الزمني. لكنها ليست رتيبة لجميع قيم الحجة. ومع ذلك، في نصف الفاصل الزمني، فهو مستمر ويزداد بشكل رتيب بشكل صارم. لذلك، إذا أخذنا المجموعة كمجال تعريف، فهناك دالة عكسية تسمى الجذر التربيعي. تحتوي الدالة العكسية على مجال ومجموعة من القيم.

مثال. إثبات وجود وتفرد جذر الدرجة n

أثبت أن المعادلة، حيث n عدد طبيعي، هو عدد حقيقي غير سالب، ولها حل فريد على مجموعة الأعداد الحقيقية، . يسمى هذا الحل بالجذر n لـ a. أي أنك تحتاج إلى إثبات أن أي رقم غير سالب له جذر فريد من الدرجة n.

النظر في وظيفة المتغير x:
(ف1) .

دعونا نثبت أنه مستمر.
وباستخدام تعريف الاستمرارية، نوضح ذلك
.
نحن نطبق صيغة نيوتن ذات الحدين:
(ف2)
.
دعونا نطبق الخصائص الحسابية لحدود الوظائف. نظرًا لأن الفصل الأول فقط هو غير صفر:
.
لقد تم إثبات الاستمرارية.

دعونا نثبت أن الوظيفة (A1) تزيد بشكل صارم.
لنأخذ أرقامًا عشوائية مرتبطة بعدم المساواة:
, , .
نحن بحاجة لإظهار ذلك. دعونا نقدم المتغيرات. ثم . وبما أن (A2) يتضح أن . أو
.
وقد ثبت زيادة صارمة.

لنجد مجموعة قيم الدالة عند .
عند نقطة ، .
دعونا نجد الحد.
للقيام بذلك، نطبق متباينة برنولي. عندما نمتلك:
.
منذ ذلك الحين و .
وبتطبيق خاصية المتباينات على الدوال الكبيرة اللانهائية، نجد أن .
هكذا، ، .

وفقا لنظرية الدالة العكسية، فإن الدالة العكسية محددة ومستمرة على فترة زمنية. أي أنه بالنسبة لأي شخص هناك شيء فريد يرضي المعادلة. نظرًا لأن لدينا ، فهذا يعني أنه لأي معادلة لها حل فريد يسمى جذر الدرجة n للرقم x:
.

البراهين من الخصائص والنظريات

إثبات ليما على الرتابة المتبادلة للوظائف المباشرة والعكسية

دع الوظيفة لها مجال التعريف X ومجموعة القيم Y. دعونا نثبت أن لها وظيفة عكسية. وبناء على ذلك، علينا أن نثبت ذلك
للجميع.

ولنفترض العكس. يجب أن تكون هناك أرقام، بحيث . فليكن كذلك. خلاف ذلك، دعونا نغير الترميز بحيث يكون . ثم، بسبب الرتابة الصارمة لـ f، يجب تلبية إحدى المتباينات:
إذا كانت f تتزايد بشكل صارم؛
إذا كان f يتناقص بشكل صارم.
إنه . نشأ تناقض. لذلك، لديها وظيفة عكسية.

دع الوظيفة تتزايد بشكل صارم. دعونا نثبت أن الدالة العكسية تتزايد أيضًا بشكل صارم. دعونا نقدم التدوين التالي:
. أي أننا بحاجة إلى إثبات أنه إذا .

ولنفترض العكس. فليكن، ولكن.

اذا ثم.

تختفي هذه الحالة.

يترك . ثم، بسبب الزيادة الصارمة في الوظيفة، أو . نشأ تناقض. لذلك، الفرصة الوحيدة ممكنة.

ثبت أن الليما تؤدي وظيفة متزايدة بشكل صارم. يمكن إثبات هذه ليما بطريقة مماثلة لوظيفة تناقصية صارمة.

إثبات خاصية تماثل الرسوم البيانية للدوال المباشرة والعكسية
(2.1) .
اسمحوا أن تكون نقطة تعسفية على الرسم البياني لوظيفة مباشرة:
.
دعونا نوضح أن النقطة المتناظرة للنقطة A بالنسبة لخط مستقيم تنتمي إلى الرسم البياني للدالة العكسية:
(2.2) .
من تعريف الدالة العكسية يتبع ذلك

ولذلك علينا أن نبين (2.2). رسم بياني للدالة العكسية y = f-1(س) متماثل مع الرسم البياني للدالة المباشرة y = f(خ)

نسبة إلى الخط المستقيم y = x.
, .

من النقطتين A و S نرسم خطوطًا متعامدة على محور الإحداثيات. ثم

من خلال النقطة A نرسم خطًا عموديًا على الخط . دع الخطوط تتقاطع عند النقطة C. نقوم ببناء نقطة S على خط مستقيم بحيث . عندها ستكون النقطة S متناظرة مع النقطة A بالنسبة للخط المستقيم.
.

النظر في المثلثات و . لهما ضلعان متساويان في الطول: و، وزوايا متساوية بينهما: . ولذلك فإنهما متطابقان. ثم
.
النظر في مثلث. منذ ذلك الحين
.
الأمر نفسه ينطبق على المثلث:
.

ثم
;
.

الآن نجد و:
(2.2)
المعادلة (2.2):
(2.1) .

راضٍ، منذ، و(2.1) راضٍ:
جميع النقاط على الرسم البياني للدالة، والتي تنعكس بشكل متماثل بالنسبة للخط المستقيم، تنتمي إلى الرسم البياني للدالة العكسية.
بعد ذلك يمكننا تغيير الأماكن. ونتيجة لذلك حصلنا على ذلك
جميع نقاط الرسم البياني للدالة، المنعكسة بشكل متماثل بالنسبة لخط مستقيم، تنتمي إلى الرسم البياني للدالة.
ويترتب على ذلك أن الرسوم البيانية للوظائف متناظرة فيما يتعلق بالخط المستقيم.

وقد ثبت العقار.

إثبات نظرية وجود واستمرارية الدالة العكسية على فترة

اسمحوا للإشارة إلى مجال تعريف الوظيفة - الجزء.

1. دعونا نبين أن مجموعة قيم الدالة هي القطعة:
,
أين .

في الواقع، بما أن الدالة متصلة على القطعة، فإنها، وفقًا لنظرية فايرستراس، تصل إلى الحد الأدنى والحد الأقصى عليها. ثم، وفقا لنظرية بولزانو-كوشي، تأخذ الدالة جميع القيم من القطعة. وهذا هو، لأي شخص موجود، والذي. نظرًا لوجود حد أدنى وحد أقصى، فإن الدالة تأخذ قيم المقطع فقط من المجموعة.

2. بما أن الدالة رتيبة تمامًا، فوفقًا لما سبق، هناك دالة عكسية، وهي أيضًا رتيبة تمامًا (تزيد إذا زادت، وتنقص إذا نقصت). مجال الدالة العكسية هو المجموعة، ومجموعة القيم هي المجموعة.

3. الآن نثبت أن الدالة العكسية مستمرة.

3.1. يجب أن تكون هناك نقطة داخلية عشوائية للقطعة: . دعونا نثبت أن الدالة العكسية مستمرة عند هذه النقطة.

دع النقطة تتوافق معها. نظرًا لأن الدالة العكسية رتيبة تمامًا، أي النقطة الداخلية للقطعة:
.
وفقا لتعريف الاستمرارية، علينا أن نثبت أن هناك دالة من هذا القبيل لأي كائن
(3.1) للجميع.

لاحظ أنه يمكننا أن نأخذها صغيرة كما نحب. في الواقع ، إذا وجدنا دالة يتم فيها استيفاء المتباينات (3.1) لقيم صغيرة بما فيه الكفاية لـ ، فسوف تكون راضية تلقائيًا عن أي قيم كبيرة لـ ، إذا وضعنا عند .

دعونا نأخذها صغيرة جدًا بحيث تكون النقاط وتنتمي إلى القطعة:
.
دعونا نقدم ونرتب التدوين:



.

دعونا نحول عدم المساواة الأولى (3.1):
(3.1) للجميع.
;
;
;
(3.2) .
وبما أنه رتيب تماما، فإنه يتبع ذلك
(3.3.1) ، إذا زاد؛
(3.3.2) ، إذا انخفض.
وبما أن الدالة العكسية رتيبة أيضًا، فإن عدم المساواة (3.3) تعني عدم المساواة (3.2).

لأي ε > 0 هناك δ، لذلك |f -1 (ص) - و -1 (ص 0) |< ε للجميع |y - y 0 | < δ .

تحدد المتباينات (3.3) فترة مفتوحة تكون نهاياتها بعيدة عن النقطة على مسافات و . يجب أن يكون هناك أصغر هذه المسافات:
.
بسبب الرتابة الصارمة لـ , . لهذا . بعد ذلك سوف يقع الفاصل الزمني في الفاصل الزمني المحدد بالمتباينات (3.3). ولجميع القيم التي تنتمي إليها سيتم استيفاء المتباينات (3.2).

لذلك وجدنا أنه بالنسبة للحجم الصغير بما فيه الكفاية، يوجد، لذلك
في .
الآن دعونا نغير الترميز.
لصغيرة بما فيه الكفاية، هناك شيء من هذا القبيل، لذلك
في .
وهذا يعني أن الدالة العكسية مستمرة عند النقاط الداخلية.

3.2. الآن فكر في نهايات مجال التعريف. هنا يبقى كل المنطق كما هو. تحتاج فقط إلى النظر في الأحياء أحادية الجانب لهذه النقاط. بدلاً من النقطة سيكون هناك أو، وبدلاً من النقطة - أو.

لذلك، للحصول على وظيفة متزايدة، .
في .
الدالة العكسية مستمرة عند هذه النقطة، حيث أنه يوجد أي نقطة صغيرة بما فيه الكفاية، لذلك
في .

بالنسبة للدالة التناقصية، .
الدالة العكسية مستمرة عند هذه النقطة، حيث أنه يوجد أي نقطة صغيرة بما فيه الكفاية، لذلك
في .
الدالة العكسية مستمرة عند هذه النقطة، حيث أنه يوجد أي نقطة صغيرة بما فيه الكفاية، لذلك
في .

لقد تم إثبات النظرية.

إثبات نظرية وجود واستمرارية الدالة العكسية على فترة

اسمحوا للإشارة إلى مجال تعريف الوظيفة - فترة مفتوحة. دع تكون مجموعة قيمها. وفقًا لما سبق، هناك دالة عكسية لها مجال تعريف، ومجموعة قيم، وهي رتيبة تمامًا (تزيد إذا زادت، وتنقص إذا نقصت). ويبقى علينا أن نثبت ذلك
1) المجموعة عبارة عن فترة مفتوحة، وذلك
2) الدالة العكسية مستمرة عليه.
هنا .

1. لنبين أن مجموعة قيم الدالة عبارة عن فترة مفتوحة:
.

مثل أي مجموعة غير فارغة تحتوي عناصرها على عملية مقارنة، فإن مجموعة قيم الدالة لها حدود دنيا وعليا:
.
هنا ويمكن أن تكون أرقامًا أو رموزًا محدودة و .

1.1. دعونا نبين أن النقاط و لا تنتمي إلى مجموعة قيم الوظيفة. أي أن مجموعة القيم لا يمكن أن تكون قطعة.

إذا أو هو نقطة في اللانهاية: أو، فإن هذه النقطة ليست عنصرًا في المجموعة. ولذلك، لا يمكن أن تنتمي إلى قيم متعددة.

دع (أو) يكون عددا منتهيا. ولنفترض العكس. دع النقطة (أو) تنتمي إلى مجموعة قيم الدالة. وهذا هو، هناك مثل هذا (أو). دعونا نأخذ النقاط ونحقق عدم المساواة:
.
نظرًا لأن الوظيفة رتيبة تمامًا، إذن
، إذا زاد f؛
، إذا كان f يتناقص.
أي أننا وجدنا نقطة تكون فيها قيمة الدالة أقل (أكبر من). ولكن هذا يخالف تعريف الحد الأدنى (الأعلى) الذي بموجبه
للجميع.
لذلك، لا يمكن أن تنتمي النقاط إلى مجموعة قيم الدالة.

1.2. الآن سوف نبين أن مجموعة القيم هي فترة، وليست اتحاد فترات ونقاط. وهذا هو، لأي نقطة هناك، والتي .

وفقا لتعريفات الحد الأدنى والأعلى، أي جوار النقاط ويحتوي على عنصر واحد على الأقل من المجموعة. اسمحوا يكون عددا تعسفيا ينتمي إلى الفاصل الزمني: . ثم للحي يوجد من أجله
.
لحي هناك , الذي
.

منذ و ثم . ثم
(4.1.1) فإذا زاد؛
(4.1.2) إذا انخفض.
من السهل إثبات عدم المساواة (4.1) عن طريق التناقض. ولكن يمكنك استخدام، والتي بموجبها توجد وظيفة عكسية في المجموعة، والتي تزيد بشكل صارم إذا زادت وتنخفض بشكل صارم إذا انخفضت. ثم نحصل على الفور على عدم المساواة (4.1).

إذن، لدينا قطعة حيث إذا زادت؛
إذا انخفض.
في نهايات المقطع تأخذ الدالة القيم و . لأنه، وفقا لنظرية بولزانو-كوشي، هناك نقطة لذلك.

وبما أن ذلك قد أظهرنا أنه لأي شيء يوجد من أجله. وهذا يعني أن مجموعة قيم الدالة هي فترة مفتوحة.

2. الآن سوف نبين أن الدالة العكسية مستمرة عند نقطة اختيارية في الفترة: . للقيام بذلك، تنطبق على هذا الجزء. وبما أن الدالة العكسية مستمرة على القطعة، بما في ذلك عند النقطة.

لقد تم إثبات النظرية.

مراجع:
أوي. بيسوف. محاضرات في التحليل الرياضي. الجزء الأول. موسكو، 2004.
سم. نيكولسكي. دورة التحليل الرياضي. المجلد الأول. موسكو، 1983.

أنظر أيضا:

دع المجموعتين $X$ و$Y$ يتم تضمينهما في مجموعة الأعداد الحقيقية. دعونا نقدم مفهوم وظيفة عكسية.

التعريف 1

الدالة $f:X\to Y$ التي تقوم بتعيين مجموعة $X$ إلى مجموعة $Y$ تسمى قابلة للعكس إذا كانت لأية عناصر $x_1,x_2\in X$، من حقيقة أن $x_1\ne x_2$ تتبعها أن $f(x_1 )\ne f(x_2)$.

الآن يمكننا أن نقدم مفهوم الدالة العكسية.

التعريف 2

اجعل الدالة $f:X\to Y$ التي تقوم بتعيين المجموعة $X$ في المجموعة $Y$ قابلة للعكس. ثم تقوم الدالة $f^(-1):Y\to X$ بتعيين المجموعة $Y$ في المجموعة $X$ المحددة بواسطة الشرط $f^(-1)\left(y\right)=x$ هي يسمى معكوس $f(x)$.

دعونا صياغة النظرية:

النظرية 1

دع الدالة $y=f(x)$ محددة، بشكل رتيب متزايد (متناقص) ومستمر في فترة ما $X$. ثم في الفاصل الزمني المقابل $Y$ لقيم هذه الوظيفة، لها دالة عكسية، والتي تزيد أيضًا (تتناقص) بشكل رتيب وتكون مستمرة على الفاصل الزمني $Y$.

دعونا الآن نقدم مباشرة مفهوم الدوال العكسية المتبادلة.

التعريف 3

في إطار التعريف 2، تسمى الوظائف $f(x)$ و $f^(-1)\left(y\right)$ بالدوال العكسية المتبادلة.

خصائص الدوال العكسية المتبادلة

افترض أن الدالتين $y=f(x)$ و$x=g(y)$ معكوستان بشكل متبادل

$y=f(g\left(y\right))$ و $x=g(f(x))$

مجال تعريف الدالة $y=f(x)$ يساوي مجال قيمة الدالة $\ x=g(y)$. ومجال تعريف الدالة $x=g(y)$ يساوي مجال قيمة الدالة $\ y=f(x)$.

الرسوم البيانية للوظائف $y=f(x)$ و$x=g(y)$ متناظرة بالنسبة إلى الخط المستقيم $y=x$.

إذا زادت إحدى الدالتين (نقصت)، فإن الدالة الأخرى تزيد (تنقص).

إيجاد الدالة العكسية

تم حل المعادلة $y=f(x)$ بالنسبة للمتغير $x$.

من الجذور التي تم الحصول عليها، تم العثور على تلك التي تنتمي إلى الفاصل الزمني $X$.

تمت مطابقة $x$ الذي تم العثور عليه مع الرقم $y$.

مثال 1

أوجد الدالة العكسية للدالة $y=x^2$ على الفترة $X=[-1,0]$

بما أن هذه الدالة متناقصة ومستمرة على الفترة $X$، ثم على الفترة $Y=$، والتي تكون أيضًا متناقصة ومستمرة على هذه الفترة (النظرية 1).

لنحسب $x$:

\ \

اختر $x$ المناسب:

إجابة:الدالة العكسية $y=-\sqrt(x)$.

مشاكل في العثور على وظائف عكسية

في هذا الجزء سننظر في الدوال العكسية لبعض الدوال الأولية. سنقوم بحل المشاكل وفقًا للمخطط الموضح أعلاه.

مثال 2

أوجد الدالة العكسية للدالة $y=x+4$

لنجد $x$ من المعادلة $y=x+4$:

مثال 3

أوجد الدالة العكسية للدالة $y=x^3$

حل.

نظرًا لأن الدالة متزايدة ومستمرة في مجال التعريف بأكمله، فوفقًا للنظرية 1، فإن لها دالة مستمرة ومتزايدة معكوسة.

لنجد $x$ من المعادلة $y=x^3$:

العثور على القيم المناسبة لـ $x$

القيمة مناسبة في حالتنا (حيث أن مجال التعريف هو كل الأرقام)

دعونا نعيد تعريف المتغيرات، نحصل على أن الدالة العكسية لها الشكل

مثال 4

أوجد الدالة العكسية للدالة $y=cosx$ على الفترة $$

حل.

خذ بعين الاعتبار الدالة $y=cosx$ في المجموعة $X=\left$. إنها مستمرة وتناقصية على المجموعة $X$ وتقوم بتعيين المجموعة $X=\left$ على المجموعة $Y=[-1,1]$، وبالتالي، من خلال نظرية وجود دالة رتيبة مستمرة عكسية، الدالة $y=cosx$ في المجموعة $ Y$ هناك دالة عكسية، وهي أيضًا مستمرة ومتزايدة في المجموعة $Y=[-1,1]$ وتقوم بتعيين المجموعة $[-1,1]$ إلى المجموعة $\left$.

لنجد $x$ من المعادلة $y=cosx$:

العثور على القيم المناسبة لـ $x$

دعونا نعيد تعريف المتغيرات، نحصل على أن الدالة العكسية لها الشكل

مثال 5

أوجد الدالة العكسية للدالة $y=tgx$ على الفترة $\left(-\frac(\pi )(2),\frac(\pi )(2)\right)$.

حل.

خذ بعين الاعتبار الدالة $y=tgx$ في المجموعة $X=\left(-\frac(\pi )(2),\frac(\pi )(2)\right)$. إنه مستمر ومتزايد على المجموعة $X$ ويعين المجموعة $X=\left(-\frac(\pi )(2),\frac(\pi )(2)\right)$ على المجموعة $Y =R$، لذلك، وفقًا لنظرية وجود دالة رتيبة مستمرة عكسية، فإن الدالة $y=tgx$ في المجموعة $Y$ لها دالة عكسية، وهي أيضًا مستمرة ومتزايدة في المجموعة $Y=R $ وتعيين المجموعة $R$ على المجموعة $\left(- \frac(\pi )(2),\frac(\pi )(2)\right)$

لنجد $x$ من المعادلة $y=tgx$:

العثور على القيم المناسبة لـ $x$

دعونا نعيد تعريف المتغيرات، نحصل على أن الدالة العكسية لها الشكل