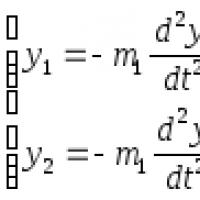اهتزازات حرة للنظام بدرجتين من الحرية. اهتزازات حرة للأنظمة بدرجتين من الحرية الانتقال إلى الإحداثيات الرئيسية

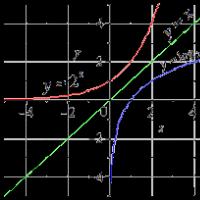
تعتبر الأنظمة ذات درجتين من الحرية حالة خاصة للأنظمة ذات درجات الحرية المتعددة. لكن هذه الأنظمة هي الأبسط، مما يسمح بالحصول على صيغ حسابية نهائية لتحديد ترددات الاهتزاز والسعات والانحرافات الديناميكية.

انحرافات yBeam بسبب قوى القصور الذاتي:

ف2=1 (1)

العلامات (-) في التعبيرات (1) ترجع إلى أن قوى القصور الذاتي ووحداتها. الحركات في الاتجاه المعاكس.

نعتقد أن الاهتزازات الجماعية تحدث وفق القانون التوافقي:

(2)

لنجد تسارع الحركة الجماعية:

(3)

استبدال التعبيرات (2) و (3) في المعادلة (1) نحصل على:

(5)

نعتبر سعة التذبذبات A 1 و A 2 مجهولة، ونحول المعادلات:

(6)

إن حل نظام المعادلات المتجانسة A 1 = A 2 =0 لا يناسبنا؛ ومن أجل الحصول على حل غير الصفر، نقوم بمساواة محددات النظام (6) بالصفر:

(7)

لنحول المعادلة (8) باعتبار التردد الدائري للاهتزازات الطبيعية  مجهول:

تسمى المعادلة (9) بالمعادلة الثنائية التوافقية للتذبذبات الحرة للأنظمة ذات درجتين من الحرية.

بالتعويض عن المتغير  2 =Z نحصل على

من هنا نحدد Z 1 و Z 2.

ونتيجة لذلك يمكن استخلاص الاستنتاجات التالية:

1. تحدث اهتزازات حرة للأنظمة ذات درجتين من الحرية بترددين  1 و  2. يُطلق على التردد الأدنى  1 النغمة الأساسية أو الأساسية، ويسمى التردد الأعلى  2 بالتردد الثاني أو النغمة الفوقية.

الاهتزازات الحرة للأنظمة ذات درجات الحرية n هي نغمة n، وتتكون من اهتزازات خالية من n.

2. يتم التعبير عن حركات الكتل م 1 و م 2 بالصيغة التالية:

أي أنه إذا حدثت تذبذبات بتردد  1، فإن حركات الكتلة لها نفس الإشارات في أي لحظة من الزمن.

إذا حدثت التذبذبات فقط بتردد  2، فإن حركات الكتلة في أي وقت لها إشارات معاكسة.

مع التذبذبات المتزامنة للكتل بترددات  1 و  2، يتأرجح النظام بشكل أساسي عند التردد  1 ويتناسب النغمة الزائدة مع التردد  2 مع هذه التذبذبات.

إذا كان النظام الذي يتمتع بدرجتين من الحرية يخضع لقوة دافعة ذات تردد ، فمن الضروري أن:

  0.7  1 .

المحاضرة 9

تذبذبات الأنظمة بعدد لا نهائي من درجات الحرية.

نظرية الاهتزازات الميكانيكية لها تطبيقات عديدة ومتنوعة للغاية في جميع مجالات التكنولوجيا تقريبًا. بغض النظر عن الغرض والحل التصميمي للأنظمة الميكانيكية المختلفة، فإن اهتزازاتها تخضع لنفس القوانين الفيزيائية، والتي تعد دراستها موضوع نظرية اهتزازات الأنظمة المرنة. لقد تم تطوير النظرية الخطية للتذبذبات بشكل كامل. تم تقديم نظرية تذبذبات الأنظمة ذات درجات الحرية المتعددة في القرن الثامن عشر من قبل لاغرانج في عمله الكلاسيكي "الميكانيكا التحليلية".

جوزيف لويس لاغرانج (1736 - 1813) - أستاذ الرياضيات في تورينو منذ سن التاسعة عشرة. منذ 1759 - عضو، ومنذ 1766 - رئيس أكاديمية برلين للعلوم؛ من عام 1787 عاش في باريس. في عام 1776 تم انتخابه عضوًا أجنبيًا فخريًا في أكاديمية سانت بطرسبرغ للعلوم.

في نهاية القرن التاسع عشر، وضع رايلي أسس النظرية الخطية لتذبذبات الأنظمة بدرجة لا حصر لها من درجات الحرية (أي مع التوزيع المستمر للكتلة في كامل حجم النظام القابل للتشوه). في القرن العشرين، يمكن القول أن النظرية الخطية قد اكتملت (طريقة بوبنوف-جاليركين، والتي تتيح أيضًا تحديد ترددات التذبذب الأعلى باستخدام التقديرات التقريبية المتعاقبة).

جون ويليام ستريت (اللورد رايلي) (1842 - 1919) - فيزيائي إنجليزي، مؤلف عدد من الأعمال حول نظرية التذبذبات.

إيفان غريغوريفيتش بوبنوف (1872 - 1919) - أحد مؤسسي ميكانيكا هياكل السفن. أستاذ في معهد سانت بطرسبرغ للفنون التطبيقية منذ عام 1910 - في الأكاديمية البحرية.

بوريس غريغوريفيتش جاليركين (1871-1945) - أستاذ في معهد لينينغراد للفنون التطبيقية.

صيغة رايلي هي الأكثر شعبية في نظرية الاهتزازات واستقرار الأنظمة المرنة. الفكرة الكامنة وراء اشتقاق صيغة رايلي تتلخص في ما يلي. مع التذبذبات الحرة أحادية التوافق (أحادية النغمة) لنظام مرن بتردد ، تحدث حركات نقاطه في الوقت المناسب وفقًا للقانون التوافقي:

حيث  1 (x,y,z),  2 (x,y,z),  3 (x,y,z) هي وظائف الإحداثيات المكانية للنقطة التي تحدد شكل التذبذب المعني (السعة).

إذا عرفت هذه الوظائف، فيمكن إيجاد تردد الاهتزازات الحرة بشرط أن يكون مجموع الطاقة الحركية والطاقة الكامنة للجسم ثابتا. ويؤدي هذا الشرط إلى معادلة تحتوي على كمية واحدة مجهولة فقط .

ومع ذلك، هذه الوظائف ليست معروفة مقدما. الفكرة التوجيهية لطريقة رايلي هي تحديد هذه الوظائف، ومطابقة اختيارها مع الشروط الحدودية والشكل المتوقع للاهتزازات.

دعونا نفكر بمزيد من التفصيل في تنفيذ هذه الفكرة فيما يتعلق باهتزازات الانحناء المستوي للقضيب؛ يتم وصف شكل الاهتزازات بواسطة الدالة =(x). يتم وصف التذبذبات الحرة بالاعتماد

الطاقة الكامنة لقضيب عازمة

(2)

الطاقة الحركية

(3)

أين ل- طول القضيب، m=m(x) شدة الكتلة الموزعة للقضيب؛

انحناء المحور المنحني للقضيب - سرعة الاهتزازات العرضية.

نظرا (1)

.

(4)

(5)

مع مرور الوقت، تتغير كل من هذه الكميات بشكل مستمر، ولكن وفقا لقانون الحفاظ على الطاقة، يبقى مجموعها ثابتا، أي.

أو عن طريق استبدال التعبيرات (4)، (5) هنا

(7)

وهذا يؤدي إلى صيغة رايلي:

(8)

إذا كانت الأحمال المركزة ذات الكتل M i مرتبطة بقضيب ذو كتلة موزعة m، فإن صيغة رايلي تأخذ الشكل:

(9)

يُظهر المسار الكامل للاشتقاق أنه، في إطار الافتراضات المقبولة (صلاحية النظرية الفنية لثني القضبان، وغياب المقاومة غير المرنة)، تكون هذه الصيغة دقيقة إذا كان (x) هو الشكل الحقيقي للاهتزازات . ومع ذلك، فإن الدالة (x) غير معروفة مسبقًا. الأهمية العملية لصيغة رايلي هي أنه يمكن استخدامها لإيجاد التردد الطبيعي ، بالنظر إلى شكل الاهتزاز (x). في الوقت نفسه، يتم تقديم عنصر القرب أكثر أو أقل خطورة في القرار. لهذا السبب، تُسمى صيغة رايلي أحيانًا بالصيغة التقريبية.

m=cosnt لنأخذ من شكل الاهتزاز الدالة: (x)=ax 2، التي تلبي شروط الحدود الحركية للمشكلة.

نحدد:

حسب الصيغة (8)

هذه النتيجة تختلف بشكل كبير عن النتيجة المحددة

الأكثر دقة هي صيغة جراميل، التي لم تصبح بعد شائعة مثل صيغة رايلي (ربما بسبب "الشباب" النسبي - تم اقتراحها في عام 1939).

دعونا نتناول مرة أخرى نفس مشكلة اهتزازات الانحناء الحر للقضيب.

اجعل (x) هو الشكل المحدد للاهتزازات الحرة للقضيب. ثم يتم تحديد شدة قوى القصور الذاتي القصوى بالتعبير m 2 ، حيث، كما كان من قبل، m=m(x) هي شدة الكتلة الموزعة للقضيب  2 هو مربع التردد الطبيعي. تصل هذه القوى إلى القيمة المحددة في اللحظة التي تصل فيها الانحرافات إلى الحد الأقصى، أي. يتم تحديدها بواسطة الدالة (x).

دعونا نكتب التعبير عن أعلى طاقة انحناء محتملة بدلالة لحظات الانحناء الناتجة عن قوى القصور الذاتي القصوى:

. (10)

هنا - لحظات الانحناء الناتجة عن الحمل m 2 . دعونا نشير إلى لحظة الانحناء الناتجة عن الحمل الشرطي m، أي.  أقل مرتين من قوة القصور الذاتي.

, (11)

ويمكن كتابة التعبير (10) على النحو التالي:

. (12)

أعلى طاقة حركية، كما هو مذكور أعلاه

. (13)

بمساواة التعبيرين (12) و (13) نصل إلى صيغة جرامل:

(14)

للحساب باستخدام هذه الصيغة، يجب عليك أولاً تحديد دالة مناسبة (x). بعد ذلك يتم تحديد الحمل الشرطي m=m(x)(x) وكتابة عبارات الانحناء الناتج عن الحمل الشرطي m. باستخدام الصيغة (14)، يتم تحديد تردد التذبذب الطبيعي للنظام.

مثال: (فكر في المثال السابق)

ذ

م(س)·(س)=حد أقصى 2

الميكانيكا النظرية

يو دي سي 531.8:621.8

دي إم كوبيليانسكي ، ف.ف. جوربونوف ، ف.أ

توافق دوران واهتزازات الأجسام مع درجة واحدة من الحرية

دعونا نفكر في جسم مسطح T، حيث تُفرض عليه ثلاثة قيود مثالية، تمنع فقط حركة الجسم في جميع الاتجاهات، كما هو موضح في الشكل 1أ. الاتصالات هي النقاط A، B، C، وتقع في رؤوس مثلث متساوي الأضلاع. بعد اختيار نظام إحداثي بحيث يتزامن مركزه مع مركز المثلث ويكون محاذيًا له (الشكل 1أ)، لدينا إحداثيات الوصلات: A(0;R), B(^l/3 /2 -R/2)، C ^-Ld/e /2؛ -I/2)، حيث I هي المسافة من مركز المثلث إلى رؤوسه، أي نصف قطر الدائرة التي تمر بالنقاط A، B، C. وفي هذا الوضع، سيكون للجسم درجة واحدة من الحرية فقط إذا كانت الخطوط الطبيعية إلى حدودها عند النقاط A، B، C تتقاطع عند نقطة واحدة، والتي ستكون المركز اللحظي للسرعات. وبخلاف ذلك، فإن عدد درجات حرية الجسم يساوي صفرًا ولا يمكنه التحرك انتقاليًا فحسب، بل يمكنه أيضًا القيام بحركة دورانية. عندما يتمتع الجسم بدرجة واحدة من الحرية، فإنه يمكن أن يبدأ في الدوران مع مركز الدوران اللحظي عند نقطة تقاطع القيم الطبيعية المذكورة أعلاه. لتكن هذه النقطة هي أصل الإحداثيات، النقطة O. إذا لم يغير مركز الدوران اللحظي موضعه، فإن الشكل الوحيد الممكن للجسم T هو دائرة نصف قطرها R ومركزها عند النقطة O.

وتنشأ المشكلة: هل هناك أشكال أخرى للجسم تسمح له بالتدوير بالنسبة إلى مركز متحرك ما بحيث

هل يمر جسم الجسم بشكل مستمر عبر النقاط الثلاث أ، ب، ج دون انقطاع هذه الوصلات؟ في الأدبيات المعروفة لنا، لم يتم النظر في مثل هذه المشكلة، ويبدو أنه يتم حلها لأول مرة.

لحل هذه المشكلة، نأخذ في الاعتبار أولاً حركة المثلث ABC كجسم صلب، نسبةً إلى نظام الإحداثيات X1O1Y1 المرتبط بالجسم T (الشكل 1ب). ثم إذا حدثت حركة المثلث بحيث تظل رؤوسه بشكل مستمر على حدود الجسم أثناء دوران المثلث بالكامل بمقدار 360 درجة، فإن الجسم أيضًا سيقوم بالحركة المطلوبة في الاتجاه المعاكس بالنسبة إلى الثابت المثلث ABC ونظام الإحداثيات المرتبط به XOU.

نحدد حركة المثلث ABC على أنها دوران بالنسبة إلى المركز O وحركة المركز O على طول المحور ОиХи بمقدار /(g)، على طول المحور ОиУи بواسطة g(t). ثم المعادلة البارامترية لمسار النقطة A سيكون لها الشكل: x = ryaSh +/(r); y=г-єо,?͑ +g(t), є (1)

بما أن النقطة O عند g=0 يجب أن تتزامن مع النقطة O1، فيجب استيفاء الشرط /(0)= g(0)=0. نشترط أنه عند التدوير بزاوية r = 2n/3، تتطابق النقطة A مع النقطة B1، وتتوافق النقطة B مع النقطة C، والنقطة C

مع النقطة A1. عند الدوران بزاوية r = 4n/3، يجب أن تنتقل النقطة A إلى النقطة C1، والنقطة B إلى النقطة A1، والنقطة C إلى النقطة B1. إن الجمع بين هذه المتطلبات لحركة رءوس المثلث يؤدي إلى شروط قيم دوال تحريك مركز الدوران /(0)=/(2 ع/3)=/(4 ع/3)= 0; g0)=g(2l/3)=g(4l/3)=0 . (2) يتم استيفاء الشروط (2) من خلال فئة واسعة من الوظائف، ولا سيما وظائف النموذج sin(3mt/2)، حيث m عدد صحيح، ومجموعاتها الخطية ذات المعاملات المتغيرة بشكل عام من النموذج:

ح (ز) = ^ بت (ز) 8Іп(3те / 2)

بالإضافة إلى ذلك، كما

رسم بياني 1. مخطط الحساب: أ) - موضع الجسم الثابت واتصالاته في نظام XOU؛ ب) - موضع النظام الثابت X1O1U1 المرتبط بالجسم، والنظام المتحرك XOU المرتبط بالمثلث ABC

الميكانيكا النظرية

الصورة 2. أشكال الأجسام ومسارات حركة مراكز دورانها

أرز. 3. موضع الجسم عند الدوران بزاوية ومسار الحركة المقابل لمركز دورانه

يمكن أخذ دوال الإزاحة، وهي الدوال التي تحدد المنحنيات المغلقة، مثل الدائريات، والتروكويدات، واللمنيسكات، مع معلمات مناسبة وفقًا للحالة (2). في هذه الحالة، يجب أن تكون جميع الوظائف الممكنة دورية بفترة 2n/3.

وهكذا فإن نظام المعادلات البارامترية (1) مع الشروط على قيم الدوال /(^, g(t) (2) أو في صورتها (3) يعطي المعادلة المطلوبة لحدود الجسم T. يوضح الشكل 2 أمثلة لأشكال الجسم المحتملة التي تلبي شروط المهمة. في وسط كل شكل، يظهر مسار مركز الدوران O1، ويتم تكبير اتصالات النقاط A وB وC لتصورها بشكل أفضل أظهر أنه حتى الأنواع البسيطة من الوظائف من الفئة المحددة بالتعبير (3) ذات المعاملات الثابتة تعطي لدينا مجموعة واسعة إلى حد ما من المنحنيات التي تصف حدود الأجسام التي تخضع للدوران و

اهتزازات متزامنة بدرجة واحدة فقط من الحرية. منحنيات الحدود أ)، ج) في الشكل. 2 تتوافق مع حركة مركز الدوران فقط على طول المحور الأفقي

أوهي وفقًا للقانون التوافقي، وكما يمكن رؤيته، لها محورين من التماثل ويمكن أن تكون إما محدبة بحتة أو بيضاوية (الشكل 2 أ) أو تجمع بين التحدب والتقعر (الشكل 2 ب). مع وجود قانون توافقي رأسي وأفقي له نفس سعة حركة مركز الدوران، تفقد المنحنيات الحدودية تماثلها (الشكل 2 ج، د). يظهر الشكل 2 د، و التأثير الكبير لتردد الاهتزازات التوافقية على شكل المنحنى الحدودي للجسم. دون إجراء تحليل كامل لتأثير السعة والتردد على الشكل والخصائص الهندسية للحدود منحنيات في هذا العمل، أود أن أشير إلى أن الأمثلة المعروضة في الشكل 2 تظهر بالفعل القدرة على حل المشاكل التقنية في اختيار الشكل المطلوب

يجمع الجسم بين حركته الدورانية والاهتزازات في مستوى الدوران.

الآن بالنظر إلى حركة الجسم بالنسبة لنظام الإحداثيات الثابت XOU المرتبط بالمثلث ABC، أي الانتقال من نظام الإحداثيات X1O1U1 إلى نظام الإحداثيات XOU، نحصل على المعادلات البارامترية التالية للمنحنى الحدودي للجسم عند زاوية الدوران المعطاة p x = cosp-

كوسب(4)

أو مع مراعاة المعادلات (1) فإن المعادلات (4) تأخذ الصيغة x = cosp-

- [ R cos(t) + g (t) - g (p)] sin p, y = sin p +

كوس ص.

تتيح المعادلات (5) وصف مسار أي نقطة من الجسم حسب قطبيتها المعطاة.

تي جي م*4<. п-і

تي-ÍLÍtWM. د-0

أرز. 4. أشكال مختلفة من الجسم مع أعداد مختلفة من الوصلات، مما يضمن توافق دوران واهتزاز الأجسام

الإحداثيات النهائية R,t. على وجه الخصوص، عند R=0، t=0 لدينا نقطة تتطابق مع أصل الإحداثيات Ob، أي مركز الدوران، والذي يتم وصف مساره في المخطط قيد النظر بالمعادلات التالية من (5) :

*0 = -f (ph) cos ph + g (ph) sin ph, y0 = - f (ph) sin ph- g (ph) cos r.

يوضح الشكل 3 مثالاً على أوضاع الجسم (الشكل 2ب) عند تدويره بزاوية φ، وفي وسط كل شكل يظهر مسار مركز الدوران

أوي، يتوافق مع دوران الجسم خلال هذه الزاوية. من الناحية الفنية ليس من الصعب صنع الرسوم المتحركة

لحركة الجسم الموضحة في الشكل 3 بدلاً من النموذج المادي، ومع ذلك، فإن إطار مقالة صحفية لا يمكن أن يسمح بذلك إلا في نسخة إلكترونية. المثال الموضح كان لا يزال

تعميم المشكلة التي تم النظر فيها هو نظام من الوصلات المثالية على شكل نقاط تقع في رؤوس مثلث منتظم، مما يمنع فقط الحركات الانتقالية للجسم. ولذلك، كما في حالة المثلث، يمكن أن يبدأ الجسم بالدوران بالنسبة إلى مركز الدوران، وهو نقطة تقاطع الأطوار مع حدود الجسم عند نقاط الاتصال. في هذه الحالة، فإن معادلة مسار نقطة الجسم A، الواقعة على المحور OU، وتقع على مسافة H من مركز الدوران، سيكون لها نفس الشكل (1). سوف تتحقق شروط قيم دوال تحريك مركز الدوران (2) في هذه الحالة

كوبيليانسكي جوربونوف

ديمتري ميخائيلوفيتش فاليري فيدوروفيتش

طالب دراسات عليا بالقسم . ثابتة و- الوثيقة. تقنية. العلوم، البروفيسور. قسم مائة

مركبات النقل والمركبات الثابتة ومركبات النقل

و(2kp/p)=g(2kp/p)=0. (7)

الحالة (7) تتوافق مع الدوال الدورية ذات الدورة 2n/n، على سبيل المثال 8m(n-m4/2)، بالإضافة إلى مجموعاتها الخطية من الشكل (3) والدوال الأخرى التي تصف المنحنيات المغلقة. إن الاستدلال المشابه لما ذكر أعلاه يؤدي إلى نفس المعادلات (4-6) التي تجعل من الممكن حساب شكل الجسم وموقعه أثناء الدوران ومسار مركز الدوران مع اهتزازات الجسم المتوافقة مع الدوران . مثال على هذه الحسابات هو الشكل 4، حيث يوضح الخط المنقط الموضع الأولي للأجسام، والخط الصلب يوضح موضع الأجسام عند الدوران بزاوية l/3، وفي وسط كل شكل يوجد المسار الكامل لمركز الدوران أثناء الدوران الكامل للجسم. وعلى الرغم من أنه في هذا المثال يتم أخذ الحركة الأفقية لمركز الدوران O فقط في الاعتبار، كمركز n-gon، إلا أن النتائج التي تم الحصول عليها تظهر مجموعة واسعة من الأشكال المحتملة لجسم بدرجة واحدة من الحرية، والجمع بين الحركة الدورانية مع تذبذبات في وجود أربعة وخمسة وستة اتصالات.

يمكن أيضًا استخدام الطريقة الناتجة لحساب مدى توافق حركات الدوران والتذبذب للأجسام بدرجة واحدة من الحرية دون أي إضافات للأجسام المكانية التي يُحظر عليها التحرك على طول الإحداثي الثالث والدوران في مستويات الإحداثيات الأخرى.

غوغولين فياتشيسلاف أناتوليفيتش

دكتور. تقنية. العلوم، البروفيسور. قسم عالم الرياضيات التطبيقية و

دع النظام ذو درجتين من الحرية يعطى وإحداثيات معممة. يتم إعطاء الطاقة الحركية والطاقة الكامنة للنظام بالصيغ (10.2):

الدالتان T وP موجبتان بالتأكيد، وبالتالي:

بالتعويض (10.2) في (10.12)، نحصل على معادلات تفاضلية للتذبذبات الصغيرة لنظام يتمتع بدرجتين من الحرية:

النظام لديه حل صفر A=B=0، الموافق لموضع التوازن المستقر. بالنسبة للحلول غير الصفرية نؤلف من (10.15) العلاقة:

بسبب متباينات الاستقرار، فإن المعادلة التربيعية (بالنسبة لـ) (10.18) لها جذرين حقيقيين موجبين. دعونا نرتبها ترتيبًا تصاعديًا:

بالنسبة للاهتزاز الرئيسي الثاني:

(10.21)

الاهتزازات الرئيسية هي الاهتزازات التوافقية.

بالتعويض وبدوره في (10.16)، نجد الروابط بين السعات A و B في الاهتزازات الرئيسية: . تسمى العوامل معاملات النموذج الذاتي (معاملات توزيع السعة). يمكن أن تكون إيجابية وسلبية. عندما تكون الإحداثيات في التذبذب الرئيسي في نفس المرحلة؛ في - في الطور المضاد.

ستكون الحركة الناتجة على طول كل إحداثي عبارة عن مجموع تذبذبين رئيسيين:

(10.22)

حيث - تعتمد على الشروط الأولية - لا تعتمد على الشروط الأولية ويتم تحديدها بواسطة معلمات النظام التذبذبي نفسه. وفي الحالة العامة فإن الترددات غير قابلة للقياس، وبالتالي فإن الحركة الناتجة لن تكون دورية.

1. تحديد الترددات الطبيعية وأنماط الاهتزاز الطبيعية (الصغيرة) لبندول رياضي مزدوج يتكون من نقطتين ماديتين متساويتين في الكتلة m وقضيبين بطول كل منهما.

تم النظر في نظام مماثل بشكل عام في المثال 2 (الفقرة 34). دعونا نستخدم الصيغ (2) و (3) التي تم الحصول عليها هناك.

عندما نصل:

وبما أن التذبذبات صغيرة، فحتى التذبذبات الصغيرة من الدرجة الثانية شاملة:

(3)

ومع مراعاة (3) من (1) نلاحظ:

(4)

وبمقارنة (4) و(2) نلاحظ:

بتوسيع المعادلة (7.52) للترددات نحصل على:

ومن (9.50) نجد معاملات التوزيع : .

التذبذب الكبير الأول:

الحركة في الطور - في كل لحظة تدور القضبان في اتجاه واحد.

التردد الرئيسي الثاني:

الحركة في الطور المضاد - في كل لحظة تدور القضبان في اتجاهين متعاكسين تمامًا.

تظهر أوضاع الاهتزاز في الشكل. 50. في الاهتزاز الرئيسي الثاني توجد نقطة خاصة F، والتي تظل بلا حراك. تسمى هذه النقاط بالعقد. نقطة النهاية O ليست عقدة.

2. جسمان صلبان ذوا كتل ونوابض ذات صلابة ويتم دمجهما في نظام يقع على مستوى أفقي أملس ويمكنه إجراء تذبذبات خطية صغيرة.

التذبذب الكبير الأول:

تتحرك الأجسام في الطور، إما إلى اليمين أو إلى اليسار. سعة تذبذب الجسم الثاني أكبر بمقدار 1.62 مرة.

التردد الرئيسي الثاني:

تتحرك الأجسام في الطور المضاد: إما تجاه بعضها البعض، أو نحو العقدة، أو تتباعد عن العقدة. سعة اهتزازات الجسم الثاني هي 0.62 من سعة الجسم الأول.

من معادلات حركة نظام ميكانيكي محافظ حول موضع توازن مستقر

في حالة درجتين من الحرية لدينا:

(1)

(وفقًا لمعيار سيلفستر:

(1) نظام المعادلات التفاضلية للتذبذبات الحرة الصغيرة لنظام ميكانيكي بدرجتين من الحرية بالقرب من موضع توازن مستقر. يتم البحث عن حلها في النموذج:

(2)

استبدال هذا الحل في نظام المعادلات التفاضلية للاهتزازات الصغيرة يعطي:

(3)

فيما يتعلق بـ A وB، فهذا نظام من المعادلات الجبرية المتجانسة. له حل غير بديهي عندما يكون محدد النظام صفرًا:

(4)

تسمى هذه المعادلة التربيعية بالمعادلة الترددية، ولها جذرين موجبين، يتوافقان مع حلين لنظام المعادلات التفاضلية للاهتزازات الصغيرة:

وبالتالي، يتم العثور على كل إحداثي معمم كمجموع ذبذبتين بترددات مختلفة، والتي تسمى التقلبات الرئيسية . في هذه الحالة، كما يلي من النظام (3)، ترتبط سعات الاهتزازات الرئيسية ببعضها البعض على النحو التالي:

(5)

أين - عوامل الشكل التقلبات الرئيسية.

ونتيجة لذلك، فإن حل معادلات الاهتزازات الحرة (1) يأخذ الشكل التالي:

(6)

البريد الوارد(6) السعات ، والمراحل الأولية ،يتم تحديد التذبذبات من الظروف الأولية.

الاهتزازات القسرية للأنظمة الميكانيكية بدرجتين من الحرية. مخمد الاهتزاز الديناميكي

يسمى القضاء على الاهتزازات غير المرغوب فيها في الأنظمة الميكانيكية حماية الاهتزاز (التخميد).تسمى الأجهزة التقنية المستخدمة في هذه الحالة مخمدات الاهتزاز (المخمدات).

يعتمد مبدأ تشغيل المثبط الديناميكي على استخدام ظاهرة الرنين المضاد، عندما يتم تحييد عمل القوة المعممة المزعجة المتغيرة بشكل دوري المقابلة لإحداثيات واحدة من خلال عمل قوة معممة محتملة تتوافق مع إحداثيات أخرى.

ليكن النظام الميكانيكي بالإضافة إلى القوى المحافظة يخضع لقوة مزعجة تتغير بمرور الزمن وفق قانون توافقي

المعادلات التفاضلية لحركة النظام الميكانيكي في هذه الحالة لها الشكل:

نحن نبحث عن حل عام لنظام المعادلات التفاضلية الخطية غير المتجانسة (في هذه الحالة) كمجموع حلين: - حل عام لنظام المعادلات التفاضلية المتجانسة؛ -الحل الجزئي لنظام المعادلات التفاضلية غير المتجانسة.

ومع مراعاة اعتماد القوة المزعجة على الزمن، يتم البحث عن حل معين في الشكل

استبداله في نظام المعادلات التفاضلية يعطي:

وبحل هذا النظام باستخدام قاعدة كرامر نحصل على

لأنه يتزامن مع الجانب الأيسر من معادلة التردد ويختفي

عندما يتطابق تردد القوة المزعجة مع أحد الترددات الطبيعية

التذبذبات أو المعاملات A و B في هذه الحالة تتحول إلى ما لا نهاية. وهكذا، في حالة تذبذبات النظام بدرجتين من الحرية، هناك اثنين من الترددات الرنانة

الحل العام لنظام المعادلات التفاضلية القسرية

الاهتزازات عند لديه النموذج:

كما يتبين، من خلال اختيار معلمات النظام المتذبذب، من الممكن تحقيق، على سبيل المثال، استيفاء الشرط A = 0، أي أن سعة التذبذبات القسرية المقابلة للإحداثيات المعممة الأولى تصبح صفرًا.

وتسمى هذه الظاهرة بالرنين العكسي.

في الحالة قيد النظر يحدث هذا إذا

المفاهيم والفرضيات الأساسية لنظرية التأثير. المعادلة الأساسية لنظرية التأثير

ظاهرة يتم فيها في فترة قصيرة من الزمن، أي. على الفور تقريبًا، تتغير سرعات نقاط الأجسام المادية إلى قيم محدودة، تسمى ينفخ .

نظرًا لأن التغيير النهائي في السرعة يحدث أثناء الاصطدام خلال فترة زمنية قصيرة جدًا، تنشأ تسارعات كبيرة جدًا، وبالتالي تنشأ قوى كبيرة جدًا. تعمل هذه القوى خلال فترة زمنية قصيرة جدًا، لكن نبضاتها خلال هذه الفترة الزمنية تكون بكميات محدودة.

تسمى القوى التي تنشأ أثناء الاصطدام خلال فترة زمنية قصيرة، ولكنها تصل في نفس الوقت إلى قيمة كبيرة، بحيث تكون نبضاتها خلال هذه الفترة الزمنية قيمًا محدودة قوى الصدمة .

تسمى الفترة القصيرة من الوقت التي تستمر فيها الضربة وقت التأثير. تسمى نبضات قوى التأثير أثناء الاصطدام نبضات الصدمة .

دع الكتلة m تعطى، والتي تتحرك تحت تأثير قوة عادية (غير صادمة). في الوقت الحالي، عندما يكون لدى MT المدروس سرعة - السرعة قبل التأثير، تبدأ قوة التأثير في التصرف عليها، والتي يتوقف عملها في الوقت الحالي. دعونا نحدد حركة MT تحت تأثير القوى وأثناء وقت التأثير.

وبتطبيق نظرية التغير في زخم نقطة ما نحصل على:

,

أين هي سرعة النقطة في اللحظة التي تلي الاصطدام.

باستخدام نظرية القيمة المتوسطة للتكامل المحدد، يمكننا أن نكتب:

,

أين و هي متوسط ​​قيم القوى و في فترة زمنية معينة. علاوة على ذلك، فهي كمية محدودة؛ تصل قوة التأثير أثناء الاصطدام إلى قيمة كبيرة جدًا (من ترتيب ). ولذلك، فإن المنتج سيكون ضئيلا مقارنة بالمنتج، وهو كمية محدودة.

دعونا نفكر في التذبذبات الصغيرة لنظام يتمتع بدرجتين من الحرية، ويخضع لقوى المجال المحتمل والقوى التي تتغير بشكل دوري مع مرور الوقت. تسمى الحركات الناتجة للنظام بالتذبذبات القسرية.

لتتغير القوى المعممة المزعجة وفق قانون توافقي مع الزمن، ولها فترات وطور ابتدائي متساويان. عندها ستكون معادلات حركة النظام قيد النظر بالشكل التالي:

معادلات الحركة في الحالة قيد النظر هي نظام من المعادلات التفاضلية الخطية من الدرجة الثانية ذات المعاملات الثابتة والجانب الأيمن.

انتقل إلى الإحداثيات الرئيسية

ولتسهيل دراسة معادلات الحركة، دعنا ننتقل إلى الإحداثيات الرئيسية للنظام، ويتم تحديد العلاقة بين الإحداثيات من خلال صيغ الفقرة السابقة من النموذج:

دعونا نشير بالمقابل إلى القوى المعممة المقابلة للإحداثيات العادية، بما أن القوى المعممة تمثل معاملات للتغيرات المقابلة للإحداثيات المعممة في التعبير عن العمل الأولي للقوى المؤثرة على النظام، إذن.

لذلك:

وبالتالي فإن معادلات الحركة في الإحداثيات الرئيسية تأخذ الشكل:

معادلات التذبذبات القسرية لنظام يتمتع بدرجتين من الحرية في الإحداثيات العادية مستقلة عن بعضها البعض ويمكن دمجها بشكل منفصل.

الترددات الحرجة للقوة المزعجة

معادلة أو تحديد الطبيعة التذبذبية للتغير في الإحداثيات العادية، تمت دراستها بالتفصيل عند النظر في التذبذب القسري لنقطة على طول خط مستقيم، حيث أن المعادلات التفاضلية للحركة هي نفسها في كلتا الحالتين. على وجه الخصوص، إذا كان تردد القوة المزعجة يساوي تردد إحدى الاهتزازات الطبيعية للنظام، أو سيتضمن الحل الوقت t كعامل. وبالتالي، فإن أحد الإحداثيات المعممة الطبيعية لـ t كبير بدرجة كافية سيكون كبيرًا بشكل تعسفي، أو لدينا ظاهرة الرنين.