একটি ফাংশনের একক বিন্দু এবং তাদের শ্রেণীবিভাগ। বিচ্ছিন্ন একবচন বিন্দু। তাদের গণনার জন্য অবশিষ্টাংশ এবং সূত্র

দুটি স্বায়ত্তশাসিত ডিফারেনশিয়াল সমীকরণের সিস্টেম দ্বারা বর্ণিত মডেল।

ফেজ সমতল ফেজ পোর্ট্রেট। আইসোক্লাইন পদ্ধতি। প্রধান আইসোলাইন। স্থির রাষ্ট্র স্থিতিশীলতা। লিনিয়ার সিস্টেম। কী পয়েন্ট প্রকার: নোড, স্যাডল, ফোকাস, সেন্টার। উদাহরণ: প্রথম অর্ডার রাসায়নিক বিক্রিয়া।

জৈবিক সিস্টেমের বৈশিষ্ট্যগুলির গুণগত মডেলিংয়ের সবচেয়ে আকর্ষণীয় ফলাফল দুটি ডিফারেনশিয়াল সমীকরণের মডেলগুলিতে প্রাপ্ত হয়েছিল, যা পদ্ধতিটি ব্যবহার করে একটি গুণগত অধ্যয়নের অনুমতি দেয়। ফেজ সমতল. সাধারণ ফর্মের দুটি স্বায়ত্তশাসিত সাধারণ ডিফারেনশিয়াল সমীকরণের একটি সিস্টেম বিবেচনা করুন

(4.1)

P(x,y), Q(x,y)- কিছু ডোমেনে সংজ্ঞায়িত ক্রমাগত ফাংশন জিইউক্লিডীয় সমতল ( x,y- কার্টেসিয়ান স্থানাঙ্ক) এবং এই এলাকায় ক্রমাগত ডেরিভেটিভস অফ অর্ডার প্রথম থেকে কম নয়।

অঞ্চল জিসীমাহীন বা সীমিত হতে পারে। ভেরিয়েবল হলে x, yএকটি নির্দিষ্ট জৈবিক অর্থ আছে (পদার্থের ঘনত্ব, প্রজাতির প্রাচুর্য), প্রায়শই এলাকা জিডান অর্ধ-সমতলের ধনাত্মক চতুর্ভুজ:

0 £ এক্স< ¥ ,0 £ y< ¥ .

পদার্থের ঘনত্ব বা প্রজাতির প্রাচুর্যও উপরে থেকে জাহাজের আয়তন বা বাসস্থানের ক্ষেত্রফল দ্বারা সীমাবদ্ধ হতে পারে। তারপর ভেরিয়েবলের পরিসরের ফর্ম আছে:

0 £ এক্স< x 0 , 0 £ y< y 0 .

ভেরিয়েবল x, yসমীকরণের সিস্টেম (4.1) অনুসারে সময়ের পরিবর্তন, যাতে সিস্টেমের প্রতিটি অবস্থা ভেরিয়েবলের মানের একটি জোড়ার সাথে মিলে যায় ( x, y).

বিপরীতভাবে, ভেরিয়েবলের প্রতিটি জোড়ার জন্য ( x, y) সিস্টেমের একটি নির্দিষ্ট অবস্থার সাথে মিলে যায়।

স্থানাঙ্ক অক্ষ সহ একটি সমতল বিবেচনা করুন যেখানে ভেরিয়েবলের মানগুলি প্লট করা হয়েছে x,y. প্রতিটি পয়েন্ট এমএই সমতল সিস্টেমের একটি নির্দিষ্ট অবস্থার সাথে মিলে যায়। এই জাতীয় সমতলকে ফেজ প্লেন বলা হয় এবং সিস্টেমের সমস্ত রাজ্যের সামগ্রিকতা চিত্রিত করে। M(x, y) বিন্দুটিকে চিত্রিত বা প্রতিনিধিত্বকারী বিন্দু বলা হয়।

প্রারম্ভিক সময়ে যাক t=t 0 প্রতিনিধিত্বকারী পয়েন্ট স্থানাঙ্ক এম 0 (এক্স(t 0),y(t 0)). সময়ের প্রতিটি পরের মুহূর্তে tভেরিয়েবলের মানের পরিবর্তন অনুসারে চিত্রিত বিন্দুটি সরবে এক্স(t),y(t). পয়েন্টের সেট এম(এক্স(t), y(t)) ফেজ প্লেনে, যার অবস্থান সময়ের সাথে পরিবর্তনশীল পরিবর্তনের প্রক্রিয়ায় সিস্টেমের অবস্থার সাথে মিলে যায় x(t), y(t)সমীকরণ অনুযায়ী (4.1), বলা হয় ফেজ ট্রাজেক্টোরি

ভেরিয়েবলের বিভিন্ন প্রারম্ভিক মানের জন্য ফেজ ট্র্যাজেক্টরির সেট সিস্টেমের একটি সহজে দৃশ্যমান "প্রতিকৃতি" দেয়। বিল্ডিং ফেজ প্রতিকৃতিআপনাকে ভেরিয়েবলের পরিবর্তনের প্রকৃতি সম্পর্কে সিদ্ধান্ত নিতে দেয় x, yসমীকরণের মূল সিস্টেমের বিশ্লেষণাত্মক সমাধান না জেনে(4.1).

একটি ফেজ পোর্ট্রেট চিত্রিত করার জন্য, ফেজ প্লেনের প্রতিটি বিন্দুতে সিস্টেম ট্র্যাজেক্টোরির জন্য একটি ভেক্টর ক্ষেত্র তৈরি করা প্রয়োজন। একটি ইনক্রিমেন্ট নির্দিষ্ট করেডি t>0,আমরা সংশ্লিষ্ট বৃদ্ধি পেতে ডি এক্সএবং ডি yঅভিব্যক্তি থেকে:

ডি x=P(x,y)ডি t,

ডি y=Q(x,y)ডি t.

ভেক্টর দিক dy/dxবিন্দুতে ( x, y) ফাংশনের চিহ্নের উপর নির্ভর করে P(x, y), Q(x, y)এবং একটি টেবিল দ্বারা দেওয়া যেতে পারে:

P(x,y)>0,Q(x,y)>0
P(x,y)<0,Q(x,y)<0
P(x,y)>0,Q(x,y)<0
P(x,y)<0,Q(x,y)>0

.(4.2)

এই সমীকরণের সমাধান y=y(x, গ), অথবা অন্তর্নিহিতভাবে চ(x,y)=গ,কোথায় সঙ্গেএকীকরণের ধ্রুবক, সমীকরণের অবিচ্ছেদ্য বক্ররেখার পরিবার দেয় (4.2) - ফেজ ট্রাজেক্টোরিসিস্টেম (4.1) প্লেনে x, y.

আইসোক্লাইন পদ্ধতি

একটি ফেজ প্রতিকৃতি নির্মাণ করতে, এক ব্যবহার করে আইসোক্লাইন পদ্ধতি -একটি নির্দিষ্ট কোণে অবিচ্ছেদ্য বক্ররেখাগুলিকে ফেজ প্লেনে ছেদ করে রেখাগুলি আঁকা হয়। আইসোক্লাইন সমীকরণটি (4.2) থেকে পাওয়া সহজ। চল রাখি

কোথায় ক– একটি নির্দিষ্ট ধ্রুবক। অর্থ কফেজ ট্রাজেক্টোরিতে স্পর্শকের ঢালের স্পর্শককে প্রতিনিধিত্ব করে এবং এর থেকে মান নিতে পারে -¥ থেকে + ¥ . পরিবর্তে প্রতিস্থাপন dy/dx(4.2) পরিমাণে কআমরা আইসোক্লাইন সমীকরণ পাই:

.(4.3)

সমীকরণ (4.3) সমতলের প্রতিটি বিন্দুতে সংশ্লিষ্ট অবিচ্ছেদ্য বক্ররেখার একমাত্র স্পর্শক নির্ধারণ করে, বিন্দু ব্যতীত যেখানে P(x,y)= 0, প্র (x,y) = 0 , যেখানে স্পর্শকের দিক অনির্দিষ্ট হয়ে যায়, যেহেতু ডেরিভেটিভের মান অনির্দিষ্ট হয়ে যায়:

.

এই বিন্দুটি সমস্ত আইসোলাইনের ছেদ বিন্দু - বিশেষ বিন্দু।এটি একই সাথে ভেরিয়েবলের সময়ের ডেরিভেটিভগুলিকে অদৃশ্য করে দেয় এক্সএবং y.

এইভাবে, একবচন বিন্দুতে, চলকের পরিবর্তনের হার শূন্যের সমান। অতএব, ফেজ ট্রাজেক্টোরিজ (4.2) এর ডিফারেনশিয়াল সমীকরণের একবচন বিন্দুর সাথে মিল রয়েছে সিস্টেমের স্থির অবস্থা(4.1), এবং এর স্থানাঙ্কগুলি হল ভেরিয়েবলের স্থির মান x, y।

বিশেষ আগ্রহ আছে প্রধান আইসোলাইন:

dy/dx=0, P(x,y)=0 – অনুভূমিক স্পর্শকগুলির আইসোলাইন এবং

dy/dx=¥ , প্র(x,y)=0 – উল্লম্ব স্পর্শকগুলির আইসোলাইন।

প্রধান আইসোলাইনগুলি তৈরি করে এবং তাদের ছেদ বিন্দু খুঁজে বের করে (x,y), যার স্থানাঙ্কগুলি শর্ত পূরণ করে:

এইভাবে আমরা ফেজ সমতলের সমস্ত আইসোলাইনগুলির ছেদ বিন্দু খুঁজে পাব, যেখানে ফেজ ট্রাজেক্টোরিজগুলির স্পর্শকগুলির দিকনির্দেশ অনির্দিষ্ট। এই - একক বিন্দু, যা অনুরূপ সিস্টেমের স্থির অবস্থা(চিত্র 4.2)।

সিস্টেমে (4.1) যতগুলি স্থির অবস্থা রয়েছে ততগুলি ফেজ প্লেনে প্রধান আইসোক্লাইনগুলির ছেদ বিন্দু রয়েছে।

প্রতিটি পর্বের গতিপথ একই অবস্থার মধ্য দিয়ে যাওয়া একটি গতিশীল সিস্টেমের গতির একটি সেটের সাথে মিলে যায় এবং শুধুমাত্র সময়ের রেফারেন্সের শুরুতে একে অপরের থেকে পৃথক হয়।

যদি কচি উপপাদ্যের শর্তগুলি সন্তুষ্ট হয়, তাহলে স্থানের প্রতিটি বিন্দুর মাধ্যমে x, y, tএকটি একক অবিচ্ছেদ্য বক্ররেখার মধ্য দিয়ে যায়। একই কথা সত্য, স্বায়ত্তশাসনের জন্য ধন্যবাদ, ফেজ ট্র্যাজেক্টোরিজগুলির জন্য: ফেজ প্লেনের প্রতিটি বিন্দুর মধ্য দিয়ে একটি অনন্য ফেজ ট্রাজেক্টোরি যায়।

স্থির রাষ্ট্র স্থিতিশীলতা

সিস্টেম ভারসাম্য রাখা যাক.

তারপরে প্রতিনিধি বিন্দুটি সিস্টেমের একক বিন্দুতে অবস্থিত, যেখানে সংজ্ঞা অনুসারে:

.

একটি একবচন বিন্দু স্থিতিশীল কি না তা স্থির অবস্থা থেকে একটি ছোট বিচ্যুতির মাধ্যমে প্রতিনিধি বিন্দুটি ছেড়ে যায় কি না তা দ্বারা নির্ধারিত হয়। দুটি সমীকরণের একটি সিস্টেমে প্রয়োগ করা হলে, ভাষায় স্থায়িত্বের সংজ্ঞাe, dনিম্নরূপ.

ভারসাম্য অবস্থা স্থিতিশীল হয় যদি ভারসাম্য অবস্থা থেকে বিচ্যুতির কোনো নির্দিষ্ট ক্ষেত্রের জন্য (e )এলাকা নির্দিষ্ট করা যেতে পারে d (e ), ভারসাম্যের অবস্থার চারপাশে এবং এমন সম্পত্তি রয়েছে যে অঞ্চলের অভ্যন্তরে শুরু হওয়া কোন গতিপথ নেই d , কখনই সীমান্তে পৌঁছাবে না e . (চিত্র 4.4)

সিস্টেমের একটি বড় শ্রেণীর জন্য - রুক্ষ সিস্টেম – যে আচরণের প্রকৃতি সমীকরণের ধরণে সামান্য পরিবর্তনের সাথে পরিবর্তিত হয় না, স্থির অবস্থার আশেপাশে আচরণের ধরণ সম্পর্কে তথ্য মূল নয়, বরং সরলীকৃত অধ্যয়ন করে পাওয়া যেতে পারে। রৈখিকপদ্ধতি.

লিনিয়ার সিস্টেম।

দুটি রৈখিক সমীকরণের একটি সিস্টেম বিবেচনা করুন:

.(4.4)

এখানে এ বি সি ডি- ধ্রুবক, x, y- ফেজ সমতলে কার্টেসিয়ান স্থানাঙ্ক।

সাধারণ সমাধান ফর্মে চাওয়া হবে:

.(4.5)

এই অভিব্যক্তিগুলিকে (4.4) এ প্রতিস্থাপন করুন এবং কমিয়ে দিন e l t:

(4.6)

অজানা সমীকরণের বীজগণিতীয় পদ্ধতি (4.6) ক, বিএকটি অশূন্য সমাধান আছে শুধুমাত্র যদি এর নির্ধারক, অজানা সহগ দ্বারা গঠিত, শূন্যের সমান হয়:

.

এই নির্ধারককে প্রসারিত করে, আমরা সিস্টেমের বৈশিষ্ট্যগত সমীকরণ পাই:

.(4.7)

এই সমীকরণের সমাধান নির্দেশকের মান দেয়l 1,2 , যার অধীনে অশূন্য মানগুলি সম্ভব কএবং খসমীকরণের সমাধান (4.6)। এই মানগুলো হলো

.(4.8)

যদি র্যাডিক্যাল অভিব্যক্তি নেতিবাচক হয়, তাহলেl 1,2 জটিল সংযোজন সংখ্যা। অনুমান করুন যে সমীকরণের (4.7) উভয় মূলেরই অশূন্য বাস্তব অংশ রয়েছে এবং কোনো একাধিক মূল নেই। তারপর সিস্টেমের সাধারণ সমাধান (4.4) সূচকের সাথে সূচকগুলির একটি রৈখিক সমন্বয় হিসাবে উপস্থাপন করা যেতে পারেl 1 , l 2 :

(4.9)

ফেজ প্লেনে সিস্টেমের সম্ভাব্য গতিপথের প্রকৃতি বিশ্লেষণ করতে, আমরা ব্যবহার করি রৈখিক সমজাতীয় স্থানাঙ্ক রূপান্তর,যা সিস্টেমে আনবে ক্যানোনিকাল ফর্ম:

,(4.10)

যা মূল সিস্টেমের (4.4) তুলনায় ফেজ প্লেনে আরও সুবিধাজনক উপস্থাপনা করতে দেয়। নতুন স্থানাঙ্ক প্রবর্তন করা যাকξ , η সূত্র অনুযায়ী:

(4.1)

রৈখিক বীজগণিতের কোর্স থেকে এটি জানা যায় যে যদি প্রকৃত অংশগুলি শূন্যের সমান না হয়l 1 , l 2 মূল সিস্টেম (4.4) রূপান্তরের সাহায্যে (4.11) সর্বদা ক্যানোনিকাল ফর্মে (4.10) রূপান্তরিত হতে পারে এবং ফেজ প্লেনে এর আচরণ অধ্যয়ন করা যেতে পারেξ , η . এখানে নিজেদের উপস্থাপন করতে পারে যে বিভিন্ন ক্ষেত্রে বিবেচনা করুন.

শিকড় λ 1 , λ 2 - বৈধ এবং একই চিহ্নের

এই ক্ষেত্রে, রূপান্তর সহগ বাস্তব, আমরা বাস্তব সমতল থেকে সরানোx,yআসল সমতলে ξ, η। সমীকরণের দ্বিতীয়টি (4.10) প্রথম দ্বারা ভাগ করলে আমরা পাই:

.(4.12)

এই সমীকরণ একত্রিত করা, আমরা খুঁজে:

কোথায়।(4.13)

আসুন আমরা λ দ্বারা বুঝতে সম্মত হই 2 একটি বড় মডুলাস সহ চরিত্রগত সমীকরণের মূল, যা আমাদের যুক্তির সাধারণতা লঙ্ঘন করে না। তারপর, যেহেতু বিবেচনাধীন ক্ষেত্রে শিকড় λ 1 , λ2 - বৈধ এবং একই চিহ্নের,ক>1 , এবং আমরা প্যারাবোলিক টাইপের অবিচ্ছেদ্য বক্ররেখা নিয়ে কাজ করছি।

সমস্ত অবিচ্ছেদ্য বক্ররেখা (অক্ষ ব্যতীত η , যা অনুরূপ ) অক্ষের উৎপত্তিস্থলে স্পর্শ করুন ξ, যা সমীকরণের একটি অবিচ্ছেদ্য বক্ররেখাও (4.11)। স্থানাঙ্কের উৎপত্তি একটি একক বিন্দু।

আসুন এখন ফেজ ট্রাজেক্টোরি বরাবর প্রতিনিধি বিন্দুর গতির দিক খুঁজে বের করা যাক। যদি λ 1, λ 2 নেতিবাচক, তাহলে, সমীকরণ (4.10), |ξ|, |η| থেকে দেখা যায় সময়ের সাথে হ্রাস প্রতিনিধিত্বকারী বিন্দুটি উত্সের কাছে যায়, কিন্তু এটি কখনই পৌঁছায় না। অন্যথায়, এটি কচির উপপাদ্যের বিরোধিতা করবে, যা বলে যে ফেজ প্লেনের প্রতিটি বিন্দুর মধ্য দিয়ে শুধুমাত্র একটি ফেজ ট্রাজেক্টোরি যায়।

এই ধরনের একটি একক বিন্দু যার মধ্য দিয়ে অবিচ্ছেদ্য বক্ররেখা চলে যায়, ঠিক যেমন প্যারাবোলার একটি পরিবার উৎপত্তির মধ্য দিয়ে যায়, একে নোড বলা হয় (চিত্র। 4.5)

λ এ নট-টাইপ ভারসাম্যের অবস্থা 1, λ 2 < 0 লিয়াপুনভের মতে স্থিতিশীল, যেহেতু প্রতিনিধিত্বকারী বিন্দুটি স্থানাঙ্কের উৎপত্তির দিকে সমস্ত অবিচ্ছেদ্য বক্ররেখা বরাবর চলে যায়। এই স্থিতিশীল গিঁট. যদি λ 1, λ 2 > 0, তারপর |ξ|, |η| সময়ের সাথে বৃদ্ধি পায় এবং প্রতিনিধি বিন্দুটি মূল থেকে দূরে সরে যায়। এই ক্ষেত্রে, একক পয়েন্ট– অস্থির নোড .

ফেজ সমতলে x, y অখণ্ড বক্ররেখার আচরণের সাধারণ গুণগত চরিত্র বজায় থাকবে, কিন্তু অখণ্ড বক্ররেখার স্পর্শক স্থানাঙ্ক অক্ষের সাথে মিলবে না। এই স্পর্শকগুলির প্রবণতার কোণটি সহগগুলির অনুপাত দ্বারা নির্ধারিত হবে α , β , γ , δ সমীকরণে (4.11)।

শিকড় λ 1 , λ 2 বৈধ এবং বিভিন্ন লক্ষণ আছে।

থেকে রূপান্তর করুনস্থানাঙ্ক x,y সমন্বয় করতে ξ, η আবার বাস্তব। ক্যানোনিকাল ভেরিয়েবলের সমীকরণের আবার ফর্ম (4.10), কিন্তু এখন চিহ্নগুলি λ 1, λ 2 ভিন্ন ফেজ ট্রাজেক্টরি সমীকরণের ফর্ম আছে:

কোথায় , (4.14)

ইন্টিগ্রেটিং (4.14), আমরা খুঁজে পাই

(4.15)

এই সমীকরণ হাইপারবোলিক ধরনের বক্ররেখার একটি পরিবারকে সংজ্ঞায়িত করে, যেখানে উভয় অক্ষ সমন্বয় করেউপসর্গগুলি (এ ক=1 আমাদের সমদ্বিবাহু হাইপারবোলাস পরিবার থাকবে). এই ক্ষেত্রে স্থানাঙ্ক অক্ষগুলিও অবিচ্ছেদ্য বক্ররেখা– এই মূলের মধ্য দিয়ে যাওয়া একমাত্র অবিচ্ছেদ্য বক্ররেখা হবে। প্রতিটিযার মধ্যে তিনটি ফেজ ট্রাজেক্টোরি রয়েছে: ভারসাম্যের অবস্থার দিকে (বা ভারসাম্যের অবস্থা থেকে দূরে) এবং ভারসাম্যের অবস্থা থেকে দুটি আন্দোলন। অন্যান্য সমস্ত অবিচ্ছেদ্য বক্ররেখা– হাইপারবোলাস যা মূলের মধ্য দিয়ে যায় না (চিত্র। 4.6) এই একবচন বিন্দু বলা হয় "স্যাডল ». পর্বত স্যাডলের কাছাকাছি স্তর রেখাগুলি স্যাডলের আশেপাশে ফেজ ট্রাজেক্টোরির মতো আচরণ করে।

ভারসাম্য অবস্থার কাছাকাছি ফেজ ট্রাজেক্টোরিজ বরাবর প্রতিনিধি বিন্দুর গতির প্রকৃতি বিবেচনা করা যাক। যেমন ধরুন,λ 1 >0 , λ 2<0 . তারপর প্রতিনিধি বিন্দু অক্ষ উপর স্থাপন ξ , উৎপত্তি থেকে দূরে সরে যাবে, এবং অক্ষের উপর স্থাপন করা হবে η – অনির্দিষ্টভাবে স্থানাঙ্কের উত্সের কাছে যাবে, নির্দিষ্ট সময়ে পৌঁছানো ছাড়াই. যেখানেই প্রতিনিধিত্বকারী বিন্দুটি প্রাথমিক মুহুর্তে (একবচন বিন্দু এবং অ্যাসিম্পটোটের বিন্দুগুলি বাদ দিয়ে) η =0), এটি শেষ পর্যন্ত ভারসাম্য অবস্থা থেকে দূরে সরে যাবে, এমনকি যদি শুরুতে এটি অবিচ্ছেদ্য বক্ররেখাগুলির একটি বরাবর একটি একক বিন্দুর দিকে চলে যায়.

এটা স্পষ্ট যে স্যাডল-টাইপ একবচন বিন্দু সবসময় অস্থির . শুধুমাত্র অ্যাসিম্পটোটে বিশেষভাবে নির্বাচিত প্রাথমিক অবস্থার অধীনেη =0 সিস্টেম ভারসাম্য একটি রাষ্ট্র কাছে যাবে. যাইহোক, এটি এই দাবির বিরোধিতা করে না যে সিস্টেমটি অস্থির। যদি আপনি গণনা করেন, যে ফেজ প্লেনে সিস্টেমের সমস্ত প্রাথমিক অবস্থা সমানভাবে সম্ভাব্য, তাহলে এমন একটি প্রাথমিক অবস্থার সম্ভাব্যতা যা অভিমুখে চলাচলের সাথে মিলে যায়প্রতি একবচন বিন্দু শূন্যের সমান। অতএব, যে কোনো বাস্তব আন্দোলন সিস্টেমকে ভারসাম্যের অবস্থা থেকে সরিয়ে দেবে।স্থানাঙ্ক ফিরে যাচ্ছেx,y,আমরা উত্সের চারপাশে গতিপথের গতিবিধির প্রকৃতির একই গুণগত চিত্র পাই।

একটি নোড এবং একটি স্যাডলের বিবেচিত ক্ষেত্রের মধ্যে সীমানা হল কেসকখন একটি চরিত্রগত সূচক, উদাহরণস্বরূপ λ 1 , অদৃশ্য হয়ে যায়, যা ঘটে যখন সিস্টেমের নির্ধারক- অভিব্যক্তি adbc=0(সূত্র 4.8 দেখুন ). এই ক্ষেত্রে, সমীকরণের (4.4) ডানদিকের সহগগুলি একে অপরের সমানুপাতিক:

এবং সিস্টেমের ভারসাম্যের জন্য লাইনের সমস্ত বিন্দু রয়েছে:

অবশিষ্ট অবিচ্ছেদ্য বক্ররেখাগুলি একটি ঢাল সহ সমান্তরাল রেখার একটি পরিবার , যার সাথে প্রতিনিধি বিন্দুগুলি হয় ভারসাম্যের অবস্থার কাছে যায় বা এটি থেকে দূরে সরে যায়, বৈশিষ্ট্যগত সমীকরণের দ্বিতীয় মূলের চিহ্নের উপর নির্ভর করে λ 2 = a+d.(চিত্র 4. 7 ) এই ক্ষেত্রে, ভারসাম্য অবস্থার স্থানাঙ্কগুলি চলকের প্রাথমিক মানের উপর নির্ভর করে।

শিকড় λ 1 , λ 2 – জটিলসংঘবদ্ধ

এই ক্ষেত্রে, বাস্তব জন্যএক্সএবং yআমরা করব জটিল কনজুগেট আছে ξ , η (4.10) . যাইহোক, আরও একটি মধ্যবর্তী রূপান্তর প্রবর্তন করে, এই ক্ষেত্রে বিবেচনাটিকে একটি বাস্তব রৈখিক সমজাতীয় রূপান্তরে হ্রাস করাও সম্ভব। চল রাখি:

(4.16)

কোথায় ক, খ,এবং u,v – বাস্তব মূল্যবোধ এটি থেকে রূপান্তর দেখানো যেতে পারেx,yপ্রতি u, v আমাদের অনুমানের অধীনে, একটি অ-শূন্য নির্ধারক সহ বাস্তব, রৈখিক, সমজাতীয়। সমীকরণের কারণে(4.10, 4.16) আমাদের আছে:

কোথায়

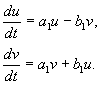(4.17)

সমীকরণের দ্বিতীয়টিকে প্রথম দ্বারা ভাগ করা, আমরা পেতে:

যা সংহত করা সহজ, যদি আমরা মেরু স্থানাঙ্ক সিস্টেমে স্যুইচ করি (আর, φ ) . প্রতিস্থাপনের পরআমরা কোথা থেকে পাই:

.(4.18)

এইভাবে, ফেজ সমতলেu, vআমরা লগারিদমিক সর্পিলগুলির একটি পরিবারের সাথে ডিল করছি, যার প্রতিটি রয়েছে৷উৎপত্তিস্থলে অ্যাসিম্পোটিক বিন্দু।একবচন বিন্দু যা সর্পিল আকার ধারণ করে সমস্ত অবিচ্ছেদ্য বক্ররেখার অসিম্পোটিক বিন্দু, নেস্টেড বন্ধুবন্ধু, ডেকেছে ফোকাস ( ডুমুর.4.8 ) .

আসুন আমরা ফেজ ট্রাজেক্টোরি বরাবর প্রতিনিধিত্বকারী বিন্দুর গতিবিধি বিবেচনা করি। সমীকরণের প্রথমটি (4.17) দ্বারা গুণ করা হচ্ছেu, এবং দ্বিতীয় থেকে vএবং যোগ করে, আমরা পাই:

কোথায়

দিন ক 1 < 0 (ক 1 = পুনঃλ ) . প্রতিনিধিত্বকারী বিন্দুটি একটি নির্দিষ্ট সময়ের মধ্যে না পৌঁছে ক্রমাগত উত্সের কাছে চলে যায়। এর মানে হল যে ফেজ ট্রাজেক্টোরিগুলি পেঁচানো সর্পিল এবং স্যাঁতসেঁতে দোলনের সাথে মিলে যায়ভেরিয়েবল এই - অবিচলিত ফোকাস .

একটি স্থিতিশীল ফোকাসের ক্ষেত্রে, একটি স্থিতিশীল নোডের ক্ষেত্রে, শুধুমাত্র লায়াপুনভ শর্তই সন্তুষ্ট নয়, তবে আরও কঠোর প্রয়োজনীয়তাও। যথা, যেকোন প্রাথমিক বিচ্যুতির জন্য, সিস্টেমটি শেষ পর্যন্ত ভারসাম্য অবস্থানের কাঙ্খিত কাছাকাছি ফিরে আসবে। এই ধরনের স্থিতিশীলতা, যেখানে প্রাথমিক বিচ্যুতিগুলি কেবল বৃদ্ধিই করে না, কিন্তু ক্ষয়, শূন্যের দিকে প্রবণতাকে বলা হয় পরম স্থিতিশীলতা .

যদি সূত্রে (4.18) ক 1 >0 , তারপর প্রতিনিধিত্বকারী বিন্দু মূল থেকে দূরে সরে যায়, এবং আমরা তার সাথে কাজ করছি অস্থির ফোকাস . যখন একটি প্লেন থেকে চলন্তu,vফেজ সমতলেএক্স, yসর্পিলও সর্পিল থাকবে, কিন্তু বিকৃত হবে।

এখন বিবেচনা যখন ক্ষেত্রেক 1 =0 . প্লেনে ফেজ ট্রাজেক্টোরিজu, vবৃত্ত থাকবে যা বিমানেx,yউপবৃত্তাকার ফিট:

এইভাবে, এএকটি 1=0 একটি বিশেষ পয়েন্টের মাধ্যমেx= 0,y= 0 কোন অবিচ্ছেদ্য বক্ররেখা পাস. এই ধরনের একটি বিচ্ছিন্ন একবচন বিন্দু, যার কাছাকাছি অবিচ্ছেদ্য বক্ররেখাগুলি বন্ধ বক্ররেখা, বিশেষত, উপবৃত্তগুলি একে অপরের মধ্যে এম্বেড করা এবং একবচন বিন্দুকে ঘেরা, একটি কেন্দ্র বলে।

এইভাবে, চরিত্রগত সমীকরণের শিকড়ের প্রকৃতির উপর নির্ভর করে ছয় ধরনের ভারসাম্য সম্ভব (4.7)। প্লেনে ফেজ ট্রাজেক্টোরির দৃশ্য x, yএই ছয়টি ক্ষেত্রে চিত্রে দেখানো হয়েছে। 4.9।

ভাত। 4.9।রৈখিক সমীকরণের সিস্টেমের জন্য একটি স্থির অবস্থার আশেপাশে ফেজ পোর্ট্রেটের ধরন (4.4)।

পাঁচ ধরনের ভারসাম্যের অবস্থা রুক্ষ, তাদের প্রকৃতি সমীকরণের ডানদিকের পর্যাপ্ত ছোট পরিবর্তনের সাথে পরিবর্তিত হয় না (4.4)। এই ক্ষেত্রে, পরিবর্তনগুলি কেবল ডানদিকে নয়, তাদের প্রথম-ক্রমের ডেরিভেটিভগুলিতেও ছোট হওয়া উচিত। ভারসাম্যের ষষ্ঠ অবস্থা - কেন্দ্র - মোটা নয়। সমীকরণের ডান দিকের প্যারামিটারে ছোট পরিবর্তনের সাথে, এটি একটি স্থিতিশীল বা অস্থির ফোকাসে যায়।

বিভাজন চিত্র

আসুন স্বরলিপি পরিচয় করিয়ে দিই:

. (4.11)

তারপর চরিত্রগত সমীকরণটি আকারে লেখা যেতে পারে:

. (4.12)

আয়তক্ষেত্রাকার কার্টেসিয়ান স্থানাঙ্ক সহ একটি সমতল বিবেচনা করুন s , ডি এবং এটিতে এক বা অন্য ধরণের ভারসাম্য অবস্থার সাথে সম্পর্কিত ক্ষেত্রগুলি চিহ্নিত করুন, যা বৈশিষ্ট্যযুক্ত সমীকরণের শিকড়ের প্রকৃতি দ্বারা নির্ধারিত হয়

.(4.13)

ভারসাম্যের স্থিতিশীলতার শর্ত হবে y-এর একটি ঋণাত্মক বাস্তব অংশের উপস্থিতিl 1 এবং l 2 . এর জন্য একটি প্রয়োজনীয় এবং পর্যাপ্ত শর্ত হল বৈষম্যের পরিপূর্ণতাs > 0, ডি > 0 . ডায়াগ্রামে (4.15), এই শর্তটি পরামিতি সমতলের প্রথম ত্রৈমাসিকে অবস্থিত পয়েন্টগুলির সাথে মিলে যায়। একবচন বিন্দু ফোকাস হবে যদিl 1 এবং l 2 জটিল এই শর্তটি সমতলের সেই পয়েন্টগুলির সাথে মিলে যায় যার জন্য , সেগুলো. একটি প্যারাবোলার দুটি শাখার মধ্যে বিন্দুs 2 = 4 ডি. সেমিয়াক্সিস পয়েন্ট s = 0, ডি>0, কেন্দ্রের প্রকারের ভারসাম্যের অবস্থার সাথে মিলে যায়। একইভাবে,l 1 এবং l 2 - বৈধ, কিন্তু বিভিন্ন লক্ষণ, যেমন একটি একবচন বিন্দু একটি স্যাডল হবে যদি ডি<0, ইত্যাদি ফলস্বরূপ, আমরা প্যারামিটার প্লেনের একটি পার্টিশন ডায়াগ্রাম পাই s, ডি, বিভিন্ন ধরনের ভারসাম্য অবস্থার সাথে সংশ্লিষ্ট অঞ্চলে।

ভাত। 4.10।বিভাজন চিত্র

রৈখিক সমীকরণের সিস্টেমের জন্য 4.4

রৈখিক পদ্ধতির সহগ হলে এ বি সি ডিকিছু প্যারামিটারের উপর নির্ভর করে, তারপর যখন এই প্যারামিটারটি পরিবর্তন করা হয়, তখন মানগুলিও পরিবর্তিত হবেs , ডি . সীমানা অতিক্রম করার সময়, ফেজ পোর্ট্রেটের প্রকৃতি গুণগতভাবে পরিবর্তিত হয়। অতএব, এই ধরনের সীমানাগুলিকে দ্বিখণ্ডিত সীমানা বলা হয় - সীমানার বিপরীত দিকে, সিস্টেমে দুটি টপোলজিক্যালি ভিন্ন ফেজ পোর্ট্রেট এবং সেই অনুযায়ী, দুটি ভিন্ন ধরনের আচরণ রয়েছে।

চিত্রটি দেখায় কিভাবে এই ধরনের পরিবর্তন ঘটতে পারে। যদি আমরা বিশেষ ক্ষেত্রে বাদ দেই - স্থানাঙ্কের উৎপত্তি - তাহলে এটা দেখা সহজ যে y-অক্ষ অতিক্রম করার সময় জিনটি একটি নোডে যেতে পারে, স্থিতিশীল বা অস্থির। একটি স্থিতিশীল নোড হয় একটি জিন বা একটি স্থিতিশীল ফোকাসে যেতে পারে, এবং তাই। মনে রাখবেন যে স্থিতিশীল নোড-স্থিতিশীল ফোকাস এবং অস্থির নোড-অস্থির ফোকাস রূপান্তর দ্বিখণ্ডিত নয়, যেহেতু ফেজ স্পেসের টপোলজি এই ক্ষেত্রে পরিবর্তিত হয় না। আমরা লেকচার 6-এ ফেজ স্পেসের টপোলজি এবং বিভার্কেশন ট্রানজিশন সম্পর্কে আরও বিস্তারিতভাবে কথা বলব।

বিভাজন পরিবর্তনের অধীনে, একবচন বিন্দুর স্থায়িত্বের প্রকৃতি পরিবর্তিত হয়। উদাহরণস্বরূপ, কেন্দ্রের মাধ্যমে একটি স্থিতিশীল ফোকাস একটি অস্থির ফোকাসে পরিণত হতে পারে। এই বিভাজন বলা হয় অ্যান্ড্রোনোভ-হপফ দ্বিখণ্ডনবিজ্ঞানীদের নাম অনুসারে যারা এটি অধ্যয়ন করেছিলেন। অরৈখিক সিস্টেমে এই বিভাজনের সাথে, একটি সীমা চক্রের জন্ম হয়, এবং সিস্টেমটি স্ব-দোলক হয়ে ওঠে (বক্তৃতা 8 দেখুন)।

উদাহরণ। রৈখিক রাসায়নিক বিক্রিয়া সিস্টেম

পদার্থ এক্সএকটি ধ্রুবক হারে বাইরে থেকে প্রবাহিত হয়, পদার্থ Y তে পরিণত হয় এবং পদার্থের ঘনত্বের সমানুপাতিক হারে Y, বিক্রিয়া ক্ষেত্র থেকে বের করা হয়। সমস্ত প্রতিক্রিয়াই প্রথম ক্রমে, বাইরে থেকে পদার্থের প্রবাহ বাদে, যার একটি শূন্য ক্রম রয়েছে। প্রতিক্রিয়া স্কিম এর মত দেখায়:

(4.14)

এবং সমীকরণ সিস্টেম দ্বারা বর্ণনা করা হয়:

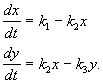(4.15)

আমরা ডানদিকের দিকগুলিকে শূন্যের সাথে সমান করে স্থির ঘনত্ব অর্জন করি:

.(4.16)

সিস্টেমের ফেজ প্রতিকৃতি বিবেচনা করুন। সিস্টেমের দ্বিতীয় সমীকরণটি (4.16) প্রথমটি দ্বারা ভাগ করা যাক। আমরা পেতে:

.(4.17)

সমীকরণ (4.17) ফেজ প্লেনে ভেরিয়েবলের আচরণ নির্ধারণ করে। আমাদের এই সিস্টেমের একটি ফেজ প্রতিকৃতি নির্মাণ করা যাক. প্রথমত, আমরা ফেজ প্লেনে প্রধান আইসোলাইনগুলি আঁকি। উল্লম্ব স্পর্শকগুলির আইসোক্লাইনের সমীকরণ:

অনুভূমিক স্পর্শকগুলির আইসোক্লাইনের জন্য সমীকরণ:

একবচন বিন্দু (স্থির অবস্থা) প্রধান আইসোলাইনগুলির সংযোগস্থলে অবস্থিত।

এখন আসুন আমরা নির্ধারণ করি যে স্থানাঙ্ক অক্ষগুলি অখণ্ড বক্ররেখাগুলিকে ছেদ করে কোন কোণে।

যদি x= 0, তারপর।

এইভাবে, স্পর্শকটির ঢালের স্পর্শক অবিচ্ছেদ্য বক্ররেখায় y=y(x), y-অক্ষ অতিক্রম করছে x=0, উপরের অর্ধেক প্লেনে ঋণাত্মক (স্মরণ করুন যে ভেরিয়েবলগুলি x, yঘনত্বের মান আছে, এবং সেইজন্য আমরা শুধুমাত্র ফেজ প্লেনের উপরের ডান চতুর্ভুজটিতে আগ্রহী)। এই ক্ষেত্রে, স্পর্শকটির প্রবণতা কোণের স্পর্শকের মান উৎপত্তি থেকে দূরত্বের সাথে বৃদ্ধি পায়।

অক্ষ বিবেচনা করুন y= 0. এই অক্ষের সংযোগস্থলে, অখণ্ড বক্ররেখা সমীকরণ দ্বারা বর্ণিত হয়

এ অ্যাবসিসা অক্ষ অতিক্রমকারী অবিচ্ছেদ্য বক্ররেখার ঢালের স্পর্শক ধনাত্মক এবং শূন্য থেকে অসীম পর্যন্ত বৃদ্ধি পায় এক্স.

এ

তারপরে, আরও বৃদ্ধির সাথে, ঢালের স্পর্শক পরম মান কমে যায়, ঋণাত্মক থাকে এবং -1-তে থাকে এক্স ® ¥ . মূল আইসোক্লাইন এবং স্থানাঙ্ক অক্ষের অবিচ্ছেদ্য বক্ররেখার স্পর্শকগুলির অভিমুখ জেনে, ফেজ ট্র্যাজেক্টোরিজগুলির সম্পূর্ণ চিত্রটি তৈরি করা সহজ।

লাইপুনভ পদ্ধতি ব্যবহার করে একবচন বিন্দুর স্থায়িত্বের প্রকৃতি প্রতিষ্ঠিত হবে। সিস্টেমের বৈশিষ্ট্যগত নির্ধারকটির ফর্ম রয়েছে:

.

নির্ধারককে প্রসারিত করে, আমরা সিস্টেমের বৈশিষ্ট্যগত সমীকরণ পাই: , অর্থাৎ চরিত্রগত সমীকরণের শিকড় উভয়ই নেতিবাচক। অতএব, সিস্টেমের স্থির অবস্থা একটি স্থিতিশীল নোড। একই সময়ে, পদার্থের ঘনত্ব এক্সএকটি স্থির অবস্থায় থাকে সবসময় একঘেয়েভাবে, Y পদার্থের ঘনত্ব ন্যূনতম বা সর্বোচ্চ অতিক্রম করতে পারে। এই ধরনের সিস্টেমে অসিলেটরি শাসন অসম্ভব।

দিন zq - ফাংশনের একবচন বিন্দু f(z), t.s। f(z)কিন্তু এই মুহুর্তে বিশ্লেষণাত্মক (বিশেষত, এটি সংজ্ঞায়িত করা যাবে না)। যদি বিন্দুর এমন একটি ছিদ্রযুক্ত পাড়া বিদ্যমান থাকে zq (অর্থাৎ, সেট O z - zq f(z) হল আলেয়াটিক, তাহলে zoডাকা বিচ্ছিন্ন একবচন বিন্দুফাংশন f(z)।এই সংজ্ঞাটি ক্ষেত্রেও সংরক্ষিত আছে zn = oo, যদি আয়োডিন একটি বিন্দু একটি punctured প্রতিবেশী হয় zq = oo সেট বুঝুন z >আমি - উৎপত্তি কেন্দ্রিক কিছু বৃত্তের চেহারা। অন্য কথায়, একক বিন্দু zq কে বিচ্ছিন্ন বলা হয় যদি এই বিন্দুর এমন একটি আশেপাশের এলাকা থাকে যেখানে অন্য একবচন বিন্দু থেকে আলাদা থাকে zq নীচের সর্বত্র, আমরা একটি একক-মূল্যবান অক্ষরের (ফাংশনটি) শুধুমাত্র একক পয়েন্ট বিবেচনা করি f(z)অনন্য বলে ধরে নেওয়া হয়েছে)।

ফাংশনের আচরণের উপর নির্ভর করে f(z)এ z -> zqএকবচন বিন্দু তিন প্রকার। বিচ্ছিন্ন একবচন বিন্দু zq ফাংশন f(z)বলা হয়:

1) অপসারণযোগ্য একক বিন্দুযদি একটি সীমাবদ্ধ সীমা থাকে

2) মেরুযদি একটি সীমা আছে

3) অপরিহার্য পয়েন্ট,যদি f(z) এর জন্য কোন সসীম বা অসীম সীমা নেই z-> zq.

উদাহরণ 26.1. আসুন দেখাই যে তিন ধরনের একবচন বিন্দু উপলব্ধি করা হয়। বিবেচনা চ(z)= বিন্দু zq = 0 বিচ্ছিন্ন

এই ফাংশনের একক বিন্দু। সূত্র ব্যবহার করে (22.12), আমরা সম্প্রসারণ পাই

যা থেকে এটি অনুসরণ করে যে সেখানে লিম রয়েছে fi(z)= 1. অতএব, zq = 0 হল

ফাংশনের একটি অপসারণযোগ্য একক বিন্দু fi(z)।

ফাংশন f'j(z) =--- একটি বিন্দুতে একটি খুঁটি আছে zo= 1 কারণ

2 r" এক্স

এখন ফাংশন বিবেচনা করুন )z(z)= e 1 ^ r এবং তা দেখান zo = O এই ফাংশনের একটি অপরিহার্য একবচন বিন্দু। যখন প্রচেষ্টা zবাস্তব অক্ষ বরাবর শূন্য পর্যন্ত, ফাংশনের বাম এবং ডান সীমা f (z)ভিন্ন: লিম সঙ্গে 1 / 1 = 0, লিম 1 /* = সহ os এই থেকেই বোঝা,

x->0-0 x->0+O

কি f:i(z) 2 এর জন্য কোন সসীম বা অসীম সীমা নেই -> ওহ, i.e. zq = 0 এই ফাংশনের একটি অপরিহার্য বিন্দু। (বিন্দু প্রবণতা হিসাবে নোট করুন z-iyকাল্পনিক অক্ষ ফাংশনে শূন্য পর্যন্ত

কোনো সীমা নেই।)

অবশ্যই, অ-বিচ্ছিন্ন একবচন বিন্দুও রয়েছে। এই ক্ষেত্রে. ফাংশন পয়েন্টে খুঁটি আছে z n = -, পৃ= ±1, ±2,...

তাই, Zq = 0 হল এই ফাংশনের একটি অ-বিচ্ছিন্ন একবচন বিন্দু: এই বিন্দুর যেকোনো (যথেচ্ছ ছোট) প্রতিবেশীতে অন্যান্য একবচন বিন্দু আছে g পি.

দিন জো-একটি ফাংশনের চূড়ান্ত বিচ্ছিন্ন একবচন বিন্দু f(z)।তারপর f(z)কিছু punctured আশেপাশের 0 Zo বিন্দুতে অনুরূপ zoএই পাড়াটিকে r = 0 অভ্যন্তরীণ ব্যাসার্ধ সহ একটি রিং হিসাবে গণ্য করা যেতে পারে। উপপাদ্য 25.1 দ্বারা, বিবেচনাধীন আশেপাশে, ফাংশনটি f(z)লরেন্ট সিরিজে প্রসারিত করা যেতে পারে (25.2)। আমরা দেখাব যে 2 এর জন্য ফাংশনের আচরণ -> zq (অর্থাৎ একবচন বিন্দুর ধরন জো)পচনের প্রধান অংশের আকারের উপর নির্ভর করে (25.2); এই পরিস্থিতিতে "প্রধান অংশ" শব্দটির উৎপত্তি ব্যাখ্যা করে।

থিওরেম 2G.2। একটি ফাংশন f(z) এর একটি বিচ্ছিন্ন একবচন বিন্দু zo অপসারণযোগ্য যদি এবং শুধুমাত্র যদি এই বিন্দুর একটি ছিদ্রযুক্ত আশেপাশে লোরাপের প্রসারণের oid থাকে

সেগুলো. শুধুমাত্র সঠিক অংশ নিয়ে গঠিত, এবং মূল অংশের সমস্ত সহগ বুলেটের সমান।

প্রমাণ। 1. যাক zoএকটি অপসারণযোগ্য একক বিন্দু। আসুন প্রমাণ করি যে লরেন্ট ফাংশনের সম্প্রসারণ f(z)ফর্ম আছে (26.1)। একবচন বিন্দু থেকে zoঅপসারণযোগ্য, তারপর একটি সীমাবদ্ধ সীমা আছে f(z) = A.তাই, f(z)বিন্দুর 0 z - zq কিছু ছিদ্রযুক্ত আশেপাশে আবদ্ধ জো,সেগুলো. )(z) সবার জন্য zএই পাড়া থেকে যে কোনো নিন আর. U р /?|, এবং লরেন্ট সিরিজের সহগগুলির জন্য সূত্রগুলি (25.3) ব্যবহার করুন:

সম্প্রসারণের প্রধান অংশের সহগগুলির জন্য n =- 1, -2,... এই ধরনের মানগুলির জন্য পৃআমাদের আছে p~n-e 0 এ আর-> 0. মান থেকে আরতারপর ইচ্ছামত ছোট নির্বাচন করা যেতে পারে জনাব ~"ইচ্ছামত ছোট হতে পারে। যেহেতু |c t,| ^ Mr~nএবং cn p এর উপর নির্ভর করে না, তারপর cn = 0 এর জন্য এবং=- 1, -2,..., যা প্রমাণ করতে হবে।

2. আসুন এখন ধরে নিই যে লরেন্ট সম্প্রসারণের ফর্ম রয়েছে (26.1)। সিরিজ (26.1) একটি পাওয়ার সিরিজ এবং। অতএব, শুধুমাত্র punctured মধ্যে নয়, কিন্তু সমগ্র প্রতিবেশী মধ্যে একত্রিত হয় জেড-zq বিন্দু সহ zo;এর পরিমাণ S(z)জন্য বিশ্লেষণাত্মক হয় z এবং S(z) = )(z) 0 z এ - zoআর.অতএব, একটি সীমাবদ্ধ সীমা আছে )(z)\u003d Pm 5 (r) \u003d 5 (r) - অতএব, একবচন বিন্দু zq

Z->Zo Z-*Zo

নিষ্পত্তিযোগ্য উপপাদ্য প্রমাণিত হয়েছে।

মন্তব্য করুন। এটি উপপাদ্যের প্রমাণ থেকে অনুসরণ করে যে একটি অপসারণযোগ্য একবচন বিন্দুর 0 z - zo ছিদ্রযুক্ত এলাকায়, ফাংশনটি f(z) S(r) ফাংশনের সাথে মিলে যায়, যা সমগ্র আশেপাশে বিশ্লেষণাত্মক z - জো অতএব, যদি আমরা /(থ) = রাখি S(zq), তারপর, ফাংশনের মান পরিবর্তন না করে f(z)ছিদ্রযুক্ত আশেপাশের যে কোনও বিন্দুতে, আমরা এই ফাংশনটিকে r-এ বিশ্লেষণাত্মক করি, অর্থাৎ বৈশিষ্ট্যটি "সরান"। এটি "অপসারণযোগ্য এককতা" শব্দটিকে ব্যাখ্যা করে। এই জাতীয় পয়েন্টগুলিকে নিয়মিত হিসাবে বিবেচনা করা স্বাভাবিক, এবং ফাংশনের একক পয়েন্ট হিসাবে নয় f(z)।

উদাহরণস্বরূপ, ফাংশন বিবেচনা করুন

উদাহরণ 26.1, এটি দেখানো হয়েছিল যে Pm (n) = 1. i.e. একক বিন্দু

zq = 0 অপসারণযোগ্য। সেটিং /i(0) = 1, আমরা এর ফলে সিঙ্গুলারিটি দূর করি এবং একটি ফাংশন পাই যা বিন্দুতে বিশ্লেষণাত্মক zq = 0 (এবং সমগ্র সমতলে C)।

আসুন এখন লরেন্ট সম্প্রসারণের পরিপ্রেক্ষিতে মেরুগুলিকে চিহ্নিত করি।

উপপাদ্য 26.3. একটি ফাংশন f(z) এর একটি বিচ্ছিন্ন একবচন বিন্দু Zo হল একটি মেরু যদি এবং শুধুমাত্র যদি, যখন কেন্দ্র Zq সহ লরেন্ট সম্প্রসারণের প্রধান অংশে শুধুমাত্র একটি সীমিত সংখ্যক স্বতন্ত্র থাকে

n সহ শূন্য সহগ থেকে:

প্রমাণ। 1. যাক zq - মেরু, i.e. লিম /( z) = oo.

আসুন প্রমাণ করি যে লরেন্ট ফাংশনের সম্প্রসারণ f(z)ফর্ম আছে (2G.2)। লিম থেকে f(z)= oo তারপর বিন্দু একটি punctured প্রতিবেশ বিদ্যমান আছে

কি zq যেখানে f(z)বিশ্লেষণাত্মক এবং কোন শূন্য নেই. তারপর ফাংশন g(z) = 1 /f(z)এছাড়াও এই punctured আশেপাশের মধ্যে বিশ্লেষণাত্মক হবে, এবং lim g(z)= 0. অতএব, জোনিষ্পত্তিযোগ্য *-? *0

ফাংশনের একক বিন্দু g(z)।এর পুনরায় সংজ্ঞায়িত করা যাক g(z)বিন্দুতে zo, বসানো g(zo)= 0. তারপর g(z)বিন্দুর সমগ্র আশেপাশে বিশ্লেষণাত্মক হয়ে ওঠে (পঞ্চার নয়) z 0,এবং z0এর বিচ্ছিন্ন শূন্য হবে। দ্বারা নির্দেশ করুন এনএই শূন্যের বহুগুণ (ক্রম)। §23 এ দেখানো হয়েছে, বিন্দুর একটি আশেপাশে zq ফাংশন g(z)ফর্মে প্রতিনিধিত্বযোগ্য (দেখুন (23.2))

এবং (z$) চ 0 এবং y>(z)বিন্দুর কিছু আশেপাশে বিশ্লেষণাত্মক জো-কারণ ip(z)বিন্দুতে অবিচ্ছিন্ন zoএবং g>(zo) F 0" তারপর ip(z)এই পয়েন্টের কিছু আশেপাশে কোন শূন্য নেই। অতএব ফাংশন 1 /-p(z)এছাড়াও এই আশেপাশে বিশ্লেষণাত্মক হবে এবং তাই, এটি একটি টেলর সিরিজে প্রসারিত হবে:

বন্ধনী খোলার এবং সহগগুলির উপাধি পরিবর্তন করে, আমরা ফর্মটিতে শেষ সম্প্রসারণ লিখি

যেখানে c_jv = 1>o চ 0. সুতরাং, f(r) এর লরেন্ট সম্প্রসারণের প্রধান অংশে শুধুমাত্র একটি সীমিত সংখ্যক পদ রয়েছে; আমরা প্রয়োজনীয় সমতায় পৌঁছেছি (26.2)।

2. একটি বিন্দু একটি punctured আশেপাশে যাক মফাংশন )(z)লরেন্ট সম্প্রসারণ (26.2) দ্বারা প্রতিনিধিত্ব করা হয় (আরও প্রসারিত আকারে, দেখুন (26.3)), যার প্রধান অংশে শুধুমাত্র একটি সীমিত সংখ্যক পদ রয়েছে এবং সঙ্গে- d" চ 0. আমাদের এটা প্রমাণ করতে হবে Zq - ফাংশন পোল f(z)।সমতা (26.3) দ্বারা গুণ করা (জি - জি o) iV, আমরা ফাংশন পাই

সিরিজটি (26.4) একটি পাওয়ার সিরিজ যা একটি বিশ্লেষণাত্মক ফাংশনে রূপান্তরিত হয় শুধুমাত্র পাংচারে নয়, বিন্দুর পুরো আশেপাশেও Zq. অতএব, ফাংশন h(z)এই আশেপাশে বিশ্লেষণাত্মক হয়ে ওঠে যদি আমরা এটিকে সেট করে তম এ প্রসারিত করি h(zo)= s_dg চ 0. তারপর

সুতরাং o বিন্দু একটি মেরু, এবং উপপাদ্য 26.3 প্রমাণিত হয়।

জিরোথ ফাংশনের বহুগুণ (ক্রম) g(z)= 1//(r) বলা হয় মেরু আদেশফাংশন /(আর)। যদি এন-মেরু এর ক্রম তম, তারপর g(z)= (আর - Zo)N ip(z),এবং যান) চ 0, এবং, উপপাদ্য 26.3 এর প্রমাণের প্রথম অংশে দেখানো হয়েছে, f(r) এর বিস্তারের ফর্ম (26.3), যেখানে c_/v চ 0. বিপরীতভাবে, যদি f(r) সিরিজে প্রসারিত হয় (26.3) এবং e-z F 0, তারপর

টি.এস. এন-ফাংশন f(r) এর পোলের ক্রম। এভাবে, ফাংশনের zq পোলের ক্রম/(জি) zq বিন্দুর ছিদ্রযুক্ত আশেপাশে লরেন্ট সম্প্রসারণের প্রধান অংশের অগ্রণী অশূন্য সহগের সংখ্যার সমান(অর্থাৎ এই জাতীয় সংখ্যার সমান এন,কি s_dg চ 0 এবং sp= 0 এ পৃ > N)।

আমাদের নিম্নলিখিত দাবি প্রমাণ করা যাক, যা সুবিধাজনক) অ্যাপ্লিকেশনের জন্য।

ফলাফল 26.4. বিন্দু zq হল কথাসাহিত্যের ক্রম N এর একটি মেরু/(জি) যদি এবং কেবল যদি/(জি) ফর্মে প্রতিনিধিত্ব করুন

যেখানে h(z) একটি বিন্দুর আশেপাশে একটি বিশ্লেষণাত্মক ফাংশনম এবং h(zo) f 0.

প্রমাণ। ফাংশন cp(z) = l/h(z)বিন্দু r-এর কিছু আশেপাশে বিশ্লেষণাত্মক। করোলারি 26.4-এর অবস্থা নিম্নলিখিতগুলির সমতুল্য:

তাই zq - বহুগুণ শূন্য এনফাংশন g(z)।এবং তাই বহুবিধ মেরু এনফাংশন /(2)।

II উদাহরণ 26.5. একটি ফাংশনের বিচ্ছিন্ন একবচন বিন্দু খুঁজুন এবং তাদের ধরন নির্ধারণ করুন।

D e u c tio n. যে পয়েন্টে (z 2 + 1 )(z+ জ) 2 ​​= 0. যদি z 2 L- 1 = 0 তারপর 2 = ±rযদি (z 4- H) 2 = 0, তারপর z=-3। অতএব, ফাংশনের তিনটি একক বিন্দু আছে z= r, 22 = -r, জেড3 = - 3. বিবেচনা করুন z:

জি -প্রথম-ক্রমের মেরু (আমরা করোলারি 26.4 ব্যবহার করেছি)। এটি একইভাবে প্রমাণ করা যেতে পারে যে 22 = -iএছাড়াও প্রথম আদেশের একটি মেরু. 2 ঘন্টার জন্য আমাদের আছে:

আসুন আমরা মূলত একক পয়েন্টের বিবেচনায় চলে যাই।

উপপাদ্য 26.6। একটি ফাংশন f(z) এর একটি বিচ্ছিন্ন একবচন বিন্দু zq মূলত একবচন হয় যদি এবং শুধুমাত্র যদি লরেন্ট সম্প্রসারণের মূল অংশটি zq কেন্দ্রিক থেকে অসীমভাবে অনেকগুলি আলাদা থাকে। শূন্য, p সহ সহগ।

প্রমাণ। উপপাদ্য 26.6 সরাসরি উপপাদ্য 26.2 এবং 26.3 থেকে অনুসরণ করে। প্রকৃতপক্ষে, যদি বিন্দু zq মূলত একবচন, তাহলে লরেন্ট সম্প্রসারণের মূল অংশটি অনুপস্থিত থাকতে পারে না বা সীমাবদ্ধ সংখ্যক পদ থাকতে পারে না (অন্যথায় বিন্দু Zq হয় অপসারণযোগ্য বা একটি মেরু হবে)। অতএব, মূল অংশে পদ সংখ্যা অসীম হতে হবে।

বিপরীতভাবে, যদি মূল অংশে অসীমভাবে অনেক সদস্য থাকে, তাহলে Zq একটি অপসারণযোগ্য বিন্দু বা একটি মেরু হতে পারে না। ফলস্বরূপ, এই বিন্দুটি মূলত একবচন।

সংজ্ঞা অনুসারে, একটি অত্যাবশ্যক একবচন বিন্দু এই সত্য দ্বারা চিহ্নিত করা হয় যে ফাংশন f(2) এর জন্য কোন সসীম বা অসীম সীমা নেই z ->zq একটি অপরিহার্য একক বিন্দুর আশেপাশে একটি ফাংশনের আচরণ কতটা অনিয়মিত তার একটি আরও সম্পূর্ণ ধারণা নিম্নলিখিত উপপাদ্য দ্বারা দেওয়া হয়েছে।

উপপাদ্য 26.7 (সোচকির উপপাদ্য)। যদি zq মূলত একবচন হয়, তাহলে ফাংশনের বিন্দু f(z), তারপর যেকোনো জটিল সংখ্যার জন্যএল, A = সহও, বিন্দুর একটি ক্রম z n যেমন z n -> zo এবংলিম f(zn) = ক.

n->ওএস

প্রমাণ। প্রথমে কেসটি বিবেচনা করুন ক = oo উপপাদ্য 2G.2 এর প্রমাণের প্রথম অংশে, আমরা প্রতিষ্ঠিত করেছি যে যদি f(z)বিন্দু r0 এর কিছু ছিদ্রযুক্ত আশেপাশে আবদ্ধ, তারপর সমস্ত সহগ c, n = -মূল অংশের 1, - 2,... শূন্যের সমান (এবং, ফলস্বরূপ, তম তে এককতা অপসারণযোগ্য)। যেহেতু অনুমান দ্বারা r0 একটি অপরিহার্যভাবে একবচন বিন্দু, ফাংশন f(r) r0 বিন্দুর যে কোনো ছিদ্রযুক্ত আশেপাশে সীমাহীন। আসুন কিছু সংকীর্ণ আশেপাশের 0 Z যেমন ধরি f(zi) > 1 (যদি |/(r)| z - zo R/2 একটি বিন্দু আছে জেড-2 , যেখানে |/(dd)| > 2, ইত্যাদি: ছিদ্রযুক্ত আশেপাশে হে 71. এটা স্পষ্ট যে rn -e go এবং lim /(r«) = oo। সুতরাং, ক্ষেত্রে A = oo, উপপাদ্য 26.7

প্রমাণিত

এখন যাক ক চ oo প্রথমে অনুমান করুন যে একটি ছিদ্রযুক্ত প্রতিবেশী 0 আছে

= -yy---- এই বিচ্ছিন্ন পাড়ায় বিশ্লেষণাত্মক হবে এবং ফলস্বরূপ,

/(জি) - ক

ফলস্বরূপ, r হল Φ(r) ফাংশনের একটি বিচ্ছিন্ন একবচন বিন্দু। দেখাই যাক। যে r0 হল Φ(r)-এর একটি অপরিহার্য বিন্দু। এটা ভুল হতে দিন. তারপর একটি সীমা লিম Φ(r), সসীম বা অসীম বিদ্যমান। কারণ

/(r) = A + , তারপর Hsh /(r)ও বিদ্যমান, যা শর্তের বিরোধিতা করে

F(g) ~ :-*z 0

উপপাদ্যের দৃষ্টিভঙ্গি। এইভাবে r0 হল Φ(r) ফাংশনের একটি অপরিহার্য বিন্দু। উপরে যা প্রমাণিত হয়েছে, সেই অনুসারে r n বিন্দুর একটি ক্রম রয়েছে যাতে r n o এবং lim Φ(r n) = oo। এখান থেকে

আমরা এই ধারণার অধীনে প্রয়োজনীয় দাবি প্রমাণ করেছি যে f(r) F Aবিন্দু r এর কিছু ছিদ্রযুক্ত আশেপাশে। আসুন এখন ধরে নিই যে এটি সত্য নয়, অর্থাৎ বিন্দু তম যে কোন ইচ্ছামত ছোট punctured আশেপাশে যেমন একটি বিন্দু আছে জি",যে f(r") = A. তারপর যেকোনোটির জন্য পৃছিদ্রযুক্ত আশেপাশে 0 f(z u) = L. এইভাবে, প্রয়োজনীয় দাবিটি সত্য পৃ-ইউও

সব ক্ষেত্রে, এবং উপপাদ্য 26.7 প্রমাণিত হয়।

(সোখোটস্কির) উপপাদ্য 26.7 অনুসারে, একটি অপরিহার্য একক বিন্দুর যে কোনো (যথেচ্ছভাবে ছোট) ছিদ্রযুক্ত এলাকায় ফাংশন f(r) বর্ধিত জটিল সমতল সি-তে যেকোনো সংখ্যার কাছাকাছি মানগুলিকে নির্বিচারে গ্রহণ করে।

বিচ্ছিন্ন একবচন বিন্দু অধ্যয়ন করতে, প্রাথমিক প্রাথমিক ফাংশনগুলির সুপরিচিত টেলর সম্প্রসারণ প্রায়ই দরকারী।

উদাহরণ 2G.8. ফাংশনের জন্য একবচন বিন্দু zq = 0 এর ধরন নির্ণয় কর

সমাধান করা হয়েছে এবং e. আমরা টেলর সিরিজে লব এবং হরকে r এর ক্ষমতায় প্রসারিত করি। প্রতিস্থাপন (22.11) 3 z r এর পরিবর্তে 1 বিয়োগ করলে আমরা পাব

(22.12) ব্যবহার করে, আমরা হরটির প্রসারণ পাই:

এই সম্প্রসারণের সিরিজ সমগ্র জটিল সমতলে একত্রিত হয় €। আমাদের আছে

এবং /2(2) বিন্দুর আশেপাশে সাদৃশ্যপূর্ণ zo = 0 (এবং এমনকি পুরো সমতলে) এবং /2(20) চ 0, তারপর h(z)বিন্দু জিএফ 0 এর কিছু আশেপাশেও বিশ্লেষণাত্মক। কোরোলারি 26.4 অনুসারে, বিন্দুটি জো = 0 হল অর্ডারের মেরু N = 4।

II উদাহরণ 26.9. একটি ফাংশনের একক পয়েন্ট খুঁজুন f(z)= sin j - এবং তাদের প্রকার নির্ধারণ করুন।

e এবং e তে P e। ফাংশনের একটি একক চূড়ান্ত একবচন বিন্দু আছে zq = 1. C থেকে অন্যান্য বিন্দুতে, ফাংশন w =--- বিশ্লেষণাত্মক; তাই পাপ ফাংশন wবিশ্লেষণাত্মক হবে।

সাইনের প্রসারণে প্রতিস্থাপন করা (22.12) - r এর পরিবর্তে, আমরা পাই

আমরা লরেন্ট সিরিজের একটি বিন্দু 20 = 1 এর ছিদ্রযুক্ত আশেপাশে সিন ফাংশনের প্রসারণ পেয়েছি। যেহেতু ফলস্বরূপ প্রসারণে নেতিবাচক শক্তি (r - 1) সহ অসীমভাবে অনেকগুলি পদ রয়েছে, তারপর zq = 1 একটি অপরিহার্য একবচন বিন্দু (এই ক্ষেত্রে, লরেন্ট সম্প্রসারণ শুধুমাত্র প্রধান অংশ নিয়ে গঠিত, এবং সঠিক অংশটি অনুপস্থিত)।

উল্লেখ্য যে এই ক্ষেত্রে সিরিজ সম্প্রসারণের অবলম্বন না করে সরাসরি সংজ্ঞা থেকে এককতার প্রকৃতি স্থাপন করাও সম্ভব ছিল। প্রকৃতপক্ষে, সেখানে ক্রম (r") এবং (2") একত্রিত হচ্ছে৷ zo= 1, এবং যেমন f(z" n)= 1, /(2") = 0 (এই ধরনের ক্রমগুলি নিজেই নির্দিষ্ট করুন) তাই, f(z)কোন সীমা আছে যখন z -> 1 এবং তাই বিন্দু zq - 1 মূলত একবচন।

আসুন একটি বিন্দুর আশেপাশে একটি ফাংশনের লরেন্ট সম্প্রসারণের ধারণাটি চালু করি Zq = 00 এবং এই বিন্দুতে বিভাজন এবং এককতার প্রকৃতির মধ্যে সংযোগ বিবেচনা করুন। নোট করুন যে একটি বিচ্ছিন্ন একবচন বিন্দুর সংজ্ঞা এবং এর ধরন (অপসারণযোগ্য, মেরু, বা অপরিহার্যভাবে একবচন) কেসটিতে বহন করে zq = oc অপরিবর্তিত। কিন্তু উপপাদ্য 26.2. 26.3 এবং 26.6, লরেন্ট সম্প্রসারণের প্রকৃতির সাথে সম্পর্কিত, পরিবর্তন করা প্রয়োজন। কথা হলো সদস্যরা c n (z - 2o) পি. পৃ= -1,-2,..., প্রধান অংশ, শেষ বিন্দুর কাছাকাছি ফাংশনের "'অনিয়ম" সংজ্ঞায়িত করে Zq, যেহেতু 2 oo এর দিকে থাকে, তারা "সঠিকভাবে" আচরণ করবে (0 এর দিকে ঝোঁক)। উল্টো অংশ নিয়ে নিয়মিত সদস্যরা পৃ= 1,2,... oo হবে; তারা সিঙ্গুলারিটির প্রকৃতি নির্ধারণ করে Zq = oo. অতএব, oo এর আশেপাশে সম্প্রসারণের প্রধান অংশটি ইতিবাচক ক্ষমতা সহ শর্তাবলী হবে পি,এবং সঠিক - নেতিবাচক সঙ্গে।

আসুন একটি নতুন পরিবর্তনশীল প্রবর্তন করা যাক w = 12। ফাংশন টিভি = 1/2, প্রসারিত যাতে u(oo) = 0, এক থেকে এক এবং আশেপাশের এলাকাকে মানচিত্র করে z > আরপয়েন্ট zq = 00 |w| এর আশেপাশে wq = 0. ফাংশন হলে f(z)একটি punctured আশেপাশে বিশ্লেষণ আর z Zq = oc, তারপর ফাংশন G(w) = f(l/w)হলুদ পাড়ায় বিশ্লেষণাত্মক হবে 0 wo = 0। যেহেতু 2 -> oo থাকবে w-> 0, তারপর

তাই G(w)পয়েন্ট এ আছে wq = 0 হল একই ধরনের একটি সিঙ্গুলারিটি f(z)বিন্দুতে Zq = 00. আসুন লরেন্ট সিরিজে G(w) ফাংশনটি wo = 0 বিন্দুর একটি ছিদ্রযুক্ত আশেপাশে প্রসারিত করি:

(26.5) এর ডান দিকের যোগফল যথাক্রমে প্রসারণের সঠিক এবং প্রধান অংশগুলিকে উপস্থাপন করে। চলক চলুন চলুন জেড,প্রতিস্থাপন w = 1/z:

denoting পৃ\u003d -A *, 6 * \u003d 6_ " \u003d সঙ্গে পিএবং যে লক্ষ্য G(l/z) = f(z), আমরা পেতে

পচনশীলতা (2G.G) বলা হয় zq বিন্দুর একটি ছিদ্রযুক্ত এলাকায় f(z) ফাংশনের লরেন্ট সম্প্রসারণ= oo প্রথম যোগফলকে (2G.6) বলা হয় ডান অংশ, এবং দ্বিতীয় যোগফল হল প্রধান অংশএই পচন। যেহেতু এই সমষ্টিগুলি সম্প্রসারণের (26.5) সঠিক এবং প্রধান অংশগুলির সাথে সঙ্গতিপূর্ণ, তাই সম্প্রসারণ (26.6) উপপাদ্য 26.2, 26.3 এবং 26.6-এর উপপাদ্যগুলিকে সন্তুষ্ট করে৷ সুতরাং, নিম্নলিখিত উপপাদ্যটি উপপাদ্য 26.2 এর একটি এনালগ।

উপপাদ্য 26.10। বিচ্ছিন্ন একবচন বিন্দুZq - os (ফাংশন/(জি) অপসারণযোগ্য যদি এবং শুধুমাত্র যদি এই বিন্দুর একটি ছিদ্রযুক্ত আশেপাশে লরেন্ট সম্প্রসারণের ফর্ম থাকে

টি.এস. শুধুমাত্র সঠিক অংশ নিয়ে গঠিত।

আমরা /(oo) = রাখি সহআশেপাশে একত্রিত হওয়া সিরিজ (26.7) দ্বারা সংজ্ঞায়িত ফাংশন z > আরপয়েন্ট 2o \u003d oc, বলা হয় বিন্দু z এ বিশ্লেষণাত্মক o = oo. (উল্লেখ্য যে এই সংজ্ঞাটি ফাংশনের বিশ্লেষণের সমতুল্য G(w) বিন্দুতে wo = 0.)

উদাহরণ 26.11। ফাংশনের একবচন বিন্দু zq = oo তদন্ত করুন

যেহেতু সীমা সীমাবদ্ধ, তাহলে zo = oo হল f(r) ফাংশনের একটি অপসারণযোগ্য একবচন বিন্দু। যদি আমরা /(oo) = lim রাখি J(z)= 0, তারপর f(z)হয়ে যাবে

বিন্দুতে টিক জো= ওএস। আসুন আমরা দেখাই কিভাবে সংশ্লিষ্ট সম্প্রসারণ (26.7) খুঁজে বের করতে হয়। চলক চলুন চলুন w = 1 fzপ্রতিস্থাপন z= 1 /?e, আমরা পাই

(শেষ সমতাটি ww = 0 বিন্দুর ছিদ্রযুক্ত আশেপাশে বৈধ, তবে আমরা সংজ্ঞাটি (7(0) = 0 প্রসারিত করব)। ফলে ফাংশনের একক বিন্দু রয়েছে w =±i, w =-1/3, এবং বিন্দুতে Wq = 0 বিশ্লেষণাত্মক। সম্প্রসারণ ফাংশন G(w)উত্তরোত্তর w(যেমন উদাহরণ 25.7 এ করা হয়েছিল) এবং ফলে পাওয়ার সিরিজে প্রতিস্থাপন করা w = 1/zকেউ ফাংশনের সম্প্রসারণ (26.7) পেতে পারে f(z)।

মামলার জন্য উপপাদ্য 26.3 zo= oo নিম্নলিখিত আকারে পুনরায় লেখা হবে।

উপপাদ্য 26.12। বিচ্ছিন্ন একবচন বিন্দু go = os ফাংশন f(z) একটি মেরু যদি এবং শুধুমাত্র যদি লরেন্ট সম্প্রসারণের প্রধান অংশ হয় (26.6) শুধুমাত্র একটি সীমিত সংখ্যক অ-শূন্য সহগ আছেসঙ্গে":

এখানে সিরিজ হল নিয়মিত অংশ, এবং বন্ধনীকৃত বহুপদী হল প্রসারণের প্রধান অংশ। oc-এ মেরুটির বহুত্বকে মেরুটির বহুগুণ হিসাবে সংজ্ঞায়িত করা হয় wq = 0 ফাংশন G(z)।এটি দেখতে সহজ যে মেরুটির বহুগুণ সংখ্যার সাথে মিলে যায় এনইন (26.8)।

Q p | (i 2 + 1) (z + 3) 2

টাস্ক। যে ফাংশন দেখান f(z) =-- -- আছে

বিন্দু zo = oo মেরু আদেশ 3.

একটি অপরিহার্য একবচন বিন্দুতে উপপাদ্য 26.6 কেসের জন্য পুনরায় লেখা হয়েছে zo= os প্রায় শব্দাত্মক, এবং আমরা বিস্তারিতভাবে এটিতে বাস করি না।

টেলর সিরিজ একটি কার্যকরী হাতিয়ার হিসাবে কাজ করে যেগুলি বৃত্তের zol-এ বিশ্লেষণাত্মক ফাংশনগুলি অধ্যয়ন করার জন্য যেগুলি একটি বৃত্তাকার অঞ্চলে বিশ্লেষণাত্মক ফাংশনগুলি অধ্যয়ন করতে, এটি দেখা যাচ্ছে যে এটির ইতিবাচক এবং নেতিবাচক শক্তিগুলিতে (z - zq) সম্প্রসারণ তৈরি করা সম্ভব। ফর্ম যা টেলর সম্প্রসারণকে সাধারণীকরণ করে। সিরিজ (1), দুটি সিরিজের যোগফল হিসাবে বোঝা, লরেন্ট সিরিজ বলা হয়। এটা স্পষ্ট যে সিরিজের (1) অভিসারণের অঞ্চলটি প্রতিটি সিরিজের (2) অভিসারণের অঞ্চলগুলির সাধারণ অংশ। আসুন তাকে খুঁজে বের করি। প্রথম সিরিজের কনভারজেন্সের ক্ষেত্র হল একটি বৃত্ত যার ব্যাসার্ধ কচি-হাদামার্ড সূত্র দ্বারা নির্ধারিত হয় কনভারজেন্সের বৃত্তের ভিতরে, সিরিজ (3) একটি বিশ্লেষণাত্মক ফাংশনে একত্রিত হয় এবং ছোট ব্যাসার্ধের যেকোনো বৃত্তে এটি একেবারে একত্রিত হয় এবং অভিন্নভাবে। দ্বিতীয় ধারাটি পরিবর্তনশীলের সাপেক্ষে একটি পাওয়ার সিরিজ। সিরিজটি (5) তার অভিসারের বৃত্তের মধ্যে জটিল পরিবর্তনশীল m-*oo এর বিশ্লেষণাত্মক ফাংশনে একত্রিত হয় এবং ছোট ব্যাসার্ধের যেকোনো বৃত্তে এটি একেবারে এবং অভিন্নভাবে একত্রিত হয়, যার অর্থ হল সিরিজের (4) অভিসারণের অঞ্চলটি হল বৃত্তের চেহারা - যদি তাহলে সিরিজের (3) এবং (4) এর অভিসারণের একটি সাধারণ অঞ্চল থাকে - একটি বৃত্তাকার বলয় যেখানে সিরিজটি (1) একটি বিশ্লেষণাত্মক ফাংশনে রূপান্তরিত হয়। তদুপরি, যে কোনও রিংয়ে, এটি একেবারে এবং অভিন্নভাবে একত্রিত হয়। উদাহরণ 1. rad লরেন্ট সিরিজের বিচ্ছিন্ন একবচন বিন্দু এবং তাদের শ্রেণীবিভাগ (z), যা একটি বৃত্তাকার বলয়ে একক-মূল্যবান এবং অরাজনৈতিক, এই রিংটিতে একটি অভিসারী সিরিজের সমষ্টি হিসাবে উপস্থাপন করা যেতে পারে যার সহগ নির্ধারণ করুন Cn স্বতন্ত্রভাবে নির্ধারিত হয় এবং সূত্র দ্বারা গণনা করা হয় যেখানে 7p ব্যাসার্ধ m একটি বৃত্ত, আসুন R-এর ভিতরে একটি নির্বিচারে বিন্দু z ঠিক করি। আমরা r বিন্দুতে কেন্দ্রগুলির সাথে বৃত্ত তৈরি করি যার রেডিই অসমতাগুলিকে সন্তুষ্ট করে এবং একটি নতুন বলয় বিবেচনা করে৷ একটি গুণিত সংযুক্ত ডোমেনের জন্য Cauchy অখণ্ড উপপাদ্য অনুসারে, আমরা প্রতিটি অখণ্ডকে যোগফল (8) আলাদাভাবে রূপান্তর করি৷ বৃত্ত 7d* বরাবর সমস্ত বিন্দুর জন্য, একটি অভিন্ন অভিসারী সিরিজ 1 1 এর যোগফলের সম্পর্কটি সন্তুষ্ট। অতএব, ভগ্নাংশ ^টিকে vi- /" / কিছুটা ভিন্ন উপায়ে উপস্থাপন করা যেতে পারে, সমস্ত বিন্দুর জন্য ξ on বৃত্ত ir> আমাদের সম্পর্ক আছে তাই, ভগ্নাংশ ^ একটি বৃত্তাকার বলয়ে বিশ্লেষণাত্মক ফাংশন (10) এবং (12) সূত্রে একটি অভিন্ন অভিসারী সিরিজের যোগফল হিসাবে উপস্থাপন করা যেতে পারে। অতএব, কচির উপপাদ্য অনুসারে, বৃত্ত 7/r এবং 7r/ যেকোনো বৃত্ত দ্বারা প্রতিস্থাপিত হলে সংশ্লিষ্ট অখণ্ডের মান পরিবর্তন হয় না। এটি আমাদেরকে (10) এবং (12) সূত্রগুলিকে একত্রিত করতে দেয়৷ সূত্র (8) এর ডান দিকের অখণ্ডগুলিকে তাদের অভিব্যক্তি (9) এবং (11) দিয়ে প্রতিস্থাপন করে, আমরা কাঙ্ক্ষিত প্রসারণ পাই৷ যেহেতু z একটি স্বেচ্ছাচারী রিংয়ের বিন্দু, এটি অনুসরণ করে যে সিরিজটি (14) এই রিংয়ের সর্বত্র f(z) ফাংশনে একত্রিত হয় এবং যে কোনও রিংয়ে সিরিজটি এই ফাংশনে একেবারে এবং অভিন্নভাবে একত্রিত হয়। আসুন এখন প্রমাণ করি যে ফর্মের (6) পচন অনন্য। অনুমান করুন যে আরও একটি পচন ঘটবে। তারপর, রিং R এর ভিতরে সর্বত্র, আমাদের পরিধির উপর, সিরিজ (15) সমানভাবে একত্রিত হয়েছে। সমতার উভয় দিককে গুণ করুন (যেখানে m একটি নির্দিষ্ট পূর্ণসংখ্যা, এবং উভয় সিরিজ পদকে পদ দ্বারা একত্রিত করুন। ফলস্বরূপ, আমরা বাম দিকে এবং ডান দিকে - Csh পাই। এইভাবে, (4, \u003d St. যেহেতু m একটি নির্বিচারে সংখ্যা, তারপর শেষ সমতা সিরিজ (6), যার সহগ সূত্র (7) দ্বারা গণনা করা হয়, লরেন্ট সিরিজের সহগগুলির জন্য রিং 7-এ f(z) ফাংশনের লরেন্ট সিরিজ বলা হয় অনুশীলনে খুব কমই ব্যবহার করা হয়, কারণ, একটি নিয়ম হিসাবে, তাদের কষ্টকর গণনার প্রয়োজন। সাধারণত, যদি সম্ভব হয়, প্রাথমিক ফাংশনের রেডিমেড টেলর সম্প্রসারণ ব্যবহার করা হয়। সম্প্রসারণের স্বতন্ত্রতার উপর ভিত্তি করে, যেকোনো বৈধ পদ্ধতি একই ফলাফলের দিকে নিয়ে যায়। উদাহরণ 2 বিভিন্ন ডোমেনের ফাংশনগুলির লরেন্ট সিরিজের সম্প্রসারণ বিবেচনা করুন, ধরে নিই Fuiscija /(z) এর দুটি একক বিন্দু রয়েছে: অতএব, তিনটি রিং ডোমেন রয়েছে এবং, r = 0 বিন্দুতে কেন্দ্রীভূত। যার প্রতিটিতে f(r) ফাংশনটি বিশ্লেষণাত্মক: ক) বৃত্ত হল বৃত্তের বহিঃস্থ (চিত্র 27)। আসুন এই প্রতিটি অঞ্চলে ফাংশন /(z) এর লরেন্ট সম্প্রসারণ খুঁজে বের করি। আমরা /(z) কে প্রাথমিক ভগ্নাংশের যোগফল হিসাবে উপস্থাপন করি ক) বৃত্ত রূপান্তর সম্পর্ক (16) নিম্নরূপ একটি জ্যামিতিক অগ্রগতির পদগুলির যোগফলের সূত্র ব্যবহার করে, আমরা পাই b) ফাংশন -z-এর জন্য রিং এই রিংটিতে অভিসারী থাকে, যেহেতু |z| এর জন্য j^j ফাংশনের জন্য সিরিজ (19) > 1 বিচ্ছিন্ন হয়। অতএব, আমরা ফাংশন /(z)কে নিম্নরূপ রূপান্তর করি: আবার সূত্র (19) প্রয়োগ করে, আমরা পাই যে এই সিরিজটির জন্য একত্রিত হয়। সম্প্রসারণ (18) এবং (21) কে সম্পর্কে (20) প্রতিস্থাপন করে, আমরা পাই > 2 diverges, এবং series (21) ফাংশনের জন্য আসুন আমরা ফাংশন /(z) কে নিম্নলিখিত আকারে উপস্থাপন করি: /<*> সূত্র (18) এবং (19) ব্যবহার করে, আমরা OR 1 প্রাপ্ত করি এই উদাহরণটি দেখায় যে একই ফাংশনের জন্য f(z) লরেন্ট সম্প্রসারণ, সাধারণভাবে বলতে গেলে, বিভিন্ন রিংয়ের জন্য একটি ভিন্ন রূপ রয়েছে। উদাহরণ 3. ফাংশন লরেন্ট সিরিজের 8 লরেন্ট সিরিজের বিচ্ছিন্ন একবচন বিন্দু এবং বৃত্তাকার অঞ্চল A-তে তাদের শ্রেণীবিভাগের পচন খুঁজুন একটি জ্যামিতিক অগ্রগতির পদগুলির যোগফলের জন্য সূত্র, আমরা পাওয়া অভিব্যক্তিগুলিকে সূত্রে (22) প্রতিস্থাপন করে পাই, আমাদের উদাহরণ 4 আছে। লরেন্ট সিরিজের পাতলা zq = 0 এর আশেপাশে ফাংশনটি প্রসারিত করুন। যেকোনো জটিল একের জন্য , আমাদের আছে Let এই সম্প্রসারণ যেকোন বিন্দু z Ф 0 এর জন্য বৈধ। এই ক্ষেত্রে, বৃত্তাকার অঞ্চল হল সম্পূর্ণ জটিল সমতল যার একটি বিন্দু z - 0 রয়েছে। এই অঞ্চলটিকে নিম্নলিখিত সম্পর্ক দ্বারা সংজ্ঞায়িত করা যেতে পারে: এই ফাংশনটি বিশ্লেষণাত্মক অঞ্চলে লরেন্ট সিরিজের সহগগুলির জন্য সূত্র (13) থেকে, পূর্ববর্তী অনুচ্ছেদের মতো একই যুক্তি দ্বারা, কেউ কুইউ অসমতা পেতে পারে। যদি f(z) ফাংশনটি একটি বৃত্তের উপর আবদ্ধ থাকে, যেখানে M একটি ধ্রুবক), তাহলে বিচ্ছিন্ন একবচন বিন্দু A বিন্দু zo কে বলা হয় f(z) ফাংশনের একটি বিচ্ছিন্ন একবচন বিন্দু যদি বিন্দুটির একটি বৃত্তাকার প্রতিবেশ থাকে ( এই সেটটিকে কখনও কখনও বিন্দু 2o-এর একটি ছিদ্রযুক্ত প্রতিবেশীও বলা হয়), যেখানে ফাংশন f(z) একক-মূল্যযুক্ত এবং বিশ্লেষণাত্মক। বিন্দু zo-এ, ফাংশনটি হয় সংজ্ঞায়িত নয় বা একক-মূল্যবান এবং বিশ্লেষণাত্মক নয়। zo বিন্দুর কাছে যাওয়ার সময় ফাংশন /(z) এর আচরণের উপর নির্ভর করে তিন ধরনের একবচন বিন্দুকে আলাদা করা হয়। একটি বিচ্ছিন্ন একবচন বিন্দু বলা হয়: 1) সসীম থাকলে অপসারণযোগ্য 2) pmusach যদি 3) একটি অপরিহার্য একবচন বিন্দু যদি f(z) ফাংশনের কোন সীমা না থাকে উপপাদ্য 16. একটি ফাংশন f(z) এর একটি বিচ্ছিন্ন একবচন বিন্দু z0 হল একটি অপসারণযোগ্য একবচন বিন্দু যদি এবং শুধুমাত্র যদি zo বিন্দুর একটি আশেপাশে ফাংশনের f(z) লরেন্ট সম্প্রসারণে একটি প্রধান অংশ না থাকে, অর্থাৎ, Let zo ফর্ম আছে - অপসারণযোগ্য একবচন বিন্দু। তারপরে একটি সসীম আছে, এবং তাই ফাংশন f(z) বিন্দু r এর একটি প্রকোলজিক্যাল আশেপাশে আবদ্ধ। আমরা কচি অসমতার কারণে সেট করেছি যেহেতু আমাদের পছন্দ মতো ছোট ρ বেছে নেওয়া সম্ভব, তারপরে সমস্ত নেতিবাচক শক্তিতে সহগ (z - 20) শূন্যের সমান: বিপরীতভাবে, লরেন্টকে zq বিন্দুর আশেপাশে ফাংশনের /(r) সম্প্রসারণ করা যাক শুধুমাত্র সঠিক অংশ রয়েছে, অর্থাৎ, এটির ফর্ম (23) আছে এবং, ফলস্বরূপ, টেলর. এটা দেখা সহজ যে z -* z0 এর জন্য ফাংশন /(r) এর একটি সীমা মান রয়েছে: উপপাদ্য 17. ফাংশন f(z) এর একটি বিচ্ছিন্ন একবচন বিন্দু zq অপসারণযোগ্য যদি এবং শুধুমাত্র যদি ফাংশন J(z) হয় বিন্দু zq কিছু punctured আশেপাশে আবদ্ধ, Zgmechai না. ধরা যাক r0 f(r) এর একটি অপসারণযোগ্য একবচন বিন্দু। ধরে নিলাম যে ফাংশনটি f(r) বিন্দুকে কেন্দ্র করে কিছু বৃত্তে বিশ্লেষণাত্মক। এটি বিন্দুর নাম নির্ধারণ করে - নিষ্পত্তিযোগ্য। উপপাদ্য 18. একটি ফাংশন f(z) এর একটি বিচ্ছিন্ন একবচন বিন্দু zq একটি মেরু যদি এবং শুধুমাত্র যদি বিন্দুর একটি পার্শ্ববর্তী অঞ্চলে ফাংশন f(z) এর লরেন্ট সম্প্রসারণের প্রধান অংশে একটি সসীম (এবং ধনাত্মক) সংখ্যা থাকে অ-শূন্য পদের, অর্থাৎ, ফর্ম 4 আছে z0 একটি মেরু হতে দিন। তারপর থেকে z0 বিন্দুর একটি ছিদ্রযুক্ত প্রতিবেশ বিদ্যমান যেখানে ফাংশন f(z) বিশ্লেষণাত্মক এবং অশূন্য। তারপর এই আশেপাশে একটি বিশ্লেষণাত্মক ফাংশন সংজ্ঞায়িত করা হয়, এবং তাই, বিন্দু zq হল ফাংশনের একটি অপসারণযোগ্য একবচন বিন্দু (শূন্য) বা যেখানে h(z) একটি বিশ্লেষণাত্মক ফাংশন, h(z0) ∩ 0. একটি আশেপাশে বিশ্লেষণাত্মক বিন্দু zq এর, এবং সেইজন্য, যেখান থেকে আমরা পেয়েছি যে এখন আমরা ধরে নিই যে ফাংশন f(z) ফর্মটির একটি পচন আছে (24) বিন্দু zo এর একটি ছিদ্রযুক্ত এলাকায়। এর মানে হল যে এই আশেপাশে ফাংশন f(z) ফাংশনের সাথে বিশ্লেষণাত্মক। ফাংশন g(z) এর জন্য, সম্প্রসারণটি বৈধ যেখান থেকে এটা স্পষ্ট যে zq হল g(z) ফাংশনের একটি অপসারণযোগ্য একবচন বিন্দু এবং বিদ্যমান তারপর ফাংশনটি 0 এ থাকে - ফাংশনের মেরুতে আরও একটি সরল রয়েছে সত্য বিন্দু Zq হল f(z) ফাংশনের একটি মেরু যদি এবং শুধুমাত্র যদি ফাংশন g(z) = y ফাংশনটি zq বিন্দুর আশেপাশে একটি বিশ্লেষণাত্মক ফাংশনে বাড়ানো যায় g(z0) = 0 সেট করে। f(z) ফাংশনের মেরুকে jfa ফাংশনের শূন্যের ক্রম বলা হয়। উপপাদ্য 16 এবং 18 নিম্নলিখিত দাবি বোঝায়। উপপাদ্য 19. একটি বিচ্ছিন্ন একবচন পাতলা মূলত একবচন হয় যদি এবং শুধুমাত্র যদি এই বিন্দুর একটি ছিদ্রযুক্ত এলাকায় লরেন্ট সম্প্রসারণের প্রধান অংশে অসীমভাবে অনেকগুলি অশূন্য পদ থাকে। উদাহরণ 5. ফাংশনের একবচন বিন্দু হল zo = 0। আমাদের কাছে লরেন্ট সিরিজ বিচ্ছিন্ন একবচন বিন্দু রয়েছে এবং তাদের শ্রেণীবিভাগ তাই, zo = 0 একটি অপসারণযোগ্য একবচন বিন্দু। শূন্য বিন্দুর আশেপাশে লরেন্ট সিরিজে ফাংশন /(z) এর বিস্তৃতিতে শুধুমাত্র সঠিক অংশ রয়েছে: উদাহরণ7। f(z) = f(z) ফাংশনের একবচন বিন্দু হল zq = 0। বাস্তব এবং কাল্পনিক অক্ষের উপর এই ফাংশনের আচরণ বিবেচনা করুন: বাস্তব অক্ষ x 0 এ, কাল্পনিক অক্ষের উপর অতএব, সসীম বা সসীম নয় z -* 0 এ অসীম সীমা f(z) বিদ্যমান নেই। তাই r0 = 0 বিন্দুটি f(z) ফাংশনের একটি অপরিহার্য বিন্দু। আসুন আমরা শূন্য বিন্দুর আশেপাশে f(z) ফাংশনের লরেন্ট সম্প্রসারণ খুঁজে পাই। যেকোন জটিল C এর জন্য আমরা সেট করেছি। তারপর লরেন্ট সম্প্রসারণে z এর ঋণাত্মক ক্ষমতা সহ অসীম সংখ্যক পদ রয়েছে।

সংজ্ঞা।ফাংশনের একবচন বিন্দুকে বলা হয় ভিন্ন, যদি এই পয়েন্টের কিছু আশেপাশে একটি বিশ্লেষণাত্মক ফাংশন হয় (অর্থাৎ, রিং এ বিশ্লেষণাত্মক)।

একটি ফাংশনের বিচ্ছিন্ন একবচন বিন্দুর শ্রেণীবিভাগ একটি একবচন বিন্দুর আশেপাশে এই ফাংশনের আচরণের সাথে সম্পর্কিত।

সংজ্ঞা।বিন্দু বলা হয় নিষ্পত্তিযোগ্য একটি ফাংশনের একক বিন্দু যদি এই ফাংশনের একটি সীমাবদ্ধ সীমা থাকে।

উদাহরণ 5দেখান যে ফাংশনটির একটি বিন্দুতে অপসারণযোগ্য এককতা রয়েছে।

সমাধান।প্রথম উল্লেখযোগ্য সীমা স্মরণ করে, আমরা গণনা করি

এর মানে হল যে প্রদত্ত ফাংশনটির বিন্দুতে একটি অপসারণযোগ্য এককতা রয়েছে।

টাস্ক 4।দেখান যে পয়েন্টটি এর জন্য অপসারণযোগ্য।

সংজ্ঞা।বিন্দু বলা হয় মেরু ফাংশন , যদি এই ফাংশনটি অনির্দিষ্টকালের জন্য বৃদ্ধি পায়, তা হল।

আসুন আমরা একটি বিশ্লেষণমূলক ফাংশনের শূন্য এবং মেরু ধারণার মধ্যে সংযোগের দিকে মনোযোগ দিই। আসুন ফাংশনটিকে হিসাবে উপস্থাপন করি।

যদি একটি বিন্দু একটি ফাংশনের একটি সরল শূন্য হয়, তাহলে ফাংশনের একটি সরল মেরু আছে

যদি পয়েন্টটি ফাংশনের জন্য ক্রম শূন্য হয়, তবে ফাংশনের জন্য এটি মেরু আদেশ

উদাহরণ 6দেখান যে ফাংশনটির একটি বিন্দুতে তৃতীয়-ক্রমের মেরু রয়েছে।

সমাধান।অনুমান, আমরা পেতে. আমরা শূন্য প্রবণতা হিসাবে, কোন আইন অনুযায়ী, আমাদের আছে. তারপর, এবং এটির সাথে ফাংশন নিজেই অনির্দিষ্টকালের জন্য বৃদ্ধি পায়। অতএব, , অর্থাৎ, একবচন বিন্দু একটি মেরু। একটি ফাংশনের জন্য, এই বিন্দুটি স্পষ্টতই একটি ট্রিপল শূন্য। সুতরাং, এই ফাংশনের জন্য, বিন্দুটি তৃতীয় ক্রমটির একটি মেরু।

টাস্ক 5।দেখান যে বিন্দুতে একটি সরল মেরু আছে।

সংজ্ঞা।বিন্দু বলা হয় মূলত বিশেষ ফাংশনের বিন্দু যদি এই বিন্দুতে ফাংশনের একটি সসীম বা অসীম সীমা না থাকে (ফাংশনের আচরণ সংজ্ঞায়িত করা হয় না)।

ফাংশনের একটি অপরিহার্য একবচন বিন্দু হতে দিন। তারপরে যেকোন পূর্ব নির্ধারিত জটিল সংখ্যার জন্য বিন্দুগুলির এমন একটি ক্রম রয়েছে যা তে রূপান্তরিত হয়, যার সাথে মানগুলি থাকে : ( সোচকির উপপাদ্য)।

উদাহরণ 7দেখান যে একটি বিন্দুতে একটি ফাংশনের একটি অপরিহার্য এককতা আছে।

সমাধান।বিন্দুর আশেপাশে একটি প্রদত্ত ফাংশনের আচরণ বিবেচনা করুন। বাস্তব অক্ষের ধনাত্মক অংশের জন্য (অর্থাৎ) আমাদের আছে এবং ; যদি বাস্তব অক্ষের নেতিবাচক অংশ বরাবর (অর্থাৎ), তারপর এবং তাই জন্য কোন সীমা নেই. সংজ্ঞা অনুসারে, একটি বিন্দুতে একটি ফাংশনের একটি অপরিহার্য এককতা রয়েছে।

সোচোকি উপপাদ্যের দৃষ্টিকোণ থেকে শূন্যে ফাংশনের আচরণ বিবেচনা করা যাক। শূন্য এবং অসীম ছাড়া অন্য যেকোন জটিল সংখ্যা হোক।

সমতা থেকে আমরা খুঁজে পাই। ধরে নিই, আমরা পয়েন্টের একটি ক্রম পাই। স্পষ্টতই, . এই ক্রমটির প্রতিটি বিন্দুতে, ফাংশনটি সমান এবং তাই

টাস্ক 6।দেখান যে ফাংশনের একটি বিন্দুতে একটি অপরিহার্য এককতা রয়েছে।

অনন্তের একটি বিন্দু সর্বদা ফাংশনের জন্য বিশেষ বিবেচিত হয়. একটি বিন্দুকে একটি ফাংশনের একটি বিচ্ছিন্ন একবচন বিন্দু বলা হয় যদি এই ফাংশনের উত্সকে কেন্দ্র করে কিছু বৃত্তের বাইরে অন্য কোনো একবচন বিন্দু না থাকে।

বিচ্ছিন্ন একবচন বিন্দুর শ্রেণীবিভাগও ক্ষেত্রে প্রসারিত করা যেতে পারে।

উদাহরণ 8দেখান যে ফাংশনটির অনন্তে একটি দ্বিগুণ মেরু রয়েছে।

সমাধান।ফাংশনটি বিবেচনা করুন, বিন্দুর আশেপাশে একটি বিশ্লেষণাত্মক ফাংশন কোথায়, এবং। এর মানে হল যে ফাংশনের অনন্তে একটি ডবল শূন্য আছে, কিন্তু তারপর ফাংশনের জন্য বিন্দুটি একটি ডবল মেরু।

উদাহরণ 9দেখান যে ফাংশনটির অসীমতায় একটি অপরিহার্য এককতা রয়েছে।

সমাধান।অনুরূপ একটি সমস্যা pr.7 এ বিবেচনা করা হয়েছে। অসীম দূরবর্তী বিন্দুর আশেপাশে একটি ফাংশনের আচরণ বিবেচনা করুন। বাস্তব অক্ষের ধনাত্মক অংশ বরাবর, এবং বাস্তব অক্ষের ঋণাত্মক অংশের জন্য। এর মানে হল একটি বিন্দুতে ফাংশনের কোন সীমা নেই এবং, সংজ্ঞা অনুসারে, এই বিন্দুটি মূলত একবচন।

একটি বিন্দুতে একটি ফাংশনের এককতার প্রকৃতি থেকে বিচার করা যেতে পারে প্রধান অংশ এই পয়েন্টের একটি আশেপাশে লরেন্টের বিস্তার।

উপপাদ্য ঘ.বিন্দু হতে নিষ্পত্তিযোগ্য ফাংশনের একক বিন্দু, এটি প্রয়োজনীয় এবং যথেষ্ট যে সংশ্লিষ্ট লরেন্ট সম্প্রসারণ প্রধান অংশ ধারণ করেনি।

টাস্ক 6।বিন্দুর আশেপাশে ফাংশনের টেলর সম্প্রসারণ ব্যবহার করে দেখান যে এটির শূন্যে একটি অপসারণযোগ্য এককতা রয়েছে।

উপপাদ্য 2।বিন্দু হতে মেরু ফাংশন, প্রয়োজনীয় এবং যথেষ্ট যাতে প্রধান অংশ অনুরূপ লরেন্ট সম্প্রসারণ সীমিত সংখ্যক সদস্য ছিল :

সর্বোচ্চ ঋণাত্মক পদের সংখ্যা মেরুটির ক্রম নির্ধারণ করে।

এই ক্ষেত্রে, ফাংশন হিসাবে উপস্থাপন করা যেতে পারে

বিন্দুতে ফাংশন বিশ্লেষণাত্মক কোথায়, , ​​মেরুটির ক্রম।

উদাহরণ 10দেখান যে ফাংশনের বিন্দুতে সরল খুঁটি রয়েছে।

সমাধান।আসুন একটি পয়েন্ট বিবেচনা করা যাক. আমরা এই বিন্দুর আশেপাশে এই ফাংশনের লরেন্ট সম্প্রসারণ ব্যবহার করি, উদাহরণ 2 এ প্রাপ্ত:

যেহেতু এই সম্প্রসারণের মূল অংশে সর্বোচ্চ (এবং একমাত্র) নেতিবাচক শক্তি একটির সমান, তাই বিন্দুটি এই ফাংশনের একটি সাধারণ মেরু।

এই ফলাফল অন্য উপায়ে প্রাপ্ত করা যেতে পারে. আসুন ফর্মে উপস্থাপন করি এবং রাখি - এটি একটি ফাংশন যা বিন্দুতে বিশ্লেষণাত্মক এবং . সুতরাং, (8) এর কারণে এই ফাংশনের বিন্দুতে একটি সরল মেরু রয়েছে।

আরেকটি উপায়: বিন্দুতে একটি সহজ শূন্য আছে এমন একটি ফাংশন বিবেচনা করুন। তাই, এই মুহুর্তে এটির একটি সাধারণ মেরু রয়েছে।

একইভাবে, যদি আমরা ফাংশনটিকে ফর্মে লিখি, যেখানে বিন্দুতে একটি ফাংশন বিশ্লেষণাত্মক এবং , তাহলে এটি অবিলম্বে স্পষ্ট যে বিন্দুটি ফাংশনের একটি সাধারণ মেরু।

টাস্ক 7।দেখান যে ফাংশনটির বিন্দুতে 2য় ক্রমটির একটি মেরু এবং বিন্দুতে 4র্থ ক্রমটির একটি পোল রয়েছে।

উপপাদ্য 3.বিন্দু হতে মূলত বিশেষ ফাংশন পয়েন্ট, এটা প্রয়োজনীয় এবং যথেষ্ট যে প্রধান অংশ বিন্দুর একটি আশেপাশে লরেন্টের বিস্তার অসীম সংখ্যক সদস্য রয়েছে .

উদাহরণ 11।ফাংশনের বিন্দুতে এককতার প্রকৃতি নির্ধারণ করুন

সমাধান।কোসাইনের সুপরিচিত সম্প্রসারণে, আমরা এর পরিবর্তে রাখি:

তাই, একটি বিন্দুর আশেপাশে লরেন্ট সম্প্রসারণের ফর্ম আছে

এখানে সঠিক অংশটি একটি পদ। এবং মূল অংশে অসীম সংখ্যক পদ রয়েছে, তাই বিন্দুটি মূলত একবচন।

টাস্ক 8।দেখান যে একটি বিন্দুতে ফাংশনের একটি অপরিহার্য এককতা আছে।

কিছু ফাংশন বিবেচনা করুন এবং বিন্দুতে এর লরেন্ট সম্প্রসারণ লিখুন:

এর একটি প্রতিস্থাপন করা যাক, যখন বিন্দু বিন্দু যায়. এখন, অসীম একটি বিন্দু একটি আশেপাশে, আমরা আছে

এটি একটি নতুন পদবী প্রবর্তন অবশেষ. আমরা পেতে

যেখানে প্রধান অংশ, এবং একটি অসীম দূরবর্তী বিন্দুর আশেপাশে ফাংশনের লরেন্ট সম্প্রসারণের নিয়মিত অংশ। সুতরাং, একটি বিন্দুর আশেপাশে একটি ফাংশনের লরেন্ট সম্প্রসারণে, প্রধান অংশটি ধনাত্মক শক্তিগুলির একটি সিরিজ, যেখানে সঠিক অংশটি নেতিবাচক শক্তিগুলির একটি সিরিজ। বিষয়টি বিবেচনায় নিয়ে

যাইহোক, এককতার প্রকৃতি নির্ধারণের জন্য উপরোক্ত মানদণ্ড একটি অসীম দূরবর্তী বিন্দুর জন্য বৈধ থাকে।

উদাহরণ 12।বিন্দুতে ফাংশনের এককতার প্রকৃতি খুঁজে বের করুন। , তারপর এক পর্যায়ে এটি অ-বিচ্ছিন্ন হতে পারে।

উদাহরণ 15একটি অসীম দূরবর্তী বিন্দুতে ফাংশন একটি অপরিহার্য এককতা আছে. দেখান যে ফাংশনের বিন্দুটি একটি বিচ্ছিন্ন একবচন বিন্দু নয়।

সমাধান।ফাংশনটির হর-এর শূন্যে অসীম সংখ্যক মেরু রয়েছে, অর্থাৎ বিন্দুতে, . যেহেতু, বিন্দু, যে কোন আশেপাশে খুঁটি আছে, খুঁটির জন্য সীমা বিন্দু।

একক বিন্দু

গণিতে

1) সমীকরণ F দ্বারা প্রদত্ত বক্ররেখার একবচন বিন্দু ( x, y) = 0, - বিন্দু M 0 ( x 0, y 0), যার মধ্যে ফাংশনের উভয় আংশিক ডেরিভেটিভ F ( x, y) অদৃশ্য:

যদি, উপরন্তু, ফাংশনের সমস্ত দ্বিতীয় আংশিক ডেরিভেটিভ না হয় ( x, y) বিন্দুতে M 0 শূন্যের সমান, তারপর O. t. কে দ্বিগুণ বলা হয়। যদি, M 0 বিন্দুতে প্রথম ডেরিভেটিভের অদৃশ্য হওয়ার সাথে সাথে, সমস্ত দ্বিতীয় ডেরিভেটিভগুলি অদৃশ্য হয়ে যায়, কিন্তু তৃতীয় ডেরিভেটিভগুলি শূন্যের সমান না হয়, তাহলে O. t. কে বলা হয় ট্রিপল, ইত্যাদি। একটি ডবল O. t. এর কাছাকাছি একটি বক্ররেখার গঠন অধ্যয়ন করার সময়, অভিব্যক্তির চিহ্ন দ্বারা একটি গুরুত্বপূর্ণ ভূমিকা পালন করা হয়

যদি Δ > 0, তাহলে O. t. কে বিচ্ছিন্ন বলা হয়; উদাহরণস্বরূপ, বক্ররেখা y 2 - x 4 + 4x 2= 0 মূল একটি বিচ্ছিন্ন O. t. (দেখুন চাল এক ) যদি Δ x 2 + y 2 + a 2) 2 - 4a 2 x 2 - a 4= 0 স্থানাঙ্কের উৎপত্তি হল নোডাল O. t. (দেখুন চাল 2 ) যদি Δ = 0 হয়, তাহলে O. t. বক্ররেখাটি হয় বিচ্ছিন্ন বা বৈশিষ্ট্যযুক্ত যে বক্ররেখার বিভিন্ন শাখার এই বিন্দুতে একটি সাধারণ স্পর্শক রয়েছে, উদাহরণস্বরূপ: স্পর্শক এবং একটি বিন্দু গঠন করে, যেমন একটি বক্ররেখা। y 2 - x 3= 0 (দেখুন চাল 3 , ক); খ) ২য় ধরনের কুসুম - বক্ররেখার বিভিন্ন শাখা সাধারণ স্পর্শকের একই পাশে অবস্থিত, বক্ররেখার মতো (y - x 2)2 - x 5= 0 (দেখুন চাল 3 , খ); গ) স্ব-যোগাযোগের বিন্দু (একটি বক্ররেখার জন্য y 2 - x 4= 0 মূল স্ব-যোগাযোগের একটি বিন্দু; (সেমি. চাল 3 , v)। নির্দিষ্ট O.t. এর সাথে বিশেষ নাম সহ আরও অনেক O.t. আছে; উদাহরণস্বরূপ, একটি অসীম সংখ্যক বাঁক সহ একটি সর্পিলের শীর্ষ হল একটি অসীম বিন্দু (চিত্র দেখুন। চাল 4 ), ব্রেক পয়েন্ট, কোণার পয়েন্ট, ইত্যাদি

2) একটি ডিফারেনশিয়াল সমীকরণের একটি একবচন বিন্দু এমন একটি বিন্দু যেখানে ডিফারেনশিয়াল সমীকরণের ডান দিকের লব এবং হর উভয়ই একই সাথে অদৃশ্য হয়ে যায় (ডিফারেনশিয়াল সমীকরণ দেখুন)

যেখানে P এবং Q ক্রমাগত পার্থক্যযোগ্য ফাংশন। অনুমান করে O.t. স্থানাঙ্কের উৎপত্তিস্থলে অবস্থিত এবং টেলর সূত্র ব্যবহার করে (টেলর সূত্র দেখুন), আমরা ফর্মে সমীকরণ (1) উপস্থাপন করতে পারি

যেখানে পি 1 ( x, y) এবং প্রশ্ন ১ ( x, y) সাপেক্ষে অসীম

যথা, যদি λ 1 ≠ λ 2 এবং λ 1 λ 2 > 0 বা λ 1 = λ 2, তাহলে O. t. একটি নোড; নোডের যথেষ্ট ছোট আশেপাশের বিন্দুর মধ্য দিয়ে যাওয়া সমস্ত অবিচ্ছেদ্য বক্ররেখা এতে প্রবেশ করে। যদি λ 1 ≠ λ 2 এবং λ 1 λ 2 i β, α ≠ 0 এবং β ≠ 0 হয়, তাহলে O. t. একটি ফোকাস; ফোকাসের পর্যাপ্ত ছোট আশেপাশের বিন্দুর মধ্য দিয়ে যাওয়া সমস্ত অবিচ্ছেদ্য বক্ররেখা হল ফোকাসের যেকোনো ইচ্ছামত ছোট পাড়ায় অসীম সংখ্যক বাঁক সহ সর্পিল। যদি, অবশেষে, λ 1,2 = ± iβ, β ≠ 0, তাহলে O. t.-এর অক্ষর P-এর সম্প্রসারণে রৈখিক পদ দ্বারা নির্ধারিত হয় না ( x, y) এবং প্রশ্ন ( x, y), উপরের সমস্ত ক্ষেত্রে যেমন ছিল; এখানে O. t. একটি ফোকাস বা কেন্দ্র হতে পারে, অথবা এটি একটি আরও জটিল চরিত্র থাকতে পারে। কেন্দ্রের আশেপাশে, সমস্ত অবিচ্ছেদ্য বক্ররেখা বন্ধ থাকে এবং তাদের ভিতরে কেন্দ্র ধারণ করে। সুতরাং, উদাহরণস্বরূপ, বিন্দু (0, 0) সমীকরণের জন্য একটি নোড এ" = 2u/x(λ 1 = 1, λ 2 = 2; দেখুন চাল 5 , ক) এবং y" = u/x(λ 1 = λ 2 = 1; দেখুন চাল 5 , b), সমীকরণের জন্য একটি স্যাডল y" = -y/x(λ 1 = -1, λ 2 = 1 ; সেমি. চাল 6 ), সমীকরণের ফোকাস y" =(x + y) / (x - y) (λ 1 = 1 - i, λ 2 = 1 + i; সেমি. চাল 7 ) এবং সমীকরণের কেন্দ্র y" = -x / y(λ 1 = -i, λ 2 = i; সেমি. চাল আট ).

যদি x, y) এবং Q ( x, y) বিশ্লেষণাত্মক, উচ্চ ক্রমবিশিষ্ট একটি O.t এর আশেপাশের অঞ্চলগুলিকে অঞ্চলে ভাগ করা যেতে পারে: D 1 - অবিচ্ছেদ্য বক্ররেখায় ভরা, যার উভয় প্রান্তই O. t. (উপবৃত্তীয় অঞ্চলে), D 2 - ভরা অখণ্ড বক্ররেখা সহ, যার একটি প্রান্ত O.t. (প্যারাবোলিক অঞ্চল) এবং D 3 - O.t.-তে অন্তর্ভুক্ত দুটি অবিচ্ছেদ্য বক্ররেখা দ্বারা আবদ্ধ অঞ্চল, যার মধ্যে হাইপারবোলাস ধরণের অবিচ্ছেদ্য বক্ররেখা রয়েছে (হাইপারবোলিক অঞ্চল) (দেখুন। চাল 9 ) যদি কোন অখণ্ড বক্ররেখা কোন O. বিন্দুতে প্রবেশ না করে, তাহলে O. বিন্দুকে স্থিতিশীল ধরনের বিন্দু বলে। একটি স্থিতিশীল O.t. এর আশেপাশে বদ্ধ অবিচ্ছেদ্য বক্ররেখা থাকে যার মধ্যে O.t. রয়েছে, যার মধ্যে সর্পিল অবস্থিত (চিত্র দেখুন। চাল 10 ).

O.t. ডিফারেনশিয়াল সমীকরণের অধ্যয়ন, অর্থাৎ, সারমর্মে, O.t. M. Lyapunov a, A. Poincare এবং অন্যান্যদের আশেপাশে অবিচ্ছেদ্য বক্ররেখার পরিবারের আচরণের অধ্যয়ন)।

3) একটি একক-মূল্যযুক্ত বিশ্লেষণাত্মক ফাংশনের একটি একবচন বিন্দু হল একটি বিন্দু যেখানে ফাংশনের বিশ্লেষণ লঙ্ঘন করা হয় (বিশ্লেষণমূলক ফাংশন দেখুন)। O. t এর পাড়া থাকলে। ক, অন্যান্য O. t. থেকে মুক্ত, তারপর বিন্দু কবিচ্ছিন্ন O. t. যদি বলা হয় কএকটি বিচ্ছিন্ন O.t. এবং সেখানে একটি সসীম a আছে যাকে অপসারণযোগ্য O.t বলা হয়। চ(ক)= খ, এটা অর্জন করা সম্ভব কসংশোধিত ফাংশনের একটি সাধারণ বিন্দু হয়ে উঠবে। উদাহরণস্বরূপ, বিন্দু z= 0 হল একটি অপসারণযোগ্য O.T. ফাংশন f 1 ( z) = চ(z), যদি z≠ 0, এবং চ 1(0),=1, বিন্দু z= 0 একটি সাধারণ বিন্দু [ চ 1 (z) বিন্দুতে বিশ্লেষণাত্মক z= 0]। যদি ক- বিচ্ছিন্ন O.t. এবং a কে একটি মেরু বা ফাংশনের একটি অপরিহার্যভাবে একক বিন্দু বলা হয় চ(z), যদি লরেন্ট সিরিজ) ফাংশন চ(z) একটি বিচ্ছিন্ন O.t এর আশেপাশে নেতিবাচক শক্তি ধারণ করে না z - ক, যদি ক- অপসারণযোগ্য O.t., সীমিত সংখ্যক নেতিবাচক শক্তি ধারণ করে z - ক, যদি ক- পোল (এই ক্ষেত্রে, পোলের ক্রম আর a এর সর্বোচ্চ শক্তি হিসাবে সংজ্ঞায়িত করা হয় - একটি অপরিহার্যভাবে একক বিন্দু। উদাহরণস্বরূপ, ফাংশনের জন্য

p = 2, 3, …)

বিন্দু z= 0 হল অর্ডারের মেরু আর, ফাংশনের জন্য

বিন্দু z= 0 একটি অপরিহার্য একবচন বিন্দু।

একটি পাওয়ার সিরিজের কনভারজেন্সের বৃত্তের সীমানায় প্রদত্ত পাওয়ার সিরিজের দ্বারা এই বৃত্তের অভ্যন্তরে উপস্থাপিত ফাংশনের কমপক্ষে একটি O.t থাকতে হবে। একটি একক-মূল্যবান বিশ্লেষণাত্মক ফাংশনের অস্তিত্বের ডোমেনের সমস্ত সীমানা বিন্দু (প্রাকৃতিক সীমানা) এই ফাংশনের সীমানা বিন্দু। এইভাবে, একক বৃত্তের সমস্ত বিন্দু | z| = 1 ফাংশনের জন্য বিশেষ

একটি বহু-মূল্যবান বিশ্লেষণাত্মক ফাংশনের জন্য, "O এর ধারণা। টি।" বেশি কঠিন. O.t. ছাড়াও, একটি ফাংশনের রিম্যান পৃষ্ঠের পৃথক শীটে (অর্থাৎ, একক-মূল্যযুক্ত বিশ্লেষণাত্মক উপাদানগুলির O. t), যেকোনো শাখা বিন্দুও ফাংশনের একটি O.t. একটি Riemann পৃষ্ঠের বিচ্ছিন্ন শাখা বিন্দু (অর্থাৎ, শাখা বিন্দু যেমন তাদের কিছু আশেপাশে কোন পাতায় অন্য কোন O.t. ফাংশন নেই) নিম্নরূপ শ্রেণীবদ্ধ করা হয়েছে। a যদি সসীম আদেশের একটি বিচ্ছিন্ন শাখা বিন্দু হয় এবং সেখানে একটি সসীম a থাকে তবে তাকে একটি সমালোচনামূলক মেরু বলা হয়। যদি কঅসীম ক্রমে একটি বিচ্ছিন্ন শাখা বিন্দু, এবং a কে ট্রান্সসেন্ডেন্টাল O. t বলা হয়। অন্যান্য সমস্ত বিচ্ছিন্ন শাখা বিন্দুকে বলা হয় সমালোচনামূলক অপরিহার্যভাবে একবচন বিন্দু। উদাহরণ: বিন্দু z= 0 হল ফাংশনের একটি সাধারণ গুরুত্বপূর্ণ বিন্দু f ( z) = লগ zএবং ফাংশনের একটি গুরুত্বপূর্ণ অপরিহার্য একবচন বিন্দু চ (z) = পাপের লগ z.

অপসারণযোগ্য একটি ব্যতীত যেকোনো O.t. বিশ্লেষণাত্মক ধারাবাহিকতার একটি বাধা, অর্থাৎ, একটি অপসারণযোগ্য O.t. এর মধ্য দিয়ে যাওয়া একটি বক্ররেখা বরাবর বিশ্লেষণাত্মক ধারাবাহিকতা অসম্ভব।

গ্রেট সোভিয়েত এনসাইক্লোপিডিয়া। - এম.: সোভিয়েত এনসাইক্লোপিডিয়া. 1969-1978 .

অন্যান্য অভিধানে "বিশেষ পয়েন্ট" কী তা দেখুন:

এখানে পয়েন্ট. এছাড়াও একবচন বিন্দু (পার্থক্য সমীকরণ) দেখুন। গণিতের একটি বৈশিষ্ট্য বা এককতা এমন একটি বিন্দু যেখানে একটি গাণিতিক বস্তু (সাধারণত একটি ফাংশন) সংজ্ঞায়িত করা হয় না বা অনিয়মিত আচরণ থাকে (উদাহরণস্বরূপ, একটি বিন্দু যেখানে ... ... উইকিপিডিয়া

একটি বিশ্লেষণাত্মক ফাংশন হল একটি বিন্দু যেখানে বিশ্লেষণের শর্ত লঙ্ঘন করা হয়। যদি একটি বিশ্লেষণাত্মক ফাংশন f(z) বিন্দু z0 এর কিছু আশেপাশে সর্বত্র সংজ্ঞায়িত করা হয় … শারীরিক বিশ্বকোষ

একটি বিশ্লেষণাত্মক ফাংশন হল একটি বিন্দু যেখানে একটি ফাংশনের বিশ্লেষণ লঙ্ঘন করা হয় ... বড় বিশ্বকোষীয় অভিধান

একক বিন্দু- — [ইয়া.এন. লুগিনস্কি, এম.এস. ফেজি ঝিলিনস্কায়া, ইউ.এস. কবিরভ। ইলেকট্রিক্যাল ইঞ্জিনিয়ারিং অ্যান্ড পাওয়ার ইন্ডাস্ট্রির ইংরেজি রাশিয়ান অভিধান, মস্কো, 1999] বৈদ্যুতিক প্রকৌশল বিষয়, মৌলিক ধারণা EN একক পয়েন্ট ... প্রযুক্তিগত অনুবাদকের হ্যান্ডবুক

1) একটি বিশ্লেষণাত্মক ফাংশন f(z) এর একটি OT এই ভেরিয়েবলের সমতলে কিছু পাথ বরাবর একটি জটিল ভেরিয়েবল z এর ফাংশন f(z) এর একটি উপাদানের বিশ্লেষণাত্মক ধারাবাহিকতার একটি বাধা। বিশ্লেষণাত্মক ফাংশন f(z) কিছু দ্বারা সংজ্ঞায়িত করা যাক ... ... গাণিতিক বিশ্বকোষ

একটি বিশ্লেষণাত্মক ফাংশন, যে বিন্দুতে ফাংশনের বিশ্লেষণ লঙ্ঘন করা হয়। * * * একক বিন্দু একটি বিশ্লেষণাত্মক ফাংশনের একক বিন্দু, একটি বিন্দু যেখানে ফাংশনের বিশ্লেষণ লঙ্ঘন করা হয় ... বিশ্বকোষীয় অভিধান

একক বিন্দু- ypatingasis taškas statusas T sritis automatika atitikmenys: engl. একক পয়েন্ট vok. singularer Punkt, m rus. একবচন বিন্দু, fpranc. বিন্দু কণা, m; পয়েন্ট singulier, m … Automatikos terminų žodynas