Емтихан формуласының логарифмдері. Логарифмдердің негізгі қасиеттері

b санының а негізі үшін логарифмі b санын алу үшін а санын көтеру керек көрсеткіш.

Егер, онда.

Логарифм – экстремалды маңызды математикалық шама, өйткені логарифмдік есептеу көрсеткіштік теңдеулерді шешуге ғана емес, сонымен қатар дәрежелермен жұмыс істеуге, көрсеткіштік және логарифмдік функцияларды дифференциациялауға, оларды интегралдауға және есептеуге қолайлырақ пішінге апаруға мүмкіндік береді.

Байланыста

Логарифмдердің барлық қасиеттері көрсеткіштік функциялардың қасиеттерімен тікелей байланысты. Мысалы, бұл факт мынаны білдіреді:

Нақты есептерді шешу кезінде логарифмдердің қасиеттері дәрежелермен жұмыс істеу ережелеріне қарағанда маңыздырақ және пайдалы болуы мүмкін екенін атап өткен жөн.

Кейбір сәйкестіктерді көрсетейік:

Мұнда негізгі алгебралық өрнектер берілген:

;

.

Назар аударыңыз! x>0, x≠1, y>0 үшін ғана болуы мүмкін.

Натурал логарифмдер дегеніміз не деген сұрақты түсінуге тырысайық. Математикаға ерекше қызығушылық екі түрін көрсетеді- біріншісінің негізі ретінде «10» саны бар және «ондық логарифм» деп аталады. Екіншісі табиғи деп аталады. Натурал логарифмнің негізі «е» саны. Бұл туралы біз осы мақалада егжей-тегжейлі айтатын боламыз.

Белгілері:

• lg x - ондық;
• ln x - табиғи.

Сәйкестікті пайдалана отырып, біз ln e = 1 екенін, сонымен қатар lg 10=1 екенін көреміз.

Натурал логарифм графигі

Нүкте бойынша стандартты классикалық әдісті қолданып, натурал логарифмнің графигін тұрғызайық. Қаласаңыз, функцияны тексеру арқылы функцияны дұрыс құрастырып жатқанымызды тексеруге болады. Дегенмен, логарифмді қалай дұрыс есептеу керектігін білу үшін оны «қолмен» құруды үйрену мағынасы бар.

Функция: y = ln x. График өтетін нүктелер кестесін жазайық:

Неліктен х аргументінің осы нақты мәндерін таңдағанымызды түсіндіріп көрейік. Мұның бәрі жеке басына қатысты: . Табиғи логарифм үшін бұл сәйкестік келесідей болады:

Ыңғайлы болу үшін біз бес анықтамалық нүктені аламыз:

;

;

.

;

.

Осылайша, натурал логарифмдерді есептеу өте қарапайым міндет, сонымен қатар ол қуаттармен операцияларды есептеуді жеңілдетеді, оларды қарапайым көбейту.

Графикті нүкте бойынша салу арқылы біз шамамен графикті аламыз:

Натурал логарифмді анықтау облысы (яғни X аргументінің барлық жарамды мәндері) нөлден үлкен барлық сандар.

Назар аударыңыз!Натурал логарифмнің анықталу облысы тек оң сандарды қамтиды! Анықтау аумағына x=0 кірмейді. Бұл логарифмнің бар болу шарттарына байланысты мүмкін емес.

Мәндер ауқымы (яғни y = ln x функциясының барлық жарамды мәндері) интервалдағы барлық сандар.

Табиғи журнал шегі

Графикті зерттей отырып, сұрақ туындайды - функция y кезінде қалай әрекет етеді<0.

Әлбетте, функцияның графигі у осін кесіп өтуге бейім, бірақ мұны істей алмайды, өйткені х-тің табиғи логарифмі<0 не существует.

Табиғи шек журналбылай жазуға болады:

Логарифм негізін ауыстыру формуласы

Табиғи логарифммен жұмыс істеу ерікті негізі бар логарифммен жұмыс істеуден әлдеқайда оңай. Сондықтан біз кез келген логарифмді натуралға келтіруді немесе оны табиғи логарифмдер арқылы ерікті негізге өрнектеуді үйренуге тырысамыз.

Логарифмдік сәйкестіктен бастайық:

Сонда кез келген сан немесе айнымалы у келесі түрде ұсынылуы мүмкін:

мұндағы х – кез келген сан (логарифмнің қасиеттері бойынша оң).

Бұл өрнекті екі жағынан да логарифмдік түрде алуға болады. Мұны ерікті z негізін қолданып көрейік:

Мүлікті қолданайық («c» орнына ғана бізде өрнек бар):

Осы жерден біз әмбебап формуланы аламыз:

.

Атап айтқанда, егер z=e болса, онда:

.

Біз екі натурал логарифмнің қатынасы арқылы логарифмді ерікті негізге бере алдық.

Біз проблемаларды шешеміз

Натурал логарифмдерді жақсы түсіну үшін бірнеше есептердің мысалдарын қарастырайық.

Мәселе 1. ln x = 3 теңдеуін шешу керек.

Шешімі:Логарифмнің анықтамасын пайдаланып: егер , онда , біз аламыз:

Мәселе 2. (5 + 3 * ln (x - 3)) = 3 теңдеуін шешіңіз.

Шешуі: Логарифмнің анықтамасын пайдаланып: егер , онда , аламыз:

.

Логарифмнің анықтамасын қайтадан қолданайық:

.

Осылайша:

.

Жауапты шамамен есептей аласыз немесе оны осы пішінде қалдыра аласыз.

3-тапсырма.Теңдеуді шеш.

Шешімі:Ауыстыруды жасайық: t = ln x. Сонда теңдеу келесі форманы алады:

.

Бізде квадрат теңдеу бар. Оның дискриминантын табайық:

Статистикада және ықтималдықтар теориясында логарифмдік шамалар өте жиі кездеседі. Бұл таңқаларлық емес, өйткені e саны көбінесе экспоненциалды шамалардың өсу қарқынын көрсетеді.

Информатикада, бағдарламалауда және компьютерлік теорияда логарифмдер жиі кездеседі, мысалы, жадта N биттерді сақтау үшін.

Фракталдар мен өлшемдер теорияларында логарифмдер үнемі қолданылады, өйткені фракталдардың өлшемдері тек олардың көмегімен анықталады.

Механика мен физикадаЛогарифмдер қолданылмаған бөлім жоқ. Барометрлік үлестірім, статистикалық термодинамиканың барлық принциптері, Циолковский теңдеуі және т.б. тек логарифмдерді қолдану арқылы математикалық сипаттауға болатын процестер.

Химияда логарифмдер Нернст теңдеуінде және тотығу-тотықсыздану процестерін сипаттауда қолданылады.

Таңқаларлық, тіпті музыкада октаваның бөліктерінің санын білу үшін логарифмдер қолданылады.

Натурал логарифм Функция y=ln x оның қасиеттері

Натурал логарифмнің негізгі қасиетін дәлелдеу

негізгі қасиеттері.

1. логакс + логай = лога(х у);
2. логакс − логая = лога (х: у).

бірдей негіздер

Log6 4 + log6 9.

Енді тапсырманы сәл күрделендіріп көрейік.

Логарифмдерді шешу мысалдары

Логарифмнің негізі немесе аргументі дәреже болса ше? Сонда бұл дәреже көрсеткішін логарифм таңбасынан келесі ережелер бойынша шығаруға болады:

Әрине, егер логарифмнің ODZ сақталса, бұл ережелердің барлығы мағыналы болады: a > 0, a ≠ 1, x >

Тапсырма. Өрнектің мағынасын табыңыз:

Жаңа негізге көшу

Логарифмдік логаксы берілсін. Сонда c > 0 және c ≠ 1 болатын кез келген c саны үшін теңдік ақиқат болады:

Тапсырма. Өрнектің мағынасын табыңыз:

Сондай-ақ қараңыз:

Логарифмнің негізгі қасиеттері

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.

Көрсеткіш 2,718281828…. Көрсеткішті есте сақтау үшін ережені зерделеуге болады: көрсеткіш 2,7-ге тең және Лев Николаевич Толстойдың туған жылына екі есе.

Логарифмдердің негізгі қасиеттері

Бұл ережені біле отырып, сіз көрсеткіштің нақты мәнін де, Лев Толстойдың туған күнін де білесіз.

Логарифмдерге мысалдар

Логарифмдік өрнектер

1-мысал.
A). x=10ac^2 (a>0,c>0).

3.5 қасиеттерін пайдаланып есептейміз

2.

3.

4. Қайда .

Мысал 2. Егер x мәнін табыңыз

Мысал 3. Логарифмдердің мәні берілсін

log(x) есептеңіз, егер

Логарифмдердің негізгі қасиеттері

Логарифмдерді кез келген сандар сияқты қосуға, азайтуға және түрлендіруге болады. Бірақ логарифмдер дәл қарапайым сандар емес болғандықтан, мұнда шақырылатын ережелер бар негізгі қасиеттері.

Сіз бұл ережелерді білуіңіз керек - оларсыз бірде-бір маңызды логарифмдік мәселені шешу мүмкін емес. Сонымен қатар, олардың саны өте аз - сіз бір күнде бәрін біле аласыз. Ендеше, бастайық.

Логарифмдерді қосу және азайту

Негіздері бірдей екі логарифмді қарастырайық: логакс және лога. Содан кейін оларды қосуға және азайтуға болады, және:

1. логакс + логай = лога(х у);
2. логакс − логая = лога (х: у).

Сонымен, логарифмдердің қосындысы көбейтіндінің логарифміне тең, ал айырмасы бөліктің логарифміне тең. Назар аударыңыз: мұнда негізгі мәселе бірдей негіздер. Себептер әртүрлі болса, бұл ережелер жұмыс істемейді!

Бұл формулалар логарифмдік өрнекті оның жеке бөліктері ескерілмегенде де есептеуге көмектеседі («Логарифм дегеніміз не» сабағын қараңыз). Мысалдарды қарап шығыңыз және қараңыз:

Логарифмдердің негіздері бірдей болғандықтан, біз қосынды формуласын қолданамыз:
log6 4 + log6 9 = log6 (4 9) = log6 36 = 2.

Тапсырма. Өрнектің мәнін табыңыз: log2 48 − log2 3.

Негіздер бірдей, біз айырмашылық формуласын қолданамыз:
log2 48 − log2 3 = log2 (48: 3) = log2 16 = 4.

Тапсырма. Өрнектің мәнін табыңыз: log3 135 − log3 5.

Тағы да негіздер бірдей, сондықтан бізде:
log3 135 − log3 5 = log3 (135: 5) = log3 27 = 3.

Көріп отырғаныңыздай, бастапқы өрнектер бөлек есептелмейтін «жаман» логарифмдерден тұрады. Бірақ түрлендірулерден кейін толығымен қалыпты сандар алынады. Көптеген сынақтар осы фактіге негізделген. Иә, Бірыңғай мемлекеттік емтиханда сынаққа ұқсас өрнектер барлық маңыздылығымен (кейде іс жүзінде ешқандай өзгеріссіз) ұсынылады.

Логарифмадан дәреже көрсеткішін шығару

Соңғы ереже алғашқы екеуіне сәйкес келетінін байқау қиын емес. Бірақ бәрібір оны есте ұстаған жөн - кейбір жағдайларда бұл есептеулердің көлемін айтарлықтай азайтады.

Әрине, егер логарифмнің ODZ сақталса, бұл ережелердің барлығы мағынасы бар: a > 0, a ≠ 1, x > 0. Және тағы бір нәрсе: барлық формулаларды солдан оңға қарай ғана емес, сонымен қатар керісінше қолдануды үйреніңіз. , яғни. Логарифмнің өзіне логарифм белгісінің алдындағы сандарды енгізуге болады. Бұл ең жиі талап етілетін нәрсе.

Тапсырма. Өрнектің мәнін табыңыз: log7 496.

Бірінші формуланы пайдаланып дәлелдегі дәрежеден құтылайық:
log7 496 = 6 log7 49 = 6 2 = 12

Тапсырма. Өрнектің мағынасын табыңыз:

Бөлгіште негізі мен аргументі дәл дәрежелер болатын логарифм бар екенін ескеріңіз: 16 = 24; 49 = 72. Бізде:

Менің ойымша, соңғы мысал кейбір нақтылауды қажет етеді. Логарифмдер қайда кетті? Соңғы сәтке дейін біз тек бөлгішпен жұмыс істейміз.

Логарифм формулалары. Логарифмдерді шешуге мысалдар.

Біз сол жерде тұрған логарифмнің негізі мен аргументін дәрежелер түрінде ұсынып, дәрежелерді алып тастадық - біз «үш қабатты» бөлшек алдық.

Енді бас бөлшекті қарастырайық. Алым мен бөлгіште бірдей сан бар: log2 7. log2 7 ≠ 0 болғандықтан, біз бөлшекті азайта аламыз - 2/4 бөлгіште қалады. Арифметика ережелері бойынша төртеуін алымға көшіруге болады, бұл орындалды. Нәтиже келесідей болды: 2.

Жаңа негізге көшу

Логарифмдерді қосу және азайту ережелері туралы айта отырып, мен олардың тек бірдей негіздермен жұмыс істейтінін ерекше атап өттім. Себептер әртүрлі болса ше? Егер олар бірдей санның дәл дәрежелері болмаса ше?

Жаңа іргетасқа өту формулалары көмекке келеді. Оларды теорема түрінде тұжырымдаймыз:

Логарифмдік логаксы берілсін. Сонда c > 0 және c ≠ 1 болатын кез келген c саны үшін теңдік ақиқат болады:

Атап айтқанда, егер c = x орнатсақ, біз мынаны аламыз:

Екінші формуладан логарифмнің негізі мен аргументін ауыстыруға болатыны шығады, бірақ бұл жағдайда бүкіл өрнек «аударылады», яғни. логарифм бөлгіште пайда болады.

Бұл формулалар қарапайым сандық өрнектерде сирек кездеседі. Олардың қаншалықты ыңғайлы екенін логарифмдік теңдеулер мен теңсіздіктерді шешкенде ғана бағалауға болады.

Дегенмен, жаңа іргетасқа көшуден басқа мүлде шешілмейтін мәселелер бар. Осылардың бірнешеуін қарастырайық:

Тапсырма. Өрнектің мәнін табыңыз: log5 16 log2 25.

Екі логарифмнің аргументтері дәл дәрежелерді қамтитынын ескеріңіз. Көрсеткіштерді шығарайық: log5 16 = log5 24 = 4log5 2; log2 25 = log2 52 = 2log2 5;

Енді екінші логарифмді «кері» көрсетейік:

Көбейткіштерді қайта орналастыру кезінде көбейтінді өзгермейтіндіктен, біз төрт пен екіні тыныштықпен көбейттік, содан кейін логарифмдермен айналыстық.

Тапсырма. Өрнектің мәнін табыңыз: log9 100 lg 3.

Бірінші логарифмнің негізі мен аргументі дәл дәрежелер болып табылады. Осыны жазып, көрсеткіштерден арылайық:

Енді жаңа негізге көшу арқылы ондық логарифмадан құтылайық:

Негізгі логарифмдік сәйкестік

Көбінесе шешу процесінде санды берілген негізге логарифм түрінде көрсету қажет. Бұл жағдайда бізге келесі формулалар көмектеседі:

Бірінші жағдайда n саны аргументтегі көрсеткішке айналады. n саны мүлдем кез келген болуы мүмкін, себебі бұл жай ғана логарифмдік мән.

Екінші формула шын мәнінде қайталанған анықтама болып табылады. Ол осылай аталады: .

Шындығында, егер b саны осы дәрежедегі b саны а санын беретіндей дәрежеге көтерілсе не болады? Дұрыс: нәтиже бірдей а саны. Осы абзацты қайтадан мұқият оқып шығыңыз - көптеген адамдар оған жабысып қалады.

Жаңа негізге көшу формулалары сияқты, негізгі логарифмдік сәйкестік кейде жалғыз мүмкін шешім болып табылады.

Тапсырма. Өрнектің мағынасын табыңыз:

Log25 64 = log5 8 - жай ғана логарифмнің негізі мен аргументінен шаршыны алғанын ескеріңіз. Дәрежелерді бірдей негізге көбейту ережелерін ескере отырып, біз аламыз:

Егер біреу білмесе, бұл Бірыңғай мемлекеттік емтиханның нақты тапсырмасы болды :)

Логарифмдік бірлік және логарифмдік нөл

Қорытындылай келе, мен қасиеттер деп атауға болмайтын екі сәйкестікті беремін - дәлірек айтқанда, олар логарифмді анықтаудың салдары. Олар үнемі проблемаларда пайда болады және таңқаларлық, тіпті «озық» студенттер үшін де қиындықтар тудырады.

1. logaa = 1. Бір рет және мәңгі есте сақтаңыз: сол негіздің кез келген а негізінің логарифмінің өзі бірге тең.
2. Лога 1 = 0. a негізі кез келген нәрсе болуы мүмкін, бірақ аргумент бір болса, логарифм нөлге тең! Өйткені a0 = 1 анықтаманың тікелей салдары болып табылады.

Міне, барлық қасиеттер. Міндетті түрде оларды іс жүзінде қолдануды үйреніңіз! Сабақтың басында көшірме парағын жүктеп алыңыз, оны басып шығарыңыз және мәселелерді шешіңіз.

Сондай-ақ қараңыз:

a негізіне b-ның логарифмі өрнекті білдіреді. Логарифмді есептеу дегеніміз теңдігі орындалатын х () дәрежесін табу

Логарифмнің негізгі қасиеттері

Жоғарыда аталған қасиеттерді білу қажет, өйткені логарифмдерге қатысты барлық дерлік есептер мен мысалдар солардың негізінде шешіледі. Қалған экзотикалық қасиеттерді осы формулалармен математикалық манипуляциялар арқылы алуға болады

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.

Логарифмдердің қосындысы мен айырмасының формуласын есептеген кезде (3.4) жиі кездеседі. Қалғандары біршама күрделі, бірақ бірқатар тапсырмаларда олар күрделі өрнектерді жеңілдету және олардың мәндерін есептеу үшін өте қажет.

Логарифмдердің жалпы жағдайлары

Кейбір қарапайым логарифмдерге негізі тіпті он, экспоненциалды немесе екі болатын логарифмдер жатады.
Ондық негізге логарифм әдетте ондық логарифм деп аталады және жай lg(x) арқылы белгіленеді.

Жазбада негіздердің жазылмағаны жазбадан көрініп тұр. Мысалы үшін

Табиғи логарифм – негізі көрсеткіші болатын логарифм (ln(x) арқылы белгіленеді).

Көрсеткіш 2,718281828…. Көрсеткішті есте сақтау үшін ережені зерделеуге болады: көрсеткіш 2,7-ге тең және Лев Николаевич Толстойдың туған жылына екі есе. Бұл ережені біле отырып, сіз көрсеткіштің нақты мәнін де, Лев Толстойдың туған күнін де білесіз.

Ал екі негізі үшін тағы бір маңызды логарифм арқылы белгіленеді

Функцияның логарифмінің туындысы айнымалыға бөлінгенге тең

Интегралдық немесе антитуынды логарифм қатынас арқылы анықталады

Берілген материал логарифмдер мен логарифмдерге қатысты есептердің кең класын шешуге жеткілікті. Материалды түсінуге көмектесу үшін мен мектеп бағдарламасы мен университеттерден бірнеше жалпы мысалдар келтіремін.

Логарифмдерге мысалдар

Логарифмдік өрнектер

1-мысал.
A). x=10ac^2 (a>0,c>0).

3.5 қасиеттерін пайдаланып есептейміз

2.
Логарифмдердің айырым қасиеті бойынша бізде

3.
3.5 қасиеттерін пайдаланып табамыз

4. Қайда .

Күрделі болып көрінетін өрнек бірнеше ережелерді қолдану арқылы оңайлатылған

Логарифм мәндерін табу

Мысал 2. Егер x мәнін табыңыз

Шешім. Есептеу үшін біз соңғы 5 және 13 қасиеттерді қолданамыз

Біз оны қағазға түсіріп, жоқтаймыз

Негіздері тең болғандықтан, өрнектерді теңестіреміз

Логарифмдер. Бастапқы деңгей.

Логарифмдердің мәні берілсін

log(x) есептеңіз, егер

Шешуі: Логарифмді оның мүшелерінің қосындысы арқылы жазу үшін айнымалының логарифмін алайық.

Бұл логарифмдермен және олардың қасиеттерімен танысуымыздың басы ғана. Есептеуге машықтаныңыз, практикалық дағдыларыңызды байытыңыз - сізге логарифмдік теңдеулерді шешу үшін жақын арада алған білім қажет болады. Осындай теңдеулерді шешудің негізгі әдістерін зерттей отырып, біз сіздің біліміңізді тағы бір маңызды тақырыпқа - логарифмдік теңсіздіктерге кеңейтеміз...

Логарифмдердің негізгі қасиеттері

Логарифмдерді кез келген сандар сияқты қосуға, азайтуға және түрлендіруге болады. Бірақ логарифмдер дәл қарапайым сандар емес болғандықтан, мұнда шақырылатын ережелер бар негізгі қасиеттері.

Сіз бұл ережелерді білуіңіз керек - оларсыз бірде-бір маңызды логарифмдік мәселені шешу мүмкін емес. Сонымен қатар, олардың саны өте аз - сіз бір күнде бәрін біле аласыз. Ендеше, бастайық.

Логарифмдерді қосу және азайту

Негіздері бірдей екі логарифмді қарастырайық: логакс және лога. Содан кейін оларды қосуға және азайтуға болады, және:

1. логакс + логай = лога(х у);
2. логакс − логая = лога (х: у).

Сонымен, логарифмдердің қосындысы көбейтіндінің логарифміне тең, ал айырмасы бөліктің логарифміне тең. Назар аударыңыз: мұнда негізгі мәселе бірдей негіздер. Себептер әртүрлі болса, бұл ережелер жұмыс істемейді!

Бұл формулалар логарифмдік өрнекті оның жеке бөліктері ескерілмегенде де есептеуге көмектеседі («Логарифм дегеніміз не» сабағын қараңыз). Мысалдарды қарап шығыңыз және қараңыз:

Тапсырма. Өрнектің мәнін табыңыз: log6 4 + log6 9.

Логарифмдердің негіздері бірдей болғандықтан, біз қосынды формуласын қолданамыз:
log6 4 + log6 9 = log6 (4 9) = log6 36 = 2.

Тапсырма. Өрнектің мәнін табыңыз: log2 48 − log2 3.

Негіздер бірдей, біз айырмашылық формуласын қолданамыз:
log2 48 − log2 3 = log2 (48: 3) = log2 16 = 4.

Тапсырма. Өрнектің мәнін табыңыз: log3 135 − log3 5.

Тағы да негіздер бірдей, сондықтан бізде:
log3 135 − log3 5 = log3 (135: 5) = log3 27 = 3.

Көріп отырғаныңыздай, бастапқы өрнектер бөлек есептелмейтін «жаман» логарифмдерден тұрады. Бірақ түрлендірулерден кейін толығымен қалыпты сандар алынады. Көптеген сынақтар осы фактіге негізделген. Иә, Бірыңғай мемлекеттік емтиханда сынаққа ұқсас өрнектер барлық маңыздылығымен (кейде іс жүзінде ешқандай өзгеріссіз) ұсынылады.

Логарифмадан дәреже көрсеткішін шығару

Енді тапсырманы сәл күрделендіріп көрейік. Логарифмнің негізі немесе аргументі дәреже болса ше? Сонда бұл дәреже көрсеткішін логарифм таңбасынан келесі ережелер бойынша шығаруға болады:

Соңғы ереже алғашқы екеуіне сәйкес келетінін байқау қиын емес. Бірақ бәрібір оны есте ұстаған жөн - кейбір жағдайларда бұл есептеулердің көлемін айтарлықтай азайтады.

Әрине, егер логарифмнің ODZ сақталса, бұл ережелердің барлығы мағынасы бар: a > 0, a ≠ 1, x > 0. Және тағы бір нәрсе: барлық формулаларды солдан оңға қарай ғана емес, сонымен қатар керісінше қолдануды үйреніңіз. , яғни. Логарифмнің өзіне логарифм белгісінің алдындағы сандарды енгізуге болады.

Логарифмдерді шешу жолдары

Бұл ең жиі талап етілетін нәрсе.

Тапсырма. Өрнектің мәнін табыңыз: log7 496.

Бірінші формуланы пайдаланып дәлелдегі дәрежеден құтылайық:
log7 496 = 6 log7 49 = 6 2 = 12

Тапсырма. Өрнектің мағынасын табыңыз:

Бөлгіште негізі мен аргументі дәл дәрежелер болатын логарифм бар екенін ескеріңіз: 16 = 24; 49 = 72. Бізде:

Менің ойымша, соңғы мысал кейбір нақтылауды қажет етеді. Логарифмдер қайда кетті? Соңғы сәтке дейін біз тек бөлгішпен жұмыс істейміз. Біз сол жерде тұрған логарифмнің негізі мен аргументін дәрежелер түрінде ұсынып, дәрежелерді алып тастадық - біз «үш қабатты» бөлшек алдық.

Енді бас бөлшекті қарастырайық. Алым мен бөлгіште бірдей сан бар: log2 7. log2 7 ≠ 0 болғандықтан, біз бөлшекті азайта аламыз - 2/4 бөлгіште қалады. Арифметика ережелері бойынша төртеуін алымға көшіруге болады, бұл орындалды. Нәтиже келесідей болды: 2.

Жаңа негізге көшу

Логарифмдерді қосу және азайту ережелері туралы айта отырып, мен олардың тек бірдей негіздермен жұмыс істейтінін ерекше атап өттім. Себептер әртүрлі болса ше? Егер олар бірдей санның дәл дәрежелері болмаса ше?

Жаңа іргетасқа өту формулалары көмекке келеді. Оларды теорема түрінде тұжырымдаймыз:

Логарифмдік логаксы берілсін. Сонда c > 0 және c ≠ 1 болатын кез келген c саны үшін теңдік ақиқат болады:

Атап айтқанда, егер c = x орнатсақ, біз мынаны аламыз:

Екінші формуладан логарифмнің негізі мен аргументін ауыстыруға болатыны шығады, бірақ бұл жағдайда бүкіл өрнек «аударылады», яғни. логарифм бөлгіште пайда болады.

Бұл формулалар қарапайым сандық өрнектерде сирек кездеседі. Олардың қаншалықты ыңғайлы екенін логарифмдік теңдеулер мен теңсіздіктерді шешкенде ғана бағалауға болады.

Дегенмен, жаңа іргетасқа көшуден басқа мүлде шешілмейтін мәселелер бар. Осылардың бірнешеуін қарастырайық:

Тапсырма. Өрнектің мәнін табыңыз: log5 16 log2 25.

Екі логарифмнің аргументтері дәл дәрежелерді қамтитынын ескеріңіз. Көрсеткіштерді шығарайық: log5 16 = log5 24 = 4log5 2; log2 25 = log2 52 = 2log2 5;

Енді екінші логарифмді «кері» көрсетейік:

Көбейткіштерді қайта орналастыру кезінде көбейтінді өзгермейтіндіктен, біз төрт пен екіні тыныштықпен көбейттік, содан кейін логарифмдермен айналыстық.

Тапсырма. Өрнектің мәнін табыңыз: log9 100 lg 3.

Бірінші логарифмнің негізі мен аргументі дәл дәрежелер болып табылады. Осыны жазып, көрсеткіштерден арылайық:

Енді жаңа негізге көшу арқылы ондық логарифмадан құтылайық:

Негізгі логарифмдік сәйкестік

Көбінесе шешу процесінде санды берілген негізге логарифм түрінде көрсету қажет. Бұл жағдайда бізге келесі формулалар көмектеседі:

Бірінші жағдайда n саны аргументтегі көрсеткішке айналады. n саны мүлдем кез келген болуы мүмкін, себебі бұл жай ғана логарифмдік мән.

Екінші формула шын мәнінде қайталанған анықтама болып табылады. Ол осылай аталады: .

Шындығында, егер b саны осы дәрежедегі b саны а санын беретіндей дәрежеге көтерілсе не болады? Дұрыс: нәтиже бірдей а саны. Осы абзацты қайтадан мұқият оқып шығыңыз - көптеген адамдар оған жабысып қалады.

Жаңа негізге көшу формулалары сияқты, негізгі логарифмдік сәйкестік кейде жалғыз мүмкін шешім болып табылады.

Тапсырма. Өрнектің мағынасын табыңыз:

Log25 64 = log5 8 - жай ғана логарифмнің негізі мен аргументінен шаршыны алғанын ескеріңіз. Дәрежелерді бірдей негізге көбейту ережелерін ескере отырып, біз аламыз:

Егер біреу білмесе, бұл Бірыңғай мемлекеттік емтиханның нақты тапсырмасы болды :)

Логарифмдік бірлік және логарифмдік нөл

Қорытындылай келе, мен қасиеттер деп атауға болмайтын екі сәйкестікті беремін - дәлірек айтқанда, олар логарифмді анықтаудың салдары. Олар үнемі проблемаларда пайда болады және таңқаларлық, тіпті «озық» студенттер үшін де қиындықтар тудырады.

1. logaa = 1. Бір рет және мәңгі есте сақтаңыз: сол негіздің кез келген а негізінің логарифмінің өзі бірге тең.
2. Лога 1 = 0. a негізі кез келген нәрсе болуы мүмкін, бірақ аргумент бір болса, логарифм нөлге тең! Өйткені a0 = 1 анықтаманың тікелей салдары болып табылады.

Міне, барлық қасиеттер. Міндетті түрде оларды іс жүзінде қолдануды үйреніңіз! Сабақтың басында көшірме парағын жүктеп алыңыз, оны басып шығарыңыз және мәселелерді шешіңіз.

(грек тілінен аударғанда λόγος - «сөз», «қатыс» және ἀριθμός - «сан») сандар бнегізделген а(журнал α б) мұндай сан деп аталады в, Және б= а с, яғни α журналын жазады б=вЖәне b=aвэквивалентті болып табылады. Логарифм мағынасы болады, егер a > 0, a ≠ 1, b > 0.

Басқа сөздермен айтқанда логарифмсандар бнегізделген Асанды көтеру керек көрсеткіш ретінде тұжырымдалған анөмірін алу үшін б(логарифм тек оң сандар үшін бар).

Бұл тұжырымнан x= log α есебі шығады б, a x =b теңдеуін шешуге тең.

Мысалы:

log 2 8 = 3, себебі 8 = 2 3.

Логарифмнің көрсетілген тұжырымы бірден анықтауға мүмкіндік беретінін атап өтейік логарифм мәні, логарифм таңбасының астындағы сан негіздің белгілі бір дәрежесі ретінде әрекет еткенде. Шынында да, логарифмді тұжырымдау егер болса, оны негіздеуге мүмкіндік береді b=a c, содан кейін санның логарифмі бнегізделген атең бірге. Логарифм тақырыбы да тақырыппен тығыз байланысты екені анық санның дәрежелері.

Логарифмді есептеу деп аталады логарифм. Логарифм – логарифм алудың математикалық операциясы. Логарифмдерді қабылдағанда көбейткіштердің көбейтінділері мүшелердің қосындыларына түрлендіріледі.

Потенциациялогарифмге кері математикалық операция болып табылады. Потенциалдау кезінде берілген база потенциация орындалатын өрнек дәрежесіне дейін көтеріледі. Бұл жағдайда терминдердің қосындылары факторлардың туындысына айналады.

Көбінесе нақты логарифмдер 2 (екілік), Эйлер саны e ≈ 2,718 (натурал логарифм) және 10 (ондық) негіздерімен қолданылады.

Бұл кезеңде қарастырған жөн логарифм үлгілеріжурнал 7 2 , лн √ 5, lg0,0001.

Ал lg(-3), log -3 3.2, log -1 -4.3 жазбалары мағынасы жоқ, өйткені олардың біріншісінде теріс сан логарифм таңбасының астына қойылады, екіншісінде теріс сан бар. негізде, ал үшіншісінде логарифм таңбасының астында теріс сан және негізде бірлігі бар.

Логарифмді анықтау шарттары.

a > 0, a ≠ 1, b > 0 шарттарын бөлек қарастырған жөн. логарифмнің анықтамасы.Бұл шектеулердің неліктен қабылданғанын қарастырайық. Бұған x = log α түріндегі теңдік көмектеседі б, жоғарыда келтірілген логарифм анықтамасынан тікелей шығатын негізгі логарифмдік сәйкестік деп аталады.

Шартты алайық a≠1. Кез келген дәреже бірге тең болғандықтан, онда x=log α теңдігі бкезде ғана болуы мүмкін b=1, бірақ журнал 1 1 кез келген нақты сан болады. Бұл екіұштылықты жою үшін біз қабылдаймыз a≠1.

Шарттың қажеттілігін дәлелдеп көрейік a>0. Сағат a=0логарифмнің тұжырымы бойынша болғанда ғана болуы мүмкін b=0. Және сәйкесінше журнал 0 0кез келген нөлге тең емес нақты сан болуы мүмкін, өйткені нөлден нөлге тең емес кез келген дәреже нөлге тең. Бұл екіұштылықты шарт арқылы жоюға болады a≠0. Және қашан а<0 логарифмнің рационал және иррационал мәндерін талдаудан бас тартуға тура келеді, өйткені рационал және иррационал көрсеткіші бар дәреже тек теріс емес негіздер үшін анықталады. Сол себепті шарт қойылып отыр a>0.

Және соңғы шарт b>0теңсіздіктен туындайды a>0, өйткені x=log α б, және оң базасы бар дәреженің мәні аәрқашан позитивті.

Логарифмдердің ерекшеліктері.

Логарифмдеререкшелігімен сипатталады Ерекше өзгешеліктері, бұл олардың күрделі есептеулерді айтарлықтай жеңілдету үшін кеңінен қолданылуына әкелді. «Логарифмдер әлеміне» көшу кезінде көбейту әлдеқайда оңай қосуға, бөлу азайтуға, ал дәреже және түбір шығару сәйкесінше дәрежеге көбейтуге және бөлуге түрленеді.

Логарифмдердің тұжырымы және олардың мәндерінің кестесі (тригонометриялық функциялар үшін) алғаш рет 1614 жылы шотланд математигі Джон Непьермен жарияланған. Басқа ғалымдар үлкейтілген және егжей-тегжейлі келтірген логарифмдік кестелер ғылыми және инженерлік есептеулерде кеңінен қолданылып, электронды есептеуіш машиналар мен есептеуіш машиналар қолданылғанға дейін өзектілігін сақтап қалды.

a (a>0, a 1-ге тең емес) негізіне оң b санының логарифмі a c = b болатындай c саны: log a b = c ⇔ a c = b (a > 0, a ≠ 1, b) > 0)       

Оң емес санның логарифмі анықталмағанын ескеріңіз. Сонымен қатар, логарифмнің негізі 1-ге тең емес оң сан болуы керек. Мысалы, егер -2 квадратын алсақ, 4 санын аламыз, бірақ бұл логарифм 4-тің негізіне -2 дегенді білдірмейді. 2-ге тең.

Негізгі логарифмдік сәйкестік

a log a b = b (a > 0, a ≠ 1) (2)

Бұл формуланың оң және сол жақтарын анықтау көлемі әртүрлі болуы маңызды. Сол жағы тек b>0, a>0 және a ≠ 1 үшін анықталады. Оң жағы кез келген b үшін анықталады және а-ға мүлдем тәуелді емес. Осылайша, теңдеулер мен теңсіздіктерді шешу кезінде негізгі логарифмдік «тұлғаны» қолдану ОД өзгеруіне әкелуі мүмкін.

Логарифмді анықтаудың екі айқын салдары

log a a = 1 (a > 0, a ≠ 1) (3)
log a 1 = 0 (a > 0, a ≠ 1) (4)

Шынында да, а санын бірінші дәрежеге көтергенде, біз бірдей сан аламыз, ал нөлдік дәрежеге көтергенде, біз аламыз.

Көбейтіндінің логарифмі және бөліндінің логарифмі

log a (b c) = log a b + log a c (a > 0, a ≠ 1, b > 0, c > 0) (5)

Log a b c = log a b − log a c (a > 0, a ≠ 1, b > 0, c > 0) (6)

Мектеп оқушыларын логарифмдік теңдеулер мен теңсіздіктерді шешуде бұл формулаларды ойланбай қолданудан сақтандырғым келеді. Оларды «солдан оңға қарай» пайдаланған кезде ОДЗ тарылады, ал логарифмдердің қосындысынан немесе айырмасынан көбейтіндінің немесе бөліктің логарифміне ауысқанда ОДЗ кеңейеді.

Шынында да, log a (f (x) g (x)) өрнегі екі жағдайда анықталады: екі функция да қатаң оң болғанда немесе f(x) және g(x) екеуі де нөлден кіші болғанда.

Бұл өрнекті log a f (x) + log a g (x) қосындысына түрлендіре отырып, біз f(x)>0 және g(x)>0 болған жағдаймен ғана шектелуге мәжбүр боламыз. Қолайлы мәндер диапазонының тарылуы бар және бұл мүлдем қолайсыз, өйткені бұл шешімдердің жоғалуына әкелуі мүмкін. Ұқсас мәселе (6) формула үшін де бар.

Дәрежені логарифмнің таңбасынан шығаруға болады

log a b p = p log a b (a > 0, a ≠ 1, b > 0) (7)

Мен тағы да дәлдікке шақырғым келеді. Келесі мысалды қарастырыңыз:

Log a (f (x) 2 = 2 log a f (x)

Теңдіктің сол жағы f(x) нөлден басқа барлық мәндер үшін анық анықталған. Оң жағы тек f(x)>0 үшін! Логарифмнен дәрежені алу арқылы біз ОДЗ-ны қайтадан тарылтамыз. Кері процедура қолайлы мәндер ауқымының кеңеюіне әкеледі. Бұл ескертулердің барлығы 2-ші қуатқа ғана емес, сонымен қатар кез келген біркелкі қуатқа да қатысты.

Жаңа негізге көшу формуласы

log a b = log c b log c a (a > 0, a ≠ 1, b > 0, c > 0, c ≠ 1) (8)

Трансформация кезінде ODZ өзгермейтін сирек жағдай. Егер сіз c негізін ақылмен таңдаған болсаңыз (оң және 1-ге тең емес), жаңа негізге көшу формуласы толығымен қауіпсіз.

Жаңа с негізі ретінде b санын таңдасақ, формуланың (8) маңызды ерекше жағдайын аламыз:

Log a b = 1 log b a (a > 0, a ≠ 1, b > 0, b ≠ 1) (9)

Логарифмдермен бірнеше қарапайым мысалдар

Мысал 1. Есептеңіз: log2 + log50.
Шешім. log2 + log50 = log100 = 2. Логарифмдердің қосындысын (5) формуласын және ондық логарифмнің анықтамасын қолдандық.

2-мысал. Есептеңіз: lg125/lg5.
Шешім. log125/log5 = log 5 125 = 3. Жаңа негізге көшу үшін формуланы қолдандық (8).

Логарифмдерге қатысты формулалар кестесі

a log a b = b (a > 0, a ≠ 1)

log a a = 1 (a > 0, a ≠ 1)

log a 1 = 0 (a > 0, a ≠ 1)

log a (b c) = log a b + log a c (a > 0, a ≠ 1, b > 0, c > 0)

log a b c = log a b − log a c (a > 0, a ≠ 1, b > 0, c > 0)

log a b p = p log a b (a > 0, a ≠ 1, b > 0)

log a b = log c b log c a (a > 0, a ≠ 1, b > 0, c > 0, c ≠ 1)

log a b = 1 log b a (a > 0, a ≠ 1, b > 0, b ≠ 1)

Логарифм оң сан N негізіне(б> 0, б 1 ) көрсеткіш деп аталады x , оған салу керекб Н алу үшін .

Логарифмдік белгілер:

Бұл жазба келесіге тең:b x = N .

Мысалдар: журнал 3 81 = 4, өйткені 3 4 = 81;

Журнал 1/3 27 = – 3, өйткені (1/3) - 3 = 3 3 = 27.

Жоғарыда келтірілген логарифм анықтамасын сәйкестендіру ретінде жазуға болады:

Логарифмдердің негізгі қасиеттері.

1) журнал б= 1 , өйткені б 1 = b.

б

2) журнал 1 = 0 , өйткені б 0 = 1 .

б

3) Көбейтіндінің логарифмі факторлардың логарифмдерінің қосындысына тең:

журнал( аб) = журнал а+ журнал б.

4) Бөліндінің логарифмі дивиденд пен бөлгіштің логарифмдерінің айырмасына тең:

журнал( а/б) = журнал а– журнал б.

5) Дәреженің логарифмі көрсеткіш пен оның табанының логарифмінің көбейтіндісіне тең:

журнал (б к ) = кжурнал б.

Бұл мүліктің салдары келесідей:түбірдің логарифмі түбірдің дәрежесіне бөлінген радикалды санның логарифміне тең:

6) Егер логарифмнің негізі дәреже болса, онда мән дәрежеге кері, журнал белгісінен шығаруға боладырифма:

Соңғы екі қасиет бір қасиетке біріктірілуі мүмкін:

7) Өтпелі модуль формуласы (яғни. e . бір негізден көшубасқа негізге логарифм):

Ерекше жағдайда қашан N=aбізде бар:

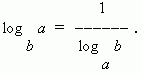
Ондық логарифм шақырды негізгі логарифм 10. Ол тағайындалған lg, яғни. журнал 10 Н = lg Н. 10, 100, 1000, ... сандарының логарифмдеріб сандар сәйкесінше 1, 2, 3, …анау. позитивтері көп

бірлік, логарифмдік санда бірден кейін неше нөл бар. 0,1, 0,01, 0,001, ... сандарының логарифмдеріб сәйкесінше –1, –2, –3, …, яғни. логарифмдік санда біреудің алдында нөл болса, сонша теріс болады ( санау және нөлдік бүтін сандар). Логарифмдер басқа сандар деп аталатын бөлшек бөлігі бар мантисса. Тұтаслогарифмнің бір бөлігі деп аталады тән. Практикалық қолдану үшінОндық логарифмдер ең қолайлы.

Натурал логарифм шақырды негізгі логарифм e. Ол тағайындалған ln, яғни. журнал eН = лн Н. Сан eқисынсыз, олжуық мән 2,718281828.Ол санның ұмтылатын шегі болып табылады(1 + 1 / n) n шексіз өсуменn(см. бірінші керемет шек ).
Біртүрлі көрінгенімен, натурал логарифмдер функцияларды талдауға байланысты әртүрлі операцияларды орындау кезінде өте ыңғайлы болып шықты.Логарифмдерді негізге есептеуeбасқа себептерге қарағанда әлдеқайда жылдам орындалады.