Wykładniczo lub wykładniczo. Postęp geometryczny. Obszerny przewodnik z przykładami (2020). Po co nam postęp geometryczny i jego historia

Rozważmy serię.

7 28 112 448 1792...

Jest absolutnie jasne, że wartość któregokolwiek z jego elementów jest dokładnie cztery razy większa niż poprzedniego. Więc ta seria to progresja.

Postęp geometryczny to nieskończony ciąg liczb, którego główną cechą jest to, że następną liczbę uzyskuje się z poprzedniej przez pomnożenie przez określoną liczbę. Wyraża się to następującym wzorem.

a z +1 =a z q, gdzie z jest numerem wybranego elementu.

Odpowiednio, z ∈ N.

Okres, w którym w szkole badany jest postęp geometryczny, to klasa 9. Przykłady pomogą ci zrozumieć koncepcję:

0.25 0.125 0.0625...

Na podstawie tego wzoru mianownik progresji można znaleźć w następujący sposób:

Ani q, ani b z nie mogą być równe zeru. Również żaden z elementów progresji nie powinien być równy zeru.

W związku z tym, aby znaleźć następną liczbę w serii, należy pomnożyć ostatnią liczbę przez q.

Aby określić tę progresję, musisz określić jej pierwszy element i mianownik. Następnie możliwe jest znalezienie dowolnego z kolejnych warunków i ich sumy.

Odmiany

W zależności od q i 1 progresja ta dzieli się na kilka typów:

• Jeśli zarówno 1, jak i q są większe od jedności, to taki ciąg jest postępem geometrycznym rosnącym z każdym kolejnym elementem. Przykład takiego przedstawiono poniżej.

Przykład: a 1 =3, q=2 - oba parametry są większe od jeden.

Następnie ciąg liczbowy można zapisać w następujący sposób:

3 6 12 24 48 ...

• Jeśli |q| mniej niż jeden, to znaczy mnożenie przez to jest równoważne dzieleniu, to postęp o podobnych warunkach jest malejącym postępem geometrycznym. Przykład takiego przedstawiono poniżej.

Przykład: a 1 = 6, q = 1/3 - a 1 jest większe niż jeden, q jest mniejsze.

Następnie ciąg liczbowy można zapisać w następujący sposób:

6 2 2/3 ... - dowolny element jest 3 razy większy niż element następujący po nim.

• Zmienna znakowa. jeśli q<0, то знаки у чисел последовательности постоянно чередуются вне зависимости от a 1 , а элементы ни возрастают, ни убывают.

Przykład: a 1 = -3 , q = -2 - oba parametry są mniejsze od zera.

Następnie sekwencję można zapisać w następujący sposób:

3, 6, -12, 24,...

Formuły

Aby wygodnie korzystać z postępów geometrycznych, istnieje wiele wzorów:

• Formuła z-tego członka. Pozwala obliczyć element pod określoną liczbą bez obliczania poprzednich liczb.

Przykład:Q = 3, A 1 = 4. Należy obliczyć czwarty element progresji.

Rozwiązanie:A 4 = 4 · 3 4-1 = 4 · 3 3 = 4 · 27 = 108.

• Suma pierwszych elementów, których liczba to z. Pozwala obliczyć sumę wszystkich elementów ciągu dozwłącznie.

Od (1-Q) jest w mianowniku, to (1 - q)≠ 0, stąd q nie jest równe 1.

Uwaga: jeśli q=1, to progresja byłaby serią nieskończenie powtarzającej się liczby.

Suma postępu geometrycznego, przykłady:A 1 = 2, Q= -2. Oblicz S 5 .

Rozwiązanie:S 5 = 22 - obliczenie według wzoru.

• Kwota, jeżeli |Q| < 1 и если z стремится к бесконечности.

Przykład:A 1 = 2 , Q= 0,5. Znajdź kwotę.

Rozwiązanie:Sz = 2 · = 4

Sz = 2 + 1 + 0.5 + 0.25 + 0.125 + 0.0625 = 3.9375 4

Niektóre właściwości:

• charakterystyczna właściwość. Jeśli następujący warunek wykonane dla dowolnegoz, to dany ciąg liczbowy jest postępem geometrycznym:

z 2 = z -1 · Az+1

• Również kwadrat dowolnej liczby ciągu geometrycznego znajduje się przez dodanie kwadratów dowolnych dwóch innych liczb w danej serii, jeśli są one w równej odległości od tego elementu.

z 2 = z - T 2 + z + T 2 , GdzieTto odległość między tymi liczbami.

• Elementyróżnią się qraz.
• Logarytmy elementów progresji również tworzą progresję, ale już arytmetyczną, to znaczy każdy z nich jest większy od poprzedniego o określoną liczbę.

Przykłady niektórych klasycznych problemów

Aby lepiej zrozumieć, czym jest postęp geometryczny, pomocne mogą być przykłady z rozwiązaniem dla klasy 9.

• Warunki:A 1 = 3, A 3 = 48. ZnajdźQ.

Rozwiązanie: każdy kolejny element jest większy od poprzedniego wQ raz.Konieczne jest wyrażenie niektórych elementów przez inne za pomocą mianownika.

Stąd,A 3 = Q 2 · A 1

Podczas zastępowaniaQ= 4

• Warunki:A 2 = 6, A 3 = 12. Oblicz S 6 .

Rozwiązanie:Aby to zrobić, wystarczy znaleźć q, pierwszy element i podstawić go do wzoru.

A 3 = Q· A 2 , stąd,Q= 2

za 2 = q 1 ,Dlatego a 1 = 3

S 6 = 189

• · A 1 = 10, Q= -2. Znajdź czwarty element progresji.

Rozwiązanie: aby to zrobić, wystarczy wyrazić czwarty element przez pierwszy i przez mianownik.

za 4 = q 3· a 1 = -80

Przykład zastosowania:

• Klient banku złożył depozyt w wysokości 10 000 rubli, zgodnie z warunkami którego co roku klient doda 6% kwoty głównej. Ile pieniędzy będzie na koncie po 4 latach?

Rozwiązanie: Początkowa kwota to 10 tysięcy rubli. Czyli rok po inwestycji na koncie będzie miała kwotę równą 10 000 + 10 000 · 0,06 = 10000 1,06

W związku z tym kwota na rachunku po kolejnym roku zostanie wyrażona w następujący sposób:

(10000 1,06) 0,06 + 10000 1,06 = 1,06 1,06 10000

Oznacza to, że każdego roku kwota wzrasta o 1,06 razy. Oznacza to, że aby znaleźć kwotę środków na koncie po 4 latach, wystarczy znaleźć czwarty element progresji, który daje pierwszy element równy 10 tys., a mianownik równy 1,06.

S = 1,06 1,06 1,06 1,06 10000 = 12625

Przykładowe zadania do obliczenia sumy:

W różnych problemach stosuje się postęp geometryczny. Przykład znalezienia sumy można podać w następujący sposób:

A 1 = 4, Q= 2, obliczS5.

Rozwiązanie: wszystkie dane potrzebne do obliczeń są znane, wystarczy je podstawić do wzoru.

S 5 = 124

• A 2 = 6, A 3 = 18. Oblicz sumę pierwszych sześciu elementów.

Rozwiązanie:

Geom. progresja, każdy kolejny element jest q razy większy od poprzedniego, czyli żeby obliczyć sumę trzeba znać elementA 1 i mianownikQ.

A 2 · Q = A 3

Q = 3

Podobnie musimy znaleźćA 1 , wiedzącA 2 IQ.

A 1 · Q = A 2

a 1 =2

S 6 = 728.

Powiązana lekcja „Nieskończenie malejący postęp geometryczny”

Cel lekcji: zapoznanie studentów z nowym rodzajem ciągu - nieskończenie malejącym postępem geometrycznym.

Zadania:

sformułowanie początkowej idei granicy ciągu liczbowego; znajomość innego sposobu zamiany nieskończonych ułamków okresowych na zwykłe za pomocą wzoru na sumę nieskończenie malejącego postępu geometrycznego;

rozwój cech intelektualnych osobowości uczniów, takich jak logiczne myślenie, zdolność do działań oceniających, uogólnianie;

wychowanie do aktywności, wzajemna pomoc, kolektywizm, zainteresowanie tematem.

Sprzęt: zajęcia komputerowe, rzutnik, ekran.

Rodzaj lekcji: Lekcja - opanowanie nowego tematu.

Podczas zajęć

I . Org. za chwilę. Wiadomość o temacie i celu lekcji.

II . Aktualizowanie wiedzy uczniów.1. Sprawdzanie pracy domowej.

1) Weryfikacja podstawowych wzorów związanych z postępami arytmetycznymi i geometrycznymi. Dwóch uczniów zapisuje formuły na tablicy.

2) Reszta uczniów tak dyktando matematyczne na temat „Formuły sumy”.

Zadania:

№1. Znajdź sumę pierwszych pięciu elementów ciągu arytmetycznego, jeśli jego pierwszy element to 6 (1. opcja), -20 (2. opcja), a piąty element to -6 (1. opcja), 20 (2. opcja).

№2. Znajdź sumę pierwszych pięciu wyrazów ciągu arytmetycznego, jeśli jego pierwszy wyraz to -20(1. opcja), 6(2. opcja), a różnica wynosi 10(1. opcja), -3(2. opcja).

№3. Znajdź sumę pierwszych pięciu wyrazów ciągu geometrycznego, jeśli jego pierwszy wyraz to 1 (opcja 1), -1 (opcja 2), a mianownik to -2 (opcja 1), 2 (opcja 2).

Na koniec dyktanda wybiórczo sprawdzane są prace dwóch uczniów do oceny, pozostali dokonują samooceny według gotowych rozwiązań zapisanych na klapach tablicy.

Rozwiązania:

Zadania

1. Postęp arytmetyczny jest określony wzorem A N = 7 – 4 N. Znajdować A 10 . (-33)

2. Postęp arytmetyczny A 3 = 7 I A 5 = 1 . Znajdować A 4 . (4)

3. Postęp arytmetyczny A 3 = 7 I A 5 = 1 . Znajdować A 17 . (-35)

4. Postęp arytmetyczny A 3 = 7 I A 5 = 1 . Znajdować S 17 . (-187)

5. Dla postępu geometrycznego
znajdź piąty wyraz.

6. Dla postępu geometrycznego
znajdować N-ty członek.

7. Wykładniczo B 3 = 8 I B 5 = 2 . Znajdować B 4 . (4)

8. Wykładniczo B 3 = 8 I B 5 = 2 . Znajdować B 1 I Q .

9. Wykładniczo B 3 = 8 I B 5 = 2 . Znajdować S 5 . (62)

III . Eksploracja nowego tematu(prezentacja demonstracyjna).

Rozważmy kwadrat o boku równym 1. Narysujmy kolejny kwadrat, którego bok jest połową pierwszego kwadratu, potem kolejny, którego bok jest połową drugiego, potem następny i tak dalej. Za każdym razem bok nowego kwadratu jest równy połowie poprzedniego.

W rezultacie otrzymaliśmy ciąg boków kwadratów tworząc postęp geometryczny z mianownikiem .

I co bardzo ważne, im więcej takich kwadratów zbudujemy, tym mniejszy będzie bok kwadratu. Na przykład,

Te. wraz ze wzrostem liczby n warunki progresji zbliżają się do zera.

Za pomocą tej figury można rozważyć jeszcze jedną sekwencję.

Na przykład sekwencja obszarów kwadratów:

. I znowu, jeśli N rośnie w nieskończoność, to pole arbitralnie zbliża się do zera.

Rozważmy jeszcze jeden przykład. Trójkąt równoboczny o boku 1 cm. Zbudujmy następny trójkąt z wierzchołkami w środkach boków pierwszego trójkąta, zgodnie z twierdzeniem o linii środkowej trójkąta - bok drugiego jest równy połowie boku pierwszego, bok trzeciego to połowa boku 2. itd. Ponownie otrzymujemy ciąg długości boków trójkątów.

Na
.

Jeśli weźmiemy pod uwagę postęp geometryczny z ujemnym mianownikiem.

Potem znowu, z rosnącą liczbą N warunki progresji zbliżają się do zera.

Zwróćmy uwagę na mianowniki tych ciągów. Wszędzie mianowniki były mniejsze niż 1 modulo.

Możemy stwierdzić: postęp geometryczny będzie malejący w nieskończoność, jeśli moduł jego mianownika jest mniejszy niż 1.

Praca z przodu.

Definicja:

Mówi się, że postęp geometryczny jest nieskończenie malejący, jeśli moduł jego mianownika jest mniejszy niż jeden.
.

Za pomocą definicji można rozwiązać pytanie, czy postęp geometryczny maleje w nieskończoność, czy nie.

Zadanie

Czy ciąg jest nieskończenie malejącym postępem geometrycznym, jeśli jest określony wzorem:

;
.

Rozwiązanie:

. Znajdźmy Q .

;
;
;
.

ten postęp geometryczny maleje w nieskończoność.

B) ta sekwencja nie jest nieskończenie malejącym postępem geometrycznym.

Rozważ kwadrat o boku równym 1. Podziel go na pół, jedną z połówek ponownie na pół i tak dalej. obszary wszystkich powstałych prostokątów tworzą nieskończenie malejący postęp geometryczny:

Suma obszarów wszystkich prostokątów uzyskanych w ten sposób będzie równa polu pierwszego kwadratu i równa 1.

Ale po lewej stronie tej równości jest suma nieskończonej liczby wyrazów.

Rozważ sumę pierwszych n wyrazów.

Zgodnie ze wzorem na sumę pierwszych n wyrazów postępu geometrycznego jest on równy .

Jeśli N wtedy rośnie w nieskończoność

Lub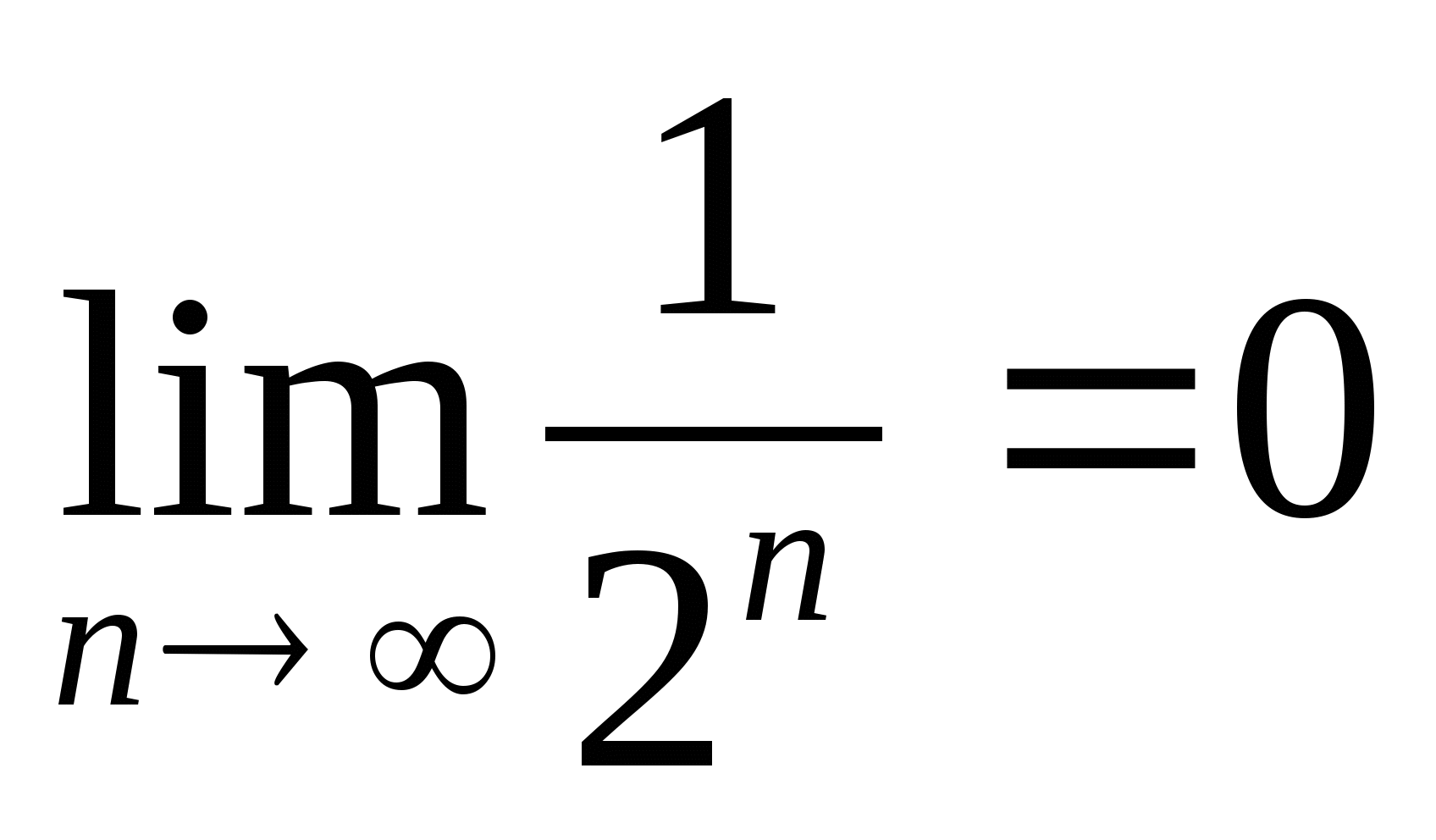
. Dlatego
, tj.
.

Suma nieskończenie malejącego postępu geometrycznego istnieje granica sekwencji S 1 , S 2 , S 3 , …, S N , … .

Na przykład dla progresji
,

Ponieważ

Suma nieskończenie malejącego postępu geometrycznego można znaleźć za pomocą wzoru
.

III . Refleksja i konsolidacja(wykonanie zadań).

Zadanie numer 2. Znajdź sumę nieskończenie malejącego postępu geometrycznego z pierwszym wyrazem 3, drugim 0,3.

Rozwiązanie:

Zadanie numer 3. podręcznik, s. 160, nr 433(1)

Znajdź sumę nieskończenie malejącego postępu geometrycznego:

Rozwiązanie:

Zadanie numer 4. Zapisz nieskończony okresowy ułamek dziesiętny 0,(5) jako ułamek zwykły.

1. sposób. Niech x = 0, (5) = 0,555 ... / 10 2. metoda. 0,(5)=0,555…=

Zadanie numer 5. podręcznik, s. 162, nr 445(3) (decyzja samodzielna)

Zapisz nieskończony okresowy ułamek dziesiętny 0,(12) jako ułamek zwykły.

Odpowiedź: 0,(12)=4/33.

IV . Zreasumowanie.

Jaką sekwencję spotkałeś dzisiaj?

Zdefiniuj nieskończenie malejący postęp geometryczny.

Jak udowodnić, że postęp geometryczny jest nieskończenie malejący?

Podaj wzór na sumę nieskończenie malejącego postępu geometrycznego.

V . Praca domowa.

Postęp geometryczny to ciąg liczbowy, którego pierwszy wyraz jest niezerowy, a każdy następny wyraz jest równy poprzedniemu wyrazowi pomnożonemu przez tę samą liczbę różną od zera. Postęp geometryczny jest oznaczony przez b1,b2,b3, …, bn, …

Własności postępu geometrycznego

Stosunek dowolnego składnika błędu geometrycznego do jego poprzedniego składnika jest równy tej samej liczbie, czyli b2/b1 = b3/b2 = b4/b3 = … = bn/b(n-1) = b(n+ 1)/bn = …. Wynika to bezpośrednio z definicji postępu arytmetycznego. Ta liczba nazywana jest mianownikiem postępu geometrycznego. Zwykle mianownik postępu geometrycznego jest oznaczony literą q.

Jednym ze sposobów wyznaczenia postępu geometrycznego jest wyznaczenie jego pierwszego wyrazu b1 i mianownika błędu geometrycznego q. Na przykład b1=4, q=-2. Te dwa warunki dają postęp geometryczny 4, -8, 16, -32, … .

Jeśli q>0 (q nie jest równe 1), to postęp jest ciągiem monotonicznym. Na przykład ciąg 2, 4,8,16,32, ... jest ciągiem rosnącym monotonicznie (b1=2, q=2).

Jeżeli mianownik q=1 w błędzie geometrycznym, to wszystkie elementy ciągu geometrycznego będą sobie równe. W takich przypadkach mówi się, że postęp jest ciągłą sekwencją.

Formuła n-tego członka progresji

Aby ciąg liczbowy (bn) był postępem geometrycznym, konieczne jest, aby każdy jego element, począwszy od drugiego, był średnią geometryczną sąsiednich elementów. Czyli trzeba spełnić równanie - (b(n+1))^2 = bn * b(n+2), dla dowolnego n>0, gdzie n należy do zbioru liczb naturalnych N.

Wzór na n-tego członka ciągu geometrycznego to:

bn=b1*q^(n-1), gdzie n należy do zbioru liczb naturalnych N.

Rozważ prosty przykład:

W postępie geometrycznym b1=6, q=3, n=8 znajdź bn.

Skorzystajmy ze wzoru n-tego elementu ciągu geometrycznego.

Postęp geometryczny to nowy rodzaj ciągu liczb, z którym musimy się zapoznać. Dla udanej znajomości nie zaszkodzi przynajmniej wiedzieć i zrozumieć. Wtedy nie będzie problemu z postępem geometrycznym.)

Co to jest postęp geometryczny? Pojęcie postępu geometrycznego.

Trasę zaczynamy, jak zwykle, od podstawówki. Piszę niedokończony ciąg liczb:

1, 10, 100, 1000, 10000, …

Czy potrafisz złapać wzór i powiedzieć, które liczby będą następne? Pieprz jest jasny, liczby 100000, 1000000 i tak dalej pójdą dalej. Nawet bez dużego stresu psychicznego wszystko jest jasne, prawda?)

OK. Inny przykład. Piszę następującą sekwencję:

1, 2, 4, 8, 16, …

Czy możesz powiedzieć, które numery pójdą dalej, po numerze 16 i imieniu ósma członek sekwencji? Jeśli zorientowałeś się, że będzie to liczba 128, to bardzo dobrze. Tak więc połowa sukcesu leży w zrozumieniu oznaczający I Kluczowe punkty postęp geometryczny już zrobiony. Możesz dalej rosnąć.)

A teraz ponownie przechodzimy od wrażeń do ścisłej matematyki.

Kluczowe momenty postępu geometrycznego.

Kluczowy moment #1

Postęp geometryczny jest sekwencja liczb. Podobnie jak postęp. Nic trudnego. Właśnie ułożyłem tę sekwencję różnie. Stąd oczywiście ma inną nazwę, tak ...

Kluczowy moment #2

W przypadku drugiego kluczowego punktu pytanie będzie trudniejsze. Cofnijmy się trochę i zapamiętajmy kluczową właściwość postępu arytmetycznego. tutaj: każdy członek różni się od poprzedniego o tę samą kwotę.

Czy można sformułować podobną kluczową właściwość dla postępu geometrycznego? Pomyśl trochę... Przyjrzyj się podanym przykładom. Zgadłeś? Tak! W postępie geometrycznym (dowolnym!) każdy z jego członków różni się od poprzedniego w tej samej liczbie razy. Zawsze!

W pierwszym przykładzie ta liczba to dziesięć. Niezależnie od tego, który wyraz ciągu wybierzesz, jest on większy niż poprzedni dziesięć razy.

W drugim przykładzie jest to dwójka: każdy element jest większy od poprzedniego. dwa razy.

Właśnie w tym kluczowym punkcie postęp geometryczny różni się od arytmetycznego. W postępie arytmetycznym uzyskuje się każdy następny wyraz dodawanie o tej samej wartości co poprzednia kadencja. I tu - mnożenie poprzednią kadencję o tę samą kwotę. Na tym polega różnica.)

Kluczowy moment #3

Ten kluczowy punkt jest całkowicie identyczny jak w przypadku postępu arytmetycznego. Mianowicie: każdy element ciągu geometrycznego jest na swoim miejscu. Wszystko jest dokładnie takie samo jak w postępie arytmetycznym i komentarze są moim zdaniem zbędne. Jest pierwszy termin, jest sto pierwszy i tak dalej. Przestawmy co najmniej dwa elementy - wzór (a wraz z nim postęp geometryczny) zniknie. To, co pozostaje, to tylko ciąg liczb bez żadnej logiki.

To wszystko. To jest cały sens postępu geometrycznego.

Terminy i oznaczenia.

A teraz, po zapoznaniu się ze znaczeniem i kluczowymi punktami postępu geometrycznego, możemy przejść do teorii. W przeciwnym razie, czym jest teoria bez zrozumienia znaczenia, prawda?

Co to jest postęp geometryczny?

Jak ogólnie zapisuje się postęp geometryczny? Bez problemu! Każdy członek progresji jest również napisany jako list. Litera jest zwykle używana tylko w postępie arytmetycznym "A", dla geometrycznej - list "B". Numer członkowski, jak zwykle, jest wskazany prawy dolny indeks. Sami członkowie progresji są po prostu wymienieni oddzieleni przecinkami lub średnikami.

Lubię to:

b1,B 2 , B 3 , B 4 , B 5 , B 6 , …

W skrócie taka progresja jest zapisana w następujący sposób: (b rz) .

Lub tak, dla skończonych postępów:

b 1 , b 2 , b 3 , b 4 , b 5 , b 6 .

b 1 , b 2 , ..., b 29 , b 30 .

Lub w skrócie:

(b rz), N=30 .

To właściwie wszystkie oznaczenia. Wszystko jest takie samo, tylko litera jest inna, tak.) A teraz przechodzimy bezpośrednio do definicji.

Definicja postępu geometrycznego.

Postęp geometryczny to ciąg liczbowy, którego pierwszy wyraz jest niezerowy, a każdy kolejny wyraz jest równy poprzedniemu wyrazowi pomnożonemu przez tę samą liczbę różną od zera.

To jest cała definicja. Większość słów i zwrotów jest dla Ciebie jasna i znana. O ile oczywiście nie rozumiesz znaczenia postępu geometrycznego „na palcach” i ogólnie. Ale jest też kilka nowych zwrotów, na które chciałbym zwrócić szczególną uwagę.

Najpierw słowa: „którego pierwszy termin różne od zera".

To ograniczenie pierwszej kadencji nie zostało wprowadzone przypadkowo. Jak myślisz, co się stanie, jeśli pierwsza kadencja B 1 wychodzi na zero? Jaki będzie drugi wyraz, jeśli każdy wyraz jest większy od poprzedniego tyle samo razy? Powiedzmy trzy razy? Zobaczmy... Pomnóż pierwszy wyraz (tj. 0) przez 3 i otrzymaj... zero! A trzeci członek? Zero też! A czwarty wyraz również jest zerowy! I tak dalej…

Dostajemy tylko worek bajgli ciąg zer:

0, 0, 0, 0, …

Oczywiście taka sekwencja ma prawo do życia, ale nie ma praktycznego znaczenia. Wszystko jest takie jasne. Każdy z jego członków jest równy zeru. Suma dowolnej liczby członków również wynosi zero... Co ciekawego można z tym zrobić? Nic…

Następujące słowa kluczowe: „pomnożone przez tę samą liczbę różną od zera”.

Ten sam numer ma również swoją specjalną nazwę - mianownik postępu geometrycznego. Zacznijmy się spotykać.)

Mianownik postępu geometrycznego.

Wszystko jest proste.

Mianownik postępu geometrycznego jest niezerową liczbą (lub wartością). ile razykażdego członka progresji więcej niż poprzedni.

Ponownie, analogicznie do postępu arytmetycznego, kluczowym słowem, na które należy zwrócić uwagę w tej definicji, jest słowo "więcej". Oznacza to, że uzyskuje się każdy wyraz postępu geometrycznego mnożenie do tego właśnie mianownika poprzedni członek.

Wyjaśniam.

Aby obliczyć, powiedzmy drugi członek do wzięcia Pierwszy członek i zwielokrotniać to do mianownika. Do obliczeń dziesiąty członek do wzięcia dziewiąty członek i zwielokrotniać to do mianownika.

Mianownik samego postępu geometrycznego może być dowolny. Absolutnie każdy! Liczba całkowita, ułamkowa, dodatnia, ujemna, irracjonalna - wszyscy. Oprócz zera. O tym mówi nam słowo „niezerowe” w definicji. Dlaczego to słowo jest potrzebne tutaj - więcej o tym później.

Mianownik postępu geometrycznego zwykle oznaczony literą Q.

Jak znaleźć ten Q? Bez problemu! Musimy przyjąć dowolny termin progresji i podzielić przez poprzedni wyraz. Podział jest frakcja. Stąd nazwa - „mianownik progresji”. W mianowniku zwykle siedzi w ułamku, tak ...) Chociaż logicznie rzecz biorąc, wartość Q należy nazwać prywatny postęp geometryczny, podobny do różnica dla postępu arytmetycznego. Ale zgodził się zadzwonić mianownik. I nie będziemy też wymyślać koła na nowo.)

Zdefiniujmy na przykład wartość Q dla tego postępu geometrycznego:

2, 6, 18, 54, …

Wszystko jest elementarne. Bierzemy każdy numer sekwencji. To, czego chcemy, to bierzemy. Poza tym pierwszym. Na przykład 18. I podziel przez poprzedni numer. To znaczy o 6.

Otrzymujemy:

Q = 18/6 = 3

To wszystko. To jest poprawna odpowiedź. Dla danego postępu geometrycznego mianownik wynosi trzy.

Znajdźmy mianownik Q dla innego postępu geometrycznego. Na przykład tak:

1, -2, 4, -8, 16, …

Wszystkie takie same. Jakiekolwiek znaki mają sami członkowie, nadal je przyjmujemy każdy kolejny numer (na przykład 16) i podzielić przez poprzedni numer(tj. -8).

Otrzymujemy:

D = 16/(-8) = -2

I tyle.) Tym razem mianownik progresji okazał się ujemny. Minus dwa. Dzieje się.)

Weźmy ten postęp:

1, 1/3, 1/9, 1/27, …

I znowu, niezależnie od rodzaju liczb w ciągu (nawet całkowitych, nawet ułamkowych, nawet ujemnych, nawet niewymiernych), bierzemy dowolną liczbę (na przykład 1/9) i dzielimy przez poprzednią liczbę (1/3). Oczywiście zgodnie z zasadami działań na ułamkach.

Otrzymujemy:

To wszystko.) Tutaj mianownik okazał się ułamkowy: Q = 1/3.

Ale taki "postęp" jak ty?

3, 3, 3, 3, 3, …

Oczywiście tutaj Q = 1 . Formalnie jest to również postęp geometryczny, tylko z ci sami członkowie.) Ale takie postępy nie są interesujące do studiowania i praktycznego zastosowania. Podobnie jak progresje z pełnymi zerami. Dlatego nie będziemy ich rozważać.

Jak widać, mianownikiem progresji może być wszystko - liczba całkowita, ułamek, dodatni, ujemny - cokolwiek! Nie może być po prostu zero. Nie zgadłeś dlaczego?

Cóż, spójrzmy na konkretny przykład, co się stanie, jeśli weźmiemy jako mianownik Q zero.) Załóżmy, że np B 1 = 2 , A Q = 0 . Jaka będzie wtedy druga kadencja?

Wierzymy:

B 2 = B 1 · Q= 2 0 = 0

A trzeci członek?

B 3 = B 2 · Q= 0 0 = 0

Rodzaje i zachowanie się postępów geometrycznych.

Ze wszystkim było mniej więcej jasne: czy różnica w progresji D jest dodatnia, progresja jest rosnąca. Jeśli różnica jest ujemna, progresja maleje. Są tylko dwie opcje. Nie ma trzeciego.)

Ale przy zachowaniu postępu geometrycznego wszystko będzie o wiele bardziej interesujące i różnorodne!)

Gdy tylko człony zachowują się tutaj: rosną i maleją, i zbliżają się do zera w nieskończoność, a nawet zmieniają znaki, na przemian pędząc albo do „plusa”, albo do „minusa”! I w całej tej różnorodności trzeba umieć dobrze się porozumieć, tak...

Rozumiemy?) Zacznijmy od najprostszego przypadku.

Mianownik jest dodatni ( Q >0)

Z dodatnim mianownikiem, po pierwsze, mogą wejść członkowie ciągu geometrycznego dodać nieskończoność(tj. rosnąć w nieskończoność) i może wejść minus nieskończoność(czyli zmniejszać się w nieskończoność). Przyzwyczailiśmy się już do takiego zachowania progresji.

Na przykład:

(b rz): 1, 2, 4, 8, 16, …

Tutaj wszystko jest proste. Każdy członek progresji jest więcej niż poprzedni. I każdy członek dostaje mnożenie poprzedni członek na pozytywny liczba +2 (tj. Q = 2 ). Zachowanie takiej progresji jest oczywiste: wszyscy członkowie progresji rosną w nieskończoność, idąc w przestrzeń. Do tego nieskończoność...

Teraz postęp:

(b rz): -1, -2, -4, -8, -16, …

Tutaj również uzyskuje się każdy termin progresji mnożenie poprzedni członek na pozytywny liczba +2. Ale zachowanie takiej progresji jest już dokładnie odwrotne: każdy członek progresji jest uzyskany mniej niż poprzednio, a wszystkie jego wyrazy maleją w nieskończoność, dążąc do minus nieskończoności.

A teraz zastanówmy się: co łączy te dwie progresje? Zgadza się, mianowniku! Tu i tam Q = +2 . Liczba dodatnia. Licho. I tu zachowanie Te dwie progresje są zasadniczo różne! Nie zgadłeś dlaczego? Tak! To wszystko o pierwszy członek! To on, jak mówią, zamawia muzykę.) Przekonaj się sam.

W pierwszym przypadku pierwszy okres progresji pozytywny(+1), a zatem wszystkie kolejne wyrażenia uzyskane przez pomnożenie przez pozytywny mianownik Q = +2 , będzie również pozytywny.

Ale w drugim przypadku pierwsza kadencja negatywny(-1). Dlatego wszyscy kolejni członkowie progresji uzyskali przez pomnożenie przez pozytywny Q = +2 , również zostanie uzyskany negatywny. Dla „minus” na „plus” zawsze daje „minus”, tak.)

Jak widać, w przeciwieństwie do postępu arytmetycznego, postęp geometryczny może zachowywać się zupełnie inaczej, nie tylko w zależności od od mianownikaQ, ale także zależne od pierwszego członka, Tak.)

Pamiętaj: zachowanie postępu geometrycznego jest jednoznacznie określone przez jego pierwszego członka B 1 i mianownikQ .

A teraz zaczynamy analizę mniej znanych, ale o wiele ciekawszych przypadków!

Weźmy na przykład następującą sekwencję:

(b rz): 1, 1/2, 1/4, 1/8, 1/16, …

Ta sekwencja jest również postępem geometrycznym! Otrzymuje się również każdego członka tej progresji mnożenie poprzednią kadencję o ten sam numer. Tylko numer jest frakcyjny: Q = +1/2 . Lub +0,5 . I (ważny!) numer, mniejszy:Q = 1/2<1.

Co jest interesującego w tym postępie geometrycznym? Dokąd zmierzają jej członkowie? spójrzmy:

1/2 = 0,5;

1/4 = 0,25;

1/8 = 0,125;

1/16 = 0,0625;

…….

Co jest tutaj interesujące? Po pierwsze, natychmiast rzuca się w oczy spadek liczby członków progresji: każdego z jej członków mniej poprzedni dokładnie 2 razy. Lub, zgodnie z definicją postępu geometrycznego, każdy termin więcej poprzedni 1/2 razy, ponieważ mianownik progresji Q = 1/2 . A od pomnożenia przez liczbę dodatnią mniejszą niż jeden wynik zwykle maleje, tak ...

Co więcej widać w zachowaniu tej progresji? Czy jej członkowie znikają? Nieograniczony, idąc do minus nieskończoności? NIE! Znikają w szczególny sposób. Najpierw maleją dość szybko, a potem coraz wolniej. I cały czas pobytu pozytywny. Choć bardzo, bardzo mały. A do czego dążą? Nie zgadłeś? Tak! Mają tendencję do zera!) I zwróćcie uwagę na członków naszej progresji nigdy nie sięgać! Tylko nieskończenie blisko niego. To jest bardzo ważne.)

Podobna sytuacja będzie w takim przebiegu:

(b rz): -1, -1/2, -1/4, -1/8, -1/16, …

Tutaj B 1 = -1 , A Q = 1/2 . Wszystko jest tak samo, tylko teraz pręty będą zbliżać się do zera od drugiej strony, od dołu. Pozostając cały czas negatywny.)

Taki postęp geometryczny, którego członkowie zbliża się do zera w nieskończoność.(nie ma znaczenia, po stronie pozytywnej lub negatywnej), w matematyce ma specjalną nazwę - nieskończenie malejący postęp geometryczny. Ta progresja jest tak ciekawa i niezwykła, że ​​w ogóle nią będzie oddzielna lekcja .)

Rozważyliśmy więc wszystkie możliwe pozytywny mianowniki są zarówno duże, jak i mniejsze. Nie uważamy tego samego za mianownik z powodów podanych powyżej (pamiętaj o przykładzie z sekwencją trójek ...)

Podsumowując:

pozytywnyI więcej niż jeden (Q>1), następnie członkowie progresji:

A) rosnąć w nieskończoność (jeśliB 1 >0);

b) zmniejszać się w nieskończoność (jeśliB 1 <0).

Jeśli mianownik postępu geometrycznego pozytywny I mniej niż jeden (0< Q<1), то члены прогрессии:

a) nieskończenie bliskie zeru powyżej(JeśliB 1 >0);

b) nieskończenie bliskie zeru od dołu(JeśliB 1 <0).

Pozostaje teraz rozpatrzyć sprawę ujemny mianownik.

Mianownik jest ujemny ( Q <0)

Nie posuniemy się daleko po przykład. Dlaczego właściwie kudłata babcia?!) Niech będzie np. pierwszym członkiem progresji B 1 = 1 i weź mianownik q = -2.

Otrzymujemy następującą sekwencję:

(b rz): 1, -2, 4, -8, 16, …

I tak dalej.) Uzyskuje się każdy termin progresji mnożenie poprzedni członek na liczba ujemna-2. W takim przypadku wszyscy członkowie na nieparzystych miejscach (pierwszy, trzeci, piąty itd.) będą pozytywny, aw miejscach parzystych (drugi, czwarty itd.) - negatywny. Znaki są ściśle przeplatane. Plus-minus-plus-minus ... Taki postęp geometryczny nazywa się - rosnący znak naprzemiennie.

Dokąd zmierzają jej członkowie? I nigdzie.) Tak, w wartości bezwzględnej (tj. modulo) warunki naszego postępu rosną w nieskończoność (stąd nazwa „rosnący”). Ale jednocześnie każdy członek progresji na przemian rzuca go w upał, a następnie w zimno. Albo plus albo minus. Nasza progresja podlega fluktuacjom... Co więcej, zakres fluktuacji rośnie gwałtownie z każdym krokiem, tak.) Dlatego też aspiracje członków progresji, by pójść gdzieś konkretnie Tutaj NIE. Ani do plus nieskończoności, ani do minus nieskończoności, ani do zera - nigdzie.

Rozważmy teraz jakiś mianownik ułamkowy między zerem a minus jeden.

Na przykład niech tak będzie B 1 = 1 , A q = -1/2.

Następnie otrzymujemy postęp:

(b rz): 1, -1/2, 1/4, -1/8, 1/16, …

I znowu mamy przemianę znaków! Ale w przeciwieństwie do poprzedniego przykładu, tutaj jest już wyraźna tendencja do zbliżania się wyrazów do zera.) Tylko tym razem nasze wyrazy zbliżają się do zera nie ściśle z góry lub z dołu, ale ponownie wahając się. Naprzemiennie przyjmując wartości dodatnie lub ujemne. Ale jednocześnie oni moduły zbliżają się coraz bardziej do upragnionego zera).

Ten postęp geometryczny nazywa się nieskończenie malejący znak naprzemienny.

Dlaczego te dwa przykłady są interesujące? I fakt, że w obu przypadkach ma miejsce naprzemienne postacie! Taki żeton jest typowy tylko dla progresji z ujemnym mianownikiem, tak.) Dlatego jeśli w jakimś zadaniu zobaczysz postęp geometryczny z naprzemiennymi wyrazami, to już na pewno będziesz wiedział, że jego mianownik jest w 100% ujemny i nie pomylisz się w znaku.)

Nawiasem mówiąc, w przypadku ujemnego mianownika znak pierwszego wyrazu w ogóle nie wpływa na zachowanie samej progresji. Bez względu na to, jaki jest znak pierwszego członka progresji, w każdym przypadku zachowany będzie znak przemiany członków. Całe pytanie jest po prostu w jakich miejscach(parzyste lub nieparzyste) będą członkowie o określonych znakach.

Pamiętać:

Jeśli mianownik postępu geometrycznego negatywny , to znaki warunków progresji są zawsze alternatywny.

Jednocześnie sami członkowie:

a) rosnąć w nieskończonośćmodulo, JeśliQ<-1;

b) dążyć do zera w nieskończoność, jeśli -1< Q<0 (прогрессия бесконечно убывающая).

To wszystko. Analizowane są wszystkie typowe przypadki.)

Analizując różne przykłady postępów geometrycznych, okresowo używałem słów: „zmierza do zera”, „zmierza do plus nieskończoności”, dąży do minus nieskończoności... W porządku.) Te zwroty mowy (i konkretne przykłady) to tylko wstępna znajomość zachowanie różne ciągi liczb. Przykład postępu geometrycznego.

Dlaczego w ogóle musimy znać zachowanie progresji? Co za różnica, dokąd pójdzie? Do zera, do plus nieskończoności, do minus nieskończoności… Co nas to obchodzi?

Rzecz w tym, że już na studiach, w ramach matematyki wyższej, przyda się umiejętność pracy z różnymi ciągami liczbowymi (z dowolnymi, nie tylko progresjami!) oraz umiejętność dokładnego wyobrażenia sobie, jak zachowuje się ten lub inny ciąg - czy rośnie w nieskończoność, czy maleje, czy dąży do określonej liczby (a niekoniecznie do zera), czy nawet wcale nie dąży do niczego... Cały rozdział jest temu tematowi poświęcony w toku zajęć matematycznych analiza - teoria granic. A dokładniej koncepcja granica ciągu liczb. Bardzo ciekawy temat! Warto iść na studia i to rozgryźć.)

Niektóre przykłady z tej sekcji (sekwencje, które mają granicę), a w szczególności nieskończenie malejący postęp geometryczny zacząć uczyć się w szkole. Przyzwyczajanie się.)

Co więcej, umiejętność dobrego studiowania zachowania sekwencji w przyszłości bardzo przyda się i będzie bardzo przydatna badania funkcji. Najbardziej zróżnicowane. Ale umiejętność kompetentnej pracy z funkcjami (obliczanie pochodnych, badanie ich w całości, tworzenie ich wykresów) już dramatycznie podnosi twój poziom matematyczny! Wątpliwość? Nie ma potrzeby. Pamiętaj też o moich słowach.)

Spójrzmy na postęp geometryczny w życiu?

W otaczającym nas życiu bardzo, bardzo często spotykamy się z postępem wykładniczym. Nawet o tym nie wiedząc.)

Na przykład różne mikroorganizmy, które otaczają nas wszędzie w ogromnych ilościach i których nawet nie widzimy bez mikroskopu, rozmnażają się dokładnie w postępie geometrycznym.

Powiedzmy, że jedna bakteria rozmnaża się, dzieląc się na pół, dając potomstwo w 2 bakteriach. Z kolei każda z nich, namnażając się, również dzieli się na pół, dając wspólne potomstwo 4 bakterii. Następne pokolenie da 8 bakterii, następnie 16 bakterii, 32, 64 i tak dalej. Z każdym kolejnym pokoleniem liczba bakterii podwaja się. Typowy przykład postępu geometrycznego).

Również niektóre owady - mszyce, muchy - rozmnażają się wykładniczo. Nawiasem mówiąc, czasami też króliki.)

Innym przykładem postępu geometrycznego, bliższego codzienności, jest tzw odsetki składane. Takie ciekawe zjawisko często spotyka się w lokatach bankowych i nazywa się kapitalizacja odsetek. Co to jest?

Ty sam jesteś oczywiście wciąż młody. Uczysz się w szkole, nie składasz wniosków do banków. Ale twoi rodzice to dorośli i niezależni ludzie. Chodzą do pracy, zarabiają na chleb codzienny, a część pieniędzy lokują w banku, oszczędzając).

Załóżmy, że twój tata chce odłożyć pewną sumę pieniędzy na rodzinne wakacje w Turcji i wpłacić do banku 50 000 rubli z oprocentowaniem 10% rocznie na okres trzech lat z roczną kapitalizacją odsetek. Co więcej, przez cały ten okres nic nie można zrobić z depozytem. Nie możesz ani uzupełnić depozytu, ani wypłacić pieniędzy z konta. Jaki zysk odniesie w ciągu tych trzech lat?

Cóż, po pierwsze, musisz dowiedzieć się, co to jest 10% rocznie. To znaczy, że za rok Bank doliczy 10% początkowej kwoty depozytu. Od czego? Oczywiście od początkowa kwota depozytu.

Oblicz kwotę konta w ciągu roku. Jeśli początkowa kwota depozytu wynosiła 50 000 rubli (tj. 100%), to za rok, ile odsetek będzie na koncie? Zgadza się, 110%! Od 50 000 rubli.

Rozważamy więc 110% z 50 000 rubli:

50 000 1,1 \u003d 55 000 rubli.

Mam nadzieję, że rozumiesz, że znalezienie 110% wartości oznacza pomnożenie tej wartości przez liczbę 1,1? Jeśli nie rozumiesz, dlaczego tak jest, przypomnij sobie piątą i szóstą klasę. Mianowicie - związek procentów z ułamkami i częściami.)

Tak więc wzrost za pierwszy rok wyniesie 5000 rubli.

Ile pieniędzy będzie na koncie po dwóch latach? 60 000 rubli? Niestety (a raczej na szczęście) nie jest to takie proste. Cała sztuczka kapitalizacji odsetek polega na tym, że przy każdym naliczaniu nowych odsetek te same odsetki będą już brane pod uwagę od nowej kwoty! Od tego, który już jest na koncie W tym momencie. A odsetki naliczone za poprzedni okres doliczane są do początkowej kwoty lokaty i tym samym same uczestniczą w naliczaniu nowych odsetek! Oznacza to, że stają się pełną częścią całkowitego konta. lub generał kapitał. Stąd nazwa - kapitalizacja odsetek.

To w ekonomii. A w matematyce takie procenty nazywają się odsetki składane. Lub procent procent.) Ich sztuczka polega na tym, że w obliczeniach sekwencyjnych procenty są obliczane za każdym razem od nowej wartości. Nie z oryginału...

Dlatego, aby obliczyć sumę przez dwa lata, musimy obliczyć 110% kwoty, która będzie na koncie za rok. To znaczy już od 55 000 rubli.

Rozważamy 110% z 55 000 rubli:

55000 1,1 \u003d 60500 rubli.

Oznacza to, że procentowy wzrost za drugi rok wyniesie już 5500 rubli, a za dwa lata - 10 500 rubli.

Teraz już można się domyślić, że za trzy lata kwota na koncie wyniesie 110% z 60 500 rubli. To znowu 110% z poprzedniego (ostatniego roku) kwoty.

Tutaj rozważamy:

60500 1,1 \u003d 66550 rubli.

A teraz budujemy nasze kwoty pieniężne według kolejnych lat:

50000;

55000 = 50000 1,1;

60500 = 55000 1,1 = (50000 1,1) 1,1;

66550 = 60500 1,1 = ((50000 1,1) 1,1) 1,1

Więc jak to jest? Dlaczego nie postęp geometryczny? Pierwszy członek B 1 = 50000 i mianownik Q = 1,1 . Każdy wyraz jest dokładnie 1,1 razy większy od poprzedniego. Wszystko jest ściśle zgodne z definicją.)

A ile dodatkowych premii procentowych „wrzuci” twój tata, podczas gdy jego 50 000 rubli było na koncie bankowym przez trzy lata?

Wierzymy:

66550 - 50000 = 16550 rubli

To złe, oczywiście. Ale dzieje się tak, jeśli początkowa kwota wkładu jest niewielka. A co jeśli jest więcej? Powiedz, nie 50, ale 200 tysięcy rubli? Wtedy wzrost za trzy lata wyniesie już 66 200 rubli (jeśli liczyć). Co już jest bardzo dobre.) A jeśli wkład jest jeszcze większy? To jest to...

Wniosek: im wyższy wkład początkowy, tym bardziej opłacalna staje się kapitalizacja odsetek. Dlatego banki udzielają lokat z kapitalizacją odsetek na długie okresy. Powiedzmy pięć lat.

Ponadto wszelkiego rodzaju groźne choroby, takie jak grypa, odra i jeszcze straszniejsze choroby (ten sam SARS na początku XXI wieku lub dżuma w średniowieczu) lubią rozprzestrzeniać się wykładniczo. Stąd skala epidemii, tak...) A wszystko przez to, że postęp geometryczny z cały dodatni mianownik (Q>1) - rzecz, która rośnie bardzo szybko! Pamiętaj o reprodukcji bakterii: z jednej bakterii uzyskuje się dwie, z dwóch - cztery, z czterech - osiem i tak dalej ... Wraz z rozprzestrzenianiem się jakiejkolwiek infekcji wszystko jest takie samo.)

Najprostsze problemy w postępie geometrycznym.

Zacznijmy, jak zawsze, od prostego problemu. Czysto, aby zrozumieć znaczenie.

1. Wiadomo, że drugi wyraz ciągu geometrycznego to 6, a mianownik to -0,5. Znajdź pierwszy, trzeci i czwarty wyraz.

Tak jest nam dane nieskończony postęp geometryczny, dobrze znany drugi członek ta progresja:

b2 = 6

Ponadto wiemy również mianownik progresji:

q = -0,5

I musisz znaleźć pierwszy, trzeci I czwarty członków tej progresji.

Tutaj działamy. Zapisujemy sekwencję zgodnie ze stanem problemu. Bezpośrednio w kategoriach ogólnych, gdzie drugim członkiem jest szóstka:

b1,6,B 3 , B 4 , …

Teraz zacznijmy szukać. Zaczynamy, jak zawsze, od najprostszego. Możesz obliczyć na przykład trzeci wyraz b3? Móc! Wiemy już (bezpośrednio w sensie postępu geometrycznego), że trzeci wyraz (b3) więcej niż sekundę (B 2 ) V "Q" raz!

Więc piszemy:

b 3 =B 2 · Q

Podstawiamy szóstkę w tym wyrażeniu zamiast b2 i zamiast tego -0,5 Q i myślimy. Oczywiście minus też nie jest ignorowany…

b 3 \u003d 6 (-0,5) \u003d -3

Lubię to. Trzecia kadencja okazała się negatywna. Nic dziwnego: nasz mianownik Q- negatywny. A plus pomnożony przez minus, to oczywiście będzie minus.)

Rozważmy teraz kolejny, czwarty okres progresji:

b 4 =B 3 · Q

b 4 \u003d -3 (-0,5) \u003d 1,5

Czwarty członek znowu z plusem. Piąty wyraz znowu będzie z minusem, szósty z plusem i tak dalej. Znaki - naprzemiennie!

Tak więc znaleziono trzeciego i czwartego członka. Rezultatem jest następująca sekwencja:

b1; 6; -3; 1,5; …

Pozostaje teraz znaleźć pierwszy wyraz b1 zgodnie ze znaną sekundą. Aby to zrobić, robimy krok w innym kierunku, w lewo. Oznacza to, że w tym przypadku nie musimy mnożyć drugiego wyrazu progresji przez mianownik, ale udział.

Dzielimy i otrzymujemy:

To wszystko.) Odpowiedź na problem będzie następująca:

-12; 6; -3; 1,5; …

Jak widać, zasada rozwiązania jest taka sama jak w . Wiemy każdy członek i mianownik postęp geometryczny - możemy znaleźć dowolny inny termin. Cokolwiek zechcemy, znajdziemy.) Jedyna różnica polega na tym, że dodawanie/odejmowanie zastępuje mnożenie/dzielenie.

Pamiętaj: jeśli znamy przynajmniej jeden element i mianownik ciągu geometrycznego, to zawsze możemy znaleźć dowolnego innego członka tego ciągu.

Następujące zadanie, zgodnie z tradycją, pochodzi z prawdziwej wersji OGE:

2.

…; 150; X; 6; 1,2; …

Więc jak to jest? Tym razem nie ma pierwszego wyrazu ani mianownika Q, podany jest tylko ciąg cyfr... Coś już znajomego, prawda? Tak! Podobny problem został już rozwiązany w postępie arytmetycznym!

Tutaj się nie boimy. Wszystkie takie same. Odwróć głowę i przypomnij sobie elementarne znaczenie postępu geometrycznego. Uważnie przyglądamy się naszemu ciągowi i ustalamy, które parametry postępu geometrycznego trzech głównych (człon pierwszy, mianownik, liczba prętów) są w nim ukryte.

Numery członkowskie? Nie ma numerów członkowskich, tak… Ale są cztery kolejny liczby. Co oznacza to słowo, nie widzę sensu wyjaśniać na tym etapie.) Czy są dwa sąsiednie znane liczby? Jeść! Są to 6 i 1,2. Więc możemy znaleźć mianownik progresji. Bierzemy więc liczbę 1,2 i dzielimy do poprzedniego numeru. Przez sześć.

Otrzymujemy:

Otrzymujemy:

X= 150 0,2 = 30

Odpowiedź: X = 30 .

Jak widać, wszystko jest dość proste. Główna trudność polega tylko na obliczeniach. Jest to szczególnie trudne w przypadku ujemnych i ułamkowych mianowników. Więc ci, którzy mają problemy, powtórz arytmetykę! Jak pracować z ułamkami zwykłymi, jak pracować z liczbami ujemnymi i tak dalej... W przeciwnym razie zwolnisz tutaj niemiłosiernie.

Teraz zmieńmy trochę problem. Teraz będzie ciekawie! Usuńmy z niego ostatnią liczbę 1.2. Rozwiążmy teraz ten problem:

3. Wypisano kilka kolejnych wyrazów postępu geometrycznego:

…; 150; X; 6; …

Znajdź termin progresji, oznaczony literą x.

Wszystko jest takie samo, tylko dwa sąsiadujące ze sobą słynny nie mamy już członków progresji. To jest główny problem. Bo wielkość Q przez dwa sąsiednie terminy, możemy już łatwo określić nie możemy. Czy mamy szansę sprostać wyzwaniu? Z pewnością!

Napiszmy nieznany termin ” X„Bezpośrednio w sensie postępu geometrycznego! Ogólnie rzecz biorąc.

Tak tak! Bezpośrednio z nieznanym mianownikiem!

Z jednej strony dla x możemy zapisać następujący stosunek:

X= 150Q

Z drugiej strony mamy pełne prawo przemalować ten sam X Następny członek, przez sześć! Podziel sześć przez mianownik.

Lubię to:

X = 6/ Q

Oczywiście teraz możemy zrównać oba te współczynniki. Ponieważ wyrażamy ten sam wartość (x), ale dwa różne sposoby.

Otrzymujemy równanie:

Mnożąc wszystko przez Q, upraszczając, redukując, otrzymujemy równanie:

q 2 \u003d 1/25

Rozwiązujemy i otrzymujemy:

q = ±1/5 = ±0,2

Ups! Mianownik jest podwójny! +0,2 i -0,2. A który wybrać? Ślepy zaułek?

Spokój! Tak, problem naprawdę istnieje dwa rozwiązania! Nic w tym złego. Zdarza się.) Nie jesteś zaskoczony, gdy na przykład otrzymujesz dwa pierwiastki, rozwiązując zwykłe? Tu jest ta sama historia.)

Dla q = +0,2 dostaniemy:

X \u003d 150 0,2 \u003d 30

I dla Q = -0,2 będzie:

X = 150 (-0,2) = -30

Otrzymujemy podwójną odpowiedź: X = 30; X = -30.

Co oznacza ten interesujący fakt? I co istnieje dwie progresje, spełniając warunek problemu!

Jak te:

…; 150; 30; 6; …

…; 150; -30; 6; …

Oba są odpowiednie. Jak myślisz, jaki jest powód rozdwojenia odpowiedzi? Właśnie z powodu wyeliminowania konkretnego członka progresji (1,2), idącego po szóstce. A znając tylko poprzedni (n-1)-ty i kolejny (n+1)-ty człon ciągu geometrycznego, nie możemy już jednoznacznie powiedzieć nic o n-tym członie stojącym między nimi. Są dwie opcje - plus i minus.

Ale to nie ma znaczenia. Z reguły w zadaniach dotyczących postępu geometrycznego znajdują się dodatkowe informacje, które dają jednoznaczną odpowiedź. Powiedzmy słowa: „progresja naprzemienna znak” Lub „postęp z dodatnim mianownikiem” i tak dalej... To właśnie te słowa powinny służyć jako wskazówka, jaki znak, plus czy minus, wybrać przy udzielaniu ostatecznej odpowiedzi. Jeśli nie ma takich informacji, to - tak, zadanie będzie miało dwa rozwiązania.)

A teraz sami decydujemy.

4. Ustal, czy liczba 20 będzie należała do ciągu geometrycznego:

4 ; 6; 9; …

5. Podano naprzemienny postęp geometryczny:

…; 5; X ; 45; …

Znajdź termin progresji wskazanej literą X .

6. Znajdź czwarty dodatni wyraz postępu geometrycznego:

625; -250; 100; …

7. Drugi wyraz ciągu geometrycznego to -360, a piąty to 23,04. Znajdź pierwszy wyraz tego ciągu.

Odpowiedzi (w nieładzie): -15; 900; NIE; 2.56.

Gratulacje, jeśli wszystko się udało!

Coś nie pasuje? Czy jest gdzieś podwójna odpowiedź? Uważnie czytamy warunki zlecenia!

Ostatnia zagadka nie działa? Nie ma tam nic skomplikowanego.) Pracujemy bezpośrednio zgodnie ze znaczeniem postępu geometrycznego. Cóż, możesz narysować obrazek. To pomaga.)

Jak widać, wszystko jest elementarne. Jeśli postęp jest krótki. A jeśli jest długi? A może liczba pożądanego członka jest bardzo duża? Chciałbym, analogicznie do ciągu arytmetycznego, uzyskać w jakiś sposób wygodny wzór, który ułatwi znalezienie każdy członkiem dowolnego postępu geometrycznego po jego numerze. Bez mnożenia wiele, wiele razy przez Q. I jest taka formuła!) Szczegóły - w następnej lekcji.

Postęp geometryczny to ciąg liczbowy, którego pierwszy wyraz jest niezerowy, a każdy następny wyraz jest równy poprzedniemu wyrazowi pomnożonemu przez tę samą liczbę różną od zera.

Postęp geometryczny jest oznaczony b1,b2,b3, …, bn, … .

Stosunek dowolnego składnika błędu geometrycznego do jego poprzedniego składnika jest równy tej samej liczbie, czyli b2/b1 = b3/b2 = b4/b3 = … = bn/b(n-1) = b(n+ 1)/bn = …. Wynika to bezpośrednio z definicji postępu arytmetycznego. Ta liczba nazywana jest mianownikiem postępu geometrycznego. Zwykle mianownik postępu geometrycznego jest oznaczony literą q.

Sekwencja monotoniczna i stała

Jednym ze sposobów wyznaczenia postępu geometrycznego jest wyznaczenie jego pierwszego wyrazu b1 i mianownika błędu geometrycznego q. Na przykład b1=4, q=-2. Te dwa warunki dają postęp geometryczny 4, -8, 16, -32, … .

Jeśli q>0 (q nie jest równe 1), to progresja jest ciąg monotonny. Na przykład ciąg 2, 4,8,16,32, ... jest ciągiem rosnącym monotonicznie (b1=2, q=2).

Jeżeli mianownik q=1 w błędzie geometrycznym, to wszystkie elementy ciągu geometrycznego będą sobie równe. W takich przypadkach mówi się o postępie stała sekwencja.

Formuła n-tego członka ciągu geometrycznego

Aby ciąg liczbowy (bn) był postępem geometrycznym, konieczne jest, aby każdy jego element, począwszy od drugiego, był średnią geometryczną sąsiednich elementów. Oznacza to, że konieczne jest spełnienie następującego równania
(b(n+1))^2 = bn * b(n+2), dla dowolnego n>0, gdzie n należy do zbioru liczb naturalnych N.

Wzór na n-tego członka ciągu geometrycznego to:

bn=b1*q^(n-1),

gdzie n należy do zbioru liczb naturalnych N.

Wzór na sumę pierwszych n wyrazów postępu geometrycznego

Wzór na sumę pierwszych n wyrazów postępu geometrycznego to:

Sn = (bn*q - b1)/(q-1) gdzie q nie jest równe 1.

Rozważ prosty przykład:

W postępie geometrycznym b1=6, q=3, n=8 znajdź Sn.

Aby znaleźć S8, używamy wzoru na sumę pierwszych n wyrazów postępu geometrycznego.

S8= (6*(3^8 -1))/(3-1) = 19680.