Halka bölümünün eylemsizlik momenti. Basit kesitlerin eylemsizlik momentleri. Bir dik üçgenin eksenel atalet momentleri
TANIM
Eksenel (veya ekvator) atalet momenti eksene göre olan bölüme şu şekilde tanımlanan bir miktar denir:
İfade (1), eksenel atalet momentini hesaplamak için, sonsuz küçük alanların () çarpımlarının toplamının, onlardan dönme eksenine olan mesafelerin kareleriyle çarpılmasının tüm S alanı üzerinden alındığı anlamına gelir:
Bölümün karşılıklı dik eksenlere göre eksenel atalet momentlerinin toplamı (örneğin, Kartezyen koordinat sistemindeki X ve Y eksenlerine göre), bu eksenlerin kesişme noktasına göre kutupsal atalet momentini () verir:
TANIM
Kutup anı Atalet, bir noktaya göre eylemsizlik kesitinin momenti olarak adlandırılır.
Eksenel atalet momentleri her zaman sıfırdan büyüktür, çünkü tanımlarında (1), integral işaretinin altında, temel alanın (), her zaman pozitif olan alanının değeri ve bu alandan uzaklığın karesi vardır. Eksen.
Karmaşık şekilli bir bölümle uğraşıyorsak, hesaplamalarda sıklıkla karmaşık bir bölümün eksene göre eksenel atalet momentinin, bu bölümün parçalarının eksenel atalet momentlerinin toplamına eşit olduğu gerçeğini kullanırız. aynı eksene göre. Ancak farklı eksen ve noktalara göre bulunan atalet momentlerini özetlemenin mümkün olmadığı unutulmamalıdır.
Kesitin ağırlık merkezinden geçen eksene göre eksenel atalet momenti, kendisine paralel eksenlere göre tüm momentler arasında en küçük değere sahiptir. Ağırlık merkezinden geçen eksene paralel olmak kaydıyla herhangi bir eksene () göre eylemsizlik momenti şuna eşittir:
bölümün ağırlık merkezinden geçen eksene göre bölümün atalet momenti nerede; - kesit alanı; - eksenler arasındaki mesafe.
Problem çözme örnekleri
ÖRNEK 1
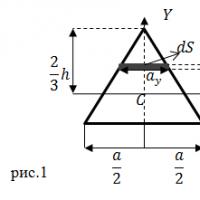
| Egzersiz yapmak | Tabanına paralel, üçgenin ağırlık merkezinden () geçen Z eksenine göre ikizkenar üçgen kesitinin eksenel atalet momenti nedir? Üçgenin yüksekliği . |
| Çözüm | Üçgen kesit üzerinde dikdörtgen bir temel alan seçelim (bkz. Şekil 1). Dönme ekseninden belirli bir mesafede bulunur, bir tarafının uzunluğu, diğer tarafının uzunluğu 2'dir. Şekil 1'den şu sonuç çıkıyor:
(1.1) dikkate alınarak seçilen dikdörtgenin alanı şuna eşittir: Eksenel atalet momentini bulmak için tanımını şu şekilde kullanırız: |
| Cevap |
ÖRNEK 2
| Egzersiz yapmak | Çapı d'ye eşit olan bir daire şeklindeki bir kesitin X ve Y dik eksenlerine (Şekil 2) göre eksenel atalet momentlerini bulun. |
| Çözüm | Sorunu çözmek için bölümün () merkezine göre kutupsal momenti bularak başlamak daha uygundur. Tüm kesiti, yarıçapı ile gösterilen sonsuz ince kalınlıktaki halkalara bölelim. Daha sonra temel alanı şu şekilde buluruz: |
Basit kesitler için statik momentler ve eylemsizlik momentleri (2.1)-(2.4) formülleri kullanılarak integral kullanılarak bulunur. Örneğin eksenel atalet momentini hesaplamayı düşünün JxŞekil 2'de gösterilen keyfi bir bölüm için. 2.9. Dikdörtgen bir koordinat sisteminde alan elemanının dF=dxdy, aldık
buradax^(y) ve (y)'de x - bazı sabit değerdeki kontur noktalarının koordinatları sen.
X üzerinden integral aldığımızda şunu buluruz:

Büyüklük ile) seviyedeki kesit genişliğini temsil eder en(bkz. Şekil 2.9) ve ürün b(y)dy = dF - eksene paralel gölgeli temel şeridin alanı Ah. Bunu dikkate alarak / formülü şu şekle dönüştürülür:

Eylemsizlik momenti için de benzer bir ifade elde edilebilir. Jy.
Dikdörtgen.Özellik 2'ye (§ 2.5) göre dikdörtgenin simetri eksenleriyle çakışan ana merkezi eksenlere göre eylemsizlik momentlerini bulalım (Şekil 2.10). Kesitin genişliği sabit olduğundan formül (2.14)'ü kullanarak şunu elde ederiz:

Eksene göre eylemsizlik momenti Ah x x x formüllerden ilkiyle (2.6) belirleriz: 


Atalet momentleri / ve J benzer şekilde bulunur. Bir dikdörtgenin eksenel eylemsizlik momentlerinin formüllerini yazalım:
Keyfi üçgen.Öncelikle eksene göre eylemsizlik momentini bulalım. 0 (xvüçgenin tabanından geçiyor (Şekil 2.11). Kesit genişliği ile()) düzeyinde sen (üçgenlerin benzerliğinden bulunur:

Bu miktarı formül (2.14)'te yerine koyup entegrasyon yaparak şunu elde ederiz:

Eksenler hakkında anlar Ah Ve 0 2x2, tabana paralel olan ve sırasıyla ağırlık merkezinden ve üçgenin tepe noktasından geçen formülleri (2.6) kullanarak buluruz:

Bu formüllerde b ( =h/ 3 ve b2 = -2h/3 - sırasıyla üçgenin ağırlık merkezinin koordinatları HAKKINDA koordinat sisteminde O x x 1 y 1 Ve 0 2 x 2 y t


1 ° 2 r Г* аУ 1
TLP *2
g >4™_ °2 1
D__V_!__*_ / ^ *3
V XV* ;-7^Лт^
U_ У-_XI - UZ__у
HAKKINDA,| B *, 0 s/b 2 %*1
Pirinç. 2.11 Pirinç. 2.12
Üçgenin tabana paralel eksenlere göre eksenel atalet momentlerinin formüllerini yazalım:
Sağ ve ikizkenar üçgenler. Dik bir üçgen için (Şekil 2.12), merkezkaç atalet momentini belirleriz J merkezi eksenlere göre Ah Ve kuruluş birimi, bacaklara paralel. Bu, formül (2.3) kullanılarak yapılabilir. Ancak aşağıdaki teknik uygulanarak sorunun çözümü basitleştirilebilir. Medyanı kullanma 0 { 0 3 Verilen üçgeni iki ikizkenar üçgene bölün 0 ( 0 3 A Ve Ofis 3B. Eksen 0 3 x 3 ve 0 3 ve 3 bu üçgenlerin simetri eksenleridir ve özellik 2'ye (§ 2.5) göre, her birinin ayrı ayrı ve dolayısıyla tüm üçgenin ana eksenleri olacaktır. O x AB. Bu nedenle merkezkaç atalet momenti J=0. Santrifüj
üçgenin eksenlere göre momenti Ah Ve kuruluş birimi formüllerin sonuncusunu (2.6) kullanarak buluruz:
Bir dik üçgenin eylemsizlik momentlerinin formüllerini yazalım: 



Bir ikizkenar üçgenin simetri eksenine göre eylemsizlik momenti kuruluş birimi(Şekil 2.13), formüllerin (2.17) dördüncüsünü kullanarak, tabanı olan bir dik üçgenin iki kat eylemsizlik momenti olarak tanımlarız. H ve yükseklik B/ 2:

Böylece, bir ikizkenar üçgenin ana merkezi eksenlere göre eylemsizlik momentleri Ah Ve kuruluş birimi formüllerle belirlenir
Daire.İlk olarak, kutupsal koordinat sistemini kullanarak (2.4) formülünü kullanarak bir dairenin kutupsal eylemsizlik momentini hesaplamak uygundur (Şekil 2.14).
Hesaba katıldığında dF-rdrdQ, bulacağız

(2.4)'e göre kutupsal moment iki eksenel momentin toplamına eşit olduğundan, şunu elde ederiz:
Yüzük. Halkanın eylemsizlik momentleri (Şekil 2.15), yarıçaplı iki çemberin eylemsizlik momentleri arasındaki fark olarak bulunur. ben 2 Ve R ( :
Yarım daire(pirinç. 2.16). Yarım daire düzleminde bir alan elemanı seçelim dF kutupsal koordinatlarla G, 0 ve Kartezyen koordinatlar x v y v bunun için, Şekil 2'ye göre. 2.16 sahibiz:
(2.1) ve (2.5) formüllerini kullanarak sırasıyla yarım dairenin eksene göre statik momentini buluruz. 0 (x( ve 0 ağırlık merkezinde hizalayın HAKKINDA koordinat sisteminde 0 ( x ( Uy

0, x ve eksenlerine göre 0 ( y v Yarım dairenin ana eksenleri olan eksenel atalet momentleri, dairenin atalet momentlerinin yarısına eşittir:

Ana merkez eksene göre eylemsizlik momenti, birinci formül (2.6) kullanılarak belirlenir:
Elips. Yarı eksenli bir elipsin eksenel eylemsizlik momentini hesaplamak için A Ve B eksene göre Ah(Şekil 2.17) şu şekilde ilerliyoruz. Elipsin etrafına bir daire çizelim ve iki temel genişlik şeridi seçelim dx ve yükseklik 2 yıl daire ve 2 için ah bir elips için. Bu iki şeridin eylemsizlik momentleri, bir dikdörtgen için formüllerden (2.15) birincisiyle belirlenebilir:
Bu ifadeleri entegre etmek -Aönce A, aldık 

Pirinç. 2.16

Pirinç. 2.17
Bir daire ve bir elipsin denklemlerinden elimizdeki

Bu düşünceyle birlikte

Eksene göre eylemsizlik momenti için de benzer bir ifade elde edilebilir. OU. Sonuç olarak elips için eksenel momentlere ilişkin aşağıdaki formüllere sahip olacağız:
Haddelenmiş çubuklar. Haddelenmiş çubukların bölümlerinin geometrik özellikleri (I-kirişler, kanallar, açılar) haddelenmiş çelik çeşitleri tablolarında verilmiştir (eke bakınız).
Bedenler M uzaklığın karesi başına D eksenler arasında:
J = J c + m d 2 , (\displaystyle J=J_(c)+md^(2),)Nerede M- toplam vücut ağırlığı.
Örneğin, bir çubuğun ucundan geçen bir eksene göre eylemsizlik momenti şuna eşittir:
J = J c + m d 2 = 1 12 m l 2 + m (l 2) 2 = 1 3 m l 2. (\displaystyle J=J_(c)+md^(2)=(\frac (1)(12))ml^(2)+m\left((\frac (l)(2))\right)^ (2)=(\frac (1)(3))ml^(2).)Bazı cisimlerin eksenel atalet momentleri
| Vücut | Tanım | Eksen konumu A | Atalet momenti Ja |
|---|---|---|---|
| Malzeme nokta kütlesi M | Mesafede R sabit bir noktadan | ||
| İçi boş ince duvarlı silindir veya yarıçap halkası R ve kitleler M | Silindir ekseni | m r 2 (\displaystyle mr^(2)) | |
| Katı silindir veya yarıçap diski R ve kitleler M | Silindir ekseni | 1 2 m r 2 (\displaystyle (\frac (1)(2))bay^(2)) | |
| İçi boş kalın duvarlı kütle silindiri M dış yarıçaplı R 2 ve iç yarıçap R 1 | Silindir ekseni | m r 2 2 + r 1 2 2 (\displaystyle m(\frac (r_(2)^(2)+r_(1)^(2))(2))) | |
| Katı silindir uzunluğu ben, yarıçap R ve kitleler M | 1 4 m ⋅ r 2 + 1 12 m ⋅ l 2 (\displaystyle (1 \over 4)m\cdot r^(2)+(1 \over 12)m\cdot l^(2)) | ||
| İçi boş ince duvarlı silindir (halka) uzunluğu ben, yarıçap R ve kitleler M | Eksen silindire diktir ve kütle merkezinden geçer | 1 2 m ⋅ r 2 + 1 12 m ⋅ l 2 (\displaystyle (1 \2'nin üzerinde)m\cdot r^(2)+(1 \12'nin üzerinde)m\cdot l^(2)) | |
| Düz İnce Uzunluk Çubuk ben ve kitleler M | Eksen çubuğa diktir ve kütle merkezinden geçer | 1 12 m l 2 (\displaystyle (\frac (1)(12))ml^(2)) | |
| Düz İnce Uzunluk Çubuk ben ve kitleler M | Eksen çubuğa diktir ve ucundan geçer | 1 3 m l 2 (\displaystyle (\frac (1)(3))ml^(2)) | |
| İnce duvarlı yarıçaplı küre R ve kitleler M | Eksen kürenin merkezinden geçer | 2 3 m r 2 (\displaystyle (\frac (2)(3))bay^(2)) | |
| Yarıçap topu R ve kitleler M | Eksen topun merkezinden geçer | 2 5 m r 2 (\displaystyle (\frac (2)(5))bay^(2)) | |
| Yarıçap konisi R ve kitleler M | Koni ekseni | 3 10 m r 2 (\displaystyle (\frac (3)(10))bay^(2)) | |
| Yüksekliği olan ikizkenar üçgen H, temel A ve kütle M | Eksen üçgenin düzlemine diktir ve tepe noktasından geçer | 1 24 m (a 2 + 12 sa 2) (\displaystyle (\frac (1)(24))m(a^(2)+12h^(2))) | |
| Kenarları olan düzgün üçgen A ve kütle M | Eksen üçgenin düzlemine diktir ve kütle merkezinden geçer | 1 12 m a 2 (\displaystyle (\frac (1)(12))ma^(2)) | |
| Kenarı olan kare A ve kütle M | Eksen karenin düzlemine diktir ve kütle merkezinden geçer | 1 6 m a 2 (\displaystyle (\frac (1)(6))ma^(2)) | |
| Kenarları olan dikdörtgen A Ve B ve kütle M | Eksen dikdörtgenin düzlemine diktir ve kütle merkezinden geçer | 1 12 m (a 2 + b 2) (\displaystyle (\frac (1)(12))m(a^(2)+b^(2))) | |
| Yarıçapın düzenli n-gonu R ve kütle M | Eksen düzleme diktir ve kütle merkezinden geçer | m r 2 6 [ 1 + 2 çünkü (π / n) 2 ] (\displaystyle (\frac (mr^(2))(6))\left) | |
| Kılavuz daire yarıçaplı simit (içi boş) R, üreten dairenin yarıçapı R ve kütle M | Eksen torus kılavuz dairesinin düzlemine diktir ve kütle merkezinden geçer | ben = m (3 4 r 2 + R 2) (\displaystyle I=m\left((\frac (3)(4))\,r^(2)+R^(2)\right)) |
Formüllerin türetilmesi
İnce duvarlı silindir (halka, çember)
Formülün türetilmesi
Bir cismin eylemsizlik momenti, onu oluşturan parçaların eylemsizlik momentlerinin toplamına eşittir. İnce duvarlı bir silindiri kütlesi olan elemanlara bölelim. DM ve eylemsizlik momentleri DJ ben. Daha sonra
J = ∑ d J ben = ∑ R ben 2 d m . (1) . (\displaystyle J=\toplam dJ_(i)=\toplam R_(i)^(2)dm.\qquad (1).)İnce duvarlı bir silindirin tüm elemanları dönme ekseninden aynı uzaklıkta olduğundan formül (1) şu şekle dönüştürülür:
J = ∑ R 2 d m = R 2 ∑ d m = m R 2 . (\displaystyle J=\toplam R^(2)dm=R^(2)\toplam dm=mR^(2).)Kalın duvarlı silindir (halka, kasnak)
Formülün türetilmesi
Dış yarıçaplı homojen bir halka olsun R, iç yarıçap R 1, kalın H ve yoğunluk ρ. İnce halkalara, kalın parçalara ayıralım doktor. İnce yarıçaplı bir halkanın kütlesi ve eylemsizlik momenti R olacak
d m = ρ d V = ρ ⋅ 2 π r h d r ; d J = r 2 d m = 2 π ρ h r 3 d r . (\displaystyle dm=\rho dV=\rho \cdot 2\pi rhdr;\qquad dJ=r^(2)dm=2\pi \rho hr^(3)dr.)Kalın halkanın eylemsizlik momentini integral olarak bulalım.
J = ∫ R 1 R d J = 2 π ρ h ∫ R 1 R r 3 d r = (\displaystyle J=\int _(R_(1))^(R)dJ=2\pi \rho h\int _ (R_(1))^(R)r^(3)dr=) = 2 π ρ sa r 4 4 | R 1 R = 1 2 π ρ h (R 4 - R 1 4) = 1 2 π ρ h (R 2 - R 1 2) (R 2 + R 1 2) . (\displaystyle =2\pi \rho h\left.(\frac (r^(4))(4))\right|_(R_(1))^(R)=(\frac (1)(2) ))\pi \rho h\left(R^(4)-R_(1)^(4)\right)=(\frac (1)(2))\pi \rho h\left(R^(2) )-R_(1)^(2)\sağ)\left(R^(2)+R_(1)^(2)\sağ).)Halkanın hacmi ve kütlesi eşit olduğundan
V = π (R 2 - R 1 2) h ; m = ρ V = π ρ (R 2 − R 1 2) h , (\displaystyle V=\pi \left(R^(2)-R_(1)^(2)\right)h;\qquad m= \rho V=\pi \rho \left(R^(2)-R_(1)^(2)\right)h,)halkanın eylemsizlik momentinin son formülünü elde ederiz
J = 1 2m (R2 + R12) . (\displaystyle J=(\frac (1)(2))m\sol(R^(2)+R_(1)^(2)\sağ).)Homojen disk (katı silindir)
Formülün türetilmesi
Bir silindiri (disk) sıfır iç yarıçaplı bir halka olarak düşünmek ( R 1 = 0), silindirin (disk) eylemsizlik momenti formülünü elde ederiz:
J = 12mR2 . (\displaystyle J=(\frac (1)(2))mR^(2).)Katı koni
Formülün türetilmesi
Koniyi kalınlıkta ince disklere ayıralım. DH, koninin eksenine dik. Böyle bir diskin yarıçapı eşittir
r = R h H , (\displaystyle r=(\frac (Rh)(H)))Nerede R– koni tabanının yarıçapı, H– koninin yüksekliği, H– koninin tepesinden diske olan mesafe. Böyle bir diskin kütlesi ve eylemsizlik momenti
d J = 1 2 r 2 d m = 1 2 π ρ r 4 d h = 1 2 π ρ (R h H) 4 d h ; (\displaystyle dJ=(\frac (1)(2))r^(2)dm=(\frac (1)(2))\pi \rho r^(4)dh=(\frac (1)( 2))\pi \rho \left((\frac (Rh)(H))\right)^(4)dh;)Entegre edersek şunu elde ederiz
J = ∫ 0 H d J = 1 2 π ρ (R H) 4 ∫ 0 H h 4 d h = 1 2 π ρ (R H) 4 h 5 5 | 0 H == 1 10 π ρ R 4 H = (ρ ⋅ 1 3 π R 2 H) 3 10 R 2 = 3 10 m R 2 . (\displaystyle (\begin(hizalanmış)J=\int _(0)^(H)dJ=(\frac (1)(2))\pi \rho \left((\frac (R)(H)) \right)^(4)\int _(0)^(H)h^(4)dh=(\frac (1)(2))\pi \rho \left((\frac (R)(H) )\right)^(4)\left.(\frac (h^(5))(5))\right|_(0)^(H)==(\frac (1)(10))\pi \rho R^(4)H=\left(\rho \cdot (\frac (1)(3))\pi R^(2)H\right)(\frac (3)(10))R^( 2)=(\frac (3)(10))mR^(2).\end(hizalanmış)))Katı homojen top
Formülün türetilmesi
Topu ince kalınlıkta disklere ayıralım DH, dönme eksenine dik. Yükseklikte bulunan böyle bir diskin yarıçapı H kürenin merkezinden itibaren formülü kullanarak buluruz
r = R 2 - h 2 . (\displaystyle r=(\sqrt (R^(2)-h^(2))).)Böyle bir diskin kütlesi ve eylemsizlik momenti
d m = ρ d V = ρ ⋅ π r 2 d h ; (\displaystyle dm=\rho dV=\rho \cdot \pi r^(2)dh;) d J = 1 2 r 2 d m = 1 2 π ρ r 4 d h = 1 2 π ρ (R 2 − h 2) 2 d h = 1 2 π ρ (R 4 − 2 R 2 h 2 + h 4) d h . (\displaystyle dJ=(\frac (1)(2))r^(2)dm=(\frac (1)(2))\pi \rho r^(4)dh=(\frac (1)( 2))\pi \rho \left(R^(2)-h^(2)\right)^(2)dh=(\frac (1)(2))\pi \rho \left(R^( 4)-2R^(2)h^(2)+h^(4)\right)dh.)Topun eylemsizlik momentini integral yoluyla buluruz:
J = ∫ − R R d J = 2 ∫ 0 R d J = π ρ ∫ 0 R (R 4 − 2 R 2 h 2 + h 4) d h = = π ρ (R 4 h − 2 3 R 2 h 3 + 1 5 sa 5) | 0 R = π ρ (R 5 − 2 3 R 5 + 1 5 R 5) = 8 15 π ρ R 5 = = (4 3 π R 3 ρ) ⋅ 2 5 R 2 = 2 5 m R 2 . (\displaystyle (\begin(aligned)J&=\int _(-R)^(R)dJ=2\int _(0)^(R)dJ=\pi \rho \int _(0)^(R )\left(R^(4)-2R^(2)h^(2)+h^(4)\right)dh=\\&=\pi \rho \left.\left(R^(4) h-(\frac (2)(3))R^(2)h^(3)+(\frac (1)(5))h^(5)\right)\right|_(0)^( R)=\pi \rho \left(R^(5)-(\frac (2)(3))R^(5)+(\frac (1)(5))R^(5)\right) =(\frac (8)(15))\pi \rho R^(5)=\\&=\left((\frac (4)(3))\pi R^(3)\rho \right) \cdot (\frac (2)(5))R^(2)=(\frac (2)(5))mR^(2).\end(hizalanmış)))İnce duvarlı küre
Formülün türetilmesi
Bunu elde etmek için homojen yarıçaplı bir topun eylemsizlik momenti formülünü kullanırız. R :
J 0 = 2 5 M R 2 = 8 15 π ρ R 5 . (\displaystyle J_(0)=(\frac (2)(5))MR^(2)=(\frac (8)(15))\pi \rho R^(5).)Sabit bir ρ yoğunluğunda yarıçapının sonsuz küçük bir miktarda artması durumunda topun eylemsizlik momentinin ne kadar değişeceğini hesaplayalım. dr. .
J = d J 0 d R d R = d d R (8 15 π ρ R 5) d R = = 8 3 π ρ R 4 d R = (ρ ⋅ 4 π R 2 d R) 2 3 R 2 = 2 3 mR2. (\displaystyle (\begin(hizalanmış)J&=(\frac (dJ_(0))(dR))dR=(\frac (d)(dR))\left((\frac (8)(15))\ pi \rho R^(5)\right)dR=\\&=(\frac (8)(3))\pi \rho R^(4)dR=\left(\rho \cdot 4\pi R^ (2)dR\right)(\frac (2)(3))R^(2)=(\frac (2)(3))mR^(2).\end(aligned)))İnce çubuk (eksen merkezden geçer)
Formülün türetilmesi
Çubuğu küçük uzunlukta parçalara ayıralım doktor. Böyle bir parçanın kütlesi ve eylemsizlik momenti eşittir
d m = m d r l ; d J = r 2 d m = m r 2 d r l . (\displaystyle dm=(\frac (mdr)(l));\qquad dJ=r^(2)dm=(\frac (mr^(2)dr)(l))).)Entegre edersek şunu elde ederiz
J = ∫ - l / 2 l / 2 d J = 2 ∫ 0 l / 2 d J = 2 m l ∫ 0 l / 2 r 2 d r = 2 m l r 3 3 | 0 l / 2 = 2 m l l 3 24 = 1 12 m l 2 . (\displaystyle J=\int _(-l/2)^(l/2)dJ=2\int _(0)^(l/2)dJ=(\frac (2m)(l))\int _ (0)^(l/2)r^(2)dr=(\frac (2m)(l))\left.(\frac (r^(3))(3))\right|_(0) ^(l/2)=(\frac (2m)(l))(\frac (l^(3))(24))=(\frac (1)(12))ml^(2.)İnce çubuk (eksen uçtan geçer)
Formülün türetilmesi
Dönme ekseni çubuğun ortasından ucuna doğru hareket ettiğinde çubuğun ağırlık merkezi eksene göre belirli bir mesafe kadar hareket eder. l ⁄ 2. Steiner teoremine göre yeni eylemsizlik momenti şuna eşit olacaktır:
J = J 0 + m r 2 = J 0 + m (l 2) 2 = 1 12 m l 2 + 1 4 m l 2 = 1 3 m l 2 . (\displaystyle J=J_(0)+mr^(2)=J_(0)+m\left((\frac (l)(2))\right)^(2)=(\frac (1)( 12))ml^(2)+(\frac (1)(4))ml^(2)=(\frac (1)(3))ml^(2.)Gezegenlerin ve uyduların boyutsuz atalet momentleri
Boyutsuz eylemsizlik momentleri, gezegenlerin ve uydularının iç yapılarının incelenmesi için büyük önem taşımaktadır. Yarıçaplı bir cismin boyutsuz eylemsizlik momenti R ve kitleler M dönme eksenine göre atalet momentinin, belirli bir mesafede bulunan sabit bir dönme eksenine göre aynı kütleye sahip bir maddi noktanın atalet momentine oranına eşittir R(eşittir Bay 2). Bu değer kütlenin derinlikteki dağılımını yansıtır. Gezegenlerin ve uyduların yakınında bunu ölçmenin yöntemlerinden biri, belirli bir gezegen veya uydunun yakınında uçan bir AMS tarafından iletilen radyo sinyalinin Doppler kaymasını belirlemektir. İnce duvarlı bir küre için boyutsuz atalet momenti 2/3 (~0,67), homojen bir top için 0,4'tür ve genel olarak, cismin kütlesi ne kadar küçükse merkezinde yoğunlaşan kütle o kadar büyük olur. Örneğin Ay'ın 0,4'e yakın (0,391'e eşit) boyutsuz bir eylemsizlik momenti vardır, dolayısıyla nispeten homojen olduğu, yoğunluğunun derinliğe göre çok az değiştiği varsayılır. Dünyanın boyutsuz eylemsizlik momenti, homojen bir topunkinden daha azdır (0,335'e eşit), bu da yoğun bir çekirdeğin varlığı lehine bir argümandır.
Merkezkaç atalet momenti
Dikdörtgen Kartezyen koordinat sisteminin eksenlerine göre bir cismin merkezkaç atalet momentleri aşağıdaki büyüklüklerdir:
J x y = ∫ (m) x y d m = ∫ (V) x y ρ d V , (\displaystyle J_(xy)=\int \limits _((m))xydm=\int \limits _((V))xy\ rho dV,) J x z = ∫ (m) x z d m = ∫ (V) x z ρ d V , (\displaystyle J_(xz)=\int \limits _((m))xzdm=\int \limits _((V))xz\ rho dV,) J y z = ∫ (m) y z d m = ∫ (V) y z ρ d V , (\displaystyle J_(yz)=\int \limits _((m))yzdm=\int \limits _((V))yz\ rho dV,)Nerede X , sen Ve z- hacimli küçük bir gövde elemanının koordinatları dV, yoğunluk ρ ve kütle DM .
OX ekseni denir vücudun eylemsizlik ana ekseni, eğer merkezkaç atalet momentleri J xy Ve Jxz aynı anda sıfıra eşittir. Cismin her noktasından üç ana atalet ekseni çizilebilir. Bu eksenler karşılıklı olarak birbirine diktir. Vücudun atalet momentleri keyfi bir noktada çizilen üç ana eylemsizlik eksenine göre Ö bedenler denir ana atalet momentleri bu bedenin.
Vücudun kütle merkezinden geçen ana atalet eksenlerine denir. vücudun ataletinin ana merkezi eksenleri ve bu eksenlere göre eylemsizlik momentleri onun ana merkezi atalet momentleri. Homojen bir cismin simetri ekseni her zaman ana merkezi atalet eksenlerinden biridir.
Geometrik atalet momentleri
Hacmin geometrik atalet momenti
J V a = ∫ (V) r 2 d V , (\displaystyle J_(Va)=\int \limits _((V))r^(2)dV,)daha önce olduğu gibi nerede R- elemandan uzaklık dV eksene A .
Alanın geometrik eylemsizlik momenti eksene göre - formülle ifade edilen vücudun geometrik bir özelliği:
J S a = ∫ (S) r 2 d S , (\displaystyle J_(Sa)=\int \limits _((S))r^(2)dS,)entegrasyonun yüzey üzerinde gerçekleştirildiği yer S, A dS- bu yüzeyin elemanı.
Boyut JSa- dördüncü kuvvete uzunluk ( d ben m J S a = L 4 (\displaystyle \mathrm (dim) J_(Sa)=\mathrm (L^(4)) )), sırasıyla SI ölçüm birimi 4'tür. İnşaat hesaplamalarında, literatürde ve haddelenmiş metal çeşitlerinde genellikle cm4 cinsinden belirtilir.
Kesitin direnç momenti, alanın geometrik atalet momenti ile ifade edilir:
W = J S a r m a x . (\displaystyle W=(\frac (J_(Sa))(r_(max))).)Burada maksimum r- yüzeyden eksene maksimum mesafe.
| Bazı şekillerin alanının geometrik atalet momentleri | |
|---|---|
| Dikdörtgen yüksekliği h (\displaystyle h) ve genişlik b (\displaystyle b): | J y = b h 3 12 (\displaystyle J_(y)=(\frac (bh^(3))(12)))
J z = h b 3 12 (\displaystyle J_(z)=(\frac (hb^(3))(12))) |
| Dış konturlar boyunca yükseklik ve genişliğe sahip dikdörtgen kutu kesiti H (\displaystyle H) Ve B (\displaystyle B) ve dahili olarak h (\displaystyle h) Ve b (\displaystyle b) sırasıyla | J z = B H 3 12 − b h 3 12 = 1 12 (B H 3 − b h 3) (\displaystyle J_(z)=(\frac (BH^(3))(12))-(\frac (bh^( 3))(12))=(\frac (1)(12))(BH^(3)-bh^(3)))
J y = H B 3 12 − h b 3 12 = 1 12 (H B 3 − h b 3) (\displaystyle J_(y)=(\frac (HB^(3))(12))-(\frac (hb^( 3))(12))=(\frac (1)(12))(HB^(3)-hb^(3))) |
| Daire çapı d (\displaystyle d) | J y = J z = π d 4 64 (\displaystyle J_(y)=J_(z)=(\frac (\pi d^(4))(64))) |
Uçağa göre eylemsizlik momenti
Katı bir cismin belirli bir düzleme göre atalet momenti, cismin her bir noktasının kütlesinin çarpımlarının, bu noktadan söz konusu düzleme olan mesafenin karesine eşit olan skaler bir niceliktir.
Eğer keyfi bir noktadan geçersek Ö (\displaystyle O) koordinat eksenlerini çiz x , y , z (\displaystyle x,y,z), daha sonra koordinat düzlemlerine göre eylemsizlik momentleri x Ö y (\displaystyle xOy), y Ö z (\displaystyle yOz) Ve z Ö x (\displaystyle zOx) formüllerle ifade edilecektir:
J x Ö y = ∑ ben = 1 n m ben z ben 2 , (\displaystyle J_(xOy)=\sum _(i=1)^(n)m_(i)z_(i)^(2)\ ,) J y Ö z = ∑ ben = 1 n m ben x ben 2 , (\displaystyle J_(yOz)=\sum _(i=1)^(n)m_(i)x_(i)^(2)\ ,) J z Ö x = ∑ ben = 1 n m ben y ben 2 . (\displaystyle J_(zOx)=\toplam _(i=1)^(n)m_(i)y_(i)^(2)\ .)Katı bir cisim durumunda, toplamanın yerini integral alma alır.
Merkezi eylemsizlik momenti
Merkezi eylemsizlik momenti (O noktasına göre eylemsizlik momenti, direğe göre eylemsizlik momenti, kutupsal eylemsizlik momenti) J Ö (\displaystyle J_(O))şu ifadeyle belirlenen miktardır:
J a = ∫ (m) r 2 d m = ∫ (V) ρ r 2 d V , (\displaystyle J_(a)=\int \limits _((m))r^(2)dm=\int \limits _((V))\rho r^(2)dV,)Merkezi atalet momenti, temel eksenel atalet momentleri cinsinden ifade edilebildiği gibi, düzlemlere ilişkin atalet momentleri cinsinden de ifade edilebilir:
J Ö = 1 2 (J x + J y + J z) , (\displaystyle J_(O)=(\frac (1)(2))\left(J_(x)+J_(y)+J_(z) \Sağ),) J Ö = J x Ö y + J y Ö z + J x Ö z . (\displaystyle J_(O)=J_(xOy)+J_(yOz)+J_(xOz.)Atalet tensörü ve atalet elipsoidi
Bir cismin kütle merkezinden geçen ve birim vektör tarafından belirlenen bir yöne sahip isteğe bağlı bir eksene göre atalet momenti s → = ‖ s x , s y , s z ‖ T , | → | = 1 (\displaystyle (\vec (s))=\left\Vert s_(x),s_(y),s_(z)\right\Vert ^(T),\left\vert (\vec (s) )\sağ\vert =1), ikinci dereceden (çift doğrusal) bir form biçiminde temsil edilebilir:
ben s = s → T ⋅ J ^ ⋅ s → , (\ displaystyle I_(s)=(\vec (s))^(T)\cdot (\hat (J))\cdot (\vec (s)) ,\qdört) (1)atalet tensörü nerede. Atalet tensör matrisi simetriktir ve boyutları vardır 3 × 3 (\displaystyle 3\times 3) ve merkezkaç momentlerinin bileşenlerinden oluşur:
Uygun koordinat sisteminin seçilmesiyle atalet tensör matrisi köşegen forma indirgenebilir. Bunu yapmak için tensör matrisinin özdeğer problemini çözmeniz gerekir. J ^ (\ displaystyle (\ şapka (J))):
Nerede S ^ (\ displaystyle (\ şapka (Q)))- Atalet tensörünün kendi tabanına dik geçiş matrisi. Uygun temelde, koordinat eksenleri atalet tensörünün ana eksenleri boyunca yönlendirilir ve ayrıca atalet tensör elipsoidinin ana yarı eksenleriyle çakışır. Miktarları J X , J Y , J Z (\displaystyle J_(X),J_(Y),J_(Z))- ana atalet momentleri. İfade (1) kendi koordinat sisteminde şu şekildedir:
buradan elipsoidin denklemini kendi koordinatlarında elde ederiz. Denklemin her iki tarafını da bölerek ben s (\displaystyle I_(s))
ve değiştirmeler yapıyoruz:
ξ = s x ben s , η = s y ben s , ζ = s z ben s , (\displaystyle \xi =(s_(x) \over (\sqrt (I_(s))))\eta =(s_(y ) \over (\sqrt (I_(s))))\zeta =(s_(z) \over (\sqrt (I_(s)))))elipsoid denkleminin kanonik formunu koordinatlarda elde ederiz ξ η ζ (\displaystyle \xi \eta \zeta ):
ξ 2 ⋅ J X + η 2 ⋅ J Y + ζ 2 ⋅ J Z = 1. (\displaystyle \xi ^(2)\cdot J_(X)+\eta ^(2)\cdot J_(Y)+\zeta ^( 2)\cdot J_(Z)=1.)Elipsoidin merkezinden belirli bir noktaya olan mesafe, elipsoidin merkezinden ve bu noktadan geçen düz bir çizgi boyunca cismin eylemsizlik momentinin değeriyle ilgilidir.
Eksenel atalet momenti, temel alanların çarpımlarının tüm bölümü ve söz konusu bölümün düzleminde yer alan belirli bir eksene olan mesafenin karesi üzerinden alınan toplamdır. Eksenel atalet momentinin büyüklüğü, kirişin bükülme deformasyonuna direnme yeteneğini karakterize eder.
J – Eksenel atalet momenti
j x = 
J y = 
Eksenel direnç momenti eksenel atalet momentinin nötr eksenden en uzak bölümün liflerine olan mesafeye oranı denir.
W – Eksenel direnç momenti.
W x = , W y =
Kutupsal eylemsizlik momenti tüm kesit üzerinden ele alındığında, temel alanların kesitin ağırlık merkezine olan uzaklıklarının karelerinin toplamına denir. Koordinat eksenleri kesişene kadar.
Polar atalet momenti, bir parçanın burulma deformasyonuna direnme yeteneğini karakterize eder.
Kutupsal eylemsizlik momenti.
= .
.
Kutupsal direnç anı kutupsal atalet momentinin, söz konusu kesitin ağırlık merkezinden kesitin en uzak noktalarına olan mesafeye oranıdır.
Kutupsal direnç anı
1. Dikdörtgen bölüm.

J y = (mm 4), J x = (mm 4)
G x =  (mm3), W y =
(mm3), W y =  (mm3)
(mm3)
2. Yuvarlak bölüm

J x = J y = (mm 4), = (mm 4)
W y = W x =  (mm3), =
(mm3), =  (mm3)
(mm3)
3. Halka bölümü

J x = J y = - =  (mm 4) , α=d/D
(mm 4) , α=d/D
W y = W x = 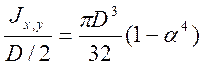 (mm3)
(mm3)
= 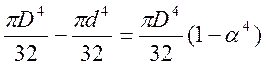 (mm4)
(mm4)
= (mm3)
(mm3)
4. Kutu bölümü.

j x =  =
= (mm4)
(mm4)
J y =  =
= (mm4)
(mm4)
G x =  (mm3)
(mm3)
W y =  (mm3)
(mm3)
Düzgün gerilim dağılımına sahip parçaların hesaplanması.
Bu tür parçalar, delikli ve pimli çubukların yanı sıra hidrolik ve pnömatik silindirler ve diğer basınçlı kaplar, bimetalik elemanlar (termal röleler) içerir.
Çekiş hesaplaması.

1) Çubuğa F çekme kuvveti uygulanıyor.
Çekiş çubuğu, etkisi altında gerildiği uzunlamasına bir yükü algılar. Bu durumda mutlak uzamanın büyüklüğü genişletilmiş Hooke yasasıyla belirlenir:
σ р =Eε. , σ р =F/A,  , σ р =F/A<=[
σ р ]= σ T / n -
, σ р =F/A<=[
σ р ]= σ T / n -
çekme çekme mukavemeti durumu, (A=H*B, A=).
Parmakla etkileşim sonucunda çıkıntılar temas alanı üzerinde ezilir.
Ezilme mukavemeti durumu:
σcm =F/A<=[σ см ]= 2σ T / n , A=d*b.
Parmaklar, gözlerle etkileşimden kaynaklanan kayma için hesaplanır:
τav =F/A<=[τ ср ]= 0,5σ T / n; A=*i, i - количество платежей среза (i=2).
2) Çubuğa F2 basınç kuvveti uygulanır.
İtme çubuğu sıkıştırmayla çalışır. Mutlak kısalmanın büyüklüğü de Hooke yasasıyla belirlenir:
σc =F/A<=[σ с ]=[σ р ]=σ T / n. – Для коротких стержней тяги.
Uzun çubuk - uzunluk, kesit boyutlarından birinin 3 katını aştığında. Burada çubuk çubuğunun anında bükülme olasılığı vardır.
σс =<=[σ с ]=[σ р ]=σ T / n, φ – коэффициент продольного изгиба, величина табличная – зависит от материала, гибкости стержня и характера закрепления концов стержня.
Delik ve parmaklar önceki hesaplamaya benzer şekilde hesaplanır.
İnce duvarlı damarların hesaplanması.
İnce duvarlı kaplar arasında hidrolik ve pnömatik silindirler, alıcılar, boru hatları vb. bulunur.
Şekle bağlı olarak gemiler şunlardır:
silindirik (hidrolik ve pnömatik silindirler, bazı alıcı türleri, boru hatları);
küresel (bazı alıcı türleri, silindirik kapların tabanları ve kapakları, membranlar vb.);
torus (boru hatlarının eğrisel bölümleri, işaretçi basınç göstergelerinin hassas elemanları).
Tüm kaplarda, sıvı veya gazın iç kuvvetlerinin etkisi altında, duvarlarda boyuna ve enine kesitlerde gerilmeler meydana gelir.
Silindirik kaplar.
 İnce silindirik bir kabuk P iç basıncıyla yüklenmiştir. - Silindirin kesiti olarak hesaplanır.
İnce silindirik bir kabuk P iç basıncıyla yüklenmiştir. - Silindirin kesiti olarak hesaplanır.
Torus gemileri.
Kavisli silindirik olarak hesaplanırlar.
15.10.04 Sıcaklık değiştiğinde ortaya çıkan gerilmelerin hesaplanması.

Sıcaklık dalgalandığında, sert destekler arasına sabitlenen bir parça, basınç veya çekme deformasyonuna maruz kalır. Sıcaklık Dt kadar arttığında (azaldığında), çubuğun mutlak uzama (kısalma) miktarı kadar uzaması (kısalması) gerekir:
Dben= AT* ben* DT, burada a t doğrusal genleşmenin sıcaklık katsayısıdır (çelik için 12*10 -6 °C -1), o zaman mutlak uzama (kısalma) değeri: Δε t = Δ ben / ben = a t* DT, ama çünkü Çubuk sert bir şekilde sabitlenirse uzayamaz (kısalamaz), bu nedenle malzemesinde değerleri Hooke yasasına göre belirlenen sıkıştırma (gerilme) gerilimleri ortaya çıkacaktır:
σ с,р =E*ε t =E*α t *Δt.
Bir kiriş kesitinin (kiriş, çubuk) atalet momentleri, kesit alanı gibi, mukavemet hesaplamalarında yer alan elemanın ana geometrik özelliklerinden biridir. Hatırlatayım ki, mukavemetli malzemelerin mukavemetinde kiriş, boyutlarından biri uzunluk olan bir elemandır...
Diğer ikisinden önemli ölçüde daha büyük - genişlik ve yükseklik. Malzemenin özellikleriyle birlikte kirişin mukavemet özelliklerini etkileyen son iki genel boyut artı şekildir.
Bir kesitin geometrik atalet momentleri, anlamları çok benzer olmasına rağmen cisimlerin atalet momentleriyle karıştırılmamalıdır. Bir cismin belirli bir eksen etrafındaki eylemsizlik momenti çarpımların toplamıdır. kitleler Vücudun temel “hacim” noktaları, eksenden bu noktalara olan mesafelerin karesi ile hesaplanır. Bir bölümün atalet momenti (düz şekil) çarpımların toplamıdır alanlar bu bölümün temel “düz” noktaları, söz konusu eksene olan uzaklıkların karesi ile hesaplanır.
Bir kirişin herhangi bir kesitinin oluşturulabileceği neredeyse otuz temel rakamın eksenel atalet momentlerinin yanı sıra atalet yarıçapları ve direnç momentlerini hesaplamak için formüller “Malzemelerin direnç elemanları” bölümünde alınabilir. makine mühendisi “Tasarımcının El Kitabı” cilt No. 1'in 1 numaralı “Genel teknik bilgiler” bölümü" V.I. Anuriev. Birkaç nesil makine mühendisinin ana referans kitabı olan ve yaklaşık on kez yeniden basılan bu üç ciltlik referans kitabı, bugün de talep görmeye ve alakalı olmaya devam ediyor. Her mühendisin buna sahip olması gerektiğini düşünüyorum, özellikle de internette bulmak sorun olmadığı için. Elbette ilgilendiğimiz formüller diğer referans literatürde de bulunabilir.
Makine mühendisliği ve inşaatta yaygın olarak kullanılan I-kirişler, kanallar, açılar, borular ve diğer haddelenmiş ve bükülmüş profiller için, atalet momentleri de dahil olmak üzere bölümlerin geometrik özellikleri GOST, OST ve diğer düzenleyici belgelerin tablolarında bulunabilir. Üretimlerini düzenleyen.
İki veya daha fazla temel profilden oluşan kirişler ve çubuklar, ağırlık ve boyut açısından tek bir profille yeterli şekilde değiştirilemeyen elemanların mukavemetini ve sertliğini arttırmak için kullanılır. Uygulamada bunlar eşleştirilmiş köşeler, iki kollu sütunlar, levha şeritle güçlendirilmiş kayışlı kirişler ve diğer durumlardır.
Kompozit kesitin geometrik özellikleri. Excel'de hesaplama.
Makalede örnek olarak bir üçgen ve yarım daire kesimli bir dikdörtgenden oluşan kompozit bir figürü ele aldık. Bu örnekle devam edelim. Her ne kadar pratikte bu kadar tuhaf bir kesite sahip bir kirişi muhtemelen hiçbir zaman göremeyecek olsanız da, çok karmaşık olmayan ve açıklayıcı bir örnek için bu bize çok yakışacaktır!

MS Excel veya OOo Calc'ı başlatın ve başlayın!
Blog makalelerinde kullanılan elektronik tabloların biçimlendirilmesine ilişkin genel kuralları burada bulabilirsiniz.
Yukarıda belirtilen makaleden ağırlık merkezlerinin koordinatlarını, kesit elemanlarının alanlarını ve tüm kompozit bölümün alanını zaten biliyoruz. Bu yazımızda başladığımız çalışmaya devam edeceğiz ve diğer geometrik özellikleri hesaplayacağız.
İlk veri:
Öğeler 1 , 2 , 3 dosyadan kopyalayın ve D3:F6 hücre aralığını doldurun.
4. Elemanların kendi merkez eksenlerine göre eksenel ve merkezkaç atalet momentlerini hesaplayalım. Ixi , iyi , Ixiyi cm4 cinsinden, V.I.'nin “Mekanik Tasarımcılar El Kitabı” ndaki formüller kullanılarak. Anuriyeva
D7 hücresinde: =80*40^3/12/10000 =42,667
Ix1 = A 1 *(B1 ^3)/12
D8 hücresinde: =40*80^3/12/10000 =170,667
Iy1 = b1 *(a1 ^3)/12
D9 hücresinde: =0 =0,000
Ix1 sen1 = 0 (eksenel simetriye sahip eleman)
E7 hücresinde: =24*42^3/36/10000 =4,939
Ix2 = A 2 *(H 2 ^3)/36
E8 hücresinde: =42*24^3/48/10000 =1,210
Iy2 = H 2 *(A 2 ^3)/48
E9 hücresinde: =0 =0,000
Ix2 sen2 = 0 (eksenel simetriye sahip eleman)
F7 hücresinde: =- (PI()/8*26^4-8/9/PI()*26^4)/10000=-5,016
Ix3 =- (π /8)*(R 3 ^4) — (8/(9* π ))*(R 3 ^4)
F8 hücresinde: =-PI()/8*26^4/10000 =-17,945
Iy3 =- (π /8)*(R 3 ^4)
F9 hücresinde: =0 =0,000
Ix3 sen3 = 0 (eksenel simetriye sahip eleman)
Üçüncü elemanın - yarım dairenin - eksenel atalet momentleri negatiftir çünkü bu bir dikdörtgenin içindeki bir kesiktir - boş bir alan!

Geometrik özelliklerin hesaplanması:
Öğeler 5 , 6 , 7 dosyadan kopyalayın ve birleştirilmiş D11E11F11...D15E15F15 hücrelerini doldurun.
8. Ağırlık merkezinden çizilen x0 ve y0 merkezi eksenlerine göre kesitin eksenel ve merkezkaç atalet momentlerini hesaplayalım. Ix 0 , Iy 0 , Ix0 sen0 cm4 cinsinden
birleştirilmiş D16E16F16 hücresinde: =((D5-D15)^2*D6+(E5-D15)^2*E6+(F5-D15)^2*F6)/10000+D7+E7+F7=90,122
Ix0 = Σ ((yci — Yc )^2* Fi )+ ΣIxi
birleştirilmiş D17E17F17 hücresinde: =((D4-D14)^2*D6+(E4-D14)^2*E6+(F4-D14)^2*F6)/10000+D8+E8+F8=159,678
Iy0 = Σ ((xci — Xc )^2* Fi )+ ΣIyi
birleştirilmiş D18E18F18 hücresinde: =((D5-D15)*(D4-D14)*D6+(E5-D15)*(E4-D14)*E6+(F5-D15)*(F4-D14)*F6)/10000+D9+E9+F9=-50,372
Ix0y0 = Σ ((yci -Yc )*(xci -Xc )*Fi )+Σ Ixiyi
9. Kesitin ana merkezi atalet momentlerini hesaplayalım IV Ve Iu cm4 cinsinden
birleştirilmiş D19E19F19 hücresinde: =($D$16+$D$17)/2+((($D$16-$D$17)/2)^2+$D$18^2)^0,5=186,111
Iv =(Ix0 +Iy0 )/2+(((Ix0 -Iy0 )/2)^2+Ix0y0 ^2)^0,5
birleştirilmiş D20E20F20 hücresinde: =($D$16+$D$17)/2- ((($D$16-$D$17)/2)^2+$D$18^2)^0,5=63,689
Iu =(Ix0 +Iy0 )/2- (((Ix0 -Iy0 )/2)^2+Ix0y0 ^2)^0,5
10. Ana eksen v'nin merkez eksen x0'a olan eğim açısını bulalım α derece olarak
birleştirilmiş D21E21F21 hücresinde: =ATAN(D18/(D20-D16))/PI()*180=62,311
α =arctg (Ix0y0 /(Iu -Ix0 ))
11. Sonuç olarak kompozit bölümün dönme yarıçapını hesaplıyoruz IV Ve ben mm cinsinden
birleştirilmiş D22E22F22 hücresinde: =(D19*10000/D11)^0,5 =26,540
IV =(IV / F 0 )^0,5
birleştirilmiş D23E23F23 hücresinde: =(D20*10000/D11)^0,5 =15,526
ben =(Iu / F 0 )^0,5
Görev tamamlandı - üç basit elemanın kompozit bölümünün atalet momentleri ve dönme yarıçapları hesaplandı! Atalet elipsinin oluşturulması için gerekli tüm veriler elde edilmiştir.
Hesaplama programına sahip bir Excel dosyası, iki veya üç basit elemandan oluşan bir kirişin kesitinin geometrik özelliklerinin tam bir hesaplamasını kolayca yapmanızı sağlar. Gerektiğinde hesaplama modülünün yeteneklerini daha fazla sayıda öğeye genişletmek kolaydır.
İçin alma yeni makaleler hakkında bilgi ve için çalışan program dosyalarını indirme lütfen abone olun Duyurular için her makalenin sonunda yer alan pencerede veya sayfanın üst kısmındaki pencerede.
Unutma onaylamak abonelik linke tıklayarak Belirtilen postayla size hemen gelecek bir mektupta (klasöre gelebilir) « İstenmeyen e-posta » )!!!
Yorumlarınızı ilgiyle okuyacağım sevgili okurlar!!! Düşüncelerini paylaş!
yalvarırım yazarın çalışmasına saygı duymak dosyayı hesaplama programıyla indirin abonelikten sonra makale duyuruları için!