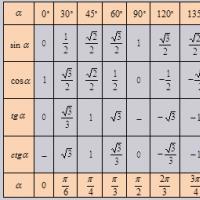
Sinüs kosinüs teğet kotanjant trigonometri değerleri tablosu

0, 30, 45, 60, 90, ... derecelik açılar için temel trigonometrik fonksiyonlar tablosu

$\sin$, $\cos$, $\tan$ ve $\cot$ fonksiyonlarının trigonometrik tanımlarından, $0$ ve $90$ derece açıları için değerlerini bulabilirsiniz:

$\sin⁡0°=0$, $\cos0°=1$, $\tan 0°=0$, $\cot 0°$ tanımlanmadı;

$\sin90°=1$, $\cos90°=0$, $\cot90°=0$, $\tan 90°$ tanımlı değil.

Bir okul geometri dersinde dik üçgenler incelenirken $0°$, $30°$, $45°$, $60°$ ve $90°$ açılarının trigonometrik fonksiyonları bulunur.

Belirtilen açılar için sırasıyla derece ve radyan cinsinden trigonometrik fonksiyonların değerleri bulundu ($0$, $\frac(\pi)(6)$, $\frac(\pi)(4)$, $\frac(\ ezberleme ve kullanım kolaylığı için pi)(3) $, $\frac(\pi)(2)$) adlı bir tabloya girilir. trigonometrik tablo, trigonometrik fonksiyonların temel değerleri tablosu ve benzeri.

İndirgeme formülleri kullanıldığında, trigonometrik tablo 360$°$'lık bir açıya ve buna göre $2\pi$ radyana kadar genişletilebilir:

Trigonometrik fonksiyonların periyodiklik özelliklerini kullanarak, bilinenden 360°$ kadar farklı olacak her açı hesaplanıp bir tabloya kaydedilebilir. Örneğin, $0°$ açısı için trigonometrik fonksiyon, $0°+360°$ açısı için, $0°+2 \cdot 360°$ açısı için ve $0°+3 \cdot 360°$ açısı için aynı değere sahip olacaktır. ve benzeri.

Trigonometrik bir tablo kullanarak birim çemberin tüm açılarının değerlerini belirleyebilirsiniz.

Bir okul geometri dersinde, trigonometrik problemleri çözme kolaylığı için trigonometrik bir tabloda toplanan trigonometrik fonksiyonların temel değerlerini ezberlemeniz beklenir.

Bir tablo kullanma

Tabloda gerekli trigonometrik fonksiyonu ve bu fonksiyonun hesaplanması gereken açı veya radyan değerini bulmanız yeterlidir. Satırın fonksiyonla ve sütunun değerle kesiştiği noktada, verilen argümanın trigonometrik fonksiyonunun istenen değerini elde ederiz.

Şekilde $\frac(1)(2)$'a eşit olan $\cos⁡60°$ değerini nasıl bulacağınızı görebilirsiniz.

Genişletilmiş trigonometrik tablo aynı şekilde kullanılır. Bunu kullanmanın avantajı, daha önce de belirtildiği gibi, hemen hemen her açının trigonometrik fonksiyonunun hesaplanmasıdır. Örneğin, $\tan 1 380°=\tan (1 380°-360°)=\tan(1 020°-360°)=\tan(660°-360°)=\tan300 değerini kolayca bulabilirsiniz. °$:

Temel trigonometrik fonksiyonların Bradis tabloları

Derece tamsayı değeri ve dakika tamsayı değeri için kesinlikle herhangi bir açı değerinin trigonometrik fonksiyonunu hesaplama yeteneği Bradis tablolarının kullanılmasıyla sağlanır. Örneğin, $\cos⁡34°7"$ değerini bulun. Tablolar 2 bölüme ayrılmıştır: $\sin$ ve $\cos$ değerleri tablosu ve $ değerleri tablosu \tan$ ve $\cot$.

Bradis tabloları, trigonometrik fonksiyonların yaklaşık değerlerini 4 ondalık basamağa kadar doğrulukla elde etmeyi mümkün kılar.

Bradis tablolarını kullanma

Sinüsler için Bradis tablolarını kullanarak $\sin⁡17°42"$'ı buluruz. Bunu yapmak için sinüs ve kosinüs tablosunun sol sütununda derece değerini - $17°$ ve üst satırda buluruz. dakikaların değerini buluyoruz - $42"$. Kesişmelerinde istenen değeri elde ederiz:

$\sin17°42"=0,304$.

$\sin17°44"$ değerini bulmak için tablonun sağ tarafındaki düzeltmeyi kullanmanız gerekir. Bu durumda tablodaki $42"$ değerine $2 düzeltmesini eklemeniz gerekir. "$, bu da $0,0006$'a eşittir. Şunu elde ederiz:

$\sin17°44"=0,304+0,0006=0,3046$.

$\sin17°47"$ değerini bulmak için tablonun sağ tarafındaki düzeltmeyi de kullanırız, ancak bu durumda $\sin17°48"$ değerini temel alır ve $1"$ düzeltmesini çıkarırız :

$\sin17°47"=0,3057-0,0003=0,3054$.

Kosinüsleri hesaplarken de benzer işlemler yapıyoruz ancak tablonun sağ sütununda derecelere, alt sütununda ise dakikalara bakıyoruz. Örneğin, $\cos20°=0,9397$.

$90°$'a kadar olan teğet değerler ve küçük açı kotanjantları için herhangi bir düzeltme yoktur. Örneğin, tabloya göre $4.967$'a eşit olan $\tan 78°37"$'ı bulalım.

Sinüs (sin), kosinüs (cos), teğet (tg), kotanjant (ctg) değer tabloları, hem teorik hem de uygulamalı birçok problemi çözmeye yardımcı olan güçlü ve kullanışlı bir araçtır. Bu makalede 0, 30, 45, 60, 90, ..., 360 derecelik (0, π 6, π 3, π) açılar için temel trigonometrik fonksiyonların (sinüsler, kosinüsler, teğetler ve kotanjantlar) tablosunu sunacağız 2,... , 2 π radyan). Sinüsler ve kosinüsler, teğetler ve kotanjantlar için ayrı Bradis tabloları da gösterilecek ve bunların temel trigonometrik fonksiyonların değerlerini bulmak için nasıl kullanılacağı açıklanacak.

0, 30, 45, 60, 90, ..., 360 derece açılar için temel trigonometrik fonksiyonlar tablosu

Sinüs, kosinüs, tanjant ve kotanjant tanımlarından yola çıkarak bu fonksiyonların 0 ve 90 derecelik açılar için değerlerini bulabilirsiniz.

sin 0 = 0, cos 0 = 1, tg 0 = 0, sıfır kotanjant tanımlı değil,

sin 90° = 1, cos 90° = 0, c t g 90° = 0, doksan derecenin tanjantı tanımlanmamıştır.

Geometri dersinde sinüs, kosinüs, teğet ve kotanjant değerleri, açıları 30, 60 ve 90 derece ve ayrıca 45, 45 ve 90 derece olan bir dik üçgenin kenarlarının oranı olarak tanımlanır.

Dik üçgende dar açı için trigonometrik fonksiyonları tanımlama

Sinüs- karşı tarafın hipotenüse oranı.

Kosinüs- bitişik bacağın hipotenüse oranı.

Teğet- karşı tarafın bitişik tarafa oranı.

Kotanjant- Bitişik tarafın karşı tarafa oranı.

Tanımlara uygun olarak fonksiyonların değerleri bulunur:

sin 30 ° = 1 2 , çünkü 30 ° = 3 2 , tg 30 ° = 3 3 , c tg 30 ° = 3 , sin 45 ° = 2 2 , çünkü 45 ° = 2 2 , tg 45 ° = 1 , c tg 45 ° = 1, sin 60° = 3 2, cos 45° = 1 2, tg 45° = 3, c tg 45° = 3 3.

Bu değerleri bir tabloya koyalım ve buna sinüs, kosinüs, tanjant ve kotanjantın temel değerlerinin tablosu diyelim.

Sinüs, kosinüs, teğet ve kotanjantların temel değerleri tablosu

α °	0	30	45	60	90
günah α	0	1 2	2 2	3 2	1
çünkü α	1	3 2	2 2	1 2	0
tgα	0	3 3	1	3	tanımsız
c t g α	tanımsız	3	1	3 3	0
α, r a d i a n	0	π 6	π4	π3	π2

Trigonometrik fonksiyonların önemli özelliklerinden biri periyodikliktir. Bu özelliğe dayanarak bu tablo indirgeme formülleri kullanılarak genişletilebilir. Aşağıda 0, 30, 60, ... , 120, 135, 150, 180, ... , 360 derece (0, π 6, π 3) açıları için ana trigonometrik fonksiyonların değerlerinin genişletilmiş bir tablosunu sunuyoruz. , π 2, ... , 2 π radyan).

Sinüs, kosinüs, teğet ve kotanjant tablosu

α °	0	30	45	60	90	120	135	150	180	210	225	240	270	300	315	330	360
günah α	0	1 2	2 2	3 2	1	3 2	2 2	1 2	0	- 1 2	- 2 2	- 3 2	- 1	- 3 2	- 2 2	- 1 2	0
çünkü α	1	3 2	2 2	1 2	0	- 1 2	- 2 2	- 3 2	- 1	- 3 2	- 2 2	- 1 2	0	1 2	2 2	3 2	1
tgα	0	3 3	1	3	-	- 1	- 3 3	0	0	3 3	1	3	-	- 3	- 1		0
c t g α	-	3	1	3 3	0	- 3 3	- 1	- 3	-	3	1	3 3	0	- 3 3	- 1	- 3	-
α, r a d i a n	0	π 6	π4	π3	π2	2 π 3	3 π 4	5 π 6	π	7 π 6	5 π 4	4 π 3	3 π 2	5 π 3	7 π 4	11 π 6	2π

Sinüs, kosinüs, tanjant ve kotanjantın periyodikliği, bu tabloyu isteğe bağlı olarak büyük açı değerlerine genişletmenize olanak tanır. Tabloda toplanan değerler en çok problem çözerken kullanılır, bu nedenle bunların ezberlenmesi önerilir.

Trigonometrik fonksiyonların temel değerleri tablosu nasıl kullanılır?

Sinüsler, kosinüsler, teğetler ve kotanjantların değer tablosunu kullanma ilkesi sezgisel düzeyde açıktır. Bir satır ile bir sütunun kesişimi, belirli bir açı için fonksiyonun değerini verir.

Örnek. Sinüs, kosinüs, teğet ve kotanjant tablosu nasıl kullanılır?

Sin 7 π 6'nın neye eşit olduğunu bulmamız gerekiyor

Tabloda son hücre değeri 7 π 6 radyan, yani 210 derece olan bir sütun buluyoruz. Daha sonra sinüs değerlerinin sunulduğu tablonun terimini seçiyoruz. Satır ve sütunun kesişiminde istenen değeri buluruz:

günah 7 π 6 = - 1 2

Bradis masaları

Bradis tablosu sinüs, kosinüs, tanjant veya kotanjant değerini bilgisayar teknolojisi kullanmadan 4 ondalık basamak hassasiyetiyle hesaplamanıza olanak tanır. Bu bir tür mühendislik hesap makinesinin yerine geçer.

Referans

Vladimir Modestovich Bradis (1890 - 1975) - Sovyet matematikçi-öğretmen, 1954'ten beri SSCB Pedagoji Bilimleri Akademisi'nin ilgili üyesi. Bradis tarafından geliştirilen dört basamaklı logaritma ve doğal trigonometrik büyüklük tabloları ilk olarak 1921'de yayınlandı.

Öncelikle sinüs ve kosinüsler için Bradis tablosunu sunuyoruz. Tamsayı derece ve dakika içeren açılar için bu fonksiyonların yaklaşık değerlerini oldukça doğru bir şekilde hesaplamanıza olanak tanır. Tablonun en soldaki sütunu dereceleri, üst satırı ise dakikaları temsil eder. Bradis tablosunun tüm açı değerlerinin altı dakikanın katları olduğuna dikkat edin.

Sinüs ve kosinüsler için Bradis tablosu

günah	0"	6"	12"	18"	24"	30"	36"	42"	48"	54"	60"	çünkü	1"	2"	3"
											0.0000	90°
0°	0.0000	0017	0035	0052	0070	0087	0105	0122	0140	0157	0175	89°	3	6	9
1°	0175	0192	0209	0227	0244	0262	0279	0297	0314	0332	0349	88°	3	6	9
2°	0349	0366	0384	0401	0419	0436	0454	0471	0488	0506	0523	87°	3	6	9
3°	0523	0541	0558	0576	0593	0610	0628	0645	0663	0680	0698	86°	3	6	9
4°	0698	0715	0732	0750	0767	0785	0802	0819	0837	0854	0.0872	85°	3	6	9
5°	0.0872	0889	0906	0924	0941	0958	0976	0993	1011	1028	1045	84°	3	6	9
6°	1045	1063	1080	1097	1115	1132	1149	1167	1184	1201	1219	83°	3	6	9
7°	1219	1236	1253	1271	1288	1305	1323	1340	1357	1374	1392	82°	3	6	9
8°	1392	1409	1426	1444	1461	1478	1495	1513	1530	1547	1564	81°	3	6	9
9°	1564	1582	1599	1616	1633	1650	1668	1685	1702	1719	0.1736	80°	3	6	9
10°	0.1736	1754	1771	1788	1805	1822	1840	1857	1874	1891	1908	79°	3	6	9
11°	1908	1925	1942	1959	1977	1994	2011	2028	2045	2062	2079	78°	3	6	9
12°	2079	2096	2113	2130	2147	2164	2181	2198	2215	2233	2250	77°	3	6	9
13°	2250	2267	2284	2300	2317	2334	2351	2368	2385	2402	2419	76°	3	6	8
14°	2419	2436	2453	2470	2487	2504	2521	2538	2554	2571	0.2588	75°	3	6	8
15°	0.2588	2605	2622	2639	2656	2672	2689	2706	2723	2740	2756	74°	3	6	8
16°	2756	2773	2790	2807	2823	2840	2857	2874	2890	2907	2924	73°	3	6	8
17°	2924	2940	2957	2974	2990	3007	3024	3040	3057	3074	3090	72°	3	6	8
18°	3090	3107	3123	3140	3156	3173	3190	3206	3223	3239	3256	71°	3	6	8
19°	3256	3272	3289	3305	3322	3338	3355	3371	3387	3404	0.3420	70°	3	5	8
20°	0.3420	3437	3453	3469	3486	3502	3518	3535	3551	3567	3584	69°	3	5	8
21°	3584	3600	3616	3633	3649	3665	3681	3697	3714	3730	3746	68°	3	5	8
22°	3746	3762	3778	3795	3811	3827	3843	3859	3875	3891	3907	67°	3	5	8
23°	3907	3923	3939	3955	3971	3987	4003	4019	4035	4051	4067	66°	3	5	8
24°	4067	4083	4099	4115	4131	4147	4163	4179	4195	4210	0.4226	65°	3	5	8
25°	0.4226	4242	4258	4274	4289	4305	4321	4337	4352	4368	4384	64°	3	5	8
26°	4384	4399	4415	4431	4446	4462	4478	4493	4509	4524	4540	63°	3	5	8
27°	4540	4555	4571	4586	4602	4617	4633	4648	4664	4679	4695	62°	3	5	8
28°	4695	4710	4726	4741	4756	4772	4787	4802	4818	4833	4848	61°	3	5	8
29°	4848	4863	4879	4894	4909	4924	4939	4955	4970	4985	0.5000	60°	3	5	8
30°	0.5000	5015	5030	5045	5060	5075	5090	5105	5120	5135	5150	59°	3	5	8
31°	5150	5165	5180	5195	5210	5225	5240	5255	5270	5284	5299	58°	2	5	7
32°	5299	5314	5329	5344	5358	5373	5388	5402	5417	5432	5446	57°	2	5	7
33°	5446	5461	5476	5490	5505	5519	5534	5548	5563	5577	5592	56°	2	5	7
34°	5592	5606	5621	5635	5650	5664	5678	5693	5707	5721	0.5736	55°	2	5	7
35°	0.5736	5750	5764	5779	5793	5807	5821	5835	5850	5864	0.5878	54°	2	5	7
36°	5878	5892	5906	5920	5934	5948	5962	5976	5990	6004	6018	53°	2	5	7
37°	6018	6032	6046	6060	6074	6088	6101	6115	6129	6143	6157	52°	2	5	7
38°	6157	6170	6184	6198	6211	6225	6239	6252	6266	6280	6293	51°	2	5	7
39°	6293	6307	6320	6334	6347	6361	6374	6388	6401	6414	0.6428	50°	2	4	7
40°	0.6428	6441	6455	6468	6481	6494	6508	6521	6534	6547	6561	49°	2	4	7
41°	6561	6574	6587	6600	6613	6626	6639	6652	6665	6678	6691	48°	2	4	7
42°	6691	6704	6717	6730	6743	6756	6769	6782	6794	6807	6820	47°	2	4	6
43°	6820	6833	6845	6858	6871	6884	6896	8909	6921	6934	6947	46°	2	4	6
44°	6947	6959	6972	6984	6997	7009	7022	7034	7046	7059	0.7071	45°	2	4	6
45°	0.7071	7083	7096	7108	7120	7133	7145	7157	7169	7181	7193	44°	2	4	6
46°	7193	7206	7218	7230	7242	7254	7266	7278	7290	7302	7314	43°	2	4	6
47°	7314	7325	7337	7349	7361	7373	7385	7396	7408	7420	7431	42°	2	4	6
48°	7431	7443	7455	7466	7478	7490	7501	7513	7524	7536	7547	41°	2	4	6
49°	7547	7559	7570	7581	7593	7604	7615	7627	7638	7649	0.7660	40°	2	4	6
50°	0.7660	7672	7683	7694	7705	7716	7727	7738	7749	7760	7771	39°	2	4	6
51°	7771	7782	7793	7804	7815	7826	7837	7848	7859	7869	7880	38°	2	4	5
52°	7880	7891	7902	7912	7923	7934	7944	7955	7965	7976	7986	37°	2	4	5
53°	7986	7997	8007	8018	8028	8039	8049	8059	8070	8080	8090	36°	2	3	5
54°	8090	8100	8111	8121	8131	8141	8151	8161	8171	8181	0.8192	35°	2	3	5
55°	0.8192	8202	8211	8221	8231	8241	8251	8261	8271	8281	8290	34°	2	3	5
56°	8290	8300	8310	8320	8329	8339	8348	8358	8368	8377	8387	33°	2	3	5
57°	8387	8396	8406	8415	8425	8434	8443	8453	8462	8471	8480	32°	2	3	5
58°	8480	8490	8499	8508	8517	8526	8536	8545	8554	8563	8572	31°	2	3	5
59°	8572	8581	8590	8599	8607	8616	8625	8634	8643	8652	0.8660	30°	1	3	4
60°	0.8660	8669	8678	8686	8695	8704	8712	8721	8729	8738	8746	29°	1	3	4
61°	8746	8755	8763	8771	8780	8788	8796	8805	8813	8821	8829	28°	1	3	4
62°	8829	8838	8846	8854	8862	8870	8878	8886	8894	8902	8910	27°	1	3	4
63°	8910	8918	8926	8934	8942	8949	8957	8965	8973	8980	8988	26°	1	3	4
64°	8988	8996	9003	9011	9018	9026	9033	9041	9048	9056	0.9063	25°	1	3	4
65°	0.9063	9070	9078	9085	9092	9100	9107	9114	9121	9128	9135	24°	1	2	4
66°	9135	9143	9150	9157	9164	9171	9178	9184	9191	9198	9205	23°	1	2	3
67°	9205	9212	9219	9225	9232	9239	9245	9252	9259	9256	9272	22°	1	2	3
68°	9272	9278	9285	9291	9298	9304	9311	9317	9323	9330	9336	21°	1	2	3
69°	9336	9342	9348	9354	9361	9367	9373	9379	9383	9391	0.9397	20°	1	2	3
70°	9397	9403	9409	9415	9421	9426	9432	9438	9444	9449	0.9455	19°	1	2	3
71°	9455	9461	9466	9472	9478	9483	9489	9494	9500	9505	9511	18°	1	2	3
72°	9511	9516	9521	9527	9532	9537	9542	9548	9553	9558	9563	17°	1	2	3
73°	9563	9568	9573	9578	9583	9588	9593	9598	9603	9608	9613	16°	1	2	2
74°	9613	9617	9622	9627	9632	9636	9641	9646	9650	9655	0.9659	15°	1	2	2
75°	9659	9664	9668	9673	9677	9681	9686	9690	9694	9699	9703	14°	1	1	2
76°	9703	9707	9711	9715	9720	9724	9728	9732	9736	9740	9744	13°	1	1	2
77°	9744	9748	9751	9755	9759	9763	9767	9770	9774	9778	9781	12°	1	1	2
78°	9781	9785	9789	9792	9796	9799	9803	9806	9810	9813	9816	11°	1	1	2
79°	9816	9820	9823	9826	9829	9833	9836	9839	9842	9845	0.9848	10°	1	1	2
80°	0.9848	9851	9854	9857	9860	9863	9866	9869	9871	9874	9877	9°	0	1	1
81°	9877	9880	9882	9885	9888	9890	9893	9895	9898	9900	9903	8°	0	1	1
82°	9903	9905	9907	9910	9912	9914	9917	9919	9921	9923	9925	7°	0	1	1
83°	9925	9928	9930	9932	9934	9936	9938	9940	9942	9943	9945	6°	0	1	1
84°	9945	9947	9949	9951	9952	9954	9956	9957	9959	9960	9962	5°	0	1	1
85°	9962	9963	9965	9966	9968	9969	9971	9972	9973	9974	9976	4°	0	0	1
86°	9976	9977	9978	9979	9980	9981	9982	9983	9984	9985	9986	3°	0	0	0
87°	9986	9987	9988	9989	9990	9990	9991	9992	9993	9993	9994	2°	0	0	0
88°	9994	9995	9995	9996	9996	9997	9997	9997	9998	9998	0.9998	1°	0	0	0
89°	9998	9999	9999	9999	9999	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	0°	0	0	0
90°	1.0000
günah	60"	54"	48"	42"	36"	30"	24"	18"	12"	6"	0"	çünkü	1"	2"	3"

Tabloda gösterilmeyen açıların sinüs ve kosinüs değerlerini bulmak için düzeltmelerin kullanılması gerekir.

Şimdi teğetler ve kotanjantlar için Bradis tablosunu sunuyoruz. 0 ila 76 derece arasındaki açıların teğet değerlerini ve 14 ila 90 derece arasındaki açıların kotanjantlarını içerir.

Teğet ve kotanjant için Bradis tablosu

tg	0"	6"	12"	18"	24"	30"	36"	42"	48"	54"	60"	ctg	1"	2"	3"
											0	90°
0°	0,000	0017	0035	0052	0070	0087	0105	0122	0140	0157	0175	89°	3	6	9
1°	0175	0192	0209	0227	0244	0262	0279	0297	0314	0332	0349	88°	3	6	9
2°	0349	0367	0384	0402	0419	0437	0454	0472	0489	0507	0524	87°	3	6	9
3°	0524	0542	0559	0577	0594	0612	0629	0647	0664	0682	0699	86°	3	6	9
4°	0699	0717	0734	0752	0769	0787	0805	0822	0840	0857	0,0875	85°	3	6	9
5°	0,0875	0892	0910	0928	0945	0963	0981	0998	1016	1033	1051	84°	3	6	9
6°	1051	1069	1086	1104	1122	1139	1157	1175	1192	1210	1228	83°	3	6	9
7°	1228	1246	1263	1281	1299	1317	1334	1352	1370	1388	1405	82°	3	6	9
8°	1405	1423	1441	1459	1477	1495	1512	1530	1548	1566	1584	81°	3	6	9
9°	1584	1602	1620	1638	1655	1673	1691	1709	1727	1745	0,1763	80°	3	6	9
10°	0,1763	1781	1799	1817	1835	1853	1871	1890	1908	1926	1944	79°	3	6	9
11°	1944	1962	1980	1998	2016	2035	2053	2071	2089	2107	2126	78°	3	6	9
12°	2126	2144	2162	2180	2199	2217	2235	2254	2272	2290	2309	77°	3	6	9
13°	2309	2327	2345	2364	2382	2401	2419	2438	2456	2475	2493	76°	3	6	9
14°	2493	2512	2530	2549	2568	2586	2605	2623	2642	2661	0,2679	75°	3	6	9
15°	0,2679	2698	2717	2736	2754	2773	2792	2811	2830	2849	2867	74°	3	6	9
16°	2867	2886	2905	2924	2943	2962	2981	3000	3019	3038	3057	73°	3	6	9
17°	3057	3076	3096	3115	3134	3153	3172	3191	3211	3230	3249	72°	3	6	10
18°	3249	3269	3288	3307	3327	3346	3365	3385	3404	3424	3443	71°	3	6	10
19°	3443	3463	3482	3502	3522	3541	3561	3581	3600	3620	0,3640	70°	3	7	10
20°	0,3640	3659	3679	3699	3719	3739	3759	3779	3799	3819	3839	69°	3	7	10
21°	3839	3859	3879	3899	3919	3939	3959	3979	4000	4020	4040	68°	3	7	10
22°	4040	4061	4081	4101	4122	4142	4163	4183	4204	4224	4245	67°	3	7	10
23°	4245	4265	4286	4307	4327	4348	4369	4390	4411	4431	4452	66°	3	7	10
24°	4452	4473	4494	4515	4536	4557	4578	4599	4621	4642	0,4663	65°	4	7	11
25°	0,4663	4684	4706	4727	4748	4770	4791	4813	4834	4856	4877	64°	4	7	11
26°	4877	4899	4921	4942	4964	4986	5008	5029	5051	5073	5095	63°	4	7	11
27°	5095	5117	5139	5161	5184	5206	5228	5250	5272	5295	5317	62°	4	7	11
28°	5317	5340	5362	5384	5407	5430	5452	5475	5498	5520	5543	61°	4	8	11
29°	5543	5566	5589	5612	5635	5658	5681	5704	5727	5750	0,5774	60°	4	8	12
30°	0,5774	5797	5820	5844	5867	5890	5914	5938	5961	5985	6009	59°	4	8	12
31°	6009	6032	6056	6080	6104	6128	6152	6176	6200	6224	6249	58°	4	8	12
32°	6249	6273	6297	6322	6346	6371	6395	6420	6445	6469	6494	57°	4	8	12
33°	6494	6519	6544	6569	6594	6619	6644	6669	6694	6720	6745	56°	4	8	13
34°	6745	6771	6796	6822	6847	6873	6899	6924	6950	6976	0,7002	55°	4	9	13
35°	0,7002	7028	7054	7080	7107	7133	7159	7186	7212	7239	7265	54°	4	8	13
36°	7265	7292	7319	7346	7373	7400	7427	7454	7481	7508	7536	53°	5	9	14°
37°	7536	7563	7590	7618	7646	7673	7701	7729	7757	7785	7813	52°	5	9	14
38°	7813	7841	7869	7898	7926	7954	7983	8012	8040	8069	8098	51°	5	9	14
39°	8098	8127	8156	8185	8214	8243	8273	8302	8332	8361	0,8391	50°	5	10	15
40°	0,8391	8421	8451	8481	8511	8541	8571	8601	8632	8662	0,8693	49°	5	10	15
41°	8693	8724	8754	8785	8816	8847	8878	8910	8941	8972	9004	48°	5	10	16
42°	9004	9036	9067	9099	9131	9163	9195	9228	9260	9293	9325	47°	6	11	16
43°	9325	9358	9391	9424	9457	9490	9523	9556	9590	9623	0,9657	46°	6	11	17
44°	9657	9691	9725	9759	9793	9827	9861	9896	9930	9965	1,0000	45°	6	11	17
45°	1,0000	0035	0070	0105	0141	0176	0212	0247	0283	0319	0355	44°	6	12	18
46°	0355	0392	0428	0464	0501	0538	0575	0612	0649	0686	0724	43°	6	12	18
47°	0724	0761	0799	0837	0875	0913	0951	0990	1028	1067	1106	42°	6	13	19
48°	1106	1145	1184	1224	1263	1303	1343	1383	1423	1463	1504	41°	7	13	20
49°	1504	1544	1585	1626	1667	1708	1750	1792	1833	1875	1,1918	40°	7	14	21
50°	1,1918	1960	2002	2045	2088	2131	2174	2218	2261	2305	2349	39°	7	14	22
51°	2349	2393	2437	2482	2527	2572	2617	2662	2708	2753	2799	38°	8	15	23
52°	2799	2846	2892	2938	2985	3032	3079	3127	3175	3222	3270	37°	8	16	24
53°	3270	3319	3367	3416	3465	3514	3564	3613	3663	3713	3764	36°	8	16	25
54°	3764	3814	3865	3916	3968	4019	4071	4124	4176	4229	1,4281	35°	9	17	26
55°	1,4281	4335	4388	4442	4496	4550	4605	4659	4715	4770	4826	34°	9	18	27
56°	4826	4882	4938	4994	5051	5108	5166	5224	5282	5340	5399	33°	10	19	29
57°	5399	5458	5517	5577	5637	5697	5757	5818	5880	5941	6003	32°	10	20	30
58°	6003	6066	6128	6191	6255	6319	6383	6447	6512	6577	6643	31°	11	21	32
59°	6643	6709	6775	6842	6909	6977	7045	7113	7182	7251	1,7321	30°	11	23	34
60°	1,732	1,739	1,746	1,753	1,760	1,767	1,775	1,782	1,789	1,797	1,804	29°	1	2	4
61°	1,804	1,811	1,819	1,827	1,834	1,842	1,849	1,857	1,865	1,873	1,881	28°	1	3	4
62°	1,881	1,889	1,897	1,905	1,913	1,921	1,929	1,937	1,946	1,954	1,963	27°	1	3	4
63°	1,963	1,971	1,980	1,988	1,997	2,006	2,014	2,023	2,032	2,041	2,05	26°	1	3	4
64°	2,050	2,059	2,069	2,078	2,087	2,097	2,106	2,116	2,125	2,135	2,145	25°	2	3	5
65°	2,145	2,154	2,164	2,174	2,184	2,194	2,204	2,215	2,225	2,236	2,246	24°	2	3	5
66°	2,246	2,257	2,267	2,278	2,289	2,3	2,311	2,322	2,333	2,344	2,356	23°	2	4	5
67°	2,356	2,367	2,379	2,391	2,402	2,414	2,426	2,438	2,450	2,463	2,475	22°	2	4	6
68°	2,475	2,488	2,5	2,513	2,526	2,539	2,552	2,565	2,578	2,592	2,605	21°	2	4	6
69°	2,605	2,619	2,633	2,646	2,66	2,675	2,689	2,703	2,718	2,733	2,747	20°	2	5	7
70°	2,747	2,762	2,778	2,793	2,808	2,824	2,840	2,856	2,872	2,888	2,904	19°	3	5	8
71°	2,904	2,921	2,937	2,954	2,971	2,989	3,006	3,024	3,042	3,06	3,078	18°	3	6	9
72°	3,078	3,096	3,115	3,133	3,152	3,172	3,191	3,211	3,230	3,251	3,271	17°	3	6	10
73°	3,271	3,291	3,312	3,333	3,354	3,376							3	7	10
							3,398	3,42	3,442	3,465	3,487	16°	4	7	11
74°	3,487	3,511	3,534	3,558	3,582	3,606							4	8	12
							3,630	3,655	3,681	3,706	3,732	15°	4	8	13
75°	3,732	3,758	3,785	3,812	3,839	3,867							4	9	13
							3,895	3,923	3,952	3,981	4,011	14°	5	10	14
tg	60"	54"	48"	42"	36"	30"	24"	18"	12"	6"	0"	ctg	1"	2"	3"

Bradis tabloları nasıl kullanılır?

Sinüsler ve kosinüsler için Bradis tablosunu düşünün. Sinüslerle ilgili her şey üstte ve soldadır. Kosinüslere ihtiyacımız varsa tablonun alt sağ tarafına bakın.

Bir açının sinüs değerlerini bulmak için, en soldaki hücrede gerekli derece sayısını içeren satır ile üst hücrede gerekli dakika sayısını içeren sütunun kesişimini bulmanız gerekir.

Tam açı değeri Bradis tablosunda yoksa düzeltmelere başvuruyoruz. Tablonun en sağ sütunlarında bir, iki ve üç dakikalık düzeltmeler verilmiştir. Tabloda olmayan bir açının sinüs değerini bulmak için ona en yakın değeri buluruz. Bundan sonra açılar arasındaki farka karşılık gelen düzeltmeyi ekler veya çıkarırız.

90 dereceden büyük bir açının sinüsünü arıyorsak, önce indirgeme formüllerini, sonra da Bradis tablosunu kullanmamız gerekir.

Örnek. Bradis tablosu nasıl kullanılır?

Diyelim ki 17 ° 44" açısının sinüsünü bulmamız gerekiyor. Tabloyu kullanarak 17 ° 42 " sinüsünün neye eşit olduğunu buluyoruz ve değerine iki dakikalık bir düzeltme ekliyoruz:

17°44" - 17°42" = 2" (gerekli düzeltme) sin 17°44" = 0. 3040 + 0 . 0006 = 0 . 3046

Kosinüsler, teğetler ve kotanjantlarla çalışma prensibi benzerdir. Ancak değişikliklerin işaretini hatırlamak önemlidir.

Önemli!

Sinüslerin değerlerini hesaplarken düzeltmenin pozitif bir işareti vardır ve kosinüsleri hesaplarken düzeltmenin negatif bir işaretle alınması gerekir.

Metinde bir hata fark ederseniz, lütfen onu vurgulayın ve Ctrl+Enter tuşlarına basın.

Makalede neye benzediğini tam olarak anlayacağız trigonometrik değerler tablosu, sinüs, kosinüs, tanjant ve kotanjant. Trigonometrik fonksiyonların temel anlamını 0,30,45,60,90,...,360 derecelik açılardan ele alalım. Ve trigonometrik fonksiyonların değerlerinin hesaplanmasında bu tabloların nasıl kullanılacağını görelim.
İlk önce şuna bakalım kosinüs, sinüs, tanjant ve kotanjant tablosu 0, 30, 45, 60, 90,... derecelik bir açıdan. Bu büyüklüklerin tanımı, 0 ve 90 derecelik açıların fonksiyonlarının değerini belirlememizi sağlar:

sin 0 0 =0, cos 0 0 = 1. tg 0 0 = 0, 0 0'dan kotanjant tanımsız olacaktır
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, 90 0'dan teğet belirsiz olacaktır

Açıları 30 ile 90 derece arasında olan dik üçgenleri alırsanız. Şunu elde ederiz:

günah 30 0 = 1/2, cos 30 0 = √3/2, tan 30 0 = √3/3, cos 30 0 = √3
günah 45 0 = √2/2, cos 45 0 = √2/2, tan 45 0 = 1, cos 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3, bebek karyolası 60 0 = √3/3

Elde edilen tüm değerleri formda temsil edelim trigonometrik tablo:

Sinüs, kosinüs, teğet ve kotanjant tablosu!

İndirgeme formülünü kullanırsak tablomuz artacak ve 360 ​​dereceye kadar olan açılar için değerler eklenecektir. Şöyle görünecek:

Ayrıca periyodiklik özelliklerine bağlı olarak açıları 0 0 +360 0 *z .... 330 0 +360 0 *z ile değiştirirsek tablo büyütülebilir; burada z bir tam sayıdır. Bu tabloda tek bir çemberdeki noktalara karşılık gelen tüm açıların değerini hesaplamak mümkündür.

Tablonun bir çözümde nasıl kullanılacağına bakalım.
Her şey çok basit. Çünkü ihtiyacımız olan değer, ihtiyacımız olan hücrelerin kesişme noktasında yatıyor. Örneğin, 60 derecelik bir açının cos değerini alın, tabloda şöyle görünecektir:

Trigonometrik fonksiyonların ana değerlerinin son tablosunda da aynı şekilde ilerliyoruz. Ancak bu tabloda 1020 derecelik açıdan tanjantın ne kadar olduğunu bulmak mümkün, = -√3 1020 0 = 300 0 +360 0 *2'yi kontrol edelim. Tabloyu kullanarak bulalım.

Daha fazla arama için dakika hassasiyetinde trigonometrik açı değerleri kullanılır. Bunların nasıl kullanılacağına ilişkin ayrıntılı talimatlar sayfada yer almaktadır.

Bradi'nin masası. Sinüs, kosinüs, teğet ve kotanjant için.

Bradis tabloları, kosinüs ve sinüs, teğet ve kotanjant tablolarından oluşan birkaç parçaya bölünmüştür - bunlar iki parçaya bölünmüştür (90 dereceye kadar açıların tg'si ve küçük açıların ctg'si).

Sinüs ve kosinüs

0 0'dan başlayıp 76 0 ile biten açının tg'si, 14 0'dan başlayıp 90 0 ile biten açının ctg'si.

90 0'a kadar tg ve küçük açılardan ctg.

Bradis tablolarını problem çözmede nasıl kullanabileceğimizi bulalım.

Tanımlama günahını (sol kenardaki sütunda tanımlama) 42 dakika (atama üst satırda) bulalım. Kesişim yoluyla atamayı ararız, bu = 0,3040.

Dakika değerleri altı dakikalık aralıklarla belirtilir, ihtiyacımız olan değer tam olarak bu aralığın içine düşerse ne yapmalıyız. 44 dakika alalım ama tabloda sadece 42 var. 42'yi baz alıyoruz ve sağ taraftaki ek sütunları kullanarak 2. değişikliği alıp 0,3040 + 0,0006'yı ekliyoruz ve 0,3046 elde ediyoruz.

Günah 47 dakika ile 48 dakikayı esas alıyoruz ve bundan 1 düzeltme çıkarıyoruz yani 0,3057 - 0,0003 = 0,3054

Cos'u hesaplarken sin'e benzer şekilde çalışıyoruz, sadece tablonun en alt sırasını baz alıyoruz. Örneğin cos 20 0 = 0,9397

90 0'a kadar olan tg açısı ve küçük açılı cot değerleri doğrudur ve bunlarda herhangi bir düzeltme yoktur. Örneğin, tg 78 0 37dk = 4,967'yi bulun


ve ctg 20 0 13 dk = 25,83

Temel trigonometrik tablolara baktık. Bu bilgilerin sizin için son derece yararlı olduğunu umuyoruz. Tablolarla ilgili sorularınız varsa yorumlara yazmayı unutmayın!

Not: Duvar tamponları - duvarları korumak için tampon paneli (http://www.spi-polymer.ru/otboyniki/)

Basitçe söylemek gerekirse bunlar, özel bir tarife göre suda pişirilen sebzelerdir. İki başlangıç ​​​​bileşenini (sebze salatası ve su) ve bitmiş sonucu - pancar çorbasını ele alacağım. Geometrik olarak bir tarafı marulu, diğer tarafı suyu temsil eden bir dikdörtgen gibi düşünülebilir. Bu iki tarafın toplamı pancar çorbasını gösterecektir. Böyle bir "pancar çorbası" dikdörtgeninin köşegeni ve alanı tamamen matematiksel kavramlardır ve asla pancar çorbası tariflerinde kullanılmaz.

Marul ve su matematiksel açıdan nasıl pancar çorbasına dönüşür? İki doğru parçasının toplamı nasıl trigonometri olabilir? Bunu anlamak için doğrusal açısal fonksiyonlara ihtiyacımız var.

Matematik ders kitaplarında doğrusal açısal fonksiyonlar hakkında hiçbir şey bulamazsınız. Ama onlar olmadan matematik olamaz. Doğa kanunları gibi matematik kanunları da onların varlığını bilsek de bilmesek de işlerler.

Doğrusal açısal fonksiyonlar toplama yasalarıdır. Cebirin nasıl geometriye, geometrinin de trigonometriye dönüştüğünü görün.

Doğrusal açısal fonksiyonlar olmadan yapmak mümkün mü? Bu mümkün çünkü matematikçiler hâlâ onlarsız da idare edebiliyorlar. Matematikçilerin püf noktası, bize her zaman yalnızca kendilerinin nasıl çözeceklerini bildikleri problemleri anlatmaları ve çözemedikleri problemler hakkında asla konuşmamalarıdır. Bakmak. Toplamanın ve bir terimin sonucunu biliyorsak, diğer terimi bulmak için çıkarma işlemini kullanırız. Tüm. Diğer sorunları bilmiyoruz ve bunları nasıl çözeceğimizi de bilmiyoruz. Yalnızca toplama işleminin sonucunu biliyorsak ve her iki terimi de bilmiyorsak ne yapmalıyız? Bu durumda toplama işleminin sonucunun doğrusal açısal fonksiyonlar kullanılarak iki terime ayrıştırılması gerekir. Daha sonra bir terimin ne olabileceğini seçiyoruz ve doğrusal açısal fonksiyonlar ikinci terimin ne olması gerektiğini gösteriyor, böylece toplama işleminin sonucu tam olarak ihtiyacımız olan şey oluyor. Bu tür terim çiftlerinden sonsuz sayıda olabilir. Günlük yaşamda toplamı ayrıştırmadan gayet iyi geçiniyoruz; çıkarma bizim için yeterli. Ancak doğa kanunları üzerine yapılan bilimsel araştırmalarda, bir toplamı bileşenlerine ayırmak çok yararlı olabilir.

Matematikçilerin bahsetmekten hoşlanmadığı bir başka toplama kanunu (hilelerinden bir diğeri), terimlerin aynı ölçü birimlerine sahip olmasını gerektirir. Salata, su ve pancar çorbası için bunlar ağırlık, hacim, değer veya ölçü birimi olabilir.

Şekil matematik için iki seviyeli farkı göstermektedir. Birinci düzey, belirtilen sayılar alanındaki farklılıklardır. A, B, C. Matematikçilerin yaptığı da budur. İkinci düzey, köşeli parantez içinde gösterilen ve harfle gösterilen ölçü birimleri alanındaki farklılıklardır. sen. Fizikçilerin yaptığı da budur. Üçüncü seviyeyi, yani tanımlanan nesnelerin alanındaki farklılıkları anlayabiliriz. Farklı nesneler aynı sayıda aynı ölçü birimine sahip olabilir. Bunun ne kadar önemli olduğunu pancar çorbası trigonometrisi örneğinde görebiliriz. Farklı nesneler için aynı birim tanımına alt simgeler eklersek, belirli bir nesneyi tam olarak hangi matematiksel niceliğin tanımladığını ve bunun zaman içinde veya eylemlerimiz nedeniyle nasıl değiştiğini söyleyebiliriz. Mektup K Suyu harfle belirteceğim S Salatayı bir harfle belirleyeceğim B- borsch. Pancar çorbası için doğrusal açısal fonksiyonlar böyle görünecek.

Suyun bir kısmını ve salatanın bir kısmını alırsak, hepsi birlikte bir porsiyon pancar çorbasına dönüşecektir. Burada pancar çorbasına biraz ara vermenizi ve uzak çocukluğunuzu hatırlamanızı öneririm. Tavşanlarla ördekleri bir araya getirmenin bize nasıl öğretildiğini hatırlıyor musun? Kaç hayvan olacağını bulmak gerekiyordu. O zaman bize ne yapmamız öğretildi? Ölçü birimlerini sayılardan ayırmamız ve sayıları toplamamız öğretildi. Evet, herhangi bir sayı başka bir sayıya eklenebilir. Bu, modern matematiğin otizmine giden doğrudan bir yoldur - bunu anlaşılmaz bir şekilde, neden, anlaşılmaz bir şekilde yapıyoruz ve bunun gerçeklikle nasıl ilişkili olduğunu çok az anlıyoruz, üç fark seviyesi nedeniyle, matematikçiler yalnızca bir tanesiyle çalışırlar. Bir ölçü biriminden diğerine nasıl geçileceğini öğrenmek daha doğru olacaktır.

Tavşanlar, ördekler ve küçük hayvanlar parça parça sayılabilir. Farklı nesneler için ortak bir ölçü birimi, onları bir araya toplamamıza olanak tanır. Bu sorunun çocuk versiyonu. Yetişkinler için de benzer bir soruna bakalım. Tavşanları ve parayı eklediğinizde ne elde edersiniz? Burada iki çözüm sunabiliriz.

İlk seçenek. Tavşanların piyasa değerini belirliyoruz ve bunu mevcut para miktarına ekliyoruz. Servetimizin toplam değerini parasal olarak aldık.

İkinci seçenek. Elimizdeki banknot sayısına tavşan sayısını da ekleyebilirsiniz. Taşınır malların miktarını parça halinde alacağız.

Gördüğünüz gibi aynı toplama kanunu farklı sonuçlar elde etmenize olanak sağlıyor. Her şey tam olarak ne bilmek istediğimize bağlı.

Ama hadi pancar çorbamıza geri dönelim. Artık doğrusal açısal fonksiyonların farklı açı değerleri için ne olacağını görebiliriz.

Açı sıfırdır. Salatamız var ama suyumuz yok. Pancar çorbası pişiremiyoruz. Pancar çorbası miktarı da sıfırdır. Bu, sıfır pancar çorbasının sıfır suya eşit olduğu anlamına gelmez. Sıfır salata ile sıfır pancar çorbası olabilir (dik açı).

Şahsen benim için bu, şu gerçeğin ana matematiksel kanıtıdır. Sıfır, eklendiğinde sayıyı değiştirmez. Bunun nedeni, yalnızca bir terim varsa ve ikinci terim eksikse toplamanın kendisinin imkansız olmasıdır. Bunu istediğiniz gibi hissedebilirsiniz, ancak unutmayın - sıfırla yapılan tüm matematiksel işlemler matematikçiler tarafından icat edilmiştir, bu yüzden mantığınızı bir kenara bırakın ve matematikçiler tarafından icat edilen tanımları aptalca tıkıştırın: "sıfıra bölmek imkansızdır", "herhangi bir sayının çarpımı" sıfır sıfıra eşittir”, “delme noktası sıfırın ötesinde” ve diğer saçmalıklar. Sıfırın bir sayı olmadığını bir kez hatırlamak yeterlidir ve bir daha asla sıfırın doğal sayı olup olmadığı sorusuyla karşılaşmazsınız çünkü böyle bir soru tüm anlamını yitirir: Sayı olmayan bir şey nasıl sayı olarak kabul edilebilir? ? Bu, görünmez bir rengin hangi renk olarak sınıflandırılması gerektiğini sormak gibidir. Bir sayıya sıfır eklemek, orada olmayan boyayla resim yapmakla aynı şeydir. Kuru bir fırça salladık ve herkese “boyama yaptık” dedik. Ama biraz dalıyorum.

Açı sıfırdan büyük ama kırk beş dereceden az. Çok fazla marulumuz var ama yeterli suyumuz yok. Sonuç olarak kalın pancar çorbası elde edeceğiz.

Açı kırk beş derecedir. Eşit miktarda su ve salatamız var. Bu mükemmel pancar çorbası (affet beni şefler, bu sadece matematik).

Açı kırk beş dereceden büyük, ancak doksan dereceden azdır. Bol suyumuz ve az salatamız var. Sıvı pancar çorbası alacaksınız.

Sağ açı. Bizim suyumuz var. Bir zamanlar salatayı işaretleyen çizginin açısını ölçmeye devam ettiğimizde, salatadan geriye kalan tek şey anılardır. Pancar çorbası pişiremiyoruz. Pancar çorbası miktarı sıfırdır. Bu durumda tutun ve elinizde su varken için)))

Burada. Bunun gibi bir şey. Burada fazlasıyla uygun olacak başka hikayeler anlatabilirim.

İki arkadaşın ortak bir işte hisseleri vardı. Birini öldürdükten sonra her şey diğerine gitti.

Gezegenimizde matematiğin ortaya çıkışı.

Bütün bu hikayeler matematik dilinde doğrusal açısal fonksiyonlar kullanılarak anlatılıyor. Başka bir zaman size bu fonksiyonların matematiğin yapısındaki gerçek yerini göstereceğim. Bu arada pancar çorbası trigonometrisine dönelim ve projeksiyonları ele alalım.

26 Ekim 2019 Cumartesi

7 Ağustos 2019 Çarşamba

Konuşmayı sonlandırırken sonsuz bir kümeyi düşünmemiz gerekiyor. Mesele şu ki, "sonsuzluk" kavramı, bir boa yılanının bir tavşanı etkilemesi gibi matematikçileri de etkiliyor. Sonsuzluğun titreten dehşeti matematikçileri sağduyudan yoksun bırakıyor. İşte bir örnek:

Orijinal kaynak bulunur. Alfa gerçek sayı anlamına gelir. Yukarıdaki ifadelerde yer alan eşittir işareti, sonsuza bir sayı veya sonsuz eklediğinizde hiçbir şeyin değişmeyeceğini, sonucun aynı sonsuz olacağını belirtir. Örnek olarak sonsuz doğal sayılar kümesini alırsak, dikkate alınan örnekler şu şekilde temsil edilebilir:

Matematikçiler haklı olduklarını açıkça kanıtlamak için birçok farklı yöntem geliştirdiler. Şahsen ben tüm bu yöntemlere teflerle dans eden şamanlar gibi bakıyorum. Esasen, bunların hepsi ya bazı odaların boş olması ve yeni misafirlerin taşınması ya da bazı ziyaretçilerin misafirlere yer açmak için koridora atılması (çok insani bir şekilde) gerçeğine dayanıyor. Bu tür kararlara ilişkin görüşlerimi Sarışın hakkında fantastik bir hikaye şeklinde sundum. Benim mantığım neye dayanıyor? Sonsuz sayıda ziyaretçinin yerini değiştirmek sonsuz miktarda zaman alır. İlk odayı bir misafir için boşalttıktan sonra, ziyaretçilerden biri, zamanın sonuna kadar her zaman koridor boyunca kendi odasından diğerine yürüyecektir. Zaman faktörü elbette aptalca göz ardı edilebilir ama bu “hiçbir kanun aptallar için yazılmaz” kategorisinde olacaktır. Her şey ne yaptığımıza bağlı: gerçekliği matematiksel teorilere göre ayarlamak veya tam tersi.

“Sonsuz otel” nedir? Sonsuz otel, kaç oda dolu olursa olsun her zaman herhangi bir sayıda boş yatağa sahip olan bir oteldir. Sonsuz "ziyaretçi" koridorundaki tüm odalar doluysa, "misafir" odalarının bulunduğu başka bir sonsuz koridor daha vardır. Bu tür koridorlardan sonsuz sayıda olacak. Üstelik “sonsuz otel”, sonsuz sayıda Tanrının yarattığı sonsuz sayıda evrende, sonsuz sayıda gezegende, sonsuz sayıda binada, sonsuz sayıda kata sahiptir. Matematikçiler sıradan günlük problemlerden uzaklaşamazlar: Her zaman tek bir Tanrı-Allah-Buda vardır, tek bir otel vardır, tek bir koridor vardır. Yani matematikçiler otel odalarının seri numaralarıyla hokkabazlık yaparak bizi "imkansızı itmenin" mümkün olduğuna ikna etmeye çalışıyorlar.

Akıl yürütmemin mantığını size sonsuz doğal sayılar kümesi örneğini kullanarak göstereceğim. Öncelikle çok basit bir soruyu yanıtlamanız gerekiyor: Kaç tane doğal sayı kümesi var - bir mi yoksa daha fazla mı? Sayıları kendimiz icat ettiğimiz için bu sorunun doğru bir cevabı yok; doğada sayılar yoktur. Evet, Doğa sayma konusunda harikadır ama bunun için bizim bilmediğimiz diğer matematiksel araçları kullanır. Doğanın ne düşündüğünü başka zaman anlatacağım. Sayıları icat ettiğimizden beri, kaç tane doğal sayı kümesinin olacağına kendimiz karar vereceğiz. Gerçek bilim adamlarına yakışır şekilde her iki seçeneği de ele alalım.

Seçenek bir. Rafta sakin bir şekilde duran tek bir doğal sayı dizisi "bize verilsin". Bu seti raftan alıyoruz. İşte bu, rafta başka doğal sayı kalmadı ve onları alacak yer yok. Zaten elimizde olduğundan bu sete bir tane ekleyemiyoruz. Ya gerçekten istersen? Sorun değil. Almış olduğumuz setten bir adet alıp rafa geri koyabiliriz. Bundan sonra raftan bir tane alıp elimizde kalanlara ekleyebiliriz. Sonuç olarak yine sonsuz bir doğal sayılar kümesi elde edeceğiz. Tüm manipülasyonlarımızı şu şekilde yazabilirsiniz:

Eylemleri cebirsel gösterimde ve küme teorisi gösteriminde, kümenin elemanlarının ayrıntılı bir listesiyle birlikte yazdım. Alt simge, tek ve tek bir doğal sayı kümesine sahip olduğumuzu gösterir. Doğal sayılar kümesinin ancak ondan bir çıkarılıp aynı birim eklenirse değişmeden kalacağı ortaya çıktı.

İkinci Seçenek. Rafımızda birçok farklı sonsuz doğal sayı kümesi var. Pratik olarak ayırt edilemez olmalarına rağmen - FARKLI olduğunu vurguluyorum. Bu setlerden birini alalım. Daha sonra başka bir doğal sayı kümesinden birini alıp daha önce almış olduğumuz kümeye ekliyoruz. İki doğal sayı kümesini bile toplayabiliriz. Elde ettiğimiz şey bu:

"Bir" ve "iki" alt simgeleri bu elemanların farklı kümelere ait olduğunu gösterir. Evet sonsuz bir kümeye bir eklerseniz sonuç yine sonsuz küme olur ama orijinal kümeyle aynı olmaz. Bir sonsuz kümeye başka bir sonsuz küme eklerseniz sonuç, ilk iki kümenin elemanlarından oluşan yeni bir sonsuz küme olur.

Doğal sayılar kümesi sayma için, cetvelin ölçme için kullanılmasıyla aynı şekilde kullanılır. Şimdi cetvele bir santimetre eklediğinizi hayal edin. Bu orijinaline eşit olmayan farklı bir çizgi olacaktır.

Benim mantığımı kabul edebilir veya kabul etmeyebilirsiniz; bu sizin kendi işinizdir. Ancak eğer matematik problemleriyle karşılaşırsanız, nesiller boyu matematikçilerin izlediği yanlış akıl yürütme yolunu takip edip etmediğinizi düşünün. Sonuçta, matematik çalışmak her şeyden önce içimizde istikrarlı bir düşünce stereotipi oluşturur ve ancak o zaman zihinsel yeteneklerimize katkıda bulunur (veya tam tersine bizi özgür düşünceden mahrum bırakır).

pozg.ru

4 Ağustos 2019 Pazar

Hakkında bir makalenin ekini bitiriyordum ve Wikipedia'da şu harika metni gördüm:

Şöyle okuyoruz: "... Babil matematiğinin zengin teorik temeli bütünsel bir karaktere sahip değildi ve ortak bir sistem ve kanıt tabanından yoksun bir dizi farklı tekniğe indirgenmişti."

Vay! Ne kadar akıllıyız ve başkalarının eksikliklerini ne kadar iyi görebiliyoruz. Modern matematiğe aynı bağlamda bakmak bizim için zor mu? Yukarıdaki metni biraz değiştirerek, kişisel olarak aşağıdakileri elde ettim:

Modern matematiğin zengin teorik temeli bütünsel değildir ve ortak bir sistem ve kanıt tabanından yoksun, birbirinden farklı bölümlere indirgenmiştir.

Sözlerimi doğrulamak için fazla uzağa gitmeyeceğim; matematiğin diğer birçok dalının dilinden ve kurallarından farklı bir dili ve kuralları var. Matematiğin farklı dallarındaki aynı isimler farklı anlamlara gelebilir. Bir dizi yayını modern matematiğin en bariz hatalarına adamak istiyorum. Yakında görüşürüz.

3 Ağustos 2019 Cumartesi

Bir küme alt kümelere nasıl bölünür? Bunu yapmak için seçilen setin bazı öğelerinde mevcut olan yeni bir ölçü birimi girmeniz gerekir. Bir örneğe bakalım.

Bolluğumuz olsun A dört kişiden oluşuyor. Bu set “kişiler” esas alınarak oluşturulmuştur. Bu setin elemanlarını harfle gösterelim. A numaralı alt simge, bu setteki her kişinin seri numarasını gösterecektir. Yeni bir ölçü birimi olan "cinsiyet"i tanıtalım ve bunu harfle belirtelim B. Cinsel özellikler tüm insanlarda doğal olduğundan, kümenin her bir öğesini çarpıyoruz A cinsiyete dayalı B. “İnsanlar” grubumuzun artık “cinsiyet özelliklerine sahip insanlar” kümesi haline geldiğine dikkat edin. Bundan sonra cinsel özellikleri erkeklere ayırabiliriz. BM ve kadınların siyah kadın cinsel özellikler. Şimdi matematiksel bir filtre uygulayabiliriz: Hangisi olursa olsun bu cinsel özelliklerden birini seçiyoruz: erkek ya da kadın. Bir kişide varsa onu bir ile çarparız, eğer böyle bir işaret yoksa sıfırla çarparız. Ve sonra normal okul matematiğini kullanıyoruz. Bak ne oldu.

Çarpma, azaltma ve yeniden düzenlemeden sonra iki alt küme elde ettik: Erkeklerin alt kümesi BM ve kadınların bir alt kümesi siyah. Matematikçiler küme teorisini pratikte uygularken yaklaşık olarak aynı şekilde mantık yürütürler. Ancak bize ayrıntıları söylemiyorlar, ancak bize nihai sonucu veriyorlar: "birçok insan, erkeklerden ve kadınlardan oluşan bir alt gruptan oluşuyor." Doğal olarak aklınıza şu soru gelebilir: Yukarıda özetlenen dönüşümlerde matematik ne kadar doğru uygulandı? Sizi temin ederim ki aslında her şey doğru yapıldı; aritmetiğin, Boole cebirinin ve matematiğin diğer dallarının matematiksel temellerini bilmek yeterlidir. Ne olduğunu? Başka bir zaman sana bundan bahsedeceğim.

Süper kümelere gelince, bu iki kümenin elemanlarında bulunan ölçü birimini seçerek iki kümeyi tek bir süper kümede birleştirebilirsiniz.

Gördüğünüz gibi ölçü birimleri ve sıradan matematik, küme teorisini geçmişin kalıntısı haline getiriyor. Küme teorisinde her şeyin yolunda olmadığının bir işareti, matematikçilerin küme teorisi için kendi dillerini ve gösterimlerini geliştirmiş olmalarıdır. Matematikçiler bir zamanlar şamanların yaptığı gibi hareket ediyorlardı. Yalnızca şamanlar "bilgilerini" nasıl "doğru" şekilde uygulayacaklarını bilirler. Bize bu “bilgiyi” öğretiyorlar.

Sonuç olarak size matematikçilerin nasıl manipüle ettiğini göstermek istiyorum.

7 Ocak 2019 Pazartesi

MÖ beşinci yüzyılda, antik Yunan filozofu Elea'lı Zenon, en ünlüsü "Aşil ve Kaplumbağa" aporia'sı olan ünlü aporialarını formüle etti. İşte kulağa nasıl geliyor:

Diyelim ki Aşil kaplumbağadan on kat daha hızlı koşuyor ve onun bin adım gerisinde. Aşil'in bu mesafeyi koştuğu süre boyunca kaplumbağa aynı yönde yüz adım kadar sürünecektir. Aşil yüz adım koştuğunda kaplumbağa on adım daha sürünür ve bu böyle devam eder. Bu süreç sonsuza kadar devam edecek, Aşil kaplumbağaya asla yetişemeyecek.

Bu akıl yürütme sonraki tüm nesiller için mantıksal bir şok oldu. Aristoteles, Diogenes, Kant, Hegel, Hilbert... Hepsi öyle ya da böyle Zeno'nun açmazını değerlendirdiler. Şok o kadar güçlüydü ki " ... tartışmalar bugüne kadar devam ediyor; bilim camiası paradoksların özü hakkında henüz ortak bir görüşe varamadı ... konunun incelenmesine matematiksel analiz, küme teorisi, yeni fiziksel ve felsefi yaklaşımlar dahil edildi. ; hiçbiri soruna genel kabul görmüş bir çözüm olmadı..."[Wikipedia, "Zeno'nun Aporia'sı". Herkes kandırıldıklarını anlıyor ama kimse aldatmanın nelerden oluştuğunu anlamıyor.

Matematiksel bir bakış açısından Zeno, çıkmazında nicelikten niceliğe geçişi açıkça gösterdi. Bu geçiş, kalıcı olanların yerine uygulamayı ima etmektedir. Anladığım kadarıyla değişken ölçü birimlerini kullanmaya yönelik matematiksel aparat ya henüz geliştirilmedi ya da Zeno'nun açmazına uygulanmadı. Her zamanki mantığımızı uygulamak bizi tuzağa düşürür. Biz, düşüncenin ataleti nedeniyle, karşılıklı değere sabit zaman birimleri uyguluyoruz. Fiziksel açıdan bakıldığında bu, Aşil'in kaplumbağaya yetiştiği anda tamamen durana kadar zamanın yavaşlaması gibi görünüyor. Zaman durursa Aşil kaplumbağadan daha fazla koşamaz.

Her zamanki mantığımızı tersine çevirirsek her şey yerli yerine oturur. Aşil sabit hızla koşar. Yolunun sonraki her bölümü bir öncekinden on kat daha kısadır. Buna göre, bunun üstesinden gelmek için harcanan süre bir öncekine göre on kat daha azdır. Bu duruma “sonsuzluk” kavramını uygularsak, “Aşil kaplumbağaya sonsuz hızla yetişecek” demek doğru olur.

Bu mantıksal tuzaktan nasıl kaçınılır? Sabit zaman birimlerinde kalın ve karşılıklı birimlere geçmeyin. Zeno'nun dilinde şöyle görünür:

Aşil'in bin adım koşması gereken sürede kaplumbağa aynı yönde yüz adım koşacaktır. Bir sonraki birinciye eşit zaman aralığında Aşil bin adım daha koşacak ve kaplumbağa yüz adım daha sürünecektir. Artık Aşil kaplumbağanın sekiz yüz adım ilerisindedir.

Bu yaklaşım, herhangi bir mantıksal paradoks olmaksızın gerçekliği yeterince tanımlamaktadır. Fakat bu soruna tam bir çözüm değildir. Einstein'ın ışık hızının karşı konulmazlığıyla ilgili açıklaması Zeno'nun "Aşil ve Kaplumbağa" açmazına çok benziyor. Hala bu sorunu incelememiz, yeniden düşünmemiz ve çözmemiz gerekiyor. Ve çözüm sonsuz büyük sayılarda değil, ölçü birimlerinde aranmalıdır.

Zeno'nun bir başka ilginç açmazı da uçan bir oktan bahseder:

Uçan ok, zamanın her anında hareketsiz olduğundan hareketsizdir ve zamanın her anında hareketsiz olduğundan daima hareketsizdir.

Bu açmazda, mantıksal paradoksun üstesinden çok basit bir şekilde gelinir - uçan bir okun, uzayın farklı noktalarında her an hareketsiz olduğunu, bunun aslında bir hareket olduğunu açıklığa kavuşturmak yeterlidir. Burada bir başka noktaya dikkat çekmek gerekiyor. Yoldaki bir arabanın bir fotoğrafından ne hareketinin gerçekliğini ne de ona olan mesafeyi belirlemek imkansızdır. Bir arabanın hareket edip etmediğini belirlemek için aynı noktadan farklı zamanlarda çekilmiş iki fotoğrafa ihtiyacınız vardır, ancak onlara olan mesafeyi belirleyemezsiniz. Bir arabaya olan mesafeyi belirlemek için, uzayın farklı noktalarından aynı anda çekilmiş iki fotoğrafa ihtiyacınız vardır, ancak bunlardan hareketin gerçekliğini belirleyemezsiniz (tabii ki hesaplamalar için yine de ek verilere ihtiyacınız var, trigonometri size yardımcı olacaktır) ). Özellikle dikkat çekmek istediğim şey, zamandaki iki nokta ile uzaydaki iki noktanın birbirine karıştırılmaması gereken farklı şeyler olmasıdır, çünkü bunlar araştırma için farklı fırsatlar sunar.
Size süreci bir örnekle göstereceğim. "Sivilce içindeki kırmızı katı" seçiyoruz - bu bizim "bütünümüz". Aynı zamanda bunların fiyonklu olduğunu ve fiyonksuz olduğunu da görüyoruz. Bundan sonra “bütünün” bir kısmını seçip “yaylı” bir set oluşturuyoruz. Şamanlar, yerleşik teorilerini gerçekliğe bağlayarak yiyeceklerini bu şekilde elde ederler.

Şimdi küçük bir numara yapalım. “Fiyonklu sivilceli katı”yı alalım ve bu “bütünleri” kırmızı unsurları seçerek renklerine göre birleştirelim. Bir sürü "kırmızı"mız var. Şimdi son soru: Sonuçta ortaya çıkan “fiyonklu” ve “kırmızı” kümeler aynı küme mi, yoksa iki farklı küme mi? Bunun cevabını yalnızca şamanlar biliyor. Daha doğrusu kendileri hiçbir şey bilmiyorlar ama dedikleri gibi öyle olacak.

Bu basit örnek, konu gerçekliğe geldiğinde küme teorisinin tamamen işe yaramaz olduğunu gösteriyor. İşin sırrı nedir? "Sivilce ve fiyonklu kırmızı katı" bir set oluşturduk. Oluşum dört farklı ölçü biriminde gerçekleşti: renk (kırmızı), sağlamlık (katı), pürüzlülük (sivilceli), dekorasyon (yaylı). Yalnızca bir dizi ölçü birimi, gerçek nesneleri matematik dilinde yeterince tanımlamamıza izin verir.. Görünüşe göre bu.

Farklı endekslere sahip "a" harfi, farklı ölçü birimlerini gösterir. Başlangıç ​​aşamasında “bütün”ün ayırt edildiği ölçü birimleri parantez içinde vurgulanmıştır. Setin oluşturulduğu ölçü birimi parantezlerden çıkarılır. Son satır nihai sonucu gösterir - kümenin bir öğesi. Gördüğünüz gibi, bir küme oluşturmak için ölçü birimlerini kullanırsak sonuç, eylemlerimizin sırasına bağlı değildir. Ve bu matematiktir, şamanların teflerle dansı değil. Şamanlar, ölçüm birimlerinin onların "bilimsel" cephaneliğinin bir parçası olmaması nedeniyle bunun "açık" olduğunu savunarak "sezgisel olarak" aynı sonuca varabilirler.

Ölçü birimlerini kullanarak bir seti bölmek veya birkaç seti tek bir süper sette birleştirmek çok kolaydır. Bu sürecin cebirine daha yakından bakalım.

Bu makale şunları içerir: sinüs, kosinüs, teğet ve kotanjant tabloları. İlk olarak, trigonometrik fonksiyonların temel değerlerinin bir tablosunu, yani 0, 30, 45, 60, 90, ..., 360 derecelik açıların sinüs, kosinüs, teğet ve kotanjant tablosunu sunacağız ( 0, π/6, π/4, π/3, π/2, …, 2π radyan). Bundan sonra V. M. Bradis'in sinüs ve kosinüs tablosunun yanı sıra teğet ve kotanjant tablosunu vereceğiz ve trigonometrik fonksiyonların değerlerini bulurken bu tabloların nasıl kullanılacağını göstereceğiz.

Sayfada gezinme.

0, 30, 45, 60, 90, ... derecelik açılar için sinüs, kosinüs, teğet ve kotanjant tablosu

Kaynakça.

• Cebir: Ders Kitabı 9. sınıf için. ortalama okul / Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; Ed. S. A. Telyakovsky. - M .: Eğitim, 1990. - 272 s.: - ISBN 5-09-002727-7.
• Bashmakov M. I. Cebir ve analizin başlangıcı: Ders kitabı. 10-11 sınıflar için. ortalama okul - 3. baskı. - M.: Eğitim, 1993. - 351 s.: hasta. - ISBN 5-09-004617-4.
• Cebir ve analizin başlangıcı: Proc. 10-11 sınıflar için. Genel Eğitim kurumlar / A.N. Kolmogorov, A.M. Abramov, Yu.P. Dudnitsyn ve diğerleri; Ed. A. N. Kolmogorov - 14. baskı - M.: Eğitim, 2004. - 384 s.: - ISBN 5-09-013651-3.
• Gusev V.A., Mordkovich A.G. Matematik (teknik okullara girenler için bir el kitabı): Proc. ödenek.- M.; Daha yüksek okul, 1984.-351 s., hasta.
• Bradis V.M. Dört basamaklı matematik tabloları: Genel eğitim için. ders kitabı kuruluşlar. - 2. baskı. - M.: Bustard, 1999.- 96 s.: hasta. ISBN 5-7107-2667-2