عدم المساواة المثلثية. أبسط وأعقد المتباينات المثلثية. معادلات متجانسة فيما يتعلق

بادئ ذي بدء ، دعنا نتذكر الصيغ لحل أبسط المعادلات المثلثية.

دولار sinx \u003d دولار

cosx دولار \u003d دولار

$ tgx \u003d $

$ ctgx \u003d $

حل أبسط المتباينات المثلثية.

لحل أبسط المتباينات المثلثية ، علينا أولًا حل المعادلة المقابلة ، ثم باستخدام الدائرة المثلثية ، إيجاد حل المتباينة. لنفكر في حلول أبسط المتباينات المثلثية بالأمثلة.

مثال 1

$ sinx \\ ge \\ frac (1) (2) $

لنجد حل المتباينة المثلثية $ sinx \u003d \\ frac (1) (2) $

\ \

الشكل 1. حل المتباينة $ sinx \\ ge \\ frac (1) (2) $.

نظرًا لأن المتباينة لها علامة "أكبر من أو يساوي" ، فإن الحل يقع على القوس العلوي للدائرة (بالنسبة إلى حل المعادلة).

الإجابة: $ \\ left [\\ frac (\\ pi) (6) +2 \\ pi n، \\ frac (5 \\ pi) (6) +2 \\ pi n \\ right] $.

مثال 2

أوجد حل المتباينة المثلثية $ cosx \u003d \\ frac (\\ sqrt (3)) (2) $

\ \

لنحدد الحل على الدائرة المثلثية

نظرًا لأن المتباينة لها علامة "أقل" ، فإن الحل يقع على قوس الدائرة الموجود إلى اليسار (بالنسبة إلى حل المعادلة).

الإجابة: $ \\ left (\\ frac (\\ pi) (6) +2 \\ pi n، \\ frac (11 \\ pi) (6) +2 \\ pi n \\ right) $.

مثال 3

$ tgx \\ le \\ frac (\\ sqrt (3)) (3) $

لنجد حل المتباينة المثلثية $ tgx \u003d \\ frac (\\ sqrt (3)) (3) $

\ \

نحتاج أيضًا إلى مجال هنا. كما نتذكر ، دالة الظل $ x \\ ne \\ frac (\\ pi) (2) + \\ pi n، n \\ in Z $

لنحدد الحل على الدائرة المثلثية

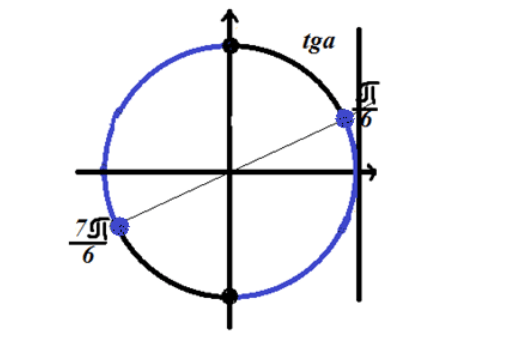
الشكل 3. حل المتباينة $ tgx \\ le \\ frac (\\ sqrt (3)) (3) $.

نظرًا لأن المتباينة لها علامة أصغر من أو يساوي ، فإن الحل يكمن في الأقواس الدائرية المميزة باللون الأزرق في الشكل 3.

الإجابة: $ \\ \\ left (- \\ frac (\\ pi) (2) +2 \\ pi n \\ right.، \\ Left. \\ Frac (\\ pi) (6) +2 \\ pi n \\ right] \\ cup \\ left (\\ frac (\\ pi) (2) +2 \\ pi n، \\ right. \\ left. \\ frac (7 \\ pi) (6) +2 \\ pi n \\ right] $

مثال 4

أوجد حل المتباينة المثلثية $ ctgx \u003d \\ sqrt (3) $

\ \

نحتاج أيضًا إلى مجال هنا. كما نتذكر ، دالة الظل $ x \\ ne \\ pi n ، n \\ in Z $

لنحدد الحل على الدائرة المثلثية

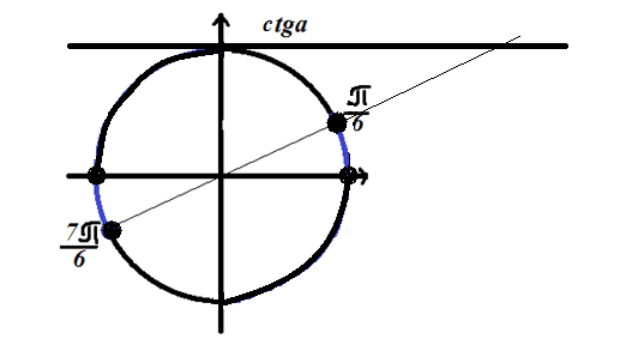
الشكل 4. حل المتباينة $ ctgx \\ le \\ sqrt (3) $.

نظرًا لأن المتباينة لها علامة "أكبر من" ، فإن الحل يكمن في الأقواس الدائرية الموضحة باللون الأزرق في الشكل 4.

الإجابة: $ \\ \\ left (2 \\ pi n، \\ frac (\\ pi) (6) +2 \\ pi n \\ right) \\ cup \\ left (\\ pi +2 \\ pi n، \\ frac (7 \\ pi) ( 6) +2 \\ pi n \\ right) $

مشروع الجبر "حل التفاوتات المثلثية" تم إكماله من قبل طالبة في الصف العاشر "ب" كازاكوفا جوليا المشرف: مدرس الرياضيات كوتشاكوفا إن إن

الغرض لتوحيد المواد حول موضوع "حل التفاوتات المثلثية" وإنشاء مذكرة للطلاب للتحضير للامتحان القادم.

الأهداف لتلخيص المواد حول هذا الموضوع. تنظيم المعلومات الواردة. ضع في اعتبارك هذا الموضوع في الامتحان.

الصلة صلة الموضوع الذي اخترته هو أن المهام المتعلقة بموضوع "حل التفاوتات المثلثية" مدرجة في مهام الاختبار.

التفاوتات المثلثية المتباينة هي علاقة تربط بين رقمين أو تعبيرين باستخدام إحدى العلامات: (أكبر من) ؛ ≥ (أكبر من أو يساوي). المتباينة المثلثية هي عدم المساواة التي تحتوي على الدوال المثلثية.

المتباينات المثلثية يتم تقليل حل المتباينات التي تحتوي على الدوال المثلثية ، كقاعدة عامة ، إلى حل أبسط المتباينات بالشكل: sin x\u003e a، sin x أ ، كوس x أ ، ت ج س أ ، ctg x

خوارزمية لحل المتباينات المثلثية على المحور المقابل لدالة مثلثية معينة ، قم بتمييز القيمة العددية المعطاة لهذه الدالة. ارسم خطًا مستقيمًا من خلال النقطة المحددة ، يتقاطع مع دائرة الوحدة. حدد نقاط تقاطع الخط والدائرة ، مع مراعاة علامة عدم المساواة الصارمة أو غير الصارمة. حدد قوس الدائرة التي توجد عليها حلول المتباينة. أوجد قيم الزوايا عند نقطتي بداية ونهاية القوس الدائري. اكتب حل المتباينة ، مع مراعاة دورية الدالة المثلثية المحددة.

صيغ حل التفاوتات المثلثية sinx\u003e a ؛ س (arcsin a + 2πn ؛ π- arcsin a + 2πn). sinx أ؛ x (- arccos a + 2πn ؛ arccos a + 2πn). كوسكس أ؛ س (أركتان أ + ن ؛ + ن). tgx أ؛ س (πn ؛ arctan + n). ctgx

الحل الرسومي للتباينات المثلثية الرئيسية sinx\u003e a

الحل الرسومي للمتباينات المثلثية الرئيسية sinx

الحل الرسومي لأهم المتباينات المثلثية cosx\u003e a

الحل الرسومي لأهم المتباينات المثلثية cosx

الحل الرسومي للتباينات المثلثية الرئيسية tgx\u003e a

الحل الرسومي للتباينات المثلثية الرئيسية tgx

الحل الرسومي للتباينات المثلثية الأساسية ctgx\u003e a

الحل الرسومي للتباينات المثلثية الرئيسية ctgx

طرق حل التفاوتات المثلثية حل المتباينات المثلثية باستخدام دائرة الأرقام ؛ حل المتباينات المثلثية باستخدام الرسم البياني للوظيفة. :

حل المتباينات المثلثية باستخدام دائرة الأرقام مثال 1 :: إجابة:

حل المتباينات المثلثية باستخدام دائرة الأرقام مثال 1: الإجابة:

حل المتباينات المثلثية باستخدام الرسم البياني للوظيفة مثال: الإجابة:

نتيجة العمل الذي عززت معرفتي حول موضوع "حل التفاوتات المثلثية". نظم المعلومات الواردة حول هذا الموضوع لتسهيل فهمه: اشتقاق خوارزمية لحل التفاوتات المثلثية ؛ حدد حلين ؛ أظهر أمثلة على الحلول. :

نتائج العمل أيضًا ، كمنتج نهائي ، يرافق مشروعي "مذكرة للطلاب استعدادًا لامتحان الجبر". مستند Microsoft Office Word (2). docx:

كتاب الأدب المستخدم في الجبر للصف العاشر "الجبر وبداية التحليل" تحرير أ.ن.كولموغوروف http://festival.1september.ru/articles/514580/ http://www.mathematics-repetition.com http: // www.calc.ru http://www.pomochnik-vsem.ru:

المتباينات هي علاقات على شكل أ ›ب ، حيث أ وب عبارة عن تعابير تحتوي على متغير واحد على الأقل. يمكن أن تكون المتباينات صارمة - ‹،› وغير صارمة - ، ≤.

المتباينات المثلثية هي تعبيرات من الشكل: F (x) ›a ، F (x)‹ a ، F (x) ≤ a ، F (x) ≥ a ، حيث يتم تمثيل F (x) بواحد أو أكثر من الدوال المثلثية.

مثال على أبسط المتباينات المثلثية هو: sin x ‹1/2. من المقبول حل مثل هذه المشاكل بيانياً ؛ لذلك ، تم تطوير طريقتين.

الطريقة 1 - حل المتباينات عن طريق رسم دالة

لإيجاد الفترة الزمنية التي تحقق شروط المتباينة sin x ‹1/2 ، يجب عليك اتباع الخطوات التالية:

على محور الإحداثيات ، قم ببناء شكل الجيب y \u003d sin x.
ارسم على نفس المحور الرسم البياني للحجة العددية للمتباينة ، أي الخط المار بالنقطة ½ للإحداثيات OY.
حدد نقاط تقاطع الرسمين البيانيين.
ظلل المقطع الذي يمثل الحل للمثال.

عند وجود إشارات قوية في تعبير ما ، فإن نقاط التقاطع ليست حلولاً. نظرًا لأن أصغر فترة موجبة للجيوب الأنفية هي 2π ، نكتب الإجابة على النحو التالي:

إذا لم تكن إشارات التعبير صارمة ، فيجب وضع الفاصل الزمني للحلول بين قوسين مربعين -. يمكن أيضًا كتابة إجابة المشكلة على أنها متباينة أخرى:

الطريقة الثانية - حل المتباينات المثلثية باستخدام دائرة الوحدة

يمكن حل مشاكل مماثلة بسهولة باستخدام الدائرة المثلثية. خوارزمية البحث عن الإجابات بسيطة للغاية:

أولاً ، ارسم دائرة وحدة.
ثم من الضروري ملاحظة قيمة دالة القوس لسعة الجانب الأيمن من المتباينة على قوس الدائرة.
من الضروري رسم خط مستقيم يمر عبر قيمة دالة القوس الموازية لمحور الإحداثي (OX).
بعد ذلك ، يبقى فقط تحديد قوس الدائرة ، وهو مجموعة حلول المتباينة المثلثية.
اكتب الإجابة في النموذج المطلوب.

دعونا نحلل خطوات الحل باستخدام مثال المتباينة sin x ›1/2. يتم وضع علامة على النقطتين α و على الدائرة - القيم

نقطتا القوس الموجودة أعلى α و هي الفترة الزمنية لحل المتباينة المعطاة.

إذا كنت بحاجة إلى حل مثال cos ، فسيتم تحديد موقع قوس الإجابات بشكل متماثل مع محور OX ، وليس OY. للنظر في الفرق بين فواصل الحلول لجيب الجيب وجيب التمام ، يمكنك استخدام المخططات أدناه في النص.

ستختلف الحلول الرسومية لمتباينات الظل والظل عن كل من الجيب وجيب التمام. هذا يرجع إلى خصائص الوظائف.

ظل القوس وظل التمام القوسي عبارة عن خطوط مماسة للدائرة المثلثية ، والحد الأدنى لفترة موجبة لكلا الدالتين هو π. لاستخدام الطريقة الثانية بشكل سريع وصحيح ، عليك أن تتذكر على أي محور يتم رسم قيم sin و cos و tg و ctg.

المماس يعمل بالتوازي مع محور OY. إذا وضعت قيمة arctan a على دائرة الوحدة ، فإن النقطة الثانية المطلوبة ستكون موجودة في الربع المائل. زوايا

هي نقاط توقف الوظيفة ، حيث يميل الرسم البياني إلى الوصول إليها ولكن لا تصل أبدًا.

في حالة ظل التمام ، يعمل الظل بالتوازي مع محور OX ، ويتم مقاطعة الوظيفة عند النقطتين π و 2π.

عدم المساواة المثلثية المعقدة

إذا تم تمثيل حجة دالة عدم المساواة ليس فقط بواسطة متغير ، ولكن بتعبير كامل يحتوي على مجهول ، فإننا نتحدث بالفعل عن متباينة معقدة. يختلف مسار الحل وترتيبه إلى حد ما عن الطرق الموضحة أعلاه. افترض أنه من الضروري إيجاد حل لعدم المساواة التالية:

يوفر الحل الرسومي لبناء الجيب العادي y \u003d sin x لقيم x المختارة بشكل عشوائي. لنحسب جدولًا بإحداثيات نقاط ارتساء الرسم البياني:

يجب أن تكون النتيجة منحنى جميل.

لسهولة إيجاد حل ، استبدل وسيطة الدالة المعقدة

يتيح لك تقاطع رسمين بيانيين تحديد منطقة القيم المرغوبة التي يتم فيها استيفاء شرط عدم المساواة.

الجزء الموجود هو حل المتغير t:

ومع ذلك ، فإن الهدف من المهمة هو العثور على جميع المتغيرات الممكنة لـ x المجهول:

حل عدم المساواة المزدوجة بسيط للغاية ، فأنت بحاجة إلى تحريك π / 3 إلى الأجزاء القصوى من المعادلة وإجراء الحسابات المطلوبة:

الإجابة على المهمة سيبدو كفترة عدم مساواة صارمة:

ستتطلب مثل هذه المهام خبرة الطلاب والبراعة في التعامل مع الدوال المثلثية. كلما تم حل المزيد من مهام التدريب في عملية التحضير ، كلما كان من الأسهل والأسرع أن يجد الطالب إجابة لسؤال اختبار الاستخدام.

طرق حل عدم المساواة المثلثية

ملاءمة. تاريخيا ، كان للمعادلات المثلثية وعدم المساواة مكانة خاصة في الدورة المدرسية. يمكننا القول أن علم المثلثات هو أحد أهم أقسام الدورة المدرسية وكل العلوم الرياضية بشكل عام.

تحتل المعادلات المثلثية وعدم المساواة أحد الأماكن المركزية في مسار رياضيات المدرسة الثانوية ، سواء في محتوى المادة التعليمية أو في أساليب النشاط التربوي والمعرفي ، والتي يمكن ويجب تشكيلها أثناء دراستها وتطبيقها على حل عدد كبير من المشاكل ذات الطبيعة النظرية والتطبيقية. ...

يخلق حل المعادلات المثلثية وعدم المساواة المتطلبات الأساسية لتنظيم معرفة الطلاب المتعلقة بجميع المواد التعليمية في علم المثلثات (على سبيل المثال ، خصائص الدوال المثلثية ، وطرق تحويل التعبيرات المثلثية ، وما إلى ذلك) ويجعل من الممكن إنشاء روابط فعالة مع المادة المدروسة في الجبر (المعادلات ، تكافؤ المعادلات ، عدم المساواة ، تحولات متطابقة التعبيرات الجبرية ، إلخ).

بعبارة أخرى ، يفترض النظر في طرق حل المعادلات المثلثية وعدم المساواة نوعًا من نقل هذه المهارات إلى محتوى جديد.

تعتبر أهمية النظرية وتطبيقاتها العديدة دليلاً على ملاءمة الموضوع المختار. وهذا بدوره يسمح لك بتحديد الأهداف والغايات وموضوع البحث لعمل الدورة.

الغرض من الدراسة: لتعميم الأنواع المتاحة من عدم المساواة المثلثية ، والطرق الأساسية والخاصة لحلها ، لاختيار مجموعة من المشاكل لحل عدم المساواة المثلثية من قبل أطفال المدارس.

أهداف البحث:

1. بناءً على تحليل المؤلفات المتوفرة حول موضوع البحث ، قم بتنظيم المادة.

2. أعط مجموعة من المهام الضرورية لتوحيد موضوع "عدم المساواة المثلثية".

كائن البحث هي عدم المساواة المثلثية في مقرر الرياضيات المدرسي.

موضوع الدراسة: أنواع عدم المساواة المثلثية وطرق حلها.

الأهمية النظرية هو تنظيم المادة.

أهمية عملية: تطبيق المعرفة النظرية في حل المشكلات ؛ تحليل الطرق الرئيسية التي يتم مواجهتها بشكل متكرر لحل التفاوتات المثلثية.

طرق البحث : تحليل الأدبيات العلمية ، تركيب وتعميم المعرفة المكتسبة ، تحليل حل المشكلات ، البحث عن الأساليب المثلى لحل التفاوتات.

§1. أنواع عدم المساواة المثلثية والطرق الأساسية لحلها

1.1. أبسط عدم المساواة المثلثية

اثنان التعبيرات المثلثيةمتصلة بعلامة أو\u003e تسمى عدم المساواة المثلثية.

حل المتباينة المثلثية يعني إيجاد مجموعة قيم المجهول المتضمنة في عدم المساواة ، والتي يتم استيفاء عدم المساواة من أجلها.

يتم حل الجزء الرئيسي من عدم المساواة المثلثية عن طريق تقليلها إلى حل أبسطها:

يمكن أن تكون هذه طريقة للتحليل ، استبدال المتغير (
,
إلخ) ، حيث يتم أولاً حل عدم المساواة المعتادة ، ثم عدم المساواة بالشكل
إلخ ، أو طرق أخرى.

يمكن حل أبسط المتباينات بطريقتين: استخدام دائرة الوحدة أو بيانياً.

اسمحوا انو (س  - إحدى الدوال المثلثية الرئيسية. لحل عدم المساواة
يكفي إيجاد حلها في فترة واحدة أي. على أي مقطع طوله يساوي فترة الدالةf  x  ... بعد ذلك ، سيتم إيجاد حل المتباينة الأصلية بالكاملx ، بالإضافة إلى تلك القيم التي تختلف عن تلك الموجودة في أي عدد صحيح لفترات الوظيفة. في هذه الحالة ، من الملائم استخدام الطريقة الرسومية.

دعونا نعطي مثالاً على خوارزمية لحل المتباينات
(
) و
.

خوارزمية لحل عدم المساواة
(
).

1. صياغة تعريف جيب الرقمx على دائرة الوحدة.

3. على المحور الإحداثي ، قم بتمييز النقطة بالإحداثياتأ .

4. من خلال هذه النقطة ، ارسم خطًا مستقيمًا موازيًا لمحور OX ، وحدد نقاط تقاطعها مع الدائرة.

5. حدد قوسًا لدائرة ، يكون إحداثيات جميع نقاطها أقل منأ .

6. حدد اتجاه التجاوز (عكس اتجاه عقارب الساعة) واكتب الإجابة ، مضيفًا فترة الوظيفة إلى نهايات الفترة2πn ,
.

خوارزمية لحل عدم المساواة
.

1. صياغة تعريف ظل الرقمx على دائرة الوحدة.

2. ارسم دائرة وحدة.

3. ارسم خطًا من الظلال وحدد نقطة بإحداثية عليهاأ .

4. قم بتوصيل هذه النقطة بالأصل وقم بتمييز نقطة تقاطع مقطع الخط الناتج مع دائرة الوحدة.

5. حدد قوسًا لدائرة ، كل نقاطها لها إحداثيات على خط المماس أقل منأ .

6. حدد اتجاه التجاوز واكتب الإجابة مع مراعاة نطاق الوظيفة ، مع إضافة فترةπn ,
(دائمًا ما يكون الرقم الموجود على اليسار في الإدخال أقل من الرقم الموجود على اليمين).

يشار إلى التفسير الرسومي لحلول أبسط المعادلات والصيغ لحل التفاوتات بشكل عام في الملحق (الملحقان 1 و 2).

مثال 1. حل المتباينة
.

ارسم خطًا مستقيمًا على دائرة الوحدة
التي تتقاطع مع الدائرة عند النقطتين A و B.

كل القيمذ على الفاصل NM أكثر ، جميع نقاط القوس AMB تحقق هذه المتباينة. في جميع زوايا الدوران ، كبير لكن أصغر ,
سيأخذ قيمًا أكبر من (لكن ليس أكثر من واحد).

رسم بياني 1

وهكذا ، فإن حل المتباينة سيكون جميع القيم في المجال
، بمعنى آخر.
... من أجل الحصول على جميع حلول هذه المتباينة ، يكفي إضافة نهايات هذه الفترة
أين
، بمعنى آخر.
,
. لاحظ أن القيم
و
هي جذور المعادلة
,

أولئك.
;
.

إجابة:
,
.

1.2 طريقة رسومية

من الناحية العملية ، غالبًا ما تكون الطريقة الرسومية لحل التفاوتات المثلثية مفيدة. لنفكر في جوهر الطريقة باستخدام مثال عدم المساواة
:

1. إذا كانت الحجة معقدة (بخلافx ) ، ثم نستبدلها بـر .

2. نبني في طائرة تنسيق واحدةعروسه لعبه الرسوم البيانية الدالة
و
.

3. نجد مثلنقطتين متجاورتين من تقاطع الرسوم البيانيةبين الذيجيبي تقعأعلى مستقيم
... ابحث عن حدود هذه النقاط.

4. اكتب المتباينة المزدوجة للوسيطةر النظر في فترة جيب التمام (ر سيكون بين الفصول الموجودة).

5. إجراء الاستبدال العكسي (العودة إلى الوسيطة الأصلية) والتعبير عن القيمةx من المتباينة المزدوجة ، نكتب الإجابة في صورة فترة عددية.

مثال 2. حل عدم المساواة:.

عند حل المتباينات باستخدام طريقة رسومية ، من الضروري رسم الرسوم البيانية للوظائف بأكبر قدر ممكن من الدقة. نقوم بتحويل عدم المساواة إلى الشكل:

دعونا نبني في نظام إحداثي واحد الرسوم البيانية للوظائف
و
(الصورة 2).

الصورة 2

الرسوم البيانية للوظيفة تتقاطع عند نقطةو مع الإحداثيات
;
... ما بين أثنين
نقاط الرسم البياني
تحت نقاط الرسم البياني
... وعندما
قيم الدالة هي نفسها. وبالتالي
في
.

إجابة:
.

1.3 الطريقة الجبرية

في كثير من الأحيان ، يمكن اختزال عدم المساواة المثلثية الأصلية إلى عدم مساواة جبرية (عقلانية أو غير عقلانية) عن طريق استبدال جيد الاختيار. تتضمن هذه الطريقة تحويل متباينة أو إدخال تعويض أو تغيير متغير.

لنلقِ نظرة على أمثلة محددة لتطبيق هذه الطريقة.

مثال 3. اختزال إلى أبسط صورة
.

(تين. 3)

تين. 3

,
.

إجابة:
,

مثال 4. حل عدم المساواة:

ODZ:
,
.

باستخدام الصيغ:
,

نكتب عدم المساواة في الشكل:
.

أو افتراض
بعد التحولات البسيطة التي نحصل عليها

لحل المتباينة الأخيرة بطريقة الفواصل ، نحصل على:

الشكل 4

على التوالي
... ثم من التين. 4 يتبع
أين
.

الشكل 5

إجابة:
,
.

1.4. طريقة التباعد

المخطط العام لحل التفاوتات المثلثية بطريقة الفاصل الزمني:

عبر الصيغ المثلثية عامل بها.

ابحث عن نقاط الفاصل والأصفار للوظيفة ، ضعها على الدائرة.

خذ أي نقطةإلى (ولكن لم يتم العثور عليها سابقًا) واكتشف علامة العمل. إذا كان الناتج موجبًا ، فضع نقطة خلف دائرة الوحدة على الشعاع المقابل للزاوية. خلاف ذلك ، ضع النقطة داخل الدائرة.

إذا حدثت نقطة لعدد زوجي من المرات ، فإننا نسميها نقطة تعدد زوجي ، إذا كان عدد مرات فردي ، نقطة تعدد فردي. ارسم الأقواس على النحو التالي: ابدأ من نقطةإلى ، إذا كانت النقطة التالية من التعددية الفردية ، فإن القوس يتقاطع مع الدائرة عند هذه النقطة ، إذا كانت نقطة التعددية الزوجية ، فإنها لا تتقاطع.

الأقواس خارج الدائرة هي امتدادات موجبة ؛ داخل الدائرة فجوات سلبية.

مثال 5. حل المتباينة

,
.

نقاط السلسلة الأولى:
.

نقاط السلسلة الثانية:
.

تحدث كل نقطة عددًا فرديًا من المرات ، أي جميع نقاط التعدد الفردي.

دعنا نتعرف على علامة المنتج على
:. دعنا نحدد جميع النقاط على دائرة الوحدة (الشكل 6):

تين. 6

إجابة:
,
;
,
;
,
.

مثال 6 ... حل المتباينة.

القرار:

أوجد أصفار التعبير .

تسلمأم :

,
;

في دائرة الوحدة ، قيم السلسلةx 1 ممثلة بالنقاط
... سلسلةx 2 يعطي نقاط
... من المسلسلx 3 نحصل على نقطتين
... أخيرا ، سلسلةx 4 سوف تمثل النقاط
... نرسم كل هذه النقاط على دائرة الوحدة ، مشيرًا بين قوسين بجانب كل منها تعددها.

الآن دع الرقم ستكون متساوية. نقوم بتقدير بواسطة العلامة:

لذا فإن النقطةأ يجب أن يتم اختياره على شعاع يشكل زاوية مع شعاعيا، خارج دائرة الوحدة. (لاحظ أن الشعاع المساعدحول أ ليس من الضروري التصوير في الصورة على الإطلاق. نقطةأ تم تحديده تقريبًا.)

الآن من هذه النقطةأ نرسم خطًا مستمرًا متموجًا بالتتابع لجميع النقاط المحددة. علاوة على ذلك ، بالنقاط
ينتقل خطنا من منطقة إلى أخرى: إذا كان خارج دائرة الوحدة ، فإنه يذهب داخلها. الوصول إلى النقطة ، يعود الخط إلى المنطقة الداخلية ، لأن تعدد هذه النقطة هو زوجي. وبالمثل في هذه النقطة (مع تعدد حتى) يجب أن يتحول الخط إلى المنطقة الخارجية. لذلك ، قمنا برسم صورة معينة موضحة في الشكل. 7. يساعد على تحديد المناطق المطلوبة في دائرة الوحدة. يتم تمييزها بعلامة "+".

الشكل 7

الجواب النهائي:

ملحوظة. إذا كان الخط المتموج ، بعد الالتفاف حول جميع النقاط المحددة على دائرة الوحدة ، لا يمكن إرجاعه إلى النقطةأ , عدم عبور الدائرة في المكان "غير القانوني" ، فهذا يعني أنه كان هناك خطأ في الحل ، ألا وهو عدم وجود عدد فردي من الجذور.

إجابة: .

§2. مجمع مشاكل حل المتباينات المثلثية

في عملية تكوين مهارات الطلاب لحل التفاوتات المثلثية ، يمكن أيضًا تمييز 3 مراحل.

1. الإعدادية ،

2. تكوين المهارات لحل أبسط التفاوتات المثلثية.

3. إدخال أنواع أخرى من عدم المساواة المثلثية.

الغرض من المرحلة الإعدادية هو أنه من الضروري تكوين قدرة الطلاب على استخدام دائرة مثلثية أو رسم بياني لحل التفاوتات ، وهي:

القدرة على حل أبسط المتباينات بالصيغة
,
,
,
, استخدام خصائص وظائف الجيب وجيب التمام ؛

القدرة على رسم عدم المساواة المزدوجة لأقواس دائرة عددية أو لأقواس الرسوم البيانية للوظائف ؛

القدرة على إجراء تحويلات مختلفة للتعبيرات المثلثية.

يوصى بتنفيذ هذه المرحلة في عملية تنظيم معرفة أطفال المدارس حول خصائص الوظائف المثلثية. يمكن أن تكون الأداة الرئيسية هي المهام التي يتم تقديمها للطلاب ويتم إجراؤها إما بتوجيه من المعلم أو بشكل مستقل ، بالإضافة إلى المهارات المكتسبة في حل المعادلات المثلثية.

فيما يلي أمثلة على هذه المهام:

1 ... ضع علامة على نقطة على دائرة الوحدة ، اذا كان

2. في أي ربع من المستوى الإحداثي تكون النقطة ، اذا كان بالتساوي:

3. ضع علامة على النقاط على الدائرة المثلثية ، اذا كان:

4. تقليل التعبير إلى الدوال المثلثيةأنا أرباع.

و)
, ب)
, في)

5. القوس مُعطى.م - وسطأناالربع الثالثر - وسطIIالربع ال. قيمة متغيرة الحدر إلى عن على: (تشكل عدم مساواة مزدوجة) أ) قوس MP ؛ ب) أقواس RM.

6. اكتب عدم المساواة المزدوجة للأقسام المحددة من الرسم البياني:

تين. 1

7. حل المتباينات
,
,
,
.

8. تحويل التعبير .

في المرحلة الثانية من التعلم لحل التفاوتات المثلثية ، يمكن اقتراح التوصيات التالية المتعلقة بمنهجية تنظيم الأنشطة الطلابية. في هذه الحالة ، تحتاج إلى التركيز على المهارات التي يتعين على الطلاب بالفعل العمل بها مع دائرة أو رسم بياني مثلثي ، تم تشكيلها أثناء حل أبسط المعادلات المثلثية.

أولاً ، من الممكن تحفيز ملاءمة الحصول على تقنية عامة لحل أبسط المتباينات المثلثية بالإشارة ، على سبيل المثال ، إلى عدم المساواة في النموذج
. باستخدام المعرفة والمهارات المكتسبة في المرحلة الإعدادية ، سيقوم الطلاب بإحضار عدم المساواة المقترحة إلى النموذج
، ولكن قد تجد صعوبة في العثور على مجموعة الحلول للتفاوت الناتج ، منذ ذلك الحين من المستحيل حلها فقط باستخدام خصائص دالة الجيب. يمكن تجنب هذه الصعوبة بالرجوع إلى الرسم التوضيحي المقابل (حل المعادلة بيانياً أو باستخدام دائرة الوحدة).

ثانيًا ، يجب على المعلم لفت انتباه الطلاب إلى الطرق المختلفة لإكمال المهمة ، وإعطاء مثال مناسب لحل التفاوتات بيانيًا واستخدام الدائرة المثلثية.

ضع في اعتبارك هذه الخيارات لحل مشكلة عدم المساواة
.

1. حل المتباينة باستخدام دائرة الوحدة.

في الدرس الأول حول حل التفاوتات المثلثية ، سنقدم للطلاب خوارزمية حل مفصلة ، والتي ، في عرض تقديمي تدريجي ، تعكس جميع المهارات الأساسية اللازمة لحل مشكلة عدم المساواة.

الخطوة 1. لنرسم دائرة وحدة ، ونضع علامة على النقطة على المحور الإحداثي وارسم خطًا مستقيمًا من خلاله ، موازيًا لمحور الإحداثي. سيتقاطع هذا الخط مع دائرة الوحدة عند نقطتين. كل نقطة من هذه النقاط تمثل أرقام جيبها .

الخطوة 2. قسم هذا الخط الدائرة إلى قوسين. دعنا نختار الرقم الذي يصور الأرقام بجيب أكبر من ... وبطبيعة الحال ، يقع هذا القوس فوق الخط المرسوم.

تين. 2

الخطوه 3.دعنا نختار أحد نهايات القوس المحدد. لنكتب أحد الأعداد الممثلة بهذه النقطة من دائرة الوحدة .

الخطوة 4. من أجل تحديد الرقم المقابل للنهاية الثانية للقوس المحدد ، سوف "نسير" على طول هذا القوس من الطرف المحدد إلى الطرف الآخر. في الوقت نفسه ، نتذكر أنه عند التحرك بعكس اتجاه عقارب الساعة ، تزداد الأرقام التي سنمر بها (عندما نتحرك في الاتجاه المعاكس ، ستنخفض الأرقام). نكتب الرقم الموضح على دائرة الوحدة بالطرف الثاني للقوس المحدد .

وهكذا نرى أن عدم المساواة
تلبية الأرقام التي من أجلها عدم المساواة
... حللنا المتباينة للأعداد الموجودة في نفس الفترة من دالة الجيب. لذلك ، يمكن كتابة جميع حلول المتباينة بالصيغة

يجب أن يُطلب من الطلاب التفكير بعناية في الرسم وفهم سبب كل حلول عدم المساواة
يمكن كتابتها كـ
,
.

تين. 3

من الضروري لفت انتباه الطلاب إلى حقيقة أنه عند حل المتباينات لوظيفة جيب التمام ، نرسم خطًا مستقيمًا موازٍ للمحور الإحداثي.

طريقة رسومية لحل عدم المساواة.

نحن نبني الرسوم البيانية
و
معتبرا أن
.

تين. 4

ثم نكتب المعادلة
وحله
,
,
وجدت باستخدام الصيغ
,
,
.

(إعطاءن القيم 0 ، 1 ، 2 ، نجد ثلاثة جذور للمعادلة). القيم
هي عبارة عن ثلاث عبارات متتالية لنقاط تقاطع الرسوم البيانية
و
... من الواضح دائمًا في الفترة الفاصلة
عدم المساواة يحمل
وفي الفترة الفاصلة
- عدم المساواة
... نحن مهتمون بالحالة الأولى ، ثم إضافة مضاعف فترة الجيب إلى نهايات هذه الفترة ، نحصل على حل للمتباينة
مثل:
,
.

تين. خمسة

لخص. لحل عدم المساواة
، من الضروري تكوين المعادلة المقابلة وحلها. أوجد الجذور من الصيغة الناتجة و ، واكتب إجابة المتباينة بالصيغة: ,
.

ثالثًا ، تم تأكيد حقيقة مجموعة جذور المتباينة المثلثية المقابلة بوضوح شديد عند حلها بيانياً.

تين. 6

من الضروري أن نوضح للطلاب أن الحلقة ، وهي حل المتباينة ، تتكرر بعد نفس الفترة الزمنية التي تساوي فترة الدالة المثلثية. يمكنك أيضًا التفكير في رسم توضيحي مشابه للرسم البياني لوظيفة الجيب.

رابعًا ، يُنصح بتنفيذ العمل على تحديث أساليب الطلاب في تحويل مجموع (فرق) الدوال المثلثية إلى منتج ، للفت انتباه الطلاب إلى دور هذه الأساليب في حل التفاوتات المثلثية.

يمكن تنظيم هذا العمل من خلال تحقيق الطلاب المستقل للمهام التي اقترحها المعلم ، والتي نبرز من بينها ما يلي:

خامساً ، يجب أن يُطلب من الطلاب توضيح الحل لكل أبسط متباينة مثلثية باستخدام رسم بياني أو دائرة مثلثية. يجب عليك بالتأكيد الانتباه إلى منفعتها ، ولا سيما لاستخدام الدائرة ، لأنه عند حل المتباينات المثلثية ، فإن الرسم التوضيحي المقابل يعمل كوسيلة ملائمة للغاية لإصلاح مجموعة حلول عدم المساواة هذه

يُنصح بتعريف الطلاب على تقنيات حل التفاوتات المثلثية التي ليست أبسطها وفقًا للمخطط التالي: الإشارة إلى متباينة مثلثية محددة تشير إلى البحث المشترك المعادل المثلثي المقابل (مدرس - طلاب) لتقنية حل النقل الذاتي للتقنية الموجودة إلى متباينات أخرى من نفس النوع.

من أجل تنظيم معرفة الطلاب حول علم المثلثات ، نوصيك بتحديد مثل هذه التفاوتات على وجه التحديد ، والتي يتطلب حلها تحويلات مختلفة يمكن تنفيذها في عملية حلها ، وتركيز انتباه الطلاب على ميزاتهم.

على هذا النحو ، يمكننا أن نقترح ، على سبيل المثال ، ما يلي:

في الختام ، نقدم مثالًا لمجموعة من المشكلات لحل المتباينات المثلثية.

1. حل عدم المساواة:

2. حل عدم المساواة: 3. البحث عن جميع الحلول لعدم المساواة: 4. البحث عن جميع الحلول لعدم المساواة:

و)
إرضاء الشرط
;

ب)
إرضاء الشرط
.

5. البحث عن جميع الحلول لعدم المساواة:

و) ;

ب) ;

في)
;

د)
;

ه)
.

6. حل عدم المساواة:

و) ;

ب) ;

في) ؛

د)
;

ه) ؛

ز)
.

7. حل عدم المساواة:

و)
;

ب) ;

في) ؛

د).

8. حل عدم المساواة:

و) ;

ب) ;

في) ؛

د)
;

ه)
;

ه) ؛

ز)
;

ح).

يُنصح بتقديم المهمتين 6 و 7 للطلاب الذين يدرسون الرياضيات على مستوى متقدم ، والمهمة 8 لطلاب الصفوف ذات الدراسة المتقدمة للرياضيات.

§3. طرق خاصة لحل المتباينات المثلثية

طرق خاصة لحل المعادلات المثلثية - أي تلك الطرق التي لا يمكن استخدامها إلا لحل المعادلات المثلثية. تعتمد هذه الطرق على استخدام خصائص الدوال المثلثية ، وكذلك استخدام الصيغ المثلثية والهويات المختلفة.

3.1. طريقة القطاع

ضع في اعتبارك طريقة القطاع لحل التفاوتات المثلثية. حل المتباينات بالشكل

أينص ( x ) وس ( x ) - الدوال المثلثية المنطقية (الجيوب ، وجيب التمام ، والظل ، والمظلات مدرجة فيها بشكل منطقي) ، على غرار حل المتباينات العقلانية. عدم المساواة العقلانية من الملائم حلها بطريقة الفواصل الزمنية على محور الأرقام. نظيره في حل المتباينات المثلثية المنطقية هو طريقة القطاعات في الدائرة المثلثية ، لsinx وكوسكس (
) أو نصف دائرة مثلثية لـtgx وctgx (
).

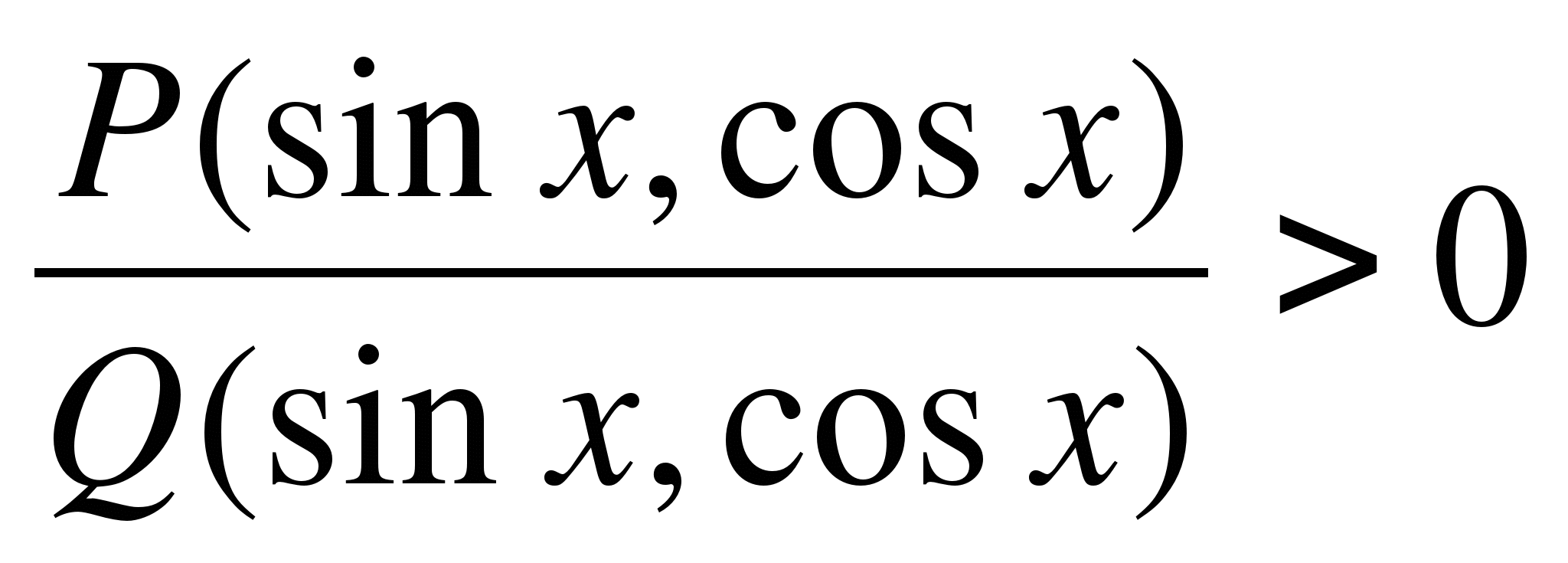
في طريقة الفواصل ، كل عامل خطي لبسط النموذج ومقامه
على المحور العددي هناك نقطة ، وعند المرور بهذه النقطة
علامة التغييرات. في طريقة القطاع ، كل عامل من أشكال النموذج
أين
- إحدى الوظائفsinx أوكوسكس و
في الدائرة المثلثية هناك تقابل زاويتين و
التي تقسم الدائرة إلى قسمين. عندما تمر و وظيفة
علامة التغييرات.

تذكر ما يلي:

أ) عوامل الشكل
و
أين
، احتفظ بالعلامة لجميع القيم ... يتم تجاهل عوامل البسط والمقام ، وتغيير (if
) لكل قطرة من هذا القبيل علامة عدم المساواة على العكس.

ب) عوامل الشكل
و
يتم التخلص منها أيضًا. علاوة على ذلك ، إذا كانت هذه عوامل المقام ، عندئذٍ تضاف عدم المساواة في الشكل إلى نظام عدم المساواة المكافئ
و
... إذا كانت هذه هي عوامل البسط ، فإنها في نظام القيود المكافئة تتوافق مع عدم المساواة
و
في حالة عدم المساواة الأولية الصارمة ، والمساواة
و
في حالة عدم المساواة الأولية التراخي. عند التخلص من المضاعف
أو
يتم عكس علامة عدم المساواة.

مثال 1. حل عدم المساواة: أ)
، ب)
. لدينا وظيفة ، ب). حل عدم المساواة لدينا ،

3.2 طريقة الدائرة المركزة

هذه الطريقة مماثلة لطريقة المحاور العددية المتوازية في حل أنظمة عدم المساواة المنطقية.

ضع في اعتبارك مثالاً لنظام عدم المساواة.

مثال 5. حل نظام أبسط المتباينات المثلثية

أولًا ، لنحل كل متباينة على حدة (الشكل 5). في الركن الأيمن العلوي من الشكل ، سنشير إلى الحجة التي يتم أخذها في الاعتبار في الدائرة المثلثية.

الشكل 5

بعد ذلك ، نقوم ببناء نظام من الدوائر متحدة المركز للحجةx ... نرسم دائرة ونظللها وفقًا لحل المتباينة الأولى ، ثم نرسم دائرة نصف قطرها أكبر ونظللها وفقًا لحل المتباينة الثانية ، ثم نرسم دائرة للمتباينة الثالثة ودائرة أساس. نرسم أشعة من مركز النظام عبر نهايات الأقواس بحيث تتقاطع مع جميع الدوائر. نشكل حلاً على الدائرة الأساسية (الشكل 6).

الشكل 6

إجابة:
,
.

خاتمة

تم الانتهاء من جميع أهداف دراسة الدورة. يتم تنظيم المادة النظرية: الأنواع الرئيسية من عدم المساواة المثلثية والطرق الرئيسية لحلها (الرسم ، والجبر ، وطريقة الفواصل ، والقطاعات وطريقة الدوائر متحدة المركز). تم إعطاء مثال لحل عدم المساواة لكل طريقة. تلا الجزء النظري الجزء العملي. يحتوي على مجموعة من المهام لحل عدم المساواة المثلثية.

يمكن للطلاب استخدام هذا المقرر الدراسي للعمل المستقل. يمكن لأطفال المدارس التحكم في مستوى إتقان هذا الموضوع ، والممارسة في إكمال المهام ذات التعقيد المتفاوت.

بعد العمل من خلال الأدبيات ذات الصلة بهذه المسألة ، من الواضح أنه يمكننا أن نستنتج أن القدرة والمهارات لحل التفاوتات المثلثية في مسار الجبر المدرسي ومبادئ التحليل مهمة للغاية ، والتي يتطلب تطويرها جهدًا كبيرًا من جانب معلم الرياضيات.

لذلك ، سيكون هذا العمل مفيدًا لمعلمي الرياضيات ، لأنه يجعل من الممكن تنظيم تدريب الطلاب بشكل فعال على موضوع "عدم المساواة المثلثية".

يمكن متابعة الدراسة بتوسيعها إلى العمل التأهيلي النهائي.

قائمة الأدب المستخدم

بوجومولوف ، ن. مجموعة من المسائل في الرياضيات [نص] / N.V. بوجومولوف. - م: بوستارد ، 2009. - 206 ص.

فيجودسكي ، م. كتيب الرياضيات الابتدائية [نص] / M.Ya. فيجودسكي. - م: بوستارد ، 2006. - 509 ص.

زوربنكو ، ل. الرياضيات في الأمثلة والمهام [نص] / ل.ن. زوربينكو. - م: Infra-M، 2009. - 373 صفحة.

إيفانوف ، أ. رياضيات ابتدائية لأطفال المدارس والطلاب والمعلمين [نص] / ..А. إيفانوف. - م: MTsNMO ، 2009. - 384 ص.

كارب ، أ. مهام الجبر وبداية التحليل لتنظيم الإعادة النهائية والشهادة في الصف 11 [نص] / A.P. الكارب. - م: التعليم ، 2005. - 79 ص.

كولانين ، إي د. 3000 مشاكل المنافسة في الرياضيات [نص] / E.D. كولانين. - م: ايريس برس ، 2007. - 624 ص.

ليبسون ، ك. مجموعة من المهام العملية في الرياضيات [نص] / K.L. ليبسون. - م: بوستارد ، 2010. - 182 ص.

لوكوت ، في. المهام مع المعلمات وحلها. علم المثلثات: المعادلات ، عدم المساواة ، النظم. الصف العاشر [نص] / V.V. مرفق. - م: أركتي ، 2008. - 64 ص.

مانوفا ، أ. رياضيات. المعلم السريع للتحضير للامتحان: كتاب مدرسي. البدل [نص] / A.N. مانوفا. - روستوف أون دون: فينيكس ، 2012. - 541 ص.

مردكوفيتش ، أ. الجبر وبداية التحليل الرياضي. 10-11 درجات. كتاب مدرسي لطلاب المؤسسات التعليمية [نص] / أ. مردكوفيتش. - م: ايريس برس ، 2009. - 201 ص.

نوفيكوف ، أ. الدوال المثلثية والمعادلات والمتباينات [نص] / A.I. نوفيكوف. - م: FIZMATLIT ، 2010. - 260 ص.

Oganesyan ، V.A. طرق تدريس الرياضيات في المرحلة الثانوية: المنهجية العامة. كتاب مدرسي. دليل للطلاب نات. - حصيرة. فاس. بيد. في tov. [نص] / V.А. هوفهانيسيان. - م: التعليم ، 2006. - 368 ص.

Olekhnik ، S.N. المعادلات وعدم المساواة. طرق الحل غير القياسية [نص] / S.N. أوليكنك. - م: دار النشر Factorial ، 1997. - 219 ص.

سيفريوكوف ، ب. المعادلات والتفاوتات المثلثية والأسية واللوغاريتمية [نص] / P.F. سيفريوكوف. - م: التعليم العام ، 2008. - 352 ص.

سيرجيف ، آي إن. امتحان الدولة الموحد: 1000 مشكلة مع الإجابات والحلول في الرياضيات. جميع مهام المجموعة C [نص] / IN. سيرجيف. - م: الفحص ، 2012. - 301 ص.

سوبوليف ، أ. الرياضيات الابتدائية [نص] / A.B. سوبوليف. - ايكاترينبرج: GOU VPO USTU-UPI، 2005. - 81 صفحة.

فينكو ، إل. طريقة الفترات في حل المتباينات ودوال الدراسة [نص] / L.M. فينكو. - م: بوستارد ، 2005. - 124 ص.

فريدمان ، إل. الأسس النظرية لطرق التدريس في الرياضيات [نص] / L.. فريدمان. - م: دار الكتاب "ليبروكوم" ، 2009. - 248 ص.

ملحق 1

التفسير البياني لحلول أبسط التفاوتات

تين. 1

تين. 2

تين. 3

الشكل 4

الشكل 5

الشكل 6

الشكل 7

الشكل 8

الملحق 2

حلول لأبسط التفاوتات

في درس عملي ، سنكرر الأنواع الرئيسية للمهام من موضوع "علم المثلثات" ، بالإضافة إلى تحليل المهام ذات التعقيد المتزايد والنظر في أمثلة لحل مختلف عدم المساواة المثلثية وأنظمتها.

سيساعدك هذا الدرس على الاستعداد لأحد أنواع المهام B5 و B7 و C1 و C3.

لنبدأ بتكرار الأنواع الرئيسية من المهام التي ناقشناها في موضوع "علم المثلثات" وسنحل العديد من المهام غير القياسية.

المشكلة رقم 1... تحويل الزوايا إلى راديان ودرجات: أ) ؛ ب).

أ) لنستخدم صيغة تحويل الدرجات إلى الراديان

دعنا نستبدل القيمة المحددة فيه.

ب) طبِّق معادلة التحويل من الراديان إلى درجات

لنقم بإجراء الاستبدال .

إجابة. و) ؛ ب).

رقم المشكلة 2... احسب: أ) ؛ ب).

أ) نظرًا لأن الزاوية أبعد بكثير من الزاوية الجدولية ، فسنقللها بطرح فترة الجيب. لان يشار إلى الزاوية بالراديان ، ثم يتم اعتبار الفترة على أنها.

ب) في هذه الحالة ، يكون الوضع مشابهًا. نظرًا لأن الزاوية محددة بالدرجات ، فسيتم اعتبار فترة الظل.

الزاوية الناتجة ، على الرغم من أنها أقل من النقطة ، تكون أكبر ، مما يعني أنها لم تعد تشير إلى الجزء الرئيسي ، بل إلى الجزء الممتد من الجدول. من أجل عدم تدريب ذاكرتنا مرة أخرى عن طريق حفظ جدول موسع لقيم دالة المثلث ، نطرح فترة الظل مرة أخرى:

استخدمنا غرابة دالة الظل.

إجابة. أ) 1 ؛ ب).

رقم المشكلة 3... احسب ، اذا كان .

نحضر المقدار بالكامل إلى المماس ، ونقسم بسط الكسر ومقامه على. في الوقت نفسه ، لا يمكننا أن نخاف ذلك ، لأنه في هذه الحالة ، لن توجد قيمة الظل.

المشكلة رقم 4... تبسيط التعبير.

يتم تحويل التعبيرات المحددة باستخدام صيغ التحويل. إنها مكتوبة بشكل غير عادي باستخدام الدرجات. التعبير الأول بشكل عام عبارة عن رقم. دعونا نبسط جميع وظائف حساب المثلثات بدورها:

لان ، ثم تتغير الوظيفة إلى دالة مشتركة ، أي إلى ظل التمام ، وتقع الزاوية في الربع الثاني ، حيث يكون للماس الأصلي إشارة سالبة.

لنفس الأسباب كما في التعبير السابق ، يتم تغيير الوظيفة إلى دالة مشتركة ، أي على ظل التمام ، وتقع الزاوية في الربع الأول ، حيث يكون للماس الأصلي إشارة موجبة.

دعنا نستبدل كل شيء في تعبير مبسط:

المشكلة رقم 5... تبسيط التعبير.

لنكتب ظل الزاوية المزدوجة وفقًا للصيغة المقابلة ونبسط التعبير:

الهوية الأخيرة هي إحدى صيغ الاستبدال الشاملة لجيب التمام.

رقم المشكلة 6... احسب.

الشيء الرئيسي هو عدم ارتكاب خطأ قياسي وعدم إعطاء إجابة بأن التعبير متساوٍ. لا يمكنك استخدام الخاصية الرئيسية لـ Arctangent طالما يوجد مضاعف على شكل اثنين بجانبه. للتخلص منها ، سنكتب المقدار وفقًا لصيغة ظل الزاوية المزدوجة ، بينما نتعامل معها على أنها حجة عادية.

يمكنك الآن استخدام الخاصية الرئيسية لـ Arctangent ، تذكر أنه لا توجد قيود على نتيجتها العددية.

رقم المشكلة 7... حل المعادلة.

عند حل معادلة كسرية تساوي صفرًا ، يُشار دائمًا إلى أن البسط يساوي صفرًا ، لكن المقام ليس كذلك ، لأن لا يمكنك القسمة على الصفر.

المعادلة الأولى هي حالة خاصة لأبسط معادلة يمكن حلها باستخدام الدائرة المثلثية. فكر في هذا الحل بنفسك. يتم حل المتباينة الثانية على أنها أبسط معادلة وفقًا للصيغة العامة لجذور الظل ، ولكن فقط عندما تكون الإشارة غير متساوية.

كما ترى ، تستبعد عائلة واحدة من الجذور عائلة أخرى من الجذور التي لا ترضي المعادلة التي لها نفس الشكل تمامًا. أولئك. لا جذور.

إجابة. لا جذور.

المشكلة رقم 8... حل المعادلة.

على الفور ، نلاحظ أنه يمكنك إخراج العامل المشترك والقيام بذلك:

تم تقليل المعادلة إلى أحد الأشكال القياسية ، عندما يكون ناتج العديد من العوامل يساوي صفرًا. نحن نعلم بالفعل أنه في هذه الحالة ، إما أن يكون أحدهما صفرًا أو الآخر أو الثالث. لنكتب هذا في صورة مجموعة معادلات:

أول معادلتين هما حالات خاصة من الأبسط ، لقد واجهنا بالفعل معادلات متشابهة عدة مرات ، لذلك سنشير إلى حلولها على الفور. يتم تقليل المعادلة الثالثة إلى دالة واحدة باستخدام صيغة الجيب المزدوجة الزاوية.

لنحل المعادلة الأخيرة بشكل منفصل:

هذه المعادلة ليس لها جذور لأن لا يمكن أن تذهب قيمة الجيب خارج الحدود .

وبالتالي ، فإن الحل هو أول عائلتين فقط من الجذور ، ويمكن دمجها في واحدة ، والتي يمكن عرضها بسهولة على الدائرة المثلثية:

هذه عائلة من جميع الأنصاف ، أي.

دعنا ننتقل إلى حل المتباينات المثلثية. أولاً ، سنقوم بتحليل نهج حل مثال دون استخدام الصيغ للحلول العامة ، ولكن باستخدام دائرة مثلثية.

المشكلة رقم 9... حل المتباينة.

ارسم على الدائرة المثلثية خطًا مساعدًا يقابل قيمة الجيب التي تساوي ، وأظهر فاصل الزوايا التي تحقق المتباينة.

من المهم جدًا أن نفهم بالضبط كيفية الإشارة إلى نطاق الزوايا الناتج ، أي ما هي بدايته وماهي نهايته. ستكون بداية الفترة الزمنية هي الزاوية المقابلة للنقطة التي سندخل عندها في بداية الفترة ، إذا تحركنا عكس اتجاه عقارب الساعة. في حالتنا ، هذه هي النقطة على اليسار لأن تتحرك عكس اتجاه عقارب الساعة وتجاوز النقطة الصحيحة ، على العكس من ذلك ، نترك النطاق المطلوب من الزوايا. وبالتالي فإن النقطة الموجودة على اليمين سوف تتوافق مع نهاية الفجوة.

الآن من الضروري فهم قيم زوايا بداية ونهاية الفترة الخاصة بحلول المتباينة. خطأ نموذجي - هذا للإشارة على الفور إلى أن النقطة اليمنى تقابل الزاوية على اليسار وتعطي إجابة. هذا ليس صحيحا! لاحظ أننا حددنا للتو الفجوة المقابلة للجزء العلوي من الدائرة ، على الرغم من أننا مهتمون بالجزء السفلي ، بمعنى آخر ، فقد خلطنا بداية ونهاية الفترة الزمنية المطلوبة للحلول.

لكي يبدأ الفاصل الزمني عند زاوية النقطة اليمنى وينتهي عند زاوية النقطة اليسرى ، يجب أن تكون الزاوية المحددة الأولى أقل من الثانية. للقيام بذلك ، سيتعين علينا قياس زاوية النقطة اليمنى في الاتجاه السلبي للإشارة ، أي في اتجاه عقارب الساعة وستكون متساوية. بعد ذلك ، بدءًا من الاتجاه الموجب في اتجاه عقارب الساعة ، سنصل إلى النقطة اليمنى بعد النقطة اليسرى ونحصل على قيمة الزاوية لها. الآن بداية الفترة الزمنية للزوايا أقل من النهاية ، ويمكننا كتابة الفاصل الزمني للحلول دون النظر إلى الفترة:

بالنظر إلى أن هذه الفواصل الزمنية ستتكرر بعدد لا حصر له من المرات بعد أي عدد صحيح من الدورات ، نحصل على حل عام مع مراعاة فترة الجيب:

نضع الأقواس لأن المتباينة صارمة ، ونقطع النقاط على الدائرة التي تتوافق مع نهايات الفترة.

قارن هذه الإجابة بصيغة الحل العام التي قدمناها في المحاضرة.

إجابة. .

هذه الطريقة جيدة لفهم من أين تأتي صيغ الحلول العامة لأبسط معاملات المثلثية. بالإضافة إلى ذلك ، من المفيد لمن هم كسالى جدًا أن يتعلموا كل هذه الصيغ المرهقة. ومع ذلك ، فإن الطريقة نفسها ليست سهلة أيضًا ، اختر الطريقة الأكثر ملاءمة لك للوصول إلى الحل.

لحل المتباينات المثلثية ، يمكنك أيضًا استخدام الرسوم البيانية للوظائف التي يُبنى عليها الخط الإضافي بطريقة مشابهة للطريقة الموضحة باستخدام دائرة الوحدة. إذا كنت مهتمًا ، فحاول اكتشاف هذا النهج بنفسك. فيما يلي ، سنستخدم الصيغ العامة لحل أبسط المتباينات المثلثية.

المشكلة رقم 10... حل المتباينة.

سنستخدم صيغة الحل العام ، مع الأخذ في الاعتبار أن عدم المساواة ليست صارمة:

ندخل في حالتنا:

إجابة.