أوجد قيمة تعبيرات المعادلات المثلثية. درس "تبسيط المقادير المثلثية"

الأقسام: رياضيات

صف دراسي: 11

الدرس 1

موضوع: الصف 11 (التحضير للامتحان)

تبسيط التعبيرات المثلثية.

أبسط حل المعادلات المثلثية... (ساعاتين)

الأهداف:

• لتنظيم وتعميم وتوسيع معارف ومهارات الطلاب المرتبطة باستخدام صيغ علم المثلثات وحل أبسط المعادلات المثلثية.

معدات الدرس:

هيكل الدرس:

1. لحظة تنظيمية
2. اختبار على أجهزة الكمبيوتر المحمولة. مناقشة النتائج.
3. تبسيط المقادير المثلثية
4. حل أبسط المعادلات المثلثية
5. عمل مستقل.
6. ملخص الدرس. شرح مهمة المنزل.

1. لحظة تنظيمية. (2 دقيقة.)

يحيي المعلم الجمهور ، ويعلن عن موضوع الدرس ، ويذكرهم بالمهمة المعطاة سابقًا لتكرار معادلات علم المثلثات ، وإعداد الطلاب للاختبار.

2. الاختبار. (15 دقيقة + 3 دقائق مناقشة)

الهدف هو اختبار المعرفة الصيغ المثلثية والقدرة على تطبيقها. كل طالب لديه جهاز كمبيوتر محمول على مكتبه بنسخة تجريبية.

يمكن أن يكون هناك أي عدد من الخيارات ، سأقدم مثالاً على أحدها:

الخيار الأول.

تبسيط التعبيرات:

أ) الهويات المثلثية الأساسية

1.sin 2 3y + cos 2 3y + 1 ؛

ب) صيغ الجمع

3.sin5x - sin3x ؛

ج) تحويل المنتج إلى مبلغ

6.2sin8y cozy3y ؛

د) صيغ زاوية مزدوجة

7.2sin5x cos5x ؛

ه) صيغ نصف زاوية

و) صيغ زاوية ثلاثية

ز) الاستبدال الشامل

ح) خفض الدرجة

16.cos 2 (3x / 7) ؛

يرى الطلاب الذين يستخدمون جهاز كمبيوتر محمول إجاباتهم أمام كل صيغة.

يتم فحص العمل على الفور بواسطة الكمبيوتر. يتم عرض النتائج على شاشة كبيرة ليراها الجميع.

أيضًا ، بعد انتهاء العمل ، يتم عرض الإجابات الصحيحة على أجهزة الكمبيوتر المحمولة الخاصة بالطلاب. يرى كل طالب مكان حدوث الخطأ وما هي الصيغ التي يحتاج إلى تكرارها.

3. تبسيط التعابير المثلثية. (25 دقيقة)

الهدف هو مراجعة وممارسة وتوحيد تطبيق الصيغ الأساسية لعلم المثلثات. حل المسائل B7 من الامتحان.

في هذه المرحلة ، يُنصح بتقسيم الفصل إلى مجموعات من الطلاب الأقوياء (العمل بشكل مستقل مع التحقق اللاحق) والطلاب الضعفاء الذين يعملون مع المعلم.

مهمة للمتعلمين الأقوياء (معدة مسبقًا على أساس مطبوع). ينصب التركيز الرئيسي على صيغ التخفيض والزاوية المزدوجة ، وفقًا لامتحان 2011.

تبسيط التعبيرات (للمتعلمين الأقوياء):

في موازاة ذلك ، يعمل المعلم مع الطلاب الضعفاء ، ويناقش ويحل المهام على الشاشة بإملاء من الطلاب.

احسب:

5) الخطيئة (270 درجة - α) + كوس (270 درجة + α)

6)

تبسيط:

جاء دور مناقشة نتائج عمل المجموعة القوية.

تظهر الإجابات على الشاشة ، وكذلك بمساعدة كاميرا الفيديو ، يتم عرض أعمال 5 طلاب مختلفين (مهمة واحدة لكل منهم).

ترى المجموعة الضعيفة الشرط وطريقة الحل. المناقشة والتحليل قيد التقدم. مع استخدام الوسائل التقنية ، يحدث هذا بسرعة.

4. حل أبسط المعادلات المثلثية. (30 دقيقة.)

الهدف هو تكرار حل أبسط المعادلات المثلثية وتنظيمها وتعميمها ، وتسجيل جذورها. حل المشكلة B3.

أي معادلة مثلثية ، بغض النظر عن كيفية حلها ، تؤدي إلى أبسط معادلة.

عند الانتهاء من المهمة ، يجب أن ينجذب الطلاب إلى تسجيل جذور معادلات الحالات الخاصة والشكل العام واختيار الجذور في المعادلة الأخيرة.

حل المعادلات:

اكتب أصغر جذر موجب في الإجابة.

5. العمل المستقل (10 دقائق)

الهدف هو اختبار المهارات المكتسبة وتحديد المشاكل والأخطاء وطرق القضاء عليها.

يتم تقديم عمل بمستويات مختلفة بناءً على اختيار الطالب.

خيار لـ "3"

1) أوجد قيمة التعبير

2) بسّط التعبير 1 - sin 2 3α - cos 2 3α

3) حل المعادلة

خيار لـ "4"

1) أوجد قيمة التعبير

2) حل المعادلة اكتب أصغر جذر موجب في الإجابة.

خيار لـ "5"

1) ابحث عن tgα إذا

2) أوجد جذر المعادلة اكتب أصغر جذر موجب في إجابتك.

6. ملخص الدرس (5 دقائق)

يلخص المعلم ما يكرره الدرس ويوحد الصيغ المثلثية ، وهو حل أبسط المعادلات المثلثية.

واجب منزلي (مُعد مسبقًا على أساس مطبوع) مع فحوصات عشوائية في الدرس التالي.

حل المعادلات:

9)

10) حدد أصغر جذر موجب في إجابتك.

الجلسة الثانية

موضوع: الصف 11 (التحضير للامتحان)

طرق حل المعادلات المثلثية. اختيار الجذور. (ساعاتين)

الأهداف:

• لتعميم وتنظيم المعرفة في حل المعادلات المثلثية بأنواعها المختلفة.
• لتعزيز تنمية التفكير الرياضي للطلاب ، والقدرة على الملاحظة والمقارنة والتعميم والتصنيف.
• شجع الطلاب على التغلب على الصعوبات في عملية النشاط العقلي ، لضبط النفس ، واستبطان أنشطتهم.

معدات الدرس: KRMu ، أجهزة كمبيوتر محمولة لكل طالب.

هيكل الدرس:

1. لحظة تنظيمية
2. مناقشة د / ح و samot. أعمال الدرس الأخير
3. تكرار طرق حل المعادلات المثلثية.
4. حل المعادلات المثلثية
5. اختيار الجذور في المعادلات المثلثية.
6. عمل مستقل.
7. ملخص الدرس. واجب منزلي.

1. لحظة تنظيمية (دقيقتان)

يحيي المعلم الجمهور ويعلن عن موضوع الدرس وخطة العمل.

2. أ) مراجعة الواجب المنزلي (5 دقائق).

الهدف هو التحقق من التنفيذ. يتم عرض عمل واحد بمساعدة كاميرا فيديو على الشاشة ، ويتم جمع الباقي بشكل انتقائي لفحص المعلم.

ب) تحليل العمل المستقل (3 دقائق)

الهدف هو تحليل الأخطاء وبيان طرق التغلب عليها.

على الشاشة ، الإجابات والحلول ، يتم تعيين عمل الطلاب مسبقًا. يتقدم التحليل بسرعة.

3. تكرار طرق حل المعادلات المثلثية (5 دقائق)

الهدف هو استدعاء طرق حل المعادلات المثلثية.

اسأل الطلاب عن الطرق التي يعرفونها لحل المعادلات المثلثية. أكد أن هناك ما يسمى بالطرق الأساسية (شائعة الاستخدام):

• استبدال متغير ،
• التحليل إلى عوامل
• معادلات متجانسة

وهناك طرق تطبيقية:

• وفقًا للصيغ الخاصة بتحويل مبلغ إلى منتج ومنتج إلى مبلغ ،
• من خلال صيغ تخفيض الدرجة ،
• استبدال عالمي مثلثي
• مقدمة من زاوية مساعدة ،
• الضرب ببعض الدوال المثلثية.

يجب أيضًا أن نتذكر أنه يمكن حل معادلة واحدة بطرق مختلفة.

4. حل المعادلات المثلثية (30 دقيقة)

الهدف هو تعميم المعرفة والمهارات حول هذا الموضوع وتوحيدها ، للتحضير لقرار C1 من الامتحان.

أعتبر أنه من المناسب حل المعادلات لكل طريقة مع الطلاب.

يفرض الطالب الحل ، يكتب المعلم على الجهاز اللوحي ، ويتم عرض العملية برمتها على الشاشة. سيسمح لك ذلك باستدعاء المواد المغطاة مسبقًا بسرعة وكفاءة.

حل المعادلات:

1) تغيير المتغير 6cos 2 x + 5sinx - 7 \u003d 0

2) تحليل 3cos (x / 3) + 4cos 2 (x / 3) \u003d 0

3) معادلات متجانسة الخطيئة 2 x + 3cos 2 x - 2sin2x \u003d 0

4) تحويل المجموع إلى حاصل ضرب cos5x + cos7x \u003d cos (π + 6x)

5) تحويل الناتج إلى مجموع 2sinx sin2x + cos3x \u003d 0

6) خفض القوة sin2x - sin 2 2x + sin 2 3x \u003d 0.5

7) الاستبدال العام المثلثي sinx + 5cosx + 5 \u003d 0.

لحل هذه المعادلة ، تجدر الإشارة إلى أن استخدام هذه الطريقة يؤدي إلى تضييق مجال التعريف ، حيث يتم استبدال الجيب وجيب التمام بـ tg (x / 2). لذلك ، قبل كتابة الإجابة ، تحتاج إلى التحقق مما إذا كانت الأرقام من المجموعة π + 2πn ، n Z هي خيول هذه المعادلة.

8) إدخال زاوية مساعدة a3sinx + cosx - √2 \u003d 0

9) الضرب ببعض الدوال المثلثية cosx cos2x cos4x \u003d 1/8.

5. اختيار جذور المعادلات المثلثية (20 دقيقة)

نظرًا لأنه في ظروف المنافسة الشرسة عند دخول الجامعات ، لا يكفي حل الجزء الأول من الاختبار ، فيجب على معظم الطلاب الانتباه إلى مهام الجزء الثاني (C1 ، C2 ، C3).

لذلك ، فإن الغرض من هذه المرحلة من الدرس هو استدعاء المواد التي تمت دراستها مسبقًا ، للتحضير لحل مشكلة C1 من USE 2011.

هناك معادلات مثلثية تحتاج فيها إلى تحديد الجذور عند كتابة إجابة. هذا بسبب بعض القيود ، على سبيل المثال: مقام الكسر ليس صفراً ، والتعبير الموجود تحت جذر قوة زوجية غير سالب ، والتعبير الموجود أسفل علامة اللوغاريتم موجب ، إلخ.

تعتبر هذه المعادلات معادلات ذات تعقيد متزايد وفي إصدار الاستخدام توجد في الجزء الثاني ، أي C1.

حل المعادلة:

إذا كان الكسر صفرًا باستخدام دائرة الوحدة ، نختار الجذور (انظر الشكل 1)

الصورة 1.

نحصل على x \u003d π + 2πn ، n Z

الجواب: π + 2πn، n Z

على الشاشة ، يظهر اختيار الجذور على دائرة في صورة ملونة.

المنتج يساوي صفرًا عندما يكون أحد العوامل على الأقل مساويًا للصفر ، ولا يفقد القوس معناه. ثم

حدد الجذور باستخدام دائرة الوحدة (انظر الشكل 2)

تم تصميم درس الفيديو "تبسيط التعبيرات المثلثية" لتطوير مهارات الطلاب في حل المشكلات المثلثية باستخدام الهويات المثلثية الأساسية. في سياق درس الفيديو ، يتم النظر في أنواع الهويات المثلثية ، وأمثلة لحل المشكلات باستخدامها. باستخدام المساعدة البصرية ، يسهل على المعلم تحقيق أهداف الدرس. يساعد العرض التقديمي الحيوي للمادة على تذكر النقاط المهمة. يتيح استخدام تأثيرات الرسوم المتحركة والدبلجة استبدال المعلم تمامًا في مرحلة شرح المادة. وبالتالي ، باستخدام هذه المساعدة البصرية في دروس الرياضيات ، يمكن للمدرس زيادة فعالية التدريس.

في بداية درس الفيديو يتم الإعلان عن موضوعه. ثم يتم استدعاء الهويات المثلثية التي تمت دراستها مسبقًا. تعرض الشاشة المساواة sin 2 t + cos 2 t \u003d 1 ، tg t \u003d sin t / cos t ، حيث t ≠ π / 2 + k لـ kϵZ ، ctg t \u003d cos t / sin t ، صالحة لـ t ≠ k ، حيث kϵZ ، tg t · ctg t \u003d 1 ، لـ t ≠ πk / 2 ، حيث kϵZ ، تسمى المتطابقات المثلثية الأساسية. يُلاحظ أن هذه الهويات تُستخدم غالبًا في حل المشكلات حيث يكون من الضروري إثبات المساواة أو تبسيط التعبير.

علاوة على ذلك ، يتم النظر في أمثلة على تطبيق هذه الهويات في حل المشكلات. أولاً ، يُقترح النظر في حل المشكلات لتبسيط التعبيرات. في المثال 1 ، من الضروري تبسيط التعبير cos 2 t- cos 4 t + sin 4 t. لحل هذا المثال ، ضع أولاً العامل المشترك cos 2 t خارج الأقواس. نتيجة لهذا التحول بين الأقواس ، يتم الحصول على التعبير 1- cos 2 t ، والتي تساوي قيمتها من الهوية الأساسية لعلم المثلثات sin 2 t. بعد تحويل التعبير ، من الواضح أن هناك عاملًا مشتركًا آخر sin 2 t يمكن وضعه بين أقواس ، وبعد ذلك يأخذ التعبير الصيغة sin 2 t (sin 2 t + cos 2 t). من نفس المتطابقة الأساسية نشتق قيمة التعبير بين الأقواس ، التي تساوي 1. نتيجة التبسيط ، نحصل على cos 2 t- cos 4 t + sin 4 t \u003d sin 2 t.

في المثال 2 ، يجب أيضًا تبسيط تعبير التكلفة / (1- sint) + cost / (1+ sint). نظرًا لأن تكلفة التعبير موجودة في بسط كلا الكسرين ، فيمكن وضعها بين قوسين كعامل مشترك. ثم يتم تقليل الكسور الموجودة بين قوسين إلى قاسم مشترك بضرب (1-sint) (1+ sint). بعد وضع هذه الحدود في البسط يبقى 2 وفي المقام 1 - sin 2 t. على الجانب الأيمن من الشاشة ، يتم تذكير المتطابقة المثلثية الأساسية sin 2 t + cos 2 t \u003d 1. وباستخدامها نجد مقام الكسر cos 2 t. بعد تقليل الكسر ، نحصل على شكل مبسط لتكلفة التعبير / (1- سينت) + التكلفة / (1+ سينت) \u003d 2 / التكلفة.

علاوة على ذلك ، يتم النظر في أمثلة إثبات الهوية ، حيث يتم تطبيق المعرفة المكتسبة حول الهويات الأساسية لعلم المثلثات. في المثال 3 ، من الضروري إثبات الهوية (tg 2 t-sin 2 t) · ctg 2 t \u003d sin 2 t. على الجانب الأيمن من الشاشة ، يتم عرض ثلاث متطابقات مطلوبة للإثبات - tg t · ctg t \u003d 1 ، ctg t \u003d cos t / sin t و tg t \u003d sin t / cos t مع القيود. لإثبات الهوية ، يتم أولاً توسيع الأقواس ، وبعد ذلك يتم تكوين منتج يعكس التعبير الرئيسي الهوية المثلثية tg t ctg t \u003d 1. بعد ذلك ، وفقًا للهوية من تعريف ظل التمام ، يتم تحويل ctg 2 t. نتيجة للتحولات ، يتم الحصول على التعبير 1-cos 2 t. باستخدام الهوية الأساسية ، نجد معنى التعبير. وهكذا ، ثبت أن (tg 2 t-sin 2 t) ctg 2 t \u003d sin 2 t.

في المثال 4 ، تحتاج إلى إيجاد قيمة التعبير tg 2 t + ctg 2 t ، إذا كانت tg t + ctg t \u003d 6. لحساب التعبير ، أولاً يتم تربيع الجانبين الأيمن والأيسر للمساواة (tg t + ctg t) 2 \u003d 6 2. تشبه صيغة الضرب المختصرة الجانب الأيمن من الشاشة. بعد فتح الأقواس على الجانب الأيسر من التعبير ، يتم تكوين المجموع tg 2 t + 2 · tg t · ctg t + ctg 2 t ، حيث يمكن تطبيق تحويل أحد المتطابقات المثلثية tg t · ctg t \u003d 1 ، حيث يتم تذكير الشكل على الجانب الأيمن من الشاشة. بعد التحويل ، نحصل على المساواة tg 2 t + ctg 2 t \u003d 34. يتطابق الجانب الأيسر من المساواة مع حالة المشكلة ، وبالتالي فإن الإجابة هي 34. تم حل المشكلة.

يوصى باستخدام درس الفيديو "Simplifying Trigonometric Expressions" في درس رياضيات المدرسة التقليدية. أيضًا ، ستكون المادة مفيدة للمعلم الذي يقوم بالتعلم عن بعد. من أجل تطوير المهارات في حل المشكلات المثلثية.

كود النص:

"تبسيط التعبيرات المثلثية".

المساواة

1) sin 2 t + cos 2 t \u003d 1 (مربع الجيب te زائد جيب التمام يساوي واحدًا)

2) tgt \u003d ، بالنسبة لـ t ≠ + k ، kϵZ (الظل te يساوي نسبة الجيب إلى جيب التمام عندما لا يساوي te pi على اثنين زائد pi ka ، ka ينتمي إلى zet)

3) ctgt \u003d ، بالنسبة لـ t ≠ πk ، kϵZ (cotangent te يساوي نسبة جيب التمام إلى الجيب عندما لا تكون te مساوية للذروة ، ka تنتمي إلى z).

4) tgt ∙ ctgt \u003d 1 لـ t ≠ ، kϵZ (ناتج الظل te و cotangent te يساوي واحدًا إذا كانت te لا تساوي القمة ، مقسومة على اثنين ، ka تنتمي إلى z)

تسمى الهويات المثلثية الأساسية.

غالبًا ما تستخدم لتبسيط وإثبات التعبيرات المثلثية.

لنلقِ نظرة على أمثلة لاستخدام هذه الصيغ لتبسيط المقادير المثلثية.

مثال 1: بسّط التعبير: cos 2 t - cos 4 t + sin 4 t. (التعبير هو مربع جيب التمام te ناقص جيب التمام من الدرجة الرابعة بالإضافة إلى الجيب من الدرجة الرابعة).

القرار. cos 2 t - cos 4 t + sin 4 t \u003d cos 2 t ∙ (1 - cos 2 t) + sin 4 t \u003d cos 2 t ∙ sin 2 t + sin 4 t \u003d sin 2 t (cos 2 t + sin 2) ر) \u003d sin 2 t 1 \u003d sin 2 t

(نحذف العامل المشترك جيب التمام التربيعي ، بين قوسين ، نحصل على الفرق بين الوحدة ومربع جيب التمام ، والذي يساوي بالمطابقة الأولى لمربع جيب التمام. نحصل على مجموع الدرجة الرابعة لجيب التمام من حاصل ضرب جيب التمام التربيعي وجيب جيب التمام. بين قوسين ، نحصل على مجموع مربعي جيب التمام والجيب بين قوسين ، والذي يساوي 1. نتيجة لذلك ، نحصل على مربع الجيب t).

مثال 2: بسّط التعبير: +.

(التعبير ba هو مجموع كسرين في بسط جيب التمام الأول te في المقام واحد ناقص جيب التمام te ، في بسط جيب التمام الثاني te في المقام الوحدة الثانية زائد جيب التمام te).

(لنأخذ العامل المشترك cosine te من الأقواس ، ونضعه بين الأقواس في المقام المشترك ، وهو حاصل ضرب واحد زائد جيب sin te واحد زائد جيب sin te.

نحصل في البسط على: واحد زائد sin te زائد واحد ناقص sin te ، ونعطي نفسًا ، البسط يساوي اثنين بعد البسط المتشابه.

في المقام ، يمكنك تطبيق معادلة الضرب المختصر (فرق المربعات) والحصول على الفرق بين الوحدة ومربع الجيب ، والتي وفقًا للهوية المثلثية الأساسية

يساوي مربع جيب التمام. بعد الإلغاء بواسطة cosine ، نحصل على الإجابة النهائية: اثنان مقسومًا على cos).

دعنا نفكر في أمثلة لاستخدام هذه الصيغ في إثبات المقادير المثلثية.

مثال 3. إثبات الهوية (tg 2 t - sin 2 t) ∙ ctg 2 t \u003d sin 2 t (حاصل ضرب الفرق بين مربعي الظل te و sine te ومربع cotangent te يساوي مربع الجيب te).

دليل.

دعنا نحول الجانب الأيسر من المساواة:

(tg 2 t - sin 2 t) ∙ ctg 2 t \u003d tg 2 t ∙ ctg 2 t - sin 2 t ∙ ctg 2 t \u003d 1 - sin 2 t ∙ ctg 2 t \u003d 1 - sin 2 t ∙ \u003d 1 - cos 2 t \u003d sin 2 t

(دعونا نفتح الأقواس ، من العلاقة التي تم الحصول عليها سابقًا ، من المعروف أن حاصل ضرب مربعات الظل te و cotangent te يساوي 1. تذكر أن cotangent te يساوي نسبة جيب التمام إلى جيب التمام ، مما يعني أن مربع ظل التمام هو نسبة مربع جيب التمام ومربع جيب التمام.

بعد إلغاء المربع te بالجيب ، نحصل على الفرق بين الوحدة وجيب التمام للمربع te ، والذي يساوي جيب المربع te). Q.E.D.

مثال 4 أوجد قيمة التعبير tg 2 t + ctg 2 t إذا كانت tgt + ctgt \u003d 6.

(مجموع مربعات الظل te و cotangent te ، إذا كان مجموع الظل و ظل التمام يساوي ستة).

القرار. (tgt + ctgt) 2 \u003d 6 2

tg 2 t + 2 ∙ tgt ∙ ctgt + ctg 2 t \u003d 36

tg 2 t + 2 + ctg 2 t \u003d 36

tg 2 t + ctg 2 t \u003d 36-2

tg 2 t + ctg 2 t \u003d 34

دعونا نضع كلا الجانبين من المساواة الأصلية:

(tgt + ctgt) 2 \u003d 6 2 (مربع مجموع tangent te و cotangent te يساوي ستة تربيع). تذكر صيغة الضرب المختصر: مربع مجموع كميتين يساوي مربع أول زائد ضعف حاصل ضرب الأول في الثانية زائد مربع الثانية. (a + b) 2 \u003d a 2 + 2ab + b 2 نحصل على tg 2 t + 2 tgt ∙ ctgt + ctg 2 t \u003d 36 (tangent square te بالإضافة إلى المنتج المزدوج لـ tangent te و cotangent te زائد cotangent تربيع t يساوي 36) ...

بما أن حاصل ضرب tangent te و cotangent te يساوي واحدًا ، إذن tg 2 t + 2 + ctg 2 t \u003d 36 (مجموع مربعي tangent te و cotangent te واثنان هو 36) ،

في تحولات متطابقة التعبيرات المثلثية يمكن استخدام الأساليب الجبرية التالية: الجمع والطرح لنفس المصطلحات ؛ إخراج العامل المشترك من الأقواس ؛ الضرب والقسمة بنفس المقدار ؛ تطبيق صيغ الضرب المختصرة ؛ اختيار مربع كامل ؛ تحليل ثلاثي الحدود إلى عوامل ؛ إدخال متغيرات جديدة من أجل تبسيط التحولات.

عند تحويل التعبيرات المثلثية التي تحتوي على كسور ، يمكنك استخدام خصائص التناسب أو اختزال الكسور أو تحويل الكسور إلى مقام مشترك. بالإضافة إلى ذلك ، يمكنك استخدام اختيار الجزء الصحيح من الكسر ، وضرب البسط والمقام في الكسر بنفس المقدار ، وإذا أمكن ، ضع في الاعتبار تجانس البسط أو المقام. إذا لزم الأمر ، يمكنك تمثيل الكسر على أنه مجموع أو فرق عدة كسور أبسط.

بالإضافة إلى ذلك ، عند تطبيق جميع الطرق اللازمة لتحويل التعبيرات المثلثية ، من الضروري أن نأخذ في الاعتبار باستمرار نطاق القيم المسموح بها للتعبيرات المحولة.

لنلق نظرة على بعض الأمثلة.

مثال 1.

احسب А \u003d (sin (2x - π) cos (3π - x) + sin (2x - 9π / 2) cos (x + π / 2)) 2 + (cos (x - π / 2) cos ( 2x - 7π / 2) +
+ الخطيئة (3π / 2 - x) الخطيئة (2x -5π / 2)) 2

القرار.

يتبع من صيغ التخفيض:

الخطيئة (2x - π) \u003d -sin 2x ؛ كوس (3π - س) \u003d -cos x ؛

الخطيئة (2x - 9π / 2) \u003d -cos 2x ؛ cos (x + / 2) \u003d -sin x ؛

cos (x - π / 2) \u003d sin x ؛ كوس (2x - 7π / 2) \u003d -sin 2x ؛

الخطيئة (3π / 2 - x) \u003d -cos x ؛ الخطيئة (2x - 5π / 2) \u003d -cos 2x.

من هنا ، بحكم الصيغ الخاصة بإضافة الحجج والهوية المثلثية الأساسية ، نحصل على

A \u003d (sin 2x cos x + cos 2x sin x) 2 + (-sin x sin 2x + cos x cos 2x) 2 \u003d sin 2 (2x + x) + cos 2 (x + 2x) \u003d
\u003d sin 2 3x + cos 2 3x \u003d 1

الجواب: 1.

مثال 2.

حوّل التعبير М \u003d cos α + cos (α + β) cos γ + cos β - sin (α + β) sin γ + cos γ إلى منتج.

القرار.

من الصيغ الخاصة بإضافة الحجج والصيغ لتحويل مجموع الدوال المثلثية إلى منتج بعد التجميع المقابل ، لدينا

М \u003d (cos (α + β) cos γ - sin (α + β) sin γ) + cos α + (cos β + cos γ) \u003d

2cos ((β + γ) / 2) cos ((β - γ) / 2) + (cos α + cos (α + β + γ)) \u003d

2cos ((+ γ) / 2) cos ((β - γ) / 2) + 2cos (α + (β + γ) / 2) cos ((+ γ) / 2)) \u003d

2cos ((β + γ) / 2) (cos ((β - γ) / 2) + cos (α + (+ γ) / 2)) \u003d

2cos ((β + γ) / 2) 2cos ((β - γ) / 2 + α + (β + γ) / 2) / 2) cos ((β - γ) / 2) - (α + ( β + γ) / 2) / 2) \u003d

4cos ((β + γ) / 2) cos ((α + β) / 2) cos ((α + γ) / 2).

الجواب: М \u003d 4cos ((α + β) / 2) cos ((α + γ) / 2) cos ((+ γ) / 2).

مثال 3.

بيّن أن التعبير A \u003d cos 2 (x + π / 6) - cos (x + π / 6) cos (x - π / 6) + cos 2 (x - π / 6) يأخذ كل x من R واحد ونفس المعنى. أوجد هذه القيمة.

القرار.

فيما يلي طريقتان لحل هذه المشكلة. بتطبيق الطريقة الأولى ، عن طريق اختيار مربع كامل واستخدام الصيغ المثلثية الأساسية المقابلة ، نحصل على

А \u003d (cos (x + / 6) - cos (x - π / 6)) 2 + cos (x - π / 6) cos (x - π / 6) \u003d

4sin 2 x sin 2/6 + 1/2 (cos 2x + cos π / 3) \u003d

Sin 2 x + 1/2 cos 2x + 1/4 \u003d 1/2 (1 - cos 2x) + 1/2 cos 2x + 1/4 \u003d 3/4.

لحل المسألة بالطريقة الثانية ، اعتبر A دالة في x من R واحسب مشتقها. بعد التحولات التي نحصل عليها

А´ \u003d -2cos (x + π / 6) sin (x + / 6) + (sin (x + / 6) cos (x - π / 6) + cos (x + / 6) الخطيئة (x + π / 6)) - 2cos (x - π / 6) sin (x - π / 6) \u003d

الخطيئة 2 (س + / 6) + الخطيئة ((س + / 6) + (س - π / 6)) - الخطيئة 2 (س - / 6) \u003d

الخطيئة 2x - (الخطيئة (2x + π / 3) + الخطيئة (2x - π / 3)) \u003d

الخطيئة 2x - 2sin 2xcos π / 3 \u003d sin 2x - sin 2x ≡ 0.

ومن ثم ، بحكم معيار ثبات دالة قابلة للتفاضل على فترة ، نستنتج ذلك

A (x) ≡ (0) \u003d cos 2/6 - cos 2/6 + cos 2/6 \u003d (√3 / 2) 2 \u003d 3/4، x € R.

الإجابة: A \u003d 3/4 لـ x € R.

الطرق الرئيسية لإثبات الهويات المثلثية هي:

و) تقليص الجانب الأيسر من الهوية إلى اليمين من خلال التحولات المناسبة ؛
ب) اختزال الجانب الأيمن من الهوية إلى اليسار ؛
في) اختزال الجانب الأيمن والأيسر من الهوية إلى نفس النوع ؛
د) تقليل الاختلاف بين الجانبين الأيمن والأيسر للهوية التي يتم إثباتها إلى الصفر.

مثال 4.

تأكد من أن cos 3x \u003d -4cos x cos (x + π / 3) cos (x + 2π / 3).

القرار.

لدينا تحويل الجانب الأيمن من هذه المتطابقة وفقًا للصيغ المثلثية المقابلة

4cos x cos (x + / 3) cos (x + 2π / 3) \u003d

2cos x (cos ((x + π / 3) + (x + 2π / 3)) + cos ((x + π / 3) - (x + 2π / 3))) \u003d

2cos x (cos (2x + π) + cos π / 3) \u003d

2cos x cos 2x - cos x \u003d (cos 3x + cos x) - cos x \u003d cos 3x.

تم تقليص الجانب الأيمن من الهوية إلى اليسار.

مثال 5.

أثبت أن sin 2 α + sin 2 β + sin 2 - 2cos α cos β cos γ \u003d 2 إذا كانت α، β، زوايا داخلية لبعض المثلث.

القرار.

مع الأخذ في الاعتبار أن α ، β ، هي الزوايا الداخلية لبعض المثلث ، نحصل على ذلك

α + β + γ \u003d ومن ثم γ \u003d π - α - β.

sin 2 α + sin 2 β + sin 2 - 2cos α cos β cos γ \u003d

الخطيئة 2 α + الخطيئة 2 β + الخطيئة 2 (π - α - β) - 2cos α cos β cos (π - α - β) \u003d

Sin 2 α + sin 2 2 + sin 2 (α + β) + (cos (α + β) + cos (α - β) (cos (α + β) \u003d

Sin 2 α + sin 2 β + (sin 2 (α + β) + cos 2 (α + β)) + cos (α - β) (cos (α + β) \u003d

1/2 · (1 - cos 2α) + · (1 - cos 2β) + 1 + 1/2 · (cos 2α + cos 2β) \u003d 2.

ثبتت المساواة الأصلية.

مثال 6.

لإثبات أنه لكي تكون إحدى زوايا المثلث α و و 60 درجة ، فمن الضروري والكافي أن تكون sin 3α + sin 3β + sin 3γ \u003d 0.

القرار.

تفترض حالة هذه المشكلة مسبقًا إثبات كل من الضرورة والكفاية.

أولا ، دعونا نثبت ضروري.

يمكن إثبات ذلك

sin 3α + sin 3β + sin 3γ \u003d -4cos (3α / 2) cos (3β / 2) cos (3γ / 2).

ومن ثم ، مع الأخذ في الاعتبار أن cos (3/2 60 °) \u003d cos 90 ° \u003d 0 ، نحصل على ذلك إذا كانت إحدى الزوايا α أو β أو 60 درجة ، إذن

cos (3α / 2) cos (3β / 2) cos (3γ / 2) \u003d 0 ، وبالتالي ، sin 3α + sin 3β + sin 3γ \u003d 0.

دعونا الآن نثبت قدرة شرط محدد.

إذا كانت sin 3α + sin 3β + sin 3γ \u003d 0 ، إذن cos (3α / 2) cos (3β / 2) cos (3γ / 2) \u003d 0 ، وبالتالي

إما cos (3α / 2) \u003d 0 ، أو cos (3β / 2) \u003d 0 ، أو cos (3γ / 2) \u003d 0.

بالتالي،

أو 3α / 2 \u003d / 2 + k ، أي α \u003d π / 3 + 2πk / 3 ،

أو 3β / 2 \u003d / 2 + k ، أي β \u003d π / 3 + 2πk / 3 ،

أو 3γ / 2 \u003d / 2 + k ،

أولئك. γ \u003d π / 3 + 2πk / 3 ، حيث k ϵ Z.

بما أن α و β و هي زوايا المثلث ، فلدينا

0 < α < π, 0 < β < π, 0 < γ < π.

لذلك ، من أجل α \u003d π / 3 + 2πk / 3 أو β \u003d π / 3 + 2πk / 3 أو

γ \u003d π / 3 + 2πk / 3 من كل kϵZ فقط k \u003d 0 يناسب.

من أين يتبع ذلك إما α \u003d π / 3 \u003d 60 درجة ، أو β \u003d π / 3 \u003d 60 درجة ، أو γ \u003d π / 3 \u003d 60 درجة.

البيان ثبت.

لا يزال لديك أسئلة؟ ألست متأكدًا من كيفية تبسيط المقادير المثلثية؟
للحصول على مساعدة من مدرس - سجل.
الدرس الأول مجاني!

الموقع ، مع النسخ الكامل أو الجزئي للمادة ، يلزم وجود رابط إلى المصدر.

الأقسام: رياضيات

صف دراسي: 11

الدرس 1

موضوع: الصف 11 (التحضير للامتحان)

تبسيط التعبيرات المثلثية.

حل أبسط المعادلات المثلثية. (ساعاتين)

الأهداف:

• لتنظيم وتعميم وتوسيع معارف ومهارات الطلاب المرتبطة باستخدام صيغ علم المثلثات وحل أبسط المعادلات المثلثية.

معدات الدرس:

هيكل الدرس:

1. لحظة تنظيمية
2. اختبار على أجهزة الكمبيوتر المحمولة. مناقشة النتائج.
3. تبسيط المقادير المثلثية
4. حل أبسط المعادلات المثلثية
5. عمل مستقل.
6. ملخص الدرس. شرح مهمة المنزل.

1. لحظة تنظيمية. (2 دقيقة.)

يحيي المعلم الجمهور ، ويعلن عن موضوع الدرس ، ويذكرهم بالمهمة المعطاة سابقًا لتكرار معادلات علم المثلثات ، وإعداد الطلاب للاختبار.

2. الاختبار. (15 دقيقة + 3 دقائق مناقشة)

الهدف هو اختبار معرفة الصيغ المثلثية والقدرة على تطبيقها. كل طالب لديه جهاز كمبيوتر محمول على مكتبه بنسخة تجريبية.

يمكن أن يكون هناك أي عدد من الخيارات ، سأقدم مثالاً على أحدها:

الخيار الأول.

تبسيط التعبيرات:

أ) الهويات المثلثية الأساسية

1.sin 2 3y + cos 2 3y + 1 ؛

ب) صيغ الجمع

3.sin5x - sin3x ؛

ج) تحويل المنتج إلى مبلغ

6.2sin8y cozy3y ؛

د) صيغ زاوية مزدوجة

7.2sin5x cos5x ؛

ه) صيغ نصف زاوية

و) صيغ زاوية ثلاثية

ز) الاستبدال الشامل

ح) خفض الدرجة

16.cos 2 (3x / 7) ؛

يرى الطلاب الذين يستخدمون جهاز كمبيوتر محمول إجاباتهم أمام كل صيغة.

يتم فحص العمل على الفور بواسطة الكمبيوتر. يتم عرض النتائج على شاشة كبيرة ليراها الجميع.

أيضًا ، بعد انتهاء العمل ، يتم عرض الإجابات الصحيحة على أجهزة الكمبيوتر المحمولة الخاصة بالطلاب. يرى كل طالب مكان حدوث الخطأ وما هي الصيغ التي يحتاج إلى تكرارها.

3. تبسيط التعابير المثلثية. (25 دقيقة)

الهدف هو مراجعة وممارسة وتوحيد تطبيق الصيغ الأساسية لعلم المثلثات. حل المسائل B7 من الامتحان.

في هذه المرحلة ، يُنصح بتقسيم الفصل إلى مجموعات من الطلاب الأقوياء (العمل بشكل مستقل مع التحقق اللاحق) والطلاب الضعفاء الذين يعملون مع المعلم.

مهمة للمتعلمين الأقوياء (معدة مسبقًا على أساس مطبوع). ينصب التركيز الرئيسي على صيغ التخفيض والزاوية المزدوجة ، وفقًا لامتحان 2011.

تبسيط التعبيرات (للمتعلمين الأقوياء):

في موازاة ذلك ، يعمل المعلم مع الطلاب الضعفاء ، ويناقش ويحل المهام على الشاشة بإملاء من الطلاب.

احسب:

5) الخطيئة (270 درجة - α) + كوس (270 درجة + α)

6)

تبسيط:

جاء دور مناقشة نتائج عمل المجموعة القوية.

تظهر الإجابات على الشاشة ، وكذلك بمساعدة كاميرا الفيديو ، يتم عرض أعمال 5 طلاب مختلفين (مهمة واحدة لكل منهم).

ترى المجموعة الضعيفة الشرط وطريقة الحل. المناقشة والتحليل قيد التقدم. مع استخدام الوسائل التقنية ، يحدث هذا بسرعة.

4. حل أبسط المعادلات المثلثية. (30 دقيقة.)

الهدف هو تكرار حل أبسط المعادلات المثلثية وتنظيمها وتعميمها ، وتسجيل جذورها. حل المشكلة B3.

أي معادلة مثلثية ، بغض النظر عن كيفية حلها ، تؤدي إلى أبسط معادلة.

عند الانتهاء من المهمة ، يجب أن ينجذب الطلاب إلى تسجيل جذور معادلات الحالات الخاصة والشكل العام واختيار الجذور في المعادلة الأخيرة.

حل المعادلات:

اكتب أصغر جذر موجب في الإجابة.

5. العمل المستقل (10 دقائق)

الهدف هو اختبار المهارات المكتسبة وتحديد المشاكل والأخطاء وطرق القضاء عليها.

يتم تقديم عمل بمستويات مختلفة بناءً على اختيار الطالب.

خيار لـ "3"

1) أوجد قيمة التعبير

2) بسّط التعبير 1 - sin 2 3α - cos 2 3α

3) حل المعادلة

خيار لـ "4"

1) أوجد قيمة التعبير

2) حل المعادلة اكتب أصغر جذر موجب في الإجابة.

خيار لـ "5"

1) ابحث عن tgα إذا

2) أوجد جذر المعادلة اكتب أصغر جذر موجب في إجابتك.

6. ملخص الدرس (5 دقائق)

يلخص المعلم ما يكرره الدرس ويوحد الصيغ المثلثية ، وهو حل أبسط المعادلات المثلثية.

واجب منزلي (مُعد مسبقًا على أساس مطبوع) مع فحوصات عشوائية في الدرس التالي.

حل المعادلات:

9)

10) حدد أصغر جذر موجب في إجابتك.

الجلسة الثانية

موضوع: الصف 11 (التحضير للامتحان)

طرق حل المعادلات المثلثية. اختيار الجذور. (ساعاتين)

الأهداف:

• لتعميم وتنظيم المعرفة في حل المعادلات المثلثية بأنواعها المختلفة.
• لتعزيز تنمية التفكير الرياضي للطلاب ، والقدرة على الملاحظة والمقارنة والتعميم والتصنيف.
• شجع الطلاب على التغلب على الصعوبات في عملية النشاط العقلي ، لضبط النفس ، واستبطان أنشطتهم.

معدات الدرس: KRMu ، أجهزة كمبيوتر محمولة لكل طالب.

هيكل الدرس:

1. لحظة تنظيمية
2. مناقشة د / ح و samot. أعمال الدرس الأخير
3. تكرار طرق حل المعادلات المثلثية.
4. حل المعادلات المثلثية
5. اختيار الجذور في المعادلات المثلثية.
6. عمل مستقل.
7. ملخص الدرس. واجب منزلي.

1. لحظة تنظيمية (دقيقتان)

يحيي المعلم الجمهور ويعلن عن موضوع الدرس وخطة العمل.

2. أ) مراجعة الواجب المنزلي (5 دقائق).

الهدف هو التحقق من التنفيذ. يتم عرض عمل واحد بمساعدة كاميرا فيديو على الشاشة ، ويتم جمع الباقي بشكل انتقائي لفحص المعلم.

ب) تحليل العمل المستقل (3 دقائق)

الهدف هو تحليل الأخطاء وبيان طرق التغلب عليها.

على الشاشة ، الإجابات والحلول ، يتم تعيين عمل الطلاب مسبقًا. يتقدم التحليل بسرعة.

3. تكرار طرق حل المعادلات المثلثية (5 دقائق)

الهدف هو استدعاء طرق حل المعادلات المثلثية.

اسأل الطلاب عن الطرق التي يعرفونها لحل المعادلات المثلثية. أكد أن هناك ما يسمى بالطرق الأساسية (شائعة الاستخدام):

• استبدال متغير ،
• التحليل إلى عوامل
• معادلات متجانسة

وهناك طرق تطبيقية:

• وفقًا للصيغ الخاصة بتحويل مبلغ إلى منتج ومنتج إلى مبلغ ،
• من خلال صيغ تخفيض الدرجة ،
• استبدال عالمي مثلثي
• مقدمة من زاوية مساعدة ،
• الضرب ببعض الدوال المثلثية.

يجب أيضًا أن نتذكر أنه يمكن حل معادلة واحدة بطرق مختلفة.

4. حل المعادلات المثلثية (30 دقيقة)

الهدف هو تعميم المعرفة والمهارات حول هذا الموضوع وتوحيدها ، للتحضير لقرار C1 من الامتحان.

أعتبر أنه من المناسب حل المعادلات لكل طريقة مع الطلاب.

يفرض الطالب الحل ، يكتب المعلم على الجهاز اللوحي ، ويتم عرض العملية برمتها على الشاشة. سيسمح لك ذلك باستدعاء المواد المغطاة مسبقًا بسرعة وكفاءة.

حل المعادلات:

1) تغيير المتغير 6cos 2 x + 5sinx - 7 \u003d 0

2) تحليل 3cos (x / 3) + 4cos 2 (x / 3) \u003d 0

3) المعادلات المتجانسة sin 2 x + 3cos 2 x - 2sin2x \u003d 0

4) تحويل المجموع إلى حاصل ضرب cos5x + cos7x \u003d cos (π + 6x)

5) تحويل الناتج إلى مجموع 2sinx sin2x + cos3x \u003d 0

6) خفض القوة sin2x - sin 2 2x + sin 2 3x \u003d 0.5

7) الاستبدال العام المثلثي sinx + 5cosx + 5 \u003d 0.

لحل هذه المعادلة ، تجدر الإشارة إلى أن استخدام هذه الطريقة يؤدي إلى تضييق مجال التعريف ، حيث يتم استبدال الجيب وجيب التمام بـ tg (x / 2). لذلك ، قبل كتابة الإجابة ، تحتاج إلى التحقق مما إذا كانت الأرقام من المجموعة π + 2πn ، n Z هي خيول هذه المعادلة.

8) إدخال زاوية مساعدة a3sinx + cosx - √2 \u003d 0

9) الضرب ببعض الدوال المثلثية cosx cos2x cos4x \u003d 1/8.

5. اختيار جذور المعادلات المثلثية (20 دقيقة)

نظرًا لأنه في ظروف المنافسة الشرسة عند دخول الجامعات ، لا يكفي حل الجزء الأول من الاختبار ، فيجب على معظم الطلاب الانتباه إلى مهام الجزء الثاني (C1 ، C2 ، C3).

لذلك ، فإن الغرض من هذه المرحلة من الدرس هو استدعاء المواد التي تمت دراستها مسبقًا ، للتحضير لحل مشكلة C1 من USE 2011.

هناك معادلات مثلثية تحتاج فيها إلى تحديد الجذور عند كتابة إجابة. هذا بسبب بعض القيود ، على سبيل المثال: مقام الكسر ليس صفراً ، والتعبير الموجود تحت جذر قوة زوجية غير سالب ، والتعبير الموجود أسفل علامة اللوغاريتم موجب ، إلخ.

تعتبر هذه المعادلات معادلات ذات تعقيد متزايد وفي إصدار الاستخدام توجد في الجزء الثاني ، أي C1.

حل المعادلة:

إذا كان الكسر صفرًا باستخدام دائرة الوحدة ، نختار الجذور (انظر الشكل 1)

الصورة 1.

نحصل على x \u003d π + 2πn ، n Z

الجواب: π + 2πn، n Z

على الشاشة ، يظهر اختيار الجذور على دائرة في صورة ملونة.

المنتج يساوي صفرًا عندما يكون أحد العوامل على الأقل مساويًا للصفر ، ولا يفقد القوس معناه. ثم

حدد الجذور باستخدام دائرة الوحدة (انظر الشكل 2)

الشكل 2.

5)

دعنا نذهب إلى النظام:

في المعادلة الأولى للنظام ، نجري التغيير 2 (sinx) \u003d y ، ثم نحصل على المعادلة ، بالعودة إلى النظام

حدد الجذور باستخدام دائرة الوحدة (انظر الشكل 5) ،

الشكل 5.

6. العمل المستقل (15 دقيقة)

الهدف هو توحيد وفحص استيعاب المواد ، لتحديد الأخطاء ، وتحديد طرق تصحيحها.

يتم تقديم العمل في ثلاث نسخ ، معدة مسبقًا على أساس مطبوع ، لاختيار الطلاب.

يمكنك حل المعادلات بأي طريقة.

خيار لـ "3"

حل المعادلات:

1) 2sin 2 x + sinx - 1 \u003d 0

2) sin2x \u003d √3cosx

خيار لـ "4"

حل المعادلات:

1) cos2x \u003d 11inx - 5

2) (2sinx + 3) log 8 (cosx) \u003d 0

خيار لـ "5"

حل المعادلات:

1) 2sinx - 3cosx \u003d 2

2)

7. ملخص الدرس ، الواجب المنزلي (5 دقائق).

يلخص المعلم الدرس ، مرة أخرى يلفت الانتباه إلى حقيقة أن المعادلة المثلثية يمكن حلها بعدة طرق. أفضل طريقة لتحقيق نتائج سريعة هي أفضل طريقة تعلمها كل طالب على حدة.

عند التحضير للاختبار ، تحتاج إلى تكرار الصيغ والأساليب بشكل منهجي لحل المعادلات.

يتم توزيع الواجب المنزلي (المُعد مسبقًا على أساس مطبوع) والتعليق على كيفية حل بعض المعادلات.

حل المعادلات:

1) cosx + cos5x \u003d cos3x + cos7x

2) 5sin (x / 6) - cos (x / 3) + 3 \u003d 0

3) 4sin 2 x + sin2x \u003d 3

4) sin 2 x + sin 2 2x - sin 2 3x - sin 2 4x \u003d 0

5) cos3x cos6x \u003d cos4x cos7x

6) 4sinx - 6cosx \u003d 1

7) 3sin2x + 4 cos2x \u003d 5

8) cosx cos2x cos4x cos8x \u003d (1/8) cos15x

9) (2sin 2 x - sinx) السجل 3 (2cos 2 x + cosx) \u003d 0

10) (2cos 2 x - √3cosx) سجل 7 (-tgx) \u003d 0

11)

فورونكوفا أولغا إيفانوفنا

مدرسة MBOU الثانوية

رقم 18 "

إنجلز ، منطقة ساراتوف.

مدرس رياضيات.

"التعبيرات المثلثية وتحولاتها"

مقدمة ………………………………………………………………………………… ... 3

الفصل 1 تصنيف المهام لاستخدام تحويلات التعبيرات المثلثية ............................................. .................. ... 5

1.1. مهام الحساب قيم التعبيرات المثلثية ……… .5

1.2. مهام لتبسيط المقادير المثلثية ... 7

1.3 مهام تحويل التعبيرات المثلثية العددية ..7

1.4 مهام مختلطة ……………………………………………………… ..... 9

الفصل 2. الجوانب المنهجية لتنظيم التكرار النهائي لموضوع "تحويل التعبيرات المثلثية" ................................... 11

2.1 الإعادة الموضوعية في الصف 10 ………………………………………… ... 11

اختبار 1 ………………………………………………………………………………………… .. 12

الاختبار 2 ………………………………………………………………………………………… .. 13

اختبار 3 ……………………………………………………………………………………… .. 14

2.2 الإعادة النهائية للصف 11 ………………………………………… ... 15

اختبار 1 …………………………………………………………………………………………… ..17

الاختبار 2 …………………………………………………………………………………………… ..17

اختبار 3 ……………………………………………………………………………………… .. 18

الخلاصة. …………………………………………………………………………… ... 19

قائمة الأدب المستعمل ………………………………………… .. …… .20

المقدمة.

في ظل ظروف اليوم ، السؤال الأهم هو: "كيف يمكننا المساعدة في إزالة بعض الفجوات في معرفة الطلاب ومنعهم من الأخطاء المحتملة في الامتحان؟" لحل هذه المشكلة ، من الضروري السعي من الطلاب ليس الاستيعاب الرسمي لمادة البرنامج ، ولكن الفهم العميق والواعي ، وتطوير سرعة الحسابات والتحولات الشفوية ، وكذلك تنمية المهارات في حل المشكلات البسيطة "في العقل". من الضروري إقناع الطلاب أنه فقط إذا كان هناك منصب نشط ، في دراسة الرياضيات ، بشرط أن يكتسبوا المهارات العملية والمهارات واستخدامها ، يمكن للمرء أن يتوقع نجاحًا حقيقيًا. من الضروري استغلال كل فرصة للتحضير لامتحان الدولة الموحدة ، بما في ذلك المواد الاختيارية في الصفوف من 10 إلى 11 ، وتحليل المهام الصعبة بانتظام مع الطلاب ، واختيار الطريقة الأكثر عقلانية للحل في الدروس والدروس الإضافية.نتيجة إيجابية فييمكن تحقيق مجالات حل المشكلات النموذجية إذا قام مدرسو الرياضيات بخلقها تدريب أساسي جيد للطلاب ، ابحث عن طرق جديدة في حل المشكلات التي فتحت أمامنا ، وقم بالتجربة بنشاط ، وتطبيق الحديث التقنيات التربويةوالأساليب والتقنيات التي تخلق ظروفًا مواتية لتحقيق الذات وتقرير المصير للطلاب في ظروف اجتماعية جديدة.

علم المثلثات هو جزء لا يتجزأ من دورة الرياضيات المدرسية. تعتبر المعرفة الجيدة والمهارات القوية في علم المثلثات دليلاً على وجود مستوى كافٍ من الثقافة الرياضية ، وهي حالة لا غنى عنها للدراسة الناجحة للرياضيات والفيزياء وعدد من التقنياتالتخصصات.

أهمية العمل. يظهر جزء كبير من خريجي المدارس من سنة إلى أخرى استعدادًا ضعيفًا للغاية في هذا القسم المهم من الرياضيات ، كما يتضح من نتائج السنوات الماضية (نسبة الإنجاز في 2011 - 48.41٪ ، 2012 - 51.05٪) ، حيث أظهر تحليل اجتياز امتحان الدولة الموحد أن يرتكب الطلاب العديد من الأخطاء عند إكمال مهام هذا القسم بالذات ، أو لا يقومون بمثل هذه المهام على الإطلاق. في واحد في امتحان الولاية ، توجد أسئلة علم المثلثات في ثلاثة أنواع تقريبًا من المهام. هذا هو حل أبسط المعادلات المثلثية في المهمة B5 ، والعمل بالتعبيرات المثلثية في المهمة B7 ، ودراسة الدوال المثلثية في المهمة B14 ، وكذلك المهمة B12 ، والتي تحتوي على صيغ تصف الظواهر الفيزيائية وتحتوي على وظائف مثلثية. وهذا ليس سوى جزء من مهام B! ولكن هناك أيضًا معادلات مثلثية مفضلة مع اختيار جذور C1 ، والمهام الهندسية "غير المفضلة جدًا" C2 و C4.

هدف. حلل مواد الامتحان المهام B7 ، المكرسة لتحويلات التعبيرات المثلثية وتصنيف المهام وفقًا لشكل عرضها في الاختبارات.

يتكون العمل من فصلين ، مقدمة وخاتمة. المقدمة تؤكد أهمية العمل. يقدم الفصل الأول تصنيفًا لمهام استخدام تحويلات التعبيرات المثلثية في الاختبار مهام الامتحان (2012).

في الفصل الثاني ، تم النظر في تنظيم تكرار موضوع "تحويل التعبيرات المثلثية" في الصفوف 10 و 11 وتم تطوير الاختبارات حول هذا الموضوع.

تتضمن قائمة الأدبيات 17 مصدرا.

الفصل الأول: تصنيف المهام لاستخدام تحويلات التعبيرات المثلثية.

وفقًا لمعيار التعليم الثانوي (الكامل) ومتطلبات مستوى تدريب الطلاب ، يشتمل برنامج ترميز المتطلبات على مهام لمعرفة أساسيات علم المثلثات.

سيكون تعلم أساسيات علم المثلثات أكثر فاعلية عندما:

سيتم توفير الدافع الإيجابي للطلاب لتكرار المواد التي سبق دراستها ؛

سيتم تنفيذ نهج موجه نحو الشخصية في العملية التعليمية ؛

سيتم تطبيق نظام المهام ، مما يساهم في توسيع وتعميق وتنظيم معرفة الطلاب ؛

سيتم استخدام تقنيات التدريس المتقدمة.

بعد تحليل الأدبيات وموارد الإنترنت للتحضير للامتحان ، اقترحنا أحد التصنيفات الممكنة للمهام B7 (KIM USE 2012 - علم المثلثات): مهام لحساب قيم التعبيرات المثلثية ؛ الاحالات لتحويل التعبيرات المثلثية العددية ؛ مهام لتحويل التعبيرات المثلثية الأبجدية ؛ مهام مختلطة.

1.1. مهام الحساب قيم التعبيرات المثلثية.

أحد أكثر أنواع مسائل علم المثلثات البسيطة شيوعًا هو حساب قيم الدوال المثلثية من خلال قيمة إحداها:

أ) استخدام الهوية المثلثية الأساسية وعواقبها.

مثال 1 ... ابحث عما إذا كان
و
.

القرار.
,
,

لان ثم
.

إجابة.

مثال 2 ... تجد
، اذا كان
و.

القرار.
,
,
.

لان ثم
.

إجابة. ...

ب) استخدام صيغ مزدوجة الزاوية.

مثال 3 ... تجد
، اذا كان
.

القرار. ، .

إجابة.
.

مثال 4 ... ابحث عن معنى التعبير
.

القرار. ...

إجابة.
.

1. تجد ، اذا كان
و
... إجابة. -0.2

2. تجد ، اذا كان
و
... إجابة. 0،4

3. تجد
، اذا كان . إجابة. -12.884. تجد
، اذا كان
... إجابة. -0.845. ابحث عن معنى التعبير:
... إجابة. 66. ابحث عن معنى التعبير
. إجابة. -تسعة عشر

1.2. مهام لتبسيط المقادير المثلثية. يجب أن يتقن الطلاب معادلات الصب جيدًا ، حيث سيجدون مزيدًا من التطبيق في دروس الهندسة والفيزياء والتخصصات الأخرى ذات الصلة.

مثال 5 . تبسيط التعابير
.

القرار. ...

إجابة.
.

مهام المساعدة الذاتية:

1. تبسيط التعبير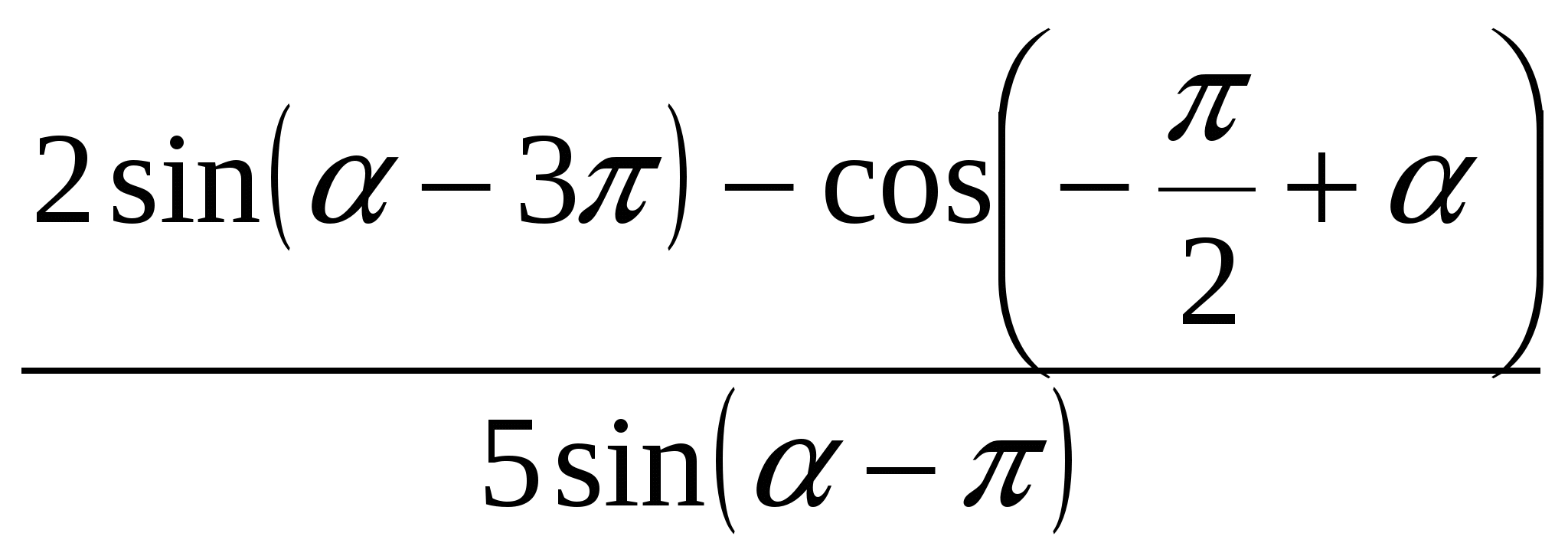
. إجابة. 0.62. تجد
، اذا كان
و ... إجابة. 10.563. ابحث عن معنى التعبير
، اذا كان
. إجابة. 2

1.3 مهام لتحويل التعبيرات المثلثية العددية.

عند ممارسة مهارات وقدرات المهام لتحويل التعبيرات المثلثية العددية ، يجب الانتباه إلى معرفة جدول قيم الدوال المثلثية ، وخصائص التكافؤ ودورية الدوال المثلثية.

أ) استخدام القيم الدقيقة للوظائف المثلثية لبعض الزوايا.

مثال 6 ... احسب
.

القرار.
.

إجابة.
.

ب) استخدام خصائص التكافؤ الدوال المثلثية.

مثال 7 ... احسب
.

القرار. .

إجابة.

في) استخدام خصائص الدوريةالدوال المثلثية.

المثال 8 . ابحث عن معنى التعبير
.

القرار. ...

إجابة.
.

مهام المساعدة الذاتية:

1. ابحث عن معنى التعبير
. إجابة. -40.52. ابحث عن معنى التعبير
. إجابة. 17

3. ابحث عن معنى التعبير
. إجابة. 6

. إجابة. -24
إجابة. -64

1.4 مهام مختلطة.

يحتوي نموذج اختبار الشهادة على ميزات مهمة جدًا ، لذلك من المهم الانتباه إلى المهام المرتبطة باستخدام العديد من الصيغ المثلثية في نفس الوقت.

المثال 9. تجد
، اذا كان
.

القرار.
.

إجابة.
.

المثال 10 ... تجد
، اذا كان
و
.

القرار. .

لان ثم
.

إجابة.
.

المثال 11. تجد
، اذا كان .

القرار. , ,
,
,
,
,
.

إجابة.

المثال 12. احسب
.

القرار. .

إجابة.
.

المثال 13. ابحث عن معنى التعبير
، اذا كان
.

القرار. .

إجابة.
.

مهام المساعدة الذاتية:

1. تجد
، اذا كان
. إجابة. -1.75
2. تجد
، اذا كان
. إجابة. 33. البحث
، اذا كان . إجابة. 0.254. ابحث عن معنى التعبير
، اذا كان
. إجابة. 0.35. ابحث عن معنى التعبير
، اذا كان
. إجابة. خمسة

الفصل 2. الجوانب المنهجية لتنظيم التكرار النهائي لموضوع "تحويل التعبيرات المثلثية".

واحدة من أهم القضايا التي تساهم في زيادة الأداء الأكاديمي ، وتحقيق معرفة عميقة ودائمة بين الطلاب هي مسألة إعادة المواد التي تم تمريرها سابقًا. تدل الممارسة على أنه من الأفضل تنظيم الإعادة الموضوعية في الصف العاشر ؛ في الصف 11 - الإعادة النهائية.

2.1. الإعادة الموضوعية في الصف العاشر.

في عملية العمل على مادة رياضية ، يصبح تكرار كل موضوع مكتمل أو قسم كامل من الدورة التدريبية أمرًا مهمًا بشكل خاص.

مع التكرار الموضوعي ، يتم تنظيم معرفة الطلاب بالموضوع في المرحلة الأخيرة من مروره أو بعد استراحة.

من أجل التكرار الموضوعي ، يتم تخصيص دروس خاصة ، حيث يتم تركيز مادة موضوع واحد وتعميمها.

يتم التكرار في الدرس من خلال محادثة بمشاركة واسعة من الطلاب في هذه المحادثة. بعد ذلك ، يُطلب من الطلاب تكرار موضوع معين ويتم تحذيرهم من إجراء اختبار.

يجب أن يتضمن الاختبار حول موضوع ما جميع أسئلته الأساسية. بعد الانتهاء من العمل ، يتم تحليل الأخطاء المميزة وتنظيم التكرار للقضاء عليها.

لدروس التكرار الموضوعي ، نقدم مطورة أوراق الاختبارحول موضوع "تحويل التعبيرات المثلثية".

اختبار رقم 1

رقم الاختبار 2

رقم الاختبار 3

جدول الإجابات

اختبار

2.2. الإعادة النهائية في الصف الحادي عشر.

يتم إجراء التكرار النهائي في المرحلة النهائية من دراسة القضايا الرئيسية لمسار الرياضيات ويتم إجراؤه بشكل منطقي مع دراسة المادة التعليمية لهذا القسم أو الدورة ككل.

يهدف التكرار النهائي للمادة التدريبية إلى الأهداف التالية:

1. تفعيل مادة الدورة التدريبية بأكملها لتوضيح هيكلها المنطقي وبناء نظام ضمن روابط الموضوع والموضوع.

2. تعميق ، وإن أمكن ، توسيع معرفة الطلاب بالقضايا الرئيسية للمقرر في عملية التكرار.

نظرًا لامتحان الرياضيات الإلزامي لجميع الخريجين ، فإن التقديم التدريجي لامتحان الدولة الموحدة يجبر المعلمين على اتباع نهج جديد لإعداد الدروس وتقديمها ، مع مراعاة الحاجة إلى ضمان إتقان جميع الطلاب للمادة التعليمية على المستوى الأساسي ، فضلاً عن إتاحة الفرصة للطلاب المتحمسين المهتمين بالحصول على درجات عالية مقابل القبول في الجامعة ، والتقدم الديناميكي في إتقان المواد على مستوى متقدم وعالي.

في دروس التكرار النهائي ، يمكنك التفكير في المهام التالية:

مثال 1 . احسب قيمة التعبير.القرار. \u003d
= =
=
=
=
=0,5. إجابة. 0.5 مثال 2. حدد أكبر قيمة عدد صحيح يمكن أن يتخذه التعبير
.

القرار. مثل
يمكن أن تأخذ أي قيمة ، قطعة [-1 ؛ 1] ، إذن
يأخذ أي قيمة للجزء [–0.4 ؛ 0.4] ، لذلك. القيمة الصحيحة للتعبير هي واحد - رقم 4.

الجواب: 4 مثال 3 . تبسيط التعبير
.

الحل: لنستخدم صيغة حساب مجموع المكعبات :. نملك

نملك:
.

الجواب: 1

مثال 4. احسب
.

القرار. ...

الجواب: 0.28

لدروس التكرار النهائي ، نقدم اختبارات مطورة حول موضوع "تحويل التعبيرات المثلثية".

الرجاء إدخال أكبر عدد صحيح لا يتجاوز 1

خاتمة.

بعد العمل من خلال الأدبيات المنهجية ذات الصلة حول هذا الموضوع ، يمكننا أن نستنتج أن القدرة والمهارات على حل المهام المتعلقة بالتحولات المثلثية في دورة الرياضيات المدرسية مهمة للغاية.

في سياق العمل المنجز ، تم تصنيف المهام B7. يتم النظر في الصيغ المثلثية الأكثر استخدامًا في CMMs لعام 2012. يتم إعطاء أمثلة على المهام مع الحلول. تم تطوير اختبارات مختلفة لتنظيم التكرار وتنظيم المعرفة استعدادًا لامتحان الدولة الموحدة.

من المستحسن مواصلة العمل الذي بدأ من خلال النظر حل أبسط المعادلات المثلثية في المهمة B5 ، ودراسة الدوال المثلثية في المهمة B14 ، والمهمة B12 ، والتي تحتوي على صيغ تصف الظواهر الفيزيائية وتحتوي على وظائف مثلثية.

في الختام ، أود أن أشير إلى أن فعالية اجتياز الامتحان تتحدد إلى حد كبير بمدى فعالية تنظيم عملية الإعداد على جميع مستويات التعليم ، مع جميع فئات الطلاب. وإذا تمكنا من تشكيل استقلالية الطلاب ومسؤوليتهم واستعدادهم لمواصلة التعلم طوال حياتهم اللاحقة ، فلن نلبي نظام الدولة والمجتمع فحسب ، بل نرفع أيضًا تقديرنا لذاتنا.

يتطلب تكرار المواد التعليمية من المعلم عمل ابداعي... يجب عليه توفير صلة واضحة بين أنواع التكرار ، وتنفيذ نظام تكرار مدروس بعمق. إن إتقان فن تنظيم التكرار مهمة المعلم. تعتمد قوة معرفة الطلاب بشكل كبير على الحل.

المؤلفات.

فيجودسكي يا ، كتيب الرياضيات الابتدائية. -M: Nauka ، 1970.

مشاكل الصعوبة المتزايدة في الجبر ومبادئ التحليل: كتاب مدرسي للصفوف 10-11 الثانوية / B.M. إيفليف ، أ. أبراموف ، يو. دودنيتسين ، إس. شوارزبورد. - م: التعليم ، 1990.

تطبيق الصيغ المثلثية الأساسية على تحويل التعبيرات (الصف العاشر) // مهرجان الأفكار التربوية. 2012-2013.

إيه جي كوريانوف ، بروكوفييف أ. نقوم بإعداد الطلاب الجيدين والطلاب المتفوقين للامتحان. - م: الجامعة التربوية "أول سبتمبر" 2012. - 103 ص.

كوزنتسوفا إي. تبسيط التعبيرات المثلثية. حل المعادلات المثلثية بطرق مختلفة (التحضير للامتحان). الصف ال 11. 2012-2013.

Kulanin E. D. 3000 مشاكل المنافسة في الرياضيات. الرابعة منهم. ، القس. و أضف. - م: رولف ، 2000.

مردكوفيتش أ. المشكلات المنهجية لدراسة علم المثلثات في المرحلة الثانوية // الرياضيات في المدرسة. 2002. رقم 6.

Pichurin L.F. حول علم المثلثات وليس فقط عنه: -M. التعليم ، 1985

ريشيتنيكوف ن. علم المثلثات في المدرسة: -M. : الجامعة التربوية "الأول من سبتمبر" 2006 ، ل 1.

شابونين إم آي ، بروكوفييف أ. رياضيات. الجبر. بداية التحليل الرياضي مستوى الملف الشخصي: كتاب مدرسي للصف العاشر - م: BINOM. معمل المعرفة 2007.

بوابة تعليمية للتحضير للامتحان.

التحضير لامتحان الدولة الموحدة في الرياضيات "أوه ، علم المثلثات هذا! http://festival.1september.ru/articles/621971/

مشروع "الرياضيات؟ سهلة !!!"http://www.resolventa.ru/