Minimum ve maksimum noktaları olmayan işlevler. Teorik materyal. Fonksiyonun ekstremumlarını birlikte aramaya devam ediyoruz

Bir fonksiyonun ekstrem noktası, fonksiyonun tanım kümesinde, fonksiyonun değerinin minimum veya maksimum değer aldığı noktadır. Fonksiyonun bu noktalardaki değerlerine fonksiyonun ekstremum (minimum ve maksimum) adı verilir.

Tanım. Nokta X1 fonksiyon alanı F(X) denir fonksiyonun maksimum noktası , eğer fonksiyonun bu noktadaki değeri, fonksiyonun kendisine yeterince yakın olan, sağında ve solunda bulunan noktalardaki değerlerinden büyükse (yani eşitsizlik geçerlidir) F(X0 ) > F(X 0 + Δ X) X1 maksimum.

Tanım. Nokta X2 fonksiyon alanı F(X) denir fonksiyonun minimum noktası, fonksiyonun bu noktadaki değeri, fonksiyonun kendisine yeterince yakın, sağında ve solunda bulunan noktalardaki değerlerinden küçükse (yani eşitsizlik geçerlidir) F(X0 ) < F(X 0 + Δ X) ). Bu durumda fonksiyonun şu noktada olduğunu söylüyoruz. X2 minimum.

nokta diyelim X1 - fonksiyonun maksimum noktası F(X). Daha sonra şuna kadar olan aralıkta X1 fonksiyon artar, dolayısıyla fonksiyonun türevi sıfırdan büyüktür ( F "(X) > 0 ) ve sonrasındaki aralıkta X1 fonksiyon azalır, bu nedenle, bir fonksiyonun türevi Sıfırdan daha az ( F "(X) < 0 ). Тогда в точке X1

Ayrıca şunu da varsayalım ki, X2 - fonksiyonun minimum noktası F(X). Daha sonra şuna kadar olan aralıkta X2 fonksiyon azalıyor ve fonksiyonun türevi sıfırdan küçük ( F "(X) < 0 ), а в интервале после X2 fonksiyon artıyor ve fonksiyonun türevi sıfırdan büyük ( F "(X) > 0). Bu durumda da bu noktada X2 fonksiyonun türevi sıfırdır veya yoktur.

Fermat teoremi (bir fonksiyonun ekstremumunun varlığının gerekli işareti). Eğer nokta X0 - fonksiyonun ekstrem noktası F(X) o zaman bu noktada fonksiyonun türevi sıfıra eşittir ( F "(X) = 0 ) veya mevcut değil.

Tanım. Bir fonksiyonun türevinin sıfır olduğu veya bulunmadığı noktalara denir. kritik noktalar .

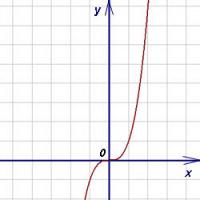
Örnek 1. Fonksiyonu ele alalım.

Noktada X= 0 fonksiyonun türevi sıfırdır, dolayısıyla nokta X= 0 kritik noktadır. Ancak fonksiyonun grafiğinde görüldüğü gibi tüm tanım kümesi boyunca artar, dolayısıyla nokta X= 0 bu fonksiyonun ekstrem noktası değildir.

Dolayısıyla, bir fonksiyonun bir noktadaki türevinin sıfıra eşit olması veya mevcut olmaması koşulları, bir ekstremum için gerekli koşullardır ancak yeterli değildir, çünkü bu koşulların sağlandığı başka fonksiyon örnekleri de verilebilir, ancak fonksiyon karşılık gelen noktada bir ekstremum yoktur. Bu yüzden yeterli kanıt olmalı Belirli bir kritik noktada bir ekstremum olup olmadığına ve bunun ne tür bir ekstremum olduğuna (maksimum veya minimum) karar verilmesini sağlar.

Teorem (bir fonksiyonun ekstremumunun varlığının ilk yeterli işareti). Kritik nokta X0 F(X) bu noktadan geçerken fonksiyonun türevi işaret değiştirirse ve işaret "artı"dan "eksi"ye değişirse, o zaman maksimum noktadır ve "eksi"den "artı"ya değişirse, o zaman minimum noktadır.

Eğer noktaya yakınsa X0 , solunda ve sağında türev işaretini korur, bu, fonksiyonun yalnızca noktanın belirli bir komşuluğunda azaldığı veya yalnızca arttığı anlamına gelir X0 . Bu durumda bu noktada X0 aşırı bir durum yok.

Bu yüzden, Fonksiyonun ekstremum noktalarını belirlemek için aşağıdakileri yapmanız gerekir: :

1. Fonksiyonun türevini bulun.
2. Türevi sıfıra eşitleyin ve kritik noktaları belirleyin.
3. Sayı doğrusu üzerinde kritik noktaları zihinsel olarak veya kağıt üzerinde işaretleyin ve ortaya çıkan aralıklarda fonksiyonun türevinin işaretlerini belirleyin. Türevin işareti “artı”dan “eksi”ye değişirse kritik nokta maksimum nokta, “eksi”den “artı”ya değişirse minimum nokta olur.
4. Fonksiyonun ekstrem noktalardaki değerini hesaplayın.

Örnek 2. Fonksiyonun ekstremumunu bulun .

Çözüm. Fonksiyonun türevini bulalım:

Kritik noktaları bulmak için türevi sıfıra eşitleyelim:

.

Herhangi bir “x” değeri için payda sıfıra eşit olmadığından payı sıfıra eşitliyoruz:

Bir kritik noktam var X= 3 . Bu noktayla sınırlanan aralıklarda türevin işaretini belirleyelim:

eksi sonsuzdan 3'e kadar - eksi işareti, yani fonksiyon azalır,

3'ten artı sonsuza kadar olan aralıkta artı işareti vardır, yani fonksiyon artar.

Yani dönem X= 3 minimum noktadır.

Fonksiyonun değerini minimum noktada bulalım:

Böylece fonksiyonun ekstrem noktası bulunur: (3; 0) ve minimum noktasıdır.

Teorem (bir fonksiyonun ekstremumunun varlığının ikinci yeterli işareti). Kritik nokta X0 fonksiyonun ekstrem noktasıdır F(X) eğer fonksiyonun bu noktadaki ikinci türevi sıfıra eşit değilse ( F ""(X) ≠ 0 ) ve ikinci türev sıfırdan büyükse ( F ""(X) > 0), o zaman maksimum nokta ve ikinci türev sıfırdan küçükse ( F ""(X) < 0 ), то точкой минимума.

Not 1. Eğer bu noktada X0 Hem birinci hem de ikinci türevler ortadan kalkarsa, bu noktada ikinci yeterli kritere dayanarak bir ekstremun varlığına karar vermek imkansızdır. Bu durumda bir fonksiyonun ekstremumu için ilk yeterli kriteri kullanmanız gerekir.

Açıklama 2. Bir fonksiyonun ekstremumu için ikinci yeterli kriter, birinci türevin durağan bir noktada mevcut olmadığı durumlarda bile uygulanamaz (bu durumda ikinci türev de mevcut değildir). Bu durumda, bir fonksiyonun ekstremumunun ilk yeterli işaretini de kullanmanız gerekir.

Fonksiyonun ekstremumunun yerel doğası

Yukarıdaki tanımlardan, bir fonksiyonun ekstremumunun doğası gereği yerel olduğu sonucu çıkar; yakındaki değerlerle karşılaştırıldığında fonksiyonun en büyük ve en küçük değeridir.

Diyelim ki bir yıllık dönemdeki kazancınıza bakıyorsunuz. Mayıs ayında 45.000 ruble, Nisan'da 42.000 ruble ve Haziran'da 39.000 ruble kazandıysanız, Mayıs ayı kazançları, yakın değerlere kıyasla kazanç fonksiyonunun maksimumudur. Ancak Ekim'de 71.000 ruble, Eylül'de 75.000 ruble ve Kasım'da 74.000 ruble kazandınız, dolayısıyla Ekim kazançları, yakındaki değerlerle karşılaştırıldığında kazanç fonksiyonunun minimumudur. Ve Nisan-Mayıs-Haziran değerleri arasında maksimumun Eylül-Ekim-Kasım minimumundan daha az olduğunu rahatlıkla görebilirsiniz.

Genel olarak konuşursak, bir aralıkta bir fonksiyonun birden fazla ekstrem değeri olabilir ve fonksiyonun bazı minimumlarının herhangi bir maksimumdan daha büyük olduğu ortaya çıkabilir. Yani yukarıdaki şekilde gösterilen fonksiyon için .

Yani, bir fonksiyonun maksimum ve minimumunun, söz konusu segmentin tamamındaki sırasıyla en büyük ve en küçük değerleri olduğu düşünülmemelidir. Maksimum noktada, fonksiyon yalnızca maksimum noktaya yeterince yakın tüm noktalarda sahip olduğu değerlerle karşılaştırıldığında en büyük değere sahiptir ve minimum noktada yalnızca bu değerlerle karşılaştırıldığında en küçük değere sahiptir. tüm noktalarının minimum noktaya yeterince yakın olması.

Bu nedenle, yukarıdaki bir fonksiyonun ekstremum noktaları kavramını açıklığa kavuşturabilir ve minimum noktaları yerel minimum noktalar ve maksimum noktaları yerel maksimum noktalar olarak adlandırabiliriz.

Fonksiyonun ekstremumlarını birlikte ararız

Örnek 3.

Çözüm: Fonksiyon tanımlıdır ve tüm sayı doğrusu üzerinde süreklidir. Türevi aynı zamanda tüm sayı doğrusunda da mevcuttur. Dolayısıyla bu durumda kritik noktalar yalnızca şu noktalardır: , nereden ve . Kritik noktalar ve fonksiyonun tüm tanım alanını üç monotonluk aralığına bölün: . Her birinde birer kontrol noktası seçip bu noktadaki türevin işaretini bulalım.

Aralık için kontrol noktası şu şekilde olabilir: bul. Aralıkta bir nokta alırsak elde ederiz ve aralıkta bir nokta alırsak elimizde olur. Yani aralıklarla ve , ve aralıkta . Bir ekstremum için ilk yeterli kritere göre, noktada bir ekstremum yoktur (çünkü türev aralıkta işaretini korur) ve noktada fonksiyonun bir minimumu vardır (çünkü türev geçerken işareti eksiden artıya değişir) bu noktadan itibaren). Fonksiyonun karşılık gelen değerlerini bulalım: , a . Aralıkta fonksiyon azalır, çünkü bu aralıktadır ve aralıkta artar, çünkü bu aralıktadır.

Grafiğin yapısını netleştirmek için koordinat eksenleriyle kesişme noktalarını buluyoruz. Kökleri ve olan bir denklem elde ettiğimizde, yani fonksiyonun grafiğinin iki noktası (0; 0) ve (4; 0) bulunmuştur. Alınan tüm bilgileri kullanarak bir grafik oluşturuyoruz (örneğin başlangıcına bakın).

Hesaplamalar sırasında kendi kendini kontrol etmek için kullanabilirsiniz. çevrimiçi türev hesaplayıcı .

Örnek 4. Fonksiyonun ekstremumlarını bulun ve grafiğini oluşturun.

Bir fonksiyonun tanım alanı, nokta hariç sayı doğrusunun tamamıdır; .

Çalışmayı kısaltmak için bu fonksiyonun eşit olduğu gerçeğini kullanabilirsiniz, çünkü . Bu nedenle grafiği eksene göre simetriktir Oy ve çalışma yalnızca aralık için yapılabilir.

Türevi bulma ve fonksiyonun kritik noktaları:

1) ;

2) ,

ancak fonksiyon bu noktada bir süreksizlikten muzdariptir, dolayısıyla bir uç nokta olamaz.

Dolayısıyla verilen fonksiyonun iki kritik noktası vardır: ve . Fonksiyonun paritesini hesaba katarak, bir ekstremum için ikinci yeterli kriteri kullanarak yalnızca noktayı kontrol edeceğiz. Bunu yapmak için ikinci türevi buluyoruz ve işaretini şu şekilde belirleriz: elde ederiz. ve olduğundan, fonksiyonun minimum noktasıdır ve .

Bir fonksiyonun grafiğinin daha eksiksiz bir resmini elde etmek için, tanım kümesinin sınırlarındaki davranışını bulalım:

(burada sembol arzuyu belirtir) X sağdan sıfıra ve X pozitif kalıyor; benzer şekilde aspirasyon anlamına gelir X soldan sıfıra ve X negatif kalır). Böylece, eğer , o zaman . Sonra buluyoruz

,

onlar. eğer öyleyse.

Bir fonksiyonun grafiğinin eksenlerle kesişme noktası yoktur. Resim örneğin başındadır.

Hesaplamalar sırasında kendi kendini kontrol etmek için kullanabilirsiniz. çevrimiçi türev hesaplayıcı .

Fonksiyonun ekstremumlarını birlikte aramaya devam ediyoruz

Örnek 8. Fonksiyonun ekstremumunu bulun.

Çözüm. Fonksiyonun tanım tanım kümesini bulalım. Eşitsizliğin sağlanması gerektiğinden,'den elde ederiz.

Fonksiyonun birinci türevini bulalım.

Teorem. (bir ekstremun varlığı için gerekli bir koşul) Eğer f(x) fonksiyonu x = x 1 noktasında türevlenebilirse ve x 1 noktası bir ekstrem nokta ise, fonksiyonun türevi bu noktada sıfırdır.

Kanıt. f(x) fonksiyonunun x = x 1 noktasında maksimuma sahip olduğunu varsayalım.

Bu durumda yeterince küçük pozitif Dх>0 için aşağıdaki eşitsizlik doğrudur:

A-tarikatı:

Onlar. Dх®0 ise ancak Dх<0, то f¢(x 1) ³ 0, а если Dх®0, но Dх>0, sonra f¢(x 1) £ 0.

Ve bu ancak Dх®0 f¢(x 1) = 0 olduğunda mümkündür.

f(x) fonksiyonunun x 2 noktasında minimuma sahip olması durumunda teorem benzer şekilde kanıtlanır.

Teorem kanıtlandı.

Sonuçlar. Tersi ifade doğru değildir. Bir fonksiyonun belirli bir noktadaki türevinin sıfıra eşit olması, fonksiyonun bu noktada bir ekstremuma sahip olduğu anlamına gelmez. Bunun güzel bir örneği, x = 0 noktasında türevi sıfıra eşit olan y = x 3 fonksiyonudur, ancak bu noktada fonksiyonun yalnızca bir bükülmesi vardır, maksimum veya minimumu yoktur.

Tanım. Kritik noktalar Fonksiyonlar, fonksiyonun türevinin bulunmadığı veya sıfıra eşit olduğu noktalardır.

Yukarıda tartışılan teorem bize bir ekstremun varlığı için gerekli koşulları verir, ancak bu yeterli değildir.

Örnek: f(x) = okxô Örnek: f(x) =

ey y

x = 0 noktasında fonksiyonun minimumu vardır, ancak x = 0 noktasında fonksiyonun minimumu yoktur.

türevi yoktur. maksimum, minimum yok, üretim yok

Genel olarak konuşursak, f(x) fonksiyonu, türevinin olmadığı veya sıfıra eşit olduğu noktalarda bir ekstrema sahip olabilir.

Teorem. (Bir ekstremun varlığı için yeterli koşullar)

f(x) fonksiyonunun x 1 kritik noktasını içeren (a, b) aralığında sürekli ve bu aralığın tüm noktalarında (belki de x 1 noktası dışında) türevlenebilir olsun.

Eğer x 1 noktasından soldan sağa geçerken f¢(x) fonksiyonunun türevinin işareti “+”dan “-“ye değişirse, o zaman x = x 1 noktasında f(x) fonksiyonu şu şekilde olur: bir maksimumdur ve eğer türevin işareti “-”den “+”ya değişirse, o zaman fonksiyonun bir minimumu olur.

Kanıt.

İzin vermek

Lagrange teoremine göre: f(x) – f(x 1) = f¢(e)(x – x 1), nerede x< e < x 1 .

O zaman: 1) Eğer x< x 1 , то e < x 1 ; f¢(e)>0; f¢(e)(x – x 1)<0, следовательно

f(x) – f(x1)<0 или f(x) < f(x 1).

2) Eğer x > x 1 ise e > x 1 f¢(e)<0; f¢(e)(x – x 1)<0, следовательно

f(x) – f(x1)<0 или f(x) < f(x 1).

Cevaplar çakıştığı için f(x) diyebiliriz.< f(x 1) в любых точках вблизи х 1 , т.е. х 1 – точка максимума.

Minimum noktaya ilişkin teoremin ispatı benzerdir.

Teorem kanıtlandı.

Yukarıdakilere dayanarak, bir segmentteki bir fonksiyonun en büyük ve en küçük değerlerini bulmak için birleşik bir prosedür geliştirebilirsiniz:

1) Fonksiyonun kritik noktalarını bulun.

2) Fonksiyonun kritik noktalardaki değerlerini bulun.

3) Parçanın uçlarındaki fonksiyonun değerlerini bulun.

4) Elde edilen değerler arasından en büyüğünü ve en küçüğünü seçin.

Bir ekstremum için bir fonksiyonun incelenmesi

yüksek mertebeden türevler.

x = x 1 noktasında f¢(x 1) = 0 olsun ve f¢¢(x 1) var olsun ve x 1 noktasının bazı komşuluklarında sürekli olsun.

Teorem. Eğer f¢(x 1) = 0 ise, x = x 1 noktasındaki f(x) fonksiyonunun maksimumu vardır, eğer f¢¢(x 1)<0 и минимум, если f¢¢(x 1)>0.

Kanıt.

f¢(x 1) = 0 ve f¢¢(x 1) olsun<0. Т.к. функция f(x) непрерывна, то f¢¢(x 1) будет отрицательной и в некоторой малой окрестности точки х 1 .

Çünkü f¢¢(x) = (f¢(x))¢< 0, то f¢(x) убывает на отрезке, содержащем точку х 1 , но f¢(x 1)=0, т.е. f¢(x) >x'te 0 x 1. Bu, x = x 1 noktasından geçerken f¢(x) türevinin işaretini “+”dan “-“ye değiştirdiği anlamına gelir, yani.

bu noktada f(x) fonksiyonunun bir maksimumu vardır.

Minimum fonksiyon durumunda teorem benzer şekilde kanıtlanır.

Eğer f¢¢(x) = 0 ise kritik noktanın doğası bilinmemektedir. Bunu belirlemek için daha fazla araştırmaya ihtiyaç vardır.

Bir eğrinin dışbükeyliği ve içbükeyliği.

Eğilme noktaları.

Tanım. Eğri dışbükeydir yukarı(a, b) aralığındaki tüm noktaları bu aralıktaki teğetlerinden herhangi birinin altındaysa. Yukarı doğru dışbükey bir eğriye denir dışbükey ve dışbükey olarak aşağı doğru bakan bir eğriye denir içbükey.

en

Şekilde yukarıdaki tanımın bir örneği gösterilmektedir.

Teorem 1. (a, b) aralığının tüm noktalarında f(x) fonksiyonunun ikinci türevi negatifse, o zaman y = f(x) eğrisi yukarı doğru dışbükeydir (dışbükey).

Kanıt. x 0 О (a, b) olsun. Bu noktada eğriye bir teğet çizelim.

Eğri denklemi: y = f(x);

Teğet denklemi:

Bunun kanıtlanması gerekir.

f(x) – f(x 0) için Lagrange teoremine göre: , x 0< c < x.

Lagrange teoremine göre

x > x 0 olsun, sonra x 0 olsun< c 1 < c < x. Т.к. x – x 0 >0 ve c – x 0 > 0 ve ayrıca koşula göre

Buradan, .

x olsun< x 0 тогда x < c < c 1 < x 0 и x – x 0 < 0, c – x 0 < 0, т.к. по условию то

Benzer şekilde, (a, b) aralığında f¢¢(x) > 0 ise, o zaman y=f(x) eğrisinin (a, b) aralığında içbükey olduğu kanıtlanmıştır.

Teorem kanıtlandı.

Tanım. Eğrinin dışbükey kısmını içbükey kısmından ayıran noktaya ne ad verilir? dönüm noktası.

Açıkçası, bükülme noktasında teğet eğriyi keser.

Teorem 2. Eğrinin y = f(x) denklemiyle tanımlanmasına izin verin. İkinci türev f¢¢(a) = 0 veya f¢¢(a) mevcut değilse ve x = a noktasından geçerken f¢¢(x) işareti değişirse, eğrinin apsisli noktası x = a bir dönüm noktasıdır.

Kanıt. 1) f¢¢(x) olsun< 0 при х < a и f¢¢(x) >x > a için 0. sonra

X< a кривая выпукла, а при x >a eğri içbükeydir, yani nokta x = a – bükülme noktası.

2) x için f¢¢(x) > 0 olsun< b и f¢¢(x) < 0 при x < b. Тогда при x < b кривая обращена выпуклостью вниз, а при x >b – yukarı doğru dışbükey. O halde x = b dönüm noktasıdır.

Teorem kanıtlandı.

Asimptotlar.

Fonksiyonları incelerken, bir eğri üzerindeki bir noktanın x koordinatı sonsuza gittiğinde, eğrinin belirli bir düz çizgiye süresiz olarak yaklaşması sıklıkla görülür.

Tanım. Düz çizgiye denir asimptot Eğrinin değişken noktasından bu düz çizgiye olan mesafe, nokta sonsuza doğru ilerledikçe sıfıra yaklaşıyorsa eğri.

Her eğrinin bir asimptotu olmadığı unutulmamalıdır. Asimptotlar düz veya eğik olabilir. Asimptotların varlığına yönelik fonksiyonları incelemek büyük önem taşır ve fonksiyonun doğasını ve eğri grafiğinin davranışını daha doğru bir şekilde belirlemenizi sağlar.

Genel olarak konuşursak, asimptotuna süresiz yaklaşan bir eğri, aşağıdaki fonksiyonun grafiğinde gösterildiği gibi onu tek bir noktada değil kesebilir. . Eğik asimptotu y = x'tir.

Eğrilerin asimptotlarını bulma yöntemlerini daha ayrıntılı olarak ele alalım.

Dikey asimtotlar.

Bir asimptotun tanımından, eğer veya veya ise, x = a düz çizgisinin y = f(x) eğrisinin asimptotu olduğu sonucu çıkar.

Örneğin bir fonksiyon için x = 5 doğrusu dikey bir asimptottur.

Eğik asimptotlar.

y = f(x) eğrisinin eğik bir asimptotu y = kx + b olduğunu varsayalım.

Eğrinin kesişme noktasını ve asimptot dikine - M, P - bu dikin asimptot ile kesişme noktasını gösterelim. Asimptot ile Ox ekseni arasındaki açıyı j olarak gösterelim. Ox eksenine dik olan MQ asimptotu N noktasında keser.

O zaman MQ = y eğri noktasının ordinatıdır, NQ = asimptot üzerindeki N noktasının ordinatıdır.

Koşula göre: , ÐNMP = j, .

j açısı sabittir ve 90 0'a eşit değildir, bu durumda

Daha sonra .

Yani y = kx + b düz çizgisi eğrinin asimptotudur. Bu çizgiyi doğru bir şekilde belirlemek için k ve b katsayılarını hesaplamanın bir yolunu bulmak gerekir.

Ortaya çıkan ifadede x'i parantezlerden çıkarıyoruz:

Çünkü x®¥, ardından , Çünkü b = sabit, o halde .

Daha sonra , buradan,

.

Çünkü , O , buradan,

Yatay asimptotların k = 0 için eğik asimptotların özel bir durumu olduğuna dikkat edin.

Örnek. .

1) Dikey asimptotlar: y®+¥ x®0-0: y®-¥ x®0+0, dolayısıyla x = 0 dikey bir asimptottur.

2) Eğik asimptotlar:

Dolayısıyla y = x + 2 düz çizgisi eğik bir asimptottur.

Fonksiyonun grafiğini çizelim:

Örnek. Asimptotları bulun ve fonksiyonun grafiğini çizin.

x = 3 ve x = -3 çizgileri eğrinin dikey asimptotlarıdır.

Eğik asimptotları bulalım:

y = 0 – yatay asimptot.

Örnek. Asimptotları bulun ve fonksiyonun grafiğini çizin .

Düz çizgi x = -2, eğrinin dikey asimptotudur.

Eğik asimptotları bulalım.

Toplamda, y = x – 4 düz çizgisi eğik bir asimptottur.

Fonksiyon çalışma şeması

Fonksiyon araştırma süreci birkaç aşamadan oluşur. Fonksiyonun davranışını ve grafiğinin doğasını en iyi şekilde anlamak için şunları bulmak gerekir:

1) Fonksiyonun varoluş alanı.

Bu kavram hem değerler alanını hem de bir fonksiyonun tanım alanını içerir.

2) Kırılma noktaları. (Mümkün ise).

3) Artış ve azalma aralıkları.

4) Maksimum ve minimum puanlar.

5) Bir fonksiyonun tanım kümesindeki maksimum ve minimum değeri.

6) Dışbükey ve içbükey alanlar.

7) Bükülme noktaları (varsa).

8) Asimptotlar (varsa).

9) Bir grafik oluşturmak.

Bir örnek kullanarak bu şemanın uygulamasına bakalım.

Örnek. Fonksiyonu keşfedin ve grafiğini oluşturun.

Fonksiyonun varlık tanım kümesini buluyoruz. Açıkça görülüyor ki tanım alanı fonksiyon alanıdır (-¥; -1) È (-1; 1) È (1; ¥).

Buna karşılık, x = 1, x = -1 düz çizgilerinin olduğu açıktır. dikey asimtotlarçarpık.

Değer aralığı bu fonksiyonun aralığı (-¥; ¥)'dir.

Kırılma noktaları fonksiyonlar x = 1, x = -1 noktalarıdır.

Bulduk kritik noktalar.

Fonksiyonun türevini bulalım

Kritik noktalar: x = 0; x = - ; x = ; x = -1; x = 1.

Fonksiyonun ikinci türevini bulalım

Eğrinin dışbükeyliğini ve içbükeyliğini aralıklarla belirleyelim.

-¥ < x < - , y¢¢ < 0, кривая выпуклая

- < x < -1, y¢¢ < 0, кривая выпуклая

1 < x < 0, y¢¢ >0, içbükey eğri

0 < x < 1, y¢¢ < 0, кривая выпуклая

1 < x < , y¢¢ >0, içbükey eğri

< x < ¥, y¢¢ >0, içbükey eğri

Boşlukları bulma artan Ve Azalan işlevler. Bunu yapmak için fonksiyonun türevinin aralıklardaki işaretlerini belirleriz.

-¥ < x < - , y¢ >0, fonksiyon artıyor

- < x < -1, y¢ < 0, функция убывает

1 < x < 0, y¢ < 0, функция убывает

0 < x < 1, y¢ < 0, функция убывает

1 < x < , y¢ < 0, функция убывает

< x < ¥, y¢¢ >0, fonksiyon artıyor

Görüldüğü gibi x = - noktası bir noktadır. maksimum ve x = noktası bir noktadır minimum. Bu noktalardaki fonksiyon değerleri sırasıyla -3/2 ve 3/2'ye eşittir.

Dikey hakkında asimptotlar yukarıda zaten söylendi. Şimdi bulalım eğik asimptotlar.

Toplamda eğik asimptotun denklemi y = x'tir.

Hadi yapalım takvimÖzellikler:

Çeşitli değişkenlerin işlevleri

Çok değişkenli fonksiyonları ele alırken kendimizi iki değişkenli fonksiyonların ayrıntılı bir tanımıyla sınırlayacağız çünkü elde edilen tüm sonuçlar isteğe bağlı sayıda değişkenin fonksiyonları için geçerli olacaktır.

Tanım: Belirli bir kümedeki her bir karşılıklı bağımsız sayı çifti (x, y), bazı kurallara göre z değişkeninin bir veya daha fazla değeriyle ilişkilendirilirse, z değişkenine iki değişkenli bir fonksiyon denir.

Tanım: Eğer bir sayı çifti (x, y) bir z değerine karşılık geliyorsa fonksiyon çağrılır. açık ve eğer birden fazla ise o zaman – çok anlamlı.

Tanım: Tanım alanı z fonksiyonu, z fonksiyonunun mevcut olduğu (x, y) çiftlerinin kümesidir.

Tanım: Bir noktanın mahallesi r yarıçapının M 0 (x 0, y 0) koşulu sağlayan tüm (x, y) noktalarının kümesidir .

Tanım: A numarası denir sınır f(x, y) fonksiyonu, M(x, y) noktası M 0 (x 0, y 0) noktasına doğru yönelirken, eğer her e > 0 sayısı için r > 0 sayısı varsa, öyle ki herhangi bir M noktası için (x, y), bunun için koşul doğrudur

durum da doğrudur .

Yazın:

Tanım: M 0 (x 0, y 0) noktasının f(x, y) fonksiyonunun tanım bölgesine ait olduğunu varsayalım. Daha sonra z = f(x, y) fonksiyonu çağrılır sürekli M 0 (x 0, y 0) noktasında, eğer

(1)

ve M(x, y) noktası M 0 (x 0, y 0) noktasına keyfi bir şekilde yönelmektedir.

Herhangi bir noktada koşul (1) sağlanmıyorsa bu noktaya denir. kırılma noktası f(x, y) fonksiyonları. Bu aşağıdaki durumlarda olabilir:

1) z = f(x, y) fonksiyonu M 0 (x 0, y 0) noktasında tanımlı değildir.

2) Sınır yoktur.

3) Bu limit mevcuttur ancak f(x 0 , y 0)'a eşit değildir.

Mülk. Eğer f(x, y, …) fonksiyonu kapalı ve

sınırlı alan D ise bu alanda en az bir nokta vardır

N(x 0 , y 0 , …), öyle ki kalan noktalar için eşitsizlik doğrudur

f(x 0 , y 0 , …) ³ f(x, y, …)

ve N 1 (x 01, y 01, ...) noktası gibi, öyle ki diğer tüm noktalar için eşitsizlik doğrudur

f(x 01 , y 01 , …) £ f(x, y, …)

bu durumda f(x 0 , y 0 , …) = M – en yüksek değer fonksiyonlar ve f(x 01 , y 01 , ...) = m – en küçük değer D bölgesinde f(x, y, …) fonksiyonları.

Kapalı ve sınırlı bir D kümesindeki sürekli bir fonksiyon, en büyük değerine en az bir kez, en küçük değerine ise bir kez ulaşır.

Mülk. F(x, y, …) fonksiyonu kapalı sınırlı bir D alanında tanımlanmış ve sürekli ise ve M ve m sırasıyla bu alandaki fonksiyonun en büyük ve en küçük değerleri ise, o zaman herhangi bir m noktası için m О bir nokta var

N 0 (x 0 , y 0 , …) öyle ki f(x 0 , y 0 , …) = m.

Basitçe söylemek gerekirse, sürekli bir fonksiyon D alanında M ile m arasındaki tüm ara değerleri alır. Bu özelliğin bir sonucu olarak, eğer M ve m sayıları farklı işaretlere sahipse, o zaman D bölgesinde fonksiyonun en az bir kez ortadan kaybolduğu sonucu çıkarılabilir.

Mülk. Kapalı sınırlı bir D bölgesinde sürekli olan f(x, y, …) fonksiyonu, sınırlı bu bölgede, bölgedeki tüm noktalar için eşitsizliğin doğru olduğu bir K sayısı varsa .

Mülk. Eğer bir f(x, y, …) fonksiyonu tanımlı ve kapalı sınırlı bir D bölgesinde sürekli ise, o zaman düzgün sürekli bu alanda, yani. herhangi bir pozitif e sayısı için bir D > 0 sayısı vardır, öyle ki bölgenin D'den daha küçük bir mesafede bulunan herhangi iki noktası (x 1, y 1) ve (x 2, y 2) için eşitsizlik geçerlidir

Yukarıdaki özellikler, bir aralıkta sürekli olan tek değişkenli fonksiyonların özelliklerine benzer. Bkz. Bir aralıkta sürekli olan fonksiyonların özellikleri.

Fonksiyonların türevleri ve diferansiyelleri

birkaç değişken.

Tanım. Bir tanım kümesinde z = f(x, y) fonksiyonu verilsin. Rasgele bir M(x, y) noktası alalım ve Dx artışını x değişkenine ayarlayalım. O halde D x z = f(x + Dx, y) – f(x, y) miktarına denir fonksiyonun x cinsinden kısmi artışı.

Yazabilirsin

.

Sonra denir kısmi türev x'te z = f(x, y) fonksiyonları.

Tanım:

Bir fonksiyonun y'ye göre kısmi türevi benzer şekilde belirlenir.

Geometrik anlamda kısmi türev (diyelim ki), N 0 (x 0, y 0, z 0) noktasında y = y 0 düzlemi tarafından yüzey bölümüne çizilen teğetin eğim açısının teğetidir.

Tam artış ve tam diferansiyel.

teğet düzlem

N ve N 0 bu yüzeyin noktaları olsun. NN 0 düz bir çizgi çizelim. N 0 noktasından geçen düzleme denir teğet düzlem Kesen NN 0 ile bu düzlem arasındaki açı sıfıra yöneliyorsa, NN 0 mesafesi sıfıra yöneliyorsa yüzeye.

Tanım. Normal N 0 noktasındaki yüzeye, bu yüzeye teğet düzleme dik N 0 noktasından geçen düz bir çizgidir.

Herhangi bir noktada yüzeyin ya tek bir teğet düzlemi vardır ya da hiç yoktur.

Yüzey z ​​= f(x, y) denklemiyle veriliyorsa, burada f(x, y) M 0 (x 0, y 0) noktasında diferansiyellenebilir bir fonksiyondur, N 0 ( noktasındaki teğet düzlem x 0,y 0, ( x 0 ,y 0)) mevcuttur ve aşağıdaki denkleme sahiptir:

Bu noktada yüzeye normalin denklemi şöyledir:

Geometrik anlamda iki değişkenli f(x, y) fonksiyonunun (x 0, y 0) noktasındaki toplam diferansiyeli, (x 0) noktasından hareket ederken teğet düzlemin yüzeye uygulanan uygulamasının (z koordinatları) artışıdır. , y 0)'dan (x 0 + Dx, y 0 +Dу) noktasına kadar.

Gördüğünüz gibi, iki değişkenli bir fonksiyonun toplam diferansiyelinin geometrik anlamı, tek değişkenli bir fonksiyonun diferansiyelinin geometrik anlamının uzaysal bir analogudur.

Örnek. Teğet düzlemin ve yüzeye normalin denklemlerini bulun

M(1, 1, 1) noktasında.

Teğet düzlem denklemi:

Normal denklem:

Toplam diferansiyelleri kullanarak yaklaşık hesaplamalar.

u fonksiyonunun toplam diferansiyeli şuna eşittir:

Bu ifadenin tam değeri: 1,049275225687319176.

Yüksek mertebeden kısmi türevler.

Eğer bir f(x, y) fonksiyonu herhangi bir D bölgesinde tanımlanmışsa, bu fonksiyonun kısmi türevleri de aynı bölgede veya onun bir kısmında tanımlanacaktır.

Bunlara türevler diyeceğiz birinci dereceden kısmi türevler.

Bu fonksiyonların türevleri şöyle olacaktır: ikinci dereceden kısmi türevler.

Ortaya çıkan eşitliklerin farklılığını almaya devam ederek daha yüksek mertebeden kısmi türevleri elde ederiz.

Anlam

En büyük

Anlam

En az

Maksimum nokta

Asgari puan

Bir ekstrem fonksiyonun noktalarını bulma problemleri standart bir şemaya göre 3 adımda çözülür.

Aşama 1. Fonksiyonun türevini bulun

• Temel fonksiyonların türev formüllerini ve türevi bulmak için türev almanın temel kurallarını hatırlayın.

y'(x)=(x3−243x+19)'=3x2−243.

Adım 2. Türevin sıfırlarını bulun

• Türevin sıfırlarını bulmak için elde edilen denklemi çözün.

3x2−243=0⇔x2=81⇔x1=−9,x2=9.

Aşama 3. Ekstrem noktaları bulun

• Türevin işaretlerini belirlemek için aralık yöntemini kullanın;
• Minimum noktada türev sıfıra eşittir ve işareti eksiden artıya, maksimum noktada artıdan eksiye değişir.

Aşağıdaki sorunu çözmek için bu yaklaşımı kullanalım:

y=x3−243x+19 fonksiyonunun maksimum noktasını bulun.

1) Türevi bulun: y′(x)=(x3−243x+19)′=3x2−243;

2) y′(x)=0 denklemini çözün: 3x2−243=0⇔x2=81⇔x1=−9,x2=9;

3) Türev x>9 ve x için pozitiftir<−9 и отрицательная при −9

Bir fonksiyonun en büyük ve en küçük değeri nasıl bulunur?

Bir fonksiyonun en büyük ve en küçük değerlerini bulma problemini çözmek gerekli:

• Fonksiyonun segment (aralık) üzerindeki uç noktalarını bulun.
• Segmentin uçlarındaki değerleri bulun ve ekstrem noktalardaki ve segmentin uçlarındaki değerlerden en büyük veya en küçük değeri seçin.

Birçok göreve yardımcı olur teorem:

Bir doğru parçası üzerinde yalnızca bir uç nokta varsa ve bu minimum nokta ise, fonksiyonun en küçük değerine bu noktada ulaşılır. Bu bir maksimum nokta ise en büyük değere orada ulaşılır.

14. Belirsiz integral kavramı ve temel özellikleri.

Eğer fonksiyon F(X X, Ve k– sayı, o zaman

Kısaca konuşursak: sabit integral işaretinden çıkarılabilir.

Eğer işlevler F(X) Ve G(X) aralığın antiderivatifleri var X, O

Kısaca konuşursak: toplamın integrali integrallerin toplamına eşittir.

Eğer fonksiyon F(X) aralığın antiderivatifi var X, daha sonra bu aralığın iç noktaları için:

Kısaca konuşursak: integralin türevi integrale eşittir.

Eğer fonksiyon F(X) aralıkta süreklidir X ve bu aralığın iç noktalarında türevlenebilirse, o zaman:

Kısaca konuşursak: Bir fonksiyonun diferansiyelinin integrali, bu fonksiyon artı integral sabitine eşittir.

Kesin bir matematiksel tanım verelim belirsiz integral kavramları.

Formun bir ifadesine denir fonksiyonun integrali f(x) , Nerede f(x) - verilen (bilinen) integral fonksiyonu, dx - diferansiyel X , sembolü her zaman mevcut olacak şekilde dx .

Tanım. Belirsiz integralçağrılan fonksiyon F(x) + C keyfi bir sabit içeren C diferansiyeli şuna eşit olan integrand ifade f(x)dx , yani veya Fonksiyon çağrılır antiderivatif fonksiyon. Bir fonksiyonun antitürevi sabit bir değere kadar belirlenir.

Şunu hatırlatalım; diferansiyel fonksiyon ve aşağıdaki gibi tanımlanır:

Sorun bulma belirsiz integral böyle bir fonksiyon bulmaktır türev bu da integrale eşittir. Bu fonksiyon bir sabite kadar doğru olarak belirlenir, çünkü sabitin türevi sıfırdır.

Mesela biliniyor, sonra ortaya çıkıyor burada keyfi bir sabit var.

Sorun bulma belirsiz integral işlevler ilk bakışta göründüğü kadar basit ve kolay değildir. Çoğu durumda, çalışma becerisinin olması gerekir belirsiz integraller, pratikle ve süreklilikle gelen bir deneyim olmalı Belirsiz integral örneklerinin çözümü.Şu gerçeği göz önünde bulundurmaya değer belirsiz integraller bazı işlevlerden (oldukça fazla vardır) temel işlevlerde alınmaz.

15. Temel belirsiz integraller tablosu.

Temel formüller

16. İntegral toplamının limiti olarak belirli integral. İntegralin geometrik ve fiziksel anlamı.

y=ƒ(x) fonksiyonunun [a; b], a< b. Выполним следующие действия.

1. x 0 = a, x 1, x 2, ..., x n = B (x 0) noktalarını kullanma

2. Her kısmi parçada, i = 1,2,...,n, i є ile rastgele bir nokta seçin ve içindeki fonksiyonun değerini, yani ƒ(i ile) değerini hesaplayın.

3. ƒ fonksiyonunun (i ile) bulunan değerini karşılık gelen kısmi parçanın ∆x i =x i -x i-1 uzunluğu ile çarpın: ƒ (i ile) ∆x i.

4. Tüm bu çarpımların toplamını S n yapalım:

(35.1) formunun toplamına, [a; B]. En büyük kısmi parçanın uzunluğunu λ ile gösterelim: λ = maksimum ∆x i (i = 1,2,..., n).

5. n → ∞ λ→0 olacak şekilde integral toplamının (35.1) limitini bulalım.

Bu durumda, S n integral toplamının bir I limiti varsa, bu, [a; b] kısmi doğru parçaları üzerinde veya içlerindeki noktaların seçimine bağlı değilse, bu durumda I sayısına, [a; b] ve şöyle gösterilir:

a ve b sayılarına sırasıyla integralin alt ve üst limitleri denir, ƒ(x) - integral fonksiyonu, ƒ(x) dx - integral, x - integralin değişkeni, segment [a; b] - entegrasyon alanı (bölümü).

y=ƒ(x) fonksiyonu, bunun için [a; b] Bu aralıkta integrallenebilir denilen belirli bir integral vardır.

Şimdi belirli bir integralin varlığına ilişkin bir teorem formüle edelim.

Teorem 35.1 (Cauchy). Eğer y = ƒ(x) fonksiyonu [a; b], o zaman belirli integral

Bir fonksiyonun sürekliliğinin integrallenebilirliği için yeterli bir koşul olduğuna dikkat edin. Bununla birlikte, bazı süreksiz fonksiyonlar için, özellikle üzerinde sonlu sayıda süreksizlik noktası bulunan bir aralıkla sınırlı herhangi bir fonksiyon için belirli bir integral de mevcut olabilir.

Belirli integralin tanımından (35.2) doğrudan çıkan bazı özelliklerini belirtelim.

1. Belirli integral, integral değişkeninin tanımından bağımsızdır:

Bu, integral toplamının (35.1) ve dolayısıyla limitinin (35.2) belirli bir fonksiyonun argümanının hangi harfle gösterildiğine bağlı olmadığı gerçeğinden kaynaklanmaktadır.

2. Aynı integral limitlerine sahip belirli bir integral sıfıra eşittir:

3. Herhangi bir gerçel sayı için c.

17. Newton-Leibniz formülü. Belirli bir integralin temel özellikleri.

Fonksiyona izin ver y = f(x) segmentte sürekli Ve F(x) bu segmentteki fonksiyonun antiderivatiflerinden biridir, o zaman Newton-Leibniz formülü: .

Newton-Leibniz formülü denir integral hesabının temel formülü.

Newton-Leibniz formülünü kanıtlamak için üst limiti değişken olan bir integral kavramına ihtiyacımız var.

Eğer fonksiyon y = f(x) segmentte sürekli , o zaman argüman için formun integrali üst sınırın bir fonksiyonudur. Bu fonksiyonu gösterelim ve bu fonksiyon süreklidir ve eşitlik doğrudur .

Aslında, argümanın artışına karşılık gelen fonksiyonun artışını yazalım ve belirli integralin beşinci özelliğini ve onuncu özelliğin sonucunu kullanalım:

Nerede .

Bu eşitliği formda yeniden yazalım. . Bir fonksiyonun türevinin tanımını hatırlarsak ve 'deki limite gidersek, şunu elde ederiz. Yani bu fonksiyonun antiderivatiflerinden biridir. y = f(x) segmentte . Böylece tüm antiderivatiflerin kümesi F(x) olarak yazılabilir, nerede İLE– keyfi sabit.

Haydi hesaplayalım F(a) belirli integralin birinci özelliğini kullanarak: , buradan, . Hesaplarken bu sonucu kullanalım F(b): , yani . Bu eşitlik kanıtlanabilir Newton-Leibniz formülünü verir .

Bir fonksiyonun artışı genellikle şu şekilde gösterilir: . Bu gösterimi kullanarak Newton-Leibniz formülü şu şekli alır:

Newton-Leibniz formülünü uygulamak için antiderivatiflerden birini bilmemiz yeterlidir. y=F(x) integral fonksiyonu y=f(x) segmentte ve bu antiderivatifin bu segment üzerindeki artışını hesaplayın. Makale entegrasyon yöntemleri, antiderivatifi bulmanın ana yollarını tartışıyor. Daha açıklayıcı olması açısından Newton-Leibniz formülünü kullanarak belirli integrallerin hesaplanmasına ilişkin birkaç örnek verelim.

Örnek.

Belirli integralin değerini Newton-Leibniz formülünü kullanarak hesaplayın.

Çözüm.

Başlangıç ​​olarak, integralin aralıkta sürekli olduğuna dikkat edelim. dolayısıyla üzerinde integrallenebilir. (Belirli bir integrali olan fonksiyonlar bölümünde integrallenebilir fonksiyonlardan bahsetmiştik.)

Belirsiz integraller tablosundan, bir fonksiyon için argümanın tüm gerçek değerleri için (ve dolayısıyla için) antitürevler kümesinin şu şekilde yazıldığı açıktır: . Bunun terstürevini alalım C=0: .

Artık belirli integrali hesaplamak için Newton-Leibniz formülünü kullanmaya devam ediyoruz: .

18. Belirli integralin geometrik uygulamaları.

BELİRLİ İNTEGRALİN GEOMETRİK UYGULAMALARI

Dikdörtgen S.K.	Parametrik olarak belirtilen fonksiyon	Polyarnaya S.K.
Düzlem figürlerin alanlarının hesaplanması
Bir düzlem eğrinin yay uzunluğunun hesaplanması
Devrimin yüzey alanının hesaplanması

Vücut hacminin hesaplanması

Paralel bölümlerin bilinen alanlarından bir cismin hacminin hesaplanması:

Dönen cismin hacmi: ; .

örnek 1. Y=sinx eğrisinin düz çizgilerle sınırladığı şeklin alanını bulun

Çözüm:Şeklin alanını bulma:

Örnek 2. Çizgilerle sınırlanmış bir şeklin alanını hesaplayın

Çözüm: Bu fonksiyonların grafiklerinin kesişim noktalarının apsisini bulalım. Bunu yapmak için denklem sistemini çözüyoruz

Buradan buluyoruz x 1 =0, x 2 =2,5.

19. Diferansiyel kontrol kavramı. Birinci mertebeden diferansiyel denklemler.

Diferansiyel denklem- bir fonksiyonun türevinin değerini fonksiyonun kendisi, bağımsız değişkenin değerleri ve sayılar (parametreler) ile birleştiren bir denklem. Denklemde yer alan türevlerin sırası farklı olabilir (resmi olarak hiçbir şeyle sınırlı değildir). Türevler, fonksiyonlar, bağımsız değişkenler ve parametreler bir denklemde çeşitli kombinasyonlarda görünebilir veya biri hariç tümü tamamen mevcut olmayabilir. Bilinmeyen bir fonksiyonun türevlerini içeren her denklem diferansiyel denklem değildir. Örneğin, diferansiyel denklem değildir.

Kısmi diferansiyel denklemler(PDF) çeşitli değişkenlerin bilinmeyen fonksiyonlarını ve bunların kısmi türevlerini içeren denklemlerdir. Bu tür denklemlerin genel formu şu şekilde temsil edilebilir:

bağımsız değişkenler nerede ve bu değişkenlerin bir fonksiyonudur. Kısmi diferansiyel denklemlerin sırası, sıradan diferansiyel denklemlerle aynı şekilde belirlenebilir. Kısmi diferansiyel denklemlerin bir diğer önemli sınıflandırması, özellikle ikinci dereceden denklemler için eliptik, parabolik ve hiperbolik tipte denklemlere bölünmesidir.

Hem adi diferansiyel denklemler hem de kısmi diferansiyel denklemler ikiye ayrılabilir doğrusal Ve doğrusal olmayan. Bilinmeyen fonksiyon ve türevleri denklemin yalnızca birinci derecesine giriyorsa (ve birbirleriyle çarpılmıyorsa) bir diferansiyel denklem doğrusaldır. Bu tür denklemler için çözümler, fonksiyonlar uzayının afin bir alt uzayını oluşturur. Doğrusal diferansiyel denklemler teorisi, doğrusal olmayan denklemler teorisinden çok daha derin bir şekilde geliştirilmiştir. Doğrusal diferansiyel denklemin genel görünümü N-inci sıra:

Nerede ben(X) denklemin katsayıları adı verilen bağımsız değişkenin bilinen fonksiyonlarıdır. İşlev R(X) sağ tarafta denir Ücretsiz Üye(bilinmeyen fonksiyona bağlı olmayan tek terim) Doğrusal denklemlerin önemli bir özel sınıfı, doğrusal diferansiyel denklemlerdir. sabit katsayılar.

Doğrusal denklemlerin bir alt sınıfı homojen diferansiyel denklemler - serbest terim içermeyen denklemler: R(X) = 0. Homojen diferansiyel denklemler için süperpozisyon ilkesi geçerlidir: böyle bir denklemin kısmi çözümlerinin doğrusal birleşimi de onun çözümü olacaktır. Diğer tüm doğrusal diferansiyel denklemlere denir heterojen diferansiyel denklemler.

Doğrusal olmayan diferansiyel denklemler genel durumda bazı özel sınıflar dışında gelişmiş çözüm yöntemlerine sahip değildir. Bazı durumlarda (belirli yaklaşımlar kullanılarak) doğrusal hale getirilebilir. Örneğin, harmonik bir osilatörün doğrusal denklemi matematiksel bir sarkacın doğrusal olmayan denkleminin bir yaklaşımı olarak düşünülebilir küçük genlikler durumunda, sen≈ günah sen.

· - sabit katsayılı ikinci dereceden homojen diferansiyel denklem. Çözüm, belirli bir çözüm için ayrı ayrı belirtilen başlangıç ​​koşullarından belirlenen ve keyfi sabitler olan bir işlevler ailesidir. Bu denklem özellikle döngüsel frekansı 3 olan harmonik bir osilatörün hareketini tanımlar.

· Newton'un ikinci yasası diferansiyel denklem şeklinde yazılabilir Nerede M- vücut kütlesi, X- koordinatı, F(X, T) - koordinatlı bir cisme etki eden kuvvet X zamanın bir noktasında T. Çözümü, belirtilen kuvvetin etkisi altında vücudun yörüngesidir.

· Bessel diferansiyel denklemi, ikinci dereceden değişken katsayılı sıradan bir doğrusal homojen denklemdir: Çözümleri Bessel fonksiyonlarıdır.

· Homojen olmayan, doğrusal olmayan, 1. dereceden adi diferansiyel denklem örneği:

Bir sonraki örnek grubunda bilinmeyen bir fonksiyon var sen iki değişkene bağlıdır X Ve T veya X Ve sen.

· Birinci dereceden homojen doğrusal kısmi diferansiyel denklem:

· Tek boyutlu dalga denklemi - ikinci dereceden hiperbolik tipte sabit katsayılı homojen bir doğrusal kısmi diferansiyel denklem, eğer - koordinatın olduğu noktada ipin sapması durumunda ipin salınımını tanımlar X zamanın bir noktasında T ve parametre A dizenin özelliklerini ayarlar:

· İki boyutlu uzayda Laplace denklemi, mekanik, termal iletkenlik, elektrostatik, hidrolik gibi birçok fiziksel problemde ortaya çıkan, sabit katsayılı, ikinci dereceden eliptik tipte homojen bir doğrusal kısmi diferansiyel denklemdir:

· Korteweg-de Vries denklemi, solitonlar da dahil olmak üzere durağan doğrusal olmayan dalgaları tanımlayan üçüncü dereceden doğrusal olmayan kısmi diferansiyel denklem:

20. Ayrılabilen diferansiyel denklemler. Doğrusal denklemler ve Bernoulli yöntemi.

Birinci dereceden doğrusal diferansiyel denklem, bilinmeyen bir fonksiyona ve onun türevine göre doğrusal olan bir denklemdir. Tam güç formuna sahiptir. Aslında, dikkate alınan türdeki denklemleri bulup yerine koyarsanız gerçek bir eşitlik elde edersiniz. Hakkında makalede belirtildiği gibi homojen denklemler Koşula göre yalnızca belirli bir çözümün bulunması gerekiyorsa, o zaman fonksiyon bariz nedenlerden dolayı bizi rahatsız etmez, ancak genel bir çözüm/integral bulunması gerektiğinde, o zaman şundan emin olmak gerekir: bu işlev kaybolmaz!

Bernoulli denkleminin tüm popüler varyasyonlarını büyük bir hediye çantasıyla getirdim ve dağıtmaya başladım. Çoraplarınızı ağacın altına asın.

örnek 1

Verilen başlangıç ​​koşuluna karşılık gelen diferansiyel denklemin özel bir çözümünü bulun.
,

Muhtemelen çoğu kişi ilk hediyenin hemen çantadan çıkarılmasına şaşırmıştı. Cauchy sorunu. Bu bir kaza değil. Bernoulli denklemi bir çözüm için önerildiğinde, bazı nedenlerden dolayı genellikle belirli bir çözüm bulmak gerekir. Koleksiyonumdan 10 Bernoulli denkleminden rastgele bir seçim yaptım ve genel çözümün (belirli bir çözüm olmadan) yalnızca 2 denklemde bulunması gerekiyor. Ancak aslında bu önemsiz bir şey çünkü her halükarda genel bir çözümün aranması gerekecek.

Çözüm: Bu difüzör şu şekle sahiptir ve dolayısıyla Bernoulli denklemidir

Ekstrem değerleri bulmak için basit bir algoritma

• Fonksiyonun türevini bulma
• Bu türevi sıfıra eşitliyoruz
• Ortaya çıkan ifadenin değişkeninin değerlerini buluyoruz (türevin sıfıra dönüştürüldüğü değişkenin değerleri)
• Bu değerleri kullanarak koordinat çizgisini aralıklara böleriz (hat üzerinde çizilmesi gereken kırılma noktalarını da unutmayın), tüm bu noktalara ekstremum için “şüpheli” noktalar denir.
• Bu aralıklardan hangisinin türevinin pozitif, hangisinin negatif olacağını hesaplıyoruz. Bunu yapmak için aralıktaki değeri türevle değiştirmeniz gerekir.

Bir ekstremum için şüpheli noktalardan bulmak gerekir. Bunu yapmak için koordinat çizgisi üzerindeki aralıklarımıza bakıyoruz. Bir noktadan geçerken türevin işareti artıdan eksiye değişirse, o zaman bu nokta şöyle olacaktır: maksimum ve eksiden artıya doğru ise, o zaman minimum.

Bir fonksiyonun en büyük ve en küçük değerlerini bulmak için fonksiyonun segmentin uçlarındaki ve ekstremum noktalarındaki değerini hesaplamanız gerekir. Daha sonra en büyük ve en küçük değeri seçin.

Bir örneğe bakalım
Türevi bulup sıfıra eşitliyoruz:

Değişkenlerin elde edilen değerlerini koordinat çizgisine çizeriz ve her aralığın türevinin işaretini hesaplarız. Mesela ilkini ele alalım-2 , o zaman türev eşit olacaktır-0,24 , ikinci olarak alacağız0 , o zaman türev olacak2 ve üçüncüyü alıyoruz2 , o zaman türev olacak-0.24. Uygun işaretleri koyduk.

-1 noktasından geçerken türevin eksiden artıya işaret değiştirdiğini yani minimum nokta olacağını, 1'den geçerken artıdan eksiye geçerken ise maksimum nokta olacağını görüyoruz.

Fonksiyon ve özelliklerinin incelenmesi, modern matematiğin en önemli bölümlerinden birini işgal etmektedir. Herhangi bir fonksiyonun ana bileşeni, yalnızca özelliklerini değil aynı zamanda bu fonksiyonun türevinin parametrelerini de gösteren grafiklerdir. Bu zor konuyu anlayalım. Peki bir fonksiyonun maksimum ve minimum noktalarını bulmanın en iyi yolu nedir?

İşlev: tanım

Bir şekilde başka bir miktarın değerlerine bağlı olan herhangi bir değişkene fonksiyon adı verilebilir. Örneğin, f(x 2) fonksiyonu ikinci derecedendir ve x kümesinin tamamı için değerleri belirler. Diyelim ki x = 9 o zaman fonksiyonumuzun değeri 9 2 = 81'e eşit olacak.

Fonksiyonlar birçok farklı türde gelir: mantıksal, vektör, logaritmik, trigonometrik, sayısal ve diğerleri. Lacroix, Lagrange, Leibniz ve Bernoulli gibi seçkin beyinler tarafından incelendiler. Onların çalışmaları, işlevlerin modern yöntemlerle incelenmesinde bir dayanak noktası görevi görüyor. Minimum noktaları bulmadan önce fonksiyonun ve türevinin anlamını anlamak çok önemlidir.

Türev ve rolü

Tüm işlevler değişkenlerine bağlıdır; bu, değerlerini istedikleri zaman değiştirebilecekleri anlamına gelir. Grafikte bu, ordinat ekseni boyunca düşen veya yükselen bir eğri olarak gösterilecektir (bu, dikey grafik boyunca "y" sayılarının tamamıdır). Yani bir fonksiyonun maksimum ve minimum noktalarının belirlenmesi tam olarak bu “salınımlarla” ilgilidir. Bu ilişkinin ne olduğunu açıklayalım.

Herhangi bir fonksiyonun türevi, temel özelliklerini incelemek ve fonksiyonun ne kadar hızlı değiştiğini (yani "x" değişkenine bağlı olarak değerini değiştirdiğini) hesaplamak için grafikle gösterilir. Fonksiyonun arttığı anda türevinin grafiği de artacaktır, ancak herhangi bir anda fonksiyon azalmaya başlayabilir ve ardından türevin grafiği azalacaktır. Türevin eksi işaretinden artı işaretine değiştiği noktalara minimum noktalar denir. Minimum puanların nasıl bulunacağını bilmek için konuyu daha iyi anlamalısınız.

Türev nasıl hesaplanır?

Tanım ve fonksiyonlar, genel olarak bir türevin tanımı şu şekilde ifade edilebilir: Bu, fonksiyonun değişim oranını gösteren niceliktir.

Bunu belirlemenin matematiksel yolu birçok öğrenci için karmaşık görünüyor, ancak gerçekte her şey çok daha basit. Herhangi bir fonksiyonun türevini bulmak için standart planı izlemeniz yeterlidir. Aşağıda türev kurallarını uygulamadan ve türev tablosunu ezberlemeden bir fonksiyonun minimum noktasını nasıl bulabileceğinizi açıklayacağız.

1. Bir fonksiyonun türevini grafik kullanarak hesaplayabilirsiniz. Bunu yapmak için, fonksiyonun kendisini tasvir etmeniz, ardından üzerinde bir nokta almanız (şekilde A noktası) apsis eksenine dikey olarak aşağıya bir çizgi çizmeniz (x 0 noktası) ve A noktasına bir teğet çizmeniz gerekir. fonksiyonun grafiği. X ekseni ve teğet belirli bir a açısı oluşturur. Bir fonksiyonun ne kadar hızlı arttığının değerini hesaplamak için bu a açısının tanjantını hesaplamanız gerekir.
2. Teğet ile x ekseninin yönü arasındaki açının tanjantının, fonksiyonun A noktası olan küçük bir alandaki türevi olduğu ortaya çıktı. Bu yöntem, türevi belirlemek için geometrik bir yöntem olarak kabul edilir.

Fonksiyonu inceleme yöntemleri

Okul matematik müfredatında bir fonksiyonun minimum noktasını iki şekilde bulmak mümkündür. Grafik kullanan ilk yöntemi daha önce tartışmıştık ama türevin sayısal değerini nasıl belirleyebiliriz? Bunu yapmak için türevin özelliklerini açıklayan ve "x" gibi değişkenleri sayılara dönüştürmeye yardımcı olan çeşitli formülleri öğrenmeniz gerekecektir. Aşağıdaki yöntem evrenseldir, dolayısıyla neredeyse tüm fonksiyon türlerine (hem geometrik hem de logaritmik) uygulanabilir.

1. Fonksiyonu türev fonksiyonuna eşitlemek ve ardından türev alma kurallarını kullanarak ifadeyi basitleştirmek gerekir.
2. Bazı durumlarda, böleni "x" değişkeni olan bir fonksiyon verildiğinde, "0" noktasını hariç tutarak kabul edilebilir değerler aralığını belirlemek gerekir (matematikte asla yapılmaması gereken basit bir nedenden dolayı) sıfıra bölme).
3. Bundan sonra, fonksiyonun orijinal formunu, ifadenin tamamını sıfıra eşitleyerek basit bir denkleme dönüştürmelisiniz. Örneğin, fonksiyon şu şekilde görünüyorsa: f(x) = 2x 3 +38x, türev kurallarına göre türevi f"(x) = 3x 2 +1'e eşittir. Daha sonra bu ifadeyi bir ifadeye dönüştürürüz. aşağıdaki formdaki denklem: 3x 2 +1 = 0 .
4. Denklemi çözüp “x” noktalarını bulduktan sonra bunları x eksenine çizip bu bölümlerde işaretli noktalar arasındaki türevin pozitif mi yoksa negatif mi olduğunu belirlemelisiniz. Atama sonrasında fonksiyonun hangi noktada azalmaya başladığı, yani işaretinin eksiden tersine değiştiği anlaşılacaktır. Bu şekilde hem minimum hem de maksimum puanları bulabilirsiniz.

Farklılaşma kuralları

Bir fonksiyonu ve onun türevini incelemenin en temel bileşeni, türev alma kurallarının bilgisidir. Yalnızca onların yardımıyla hantal ifadeleri ve büyük karmaşık işlevleri dönüştürebilirsiniz. Onları tanıyalım, oldukça fazla var ama hem güç hem de logaritmik fonksiyonların doğal özellikleri nedeniyle hepsi çok basit.

1. Herhangi bir sabitin türevi sıfıra eşittir (f(x) = 0). Yani f(x) = x 5 + x - 160 türevi şu formu alacaktır: f" (x) = 5x 4 +1.
2. İki terimin toplamının türevi: (f+w)" = f"w + fw".
3. Logaritmik bir fonksiyonun türevi: (log a d)" = d/ln a*d. Bu formül tüm logaritma türleri için geçerlidir.
4. Gücün türevi: (x n)"= n*x n-1. Örneğin, (9x 2)" = 9*2x = 18x.
5. Sinüzoidal fonksiyonun türevi: (sin a)" = cos a. Eğer a açısının günahı 0,5 ise türevi √3/2 olur.

Ekstrem noktalar

Minimum noktaların nasıl bulunacağını zaten tartıştık, ancak aynı zamanda bir fonksiyonun maksimum noktaları kavramı da var. Minimum, fonksiyonun eksi işaretinden artıya değiştiği noktaları gösteriyorsa, maksimum noktalar, fonksiyonun türevinin artıdan zıt eksiye değiştiği x ekseni üzerindeki noktalardır.

Yukarıda açıklanan yöntemi kullanarak bulabilirsiniz, ancak fonksiyonun azalmaya başladığı alanları, yani türevin sıfırdan küçük olacağını belirttiklerini dikkate almalısınız.

Matematikte, her iki kavramı da genelleştirmek ve bunların yerine "ekstrem noktalar" ifadesini koymak gelenekseldir. Bir görev sizden bu noktaları belirlemenizi istediğinde, belirli bir fonksiyonun türevini hesaplamanız ve minimum ve maksimum noktaları bulmanız gerektiği anlamına gelir.