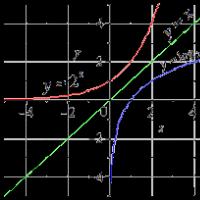
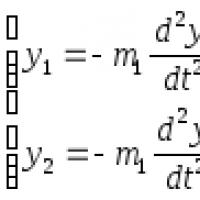Ikki erkinlik darajasiga ega tizimning erkin tebranishlari. Ikki erkinlik darajasiga ega tizimlarning erkin tebranishlari Bosh koordinatalarga o'tish

Ikki erkinlik darajasiga ega tizimlar bir necha erkinlik darajasiga ega bo'lgan tizimlarning alohida holatidir. Ammo bu tizimlar eng sodda bo'lib, yakuniy shaklda tebranish chastotalari, amplitudalari va dinamik burilishlarini aniqlash uchun hisoblash formulalarini olish imkonini beradi.

yInersiya kuchlari ta’sirida nurning burilishlari:

P 2 =1 (1)

(1) ifodalardagi (-) belgilari inersiya kuchlari va birliklari bilan bog'liq. harakatlar teskari yo'nalishda.

Biz massa tebranishlari garmonik qonunga muvofiq sodir bo'lishiga ishonamiz:

(2)

Massa harakatining tezlanishini topamiz:

(3)

(2) va (3) ifodalarni (1) tenglamaga qo'yib, biz quyidagilarni olamiz:

(5)

A 1 va A 2 noma'lum tebranishlarning amplitudalarini ko'rib chiqamiz va tenglamalarni o'zgartiramiz:

(6)

A 1 = A 2 =0 bir jinsli tenglamalar sistemasi yechimi bizga mos kelmaydi, nolga teng bo‘lmagan yechimni olish uchun (6) sistemaning determinantlarini nolga tenglashtiramiz;

(7)

Tabiiy tebranishlarning  noma'lum doiraviy chastotasini hisobga olgan holda (8) tenglamani o'zgartiramiz:

(9) tenglama ikki erkinlik darajasiga ega sistemalarning erkin tebranishlarining bigarmonik tenglamasi deyiladi.

 2 =Z o'zgaruvchisini almashtirsak, olamiz

bu yerdan Z 1 va Z 2 ni aniqlaymiz.

Natijada quyidagi xulosalar chiqarish mumkin:

1. Ikki erkinlik darajasiga ega tizimlarning erkin tebranishlari ikkita  1 va  2 chastotalarda sodir bo'ladi. Past chastota 1 asosiy yoki asosiy ton, yuqori chastota 2 ikkinchi chastota yoki overton deb ataladi.

Erkinlik darajasi n bo'lgan tizimlarning erkin tebranishlari n-ton bo'lib, n-erkin tebranishlardan iborat.

2. m 1 va m 2 massalarning harakati quyidagi formulalar bilan ifodalanadi:

ya'ni, tebranishlar  1 chastotada sodir bo'lsa, u holda har qanday vaqtda ommaviy harakatlar bir xil belgilarga ega.

Agar tebranishlar faqat  2 chastotada sodir bo'lsa, u holda har qanday vaqtda massa harakati qarama-qarshi belgilarga ega.

 1 va  2 chastotali massalarning bir vaqtda tebranishlari bilan tizim asosan  1 chastotada tebranadi va bu tebranishlarga  2 chastotali overton mos keladi.

Agar ikki erkinlik darajasiga ega bo'lgan tizim  chastotali harakatlantiruvchi kuchga tobe bo'lsa, unda quyidagilar zarur:

  0,7  1 .

9-ma'ruza

Cheksiz erkinlik darajasiga ega tizimlarning tebranishlari.

Mexanik tebranishlar nazariyasi texnologiyaning deyarli barcha sohalarida juda ko'p va juda xilma-xil qo'llanilishiga ega. Har xil mexanik tizimlarning maqsadi va konstruktiv yechimidan qatʼi nazar, ularning tebranishlari bir xil fizik qonunlarga boʻysunadi, ularni oʻrganish elastik sistemalarning tebranishlari nazariyasining predmeti hisoblanadi. Tebranishlarning chiziqli nazariyasi eng to'liq ishlab chiqilgan. Bir necha erkinlik darajasiga ega tizimlarning tebranishlari nazariyasi 18-asrda Lagranj tomonidan o'zining "Analitik mexanika" klassik asarida berilgan.

Jozef Lui Lagranj (1736 - 1813) - 19 yoshidan Turindagi matematika professori. 1759 yildan - Berlin Fanlar akademiyasining a'zosi, 1766 yildan - prezident; 1787 yildan Parijda yashagan. 1776 yilda u Sankt-Peterburg Fanlar akademiyasining faxriy xorijiy a'zosi etib saylandi.

19-asrning oxirida Rayleigh cheksiz erkinlik darajasiga ega (ya'ni, deformatsiyalanuvchi tizimning butun hajmi bo'ylab massaning uzluksiz taqsimlanishi bilan) tizimlarning tebranishlarining chiziqli nazariyasiga asos soldi. 20-asrda chiziqli nazariya tugallangan deb aytish mumkin (Bubnov-Galerkin usuli, bu ham ketma-ket yaqinlashishlar yordamida yuqori tebranish chastotalarini aniqlash imkonini beradi).

Jon Uilyam Strett (Lord Rayleigh) (1842 - 1919) - ingliz fizigi, tebranishlar nazariyasi bo'yicha bir qator ishlar muallifi.

Ivan Grigorievich Bubnov (1872 - 1919) - kema qurilish mexanikasi asoschilaridan biri. Sankt-Peterburg politexnika instituti professori, 1910 yildan - Dengizchilik akademiyasida.

Boris Grigoryevich Galerkin (1871-1945) - Leningrad politexnika instituti professori.

Reyli formulasi elastik tizimlarning tebranishlari va barqarorligi nazariyasida eng mashhur hisoblanadi. Rayleigh formulasining kelib chiqishiga asos bo'lgan g'oya quyidagilarga to'g'ri keladi.  chastotali elastik tizimning monoharmonik (bir tonna) erkin tebranishlari bilan uning nuqtalarining harakati garmonik qonunga muvofiq vaqt ichida sodir bo'ladi:

Bu yerda  1 (x,y,z),  2 (x,y,z),  3 (x,y,z) nuqtaning fazoviy koordinatalarining ko’rilayotgan tebranish shaklini (amplitudasini) aniqlovchi funksiyalaridir.

Agar bu funksiyalar ma'lum bo'lsa, u holda tananing kinetik va potensial energiyasi yig'indisi doimiy bo'lgan shartdan erkin tebranishlarning chastotasini  topish mumkin. Bu shart faqat bitta noma'lum miqdorni o'z ichiga olgan tenglamaga olib keladi.

Biroq, bu funktsiyalar oldindan ma'lum emas. Rayleigh usulining asosiy g'oyasi bu funktsiyalarni belgilash, ularning tanlovini chegara shartlari va tebranishlarning kutilgan shakli bilan moslashtirishdir.

Tayoqning tekis egilish tebranishlari uchun ushbu fikrni amalga oshirishni batafsil ko'rib chiqaylik, tebranishlarning shakli =(x) funktsiyasi bilan tavsiflanadi; Erkin tebranishlar qaramlik bilan tavsiflanadi

egilgan tayoqning potentsial energiyasi

(2)

kinetik energiya

(3)

Qayerda l- novda uzunligi, m=m(x) tayoqning taqsimlangan massasining intensivligi;

Rodning egri o'qining egriligi - ko'ndalang tebranishlar tezligi;

Berilgan (1)

.

(4)

(5)

Vaqt o'tishi bilan bu miqdorlarning har biri doimiy ravishda o'zgarib turadi, lekin energiyaning saqlanish qonuniga ko'ra, ularning yig'indisi doimiy bo'lib qoladi, ya'ni.

yoki bu yerda (4), (5) iboralar o‘rniga qo‘yiladi

(7)

Bu Rayleigh formulasiga olib keladi:

(8)

Agar M i massali kontsentrlangan yuklar taqsimlangan massa m bo'lgan novda bilan bog'langan bo'lsa, Rayleigh formulasi quyidagi shaklni oladi:

(9)

Chiqarishning butun yo'nalishi shuni ko'rsatadiki, qabul qilingan taxminlar doirasida (tayoqlarning egilishining texnik nazariyasining haqiqiyligi, elastik qarshilikning yo'qligi), agar  (x) tebranishlarning haqiqiy shakli bo'lsa, bu formula aniq bo'ladi. . Biroq,(x) funksiyasi oldindan noma’lum. Reyli formulasining amaliy ahamiyati shundaki, u tebranish shakli(x) ni hisobga olgan holda tabiiy chastota ni topish uchun ishlatilishi mumkin. Shu bilan birga, qarorga ko'proq yoki kamroq jiddiy yaqinlik elementi kiritilgan. Shu sababli, Reyli formulasi ba'zan taxminiy formula deb ataladi.

m=cosnt Funksiyani tebranish shakli sifatida qabul qilaylik:(x)=ax 2, masalaning kinematik chegara shartlarini qanoatlantiradi.

Biz aniqlaymiz:

Formula bo'yicha (8)

Bu natija aniq natijadan sezilarli darajada farq qiladi

Grammel formulasi aniqroq bo'lib, u hali Rayleigh formulasi kabi mashhur bo'lmagan (ehtimol, nisbiy "yoshligi" tufayli - 1939 yilda taklif qilingan).

Keling, novdaning erkin egilish tebranishlari muammosiga yana to'xtalib o'tamiz.

(x) sterjenning erkin tebranishlarining belgilangan shakli bo'lsin. U holda maksimal inersiya kuchlarining intensivligi m 2  ifodasi bilan aniqlanadi, bunda avvalgidek m=m(x) sterjenning taqsimlangan massasining intensivligi  2 tabiiy chastotaning kvadrati; Bu kuchlar burilishlar maksimal bo'lgan paytda belgilangan qiymatga etadi, ya'ni. (x) funksiya bilan aniqlanadi.

Maksimal inertial kuchlar ta’sirida yuzaga kelgan egilish momentlari bo‘yicha eng yuqori potentsial egilish energiyasining ifodasini yozamiz:

. (10)

Bu yerga - m 2  yuk ta’sirida yuzaga keladigan egilish momentlari. Shartli yuklama m ta’sirida yuzaga kelgan egilish momentini belgilaymiz, ya’ni.  inersiya kuchidan 2 marta kam.

, (11)

va ifoda (10) quyidagicha yozilishi mumkin:

. (12)

Yuqoridagi kabi eng yuqori kinetik energiya

. (13)

(12) va (13) ifodalarni tenglashtirib, Grammel formulasiga kelamiz:

(14)

Ushbu formuladan foydalanib hisoblash uchun avvalo mos keladigan (x) funksiyani ko'rsatish kerak. Shundan so'ng shartli yuk m=m(x)(x) aniqlanadi va shartli yuk m ta'sirida yuzaga keladigan egilish ifodalari yoziladi. (14) formuladan foydalanib, tizimning tabiiy tebranish chastotasi aniqlanadi.

Misol: (oldingisini ko'rib chiqing)

y

m(x)·(x)=max 2

NAZARIY MEXANIKA

UDC 531.8: 621.8

D.M.Kobylyanskiy, V.F.Gorbunov, V.A

JANLARNING BIR DARAJASI ERKINLIK BILAN AYLANISHI VA VIBRASYONLARINI MUVOSLIGI.

Keling, 1a-rasmda ko'rsatilgandek, faqat tananing barcha yo'nalishlarda harakatlanishiga to'sqinlik qiladigan uchta ideal cheklov qo'yilgan tekis jism T ni ko'rib chiqaylik. Bog'lanishlar teng tomonli uchburchakning uchlarida joylashgan A, B, C nuqtalaridir. Koordinatalar tizimini tanlab, uning markazi uchburchakning markaziga to'g'ri keladi va unga to'g'ri keladi (1a-rasm), biz ulanishlarning koordinatalariga ega bo'lamiz: A(0;R), B(^l/3 /2). -R/2), C ^-Ld/e /2; -I/2), bu erda I uchburchak markazidan uning cho'qqilarigacha bo'lgan masofa, ya'ni A, B, C nuqtalardan o'tuvchi aylana radiusi. Bu holatda jism bir daraja erkinlikka ega bo'ladi. faqat uning chegarasining A, B, C nuqtalaridagi normallari bir nuqtada kesishsa, bu tezliklarning oniy markazi bo'ladi. Aks holda, tananing erkinlik darajalari soni nolga teng bo'ladi va u nafaqat translyatsion harakatni, balki aylanish harakatini ham amalga oshira olmaydi. Jism bir daraja erkinlikka ega bo'lganda, u yuqoridagi normalarning kesishish nuqtasida oniy aylanish markazi bilan aylana boshlashi mumkin. Bu nuqta koordinatalarning boshi bo'lsin, O nuqta. Agar lahzali aylanish markazi o'z o'rnini o'zgartirmasa, u holda T jismning yagona mumkin bo'lgan shakli markazi O nuqtada bo'lgan R radiusli doiradir.

Muammo tug'iladi: tananing harakatlanuvchi markazga nisbatan aylanishiga imkon beradigan boshqa shakllari bormi?

tananing tanasi bu bog'lanishlarni uzmasdan A, B, C uchta nuqtadan doimiy ravishda o'tib ketganmi? Bizga ma'lum bo'lgan adabiyotlarda bunday muammo ko'rib chiqilmagan va, ehtimol, birinchi marta hal qilinmoqda.

Bu masalani yechish uchun biz birinchi navbatda ABC uchburchakning harakatini qattiq jism sifatida, T jism bilan bog'langan X1O1Y1 koordinata tizimiga nisbatan ko'rib chiqamiz (1b-rasm). Keyin, agar uchburchakning harakati shunday sodir bo'lsa, uning uchlari uchburchakning 360 ° ga to'liq aylanishida doimiy ravishda tananing chegarasida qoladigan bo'lsa, u holda tana kerakli harakatni qo'zg'almas harakatga nisbatan teskari yo'nalishda ham bajaradi. uchburchak ABC va tegishli koordinatalar tizimi XOU.

ABC uchburchakning harakatini O markazga nisbatan aylanish va O markazning OíHi oʻqi boʻylab /(g), OíUí oʻqi boʻyicha g(t) ga harakatini aniqlaymiz. U holda A nuqta traektoriyasining parametrik tenglamasi quyidagi ko rinishga ega bo ladi: x = ryaSh +/(r); u=g-êo,?g̀ +g(t), g̀ê (1)

G=0 nuqtada O nuqta O1 nuqtaga to‘g‘ri kelishi kerak ekan, u holda /(0)= g(0)=0 sharti bajarilishi kerak. Biz r = 2n/3 burchak orqali aylantirilganda A nuqta B1 nuqtaga, B nuqta C nuqtaga va C nuqtaga to'g'ri kelishini talab qilamiz.

A1 nuqtasi bilan. Burchak r = 4n/3 bo'ylab burilganda, A nuqtasi C1 nuqtasiga, B nuqtasi A1 nuqtasiga va C nuqtasi B1 nuqtasiga o'tishi kerak. Uchburchak uchlari harakati uchun ushbu talablarni birlashtirish aylanish markazini harakatlantirish funktsiyalari qiymatlari uchun shartlarga olib keladi /(0)=/(2 p/3)=/(4 p/3)= 0; g0)=g(2l/3)=g(4l/3)=0 . (2) (2) shartlar keng funksiyalar sinfi, xususan, sin(3mt/2) ko‘rinishidagi funksiyalar bilan qanoatlantiriladi, bunda m butun son bo‘lib, ularning chiziqli birikmalari shaklning umumiy o‘zgaruvchan koeffitsientlari bilan:

H (g) = ^ bt (g) 8Ip(3thg / 2)

Bundan tashqari, kabi

1-rasm. Hisoblash sxemasi: a) - harakatsiz jismning holati va uning XOU tizimidagi ulanishlari; b) - X1O1U1 qo'zg'almas tizimning tana bilan bog'langan holati va ABC uchburchagi bilan bog'langan harakatlanuvchi XOU tizimi.

Nazariy mexanika

2-rasm. Jismlarning shakllari va ularning aylanish markazlarining harakat traektoriyalari

Guruch. 3. Burchakda burilganda jismning holati va uning aylanish markazining tegishli harakat traektoriyasi.

siljish funksiyalari, (2) shartga muvofiq parametrlari bilan sikloidlar, troxoidlar, lemniskatlar kabi yopiq egri chiziqlarni aniqlovchi funksiyalar olinishi mumkin. Bunday holda, barcha mumkin bo'lgan funktsiyalar 2n/3 davr bilan davriy bo'lishi kerak.

Shunday qilib, parametrik tenglamalar tizimi (1) funktsiyalar qiymatlari bo'yicha shartlar bilan /(^, g(t) (2) yoki ularning ko'rinishida (3) T tanasining chegarasi uchun kerakli tenglamani beradi. 2-rasmda vazifani bajarish shartlarini qondiradigan mumkin bo'lgan tana shakllarining misollari ko'rsatilgan. Har bir rasmning markazida aylanish markazining traektori O1 ko'rsatilgan va ularni yaxshiroq ko'rish uchun A, B, C nuqta ulanishlari kengaytirilgan doimiy koeffitsientlarga ega bo'lgan (3) ifoda bilan aniqlangan sinfdan oddiy funksiya turlari ham aylanayotgan jismlarning chegaralarini tavsiflovchi juda keng egri chiziqlarga ega ekanligini ko'rsating

faqat bitta erkinlik darajasi bilan bir vaqtning o'zida tebranishlar. 2-rasmdagi a), c) chegara egri chiziqlari aylanish markazining faqat gorizontal o'q bo'ylab harakatiga mos keladi.

OíXi garmonik qonunga koʻra va koʻrinib turganidek, ikkita simmetriya oʻqiga ega boʻlib, sof qavariq, tasvirlar (2a-rasm) yoki qavariqlik bilan botiqlikni birlashtirishi mumkin (2b-rasm). Aylanish markazining bir xil harakat amplitudasi bilan vertikal va gorizontal garmonik qonun bilan chegaraviy egri chiziqlar simmetriyani yo'qotadi (2-rasm c, d). Garmonik tebranishlar chastotasining jismning chegaraviy egri chizig'ining shakliga sezilarli ta'siri 2-rasmda ko'rsatilgan d, f chegaraning shakli va geometrik xususiyatlariga amplituda va chastotaning ta'sirini to'liq tahlil qilmasdan. bu ishda egri chiziqlar, shuni ta'kidlashni istardimki, 2-rasmda keltirilgan misollar allaqachon kerakli shaklni tanlashda texnik muammolarni hal qilish qobiliyatini ko'rsatadi.

tananing aylanish harakatini aylanish tekisligidagi tebranishlar bilan birlashtirish uchun.

Endi tananing ABC uchburchagi bilan bog'langan XOU qo'zg'almas koordinatalar tizimiga nisbatan harakatini, ya'ni X1O1U1 koordinatalar tizimidan XOU koordinatalar tizimiga o'tishni hisobga olsak, tananing chegara egri chizig'ining quyidagi parametrik tenglamalarini olamiz. berilgan aylanish burchagi p x = cosp-

Kosp(4)

yoki (1) tenglamalarni hisobga olgan holda (4) tenglamalar x = cosp- shaklini oladi.

- [ R cos(t) + g (t) - g (p)] sin p, y = sin p +

Cos p.

(5) tenglamalar tananing istalgan nuqtasining traektoriyasini berilgan qutblarga ko'ra tasvirlash imkonini beradi.

t-g.i m*4<. п-і

t-ÍLÍtWM. d-0

Guruch. 4. Jismlarning aylanishi va tebranishlarining mos kelishini ta'minlovchi turli xil bog'lanishlar soniga ega tana shakllarining variantlari

nal koordinatalari R,t. Xususan, R=0, t=0 da bizda Ob koordinatalarining kelib chiqishiga to‘g‘ri keladigan nuqta, ya’ni aylanish markazi bo‘lib, uning traektoriyasi ko‘rib chiqilayotgan sxemada (5) dan kelib chiqadigan tenglamalar bilan tavsiflanadi. :

*0 = -f (ph) cos ph + g (ph) sin ph, y0 = - f (ph) sin ph- g (ph) cos r.

3-rasmda ph burchagi bo'ylab aylantirilganda tananing pozitsiyalari misoli (2b-rasm) ko'rsatilgan va har bir rasmning markazida aylanish markazining traektoriyasi ko'rsatilgan.

Oi, bu burchak orqali tananing aylanishiga mos keladi. Texnik jihatdan animatsiya qilish qiyin emas

jismoniy model o'rniga 3-rasmda ko'rsatilgan tana harakatining, ammo jurnal maqolasining ramkasi bunga faqat elektron versiyada ruxsat berishi mumkin. Ko'rsatilgan misol hali ham edi

Ko'rib chiqilayotgan muammoni umumlashtirish - bu muntazam uchburchakning cho'qqilarida joylashgan nuqtalar ko'rinishidagi n ideal bog'lanishlar tizimi, bu tananing faqat translatsion harakatlarini oldini oladi. Shuning uchun, uchburchak holatida bo'lgani kabi, tananing aylanish nuqtasiga nisbatan aylana boshlashi mumkin, bu esa ulanish nuqtalarida tananing chegarasiga normallarning kesishish nuqtasidir. Bunda OU o'qida joylashgan va aylanish markazidan H masofada joylashgan A jismning nuqta traektoriyasi tenglamasi (1) ko'rinishga ega bo'ladi. Bu holda aylanish markazini (2) harakatlantirish funktsiyalarining qiymatlari uchun shartlar olinadi

Kobilyanskiy Gorbunov

Dmitriy Mixaylovich Valeriy Fedorovich

Kafedra aspiranti. statsionar va - doc. texnologiya. fanlar, prof. Bo'lim yuz

transport vositalari, statsionar va transport vositalari

f(2kp/p)=g(2kp/p)=0. (7)

Shart (7) 2n/n davriga ega davriy funksiyalarga, masalan, 8m(n-m4/2), shuningdek, ularning (3) shakldagi chiziqli birikmalariga va yopiq egri chiziqlarni tavsiflovchi boshqa funksiyalarga mos keladi. Yuqorida aytib o'tilganlarga o'xshash fikrlash bir xil tenglamalarga (4-6) olib keladi, bu esa tananing shaklini, aylanish paytidagi holatini va aylanish markazining aylanish jarayoniga mos keladigan tebranishlari bilan aylanish markazining traektoriyasini hisoblash imkonini beradi. . Bunday hisob-kitoblarga misol qilib 4-rasmni keltirish mumkin, unda nuqtali chiziq jismlarning dastlabki holatini, qattiq chiziq jismlarning l/3 burchak ostida aylanayotgandagi holatini va har bir rasmning markazida tananing to'liq aylanishida aylanish markazining to'liq traektoriyasi. Garchi bu misolda n-gonning markazi sifatida faqat O aylanish markazining gorizontal harakati ko'rib chiqilsa-da, olingan natijalar aylanish harakatini birlashtirgan bir erkinlik darajasiga ega bo'lgan tananing mumkin bo'lgan shakllarining keng doirasini ko'rsatadi. to'rt, besh va oltita ulanishlar mavjudligida tebranishlar bilan.

Bir darajadagi erkinlikka ega jismlarning aylanish va tebranish harakatlarining mosligini hisoblashning natijaviy usuli, uchinchi koordinata bo'ylab harakatlanish va boshqa koordinata tekisliklarida aylanish taqiqlangan fazoviy jismlar uchun ham qo'shimchalarsiz qo'llanilishi mumkin.

Gogolin Vyacheslav Anatolevich

Dr. texnologiya. fanlar, prof. Bo'lim amaliy matematik va

Ikki erkinlik darajasiga ega bo'lgan sistema umumiy koordinatalar bo'lsin. Tizimning kinetik va potentsial energiyasi (10.2) formulalar bilan ifodalanadi:

T va P funktsiyalari aniq ijobiy, shuning uchun:

(10.2) ni (10.12) ga almashtirib, ikkita erkinlik darajasiga ega tizimning kichik tebranishlari uchun differentsial tenglamalarni olamiz:

Tizim barqaror muvozanat holatiga mos keladigan A=B=0 nol yechimga ega. Nolga teng bo'lmagan yechimlar uchun (10.15) dan munosabat tuzamiz:

Barqarorlik tengsizliklari tufayli (10.18 ga nisbatan) kvadratik tenglama ikkita haqiqiy musbat ildizga ega. Keling, ularni o'sish tartibida joylashtiramiz:

Ikkinchi asosiy tebranish uchun:

(10.21)

Asosiy tebranishlar garmonik tebranishlardir.

(10.16) o rniga va navbat bilan asosiy tebranishlarda A va B amplitudalar orasidagi bog lanishlarni topamiz: . Faktorlar xos koeffitsientlar (amplituda taqsimot koeffitsientlari) deb ataladi. Ular ham ijobiy, ham salbiy bo'lishi mumkin. Asosiy tebranishdagi ikkala koordinata ham bir fazada bo'lganda; at - antifazada.

Har bir koordinata bo'ylab hosil bo'lgan harakat ikkita asosiy tebranishlarning yig'indisi bo'ladi:

(10.22)

Bu erda - boshlang'ich shartlarga bog'liq, - boshlang'ich shartlarga bog'liq emas va tebranish tizimining o'zi parametrlari bilan belgilanadi. Umumiy holda, chastotalar va o'lchovsizdir va shuning uchun natijada harakat davriy bo'lmaydi.

1. Massasi m teng bo‘lgan ikkita moddiy nuqta va har birining uzunligi ikkita tayoqchadan hosil bo‘lgan qo‘sh matematik mayatnikning tabiiy chastotalari va tabiiy tebranish usullarini (kichik) aniqlang.

Umumiy shakldagi shunga o'xshash tizim 2-misolda (§34) ko'rib chiqilgan. Keling, u erda olingan (2) va (3) formulalardan foydalanamiz.

Qachon, biz olamiz:

Tebranishlar kichik bo'lgani uchun, ikkinchi darajali kichiklarga qadar:

(3)

(1) dan (3) ni hisobga olgan holda biz quyidagilarni qayd etamiz:

(4)

(4) va (2) ni taqqoslab, biz quyidagilarni ko'ramiz:

(7.52) chastotalar tenglamasini kengaytirib, biz quyidagilarni olamiz:

(9.50) dan taqsimot koeffitsientlarini topamiz: .

Birinchi katta tebranish:

Fazali harakat - har bir daqiqada novdalar bir yo'nalishda aylanadi.

Ikkinchi asosiy ikkilanish:

Antifazada harakat - har daqiqada novdalar mutlaqo qarama-qarshi yo'nalishda aylanadi.

Tebranish rejimlari rasmda ko'rsatilgan. 50. Ikkinchi asosiy tebranishda harakatsiz qoladigan maxsus F nuqta mavjud. Bunday nuqtalar tugunlar deb ataladi. Oxirgi nuqta O tugun emas.

2. Massali ikkita qattiq jism va qattiqligi bo'lgan ikkita prujinali va silliq gorizontal tekislikda joylashgan va kichik chiziqli tebranishlarni bajara oladigan tizimga birlashtirilgan.

Birinchi katta tebranish:

Jismlar o'ngga yoki chapga bosqichma-bosqich harakat qiladi. Ikkinchi jismning tebranish amplitudasi 1,62 marta katta.

Ikkinchi asosiy ikkilanish:

Jismlar antifazada harakatlanadi: yoki bir-biriga, tugun tomon yoki tugundan ajralib chiqadi. Ikkinchi jismning tebranishlar amplitudasi birinchisining amplitudasining 0,62 ga teng.

Konservativ mexanik tizimning barqaror muvozanat holati atrofidagi harakat tenglamalaridan

Ikki erkinlik darajasida bizda:

(1)

(Silvester mezoniga ko'ra:

(1) barqaror muvozanat holatiga yaqin ikki erkinlik darajasiga ega mexanik tizimning kichik erkin tebranishlarining differentsial tenglamalari tizimi. Uning yechimi quyidagi shaklda izlanadi:

(2)

Ushbu yechimni kichik tebranishlarning differensial tenglamalari tizimiga almashtirish quyidagilarni beradi:

(3)

A va B ga nisbatan bu bir hil algebraik tenglamalar tizimidir. Tizimning determinanti nolga teng bo'lsa, u noan'anaviy yechimga ega:

(4)

Ushbu bikvadrat tenglama chastotali tenglama deb ataladi, uning ikkita musbat ildizi bor, ular kichik tebranishlarning differentsial tenglamalari tizimining ikkita echimiga mos keladi:

Shunday qilib, har bir umumlashtirilgan koordinata turli chastotali ikkita tebranish yig'indisi sifatida topiladi, ular deyiladi. asosiy tebranishlar . Bunday holda, (3) tizimdan kelib chiqqan holda, asosiy tebranishlarning amplitudalari bir-biri bilan quyidagicha bog'langan:

(5)

Qaerda - shakl omillari asosiy tebranishlar.

Natijada, erkin tebranishlar (1) tenglamalarining yechimi nihoyat quyidagi shaklni oladi:

(6)

Kiruvchi quti(6) amplitudalar va boshlang'ich fazalar, tebranishlar dastlabki shartlardan aniqlanadi.

Ikkita erkinlik darajasiga ega mexanik tizimlarning majburiy tebranishlari. Dinamik tebranish damperi

Mexanik tizimlarda kiruvchi tebranishlarni yo'q qilish deyiladi tebranishdan himoya qilish (damping). Bu holda ishlatiladigan texnik qurilmalar deyiladi tebranish damperlari (damperlar).

Dinamik amortizatorning ishlash printsipi bir koordinataga mos keladigan vaqti-vaqti bilan o'zgarib turadigan bezovta qiluvchi umumlashtirilgan kuchning ta'siri boshqa koordinataga mos keladigan potentsial umumlashtirilgan kuchning ta'sirida neytrallanganda aks-rezonans hodisasidan foydalanishga asoslangan.

Mexanik tizim, konservativ kuchlardan tashqari, garmonik qonunga muvofiq vaqt o'tishi bilan o'zgarib turadigan bezovta qiluvchi kuchga ham ta'sir qilsin.

Bu holda mexanik tizim harakatining differentsial tenglamalari quyidagi shaklga ega:

Ikki yechim yig'indisi sifatida chiziqli differensial bir jinsli bo'lmagan (bu holda) tenglamalar sistemasining umumiy yechimini qidiramiz: , - bir jinsli differentsial tenglamalar sistemasining umumiy yechimi; -bir jinsli differensial tenglamalar sistemasini qisman yechish.

Bezovta qiluvchi kuchning vaqtga bog'liqligini hisobga olgan holda, shaklda ma'lum bir yechim izlanadi.

Uni differensial tenglamalar tizimiga qo'yish quyidagilarga olib keladi:

Ushbu tizimni Kramer qoidasi yordamida hal qilib, biz olamiz

Chunki u chastota tenglamasining chap tomoniga to'g'ri keladi va yo'qoladi

bezovta qiluvchi kuchning chastotasi tabiiy chastotalardan biriga to'g'ri kelganda

tebranishlar yoki A va B koeffitsientlari bu holda cheksizlikka aylanadi. Shunday qilib, ikkita erkinlik darajasiga ega bo'lgan tizimning tebranishlari mavjud ikkita rezonans chastotasi

Majburiy differensial tenglamalar sistemasining umumiy yechimi

da tebranishlar shaklga ega:

Ko'rinib turibdiki, tebranuvchi tizimning parametrlarini tanlash orqali, masalan, A = 0 shartining bajarilishiga erishish mumkin, ya'ni birinchi umumlashtirilgan koordinataga mos keladigan majburiy tebranishlar amplitudasi nolga aylanadi.

Bu hodisa antirezonans deb ataladi.

Ko'rib chiqilayotgan holatda bu sodir bo'ladi, agar

Ta'sir nazariyasining asosiy tushunchalari va farazlari. Ta'sir nazariyasining asosiy tenglamasi

Qisqa vaqt ichida, ya'ni. deyarli bir zumda, moddiy ob'ektlar nuqtalarining tezligi cheklangan qiymatlarga o'zgaradi, deyiladi puflamoq .

Ta'sir paytida tezlikning yakuniy o'zgarishi juda qisqa vaqt ichida sodir bo'lganligi sababli, juda katta tezlanishlar va shuning uchun juda katta kuchlar paydo bo'ladi. Bu kuchlar juda qisqa vaqt oralig'ida harakat qiladilar, lekin ularning bu vaqt oralig'idagi impulslari cheklangan miqdorlardir.

Qisqa vaqt ichida ta'sir qilish paytida paydo bo'ladigan, lekin ayni paytda katta qiymatga erishadigan, shuning uchun ularning bu vaqt oralig'idagi impulslari cheklangan qiymatlar deyiladi. zarba kuchlari .

Zarba davom etadigan qisqa vaqt davri deyiladi ta'sir qilish vaqti. Ta'sir paytida ta'sir kuchlarining impulslari deyiladi zarba zarbalari .

Oddiy (zarba bo'lmagan) kuch ta'sirida harakatlanuvchi m massali MT berilgan bo'lsin. Ko'rib chiqilayotgan MT tezlikka ega bo'lgan paytda - zarbadan oldingi tezlik, zarba kuchi unga ta'sir qila boshlaydi, uning harakati hozirgi vaqtda to'xtaydi. MTning kuchlar ta'sirida va zarba vaqtidagi harakatini aniqlaylik.

Nuqta impulsining o'zgarishi haqidagi teoremani qo'llash orqali biz quyidagilarga erishamiz:

,

zarbadan keyingi momentdagi nuqtaning tezligi qayerda.

Aniq integralning o'rtacha qiymati haqidagi teoremadan foydalanib, quyidagilarni yozishimiz mumkin:

,

bu erda va ma'lum bir vaqt oralig'idagi kuchlarning o'rtacha qiymatlari. Bundan tashqari, u cheklangan miqdordir; Ta'sir paytida zarba kuchi juda katta qiymatga etadi (tartibda). Shuning uchun mahsulot cheklangan miqdor bo'lgan mahsulotga nisbatan ahamiyatsiz bo'ladi.

Potensial maydon kuchlariga va vaqt o'tishi bilan davriy ravishda o'zgarib turadigan kuchlarga bo'ysunadigan ikki erkinlik darajasiga ega bo'lgan tizimning kichik tebranishlarini ko'rib chiqaylik. Tizimning hosil bo'lgan harakatlari majburiy tebranishlar deb ataladi.

Bezovta qiluvchi umumlashgan kuchlar teng davrlar va boshlang'ich fazaga ega bo'lgan vaqt bo'yicha garmonik qonunga muvofiq o'zgarib tursin. Keyin ko'rib chiqilayotgan tizimning harakat tenglamalari quyidagi shaklda bo'ladi:

Ko'rib chiqilayotgan ishdagi harakat tenglamalari doimiy koeffitsientli va o'ng tomonli chiziqli ikkinchi tartibli differensial tenglamalar tizimidir.

Asosiy koordinatalarga o'ting

Harakat tenglamalarini o'rganish qulayligi uchun tizimning asosiy koordinatalariga o'tamiz.

Oddiy koordinatalarga mos keladigan umumlashtirilgan kuchlarni belgilaymiz, chunki u tizimga ta'sir qiluvchi kuchlarning elementar ishini ifodalashda umumlashtirilgan koordinatalarning mos keladigan o'zgarishlari uchun koeffitsientlarni ifodalaydi.

Demak:

Shunday qilib, asosiy koordinatalarda harakat tenglamalari quyidagi shaklni oladi:

Oddiy koordinatalarda ikki erkinlik darajasiga ega sistemaning majburiy tebranishlar tenglamalari bir-biridan mustaqil va alohida integrallanishi mumkin.

Bezovta qiluvchi kuchning kritik chastotalari

Tenglama normal koordinatalar o'zgarishining tebranish xususiyatini aniqlaydi, to'g'ri chiziq bo'ylab nuqtaning majburiy tebranishini ko'rib chiqishda batafsil o'rganiladi, chunki harakatning differentsial tenglamalari ikkala holatda ham bir xil bo'ladi. Xususan, agar bezovta qiluvchi kuchning chastotasi tizimning tabiiy tebranishlaridan birining chastotasiga teng bo'lsa yoki u holda yechim t vaqtini omil sifatida o'z ichiga oladi. Binobarin, etarlicha katta t uchun normal umumlashtirilgan koordinatalardan biri ixtiyoriy ravishda katta bo'ladi yoki bizda rezonans hodisasi mavjud.